14 R Modulo 5

Relativizações e transformações

RESUMO

Transformações e relativizações de dados são técnicas essenciais na análise de dados em Ecologia Numérica, permitindo comparar diferentes variáveis que estão em escalas diferentes ou que possuem unidades distintas.

Apresentação

O R é uma ferramenta poderosa para realização dessas operações, com diversos pacotes disponíveis para essa finalidade. Neste tutorial, iremos explorar algumas das principais funções do pacote vegan, que permite realizar transformações e relativizações de dados de forma simples e eficiente. Além disso, também utilizaremos outras bibliotecas importantes para reorganização e visualozação de dados. O tutorial irá abordar desde as operações básicas, como filtragem e seleção de dados, até as transformações mais complexas, como a normalização de dados e a relativização por medidas de biomassa ou área. Com exemplos práticos e ilustrações gráficas, o objetivo é permitir que os usuários do R possam aplicar essas técnicas em suas próprias análises e estudos de Ecologia Numérica. Ao final do tutorial, espera-se que o usuário esteja apto a realizar transformações e relativizações de dados em suas próprias análises, aumentando a qualidade e a precisão dos resultados obtidos.

14.1 Organização básica

dev.off() #apaga os graficos, se houver algum
rm(list=ls(all=TRUE)) #limpa a memória
cat("\014") #limpa o console

Instalando os pacotes necessários para esse módulo

install.packages("openxlsx") #importa arquivos do excel
install.packages("moments") #calcula assimetria e curtose dos dados
install.packages("vegan") #estatisticas para ecologia de comunidades

Agora vamos definir o diretório de trabalho. Esse código é usado para obter e definir o diretório de trabalho atual no R. O comando getwd() retorna o caminho do diretório onde o R está lendo e salvando arquivos. O comando setwd() muda esse diretório de trabalho para o caminho especificado entre aspas. No seu caso, você deve ajustar o caminho para o seu próprio diretório de trabalho. Lembre de usar a barra “/” entre os diretórios. E não a contra-barra “\”.

Definindo o diretório de trabalho e installando os pacotes necessários:

getwd()
setwd("C:/Seu/Diretório/De/Trabalho")

14.1.1 Importando a planilha

Note que o símbolo # em programação R significa que o texto que vem depois dele é um comentário e não será executado pelo programa. Isso é útil para explicar o código ou deixar anotações.
- Ajuste a primeira linha do código abaixo para refletir “C:/Seu/Diretório/De/Trabalho/Planilha.xlsx”.
- Ajuste o parâmetro sheet = "Sheet1" para refletir a aba correta do arquivo .xlsx a ser importado.

library(openxlsx)
#dir <- getwd() #criamos um vetor com o diretório  de trbalho 
#shell.exec(dir) #abre o diretorio de trabalho no Windows Explorer
m_bruta <- read.xlsx("D:/Elvio/OneDrive/Disciplinas/_EcoNumerica/5.Matrizes/ppbio06-peixes.xlsx",
                   rowNames = T, colNames = T,
                   sheet = "Sheet1")
str(m_bruta)
#View(m_bruta)
m_bruta[1:5,1:5] #[1:5,1:5] mostra apenas as linhas e colunas de 1 a 5.
## 'data.frame':    26 obs. of  35 variables:
##  $ ap-davis : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ as-bimac : num  1 99 194 19 23 142 5 46 206 16 ...
##  $ as-fasci : num  0 0 55 0 1 3 1 0 64 0 ...
##  $ ch-bimac : num  0 0 0 0 13 3 0 178 0 0 ...
##  $ ci-ocela : num  0 0 0 0 0 0 40 0 0 13 ...
##  $ ci-orien : num  0 0 5 0 0 69 9 0 25 24 ...
##  $ co-macro : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ co-heter : num  0 0 1 0 0 0 0 0 0 0 ...
##  $ cr-menez : num  0 0 14 0 0 4 0 0 8 0 ...
##  $ cu-lepid : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ cy-gilbe : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ ge-brasi : num  0 0 3 0 0 0 0 0 1 0 ...
##  $ he-margi : num  0 0 0 0 0 1 0 0 0 0 ...
##  $ ho-malab : num  0 0 1 5 0 17 10 2 31 4 ...
##  $ hy-pusar : num  0 0 9 2 0 43 2 0 11 0 ...
##  $ le-melan : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ le-piau  : num  0 0 3 0 0 1 3 0 2 1 ...
##  $ le-taeni : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ mo-costa : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ mo-lepid : num  0 1 39 0 0 1 0 0 0 0 ...
##  $ or-nilot : num  0 2 36 0 0 77 0 0 138 0 ...
##  $ pa-manag : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ pimel-sp : num  0 0 6 0 0 0 0 0 0 0 ...
##  $ po-retic : num  0 0 0 0 0 20 0 0 5 0 ...
##  $ po-vivip : num  0 0 47 15 0 221 32 0 326 10 ...
##  $ pr-brevi : num  9 0 5 0 1 15 5 2 164 0 ...
##  $ ps-rhomb : num  0 0 0 0 0 0 0 0 1 0 ...
##  $ ps-genise: num  0 0 0 0 0 0 0 0 1 0 ...
##  $ se-heter : num  0 0 40 14 4 60 0 0 38 0 ...
##  $ se-piaba : num  0 0 68 0 0 0 0 0 0 0 ...
##  $ se-spilo : num  0 0 0 0 0 0 0 0 1 0 ...
##  $ st-noton : num  0 0 1 0 0 25 0 0 115 0 ...
##  $ sy-marmo : num  0 0 0 0 0 0 1 0 0 0 ...
##  $ te-chalc : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ tr-signa : num  0 0 18 0 0 15 0 0 7 0 ...
##         ap-davis as-bimac as-fasci ch-bimac ci-ocela
## S-A-ZA1        0        1        0        0        0
## S-R-CC1        0       99        0        0        0
## S-R-CT1        0      194       55        0        0
## S-R-CP1        0       19        0        0        0
## S-A-TA1        0       23        1       13        0

Exibindo os dados importados (esses comando são “case-sensitive” ignore.case(object)).

#View(m_bruta)
print(m_bruta[1:8,1:8])
m_bruta[1:10,1:10]
str(m_bruta)
mode(m_bruta)
class(m_bruta)

Podemos exibir a planilha depois de ter sido importada para o ambiente R/RStudio usando as funções View(), print() ou head(). Note que essas funções são case-sensitive. A função ignore.case() é uma função do pacote stringr que modifica um padrão para que ele não considere o caso das letras nas correspondências. Por exemplo, se você quiser encontrar todas as ocorrências da letra “a” em um vetor de caracteres, independente de ser “A” ou “a”, você pode usar essa função.

#View(m_bruta)
print(m_bruta)
head(m_bruta)

A função head() no RStudio é uma forma de ver as primeiras (n=6) linhas de um objeto, como um vetor, uma matriz, um data frame ou uma lista. Ela é útil para ter uma ideia do conteúdo e da estrutura do objeto.

Também podemos explorar as características da planilha usando as funções str(), mode(), class() e length(). O número de observações ou tamanho do vetor depende do tipo de dados, se eles são uma matrix ou um data.frame.

Abreviações

No interesse de sistematizar o código R das várias matrizes que são comumente usadas em uma AMD, a tabela a seguir (Tabela @ref(tab:5tblm_2)) resume seus tipos e abreviações.

(#tab:5tblm_2)Nomenclatura das matrizes em AMD em relação aos atributos das colunas
Nome Atributos (colunas) Abreviação no R
Matriz comunitaria Os atributos são táxons ou OTU’s (Unidades Taxonômicas Operacionais) (ex. espécies, gêneros, morfotipos) m_com
Matriz ambiental Os atributos são dados ambientais e variáveis físicas e químicas (ex. pH, condutividade, temperatura) m_amb
Matriz de habitat Os atributos são elementos da estrutura do habitat (ex. macróficas, algas, pedras, lama, etc) m_hab
Matriz bruta Os atributos ainda não receberam nenhum tipo de tratamento estatísco (valores brutos, como coletados) m_bruta
Matriz transposta Os atributos foram transpostos para as linhas m_t
Matriz relativizada Os atributos foram relativizados por um critério de tamanho ou de variação (ex. dividir os valores de cada coluna pela soma) m_rel, m_relcol, m_rellin
Matriz transformada Foi aplicado um operador matemático a todos os atributos (ex. raiz quadrada, log) m_trns, m_log10, m_asrq
Matriz de distâncias Matriz de m x m similaridades ou de distâncias (ex. Euclidiana, Manhattan, Bray-Curtis, etc) m_dists, m_euclid, m_bray
Matriz de trabalho Qualquer matriz que seja o foco da análise atual (ex. comunitária, relativizada, etc) m_trab
Matriz particionada Foram removidas linhas ou colunas (ex. linhas que são outliers e espécies zeradas) m_part
Base de dados Arquivo do Excel planilhado a partir de dados de campo ou de laboratório. Será manejada e particionada no R, para criar a Matriz bruta ppbio06.xlsx, zoorebio.xlsx, bentos06.xlsx

14.2 Tamanho da matriz

Podemos agora calcular o número e a proporção de zeros na matriz usando as funções sum() e length() (Você pode pesquisar o que faz a função length() usando o comando ?length).

range(m_bruta) #menor e maior valores
length(m_bruta) #no. de colunas
ncol(m_bruta) #no. de N colunas
nrow(m_bruta) #no. de M linhas
sum(lengths(m_bruta)) #soma os nos. de colunas
length(as.matrix(m_bruta)) #tamanho da matriz m x n
sum(m_bruta == 0) # número de observações igual a zero
sum(m_bruta > 0) # número de observações maiores que zero
zeros <- (sum(m_bruta == 0)/length(as.matrix(m_bruta)))*100 # proporção de zeros na matriz
zeros
## [1]   0 511
## [1] 35
## [1] 35
## [1] 26
## [1] 910
## [1] 910
## [1] 716
## [1] 194
## [1] 78.68132

Tabela que resume as informações geradas (14.1).

tamanho <- data.frame(
  Função = c("range", "lenght", "m cols", "n linhas", "Tamanho", "Tamanho",
             "Zeros", "Nao zeros", "% Zeros"),
  Resultado = c(paste(range(m_bruta), collapse = " - "), length(m_bruta), ncol(m_bruta),
                nrow(m_bruta), sum(lengths(m_bruta)), length(as.matrix(m_bruta)), sum(m_bruta == 0),
                sum(m_bruta > 0), round(zeros, 1)))
tamanho
##      Função Resultado
## 1     range   0 - 511
## 2    lenght        35
## 3    m cols        35
## 4  n linhas        26
## 5   Tamanho       910
## 6   Tamanho       910
## 7     Zeros       716
## 8 Nao zeros       194
## 9   % Zeros      78.7
Tabela 14.1: Resumo das informações geradas.
Função Resultado
range 0 - 511
lenght 35
m cols 35
n linhas 26
Tamanho 910
Tamanho 910
Zeros 716
Nao zeros 194
% Zeros 78.7

Ou seja, temos uma matriz de tamanho m x n igual a 26 objetos por 35 atributos, onde 78.68% dos valores da matriz são iguais a zero!

14.3 Reset point 1

m_trab <- m_bruta

Aqui cria-se um novo objeto do R (m_trab, ou a matriz de trabalho, para esse momento) que substitui a matriz de dados original, por uma nova matriz que pode ser a matriz relativizada, transformada, transposta, etc. Dessa forma, mantemos a matriz de dados original caso precisemos dela novamente (Veja a Tabela Tabela @ref(tab:5tblm_2)).

14.4 Cálculo da matriz de distâncias

Agora vamos calcular a matriz de distâncias euclidiana (Legendre and Legendre (1998), Borcard, Gillet, and Legendre (2018)) entre as UA´s usando a função dist() (pesquise o que faz essa função usando o comando ?dist).

m_dists <- dist(m_trab, method = "euclidian", diag = TRUE, upper = FALSE)

Pronto, calculamos a matriz de distâncias (euclidiana). Agora podemos visualizar a matriz.

#m_dists
str(m_dists)
mode(m_dists)
class(m_dists)
length(as.matrix(m_dists))
as.matrix(m_dists)[1:10, 1:10]
##  'dist' num [1:325] 98.4 228.5 29.2 27.1 294.1 ...
##  - attr(*, "Size")= int 26
##  - attr(*, "Labels")= chr [1:26] "S-A-ZA1" "S-R-CC1" "S-R-CT1" "S-R-CP1" ...
##  - attr(*, "Diag")= logi TRUE
##  - attr(*, "Upper")= logi FALSE
##  - attr(*, "method")= chr "euclidean"
##  - attr(*, "call")= language dist(x = m_trab, method = "euclidian", diag = TRUE, upper = FALSE)
## [1] "numeric"
## [1] "dist"
## [1] 676
##           S-A-ZA1   S-R-CC1  S-R-CT1   S-R-CP1   S-A-TA1  S-R-CT2   S-R-CP2
## S-A-ZA1   0.00000  98.43780 228.5235  29.24038  27.09243 294.0629  53.40412
## S-R-CC1  98.43780   0.00000 154.2433  82.79493  77.25283 261.3905 108.10180
## S-R-CT1 228.52352 154.24331   0.0000 208.52338 209.69263 224.9133 224.09150
## S-R-CP1  29.24038  82.79493 208.5234   0.00000  23.25941 271.4922  49.22398
## S-A-TA1  27.09243  77.25283 209.6926  23.25941   0.00000 283.7869  57.82733
## S-R-CT2 294.06292 261.39051 224.9133 271.49217 283.78689   0.0000 268.95167
## S-R-CP2  53.40412 108.10180 224.0915  49.22398  57.82733 268.9517   0.00000
## S-A-TA2 183.74439 185.75791 261.8301 181.24845 166.66133 326.3327 190.15257
## S-R-CT3 460.42155 428.64437 366.6429 443.90877 453.59674 238.3799 438.54532
## S-R-CP3  34.17601  88.06816 215.2557  31.32092  33.13608 275.0436  40.37326
##          S-A-TA2  S-R-CT3   S-R-CP3
## S-A-ZA1 183.7444 460.4215  34.17601
## S-R-CC1 185.7579 428.6444  88.06816
## S-R-CT1 261.8301 366.6429 215.25566
## S-R-CP1 181.2484 443.9088  31.32092
## S-A-TA1 166.6613 453.5967  33.13608
## S-R-CT2 326.3327 238.3799 275.04363
## S-R-CP2 190.1526 438.5453  40.37326
## S-A-TA2   0.0000 478.9008 182.86060
## S-R-CT3 478.9008   0.0000 449.24826
## S-R-CP3 182.8606 449.2483   0.00000

Uma matriz do tipo dist no R é um objeto que armazena as distâncias entre as linhas de uma matriz ou um data frame. Ela é criada pela função dist(), que calcula as distâncias usando diferentes medidas, como “euclidean”, “manhattan”, “canberra”, “binary” ou “minkowski” (Horton and Kleinman 2015).

range(m_trab)
range(m_dists)
min(m_dists)
max(m_dists)
mean(m_dists) #CENTROIDE!! ou Grand mean
sd(m_dists)  #standard deviation
centroide <- mean(m_dists)
centroide
## [1]   0 511
## [1]  16.27882 707.32666
## [1] 16.27882
## [1] 707.3267
## [1] 285.9043
## [1] 172.9708
## [1] 285.9043

A função mean() calcula a média de todos os valores da matriz de distâncias, ou seja, a média multivariada, que é o centróide. Nesse caso o centroide assume o valor de 285.9. Usamos agora a fórmula m*(m-1)/2, onde m é o no. de objetos sendo comparados, para calcular quantas distâcias temos na nossa matriz.

length(m_dists)
m <- nrow(as.matrix(m_dists))
m
m*(m-1)/2
summary(m_dists)
## [1] 325
## [1] 26
## [1] 325
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   16.28  142.70  242.82  285.90  423.64  707.33

Temos então que m é 26 objetos (ou linhas), e portanto, a matriz de distâncias tem 325 valores. Fazemos agora um breve sumário do que foi calculado até agora com base na matriz de distâncias.

Sumario1 <- cbind(min(m_dists),
                  max(m_dists),
                  sd(m_dists),
                  mean(m_dists),
                  length(m_dists))
colnames(Sumario1) <- c("Minimo", "Maximo", "Desv.Padr", "Media", "m(m-1)/2")
rownames(Sumario1) <- ("Valores")
Sumario1
##           Minimo   Maximo Desv.Padr    Media m(m-1)/2
## Valores 16.27882 707.3267  172.9708 285.9043      325

A matriz m_dists está como uma classe dist, mas podemos transformá-la em uma classe matrix usando a função as.matrix().

dist <- (as.matrix(m_dists))
#View(dist)
str(dist)
mode(dist)
class(dist)
#head(dist)
dist[1:5, 1:5] #mostra as 5 primeiras linhas e colunas da matriz
##  num [1:26, 1:26] 0 98.4 228.5 29.2 27.1 ...
##  - attr(*, "dimnames")=List of 2
##   ..$ : chr [1:26] "S-A-ZA1" "S-R-CC1" "S-R-CT1" "S-R-CP1" ...
##   ..$ : chr [1:26] "S-A-ZA1" "S-R-CC1" "S-R-CT1" "S-R-CP1" ...
## [1] "numeric"
## [1] "matrix" "array" 
##           S-A-ZA1   S-R-CC1  S-R-CT1   S-R-CP1   S-A-TA1
## S-A-ZA1   0.00000  98.43780 228.5235  29.24038  27.09243
## S-R-CC1  98.43780   0.00000 154.2433  82.79493  77.25283
## S-R-CT1 228.52352 154.24331   0.0000 208.52338 209.69263
## S-R-CP1  29.24038  82.79493 208.5234   0.00000  23.25941
## S-A-TA1  27.09243  77.25283 209.6926  23.25941   0.00000

Visualizando a matriz de distâncias, observamos que ela é uma matriz quadrada que contém as distâncias entre cada par de elementos do conjuto de dados. A matriz de distâncias terá dimensão m x m, e cada elemento da matriz será a distância entre cada par de observações ou objetos. A matriz de distâncias é simétrica, pois a distância entre i e j é igual à distância entre j e i. A matriz de distâncias também tem diagonal zero, pois a distância entre uma observação e ela mesma é zero.

14.5 Distribuição de frequência da matriz de distâncias

Por fim, vamos produzir uma distribuição de frequência da matriz de distâncias, mas antes vamos explorar alguns parâmetros básicos da matriz de distâncias, como o intervalo, a média e o desvio padrão. Para isso, usamos as funções range(), mean() e sd() do R.

14.5.1 Calculando alguns parâmetros básicos

range(m_dists) # intervalo dos valores da matriz
mean(m_dists) # média dos valores da matriz
sd(m_dists) # desvio padrão dos valores da matriz
## [1]  16.27882 707.32666
## [1] 285.9043
## [1] 172.9708

Esses comandos mostram que o menor, maior valores na matriz de distância foram 16.28, 707.33, enquanto que a média foi de 285.9 com um desvio padrão de 172.97.

IMPORTANTE Lembre que no R e RStudio, a vírgula é usada como separador de decimal e o ponto é apenas indicador de milhar. Por exemplo, 2.500,50 lê-se dois mil e quinhentos e 50 décimos.

Também podemos calcular a assimetria e a curtose da matriz de distâncias, que são medidas que indicam o grau de desvio da normalidade da distribuição. Para isso, precisamos carregar o pacote moments, que contém as funções skewness() (assimetria) e kurtosis() (curtose).

14.5.2 Calculando a assimetria e a curtose

library(moments)
sk <- skewness(as.matrix(m_dists)) #calcula a assimetria da matriz
ku <- kurtosis(as.matrix(m_dists)) #calcula a curtose da matriz
sku <- cbind(sk,ku) # junta os dois valores em um vetor
colnames(sku) <- c("assimetria", "curtose") # nomeia as colunas do vetor
sku[1:10, ] # mostra as primeiras 10 linhas desse vetor
summary(sku) # mostra um resumo estatístico do vetor
##          assimetria   curtose
## S-A-ZA1  1.03617037  3.101029
## S-R-CC1  1.21511849  3.852134
## S-R-CT1  0.91278496  6.263889
## S-R-CP1  1.06839482  3.177206
## S-A-TA1  1.07960546  3.220821
## S-R-CT2  0.05290597  6.265832
## S-R-CP2  1.08571040  3.241712
## S-A-TA2  1.25111833  4.838956
## S-R-CT3 -2.35918827 10.736848
## S-R-CP3  1.06511174  3.178170
##    assimetria         curtose      
##  Min.   :-3.9660   Min.   : 2.946  
##  1st Qu.: 0.1891   1st Qu.: 3.226  
##  Median : 1.0531   Median : 3.793  
##  Mean   : 0.3625   Mean   : 5.248  
##  3rd Qu.: 1.1593   3rd Qu.: 5.659  
##  Max.   : 1.2826   Max.   :18.799

14.6 Distribuição de frequências da matriz de distâncias

Agora que temos uma ideia dos parâmetros básicos da matriz de distâncias, vamos entender sua distribuição de frequência usando um histograma e um boxplot. O histograma mostra a frequência relativa de cada intervalo de valores da matriz, enquanto o boxplot mostra a mediana, os quartis e os valores extremos da matriz.

Para fazer os gráficos, usamos as funções hist() e boxplot.default() do R. Também usamos a função curve() para sobrepor uma curva de normalidade ao histograma, e a função par para ajustar os parâmetros gráficos.

Nas linhas xlim = (), # limites dos eixos do código abaixo, os limites dos eixos do gráfico a ser criado foram definidos entre 0 e 707.3266572. No seu caso, você deve ajustar os valores de xlim para que eles sejam os limites dos valores da sua matriz, definidos pela linha range(dist) (primeira linha do código abaixo).

Em resumo, o código abaixo plota um histograma e um boxplot da distribuição de dados armazenada na matriz de distâncias. Também é adicionada uma curva normal teórica ao histograma utilizando a média e o desvio padrão dos dados (Figura 14.1. As funções floor(min(m_dists)) e ceiling(max(m_dists)) definem os limites dos graficos pelo valores mínimo e máximo do objeto.

range(m_dists)
par(mfrow=c(2,1)) # esse comando faz os gráficos aparecerem um acima do outro
hist(m_dists,
     breaks = 20, # determina o número de colunas do histograma
     xlim = range(floor(min(m_dists)), ceiling(max(m_dists))), # limites dos eixos
     xlab = "Distr. de Frequências",
     freq = FALSE, # mostra as frequências relativas em vez das absolutas
     main = "Histograma e boxplot da matriz de distâncias")
curve(dnorm(x, mean=mean(m_dists), sd=sd(m_dists)), add=TRUE) # sobrepõe a curva de normalidade
boxplot.default(m_dists, horizontal = TRUE, frame = FALSE,
                xlab="Distr. de Frequências",
                ylim=c(floor(min(m_dists)), ceiling(max(m_dists)))) # limites dos eixos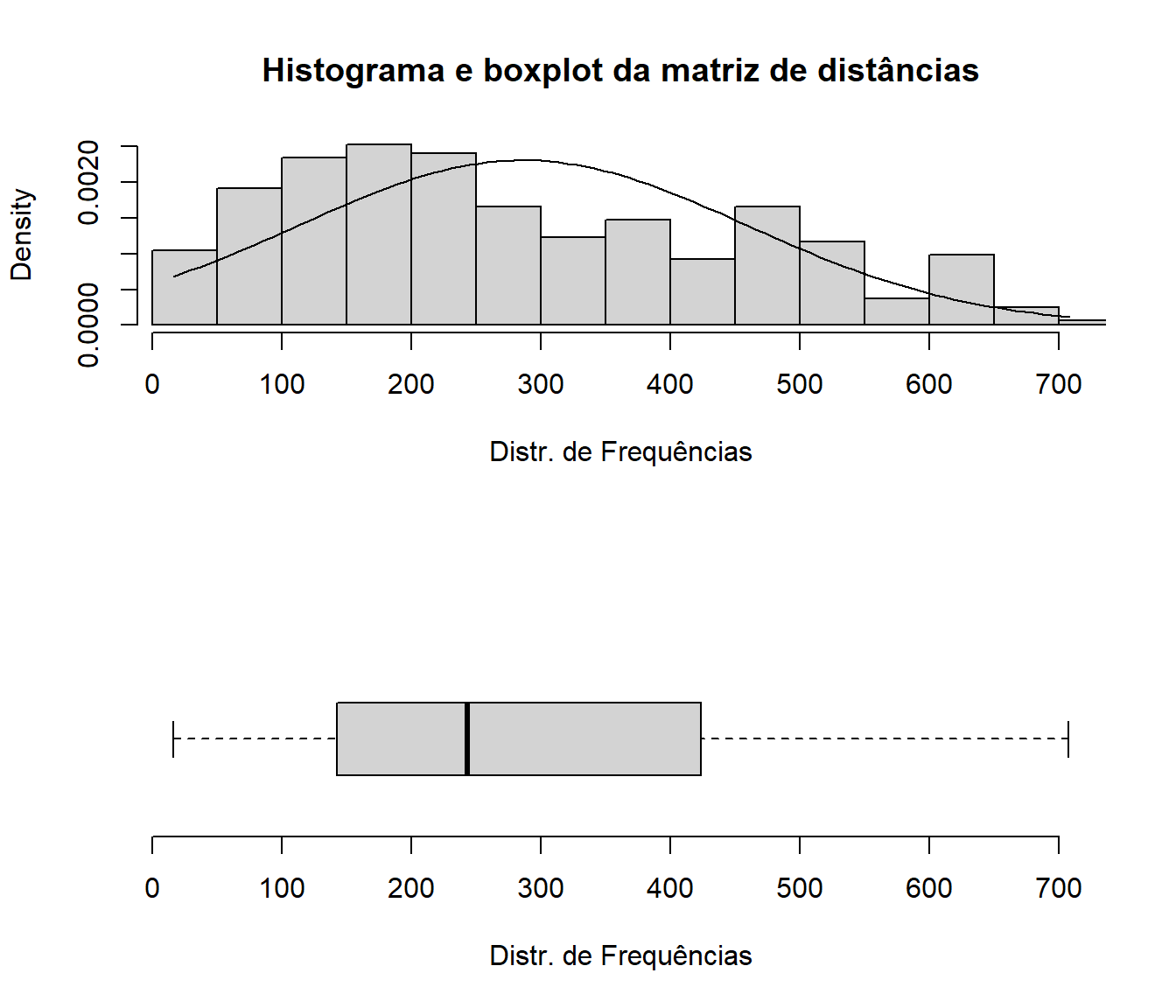
Distribuições de frequências da matriz de distâncias

Figura 14.1: Distribuições de frequências da matriz de distâncias 

## [1]  16.27882 707.32666

IMPORTANTE [Atenção:] Se você recebeu a mensagem de erro “Error in plot.new() : figure margins too large”, aumente o tamanho da janela do gráfico e execute o bloco de comandos novamente.

O comando abaixo apaga os gráficos.

dev.off()

14.7 Relativizando e transformando a base de dados

Na sequencia de códigos a seguir o R realiza relativizações e transformações em dados biológicos (R. R. Sokal and Rohlf (1995)). Vamos ver passo a passo o que cada seção do código faz. Os códigos para as demais principais relativizações estão AQUI

library(vegan)

Essa linha carrega o pacote vegan no ambiente R, permitindo o uso de suas funções. O pacote vegan é um pacote do R para análise de ecologia numérica e comunidades biológicas. Ele fornece uma ampla variedade de funções para análise de dados ecológicos, como análise de diversidade, ordenação de espécies, análise de similaridade, entre outras.

A função decostand() é usada para relativizar os dados armazenados na matriz de trabalho (m_trab). O parâmetro method especifica o método de relativização, neste caso “total” (relativização pelo total de cada coluna). Outros métodos disponíveis são max, normalize, range e rankm (@ref(tab:(5tbl-rel)). O parâmetro MARGIN especifica em qual dimensão os cálculos devem ser feitos (1 para linhas, 2 para colunas). Neste caso, MARGIN=2 (colunas). A variável m_relcol armazena o resultado da relativização. Sokal e Rohlf (Robert R. Sokal and Rohlf (1987)) tratam dos diversos tipos de relativizações e transformações em dados ecológicos.

14.7.1 Relativização pelo total

m_relcol <- decostand(m_trab,
                         method="total",
                         MARGIN = 2)
#View(m_relcol)
m_relcol
##          ap-davis     as-bimac    as-fasci    ch-bimac   ci-ocela   ci-orien
## S-A-ZA1 0.0000000 0.0004191115 0.000000000 0.000000000 0.00000000 0.00000000
## S-R-CC1 0.0000000 0.0414920369 0.000000000 0.000000000 0.00000000 0.00000000
## S-R-CT1 0.0000000 0.0813076278 0.348101266 0.000000000 0.00000000 0.03496503
## S-R-CP1 0.0000000 0.0079631182 0.000000000 0.000000000 0.00000000 0.00000000
## S-A-TA1 0.0000000 0.0096395641 0.006329114 0.018439716 0.00000000 0.00000000
## S-R-CT2 0.0000000 0.0595138307 0.018987342 0.004255319 0.00000000 0.48251748
## S-R-CP2 0.0000000 0.0020955574 0.006329114 0.000000000 0.57142857 0.06293706
## S-A-TA2 0.0000000 0.0192791282 0.000000000 0.252482270 0.00000000 0.00000000
## S-R-CT3 0.0000000 0.0863369656 0.405063291 0.000000000 0.00000000 0.17482517
## S-R-CP3 0.0000000 0.0067057837 0.000000000 0.000000000 0.18571429 0.16783217
## S-A-TA3 0.0000000 0.0980720872 0.044303797 0.337588652 0.00000000 0.00000000
## S-R-CT4 0.0000000 0.0000000000 0.006329114 0.000000000 0.00000000 0.03496503
## S-R-CP4 0.0000000 0.0000000000 0.000000000 0.000000000 0.15714286 0.04195804
## S-A-TA4 0.0000000 0.1651299246 0.000000000 0.387234043 0.00000000 0.00000000
## B-A-MU1 0.0000000 0.0050293378 0.000000000 0.000000000 0.00000000 0.00000000
## B-R-ET1 0.0000000 0.0012573345 0.000000000 0.000000000 0.00000000 0.00000000
## B-A-GU1 0.0000000 0.0008382230 0.012658228 0.000000000 0.00000000 0.00000000
## B-R-PC2 0.1851852 0.0184409053 0.000000000 0.000000000 0.02857143 0.00000000
## B-A-MU2 0.0000000 0.0414920369 0.000000000 0.000000000 0.00000000 0.00000000
## B-A-GU2 0.0000000 0.0000000000 0.000000000 0.000000000 0.00000000 0.00000000
## B-R-PC3 0.8148148 0.0314333613 0.044303797 0.000000000 0.05714286 0.00000000
## B-A-MU3 0.0000000 0.2141659681 0.000000000 0.000000000 0.00000000 0.00000000
## B-A-GU3 0.0000000 0.0025146689 0.000000000 0.000000000 0.00000000 0.00000000
## B-R-PC4 0.0000000 0.0029337804 0.107594937 0.000000000 0.00000000 0.00000000
## B-A-MU4 0.0000000 0.0984911987 0.000000000 0.000000000 0.00000000 0.00000000
## B-A-GU4 0.0000000 0.0054484493 0.000000000 0.000000000 0.00000000 0.00000000
##         co-macro co-heter   cr-menez cu-lepid  cy-gilbe     ge-brasi he-margi
## S-A-ZA1        0        0 0.00000000        0 0.0000000 0.0000000000      0.0
## S-R-CC1        0        0 0.00000000        0 0.0000000 0.0000000000      0.0
## S-R-CT1        0        1 0.50000000        0 0.0000000 0.0029411765      0.0
## S-R-CP1        0        0 0.00000000        0 0.0000000 0.0000000000      0.0
## S-A-TA1        0        0 0.00000000        0 0.0000000 0.0000000000      0.0
## S-R-CT2        0        0 0.14285714        0 0.0000000 0.0000000000      0.5
## S-R-CP2        0        0 0.00000000        0 0.0000000 0.0000000000      0.0
## S-A-TA2        0        0 0.00000000        0 0.0000000 0.0000000000      0.0
## S-R-CT3        0        0 0.28571429        0 0.0000000 0.0009803922      0.0
## S-R-CP3        0        0 0.00000000        0 0.0000000 0.0000000000      0.0
## S-A-TA3        1        0 0.00000000        0 0.0000000 0.0000000000      0.0
## S-R-CT4        0        0 0.03571429        0 0.3816794 0.0029411765      0.5
## S-R-CP4        0        0 0.00000000        0 0.0000000 0.0000000000      0.0
## S-A-TA4        0        0 0.03571429        0 0.0000000 0.0009803922      0.0
## B-A-MU1        0        0 0.00000000        0 0.0000000 0.1862745098      0.0
## B-R-ET1        0        0 0.00000000        0 0.0000000 0.0000000000      0.0
## B-A-GU1        0        0 0.00000000        0 0.0000000 0.0068627451      0.0
## B-R-PC2        0        0 0.00000000        0 0.0000000 0.0078431373      0.0
## B-A-MU2        0        0 0.00000000        0 0.0000000 0.0656862745      0.0
## B-A-GU2        0        0 0.00000000        0 0.0000000 0.0225490196      0.0
## B-R-PC3        0        0 0.00000000        1 0.0000000 0.0156862745      0.0
## B-A-MU3        0        0 0.00000000        0 0.0000000 0.1421568627      0.0
## B-A-GU3        0        0 0.00000000        0 0.0000000 0.0313725490      0.0
## B-R-PC4        0        0 0.00000000        0 0.6183206 0.0049019608      0.0
## B-A-MU4        0        0 0.00000000        0 0.0000000 0.4990196078      0.0
## B-A-GU4        0        0 0.00000000        0 0.0000000 0.0098039216      0.0
##            ho-malab   hy-pusar le-melan    le-piau le-taeni mo-costa   mo-lepid
## S-A-ZA1 0.000000000 0.00000000        0 0.00000000        0        0 0.00000000
## S-R-CC1 0.000000000 0.00000000        0 0.00000000        0        0 0.02439024
## S-R-CT1 0.009174312 0.12676056        0 0.20000000        0        0 0.95121951
## S-R-CP1 0.045871560 0.02816901        0 0.00000000        0        0 0.00000000
## S-A-TA1 0.000000000 0.00000000        0 0.00000000        0        0 0.00000000
## S-R-CT2 0.155963303 0.60563380        0 0.06666667        0        0 0.02439024
## S-R-CP2 0.091743119 0.02816901        0 0.20000000        0        0 0.00000000
## S-A-TA2 0.018348624 0.00000000        0 0.00000000        0        0 0.00000000
## S-R-CT3 0.284403670 0.15492958        0 0.13333333        0        0 0.00000000
## S-R-CP3 0.036697248 0.00000000        0 0.06666667        0        0 0.00000000
## S-A-TA3 0.183486239 0.00000000        0 0.00000000        0        0 0.00000000
## S-R-CT4 0.036697248 0.04225352        0 0.00000000        0        0 0.00000000
## S-R-CP4 0.018348624 0.00000000        0 0.13333333        0        0 0.00000000
## S-A-TA4 0.082568807 0.00000000        0 0.13333333        0        0 0.00000000
## B-A-MU1 0.000000000 0.00000000        0 0.00000000        0        0 0.00000000
## B-R-ET1 0.000000000 0.00000000        0 0.00000000        0        0 0.00000000
## B-A-GU1 0.000000000 0.00000000        0 0.00000000        0        0 0.00000000
## B-R-PC2 0.000000000 0.00000000        1 0.00000000        1        0 0.00000000
## B-A-MU2 0.009174312 0.00000000        0 0.00000000        0        0 0.00000000
## B-A-GU2 0.000000000 0.00000000        0 0.00000000        0        0 0.00000000
## B-R-PC3 0.018348624 0.01408451        0 0.00000000        0        1 0.00000000
## B-A-MU3 0.000000000 0.00000000        0 0.00000000        0        0 0.00000000
## B-A-GU3 0.000000000 0.00000000        0 0.00000000        0        0 0.00000000
## B-R-PC4 0.009174312 0.00000000        0 0.06666667        0        0 0.00000000
## B-A-MU4 0.000000000 0.00000000        0 0.00000000        0        0 0.00000000
## B-A-GU4 0.000000000 0.00000000        0 0.00000000        0        0 0.00000000
##            or-nilot    pa-manag pimel-sp   po-retic    po-vivip    pr-brevi
## S-A-ZA1 0.000000000 0.000000000        0 0.00000000 0.000000000 0.032258065
## S-R-CC1 0.002358491 0.000000000        0 0.00000000 0.000000000 0.000000000
## S-R-CT1 0.042452830 0.000000000        1 0.00000000 0.048057260 0.017921147
## S-R-CP1 0.000000000 0.000000000        0 0.00000000 0.015337423 0.000000000
## S-A-TA1 0.000000000 0.000000000        0 0.00000000 0.000000000 0.003584229
## S-R-CT2 0.090801887 0.000000000        0 0.05249344 0.225971370 0.053763441
## S-R-CP2 0.000000000 0.000000000        0 0.00000000 0.032719836 0.017921147
## S-A-TA2 0.000000000 0.000000000        0 0.00000000 0.000000000 0.007168459
## S-R-CT3 0.162735849 0.000000000        0 0.01312336 0.333333333 0.587813620
## S-R-CP3 0.000000000 0.000000000        0 0.00000000 0.010224949 0.000000000
## S-A-TA3 0.000000000 0.000000000        0 0.00000000 0.000000000 0.000000000
## S-R-CT4 0.086084906 0.000000000        0 0.00000000 0.028629857 0.211469534
## S-R-CP4 0.000000000 0.000000000        0 0.00000000 0.081799591 0.000000000
## S-A-TA4 0.001179245 0.000000000        0 0.00000000 0.000000000 0.010752688
## B-A-MU1 0.007075472 0.000000000        0 0.00000000 0.000000000 0.000000000
## B-R-ET1 0.009433962 0.001805054        0 0.08923885 0.000000000 0.000000000
## B-A-GU1 0.003537736 0.019855596        0 0.00000000 0.000000000 0.000000000
## B-R-PC2 0.005896226 0.000000000        0 0.00000000 0.000000000 0.032258065
## B-A-MU2 0.001179245 0.000000000        0 0.02624672 0.008179959 0.000000000
## B-A-GU2 0.042452830 0.184115523        0 0.00000000 0.000000000 0.000000000
## B-R-PC3 0.076650943 0.000000000        0 0.00000000 0.000000000 0.021505376
## B-A-MU3 0.012971698 0.000000000        0 0.12073491 0.049079755 0.003584229
## B-A-GU3 0.291273585 0.451263538        0 0.00000000 0.000000000 0.000000000
## B-R-PC4 0.010613208 0.000000000        0 0.00000000 0.000000000 0.000000000
## B-A-MU4 0.001179245 0.000000000        0 0.69816273 0.166666667 0.000000000
## B-A-GU4 0.152122642 0.342960289        0 0.00000000 0.000000000 0.000000000
##         ps-rhomb ps-genise   se-heter se-piaba se-spilo    st-noton sy-marmo
## S-A-ZA1        0         0 0.00000000        0        0 0.000000000        0
## S-R-CC1        0         0 0.00000000        0        0 0.000000000        0
## S-R-CT1        0         0 0.13513514        1        0 0.004878049        0
## S-R-CP1        0         0 0.04729730        0        0 0.000000000        0
## S-A-TA1        0         0 0.01351351        0        0 0.000000000        0
## S-R-CT2        0         0 0.20270270        0        0 0.121951220        0
## S-R-CP2        0         0 0.00000000        0        0 0.000000000        1
## S-A-TA2        0         0 0.00000000        0        0 0.000000000        0
## S-R-CT3        1         1 0.12837838        0        1 0.560975610        0
## S-R-CP3        0         0 0.00000000        0        0 0.000000000        0
## S-A-TA3        0         0 0.00000000        0        0 0.000000000        0
## S-R-CT4        0         0 0.01013514        0        0 0.312195122        0
## S-R-CP4        0         0 0.01013514        0        0 0.000000000        0
## S-A-TA4        0         0 0.00000000        0        0 0.000000000        0
## B-A-MU1        0         0 0.00000000        0        0 0.000000000        0
## B-R-ET1        0         0 0.00000000        0        0 0.000000000        0
## B-A-GU1        0         0 0.00000000        0        0 0.000000000        0
## B-R-PC2        0         0 0.03378378        0        0 0.000000000        0
## B-A-MU2        0         0 0.00000000        0        0 0.000000000        0
## B-A-GU2        0         0 0.00000000        0        0 0.000000000        0
## B-R-PC3        0         0 0.31418919        0        0 0.000000000        0
## B-A-MU3        0         0 0.00000000        0        0 0.000000000        0
## B-A-GU3        0         0 0.00000000        0        0 0.000000000        0
## B-R-PC4        0         0 0.10472973        0        0 0.000000000        0
## B-A-MU4        0         0 0.00000000        0        0 0.000000000        0
## B-A-GU4        0         0 0.00000000        0        0 0.000000000        0
##          te-chalc   tr-signa
## S-A-ZA1 0.0000000 0.00000000
## S-R-CC1 0.0000000 0.00000000
## S-R-CT1 0.0000000 0.08653846
## S-R-CP1 0.0000000 0.00000000
## S-A-TA1 0.0000000 0.00000000
## S-R-CT2 0.0000000 0.07211538
## S-R-CP2 0.0000000 0.00000000
## S-A-TA2 0.0000000 0.00000000
## S-R-CT3 0.0000000 0.03365385
## S-R-CP3 0.0000000 0.00000000
## S-A-TA3 0.0000000 0.00000000
## S-R-CT4 0.0000000 0.67788462
## S-R-CP4 0.0000000 0.00000000
## S-A-TA4 0.0000000 0.00000000
## B-A-MU1 0.0000000 0.00000000
## B-R-ET1 0.0000000 0.00000000
## B-A-GU1 0.0000000 0.00000000
## B-R-PC2 0.5671642 0.11057692
## B-A-MU2 0.0000000 0.00000000
## B-A-GU2 0.0000000 0.00000000
## B-R-PC3 0.4328358 0.00000000
## B-A-MU3 0.0000000 0.00000000
## B-A-GU3 0.0000000 0.00000000
## B-R-PC4 0.0000000 0.01923077
## B-A-MU4 0.0000000 0.00000000
## B-A-GU4 0.0000000 0.00000000
#colSums(m_relcol)
#range(m_relcol)

14.7.2 Transformação pelo arcoseno da raiz quadrada

A seguir é realizada a transformação pelo arcoseno da raiz quadrada, apropriada para ados em proporção como os ados previamente relativisados. Para cada transformação, a função é aplicada aos dados de interesse e o resultado é armazenado em uma nova variável. A função View() é usada para visualizar o resultado de cada transformação na forma de uma tabela. Os códigos para as demais principais transformações estão AQUI

m_relcol_asrq <- asin(sqrt(m_relcol))
#View(m_relcol_asrq)
m_relcol_asrqpi <- 2/pi*(asin(sqrt(m_relcol)))
#View(m_relcol_asrqpi)
#colSums(m_relcol_asrqpi)
#range(m_relcol_asrqpi)

14.8 Reset point 2

Aqui estabelecemos a matriz transformada depois de ter sido relativisada como m_trns.

m_trns <- m_relcol_asrqpi
#m_dists <- dist(m_trns, method = "euclidian", diag = TRUE, upper = FALSE)

Agora é com você…Refaça toda a análise com as relativizações e transformações adequadas para a matriz de dados fornecida.

Apêndices

Relativizações

Total das colunas

m_relcol <- decostand(m_bruta,
                         method="total",
                         MARGIN = 2)
View(m_relcol)
m_relcol

A função decostand() é usada para relativizar os dados armazenados no vetor m_bruta. O parâmetro method especifica o método de relativização, neste caso “total” (relativização pelo total de cada coluna). Outros métodos disponíveis são max, normalize, range e rankm (Figura 14.2). O parâmetro MARGIN especifica em qual dimensão os cálculos devem ser feitos (1 para linhas, 2 para colunas). Neste caso, MARGIN=2 (colunas). A variável m_relcol armazena o resultado da relativização. Sokal e Rohlf (1995) tratam dos diversos tipos de relativizações e transformações em dados ecológicos.

Tabela 14.2: Métodos de relativização da função decostand
Função Descrição Uso adequado
max Divide cada valor pela maior observação da coluna em que está localizado. Todos os valores resultantes serão menores ou iguais a 1. Adequada para análise em escala relativa Quando a escala de cada variável é conhecida e a análise deve ser feita em uma escala relativa
normalize Divide cada valor pelo comprimento do vetor. Isso resulta em valores cujo comprimento é sempre igual a 1. Adequada para análise de dados de frequência Para análise de dados de frequência
range Subtrai o valor mínimo da coluna de cada valor e, em seguida, divide pelo intervalo (ou amplitude) dos valores da coluna. Isso resulta em valores entre 0 e 1. Quando a amplitude dos valores em cada coluna é importante para a análise
rankm Transforma os valores em suas posições dentro da coluna, em ordem crescente. O menor valor recebe o valor 1 e o maior valor recebe o valor igual ao comprimento da coluna. Quando a escala absoluta dos valores não é importante, mas a ordem dos valores é significativa.

Transformações

Essa seção mostra as diversas transformações nos dados armazenados no vetor m_bruta. Para cada transformação, a função é aplicada aos dados da matriz e o resultado é armazenado em uma nova variável. A função View() pode ser usada para visualizar o resultado de cada transformação na forma de uma tabela. Ela mostra o código que realiza diversas transformações na matriz de dados. Para cada transformação, a função é aplicada aos dados e o resultado é armazenado em uma nova variável.

Log10

Não aceita zeros, porque o log de zero é indeterminado. Por isso devemos substituir os valores com erro (infinito negativo) por zero, usando a função replace().

m_lg10 <- log10(m_bruta)
#View(m_lg10)
m_lg10 <- replace(m_lg10, is.infinite(m_lg10), 0)
head(m_lg10)

Log(x+1)

Desaconselhavel para valores que variam entre 0-1.

m_lgx1 <- log(m_bruta+1)
#View(m_lgx1)

Exponenciais

“Power transformations”, onde o valor de p estabelece a compressão dos dados.

m_bruta_P1 <- m_bruta^1 #p=1
#View(m_bruta_P1)
m_bruta_P05 <- m_bruta^0.5 #p=0,5
#View(m_bruta_P05)
m_bruta_P01 <- m_bruta^0.1 #p=0,1
#View(m_bruta_P01)

Presença/Ausência

m_pa <- (m_bruta>0)*1L
#View(m_pa)

Raiz quadrada

m_rq <- sqrt(m_bruta)
#View(m_rq)

Arcoseno da raiz quadrada

Os valores de entrada tem que variar entre 0 e 1. Ideal para matrizes relativizadas. Duas formulações estão disponíveis, com e sem a multiplicação por 2/pi. A segunda opção costuma ter melhor efeito na normalização dos dados.

m_asrq <- asin(sqrt(m_relcol))
#View(m_asrq)
m_asrqpi <- 2/pi*(asin(sqrt(m_relcol)))
View(m_asrqpi)

Script limpo

Aqui apresento o scrip na íntegra sem os textos ou outros comentários. Você pode copiar e colar no R para executa-lo. Lembre de remover os # ou ## caso necessite executar essas linhas.

## dev.off() #apaga os graficos, se houver algum
## rm(list=ls(all=TRUE)) #limpa a memória
## cat("\014") #limpa o console
## install.packages("openxlsx") #importa arquivos do excel
## install.packages("moments") #calcula assimetria e curtose dos dados
## install.packages("vegan") #estatisticas para ecologia de comunidades
## getwd()
## setwd("C:/Seu/Diretório/De/Trabalho")
library(openxlsx)
#dir <- getwd() #criamos um vetor com o diretório  de trbalho 
#shell.exec(dir) #abre o diretorio de trabalho no Windows Explorer
m_bruta <- read.xlsx("D:/Elvio/OneDrive/Disciplinas/_EcoNumerica/5.Matrizes/peixes06.xlsx",
                   rowNames = T, colNames = T,
                   sheet = "Sheet1")
str(m_bruta)
#View(m_bruta)
m_bruta[1:5,1:5] #[1:5,1:5] mostra apenas as linhas e colunas de 1 a 5.
## #View(m_bruta)
## print(m_bruta[1:8,1:8])
## m_bruta[1:10,1:10]
## str(m_bruta)
## mode(m_bruta)
## class(m_bruta)
#View(m_bruta)
print(m_bruta)
head(m_bruta)
range(m_bruta) #menor e maior valores
length(m_bruta) #no. de colunas
ncol(m_bruta) #no. de N colunas
nrow(m_bruta) #no. de M linhas
sum(lengths(m_bruta)) #soma os nos. de colunas
length(as.matrix(m_bruta)) #tamanho da matriz m x n
sum(m_bruta == 0) # número de observações igual a zero
sum(m_bruta > 0) # número de observações maiores que zero
zeros <- (sum(m_bruta == 0)/length(as.matrix(m_bruta)))*100 # proporção de zeros na matriz
zeros
tamanho <- data.frame(
  Função = c("range", "lenght", "m cols", "n linhas", "Tamanho", "Tamanho",
             "Zeros", "Nao zeros", "% Zeros"),
  Resultado = c(paste(range(m_bruta), collapse = " - "), length(m_bruta), ncol(m_bruta),
                nrow(m_bruta), sum(lengths(m_bruta)), length(as.matrix(m_bruta)), sum(m_bruta == 0),
                sum(m_bruta > 0), round(zeros, 1)))
tamanho
m_trab <- m_bruta
m_dists <- dist(m_trab, method = "euclidian", diag = TRUE, upper = FALSE)
#m_dists
str(m_dists)
mode(m_dists)
class(m_dists)
length(as.matrix(m_dists))
as.matrix(m_dists)[1:10, 1:10]
range(m_trab)
range(m_dists)
min(m_dists)
max(m_dists)
mean(m_dists) #CENTROIDE!! ou Grand mean
sd(m_dists)  #standard deviation
centroide <- mean(m_dists)
centroide
length(m_dists)
m <- nrow(as.matrix(m_dists))
m
m*(m-1)/2
summary(m_dists)
Sumario1 <- cbind(min(m_dists),
                  max(m_dists),
                  sd(m_dists),
                  mean(m_dists),
                  length(m_dists))
colnames(Sumario1) <- c("Minimo", "Maximo", "Desv.Padr", "Media", "m(m-1)/2")
rownames(Sumario1) <- ("Valores")
Sumario1
dist <- (as.matrix(m_dists))
#View(dist)
str(dist)
mode(dist)
class(dist)
#head(dist)
dist[1:5, 1:5] #mostra as 5 primeiras linhas e colunas da matriz
range(m_dists) # intervalo dos valores da matriz
mean(m_dists) # média dos valores da matriz
sd(m_dists) # desvio padrão dos valores da matriz
library(moments)
sk <- skewness(as.matrix(m_dists)) #calcula a assimetria da matriz
ku <- kurtosis(as.matrix(m_dists)) #calcula a curtose da matriz
sku <- cbind(sk,ku) # junta os dois valores em um vetor
colnames(sku) <- c("assimetria", "curtose") # nomeia as colunas do vetor
sku[1:10, ] # mostra as primeiras 10 linhas desse vetor
summary(sku) # mostra um resumo estatístico do vetor
range(m_dists)
par(mfrow=c(2,1)) # esse comando faz os gráficos aparecerem um acima do outro
hist(m_dists,
     breaks = 20, # determina o número de colunas do histograma
     xlim = range(floor(min(m_dists)), ceiling(max(m_dists))), # limites dos eixos
     xlab = "Distr. de Frequências",
     freq = FALSE, # mostra as frequências relativas em vez das absolutas
     main = "Histograma e boxplot da matriz de distâncias")
curve(dnorm(x, mean=mean(m_dists), sd=sd(m_dists)), add=TRUE) # sobrepõe a curva de normalidade
boxplot.default(m_dists, horizontal = TRUE, frame = FALSE,
                xlab="Distr. de Frequências",
                ylim=c(floor(min(m_dists)), ceiling(max(m_dists)))) # limites dos eixos
## dev.off()
library(vegan)
m_relcol <- decostand(m_trab,
                         method="total",
                         MARGIN = 2)
#View(m_relcol)
m_relcol
#colSums(m_relcol)
#range(m_relcol)
m_relcol_asrq <- asin(sqrt(m_relcol))
#View(m_relcol_asrq)
m_relcol_asrqpi <- 2/pi*(asin(sqrt(m_relcol)))
#View(m_relcol_asrqpi)
#colSums(m_relcol_asrqpi)
#range(m_relcol_asrqpi)
m_trns <- m_relcol_asrqpi
#m_dists <- dist(m_trns, method = "euclidian", diag = TRUE, upper = FALSE)
## m_relcol <- decostand(m_bruta,
##                          method="total",
##                          MARGIN = 2)
## View(m_relcol)
## m_relcol
## m_lg10 <- log10(m_bruta)
## #View(m_lg10)
## m_lg10 <- replace(m_lg10, is.infinite(m_lg10), 0)
## head(m_lg10)
## m_lgx1 <- log(m_bruta+1)
## #View(m_lgx1)
## m_bruta_P1 <- m_bruta^1 #p=1
## #View(m_bruta_P1)
## m_bruta_P05 <- m_bruta^0.5 #p=0,5
## #View(m_bruta_P05)
## m_bruta_P01 <- m_bruta^0.1 #p=0,1
## #View(m_bruta_P01)
## m_pa <- (m_bruta>0)*1L
## #View(m_pa)
## m_rq <- sqrt(m_bruta)
## #View(m_rq)
## m_asrq <- asin(sqrt(m_relcol))
## #View(m_asrq)
## m_asrqpi <- 2/pi*(asin(sqrt(m_relcol)))
## View(m_asrqpi)

Referências

Bibliografia

Borcard, Daniel, François Gillet, and Pierre Legendre. 2018. Numerical Ecology with r. Book. 2nd ed. Use r! Springer.
Horton, Nicholas J., and Ken Kleinman. 2015. Using r and RStudio for Data Management, Statistical Analysis, and Graphics. Book. 2nd ed. CRC Press.
Legendre, P., and L. Legendre. 1998. Numerical Ecology. Book. 2nd English ed. Developments in Environmental Modelling 20. Amsterdam, The Netherlands ; New York ; Oxford.
Sokal, R. R., and F. J. Rohlf. 1995. Biometry: The Principles and Practice of Statistics in Biological Research. Book. 3rd ed. New York: W.H. Freeman; Company.
Sokal, Robert R., and F. James Rohlf. 1987. Introduction to Biostatistics. Book. 2nd ed. Mineola, New York: Dover Publications.