10 R Modulo 3-2

Testes Estatísticos

RESUMO

Apresentação

A estatística descritiva tem um papel importante a desempenhar na ciência. Quando problemas específicos são tratados na ciência, os dados precisam ser coletados, analisados e apresentados de forma concisa para que outros possam se beneficiar do que foi encontrado. Geralmente não é possível apresentar um conjunto de dados completo em uma publicação ou em um seminário e, mesmo que fosse, é improvável isso permitisse uma boa comunicação dos resultados da pesquisa. Em vez disso, os dados são geralmente resumidos como tabelas de frequência, histogramas e estatísticas descritivas que os leitores ou ouvintes podem assimilar prontamente, mas que ainda transmitem os elementos essenciais do conjunto de dados original. O principal objetivo do cálculo das estatísticas descritivas é transmitir informações essenciais contidas em um conjunto de dados da forma mais concisa e clara possível.

10.1 Sobre os dados

Considere os dados merísticos (ou médições morfológicas) da espécie de peixe Cichla ocellaris (tucunaré amarelo) do reservatório da barragem de Gramame, PB (Bradstock, Tozer, and Keith 1997) (Figura 11.1). Existem 421 medições do comprimemto total (CT), comprimento padrão (CP) e peso total (PT), além do sexo (MACHO, FÊMEA ou imaturo), e outros descritores da estrutura populacional da pespécie, um conjunto de dados formidável.

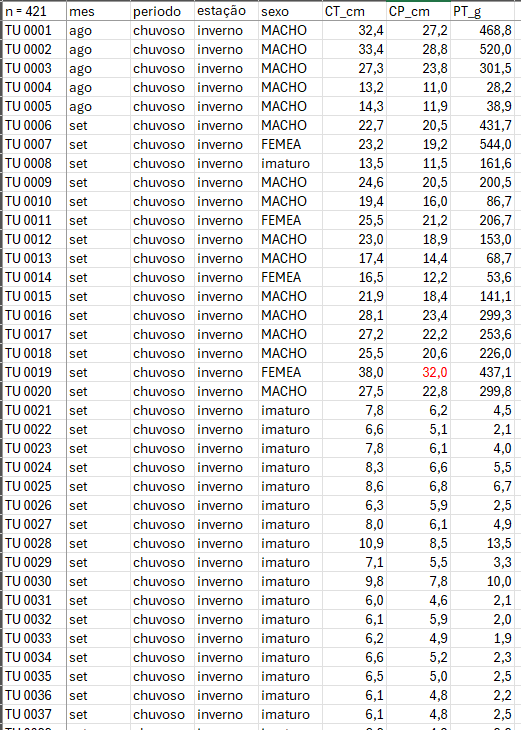
Figura 10.1: Dados merísticos da espécie de peixe Cichla ocellaris (tucunaré amarelo) do reservatório da barragem de Gramame, PB.

10.2 Organização básica

dev.off() #apaga os graficos, se houver algum
rm(list=ls(all=TRUE)) #limpa a memória
cat("\014") #limpa o console

Instalando os pacotes necessários para esse módulo

install.packages("openxlsx") #importa arquivos do excel
install.packages("fdth")
install.packages("ggpubr")
install.packages("multcomp")

library(openxlsx)

Os códigos acima, são usados para instalar e carregar os pacotes necessários para este módulo. Esses códigos são comandos para instalar pacotes no R. Um pacote é uma coleção de funções, dados e documentação que ampliam as capacidades do R (R CRAN (R. C. Team 2017) e RStudio (R. S. Team 2022)). No exemplo acima, o pacote openxlsx permite ler e escrever arquivos Excel no R. Para instalar um pacote no R, você precisa usar a função install.packages().

Depois de instalar um pacote, você precisa carregá-lo na sua sessão R com a função library(). Por exemplo, para carregar o pacote openxlsx, você precisa executar a função library(openxlsx). Isso irá permitir que você use as funções do pacote na sua sessão R. Você precisa carregar um pacote toda vez que iniciar uma nova sessão R e quiser usar um pacote instalado.

Agora vamos definir o diretório de trabalho. Esse código é usado para obter e definir o diretório de trabalho atual no R. O comando getwd() retorna o caminho do diretório onde o R está lendo e salvando arquivos. O comando setwd() muda esse diretório de trabalho para o caminho especificado entre aspas. No seu caso, você deve ajustar o caminho para o seu próprio diretório de trabalho. Lembre de usar a barra “/” entre os diretórios. E não a contra-barra “\”.

getwd()
setwd("C:/Seu/Diretório/De/Trabalho")

10.3 Importando a planilha

Vamos importar a planilha de dados univariados univ*.xlsx. Note que o símbolo # em programação R significa que o texto que vem depois dele é um comentário e não será executado pelo programa. Isso é útil para explicar o código ou deixar anotações. Ajuste a segunda linha do código abaixo para refletir “C:/Seu/Diretório/De/Trabalho/Planilha.xlsx”.

library(openxlsx)
univ <- read.xlsx("D:/Elvio/OneDrive/Disciplinas/_EcoNumerica/5.Matrizes/univ.xlsx",
                    rowNames = F, colNames = T,
                    sheet = "tucuna")
head(univ,10)
head(univ[, 1:5], 10)

##    n.=.434 CT_cm  PT_g CP_cm Ctubo_cm  PC_g      %PT Pest_g Cest_cm gr_est
## 1    TU001  32.4 468.8  27.2     39.8 458.9 2.111775    3.9     7.7      I
## 2    TU002  33.4 520.0  28.8     14.3 507.4 2.423077    5.9    10.0      I
## 3    TU003  27.3 301.5  23.8     13.0 283.4 6.003317   15.5    10.2    III
## 4    TU004  13.2  28.2  11.0     16.5  27.7 1.773050    0.3     4.3      I
## 5    TU005  14.3  38.9  11.9     15.5  37.7 3.084833    0.8     4.5    III
## 6    TU006  22.7 431.7  20.5     24.2 418.7 3.011350    9.9     6.4    III
## 7    TU007  23.2 544.0  19.2     25.0 520.1 4.393382    6.8     7.5     II
## 8    TU008  13.5 161.6  11.5     17.5 157.0 2.846535    4.1     6.8     II
## 9    TU009  24.6 200.5  20.5     25.7 195.9 2.294264    2.5     7.6     II
## 10   TU010  19.4  86.7  16.0     18.3  84.5 2.537486    0.7     5.1      I
##       ir_est Pint_g Cint_cm gr_int    ir_int Pgon_g Cgon_cm          emg
## 1  0.8319113    4.8    38.3     II 1.0238908    1.2       7      IMATURO
## 2  1.1346154    5.3    13.3     II 1.0192308    1.4     6.5       MADURO
## 3  5.1409619    2.4    12.0     II 0.7960199    0.2     7.7 EM MATURACAO
## 4  1.0638298    0.1    16.0     II 0.3546099    0.1       5      IMATURO
## 5  2.0565553    0.3    15.0     II 0.7712082    0.1     3.2      IMATURO
## 6  2.2932592    2.7    23.7     II 0.6254343    0.4     7.8 EM MATURACAO
## 7  1.2500000    3.3    24.5     II 0.6066176   13.8     7.9       MADURO
## 8  2.5371287    0.4    17.0      I 0.2475248    0.1     2.5      IMATURO
## 9  1.2468828    2.0    25.3     II 0.9975062    0.1     6.5 EM MATURACAO
## 10 0.8073818    1.4    17.7     II 1.6147636    0.1       6      IMATURO
##            ig mes periodo estação    sexo
## 1  0.25597270 ago chuvoso inverno   MACHO
## 2  0.26923077 ago chuvoso inverno   MACHO
## 3  0.06633499 ago chuvoso inverno   MACHO
## 4  0.35460993 ago chuvoso inverno   MACHO
## 5  0.25706941 ago chuvoso inverno   MACHO
## 6  0.09265694 set chuvoso inverno   MACHO
## 7  2.53676471 set chuvoso inverno   FEMEA
## 8  0.06188119 set chuvoso inverno imaturo
## 9  0.04987531 set chuvoso inverno   MACHO
## 10 0.11534025 set chuvoso inverno   MACHO
##    n.=.434 CT_cm  PT_g CP_cm Ctubo_cm
## 1    TU001  32.4 468.8  27.2     39.8
## 2    TU002  33.4 520.0  28.8     14.3
## 3    TU003  27.3 301.5  23.8     13.0
## 4    TU004  13.2  28.2  11.0     16.5
## 5    TU005  14.3  38.9  11.9     15.5
## 6    TU006  22.7 431.7  20.5     24.2
## 7    TU007  23.2 544.0  19.2     25.0
## 8    TU008  13.5 161.6  11.5     17.5
## 9    TU009  24.6 200.5  20.5     25.7
## 10   TU010  19.4  86.7  16.0     18.3

Exibindo os dados importados (esses comando são “case-sensitive” ignore.case(object)).

#View(univ)
print(univ[1:5,1:5])
univ
str(univ)
mode(univ)
class(univ)

Vamos escolher uma coluna como a variável de interesse para trabalhar com ela. No código abaixo, essa coluna é descrita pelo seu nome apresentado depois do $. Antes do $ especificamos e qual data frame está a variável. Depois disso, a convertemos para um vertor.

var <- univ$CP_cm
var_v <- as.vector(var)
range(var_v)

## [1]  3.5 36.1

E agora visualizando nossos dados.

#View(var)
print(var_v)
var_v
str(var_v)
mode(var_v)
class(var_v)
range(var_v)

Por inspeção, o comprimento total mínimo do peixe é 3.5 cm e o máximo é 36.1 cm. Esses valores definem o intervalo da amostra. Agora precisamos subdividir os dados em intervalos ou classes, cada um com o mesmo tamanho. Geralmente, é aconselhável arredondar o valor mínimo para baixo e o valor máximo para cima, para valores apropriados ao decidir as classes de intervalos. Nesse caso, parece sensato dividir a faixa de range(var_v) cm em sete intervalos a cada 5 cm de largura. Se contarmos o número de peixes que se encontram em cada um dos sete intervalos, temos a base para a tabulação da frequência.

A coluna de frequência será obtida contando o número de medições que existem dentro de cada classe. A coluna de frequência percentual será obtida representando cada contagem como uma porcentagem da contagem total. A frequência cumulativa e as frequências percentuais cumulativas serão obtidas somando progressivamente as frequências correspondentes.

Tendo em mãos o conjunto total de 434 valores merísticos da variável de interesse agora podemos tirar uma subamostra aleatória de uma parte dos 434 valores. Essa subamostra é tirada usando o comando size= no código subsequente, que estabelece o tamanho da subamostra a ser tirada do total de dados. Esse tamanho é estabelecido no quiz. Inclua esse valor de acordo com o que é pedido no quiz. Por exemplo, se for pedido uma subamostra de 150 comprimentos, então size = 150. Nesse tutorial usaremos todos os 434 comprimentos. Podemos ainda escolher uma das colunas da base de dados, no caso desse vamos usar a coluna

Subsitua em n <- o valor de size= desejado. Aqui n <- será todo o conjunto de dados length(var_v).

n <- length(var_v)
set.seed(666)
var_sub <- sample(var_v, size = n, replace = F) #atualize o valor de 'size=' se necessário
#OU
#var_sub <- univ[univ$CP_cm >0 & univ$CP_cm <20,] #data.frame
#var_sub <- var_v[var_v>=5 & var_v <=15] #vector

Para fazermos uma tabela de frequência dos valores merísticos carregamos o pacote fdth e pedimos a função range que retorna o valor máximo e mínimo no vetor.

library(fdth)
range(var_sub) #retorna o valor máximo e mínimo
#?range

## [1]  3.5 36.1

Agora é necessário que você substitua os valores de range 3.5, 36.1 nos valores de início e fim da distribuição de frequência. Os comandos abaixo criam uma tabela de frequência chamada tf com valores máximos e mínimos definidos por range(var_v) em intervalor definidos por h=5, e o comando print(tf) exibe a tabela de frequência.

tf <- fdt(var_sub, start=0, end=40, h=5) #tabela de frequência
#?fdt #atente para o uso de k, por exemplo tf <- fdt(var_sub, k=5)
print(tf)

##  Class limits   f   rf rf(%)  cf  cf(%)
##         [0,5)  57 0.13 13.13  57  13.13
##        [5,10) 154 0.35 35.48 211  48.62
##       [10,15) 109 0.25 25.12 320  73.73
##       [15,20)  38 0.09  8.76 358  82.49
##       [20,25)  33 0.08  7.60 391  90.09
##       [25,30)  23 0.05  5.30 414  95.39
##       [30,35)  15 0.03  3.46 429  98.85
##       [35,40)   5 0.01  1.15 434 100.00

Class limits = limites de classe, f = frequência de classe, rf = frequência relativa da classe, rf(%) = frequência relativa percentual da classe, cf = frequência cumulativa da classe, cf(%) = frequência cumulativa percentual da classe.

Se contarmos o número de brotos que se encontram em cada um dos sete intervalos, temos a base para a tabulação da frequência. Essa tabulação é mostrada na tabela gerada pelos códigos acima. A coluna de frequência foi obtida contando o número de medições que existem dentro de cada classe. A coluna de frequência percentual foi obtida representando cada contagem como uma porcentagem da contagem total. A frequência cumulativa e as frequências percentuais cumulativas foram obtidas somando progressivamente as frequências correspondentes.

10.4 Gráficos de histograma e boxplot

No código abaixo se define o layout dos gráficos para serem exibidos lado a lado, e na sequência criamos um gráfico de histograma com base na tabela de frequência tf. O comando boxplot() cria um gráfico de boxplot para os valores em var_v. O argumento “horizontal = TRUE” indica que o boxplot deve ser horizontal.

par(mfrow = c(1,2)) #gráficos lado a lado
plot(tf) #distribuição de frequências
boxplot(var_sub, horizontal = TRUE,
        xlab="Class limits") #boxplot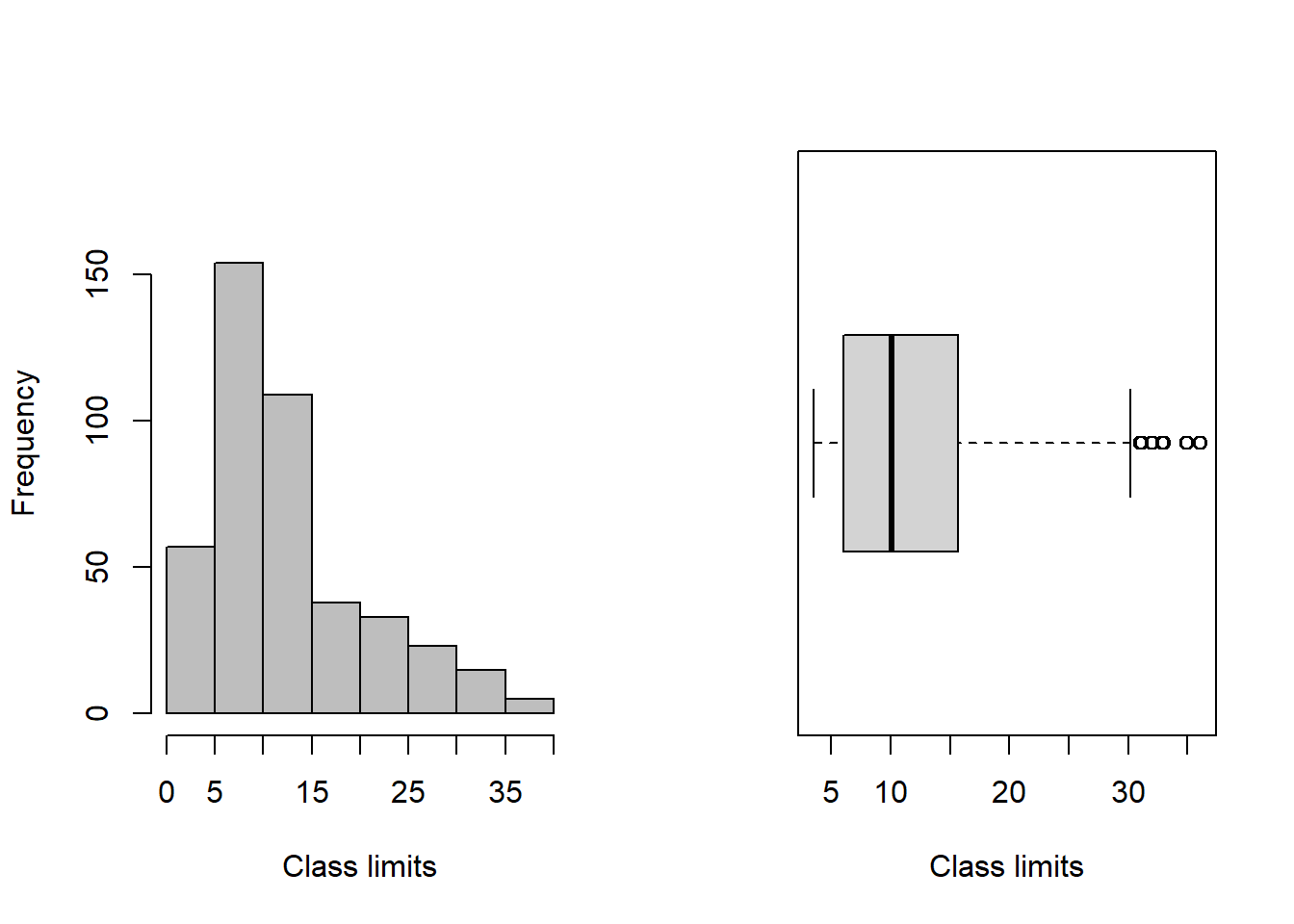

par(mfrow = c(1,1)) #gráficos de volta ao normal

IMPORTANTE Se você recebeu a mensagem de erro “Error in plot.new() : figure margins too large”, aumente o tamanho da janela do gráfico e execute as últimas três linhas de comando novamente.

10.5 Sumário estatístico geral

summary(var_sub)
#?summary
sd(var_sub) #desvio padrão
var(var_sub) #variância

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    3.50    6.00   10.10   12.32   15.70   36.10 
## [1] 7.845708
## [1] 61.55514

10.6 Testando normalidade

10.6.1 Q-Q plots

par(mfrow=c(3,1))
qqnorm(var_sub, main='Normal')
qqline(var_sub)
boxplot(var_sub, horizontal = TRUE,
        xlab="Class limits") #boxplot
hist(var_sub)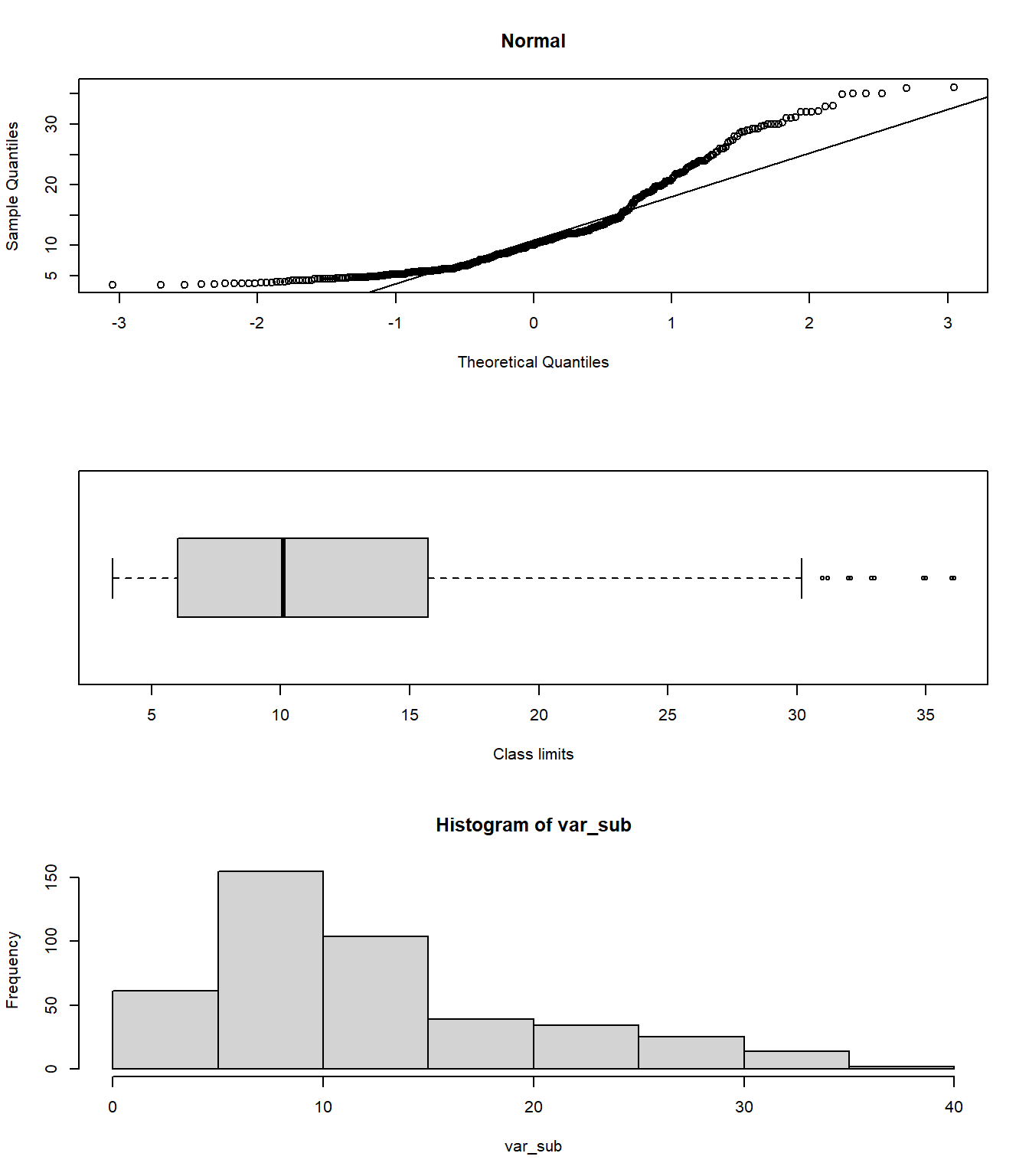

par(mfrow=c(1,1))
library(ggpubr)

## Warning: package 'ggpubr' was built under R version 4.3.3

ggdensity(var_sub)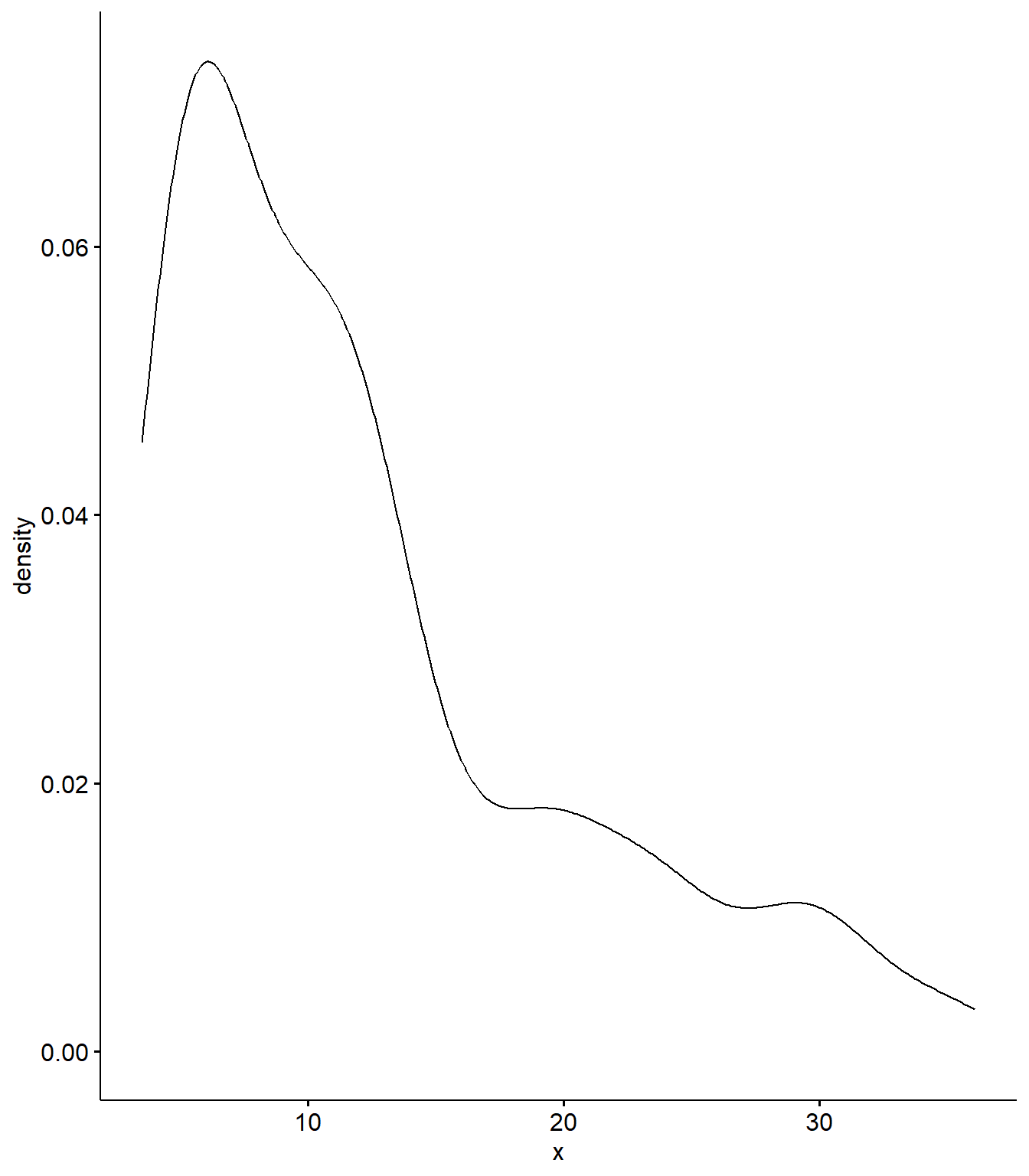

ggqqplot(var_sub)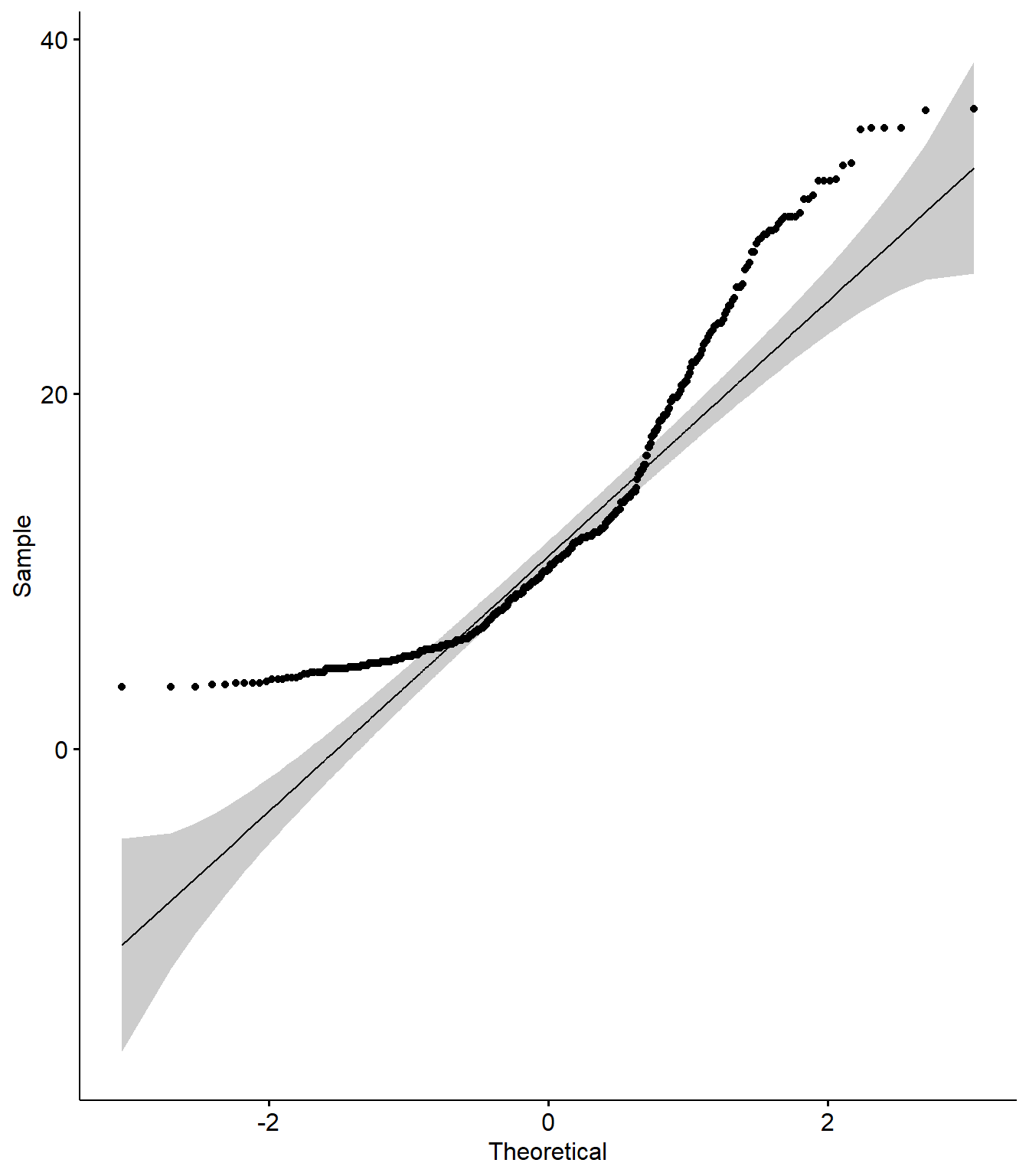

library(car)

## Carregando pacotes exigidos: carData

## 
## Attaching package: 'car'

## The following object is masked from 'package:dplyr':
## 
##     recode

## The following object is masked from 'package:purrr':
## 
##     some

qqPlot(var_sub)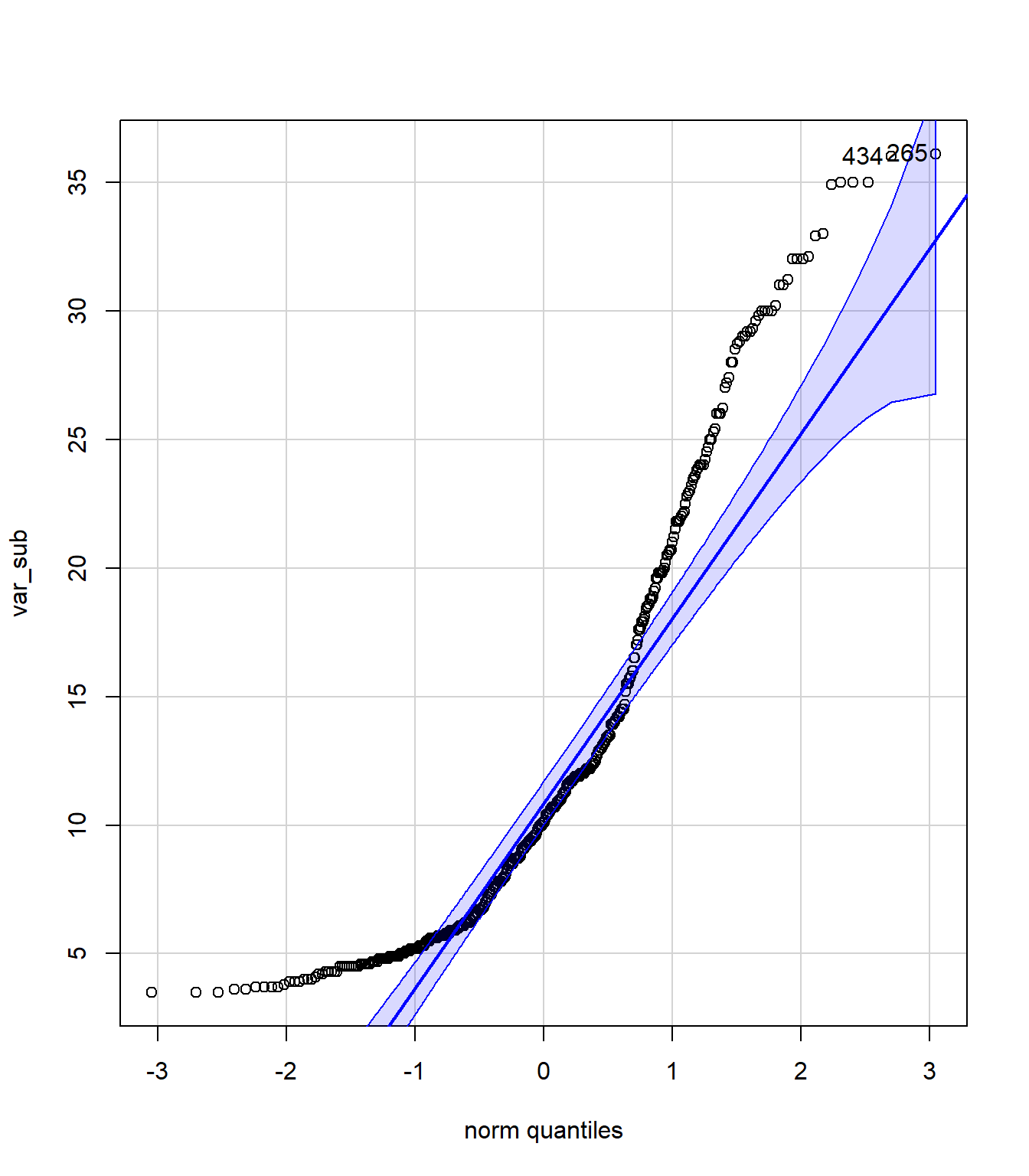

## [1] 265 434

10.6.2 Testes de Shapiro-Wilk e Kolmogorov-Smirnov

shap <- shapiro.test(var_sub)
shap
p <- format(shap$p.value, scientific = FALSE)
p
ks.test(var_sub, "pnorm")

## Warning in ks.test.default(var_sub, "pnorm"): ties should not be present for the
## Kolmogorov-Smirnov test

## 
##  Shapiro-Wilk normality test
## 
## data:  var_sub
## W = 0.86837, p-value < 2.2e-16
## 
## [1] "0.00000000000000000107347"
## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  var_sub
## D = 0.99977, p-value < 2.2e-16
## alternative hypothesis: two-sided

10.7 Testando diferenças entre médias

10.7.1 Testando homogeneidade de variâncias

# F-test
#var.test(CT_cm ~ sexo, data = univ) com erro
#Interpretação: Um valor de p maior que o nível de significância de 0.05 significa que, NÃO HÁ diferença significativa entre as duas variâncias.

# Levene
library(car)
#univ$sexo <- as.factor(univ$sexo) #evita o Warning de "group coerced to factor"  
lev <- leveneTest(CT_cm ~ sexo, data = univ)

## Warning in leveneTest.default(y = y, group = group, ...): group coerced to
## factor.

lev

# Teste de Levene entre dois de tres grupos
machos_CT_cm <- na.omit(univ$CT_cm[univ$sexo == "MACHO"])
femeas_CT_cm <- na.omit(univ$CT_cm[univ$sexo == "FEMEA"])
imat_CT_cm <- na.omit(univ$CT_cm[univ$sexo == "imaturo"])
lev2 <- leveneTest(CT_cm ~ sexo, data = univ[univ$sexo %in% c("MACHO", "FEMEA"), ])

## Warning in leveneTest.default(y = y, group = group, ...): group coerced to
## factor.

lev2
#Interpretação: Um valor de p maior que o nível de significância de 0.05 significa que, a hipótese nula é mantida e NÃO HÁ diferença significativa entre as variâncias.
univ$sexo <- factor(univ$sexo, levels = c("MACHO", "FEMEA", "imaturo"))
boxplot(CT_cm ~ sexo, data = univ)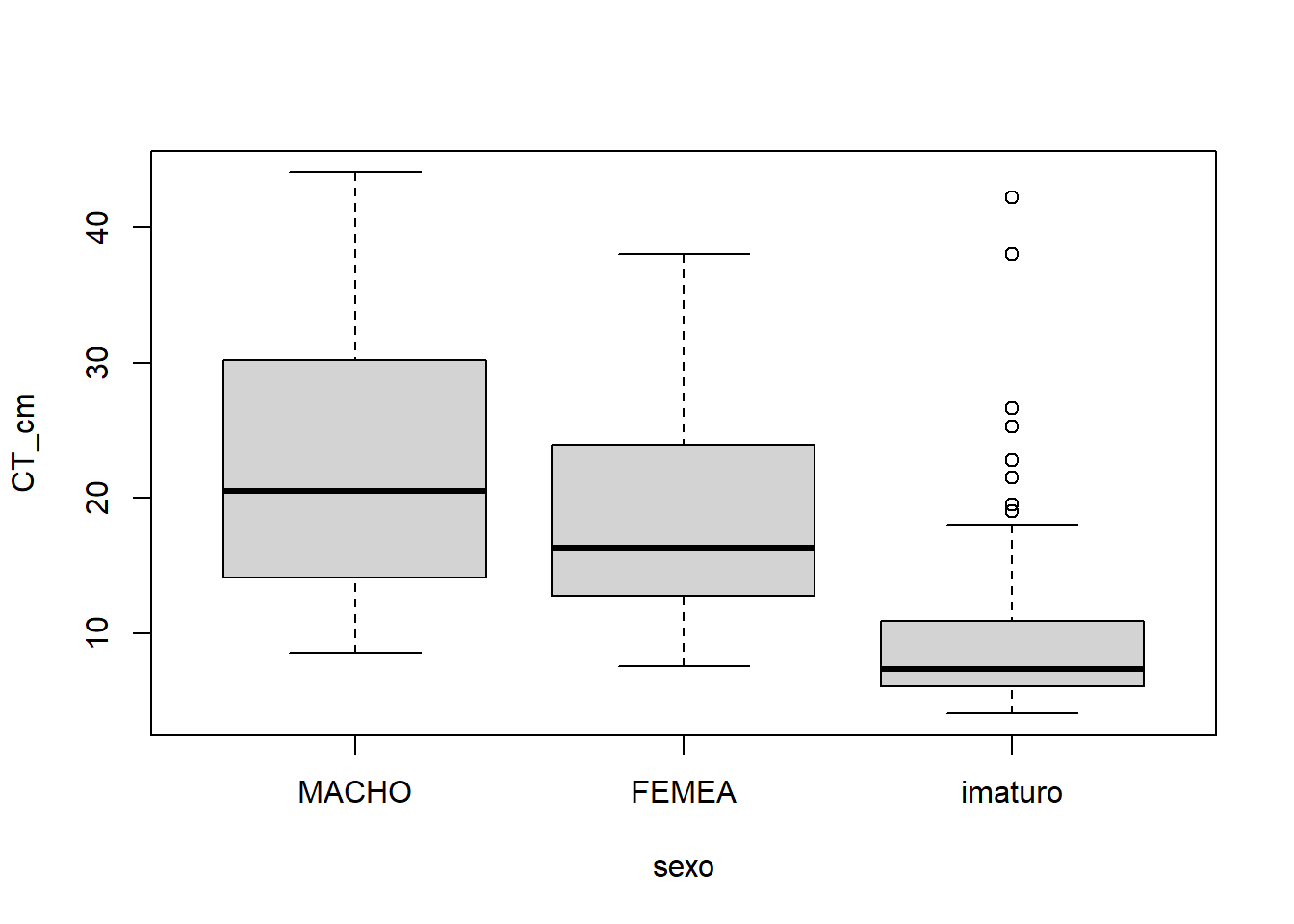

## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value    Pr(>F)    
## group   2  45.395 < 2.2e-16 ***
##       431                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value   Pr(>F)   
## group   1  10.826 0.001173 **
##       211                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

10.7.2 Teste entre duas médias (t-Student)

t.test(machos_CT_cm, femeas_CT_cm,
      alternative = c("two.sided", "less", "greater"),
      mu = 0, paired = FALSE, var.equal = FALSE,
      conf.level = 0.95)

## 
##  Welch Two Sample t-test
## 
## data:  machos_CT_cm and femeas_CT_cm
## t = 3.4342, df = 210.89, p-value = 0.0007155
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  1.747453 6.456834
## sample estimates:
## mean of x mean of y 
##  22.70984  18.60769

10.7.3 Teste entre três médias (ANOVA)

ANOVA

levels(univ$sexo)
univ$sexo <- ordered(univ$sexo,
                         levels = c("MACHO", "FEMEA", "imaturo"))
library(dplyr)
group_by(univ, sexo) %>%
  summarise(
    count = n(),
    mean = mean(CP_cm, na.rm = TRUE),
    sd = sd(CP_cm, na.rm = TRUE)
  )
# Conjunto de gráficos
library("ggpubr")
ggboxplot(univ, x = "sexo", y = "CP_cm",
          color = "sexo", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
          order = c("MACHO", "FEMEA", "imaturo"),
          ylab = "CP_cm", xlab = "Sexo")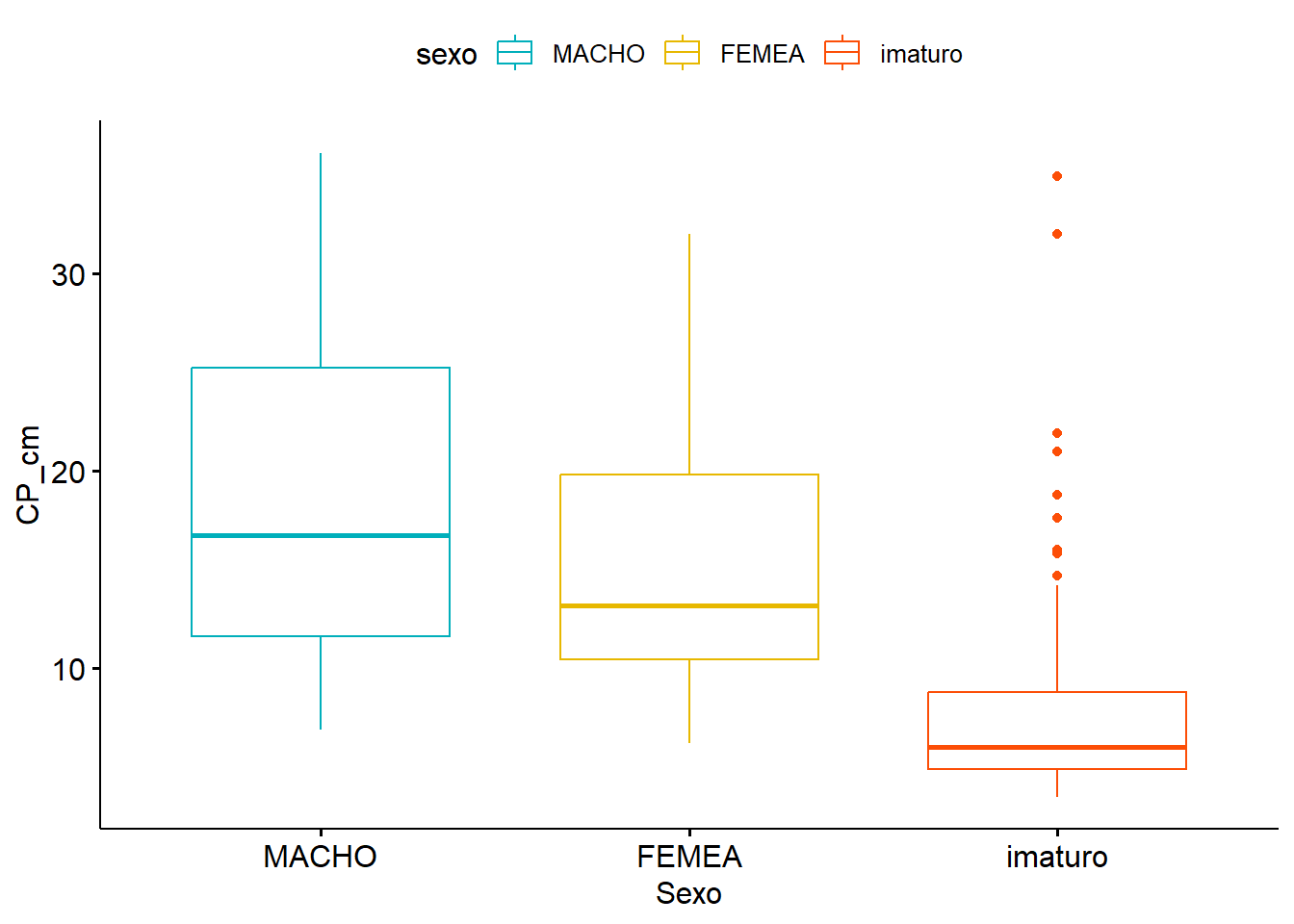

ggline(univ, x = "sexo", y = "CP_cm",
       add = c("mean_se", "jitter"),
       order = c("MACHO", "FEMEA", "imaturo"),
       ylab = "Weight", xlab = "Treatment")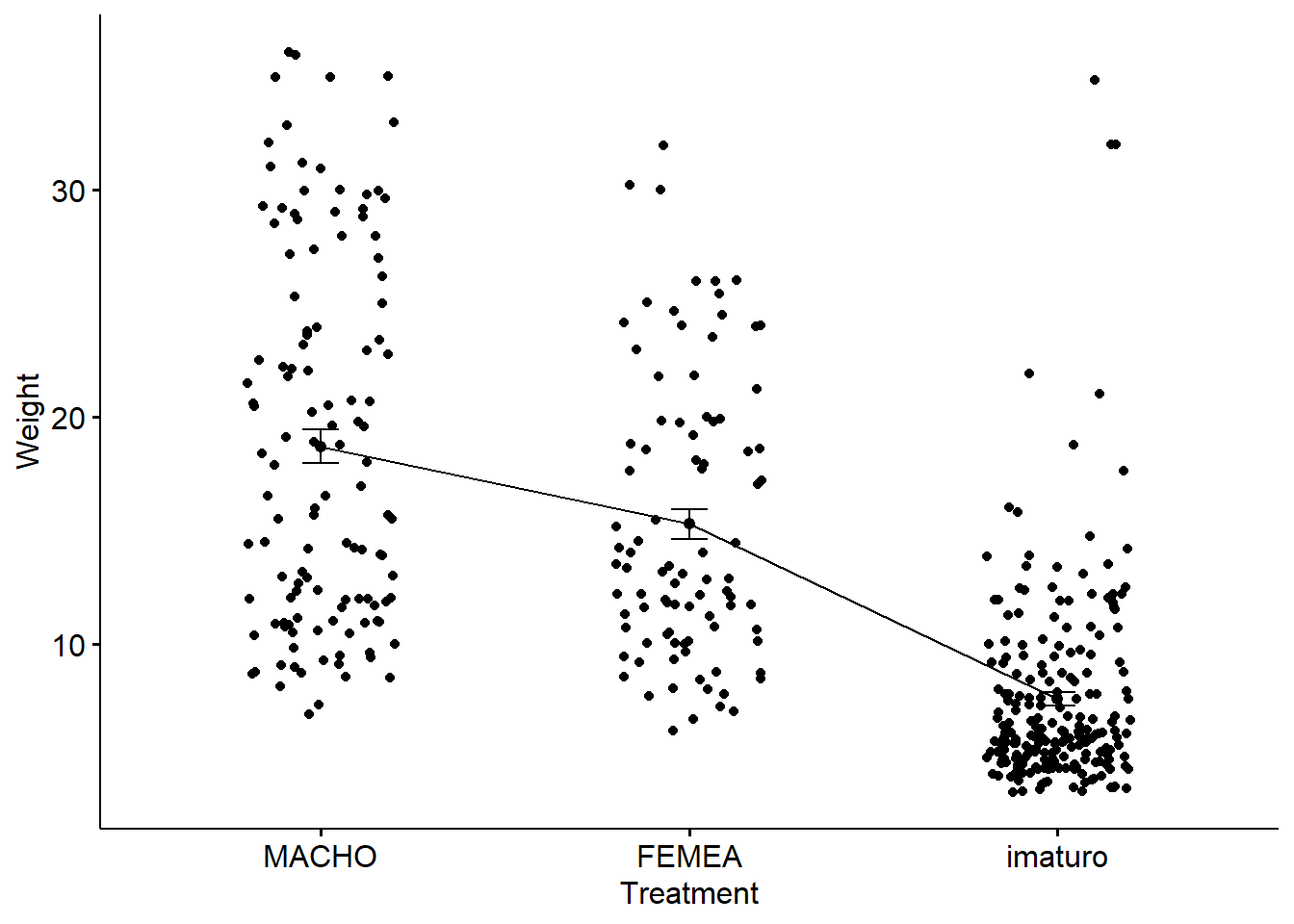

boxplot(CP_cm ~ sexo, data = univ,
        xlab = "Sexo", ylab = "CP_cm",
        frame = FALSE, col = c("#00AFBB", "#E7B800", "#FC4E07"))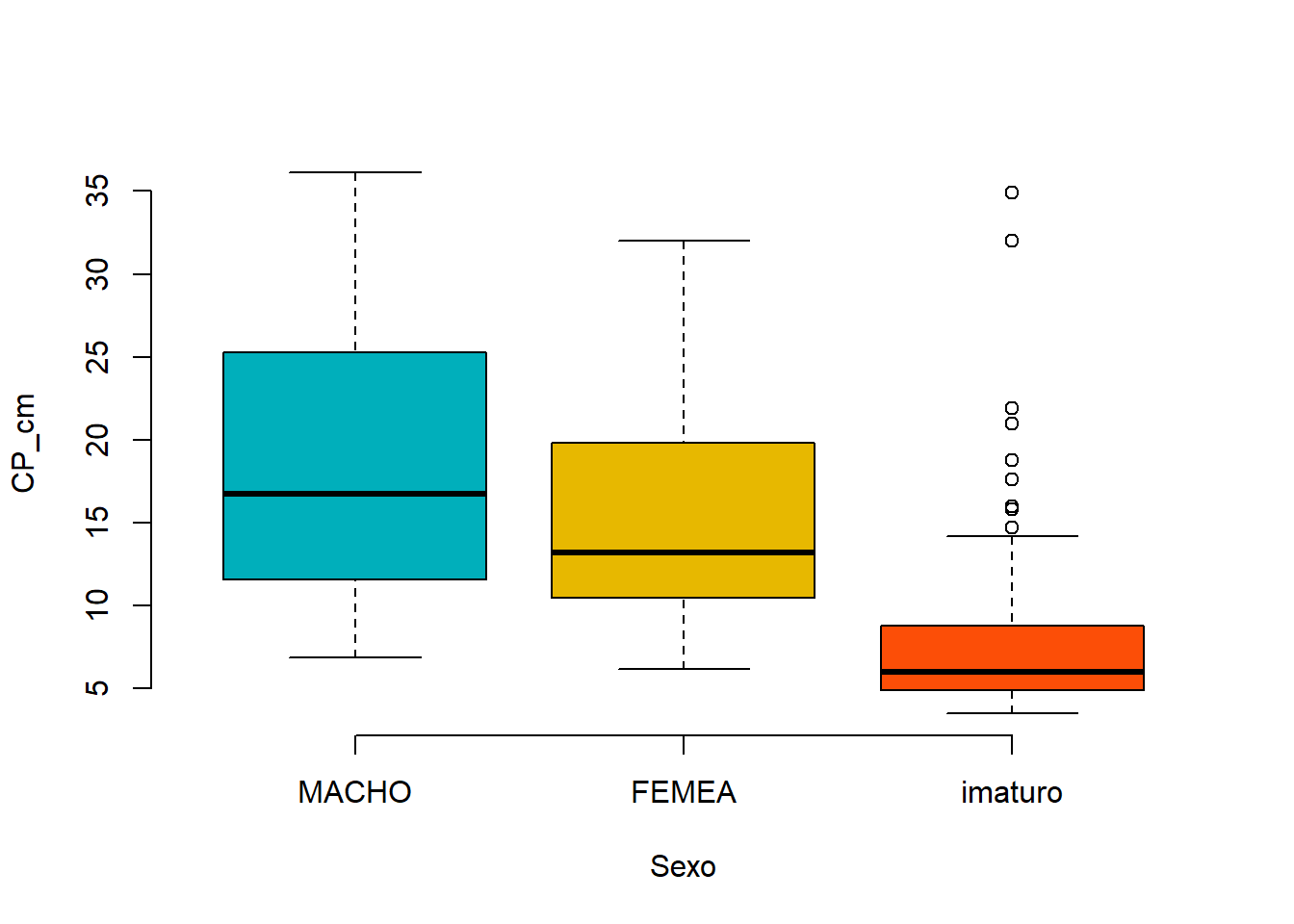

library(gplots)
plotmeans(CP_cm ~ sexo, data = univ, frame = FALSE,
          xlab = "Sexo", ylab = "CP_cm",
          main="Mean Plot with 95% CI")

## Warning in plot.xy(xy.coords(x, y), type = type, ...): "frame" não é um parâmetro
## gráfico

## Warning in axis(1, at = 1:length(means), labels = legends, ...): "frame" não é um
## parâmetro gráfico

## Warning in plot.xy(xy.coords(x, y), type = type, ...): "frame" não é um parâmetro
## gráfico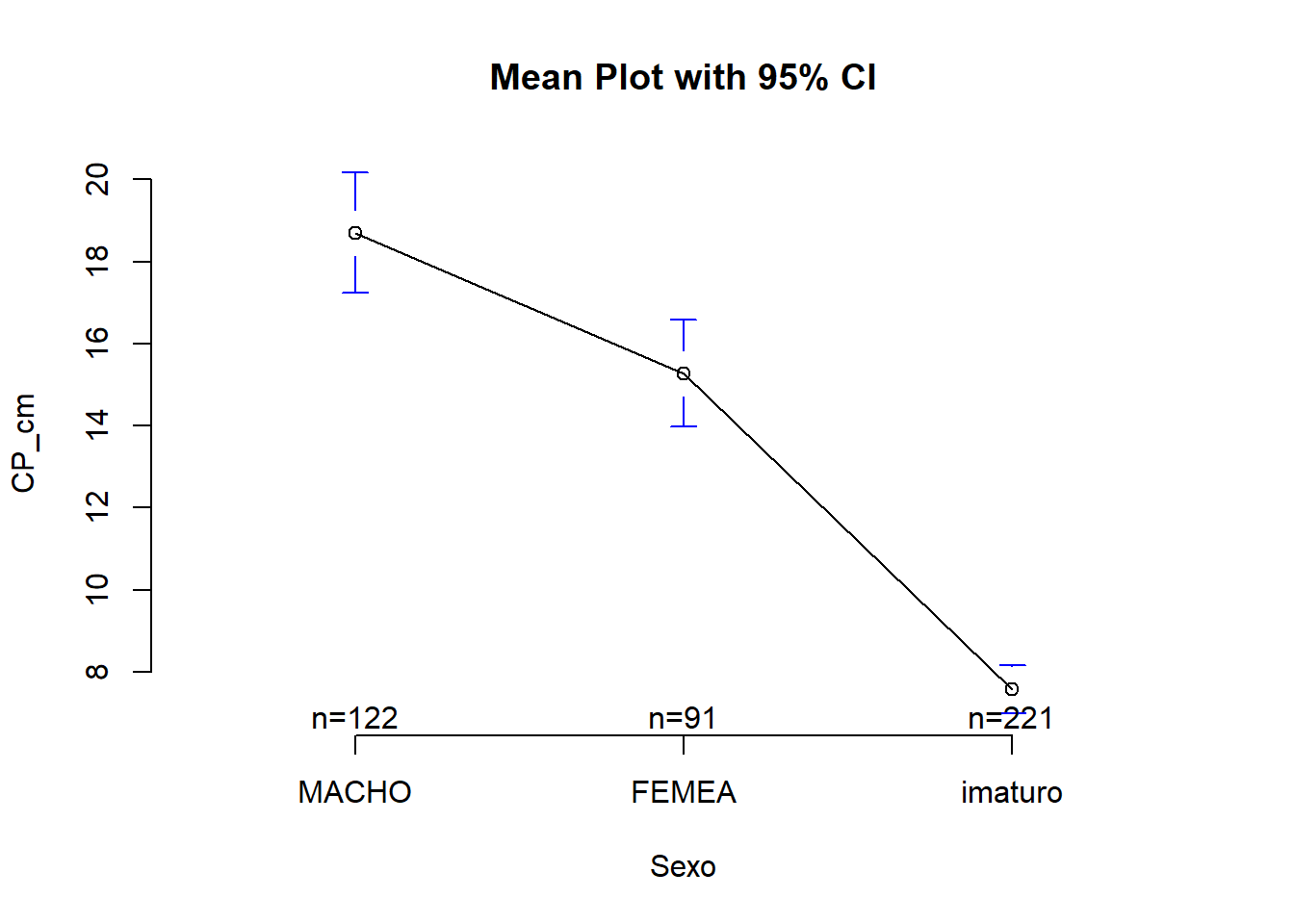

# ANOVA
anova <- aov(CP_cm ~ sexo, data = univ)
summary(anova)
#Interpretação: Um valor de p MENOR que o nível de significância de 0.05 significa que,
#EXISTE diferença significativa entre as três grupos de médias.

# Comparações multiplas
TukeyHSD(anova)
library(multcomp)

## Warning: package 'multcomp' was built under R version 4.3.3

## Carregando pacotes exigidos: mvtnorm

## Carregando pacotes exigidos: survival

## Carregando pacotes exigidos: TH.data

## Warning: package 'TH.data' was built under R version 4.3.3

## Carregando pacotes exigidos: MASS

## 
## Attaching package: 'MASS'

## The following object is masked from 'package:dplyr':
## 
##     select

## 
## Attaching package: 'TH.data'

## The following object is masked from 'package:MASS':
## 
##     geyser

library(multcomp)
summary(glht(anova, linfct = mcp(sexo = "Tukey")))
# T-test entre pares
pairwise.t.test(univ$CP_cm, univ$sexo,
                 p.adjust.method = "BH")
# Pressupostos
## Homogeneidade de variâncias 
plot(anova, 1) #valores numerados são outliers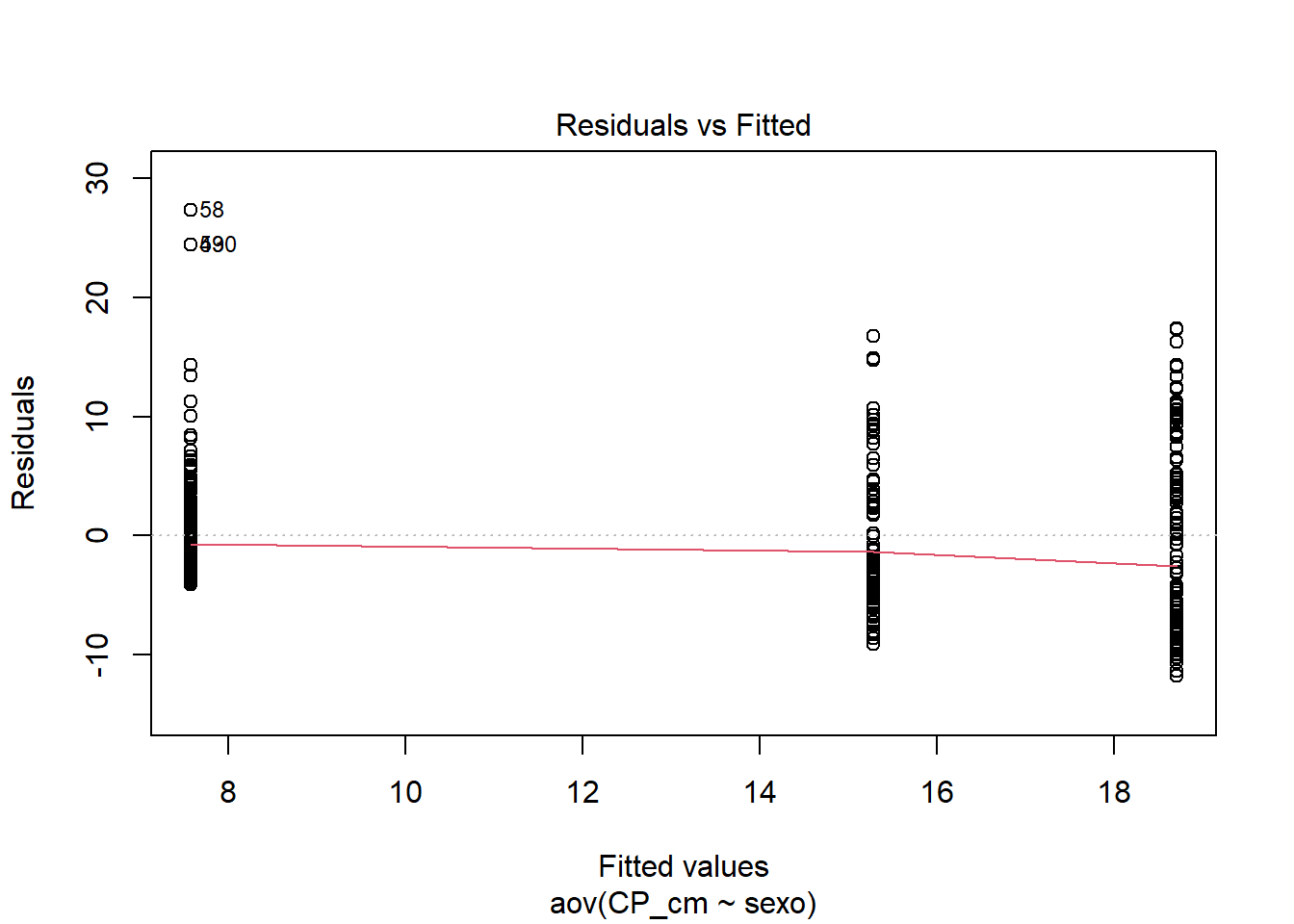

library(car)
leveneTest(CP_cm ~ sexo, data = univ)
# ANOVA sem o pressuposto de equalidade de variâncias
oneway.test(CP_cm ~ sexo, data = univ)
# Testes pareados sem o pressuposto de equalidade de variâncias
pairwise.t.test(univ$CP_cm, univ$sexo,
                p.adjust.method = "BH", pool.sd = FALSE)
# Normalidade pelos resíduos (Q-Q plot)
plot(anova, 2)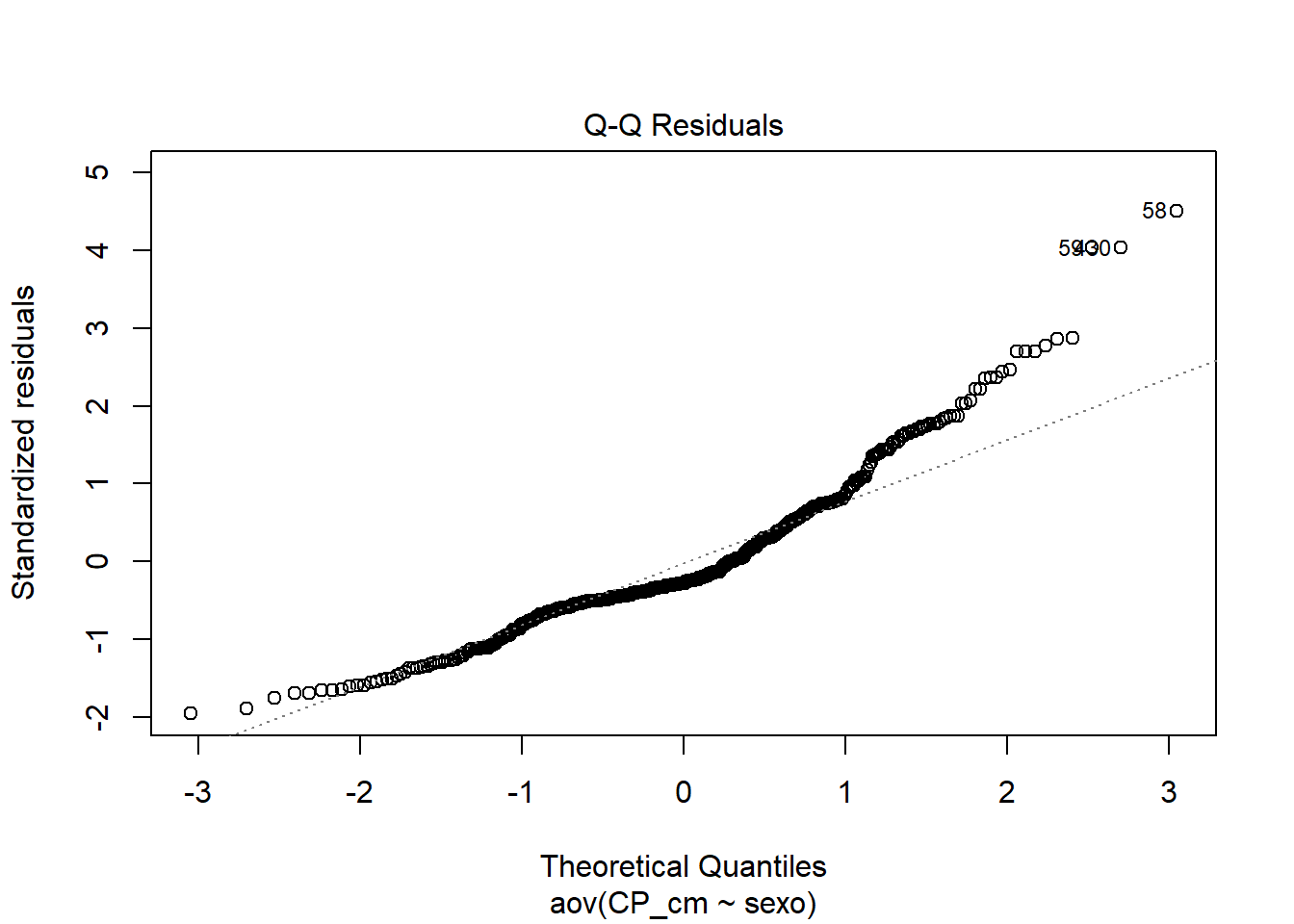

# Extraindo os resíduos e rodando o Shapiro-Wilk neles
anova_residuals <- residuals(object = anova)
shapiro.test(x = anova_residuals)
# ANOVA não-paramétrica (Kruskal-Wallis)
kruskal.test(CP_cm ~ sexo, data = univ)

## [1] "MACHO"   "FEMEA"   "imaturo"
## # A tibble: 3 × 4
##   sexo    count  mean    sd
##   <ord>   <int> <dbl> <dbl>
## 1 MACHO     122 18.7   8.16
## 2 FEMEA      91 15.3   6.25
## 3 imaturo   221  7.57  4.44
##              Df Sum Sq Mean Sq F value Pr(>F)    
## sexo          2  10743    5371   145.5 <2e-16 ***
## Residuals   431  15911      37                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = CP_cm ~ sexo, data = univ)
## 
## $sexo
##                     diff        lwr       upr     p adj
## FEMEA-MACHO    -3.424716  -5.403982 -1.445451 0.0001655
## imaturo-MACHO -11.127884 -12.739590 -9.516177 0.0000000
## imaturo-FEMEA  -7.703167  -9.482984 -5.923350 0.0000000
## 
## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: aov(formula = CP_cm ~ sexo, data = univ)
## 
## Linear Hypotheses:
##                      Estimate Std. Error t value Pr(>|t|)    
## FEMEA - MACHO == 0    -3.4247     0.8416  -4.069 0.000161 ***
## imaturo - MACHO == 0 -11.1279     0.6853 -16.238  < 1e-04 ***
## imaturo - FEMEA == 0  -7.7032     0.7568 -10.179  < 1e-04 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)
## 
## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  univ$CP_cm and univ$sexo 
## 
##         MACHO   FEMEA  
## FEMEA   5.6e-05 -      
## imaturo < 2e-16 < 2e-16
## 
## P value adjustment method: BH 
## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value    Pr(>F)    
## group   2  45.138 < 2.2e-16 ***
##       431                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##  One-way analysis of means (not assuming equal variances)
## 
## data:  CP_cm and sexo
## F = 134.26, num df = 2.00, denom df = 180.92, p-value < 2.2e-16
## 
## 
##  Pairwise comparisons using t tests with non-pooled SD 
## 
## data:  univ$CP_cm and univ$sexo 
## 
##         MACHO   FEMEA  
## FEMEA   0.00063 -      
## imaturo < 2e-16 < 2e-16
## 
## P value adjustment method: BH 
## 
##  Shapiro-Wilk normality test
## 
## data:  anova_residuals
## W = 0.93021, p-value = 2.35e-13
## 
## 
##  Kruskal-Wallis rank sum test
## 
## data:  CP_cm by sexo
## Kruskal-Wallis chi-squared = 217.39, df = 2, p-value < 2.2e-16

10.7.4 Teste entre três médias e dois fatores (Two-Way ANOVA)

Two-way ANOVA

univ$sexo <- factor(univ$sexo,
                  labels = c("MACHO", "FEMEA", "imaturo"))
univ$periodo <- factor(univ$periodo,
                  labels = c("chuvoso", "seco"))
str(univ)
table(univ$sexo,univ$periodo)

library("ggpubr")
ggboxplot(univ, x = "sexo", y = "CP_cm", color = "periodo",
          palette = c("#00AFBB", "#E7B800"))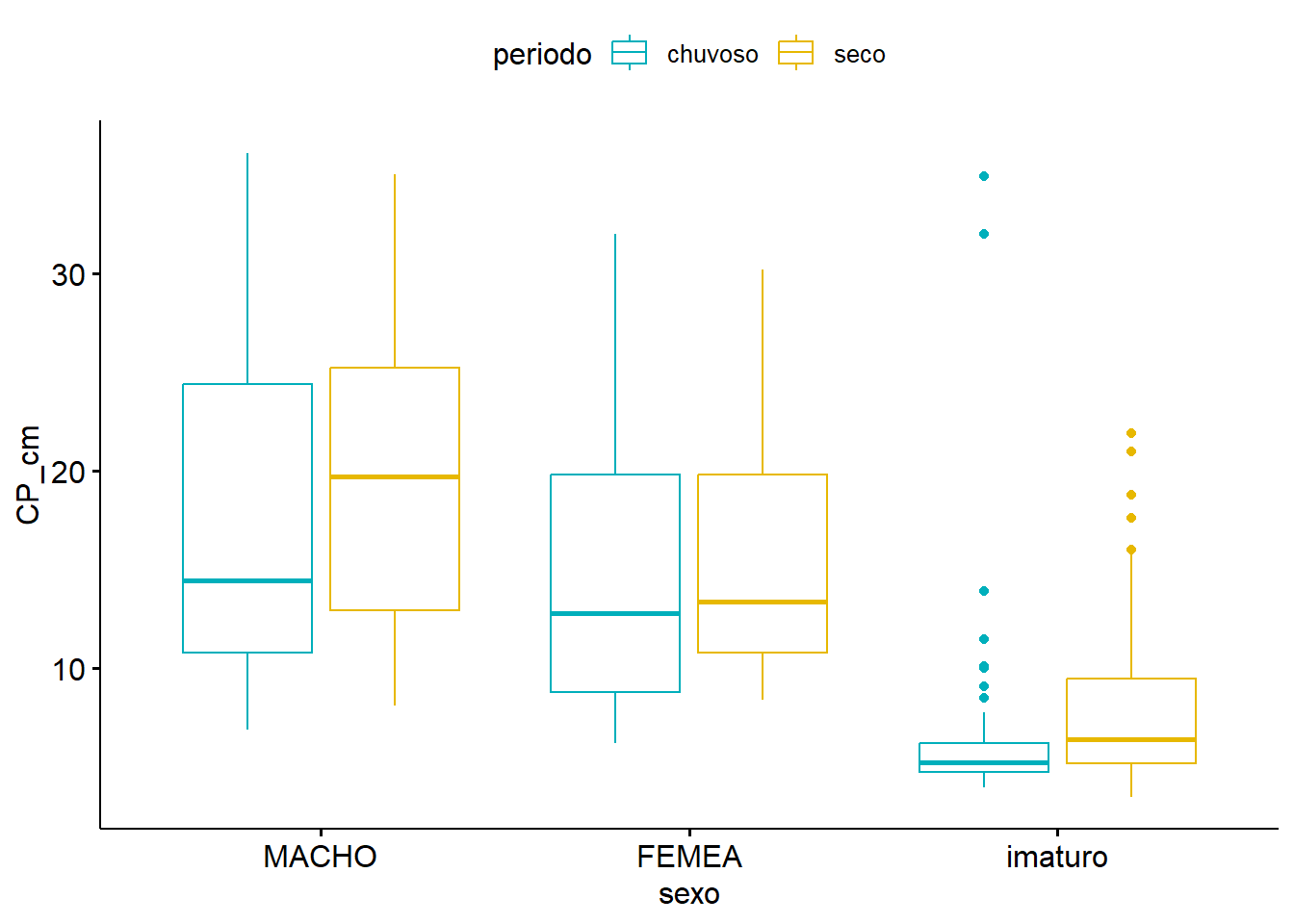

ggline(univ, x = "sexo", y = "CP_cm", color = "periodo",
       add = c("mean_se", "dotplot"),
       palette = c("#00AFBB", "#E7B800"))

## Bin width defaults to 1/30 of the range of the data. Pick better value with
## `binwidth`.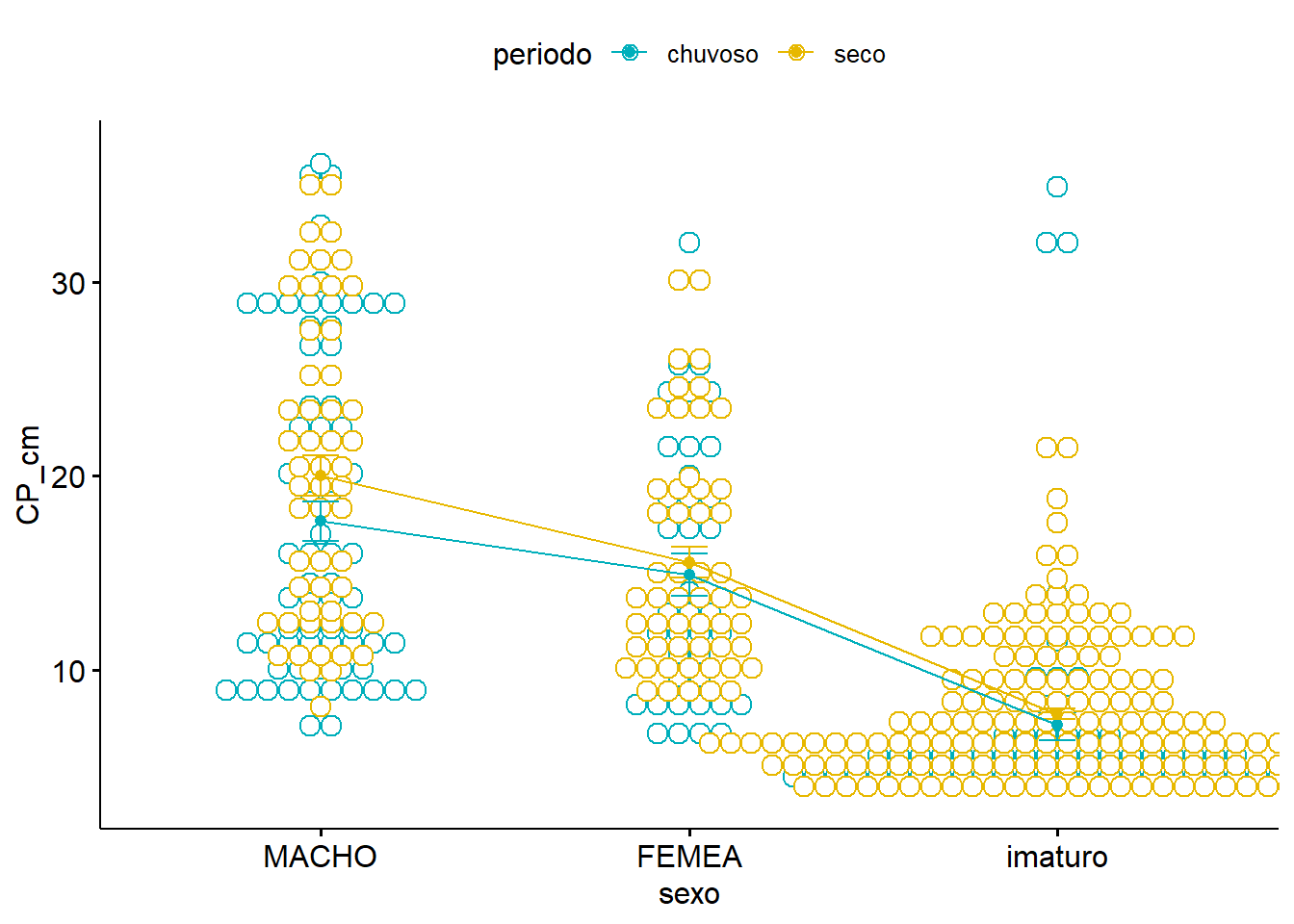

boxplot(CP_cm ~ periodo * sexo, data=univ, frame = FALSE,
        col = c("#00AFBB", "#E7B800"), ylab="CP_cm")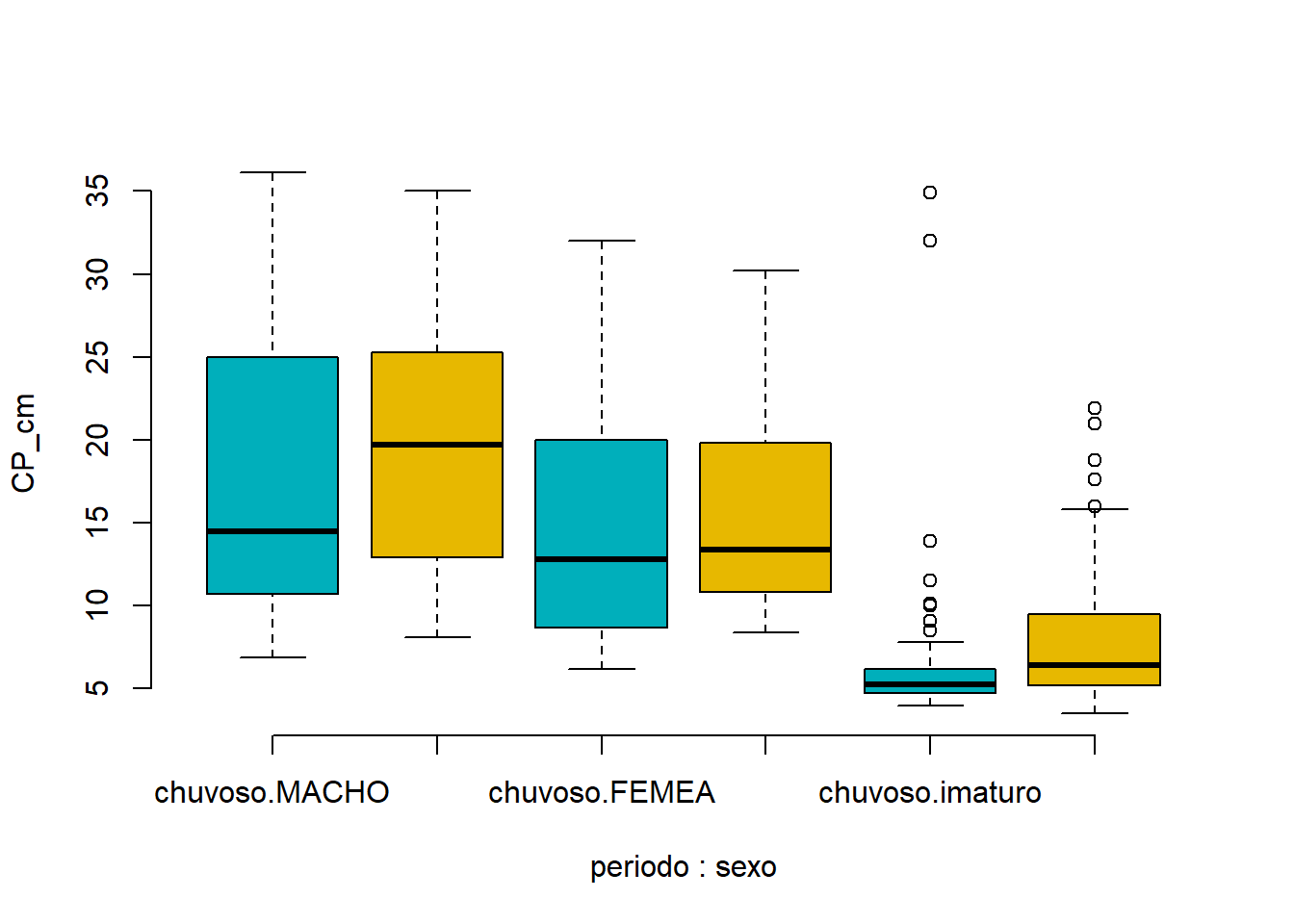

# Gráfico das interações
interaction.plot(x.factor = univ$sexo, trace.factor = univ$periodo,
                 response = univ$CP_cm, fun = mean,
                 type = "b", legend = TRUE,
                 xlab = "Sexo", ylab="CP_cm",
                 pch=c(1,19), col = c("#00AFBB", "#E7B800"))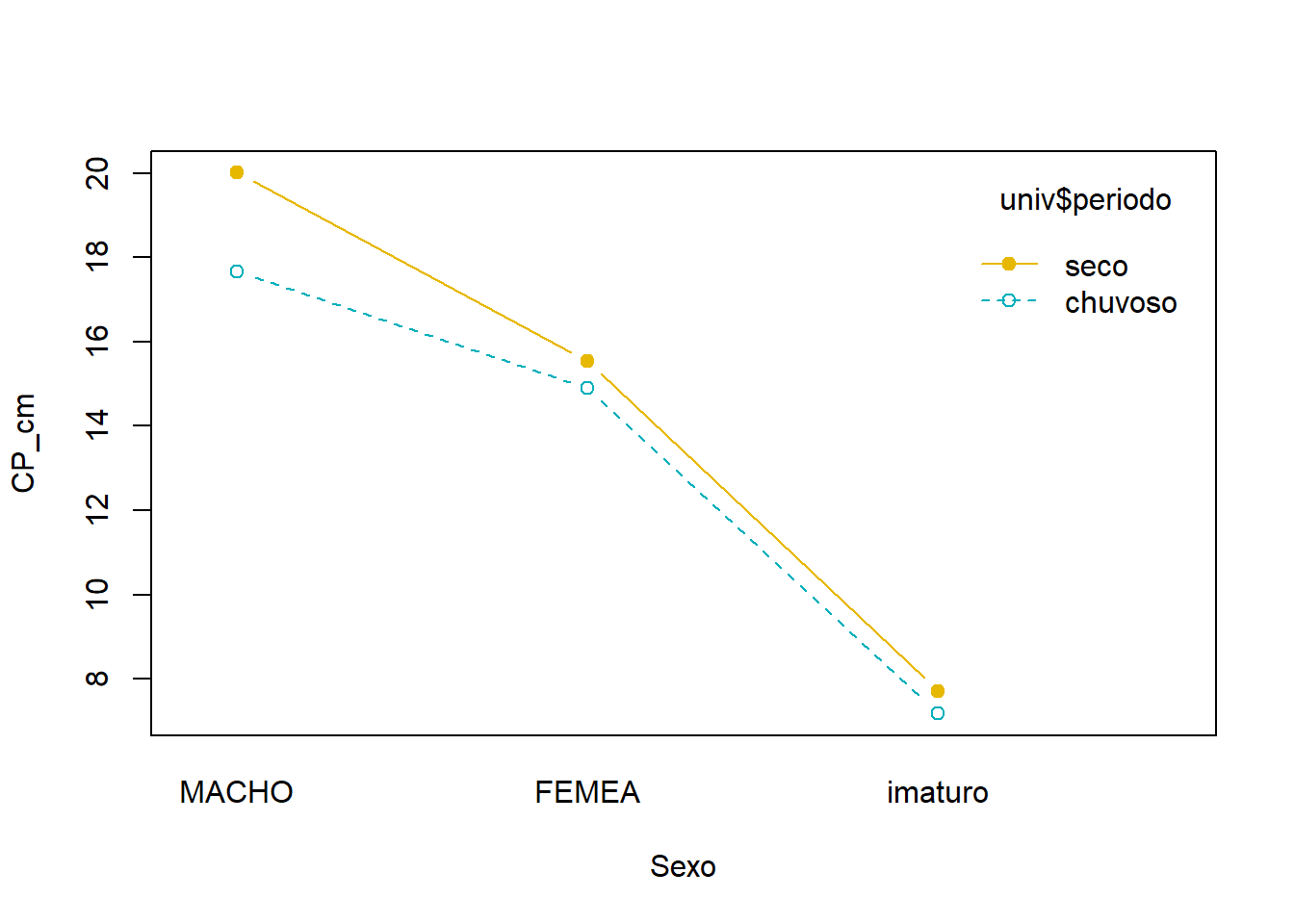

# ANOVA Two-way
anova2 <- aov(CP_cm ~ periodo + sexo, data = univ)
summary(anova2)

#The above-fitted model is not referred to as an additive model.
#It is presumptively assumed that the two-factor variables are unrelated.
#Replace the plus symbol (+) with an asterisk (*) if you think
#these two variables will interact to create a synergistic effect.

anova3 <- aov(CP_cm ~ periodo * sexo, data = univ)
summary(anova3)

require("dplyr")
group_by(univ, periodo, sexo) %>%
  summarise(
    count = n(),
    mean = mean(CP_cm, na.rm = TRUE),
    sd = sd(CP_cm, na.rm = TRUE)
  )

# Comparações múltiplas pares: Tukey
TukeyHSD(anova3, which = "sexo")

# Comparações múltiplas pares
library(multcomp)
summary(glht(anova2, linfct = mcp(sexo = "Tukey")))

# T-test entre pares
pairwise.t.test(univ$CP_cm, univ$sexo,
                p.adjust.method = "BH")

# Pressupostos
## Homogeneidade de variâncias
plot(anova3, 1)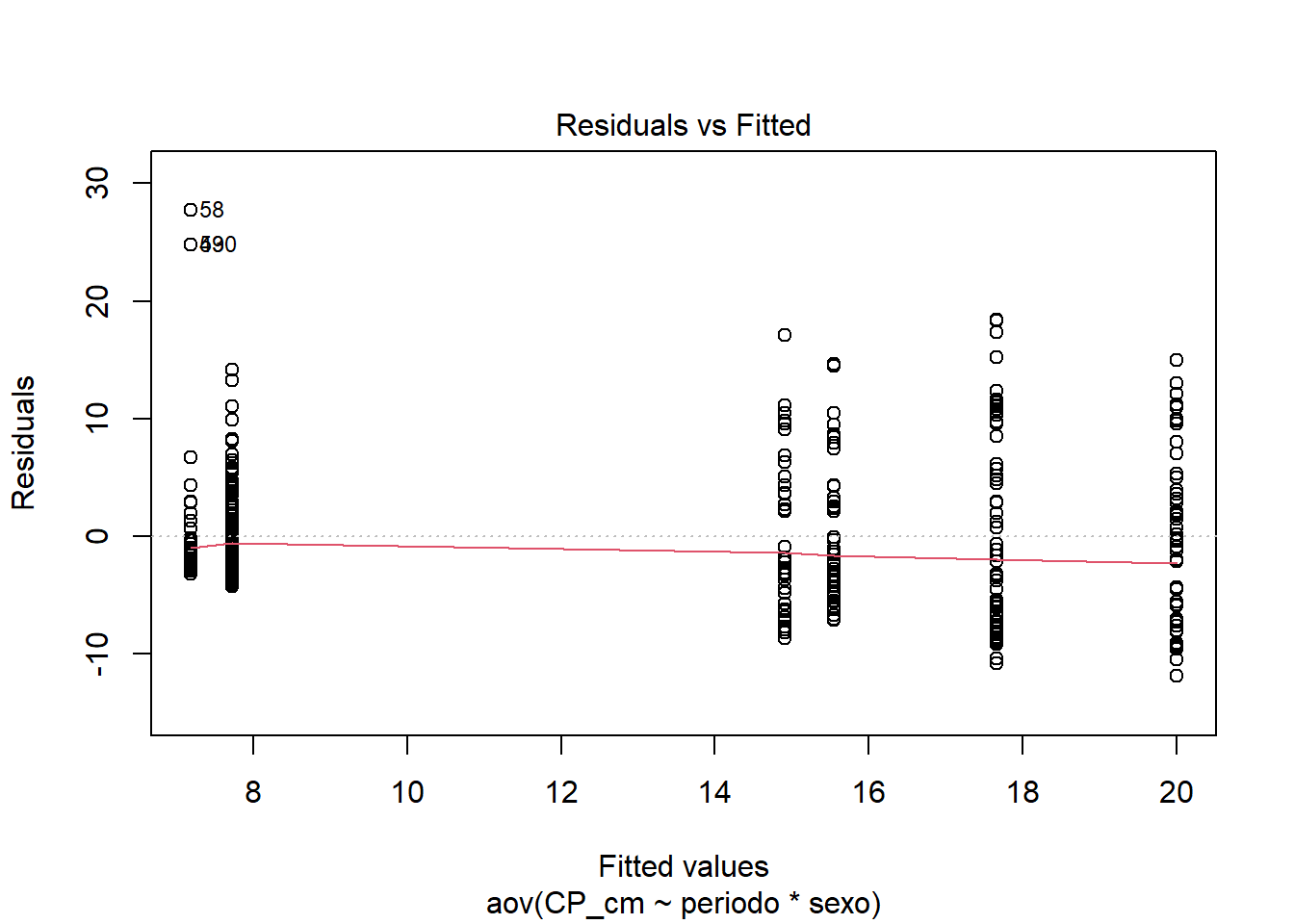

library(car)
leveneTest(CP_cm ~ periodo*sexo, data = univ)
# Normalidade pelos resíduos (Q-Q plot)
plot(anova3, 2)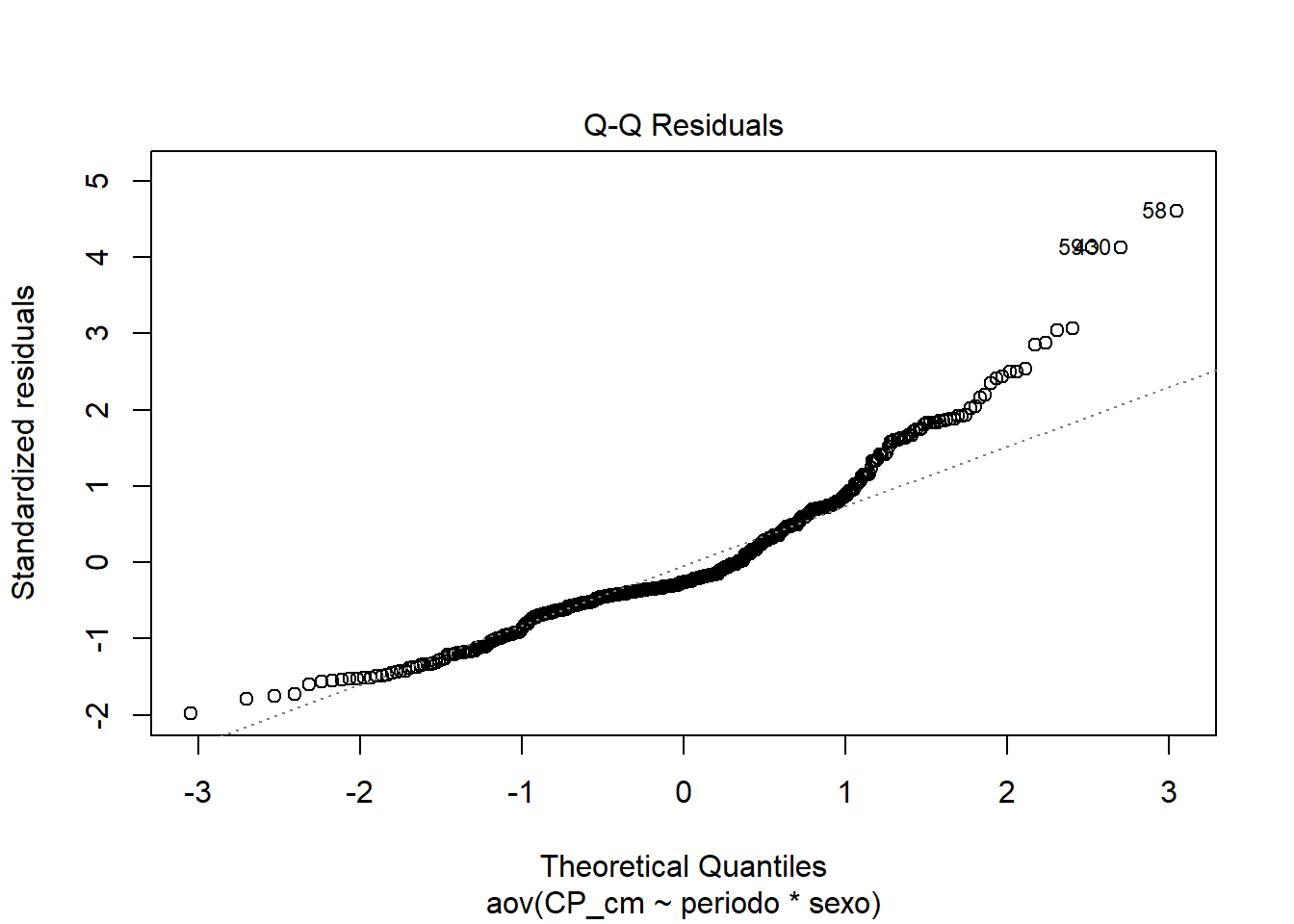

# Extraindo os resíduos e rodando o Shapiro-Wilk neles
anova3_residuals <- residuals(object = anova3)
shapiro.test(x = anova3_residuals )

# ANOVA para desenhos não balanceados
library(car)
nb_anova <- aov(CP_cm ~ periodo * sexo, data = univ)
Anova(nb_anova, type = "III")

## 'data.frame':    434 obs. of  23 variables:
##  $ n.=.434 : chr  "TU001" "TU002" "TU003" "TU004" ...
##  $ CT_cm   : num  32.4 33.4 27.3 13.2 14.3 22.7 23.2 13.5 24.6 19.4 ...
##  $ PT_g    : num  468.8 520 301.5 28.2 38.9 ...
##  $ CP_cm   : num  27.2 28.8 23.8 11 11.9 20.5 19.2 11.5 20.5 16 ...
##  $ Ctubo_cm: num  39.8 14.3 13 16.5 15.5 24.2 25 17.5 25.7 18.3 ...
##  $ PC_g    : num  458.9 507.4 283.4 27.7 37.7 ...
##  $ %PT     : num  2.11 2.42 6 1.77 3.08 ...
##  $ Pest_g  : num  3.9 5.9 15.5 0.3 0.8 9.9 6.8 4.1 2.5 0.7 ...
##  $ Cest_cm : num  7.7 10 10.2 4.3 4.5 6.4 7.5 6.8 7.6 5.1 ...
##  $ gr_est  : chr  "I" "I" "III" "I" ...
##  $ ir_est  : num  0.832 1.135 5.141 1.064 2.057 ...
##  $ Pint_g  : num  4.8 5.3 2.4 0.1 0.3 2.7 3.3 0.4 2 1.4 ...
##  $ Cint_cm : num  38.3 13.3 12 16 15 23.7 24.5 17 25.3 17.7 ...
##  $ gr_int  : chr  "II" "II" "II" "II" ...
##  $ ir_int  : num  1.024 1.019 0.796 0.355 0.771 ...
##  $ Pgon_g  : num  1.2 1.4 0.2 0.1 0.1 0.4 13.8 0.1 0.1 0.1 ...
##  $ Cgon_cm : chr  "7" "6.5" "7.7" "5" ...
##  $ emg     : chr  "IMATURO" "MADURO" "EM MATURACAO" "IMATURO" ...
##  $ ig      : num  0.256 0.2692 0.0663 0.3546 0.2571 ...
##  $ mes     : chr  "ago" "ago" "ago" "ago" ...
##  $ periodo : Factor w/ 2 levels "chuvoso","seco": 1 1 1 1 1 1 1 1 1 1 ...
##  $ estação : chr  "inverno" "inverno" "inverno" "inverno" ...
##  $ sexo    : Ord.factor w/ 3 levels "MACHO"<"FEMEA"<..: 1 1 1 1 1 1 2 3 1 1 ...
##          
##           chuvoso seco
##   MACHO        68   54
##   FEMEA        38   53
##   imaturo      60  161
##              Df Sum Sq Mean Sq F value Pr(>F)    
## periodo       1    231     231    6.29 0.0125 *  
## sexo          2  10634    5317  144.80 <2e-16 ***
## Residuals   430  15789      37                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##               Df Sum Sq Mean Sq F value Pr(>F)    
## periodo        1    231     231   6.287 0.0125 *  
## sexo           2  10634    5317 144.714 <2e-16 ***
## periodo:sexo   2     64      32   0.874 0.4180    
## Residuals    428  15725      37                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## # A tibble: 6 × 5
## # Groups:   periodo [2]
##   periodo sexo    count  mean    sd
##   <fct>   <ord>   <int> <dbl> <dbl>
## 1 chuvoso MACHO      68 17.7   8.41
## 2 chuvoso FEMEA      38 14.9   6.78
## 3 chuvoso imaturo    60  7.18  6.25
## 4 seco    MACHO      54 20.0   7.70
## 5 seco    FEMEA      53 15.5   5.90
## 6 seco    imaturo   161  7.72  3.56
##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = CP_cm ~ periodo * sexo, data = univ)
## 
## $sexo
##                     diff        lwr       upr     p adj
## FEMEA-MACHO    -3.214875  -5.189460 -1.240291 0.0004334
## imaturo-MACHO -10.698753 -12.306648 -9.090859 0.0000000
## imaturo-FEMEA  -7.483878  -9.259486 -5.708270 0.0000000
## 
## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: aov(formula = CP_cm ~ periodo + sexo, data = univ)
## 
## Linear Hypotheses:
##                      Estimate Std. Error t value Pr(>|t|)    
## FEMEA - MACHO == 0    -3.5823     0.8438  -4.246  7.4e-05 ***
## imaturo - MACHO == 0 -11.4502     0.7060 -16.219  < 1e-05 ***
## imaturo - FEMEA == 0  -7.8679     0.7601 -10.351  < 1e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)
## 
## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  univ$CP_cm and univ$sexo 
## 
##         MACHO   FEMEA  
## FEMEA   5.6e-05 -      
## imaturo < 2e-16 < 2e-16
## 
## P value adjustment method: BH 
## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value   Pr(>F)    
## group   5  16.044 1.67e-14 ***
##       428                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##  Shapiro-Wilk normality test
## 
## data:  anova3_residuals
## W = 0.92359, p-value = 4.653e-14
## 
## Anova Table (Type III tests)
## 
## Response: CP_cm
##               Sum Sq  Df  F value Pr(>F)    
## (Intercept)  27390.0   1 745.5129 <2e-16 ***
## periodo        122.3   1   3.3281 0.0688 .  
## sexo          3641.5   2  49.5584 <2e-16 ***
## periodo:sexo    64.2   2   0.8741 0.4180    
## Residuals    15724.6 428                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

10.8 Correlação e regressão simples

Correlação e regressão

df<-data.frame(univ$CT_cm, univ$CP_cm, univ$PT_g)
plot(df[,1:3])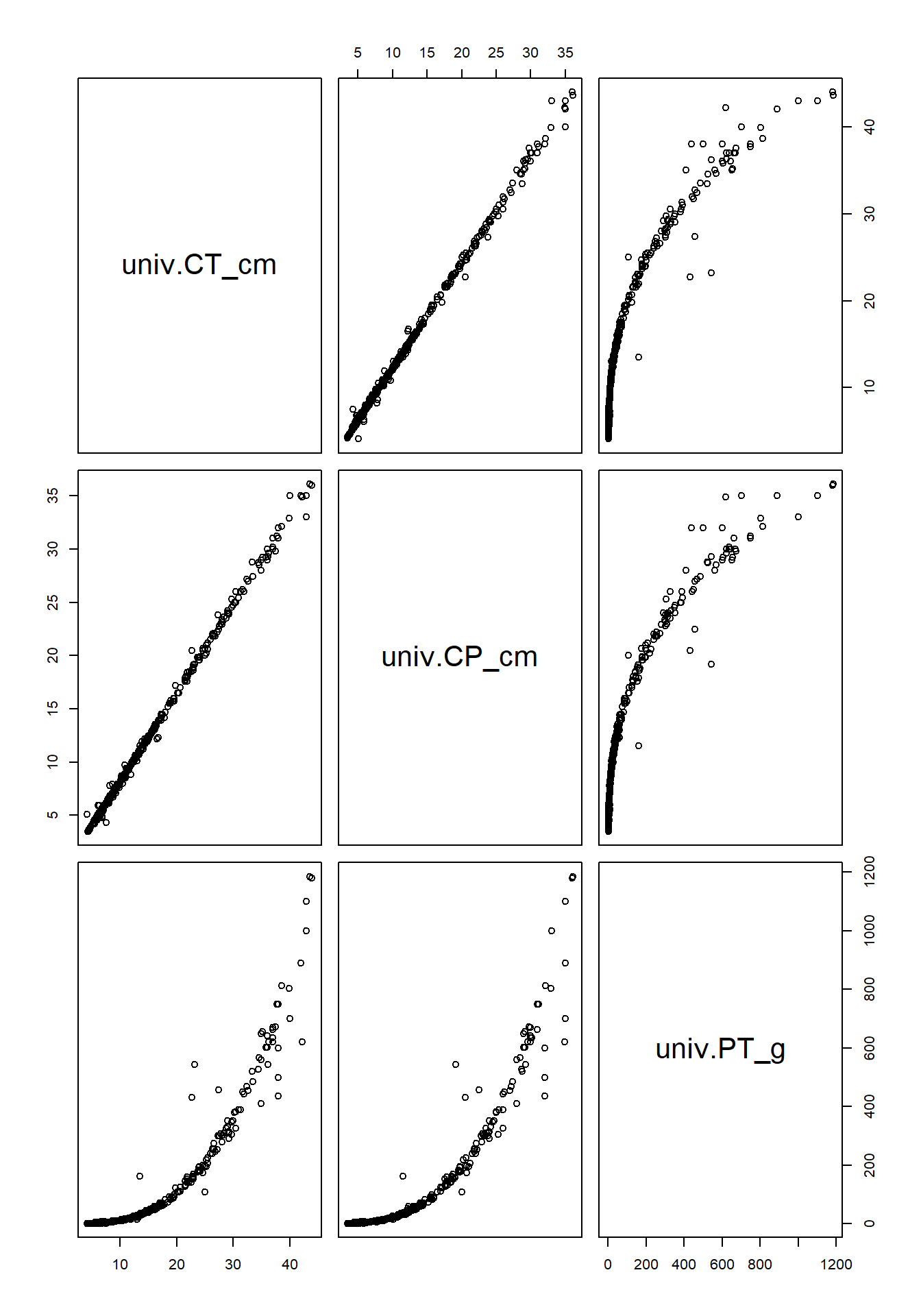

cor(df,method="pearson")
cor(df[,1:3], method="spearman")
cor.test(univ$CT_cm, univ$CP_cm, method="pearson")
cor.test(univ$CT_cm, univ$CP_cm, method="spearman")

## Warning in cor.test.default(univ$CT_cm, univ$CP_cm, method = "spearman"):
## Impossível calcular o valor exato de p com empates

m1 <- lm(univ$CT_cm ~ univ$CP_cm, data=univ)
summary(m1)
par(mfrow=c(2,2))
plot(m1)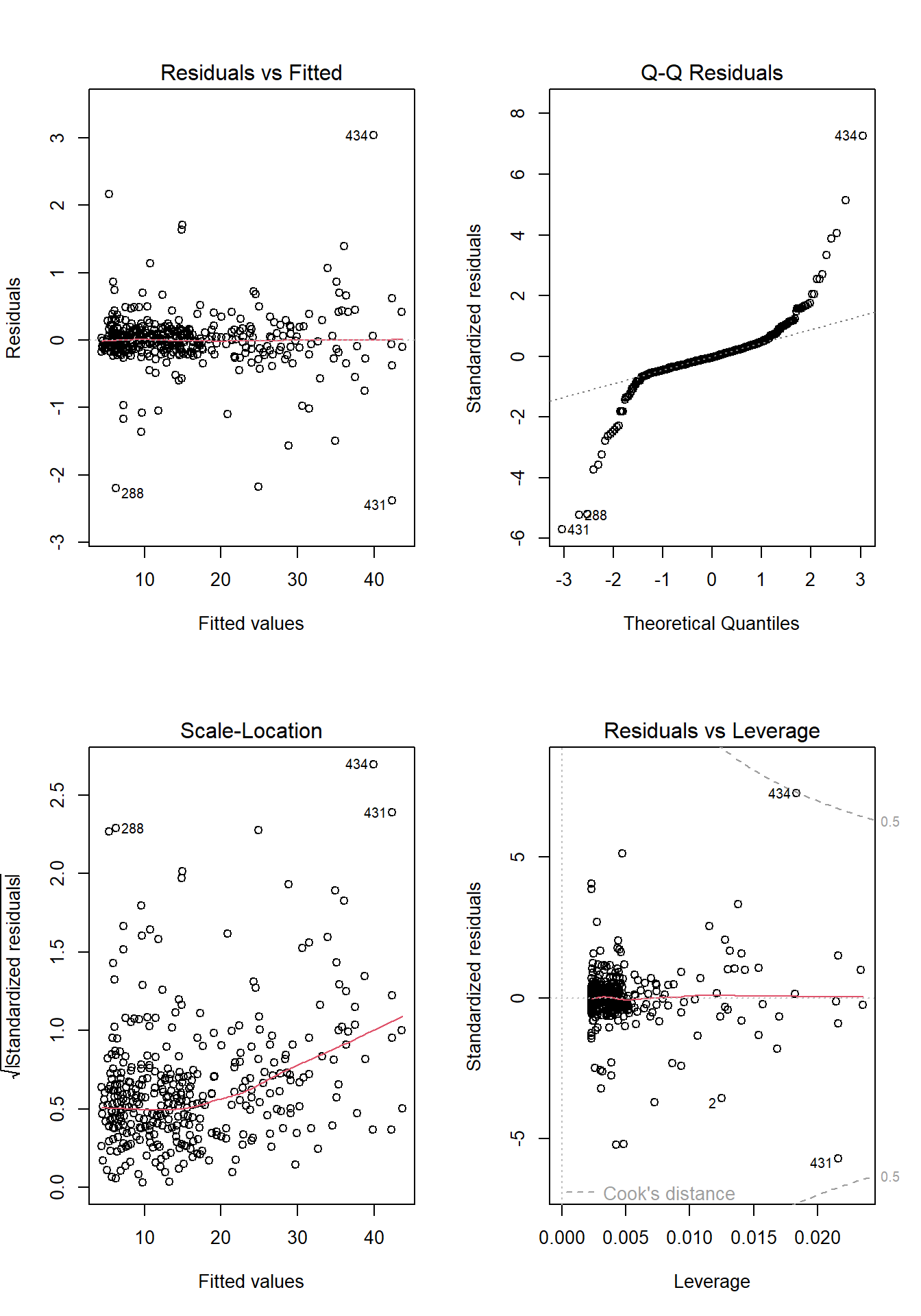

par(mfrow=c(1,1))
univ$CT_cm <- log(univ$CT_cm)
plot(univ$CT_cm ~ CP_cm, univ)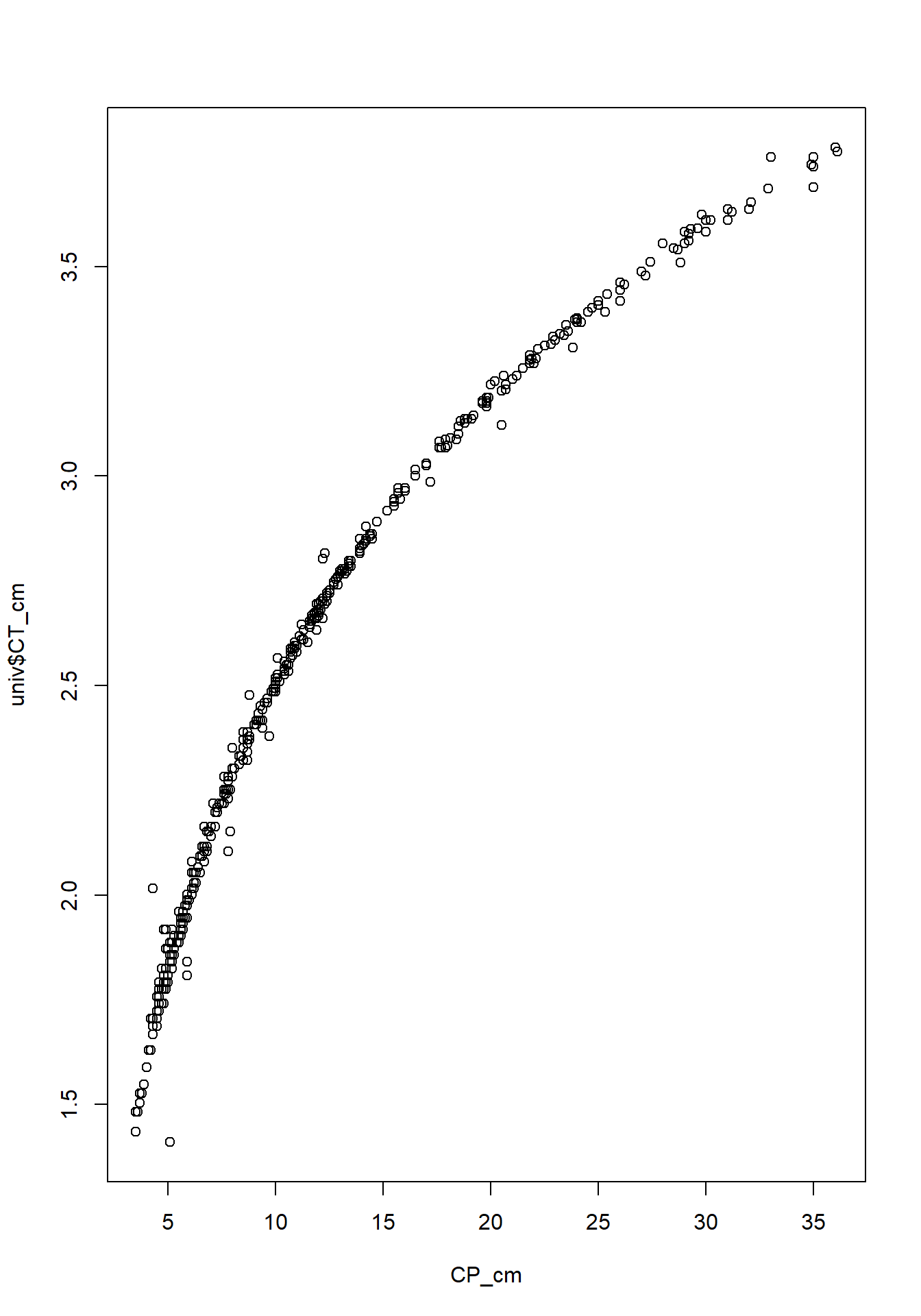

anova(m1) 
library(car)
Anova(m1)
Anova(m1, white.adjust=TRUE)

## Coefficient covariances computed by hccm()

univ <- univ[univ$CT_cm!=max(univ$CT_cm),]

##            univ.CT_cm univ.CP_cm univ.PT_g
## univ.CT_cm  1.0000000  0.9990120 0.9057485
## univ.CP_cm  0.9990120  1.0000000 0.9039503
## univ.PT_g   0.9057485  0.9039503 1.0000000
##            univ.CT_cm univ.CP_cm univ.PT_g
## univ.CT_cm  1.0000000  0.9976789 0.9924823
## univ.CP_cm  0.9976789  1.0000000 0.9934510
## univ.PT_g   0.9924823  0.9934510 1.0000000
## 
##  Pearson's product-moment correlation
## 
## data:  univ$CT_cm and univ$CP_cm
## t = 467.22, df = 432, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.9988068 0.9991819
## sample estimates:
##      cor 
## 0.999012 
## 
## 
##  Spearman's rank correlation rho
## 
## data:  univ$CT_cm and univ$CP_cm
## S = 31624, p-value < 2.2e-16
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.9976789 
## 
## 
## Call:
## lm(formula = univ$CT_cm ~ univ$CP_cm, data = univ)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.3777 -0.1281 -0.0147  0.1260  3.0354 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.147883   0.037700   3.923 0.000102 ***
## univ$CP_cm  1.206566   0.002582 467.221  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4216 on 432 degrees of freedom
## Multiple R-squared:  0.998,  Adjusted R-squared:  0.998 
## F-statistic: 2.183e+05 on 1 and 432 DF,  p-value: < 2.2e-16
## 
## Analysis of Variance Table
## 
## Response: univ$CT_cm
##             Df Sum Sq Mean Sq F value    Pr(>F)    
## univ$CP_cm   1  38802   38802  218295 < 2.2e-16 ***
## Residuals  432     77       0                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Anova Table (Type II tests)
## 
## Response: univ$CT_cm
##            Sum Sq  Df F value    Pr(>F)    
## univ$CP_cm  38802   1  218295 < 2.2e-16 ***
## Residuals      77 432                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Analysis of Deviance Table (Type II tests)
## 
## Response: univ$CT_cm
##             Df     F    Pr(>F)    
## univ$CP_cm   1 75315 < 2.2e-16 ***
## Residuals  432                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Apêndices

Sites consultados

Script limpo

Aqui apresento o scrip na íntegra sem os textos ou outros comentários. Você pode copiar e colar no R para executa-lo. Lembre de remover os # ou ## caso necessite executar essas linhas.

Referências

Bibliografia

Bradstock, R. A., M. G. Tozer, and D. A. Keith. 1997. “Effects of High Frequency Fire on Floristic Composition and Abundance in a Fire-Prone Heathland Near Sydney.” Journal Article. Australian Journal of Botany 45: 641–55.

———. 2017. R: A Language and Environment for Statistical Computing. Book. Austria: R Foundation for Statistical Computing. https://www.r-project.org/.

Team, R Studio. 2022. RStudio: Integrated Development Environment for r. Book. Boston, MA: RStudio, PBC. https://posit.co/products/open-source/rstudio/.