7 R Modulo 12
Apresentação
A Análise de Espécies Indicadoras (ISA) foi originalmente desenvolvida por Dufrene and Legendre (1997) como uma técnica para identificar espécies que estão fortemente associadas a um grupo específico. Uma motivação para o desenvolvimento dessa técnica foi fornecer uma ferramenta para determinar quantos grupos focar em uma análise de agrupamento.
Antes do desenvolvimento do ISA, a principal técnica estatística para identificar espécies associadas a grupos era a Análise de Espécies Indicadoras de Duas Vias ou Two-Way INdicator SPecies ANalysis(TWINSPAN) McCune and Grace (2002). O TWINSPAN é uma abordagem divisiva - parte do pressuposto de que tudo está em um grupo e depois procura maneiras de dividir esse grupo. No entanto, vários aspectos do TWINSPAN limitam muito sua utilidade:
- Não pode ser usado para grupos predefinidos.
- Apresenta desempenho ruim com mais de um gradiente.
- Envolve detalhes analíticos complexos.
- Baseia-se na Análise de Correspondência (CA) e, portanto, em distâncias qui-quadrado.
- Requer “pseudoespécies” para converter dados de abundância quantitativa em dados de presença/ausência qualitativos (colocando abundâncias em classes e considerando cada classe equivalente a uma pseudoespécie).
7.1 Organização básica
dev.off() #apaga os graficos, se houver algum
rm(list=ls(all=TRUE)) #limpa a memória
cat("\014") #limpa o consoleInstalando os pacotes necessários para esse módulo
install.packages("indicspecies")
install.packages("gt")Agora vamos definir o diretório de trabalho. Esse código é usado para obter e definir o diretório de trabalho atual no R. O comando getwd() retorna o caminho do diretório onde o R está lendo e salvando arquivos. O comando setwd() muda esse diretório de trabalho para o caminho especificado entre aspas. No seu caso, você deve ajustar o caminho para o seu próprio diretório de trabalho. Lembre de usar a barra “/” entre os diretórios. E não a contra-barra “\”.
Definindo o diretório de trabalho e installando os pacotes necessários:
getwd()
setwd("C:/Seu/Diretório/De/Trabalho")7.1.1 Sobre os dados do PPBio
A planilha ppbio contém os dados de abundância de espécies em diferentes unidades amostrais (UA’s). A base teórica dos dados do PPBio para o presente estudo pode ser vista em Base Teórica. Leia antes de prosseguir.
7.1.2 A planilha PPBio Grupos
Para esse módulo também usaremos a planilha ppbio06-grupos. Esta é uma tabela de agrupamentos guardada no arquivo ppbio06-grupos.xlsx, que traz os agrupamentos das UA’s definidos a priori no delineamento amostral do PPBio (veja a figura 7.1. Essa tabela contem as ~26 localidades (UAs) em períodos diferentes (linhas) x ~5 tipos de grupos aos quais cada UA foi atribuida (colunas) (dados publicados por Medeiros, Silva, and Ramos (2008))(veja o quadro da figura 7.2). As bases teóricas dos dados do PPBio para o presente estudo pode ser vista em Base Teórica. Leia antes de prosseguir.
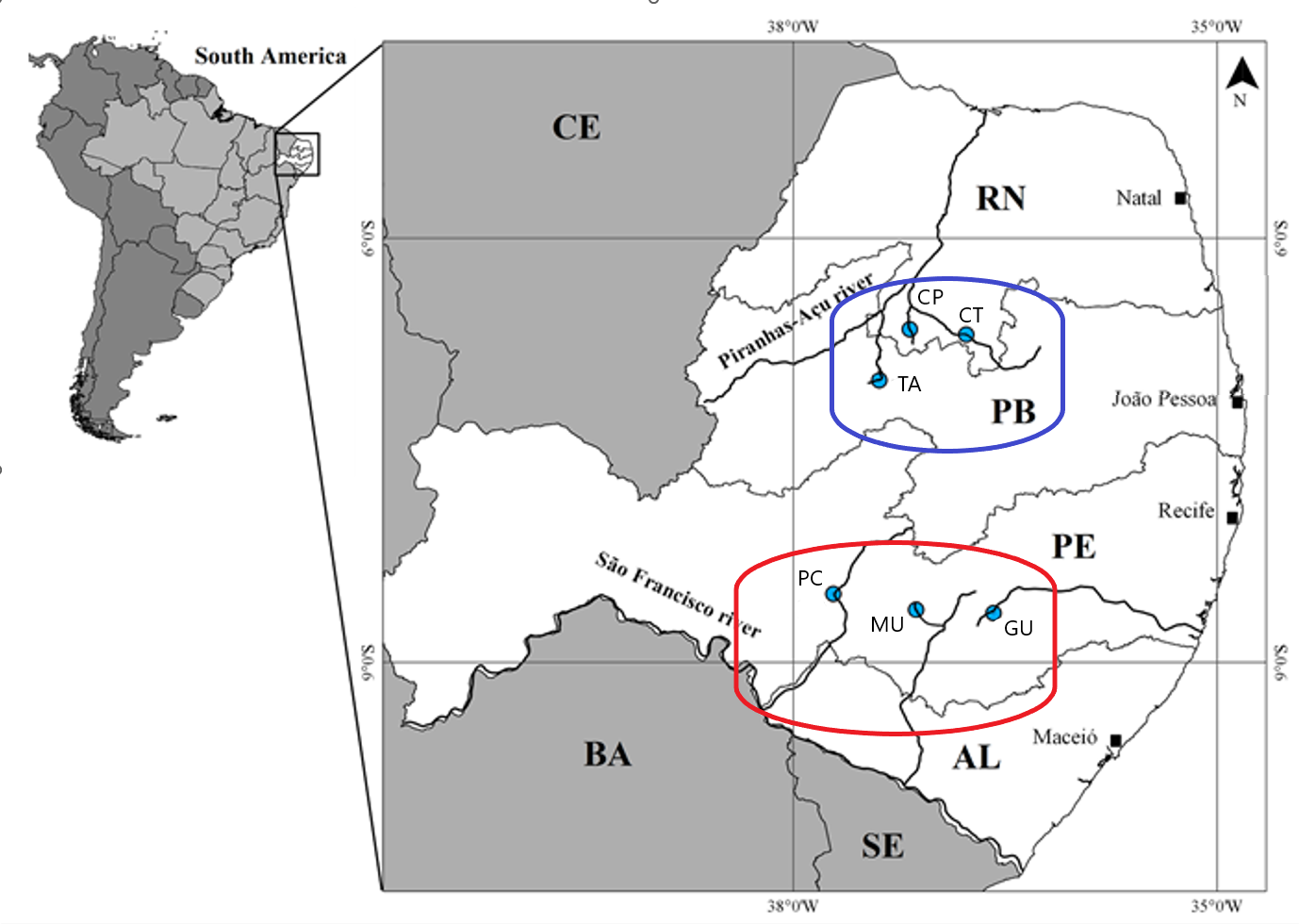
Figura 7.1: Mapa com a distribuição das Unidades Amostrais entre as duas áreas prioritárias para a conservação da Caatinga (sensu PROBIO) estudadas: Buíque/Vale do rio Ipojuca (em vermelho) e Seridó/Borborema (em azul).
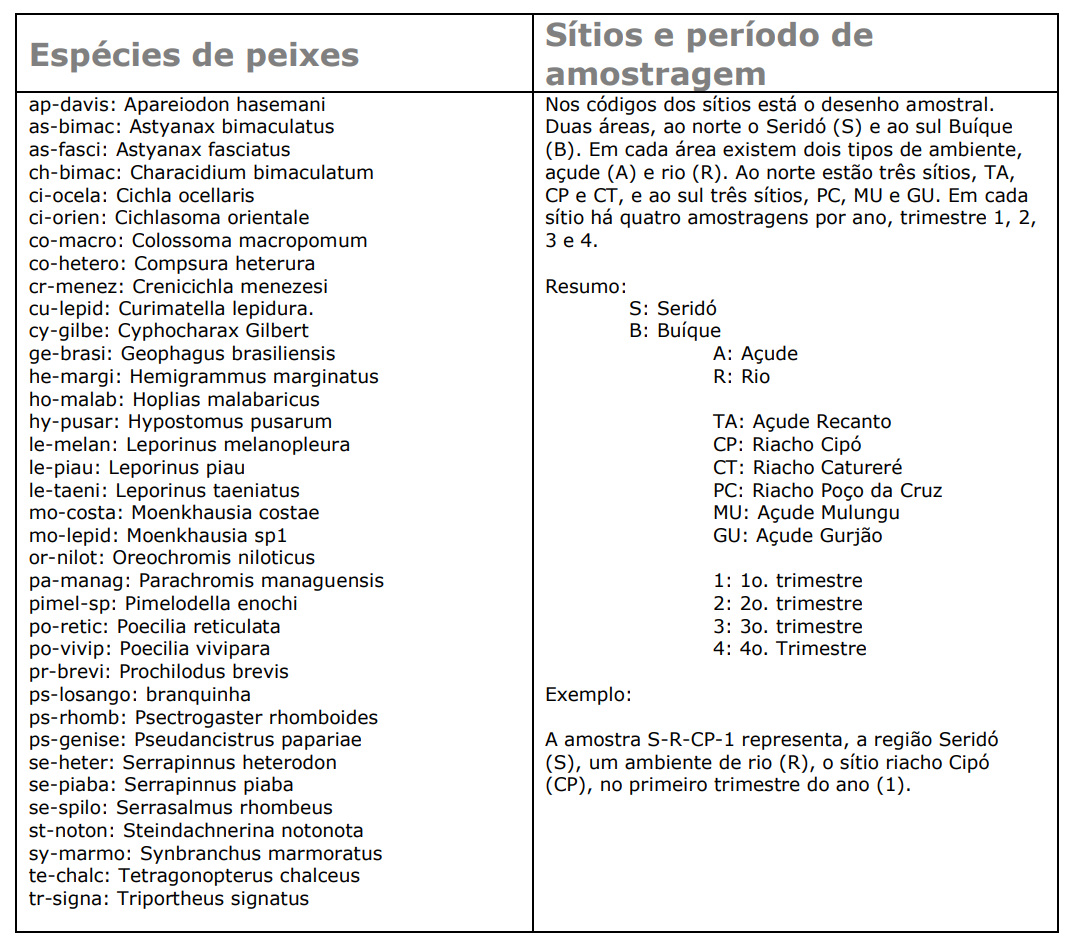
Figura 7.2: Quadro com a descrição do desenho amostral do primeiro ano do PPBio Semiárido (2006) e codificação dos agrupamentos a priori.
7.1.3 Importando as planilhas
Note que o símbolo # em programação R significa que o texto que vem depois dele é um comentário e não será executado pelo programa. Isso é útil para explicar o código ou deixar anotações.
- Ajuste a primeira linha do código abaixo para refletir “C:/Seu/Diretório/De/Trabalho/Planilha.xlsx”.
- Ajuste o parâmetro sheet = "" para refletir a aba correta do arquivo .xlsx a ser importado.
Alternativamente você pode ir na barra de tarefas e escolhes as opções:
SESSION -> SET WORKING DIRECTORY -> CHOOSE DIRECTORY
library(openxlsx)
ppbio <- read.xlsx("D:/Elvio/OneDrive/Disciplinas/_EcoNumerica/5.Matrizes/ppbio06p-peixes.xlsx",
rowNames = T,
colNames = T,
sheet = "Sheet1")
t_grps <- read.xlsx("D:/Elvio/OneDrive/Disciplinas/_EcoNumerica/5.Matrizes/ppbio06-grupos.xlsx",
rowNames = T,
colNames = T,
sheet = "peixesp")
ppbio[1:5,1:5] #[1:5,1:5] mostra apenas as linhas e colunas de 1 a 5.
t_grps## ap-davis as-bimac as-fasci ch-bimac ci-ocela
## S-R-CT1 0 194 55 0 0
## S-R-CP1 0 19 0 0 0
## S-A-TA1 0 23 1 13 0
## S-R-CT2 0 142 3 3 0
## S-R-CP2 0 5 1 0 40
## area ambiente UA coleta
## S-R-CT1 Serido rio CT 1
## S-R-CP1 Serido rio CP 1
## S-A-TA1 Serido acude TA 1
## S-R-CT2 Serido rio CT 2
## S-R-CP2 Serido rio CP 2
## S-A-TA2 Serido acude TA 2
## S-R-CT3 Serido rio CT 3
## S-R-CP3 Serido rio CP 3
## S-A-TA3 Serido acude TA 3
## S-R-CT4 Serido rio CT 4
## S-R-CP4 Serido rio CP 4
## S-A-TA4 Serido acude TA 4
## B-A-MU1 Buique acude MU 1
## B-A-GU1 Buique acude GU 1
## B-R-PC2 Buique rio PC 2
## B-A-MU2 Buique acude MU 2
## B-A-GU2 Buique acude GU 2
## B-R-PC3 Buique rio PC 3
## B-A-MU3 Buique acude MU 3
## B-A-GU3 Buique acude GU 3
## B-R-PC4 Buique rio PC 4
## B-A-MU4 Buique acude MU 4
## B-A-GU4 Buique acude GU 47.2 REINÍCIO 1
m_bruta <- (ppbio) # <1>- Aqui usaremos as matrizes relativizadas/transformadas/particionadas, etc
Podemos exibir a planilha depois de ter sido importada para o ambiente R/RStudio usando as funções View(), print() ou head(). Note que essas funções são case-sensitive. A função ignore.case() é uma função do pacote stringr que modifica um padrão para que ele não considere o caso das letras nas correspondências. Por exemplo, se você quiser encontrar todas as ocorrências da letra “a” em um vetor de caracteres, independente de ser “A” ou “a”, você pode usar essa função.
#View(m_bruta)
print(m_bruta)
head(m_bruta)A função head() no RStudio é uma forma de ver as primeiras (n=6) linhas de um objeto, como um vetor, uma matriz, um data frame ou uma lista. Ela é útil para ter uma ideia do conteúdo e da estrutura do objeto.
Também podemos explorar as características da planilha usando as funções str(), mode(), class() e length(). O número de observações ou tamanho do vetor depende do tipo de dados, se eles são uma matrix ou um data.frame.
str(m_bruta)
mode(m_bruta)
class(m_bruta)
#?str## 'data.frame': 23 obs. of 35 variables:
## $ ap-davis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ as-bimac : num 194 19 23 142 5 46 206 16 234 0 ...
## $ as-fasci : num 55 0 1 3 1 0 64 0 7 1 ...
## $ ch-bimac : num 0 0 13 3 0 178 0 0 238 0 ...
## $ ci-ocela : num 0 0 0 0 40 0 0 13 0 0 ...
## $ ci-orien : num 5 0 0 69 9 0 25 24 0 5 ...
## $ co-macro : num 0 0 0 0 0 0 0 0 2 0 ...
## $ co-heter : num 1 0 0 0 0 0 0 0 0 0 ...
## $ cr-menez : num 14 0 0 4 0 0 8 0 0 1 ...
## $ cu-lepid : num 0 0 0 0 0 0 0 0 0 0 ...
## $ cy-gilbe : num 0 0 0 0 0 0 0 0 0 50 ...
## $ ge-brasi : num 3 0 0 0 0 0 1 0 0 3 ...
## $ he-margi : num 0 0 0 1 0 0 0 0 0 1 ...
## $ ho-malab : num 1 5 0 17 10 2 31 4 20 4 ...
## $ hy-pusar : num 9 2 0 43 2 0 11 0 0 3 ...
## $ le-melan : num 0 0 0 0 0 0 0 0 0 0 ...
## $ le-piau : num 3 0 0 1 3 0 2 1 0 0 ...
## $ le-taeni : num 0 0 0 0 0 0 0 0 0 0 ...
## $ mo-costa : num 0 0 0 0 0 0 0 0 0 0 ...
## $ mo-lepid : num 39 0 0 1 0 0 0 0 0 0 ...
## $ or-nilot : num 36 0 0 77 0 0 138 0 0 73 ...
## $ pa-manag : num 0 0 0 0 0 0 0 0 0 0 ...
## $ pimel-sp : num 6 0 0 0 0 0 0 0 0 0 ...
## $ po-retic : num 0 0 0 20 0 0 5 0 0 0 ...
## $ po-vivip : num 47 15 0 221 32 0 326 10 0 28 ...
## $ pr-brevi : num 5 0 1 15 5 2 164 0 0 59 ...
## $ ps-rhomb : num 0 0 0 0 0 0 1 0 0 0 ...
## $ ps-genise: num 0 0 0 0 0 0 1 0 0 0 ...
## $ se-heter : num 40 14 4 60 0 0 38 0 0 3 ...
## $ se-piaba : num 68 0 0 0 0 0 0 0 0 0 ...
## $ se-spilo : num 0 0 0 0 0 0 1 0 0 0 ...
## $ st-noton : num 1 0 0 25 0 0 115 0 0 64 ...
## $ sy-marmo : num 0 0 0 0 1 0 0 0 0 0 ...
## $ te-chalc : num 0 0 0 0 0 0 0 0 0 0 ...
## $ tr-signa : num 18 0 0 15 0 0 7 0 0 141 ...
## [1] "list"
## [1] "data.frame"O símbolo ? é usado para acessar a documentação de uma função ou um pacote no R. Como mostrado acima você pode saber mais sobre a função str(), usando o comando ?str. Isso vai abrir uma página no menu de ajuda com a descrição, os argumentos, os valores de retorno e os exemplos da função str(). Você também pode usar o símbolo ? para obter informações sobre um pacote inteiro. Por exemplo, se você quiser saber mais sobre o pacote openxlsx, você pode digitar ?openxlsx. Isso vai abrir uma página com a visão geral, a instalação, os recursos e as referências do pacote solicitado.
Podemos agora calcular o número e a proporção de zeros na matriz usando as funções sum() e length() (Você pode pesquisar o que faz a função length() usando o comando ?length).
7.2.1 Tamanho da matriz
range(m_bruta) #menor e maior valores
length(m_bruta) #no. de colunas
ncol(m_bruta) #no. de N colunas
nrow(m_bruta) #no. de M linhas
sum(lengths(m_bruta)) #soma os nos. de colunas
length(as.matrix(m_bruta)) #tamanho da matriz m x n
sum(m_bruta == 0) # número de observações igual a zero
sum(m_bruta > 0) # número de observações maiores que zero
zeros <- (sum(m_bruta == 0)/length(as.matrix(m_bruta)))*100 # proporção de zeros na matriz
zeros## [1] 0 511
## [1] 35
## [1] 35
## [1] 23
## [1] 805
## [1] 805
## [1] 620
## [1] 185
## [1] 77.01863A matriz de dados apresenta um total de 805 valores que variam entre 0, 511 (menor e maior valores). A matriz m x n tem 23 linhas e 35 colunas. Existem 620 observações iguais a zero e 185 observações maiores que zero, representando um percentual de 77% dos valores sendo zeros.
Essas informações podem ser resumidas na Tabela 7.1 que será gerada abaixo.
tamanho <- data.frame(
Função = c("range", "lenght", "m cols", "n linhas", "Tamanho", "Tamanho",
"Zeros", "Nao zeros", "% Zeros"),
Resultado = c(paste(range(m_bruta), collapse = " - "), length(m_bruta), ncol(m_bruta),
nrow(m_bruta), sum(lengths(m_bruta)), length(as.matrix(m_bruta)), sum(m_bruta == 0),
sum(m_bruta > 0), round(zeros, 1))
)
tamanho## Função Resultado
## 1 range 0 - 511
## 2 lenght 35
## 3 m cols 35
## 4 n linhas 23
## 5 Tamanho 805
## 6 Tamanho 805
## 7 Zeros 620
## 8 Nao zeros 185
## 9 % Zeros 77| Função | Resultado |
|---|---|
| range | 0 - 511 |
| lenght | 35 |
| m cols | 35 |
| n linhas | 23 |
| Tamanho | 805 |
| Tamanho | 805 |
| Zeros | 620 |
| Nao zeros | 185 |
| % Zeros | 77 |
Ou seja, temos uma matriz de tamanho m x n igual a 23 objetos por 35 atributos, onde 77.02% dos valores da matriz são iguais a zero!
7.3 Classificação
Criando uma classificação baseada na distância Bray-Curtis e UPGMA como método de fusão, criada a partir da matriz de dados relativizada pelo total das colunas e transformada pelo arco seno da raiz quadrada.
library(vegan)
m_trns <- asin(sqrt(decostand(m_bruta,
method="total", MARGIN = 2)))
vegdist <- vegdist(m_trns, method = "bray",
diag = TRUE,
upper = FALSE)
cluster <- hclust(vegdist, method = "average")
plot(cluster, main = "Cluster Dendrogram - Bray-Curtis")
#rect.hclust(cluster, k = 3, h = NULL)
#h = 0.8 fornece os grupos formados na altura h
as.matrix(vegdist)[1:6, 1:6]## S-R-CT1 S-R-CP1 S-A-TA1 S-R-CT2 S-R-CP2 S-A-TA2
## S-R-CT1 0.0000000 0.8743721 0.9338269 0.6274997 0.8106894 0.9420728
## S-R-CP1 0.8743721 0.0000000 0.6833816 0.7759468 0.7726098 0.7342613
## S-A-TA1 0.9338269 0.6833816 0.0000000 0.8789631 0.9178304 0.5700984
## S-R-CT2 0.6274997 0.7759468 0.8789631 0.0000000 0.7280378 0.8836068
## S-R-CP2 0.8106894 0.7726098 0.9178304 0.7280378 0.0000000 0.8915271
## S-A-TA2 0.9420728 0.7342613 0.5700984 0.8836068 0.8915271 0.0000000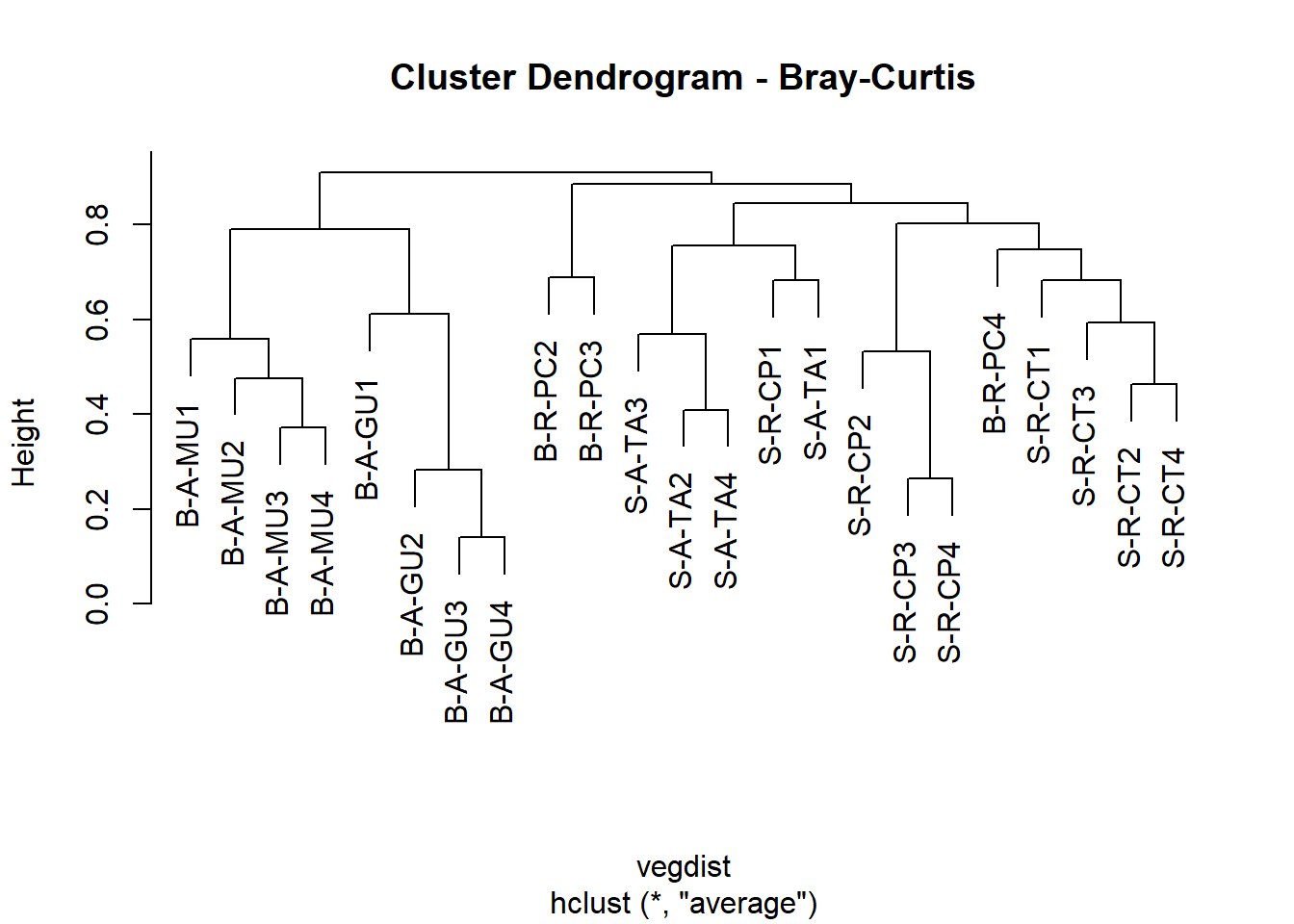
7.4 Histórico das fusões
Criamos agora o histórico das fusões dos objetos. Na tabela gerada, as duas primeiras colunas (No. e UA) representam o número (No.) atribuido a cada unidade amostral (UA). As duas colunas subsequentes (Cluster1 e Cluster2) representam o par de objetos (indicado pelo sinal de “-”) ou grupo de objetos (indicado pela ausência do sinal de “-”) que foram agrupadas. A coluna Height, indica o valor de similaridade na qual um dado par de objetos (ou grupo de objetos) foi agrupado. O valor aproximado de Height também pode ser visualizado no eixo do dendrograma. Por último, na coluna Histórico, é mostrada a sequência das fusões da primeira até a m-1 última fusão entre os dois últimos grupos. Nesse caso, 22.
merge <- as.data.frame(cluster$merge)
merge[nrow(merge)+1,] = c("0","0")
height <- as.data.frame(round(cluster$height, 2))
height[nrow(height)+1,] = c("1.0")
fusoes <- data.frame(Cluster = merge, Height = height)
colnames(fusoes) <- c("Cluster1", "Cluster2", "Height")
UA <- rownames_to_column(as.data.frame(m_trns[, 0]))
colnames(UA) <- c("No. e UA")
fusoes <- cbind(UA, fusoes)
fusoes$Histórico <- 1:nrow(fusoes)
fusoes## No. e UA Cluster1 Cluster2 Height Histórico
## 1 S-R-CT1 -20 -23 0.14 1
## 2 S-R-CP1 -8 -11 0.26 2
## 3 S-A-TA1 -17 1 0.28 3
## 4 S-R-CT2 -19 -22 0.37 4
## 5 S-R-CP2 -6 -12 0.41 5
## 6 S-A-TA2 -4 -10 0.46 6
## 7 S-R-CT3 -16 4 0.48 7
## 8 S-R-CP3 -5 2 0.53 8
## 9 S-A-TA3 -13 7 0.56 9
## 10 S-R-CT4 -9 5 0.57 10
## 11 S-R-CP4 -7 6 0.59 11
## 12 S-A-TA4 -14 3 0.61 12
## 13 B-A-MU1 -2 -3 0.68 13
## 14 B-A-GU1 -1 11 0.68 14
## 15 B-R-PC2 -15 -18 0.69 15
## 16 B-A-MU2 -21 14 0.75 16
## 17 B-A-GU2 10 13 0.76 17
## 18 B-R-PC3 9 12 0.79 18
## 19 B-A-MU3 8 16 0.8 19
## 20 B-A-GU3 17 19 0.85 20
## 21 B-R-PC4 15 20 0.89 21
## 22 B-A-MU4 18 21 0.91 22
## 23 B-A-GU4 0 0 1.0 23No código acima, h = 0.8 fornece os grupos formados na altura h do eixos das distâncias do dendrograma. Ou seja, no dendrograma, o eixo y (HEIGHT, “h”) representa o valor da distancia escolhida entre os objetos ou grupos de objetos. Portanto, se dois objetos ou grupos de objetos foram agrupados num dado valor (0.8, por exemplo) no eixo height, isso significa que a distancia entre esses objetos é 0.8.
7.6 REINÍCIO 2
m_trab <- (m_bruta) # <1>- Aqui usaremos as matrizes relativizadas/transformadas/particionadas, etc
library(vegan)
t_grps
grp <- t_grps$area
mrpp <- with(t_grps, mrpp(m_trab, grp, distance="bray"))
mrpp
#teste de hipótese
str(mrpp)
p_value <- mrpp$Pvalue
print(sprintf("p-value: %.10f", p_value))
# Conditional statement to check the p-value and print the appropriate message
if (p_value < 0.05) {
print(sprintf("Existe diferença significativa porquê o valor de p é %.10f, sendo menor que o nível de significância de 0.05.", p_value))
} else {
print(sprintf("Não existe diferença significativa porquê o valor de p é %.10f, sendo maior ou igual ao nível de significância de 0.05.", p_value))
}## area ambiente UA coleta
## S-R-CT1 Serido rio CT 1
## S-R-CP1 Serido rio CP 1
## S-A-TA1 Serido acude TA 1
## S-R-CT2 Serido rio CT 2
## S-R-CP2 Serido rio CP 2
## S-A-TA2 Serido acude TA 2
## S-R-CT3 Serido rio CT 3
## S-R-CP3 Serido rio CP 3
## S-A-TA3 Serido acude TA 3
## S-R-CT4 Serido rio CT 4
## S-R-CP4 Serido rio CP 4
## S-A-TA4 Serido acude TA 4
## B-A-MU1 Buique acude MU 1
## B-A-GU1 Buique acude GU 1
## B-R-PC2 Buique rio PC 2
## B-A-MU2 Buique acude MU 2
## B-A-GU2 Buique acude GU 2
## B-R-PC3 Buique rio PC 3
## B-A-MU3 Buique acude MU 3
## B-A-GU3 Buique acude GU 3
## B-R-PC4 Buique rio PC 4
## B-A-MU4 Buique acude MU 4
## B-A-GU4 Buique acude GU 4
##
## Call:
## mrpp(dat = m_trab, grouping = grp, distance = "bray")
##
## Dissimilarity index: bray
## Weights for groups: n
##
## Class means and counts:
##
## Buique Serido
## delta 0.8246 0.796
## n 11 12
##
## Chance corrected within-group agreement A: 0.04612
## Based on observed delta 0.8097 and expected delta 0.8488
##
## Significance of delta: 0.002
## Permutation: free
## Number of permutations: 999
##
## List of 13
## $ call : language mrpp(dat = m_trab, grouping = grp, distance = "bray")
## $ delta : num 0.81
## $ E.delta : num 0.849
## $ CS : logi NA
## $ n : Named int [1:2] 11 12
## ..- attr(*, "names")= chr [1:2] "Buique" "Serido"
## $ classdelta : Named num [1:2] 0.825 0.796
## ..- attr(*, "names")= chr [1:2] "Buique" "Serido"
## $ Pvalue : num 0.002
## $ A : num 0.0461
## $ distance : chr "bray"
## $ weight.type : num 1
## $ boot.deltas : num [1:999] 0.857 0.853 0.842 0.857 0.84 ...
## $ permutations: int 999
## $ control :List of 12
## ..$ within :List of 6
## .. ..$ type : chr "free"
## .. ..$ constant: logi FALSE
## .. ..$ mirror : logi FALSE
## .. ..$ ncol : NULL
## .. ..$ nrow : NULL
## .. ..$ call : language Within()
## .. ..- attr(*, "class")= chr "Within"
## ..$ plots :List of 7
## .. ..$ strata : NULL
## .. ..$ type : chr "none"
## .. ..$ mirror : logi FALSE
## .. ..$ ncol : NULL
## .. ..$ nrow : NULL
## .. ..$ plots.name: chr "NULL"
## .. ..$ call : language Plots()
## .. ..- attr(*, "class")= chr "Plots"
## ..$ blocks : NULL
## ..$ nperm : num 999
## ..$ complete : logi FALSE
## ..$ maxperm : num 9999
## ..$ minperm : num 5040
## ..$ all.perms : NULL
## ..$ make : logi TRUE
## ..$ observed : logi FALSE
## ..$ blocks.name: chr "NULL"
## ..$ call : language how(nperm = 999)
## ..- attr(*, "class")= chr "how"
## - attr(*, "class")= chr "mrpp"
## [1] "p-value: 0.0020000000"
## [1] "Existe diferença significativa porquê o valor de p é 0.0020000000, sendo menor que o nível de significância de 0.05."7.6.1 Interpretação da MRPP
Os resultados da análise MRPP fornecem várias informações importantes sobre a dissimilaridade entre grupos e a significância dessa dissimilaridade:
Foi usada a medida de distância de bray.
Sobre as médias e contagens das classes: Esta seção fornece as médias de dissimilaridade (delta) e as contagens (n) para cada grupo. Neste caso, os grupos e suas contagens foram 11, 12, e a média de dissimilaridade foi de 0.8245795, 0.7960057 para seu respectivo grupo. A contagem indica o número de amostras em cada grupo.
Concordância Dentro do Grupo Corrigida para o Acaso (A) ou “Chance Corrected Within-Group Agreement”: Esta métrica, que varia de 0 a 1, mede a concordância dentro dos grupos após considerar o acaso. Um valor próximo de 1 indica alta concordância dentro dos grupos, enquanto um valor próximo de 0 indica baixa concordância além do que seria esperado apenas pelo acaso.
De acordo com MCCUNE um valor esperado seria de XXX para o caso de XXX. Para esse análise o valore de A observado foi de 0.0461153
Significância do Delta: A significância do índice de dissimilaridade observado (delta) é avaliada usando um teste de permutação (“Bootstrapping”). Neste caso, o valor p associado ao índice de dissimilaridade observado foi de 0.002, sugerindo que a dissimilaridade observada não é estatisticamente significativa no nível de significância convencional de 0.05.
Permutação: O método de permutação usado para avaliar a significância é indicado como free, o que significa que o número de permutações não foi restrito a um valor específico, mas sim foi permitido variar com base nos recursos computacionais disponíveis.
Número de Permutações: O número de permutações realizadas na análise foi de 999.
7.6.2 Gráfico da MRPP
def.par <- par(no.readonly = TRUE)
layout(matrix(1:2,nr=1))
plot(ord <- metaMDS(m_trab, distance="bray"), type="text", display="sites")
with(t_grps, ordihull(ord, grp))
with(mrpp, {
fig.dist <- hist(boot.deltas, xlim=range(c(delta,boot.deltas)),
main="Test of Differences Among Groups")
abline(v=delta);
text(delta, 2*mean(fig.dist$counts), adj = -0.5,
expression(bold(delta)), cex=1.5 ) }
)
par(def.par)## Square root transformation
## Wisconsin double standardization
## Run 0 stress 0.1474521
## Run 1 stress 0.2218076
## Run 2 stress 0.1474521
## ... Procrustes: rmse 4.590164e-06 max resid 1.417907e-05
## ... Similar to previous best
## Run 3 stress 0.1872215
## Run 4 stress 0.1474521
## ... Procrustes: rmse 1.026737e-05 max resid 3.162571e-05
## ... Similar to previous best
## Run 5 stress 0.1474521
## ... Procrustes: rmse 4.718408e-06 max resid 1.62862e-05
## ... Similar to previous best
## Run 6 stress 0.1474521
## ... Procrustes: rmse 1.147756e-05 max resid 3.650901e-05
## ... Similar to previous best
## Run 7 stress 0.1872276
## Run 8 stress 0.2014592
## Run 9 stress 0.1474521
## ... Procrustes: rmse 1.963767e-05 max resid 5.170984e-05
## ... Similar to previous best
## Run 10 stress 0.1968761
## Run 11 stress 0.1872272
## Run 12 stress 0.1474521
## ... Procrustes: rmse 1.08559e-05 max resid 3.473127e-05
## ... Similar to previous best
## Run 13 stress 0.1474521
## ... Procrustes: rmse 1.020077e-05 max resid 3.019864e-05
## ... Similar to previous best
## Run 14 stress 0.1474521
## ... Procrustes: rmse 4.679741e-06 max resid 1.186286e-05
## ... Similar to previous best
## Run 15 stress 0.1474521
## ... Procrustes: rmse 8.205253e-06 max resid 1.961544e-05
## ... Similar to previous best
## Run 16 stress 0.1474521
## ... Procrustes: rmse 2.306956e-05 max resid 5.753558e-05
## ... Similar to previous best
## Run 17 stress 0.1474521
## ... Procrustes: rmse 2.522681e-05 max resid 6.454723e-05
## ... Similar to previous best
## Run 18 stress 0.1474521
## ... Procrustes: rmse 2.16497e-05 max resid 6.503519e-05
## ... Similar to previous best
## Run 19 stress 0.1474521
## ... Procrustes: rmse 2.216716e-06 max resid 5.263279e-06
## ... Similar to previous best
## Run 20 stress 0.1474521
## ... Procrustes: rmse 7.032083e-06 max resid 1.685117e-05
## ... Similar to previous best
## *** Best solution repeated 14 times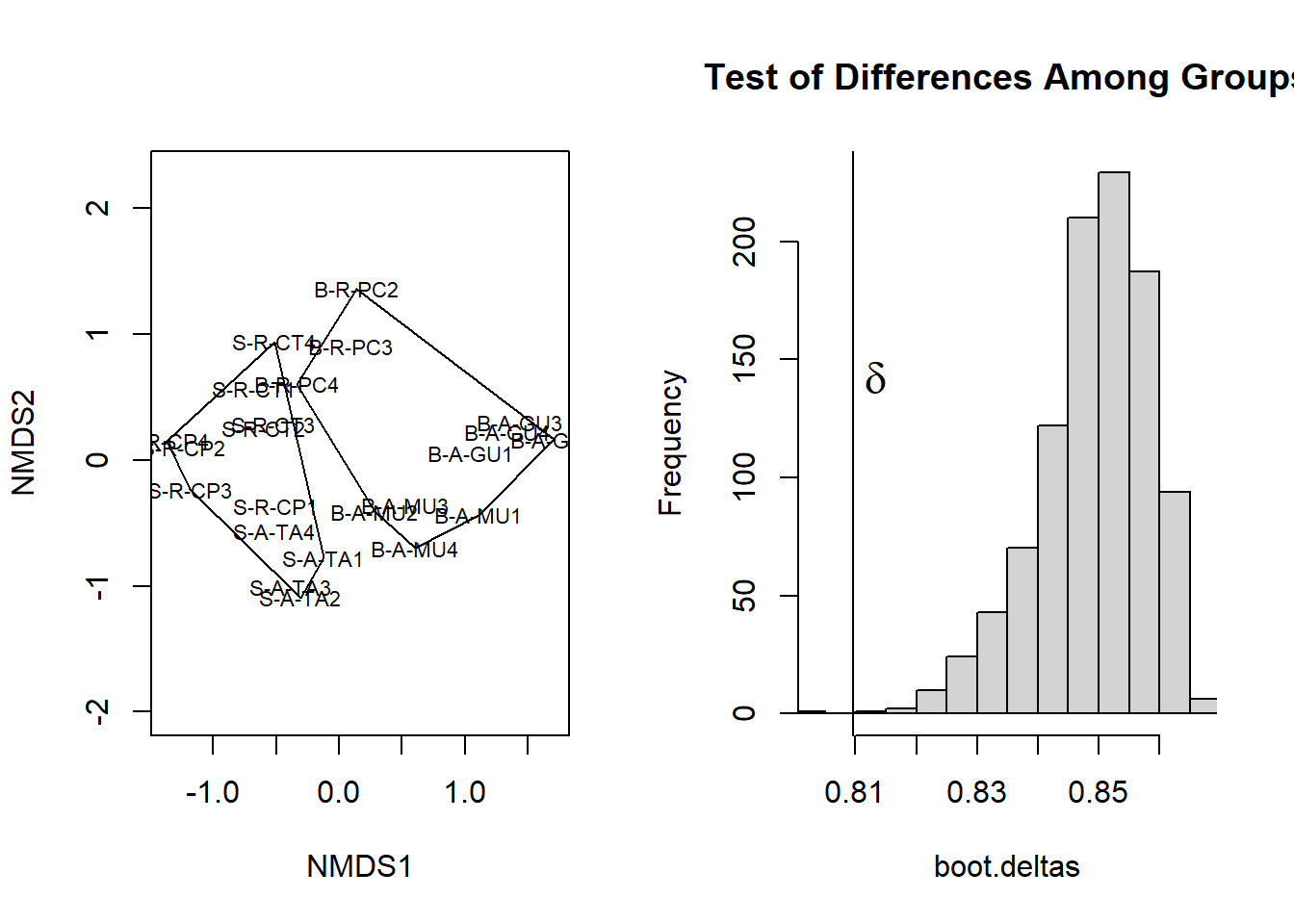
Figura 7.3: Ordenação dos dados mostrando o agrupamento escolhido (r print(grp) da tabela de grupos e teste (sigma) de diferenças entre os grupos.
Na figura 7.3 observa-se (a esquerda) a distribuição da UA’s no espaço da Ordenação e o agrupamento de acordo com . A direita observa-se a distribuição de frequência de delta. O delta esperado foi de 0.8488147, enquanto que o delta observado foi de 0.8096714 sifnificativamente menor, com um valor de p de 0.002 (A=0.0461153).
No geral, esses resultados indicam que há diferença estatisticamente significativa entre os grupos avaliados para essa comparação específica com base nas relativizações e transformações utilizadas e na medida de distância escolhida, pois a dissimilaridade observada não é significativamente diferente do que seria esperado apenas pelo acaso.
7.6.3 Avaliando as distâncias médias meandist
md <- with(t_grps, meandist(vegdist(m_trab), grp))
md
summary(md)
par(mfrow=c(1,2))
plot(md)
plot(md, kind="histogram")
par(mfrow=c(1,1))## Buique Serido
## Buique 0.8245795 0.8853173
## Serido 0.8853173 0.7960057
## attr(,"class")
## [1] "meandist" "matrix"
## attr(,"n")
## grouping
## Buique Serido
## 11 12
##
## Mean distances:
## Average
## within groups 0.8089938
## between groups 0.8853173
## overall 0.8488147
##
## Summary statistics:
## Statistic
## MRPP A weights n 0.04611526
## MRPP A weights n-1 0.04618495
## MRPP A weights n(n-1) 0.04691359
## Classification strength 0.07564585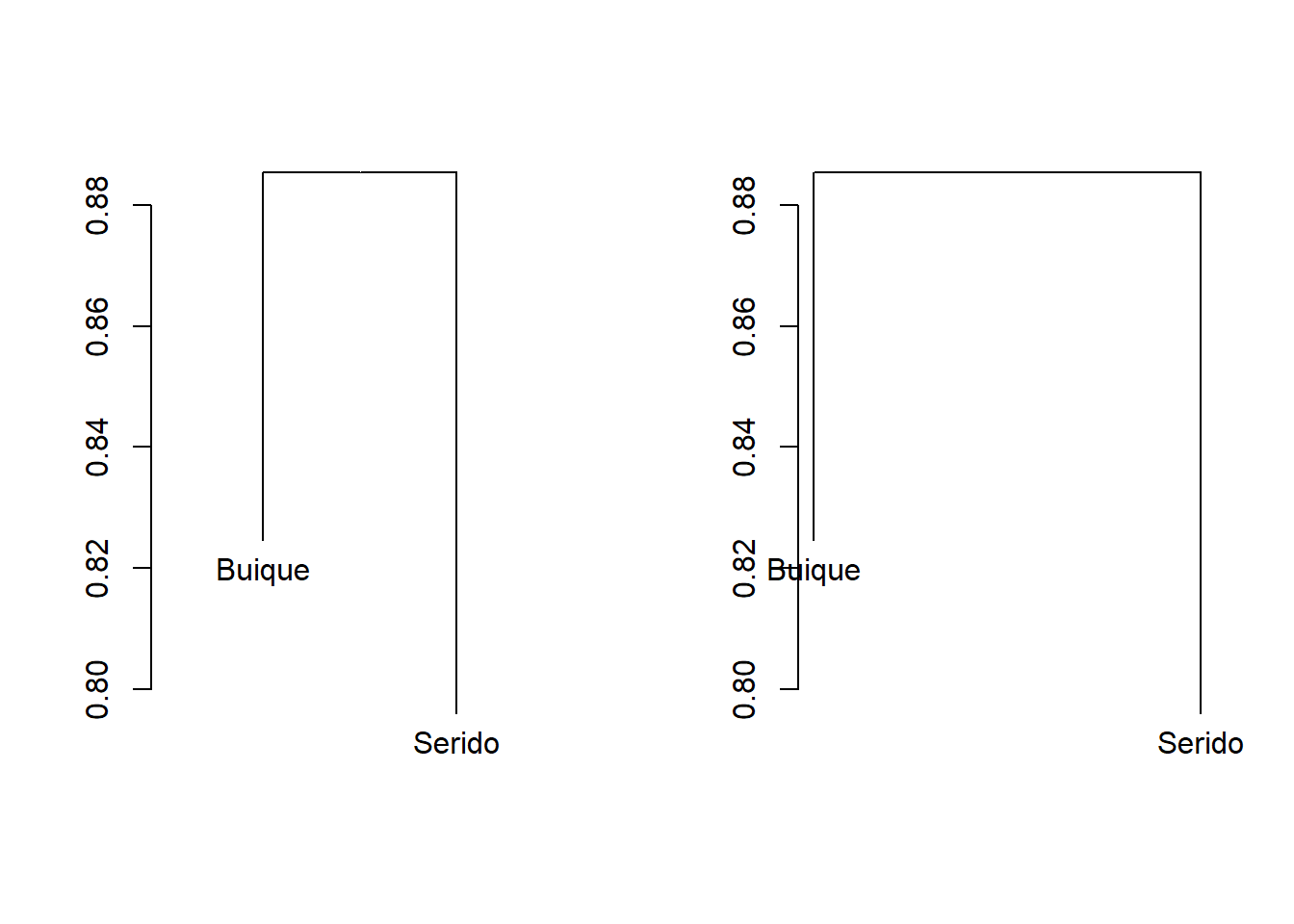
Podemos partir para uma Análise de Espécies Indicadoras (ISA) se as diferenças entre grupos são significativas.
7.7 ISA
Indicator Species Analisys
Ver indicspecies
7.7.1 Organizando os grupos
library(indicspecies)## Warning: package 'indicspecies' was built under R version 4.3.3# Grupos a priori
groups <- grp
groups
#OU
rep <- c(rep("Serido", 12), rep("Buique", 11))
rep
#OU
levs <- factor(c(rep(1,12), rep(2,11)), labels = c("Serido","Buique"))
levs
#OU Grupos a posteriori
km <- kmeans(m_trab, centers=3)
groupskm <- km$cluster
groupskm## [1] "Serido" "Serido" "Serido" "Serido" "Serido" "Serido" "Serido" "Serido"
## [9] "Serido" "Serido" "Serido" "Serido" "Buique" "Buique" "Buique" "Buique"
## [17] "Buique" "Buique" "Buique" "Buique" "Buique" "Buique" "Buique"
## [1] "Serido" "Serido" "Serido" "Serido" "Serido" "Serido" "Serido" "Serido"
## [9] "Serido" "Serido" "Serido" "Serido" "Buique" "Buique" "Buique" "Buique"
## [17] "Buique" "Buique" "Buique" "Buique" "Buique" "Buique" "Buique"
## [1] Serido Serido Serido Serido Serido Serido Serido Serido Serido Serido Serido
## [12] Serido Buique Buique Buique Buique Buique Buique Buique Buique Buique Buique
## [23] Buique
## Levels: Serido Buique
## S-R-CT1 S-R-CP1 S-A-TA1 S-R-CT2 S-R-CP2 S-A-TA2 S-R-CT3 S-R-CP3 S-A-TA3 S-R-CT4
## 2 3 3 2 3 3 2 3 2 3
## S-R-CP4 S-A-TA4 B-A-MU1 B-A-GU1 B-R-PC2 B-A-MU2 B-A-GU2 B-R-PC3 B-A-MU3 B-A-GU3
## 3 2 3 3 3 3 3 3 2 3
## B-R-PC4 B-A-MU4 B-A-GU4
## 3 1 3Usaremos a oppção grupos
7.7.2 Valores indicativos (IV)
indval <- multipatt(m_trab, groups,
control = how(nperm=999))
indval
# Ordena pelo menor valor de P
indval$sign[order(indval$sign$p.value), ]
library("gt")
gt(indval$sign[order(indval$sign$p.value), ], rownames_to_stub=TRUE)## $call
## multipatt(x = m_trab, cluster = groups, control = how(nperm = 999))
##
## $func
## [1] "IndVal.g"
##
## $cluster
## [1] "Serido" "Serido" "Serido" "Serido" "Serido" "Serido" "Serido" "Serido"
## [9] "Serido" "Serido" "Serido" "Serido" "Buique" "Buique" "Buique" "Buique"
## [17] "Buique" "Buique" "Buique" "Buique" "Buique" "Buique" "Buique"
##
## $comb
## Buique Serido Buique+Serido
## [1,] 0 1 1
## [2,] 0 1 1
## [3,] 0 1 1
## [4,] 0 1 1
## [5,] 0 1 1
## [6,] 0 1 1
## [7,] 0 1 1
## [8,] 0 1 1
## [9,] 0 1 1
## [10,] 0 1 1
## [11,] 0 1 1
## [12,] 0 1 1
## [13,] 1 0 1
## [14,] 1 0 1
## [15,] 1 0 1
## [16,] 1 0 1
## [17,] 1 0 1
## [18,] 1 0 1
## [19,] 1 0 1
## [20,] 1 0 1
## [21,] 1 0 1
## [22,] 1 0 1
## [23,] 1 0 1
##
## $str
## Buique Serido Buique+Serido
## ap-davis 0.42640143 0.00000000 0.2948839
## as-bimac 0.64758904 0.67000701 0.9325048
## as-fasci 0.21963032 0.69293487 0.6593805
## ch-bimac 0.00000000 0.64549722 0.4662524
## ci-ocela 0.12988352 0.47623957 0.4662524
## ci-orien 0.00000000 0.76376262 0.5516773
## co-macro 0.00000000 0.28867513 0.2085144
## co-heter 0.00000000 0.28867513 0.2085144
## cr-menez 0.00000000 0.64549722 0.4662524
## cu-lepid 0.30151134 0.00000000 0.2085144
## cy-gilbe 0.24095141 0.17353353 0.2948839
## ge-brasi 0.99639638 0.04897021 0.8075729
## he-margi 0.00000000 0.40824829 0.2948839
## ho-malab 0.10431628 0.93813189 0.7801895
## hy-pusar 0.03735003 0.70166043 0.5516773
## le-melan 0.30151134 0.00000000 0.2085144
## le-piau 0.08106628 0.73563895 0.5897678
## le-taeni 0.30151134 0.00000000 0.2085144
## mo-costa 0.30151134 0.00000000 0.2085144
## mo-lepid 0.00000000 0.40824829 0.2948839
## or-nilot 0.79537250 0.39124938 0.8340577
## pa-manag 0.60302269 0.00000000 0.4170288
## pimel-sp 0.00000000 0.28867513 0.2085144
## po-retic 0.50458592 0.10523083 0.4662524
## po-vivip 0.25552602 0.71208161 0.6915641
## pr-brevi 0.13242500 0.78981008 0.6915641
## ps-rhomb 0.00000000 0.28867513 0.2085144
## ps-genise 0.00000000 0.28867513 0.2085144
## se-heter 0.35967269 0.55374829 0.6593805
## se-piaba 0.00000000 0.28867513 0.2085144
## se-spilo 0.00000000 0.28867513 0.2085144
## st-noton 0.00000000 0.57735027 0.4170288
## sy-marmo 0.00000000 0.28867513 0.2085144
## te-chalc 0.42640143 0.00000000 0.2948839
## tr-signa 0.15952019 0.53542606 0.5107539
##
## $A
## Buique Serido Buique+Serido
## ap-davis 1.00000000 0.000000000 1
## as-bimac 0.46130873 0.538691274 1
## as-fasci 0.17687075 0.823129252 1
## ch-bimac 0.00000000 1.000000000 1
## ci-ocela 0.09278351 0.907216495 1
## ci-orien 0.00000000 1.000000000 1
## co-macro 0.00000000 1.000000000 1
## co-heter 0.00000000 1.000000000 1
## cr-menez 0.00000000 1.000000000 1
## cu-lepid 1.00000000 0.000000000 1
## cy-gilbe 0.63863338 0.361366623 1
## ge-brasi 0.99280576 0.007194245 1
## he-margi 0.00000000 1.000000000 1
## ho-malab 0.03990025 0.960099751 1
## hy-pusar 0.01534527 0.984654731 1
## le-melan 1.00000000 0.000000000 1
## le-piau 0.07228916 0.927710843 1
## le-taeni 1.00000000 0.000000000 1
## mo-costa 1.00000000 0.000000000 1
## mo-lepid 0.00000000 1.000000000 1
## or-nilot 0.63261741 0.367382592 1
## pa-manag 1.00000000 0.000000000 1
## pimel-sp 0.00000000 1.000000000 1
## po-retic 0.93355883 0.066441169 1
## po-vivip 0.23940967 0.760590325 1
## pr-brevi 0.06430007 0.935699933 1
## ps-rhomb 0.00000000 1.000000000 1
## ps-genise 0.00000000 1.000000000 1
## se-heter 0.47433628 0.525663717 1
## se-piaba 0.00000000 1.000000000 1
## se-spilo 0.00000000 1.000000000 1
## st-noton 0.00000000 1.000000000 1
## sy-marmo 0.00000000 1.000000000 1
## te-chalc 1.00000000 0.000000000 1
## tr-signa 0.13995680 0.860043197 1
##
## $B
## Buique Serido Buique+Serido
## ap-davis 0.18181818 0.00000000 0.08695652
## as-bimac 0.90909091 0.83333333 0.86956522
## as-fasci 0.27272727 0.58333333 0.43478261
## ch-bimac 0.00000000 0.41666667 0.21739130
## ci-ocela 0.18181818 0.25000000 0.21739130
## ci-orien 0.00000000 0.58333333 0.30434783
## co-macro 0.00000000 0.08333333 0.04347826
## co-heter 0.00000000 0.08333333 0.04347826
## cr-menez 0.00000000 0.41666667 0.21739130
## cu-lepid 0.09090909 0.00000000 0.04347826
## cy-gilbe 0.09090909 0.08333333 0.08695652
## ge-brasi 1.00000000 0.33333333 0.65217391
## he-margi 0.00000000 0.16666667 0.08695652
## ho-malab 0.27272727 0.91666667 0.60869565
## hy-pusar 0.09090909 0.50000000 0.30434783
## le-melan 0.09090909 0.00000000 0.04347826
## le-piau 0.09090909 0.58333333 0.34782609
## le-taeni 0.09090909 0.00000000 0.04347826
## mo-costa 0.09090909 0.00000000 0.04347826
## mo-lepid 0.00000000 0.16666667 0.08695652
## or-nilot 1.00000000 0.41666667 0.69565217
## pa-manag 0.36363636 0.00000000 0.17391304
## pimel-sp 0.00000000 0.08333333 0.04347826
## po-retic 0.27272727 0.16666667 0.21739130
## po-vivip 0.27272727 0.66666667 0.47826087
## pr-brevi 0.27272727 0.66666667 0.47826087
## ps-rhomb 0.00000000 0.08333333 0.04347826
## ps-genise 0.00000000 0.08333333 0.04347826
## se-heter 0.27272727 0.58333333 0.43478261
## se-piaba 0.00000000 0.08333333 0.04347826
## se-spilo 0.00000000 0.08333333 0.04347826
## st-noton 0.00000000 0.33333333 0.17391304
## sy-marmo 0.00000000 0.08333333 0.04347826
## te-chalc 0.18181818 0.00000000 0.08695652
## tr-signa 0.18181818 0.33333333 0.26086957
##
## $sign
## s.Buique s.Serido index stat p.value
## ap-davis 1 0 1 0.4264014 0.212
## as-bimac 1 1 3 0.9325048 NA
## as-fasci 0 1 2 0.6929349 0.140
## ch-bimac 0 1 2 0.6454972 0.042
## ci-ocela 0 1 2 0.4762396 0.322
## ci-orien 0 1 2 0.7637626 0.006
## co-macro 0 1 2 0.2886751 1.000
## co-heter 0 1 2 0.2886751 1.000
## cr-menez 0 1 2 0.6454972 0.046
## cu-lepid 1 0 1 0.3015113 0.489
## cy-gilbe 1 1 3 0.2948839 NA
## ge-brasi 1 0 1 0.9963964 0.001
## he-margi 0 1 2 0.4082483 0.494
## ho-malab 0 1 2 0.9381319 0.001
## hy-pusar 0 1 2 0.7016604 0.038
## le-melan 1 0 1 0.3015113 0.487
## le-piau 0 1 2 0.7356389 0.013
## le-taeni 1 0 1 0.3015113 0.487
## mo-costa 1 0 1 0.3015113 0.489
## mo-lepid 0 1 2 0.4082483 0.511
## or-nilot 1 1 3 0.8340577 NA
## pa-manag 1 0 1 0.6030227 0.044
## pimel-sp 0 1 2 0.2886751 1.000
## po-retic 1 0 1 0.5045859 0.313
## po-vivip 0 1 2 0.7120816 0.106
## pr-brevi 0 1 2 0.7898101 0.049
## ps-rhomb 0 1 2 0.2886751 1.000
## ps-genise 0 1 2 0.2886751 1.000
## se-heter 1 1 3 0.6593805 NA
## se-piaba 0 1 2 0.2886751 1.000
## se-spilo 0 1 2 0.2886751 1.000
## st-noton 0 1 2 0.5773503 0.101
## sy-marmo 0 1 2 0.2886751 1.000
## te-chalc 1 0 1 0.4264014 0.212
## tr-signa 0 1 2 0.5354261 0.396
##
## attr(,"class")
## [1] "multipatt"
## s.Buique s.Serido index stat p.value
## ge-brasi 1 0 1 0.9963964 0.001
## ho-malab 0 1 2 0.9381319 0.001
## ci-orien 0 1 2 0.7637626 0.006
## le-piau 0 1 2 0.7356389 0.013
## hy-pusar 0 1 2 0.7016604 0.038
## ch-bimac 0 1 2 0.6454972 0.042
## pa-manag 1 0 1 0.6030227 0.044
## cr-menez 0 1 2 0.6454972 0.046
## pr-brevi 0 1 2 0.7898101 0.049
## st-noton 0 1 2 0.5773503 0.101
## po-vivip 0 1 2 0.7120816 0.106
## as-fasci 0 1 2 0.6929349 0.140
## ap-davis 1 0 1 0.4264014 0.212
## te-chalc 1 0 1 0.4264014 0.212
## po-retic 1 0 1 0.5045859 0.313
## ci-ocela 0 1 2 0.4762396 0.322
## tr-signa 0 1 2 0.5354261 0.396
## le-melan 1 0 1 0.3015113 0.487
## le-taeni 1 0 1 0.3015113 0.487
## cu-lepid 1 0 1 0.3015113 0.489
## mo-costa 1 0 1 0.3015113 0.489
## he-margi 0 1 2 0.4082483 0.494
## mo-lepid 0 1 2 0.4082483 0.511
## co-macro 0 1 2 0.2886751 1.000
## co-heter 0 1 2 0.2886751 1.000
## pimel-sp 0 1 2 0.2886751 1.000
## ps-rhomb 0 1 2 0.2886751 1.000
## ps-genise 0 1 2 0.2886751 1.000
## se-piaba 0 1 2 0.2886751 1.000
## se-spilo 0 1 2 0.2886751 1.000
## sy-marmo 0 1 2 0.2886751 1.000
## as-bimac 1 1 3 0.9325048 NA
## cy-gilbe 1 1 3 0.2948839 NA
## or-nilot 1 1 3 0.8340577 NA
## se-heter 1 1 3 0.6593805 NA| s.Buique | s.Serido | index | stat | p.value | |
|---|---|---|---|---|---|
| ge-brasi | 1 | 0 | 1 | 0.9963964 | 0.001 |
| ho-malab | 0 | 1 | 2 | 0.9381319 | 0.001 |
| ci-orien | 0 | 1 | 2 | 0.7637626 | 0.006 |
| le-piau | 0 | 1 | 2 | 0.7356389 | 0.013 |
| hy-pusar | 0 | 1 | 2 | 0.7016604 | 0.038 |
| ch-bimac | 0 | 1 | 2 | 0.6454972 | 0.042 |
| pa-manag | 1 | 0 | 1 | 0.6030227 | 0.044 |
| cr-menez | 0 | 1 | 2 | 0.6454972 | 0.046 |
| pr-brevi | 0 | 1 | 2 | 0.7898101 | 0.049 |
| st-noton | 0 | 1 | 2 | 0.5773503 | 0.101 |
| po-vivip | 0 | 1 | 2 | 0.7120816 | 0.106 |
| as-fasci | 0 | 1 | 2 | 0.6929349 | 0.140 |
| ap-davis | 1 | 0 | 1 | 0.4264014 | 0.212 |
| te-chalc | 1 | 0 | 1 | 0.4264014 | 0.212 |
| po-retic | 1 | 0 | 1 | 0.5045859 | 0.313 |
| ci-ocela | 0 | 1 | 2 | 0.4762396 | 0.322 |
| tr-signa | 0 | 1 | 2 | 0.5354261 | 0.396 |
| le-melan | 1 | 0 | 1 | 0.3015113 | 0.487 |
| le-taeni | 1 | 0 | 1 | 0.3015113 | 0.487 |
| cu-lepid | 1 | 0 | 1 | 0.3015113 | 0.489 |
| mo-costa | 1 | 0 | 1 | 0.3015113 | 0.489 |
| he-margi | 0 | 1 | 2 | 0.4082483 | 0.494 |
| mo-lepid | 0 | 1 | 2 | 0.4082483 | 0.511 |
| co-macro | 0 | 1 | 2 | 0.2886751 | 1.000 |
| co-heter | 0 | 1 | 2 | 0.2886751 | 1.000 |
| pimel-sp | 0 | 1 | 2 | 0.2886751 | 1.000 |
| ps-rhomb | 0 | 1 | 2 | 0.2886751 | 1.000 |
| ps-genise | 0 | 1 | 2 | 0.2886751 | 1.000 |
| se-piaba | 0 | 1 | 2 | 0.2886751 | 1.000 |
| se-spilo | 0 | 1 | 2 | 0.2886751 | 1.000 |
| sy-marmo | 0 | 1 | 2 | 0.2886751 | 1.000 |
| as-bimac | 1 | 1 | 3 | 0.9325048 | NA |
| cy-gilbe | 1 | 1 | 3 | 0.2948839 | NA |
| or-nilot | 1 | 1 | 3 | 0.8340577 | NA |
| se-heter | 1 | 1 | 3 | 0.6593805 | NA |
7.7.3 Multi-level Pattern Analysis
summary(indval)
summary(indval, indvalcomp=TRUE)
summary(indval, alpha=1)
pa <- ifelse(m_trab>0,1,0)
phi <- multipatt(pa, groups, func = "r",
control = how(nperm=999))
phi
phi <- multipatt(pa, groups, func = "r.g",
control = how(nperm=999))
summary(phi)
round(head(phi$str),3)
round(head(indval$str),3)##
## Multilevel pattern analysis
## ---------------------------
##
## Association function: IndVal.g
## Significance level (alpha): 0.05
##
## Total number of species: 35
## Selected number of species: 9
## Number of species associated to 1 group: 9
##
## List of species associated to each combination:
##
## Group Buique #sps. 2
## stat p.value
## ge-brasi 0.996 0.001 ***
## pa-manag 0.603 0.044 *
##
## Group Serido #sps. 7
## stat p.value
## ho-malab 0.938 0.001 ***
## pr-brevi 0.790 0.049 *
## ci-orien 0.764 0.006 **
## le-piau 0.736 0.013 *
## hy-pusar 0.702 0.038 *
## ch-bimac 0.645 0.042 *
## cr-menez 0.645 0.046 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Multilevel pattern analysis
## ---------------------------
##
## Association function: IndVal.g
## Significance level (alpha): 0.05
##
## Total number of species: 35
## Selected number of species: 9
## Number of species associated to 1 group: 9
##
## List of species associated to each combination:
##
## Group Buique #sps. 2
## A B stat p.value
## ge-brasi 0.9928 1.0000 0.996 0.001 ***
## pa-manag 1.0000 0.3636 0.603 0.044 *
##
## Group Serido #sps. 7
## A B stat p.value
## ho-malab 0.9601 0.9167 0.938 0.001 ***
## pr-brevi 0.9357 0.6667 0.790 0.049 *
## ci-orien 1.0000 0.5833 0.764 0.006 **
## le-piau 0.9277 0.5833 0.736 0.013 *
## hy-pusar 0.9847 0.5000 0.702 0.038 *
## ch-bimac 1.0000 0.4167 0.645 0.042 *
## cr-menez 1.0000 0.4167 0.645 0.046 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Multilevel pattern analysis
## ---------------------------
##
## Association function: IndVal.g
## Significance level (alpha): 1
##
## Total number of species: 35
## Selected number of species: 31
## Number of species associated to 1 group: 31
##
## List of species associated to each combination:
##
## Group Buique #sps. 9
## stat p.value
## ge-brasi 0.996 0.001 ***
## pa-manag 0.603 0.044 *
## po-retic 0.505 0.313
## ap-davis 0.426 0.212
## te-chalc 0.426 0.212
## cu-lepid 0.302 0.489
## le-melan 0.302 0.487
## le-taeni 0.302 0.487
## mo-costa 0.302 0.489
##
## Group Serido #sps. 22
## stat p.value
## ho-malab 0.938 0.001 ***
## pr-brevi 0.790 0.049 *
## ci-orien 0.764 0.006 **
## le-piau 0.736 0.013 *
## po-vivip 0.712 0.106
## hy-pusar 0.702 0.038 *
## as-fasci 0.693 0.140
## ch-bimac 0.645 0.042 *
## cr-menez 0.645 0.046 *
## st-noton 0.577 0.101
## tr-signa 0.535 0.396
## ci-ocela 0.476 0.322
## he-margi 0.408 0.494
## mo-lepid 0.408 0.511
## co-macro 0.289 1.000
## co-heter 0.289 1.000
## pimel-sp 0.289 1.000
## ps-rhomb 0.289 1.000
## ps-genise 0.289 1.000
## se-piaba 0.289 1.000
## se-spilo 0.289 1.000
## sy-marmo 0.289 1.000
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## $call
## multipatt(x = pa, cluster = groups, func = "r", control = how(nperm = 999))
##
## $func
## [1] "r"
##
## $cluster
## [1] "Serido" "Serido" "Serido" "Serido" "Serido" "Serido" "Serido" "Serido"
## [9] "Serido" "Serido" "Serido" "Serido" "Buique" "Buique" "Buique" "Buique"
## [17] "Buique" "Buique" "Buique" "Buique" "Buique" "Buique" "Buique"
##
## $comb
## Buique Serido
## [1,] 0 1
## [2,] 0 1
## [3,] 0 1
## [4,] 0 1
## [5,] 0 1
## [6,] 0 1
## [7,] 0 1
## [8,] 0 1
## [9,] 0 1
## [10,] 0 1
## [11,] 0 1
## [12,] 0 1
## [13,] 1 0
## [14,] 1 0
## [15,] 1 0
## [16,] 1 0
## [17,] 1 0
## [18,] 1 0
## [19,] 1 0
## [20,] 1 0
## [21,] 1 0
## [22,] 1 0
## [23,] 1 0
##
## $str
## Buique Serido
## ap-davis 0.32232919 -0.32232919
## as-bimac 0.11236664 -0.11236664
## as-fasci -0.31298622 0.31298622
## ch-bimac -0.50460839 0.50460839
## ci-ocela -0.08257228 0.08257228
## ci-orien -0.63327851 0.63327851
## co-macro -0.20412415 0.20412415
## co-heter -0.20412415 0.20412415
## cr-menez -0.50460839 0.50460839
## cu-lepid 0.22268089 -0.22268089
## cy-gilbe 0.01343038 -0.01343038
## ge-brasi 0.69920590 -0.69920590
## he-margi -0.29546842 0.29546842
## ho-malab -0.65909298 0.65909298
## hy-pusar -0.44411739 0.44411739
## le-melan 0.22268089 -0.22268089
## le-piau -0.51645890 0.51645890
## le-taeni 0.22268089 -0.22268089
## mo-costa 0.22268089 -0.22268089
## mo-lepid -0.29546842 0.29546842
## or-nilot 0.63327851 -0.63327851
## pa-manag 0.47923384 -0.47923384
## pimel-sp -0.20412415 0.20412415
## po-retic 0.12844577 -0.12844577
## po-vivip -0.39393939 0.39393939
## pr-brevi -0.39393939 0.39393939
## ps-rhomb -0.20412415 0.20412415
## ps-genise -0.20412415 0.20412415
## se-heter -0.31298622 0.31298622
## se-piaba -0.20412415 0.20412415
## se-spilo -0.20412415 0.20412415
## st-noton -0.43929769 0.43929769
## sy-marmo -0.20412415 0.20412415
## te-chalc 0.32232919 -0.32232919
## tr-signa -0.17236256 0.17236256
##
## $A
## NULL
##
## $B
## NULL
##
## $sign
## s.Buique s.Serido index stat p.value
## ap-davis 1 0 1 0.32232919 0.234
## as-bimac 1 0 1 0.11236664 1.000
## as-fasci 0 1 2 0.31298622 0.198
## ch-bimac 0 1 2 0.50460839 0.035
## ci-ocela 0 1 2 0.08257228 1.000
## ci-orien 0 1 2 0.63327851 0.005
## co-macro 0 1 2 0.20412415 1.000
## co-heter 0 1 2 0.20412415 1.000
## cr-menez 0 1 2 0.50460839 0.037
## cu-lepid 1 0 1 0.22268089 0.530
## cy-gilbe 1 0 1 0.01343038 1.000
## ge-brasi 1 0 1 0.69920590 0.004
## he-margi 0 1 2 0.29546842 0.448
## ho-malab 0 1 2 0.65909298 0.003
## hy-pusar 0 1 2 0.44411739 0.064
## le-melan 1 0 1 0.22268089 0.454
## le-piau 0 1 2 0.51645890 0.029
## le-taeni 1 0 1 0.22268089 0.454
## mo-costa 1 0 1 0.22268089 0.530
## mo-lepid 0 1 2 0.29546842 0.474
## or-nilot 1 0 1 0.63327851 0.006
## pa-manag 1 0 1 0.47923384 0.038
## pimel-sp 0 1 2 0.20412415 1.000
## po-retic 1 0 1 0.12844577 0.627
## po-vivip 0 1 2 0.39393939 0.081
## pr-brevi 0 1 2 0.39393939 0.094
## ps-rhomb 0 1 2 0.20412415 1.000
## ps-genise 0 1 2 0.20412415 1.000
## se-heter 0 1 2 0.31298622 0.217
## se-piaba 0 1 2 0.20412415 1.000
## se-spilo 0 1 2 0.20412415 1.000
## st-noton 0 1 2 0.43929769 0.086
## sy-marmo 0 1 2 0.20412415 1.000
## te-chalc 1 0 1 0.32232919 0.234
## tr-signa 0 1 2 0.17236256 0.669
##
## attr(,"class")
## [1] "multipatt"
##
## Multilevel pattern analysis
## ---------------------------
##
## Association function: r.g
## Significance level (alpha): 0.05
##
## Total number of species: 35
## Selected number of species: 8
## Number of species associated to 1 group: 8
##
## List of species associated to each combination:
##
## Group Buique #sps. 3
## stat p.value
## ge-brasi 0.707 0.003 **
## or-nilot 0.642 0.008 **
## pa-manag 0.471 0.034 *
##
## Group Serido #sps. 5
## stat p.value
## ho-malab 0.656 0.002 **
## ci-orien 0.642 0.005 **
## le-piau 0.521 0.028 *
## ch-bimac 0.513 0.042 *
## cr-menez 0.513 0.046 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Buique Serido
## ap-davis 0.316 -0.316
## as-bimac 0.113 -0.113
## as-fasci -0.314 0.314
## ch-bimac -0.513 0.513
## ci-ocela -0.083 0.083
## ci-orien -0.642 0.642
## Buique Serido Buique+Serido
## ap-davis 0.426 0.000 0.295
## as-bimac 0.648 0.670 0.933
## as-fasci 0.220 0.693 0.659
## ch-bimac 0.000 0.645 0.466
## ci-ocela 0.130 0.476 0.466
## ci-orien 0.000 0.764 0.552Outras funções podem ser usadas para estimar e testar a associação entre espécies e grupos de Unidades Amostrais, mas estas funções estão além do interesse desse livro. Mais importante, é que quarto Índices de Associações (IA) são possíveis no pacote indicspecies (func=)(CITA):
IndVal: o Valor Indicativo (IV), originalmente proposto por (CITA),
IndVal.g: uma extenção do IV (CITA), que é usada como padrão (default) pela funçãomultipatt(CITA),
re,
r.g.
O Índice de Associação escolhido na Análise de Espécies Indicadoras deve ser reportado na metodologia quando o trabalho é publicado. Para ver mais detalhes e exemplos desses IA’s ?indicspecies e ?multipatt.
Até o momento temos usado o IA padrão, IndVal.g.
7.8 ANOSIM e SIMPER
SIMPER (“SIMilarity PERrcentages)
dist <- vegdist(m_trab)
ano <- with(t_grps, anosim(dist, grp))
ano
summary(ano)
plot(ano)
sim_total <- with(t_grps, simper(m_trab, permutations = 999))
sim_total
sim <- with(t_grps, simper(m_trab, grp, permutations = 999))
sim
summary(sim, ordered = TRUE)##
## Call:
## anosim(x = dist, grouping = grp)
## Dissimilarity: bray
##
## ANOSIM statistic R: 0.3022
## Significance: 0.002
##
## Permutation: free
## Number of permutations: 999
##
##
## Call:
## anosim(x = dist, grouping = grp)
## Dissimilarity: bray
##
## ANOSIM statistic R: 0.3022
## Significance: 0.002
##
## Permutation: free
## Number of permutations: 999
##
## Upper quantiles of permutations (null model):
## 90% 95% 97.5% 99%
## 0.0831 0.1154 0.1323 0.1977
##
## Dissimilarity ranks between and within classes:
## 0% 25% 50% 75% 100% N
## Between 6 78 154.5 209.5 248 132
## Buique 2 60 115.0 158.5 228 55
## Serido 1 38 94.0 157.5 241 66
##
## cumulative contributions of most influential species:
##
## $total
## as-bimac ge-brasi po-vivip ch-bimac or-nilot pa-manag se-heter
## 0.2023113 0.3166006 0.4155793 0.5132010 0.6057372 0.6948231 0.7349352
##
## cumulative contributions of most influential species:
##
## $Serido_Buique
## as-bimac ge-brasi pa-manag po-vivip ch-bimac or-nilot
## 0.1903761 0.3214618 0.4192176 0.5159272 0.6104916 0.7026686
##
##
## Contrast: Serido_Buique
##
## average sd ratio ava avb cumsum p
## as-bimac 0.16854 0.15123 1.11450 106.58000 91.27000 0.190 0.625
## ge-brasi 0.11605 0.15749 0.73690 0.67000 92.00000 0.322 0.008 **
## pa-manag 0.08654 0.14784 0.58540 0.00000 50.27000 0.419 0.033 *
## po-vivip 0.08562 0.10015 0.85490 63.25000 19.91000 0.516 0.260
## ch-bimac 0.08372 0.14759 0.56720 58.75000 0.00000 0.611 0.273
## or-nilot 0.08161 0.10024 0.81410 27.08000 46.64000 0.703 0.134
## se-heter 0.03378 0.04825 0.70000 13.50000 12.18000 0.741 0.503
## te-chalc 0.02516 0.06544 0.38450 0.00000 12.18000 0.769 0.123
## cy-gilbe 0.02430 0.07348 0.33070 4.17000 7.36000 0.797 0.366
## tr-signa 0.02428 0.05666 0.42860 15.08000 2.45000 0.824 0.763
## po-retic 0.02355 0.05185 0.45410 2.08000 29.27000 0.851 0.213
## pr-brevi 0.02129 0.03600 0.59130 21.17000 1.45000 0.875 0.757
## ci-orien 0.01908 0.03370 0.56610 11.92000 0.00000 0.896 0.213
## ci-ocela 0.01690 0.04108 0.41140 5.33000 0.55000 0.915 0.497
## st-noton 0.01612 0.03247 0.49660 17.08000 0.00000 0.934 0.513
## as-fasci 0.01507 0.02321 0.64920 11.00000 2.36000 0.951 0.465
## ho-malab 0.01222 0.01219 1.00260 8.75000 0.36000 0.964 0.011 *
## se-piaba 0.00678 0.02344 0.28910 5.67000 0.00000 0.972 0.754
## hy-pusar 0.00655 0.01194 0.54850 5.83000 0.09000 0.980 0.392
## ap-davis 0.00426 0.01123 0.37940 0.00000 2.45000 0.984 0.124
## mo-lepid 0.00397 0.01342 0.29570 3.33000 0.00000 0.989 0.750
## cu-lepid 0.00301 0.01032 0.29150 0.00000 1.91000 0.992 0.292
## cr-menez 0.00238 0.00487 0.48800 2.33000 0.00000 0.995 0.446
## le-piau 0.00221 0.00332 0.66450 1.17000 0.09000 0.997 0.125
## pimel-sp 0.00060 0.00207 0.28910 0.50000 0.00000 0.998 0.753
## le-melan 0.00044 0.00161 0.27510 0.00000 0.18000 0.999 0.233
## sy-marmo 0.00025 0.00097 0.25600 0.08000 0.00000 0.999 0.678
## le-taeni 0.00022 0.00081 0.27510 0.00000 0.09000 0.999 0.233
## co-macro 0.00021 0.00073 0.28810 0.17000 0.00000 0.999 0.766
## he-margi 0.00020 0.00047 0.41840 0.17000 0.00000 1.000 0.491
## mo-costa 0.00014 0.00049 0.29150 0.00000 0.09000 1.000 0.292
## co-heter 0.00010 0.00034 0.28910 0.08000 0.00000 1.000 0.752
## ps-rhomb 0.00006 0.00019 0.29560 0.08000 0.00000 1.000 0.813
## ps-genise 0.00006 0.00019 0.29560 0.08000 0.00000 1.000 0.813
## se-spilo 0.00006 0.00019 0.29560 0.08000 0.00000 1.000 0.813
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Permutation: free
## Number of permutations: 999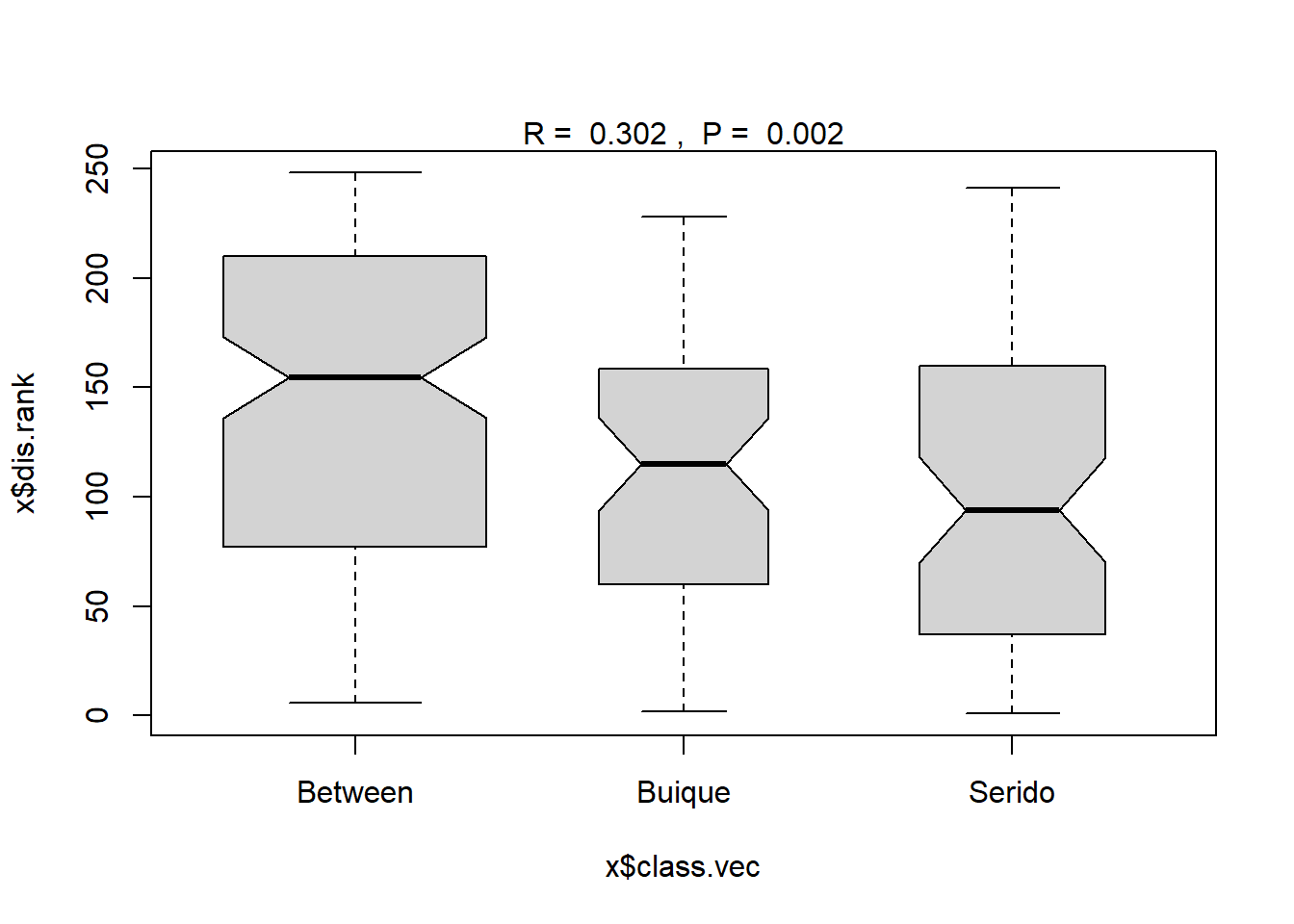
7.9 PerMANOVA usando Matrizes de Distâncias adonis2
Permutational Multivariate ANalysis 0f VAriance using Distance Matrices
adonis2(m_trab ~ area, data = t_grps, method = "bray")
## default test by terms
adonis2(m_trab ~ area*ambiente, data = t_grps)
## overall tests
adonis2(m_trab ~ area*ambiente, data = t_grps, by = NULL)## Permutation test for adonis under reduced model
## Terms added sequentially (first to last)
## Permutation: free
## Number of permutations: 999
##
## adonis2(formula = m_trab ~ area, data = t_grps, method = "bray")
## Df SumOfSqs R2 F Pr(>F)
## area 1 0.9772 0.11983 2.8589 0.001 ***
## Residual 21 7.1781 0.88017
## Total 22 8.1554 1.00000
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Permutation test for adonis under reduced model
## Terms added sequentially (first to last)
## Permutation: free
## Number of permutations: 999
##
## adonis2(formula = m_trab ~ area * ambiente, data = t_grps)
## Df SumOfSqs R2 F Pr(>F)
## area 1 0.9772 0.11983 3.3624 0.001 ***
## ambiente 1 0.8867 0.10872 3.0508 0.001 ***
## area:ambiente 1 0.7694 0.09435 2.6475 0.003 **
## Residual 19 5.5220 0.67710
## Total 22 8.1554 1.00000
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Permutation test for adonis under reduced model
## Permutation: free
## Number of permutations: 999
##
## adonis2(formula = m_trab ~ area * ambiente, data = t_grps, by = NULL)
## Df SumOfSqs R2 F Pr(>F)
## Model 3 2.6333 0.3229 3.0202 0.001 ***
## Residual 19 5.5220 0.6771
## Total 22 8.1554 1.0000
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Anderson (2001, Fig. 4) warns that the method may confound location and dispersion effects: significant differences may be caused by different within-group variation (dispersion) instead of different mean values of the groups (see Warton et al. 2012 for a general analysis). However, it seems that adonis2 is less sensitive to dispersion effects than some of its alternatives (anosim, mrpp). Function betadisper is a sister function to adonis2 to study the differences in dispersion within the same geometric framework.
7.9.1 Usando função betadisper
## Bray-Curtis distances between samples
dis <- vegdist(m_trab)
## Calculate multivariate dispersions
mod <- betadisper(dis, groups)
mod
## Perform test
anova(mod)
## Permutation test for F
permutest(mod, pairwise = TRUE, permutations = 99)
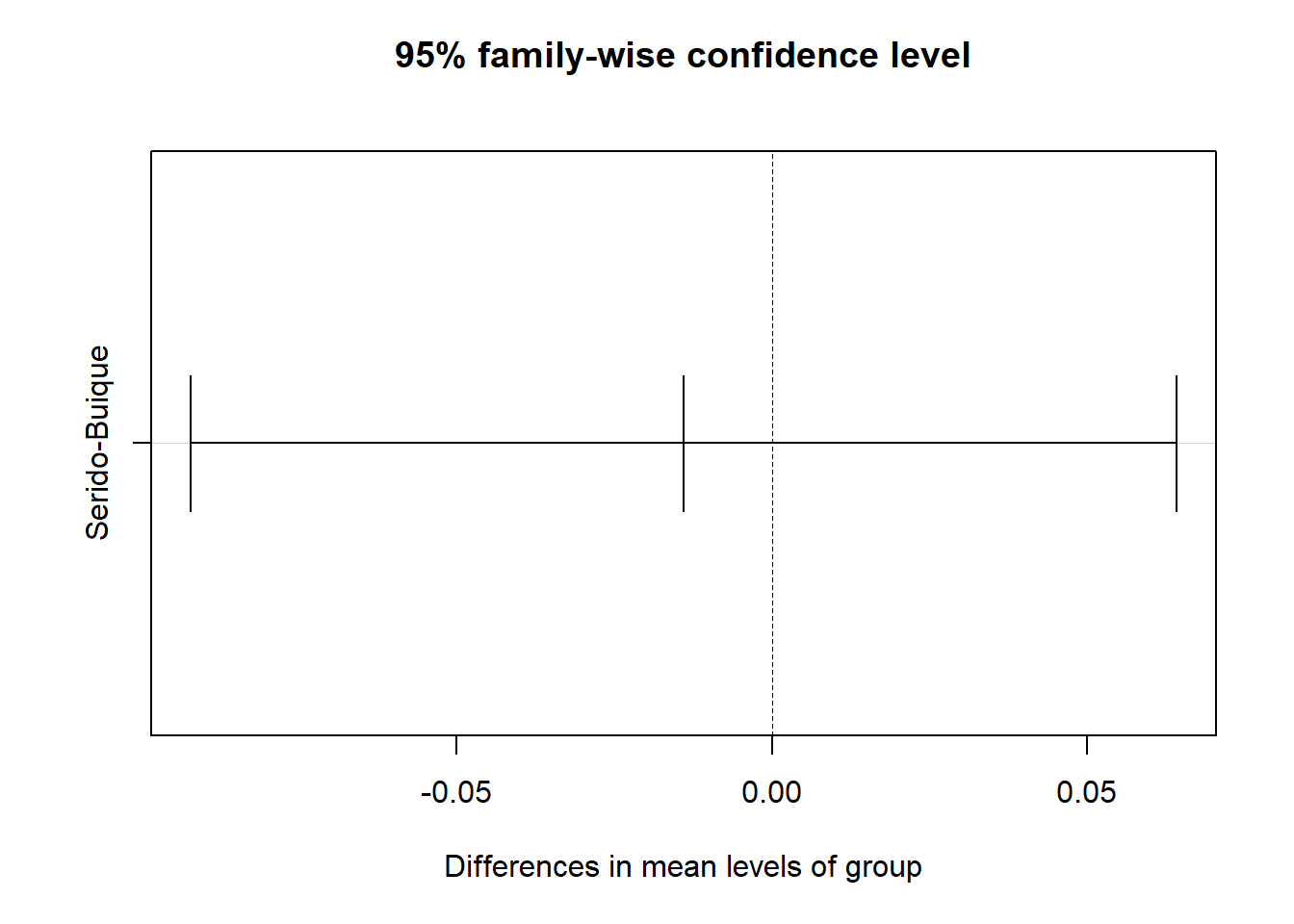
## Tukey's Honest Significant Differences
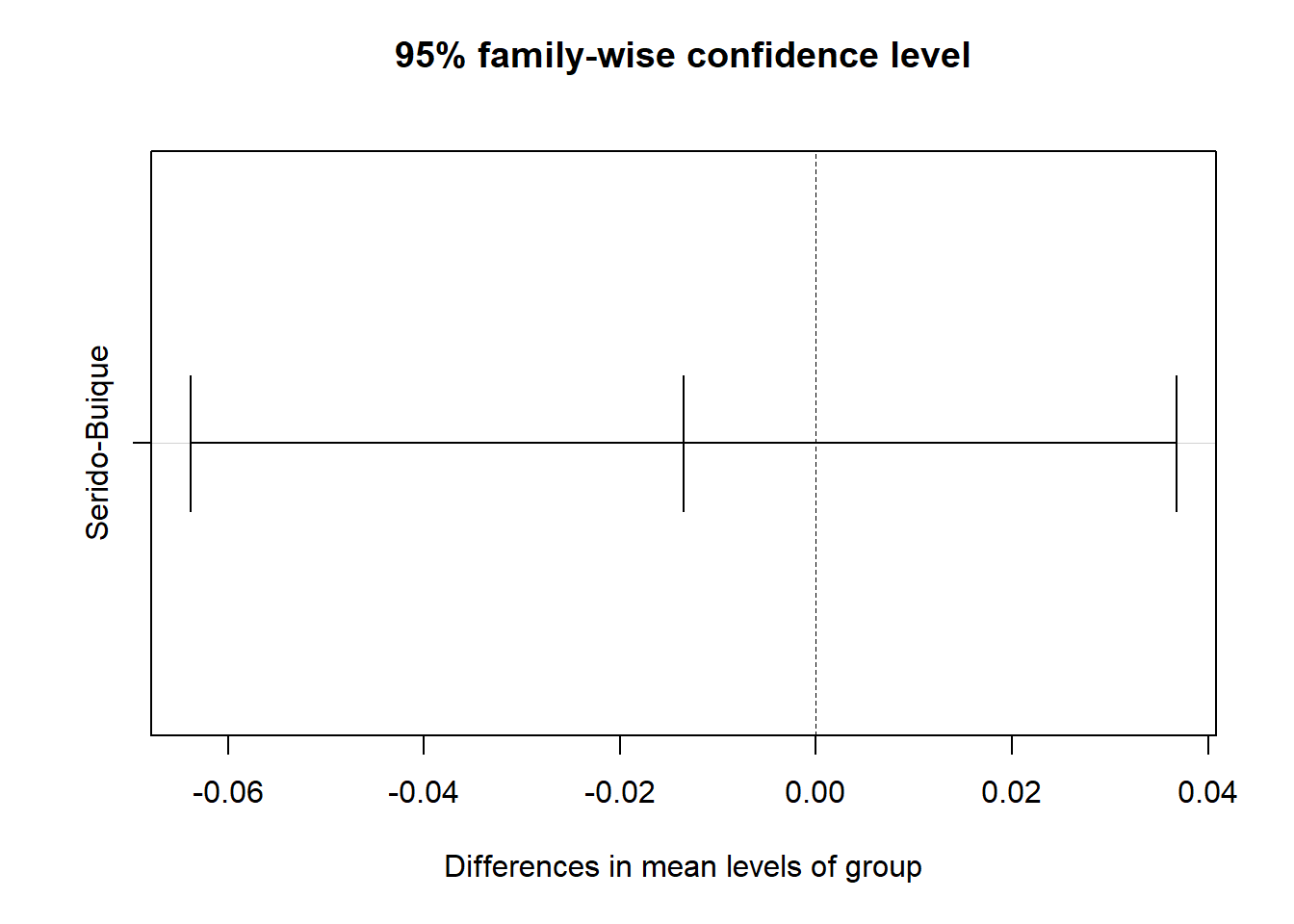
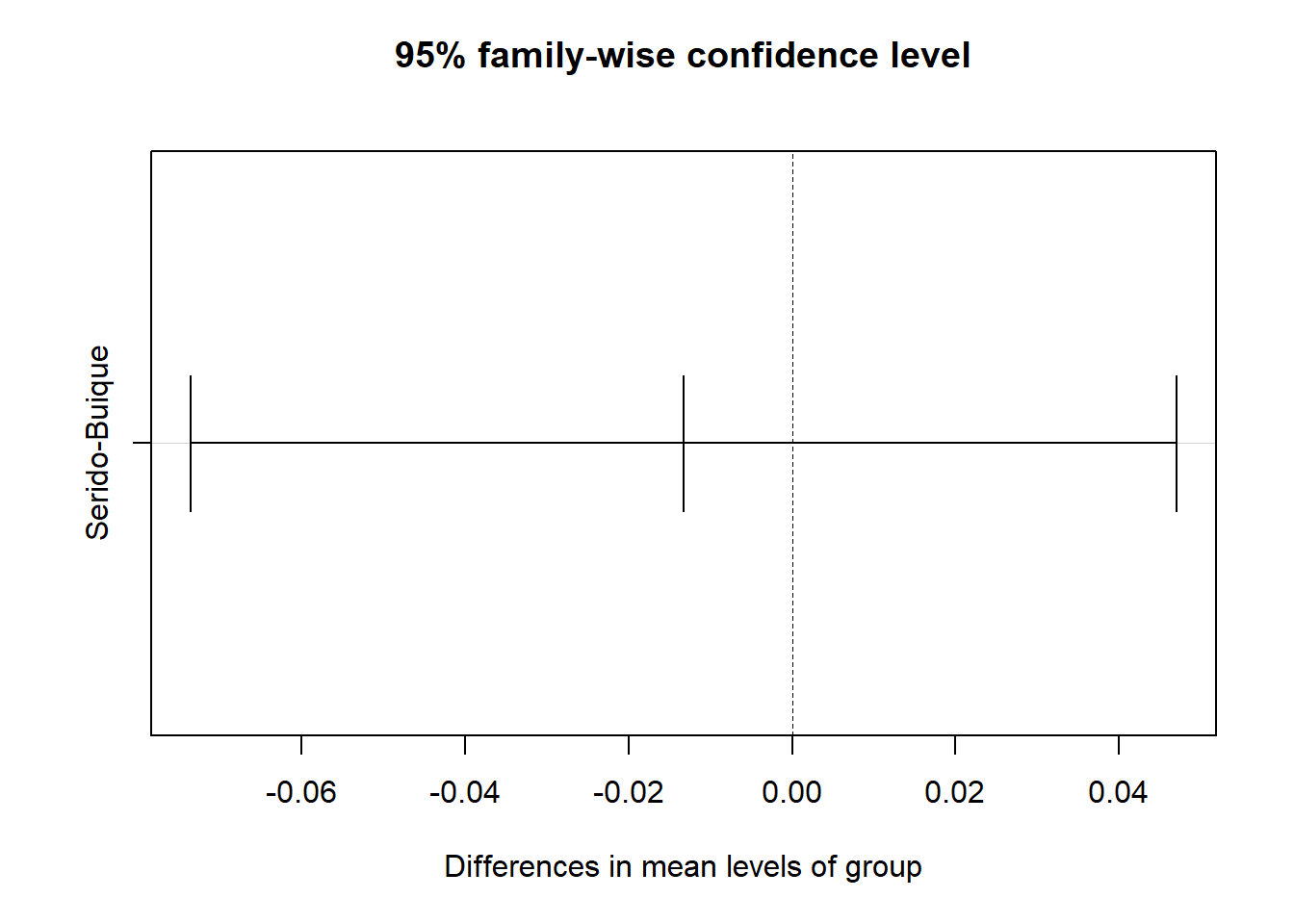
mod.HSD <- TukeyHSD(mod)
plot(mod.HSD)
## Plot the groups and distances to centroids on the
## first two PCoA axes
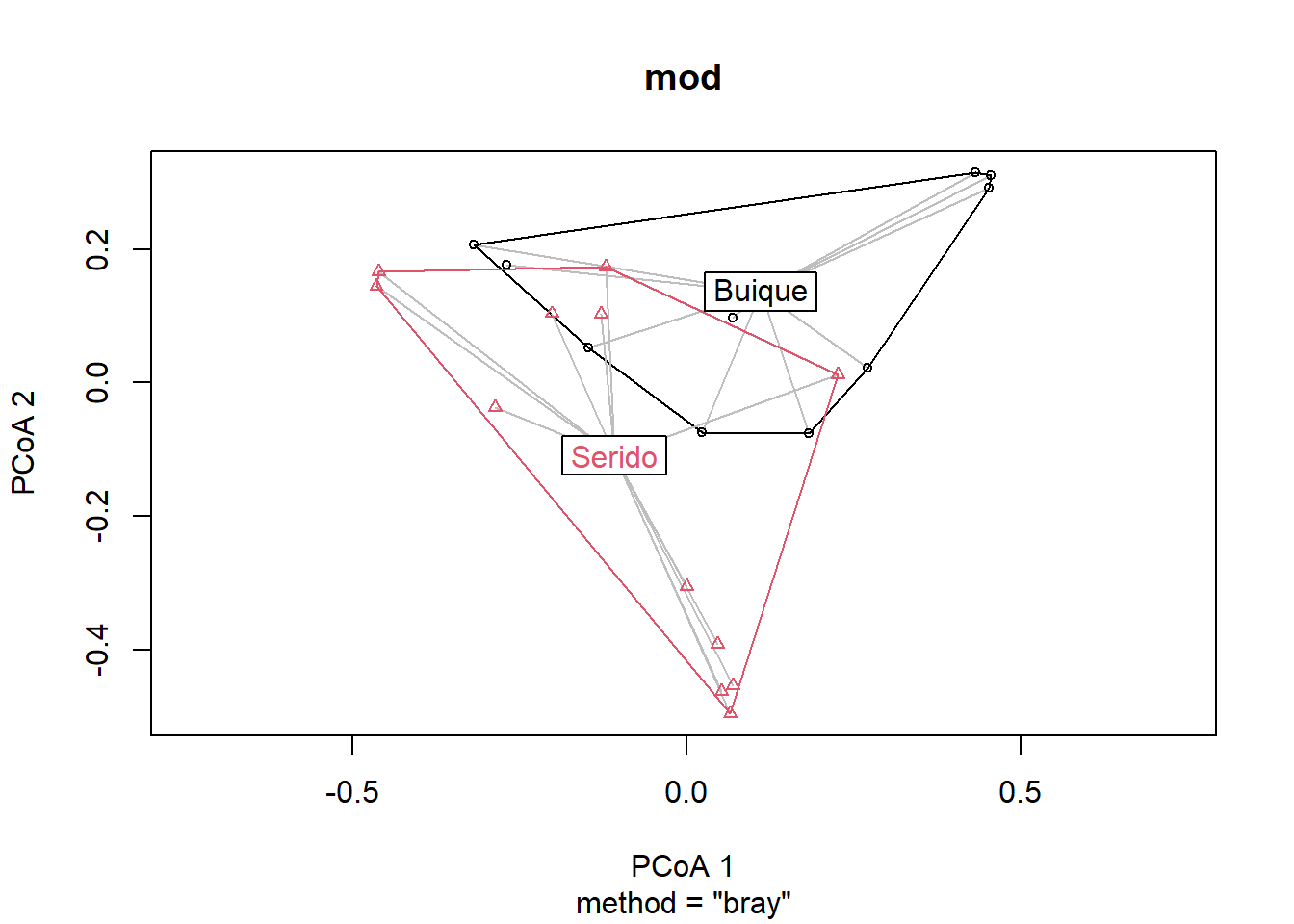
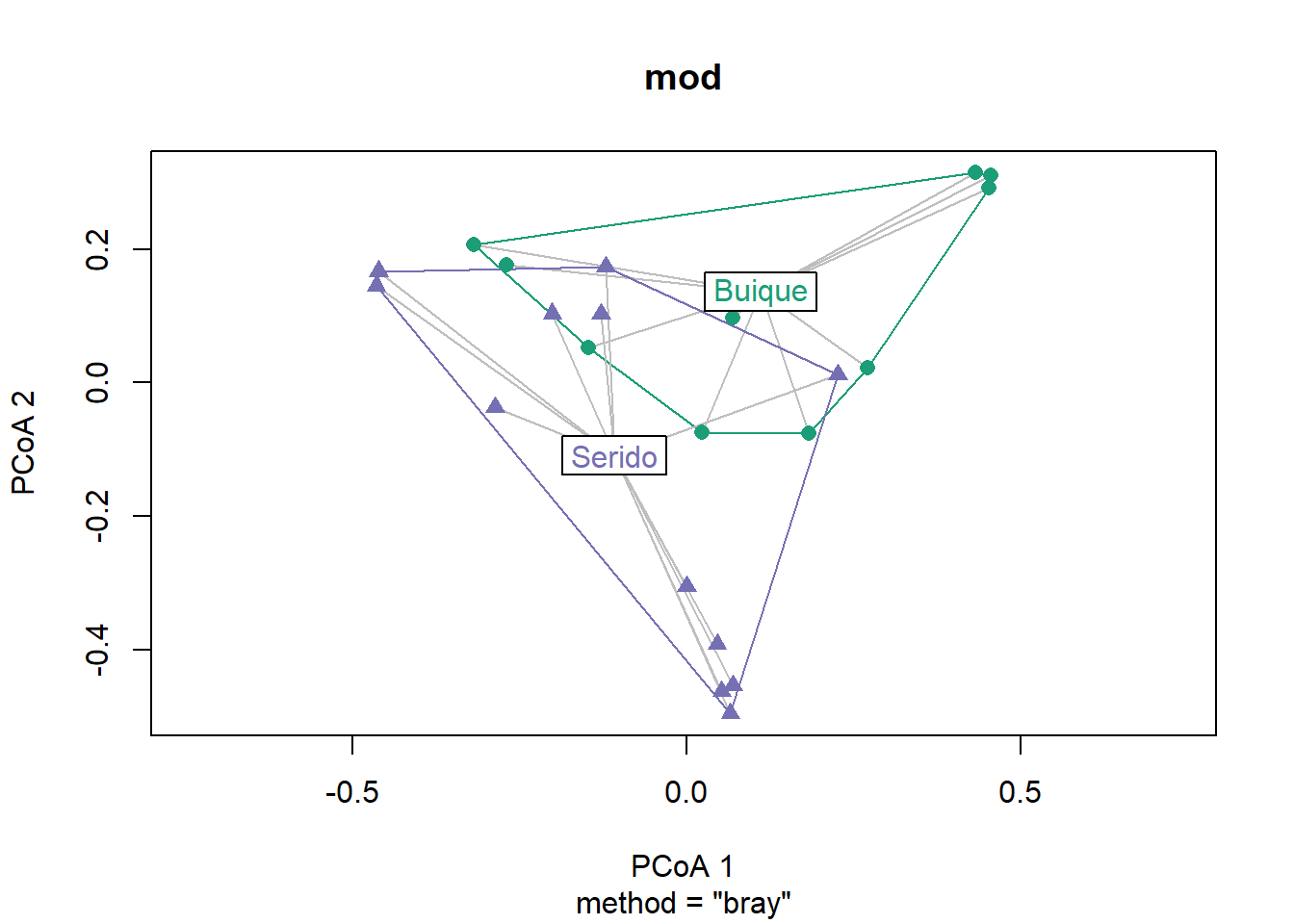
plot(mod)
## with data ellipses instead of hulls
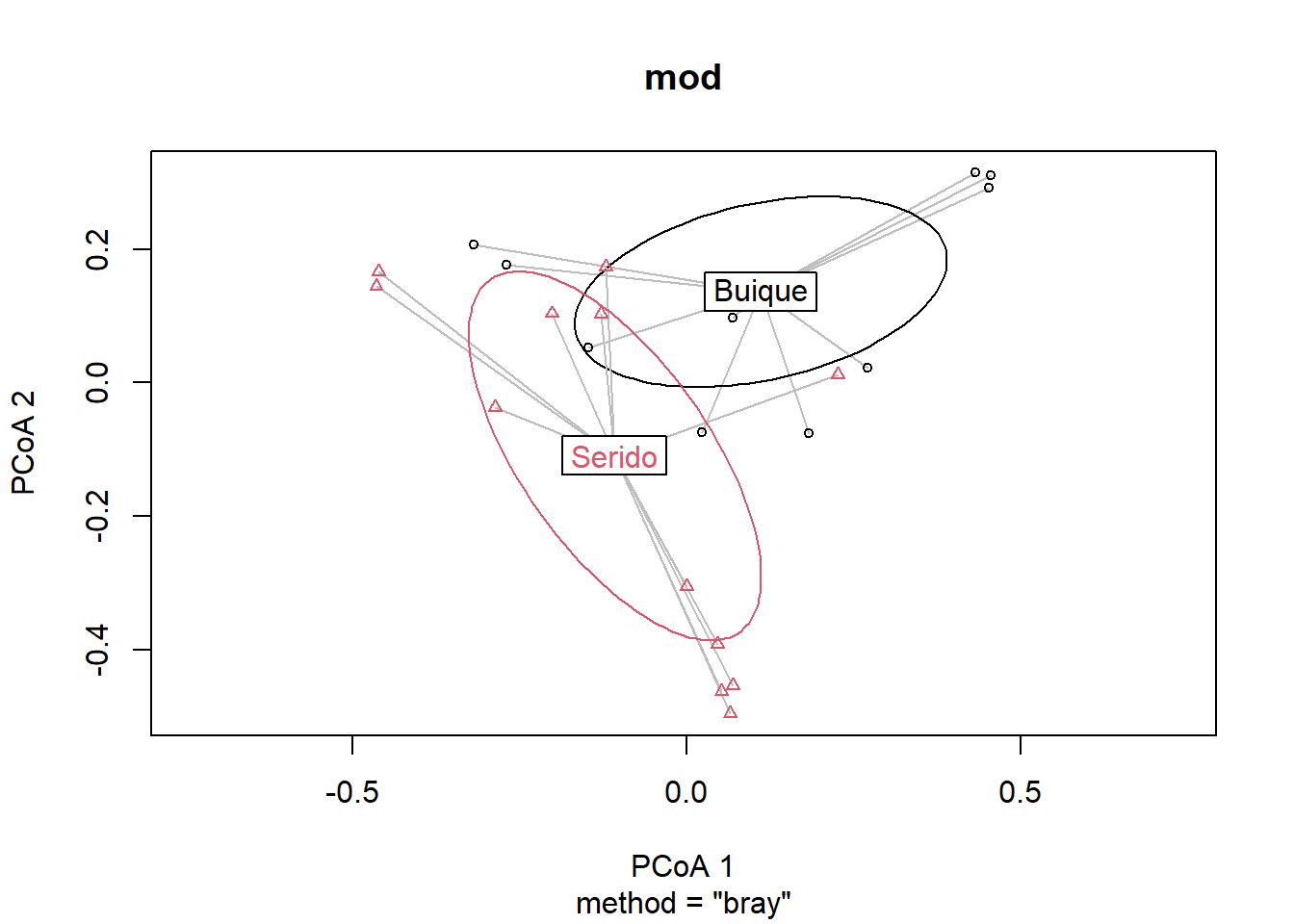
plot(mod, ellipse = TRUE, hull = FALSE) # 1 sd data ellipse
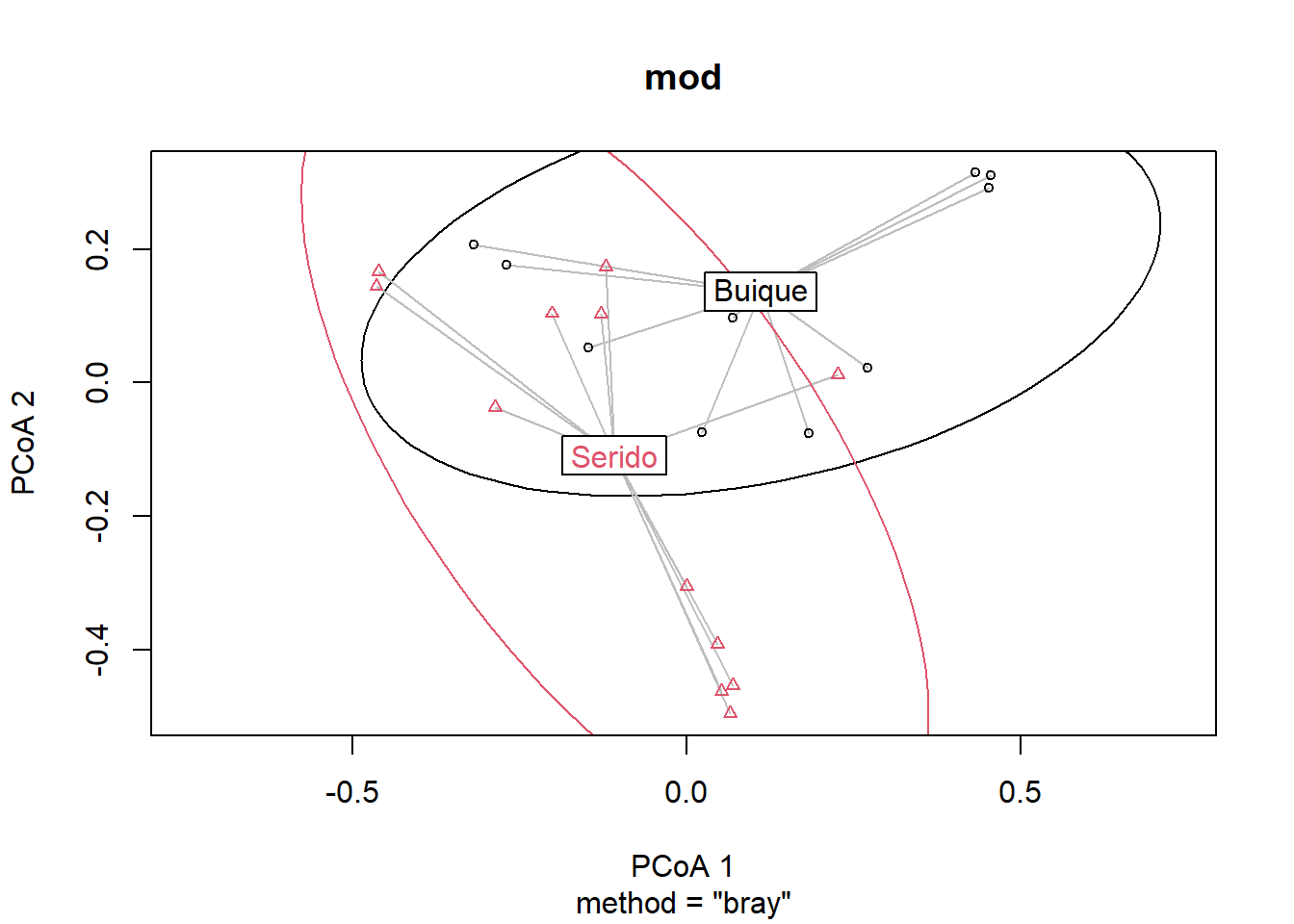
plot(mod, ellipse = TRUE, hull = FALSE, conf = 0.90) # 90% data ellipse
# plot with manual colour specification
my_cols <- c("#1b9e77", "#7570b3")
plot(mod, col = my_cols, pch = c(16,17), cex = 1.1)
## can also specify which axes to plot, ordering respected
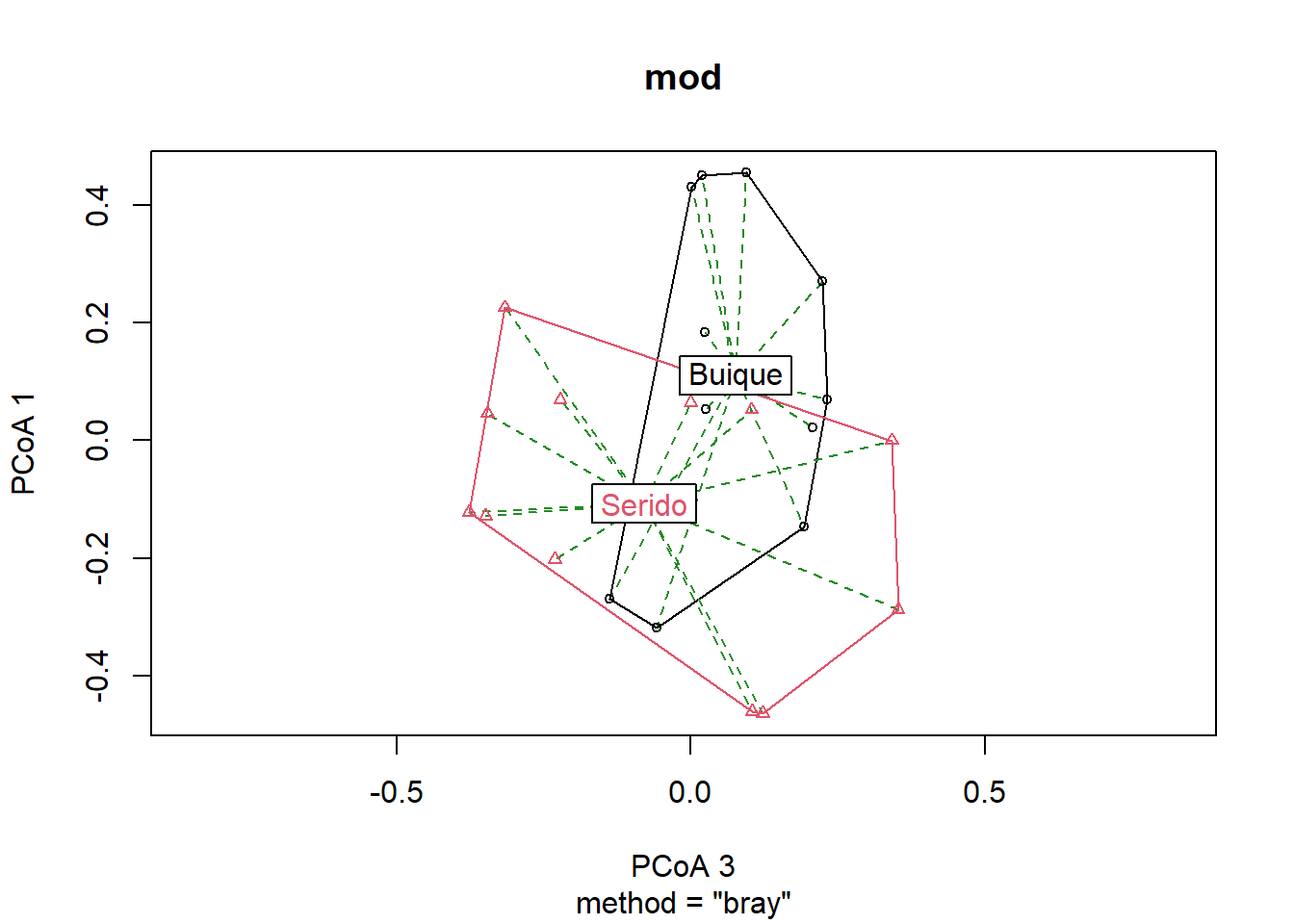
plot(mod, axes = c(3,1), seg.col = "forestgreen", seg.lty = "dashed")
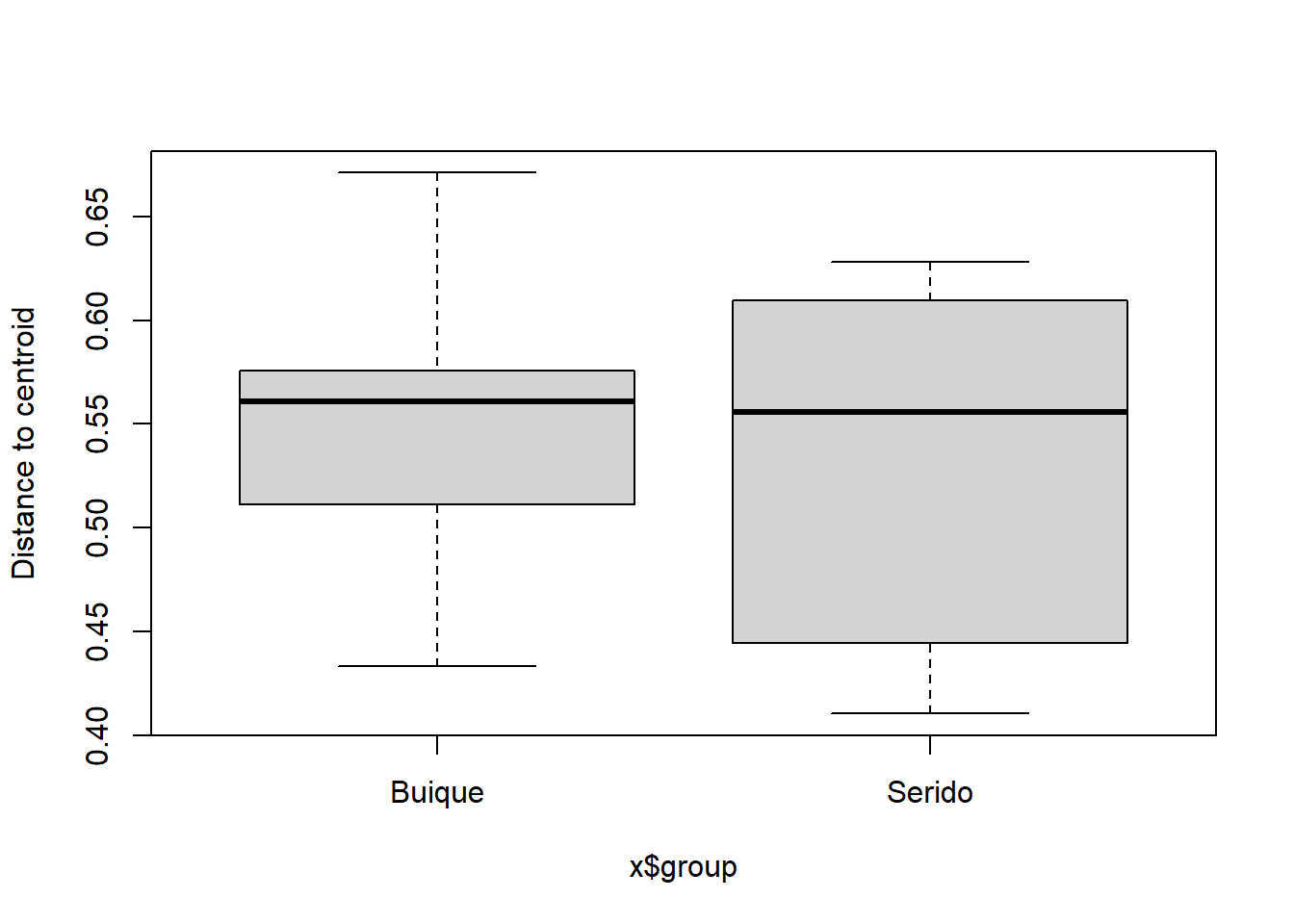
## Draw a boxplot of the distances to centroid for each group
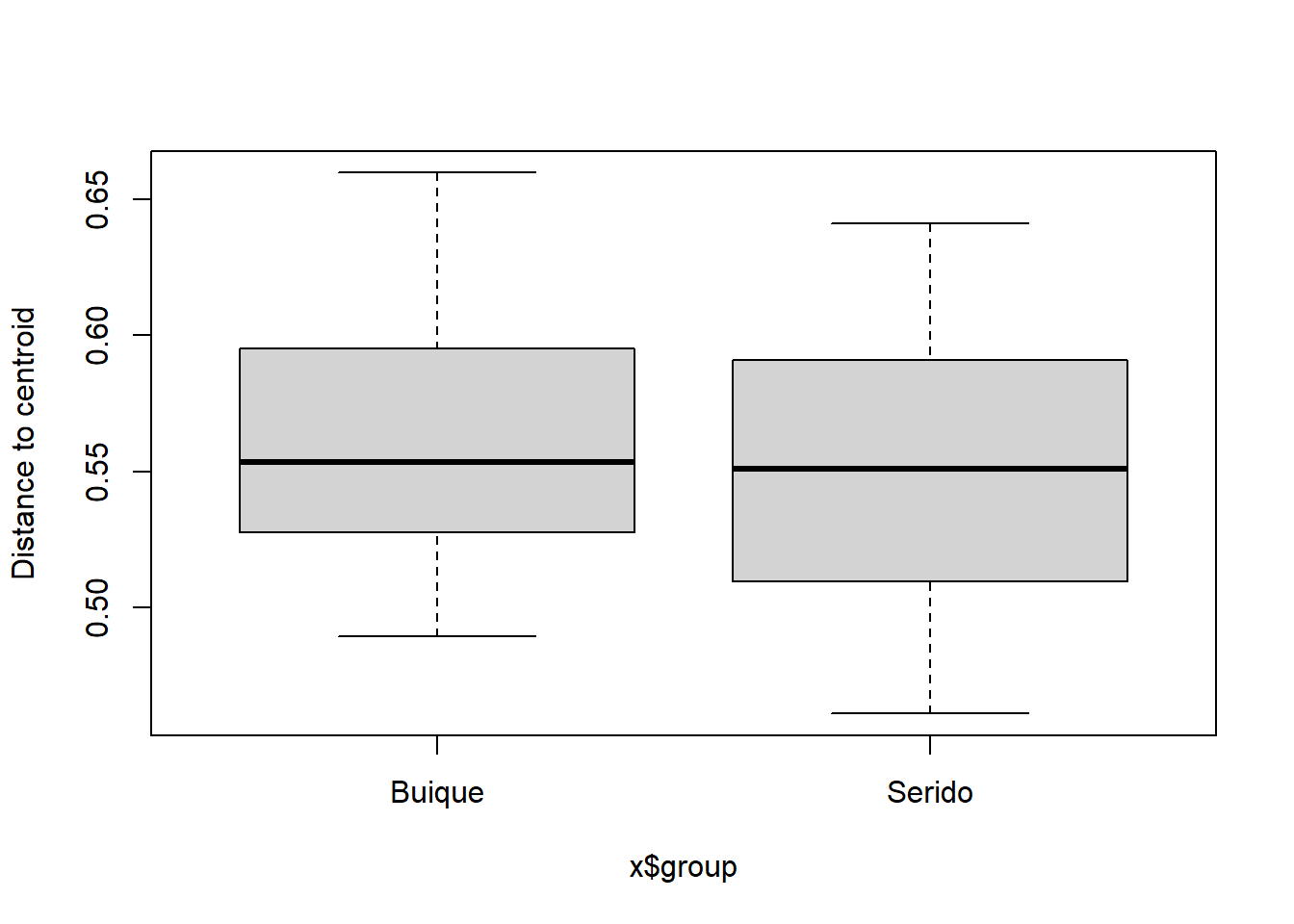
boxplot(mod)
## `scores` and `eigenvals` also work
scrs <- scores(mod)
str(scrs)
head(scores(mod, 1:4, display = "sites"))
# group centroids/medians
scores(mod, 1:4, display = "centroids")
# eigenvalues from the underlying principal coordinates analysis
eigenvals(mod)
## try out bias correction; compare with mod3
mod3B <- betadisper(dis, groups, type = "median", bias.adjust=TRUE)
anova(mod3B)
permutest(mod3B, permutations = 99)
## should always work for a single group
group <- factor(rep("Serido", NROW(m_trab)))
tmp <- betadisper(dis, group, type = "median")
tmp <- betadisper(dis, group, type = "centroid")
## simulate missing values in 'd' and 'group'
## using spatial medians
groups[c(2,20)] <- NA
dis[c(2, 20)] <- NA
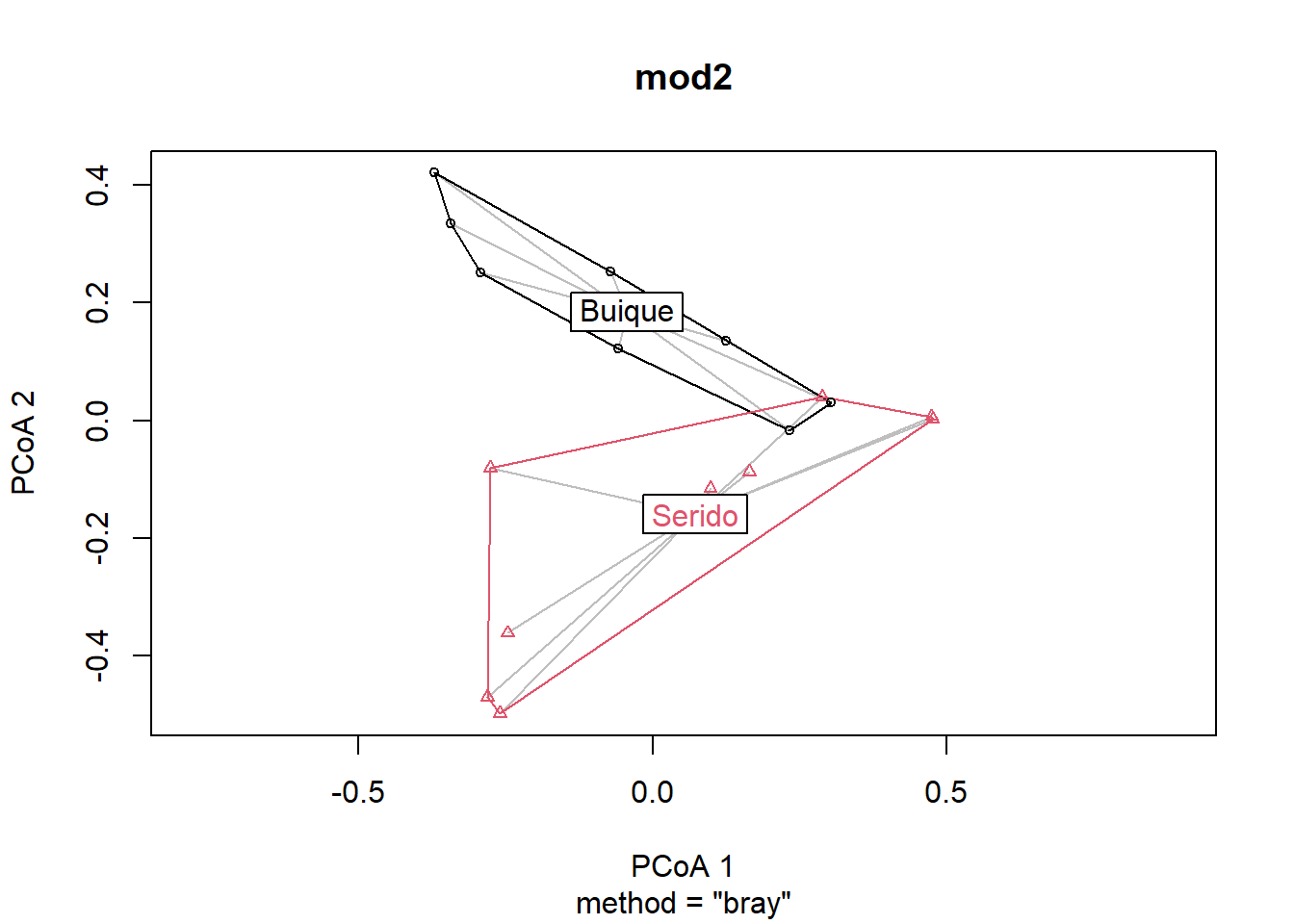
mod2 <- betadisper(dis, groups) ## messages## missing observations due to 'group' removed## missing observations due to 'd' removedmod2
permutest(mod2, permutations = 99)
anova(mod2)
plot(mod2)
boxplot(mod2)
plot(TukeyHSD(mod2))
## Using group centroids
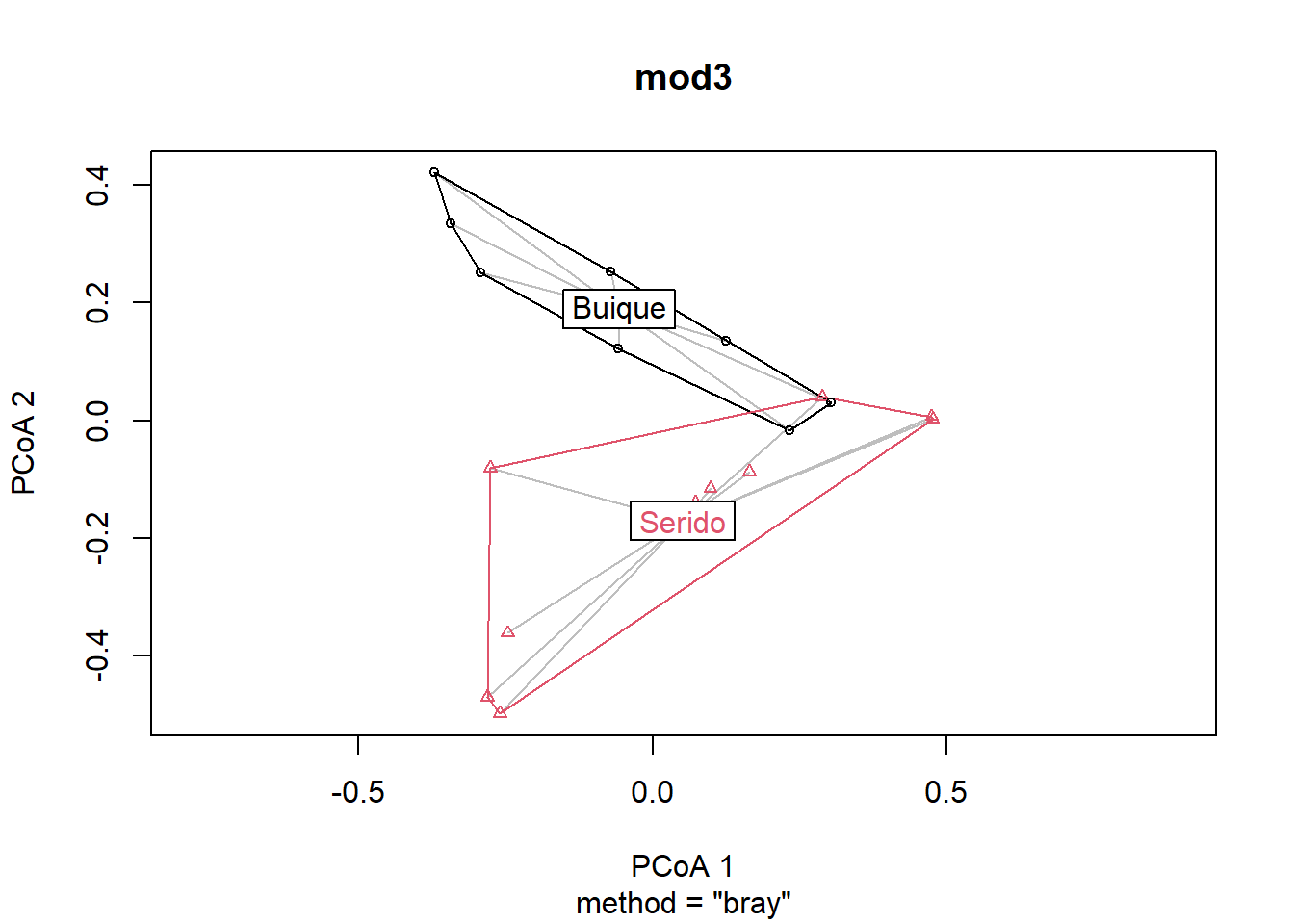
mod3 <- betadisper(dis, groups, type = "centroid")## missing observations due to 'group' removed
## missing observations due to 'd' removedmod3
permutest(mod3, permutations = 99)
anova(mod3)
plot(mod3)
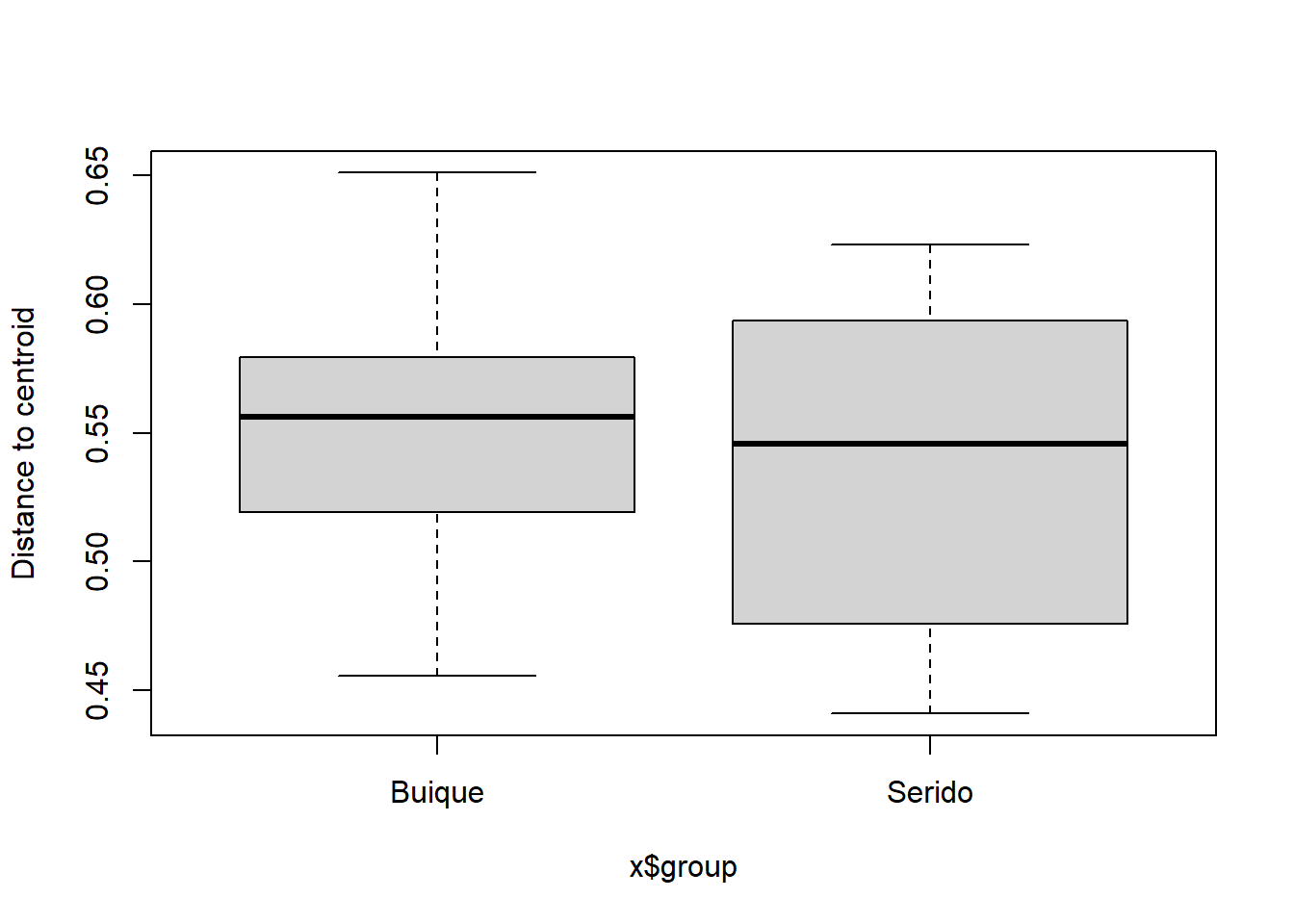
boxplot(mod3)
plot(TukeyHSD(mod3))##
## Homogeneity of multivariate dispersions
##
## Call: betadisper(d = dis, group = groups)
##
## No. of Positive Eigenvalues: 19
## No. of Negative Eigenvalues: 3
##
## Average distance to median:
## Buique Serido
## 0.5633 0.5497
##
## Eigenvalues for PCoA axes:
## (Showing 8 of 22 eigenvalues)
## PCoA1 PCoA2 PCoA3 PCoA4 PCoA5 PCoA6 PCoA7 PCoA8
## 1.5581 1.4071 1.0818 0.8493 0.7219 0.5358 0.3977 0.3573
## Analysis of Variance Table
##
## Response: Distances
## Df Sum Sq Mean Sq F value Pr(>F)
## Groups 1 0.001048 0.0010480 0.3123 0.5822
## Residuals 21 0.070467 0.0033556
##
## Permutation test for homogeneity of multivariate dispersions
## Permutation: free
## Number of permutations: 99
##
## Response: Distances
## Df Sum Sq Mean Sq F N.Perm Pr(>F)
## Groups 1 0.001048 0.0010480 0.3123 99 0.65
## Residuals 21 0.070467 0.0033556
##
## Pairwise comparisons:
## (Observed p-value below diagonal, permuted p-value above diagonal)
## Buique Serido
## Buique 0.64
## Serido 0.58218
## List of 2
## $ sites : num [1:23, 1:2] -0.201726 0.052322 -0.000111 -0.128525 0.069086 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:23] "S-R-CT1" "S-R-CP1" "S-A-TA1" "S-R-CT2" ...
## .. ..$ : chr [1:2] "PCoA1" "PCoA2"
## $ centroids: num [1:2, 1:2] 0.111 -0.108 0.136 -0.109
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:2] "Buique" "Serido"
## .. ..$ : chr [1:2] "PCoA1" "PCoA2"
## PCoA1 PCoA2 PCoA3 PCoA4
## S-R-CT1 -0.2017256132 0.10351405 -0.2321564 -0.12321307
## S-R-CP1 0.0523216794 -0.46253086 0.1031103 -0.03425336
## S-A-TA1 -0.0001105738 -0.30528913 0.3413382 -0.11053590
## S-R-CT2 -0.1285245294 0.10255946 -0.3491635 -0.11933450
## S-R-CP2 0.0690861087 -0.45374951 -0.2225214 0.12328578
## S-A-TA2 -0.2871743927 -0.03736118 0.3523556 -0.22773557
## PCoA1 PCoA2 PCoA3 PCoA4
## Buique 0.1107821 0.1362774 0.07608946 0.06671195
## Serido -0.1076160 -0.1092139 -0.07921639 -0.06354072
## PCoA1 PCoA2 PCoA3 PCoA4 PCoA5 PCoA6 PCoA7
## 1.5581366 1.4071471 1.0818039 0.8492572 0.7218736 0.5358491 0.3976945
## PCoA8 PCoA9 PCoA10 PCoA11 PCoA12 PCoA13 PCoA14
## 0.3572736 0.2888030 0.2084683 0.1972004 0.1604109 0.1094020 0.1042547
## PCoA15 PCoA16 PCoA17 PCoA18 PCoA19 PCoA20 PCoA21
## 0.0875008 0.0806762 0.0506834 0.0308129 0.0195090 -0.0042791 -0.0237525
## PCoA22
## -0.0633588
## Analysis of Variance Table
##
## Response: Distances
## Df Sum Sq Mean Sq F value Pr(>F)
## Groups 1 0.001574 0.0015739 0.4282 0.52
## Residuals 21 0.077190 0.0036757
##
## Permutation test for homogeneity of multivariate dispersions
## Permutation: free
## Number of permutations: 99
##
## Response: Distances
## Df Sum Sq Mean Sq F N.Perm Pr(>F)
## Groups 1 0.001574 0.0015739 0.4282 99 0.51
## Residuals 21 0.077190 0.0036757
##
## Homogeneity of multivariate dispersions
##
## Call: betadisper(d = dis, group = groups)
##
## No. of Positive Eigenvalues: 16
## No. of Negative Eigenvalues: 2
##
## Average distance to median:
## Buique Serido
## 0.5474 0.5334
##
## Eigenvalues for PCoA axes:
## (Showing 8 of 18 eigenvalues)
## PCoA1 PCoA2 PCoA3 PCoA4 PCoA5 PCoA6 PCoA7 PCoA8
## 1.3690 1.1263 0.9269 0.8041 0.6184 0.4063 0.3270 0.2469
##
## Permutation test for homogeneity of multivariate dispersions
## Permutation: free
## Number of permutations: 99
##
## Response: Distances
## Df Sum Sq Mean Sq F N.Perm Pr(>F)
## Groups 1 0.000931 0.0009314 0.1433 99 0.7
## Residuals 17 0.110468 0.0064981
## Analysis of Variance Table
##
## Response: Distances
## Df Sum Sq Mean Sq F value Pr(>F)
## Groups 1 0.000931 0.0009314 0.1433 0.7097
## Residuals 17 0.110468 0.0064981
##
## Homogeneity of multivariate dispersions
##
## Call: betadisper(d = dis, group = groups, type = "centroid")
##
## No. of Positive Eigenvalues: 16
## No. of Negative Eigenvalues: 2
##
## Average distance to centroid:
## Buique Serido
## 0.5480 0.5348
##
## Eigenvalues for PCoA axes:
## (Showing 8 of 18 eigenvalues)
## PCoA1 PCoA2 PCoA3 PCoA4 PCoA5 PCoA6 PCoA7 PCoA8
## 1.3690 1.1263 0.9269 0.8041 0.6184 0.4063 0.3270 0.2469
##
## Permutation test for homogeneity of multivariate dispersions
## Permutation: free
## Number of permutations: 99
##
## Response: Distances
## Df Sum Sq Mean Sq F N.Perm Pr(>F)
## Groups 1 0.000833 0.0008334 0.2153 99 0.7
## Residuals 17 0.065793 0.0038702
## Analysis of Variance Table
##
## Response: Distances
## Df Sum Sq Mean Sq F value Pr(>F)
## Groups 1 0.000833 0.0008334 0.2153 0.6485
## Residuals 17 0.065793 0.0038702