9 R Modulo 3-1

Estatísticas descritivas e Normalidade

RESUMO

Apresentação

A estatística descritiva tem um papel importante a desempenhar na ciência. Quando problemas específicos são tratados na ciência, os dados precisam ser coletados, analisados e apresentados de forma concisa para que outros possam se beneficiar do que foi encontrado. Geralmente não é possível apresentar um conjunto de dados completo em uma publicação ou em um seminário e, mesmo que fosse, é improvável isso permitisse uma boa comunicação dos resultados da pesquisa. Em vez disso, os dados são geralmente resumidos como tabelas de frequência, histogramas e estatísticas descritivas que os leitores ou ouvintes podem assimilar prontamente, mas que ainda transmitem os elementos essenciais do conjunto de dados original. O principal objetivo do cálculo das estatísticas descritivas é transmitir informações essenciais contidas em um conjunto de dados da forma mais concisa e clara possível.

9.1 Sobre os dados

Considere os dados sobre o comprimento dos brotos de Banksia ericifolia de charnecas³ na Baía de Jervis, Austrália (Bradstock, Tozer, and Keith 1997) (Figura 9.1). Existem 500 medições, um conjunto de dados formidável. Por inspeção, o comprimento mínimo do broto é 10,0 e o máximo é 44,9 cm. Esses valores definem o intervalo da amostra. Agora precisamos subdividir o intervalo em intervalos ou classes, cada um com o mesmo tamanho. Geralmente, é aconselhável arredondar o valor mínimo para baixo e o valor máximo para valores apropriados ao decidir as classes de intervalos. Nesse caso, parece sensato dividir a faixa de 10 a 45 cm em sete intervalos a cada 5 cm de largura. Se contarmos o número de brotos que se encontram em cada um dos sete intervalos, temos a base para a tabulação da frequência. A coluna de frequência foi obtida contando o número de medições que existem dentro de cada classe. A coluna de frequência percentual foi obtida representando cada contagem como uma porcentagem da contagem total. A frequência cumulativa e as frequências percentuais cumulativas foram obtidas somando progressivamente as frequências correspondentes.

Figura 9.1: Comprimentos (cm) de 500 brotos do arbusto Banksia ericifolia de charnecas na Baía de Jervis, Austrália.

9.2 Organização básica

rm(list=ls(all=TRUE)) #limpa a memória

Instalando os pacotes necessários para esse módulo

install.packages("openxlsx") #importa arquivos do excel
install.packages("fdth")

library(openxlsx)

Os códigos acima, são usados para instalar e carregar os pacotes necessários para este módulo. Esses códigos são comandos para instalar pacotes no R. Um pacote é uma coleção de funções, dados e documentação que ampliam as capacidades do R (R CRAN (R. C. Team 2017) e RStudio (R. S. Team 2022)). No exemplo acima, o pacote openxlsx permite ler e escrever arquivos Excel no R. Para instalar um pacote no R, você precisa usar a função install.packages().

Depois de instalar um pacote, você precisa carregá-lo na sua sessão R com a função library(). Por exemplo, para carregar o pacote openxlsx, você precisa executar a função library(openxlsx). Isso irá permitir que você use as funções do pacote na sua sessão R. Você precisa carregar um pacote toda vez que iniciar uma nova sessão R e quiser usar um pacote instalado.

Agora vamos definir o diretório de trabalho. Esse código é usado para obter e definir o diretório de trabalho atual no R. O comando getwd() retorna o caminho do diretório onde o R está lendo e salvando arquivos. O comando setwd() muda esse diretório de trabalho para o caminho especificado entre aspas. No seu caso, você deve ajustar o caminho para o seu próprio diretório de trabalho. Lembre de usar a barra “/” entre os diretórios. E não a contra-barra “\”.

getwd()
setwd("C:/Seu/Diretório/De/Trabalho")

9.3 Importando a planilha

Note que o sómbolo # em programação R significa que o texto que vem depois dele é um comentário e não será executado pelo programa. Isso é útil para explicar o código ou deixar anotações. Ajuste a segunda linha do código abaixo para refletir “C:/Seu/Diretório/De/Trabalho/Planilha.xlsx”.

library(openxlsx)
brotos <- read.xlsx("D:/Elvio/OneDrive/Disciplinas/_EcoNumerica/5.Matrizes/brotos.xlsx",
                    rowNames = F, colNames = F,
                    sheet = "Planilha1")
head(brotos,10)
head(brotos[, 1:5], 10)

##      X1   X2   X3   X4   X5   X6   X7   X8   X9  X10
## 1  28.4 29.1 25.7 26.2 25.8 30.2 26.2 35.8 33.4 29.0
## 2  25.1 36.8 29.9 38.3 27.1 32.3 29.0 27.7 28.1 28.9
## 3  29.9 36.3 26.0 21.2 19.8 36.7 21.1 34.6 29.6 32.6
## 4  25.8 23.2 28.8 38.2 32.7 38.7 33.2 24.5 21.6 28.6
## 5  35.0 25.1 24.7 29.5 24.9 29.2 19.5 20.1 30.3 38.9
## 6  36.4 31.8 31.0 39.4 28.8 31.8 28.7 37.0 25.5 19.3
## 7  29.1 21.1 30.4 31.2 38.0 39.0 19.3 27.6 19.1 32.5
## 8  33.2 26.5 38.1 14.9 33.2 27.8 24.7 24.9 25.0 33.1
## 9  26.9 22.5 25.5 33.0 19.4 26.8 24.6 37.5 19.8 43.7
## 10 34.2 33.6 42.5 19.0 25.8 34.0 34.4 42.0 35.4 31.5
##      X1   X2   X3   X4   X5
## 1  28.4 29.1 25.7 26.2 25.8
## 2  25.1 36.8 29.9 38.3 27.1
## 3  29.9 36.3 26.0 21.2 19.8
## 4  25.8 23.2 28.8 38.2 32.7
## 5  35.0 25.1 24.7 29.5 24.9
## 6  36.4 31.8 31.0 39.4 28.8
## 7  29.1 21.1 30.4 31.2 38.0
## 8  33.2 26.5 38.1 14.9 33.2
## 9  26.9 22.5 25.5 33.0 19.4
## 10 34.2 33.6 42.5 19.0 25.8

Exibindo os dados importados (esses comando são “case-sensitive” ignore.case(object)).

#View(brotos)
print(brotos[1:5,1:5])
brotos
str(brotos)
mode(brotos)
class(brotos)

Precisaremos converter para um vetor.

brotos_v <- c(t(brotos))
brotos_v

##   [1] 28.4 29.1 25.7 26.2 25.8 30.2 26.2 35.8 33.4 29.0 25.1 36.8 29.9 38.3 27.1
##  [16] 32.3 29.0 27.7 28.1 28.9 29.9 36.3 26.0 21.2 19.8 36.7 21.1 34.6 29.6 32.6
##  [31] 25.8 23.2 28.8 38.2 32.7 38.7 33.2 24.5 21.6 28.6 35.0 25.1 24.7 29.5 24.9
##  [46] 29.2 19.5 20.1 30.3 38.9 36.4 31.8 31.0 39.4 28.8 31.8 28.7 37.0 25.5 19.3
##  [61] 29.1 21.1 30.4 31.2 38.0 39.0 19.3 27.6 19.1 32.5 33.2 26.5 38.1 14.9 33.2
##  [76] 27.8 24.7 24.9 25.0 33.1 26.9 22.5 25.5 33.0 19.4 26.8 24.6 37.5 19.8 43.7
##  [91] 34.2 33.6 42.5 19.0 25.8 34.0 34.4 42.0 35.4 31.5 32.0 38.4 29.1 29.4 29.3
## [106] 26.8 32.4 25.2 28.5 29.8 31.7 22.4 21.7 20.1 21.6 23.5 33.2 33.0 29.6 36.9
## [121] 23.6 16.2 27.3 33.3 21.6 30.2 22.5 33.0 38.3 29.5 31.1 31.7 31.6 41.7 25.9
## [136] 32.3 35.7 31.6 26.0 26.6 29.1 15.8 22.1 23.2 25.4 28.4 20.2 25.5 26.9 32.7
## [151] 29.8 27.1 36.9 32.7 24.8 18.0 40.2 28.0 26.8 41.9 31.5 27.4 37.2 30.6 32.2
## [166] 34.8 28.2 31.3 34.3 32.0 20.6 27.2 25.0 26.1 34.5 44.9 40.5 32.1 40.4 35.7
## [181] 29.3 24.7 37.0 36.9 34.8 29.8 22.8 32.3 34.8 29.6 24.0 30.5 31.6 28.7 20.8
## [196] 14.6 23.4 26.3 31.9 32.5 32.4 36.4 24.1 33.1 26.3 35.7 26.4 34.7 27.5 39.6
## [211] 30.5 30.1 21.3 27.1 19.0 25.4 36.5 22.6 25.5 30.0 29.2 30.2 20.8 30.3 27.8
## [226] 32.9 28.2 20.6 33.6 22.2 26.1 29.7 32.0 22.2 29.2 21.5 31.4 43.1 35.9 14.9
## [241] 38.8 21.9 25.6 29.7 29.9 32.5 30.4 29.2 40.9 14.1 22.4 19.9 34.8 33.4 28.0
## [256] 29.1 27.2 18.8 36.2 27.8 29.9 21.8 33.1 30.4 30.8 33.9 27.1 27.6 37.2 30.9
## [271] 28.3 34.3 34.0 29.0 30.9 24.4 29.0 25.4 30.5 31.1 26.3 38.3 24.8 23.5 29.3
## [286] 37.8 29.9 28.6 27.4 29.9 24.3 20.7 22.5 39.5 32.0 27.6 36.3 22.0 28.4 19.1
## [301] 16.8 43.9 27.9 44.4 29.7 23.0 26.8 43.4 29.4 26.7 27.8 33.1 34.9 20.5 25.4
## [316] 10.0 28.2 31.0 10.6 28.4 21.9 27.0 26.5 29.2 24.9 18.4 24.1 28.3 29.0 29.1
## [331] 26.2 32.6 22.3 31.7 37.1 35.6 19.5 26.9 24.8 19.2 29.9 42.1 36.6 25.5 34.2
## [346] 22.4 40.5 21.2 32.3 31.5 29.3 34.8 34.8 22.6 33.6 23.0 33.8 21.9 31.6 16.5
## [361] 31.6 26.8 37.3 23.2 20.5 17.6 25.0 41.9 21.8 34.4 23.2 27.6 34.3 26.7 28.1
## [376] 24.7 34.2 15.7 27.2 37.5 32.1 25.5 34.7 43.7 31.6 37.9 27.4 17.0 19.4 24.6
## [391] 20.3 22.4 37.7 29.4 36.0 39.2 26.2 25.7 28.2 22.1 27.8 36.5 23.7 28.6 23.8
## [406] 16.2 38.0 22.1 44.0 20.2 22.9 41.5 30.4 36.1 32.7 30.1 39.9 22.3 26.8 31.4
## [421] 32.5 31.4 18.8 19.1 24.2 29.3 19.7 36.7 24.1 33.9 24.5 22.8 29.9 34.5 33.4
## [436] 22.8 30.8 22.1 38.1 33.5 36.5 33.5 28.6 24.9 24.3 25.7 19.2 34.5 40.6 25.8
## [451] 39.4 33.3 21.9 29.6 27.0 30.2 17.1 15.8 22.8 16.5 24.2 21.2 25.8 29.8 24.7
## [466] 30.6 38.1 33.3 26.8 16.5 23.2 24.5 29.9 26.0 40.5 30.0 30.3 33.9 34.9 18.8
## [481] 28.3 40.2 30.9 22.0 34.1 26.2 19.6 33.6 26.3 25.1 29.3 31.9 43.0 31.9 33.9
## [496] 20.0 39.6 34.3 28.8 34.2

E agora visualizando nossos dados.

#View(brotos_v)
print(brotos_v)
brotos_v
str(brotos_v)
mode(brotos_v)
class(brotos_v)

Tendo em mãos o conjunto total de 500 comprimentos medidos de brotos de Banksia, agora vamos tirar uma subamostra aleatória de uma parte dos 500 valores. Essa subamostra é tirada usando o comando size= no código subsequente, que estabelece o tamanho da subamostra a ser tirada do total de dados. Esse tamanho é estabelecido no quiz. Inclua esse valor de acordo com o que é pedido no quiz. Por exemplo, se for pedido uma subamostra de 150 comprimentos, então size = 150. Nesse tutorial usaremos todos os 500 comprimentos.

set.seed(666)
brotos_sub <- sample(brotos_v, size = 500, replace = F) #atualize o valor de 'size=' se necessário
brotos_sub

##   [1] 21.1 30.2 34.0 36.0 27.3 34.6 15.8 19.4 31.6 26.6 31.5 38.9 31.1 32.0 29.9
##  [16] 24.5 21.2 19.3 22.1 24.7 24.7 37.0 22.4 32.5 35.9 36.9 24.2 33.0 27.6 22.8
##  [31] 26.5 31.6 32.3 38.1 27.4 32.3 24.8 25.5 33.1 34.5 24.4 27.1 43.9 28.6 28.4
##  [46] 33.4 29.3 24.9 36.2 24.6 30.0 32.6 25.6 26.0 25.8 37.0 26.4 22.5 23.2 38.2
##  [61] 23.0 44.4 27.6 20.2 29.0 25.9 22.3 27.4 14.9 33.3 40.9 33.5 36.3 28.0 28.4
##  [76] 41.5 28.5 34.8 29.1 31.6 36.7 30.1 35.4 19.2 39.4 16.5 25.1 28.4 31.9 16.2
##  [91] 31.7 29.3 33.9 22.3 33.6 25.5 33.0 30.0 33.3 34.0 44.0 29.5 33.6 26.7 42.0
## [106] 33.2 24.8 26.9 25.4 43.0 29.4 15.8 28.8 39.5 31.8 20.3 38.3 19.8 37.8 26.7
## [121] 23.0 19.8 39.6 18.4 31.0 29.1 24.0 32.4 22.6 30.9 26.2 29.1 28.2 33.4 25.7
## [136] 30.9 34.8 34.1 24.1 29.9 20.0 29.3 28.7 28.6 36.5 25.1 17.1 24.7 29.2 38.7
## [151] 26.8 30.6 17.0 25.5 26.2 31.5 32.5 34.7 30.2 36.6 36.5 29.1 32.3 35.0 33.9
## [166] 19.1 25.0 26.1 40.2 30.4 31.4 33.6 37.5 29.8 20.8 29.3 39.6 28.4 31.0 24.9
## [181] 27.5 33.4 33.3 34.3 21.6 40.5 29.4 26.3 22.5 42.5 20.5 44.9 29.8 30.4 28.6
## [196] 27.6 39.4 33.2 34.2 20.1 18.8 26.8 22.9 25.7 21.9 34.9 34.8 33.2 40.6 26.9
## [211] 20.2 19.1 27.2 23.2 37.3 32.5 25.4 32.0 34.5 29.7 28.1 31.2 27.2 25.8 27.0
## [226] 26.3 32.2 43.7 42.1 38.4 19.0 28.9 31.8 34.5 22.1 29.0 25.2 38.1 29.2 34.3
## [241] 27.9 24.5 34.4 40.2 36.1 29.6 33.1 28.8 22.8 38.0 20.1 28.6 34.4 30.5 19.5
## [256] 30.2 30.4 22.4 35.6 17.6 28.2 29.5 37.7 19.5 28.0 37.1 20.6 34.3 40.5 27.8
## [271] 29.9 27.1 36.9 25.0 29.9 32.7 33.2 24.7 30.9 27.0 29.9 29.6 29.7 23.8 22.2
## [286] 34.8 38.8 31.1 26.8 19.0 22.4 36.9 35.7 22.0 24.1 26.1 34.3 25.5 18.0 41.7
## [301] 29.8 32.0 31.4 21.8 27.7 33.1 28.7 29.2 31.6 23.6 34.2 25.8 21.3 26.3 23.5
## [316] 21.6 32.7 27.8 32.7 30.3 16.8 33.0 10.0 30.4 25.4 26.2 22.1 37.5 26.0 33.5
## [331] 29.0 36.7 29.8 24.8 31.9 32.6 36.4 32.1 31.5 33.8 43.4 29.4 24.2 25.0 34.9
## [346] 22.0 24.9 16.2 28.3 16.5 29.1 24.6 19.3 25.8 29.0 29.3 29.9 32.7 35.8 32.3
## [361] 19.9 30.2 21.2 24.3 32.5 27.6 25.8 39.9 34.7 25.5 29.3 21.9 23.2 26.2 19.4
## [376] 19.2 32.1 26.3 26.8 38.0 28.3 34.8 19.6 35.7 35.7 23.2 32.9 27.4 22.8 40.4
## [391] 37.9 28.2 43.7 21.7 21.1 31.6 24.9 25.5 29.6 40.5 39.2 39.0 29.1 33.9 25.7
## [406] 29.6 29.7 19.7 38.3 22.6 36.4 16.5 28.3 30.8 21.2 14.9 34.8 33.6 24.1 25.4
## [421] 43.1 20.7 30.3 41.9 31.3 27.1 34.2 27.8 18.8 31.7 30.6 27.8 21.6 30.1 30.8
## [436] 27.2 28.8 37.2 14.6 18.8 26.9 22.1 14.1 25.1 22.2 36.5 23.4 29.9 33.9 24.3
## [451] 33.1 26.2 28.1 24.5 34.2 15.7 32.0 22.8 21.9 26.0 23.2 20.8 21.5 38.1 30.3
## [466] 19.1 31.6 27.1 32.4 23.5 36.8 37.2 21.8 26.8 31.9 22.4 24.7 20.6 30.5 26.8
## [481] 30.5 29.0 26.5 29.2 31.4 20.5 26.8 10.6 27.8 21.9 28.2 23.7 29.9 29.9 36.3
## [496] 31.7 38.3 29.2 22.5 41.9

Para fazermos uma tabela de frequência do comprimento dos brotos carregamos o pacote fdth e pedimos a função range que retorna o valor máximo e mínimo no vetor.

library(fdth)

## Warning: package 'fdth' was built under R version 4.3.1

## 
## Attaching package: 'fdth'

## The following objects are masked from 'package:stats':
## 
##     sd, var

range(brotos_sub) #retorna o valor máximo e mínimo
#?range

## [1] 10.0 44.9

Agora é necessário que você substitua os valores de range 10, 44.9 nos valores de início e fim da distribuição de frequência. Os comandos abaixo criam uma tabela de frequência chamada tf com valores máximos e mínimos definidos por range(brotos_v) em intervalor definidos por h=5, e o comando print(tf) exibe a tabela de frequência.

tf <- fdt(brotos_sub, start=10, end=45, h=5) #tabela de frequência
#?fdt #atente para o uso de k, por exemplo tf <- fdt(brotosv, k=5)
print(tf)

##  Class limits   f   rf rf(%)  cf cf(%)
##       [10,15)   6 0.01   1.2   6   1.2
##       [15,20)  35 0.07   7.0  41   8.2
##       [20,25)  93 0.19  18.6 134  26.8
##       [25,30) 155 0.31  31.0 289  57.8
##       [30,35) 130 0.26  26.0 419  83.8
##       [35,40)  57 0.11  11.4 476  95.2
##       [40,45)  24 0.05   4.8 500 100.0

Class limits = limites de classe, f = frequência de classe, rf = frequência relativa da classe, rf(%) = frequência relativa percentual da classe, cf = frequência cumulativa da classe, cf(%) = frequência cumulativa percentual da classe.

Se contarmos o número de brotos que se encontram em cada um dos sete intervalos, temos a base para a tabulação da frequência. Essa tabulação é mostrada na tabela gerada pelos códigos acima. A coluna de frequência foi obtida contando o número de medições que existem dentro de cada classe. A coluna de frequência percentual foi obtida representando cada contagem como uma porcentagem da contagem total. A frequência cumulativa e as frequências percentuais cumulativas foram obtidas somando progressivamente as frequências correspondentes.

9.4 Gráficos de histograma e boxplot

No código abaixo se define o layout dos gráficos para serem exibidos lado a lado, e na sequência criamos um gráfico de histograma com base na tabela de frequência tf. O comando boxplot() cria um gráfico de boxplot para os valores em brotos_v. O argumento “horizontal = TRUE” indica que o boxplot deve ser horizontal.

par(mfrow = c(1,2)) #gráficos lado a lado
plot(tf) #distribuição de frequências
boxplot(brotos_sub, horizontal = TRUE,
        xlab="Class limits") #boxplot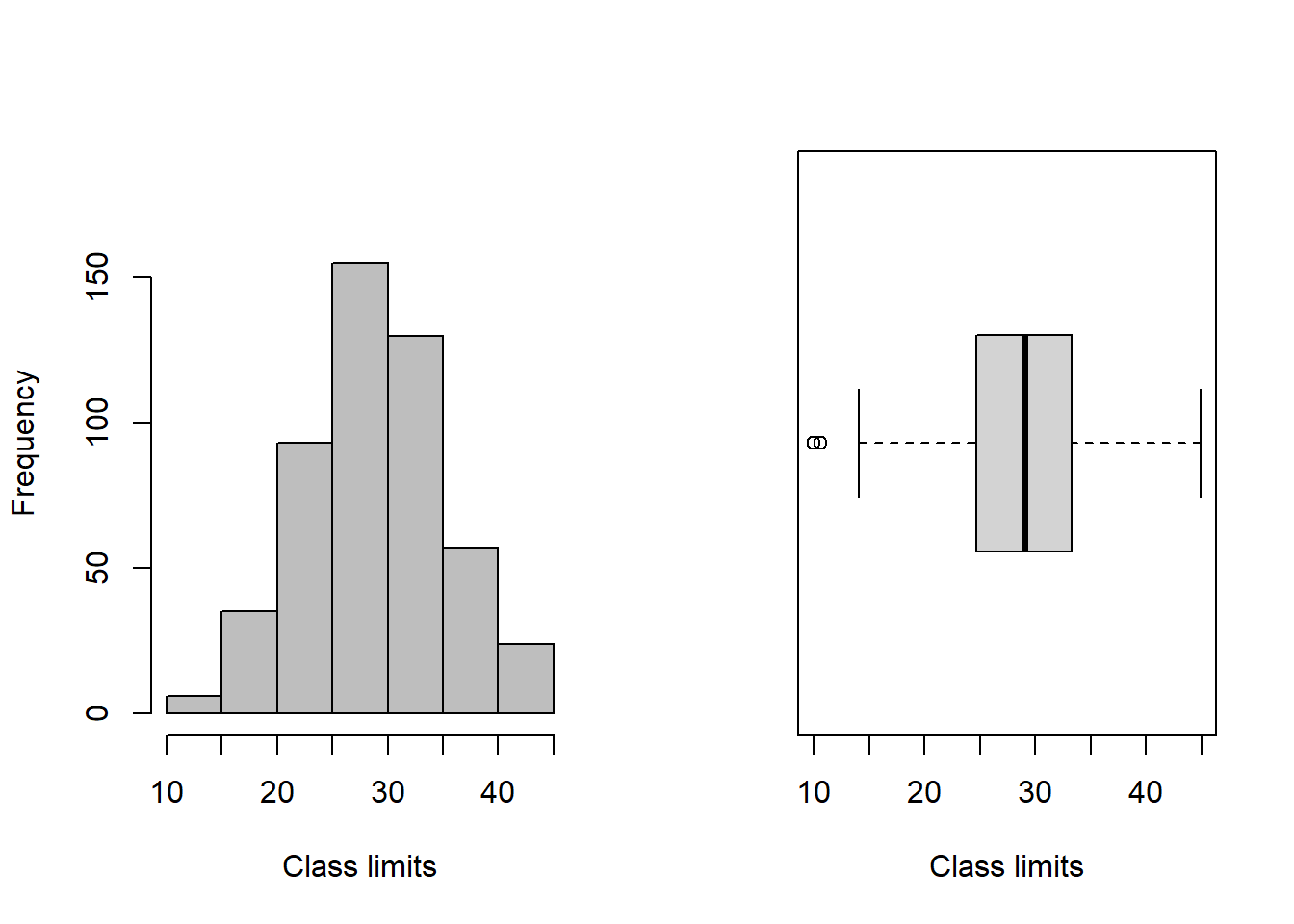

par(mfrow = c(1,1)) #gráficos de volta ao normal

Se você recebeu a mensagem de erro “Error in plot.new() : figure margins too large”, aumente o tamanho da janela do gráfico e execute as últimas três linhas de comando novamente.

9.5 Sumário estatístico geral

summary(brotos_v)
#?summary
sd(brotos_v) #desvio padrão
var(brotos_v) #variância

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   10.00   24.70   29.10   28.97   33.23   44.90 
## [1] 6.373581
## [1] 40.62254

Apêndices

Sites consultados

Script limpo

Aqui apresento o scrip na íntegra sem os textos ou outros comentários. Você pode copiar e colar no R para executa-lo. Lembre de remover os # ou ## caso necessite executar essas linhas.

## rm(list=ls(all=TRUE)) #limpa a memória
## install.packages("openxlsx") #importa arquivos do excel
## install.packages("fdth")
library(openxlsx)
## getwd()
## setwd("C:/Seu/Diretório/De/Trabalho")
library(openxlsx)
brotos <- read.xlsx("D:/Elvio/OneDrive/Disciplinas/_EcoNumerica/5.Matrizes/brotos.xlsx",
                    rowNames = F, colNames = F,
                    sheet = "Planilha1")
head(brotos,10)
head(brotos[, 1:5], 10)
## #View(brotos)
## print(brotos[1:5,1:5])
## brotos
## str(brotos)
## mode(brotos)
## class(brotos)
brotos_v <- c(t(brotos))
brotos_v
## #View(brotosv)
## print(brotos_v)
## brotos_v
## str(brotos_v)
## mode(brotos_v)
## class(brotos_v)
set.seed(666)
brotos_sub <- sample(brotos_v, size = 500, replace = F) #atualize o valor de 'size=' se necessário
brotos_sub
library(fdth)
range(brotos_sub) #retorna o valor máximo e mínimo
#?range
tf <- fdt(brotos_sub, start=10, end=45, h=5) #tabela de frequência
#?fdt #atente para o uso de k, por exemplo tf <- fdt(brotosv, k=5)
print(tf)
par(mfrow = c(1,2)) #gráficos lado a lado
plot(tf) #distribuição de frequências
boxplot(brotos_sub, horizontal = TRUE,
        xlab="Class limits") #boxplot
par(mfrow = c(1,1)) #gráficos de volta ao normal
summary(brotos_v)
#?summary
sd(brotos_v) #desvio padrão
var(brotos_v) #variância

Referências

Bibliografia

Bradstock, R. A., M. G. Tozer, and D. A. Keith. 1997. “Effects of High Frequency Fire on Floristic Composition and Abundance in a Fire-Prone Heathland Near Sydney.” Journal Article. Australian Journal of Botany 45: 641–55.

———. 2017. R: A Language and Environment for Statistical Computing. Book. Austria: R Foundation for Statistical Computing. https://www.r-project.org/.

Team, R Studio. 2022. RStudio: Integrated Development Environment for r. Book. Boston, MA: RStudio, PBC. https://posit.co/products/open-source/rstudio/.

O RStudio Cloud é uma plataforma online que fornece um ambiente de desenvolvimento integrado para o R, permitindo que os usuários executem análises, desenvolvam código e colaborem com outras pessoas, sem a necessidade de instalar o R e o RStudio em seus próprios computadores. É uma solução conveniente e acessível, especialmente para iniciantes ou usuários que desejam compartilhar projetos e colaborar de forma eficiente.↩︎