Chapter 6 Classical and Bayesian Inference

Figure 6.1: Frequentists vs. Bayesians

Let’s carefully examine a fake experiment:

A scientist is interested the rate at which radioactive ooze turns ordinary turtles into mutant ninja turtles (the age of the turtles is irrelevant but if you must know they are between 13 and 19 years old).

20 turtles are exposed to radioactive ooze.

16 of them show signs of mutation (the fun kind not the sad kind).

Figure 6.2: Experimental Results ($n = 4$)

So, we have a proportion with $s=16$ (let’s call mutation a “success”) and $N=20$. Let’s call that proportion $\hat{\pi}$: ¹²⁵

\[\hat{\pi}=\frac{16}{20}=0.8\] If we were to mutate 16 turtles into pizza-loving ninjas, that would be scientifically noteworthy in and of itself. But, let’s suppose it is not necessarily the mutation itself that we are interested in but the rate of mutations. As noted in Categorizing and Summarizing Information, scientific inquiry is in most cases about generalizing the results from a sample to a population. In that light, what we would want to infer from these experimental results is the population-level rate of turtle mutation.

And what we can say about the population-level rate is at the heart of the fight between proponents of relative-frequency-based statistical inference and proponents of subjective-probability-based statistics – or, more simply, between Classical Statisticians and Bayesian Statisticians.

Figure 6.3: Artist’s Rendering

6.0.1 Different Approaches to Analyzing the Same Data

If the results of an experiment suggest that, for the particular participants and under the specific conditions of the experiment, a rate of 80% (as in the example of the turtles), there are a few ways to interpret that:

The true rate is exactly 80%: no further analysis needed.¹²⁶

This is both one of the simplest and one of the least believable inferences we could make. It is simple because it technically does precisely what we are trying to do with scientific experimentation – to study a sample and generalize to the population – in the most straightforward possible way. However, this approach would fail to withstand basic scientific scrutiny because (among other reasons, but mainly) the sample of participants is highly unlikely to be representative of the entire population. And, even if the sample were somehow perfectly representative, it would also fail from the perspective of probability theory. Consider, yet again, a coin flip.¹²⁷ The probability of flipping a perfectly fair coin 20 times and getting other than exactly 10 heads is:

\[p(s\ne 10|N=20, \pi=0.5)=1-\frac{20!}{10!10!}(0.5)^{10}(0.5)^{10} = 0.8238029\]

so there is an approximately 82.4% chance that in a study of 20 flips of a fair coin, the result by itself will imply that the probability of heads is not 50%. We know that wouldn’t be true: if we got 8 heads in 20 flips of a coin, we would be wrong to think there is something unusual about the coin. Likewise, the results of one experiment with $N=20$ trials should not convince us that the true rate is exactly 80%. Both of these problems – a lack of representativeness and relatively high statistical uncertainty – can be somewhat ameliorated by increasing the sample size, but neither can be completely eliminated short of testing the entire population at all times in history. Thus, approach #1 is out.

Based on our experiment, the true rate is probably somewhere around 80%, give or take some percentage based on the level of certainty afforded by the size of our sample.

The second approach takes the fact that a rate $80\%$ was observed in one sample of size $N=20$ and extrapolates that information based on what we know about probability theory to make statements about the true rate. In this specific case, we could note that $80\%$ is a proportion, and that proportions can be modeled using the $\beta$ distribution. We can use the observed $s$ and $f$ – 16 and 4, respectively – as the sufficient statistics, also known in the case of the $\beta$ (and other distributions) as shape parameters, for a $beta$ distribution. The shape parameters for a $\beta$ distribution are $s+1$ and $f+1$, also known as $\alpha$ and $\beta$ where $\alpha=s+1$ and $\beta=f+1$.¹²⁸ Based on our experiment, we would expect this to be the probability density of proportions:

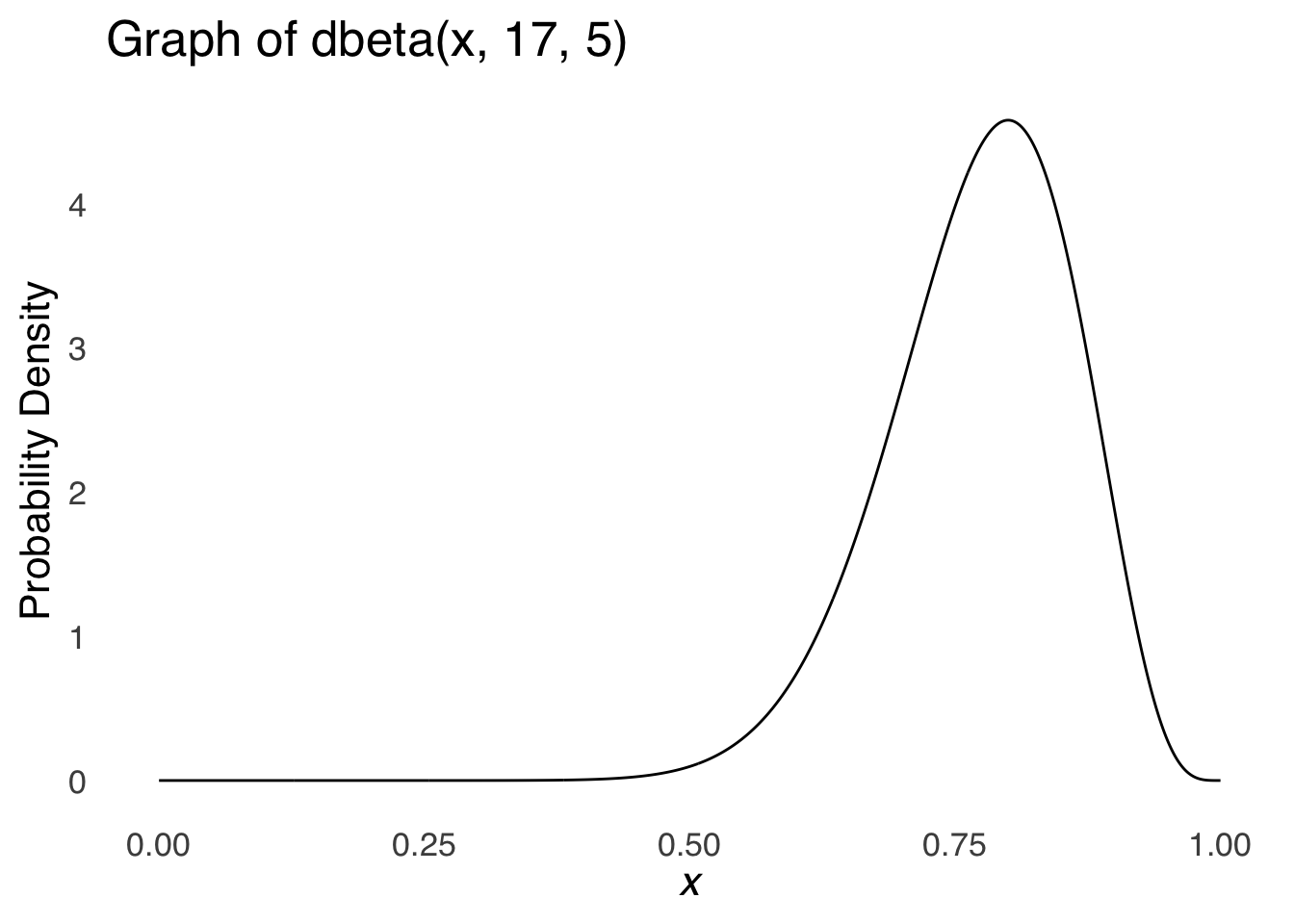
$A $\beta$ distribution with $s+1=17$ and $f+1=5$$

Figure 6.4: A $\beta$ distribution with $s+1=17$ and $f+1=5$

Based on the $\beta$ distribution depicted in Figure 6.4, we can determine that the probability that the true rate is exactly 80% is 0 and this approach is useless. No! That’s just a funny funny joke about the probability of any one specific value in a continuous probability distribution. What fun!

Seriously, folks, based on the $\beta$ distribution depicted in Figure 6.4, we can determine the following probabilities of the true rate $\pi$:

$p(0.79<\pi<0.81)=$ pbeta(0.81, 17, 5) - pbeta(0.79, 17, 5) $= 0.0914531$

$p(0.70<\pi<0.9)=$ pbeta(0.9, 17, 5) - pbeta(0.7, 17, 5) $= 0.7494661$

$p(0.65<\pi<0.65)=$ pbeta(0.95, 17, 5) - pbeta(0.65, 17, 5) $= 0.9044005$

$p(\pi>0.5)=$ pbeta(0.5, 17, 5, lower.tail=FALSE) $= 0.9964013$

Thus, we would be about 90% sure that the true value of $\pi$ is within 0.15 of 0.8, and over 99.5% sure that the true value of $\pi$ is greater than 0.5.

We could also use Bayes’s Theorem to determine various values of $p(H|D)$ – in this case, $p(\pi|Data)$ – and would get the same results as using the $\beta$. Approach #2 is the Bayesian Approach.

The true rate is a single value that cannot be known without measuring the entire population: there is a chance that our results behaved according to the true rate and a chance that our results were weird. Therefore, the results of our experiment cannot prove or disprove anything about the true rate. We can rule out – with some uncertainty – some possibilities for the true rate if our results are unlikely to have been observed given those possible true rates.

In this approach, the true rate is unknowable based on the results of a single experiment, so we can’t make any direct statements about it. Instead, the scientific question focuses on the probability of the data rather than the probability of the hypothesis. This approach starts by establishing what the expectations of the results would be in a scenario where nothing special at all is happening. If the experiment results in a situation where anything at least as likely as the observations are extremely unlikely to have happened given our hypothetical nothing-special-at-all assumption, then we have evidence to question the nothing special assumption,¹²⁹ and support for the idea that something special is indeed happening.

Going back to our example: we might reasonably assert that a state of affairs in which the radioactive ooze is just as likely to cause a mutation as not to cause a mutation. In that case, the $p(mutate)=p(\neg mutate)=0.5$: essentially a coin flip. As above, we collect the data and find that 16 out of the 20 turtles show signs of mutation. Given our assumption that the rate is 0.5, then the probability of observing 16 successes in 20 trials is:

\[p(s=16|N=20, \pi=0.5)=\frac{20!}{16!4!}(0.5)^16(0.5)^4=0.004620552.\] That’s pretty unlikely! But, it can be misleading: for one, the probability of any specific $s$ is pretty small and vanishingly small for increasing $N$ and it’s not like if we instead observed 17, 18, 19, or 20 mutations that we would change our scientific theories about the experiment. So, we are instead going to be interested in the probability of the number of observed $s$ or more given our assumption that $\pi=0.5$:

\[p(s\ge 16|N=20, \pi=0.5)= 0.005909\] which is still super-unlikely. It is unlikely enough that we would reject the notion that the rate of turtle-mutation following exposure to the ooze is 50% (or, by extension, less than 50%) – the results are too unlikely to support that idea – in favor of a notion that the true rate is somewhere greater than 0.5.

How unlikely is unlikely enough to reject the notion of nothing-special-at-all going on? That depends on how often we are willing to be wrong. If we’re ok with being wrong on 5% of our claims, then any result with a cumulative probability of at least the observation happening less than or equal to 5% is unlikely enough. If we’re ok with being wrong on 1% of our claims, then any result with a cumulative probability less than or equal to 1% is unlikely enough. Basically, if we say “this didn’t happen randomly” every time an event has a cumulative probability less than $x\%$, then it will have happened randomly $x\%$ of the time and we will have been wrong in our claim of nonrandomness.

This third approach is the most popular in applied statistics. It is the Classical Null Hypothesis Testing Approach.

We cannot make statements about the true rate, but based on the observed results and what we know about the distribution of the data (in this case, the binomial distribution), we can estimate an interval for which a given proportion of theoretical future samples will produce similar interval estimates that contain the true rate (whatever it may be).

As in approach #3, we assume that the true rate is a fixed value that cannot vary and cannot be known without measuring the entire population at all points in time. But, given that we observed 16 successes in 20 trials, we can make some statements about what future replications of the experiments will show. For example, we know that the true rate is not 0 or 1: otherwise, all of our trials would have resulted in failure (if $\pi=0$) or in success (if $\pi=1$).

Let’s say, for example, that we want to produce an interval such that 95% of future repetitions of our experiment will produce 95% intervals that include the true rate (whatever it is). The lowest possible value of $\pi$ in that interval is going to be the value that leads to the cumulative likelihood of the observed $s$ or greater being $2.5\%$, and the highest possible value of $\pi$ is going to be the value that leads to the cumulative likelihood of the observed $s$ or less being $2.5\%$. Thus, the cumulative probability of the data in the middle is $1-2.5\%-2.5%=95\%$.

For $N>20$, there are algebraic methods for estimating the width of this interval,¹³⁰, but if software is available, the best method regardless of the size of $N$ is known as the Clopper-Pearson Exact Method. Without software, the Exact Method is an interminable ordeal of trial-and-error to get the lower and upper values of $\pi$, but it’s easy enough with software:

library(binom)
binom.confint(16, 20, 0.95, methods="exact")

##   method  x  n mean    lower    upper
## 1  exact 16 20  0.8 0.563386 0.942666

The lower limit of the interval is 0.563386, and the cumulative probability of $s\ge 16$ is:

pbinom(15, 20, 0.563386, lower.tail=FALSE) $= 0.025$

The upper limit of the interval is 0.942666, and the cumulative probability of $s\le 16$ is:

pbinom(16, 20, 0.942666, lower.tail=TRUE) $= 0.025$

Thus, the math checks out.

The interval estimate created by this method is known as the Confidence Interval. It’s similar to intervals tested using the Bayesian approach, except that the interpretation is different due to the philosophical objection (that it shares with the Classical Null Hypothesis Testing approach) against making probabilistic statements about the true rate. The confidence interval is not a range in which one is $x/%$ confident that the true rate is in: that would imply a degree of belief about the value of the true rate. Instead, the confidence interval¹³¹ is a statement about the ranges produced by future estimates based on repeated use of the same scientific algorithm. And if that sounds overly complicated and/or semantically twisted, that’s because it kind of is.

The confidence interval approach is, like Null Hypothesis Testing, a Classical approach.

6.0.2 The Essential Difference

The key difference between Bayesian Statistics and Classical Statistics (both Null Hypothesis Testing and Confidence Intervals) that informs all of the analyses used by both camps and the math involved in both lies in the treatment of what was referred to as the true rate in the specific example above and is more generally known as the population parameter. Population parameters can be descriptions of rates, but also can be things like differences between means, or variances, or regression coefficients.

The classical (or relative frequentist, or simply _frequentist) theorists of the late 19th and early 20th centuries – who almost to a man held and promoted horrible beliefs about humanity¹³² – collectively objected to the idea that a parameter could be described in any probabilistic way. And that is a fair point! A parameter is a fixed value that could only be known by measuring the entire population at all points in time.

Bayesians believe that population parameters can be described using probability distributions: it’s not so much that they think that population parameters vary back and forth along curves as that it is reasonable to express a degree of belief about a parameter or a range of parameter values, and that belief can be represented by a distribution. The paradox of describing a fixed state with a probability distribution was explained well after the establishment of classical statistics by Bruno de Finetti (the fascist from the sidenote). Please imagine that somebody asked you about some minor thing in your life that you either did or did not do, for example: whether you remembered to lock your front door last Tuesday, and they asked you to put a probability value on whether you did it or not. Even though it is essentially a yes or no question, we tend to be ok with assigning a probability value to it based on things like what we know about our tendencies and what the context was on a given day. That is a case of making a probabilistic statement about a factual thing, which is how Bayesian statisticians approach placing parameters in the context of probability distributions.

6.0.3 Consequences of the Difference

6.0.3.1 $p(H|D)$ vs. $p(D|H)$

Bayesian statisticians get their name because Bayes’s Theorem is fundamental to the way that they treat scientific inquiry: they are interested in the probability of various hypothesis ($H$) given the data ($D$): $p(H|D)$. As covered in the section on Bayes’s Theorem in Probability Theory, there are four parts to the theorem:

$p(H)$: the Prior Probability

The prior probability is the most subjective element of Bayesian analysis. Bayesian analyses often employ priors that represent scenarios where each hypothesis starts out as equally likely: these include flat or noninformative priors. Such analyses do, however, include the option to add information from scientific theory or prior studies. For example: a Bayesian analyst might choose a prior that weighs the probabilities against an extraordinarily unlikely hypothesis (like the existence of extrasensory perception or time travel), or (more commonly) that includes probabilities obtained in earlier studies.

$p(D|H)$: the Likelihood

The likelihood is the conditional probability of the observed data given the hypothesis. Typically, the likelihood is not a single value but a likelihood function, as Bayesian analyses are often based on evaluating a range of possibilities that need to be fed into a function. In an example like the mutating-turtle experiment described above where the hypothesis is about a rate parameter, the likelihood function would be the binomial likelihood function. In other studies, the likelihood function might be based on other probability density functions like that of the normal distribution. Like the prior, there is some expertise required to choose the proper likelihood function (in my experience, this is the part that Bayesians argue the most about with other Bayesians).

$p(D)$: the Base Rate

The base rate is the overall probability of the data under the conditions of all hypotheses under consideration. It’s actually the least controversial term of Bayes’s Theorem: once the prior and the likelihood are established, the base rate is just the normalizing factor that makes the sum of all the posterior probabilities of all the hypotheses under consideration equal to 1.

$p(H|D)$: the Posterior Probability

The posterior probability is the result of the analysis. It is the probability or probability distribution that allows us to evaluate different hypotheses.

In the Bayesian approach, $p(H|D)$ implies that there is probability associated with the hypothesis but the data are facts. Classical Statisticians, famously, refuse the notion that there can be a probability of a hypothesis. Thus, for Classicists, the probability in statistics is associated with the data and not the hypothesis. That means that the focus of Classical Statistics is on the likelihood function $p(D|H)$ alone. That is, Classical techniques posit a hypothesis (actually, a null hypothesis) and assess the probability of the data based on that hypothesis.

6.0.3.2 Mathematical Implications

Classical approaches focus on the likelihood of the data and typically use likelihood functions (that give rise to probability distribuions) that describe the distribution of the data given certain assumptions. The most common such assumption is that data are sampled from normal distributions. For example, we may assume that the data are sampled from a standard normal distribution. If an experiment results in an observed value with a $z$-score of 5, then the likelihood of sampling that value from the standard normal is pnorm(5, lower.tail=FALSE)=$2.8665157\times 10^{-7}$: not impossible, but seriously unlikely. In fact, that is so unlikely that we would reject the assumption that this value came from the standard normal in favor of the idea that the value came from some other normal distribution.

Classical approaches have been around so long and have become so widely used that the procedures have been made computationally simple relative to Bayesian approaches.¹³³ Part of that relative simplicity is due to the assumptions made about the probability distributions of the data. Another part of the relative simplicity is that most of the most complicated work – for example, all of the calculus that goes into estimating areas under the standard normal curve – has been done for us. If you ever happen to read some of the seminal papers in classical statistics (1/10 I can’t recommend it), you may note the stunning mathematical complexity of the historical work on the concepts. Classical statistical methods have been made easier (again, relatively speaking) to meet the demands of the overwhelming growth of applications of the field over the past century or so. Bayesian methods might get there eventually.

Bayesian methods tend to be much more computationally demanding than their Classical counterparts. There are two main reasons that Bayesian approaches are more complex: 1. there are more moving parts to calculating $p(H|D)$ than calculating $p(D|H)$, and 2. they rely less on assumptions about probability distributions.¹³⁴ In terms of marbles-in-jars problems using Bayes’s Theorem, there are lots of possible jars, and lots of different relative proportions of different marbles in those jars, so calculating posterior probabilities involves lots of calculus and/or computer simulations. A substantial amount of the analyses that we can do today using modern computing and Monte Carlo sampling were difficult-to-impossible decades ago (to be fair, the same can be said for some classical analyses as well). The good news is that with modern software, the calculations are much easier to do.

6.0.3.3 Comparability of Results

The decades of internecine fighting among statisticians belies the fact that the results usually aren’t wildly different between Bayesian and Classical analyses of the same data. Bayesian analyses tend to produce more precise estimates, either because they don’t have to content with the sample size required to reject a null hypothesis or because they provide more concise interval estimates.

Bayesian approaches are more flexible in that one can construct their own evaluation of posterior probabilities to fit their study design needs. Classical approaches are in a sense easier in that regard because their popularity has led to the development of tools for almost any experimental design that a behavioral scientist would use.

Classical approaches offer the authority of statistical significance, a concept that Bayesian approaches do not have. The upside there for Bayesian approaches is that without a null-hypothesis testing framework, they don’t carry concerns about type-I and type-II errors.

6.1 Examples of Classical and Bayesian Analyses

In this section, we will elaborate on the example above of an experiment with $s=16$ successes in $N=20$ trials, analyzing the data using both Classical and Bayesian methods.

6.1.1 Classical Null Hypothesis Testing

In Classical Hypothesis Testing, a hypothesis is a statement about a population tested with information (statistics) from a sample.¹³⁵ In the Classical paradigm, two mutually exclusive hypotheses are posited: a null hypothesis (abbreviated $H_0$) and an alternative hypothesis (abbreviated $H_1$).

6.1.1.1 Null and Alternative Hypotheses

The null hypothesis is a description of a state where nothing is happening. In a study design that investigates the correlation between variables, nothing is happening means that there is no relationship between the variables, and the null hypothesis statement describes the mathematical state of affairs that would result from variables having no relationship: i.e., that the statistical correlation between the variables is equal to 0. In a study design that investigates differences between variables, nothing is happening means that there is no difference between the variables, and the null hypothesis is a mathematical statement that reflects that: i.e., that the statistics describing the variables are equal to each other. The alternative hypothesis is the opposite of the null hypothesis: it describes a state where something is happening: i.e., that the correlation between variables is not equal to 0, or that the statistics describing variables are different from each other.

The null and alternative hypotheses are both statements about populations. They are, more specifically than described above, statements about whether nothing (in the case of the null) or something (in the case of the alternative) is going on in the population. In a case of an experiment designed to see if there are differenes between the mean results under two conditions, for example, the null hypothesis might be that there is no difference between the population means for each condition, stated as $\mu_{condition~1}-\mu_{condition~2}=0$ (note the use of Greek letters to indicate population means). That means that if the entire world population were subjected to each of these conditions and we were to measure the population-level means $\mu_{condition~1}$ and $\mu_{condition~2}$, that the difference between the two would be precisely 0. However, even if the null hypothesis $\mu_{condition~1}-\mu_{condition~2}$ were true, it would be extraordinary unlikely that the difference between the sample means – $\bar{x}_{condition~1}-\bar{x}_{condition~2}=0$: if we take two groups of, say, 30 random samples from the same distribution, it’s almost impossible that the mean of both of those groups will be exactly equal to each other.

Thus, it is pretty much a given that two samples will neither be completely uncorrelated with each other nor that two samples will be completely identical to each other. But, based on a combination of how correlated to or how different from each other the samples are, the size of the samples, and the variation in the measurement of the samples, we can generalize our sample results to determine whether there are correlations or differences on the population level.

6.1.1.1.1 Types of Null and Alternative Hypotheses

The null, and by extension, the alternative hypotheses we choose can indicate either a directional hypothesis or a point hypothesis. A directional hypothesis is one in which we believe that the population parameter will be either greater than the value indicated in the null hypothesis or less than the value indicated in the null hypothesis but not both. For example, consider a drug study where the baseline rate of improvement for the condition to be treated by the drug in the population is 33%. In that case, 33% would be a reasonable value for the rate in the null hypothesis: if the results from the sample indicate that the success rate of the drug in the population would be 33%, that would indicate that the drug does nothing. If, in a large study with lots of people, the observed success rate were something like 1%, there might be a very small likelihood of observing that rate or smaller rates, but the scientists developing that drug certainly would not want to publish those results. Instead, that would be a case suited for a directional hypothesis that would lead to rejection of the null hypothesis if the likelihood of the observed successes or more was less than would be expected with a rate of 33%. The null and alternative hypotheses for that example might be:

\[H_0: \pi \le 0.33\] \[H_1: \pi>0.33\] Directional hypotheses are also known as one-tailed hypotheses because only observations on one side of the probability distribution suggested by the null hypothesis can potentially lead to rejecting the null.

Point hypotheses indicate that the population parameter is in any way different – greater than or less than – the value stated in the null hypothesis. For example: a marketing firm might be interested in whether a new ad campaign changes people’s minds about a product. They may have a null hypothesis that indicates a 50/50 chance of either improving opinions or not improving opinions. In that case, evidence from sample data that indicates highly improved opinions or highly declined opinions would indicate substantial change and may – based on the cumulative likelihood of high numbers of positive opinions or higher or on the cumulative likelihood of low numbers of positive opinions or lower – lead to rejection of the null hypothesis. A set of null and alternative hypotheses for that scenario may look like this:

\[H_0: \pi=0.5\] \[H_1: \pi \ne 0.5\] A point hypothesis is also known as a two-tailed hypothesis because values in the upper range or values in the lower range of the probability distribution suggested by the null hypothesis can lead to rejection of the null.

The choice of whether to use a point hypothesis or a directional hypothesis should depend on the nature of the scientific inquiry (although there are some that will prescribe always using one or the other). Personally, I think that cases where scientists are genuinely ambivalent as to whether a result will be either small or large – which would suggest using a point hypothesis – are legitimate but less frequent than cases where scientists have a good idea of which direction the data should point, which would produce more directional hypotheses than point hypotheses. But, that is a matter of experimental design more than a statistical concern.

Classical Null Hypothesis testing follows an algorithm known as the six-step hypothesis testing procedure.

Figure 6.5: There are few things in this world I love as much as a clever setup to a dumb punchline.

This algorithm should be considered a basic guideline for the hypothesis testing procedure: the six steps are not etched in stone¹³⁶, the wording of them varies from source to source, and sometimes the number of steps is cited as 5 instead of 6, but the basic procedure is always the same. The next section outlines the procedure, using the mutating-turtles example to help illustrate.

6.1.2 The Six (sometimes Five) Step Procedure

The basic logic of the six-step procedure is this: we start by defining the null and alternative hypotheses and laying out all of the tests we are going to do and standards by which we are going to make decisions.

We then proceed to evaluate the cumulative probability of at least the observed data (more on that in a bit) given the null hypothesis. This cumulative probability is known as the $p$-value: if the $p$-value is less than a predetermined rate value known as the $\alpha$-rate, then we reject the null hypothesis in favor of the alternative hypothesis.

Rejecting the null hypothesis means that we have assumed a world where there is no effect of whatever we are investigating and have analyzed the cumulative likelihood of the observed data in that context and come to the conclusion that it’s unlikely – based on the observed data – that there really is no effect of whatever we are investigating. Given that we have rejected the null, then the alternative is all that is left. In cases where we reject the null hypothesis, we may also say that there is a statistically significant effect of whatever it is we are studying.

If we analyze the cumulative likelihood of the data under the assumptions of the null hypothesis and find that it exceeds the $\alpha$ rate, then we would not be able to rule out the null hypothesis: the data would be pretty likely if there were no effect so we continue to assume no effect. In such cases, we continue to assume the null hypothesis.

Please note that in the preceding paragraphs there is no mention of the terms prove or accept or any form, derivation, or synonym of either of them. In the Classical framework (and in the Bayesian framework, too), we never prove anything, neither do we ever accept anything. That practice is consistent with principles of early-20th century philosophy of science in that no scientific theory is ever considered to be 100% proven, and it’s also consistent with the notion that statistical findings are always, in some way, probabilistic rather than deterministic in nature. The rejection of a null hypothesis, for example, is not so much there’s no way the null can be true as the null is unlikely enough given the likelihood threshold we have set.

6.1.2.1 $p$-values

As noted above, the decision as to whether to reject or to continue to assume the null hypothesis depends on the cumulative likelihood of the data, and that the value of the cumulative likelihood given the null hypothesis is known as the $p$-value. $P$-values are the stiffest competition to confidence intervals for most famously misunderstood concept in statistics: like the confidence interval, it’s pretty poorly named.

The $p$-value is a cumulative likelihood: if it weren’t a cumulative likelihood, we would be rejecting null hypotheses in just about every scientific investigation. The probability of any one specific event is vanishingly small, especially for continuous variables but for discrete variables with large $N$ as well.¹³⁷ Generally speaking, ranges produce much more meaningful probabilities than do single values.

The range of the cumulative likelihood of a $p$-value is defined as the observed event plus more extreme unobserved events. That might sound odd, particularly the part about unobserved events. How can unobserved events affect our understanding of science? First, as noted in the preceding paragraph, the probability of just the observed event would be misleadingly small. Second, that reasoning isn’t terribly unusual: you or someone you know might be or might have been in a situation where you or they need a certain grade on an upcoming assessment to get a certain grade in a course. You may have said or you may have heard somebody else say, “I need to score $x\%$ on this test to pass [or get a D in or an A in, etc.] this class.” Let’s say a student needs an 80% to get a C for the semester in a class. Would they be upset if they scored an 81%, or an 82%, or a 100%? No, they would not. In the context of classical statistics, the likelihood of interest is more like at least the observed data.

That the $p$-value is a likelihood means that it is conditioned on something. That something is the conditions of the null hypothesis. The null hypothesis is a mathematical description of what would be expected if nothing were special at the population level. To some extent, researchers need to make choices about the null hypothesis. Sometimes these decisions are relatively straightforward: in the case of a cognitive task where participants have four options to choose from, a null hypothesis that states that the population parameter is equal to $1/4$ makes sense (that would be what would happen if people guessed purely at random). Other times, the decisions are not as straightforward: in the fictional case of our mutating-turtles example, the null hypothesis might be based on a population parameter of $1/2$, indicating that the ooze is just as likely to cause a mutation as not. But, we might instead define pure chance as something much smaller than $1/2$ or much bigger than $1/2$ based on what we know about turtle-mutating-ooze ¹³⁸. What we choose as the null hypothesis parameter matters enormously to the likelihood of the data.

The misconception about $p$-values is usually expressed in one of two ways: 1. that the $p$-value is the probability of the observed data and 2. that the $p$-value is the probability that the results of an experiment were arrived at by pure chance. Both statements are wrong. Firstly, the $p$-value refers not just to the data but at least the data because it’s a cumulative likelihood. Secondly (and probably more importantly): the $p$-value can’t be the probability of the data nor the probability that the data were a fluke because the $p$-value is conditioned on the choice of the null hypothesis. If you can change the null hypothesis (which includes the choice between using a point hypothesis or a directional hypothesis: the two types of hypotheses will always alter the $p$-value and may mean the difference between statistical significance and continuing to assume the null) and in doing so change the $p$-value, then the probability expressed cannot be a feature of the data themselves.

6.1.2.2 $\alpha$-rates and Type-I Errors

The $\alpha$-rate is also known as the false alarm rate or the Type I error rate. It is the rate of long-run repetitions of an experiment that will falsely reject the null hypothesis. No research study in the behavioral sciences produces definitive results: we never prove an alternative hypothesis. Thus, we have to have some standard for how small a $p$-value is to declare the data (cumulatively) unlikely enough to reject the null hypothesis. Whatever value for that threshold that we choose is also going to be the rate at which we are wrong about rejecting the null.

Let’s say we choose an $\alpha$ rate of 0.05. Figure 6.6 is a representation of a standard normal distribution with the most extreme 5% of distribution highlighted in the right tail. The distribution represents a null hypothesis that the population mean and standard deviation are 0 and 1, respectively, and the shaded area indicates all values that have a cumulative likelihood of 0.05 or less. Any result that shows up in the shaded region (that is, if the value of greater than or equal to 1.645) will lead to rejecting the null hypothesis: the shaded area is what is known as a rejection region.

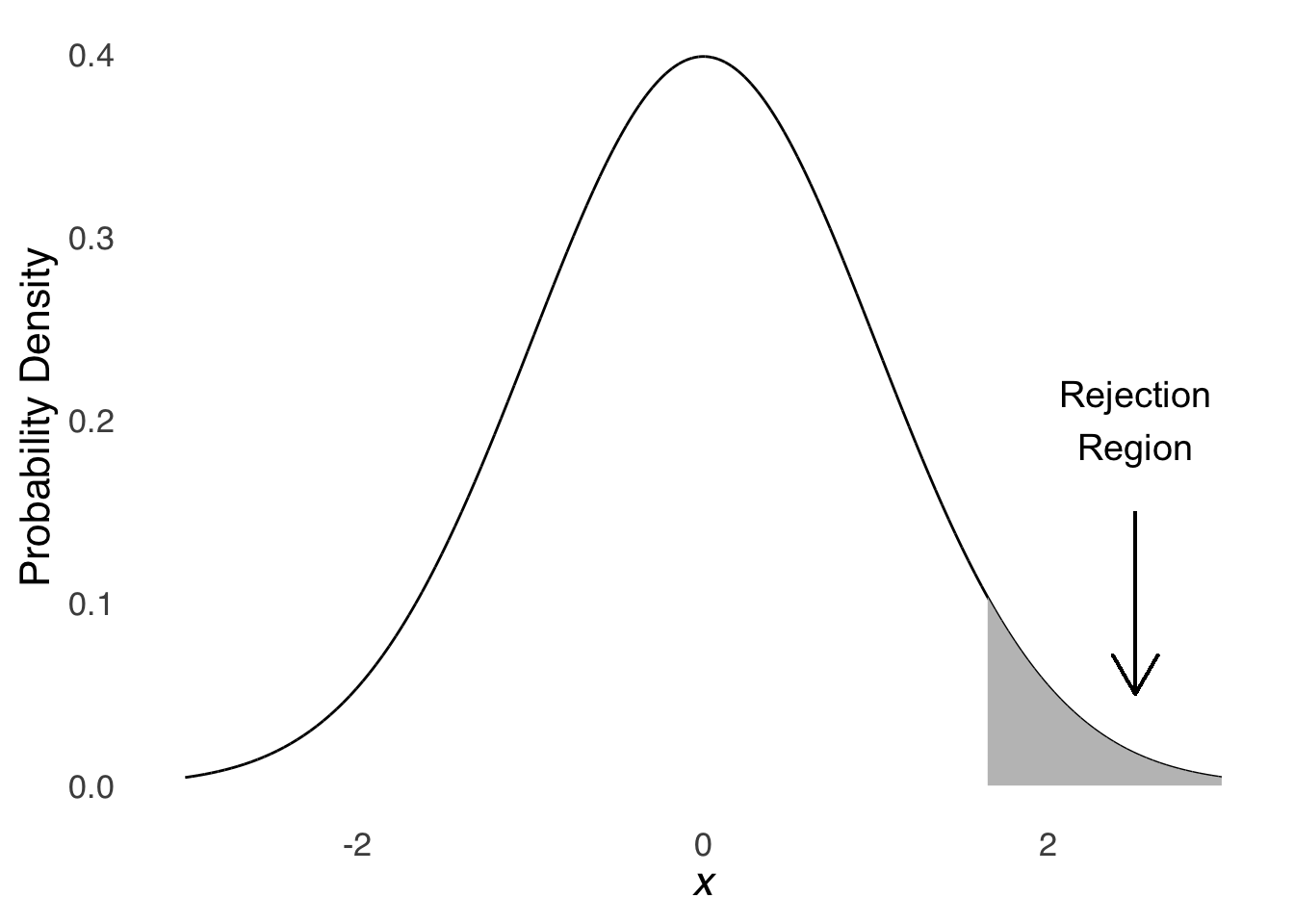
Figure 6.6: Normal Distribution with an Upper-tail 5% Rejection Region

Again, anytime we have an observed value pop up somewhere in the rejection region, we will reject the null hypothesis in favor of the alternative hypothesis. Rejecting the null means that we have some reason to believe that the value was not sampled from the distribution suggested by the null hypothesis but rather that it came from some other distribution with different parameters. We might be right about that. But as illustrated in Figure 6.6, we will be wrong 5% of the time. Five percent of the values in the distribution just live in that region. If there were no other distribution, we would sample a value from that part of the curve 5% of the time.

So, what should we choose to be the $\alpha$-rate? The most common choice is $\alpha=0.05$, which is a legacy of a decision made by R.A. Fisher (dick) that was partly informed by how easy it made calculations that had to be done using a slide rule.¹³⁹ It’s still common today largely because it has been handed down from stats teacher to stats teacher through the generations. Choosing $\alpha=0.05$ means that, on average, 5% of results declared statistically significant will be false alarms. It may not surprise you to learn that psychologists are increasingly tending towards choosing more stringent – i.e., smaller – $\alpha$ rates.

6.1.2.3 Type-II Errors

The complement to the Type-I error is the type-II error, also known as the $\beta$ error, or a miss. A type-II error occurs when there is a real, population-level effect of whatever is being tested. Figure 6.7 depicts a situation where the population distribution is different from the distribution represented by the null hypothesis. Whenever a value is sampled from this population distribution that is less than the values indicated by the rejection region under the null distribution, we will continue to assume the null hypothesis and be wrong about it.

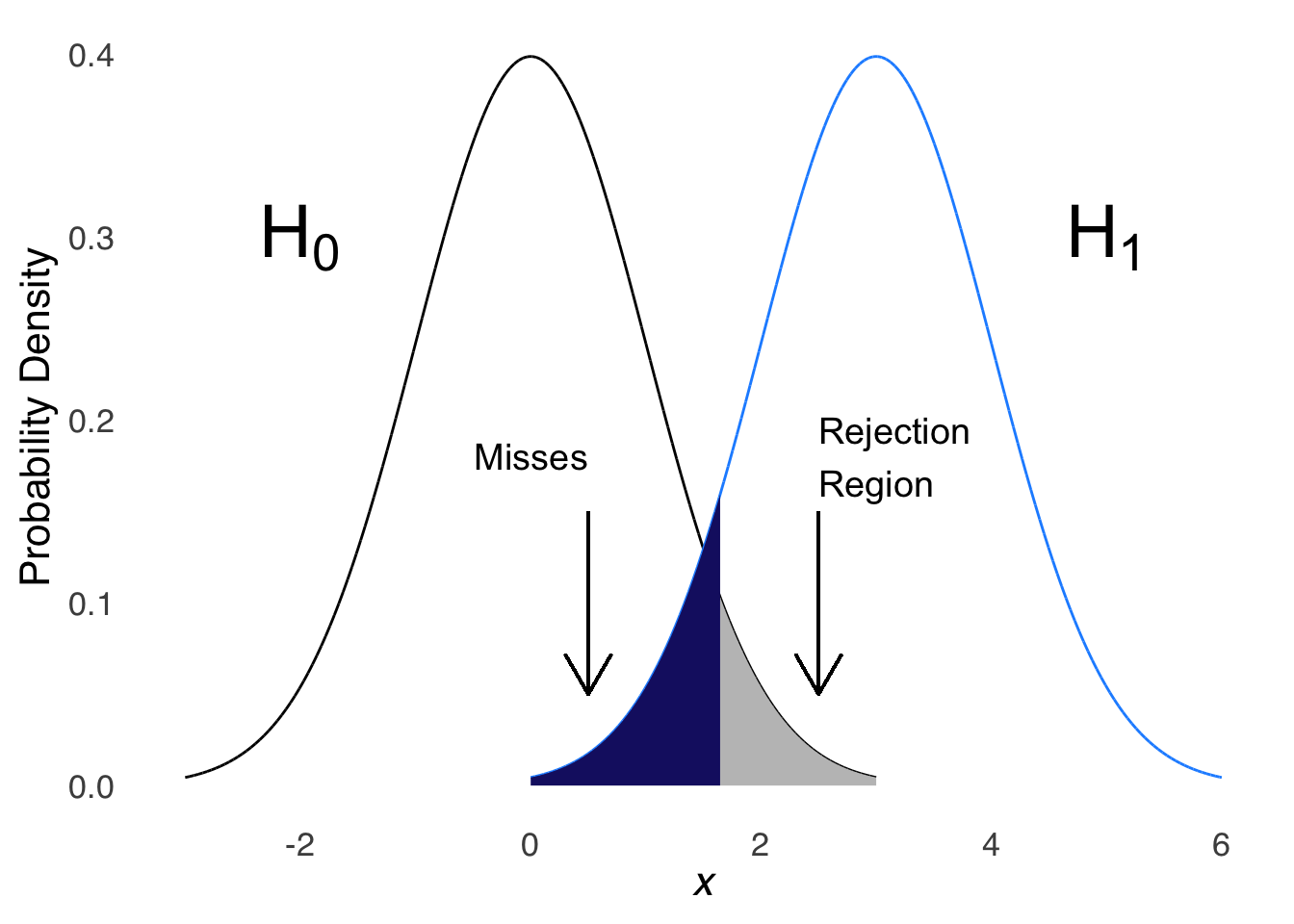
Figure 6.7: Normal Distribution with an Upper-tail 5% Rejection Region and an Alternative Distribution with Highlighted Misses

The long-term rate of misses is known as the $\beta$ rate. The complement of the $\beta$ rate – or $1-\beta$, is the rate of times when the null hypothesis will be correctly rejected. In the sense that it is the opposite of the miss rate we might call that the hit rate, but it is usually referred to as the power.

The table below indicates the matrix of possibilities based on whether or not there is a real, population-level effect (columns) and what the decision is regarding $H_0$ (rows).

		Real Effect?
		Yes	No
Decision	Reject $H_0$	Correct Rejection of $H_0$	False Alarm
Decision	Continue to Assume $H_0$	$Miss$	$H_0$ Correctly Assumed

There is a tradeoff between type-I and type-II errors: the more stringent we are about preventing false alarms (by adopting smaller $\alpha$-rates), the more frequently we will miss real effects, and the more lenient we are about preventing false alarms (by adopting larger $\alpha$ rates), the less frequently we will miss real effects. Which error – false alarm or miss – is worse? There are deontological prescriptions to answer that question – some believe that hits are worth the false alarms, others believe that avoiding false alarms are worth the misses – but I prefer a consequentialist viewpoint: it depends on the implications of the experiment.

And now, with no further ado, the six-step procedure:

Describe the null and the alternative hypotheses
Set the Type-I error rate
Identify the statistical test you will use
Identify a rule for deciding between the null and the alternative hypotheses
Obtain data and make calculations
Make a decision

In step 1, we state the null and the alternative. In the running example for this page (turtles and ooze), we will adopt a directional hypothesis: we will reject the null if the likelihood of the observed data or larger unobserved data is less than our $\alpha$ rate (but not if the observed data indicate a rate less than what is specified in the null). Thus, our null and alternative are:

\[H_0: \pi \le 0.5\] \[H_1: \pi=0.5\] In step 2, we define our $\alpha$-rate. Let’s save the breaks from tradition for a less busy time and just say $\alpha=0.05$.

In step 3, we indicate the statistical test we are going to use. Since we have binomial data, we will be doing a binomial test.

In step 4, we lay out the rules for whether or not we will reject the null. In this case, we are going to reject the null if the cumulative likelihood of the observed data or more extreme (in this case, larger values of $s$) data is less than the $\alpha$-rate (which, as declared in step 2, is $\alpha=0.05$). Symbolically speaking, we can write out our step 4 as:

\[\left\{ \begin{array}{ll} \mbox{if } p(s\ge s_{obs}|\pi=0.5, N=20) \leq 0.05~ & \mbox{reject}~H_0 \mbox{in favor of}~H_1 & \\ \mbox{else} & \mbox{continue to assume}~ H_0 \end{array} \right.\]

In step 5, we get the data and do the math. For our example, the data are:

\[s=16, N=20\]

And the cumulative likelihood of $s\ge16|\pi=0.5, N=20$¹⁴⁰ is:

pbinom(15, 20, 0.5, lower.tail=FALSE)$= 0.005909$

In step 6, we make our decision. Because the cumulative likelihood – our $p$-value – is 0.0059 and is less than $\alpha$, we reject the null hypothesis in favor of the alternative hypothesis.

There is a statistically significant effect of the ooze.

6.1.3 Confidence Intervals

A $1-\alpha\%$ confidence interval represents the range in which $1-\alpha\%$ of future samples using the same algorithm will generate similar interval estimates that capture the true population parameter $1-\alpha\%$ of the time. It would make a lot more sense – especially given the name confidence interval – if the interval represented a range where we were 95% confident that the true population parameter was. But, making such a statement would invalidate the very core of the classicist philosophy: that a parameter cannot be described using probability. The distinction in the language is not just philosophical, though: the range of future interval estimates produces different values than would an interval estimate about the true parameter value. We know that because Bayesians do calculate such intervals, and they are frequently different than corresponding Classical confidence interval estimates for the same data.

The term $1-\alpha\%$ refers to the false alarm rate used in a statistical analysis. If the false alarm rate $\alpha=0.05$, then the Classical interval estimate is a $1-0.05=95\%$ confidence interval. If $\alpha=0.01$, then the estimate is a $1-0.01=99\%$ confidence interval. Just as $0.05$ is the most popular $\alpha$ rate, $95\%$ is the most popular value for the Classical confidence interval. The value of the lower limit of the 95% confidence interval (0.563386) is the value of $\pi$ for which $p(\ge 16)=2.5\%$. The value of the upper limit of the 95% confidence interval (0.942666) is the value of $\pi$ for which $p(s\le 16)=2.5\%$.

Confidence intervals are useful for comparison: a narrower confidence interval indicates higher precision; and a wider confidence interval indicates lower precision. Confidence intervals that don’t include values of interest – in this case, 0.5 might be considered interesting because it suggests pure chance – are indicators of statistical significance (even though the 6-step procedure hasn’t been strictly followed) Confidence intervals for multiple samples that don’t overlap indicate significant differences; confidence intervals that do overlap indicate lack of significant differences.

6.2 Bayesian Inference

6.2.1 Posterior Probabilities

The Classical approach focuses on likelihoods: $p(D|H)$, the probability of the data given the hypothesis (namely, the null hypothesis). It places all of the probability on the observation of data. Data, in the classical approach, are probabilistic events – they depend on randomness in sampling or in unexpected changes in experimental procedures – and hypotheses are fixed elements, things that either are something or are not. The Bayesian approach focuses on posterior probabilities: $p(H|D)$, which are the conditional-probability antonyms of likelihoods. In the Bayesian approach, it is hypotheses that are described with probability based on the data, which are considered fixed facts: observations that happened with certainty.

This is how Bayesians get their name: the focus on the probability of hypotheses invokes the use of Bayes’s Theorem – $p(H|D)=\frac{p(H)p(D|H)}{p(D)}$ – to use posterior probabilities to describe hypotheses given the observed data.

As described in the page on probability theory, there are four parts to Bayes’s Theorem: the prior probability, the likelihood, the base rate, and the posterior probability. Using the turtle-mutating ooze experiment example, the next section will illustrate how we use Bayes’s Theorem to investigate a scientific hypothesis.

The scientific investigation represented by this example is centered around a proportion: given that $s=16$ successes were observed in $N=20$ trials, what can we say about the population-level probability parameter? That is: what is the overall probability that the ooze will turn a teenaged turtle into a teenaged mutant turtle (that may or may not practice ninjitsu)?

We will start with the prior probability. A common practice in Bayesian statistics is to choose priors that indicate that each possibility is equally likely, and that’s what we’ll do here. The population parameter has to be a value between 0 and 1. Let’s take evenly-spaced possible values of $\pi$ – generating 11 candidate values $\pi_i=\{0,~0.1,~0.2,~0.3,~0.4,~0.5,~0.6,~0.7,~0.8,~0.9,~1\}$ – and use a uniform prior probability $p(H)$ distribution that makes all 11 equally likely, as shown in Figure 6.8:

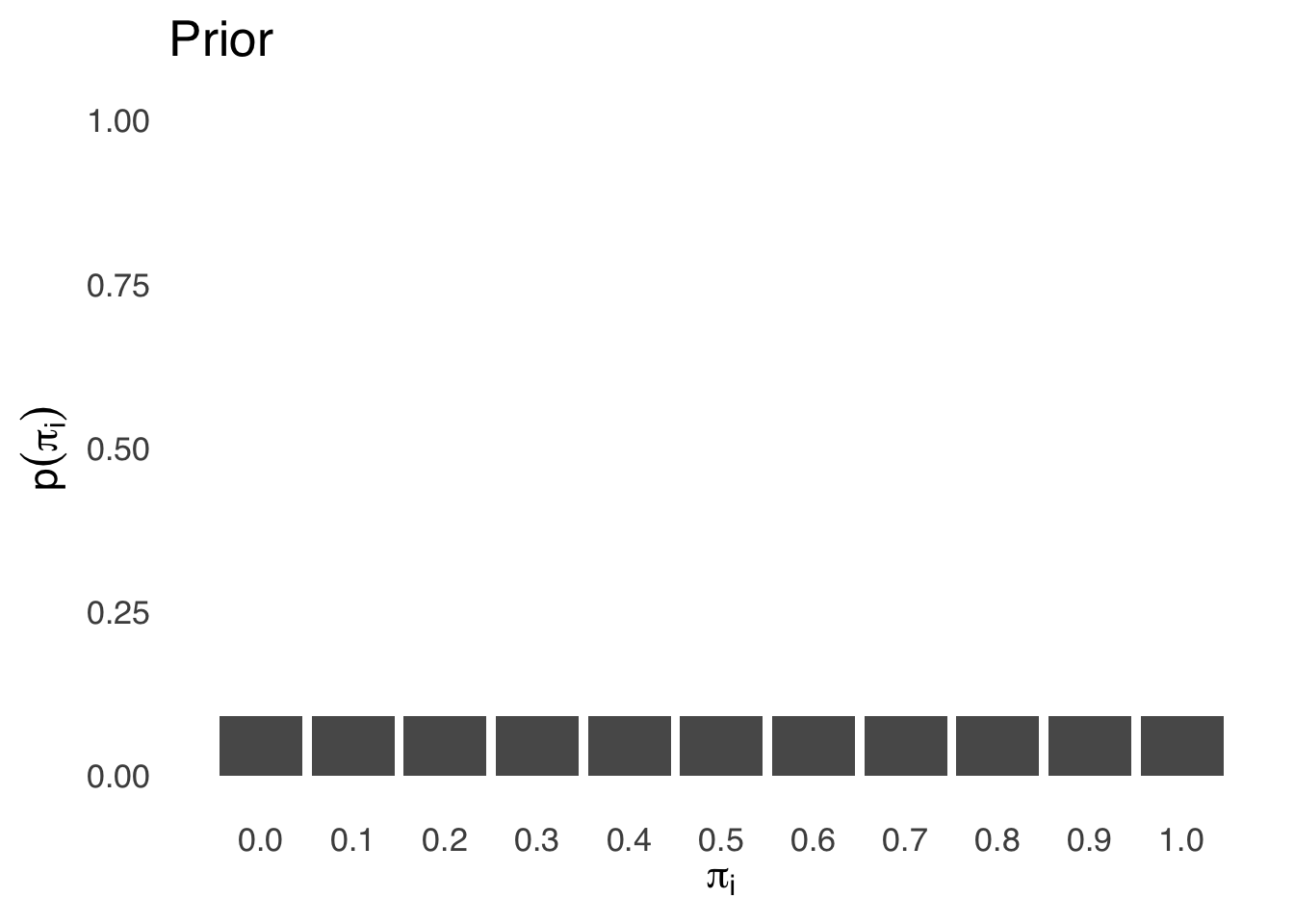
$Prior Probability Distribution for $\pi_i$$

Figure 6.8: Prior Probability Distribution for $\pi_i$

Next, let’s calculate the likelihood $p(D|H)$ for each of the 11 possible values of $\pi$ using the binomial likelihood function:

\[p(s=16|N=20, \pi=pi_i)=\frac{20!}{16!4!}(\pi_i)^{16}(1-\pi_i)^4\] The resulting likelihood distribution is shown in Figure 6.9.

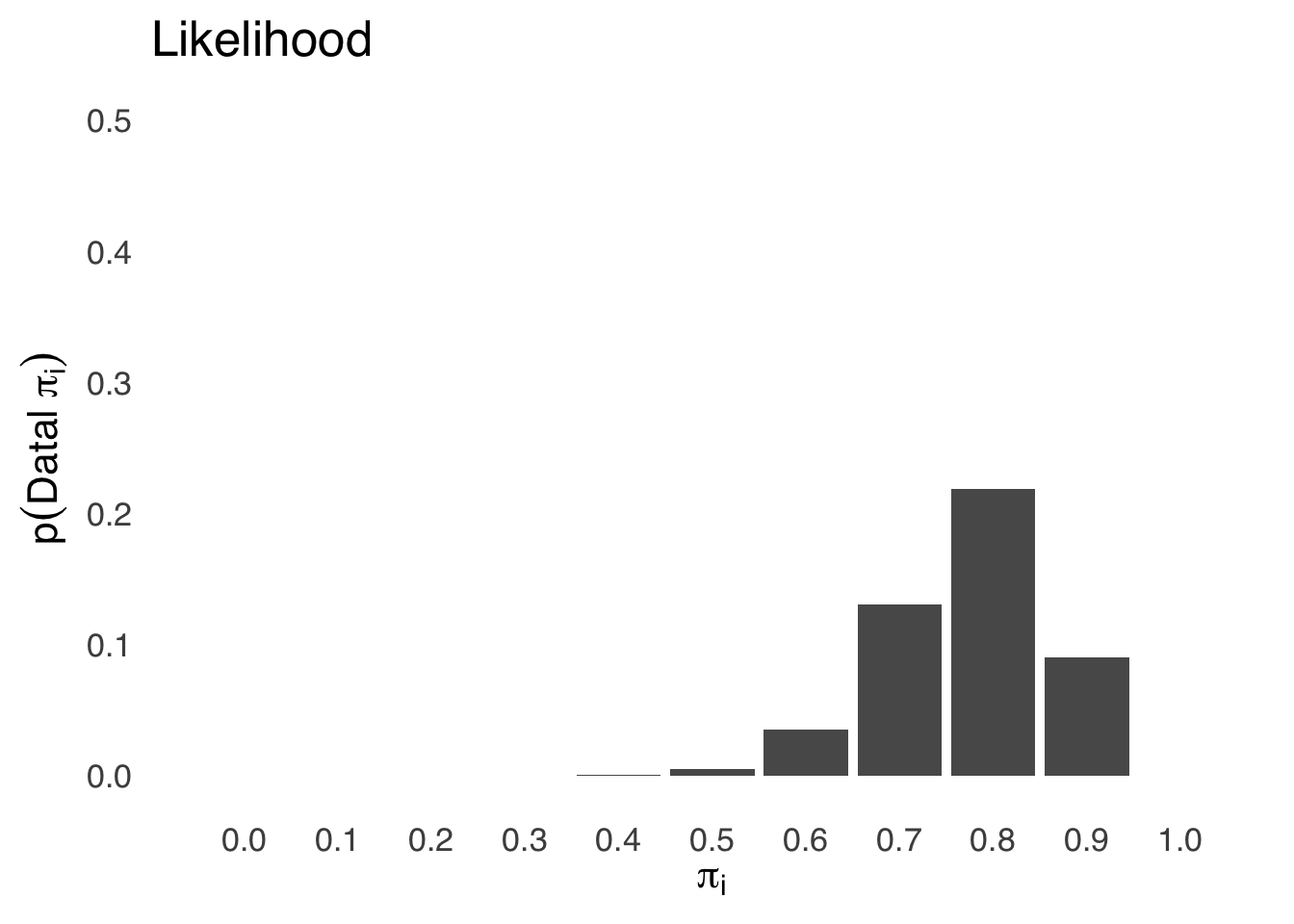
$Likelihood Distribution for $\pi_i$$

Figure 6.9: Likelihood Distribution for $\pi_i$

The base rate $p(D)$ is the value that will make all of the posterior probabilities that we calculate for each $\pi_i$ sum to 1. To get that, we take the sum of the products $p(H)p(D|H)$ for each value of $\pi_i$:

\[p(D)=\sum_{i=1}^{11} p(\pi_i)p(D|\pi_i)=0.0434\] Finally, for each value of $\pi_i$, we multiply the prior probability by the likelihood and divide each value by $p(D)$ (which is the constant 0.0434) to get the posterior probability distribution shown in Figure 6.10:

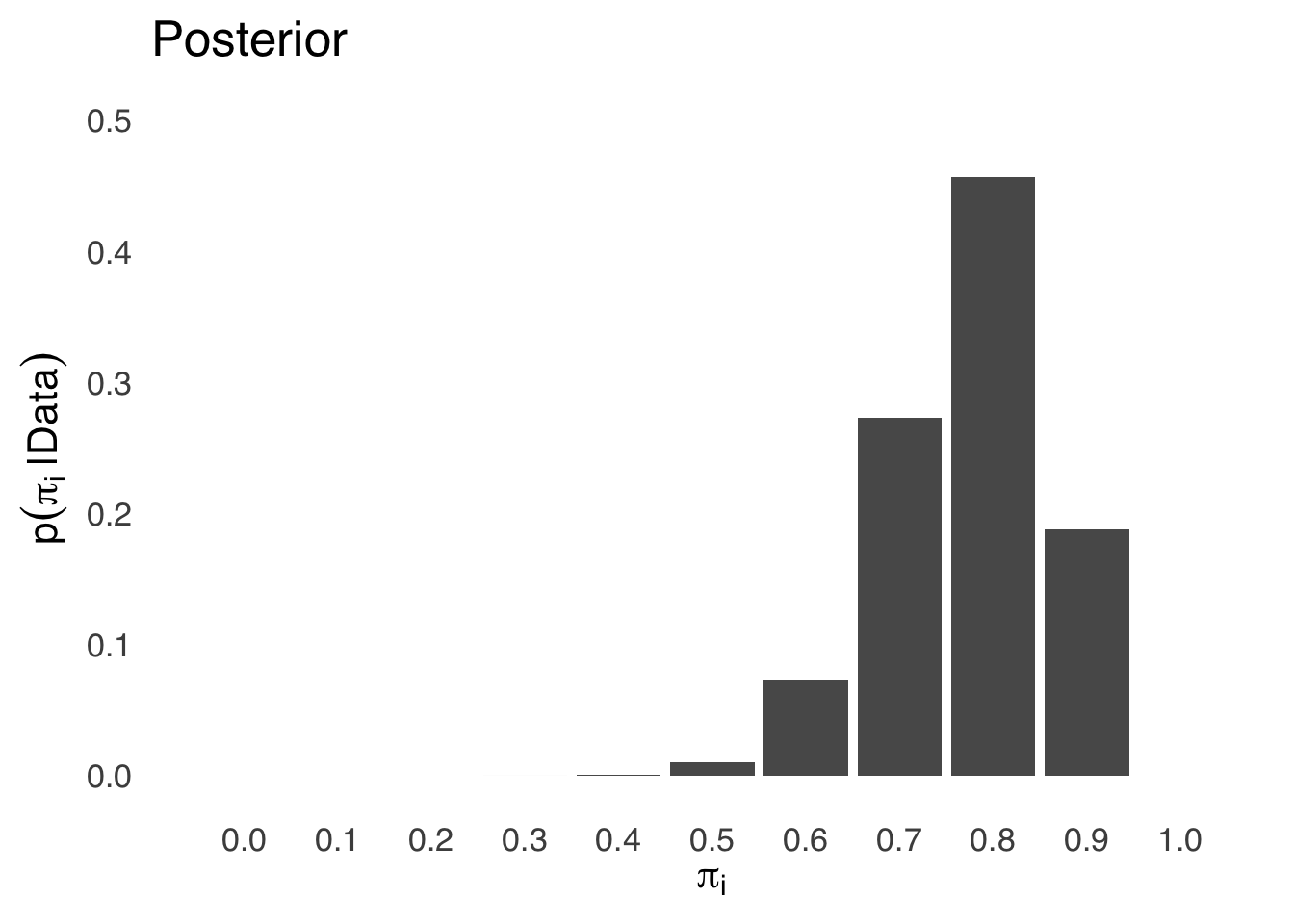
$Posterior Probability Distribution for $\pi_i$$

Figure 6.10: Posterior Probability Distribution for $\pi_i$

And, wouldn’t you know it? That looks an awful lot like the $\beta$ distribution for $s=16$ and $f=4$ (see Figure 6.4 above). In fact, if we divided the $[0, 1]$ more and took 101 values of $\pi_i$, it would look more like the $\beta$. And if we had infinite values of $\pi_i$, it would be the $\beta$. The $\beta$ distribution is the natural conjugate function for binomial data, meaning that it’s the result of Bayes’s thorem when you have binomial data. As a result, binomial data are pretty much the easiest thing to analyze with Bayesian methods.

As a natural conjugate function, if the prior distribution is a $\beta$ then the posterior distribution is also a $\beta$. When the $\beta$ is used as a prior, we use the symbols $s'$ (“s prime”) and $f'$ (“f prime”) to indicate that they are parameters for a prior distribution. The observed data from an experiment are still called $s$ and $f$. The resulting posterior distribution uses the symbols $s''$ (“s double prime”) and $f''$ (“f double prime”). In our example, we want to start with a prior probability that indicates that everything is equally likely. To do so, we will use a flat prior (the Bayesian term for a uniform prior distribution), specifically, the $\beta$ distribution with $s'=0$ and $f'=0$.¹⁴¹

To our prior $\beta$ shape parameters $s'$ and $f'$, we add our experimental data $s$ and $f$ to get the posterior shape parameters $s''$ and $f''$:

\[s''=s'+s=0+16=16\] \[f''=f'+f=0+4=4\] The resulting posterior $\beta$ distribution is therefore based on the sufficient statistics $s''=16$ and $f''=4$.¹⁴² The mean of the posterior distribution is:

\[mean(\pi)=\frac{s''+1}{s''+f''+2}=\frac{17}{22}\] the variance is:

\[var(\pi)=\frac{\pi(1-\pi)}{s''+f''+3}=0.0061\] and the standard deviation is:

\[sd(\pi)=\sqrt{\frac{\pi(1-\pi)}{s''+f''+3}}=0.078.\] Using the posterior $\beta$ distribution, we can make all kinds of probabilistic statements about the population parameter $\pi$. For example, we may want to know what the probability is that $\pi>0.5$:

pbeta(0.5, 17, 5, lower.tail=FALSE) $= 0.9964013$

6.2.2 Bayesian Interval Estimates

We also might be interested in the Bayesian counterpart to the confidence interval, known as the the highest density interval (abbreviated HDI), or the credible interval (abbreviated CI, the same as confidence interval is, which is obnoxious). The Bayesian HDI differs from the classical confidence interval in a couple of ways. The first is philosophical: the Bayesian HDI is the range in which we are $x\%$ confident that the population parameter is. The second is mathematical: the highest density interval is not necessarily symmetric (as most Classical confidence intervals are) but represent the narrowest possible interval that defines x% of the area under a posterior probability curve. That doesn’t make much difference for distributions that are themselves symmetric, but for skewed distributions (like the $\beta$ in our example), the HDI can be substantially narrower than a symmetric interval would be, allowing for more precise evalutation of the population parameter.

To calculate the HDI (or credible interval, if you prefer. I don’t.), we’re going to need some software help.¹⁴³ We can install the R package HDInterval to find HDI limits:

library(HDInterval) #load package
x<-seq(0, 1, 1/1000) #create a vector of x values to help define the probability function
hdi(qbeta(x, 17, 5), 0.95) #get the 95% HDI associated with the quantile distribution for a beta with shape parameters s+1=17 and f+1=5 across the range defined by x

##     lower     upper 
## 0.6000603 0.9303378 
## attr(,"credMass")
## [1] 0.95

Thus, the tightest possible range that defines 95% of the area under the $\beta$ curve for $s=16, f=4$ has a lower limit of 0.60 and an upper limit of 0.93. By convention, we report Bayesian intervals as:

\[p(0.60\le \pi \le 0.93)=0.95\]

6.2.2.1 The Metropolis-Hastings Markov-Chain Monte Carlo Algorithm

The $\beta$ distribution is relatively painless to use for Bayesian analyses: the shape parameters of the $\beta$ come straight from the data. Unfortunately, the proper distribution isn’t always so clear, especially in cases where there are multiple population parameters that we’re trying to learn about.

In those cases, Bayesians often turn to Markov Chain Monte Carlo methods to estimate posterior probability distributions on parameters. The most broadly useful Monte Carlo method for estimating probability distributions is the Metropolis-Hastings Algorithm.

Figure 6.11: Can’t stop, won’t stop

The Metropolis-Hastings Algorithm, like all Markov Chain Monte Carlo (MCMC) methods, is a sophisticated version of a random walk model. In this case, the steps are between parameter estimates, and the path is guided by the relative likelihoods of the data given the parameter estimate option. We start by choosing a starting value for our parameters – it doesn’t super-matter what we choose, but if we make more educated guesses then the algorithm works a little more efficiently. Then, we generate another set of parameters: if the new set of parameters increases the likelihood of the data or results in the same likelihood, then we accept the new set of parameters. If the new set of parameters decreases the likelihood of the data, then we will still accept the new parameters if the ratio of the new likelihood and the old likelihood is greater than a randomly generated number from a uniform distribution between 0 and 1. The second part – sometimes accepting new parameters if they decrease the likelihood of the data – is the key to generating the target probability distribution: if we only ever accepted parameters that increase the likelihood of the data, then the estimates would converge on a single value rather than the distribution. Accepting new parameters if the likelihood ratio exceeds a random number between 0 and 1 means that parameters that decrease the likelihood of the model are more likely to be accepted if they slightly decrease the likelihood than if they decrease the likelihood by a lot.¹⁴⁴ Then, we repeat the process again and again about a million times (deciding on how many iterations to use is more art than science, but the answer is usually: a lot).

Let’s pretend for now that we were unaware of the Bayesian magic of the $\beta$ distribution and its shape parameters and had to generate it from scratch. Here is how we would proceed:

Choose a semi-random starting parameter. We’ll call it $\pi_1$ and start it at 0.5 (can’t be too far off to start if we start in the middle of the range).
Randomly sample a candidate replacement parameter. We’ll call that $\pi_2$ and generate it by taking a random number from a uniform distribution between 0 and 1.
Calculate the likelihood ratio $r$:

\[r=\frac{p(D|\pi_2)}{p(D|\pi_1)}\] between the probability density using the new parameter and the old parameter. For our data, the probability densities are given by:

\[p(D|\pi_i)=\frac{20!}{16!4!}\pi^{16}(1-\pi)^4\] 4. If the ratio $r$ is $\ge 1$, we will accept the new parameter. $\pi_2$ would be the new $\pi_1$. We’ll write it down (with software, of course) before we move on.

If the ratio $r$ is $<1$, randomly sample a number we’ll call $u$ between 0 and 1 from a uniform distribution.
Then, if the ratio $r$ is $>u$, then we will accept the new parameter. $\pi_2$ is the new $\pi_1$. We’ll write it down.
If the ratio $r$ is $\le u$, then we will reject the new parameter. $\pi_1$ stays $\pi_1$. We’ll write that down.

Repeat steps 1 – 4 like a million times, writing down either $\pi_1$ or $\pi_2$ – whichever wins the algorithm – each time.

Here’s how that looks in R code:

set.seed(77)
s<-16
N<-20
theta<-c(0.5, rep(NA, 999))
for (i in 2:1000000){ #Number of MCMC Samples
  theta2<-runif(1) #Sample theta from a uniform distribution
  r<-dbinom(s, N, theta2)/dbinom(s, N, theta[i-1]) #calculate likelihood ratio
  u<-runif(1) #Sample u from a uniform distribution
  theta[i]<-ifelse(r>=1, theta2, #replace theta according to MH algorithm
                   ifelse(r>u, theta2, theta[i-1]))
}

And the resulting distribution of the samples is shown in Figure 6.12.

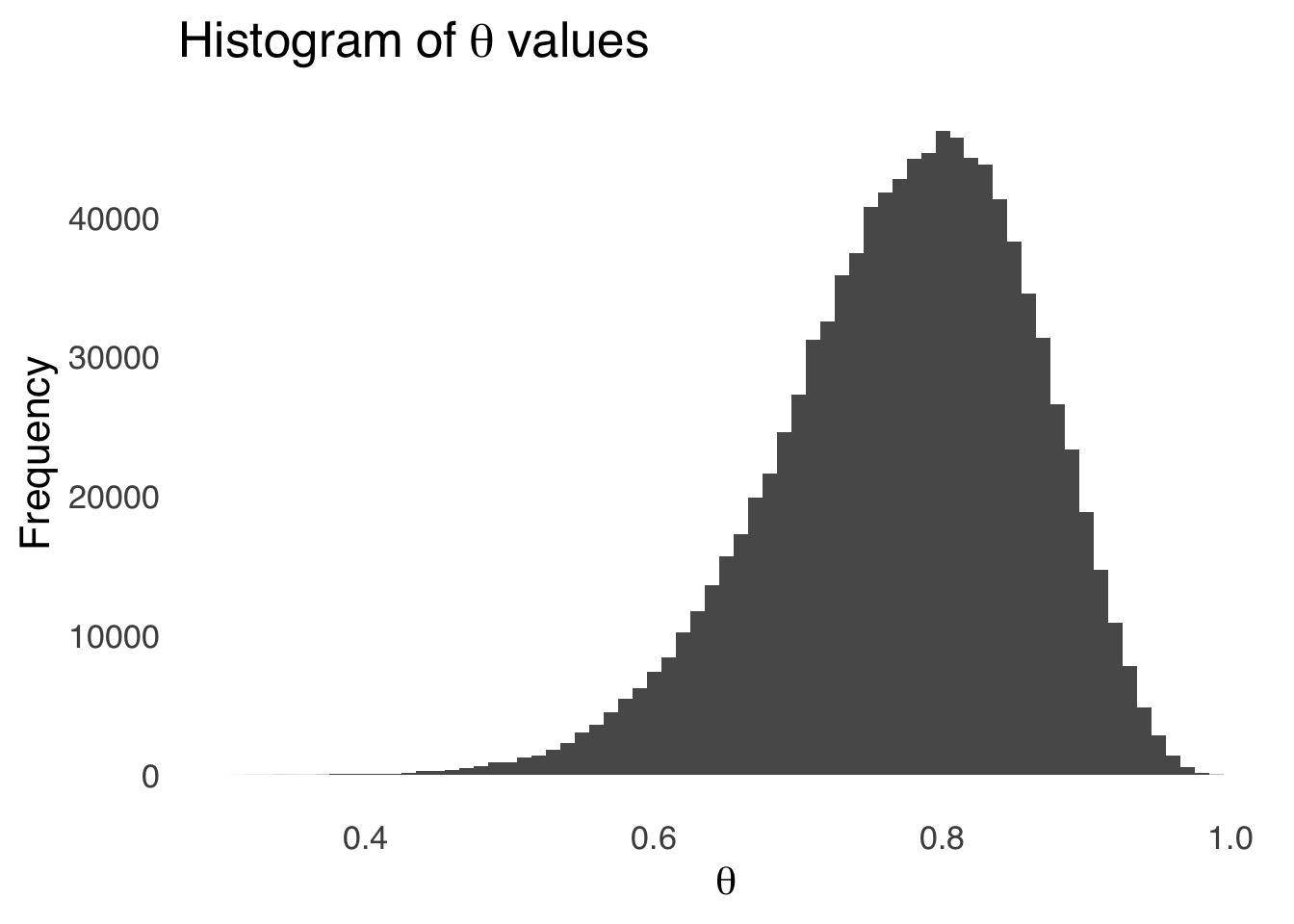
Figure 6.12: Results of 1,000,000 Markov Chain Monte Carlo Samples Selected Using the Metropolis-Hastings Algorithm

6.2.3 Bayes Factor

The last major Bayesian tool we’ll discuss in this introduction is the Bayes Factor. The Bayes Factor is a way of evaluating competing models.

Let’s posit a hypothetical model $H_1$. The odds in favor of the prior $H_1$ are $\frac{p(H_1)}{1-p(H_1)}$. If there are two models – $H_1$ and $H_2$, then the prior probability of $H_2$ is equal to $1-p(H_1)$, and the prior odds in favor of $H_1$ are:

\[\frac{p(H_1)}{p(H_2)}\].

Likewise, the posterior odds in favor of $H_1$ given the data are $\frac{p(H_1|D)}{1-p(H_1|D)}$, the prior probability of $H_2$ given the data $D$ is equal to $1-p(H_1|D)$, and the posterior odds in favor of $H_1$ are:

\[\frac{p(H_1|D)}{p(H_2|D)}\] Using Bayes’s Theorem, we can derive the following relationship between the prior odds and the posterior odds (note that $p(D)$ cancels out in the numerator and denominator – that’s why it’s missing):

\[\frac{p(H_1|D)}{p(H_2|D)}=\frac{p(H_1)}{p(H_2)}\frac{p(D|H_1)}{p(D|H_2)}\] The Bayes Factor is the factor by which the likelihood of model $H_1$ increases the posterior odds from the prior odds relative to the likelihood of model $H_2$ – it’s the rightmost part of the equation above.

\[B.F.=\frac{p(D|H_1)}{p(D|H_2)}\] Generally, the Bayes Factor is calculated by integrating both likelihoods over the range of all of their possible parameters:

\[B.F.=\frac{\int p(D|H_1)}{\int p(D|H_2)}\]

All things being equal, the integrated likelihood of a more complex model will be smaller than the integrated likelihood of a simpler model – a model with more parameters will stretch its likelihood across a much larger space. That means that the Bayes Factor naturally favors simpler models.

Which model is $H_1$ and which is $H_2$ is arbitrary. In practice, the model with the larger likelihood goes in the numerator so that Bayes Factor is always reported as being $\ge 1$: so the larger the Bayes Factor, the greater the evidence in favor of the more likely model. There are two sets of guidelines for interpreting Bayes Factors. Both are kind of arbitrary. I don’t have a preference.

Jeffreys (1961)		Kass & Raftery (1995)
Bayes Factor	Interpretation	Bayes Factor	Interpretation
1 to 3.2	Not worth more than a bare mention	1 to 3	Not worth more than a bare mention
3.2 to 10	Substantial	3 to 20	Positive
10 to 100	Strong	20 to 150	Strong
> 100	Decisive	> 150	Very Strong

Happily, we don’t need to use calculus for the example that wraps up this discussion of Bayesian inference. Let’s go to the ooze one more time!

Suppose we had two competing hypotheses for the population parameter $\pi$ that describes the probability of a turtle mutating when coming into contact with radioactive ooze. The first hypothesis is $H_1: \pi=0.8$. The second hypothesis is $H_2: \pi=0.5$. We can use Bayes’s theorem to compare them, and, because the likelihood functions of the two hypotheses (both binomial likelihood functions) differ only by the parameter value, a simple likelihood ratio gives the Bayes Factor:

\[B.F.=\frac{p(D|H_1)}{p(D|H_2)}=\frac{\frac{20!}{16!4!}(0.8)^{16}(0.2)^4}{\frac{20!}{16!4!}(0.5)^{16}(0.5)^4}=\frac{(0.8)^{16}(0.2)^4}{(0.5^{16}(0.5)^4)}\] \[B.F.=47.22366\]

That Bayes Factor is considered strong evidence in favor of the $\pi=0.8$ model by both the Jeffreys (1961) guidelines and the Kass & Raftery (1995) guidelines.

Please note that the little hat thing ($\hat{}$) is supposed to be right on top of $\pi$. Html, for some reason, doesn’t render that correctly.↩︎
The scientific principle of parsimony motivates explanations of phenomena to be as simple as possible but no simpler. We’ll cover the importance of parsimony and how it is emphasized in statistical analysis, but there is such a thing as too simple.↩︎
I am well aware that the most important problem associated with becoming a cashless society is worsening income inequality. But also: I would be left with pretty much no ability to explain statistics without the existence of coins.↩︎
I prefer using $s+1$ and $f+1$ to describe the shape parameters because it makes it easier to connect the distribution of proportions to observed successes and failures, but from my reading, $\alpha$ and $\beta$ are more common, and also the input that software packages including R expect.↩︎
This kind of logic is formally known as modus tollens, a Latin phrase that roughly translates to “the way that denies by denying.” If the statement if p then q is true, then the contrapositive of the statement if not q _then not p must be true. For example, the statement if it rained, then the street will be wet implies that if the street is not wet, then it did not rain. In the case of hypothesis testing, to say if not the data we expect, then not the hypothesis is a useful tool when your philosophy prevents you from directly evaluating the hypothesis itself.↩︎
Two such methods that we will talk about in future content are the Wilson Score Interval and the Normal Approximation (or Asymptotic) Method.↩︎
Now is an excellent time to point out that the “confidence interval” is perhaps the worst-named thing in statistics.↩︎
The founders of Classical Statistic are famously and rightly associated with the eugenics movement: I include that here not as evidence that Frequentism is an inferior approach to statistics but because I think it merits mention as often as possible. Also, at least one prominent Bayesian was a literal fascist.↩︎
To be clear: Classical statistics are not what most would consider simple: but they are, by and large, simple relative to the Bayesian alternative.↩︎
On the relatively rare occasions in which Classical analyses can’t rely on assumptions about data distributions, they can become super complex↩︎
The term hypothesis testing is generally broad and can include any scientific inquiry where an idea is tested with observations and/or experimentation. In the context of statistics, however, hypothesis testing has come to be synonymous with classical null hypothesis testing and is used as a shorthand for that approach.↩︎
I should say not etched in stone yet but keep refreshing this link.↩︎
For example, the probability of seeing exactly 1,000,000 heads in 2,000,000 coin flips is 0.0005641895.↩︎
I have to confess that all I know about turtle mutation comes from watching cartoons (and movies and also playing both video games) as a child and based on that I would guess that the mutation rate of radioactive ooze is 100%.↩︎
If you have a moment, you’re gonna wanna click on that slide rule link.↩︎
We use $\pi=0.5$ because that is the number in the statement of the null hypothesis.↩︎
$S'=f'=0$ indicates that we have no information included in the prior distribution. For that reason, this particular prior is an example of a noninformative prior because it does not sway the shape of the posterior distribution in anyway. This specific prior is also known as the ignorance prior, which is just rude.↩︎
Or in the other terms used to describe the shape parameters of the $\beta$, $\alpha=s''+1=17$, $\beta=f''+1=5$.↩︎
There are some HDI tables, but as with all tables, they are limited to a certain amount of possible parameter values.↩︎
For a proof of how generating a random number from a uniform distribution between 0 and 1 generates the desired probability distribution, see Chechile, R. (2020) Bayesian Statistics for Experimental Scientists. Cambridge, MA: MIT Press.↩︎

Advanced Statistics I & II