Chapter 6 Point Estimation
6.1 Descriptive Statistics
Descriptive statistics is the branch of statistics that involves ‘describing a situation’. Most of the methods used in descriptive statistics are relatively simple, such as finding averages or constructing a graph.
A distribution consists of the values that a random variable takes on and how often it takes those values. We will use three techniques to describe a distribution: a table, graph, or mathematical function.
Part of a data table is presented. Each row represents a student, and each column is a variable (one of the questions you were asked).
## Class Sex Color Texts Chocolate Height Temperature
## 1 9:30 Male Green 10 3 70 86
## 2 9:30 Female Purple 2 3 67 76
## 3 9:30 Female Green 2 10 67 90
## 4 9:30 Female Blue 4 7 66 85
## 5 9:30 Male Purple 30 6 67 90
## 6 9:30 Female Red 4 7 67 83A common way to display a quantitative data set is with a stem-and-leaf plot, also known as a stemplot. Each data value is divided into two pieces. The leaf consists of the final significant digit, and the stem the remaining digits.
If we were going to do a stemplot of ages and we had a 42 year-old man, the stem would be the ‘4’ and the leaf the ‘2’. If we had a 9 year-old girl, the stem would be ‘0’ and the leaf the ‘9’.
Here is a stemplot for the number of text messages sent by studentss.
## 1 | 2: represents 12
## leaf unit: 1
## n: 71
## 0 | 00000011112222223344444555556667788889999
## 1 | 0000122236777
## 2 | 00000333788
## 3 | 0234
## 4 |
## 5 |
## 6 |
## 7 |
## 8 | 7
## 9 |
## 10 | 0## ________________________________________________________
## 1 | 2: represents 12, leaf unit: 1
## Texts[Sex == "Male"] Texts[Sex == "Female"]
## ________________________________________________________
## 98765554332221100000| 0 |011222444455667888999
## 21000| 1 |02236777
## 7300| 2 |0003388
## 0| 3 |234
## | 4 |
## | 5 |
## | 6 |
## | 7 |
## 7| 8 |
## | 9 |
## 0| 10 |
## ________________________________________________________
## n: 32 39
## ________________________________________________________We often are interested in the central value, or ‘average’, of a distribution. Common statistics used to measure the center of a distribution include:
- mean
- median
- mode
The mean (or arithmetic mean) of a dataset is just the average, computed as you would expect (i.e. add up the values and divide by sample size).
The mean of a sample is referred to as a statistic (a characteristic of a sample) and is computed as \[\bar{x}=\frac{\sum x}{n}\]
The mean of a population is referred to as a parameter (a characteristic of a population) and is computed as \[\mu=\frac{\sum x}{N}\]
Notice we are using Greek letters for population parameters. This is the usual convention (although exceptions do exist). We usually can’t calculate a parameter because we usually don’t have data on the entire population.
The median is the middle value in an ordered data set. The median is often used if outliers (i.e. unusually small or large values) exist in the dataset. Outliers will affect the mean more than the median. We say the median is more resistant, or robust, to the effect of outliers.
The median is computed by taking the \(\frac{n+1}{2}\)th ordered data value, averaging the two middle values if \(\frac{n+1}{2}\) is not an integer.
The mode is the most frequent value in the data set. A data set may have mulitple modes, and the mode may not necessarily be found in the center of the distribution.
Here, instead of using data I collected from the class, the data below are hypothetical exam scores that a class with \(n=35\) students might have earned.
Mean: \(\bar{x}=\frac{2603}{35}=74.4\)
Median: \(M=77\) (the \(\frac{35+1}{2}=18\)th ordered value)
Mode: 71 and 87 (both occur three times)
## 1 | 2: represents 12
## leaf unit: 1
## n: 35
## 2 | 9
## 3 |
## 4 | 579
## 5 | 3
## 6 | 233578
## 7 | 11124578
## 8 | 011236677789
## 9 | 367
## 10 | 0In addition to central tendency, we are also interested in the amount of spread, or variability, in the data. Are the data clustered close to the mean or is there a wide range?
Statistics for measuring variability include:
- Range
- Five-Number Summary and IQR
- Variance and Standard Deviation
The five-number summary is a set of five statistics that gives information about the center, spread, and shape of a distribution. It consists of the following values:
Minimum (\(Min\))
First Quartile (\(Q_1\))
Median (\(M\))
Third Quartile (\(Q_3\))
Maximum (\(Max\))
We will at first use the simplest way to compute the quartiles, which is the way found on a TI-84 calculator and in most lower level math and statistics textbooks. The STA 540 textbook and R’s default will compute the quartiles with a more complex method and get slightly different answers, which we will consider later.
We already know how to compute the median, and the minimum and maximum are just the smallest and largest values in the data set.
The first quartile, \(Q_1\), is the 25th percentile of the data set. We will compute it by taking the median of the lower half of the data set. For example, the exam scores data set has \(n=35\) data values. The median, \(M=77\), was the 18th data value. So \(Q_1\) will be the median of the 17 values below 77.
Similarly, the third quartile, \(Q_3\), is the 75th percentile of the data set. It is the median of the data values greater than the median.
The five-number summary of the exam scores data set.
1.\(Min=29\) (the 1st or minimum value)
\(Q_1=65\) (the 9th value)
\(M=77\) (the 18th or middle value)
\(Q_3=87\) (the 27th value)
\(Max=100\) (the 35th or largest value)
The range is a simple measure of variability that is \(Range=Max-Min\). The interquartile range is \(IQR=Q_3-Q_1\), which measures the variability of the middle 50% of the distribution. Here, the range=71 and \(IQR=22\).
The famous statistician John Tukey has a simple rule for determining if a point in a data set is small/large enough to be an outlier.
First, compute the Step, where \(Step=1.5*IQR\). In the exam scores example, Step=33.
Next, subtract the step from the first quartile. \(Q_1-Step=65-33=32\). Any exam scores below 32 are outliers. In our problem, the score of 29 is an outlier on the low end.
Finally, add the step to the third quartile. \(Q_3+Step=87+33=120\). Any exam scores above 120 are outliers. In our problem, no points qualify as outliers on the high end. These values 32 and 120 are sometimes called fences; outliers are ‘outside’ the fences.
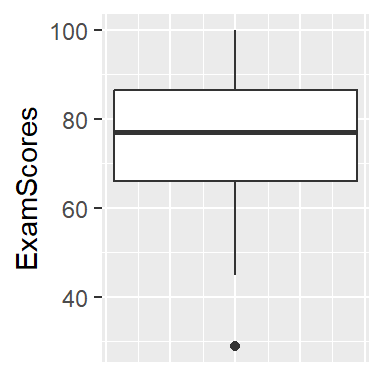
The boxplot is a graph that displays information from the five-number summary, along with outliers. The vertical, or y-axis, has the range of data values. Horizontal lines are drawn at the first quartile, median, and third quartile, and are connected with vertical lines to form a ‘box’. Sometimes the boxplot is oriented such that the x-axis is used to display the range of values rather than the y-axis.
‘Whiskers’ are vertical lines that are drawn from the quartiles to the smallest/largest values that are NOT outliers.
Points that are outliers are displayed with a symbol such as an asterisk or circle to clearly identify their outlier status.
The student who got a very low score of 29, is indicated as an outlier.
A weakness of the range is that it only uses the two most extreme values in the data set. The IQR is better, but it would be preferable to have a statistic that uses all values in the data set in an effort to measure the `average deviation’ or distance from the mean.
The deviation is defined as \(x-\bar{x}\). For example, if Dr. X is 42 and the average college professor is 48, the deviation is 42-48=-6, or Dr. X is six years younger than average.
Unfortunately, the sum of deviations, \(\sum (x-\bar{x})\) will equal zero for all data sets. Therefore, we cannot just compute the `average deviation’.
Occasionally we take the absolute value of the deviations, but the standard method for computing variability is based on squared deviations.
If we have a sample of data (i.e. a portion of a larger population), the variance is computed as: \[s^2=\frac{\sum (x-\bar{x})^2}{n-1}\]
Less commonly, if our data represents an entire population, the variance is: \[\sigma^2=\frac{\sum (x-\mu)^2}{N}\]
The standard deviation (either \(s\) or \(\sigma\)) is the square root of variance.
An example of computing the variance for a sample of \(n=5\) ages, where \(\bar{x}=44.2\) years.
| \(x\) | \(x-\bar{x}\) | \((x-\bar{x})^2\) |
|---|---|---|
| 29 | -15.2 | 231.04 |
| 35 | -9.2 | 84.64 |
| 42 | -2.2 | 4.84 |
| 50 | 5.8 | 33.64 |
| 65 | 20.8 | 432.64 |
| \(\sum\): 221 | 0 | 786.80 |
So the variance is \[s^2=\frac{786.8}{5-1}=196.7\] where the unit is years squared.
It is usually more convenient to take the square root. The standard deviation is \(s=\sqrt{196.7}=14.02\) years.
Obviously we want to use technology for large data sets.
6.2 Exploratory Data Analysis with R, Including Percentiles
It is very easy to compute the mean in R. R will assume your data represents a sample and you are therefore computing the sample statistic \(\bar{x}\), rather than the population parameter \(\mu\). Of course, both are computed with the same formula, \(\bar{x}=\frac{\sum x_i}{n}\).
You can use the by function to separate by levels of another variable. median does (you guees it!) the median of your distribution. var and sd will compute the sample variance \[s^2 = \frac{\sum_{i=1}^n (x_i-\bar{x})^2}{n=1}\] and \(s=\sqrt{s^2}\).
## [1] 261.3099aggregate(x = chickwts$weight, # Specify data column
by = list(chickwts$feed), # Specify group indicator
FUN = mean) ## Group.1 x
## 1 casein 323.5833
## 2 horsebean 160.2000
## 3 linseed 218.7500
## 4 meatmeal 276.9091
## 5 soybean 246.4286
## 6 sunflower 328.9167## [1] 258aggregate(x = chickwts$weight, # Specify data column
by = list(chickwts$feed), # Specify group indicator
FUN = median) ## Group.1 x
## 1 casein 342.0
## 2 horsebean 151.5
## 3 linseed 221.0
## 4 meatmeal 263.0
## 5 soybean 248.0
## 6 sunflower 328.0## [1] 6095.503## [1] 78.0737Now, let’s set aside our baby chicks and look at a small data set involving exam scores. I will manually enter in these scores into both a list in the TI-84 calculator and a vector in R.
## [1] 25 60 62 65 72 76 78 78 78 83 84 86 92 93 96## [1] 75.2## [1] 78## [1] 15The five number summary is a set of five simple statistics that quickly summarize the central tendency, the spread, and the shape of a distribution. The statistics used are: 1. minimum (or the 0th percentile) 2. first quartile \(Q_1\) (the 25th percentile) 3. median \(M\) (the 50th percentile) 4. third quartile \(Q_3\) (the 75th percentile) 5. maximum (or the 100th percentile)
We will define the quantile:
Let \(p \in [0,1]\). The \(p\)-quantile of a distribution is a number \(q\) such that the proportion of the distribution that is less than \(q\) is p.
Seems easy enough, but is tricky to compute in practice. As you will soon see, the way common quantiles (such as the first and third quartiles of the five-number summary) will be different between a TI-84 calculator and R, with other methods found in other software packages.
First, we’ll discuss how this is computed on your calculator, which corresponds to the discussion found in many (but not all) low-level statistics textbooks.
The minimum and maximum are easy: just take the smallest and largest numbers, i.e. your 1st and \(n\)th order statistics. For the exams, \(Min=25\) and \(Max=96\).
The median isn’t very hard either. With a sample of \(n=15\) students, we use the \(\frac{n+1}{2}\) th order statistic. The 8th order statistic is \(M=78\).
The TI-84 computes the first quartile \(Q_1\) in this fashion. Take all of the data values less than the median (i.e. exclusive of the median). This is our first seven order statistics \(25,60,62,65,72,76,78\). Take the median of those seven values. When you do so, \(Q_1=65\).
The third quartile is found in a similar fashion using the seven values greater than the median, again excluding the median. Doing this, \(Q_3=86\).
You are thinking “I bet R has a function for computing these values”. It has several, including summary, quantile, and fivenum.
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 25.0 68.5 78.0 75.2 85.0 96.0## 0% 25% 50% 75% 100%
## 25.0 68.5 78.0 85.0 96.0## [1] 25.0 68.5 78.0 85.0 96.0OH NO!!! The first and third quartiles (i.e. the 25th and 75th percentiles or the 0.25-quantile and 0.75-quantile) are different than my calculator!!! What is R doing???
It turns out there are many ways (type in help(quantile) to learn a bunch of them) to compute quantiles. Your TI-84 calculator and most lower-level math and stats textbooks are using “Type 2”. Here’s how R does it.
## 0% 25% 50% 75% 100%
## 25 65 78 86 96R is using “Type 7”, as is your textbook.
To find the 25th percentile, we have \(n=15\) and \(p=0.25\). The texxtbook notation is: \[\tilde{\pi}_p = y_{(r)} + (a/b)(y_{(r+1)} - y_{(r)})\]
Take the \(r=[(n-1)p]+1\) th order statistic. In our case, you end up with \(r=14(.25)+1=4.5\). The non-integer portion \(a/b=0.5\), so the 25th percentile (or first quartile) is a weighted average of the 4th and 5th order statistics. \[\tilde{\pi}_{0.25} = y_{(4)} + (0.5)(y_{(5)} - y_{(4)}) = 0.5y_{(4)} + 0.5y_{(5)} = 0.5(65) + 0.5(72) = 68.5\]
Similarly with \(p=0.75\), we use \(r=14(.75)+1=11.5\), and thus the 75th percentile (third quartile) is the average of the 11th and 12th order statistics.
\[\tilde{\pi}_{0.75} = y_{(11)} + (0.5)(y_{(12)} - y_{(11)}) = 0.5y_{(11)} + 0.5y_{(12)} = 0.5(84) + 0.5(86) = 85\]
What if the fractional remainder \(a/b\) is something other than 0.5? Let’s take the 90th percentile of the exams, so \(p=0.90\) and \(r=14(.9)+1=13.6\). This is telling us that the 90th percentile lies between the 13th and 14th order statistics, and since 0.6 is more than half, it will be closer to the 14th order statsitics than the 13th order statistics.
\[\tilde{\pi}_{0.9} = y_{(13)} + (0.6)(y_{(14)} - y_{(13)}) = 0.6y_{(14)} + 0.4y_{(13)} = 0.6(93) + 0.4(92) = 92.6\]
## 10% 90%
## 60.8 92.6A common measure of spread, or variability, of a distribution is the range, which is just \(Range=Max-Min\). An obvious flaw of this statistic is that it is completely distorted by outliers. If I tell you after an exam that the range was 71, that could be caused by a single individual (i.e. 14 out of 15 students got very high scores and one person did terrible, or vice-versa).
One solution is to use the interquartile range. \(IQR=Q_3-Q_1\) which tells us the spread in the middle 50% of the distribution. The major use of this statistic is in determining whether or not outliers exist in the data.
The famous statistician John Tukey devised a simple rule for detecting outliers based on the \(IQR\). For the purposes of my example, let’s use the exam scores and R’s version of the five-number summary.
- Find the interquartile range. \(IQR=Q_3-Q_1=85-68.5=16.5\)
- Find the step. \(Step=1.5IQR=1.5 \times 16.5 = 24.75\).
- Any points more than one step, or 1.5 IQR, from a quartile are outliers. These are called inner fences.
- \(Q_1-Step=68.5-24.75=43.75\)
- \(Q_3+Step=85+24.47=109.75\)
- The exam score of 25 is below 43.75, and is an outlier. A score would have to have been greater than 109.75 to be an outlier in the other direction.
Tukey constructed a graph known as a boxplot or box-and-whisker display that combines information from the five-number summary and outliers. Bars are drawn representing the median and the first/third quartiles, forming a ‘box’. ‘Whiskers’ are extended to the smallest/largest data values that are NOT outliers; in our case, with no outliers the whiskers extend to the minimum and maximum.
The base graphics packages uses the boxplot function.
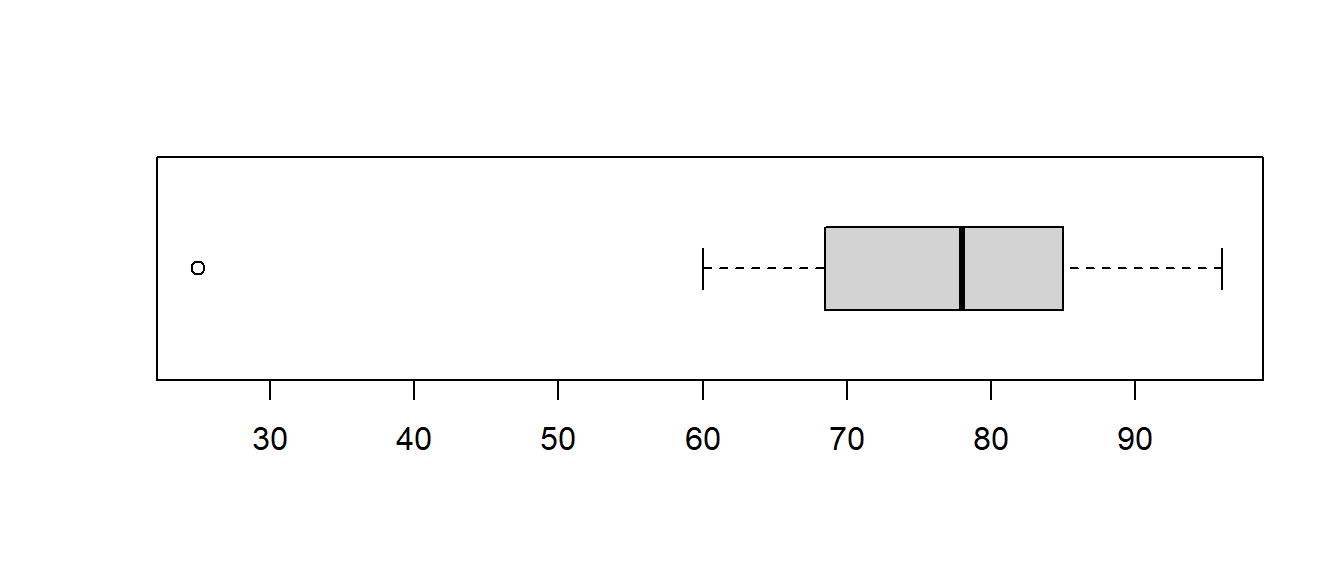
I am going to change one of the exam scores to show you how the plot will change without an outlier. Let’s suppose the first student actually got a 55, not a 25.
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 55.0 68.5 78.0 77.2 85.0 96.0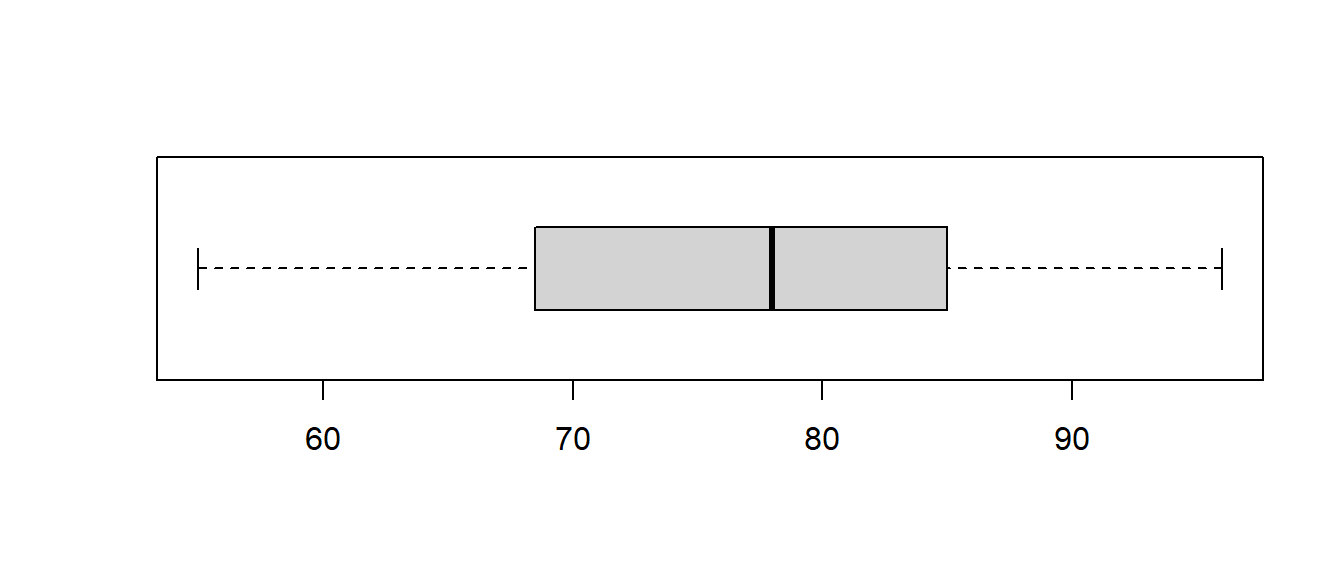
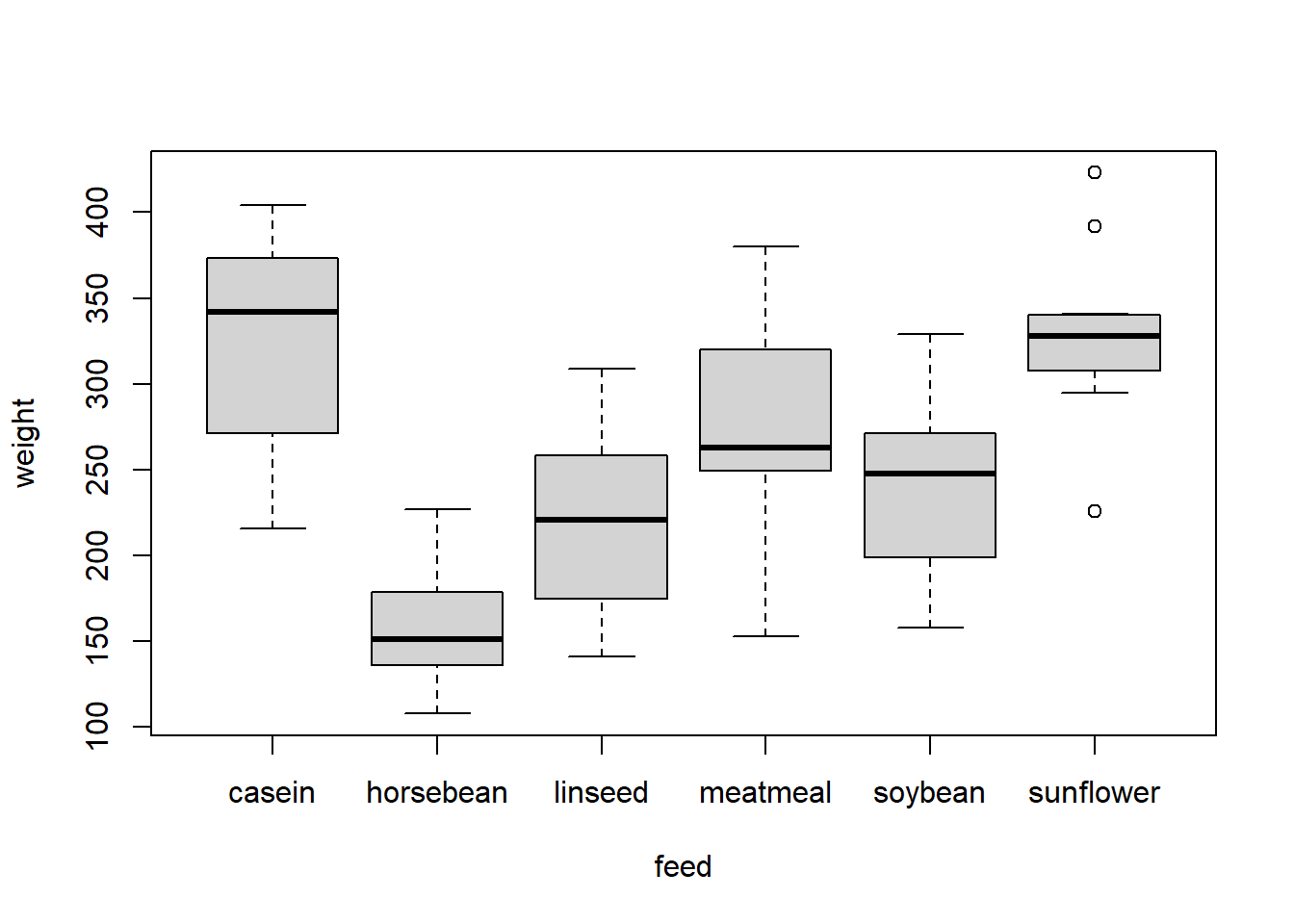
A great way of using boxplots is to draw side-by-side boxplots to compare two or more distributions. Let’s go back to our chick weights and compare the weight for different types of feed. Notice that there are several outliers when the chicks are given sunflower as the feed.
6.4 Maximum Likelihood Estimation
In statistics, we often seek to estimate the parameters of probability distributions and statistical models. Some examples:
I want to estimate the mean and standard deviation for the height of adult men, assuming \(X \sim N(\mu,\sigma)\)
I want to estimate the rate (in failures/day) at which my Internet connection at home ‘goes down’, assuming \(X \sim POI(\lambda)\)
I want to estimate the 2 shape parameters of a beta distribution to try to model the proportion of Americans that support the president, \(X \sim BETA(\alpha,\beta)\)
I want to estimate the lifespan of my laptop–where this might follow a Weibull distribution \(X \sim(\alpha,\beta)\) or a mixture of various distributions
Generically, we will refer to unknown parameters as \(\theta\). For example, I do not know precisely what the rate of failures per day for my Internet connection is. This unknown parameter is sometimes referred to as an estimand.
In order to estimate (i.e. make educated guesses) about the values of unknown parameters, we collect data and compute statistics based on the observed data X. A function of the observed data X that serves as a prediction for \(\theta\) is a called an estimator or point estimator and is denoted as \(\hat{\theta}\). That is, \[\hat{\theta}=f(X;\theta)\] A value that arises from a particular data set is called an estimate or point estimate.
Example: I want to know how many failures per day my Internet connection has, assuming \(X \sim POI(\lambda)\). The estimand \(\lambda\) is not known. I collect data for \(n=10\) days and get X=(3,4,0,1,6,2,1,0,0,1). An estimator that seems reasonable is to use \(\hat{\lambda}=\bar{X}\), the sample mean of the observed data. Later, we will learn why this point estimator satistifies various desirable mathematical properties.
\(\bar{X}=\frac{19}{10}=1.9\) is my point estimate; my single number best guess for the value of \(\lambda\).
How did I know to use \(\bar{X}\) as my estimator for the unknown parameter rather than the sample median or the sample variance or some other statistic? At this point, we don’t have any reason or justification beyond the fact that the sample mean is ‘easy’ to calculate and interpret and the fact that we know \(\lambda\) represents the rate of occurences per interval (i.e. the average number of events).
Statisticians have a variety of methods to derive estimators. The two most popular are:
method of moments estimation (MME), which we will consider now
method of maximum likelihood (MLE), which is the most used method
In order to learn the method of moments, we need to define what sample moments are.
The kth sample moment about zero is \[\hat{\mu}_k=\frac{1}{n} \sum_{i=1}^n (x_i)^k\]
Notice that \(\hat{\mu}_1=\frac{1}{n}\sum x_i=\bar{x}\), the sample mean.
The kth sample moment about the sample mean is \[\hat{\mu}'_k=\frac{1}{n} \sum_{i=1}^n (x_i-\bar{x})^n\]
Notice that \(\hat{\mu}'_2=\frac{\sum(x_i-\bar{x})^2}{n}=v \neq s^2\). This is not quite equal to the sample variance; in fact, \(v=\frac{n-1}{n} s^2\).
Using the method of moments is quite easy for single parameter models, i.e. only one unknown parameter \(\theta\) for \(X \sim f(x;\theta)\).
The process is:
Find the 1st moment of the population, i.e. find \(E(X)\) in terms of \(\theta\)
Find the 1st sample moment, i.e. \(\bar{x}\)
Set the sample moment equal to the population moment and solve for \(\hat{\theta}\). This solution is called the MME (method of moments estimator).
Example #1: \(X \sim POI(\lambda)\), so \(E(X)=\lambda\). The resulting equation is \(\hat{\lambda}=\bar{x}\) and we immediately see that \(\bar{x}\) is the MME for the Poisson distribution.
Example #2: \(X \sim EXP(\lambda)\), so \(E(X)=\frac{1}{\lambda}\). The resulting equation is \(\frac{1}{\hat{\lambda}}=\bar{x}\) and we see that \(\hat{\lambda}=\frac{1}{\bar{x}}\) is the MME for the exponential distribution.
Example #3: \(X \sim UNIF(\theta,10\)), where the maximum is known to be \(b=10\) but the minimum \(\theta=a\) is not known. \(E(X)=\frac{a+b}{2}=\frac{\theta+10}{2}\), so the MME equation is \(\frac{\hat{\theta}+10}{2}=\bar{x}\) with solution \(\hat{\theta}=2\bar{x}-10\).
Suppose I have an i.i.d. sample of size \(n=4\) from \(X \sim UNIF(\theta,10)\) such that X=(3.2,5.0,7.2,9.6). Clearly, \(\bar{x}=\frac{25}{4}=6.25\) and the MME is \(\hat{\theta}=2(6.25)-10=12.5-10=2.5\). Our estimate for the minimum of our uniform distribution is 2.5.
However, suppose my data were X=(2.2,6.0,7.2,9.6) instead. Notice that \(\bar{x}=6.25\) and \(\hat{\theta}=2.5\) remain unchanged, but now my MME is clearly an incorrect estimate. I observed a data value \(x=2.2\) which is less than the estimated minimum value \(\hat{\theta}=2.5\). This is an unfortunate reality with MME and also with MLE, in that sometimes the estimates end up being impossible. Sometimes in complicated models using MLE, parameters end up with negative estimates in contexts where negative values are impossible.
#require(fastR)
#similar to 4.3, but X ~ UNIF(theta,10), estimating the minimum
#I wrote a function that generates a random sample with n=size and minimum=theta
#it then computes the MME and returns if the MME is greater than the observed minimum
#(which it shouldn't be)
simulate<- function(theta,size) {
rdata<- runif(n=size,min=theta,max=10)
MME <- 2*mean(rdata)-10
MME > min(rdata)
results <- list(rdata,min(rdata),MME,MME>min(rdata))
names(results) <- c("Data","Minimum","MME","Too Big?")
return(results)
}
simulate(theta=0,size=4) #do once, TRUE means the MME is "too big"## $Data
## [1] 6.896993 5.101379 4.694002 2.717308
##
## $Minimum
## [1] 2.717308
##
## $MME
## [1] -0.2951592
##
## $`Too Big?`
## [1] FALSE## $Data
## [1] 6.439965 8.802370 5.436307 8.485617 6.022285 6.629783 5.697249 6.235657
## [9] 8.238171 7.963206 8.728013 6.108386 7.252373 5.134514 5.422075 8.377848
## [17] 6.280657 8.369689 8.962440 9.559883
##
## $Minimum
## [1] 5.134514
##
## $MME
## [1] 4.414649
##
## $`Too Big?`
## [1] FALSETwo Parameter Models:
Using the method of moments is not too much harder for two parameter models, i.e. two unknown parameters \(\theta_1,\theta_2\) for \(X \sim f(x;\theta_1,\theta_2)\).
The process is:
Find the 1st 2 moments of the population, i.e. find \(E(X)\) and \(Var(X)\) in terms of \(\theta_1,\theta_2\)
Find the 1st 2 sample (data) moments, i.e. \(\bar{x}\) and \(v=\frac{\sum (x_i-\bar{x})^2}{n}\)
Set the sample moments equal to the population moments and solve the resulting system of equations for \(\hat{\theta_1}\) and \(\hat{\theta_2}\).
Example #1: \(X \sim N(\mu, \sigma)\). We know that \(E(X)=\mu\) and \(Var(X)=\sigma^2\). We obtain the system of equations \(\hat{\mu}=\bar{x}, \hat{\sigma}=\sqrt{v}\). The MME for the mean of a normal is clearly just the sample mean. But the MME for the standard deviation is \(\hat{\sigma}=\sqrt{v}=\sqrt{\frac{n-1}{n}s^2}=\sqrt{\frac{\sum(x_i-\bar{x})^2}{n}}\), which is not quite the sample variance that we usually teach (i.e. we are dividing by \(n\) rather than \(n-1\)). In the next section, we will see a theoretical reason why we usually divide by \(n-1\) and do not use the MME for estimating variance/standard deviation of a normal distribution.
Example #2: \(X \sim BETA(\alpha,\beta)\). We know that \[E(X)=\frac{\alpha}{\alpha+\beta}, Var(X)=\frac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\] Setting these two population moments equal to \(\bar{x}\) and \(v\), respectively, yields (after tedious algebra) \[\hat{\alpha}=\bar{x}(\frac{\bar{x}(1-\bar{x})}{v}-1), \hat{\beta}=(1-\bar{x})((\frac{\bar{x}(1-\bar{x})}{v}-1))\]
Maximum Likelihood Estimation
Motivating Example (coin flipping/binomial): In statistics, we often have an unknown parameter (or paramters) \(\theta\) from a distribution that we wish to estimate. Last semester, we considered the method of moments as a systematic way of determining the estimate. Now, we will consder a method known as maximum likelihood estimation (MLE), which is probably the most common technique used in this scenario to obtain estimate \(\hat{\theta}\) for unknown parameter \(\theta\).
Basically, the idea is to determine the likelihood function that corresponds to the distribution you are sampling from and to find the value \(\hat{\theta}\) from the possible values of that parameter \(\theta\) that maximizes the likelihood function.
Suppose I am from Mars and I am unfamiliar with probabilities associated with flipping a fair coin. You, as an Earthling, know that if a fair coin is flipped, the probability of obtaining heads is \(\pi=0.50\). I, as a Martian, do not have that intuition and I will instead collect a sample (i.e. I will flip a coin several times) and I will use MLE to determine an estimate \(\hat{\pi}\) for the probability of getting heads.
If I flip a coin one time, the Bernoulli distribution (which is just the binomial distribution with \(n=1\)) models the probability of getting heads or tails. Letting \(X=0\) for tails (failure) and \(X=1\) for heads (success), then the Bernoulli density function for \(X_i \sim BERN(\pi)\) is:
\[f(x; \pi)=\pi^x (1-\pi)^{1-x} \qquad x=0,1; \qquad \pi \in (0,1)\]
The parameter space (i.e. possible values) for \(\pi\) is the interval \((0,1)\). We use \(\Omega\) to represent this space and in this situation say \(\Omega=\{\pi: 0 < \pi < 1\}\). For other distributions, \(\Omega\) could be all positive real numbers (such as the parameter \(\lambda\) in the exponential distribution) or all real numbers (such as \(\mu\) in a normal distribution). The example on page 251 of the text is a situation where the parameter space is finite (i.e. \(\Omega=\{1/2,1/3,1/5\}\) as the parameter represented the probability of getting a 1 or 2 from a 4-sided, 6-sided, or 10-sided die).
The likelihood function is the joint density function of our random sample from the specified distribution.
\[L(\theta)=\prod_{i=1}^n f(x_i; \theta)=f(x_1)\cdot f(x_2) \cdots f(x_n)\]
The Martian flips a coin three times, obtaining HTH (i.e. \(x_1=1, x_2=0, x_3=1\)). The Martian then constructs and maximizes a likelihood function for his observed data.
\[ \begin{aligned} L(\pi) & = \prod_{i=1}^3 f(x_i; \pi) \\ & = f(x_1) \cdot f(x_2) \cdot f(x_3) \\ & = f(1) \cdot f(0) \cdot f(1) \\ & = \pi^1 (1-\pi)^{1-1} \cdot \pi^0 (1-\pi)^{1-0} \cdot \pi^1 (1-\pi)^{1-1} \\ & = \pi (1-\pi) \pi \\ & = \pi^2 (1-\pi) \\ & = \pi^2-\pi^3 \\ \end{aligned} \]
I will graph this function and use some simple calculus to maximize it.
pi.hat<-seq(0,1,by=0.0001)
like<-pi.hat^2-pi.hat^3
MLE<-data.frame(pi.hat,like)
max<-which(like==max(like))
(pi.hat.max<-pi.hat[max]) #MLE## [1] 0.6667## [1] 0.1481481plot(like~pi.hat,type="l",lwd=2,xlab=expression(paste("Probability of Heads, ",pi)),
ylab="Likelihood",main="Maximum Likelihood Estimation")
abline(h=like.max,col="red",lty=2)
abline(v=pi.hat.max,col="red",lty=2)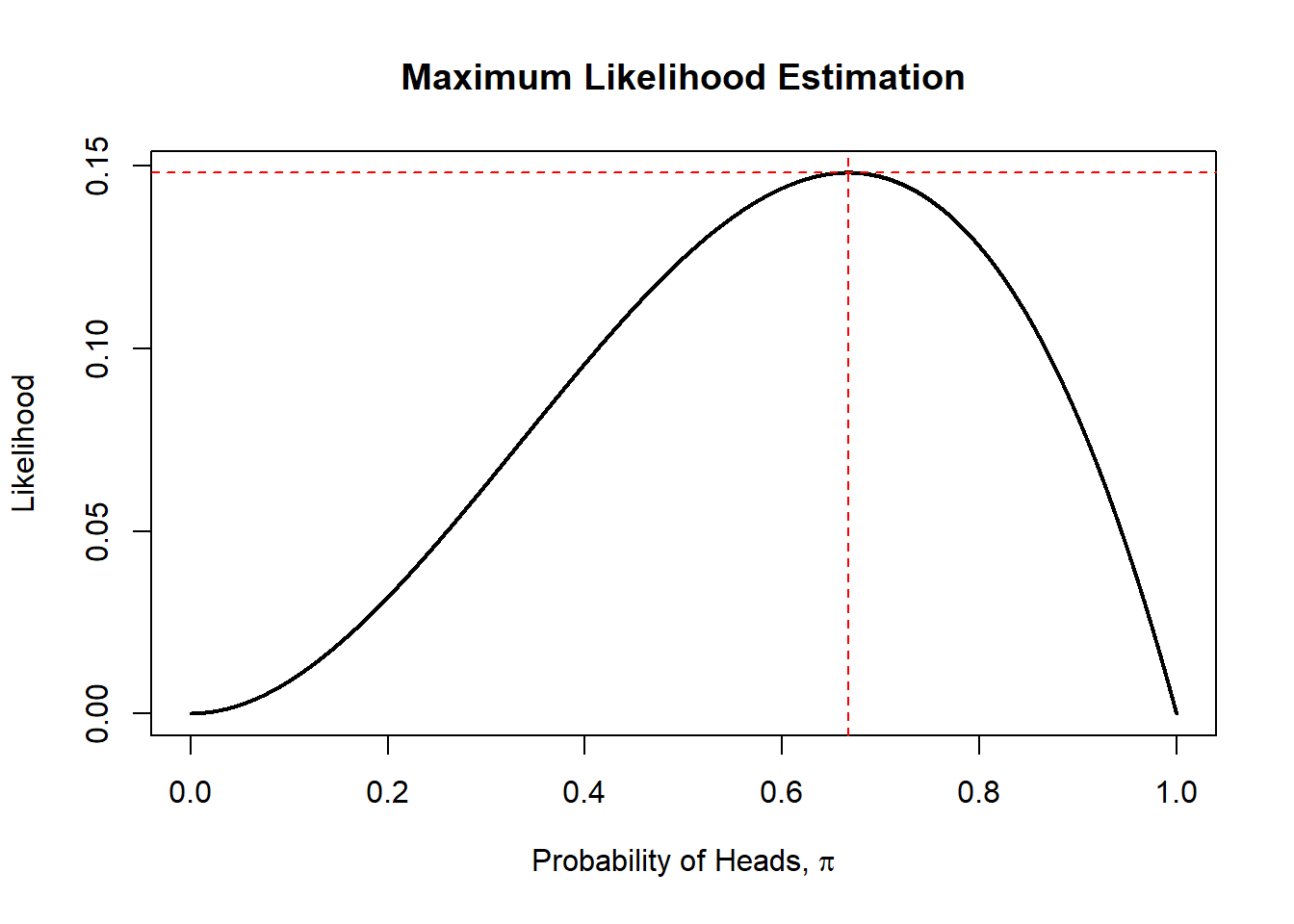
The function seems to be maximized at about \(\hat{\pi}=0.6667\). We can verify this with calculus; take the first derivative of the likelihood function, set that derivative equal to zero, and solve for \(\hat{pi}\) in the resulting equation.
\[ \begin{aligned} L(\pi) & = \pi^2-\pi^3 \\ \frac{d L(\pi)}{d\pi} & = 2\pi-3\pi^2 \\ 2\hat{\pi}-3\hat{\pi}^2 & = 0 \\ \hat{\pi} & = \frac{2}{3} \\ \end{aligned} \]
So in our example, \(\hat{\pi}=\frac{2}{3}\). The Martian flipped his coin 3 times, got heads twice, and thus the MLE for the probability of heads, based on this limited data, is \(2/3\). Obviously, repeated flipping of a coin would result in the MLE approaching \(1/2\).
We can generalize for \(n\) flips of a coin. When we do so, the likelihood function will be difficult to differentitate. What is usually done is to take the natural log of the likelihood and to maximize this log-likelihood function instead. Since the natural logarithm is a monotonically increasing function, we will obtain the same maximum whether we maximize \(L(\theta)\) or \(\ln L(\theta)\).
\[ \begin{aligned} L(\pi) & = f(x_1) \cdot f(x_2) \cdots f(x_n) \\ & = \pi^{x_1} (1-\pi)^{1-x_1} \cdot \pi^{x_2} (1-\pi)^{1-x_2} \cdots \pi^{x_n} (1-\pi)^{1-x_n} \\ & = \pi^{\sum x_i} (1-\pi)^{n-\sum x_i} \\ \ln L(\pi) & = \sum x_i \ln(\pi) + (n-\sum x_i) \ln(1-\pi) \\ \frac{d \ln L(\pi)}{d\pi} & = \sum x_i \frac{1}{\pi} + (n-\sum x_i)\frac{1}{1-\pi}(-1) \\ & = \frac{\sum x_i}{\pi}-\frac{n-\sum x_i}{1-\pi} \\ \frac{\sum x_i}{\hat{\pi}}-\frac{n-\sum x_i}{1-\hat{\pi}} & = 0 \\ \frac{\sum x_i}{\hat{\pi}} & = \frac{n-\sum x_i}{1-\hat{\pi}} \\ (1-\hat{\pi})\sum x_i & = \hat{\pi}(n-\sum x_i) \\ \sum x_i -\hat{\pi}\sum x_i & = \hat{\pi}n-\hat{\pi}\sum x_i \\ \sum x_i & = n \hat{\pi} \\ \hat{\pi} & = \frac{\sum x_i}{n} \\ \end{aligned} \]
We see that the MLE for the probability of success is equal to the sum of the \(x_i\)’s (which is the number of observed successes) divided by the total number of trials. In this case, the MLE has an intuitive explananation and is probably what somebody with no background in statistics might come up with for estimating the probability of success.
Basically, the idea is to determine the likelihood function that corresponds to the distribution you are sampling from and to find the value \(\hat{\theta}\) from the possible values of that parameter \(\theta\) that maximizes the likelihood function.
The parameter space is the set of all possible values of the parameter. We use \(\Omega\) to represent this space; if \(\theta\) is the probability of success of a Bernoulli process, then \(\Omega=\{\pi: 0 < \pi < 1\}\). For other distributions, \(\Omega\) could be all positive real numbers (such as the parameter \(\lambda\) in the exponential distribution) or all real numbers (such as \(\mu\) in a normal distribution). A situation where the parameter space is finite (i.e. \(\Omega=\{1/2,1/3,1/5\}\) could be if the parameter \(\pi\) represented the probability of getting a 1 or 2 from a 4-sided, 6-sided, or 10-sided die).
Regularity Conditions
(R0) The pdfs are distinct; i.e. \(\theta \neq \theta' \rightarrow f(x; \theta) \neq f(x; \theta')\)
(R1) The pdfs have common support for all \(\theta\), i.e. the support for \(X\) does not depend on \(\theta\)
(R2) The point \(\theta_0\) is an interior point in \(\Omega\).
These three regularity conditions are used in the following theorem (will not be proved here) which basically explains why maximum likelihood “works”.
Theorem: Let \(\theta_0\) be the true value of parameter \(\theta\). Under regularity conditions (R0) and (R1), \[lim_{n \rightarrow \infty} P_{\theta_0}[L(\theta_0,X)>L(\theta,X)]=1 \qquad \forall \theta \neq \theta_0\]
This theorem says that asymptotically the likelihood function is maximized at the true value of the parameter.
Definition: \(\hat{\theta}\) is a MLE of \(\theta\) is \(\hat{\theta}=argmax L(\theta,X)\) (i.e. \(L(\theta,X)\) achieves its maximum at \(\hat{\theta}\)), where \(argmax f(x)=\{x| \forall y: f(y) \leq f(x) \}\)
If we set \(\frac{\partial \ln L(\theta)}{\partial \theta}=0\), we obtain the estimating equation(s). We take the derivative of \(\ln L(\theta)\) w.r.t. \(\theta\), set equal to zero, and solve for \(\hat{\theta}\). If there are 2 or more paraemters, we have a system of equations to solve, based on setting the partial derivatives equal to zero.
Example: Let’s take an unfamiliar probability distribution such that you will probably not have any intuition about what a reasonable estimator for \(\theta\) might be.
\[f(x;\theta)=\frac{1}{\theta}x^{\frac{1-\theta}{\theta}}, 0 < x < 1, \theta > 0\]
I will utilize maximum likelihood estimation to find \(\hat{\theta}\).
\[ \begin{aligned} L(\theta) & = \frac{1}{\theta}x_1^{\frac{1-\theta}{\theta}} \cdot \frac{1}{\theta}x_2^{\frac{1-\theta}{\theta}} \cdots \frac{1}{\theta}x_n^{\frac{1-\theta}{\theta}} \\ & = (\frac{1}{\theta})^n \prod_{i=1}^n x_i^{\frac{1-\theta}{\theta}} \\ & = \theta^{-n} \prod_{i=1}^n x_i^{\frac{1-\theta}{\theta}} \\ \ln L(\theta) & = -n \ln \theta + (\frac{1-\theta}{\theta}) \ln (\prod x_i) \\ & = -n \ln \theta + (\frac{1-\theta}{\theta}) \sum \ln x_i \\ & = -n \ln \theta + \frac{1}{\theta} \sum \ln x_i - \sum \ln x_i \\ \end{aligned} \]
\[ \begin{aligned} \frac{d \ln L(\theta)}{d\theta} & = \frac{-n}{\theta}-\frac{1}{\theta^2} \sum \ln x_i \\ \frac{-n}{\hat{\theta}}-\frac{1}{\hat{\theta^2}} \sum \ln x_i & = 0 \\ -n & = \frac{1}{\hat{\theta}} \sum \ln x_i \\ \hat{\theta} & = -\frac{1}{n} \sum \ln x_i \\ \end{aligned} \]
Thus, the MLE is \(\hat{\theta}=-\frac{1}{n} \sum \ln x_i=-\frac{1}{n} \ln \prod x_i\). I didn’t have any intuition that that would be the result.
Is it unbiased for \(\theta\)?
\[ \begin{aligned} E(\hat{\theta}) & = E[-\frac{1}{n}\sum \ln X_i] \\ & = -\frac{1}{n} \sum E(\ln X_i) \\ & = -\frac{1}{n}\cdot n E(\ln X_i) \\ & = -E(\ln X_i) \\ \end{aligned} \]
This means that if the negative of the expected value of \(\ln X\) is equal to \(\theta\), then our MLE is unbiased.
\[ \begin{aligned} E(\ln X) & = \int_0^1 \ln x f(x) dx \\ & = \int_0^1 \ln x \frac{1}{\theta} x^{\frac{1-\theta}{\theta}} \\ \end{aligned} \]
We use everyone’s favorite integration technique (integration by parts). \[u=\ln x, du=\frac{1}{x}dx \qquad dv=\frac{1}{\theta}x^{\frac{1-\theta}{\theta}} dx, v=x^{frac{1}{\theta}}\]
\[ \begin{aligned} E(\ln X) & = [\ln x \cdot x^{\frac{1-\theta}{\theta}}]_0^1-\int_0^1 x^{\frac{1}{\theta}}\cdot \frac{1}{x} dx \\ & = -\int_0^1 x^{\frac{1}{\theta}-1} dx \\ -E(\ln X) & = \int_0^1 x^{\frac{1}{\theta}-1} dx \\ & = \frac{x^{1/\theta}}{1/\theta}|_0^1 \\ & = \theta x^{\frac{1}{\theta}}|_0^1 \\ & = \theta \end{aligned} \]
Our MLE is unbiased (yay!).
Example: Uniform Let’s look at an example similar to Exercise 5.1. Suppose we take an i.i.d sample of size \(n\) from \(X_i \sim UNIF(\theta,10)\). We have a uniform distribution where we know the upper bound of the support (i.e. the maximum) but do not know the lower bound of the support (the minimum).
\[f(x)=\frac{1}{(10-\theta)}, \theta < x < 10\] \[L(\theta)=\frac{1}{(10-\theta)^n}=(10-\theta)^{-n} \] \[\ln L(\theta)=-n \ln (10-\theta) \] \[\frac{d \ln L(\theta)}{d \theta}=\frac{n}{10-\theta}\]
If we set the derivative equal to zero and attempt to solve for \(\hat{\theta}\), it doesn’t work?
However, unlike MME, we can still find the MLE because we can still maximize the likelihood function.
It is not possible for the parameter \(\theta > \min(X_i)\). Why? Because if our smallest observed data value is \(x_i=5\), we know that the parameter \(\theta\) cannot be larger than 5 because \(\theta\) is the minimum of our uniform distribution.
Thus, \(L(\theta)=0\) if \(\theta > min(X_i)\) (i.e. those are impossible values).
What about values of \(\theta\) that are less than the smallest observed data value which are possible values for \(\theta\).
Well, the likelihood function is \[L(\theta)=\frac{1}{(10-\theta)^n}\]
If we choose \(\theta < min(X_i)\) and call that choice \(\theta^*\), then \(L(\theta^*) < L(\min(X_i))\).
Thus, the MLE must be \(\hat{\theta}=\min(X_i)\).
Also note that this is an example where the MME and MLE are not equal. The MME would be:
\[ \begin{aligned} E(X) & = \frac{\theta+10}{2} \\ \bar{x} & = \frac{\tilde{\theta}+10}{2} \\ \tilde{\theta} & = 2\bar{x}-10 \\ \end{aligned} \]
Example: (Normal, two unknown parameters)
Suppose we have an i.i.d. random sample of size \(n\) from a normal distribution, \(X_i \sim N(\mu, \sigma^2)\) where both the mean and variance parameters are unknown. For convenience, I will set \(\mu=\theta_1\) and \(\sigma^2=\theta_2\) and thus \(X_i \sim N(\theta_1,\theta_2)\).
The density function is \[f(x; \theta_1, \theta_2)=\frac{1}{\sqrt{2 \pi \theta_2}} \exp(-\frac{(x-\theta_1)^2}{2 \theta_2})\]
The likelihood function is \[L(\theta_1, \theta_2)=(2\pi \theta_2)^{-n/2} \exp(-\frac{\sum (x_i-\theta_1)^2}{2 \theta_2})\]
The log-likelihod function is \[\ln L(\theta_1, \theta_2)=-\frac{n}{2} \ln(2\pi \theta_2)-\frac{\sum (x_i-\theta_1)^2}{2 \theta_2}\]
Now we take two partial derivatives, with respect to \(\theta_1\) and \(\theta_2\), respectively, and set the partial derivatives equal to zero and solve the system of two equations in two unknowns for \(\hat{\theta_1}\) and \(\hat{\theta_2}\). In general, with \(p\) unknown parameters, we would have \(p\) partial derivativets and a system of \(p\) equations in \(p\) unknowns to solve to determine the \(p\) MLEs.
The partials w.r.t. \(\theta_1\) and \(\theta_2\) are:
\[\frac{\partial \ln L(\theta_1,\theta_2)}{\partial \theta_1}=\frac{\sum(x_i-\theta_1)}{\theta_2}\] \[\frac{\partial \ln L(\theta_1,\theta_2)}{\partial \theta_2}=\frac{-n}{2\theta_2}+\frac{\sum(x_i-\theta_1)^2}{2\theta_2^2}\]
Setting the partials equal to zero, we get the system \[ \begin{aligned} \frac{\sum(x_i-\hat{\theta_1})}{\hat{\theta_2}} & = 0 \\ \frac{-n}{2\hat{\theta_2}}+\frac{\sum(x_i-\hat{\theta_1})^2}{2\hat{\theta_2^2}} & = 0 \\ \end{aligned} \]
Taking the first equation: \[ \begin{aligned} \frac{\sum(x_i-\hat{\theta_1})}{\hat{\theta_2}} & = 0 \\ \sum(x_i-\hat{\theta_1}) & =0 \\ \sum x_i - n\hat{\theta_1} & = 0 \\ \hat{\theta_1} & = \frac{\sum x_i}{n} = \bar{x} \\ \end{aligned} \]
Unsurprisinly, the MLE for \(\theta_1\), the mean of a normal distribution, ends up just being the sample mean \(\bar{x}\). It is unbiased for \(\mu=\theta_1\).
Now taking the second equation and substituting \(\hat{\theta_1}=\bar{x}\):
\[ \begin{aligned} \frac{-n}{2\hat{\theta_2}}+\frac{\sum(x_i-\bar{x})^2}{2\hat{\theta_2^2}} & = 0 \\ -n + \frac{\sum(x_i-\bar{x})^2}{\hat{\theta_2}} & = 0 \\ \hat{\theta_2} & = \frac{\sum(x_i-\bar{x})^2}{n} \\ \end{aligned} \]
You might notice that the MLE for \(\theta_2\), the variance of the normal distribution, is not quite the sample variance, which is \(s^2=\frac{\sum(x_i-\bar{x})^2}{n-1}\). Why not?
It turns out that the MLE in this case is biased and we typically `adjust’ the MLE in order to obtain an unbiased estimator. The property of being unbiased is important enough such that we typically teach people to divide by \(n-1\) rather than \(n\) in introductory statistics courses, although it is hard to justify it in those classes, as these details are too technical for them. We end up saying stuff like ‘the sample probably isn’t as spread out as the population and we underestimate the variance, so dividing by \(n-1\) “fixes” that underestimation’.
Notice that the usual unbiased estimate of sample variance is a function of the MLE–we just ended up multiplying the MLE by a correction factor. \[\frac{n}{n-1}\hat{\theta_2}=\frac{n}{n-1}\frac{\sum(x_i-\bar{x})^2}{n}=\frac{\sum(x_i-\bar{x})^2}{n}=s^2\]
Notice that this correction factor \(\frac{n}{n-1} \to 1\) as \(n \to \infty\) (i.e. as the sample gets bigger, the amount of bias in the MLE will disappear).
Example: (Gamma, two unknown parameters)
Suppose we have an i.i.d. random sample of size \(n\) from a gamma distribution, \(X_i \sim GAMMA(\alpha,\theta)\) where both parameters are unknown. Recall that \(\mu=\alpha\theta\) and \(\sigma^2=\alpha \theta^2\).
Let’s first use the methods of moments. \[E(X)=\mu=\alpha\theta\] \[E(X^2)=\sigma^2+\mu^2=\alpha \theta^2+(\alpha \theta)^2\]
So the system of equations for MME is: \[\bar{x}=\alpha \theta\] \[\frac{\sum x_i^2}{n}=\alpha \theta^2+\alpha^2 \theta^2\]
First, solve for \(\tilde{\theta}\) \[ \begin{aligned} \frac{\sum x_i^2}{n} & = \bar{x}\tilde{\theta} + \bar{x}^2 \\ \tilde{\theta} & = \frac{\frac{\sum x_i^2}{n}-\bar{x}^2}{\bar{x}} \\ \end{aligned} \]
Now solve for \(\tilde{\alpha}\) \[ \begin{aligned} \tilde{\alpha} & = \frac{\bar{x}}{\tilde{\theta}} \\ & = \frac{\bar{x}^2}{\frac{\sum x_i^2}{n}-\bar{x}^2} \\ \end{aligned} \]
Now let’s use MLE.
The density function is \[f(x; \alpha, \theta)=\frac{1}{\Gamma(\alpha) \theta^\alpha} x^{\alpha-1} e^{-x/\theta}\]
The likelihood function is \[L(\alpha, \theta)=[\frac{1}{\Gamma(\alpha) \theta^\alpha}]^n [\prod_{i=1}^n x_i^{\alpha-1}] e^{-\sum x_i/\theta}\]
The log-likelihood function is \[\ln L(\alpha, \theta)=-n \ln \Gamma(\alpha) - n \alpha \ln \theta + (\alpha-1) \sum \ln x_i - \sum x_i/\theta\]
Now we take two partial derivatives, with respect to \(\alpha\) and \(\theta\), respectively, and set the partial derivatives equal to zero and solve the system of two equations in two unknowns for \(\hat{\alpha}\) and \(\hat{\theta}\). In general, with \(p\) unknown parameters, we would have \(p\) partial derivativets and a system of \(p\) equations in \(p\) unknowns to solve to determine the \(p\) MLEs.
The partials w.r.t. \(\theta\) is:
\[\frac{\partial \ln L(\alpha,\theta)}{\partial \theta}=\frac{-n \alpha}{\theta}+\frac{\sum x_i}{\theta^2}\]
Setting the partial equal to zero, we get \[ \begin{aligned} \frac{-n \alpha}{\hat{\theta}}+\frac{\sum x_i}{\hat{\theta}^2} & = 0 \\ \frac{\sum x_i}{\hat{\theta}} & = n \alpha \\ \hat{\theta} & = \frac{\bar{x}}{\alpha} \\ \end{aligned} \]
Substituting, we get \[\ln L(\alpha)=-n \ln \Gamma(\alpha) - n \alpha \ln(\frac{\bar{x}}{\alpha}) + (\alpha-1) \ln \sum x_i - n \alpha\]
We need the derivative of this w.r.t. \(\alpha\) (how do you take the derivative of the log of the gamma function of something??? I don’t know!)
I can’t solve analytically, this can be solved numerically and this is frequently done for complicated likelihood functions involving several parameters.
Restricted MLE:
The method of maximum likelihood is designed to find the value \(\hat{\theta} \in \Omega\) that maximizes \(L(\theta)\) or equivalently \(\ln L(\theta)\). However, often in applications there will be further limitations put on the parameter space; for example, while the mean of a normal distributions can theoretically take on any real number, we might be using the normal distribution to model a real-life scenario where the variable can only take on positive values and hence a negative estimate for \(\theta\) would not “make sense”. We can find the restricted MLE in this situation; we’ll see later the usefulness of restricted estimates in hypothesis testing.
Lets take a random sample of size \(n\) from \(X \sim N(\theta,\sigma^2)\), where \(\theta\) is an unknown parameter that represents the mean that we wish to estimate, and \(\Omega\) is all real numbers, while \(\sigma^2\) is assumed to be a known fixed constant that represents the variance.
We will first show that the unrestricted MLE of \(\theta\) is the sample statistic \(\bar{x}\).
Let \(k=\sigma^2\).
\[ \begin{aligned} f(x;\theta) & = \frac{1}{\sqrt{2\pi k}} \exp(-\frac{1}{2k}(x_i-\theta)^2) \\ L(\theta) & = (2 \pi k)^{-n/2} \exp(-\frac{1}{2k} \sum (x_i-\theta)^2) \\ \ln L(\theta) & = -\frac{n}{2}\ln (2 \pi k) - \frac{1}{2k}\sum(x_i-\theta)^2 \\ \frac{d \ln L(\theta)}{d\theta} & = -\frac{1}{2k}(2)\sum(x_i-\theta) \\ -\frac{\sum (x_i-\hat{\theta})}{k} & = 0 \\ \sum x_i - n \hat{\theta} & = 0 \\ \hat{\theta} & = \frac{\sum x_i}{n} \\ \hat{\theta} & = \bar{x} \\ \end{aligned} \]
If we restricted the parameter space of \(\theta\) to be \(\Omega_0=\{\theta|\theta \geq 0\}\) (i.e. the mean must be non-negative), the restricted MLE needs to be found.
From before: \[ \begin{aligned} \ln L(\theta) & = -\frac{n}{2}\ln (2 \pi k) - \frac{1}{2k}\sum(x_i-\theta)^2 \\ & = k_1 - k_2 Q(\theta) \\ \end{aligned} \]
where \(k_1\) and \(k_2\) are constants such that \(k_2 >0\), remembering that \(k=\sigma^2 > 0\), and \(Q(\theta)=\sum(x_i-\theta)^2\).
Therefore, we can maximize \(\ln L(\theta)\) by minimizing \(Q(\theta)\)
\[ \begin{aligned} Q(\theta) & = \sum (x_i-\theta)^2 \\ Q'(\theta) & = 2 \sum (x_i-\theta) \\ 2 \sum(x_i-\hat{\theta}) & = 0 \\ \sum x_i - n \hat{\theta} & = 0 \\ \hat{\theta} & = \bar{x} \\ \end{aligned} \]
This minimizes the function \(Q(\theta)\), which is concave up. You can use the 2nd derivative test.
If we obtain data such that \(\hat{\theta}=\bar{x} < 0\), then \(Q(\theta)\) is minimized at zero in the restricted space and \(\hat{\theta_R}=0\).
Below, the data is \(x=\{-30,-25,-20,-15,-10,0,5,10,15,20\}\) such that \(\bar{x}=-5\). \(Q(\theta)\) is minimzed at \(\hat{\theta}=5\), and if we restrict to \(\theta>0\), then \(Q(\theta)\) is minimzed at \(\hat{\theta}=0\).
x<-c(-30,-25,-20,-15,-10,0,5,10,15,20)
theta<-seq(-10,10,by=0.01)
Q<-1:length(theta)
for (i in 1:length(theta)){
Q[i]<-sum((x-theta[i])^2)
}
theta.rest<-seq(0,10,by=0.01)
Q.rest<-1:length(theta.rest)
for (i in 1:length(theta.rest)){
Q.rest[i]<-sum((x-theta.rest[i])^2)
}
plot(Q~theta,type="l",lty=2,lwd=2,xlab=expression(theta),ylab="Q(theta)")
points(Q.rest~theta.rest,type="l",col="red",lwd=2)
abline(v=-5,lty=2)
abline(h=min(Q),lty=2)
abline(v=0,lty=3,col="red")
abline(h=min(Q.rest),lty=3,col="red")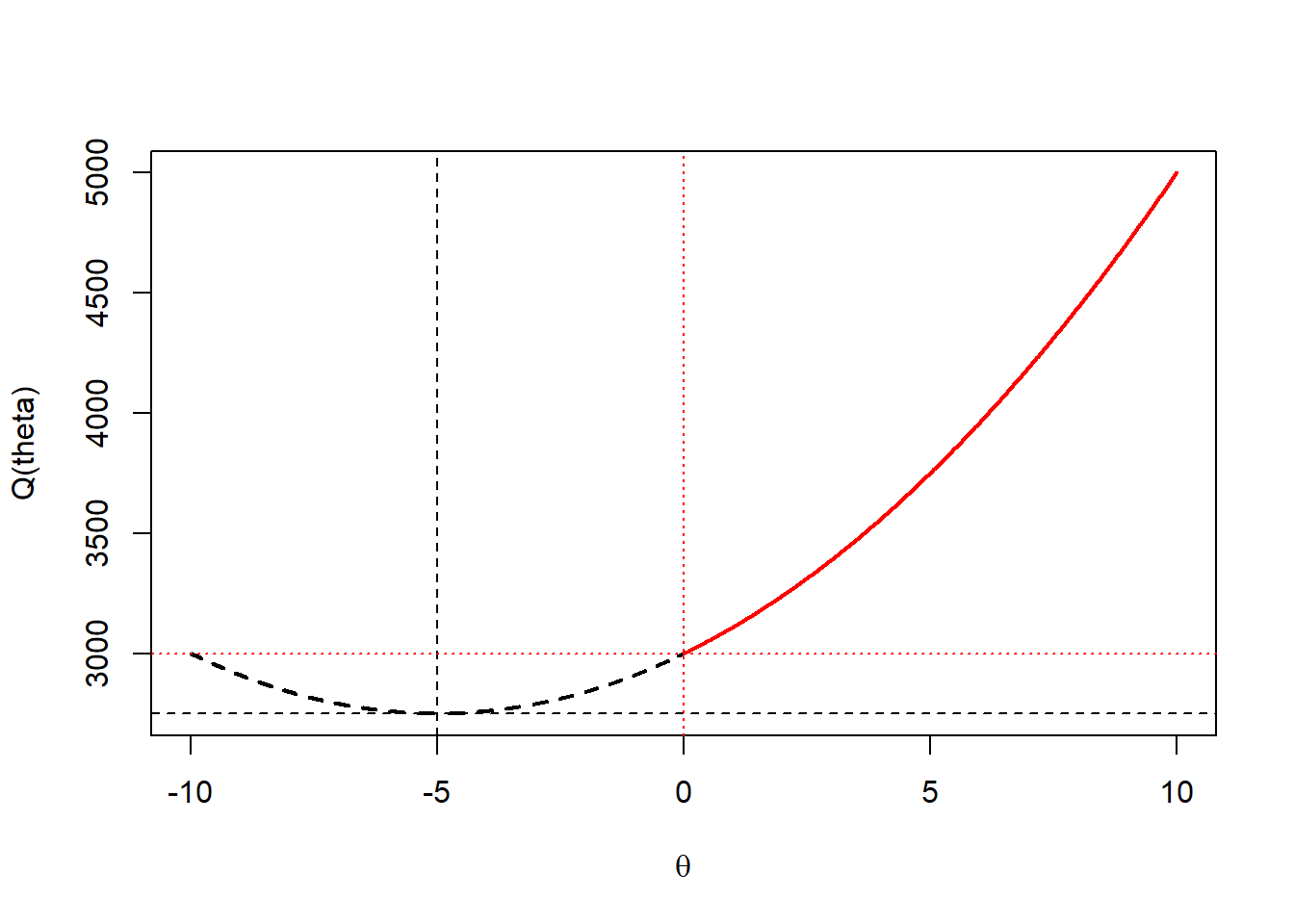
If we chose to maximize \(\ln L(\theta)\) instead, we get the same restricted and unrestricted MLEs.
x<-c(-30,-25,-20,-15,-10,0,5,10,15,20)
theta<-seq(-10,10,by=0.01)
log.lik<-dnorm(x=theta,mean=mean(x),sd=sd(x),log=TRUE)
theta.rest<-seq(0,10,by=0.01)
log.lik.rest<-dnorm(x=theta.rest,mean=mean(x),sd=sd(x),log=TRUE)
plot(log.lik~theta,type="l",lty=2,lwd=2,xlab=expression(theta),ylab="log-likelihood")
points(log.lik.rest~theta.rest,type="l",col="red",lwd=2)
abline(v=-5,lty=2)
abline(h=max(log.lik),lty=2)
abline(v=0,lty=3,col="red")
abline(h=max(log.lik.rest),lty=3,col="red")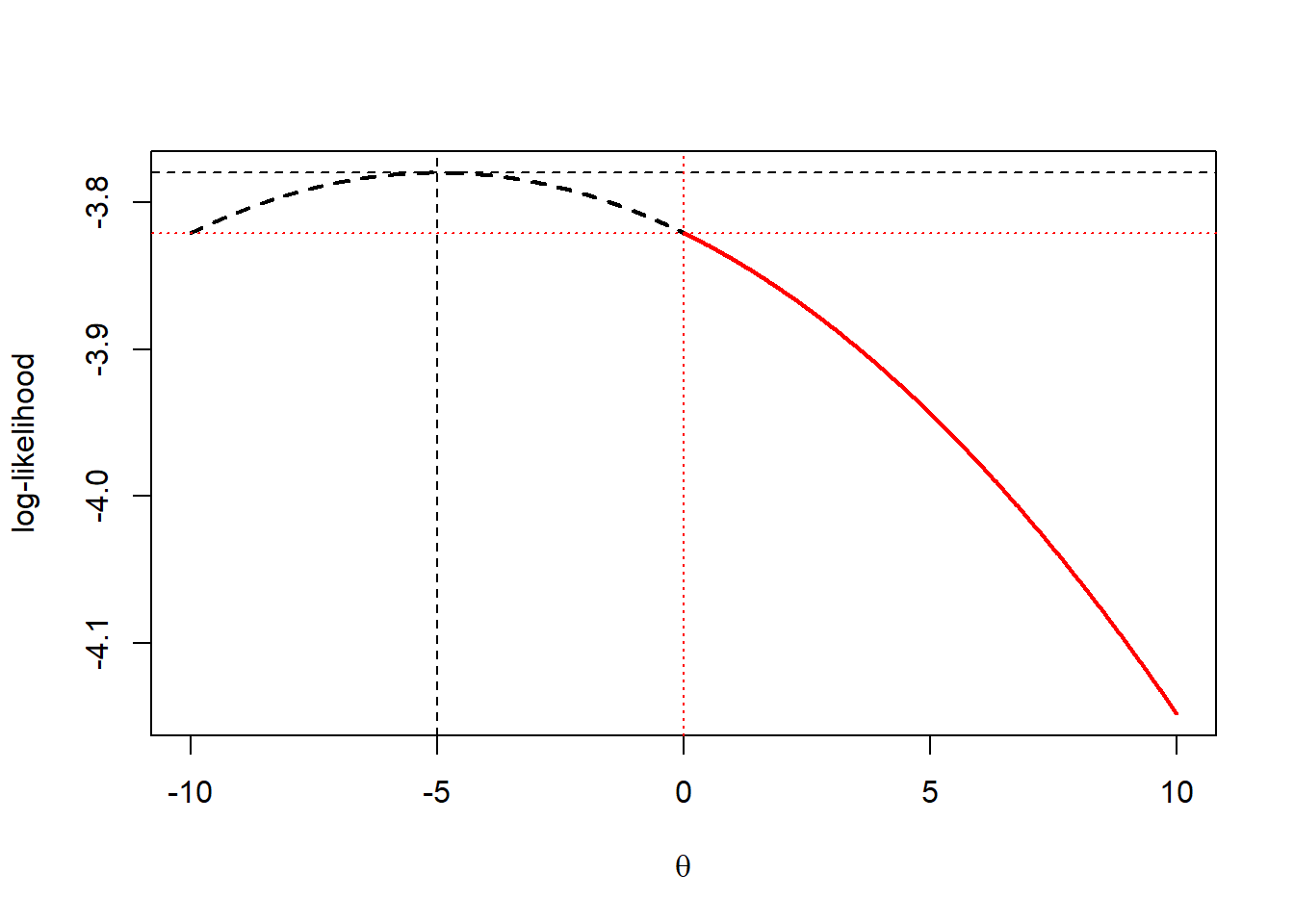
6.6 Asymptotic Distribution of Maximum Likelihood Estimators
NOTE: I will go into a lot more detail than the textbook does in Sections 6.6 and 6.7 in terms of the “Theory of Point Estimation”.
We have already defined several properties of point estimates, but will repeat them here, along with the introduction of others. We also have two methods for determining the point estimator, namely Method of Moments (MME) and Maximum Likelihood (MLE).
Definition: A point estimate \(\hat{\theta}\) is said to be unbiased for \(\theta\) if \(E(\theta)=\theta\).
Definition: A point estimate \(\hat{\theta}\) is said to have minimum variance if \(Var(\hat{\theta}) \leq Var(\theta^*)\), where \(\theta^*\) is any other estimator besides \(\hat{\theta}\).
Definition: A point estimate \(\hat{\theta}\) is said to be consistent if \[\hat{\theta} \overset{P}{\to} \theta\]
For example, the Weak Law of Large Numbers tells us that \[\bar{x} \overset{P}{\to} \mu\]
Definition: A point estimate \(\hat{\theta}\) is said to be the minimum variance unbiased estimator, or MVUE, when it is both unbiased AND has minimum variance when compared to all other unbiased estimators. MVUEs combined two valued properties and much effort is expended in finding them, when possible.
Let us define two additional regularity conditions.
(R3) The pdf \(f(x;\theta)\) is twice differentiable as a function of \(\theta\).
(R4) The integral \(\int f(x;\theta) dx\) can be differentiate twice under the integral sign as a function of \(\theta\).
Let \(X_1,X_2,\cdots,X_n\) be a random sample of size \(n\) from some function \[X \sim f(x;\theta), \theta \in \Omega = \{\theta: c<\theta<d \}\]
When the support space of \(X\) does not depend on \(\theta\), it can be shown that for all unbiased estimators \(T\) of \(\theta\),
\[Var(T) \geq \frac{1}{n E\{[\frac{\partial \ln f(x;\theta)}{\partial \theta}]^2\}} = \frac{1}{-n E\{[\frac{\partial^2 \ln f(x;\theta)}{\partial \theta^2}]\}}\]
The function \(\frac{\partial \ln f(x;\theta)}{\partial \theta}\) is called the score function.
It can be shown that the expected value of the score function is zero. \[E[\frac{\partial \ln f(x;\theta)}{\partial \theta}]=0\]
The variance of the score function is called Fisher information. \[I(\theta)=Var[\frac{\partial \ln f(x;\theta)}{\partial \theta}]\]
Since the mean of the score function is conveniently always equal to zero, we can compute the variance of the score function either by finding the expected value of the squared score function OR by taking the negative second derivative of the log-density function. In practice, choose whichever is easier to evaluate.
\[I(\theta)=E[\frac{\partial \ln f(x;\theta)}{\partial \theta}]^2=-E[\frac{\partial^2 \ln f(x;\theta)}{\partial \theta^2}]\]
What is Fisher information? Roughly speaking, if \(I(\theta)\) is highly peaked (i.e. the density curve is “sharp” near \(\theta\)), we have high information. If it is not highly peaked or is blunt, we have low information about \(\theta\).
When we have multiple parameters, the Fisher information is a matrix of second partial derivatives which is also called the Hessian matrix. This matrix is important in certain types of hypothesis tests such as the likelihood ratio test (or LRT) and the Wald test that we will study later.
Theorem: Let \(X_1,X_2,\cdots,X_n\) be iid from pdf \(f(x;\theta)\) for \(\theta \in \Omega\). Assume the regularity conditions R0 through R4 all hold.
Let \(T=u(X_1,X_2,\cdots,X_n)\) be some statistic (i.e. some function of the random sample) with expected value \[E(T)=E[u(X_1,X_2,\cdots,X_n)]=k(\theta)\]
Then the variance of that statistic is \[Var(T) \geq \frac{[k'(\theta)]^2}{nI(\theta)}\]
Proof: omitted
This theorem gives us the lower bound for the variance of a point estimator. This theorem is primarily useful if we are considering the variance of an unbiased estimator. If \(T\) is unbaised, then \(E(T)=k(\theta)=\theta\) (by defintion of unbiased) and hence \(k'(\theta)=1\). So the lower bound is \[Var(T) \geq \frac{1}{nI(\theta)}\] and this is known as the Cramer-Rao Lower Bound (CRLB).
There are two main uses for the Cramer-Rao Lower Bound.
To help in finding minimum variance unbiased estimators or MVUEs. Essentially, if we have an unbiased estimator \(T\) and we can show that the variance of \(T\) is equal to the Cramer-Rao Lower Bound, then \(T\) is a MVUE (and we celebrate).
To compute the efficiency of an estimator.
Definition: An estimator \(T\) of \(\theta\) is said to be efficient iff \(Var(T)=\frac{1}{nI(\theta)}\) (i.e. if the variance is equal to the CRLB).
\[eff(T)=\frac{CRLB}{Var(T)} \times 100 \% \]
We obtain 100% efficiency for an estimator only when the variance is the estimator is equal to the Cramer-Rao Lower Bound. As \(Var(T)\) increases w.r.t. the CRLB, the efficiency will decrease.
Example: Consider \(X_i \sim GAMMA(\alpha=1, \theta=1/\lambda)\). Essentially, this is the exponential distribution (since \(\alpha=1\)) with the rate parameter \(\lambda\) re-parameterized as the mean waiting time \(\theta=1/\lambda\).
\[f(x;\theta)=\frac{1}{\Gamma(1)\theta^1}x^{1-1} e^{-x/\theta}=\frac{1}{\theta} e^{-x/\theta}, x>0, \theta >0\]
Note that \(E(X)=1/\lambda=\theta\) and \(Var(X)=1/\lambda^2=\theta^2\).
Let’s find the Fisher information for this distribution.
Assume an iid random sample of size \(n\) from \(X \sim GAMMA(1,\theta)\)
Obtain the score function.
\[ \begin{aligned} \ln f(x;\theta) & = \ln(\frac{1}{\theta})-\frac{x}{\theta} \\ & = -\ln \theta - \frac{x}{\theta} \\ \frac{d \ln f(x;\theta)}{d \theta} & = -\frac{1}{\theta} + \frac{x}{\theta}^2 \\ & = \frac{x-\theta}{\theta^2} \\ \end{aligned} \]
We can find the Fisher information by finding the expected value of the squared score function.
\[ \begin{aligned} I(\theta) & = E[(\frac{d}{d \theta} \ln f(x; \theta))^2] \\ & = E[(\frac{X-\theta}{\theta^2})^2] \\ & = \frac{1}{\theta^4} E[(X-\theta)^2] \\ & = \frac{1}{\theta^4} Var(X) \\ & = \frac{1}{\theta^4} \theta^2 \\ I(\theta) & = 1/\theta^2 \\ \end{aligned} \]
So the Cramer-Rao Lower Bound is \[\frac{1}{nI(\theta)}=\frac{\theta^2}{n}\]
Alternatively, we can find Fisher information by finding the negative expected value of the second derivative of the log-density function.
\[ \begin{aligned} \frac{d^2 \ln f(x;\theta)}{d \theta^2} & = \frac{1}{\theta^2}-\frac{2X}{\theta^3} \\ I(\theta) & = -E[\frac{1}{\theta^2}-\frac{2X}{\theta^3}] \\ & = -E[\frac{1}{\theta^2}]+E[\frac{2X}{\theta^3}] \\ & = -\frac{1}{\theta^2}+ \frac{2}{\theta^3}E(X) \\ & = -\frac{1}{\theta^2}+ \frac{2}{\theta^3}\theta \\ & = \frac{1}{\theta^2} \end{aligned} \]
Obviously, the Fisher information and hence the Cramer-Rao Lower Bound are the same as before. In practice, pick which of the two methods is easier for the problem at hand.
So if we can somehow find an unbiased estimator \(T\) for \(X \sim GAMMA(\alpha=1,\theta=1/\lambda)\) such that \(Var(T)=CRLB\), then it is the MVUE. There is no guarantee that such an estimator exists; it is possible that no unbiased estimator will have a variance equal to CRLB.
In our case, let’s choose \(T=\bar{x}\).
First, verify that \(T\) is unbiased.
\[E(\bar{x})=E(\frac{\sum x_i}{n})=\frac{1}{n}\sum E(X_i)=\frac{1}{n} n \theta = \theta\]
Now, find the variance and hope that it is equal to Cramer-Rao Lower Bound.
\[Var(\bar{x})=Var(\frac{\sum x_i}{n})=\frac{1}{n^2}\sum Var(X_i)=\frac{1}{n^2}n \theta^2 = \frac{\theta^2}{n}\]
YAY! REJOICE! WE FOUND THE MVUE!
Example: Let \(X_1,X_2,\cdots,X_n\) be an iid random sample from \(X \sim N(\mu,\sigma^2)\) where \(\sigma^2\) is a known, fixed constant.
Consider the estimator \(T=\frac{X_1+X_n}{2}\), which is the average of the first and last numbers in the random sample that I will call the “lazy mean”.
Is the lazy mean unbiased?
\(E(T)=E(\frac{X_1+X_n}{2})=\frac{1}{2}[E(X_1)+E(X_n)]=\frac{1}{2}[\mu + \mu]=\mu\)
Yes, the lazy mean is unbiased. I wonder if it is also the MVUE, as I would love to be lazy when I average numbers. So, we’ll find the Fisher information for our distribution (normal distribution with known variance) and then will compute the CRLB.
Take the density function. \[f(x;\mu)=\frac{1}{\sqrt{2\pi \sigma^2}} \exp[-\frac{1}{2\sigma^2}(x-\mu)^2]\]
Find the log-density function. \[\ln f(x; \mu)=-\frac{1}{2} \ln (2\pi \sigma^2) - \frac{1}{2 \sigma^2}(x-\mu)^2\]
Find the first derivative of the log-density (this is the score function). \[\frac{d \ln f(x;\mu)}{d \mu} = -\frac{1}{\sigma^2}(2)(x-\mu)^1 (-1)=\frac{x-\mu}[\sigma^2]=\frac{x}{\sigma^2}-\frac{\mu}{\sigma^2}\]
The score function looks like it will be easy to take another derivative of w.r.t. \(\mu\), so I will do so: \[\frac{d^2 \ln f(x;\mu)}{d \mu}^2 = -\frac{1}{\sigma^2}\]
The Fisher information is the negative expected value of this second derivative of the log-density. \[I(\mu)=-E(-\frac{1}{\sigma^2})=-(-\frac{1}{\sigma^2})=\frac{1}{\sigma^2}\]
Hence, the Cramer-Rao Lower Bound is: \[CRLB=\frac{1}{nI(\mu)}=\frac{\sigma^2}{n}\]
But the variance of the lazy mean is: \[Var(T)=Var(\frac{X_1+X_2}{2})=\frac{1}{4}[Var(X_1)+Var(X_2)]=\frac{1}{4}[\sigma^2+sigma^2]=\frac{\sigma^2}{2}\]
This is not equal to the Rao-Cramer Lower Bound unless \(n=2\) (where the lazy mean is equivalent to the sample mean).
The efficiency of the lazy mean is: \[eff(T)=\frac{CRLB}{Var(T)}=\frac{\sigma^2/n}{\sigma^2/2}=\frac{2}{n}\]
As \(n \rightarrow \infty\), the efficiency decreases; \(eff(T) \rightarrow 0\).
We have already seen that one method for showing that \(\hat{\theta}\) is the MVUE is by showing that its variance \(Var(\theta)\) is equal to the Cramer-Rao Lower Bound (CRLB). Unfortunately, in many situations no unbiased estimator will exist with a variance equal to the CRLB and thus other methods will be needed to find the MVUE.
We saw that if \(X \sim N(\mu,\sigma^2)\) with known variance \(\sigma^2\), that the sample mean \(\bar{x}\) was an efficient estimator of \(\mu\), while the “lazy mean” \(T=\frac{X_1+X_n}{2}\) is not as long as the sample size \(n>2\).
Definition: The relative efficiency of two estimators is \[re(\hat{\theta_1},\hat{\theta_2})=\frac{Var(\hat{\theta_1})}{Var(\hat{\theta_2})}\] The estimator \(\theta_1\) is more efficient than \(\theta_2\) when \(re(\hat{\theta_1},\hat{\theta_2}) < 1\), or in other words, when the variance of the first estimator is less than the variance of the second estimator.
If \(re(\hat{\theta_1},\hat{\theta^*}) \leq 1\) for all unbiased estimators \(\hat{\theta_1}\) and \(\theta^*\), then \(\hat{\theta_1}\) is the MVUE.
Example: For our normal example, the relative efficienty of the sample mean compared to the lazy mean is \[re(\bar{x},T)=\frac{Var(\bar{x})}{Var(T)}=\frac{\sigma^2/n}{\sigma^2/2}=\frac{2}{n}\]
This by itself is not sufficient evidence that \(\bar{x}\) is the MVUE, as there could another unbiased estimator with lower variance. The fact that the variance of sample mean is equal to the CRLB does establish it as the MVUE.
Now let’s consider a slightly different version of our example. Let \(X \sim N(\mu, \sigma^2=1)\). We know by Central Limit Theorem that the sampling distribution of \(\bar{x}\) is \(\bar{X} sim N(\mu_{\bar{x}}=\mu,\sigma^2_{\bar{x}}=\frac{1}{n})\). It is not hard to show \(\bar{x}\) is efficient.
\[I(\mu)=\frac{1}{\sigma^2}=1, CRLB=\frac{1}{nI(\mu)}=\frac{1}{n}\]
\[Var(\bar{x})=\frac{1}{n}\]
\[eff(\bar{x})=\frac{CRLB}{Var(\bar{X})} = \frac{1/n}{1/n}=1\]
It probably seemed intuitive that the lazy mean (averaging some but not all of the numbers in the sample) was not efficient. However, we could use the sample median \(\tilde{x}\) instead; it is also an unbiased estimator for \(\mu\) and it does use all of the data in the sample.
What is known about the sampling distribution of the sample median \(\tilde{x}\)? Well, we’ll use without proof a result due to LaPlace that states for \(X \sim f(x)\), the sampling distribution of the median is approximately \[ \tilde{X} \sim N(\mu_{\tilde{x}}=m,\sigma^2_{\tilde{x}}=\frac{1}{4nf(m)^2}\] where \(m\) is the median of \(f(x)\).
In our case, \(f(x)\) is \(N(\mu,\sigma^2=1)\) and since the normal distribution is symmetric, \(m=\mu\). Hence, the variance of the sampling distribution of the sample median is \[Var(\tilde{x})=\frac{1}{4nf(\mu)^2}\]
Note that \[f(\mu)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2}(\mu-\mu)^2}=\frac{1}{\sqrt{2 \pi}}\]
Hence \[Var(\tilde{x})=\frac{1}{4n(1/\sqrt{2 \pi})^2}=\frac{\pi}{2n}\]
The efficiency of the sample median is: \[eff(\tilde{x})=\frac{CRLB}{Var(\tilde{x})}=\frac{1/n}{\pi/2n}=\frac{2}{\pi}\approx 64\%\]
The relative efficiency of the sample mean to sample median is: \[re(\bar{x},\tilde{x})=\frac{1/n}{\pi/2n}=\frac{2}{\pi}\]
The relative efficienty of the sample median to the lazy mean in this situation is: \[re(\tilde{x},T)=\frac{\pi/2n}{1/2}=\frac{\pi}{n}\] This will be less than 1 as long as \(n>\pi\), so the sample median is more efficient than the lazy mean as long as the sample size is at least 4.
Comparing Biased and Unbiased Estimators:
Although we traditionally give a lot of attention and emphasis to unbiased estimators, it is possible that a biased estimator might be “better” in some situations.
In order to compare unbiased and biased estimators, another common property is the mean-squared-error, or \(MSE\), of the estimator. \(MSE\) is defined as the variance plus squared bias, where bias is \(Bias(\hat{\theta})=\theta-E(\hat{\theta})\). Naturally, the bias of unbiased estimators is zero.
\[MSE(\hat{\theta}) = Var(\hat{\theta}) + Bias(\hat{\theta})^2\]
It is desirable to minimize the MSE of an estimator, where we think of the variance as being the “precision” of the estimate, and the bias as the “accuracy” of the estimate.
Example: Take a random sample of size \(n\) from \(X \sim N(\mu,\sigma^2\) (i.e. both mean and variance unknown).
The maximum likelihood estimator for \(\sigma^2\) is \[\hat{\sigma^2}=\frac{\sum(x-\bar{x})^2}{n}\]
Note that the MLE is biased. \[E(\hat{\sigma^2})=\sigma^2-\frac{\sigma^2}{n}=\sigma^2(1-\frac{1}{n})\] \[Bias(\sigma^2)=\sigma^2-[\sigma^2-\frac{\sigma^2}{n}]=\frac{\sigma^2}{n}\]
As \(n \to \infty\) then \(Bias \to 0\).
In introductory statistics course, we usually teach the following statisic as the “sample variance”, because it is unbiased (although we don’t tell them that!). This is why we routinely divide the sum of squared deviations by \(n-1\) rather than \(n\).
\[s^2=\frac{\sum(x-\bar{x})^2}{n-1}\] \[Bias(s^2)=0\]
Note that the MLE \(\hat{\sigma^2}\) is a function of the unbiased statistic \(s^2\).
\[\hat{\sigma^2}=\frac{n-1}{n-1} \frac{\sum(x-\bar{x})^2}{n} = \frac{n-1}{n} s^2\]
\[Var(\sigma^2)=Var(\frac{n-1}{n} s^2)=(\frac{n-1}{n})^2 Var(s^2)\]
Thus \(Var(\sigma^2) < Var(s^2)\). The MLE is more “precise” (because of lower variance) but is less accurate (because it is biased). Basically, one of these statistics (\(s^2\)) is unbiased, which we want, but the other statistic \(\hat{\sigma^2}\) has lower variance, which we also want. How can we decide which is better?
We will use the \(MSE\) as our “tiebreaker”.
Since \[\frac{(n-1)s^2}{\sigma^2} \sim \chi^2(n-1)\] then
\[ \begin{aligned} Var(\frac{(n-1)s^2}{\sigma^2}) & = 2(n-1) \\ \frac{(n-1)^2}{(\sigma^2)^2} Var(s^2) & = 2(n-1) \\ Var(s^2) & = \frac{2(n-1)(\sigma^2)^2}{(n-1)^2} \\ Var(s^2) & = \frac{2\sigma^4}{n-1} \\ MSE(s^2) & =Var(s^2)+Bias^2(s^2) \\ MSE(s^2) & = \frac{2\sigma^4}{n-1}+0^2 \\ \end{aligned} \]
The MSE for the biased MLE \(\hat{\sigma^2}\) is
\[ \begin{aligned} \hat{\sigma^2} & = \frac{n-1}{n} s^2 \\ MSE(\hat{\sigma^2}) & = Var(\hat{\sigma^2}) + Bias^2(\hat{\sigma^2}) \\ & = (\frac{n-1}{n})^2 \frac{2\sigma^4}{n-1} + (\frac{\sigma^2}{n})^2 \\ & = (\frac{n-1}{n^2}) 2\sigma^4 + \frac{\sigma^4}{n^2} \\ & = \frac{\sigma^4}{n^2}[2(n-1)+1] \\ & = \frac{\sigma^4}{n^2}(2n-1) \\ \end{aligned} \]
Which MSE is smaller? I will subtract the two MSEs to find out.
\[ \begin{aligned} MSE(s^2)-MSE(\hat{\sigma^2}) & = \frac{2\sigma^4}{n-1} - \frac{\sigma^4}{n^2}(2n-1) \\ & = \sigma^4[\frac{2}{n-1}-{2n-1}{n^2}] \\ & = \sigma^4[\frac{2n^2-(2n-1)(n-1)}{n^2(n-1)}] \\ & = \sigma^4[\frac{2n^2-2n^2+3n-1}{n^2(n-1)}] \\ & = \sigma^4[\frac{3n-1}{n^2(n-1)}] \\ & = >0 \forall n>1 \\ \end{aligned} \]
Thus \(MSE(s^2) > MSE(\hat{sigma^2})\), i.e. if you want to minimize MSE, you would prefer dividing by \(n\) rather than \(n-1\) and choose the biased estimator \(\hat{\sigma^2}\) despite the fact we usually stick with the unbiased estimator \(s^2\).
Definition: Let \(Y=u(X_1,X_2,\cdots,X_n)\) be a statistic that is used as a point estimate for \(\theta\). Let \(\delta(y)\) be the function of the observed value of statistic \(Y\) which is the point estimate. The function \(\delta(\cdot)\) decides the value of the point estimate and is called the decision function or decision rule.
Is our “decision” about the value of the unknown parameter \(\theta\) correct?
For each pair \(\theta, \delta(y), \theta \in \Omega\), asssociate a nonnegative value \(\mathcal{L}(\theta,\delta(y))\) with the seriousness of making an incorrect decision.
\(\mathcal{L}(\cdot)\) is the loss function. The expected value of the loss, \(E(\mathcal{L}(\cdot))\) is the risk function.
The loss function quantifies the error made using \(T=\delta(y)\) as an estimate of \(\theta\). Minimization of the risk function \(R_T(\theta)=E[\mathcal{L}(T;\theta)]\) is desirable.
Some common loss functions include:
squared error loss \[\mathcal{L}(T;\theta)=(T-\theta)^2\]
absolute deviation loss \[\mathcal{L}(T;\theta)=|T-\theta|\]
binary loss (equals 1 if the loss is complete/unacceptable, 0 if the loss is acceptable) \[\mathcal{L}(T;\theta)=1, |T-\theta|>k\] \[\mathcal{L}(T;\theta)=0, |T-\theta|\leq k\]
It would be ideal to find statistic \(T\) such that \(R_T(\theta) \leq R_{T^*}(\theta), \forall \theta \in \Omega\), where \(T^*\) is any other statistic. Usually we cannot find such an estimate \(T\).
Definition: if \(T_1\) and \(T_2\) are estimates of \(\theta\) such that \(R_{T_1}(\theta) \leq R_{T_2}(\theta) \forall \theta \in \Omega\), and for at least one value of \(\theta in \Omega\), that inequality is strictly less than,\(R_{T_1}(\theta) < R_{T_2}(\theta)\), then we say \(T_1\) is, in a sense, a “better” estimator than \(T_2\).
\(T_1\) is an admissable estimator iff there is never a “better” estimate that is available. \(T_2\) would be said to be inadmissable iff there is always a “better” estimate that is available.
Definition: \(T\) is a minimax estimator of \(\theta\) if: \[\underset{\theta \in \Omega}{\max} \quad R_T(\theta) \leq \underset{\theta \in \Omega}{\max} \quad R_{T^*}(\theta), \forall \quad T^*\]
Basically, we want to choose an estimator that has the smallest possible maximum value of the risk.
Example: Take a random sample of size \(n=25\) from \(X \sim N(\theta,\sigma^2=100)\).
Let \(T_1=\bar{x}\) (the sample mean, which is unbiased and is both the MLE and MME)
Let \(T_2=X_1\) (the first data value or a “very lazy” mean with \(n=1\))
Let \(T_3=10\) (we just guess the parameter \(\theta\) is equal to some constant, in this case 10, and ignore the data)
We will compute the risk for each of the three estimators and graph the risk.
\[ \begin{aligned} R_{T_1}(\theta) = & E[\mathcal{L}(T_1,\theta)] \\ & = E[(T_1-\theta)^2] \\ & = E((\bar{x}-\theta)^2) \\ & = Var(\bar{x}) \\ & = \sigma^2/n \\ & = 100/25 \\ & = 4 \\ R_{T_2}(\theta) = & E[\mathcal{L}(T_2,\theta)] \\ & = E[(T_2-\theta)^2] \\ & = E[(X_1-\theta)^2] \\ & = Var(X_1) \\ & = \sigma^2 \\ & = 100 R_{T_3}(\theta) = & E[\mathcal{L}(T_3,\theta)] \\ & = E[(T_3-\theta)^2] \\ & = E[(10-\theta)^2] \\ & = (10-\theta)^2 \\ \end{aligned} \]
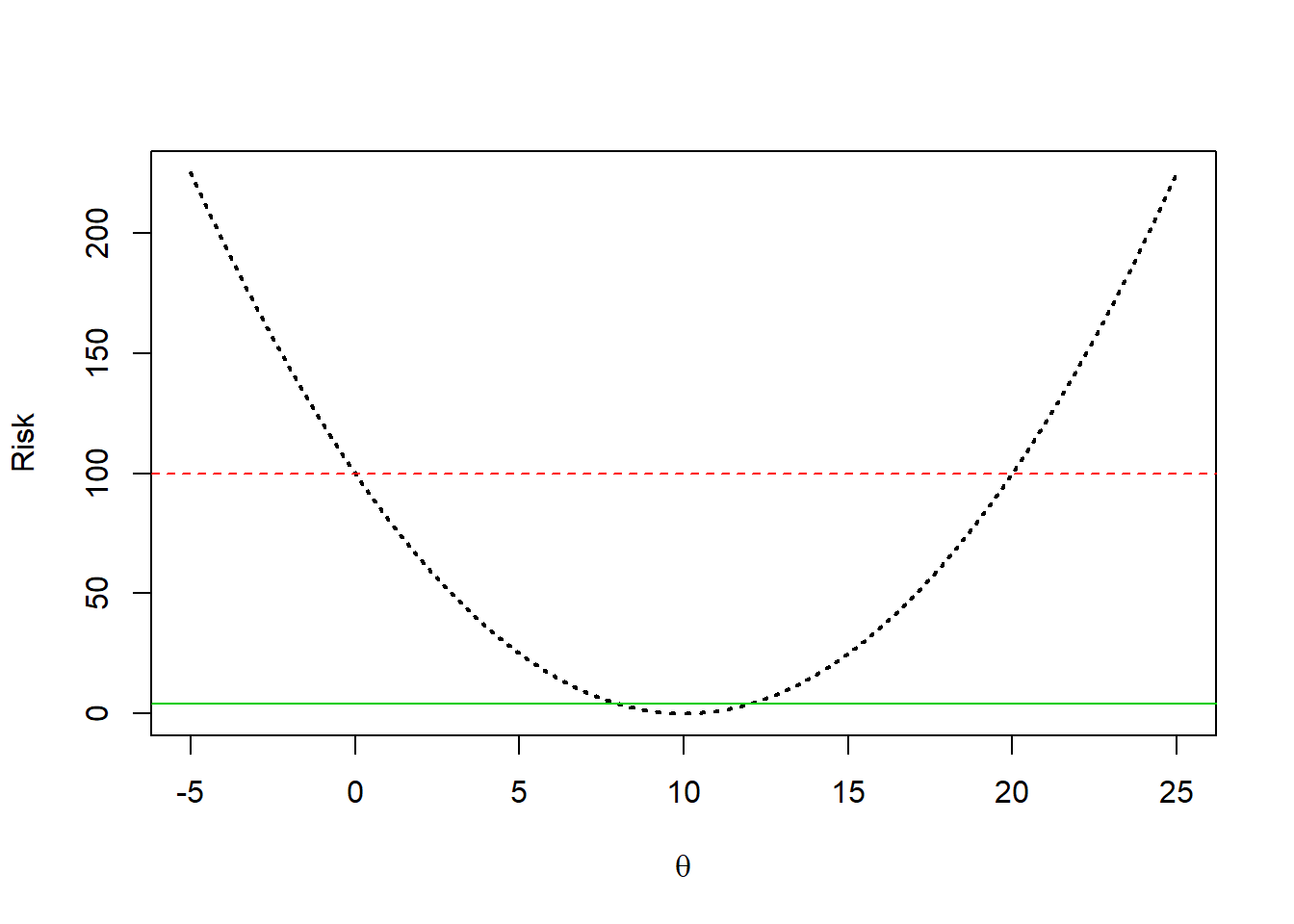
Notice that the risk of \(T_2\) (the red dashed line) is always greater than the risk of \(T_1\) (the green solid line). Thus, \(T_2\) is not admissable; \(T_1\) is “better” for every possible value of \(\theta\).
However, the black dotted parabola that represents the risk of \(T_3\) is sometimes less than the green solid line which is the risk of \(T_1\). If our “guess” of 10 happens to be very close to the true value of \(\theta\), then our “lucky” guess has low risk. However, if the true value of \(\theta\) is far from 10, the risk with \(T_3\) is much higher than the risk of \(T_1\) or even \(T_2\) and the risk approaches infinity.
\(T_1\) is the minimax estimator; the largest the risk ever is when using \(T_1\) is 4, while the maximum risk is 100 for \(T_2\) and \(\infty\) for \(T_3\).
6.7 Sufficient Statistics
Sufficiency:
When we compute a statistic \(Y=u(X_1,X_2,\cdots,X_n)\), this is really a form of data reduction; for example, we usually just report \(\bar{x}\) rather than an entire list of data values if we were interested in something like the average salary of a random sample of people. We can think of statistic \(Y\) as partitioning the sample space of \(X_1,X_2,\cdots,X_n\).
Definition: A sufficient statistic \(Y=u(X_1,X_2,\cdots,X_n)\) partitions the sample space in such a way that \[(X_1,X_2,\cdots,X_n) \in \{(x_1,x_2,\cdots,x_n): u(x_1,x_2,\cdots,x_n)=y\}\] where the conditional probability of \(X_1,X_2,\cdots,X_n\) does not depend on the unknown parameter \(\theta\).
Basically, statistic \(Y\) extracts all of the information available about \(\theta\) that is contained in the sample and is therefore described as being “sufficient”.
Fisher-Neyman Factorization Theorem: Let \(X_1,X_2,\cdots,X_n\) be an iid random sample from a distribution with pdf \(f(x;\theta), \theta \in \Omega\). Then statistic \(Y=u(X_1,X_2,\cdots,X_n)\) is a sufficient statistic for \(\theta\) iff \[f(x_1,x_2,\cdots,x_n;\theta)=k_1[u(x_1,x_2,\cdots,x_n;\theta)] k_2(x_1,x_2,\cdots,x_n)\]
Essentially, the joint pdf of the random sample (the likelihood function) can be factored into two pieces, \(k_1(\cdot)\) which involves both the data through function \(u(\cdot)\) and the unknown parameter \(\theta\) and \(k_2(\cdot)\) which is only a fucntion of the data and is free of parameter \(\theta\).
Example: Let \(X_1,X_2,\cdots,X_n\) be an iid random sample from the geometric distribution with \(f(x;\theta)=(1-\theta)^x \theta, x=0,1,2,\cdots, 0<\theta<1\). Find the sufficient statistic for \(\theta\).
\[ \begin{aligned} f(x_1,x_2,\cdots,x_n;\theta) & = f(x_1;\theta) f(x_2;\theta) \cdots f(x_n;\theta) \\ & = (1-\theta)^{x_1} \theta (1-\theta)^{x_2} \theta \cdots (1-\theta)^{x_n} \theta \\ & = (1-\theta)^{\sum x_i} \theta^n \cdot 1 \\ \end{aligned} \]
Notice in this case when we use the Fisher-Neyman Factorization Theorem that \(k_2(\cdot)=1\), a trivial function of the data that is free of \(\theta\).
In the portion \(k_1(\cdot)\) that involves both the data values and \(\theta\), \(u(x_1,x_2,\cdot,x_n)=\sum x_i\), hence the sufficient statisic is \(Y=\sum x_i\). The sum of the \(x\)’s or some function of that sum (such as the sample mean \(\bar{x}\)) is sufficient for estimating \(\theta\), which for the geometric distribution is the probability of success on a given trial.
Example: Let \(X_1,X_2,\cdots,X_n\) be an iid random sample from the normal distribution with known varaince \(\sigma^2\) and unknown mean \(\mu\). Find the sufficient statistic for \(\mu\), the mean of the normal distribution with known variance (so we need just one sufficient statistic).
\[ \begin{aligned} f(x;\mu) & = \frac{1}{\sqrt{2\pi \sigma^2}}e^{-1/2(\frac{x-\mu}{\sigma})^2} \\ & = (2\pi \sigma^2)^{-1/2} \exp(-\frac{(x-\mu)^2}{2 \sigma^2}) \\ L(\mu) & = (2\pi \sigma^2)^{-n/2} \exp(-\frac{\sum(x_i-\mu)^2}{2 \sigma^2}) \\ & = (2\pi \sigma^2)^{-n/2} \exp(-\frac{\sum(x_i-\bar{x}+\bar{x}-\mu)^2}{2 \sigma^2}) \\ & = (2\pi \sigma^2)^{-n/2} \exp(-\frac{\sum(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2 \sigma^2}) \\ & = (2\pi \sigma^2)^{-n/2} \exp(-\frac{\sum(x_i-\bar{x})^2}{2 \sigma^2}) \exp(-\frac{n(\bar{x}-\mu)^2}{2 \sigma^2}) \\ \end{aligned} \]
The second exponential term in the above factorization is \(k_1(\cdot)\), so \(Y=\bar{x}\) or \(Y=\sum x_i\) is sufficient for \(\mu\).
More generally, both \(\mu\) and \(\sigma^2\) (the mean and variance) of a normal distribution would be unknown and will require estimation. We will need 2 sufficient statistics.
\[L(\mu,\sigma^2)=(2\pi \sigma^2)^{-n/2} \exp(-\frac{\sum(x_i-\mu)^2}{2 \sigma^2})\]
\[\sum(x_i-\mu)^2 = \sum x_i^2 - 2\mu \sum x_i + n\mu^2\]
\[L(\mu,\sigma^2)=(2\pi \sigma^2)^{-n/2} \exp[-\frac{1}{2\sigma^2}(\sum x_i^2 - 2\mu \sum x_i + n\mu^2)] \cdot 1\]
The sufficient statistics for \((\mu,\sigma^2)\) are \((\sum x_i, \sum x_i^2)\). Usually, we choose \((\bar{x},s^2)\), function of the sufficient statistics that are also unbiased.
Definition: A sufficient statistic \(T=u(X)\) is complete iff \(E[u(X)]=0\) implies that \(u(x)=0\); i.e. there are no nontrivial unbiased estimators of zero–this prevents two different functions of a sufficient statistic from having the same expected value.
If \(E[u_1(x)=\tau(\theta)]\) and \(E[u_2(x)=\tau(\theta)]\), then \[E[u_1(x)-u_2(x)]=0\] which implies that \[ \begin{aligned} u_1(x)-u_2(x) & = 0 \\ u_1(x) & = u_2(x) \\ T_1 & = T_2 \\ \end{aligned} \]
A statistic \(T\) that is both complete and sufficient is desirable. Why? Because a complete and sufficient statistic can serve as another path to finding the MVUE (the statistic that is both unbiased and minimum variance) in those situations where we cannot find any statistic whose variance is equal to the Cramer-Rao Lower Bound.
Defintion: A density function that can be written in the form \[f(x;\theta)=\exp[k(x)p(\theta)+H(x)+q(\theta)]\] is said to be a member of the regular exponential class (REC) if the following conditions are met:
the support of \(X\) does not depend on \(\theta\)
\(p(\theta)\) is a nontrivial continuous function of \(\theta\)
if \(X\) is continuous, then both \(k'(x) \neq 0\) and \(H(X)\) are continuous functions; if \(X\) is discrete, then \(k(x)\) is a nontrivial function of \(X\)
Example: You might guess that the exponential distribution would be a member of the regular exponential class. We will algebraically manipulate the usual format of the pdf of the exponential to fit the format in the definition of the REC.
\[ \begin{aligned} f(x; \lambda) & = \lambda e^{-\lambda x}, x>0, \lambda>0 \\ f(x; \lambda) & = e^{\ln \lambda} e^{-\lambda x} \\ & = e^{\ln \lambda-\lambda x} \\ & = e^{-x \lambda + 0 + \ln \lambda} \\ \end{aligned} \]
So: \(k(x)=-x\), \(p(\lambda)= \lambda\), \(H(x)=0\), and \(q(\lambda)=\ln \lambda\).
The support of the exponential distribution is \(x>0\), which does not depend on \(\lambda\). \(p(\lambda)=\lambda\) is a nontrivial continuous function of the parameter \(\lambda\). Since \(X\) is continuous and \(k'(x)=-1\) and \(H(x)=0\) are continuous functions, we satisfy all condtions and the exponential distribution is a member of the regular exponential class.
Example: Is the Bernoulli distribution, a discrete distribution that is the special case of the binomial with \(n=1\), a member of the REC?
\[ \begin{aligned} f(x; \theta) & = \theta^x (1-\theta)^{1-x}, x=0,1 \quad 0< \theta <1 \\ f(x; \theta) & = e^{\ln[\theta^x (1-\theta)^{1-x}]} \\ & = e^{x \ln \theta +(1-x) \ln(1-\theta)} \\ & = e^{x \ln \theta + \ln(1-\theta) -x \ln(1-\theta)} \\ & = e^{x \ln(\frac{\theta}{1-\theta})+0+\ln(1-\theta)} \\ \end{aligned} \]
So: \(k(x)=x\), \(p(\lambda)= \ln(\frac{\theta}{1-\theta})\), \(H(x)=0\), and \(q(\lambda)=\ln(1-\theta)\).
The support of the Bernoulli distribution is \(x=0,1\), which does not depend on \(\lambda\). \(p(\theta)= \ln(\frac{\theta}{1-\theta})\) is a nontrivial continuous function of the parameter \(\theta\). Since \(X\) is discrete and \(k(x)=x\) is a nontrivial function of \(X\), we satisfy all condtions and the Bernoulli distribution is a member of the regular exponential class.
Example Consider \(Y \sim UNIF(0,\theta), 0<y<\theta,\theta>0\). This distribution is clearly NOT a member of the regular exponential class since the support of \(Y\) contains \(\theta\).
If a sufficient statistic exists, then the likelihood function \[L(\theta)=f(x_1,x_2,\cdots,x_n;\theta)=k_1[u(x_1,x_2,\cdots,x_n;\theta)] k_2(x_1,x_2,\cdots,x_n)\] due to the Fisher-Neyman Factorization Theorem. Since \(k_2(\cdot)\) does not depend on \(\theta\), we can maximize the likelihood function \(L(\theta)\) merely by maximizing \(k_1(\cdot)\). Recall that \(k_1(\cdot)\) is a function of \(X\) only through the sufficient statistic for \(\theta\).
Thus, if there is a unique value of \(\theta\) that maximizes \(k_1(\cdot)\) (i.e. there is a unique MLE), then that MLE is a function of the sufficient statistic.
Example: Suppose we have a random sample from \(X_i \sim N(0,\sigma^2)\) where the mean is known to be zero, and the variance parameter \(\sigma^2\) is unknown.
It can be shown that this normal distribution with known mean, unknown variance is a member of the regular exponential class and that \(\sum x_i^2\) is the sufficient statistic for \(\sigma^2\).
Recall the MLE, which is biased in this situation, is \[\hat{\sigma}^2 = \frac{\sum(x_i-\mu)^2}{n}=\frac{\sum x_i^2}{n}\] and notice that it a function of the sufficient statistic.
The usual unbiased estimator is \[s^2=\frac{n}{n-1}\hat{\sigma}^2=\frac{\sum x_i^2}{n-1}\] and it is also a function of the sufficient statistic.
The Cramer-Rao Lower bound for the variance of estimators for this situation (normal distribution with known mean) is \[CRLB = \frac{2(\sigma^2)^2}{n}\]
However, the variance of our unbiased estimator, that is function of the sufficient statistic, is \[Var(s^2)=\frac{2(\sigma^2)^2}{n-1}\] which unfortunately is greater than the CRLB. Hence we are not sure if \(s^2\) is the MVUE. At this point, it is possible that there might be some other unbiased estimator we don’t know about whose variance is equal to the CRLB. If such an estimator exists, it would be the MVUE.
Some Important Theorems in Point Estimation:
Rao-Blackwell Theorem: Let \(X_1,X_2,\cdots,X_n\) be a random sample from \(f(x;\theta), \theta \in \Omega\).
Let \(Y_1=u_1(x_1,x_2,\cdots,x_n)\) be a sufficient statistic for \(\theta\).
Let \(Y_2=u_2(x_1,x_2,\cdots,x_n)\) be unbiased for \(\theta\), where \(Y_2\) is not simply a function of \(Y_1\) alone.
Then \(E(Y_2|y_1)=\phi(y_1)\) defines a statistic \(\phi(y_1)\) which is a function of the sufficient statistic that is unbiased and has variance less than or equal to \(Y_2\).
Proof: omitted
Point: When hunting for the MVUE, if a sufficient statistic exists, we only need consider functions of the sufficient statistic!
So, if we begin with unbiased estimator \(Y_2\), we can improve by computing \(\phi(y_1)\).
Theorem: Let \(X_1,X_2,\cdots,X_n\) be a random sample from \(f(x;\theta), \theta \in \Omega\). If a sufficient statistic \(Y_1=u_1(X_1,X_2,\cdots,X_n)\) exists and if a MLE \(\hat{\theta}\) exists uniquely, then \(\hat{\theta}\) will be a function of \(Y_1\).
Proof: omitted
Point: The maximum likelihood estimator \(\hat{\theta}\) is usually a function of the sufficient statistic.
Lehmann-Scheffe Theorem: Let \(X_1,X_2,\cdots,X_n\) be a random sample from \(f(x;\theta), \theta \in \Omega\). If \(Y_1=u_1(X_1,X_2,\cdots,X_n)\) is both complete and sufficient for \(\theta\), and if \(T^*=f(y_1)\) is unbiased for \(\theta\), then \(T^*\) is the MVUE>
Proof: omitted
Point: If you have a statistic that is both complete and sufficient for \(\theta\), find the unbiased function of that statistic. As long as \(f(x;\theta)\) is from the regular exponential class, then this unbiased version of the complete and sufficient statistic is the MVUE.
So, in the case we considered regarding the normal distribution with known mean, since \(Y_1=\sum x_i^2\) is the complete and sufficient statistic for \(\sigma^2\) and the normal distribution is a member of the REC, then find an unbiased function of \(Y_1\).
It’s \(s^2=\frac{\sum x_i^2}{n}\). Even though \(Var(s^2)>CRLB\), by the Lehmann-Scheffe Theorem, it must be the MVUE for \(\sigma^2\) (this means there was no unbiased estimator whose variance equalled the CRLB).
Example: Suppose we have an iid random sample \(X_1,X_2,\cdots,X_n\) from \(X_i \sim BIN(1,\theta)\) and we want the MVUE for \(n \theta(1-\theta)\) (i.e. the variance of the binomial distribution).
We already know that the binomial distribution is a member of the REC.
So \(T=\sum x_i\) is the complete and sufficient statistic for \(\theta\).
The distribution of \(T\) is \(T \sim BIN(n,\theta)\), so \(E(T)=n \theta\) and \(E(T/n)=\theta\). Hence, the MVUE for \(\theta\), due to Rao-Blackwell and Lehmann-Scheffe, is \[\frac{T}{n}=\frac{\sum x_i}{n}=\bar{x}\]
Since we actually want the MVUE for \(n \theta(1-\theta)\), we need to find some function \(u(T)\) such that \(E[u(T)]=n \theta (1-\theta)\).
As an initial guess, I’m just going to “plug-in” \(\frac{T}{n}\) in place of \(\theta\) and see if that’s what I need, i.e. my guess is \[u_1(T)=n \frac{T}{n}(1-\frac{T}{n})\]
Find the expected value of this “guess”:
\[ \begin{aligned} E[u_1(T)] & = E[n \frac{T}{n}(1-\frac{T}{n})] \\ & = E[T(1-\frac{T}{n})] \\ & = E[T-\frac{T^2}{n}] \\ & = E(T)-\frac{1}{n}E(T^2) \\ & = E(T)-\frac{1}{n}[Var(T)+(E(T))^2] \\ & = n \theta - \frac{1}{n}[n \theta(1-\theta)+n^2 \theta^2] \\ & = n\theta - \theta(1-\theta) - n\theta^2 \\ & = n\theta(1-\theta)-\theta(1-\theta) \\ & = \theta(n-1)(1-\theta) \\ \end{aligned} \]