Chapter 2 Discrete Distributions

2.1 Random Variables of the Discrete Type

A random variable is a measurement of an outcome that is associated with a random experiment. It is pretty standard to denote random variables with capital letters from the end of the alphabet, $X$, $Y$, $Z$ are pretty common choices.

As an example, we might let $X$ represent the age of a person. If I picked a student at random and asked how old they are, I will not get the same numerical value for each student.

It is customary to use lower case letters to denote a measurement for a particular trial of an experiment, such as $x_i,y_i,z_i$. For our age example, if I reported my age as 54 years old and I am individual $i=1$, it would be $x_1=52$. If a student said they were 21 years old, then $x_2=21$. If a different student said that they were 19, then $x_3=19$.

If we let $Y$ represent the number obtained when rolling a standard six-sided die and then rolled the die $n=4$ times, we would observed 4 values. For instance, it could be $y_1=3, y_2=6, y_3=6, y_4=4$.

A more technical definition of a random variable is as follows: we have a random experiment with possible outcomes contained in sample space $\mathcal{C}$. A function $X$ that assigns to each element $c \in \mathcal{C}$ one and only one real number $x$ is a random variable. For example, take people born on January 1, 2000. This is one possible outcome (i.e. birthday) of all possible birthdays of people that are alive that could be contained in $\mathcal{C}$.

It is customary to truncate our age down to the year (although with babies and small children, we might talk about age in weeks or months or half-years). Before my recent birthday, I would have told you that I was $x=53$ years old, as I had not yet had my birthday for the year, even though my age was really almost 54. Now that my birthday for this year has occurred, I will now tell you that I am $x=54$ years old, and everyone else that was born on the same day as me will be assigning the real number $x=54$ to their age (assuming they are using the typical convention in reporting age).

The space or range of $X$ is a set of real numbers \[S = \{x: x=X(c), c \in \mathcal{C}\}\]

Given a random variable $X$, we are interested in a range $S$ that “induces” a probability density function (p.d.f.), a function that will tell us how likely certain values of the random variable are. For instance, I might want to know how likely it is for someone in the population to be $x=54$ years old or how likely it is to roll a four, $y=4$, with a six-sided die.

In Chapter 2, we will focus on discrete random variables, where the word discrete means that the set of values in the range $S$ is a countable set. Usually it is a finite set: if I roll a six-sided die, there are only 6 possible outcomes to consider: $S=\{1,2,3,4,5,6\}$. Occasionally it is an countably infinite set: we could let random variable $X$ represent the number of tosses of a fair coin needed to obtain the first result of “heads”. Here, $S=\{1,2,3,\cdots\}$.

In Chapter 3, we will focus on continuous random variables, where the word *continuous means that the set of values in the range $S$ is an interval. For example, the pseudo-random number generator rand on a TI-84 calculator has space $S=\{x: 0<x<1\}$.

When $X$ is a person’s age, we might think of it as a discrete random variable, as conventionally we truncate our age to an integer value, but we could think of it as a continuous random variable. If several students in the class are $x=21$ years old, their age could be reported more precisely by figuring out how many years, months, days, hours, etc. old they are, and possibly reporting your age as $x=21.66849$ years if you are 21 years and 244 days old.

Dice rolling example Suppose we roll 2 standard six-sided dice, and let random variable $X$ be the product of the two numbers.

The sample space $\mathcal{C}$ would consist of ordered pairs describing the $6 \times 6=36$ possible rolls. \[\mathcal{C} = \{(i,j):i,j=1,2,3,4,5,6\}\]

\[X = X(i,j)=i \times j\] I’ll draw a grid representing this situation in class, with $i$ (the first die) on the horizontal axis and $j$ (the second die) on the vertical axis. Each ordered pair $(i,j)$ is assigned one and one one real number value. For instance, for $(i=4,j=2)$, I assign the numerical value $x=8$.

The space or range $S$ for $X$ is the set of all possible products we could obtain. The smallest such value is $x=1$ and the largest such value is $x=36$, and not all integers between 1 and 36 will be contained in $S$.

\[S_X = \{1,2,3,4,5,6,8,9,10,12,15,16,18,20,24,25,30,36\}\] The possible values $x$ of $X$ are not equally likely. For instance, we can obtain $x=12$ several ways: $(2,6),(3,4),(4,3),(6,2)$ but can only obtain $x=25$ with the roll $(5,5)$.

The table below is the probability density function (pdf) of $X$. Often for discrete random variables, it will be referred to as a probability mass function or p.m.f instead. Some authors do this to distinguish probability functions for discrete random variables from probability functions for continuous random variables.

This table was found merely by counting the number of occurences of each product in $\mathcal{C}$ and dividing by the 36 possible dice rolls, which are assumed to be equally likely. Later, this probability function $P(x)$ will often be a mathematical formula.

$x$	$P(x)$	$x$	$P(x)$
1	1/36	12	4/36
2	2/36	15	2/36
3	2/36	16	1/36
4	3/36	18	2/36
5	2/26	20	2/36
6	4/36	24	2/36
7	0	25	1/36
8	2/36	30	2/36
9	1/36	36	1/36
10	2/36

The probability mass function or p.m.f. of a discrete random variable $X$ with space $S_X$ is a non-negative function $f(x)$ or $P(x)$ such that:

$f(x)>0, x \in S_X$
$\sum_{x \in S_X} f(x)=1$
$P(X=u_i)=f(u_i)$

Note that if I sum the probabilities of all possible products, I will get 1.

\[\sum_{x \in S_X}=f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(8)+\cdots+f(30)+f(36)=1\]

Suppose we define events $B_1=\{x: x \leq 10\}$ and $B_2=\{x: x>20\}$ (will show on the diagram)

\[P(B_1)=f(1) + f(2) + \cdots + f(10) =1/36 + 2/36 + \cdots + 2/36 = 19/36\] \[P(B_2)=f(24) + f(25) + f(30) + f(36) = 2/36 + 1/36 + 2/36 + 1/36 = 6/36 = 1/6\]

Discrete Uniform Distribution

A discrete random variable $X$ is said to be a discrete uniform distribution when it can take on the integer values $1,2,\cdots,m$ in an equally likely manner. Rolling a standard six-sided die is an example where $m=6$. Notation is $X \sim DU(m)$

The probability mass function for a discrete uniform distribution is: \[f(x)=P(X=x)\frac{1}{m}, x=1,2,\cdots,m\] and equal to 0 otherwise. This can be shown with a graph of points that all have the same height, reflecting the fact that the possible outcomes are equally likely (or uniformly likely).

If \[X \sim DU(m=10)\] (imagine a 10-sided die, often used in role-playing games), then \[P(X=3)=f(3)=\frac{1}{10}\]

If you wanted to know $P(X \leq 3)$, you could just sum the probabilities of the appropriate outcomes.

\[P(X \leq 3)=f(1)+f(2)+f(3)=\frac{1}{10}+\frac{1}{10}+\frac{1}{10}=\frac{3}{10}\]

The Cumulative Distribution Function (CDF) of a random variable is defined as:

\[F_X(x)=P_X((-\infty,x])=P(\{c \in \mathcal{C}: X(c) \leq x\})\]

or, in less technical notation

\[F(x)=P(X \leq x)\] So, when $X$ is discrete, then \[F(x)=\sum_{X \leq x} f(x)\]

So, the probability of getting a 3 or less on a roll of the ten-sided die is \[F(3)=P(X \leq 3)\] as evaluated before.

Discrete Example, pmf given as a formula

Let discrete random variable $X$ have the probability mass function

\[f(x)=\frac{2^x}{c}, x=0,1,2,3\] and 0 otherwise. We’ll find the following: (1) the value of the constant $c$ that makes this a valid p.m.f., (2) $f(2)$, which is $P(X=2)$, and (3) $F(2)$, which is $P(X \leq 2)$.

\[\frac{2^0}{c} + \frac{2^1}{c} + \frac{2^2}{c} + \frac{2^3}{c} = 1\] \[\frac{1}{c} + \frac{2}{c} + \frac{4}{c} + \frac{8}{c} = 1\] \[\frac{15}{c} = 1\] \[c = 15\]

\[f(2)=\frac{2^2}{15}=\frac{4}{15}\]

\[F(2)=\frac{2^0}{15} + \frac{2^1}{15} + \frac{2^2}{15} = \frac{1+2+4}{15}=\frac{7}{15}\]

Hypergeometric Distribution Another specical type of a discrete random variable is the hypergeometric, where $N$ objects can be divided into two mutually exclusive sets with $N_1$ and $N_2$ objects, respectively. The probability mass function for the hypergeometric that describes the probability of drawing $x$ objects from the first set when drawing $n$ objects without replacement is:

\[f(x)=\frac{\binom{N_1}{x}\binom{N_2}{n-x}}{\binom{N}{n}}\]

where $N=N_1 + N_2$, $N_1>0$, $N_2>0$, $x \leq n$, $x \leq N_1$, and $n-x \leq N_2$.

An example would be if we had a jar with $N=40$ jelly beans, with $N_1=25$ green jelly beans and $N_2=15$ purple jelly beans. If we choose $n=3$ jelly beans randomly without replacement, then $P(X=x)$, the number of green jelly beans chosen, is:

\[f(x) = \frac{{\binom{25}{x}\binom{15}{3-x}}}{\binom{40}{3}}\]

The probability of exactly $x=2$ green jelly beans and $n-x=3-2=1$ purple jelly bean is: \[f(2) = \frac{\binom{25}{2}\binom{15}{1}}{\binom{40}{3}}\]

The cumulative probability of 2 or fewer green jelly beans is:

\[F(2)=f(0)+f(1)+f(2)=\frac{\binom{25}{0}\binom{15}{3}}{\binom{40}{3}}+\frac{\binom{25}{1}\binom{15}{2}}{\binom{40}{3}}+\frac{\binom{25}{2}\binom{15}{1}}{\binom{40}{3}}\] We could also use the complement rule since $P(X \leq 2)=1-P(X=3)$: \[F(2)=1-f(3)=1-\frac{\binom{25}{3}\binom{15}{0}}{\binom{40}{3}}\]

2.2 Mathematical Expectation

If $X$ is a discrete random variable with space $S$ and probability mass function $f(x)$, then the expected value or the mean of the distribution is:

\[\mu_x = E(X) = \sum_{x \in S} x f(x)\]

Example: If $f(x)=\frac{2^x}{15}, x=0,1,2,3$ and 0 otherwise, then

\[\mu_X = E(X) = 0(\frac{1}{15}) + 1(\frac{2}{15}) + 2(\frac{4}{15}) + 3(\frac{8}{15}) = \frac{34}{15}\]

The expected value of $u(X)$ is: \[E[u(X)]=\sum_{x \in S} u(x)f(x)\]

For instance, if $u(x)=x^2$, then the expected value of $X^2$ is: \[E(X^2)=0^2(\frac{1}{15}) + 1^2(\frac{2}{15}) + 2^2(\frac{4}{15}) + 3^2(\frac{8}{15}) = \frac{90}{15}=6\] ———————————————————————————————————-

The expected value of the discrete uniform distribution is: \[E(X) = \sum_{x=1}^m x f(x)\] \[E(X) = \sum_{x=1}^m x \frac{1}{m}\]

\[E(X) = \frac{1}{m} \sum_{x=1}^m\]

The sum of the first $m$ positive integers is $\sum_{x=1}^m = \frac{m(m+1)}{2}$ (can show by mathematical induction). So:

\[E(X) = \frac{1}{m} \frac{m(m+1)}{2} = \frac{m+1}{2}\]

So, for $X \sim DU(m=10)$, the expected value is: \[E(X) = \frac{10+1}{2}=5.5\]

Geometric Distribution

A random experiment has a probability of success $p$, where $0 < p < 1$ and a probability of failure $q=1-p$. A trivial example is flipping a coin with heads defined as success and tails as failure, with $p=q=0.5$. A basketball player that always makes 70% of their free throws would have $p=0.7, q=0.3$.

Suppose the experiment is repeated until the first success is observed and random variable $X$ is the number of trials needed to obtain this success. The space of $X$ is $S_X = \{1,2,3,\cdots \}$. In order to define the probability mass function $f(x)$ to find $P(X=x)$, notice that we will have observed failures on the first $x-1$ trials before a success on the $x$th trial. Thus:

\[f(x) = q^{x-1} p, x \in S_X\] and zero otherwise. $X$ is said to follow the geometric distribution, where $X \sim GEO(p)$.

We can derive the expected value for the geometric distribution, which will require remembering a bit about the geometric series.

First, let’s verify that the probabilities sum to one.

\[\sum_{x=1}^\infty f(x) = q^0 p + q^1 p + q^2 p + \cdots = p(1+q+q^2+\cdots)\] Recall the geometric series, where \[\sum_{k=0}^\infty a r^k = \frac{a}{1-r}, |r|<1\]

Note that $p(1+q+q^2+\cdots)$ can be written as \[\sum_{k=0}^\infty p q^k\]

Letting $p=a$ and $q=r$, noting that $q<1$, then \[\sum_{x=1}^\infty f(x)=\frac{p}{1-q}=\frac{p}{p}=1\]

\[E(X)=\sum_{x=1}^\infty x f(x)\] \[\mu = E(X)=1 q^0 p + 2 q^1 p + 3 q^2 p + \cdots\]

If you multiply both sides by $q$, you obtain \[q \mu = qp + 2q^2 p + 3q^3 p + \cdots\]

Subtracting the second quuation from the first, you get: \[\mu - q \mu = (p+2qp+3q^2p+\cdots) - (qp+2q^2p+3q^3p + \cdots)\] \[\mu(1-q)=p(1-q+2q-2q^2+3q^2-3q^3+\cdots...)\] \[\mu(1-q)=p(1+q+q^2+q^3+\cdots)\]

\[\mu(1-q)=p \frac{1}{1-q}=1\] So \[\mu=\frac{1}{1-q}=\frac{1}{p}\]

For example, when $p=1/6$, we expect to need $\mu=\frac{1}{1/6}=6$ trials before observing the first success.

2.3 Special Mathematical Expectations

The variance of a discrete random variable is defined as:

\[\sigma^2_X = Var(X) = \sum_{x \in S}[X-E(X)]^2 f(x) = \sum_{x \in S} (X-\mu_X)^2 f(x)\] Example: If $f(x)=\frac{2^x}{15}, x=0,1,2,3$ and 0 otherwise, then we have already shown that $\mu_X = E(X) = \frac{34}{15}$. Using the defintion of variance: \[\sigma^2_X = Var(X) = \sum_{x=0}^2 (X-\mu_X)^2 f(x)\] \[\sigma^2_X = (0-34/15)^2 f(0) + (1-34/15)^2 f(1) + (2-34/15)^2 f(2) + (3-34/15)^2 f(3)\] \[\sigma^2_X = \frac{1156}{225}(\frac{2^0}{15})+\frac{361}{225}(\frac{2^1}{15})+\frac{16}{225}(\frac{2^2}{15})+\frac{121}{225}(\frac{2^3}{15})\] \[\sigma^2_X = \frac{1156+722+64+968}{3375}=\frac{2910}{3375}=\frac{194}{225}\] One disadvantage of the variance is that the unit of the problem is squared. For example, if $X$ in this discrete probability distribution represented the number of different classes I received an email from in a day, if I teach 3 classes, then the variance would be $\sigma^2_X = \frac{194}{225}$ squared classes per day. Typically, we take the square root of this quantity, which is referred to as the standard deviation.

\[\sigma_X = SD(X) = \sqrt{Var(X)} = \sqrt{\frac{194}{225}}=\frac{\sqrt{194}}{15}\approx 0.929\]

The standard deviation is about 0.929 classes per day.

As you can see, the variance and standard deviation can be quite tedious to compute for discrete random variables. Thus, we will try to find formulas to make computing the variance and standard deviation easier for particular probability distributions. Many of the well-known probability distributions have what I call “short-cut” formulas for finding the variance.

Let’s try to find more ways to compute the variance.

\[\sigma_X^2 = \sum_{x \in S} (X-\mu_X)^2 f(x)\] \[\sigma_X^2 = \sum_{x \in S} (X^2 - 2 \mu_X X + \mu_X^2) f(x)\] \[\sigma_X^2 = \sum_{x \in S} X^2 f(x) - 2\mu_X \sum_{x \in S}X f(x) + \mu^2_X \sum_{x \in S} f(x)\] \[\sigma_X^2 = E(X^2) - 2 \mu_X \mu_X + \mu_X^2 (1)\]

\[\sigma_X^2 = E(X^2) - \mu_X^2\]

\[\sigma_X^2 = E(X^2) - [E(X)]^2\]

This formula, which is often easier to compute than the variance via the defintion, uses absolute moments.

The $k$th absolute moment is $E(X^k)$.

When $k=1$, the first absolute moment is \[E(X^1)=E(X)=\sum_{x \in S} x f(x)\] which is the mean or expected value of the random variable.

When $k=2$, the second absolute moment is \[E(X^2)=\sum_{x \in S} x^2 f(x)\]

The $k$th central moment about the mean is $E[(X-\mu_X)^k]$.

When $k=1$, then \[E[(X-\mu_X)^1] = E(X-\mu_X)=E(X)-E(\mu_X)=\mu_X - \mu_X = 0\] The first central moment is equal to zero.

When $k=2$, then \[E[(X-\mu_X)^2] = \sigma_X^2\] The second central moment is equal to the variance.

When $k=3$ and $k=4$, the third and fourth central moments are measures of skewness and kurtosis, respectively.

Properties of Mathematical Expectation

Below, $X$ is a random variable with p.m.f. or p.d.f. $f(x)$, $g(x),h(x),u(x)$ are real-valued functions and $k$ is a real-valued constant, then:

\[E[g(x) + h(x)] = E[g(x)] + E[h(x)]\]

\[E[k u(x)]=k E[u(x)]\] \[E(k) = k\] \[Var(k)=0\] \[Var(kX)=k^2 Var(X)\]

What happens if we add/subtract a constant to all value of $X$, such as if an instructor added $k=5$ points to all exam scores? It seems intutitive that the expected value should increase by 5 points, and the variance/standard deviation should remain the same.

\[E(X+5)=E(X)+E(5)=\mu_x +5\]

\[Var(X+5)=Var(X) + Var(5) = \sigma^2_X + 0 = \sigma^2_X\] What about multiplication or division? For example, suppose inches are converted to centimeters by multiplying by $k=2.54$.

\[E(2.54X)=2.54E(X)=2.54\mu_X\] \[Var(2.54X)=2.54^2 Var(X)=2.54^2 \sigma^2_X\]

\[SD(2.54X)=2.54 \sigma_X\] Suppose I convert from degrees Celsius to degrees Fahrenheit by using the formula \[F=1.8C+32\]

\[E(F)=E(1.8C+32)=E(1.8C)+E(32)=1.8E(C)+32\] \[Var(F)=Var(1.8C+32)=Var(1.8C)+Var(32)=1.8^2Var(C)+0=1.8^2 Var(C)\]

\[SD(F)=1.8 SD(C)\] So, if the temperature in a particular month in Toronto had $E(C)=10$ degrees Celsius and $SD(C)=3$ degrees Celsius, then the mean and standard deviation in degrees FahrenheiT is $E(F)=1.8(10)+32 = 18+32=50$ and $SD(F)=1.8(3)=5.4$

Another technique that often makes finding expected values and variances easier is the use of what is called a moment generating function.

Suppose $X$ is a discrete random variable that takes on $n$ values with positive probability:

\[ \begin{aligned} f(x) & = a_i, x=x_1 \\ & = a_2, x=x_2 \\ & \:\:\: \: \: \: \: \: \:\vdots \\ & = a_n, x=x_n \\ & = 0 \: \: \: \: \text{otherwise} \\ \end{aligned} \] The space of $X$ is $S_X=\{x_1,x_2,\cdots,x_n\}$, where $\sum_{i=1}^n a_i=1$. Then the moment generating function of $X$, denoted as $M_X(t)$ is:

\[ \begin{aligned} M_X(t) & = E(e^{tx}) \\ & = \sum_{x \in S_X} e^{tx} f(x) \\ & = \ e^{tx_1}f(x_1) + e^{tx_2}f(x_2)+\cdots+e^{tx_n}f(x_n)\\ \end{aligned} \] So, for a discrete probability mass function, \[M_X(t)=a_1 e^{tx_1} + a_2 e^{tx_2} + \cdots + a_n e^{tx_n}\]

Suppose we have the following moment generating function: \[M_X(t)=\frac{1}{12}e^t + \frac{1}{3}e^{-t}+\frac{1}{2}e^{3t}+\frac{1}{12}e^{5t}\]

This moment generating function describes a unique probability mass function, in this case one that has 4 points of positive probability.

\[ \begin{aligned} f(x) & = \frac{1}{12}, x=1,5 \\ & = \frac{1}{3}, x=-1 \\ & = \frac{1}{2}, x=3 \\ & = 0 \: \: \: \text{otherwise} \\ \end{aligned} \] Let’s see what happens if we take the derivative of a moment generating function for a discrete random variable. A very similar argument will exist when $X$ is continuous, replacing the summation in the expected value with an appropriate integral. A “handwave” argument is used to allow interchanging the order of summation and differentiation.

\[ \begin{aligned} M_X(t) = E(e^{tx}) = \sum_{x \in S_X} e^{tx} f(x) \\ \frac{dM_X(t)}{dt} = M'_X(t) = \frac{d(\sum e^{tx}f(x))}{dt} \\ = \frac{\sum d(e^{tx}f(x))}{dt} \\ = \sum x e^{tx}f(x) \\ M'_X(0) = \sum x e^{0 \cdot x} f(x) \\ = \sum x f(x) \\ = E(X) \\ \end{aligned} \] So, when we take the first derivative of the moment generating function and evaluate it at $t=0$, we get the expected value of the probability mass (or density) function. This gives us another tool to find the expected value!

When would this be handy? Suppose you know the moment generating function but not the probability mass function.

\[ \begin{aligned} M_X(t) = (\frac{3}{4}e^t+\frac{1}{4})^3 \\ M'_X(t) = 3(\frac{3}{4}e^t+\frac{1}{4})^2(\frac{3}{4}e^t) \\ E(X) = M'_X(0) = 3(\frac{3}{4}e^0+\frac{1}{4})^2(\frac{3}{4}e^0) \\ E(X)=M'_X(0) = 3(\frac{3}{4}+\frac{1}{4})^2 (\frac{3}{4}\cdot 1) \\ E(X)=M'_X(0) = 3(1)^2\frac{3}{4} = \frac{9}{4} \\ \end{aligned} \] So the expected value, or mean, of $X$ is $\mu_X=\frac{9}{4}$. Unfortunately, there is no way in general to use the moment generating function to derive the probability mass/density function $f(x)$, although in certain special cases we will recognize the form of $M_X(t)$ as following the form of a m.g.f. of a known type of probability distribution.

It turns out taking the second derivative of the moment generating function will be useful in finding the variance.

\[ \begin{aligned} M'_X(t) = \sum f(x)e^{tx}\cdot x \\ \frac{d^2(M_X(t))}{dt^2} = M''_X(t) = \frac{d(\sum f(x)e^{tx}\cdot x)}{dt} \\ = \frac{\sum d(f(x)e^{tx}\cdot x)}{dt} \\ = \sum(x f(x)e^{tx}\cdot x) \\ M''_X(t) = \sum x^2 f(x)e^{tx} \\ M''_X(0) = \sum x^2 f(x)e^{0\cdot x} \\ M''_X(0) = \sum x^2 f(x) = E(X^2) \\ \end{aligned} \] So the second derivative of the moment generating function is $E(X^2)$, the second absolute moment. So:

\[\sigma^2_X = Var(X) = E(X^2) - [E(X)]^2\] \[\sigma^2_X = Var(X) = M''_X(0) - [M'_X(t)]^2\] So now we can find the second absolute moment and eventually the variance and standard deviation of $X$.

\[ \begin{aligned} M_X(t) = (\frac{3}{4}e^t+\frac{1}{4})^3 \\ M'_X(t) = 3(\frac{3}{4}e^t+\frac{1}{4})^2 \cdot \frac{3}{4}e^t = \frac{9}{4}e^t(\frac{3}{4}e^t+\frac{1}{4})^2 \\ M''_X(t) = \frac{9}{4}e^t \cdot 2(\frac{3}{4}e^t+\frac{1}{4})^1\cdot \frac{3}{4}e^t+\frac{9}{4}e^t(\frac{3}{4}e^t+\frac{1}{4})^2 \\ M''_X(t) = \frac{27}{8}e^{2t}(\frac{3}{4}e^t+\frac{1}{4})+\frac{9}{4}e^t(\frac{3}{4}e^t+\frac{1}{4})^2 \\ E(X^2) = M''_X(0) = \frac{27}{8}(\frac{3}{4}+\frac{1}{4})+\frac{9}{4}(\frac{3}{4}+\frac{1}{4})^2 \\ E(X^2) = \frac{27}{8} + \frac{9}{4} = \frac{27}{8}+\frac{18}{8} = \frac{45}{8} \\ \end{aligned} \] Use this value $E(X^2)=\frac{45}{8}$ along with $E(X)=\frac{9}{4}$ that we found earlier to get the variance.

\[ \begin{aligned} \sigma^2_X = Var(X) = E(X^2) - [E(X)]^2 \\ \sigma^2_X = Var(X) = \frac{45}{8} - (\frac{9}{4})^2 = \frac{45}{8} - \frac{81}{16} \\ \sigma^2_X = Var(X)= \frac{90}{16} - \frac{81}{16} = \frac{9}{16} \\ \sigma_X = SD(X) = \sqrt{\frac{9}{16}} = \frac{3}{4} \\ \end{aligned} \] So the mean and variance of $X$ are $\mu_X = \frac{9}{4}$ and $\sigma^2_X=\frac{9}{16}$, respectively, with standard deviation $\sigma_X=\frac{3}{4}$.

Another example of using the moment generating function to find the expected value and variance of a discrete random variable $X$.

\[f(x)=(\frac{1}{2})^x, \: \: \: x=1,2,3,\cdots\] Find the moment generating function, then take the first and second derivatives of it.

\[ \begin{aligned} M_X(t)=E(e^{tx}) \\ = \sum_{x=1}^\infty e^{tx}(\frac{1}{2})^x \\ = \sum_{x=1}^\infty (\frac{1}{2}e^t)^x \\ \end{aligned} \] Let $y=x-1$ (as our goal is to be able to evaluate this summation using the geometric series)

\[ \begin{aligned} = \sum_{y=0}^\infty (\frac{1}{2}e^t)^{y+1} \\ = \sum_{y=0} (\frac{1}{2}e^t)(\frac{1}{2}e^t)^ y \\ \end{aligned} \] Now we have the moment generating function in the geometric series form \[\sum_{k=0}^\infty a r^k=\frac{a}{1-r}, |r|<1\] with $a=\frac{1}{2}e^t$ and $r=\frac{1}{2}e^t$ with $\frac{1}{2}e^t <1$.

\[ \begin{aligned} = \frac{\frac{1}{2}e^t}{1-\frac{1}{2}e^t} \\ = \frac{\frac{1}{2}e^t}{\frac{2-e^t}{2}} \\ M_X(t) = \frac{e^t}{2-e^t} \\ \frac{1}{2}e^t < 1 \\ e^t < 2\\ t < \ln 2 \\ t < -\ln \frac{1}{2} \\ \end{aligned} \] So we can have some quotient rule fun to find the first two derivatives of this moment generating function.

\[ \begin{aligned} M'_X(t) = \frac{(2-e^t)e^t - e^t(-e^t)}{(2-e^t)^2} \\ = \frac{2e^t-e^{2t}+e^{2t}}{(2-e^t)^2} \\ =\frac{2e^t}{(2-e^t)^2} \\ E(X) = M'_X(0) = \frac{2 \cdot 1}{(2-1)^2} = 2\\ M''_X(t) = \frac{(2-e^t)^2 \cdot 2e^t - 2e^t \cdot 2(2-e^t)(-e^t)}{(2-e^t)^4} \\ = \frac{(2-e^t)^2 \cdot 2e^t + 4e^{2t}(2-e^t)}{(2-e^t)^4} \\ E(X^2) = M''_X(0) = \frac{(2-1)^2 \cdot 2 \cdot 1 + 4 \cdot 1(2-1)}{(2-1)^4} \\ = \frac{2+4}{1} = 6 \\ Var(X) = E(X^2) - [E(X)]^2 = 6 - 2^2 = 6-4 = 2 \\ \end{aligned} \]

If you check the inside front cover of the textbook, you should notice that our probability mass function $f(x)=\frac{1}{2}^x, x=1,2,3,\cdots$ is the geometric distribution with $p=\frac{1}{2}$, or $X \sim GEO(p=\frac{1}{2})$. Notice that the given equations for the moment generating function, mean, and variance yield the same results as the calculations that we just did, and we could have generated those equations by repeating the above work using $p$ as the general probability of success rather than the specific value $p=\frac{1}{2}$.

2.4 The Binomial Distribution

A random experiment is said to be based on Bernouli trials when the following three conditions are met:

each trial of the experiment has 2 and only 2 possible outcomes, where these outcomes are generally referred to as “success” and “failure”
each trial of the experiment is independent of every other trial
each trial has a known probability of success $p$ that remains the same for all trials

Since we denote the probability of success as $p$, the probability of failure is $q=1-p$.

When we have a random experiment with exactly $n=1$ Bernoulli trial and let random variable $X$ represent the number of successes that were observed, then $S_X = \{0,1\}$ and the probability mass function is: \[f(x)=p^x (1-p)^{1-x}, x=0,1\] and 0 otherwise. This is referred to as the Bernoulli distribution, $X \sim BERN(p)$.

We can use the definition of expected value to find the mean of the Bernoulli distribution.

\[ \begin{aligned} E(X) = & \sum_{x=0}^1 x f(x) \\ E(X) = & 0 \cdot f(0) + 1 \cdot f(1) \\ E(X) = & 0 + p^1 (1-p)^{1-1} \\ E(X) = & p \\ \end{aligned} \] Next, find the second absolute moment $E(X^2)$ in order to find the variance of the Bernoulli distribution.

\[ \begin{aligned} E(X^2) = & \sum_{x=0}^1 x^2 f(x) \\ E(X^2) = & 0^2 \cdot f(0) + 1^2 \cdot f(1) \\ E(X^2) = & p \\ Var(X) = & E(X^2) -[E(X)]^2 \\ Var(X) = & p - p^2 \\ Var(X) = & p(1-p) \\ \end{aligned} \] We can also find the moment generating function.

\[ \begin{aligned} M_X(t) = & E(e^{tX}) \\ M_X(t) = & \sum{x=0}^1 e^{tx} \cdot p^x (1-p)^{1-x} \\ M_X(t) = & e^0 p^0 (1-p)^1 + e^t p^1 (1-p)^0 \\ M_X(t) = & (1-p) + pe^t \\ \end{aligned} \]

We can generalize these results to a random experiment with $n$ such Bernoulli trials with success probability $p$. This will be called the binomial distribution, $X \sim BIN(n,p)$. The random variable $X$ represents the number of successes counted in a fixed number of trials. Notice that the Bernoulli distribution is a special case of the binomial with $n=1$.

The probability mass function for the binomial distribution is:

\[f(x) = \binom{n}{x} p^x (1-p)^{n-x}, x=0,1,2,\cdots,n\] and zero otherwise. Note that $x$ is the observed number of successes and $n-x$ is the observed number of failures.

We can find the moment generating function of the binomial distribution.

\[ \begin{aligned} M_X(t) = & E(e^{tX}) \\ M_X(t) = & \sum_{x=0}^n e^{tx} \binom{n}{x} p^x (1-p)^{n-x} \\ M_X(t) = & \sum_{x=0}^n \binom{n}{x} (pe^t)^x (1-p)^{n-x} \\ \end{aligned} \]

This is a binomial expansion \[(a+b)^n = \sum_{x=0}^n \binom{n}{x} b^x a^{n-x}\] with $a=1-0$ and $b=pe^t$. So \[M_X(t) = ((1-p)+pe^t)^n, -\infty < t < \infty\]

Now, we’ll use this moment generating function to “generate” the first two absolute moments of the binomial distribution, and use those to find formulas for the mean and the variance.

\[ \begin{aligned} M'_X(t) = & n [(1-p)+pe^t]^{n-1} \cdot (pe^t) \\ E(X) & = n[(1-p)+pe^0]^{n-1} \cdot (pe^0) \\ E(X) & = np \\ M''_X(t) = & n(n-1)[(1-p)+pe^t]^{n-2}(pe^t)^2 + n[(1-p)+pe^t]^{n-1} \cdot pe^t \\ E(X^2) = & n(n-1)[(1-p)+pe^0]^{n-2}(pe^0)^2 + n[(1-p)+pe^0]^{n-1} \cdot pe^0 \\ E(X^2) = & n(n-1)p^2 + np \\ Var(X) = & n(n-1)p^2 + np - (np)^2 \\ Var(X) = & n(n-1)p^2 + np - n^2 p^2 \\ Var(X) = & np[(n-1)p + 1 - np] \\ Var(X) = & np[np - p + 1 - np] \\ Var(X) = & np(1-p) \\ \end{aligned} \]

For an applied example, suppose a student is taking a multiple choice exam with $n=20$ questions. Each question has 4 choices, one of which is correct (success) and the other three which are incorrect (failure). The student has not studied and decides to guess on every problem without reading it, so $p=0.25$. While this is unwise on the student’s part, we do have $n=20$ Bernoulli trials and if $X$ represents the number of correct answers, then $X \sim BIN(n=20,p=0.25)$.

The mean number of correct answers is $\mu_X = E(X) = np = 20(.25) = 5$, with variance $\sigma^2_X = Var(X) = np(1-p) = 20(.25)(1-.25)=3.75$ and standard deviation $\sigma_X = SD(X) = \sqrt{3.75}$.

If we wanted to know the probability that the student guesses correctly on exactly 3 of the 20 questions, we could draw a tree diagram with 2^20 branches, or use the binomial p.m.f. Then \[f(3)=P(X=3)=\binom{20}{3}(.25)^3 (.75)^{17} = 1140(.25)^3 (.75)^17 = 0.1339\]

The function binompdf(20,0.25,3) on a TI-84 calculator or dbinom(x=3,size=20,prob=0.25) can be used to make this calculation.

dbinom(x=3,size=20,prob=0.25)

## [1] 0.1338956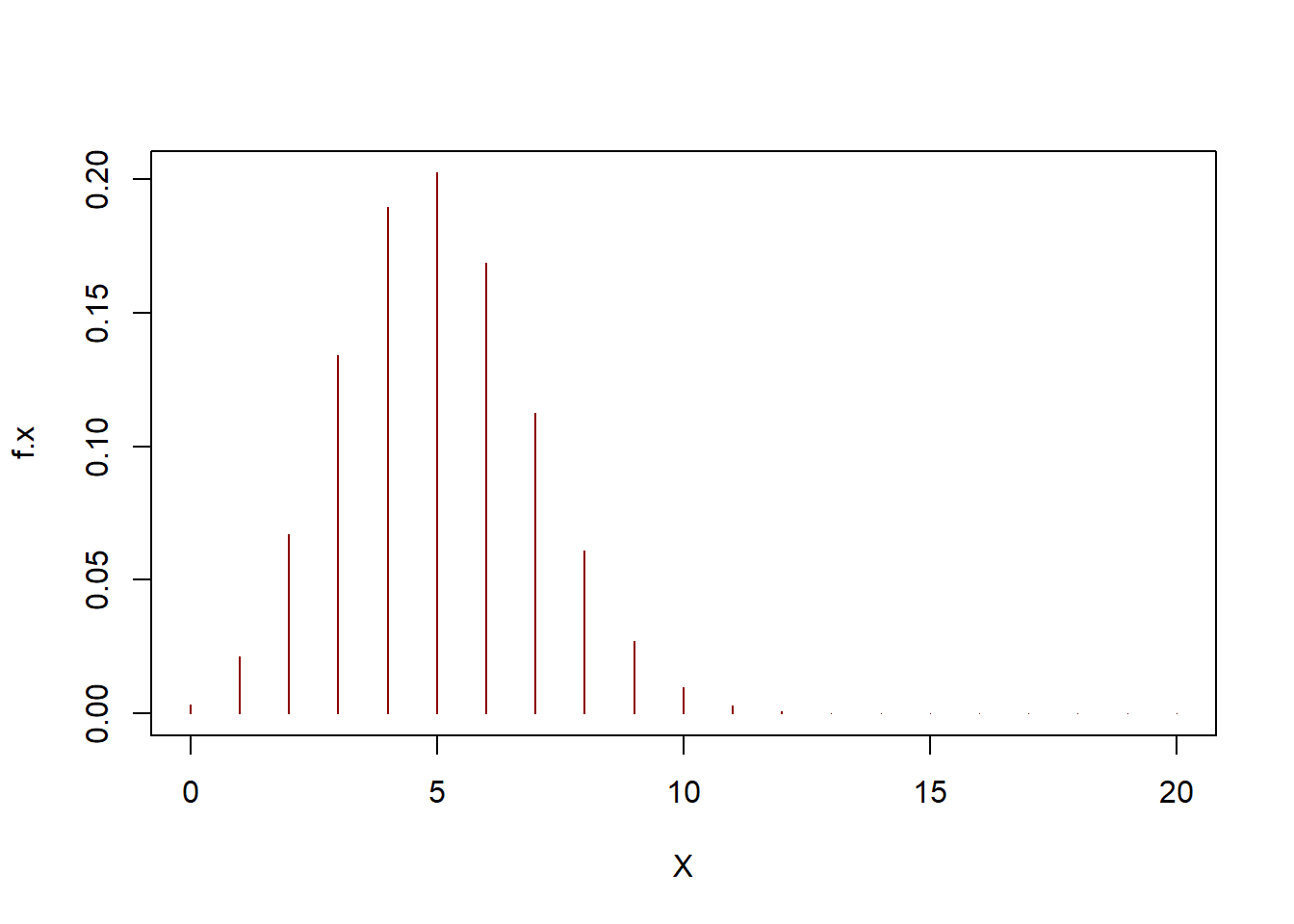

X <- 0:20
f.x <- dbinom(x=X,size=20,prob=0.25)
plot(f.x ~ X, type="h", col="red4")

If the student needed to get at least 12 questions correct to pass the exam, they have very little chance of passing by random guesses.

Suppose we want to know the probability that the guessing students fails the exam, $P(X \leq 11)=F(11)$.

We could find this by repeated use of the probability mass function or the binompdf or dbinom functions, adding all the answers together.

\[F(11) = P(X \leq 11) = P(X=0) + P(X=1) + \cdots + P(X=11) = \sum_{x=0}^{11} \binom{20}{x} (.25)^x (.75)^{20-x}\]

Functions for the cumulative distribution function, or CDF $F(x)$ exist to do these tedious calculations. Either binomcdf(20,0.25,11) or pbinom(q=11,size=20,prob=0.25) will compute this for us.

X <- 0:11
sum(dbinom(x=X,size=20,prob=0.25))

## [1] 0.9990646

pbinom(q=11,size=20,prob=0.25)

## [1] 0.9990646

As we see, the guessing student almost assuredly fails, the probability of passing $P(X \geq 12) = 1-P(X \leq 11) = 1 - .9990646 = 0.0009354$.

2.5 The Negative Binomial Distribution

Now, instead of fixing the number of trials and counting successes, let us fix the number of successes to be $r$ and count the number of trials $X$ needed to obtain the $r$th success.

Which would be larger?

The probability of 4 successes (heads) in $n=10$ tosses of a coin (where the number of tosses was fixed to 10) with probability of success $p$.

This is binomial, \[f(4)=P(X=4)=\binom{10}{4}p^4 (1-p)^{10-4}=210 p^4 (1-p)^6\]

The probability of obtaining the $r=4$th success on the $x=10$th flip of that coin (where the number of successes was fixed to 4).

Notice that for this to happen, we must have had exactly 3 successes (and hence 9-3=6 failures) in the first 9 trials, and the 4th success on exactly the 10th trial.

\[P(X=10)=\binom{9}{3} p^3 (1-p)^6 \cdot p = 84 p^4 (1-p)^4\]

Scenario (b) clearly has a lower probability and is actually a subset of scenario (a).

When we fix the number of successes needed as $r$ and count the number of trials needed as random variable $X$, we have the negative binomial distribution, $X \sim NB(r,p)$. The probability mass function is

\[f(x)=P(X=x)=\binom{x-1}{r-1} p^r (1-p)^{x-r}, x=r,r+1,\cdots\]

and 0 otherwise.

A mathematical fact we will use when finding the moment generating function of the negative binomial is that if one differentiates a geometric series $k$ times, we obtain: \[\sum_{y=0}^\infty (y+k)(y+k-1)\cdot \cdots \cdot (y+1)x^y = \frac{k!}{(1-x)^{k+1}}, |x| < 1\]

Let’s find the moment generating function, where we will let $y=x-r$ so that $x=y+r$ and eventually $k=r-1$ and $x=(1-p)e^t$:

\[ \begin{aligned} M_X(t) = & \sum_{x=r}^\infty e^{tx} \binom{x-1}{r-1}p^r (1-p)^{x-r} \\ = & \sum_{y=0}^\infty e^{t(y+r)} \binom{y+r-1}{r-1} p^r (1-p)^y \\ = & \frac{e^{tr} p^r}{(r-1)!} \sum_{y=0}^\infty e^{ty} (y+r-1)(y+r-2)\cdot \cdots \cdot (y+1)(1-p)^y \\ = & \frac{(pe^t)^r}{(r-1)!} \sum_{y=0}^\infty (y+r-1)(y+r-2)\cdot \cdots \cdot (y+1)[(1-p)e^t]^y \\ = & \frac{(pe^t)^r}{(r-1)!} \frac{(r-1)!}{[1-(1-p)e^t]^r} \\ = & \frac{(pe^t)^r}{[1-(1-p)e^t]^r}, t < \ln(1-p) \\ \end{aligned} \]

Now that we have the moment generating function for the negative binomial, straightforward but tedious differentiation will give us the first two absolute moments $E(X),E(X^2)$ and hence the mean and variance. Many of the details involving the Product and Quotient Rules are skipped below.

\[M'_X(t) = r (\frac{pe^t}{1-(1-p)e^t})^{r-1} [\frac{pe^t}{(1-(1-p)e^t)^2}]\] \[\mu = E(X) = M'_X(0) = r(\frac{p}{1-(1-p)})^{r-1}[\frac{p}{(1-(1-p))^2}] = r \cdot \frac{p}{p} \cdot \frac{p}{p^2} = \frac{r}{p}\] \[E(X^2) = M''_X(0) = \frac{r}{p^2}[r+(1-p)]\]

\[\sigma^2 = Var(X) = M''_X(0)-[M'_X(0)]^2 = \frac{r}{p^2}[r+(1-p)]-(\frac{r}{p})^2 = \frac{r(1-p)}{p^2}\]

An important special case of the negative binomial is when $r=1$. The number of trials needed to obtain the first success has already been described as the geometric distribution. Recapping $X \sim GEO(p)$ or equivalently $X \sim NB(r=1,p)$: \[f(x)=p(1-p)^{x-1}, x=1,2,3,\cdots\] \[\mu=E(X)=\frac{1}{p}\]

\[\sigma^2=Var(X)=\frac{1-p}{p^2}\]

Suppose that we are considering $X \sim NB(r=2,p=1/3)$ and we wish to find the probability that 5 trials were needed to obtain 2 successes. This, of course, means that the first 4 trials consisting of 1 success and 3 failures (in any possible order) and that the 5th trial was the 2nd success.

\[f(5)=P(X=5)=\binom{5-1}{2-1}(\frac{1}{3})^2 (\frac{2}{3})^{5-2} = \binom{4}{1}(\frac{1}{3})^2 (\frac{2}{3})^3 = 4 \cdot \frac{1}{3^2} \cdot \frac{2^3}{3^3} = \frac{32}{243} = .1317\]

There is no function on the TI-84 calculator for the probability mass function or cumulative distribution function of the negative binomial. There are such d- (p.m.f $f(x)$ and p- (CDF $F(x)$) in R, but we need to be careful in using them!

dnbinom(x=5,size=2,prob=1/3)

## [1] 0.0877915

As you see (with $r$ called size) that the dnbinom function is not returning the same answer as we got plugging into the negative binomial’s p.m.f. The reason for this discrepancy is that R uses a different parameterization of the negative binomial that counts the number of FAILURES (rather than trials) before the $r$th success. Let $Y$ represent this number of failures, $Y ~ NB(r,p)$.

\[f(y)=P(Y=y)= \binom{y+r-1}{y} p^r (1-p)^y, y=0,1,2,\cdots\] \[\mu_Y = \frac{r(1-p)}{p}, \sigma^2_Y = \frac{r(1-p)}{p^2}\] If we recompute our probability of $f_X(5)=P(X=5)$, note that when $X=5$, that $Y=5-2=3$.

\[f_Y(3)=P(Y=3)=\binom{3+2-1}{3}(\frac{1}{3})^2 (\frac{2}{3})^3 = \binom{4}{3}(\frac{1}{3})^2 (\frac{2}{3})^ 3 = 4 \cdot \frac{1}{3^2}=\frac{2^3}{3^3} = \frac{32}{243}\]

Ah, the same as before. We can use R, as long as we are sure to remember that R wants the number of failures it takes for the $r$th success, not the total number of trials.

dnbinom(x=3,size=2,prob=1/3) # exactly 3 failures before 2nd success

## [1] 0.1316872

pnbinom(q=3,size=2,prob=1/3) # less than or equal to 3 failures

## [1] 0.5390947

x <- 0:20
f.x <- dnbinom(x=x,size=2,prob=1/3)
plot(f.x~x,type="h",xlab="Number of failures before 2nd success")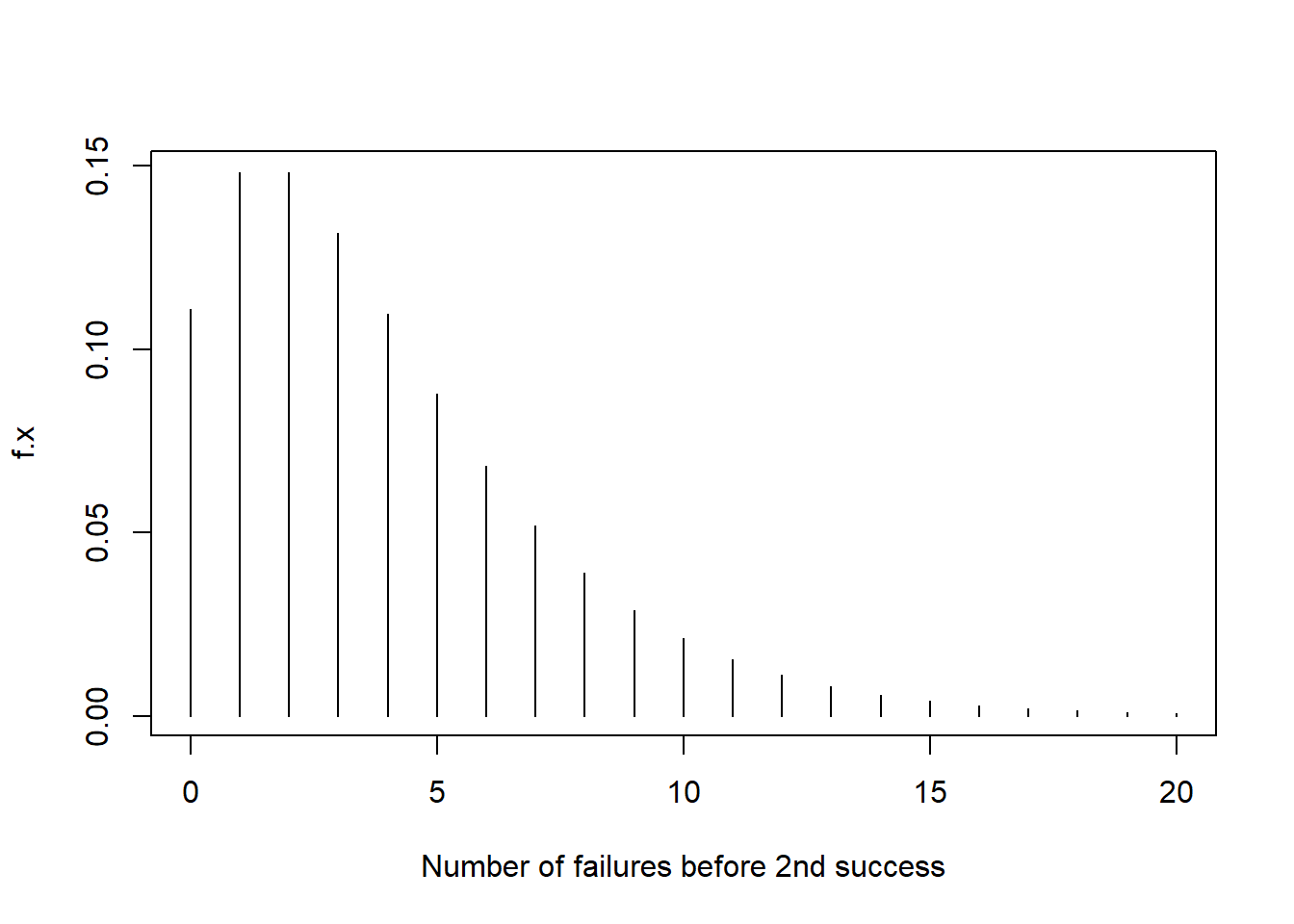

2.6 The Poisson Distribution

The Poisson distribution is a discrete probability distribution that is often used to model the number of occurences of an event of interest within a given interval. The interval is usually a period of time, but can also be a length or area.

Examples:

(historical) model the number of soldiers from the Prussian cavalry that are killed yearly by being kicked by their horse
model the number of accidents per month at a certain intersection
describe the number of people someone with an infectious disease spreads it to
predict the number of flaws in a 1 meter length of wire

We will state some technical assumptions of the Poisson Process, and use those to derive the probability mass function $f(x)$.

Assumptions:

Assume $p_n(t)=P(x(t)=n$, where $X(t)$ the count of the number of occurences of the event in an interval of length $t$.
Assume the probability of a single event in time period $\Delta t$ is given by $\lambda \Delta t + o(\Delta t)$, where “little o”, $o(\Delta t)$ is a representation of a function $f(\Delta t)$ such that \[\lim_{\Delta t \rightarrow 0} \frac{f(\Delta t)}{\Delta t}=0\] (i.e. $o(\Delta t)$ is essentially zero)
Assume the probability of two or more events in time period $\Delta t$ is $o(\Delta t)$ (i.e. neglible)
Assume the count of the number of occurences of the event in disjoint time intervals are independent. Note that this is often violated in real-life applications. For example, we would expect more accidents per month at the Five Points intersection in Murray during the winter months, both due to weather and heavier traffic because of school being in session.
The probability of a zero count in $\Delta t$ is $1 - \lambda \Delta t - o(\Delta t)$.

So this means: \[p_n(t + \Delta t) = p_n(t)(1-\lambda\Delta t - o(\Delta t)) + p_{n-1}(t)(\lambda \Delta t + o(\Delta t))\]

where the first term in the right hand sum is the probability of $n$ events in interval $(0,t)$ times the probability of no events in interval $(t,t+\Delta t)$ and the second term is the probability of $n-1$ events from $(0,t)$ times one event in $(t,t+\Delta t)$.

So: \[ \begin{aligned} f'(x) = & \frac{d f(x)}{dx} = \lim_{\Delta x \rightarrow 0} \frac{f(x + \Delta x)-f(x)}{\Delta x} \\ p'_n(t) = & \frac{d p_n(t)}{dt} = \lim_{\Delta t \rightarrow 0} \frac{p_n(t+\Delta t)-p_n(t)}{\Delta t} \\ = & \lim_{\Delta t \rightarrow 0} [\frac{p_n(t)[1-\lambda \Delta t-o(\Delta t)]+p_{n-1}(t)[\lambda \Delta t + o(\Delta t)]-p_n(t)}{\Delta t}] \\ = & \lim_{\Delta t \rightarrow 0}[\frac{p_n(t)-\lambda \Delta t p_n(t)-o(\Delta t)p_n(t)+ \lambda \Delta t p_{n-1}(t) + o(\Delta t)p_{n-1}(t)-p_n(t)]}{\Delta t}] \\ = & \lim_{\Delta t \rightarrow 0} -\lambda p_n(t) - \frac{o(\Delta t)p_n(t)}{\Delta t} + \lambda p_{n-1}(t) + \frac{o(\Delta t)p_{n-1}(t)}{\Delta t} \\ \frac{d p_n(t)}{dt} = & \lambda p_{n-1}(t) - \lambda p_n(t) \\ \end{aligned} \]

We can either derive a formula for $p_n(t)$ by mathematical induction, or (as will be done here), use some basic differential equations and a few “handwaves” to find $p_0(t), p_1(t), p_2(t), \cdots$ and notice a pattern. Yet another approach is used in the textbook, which considers dividing the interval into increasing smaller subintervals and considering each small subinterval as a Bernoulli trial where either a success (occurence of the event) or failure is observed.

For our approach, since $p_n(0)=0$ for $n>0$ (i.e. the probability of observing one or more events in an interval of length 0 is zero), then we have the boundary conditions $p_0(0)=1$ and $p_{-1}(t)=0$.

First suppose $n=0$. Along the way, let $e^C = k$. \[ \begin{aligned} \frac{d p_0(t)}{dt} = & \lambda p_{-1}(t) - \lambda p_0(t)\\ \frac{d p_0(t)}{dt} = & - \lambda p_0(t)\\ \int \frac{1}{p_0(t)} dp_0(t) = & \int -\lambda dt \\ \ln p_0(t) = & -\lambda t + C \\ p_0(t) = & e^{-\lambda t}\cdot e^C \\ p_0(t) = & ke^{-\lambda t} \\ \end{aligned} \]

If $t=0$, then $p_0(0)=ke^{\lambda \cdot 0}=k=1$, so the probability of zero events in the interval $(0,t)$ is: \[p_0(t) = e^{\lambda t}\]

Now let $n=1$, obtain a first order linear differential equation, and handwave some D.E. details.

\[ \begin{aligned} \frac{dp_1(t)}{dt} = & \lambda p_0(t) - \lambda p_1(t) \\ \frac{dp_1(t)}{dt} = & \lambda[e^{-\lambda t}-p_1(t)] \\ p_1(t) = & \lambda t e^{-\lambda t} + ce^{\lambda t} \\ \end{aligned} \]

Let $t=0$, and since $p_1(0)=0$, then $0 + c = 0$ and thus $c=0$.

Hence the probability of exactly one event in interval $(0,t)$ is \[p_1(t) = \lambda t e^{-\lambda t}\]

If we continues this process for $n=2,3,\cdots,n$

\[ \begin{aligned} \frac{dp_2(t)}{dt} = & \lambda[p_1(t)-p_2(t)] \\ = & \: \: \: \: \: handwave \\ p_2(t) = & \frac{(\lambda t)^2}{2} e^{-\lambda t} \\ \vdots & \: \: \: \: \: handwaving\\ p_n(t) = & \frac{(\lambda t)^n}{n!} e^{-\lambda t}, n=0,1,2,\cdots \\ \end{aligned} \]

The number of changes of $X$ in an interval of size $t$ is $m=\lambda t$. Thus $X(t) \sim POI(\lambda t)$, where $\mu = E[X(t)]=\lambda t$.

$\lambda$ is a proportionality constant which is the rate of occurence or intensity of the Poission process. $\lambda$ is close to zero when events are rare, and becomes larger as event are more common. Because $\lambda$ is assumed to be constant over time, we have a *homogeneous Poisson process$.

If we let $\mu = \lambda t$, then the probability mass function of the Poisson distribution is \[f(x) = P(X=x) = \frac{\mu^x e^{-\mu}}{x!}, x=0,1,2,\cdots\]

where $\mu$ is the average count of the number of occurence of the event per unit of measure. Often we assume $t=1$ (one day, one month, one year, one meter, etc.) and use $\lambda$ as the Poisson distribution’s parameter, as you will find in your textbook. We say $X \sim POI(\lambda)$.

\[f(x) = \frac{\lambda^x e^{-\lambda}}{x!}, x= 0,1,2,\cdots\]

Let’s establish that $f(x)$ is a valid p.m.f. Note that $f(x) > 0$ for all values of $x$ in $S_X$. Do they sum to one?

Before we check, here’s a reminder about the sum of the exponential series. \[\sum_{n=0}^\infty \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = e^x\]

Let’s sum the Poisson p.m.f.

\[\sum_{x=0}^\infty f(x) = \sum_{x=0}^\infty \frac{\lambda^x e^{-\lambda}}{x!} = e^{-\lambda} \sum_{x=0}^\infty \frac{\lambda^x}{x!} = e^{-\lambda} \cdot e^\lambda = 1\]

Now let’s find the moment generating function.

\[ \begin{aligned} M_X(t) = & \sum_{x=0}^\infty e^{tx} \frac{e^{-\lambda} \lambda^x}{x!} \\ = & e^{-\lambda} \sum_{x=0}^\infty \frac{(\lambda e^t)^x}{x!} \\ = & e^{-\lambda} e^{\lambda e^t} \\ M_X(t) = & e^{\lambda(e^t-1)}, -\infty < t < \infty \\ \end{aligned} \] We can take the first two derivatives to determine the expected value and variance of the Poisson distribution.

\[ \begin{aligned} M'_X(t) = & e^{\lambda(e^t-1)} \cdot \lambda e^t \\ E(X) = M'_X(0) = & e^{\lambda(e^0-1)} \cdot \lambda e^0 = \lambda \\ M''_X(t) = & e^{\lambda(e^1-1)} \cdot \lambda e^t + e^{\lambda(e^t-1)} \cdot \lambda e^t \cdot \lambda e^t \\ E(X^2) = M''_X(0) = & \lambda + \lambda^2 \\ Var(X) = & E(X^2) - [E(X)]^2 = \lambda + \lambda^2 -(\lambda)^2 = \lambda \\ \end{aligned} \] So the Poisson distribution has the unusual property that the mean and the variance are equal to each other. This ends up being problematic in applied statistics, as real-life count data tends to have a variance that is greater than the mean. This is known as being overdispersed, and a variety of variations of the Poisson distribution and negative binomial distribution, including the zero-inflated Poisson, exist to attempt to more accurately model actual count data.

Suppose $X$ represents the number of flaws found in a 10 meter length of wire, where $\lambda=1.6$.

The probability of exactly 2 flaws is: \[f(2)=P(X=2)=\frac{e^{-1.6}(1.6)^2}{2!}=0.2584\]

We can compute this with either poissonpdf(1.6,2) on a TI-84 or by using the dpois function in R.

r dpois(x=2,lambda=1.6)

## [1] 0.2584275

If I wanted to know the probability of 2 or fewer flaws in the 10 meter length, you can either use the p.m.f. 3 times and sum the results, or use the cumulative distribution function.

\[F(2)=P(X \leq 2) = P(X=0) + P(X=1) + P(X=2)\]

Table III provided on pages 490-491 of our textbook have tabulated the Poisson CDF for certain values of the rate parameter $\lambda$. There are similar tables on pages 485-489 for certain combinations of $n$ and $p$ for the binomial distribution. The entry for $F(2)$ when $\lambda=1.6$ is 0.783 This can also be done with poissoncdf(2,1.6) or the ppois function in R.

r ppois(q=2,lambda=1.6)

## [1] 0.7833585

If we wanted to know the probability of more than 3 flaws in the 10 meter length, then $P(X>3)=1-P(X \leq 3)$. Via the table, this is $1-0.921=0.079$.

r 1-ppois(q=3,lambda=1.6)

## [1] 0.07881349 R can be used to graph either the p.m.f. or CDF.

r X <- 0:10 f.x <- dpois(x=X,lambda=1.6) plot(f.x~X,type="h",col="blue")

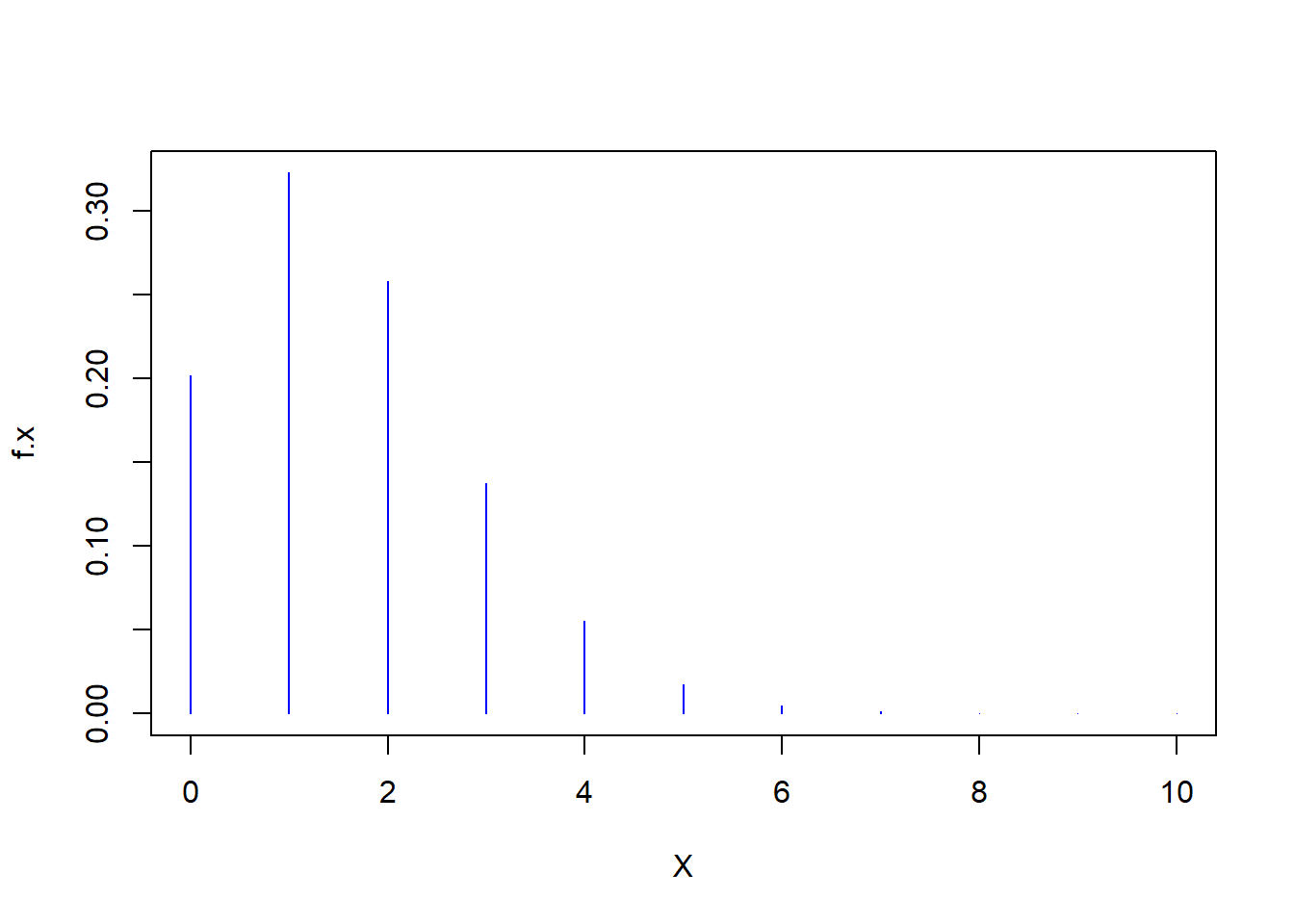r F.x <- ppois(q=X,lambda=1.6) plot(F.x~X,type="s",col="red")

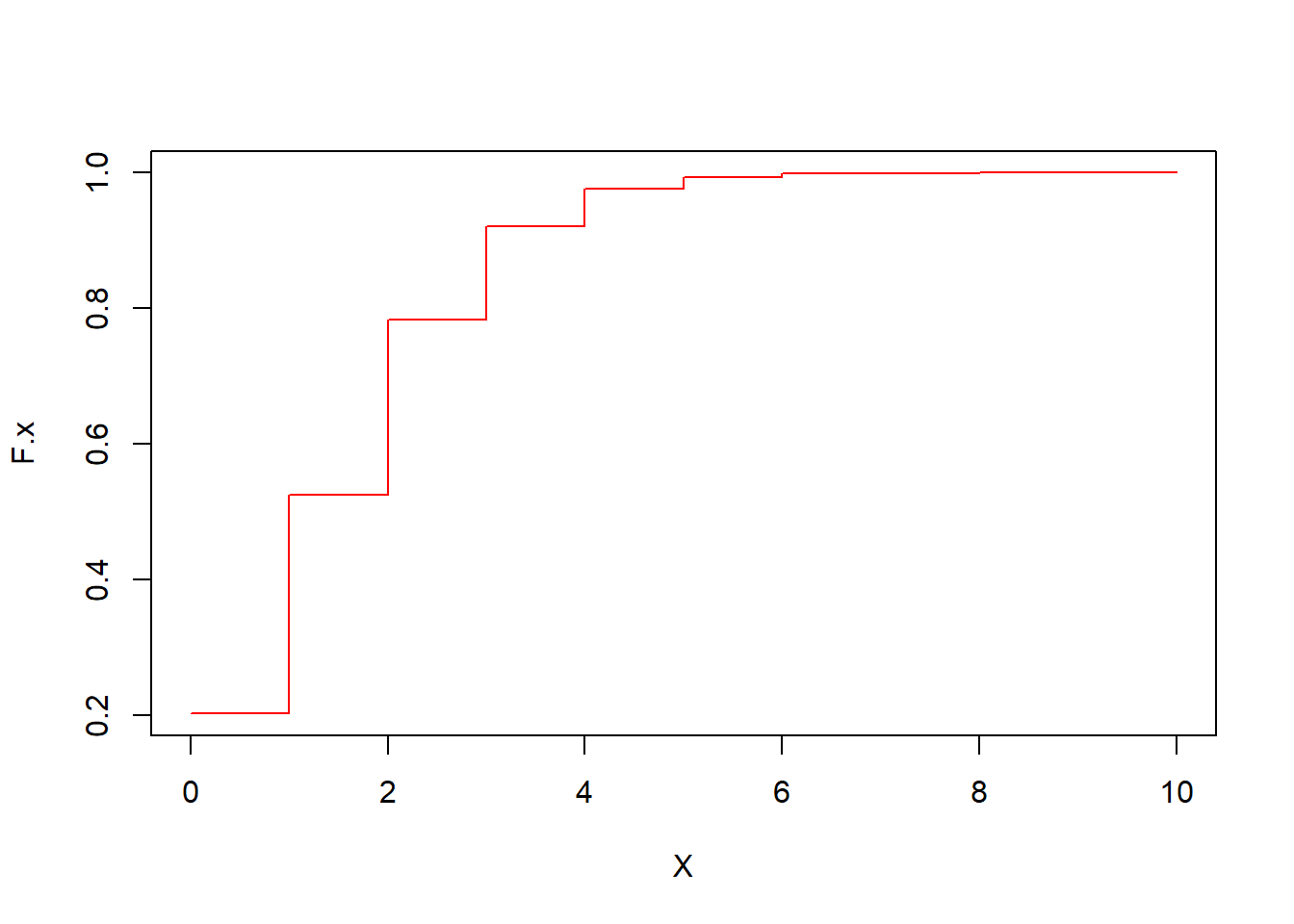If we change the size of the interval (such as looking at a different length of wire or a different unit of time), we can just adjust the rate parameter $\lambda$ since we are assuming a homogeneous Poisson process. For instance, suppose I want to know the probability of at least 1 flaw in a 1 metere length of wire. I adjust $\lambda=1.6 \times 0.1 = 0.16$.

\[P(X \geq 1) = 1 - P(X=0) = 1-f(0) = 1 - \frac{e^{-0.16}(0.16)^0}{0!} = 1 - e^{-0.16} = 0.1479\]

r 1-dpois(x=0,lambda=0.16)

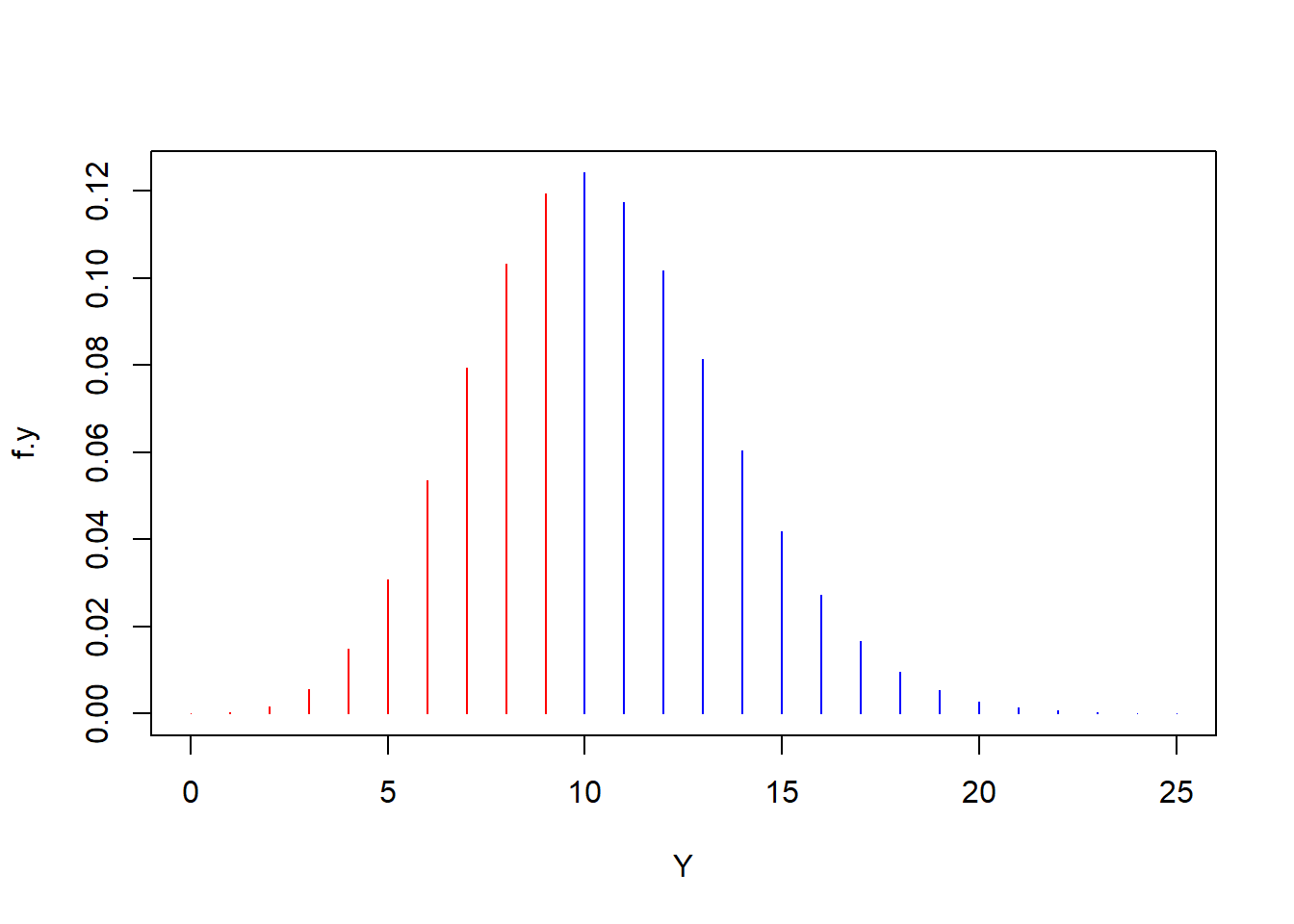
## [1] 0.1478562 One would make a similar adjustment if the interval is a length of time. For instance, suppose that the number of accidents per week at a given intersection is $X \sim POI (\lambda=0.2)$ and we wanted to know the probability of less than 10 accidents in a year. Letting $Y$ represent the number of accidents per year and assuming the rate of 0.2 accidents per week is constant across all weeks, then $Y \sim POI(\lambda=52 \times 0.2=10.4)$

\[P(Y < 10) = P(Y \leq 9)=F_Y(9)=0.409\]

r ppois(q=9,lambda=10.4)

## [1] 0.4089874

r Y <- 0:25 f.y <- dpois(x=Y,lambda=10.4) plot(f.y ~ Y, type="h",col=c(rep("red",10),rep("blue",16)))

There are a various ways to derive the Poisson distribution; one method shown earlier involves differential equations, but here we will look at a method that builds upon the now familiar binomial distribution.

Divide our interval into $n$ sub-intervals, so the rate of an occurence in a sub-interval is equal to $\frac{\lambda}{n}$. In the wire example with $\lambda=2$ flaws per 10 meters of wire, if $n=10$, then the rate of an occurence in each 1 meter of wire is $\frac{2}{10}=0.2$
If $n$ is large (i.e. we are looking at very short lengths of wire or short periods of time), then the probability of two occurences in the sub-interval is essentially zero (an assumption of a Poisson process).
Since each subinterval is assumed to be independent of one another, then we can approximate the distribution of $X$ by using the binomial model with $n$ trials and probability of success $\frac{\lambda}{n}$. \[X \sim BIN(n,\pi=\lambda/n)\]
This approximation gets better as $n \rightarrow \infty$. When $n$ is very large relative to $x$ and recalling that \[e=\lim_{t \to 0} (1+t)^{1/t}=\lim_{n \to \infty}(1+\frac{1}{n})^n\] and that \[e^b=\lim_{n \to \infty} (1+\frac{b}{n})^n\] then

\[ \begin{aligned} P(X=x) & \approx{n \choose x}(\frac{\lambda}{n})^x (1-\frac{\lambda}{n})^{n-x} \\ & \approx \lim_{n \to \infty} \frac{n!}{x!(n-x)!} \frac{\lambda^x}{n^x} (1-\frac{\lambda}{n})^n (1-\frac{\lambda}{n})^{-x} \\ & = \lim_{n \to \infty} \frac{\lambda^x}{x!} \frac{n(n-1)\cdots(n-x+1)}{n^x} (1-\frac{\lambda}{n})^n (1-\frac{\lambda}{n})^{-x} \\ & = \frac{\lambda^x}{x!} \lim_{n \to \infty} \frac{n(n-1)\cdots(n-x+1)}{n^x} \lim_{n \to \infty} (1-\frac{\lambda}{n})^n \lim_{n \to \infty} (1-\frac{\lambda}{n})^{-x} \\ & = \frac{\lambda^x}{x!} \times 1 \times e^{-\lambda} \times 1 \\ & = \frac{e^{-\lambda} \lambda^x}{x!}, x=0,1,2,\cdots; \lambda>0 \\ \end{aligned} \]

Notice that \[\lim_{n \to \infty} \frac{n(n-1)\cdots(n-x+1)}{n^x} = \lim_{n \to \infty} [(\frac{n}{n})(\frac{n-1}{n})\cdots(\frac{n-x+1}{n})] = 1\]

There are situations where the Poisson distribution can be used to approximate a binomial distribution. The Poisson Limit Theorem states (without proof here) that as $n \rightarrow \infty$ and $p \rightarrow 0$ such that $np \rightarrow \lambda$, then \[\binom{n}{x}p^x (1-p)^{n-x} \rightarrow \frac{e^{-\lambda} \lambda^x}{x!}\] So, for large $n$ and small $p$, \[BIN(n,p) \rightarrow POI(\lambda=np)\] This approximation works well when $n \geq 100$ and $p \leq 0.05$.

As an example, suppose an email scammer sends $n=10000$ emails in an attempt to get people to reveal information. The email scammer will have a very low success rate, as most people will not fall for such a scam. Suppose $p=0.001$.

If we want to know $P(X=10)$ and $P(X \leq 10)$, we can try using the binomial distribution $X \sim BIN(n=10000,p=0.001)$ or the Poisson approximation $X \sim POI(\lambda=10)$.

To find $f(10)=P(X=10)$, you could use binompdf(10000,0.001,10) or poissonpdf(10,0.001) on a TI-84 calculator, or:

dbinom(x=10,size=10000,prob=0.001)

## [1] 0.1251726

dpois(x=10,lambda=10)

## [1] 0.12511

Note the Poisson approximation is accurate to 4 decimal places. To find $P(X \leq 10) = F(10)$, use binomcdf(10000,0.001,10) or poissoncdf(10,0.001) on the TI-84, or:

pbinom(q=10,size=10000,prob=0.001)

## [1] 0.5830398

ppois(q=10,lambda=10)

## [1] 0.5830398

Again, the Poisson distribution is very accurate.

Let’s plot the probability mass functions.

x <- 0:20
f.x1 <- dbinom(x=x,size=10000,p=0.001)
f.x2 <- dpois(x=x,lambda=10)
plot(f.x1~x,col="blue",type="h")
points(f.x2~x,col="red")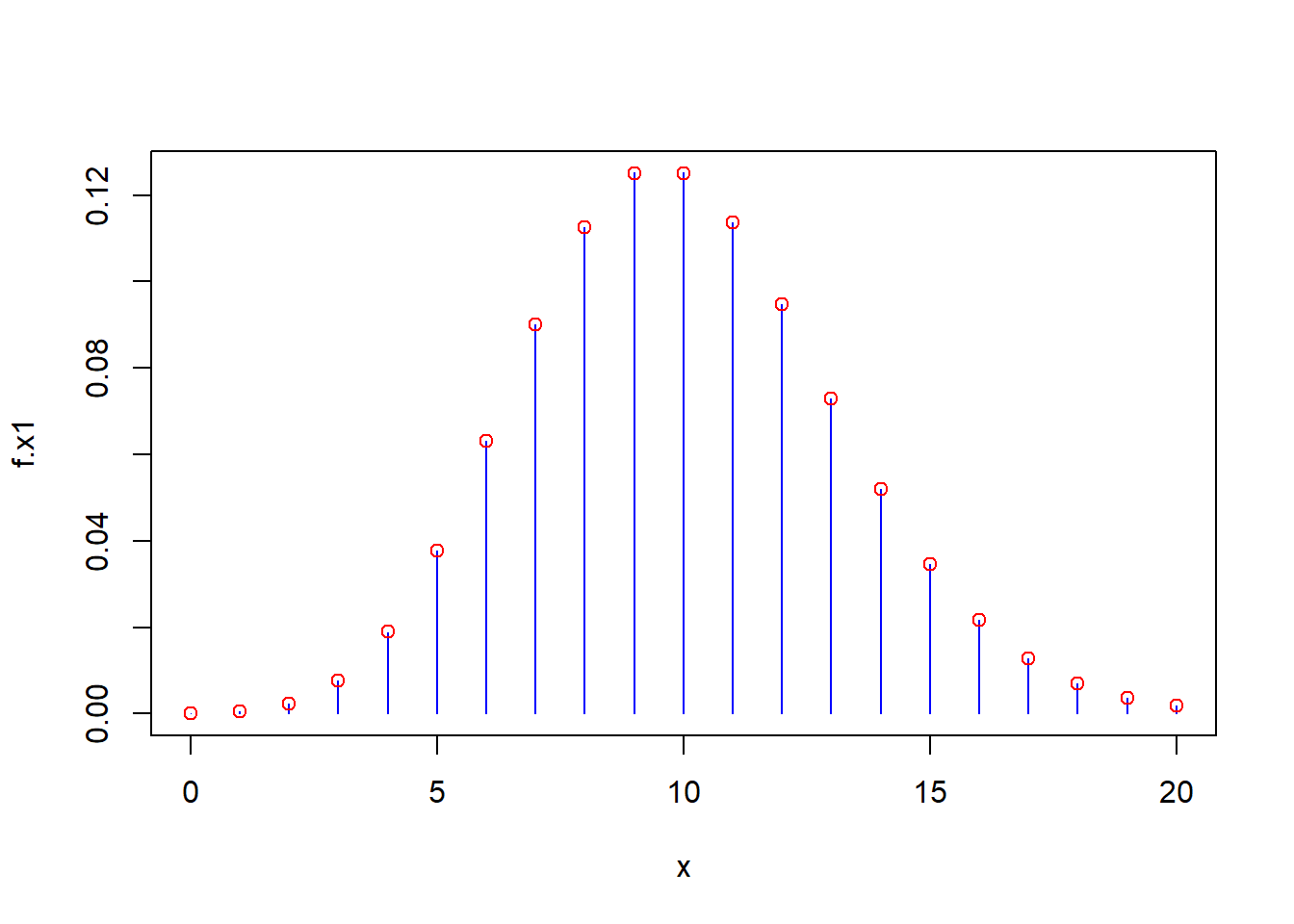

The red points (representing the Poisson probabilities) match the height of the blue spikes (the binomial probabilities) virtually exactly. You might notice the graph looks like a bell-shaped mound, and we’ll encounter that “normal” or “Gaussian” distribution soon.