第 2 章 R in OLS

下載

2.1 參考資料

2.2 setup

library("AER")
library("ggplot2")
library("dplyr")
library("knitr")

2.3 dataframe物件

data("Journals")

Journal這個dataframe的結構(structure)是什麼？有幾個變數？每個變數物件的類別(class)又是什麼？


找出Journal資料的詳細說明。

2.4 資料處理：產生新變數 dplyr::mutate

Journals %>% mutate(citeprice=price/citations) -> journals
summary(journals)

2.5 因果問句

期刊的價格(citeprice，平均文獻引用價格)如何影響其圖書館訂閱量(subs)?


library(psych)
journals %>% 
  select(citeprice,subs) %>%
  pairs.panels()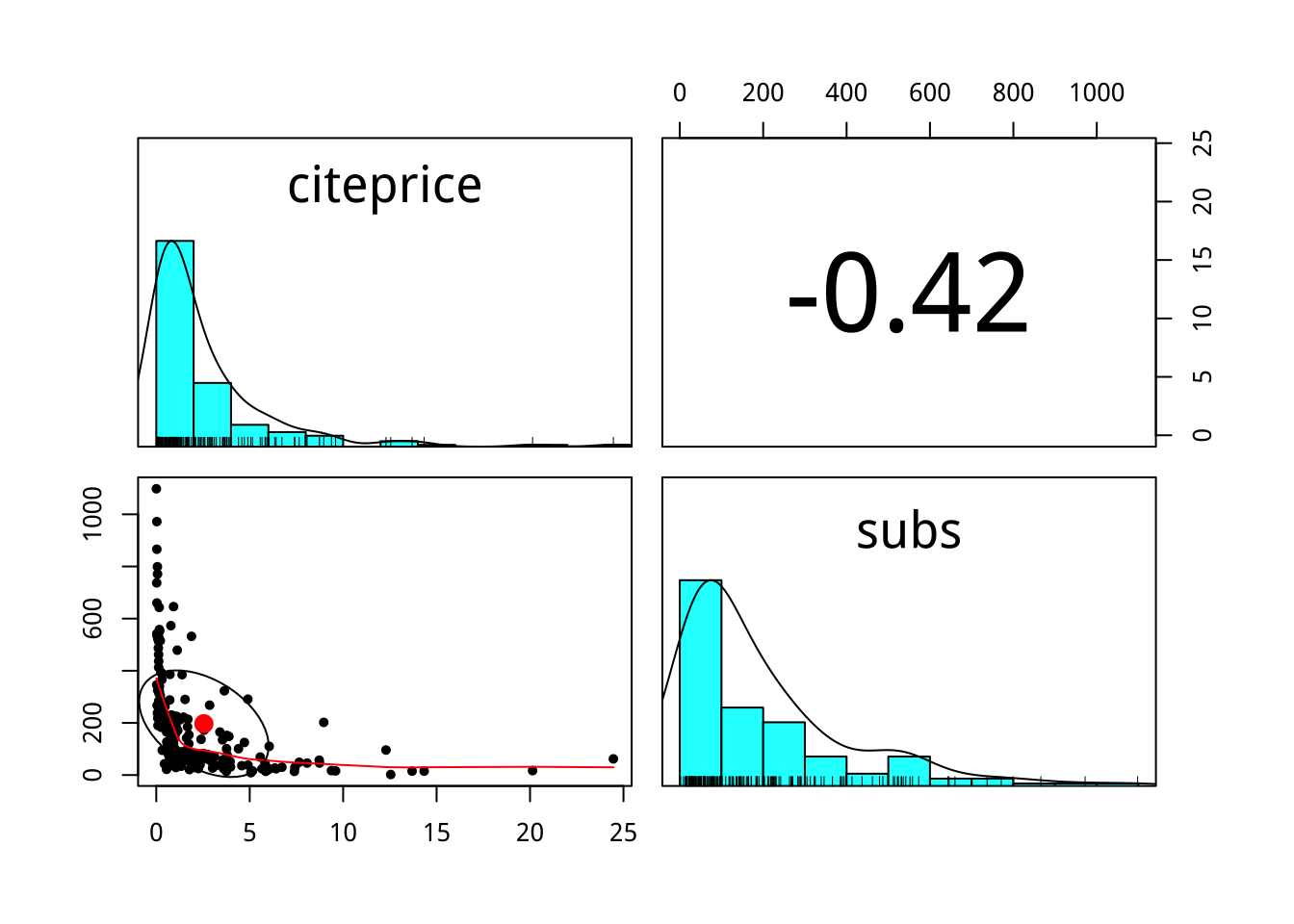

journals %>% 
  select(citeprice,subs) %>%
  mutate_all(log) %>%
  pairs.panels()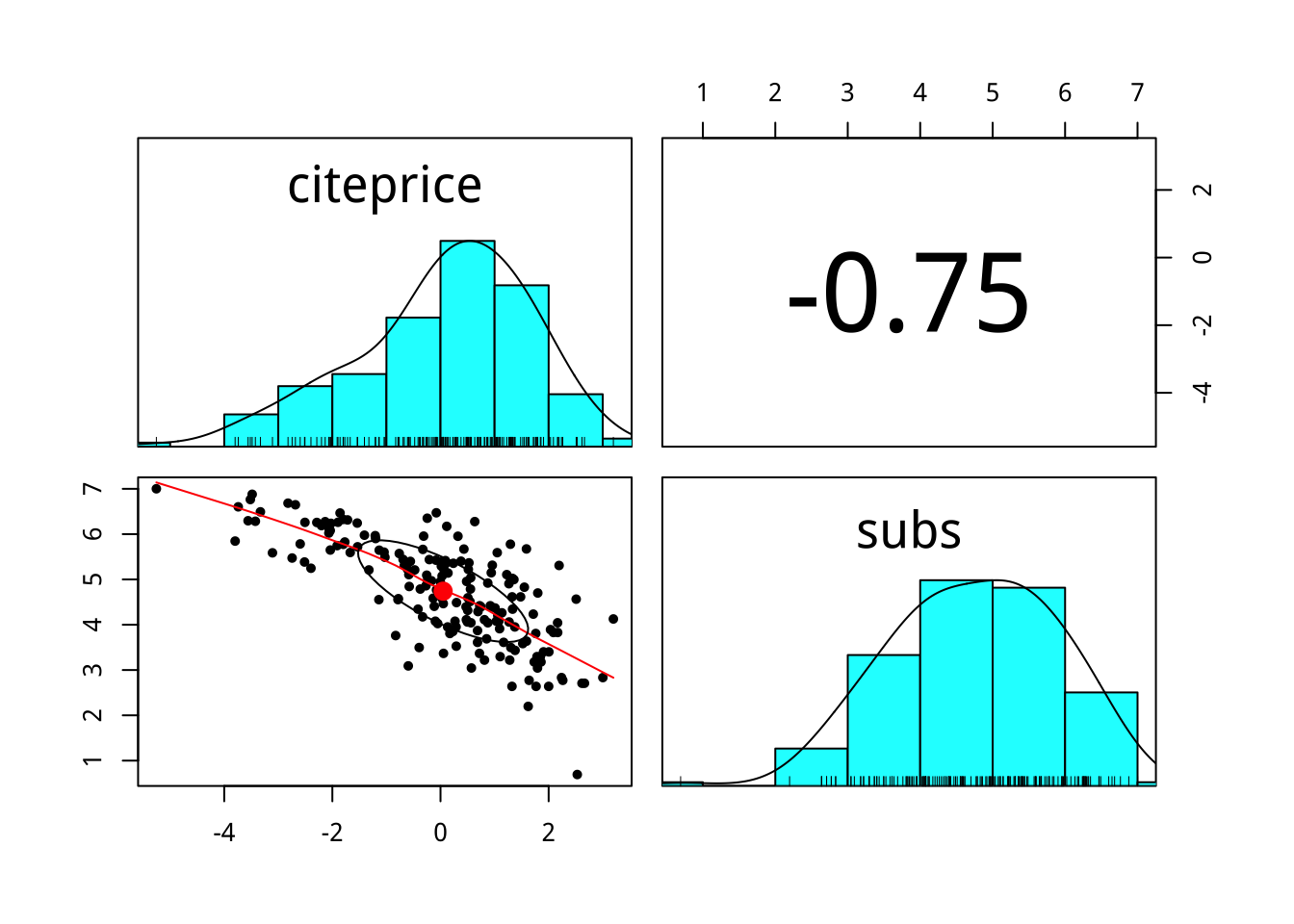

為什麼取log後，兩者的相關度變高？它表示兩個變數變得更不獨立嗎？

2.6 效應評估

當解釋變數並非直接代表有沒有受試的dummy variable(即只有0或1可能值)時，可以用以下的間斷例子來思考迴歸模型的係數含意：

假設\(P_i\)就只有高價（\(P_H\)）及低價（\(P_L\)）兩種，\(Y_{Hi},Y_{Li}\)分別代表期刊\(i\)在在高價及低價的訂閱量，我們觀察到的訂量\(Y_i\)只會是\(Y_{Hi},Y_{Li}\)其中一個。我們可以將\(Y_i\)與\(P_i\)寫成如下的效應關係：

\[Y_i=Y_{Li}+\frac{Y_{Hi}-Y_{Li}}{P_H-P_L}(P_i-P_L)\]

若假設價格對每個期刊帶來的單位變化固定，即： \[\frac{Y_{Hi}-Y_{Li}}{P_H-P_L}=\beta_1^*\]

則 \[Y_i=Y_{Li}+\beta_1^*(P_i-P_L)\]

單純比較不同「期刊價格」(citeprice)的期刊所獨得的圖書館「訂閱數」(subs)變化並無法反應真正的「期刊價格」效應，原因是「立足點」並不與「期刊價格」獨立。

這裡「立足點」指得是什麼？

「低價格下的訂閱數」（包含高價格期刊若採低價格的訂閱情境）。


你認為高價期刊，若採低價，它的訂閱數會與目前低價期刊相同嗎？為什麼？

2.7 進階關連分析

數值變數v.s.數值變數

# 判斷變數是否為數值類別
is_numeric<-function(x) all(is.numeric(x))
# 計算數數與citeprice的相關係數
cor_citeprice<-function(x) cor(x,journals$citeprice)

journals %>%  
  select_if(is_numeric) %>%
  summarise_all(cor_citeprice) %>%
  kable()

期刊越重要，其引用次數越高，因此高引用次數的期刊，你認為它在「低價格下的訂閱數」（立足點）會比較高還是低？


承上題，單純比較「期刊引用單價」高低間的「訂閱數量」差別，所估算出來的價格效果以絕對值來看會高估、還是低估？為什麼？

2.8 複迴歸模型

journals %>% 
  lm(log(subs)~log(citeprice),data=.) -> model1

journals %>%
  lm(log(subs)~log(citeprice)+foundingyear,data=.) -> model2

2.9 broom

  • tidy()

  • augment()

  • glance()

library(broom)
tidy(model1)
## # A tibble: 2 x 5
##   term           estimate std.error statistic   p.value
##   <chr>             <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept)       4.77     0.0559      85.2 2.95e-146
## 2 log(citeprice)   -0.533    0.0356     -15.0 2.56e- 33
augment(model1)
## # A tibble: 180 x 9
##    log.subs. log.citeprice. .fitted .se.fit .resid
##        <dbl>          <dbl>   <dbl>   <dbl>  <dbl>
##  1     2.64          1.77      3.82  0.0829 -1.18 
##  2     4.08         -0.0953    4.82  0.0561 -0.739
##  3     2.83          3.00      3.17  0.119  -0.332
##  4     0.693         2.53      3.42  0.105  -2.72 
##  5     4.56          2.51      3.43  0.104   1.14 
##  6     2.71          2.66      3.35  0.109  -0.639
##  7     2.64          1.32      4.06  0.0720 -1.42 
##  8     5.31          2.19      3.60  0.0946  1.71 
##  9     3.83          2.09      3.65  0.0917  0.176
## 10     3.83          2.17      3.61  0.0939  0.218
## # … with 170 more rows, and 4 more variables:
## #   .hat <dbl>, .sigma <dbl>, .cooksd <dbl>,
## #   .std.resid <dbl>
glance(model1)
## # A tibble: 1 x 11
##   r.squared adj.r.squared sigma statistic  p.value
##       <dbl>         <dbl> <dbl>     <dbl>    <dbl>
## 1     0.557         0.555 0.750      224. 2.56e-33
## # … with 6 more variables: df <int>, logLik <dbl>,
## #   AIC <dbl>, BIC <dbl>, deviance <dbl>,
## #   df.residual <int>

2.10 模型比較

journals %>% 
  lm(log(subs)~log(citeprice),data=.) -> model_1
journals %>%
  lm(log(subs)~log(citeprice)+foundingyear,data=.) -> model_2

library(sandwich)
library(lmtest)
library(stargazer)

#使用vcovHC函數來計算HC1型的異質變異（即橫斷面資料下的線性迴歸模型）
coeftest(model_1, vcov. = vcovHC, type="HC1") -> model_1_coeftest
coeftest(model_2, vcov. = vcovHC, type="HC1") -> model_2_coeftest

stargazer(model_1, model_2, 
          se=list(model_1_coeftest[,"Std. Error"], model_2_coeftest[,2]),
          type="html",
          align=TRUE)

關於vcovHC()更多type的探討，請見： Zeileis A (2006), Object-Oriented Computation of Sandwich Estimators. Journal of Statistical Software, 16(9), 1–16. URL http://www.jstatsoft.org/v16/i09/.