第 3 章 IV

3.1 效應評估模型

提高香煙（含稅）售價對香煙銷售量的影響？

假設香煙銷售量\(Y_i\)與香煙售價\(P_i\)的因果模型可以寫成：

\[Y_{i}={Y}_{-p,i}+\beta_iP_{i}\]

其中\(Y_{-p,i}\)代表i州的「非價格催生之香煙銷售量」，也就是價格「以外」的其他因素所決定之銷量。

假設齊質價格效果：\(\beta_i=\beta\)

則因果模型可以寫成：

\[ Y_{i}={Y}_{-p,i}+\beta P_{i}\]

在做效應評估時，只有因果關係式的\(\beta\)值才是「真實」值。

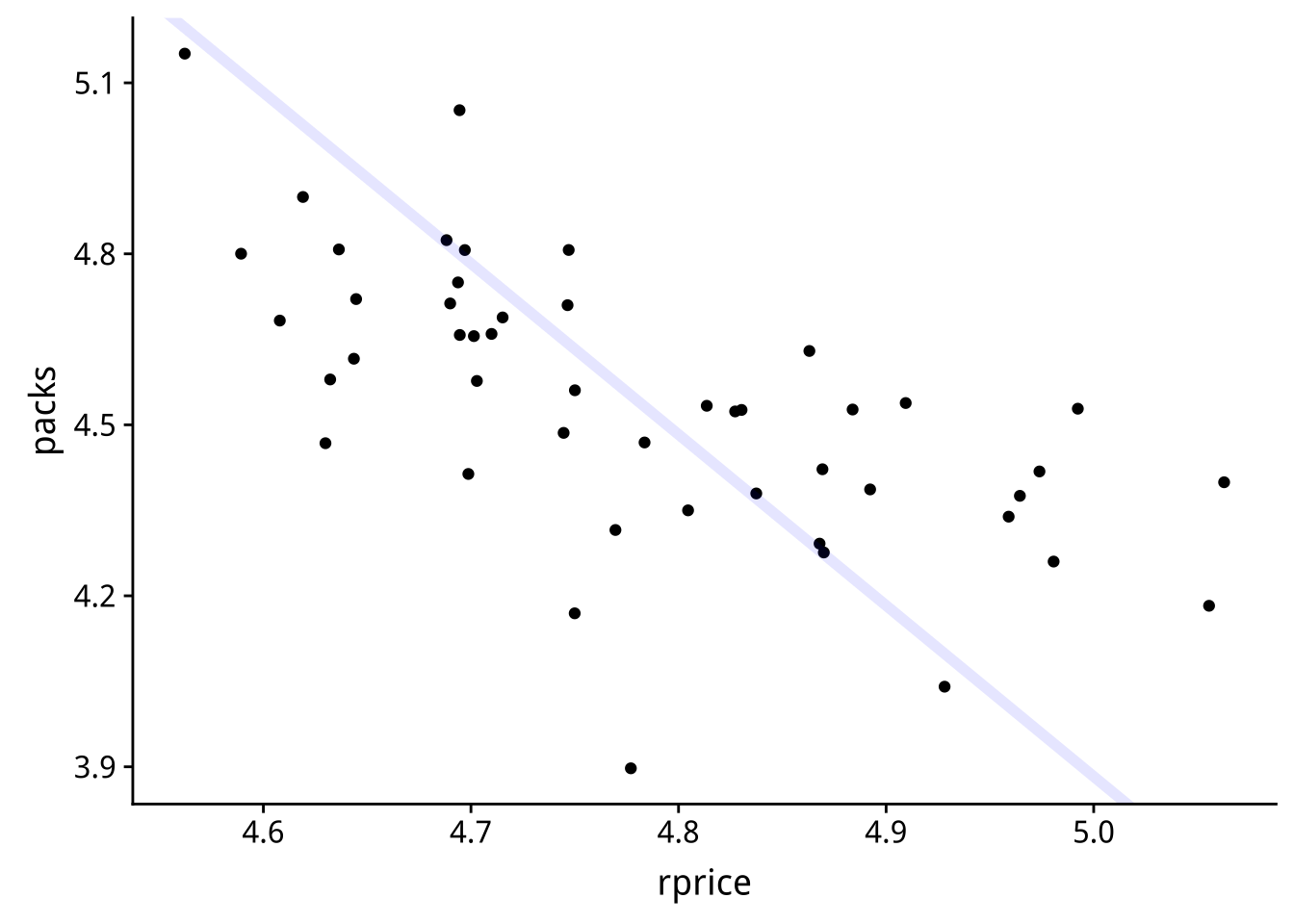
真實效應(淺藍線)與資料

圖 3.1: 真實效應(淺藍線)與資料

3.2 最小平方法估計式

為方便討論，我們進一步去除下標0：

\[ Y_{i}={Y}_{-p,i}+\beta P_{i}\]

考慮最小平方法估計式： \[\hat{\beta}=\frac{\sum_i(Y_i-\bar{Y})(P_i-\bar{P})}{\sum_i(P_i-\bar{P})^2}\] 經過整理： \[ \hat{\beta}=\sum_{i}\left\{ \frac{(P_{i}-\bar{P})^{2}}{\sum_{i}(P_{i}-\bar{P})^{2}}\right\} \times\frac{(Y_{i}-\bar{Y})}{(P_{i}-\bar{P})} \]

它的幾何意義是什麼？

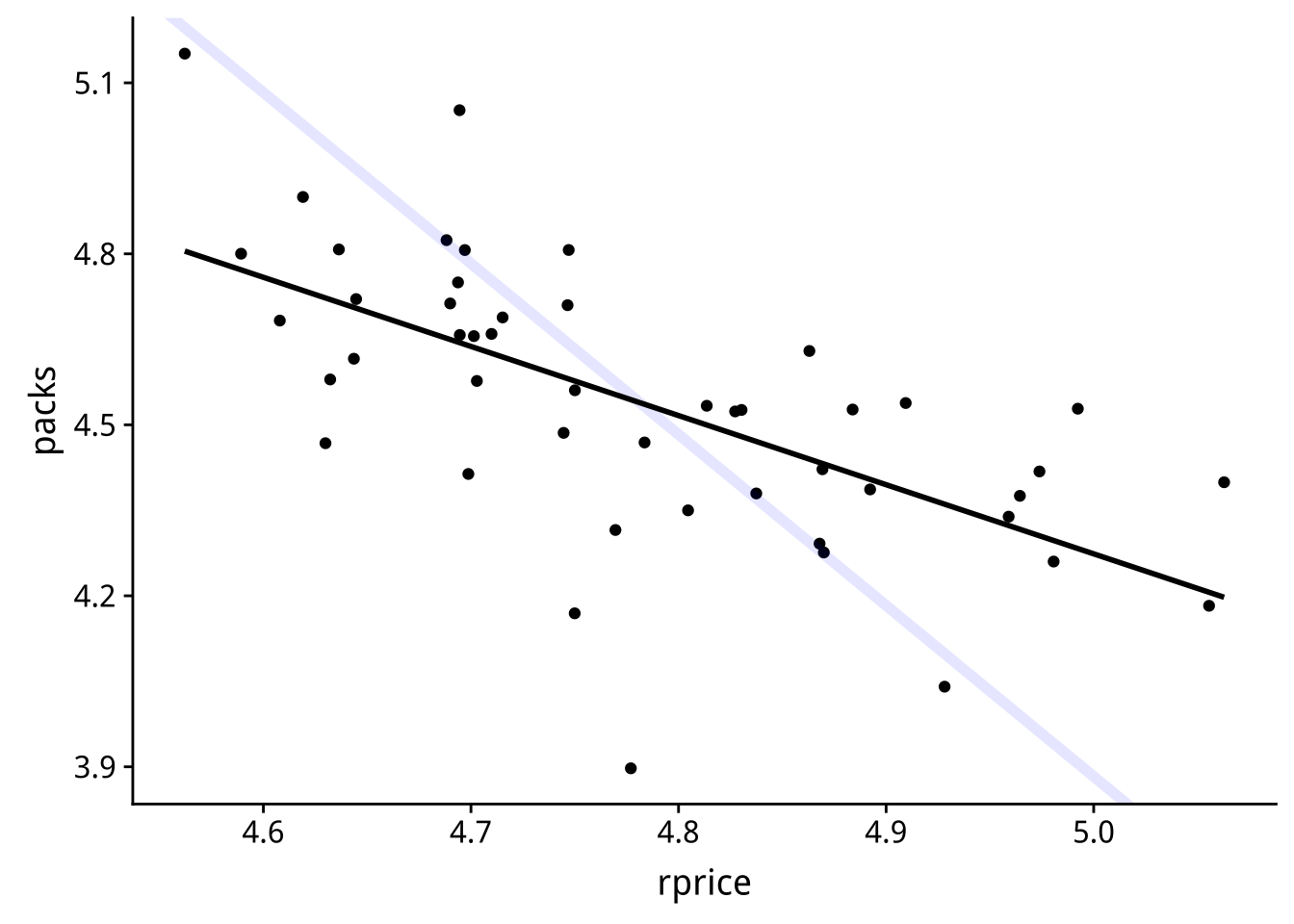
一般化最小平方法（OLS）的斜率項估計式是所有觀測點與平均點連線斜率的「加權平均」。


OLS估試式的斜率會比真實質陡還是緩？

3.3 選擇性偏誤

下圖是GA和MA兩州的香煙訂價與銷量：

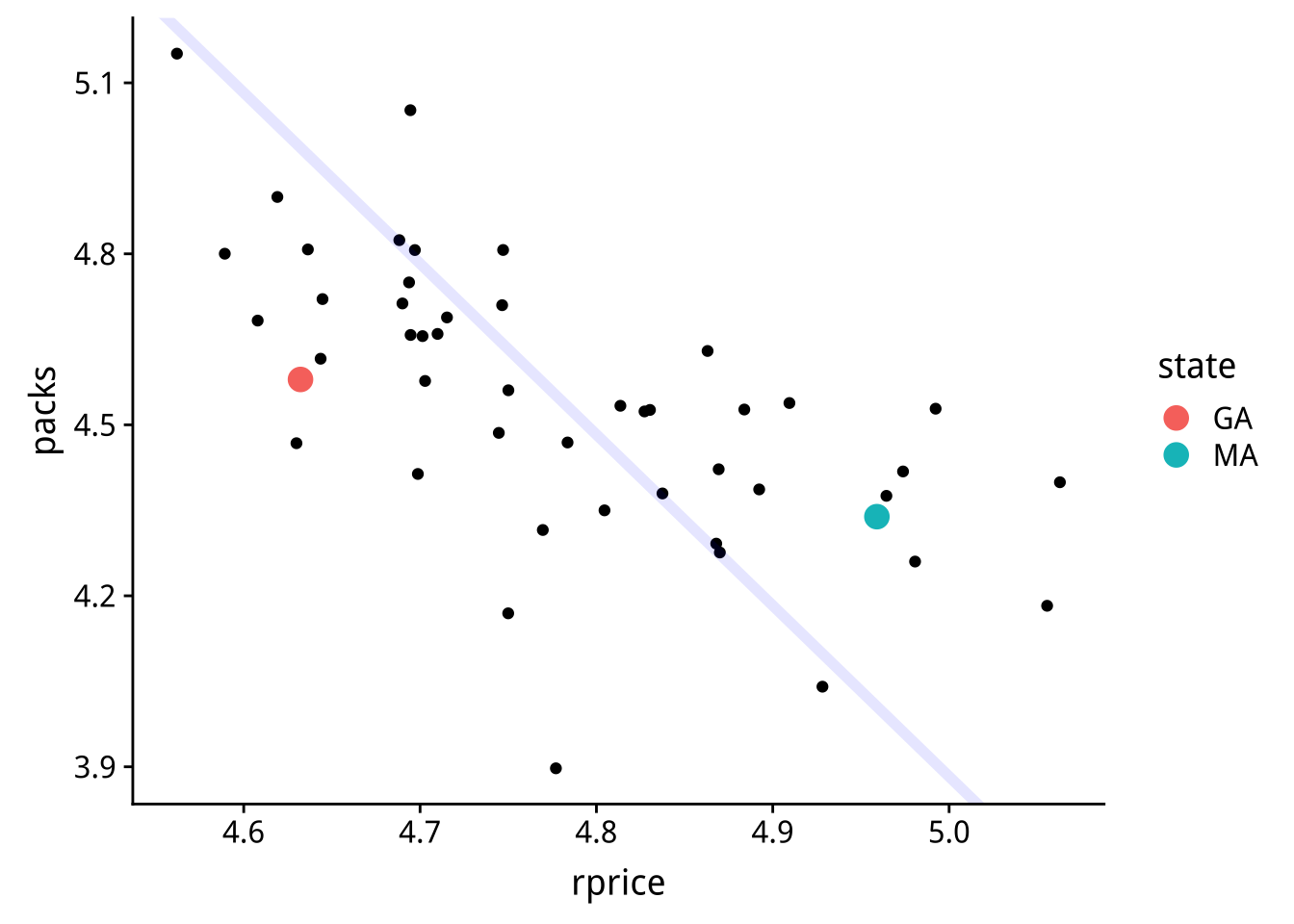
請問這兩州「售價（\(P_i\)）」與「非售價效應之銷量（\(Y_{-p,i}\)）之間有什麼關連？整體來看（所有觀測點），兩者間的關連性為何？

麻州「售價（\(P\)）」較高，同時「非售價效應之銷量（\(Y_{-p}\)）」也比較高。整體來看兩者間有正向關連。


注意這裡我們是先假設我們已經知道真實值（藍線），這樣才能得知以上\(P\)與\(Y_{-p}\)有關（即選擇性偏誤）的觀察，現實應用上是不可能的，只能用邏輯判斷是否有此偏誤可能。

3.4 複迴歸模型

邏輯推論潛在「選擇性偏誤」

一個造成\(P\)與\(Y_{-p}\)有正向關連的可能原因是影響\(Y_{-p}\)的「州所得(rincome)」。下圖顯示「州所得(rincome)」，與香煙售價及售量的關係。

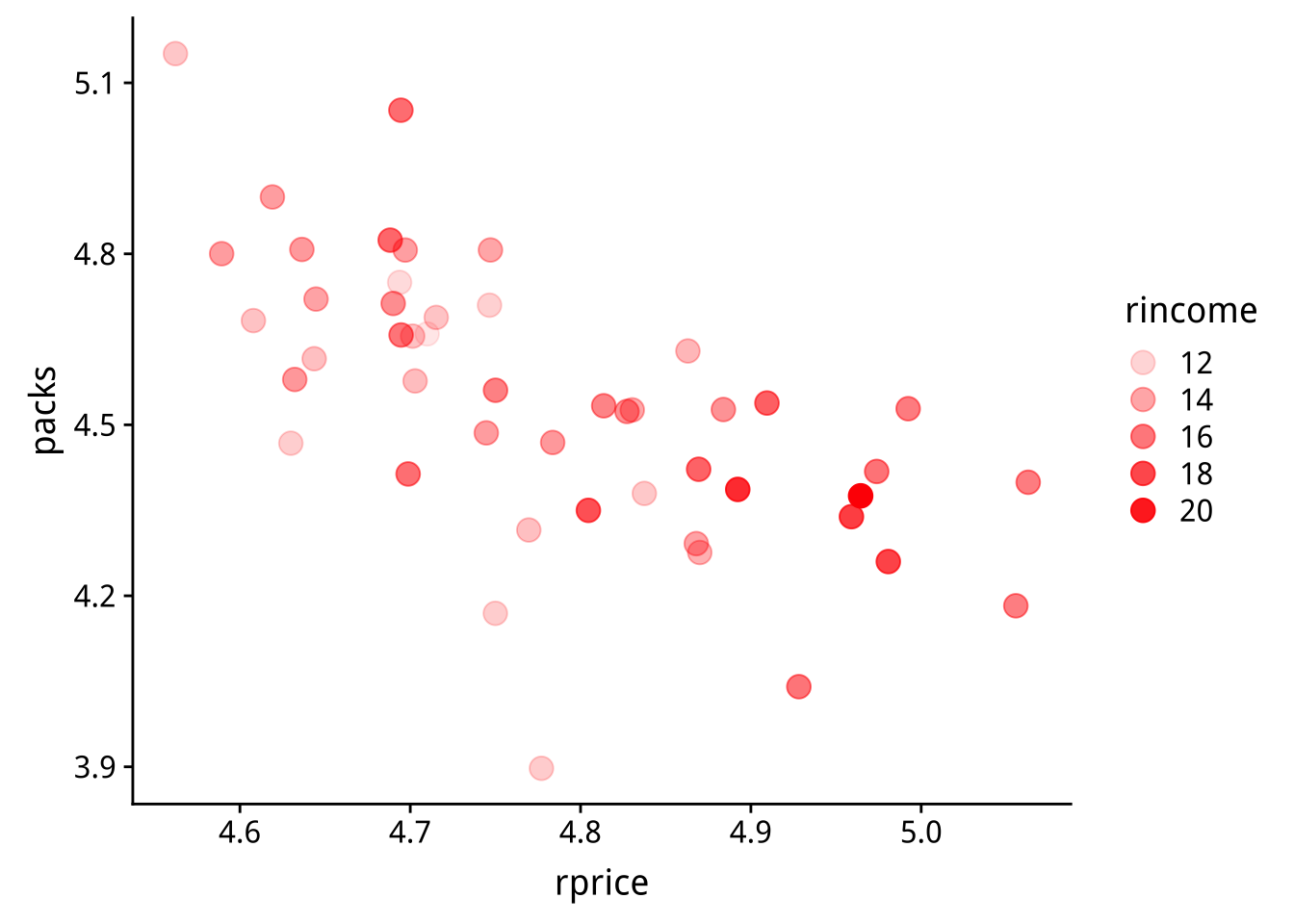
你觀察到什麼？它在「售價」與「非價格效應的銷售量」的關連上扮演什麼經濟直觀角色？

深紅色在圖面偏右上塊，有可能「所得」越高的州越負擔得起香煙，故香煙「售價」及「銷售」都會比較高。


因此我們在估算效應模型時，至少得加入rincome變數： \[\begin{equation} Y_i=\beta_0+\beta_1P_i+\beta_2 rincome+\varepsilon \tag{3.1} \end{equation}\] 以上只是基本要有的複迴歸模型，當然導致「香煙價格(\(P_i\))」與「非價格效應的銷售量(\(Y_i\))」相關的因素不只有「州所得(rincome)」，其他有可能的因素都要不斷加入擴充複迴歸模型。

由於選擇性偏誤指\(Y_{-p}\)中有些影響變數，如「州所得」，會同時影響\(P\)，在迴歸時若不包含「州所得」於迴歸模型中會造成\(P\)的效應估計偏誤，故選擇性偏誤又稱「遺漏變數偏誤」（Omitted variable bias）。

以下面的模型為例， \[\begin{equation} Y_i=\beta_0+\beta_1P_i+w_i'\gamma+\varepsilon \tag{3.2} \end{equation}\] 複迴歸模型下的OLS估計若可以得到效應評估模型下的\(\beta\)合理估計，

它所要求的條件是什麼？

在\(w_i\)條件下，「香煙售價」(\(P_i\))必需要與「非價格效應的香煙銷售量」(\(Y_{-p,i}\)) 獨立，即： \[P_i\perp Y_{-p,i} | w_i\] 另一個同義說法是：「香煙售價」(\(P_i\))必需要與「控制\(w_i\)條件後的非價格效應香煙銷售量」獨立。

變數訊息拆解

考慮效應模型： \[Y_i=Y_{-P,i}+\beta^* P_i\] 對\(Y_{-P}\)進行rincome條件下的訊息拆解： \[\begin{equation} Y_{i}=Y_{-P,i}-\mathbb{E}(Y_{-P,i}|rincome_{i})+\beta^{*}P_{i}+\mathbb{E}(Y_{-P,i}|rincome_{i}) \tag{3.3} \end{equation}\]

對照(3.3)，(3.1)迴歸模型的誤差項\(\epsilon\)及控制項\(\beta_0+\beta_2 rincome\)分別代表(3.3)效應模型中的什麼？

\(\epsilon=Y_{-P,i}-\mathbb{E}(Y_{-P,i}|rincome_{i})\), \(\beta_0+\beta_2 rincome=\mathbb{E}(Y_{-P,i}|rincome_{i})\); 後者還需要條件期望值的函數形式為線性的假設。


複迴歸模型下的最小平方估計是在進行\(\mathbb{E}(Y|\mbox{all regressors})\)的母體迴歸線估計。

對照(3.3)，這裡\(\mathbb{E}(Y_i|P_i,rincome_i)\)會等於什麼？

\[\begin{align*} \mathbb{E}\left(Y_{-P,i}-\mathbb{E}(Y_{-P,i}|rincome_{i})|P_{i},rincome_{i}\right)\\ = & \mathbb{E}\left(Y_{-P,i}|P_{i},rincome_{i}\right)-\mathbb{E}\left(\mathbb{E}(Y_{-P,i}|rincome_{i})|P_{i},rincome_{i}\right)\\ = & \mathbb{E}\left(Y_{-P,i}|P_{i},rincome_{i}\right)-\mathbb{E}(Y_{-P,i}|rincome_{i})\\ = & \mathbb{E}\left(Y_{-P,i}|P_{i},rincome_{i}\right)-\mathbb{E}(Y_{-P,i}|rincome_{i}) \end{align*}\] 故 \[\mathbb{E}(Y_{i}|P_{i},rincome_{i})=\beta_{0}+\beta^{*}P_{i}+\beta_{2}rincome_{i}+\mathbb{E}\left(Y_{-P,i}|P_{i},rincome_{i}\right)-\mathbb{E}(Y_{-P,i}|rincome_{i})\]


若我們相信：

控制「州所得(rincome)」後「香煙售價(P)」與「非香煙售價效果的銷售量(\(Y_{-P}\))」無關

則：

\(\mathbb{E}(Y_i|P_i,rincome_i)\)會等於什麼？

此時\[\mathbb{E}\left(Y_{-P,i}|P_{i},rincome_{i}\right)-\mathbb{E}(Y_{-P,i}|rincome_{i})=0\] 故 \[\mathbb{E}(Y_{i}|P_{i},rincome_{i})=\beta_{0}+\beta^{*}P_{i}+\beta_{2}rincome_{i}\] 因此(3.2)迴歸模型的\(\beta_1=\beta^*\)，即最小平方法所估計的\(\beta_1\)會代表效應值\(\beta^*\)。

3.5 工具變數

  • 複迴歸模型

    把資料依\(w_i\)條件變數不同, 分群觀察「香煙售價」(\(P_i\))與「香煙銷售量」(\(Y_i\))之間的斜率。如果\(w_i\)變數選得好，同一群資料\(P_i\)與\(Y_i\)間的關連會反映應有的效應斜率——雖然有時\(Y_i\)會因為\(Y_{-p,i}\)的干擾影響我們對斜率高低的觀察，但因為\(Y_{-p,i}\)不會與\(P_i\)有關了，這些觀察干擾在大樣本下會互相抵消掉而還原應有的效應斜率值。

如果不管我們怎麼選擇\(w_i\)還是無法控制住\(Y_{-p,i}\)對\(P_i\)與\(Y_i\)關連的干擾，那我們就要進行【資料轉換】直接從原始資料中【去除這些干擾】，其中最常見的兩種去除法為：工具變數法、追蹤資料固定效果模型。

  • 工具變數法：透過工具變數留下\(P\)不與\(Y_{-p}\)相關的部份。

  • 追蹤資料：透過變數轉換去除\(P\)中與\(Y_{-p}\)相關的部份。

變數訊息拆解

\[Y_i=Y_{-p,i}+\beta P_i\] 考慮使用變數\(z_i\)來對\(P_i\)進行訊息拆解。

拆解結果為何？

\(P_i=\mathbb{E}(P_i|z_i)+(P_i-\mathbb{E}(P_i|z_i))\).


藉由訊息拆解， \[Y_i=Y_{-p,i}+\beta\mathbb{E}(P_i|z_i)+\beta (P_i-\mathbb{E}(P_i|z_i))\]

3.5.1 相關性條件(Relevance condition)

若\(z\)對\(P\)具有訊息價值，則:

\(\mathbb{E}(P|z)\neq\) 常數

3.5.2 排除條件(Exclusion condition)

若\(z\)與\(Y_{-p}\)無關, 則:

\(Y_{-p,i}+\beta(P_i-\mathbb{E}(P_i|z_i))\)與\(z_i\)無關。

令 \[P_z\equiv\mathbb{E}(P|z)\] \[Y_{-P_z}\equiv Y_{-p}+\beta(P-\mathbb{E}(P|z))\] 則 \[Y=Y_{-P_z}+\beta P_z\]

上述表示式裡，\(Y_{-P_z}\)與\(P_z\)會無關嗎？

會。

3.5.3 兩階段最小平方法

  1. 第一階段：取得\(P_z\)估計
  2. 第二階段：以\(P_z\)為\(Y\)的解釋變數，進行OLS估計

為什麼第二階段可以得到效應值\(\beta\)的合理（一致性）估計？排除條件和相關性條件各用在哪裡來保證估計式的一致性？

工具變數：香煙稅

為什麼香煙稅可排除「非價格效應的銷售量（\(Y_{-p}\)）」？

因為售價含稅，若香煙稅會影響「非價格效應的銷售量（\(Y_{-p}\)）」，表示同樣消費者要實付10美元一包的香煙，他會因為被政府拿走多少而改變他的購買意願——不太可能。


為什麼香煙稅滿足認定條件？

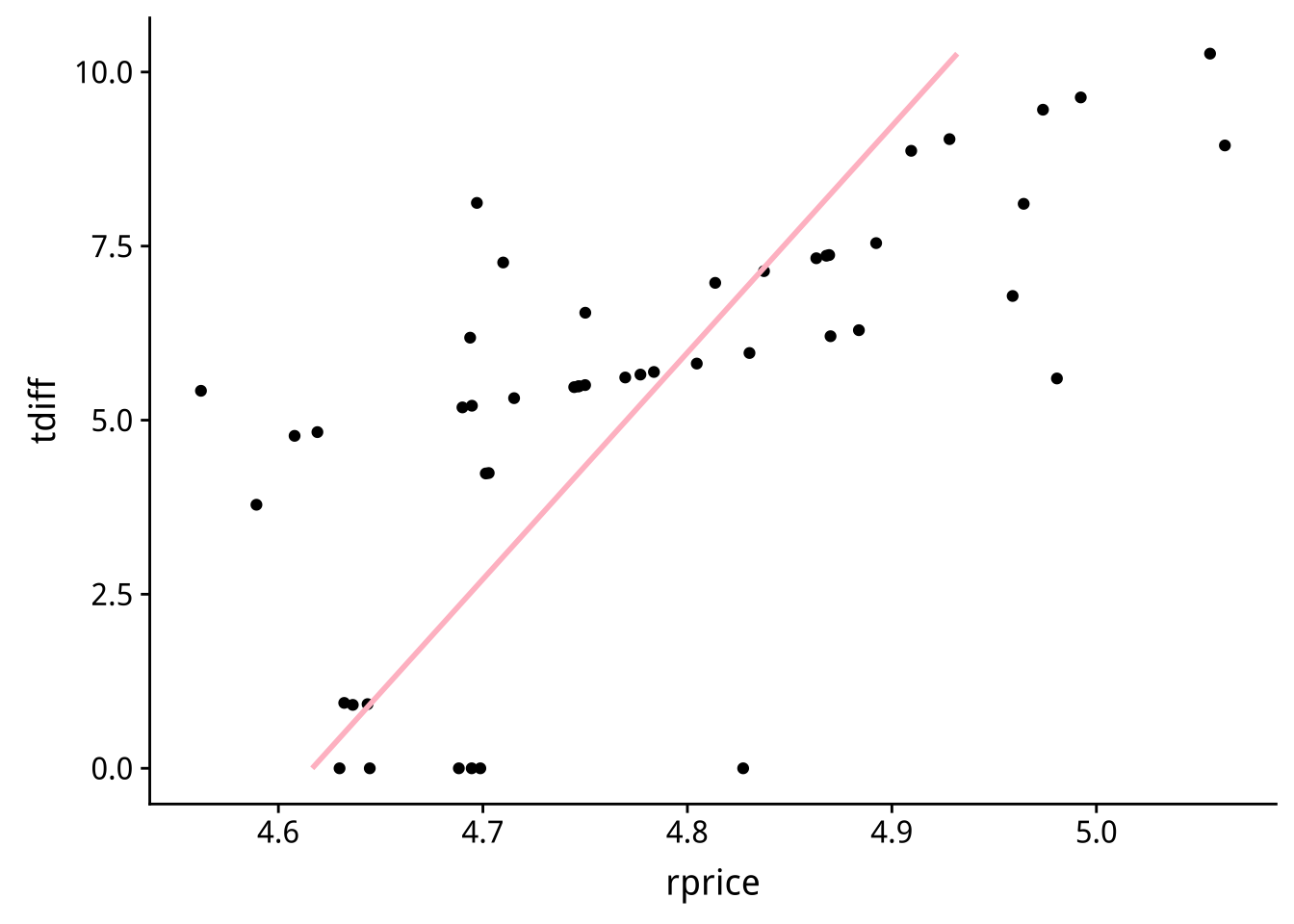
認定條件：香煙稅率（tdiff）與香煙價格（rprice）

圖 3.2: 認定條件：香煙稅率（tdiff）與香煙價格（rprice）

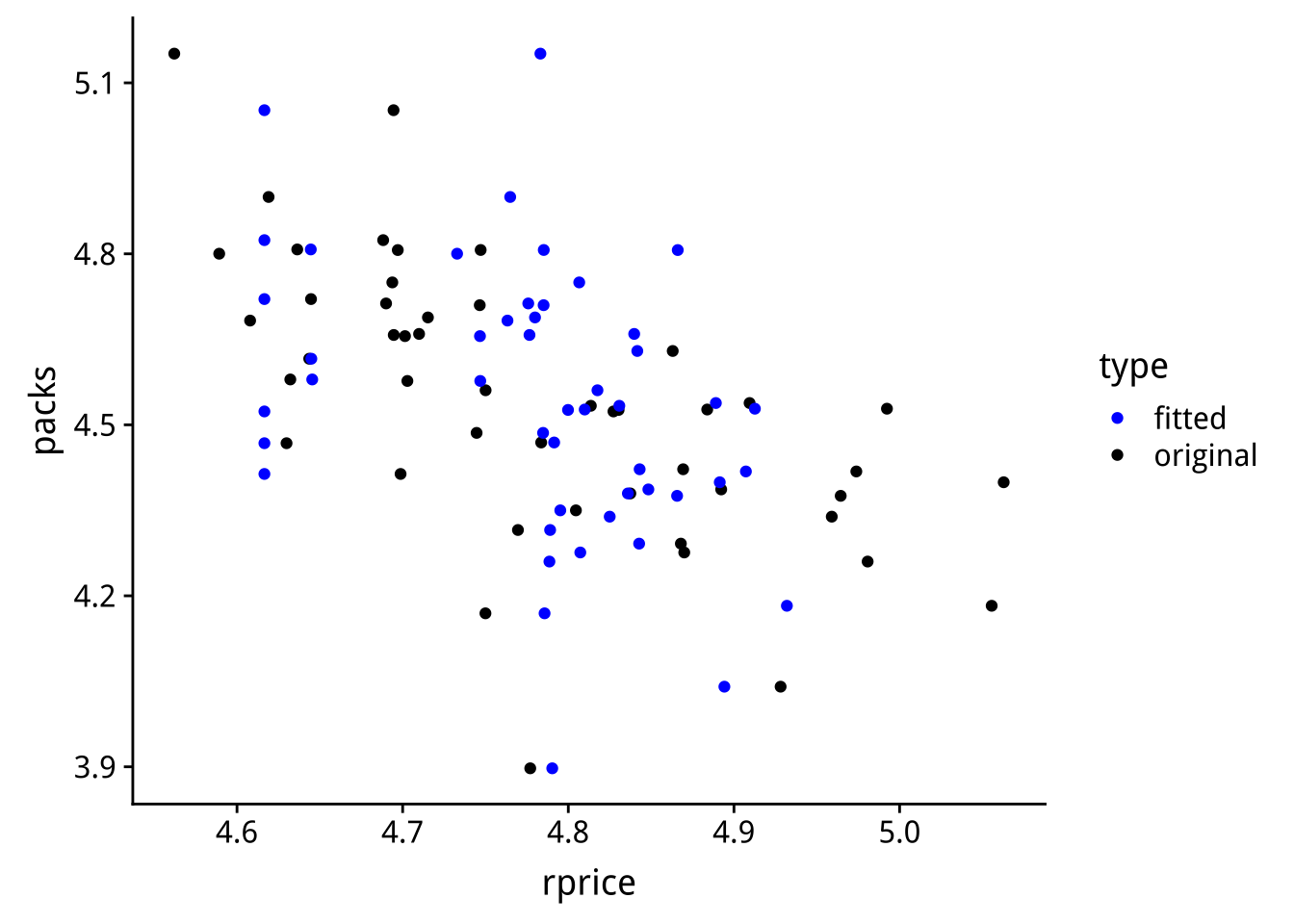
原始資料的關連(original)與只留下工具變數所造成的關連(fitted)

圖 3.3: 原始資料的關連(original)與只留下工具變數所造成的關連(fitted)

由於「藍色」的資料是由工具變數「香煙稅」所造成的「香煙（含稅）售價」變動，而「香煙稅」並不與「非價格效應的香煙售量」有關，所以「藍色」資料所呈現的「香煙價格」與「香煙售量」的關連較能反應價格對售量的效應。

3.6 兩階段最小平方法

考慮一個廣義的迴歸模型： \[\begin{equation} \underset{1\times1}{\underbrace{Y_{i}}}=\underset{1\times K}{\underbrace{X_i^{'}}\beta}+\underset{1\times P}{\underbrace{W_i^{'}}\gamma}+\underset{1\times1}{\underbrace{\epsilon_{i}}}, \tag{3.4} \end{equation}\] 其中\(X\)為要進行效應評估的變數群，\(W\)為控制變數群，故\(\epsilon\)為「\(W\)控制條件下排除\(X\)效果的Y值」。

我們面臨無法產生條件式獨立的問題，即

\[X_i\not\perp\epsilon_{i} | W_i.\] 也可寫成\(\mathbb{E}(\epsilon_i|X_i,W_i)\neq\mathbb{E}(\epsilon_i|W_i)\)。

注意：根據訊息拆解，\(\epsilon_i\)會與\(W_i\)無關，即\(\mathbb{E}(\epsilon_i|W_i)=0\).

請問\(W_i\)本身會是合格的工具變數嗎？

會～～～！


令\(z_{i}(M\times1)\)為另外找的工具變數（如香煙稅），則我們可用的工具變數群可以寫成更大的\({\bf Z}_{i}\)（包含了控制變數群，例如香煙稅和州所得一起當工具變數），其中

\[{\bf Z}_{i}: {\bf Z}_{i}(\left(M+P\right)\times1) =\left[\begin{array}{c} z_{i}\\ W_i \end{array}\right], {\bf Z}(n\times\left(M+P\right)) =\left[\begin{array}{c} {\bf Z}_{1}'\\ \vdots\\ {\bf Z}_{n}' \end{array}\right].\]

兩階段最小平方法(Two-stage least square estimation, TSLS)：

  1. X 迴歸在 \({\bf Z}\Rightarrow\hat{\gamma}=({\bf Z}^{'}{\bf Z})^{^{-1}}({\bf Z}^{'}X)\Rightarrow\hat{X}={\bf Z}\hat{\gamma}\)

  2. Y 迴歸在工具變數保留下的\(\hat{X}\)和控制變數\(W\) \(\Rightarrow\hat{\beta}_{IV}\)

3.7 認定條件

在香煙的例子，即然控制變數「州所得」是合格的工具變數，那可不可以不用再找其他工具變數（即不使用「香煙稅」）來進行TSLS估計？

不行！在第二階段迴歸會有完美線性(perfect multicollinearity)重合問題。


在廣義的(3.4)模型下，要額外找的工具變數數目要大於等於K。

3.8 幾個範例

Endogeneity Bias

One common source of OVB is Endogeneity Bias.

Exercise. \[\begin{cases} Supply\ function\ : & Q_{i}=\alpha P_{i}+\epsilon_{i}^{S},\\ Demand\ function\ : & P_{i}=\beta Q_{i}+\epsilon_{i}^{D} \end{cases} \]

Both prices and quantities are endogenous. In other words,\(P_{i} =P(\alpha,\beta,\epsilon_{i}^{S},\epsilon_{i}^{D})\) \(Q_{i} =Q(\alpha,\beta,\epsilon_{i}^{S},\epsilon_{i}^{D})\)

To be precise, their solutions are: \[Q_{i} =\alpha(\beta Q_{i}+\epsilon_{i}^{D})+\epsilon_{i}^{S}\Rightarrow Q_{i}=\frac{\alpha\epsilon_{i}^{D}+\epsilon_{i}^{s}}{1-\alpha\beta},\] \[P_{i} =\beta[\frac{\alpha\epsilon_{i}^{D}+\epsilon_{i}^{S}}{1-\alpha\beta}]+\epsilon_{i}^{D}.\] Regressing \(P_{i}\) on \(Q_{i}\) does not give you consistent estimate of \(\beta\) on the demand function since \(Q_{i}\not\perp\epsilon_{i}^{D}\).Regressing \(Q_{i}\) on \(P_{i}\) does not give you consistent estimate of \(\alpha\) on the supply function either since \(P_{i}\not\perp\epsilon_{i}^{S}\).

Neutrality of money

\(\frac{\bigtriangleup Y}{Y}=\alpha_{0}+\alpha_{1}\cdot\frac{\bigtriangleup M}{M}+u\)

Income normally affect demand but not supply. It is intuitive to assume \(I_{i}\perp\varepsilon_{i}^{s}\). As a result, it can be an IV for \(P_{i}\) in the supply function.

TSLS:

  1. \(P_{i}\) regresses on \(I_{i}\Rightarrow\hat{P_{i}}\Rightarrow\)recover the change of \(P_{i}\) that is solely due to the demand side change, i.e. controling Supply side, only move Demand side

  2. \(Q_{i}=\alpha\hat{P_{i}}+\varepsilon_{i}^{s}\). (\(Q_{i}\),\(\hat{P_{i}}\)) variation is coming from the demand side variation

Labor supply and labor demand

Labor Supply: \[wks=r_{1}+r_{2}\ln wage+r_{3}Ed+r_{4}union+r_{5}Fem+u^{S}.\]

Labor Demand: \[\ln wage =\beta_{1}+\beta_{2}wks+\beta_{3}Exp+\beta_{4}Exp^{2}+\beta_{5}Occ +\beta_{6}Ind+\beta_{7}SMSA+u^{D}.\]

To estimate labor supply,

• \(Z_{1}=\left[Ind\ |\ Ed,\ union,\ Fem\right]\): Exactly identified.

• \(Z_{2}=\left[Ind,\ SMSA\ |\ Ed,\ union,\ Fem\right]\): Overly identified.

How about estimating labor demand?

3.9 最小平方法的幾何意義

以三筆資料，二個變數為例

target_y regressor_x1 iv_z1 iv_z2
-0.1012 -2.3024 -0.4458 0.6394
-0.5270 -0.2312 -1.2059 -0.7866
-1.4004 -0.3679 0.0411 -0.3855

  1. 每筆資料是一個點

    • 圖面維度：資料變數個數決定

    • 範例: 呈現y, x1兩個變數；3筆資料

  1. 每個變數是一個點

    • 圖面維度：由資料樣本數決定

    • 範例：呈現3筆資料；顯示2個變數

正交投射

兩個向量X,Y若正交（orthogonal），則\(X'Y=0\)。

迴歸模型： \[Y=X\beta+\varepsilon\]
證明：使誤差平方和（即\((Y-\hat{Y})'(Y-\hat{Y})\)）極小的\(\hat{\beta}\)，將使\((Y-\hat{Y})\)與\(X\)正交。

範例1：最小平方法

\[ Y=\beta X1+\epsilon\]

範例2：一個工具變數下的TSLS

一個工具變數：\(Z1\)

範例3：二個工具變數下的TSLS

一個工具變數：\(Z1\)，\(Z2\)

3.10 三個檢定

\[\begin{equation} Y_i=\beta_0+\beta_1 P_i + \gamma_1 rincome_i + \epsilon_i \tag{3.5} \end{equation}\] 其中\(\epsilon=Y_{-P}-\mathbb{E}(Y_{-P}|rincome)-\beta_0\)，即「非售價因素銷量」扣除「州所得」可補捉的部份，簡稱為「控制州所得條件下的非售價因素銷量」。上面的迴歸式，OLS\(\hat{\beta}_1\)若要能代表價格效應，我們需要\(P_i\)與\(\epsilon_i\)無關。

Q1: 我的工具變數有滿足排除條件（或外生條件）嗎?

香煙稅是否與控制條件下的「非售價因素銷售」無關？

Q2: 我的工具變數關聯性夠強嗎？

香煙稅真的與「售價」很有關連嗎？

Q3: 我對遺漏變數偏誤的擔心是否多餘？

或許根本沒有必要用工具變數，在(3.5)迴歸模型下，\(P\)早已和\(\epsilon\)（即「控制條件下的非售價因素銷售」）無關——直接對(3.5)進行最小平方法估計即可。

Q1: 排除條件檢定

Q1: 我的工具變數有滿足排除條件（或外生條件）嗎?

考慮如下的複迴歸模型： \[Y =\underset{(\times k)}{X}\beta+\underset{(\times p)}{W}\gamma +\epsilon\] 其中\(X\)為要進行效應評估的變數群，\(W\)為控制變數群，故\(\epsilon\)為「\(W\)控制條件下排除\(X\)效果的Y值」。另外，我們額外找了工具變數: \(\underset{\times m)}{Z}\), 要驗證：

\({\bf H}_0\): 工具變數\(Z\)與迴歸模型誤差項\(\epsilon\)無關

  1. 進行TSLS，取得 \(\hat{\epsilon}_{_{TSLS}}=Y-\hat{Y}_{TSLS}\).

  2. 將\(\hat{\epsilon}_{TSLS}\)迴歸在總工具變數群（即\(Z\)與\(W\)）並進行所有係數為0的聯立檢定，計算檢定量 \(J=mF\sim\chi^{2}(m-k)\)，其中F係數聯立檢定的F檢定值。

此檢定的自由度為\(m-k\)，所以\(m\)要大於\(k\)。“等於”時是無法進行檢定的。

在香煙的例子，我們可以檢定「香煙稅」為滿足排除條件的工具變數嗎？

Q2: 工具變數關聯性檢定

工具變數\(Z\)必需要與效應解釋變數\(X\)有「足夠強」的關聯，否則\(\hat{\beta}_{TSLS}\)的大樣本漸近分配不會是常態分配。

考慮TSLS中的第一階段迴歸模型： \[X=Z\alpha_z+W\alpha_w+u\] 我們希望\(\alpha_z\)聯立夠顯著。

檢定原則

\({\bf H}_0: Z\) 工具變數只有微弱關聯性。

  1. \(X\)迴歸在「總」工具變數群(\(Z,W\))，進行\(\alpha_z=0\)的聯立F檢定。
  2. \(F>10\)拒絕\({\bf H}_0\)。

Q3: 遺漏變數偏誤（OVB）檢定

\[\begin{equation} Y =X\beta+W\gamma +\epsilon \tag{3.6} \end{equation}\]

若沒有OVB問題，還可以使用TSLS嗎？

可以。


\({\bf H}_0\): 迴歸模型(3.6)中的\(\beta\)係數估計「沒有」面臨OVB。
\({\bf H}_1\): 迴歸模型(3.6)中的\(\beta\)係數估計「有」面臨OVB。

\({\bf H}_0\): 用OLS或TSLS都可以。
\({\bf H}_1\): 只能用TSLS。

\({\bf H}_0\): 在大樣本下，\(\hat{\beta}_{OLS}\approx\hat{\beta}_{TSLS}\)。
\({\bf H}_1\): 在大樣本下，\(\hat{\beta}_{OLS}\)與\(\hat{\beta}_{TSLS}\)差很多。

Hausman檢定統計量:

\[H\equiv\left(\hat{\beta}_{IV}-\hat{\beta}_{OLS}\right)^{'}\left[V(\hat{\beta}_{IV}-\hat{\beta}_{OLS})\right]^{-1}\left(\hat{\beta}_{IV}-\hat{\beta}_{OLS}\right)\sim\chi_{(df)}^{2}.\]

– df： \(\beta\)係數個數.

  • 當\(H>\chi_{(df)}^{2}(\alpha)\)才拒絕\({\bf H}_0\)。

3.11 幾個觀念

  1. 有時資料並沒有所要的變數，但有其他具有代表性的替代變數（proxies）。如所要變數為「智商」，替代數變為「IQ測驗成績」。以下變數使用替代變數會有問題嗎：
    • 效應變數
    • 控制變數
  2. TSLS會是不偏估計嗎？會有一致性嗎？