第 6 章 R for panel data
參考資料:
Panel Data Econometrics in R: The plm Package, Yves Croissant and Giovanni Millo.
library(dplyr)
library(tidyverse)
library(magrittr)6.1 引入資料
library(readr)
fatality <- read_csv("https://raw.githubusercontent.com/tpemartin/Econometric-Analysis/master/Part%20II/fatality.csv")檢查資料
fatality %>% summarise_all(funs(class))## # A tibble: 1 x 43
## state year spircons unrate perinc emppop beertax
## <chr> <chr> <chr> <chr> <chr> <chr> <chr>
## 1 nume… nume… numeric numer… numer… numer… numeric
## # … with 36 more variables: sobapt <chr>,
## # mormon <chr>, mlda <chr>, dry <chr>, yngdrv <chr>,
## # vmiles <chr>, breath <chr>, jaild <chr>,
## # comserd <chr>, allmort <chr>, mrall <chr>,
## # allnite <chr>, mralln <chr>, allsvn <chr>,
## # a1517 <chr>, mra1517 <chr>, a1517n <chr>,
## # mra1517n <chr>, a1820 <chr>, a1820n <chr>,
## # mra1820 <chr>, mra1820n <chr>, a2124 <chr>,
## # mra2124 <chr>, a2124n <chr>, mra2124n <chr>,
## # aidall <chr>, mraidall <chr>, pop <chr>,
## # pop1517 <chr>, pop1820 <chr>, pop2124 <chr>,
## # miles <chr>, unus <chr>, epopus <chr>, gspch <chr>6.2 載入Panel套件:plm
library(plm)宣告資料為Panel data frame
fatality<-pdata.frame(fatality,c("state","year"))6.3 初步資料觀察
#各州啤酒稅(beertax)與車禍死亡率(mrall)
library(ggplot2)
fatality %>%
ggplot()+
geom_point(aes(x=beertax,y=I(mrall*1000)))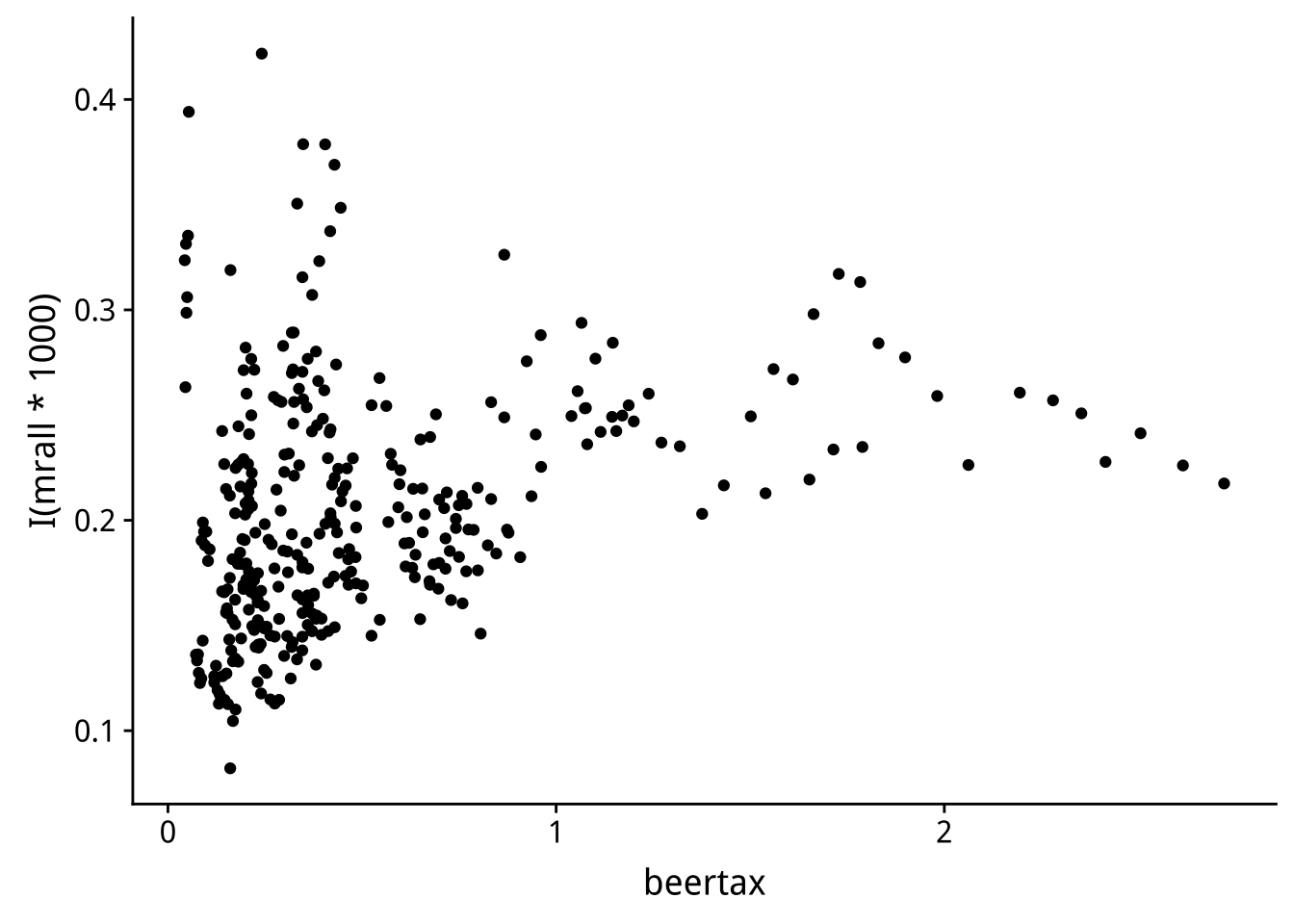
不同州用不同顏色畫離散圖
fatality %>%
ggplot()+
geom_point(aes(x=beertax,y=I(mrall*1000),color=state))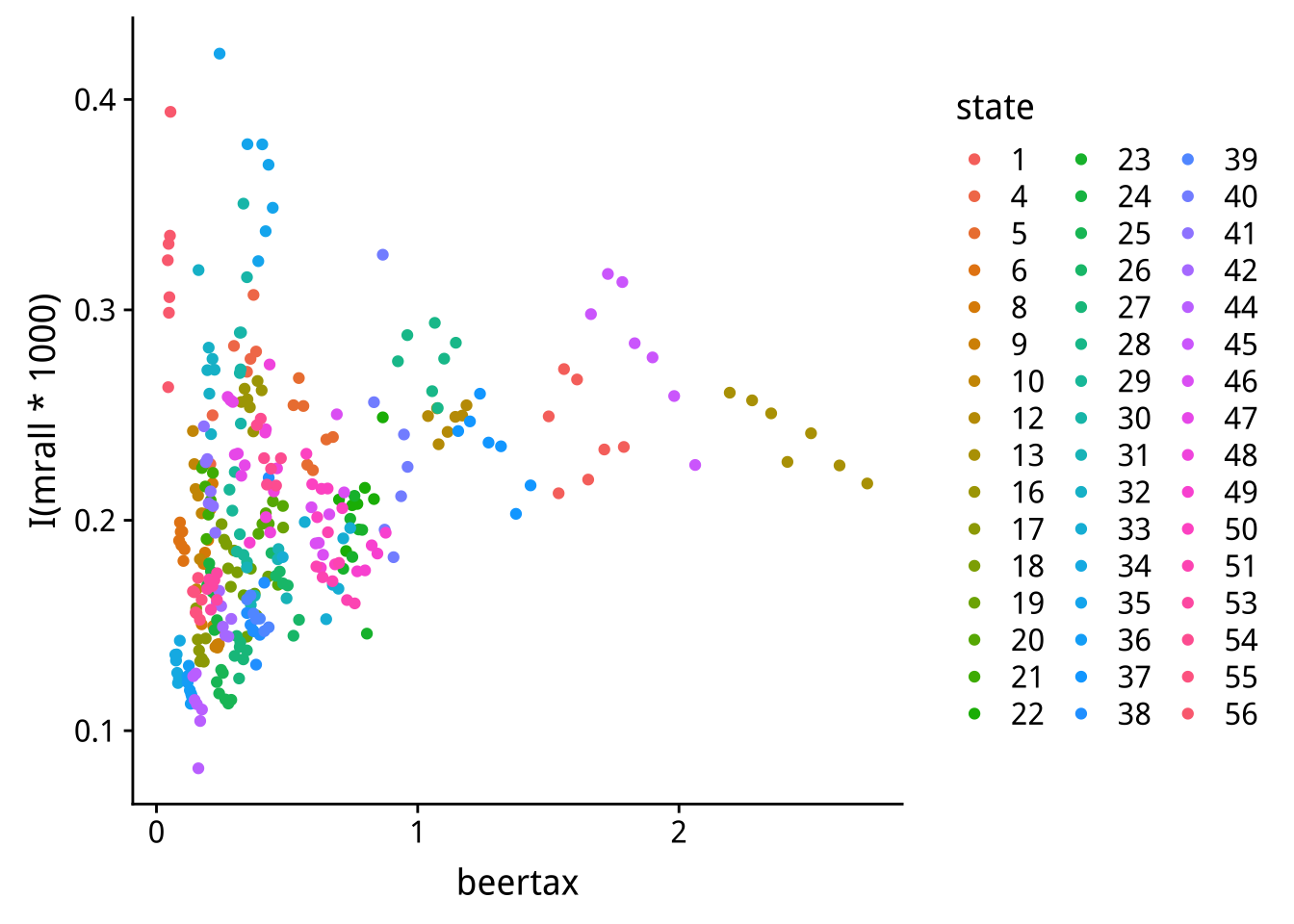
不同年用不同顏色畫離散圖
fatality %>%
ggplot()+
geom_point(aes(x=beertax,y=I(mrall*1000),color=year))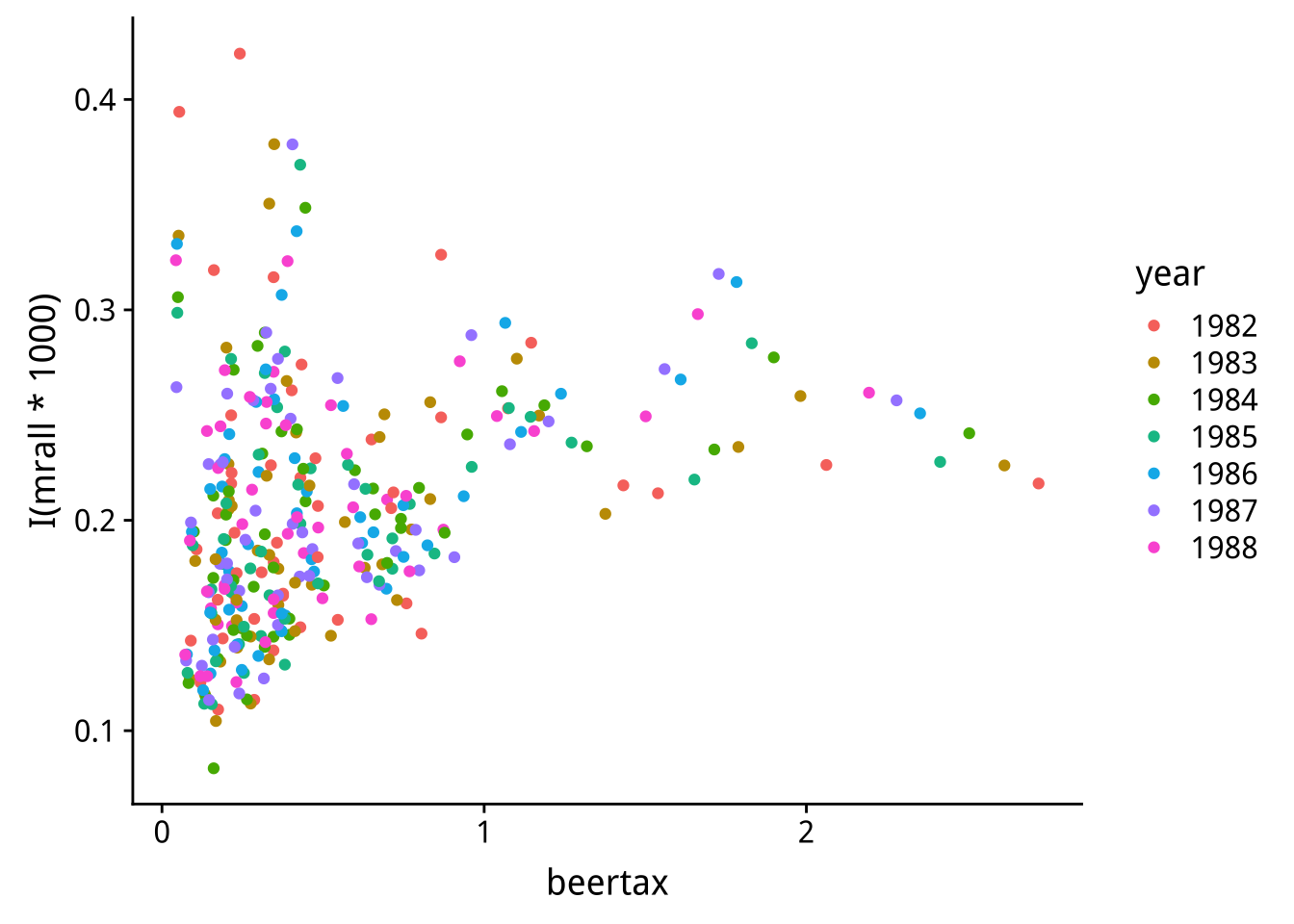
6.4 組內差異
去除每個州的中間點,即進行Demean
fatality %>%
group_by(state) %>% #依state分組進行以下程序:
mutate(
mrall_demean=mrall-mean(mrall),
beertax_demean=beertax-mean(beertax)
) %>%
select(mrall_demean,beertax_demean) %>%
ungroup() -> demean_results # grouping variable會被保留Demean 之後再畫一次離散圖
demean_results %>%
ggplot()+
geom_point(aes(x=beertax_demean,y=mrall_demean,color=state))+
geom_smooth(aes(x=beertax_demean,y=mrall_demean),method = "lm",se=FALSE)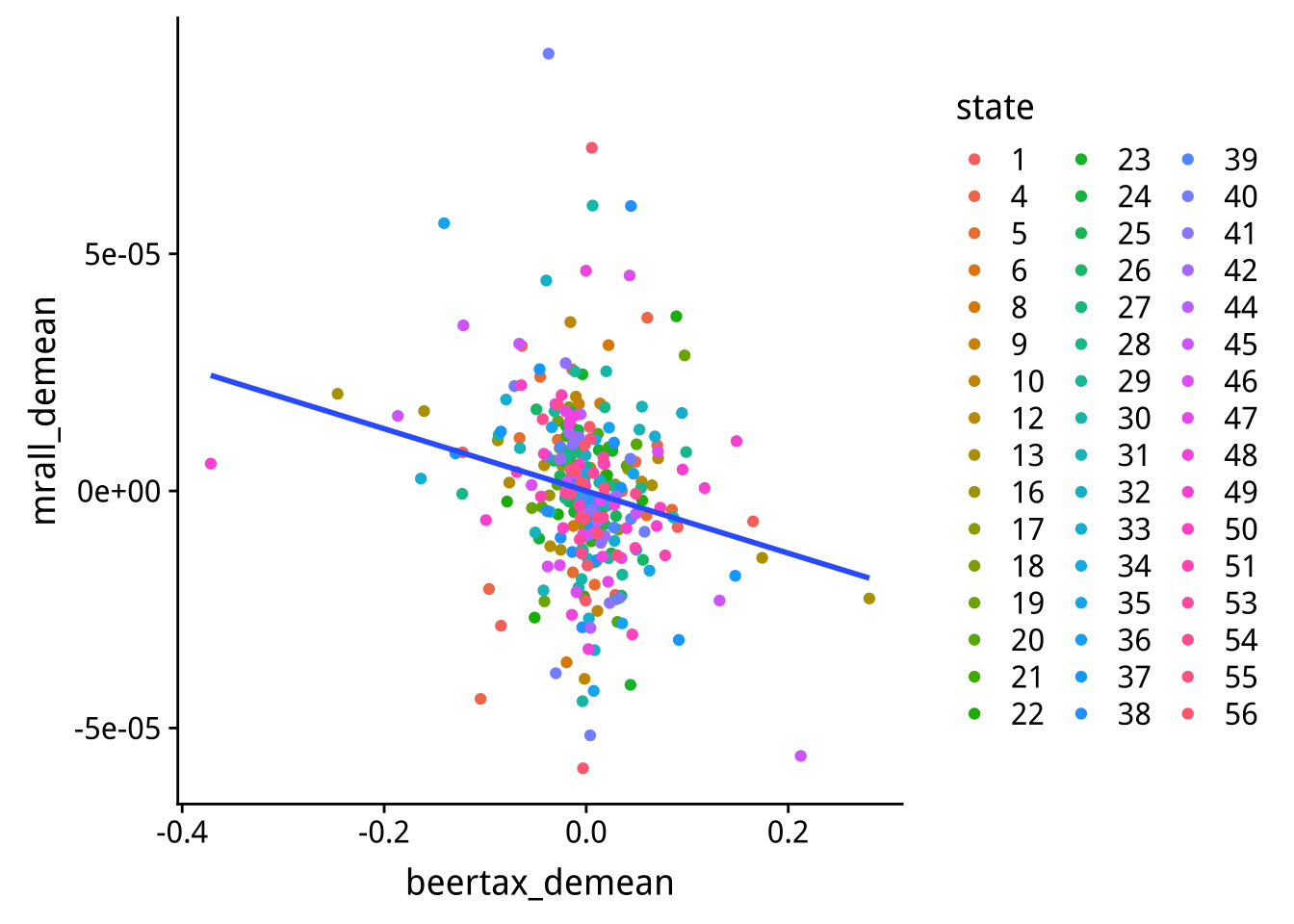
6.5 使用Dummies
fatality %>% lm(data=., mrall~factor(state)) -> results
# results$residuals 也會是demean的結果##模型估計 迴歸模型設定
model<-mrall~beertaxOLS
迴歸模型: \[mrall_{it}=\beta_0+\beta_1 BeerTax_{it}+\nu_{it}\]
pool1<-plm(model, data=fatality, model='pooling')
summary(pool1)Random effect
迴歸模型: \[mrall_{it}=\beta_0+\beta_1 BeerTax_{it}+\nu_{it}\] 且\(\nu_{it}=\alpha_i+\epsilon_{it}\),其中假設:
- \(\nu_{it}\perp BeerTax_{it}\)
- \(var(\alpha_i|X)=\sigma_{\alpha}^2\)
- \(var(\epsilon_{it}|X)=\sigma^2\)
- \(cov(\epsilon_{it},\epsilon_{is}|X)=0\)
re1<-plm(model, data=fatality, model='random')
summary(re1)Fixed effect
迴歸模型: \[mrall_{it}=\alpha_i+\beta_1 BeerTax_{it}+\epsilon_{it}\]
fe1<-plm(model, data=fatality, model='within', effect='individual')
summary(fe1)迴歸模型: \[mrall_{it}=\alpha_i+\delta_t+\beta_1 BeerTax_{it}+\epsilon_{it}\]
fe2<-plm(model, data=fatality, model='within', effect='twoways')
summary(fe2)模型比較
library(stargazer)
stargazer(pool1,re1,fe1,fe2,type='html',
column.labels = c("Pooled OLS","RE","FE-individual","FE-two-ways"))| Dependent variable: | ||||
| mrall | ||||
| Pooled OLS | RE | FE-individual | FE-two-ways | |
| (1) | (2) | (3) | (4) | |
| beertax | 0.00004*** | -0.00001 | -0.0001*** | -0.0001*** |
| (0.00001) | (0.00001) | (0.00002) | (0.00002) | |
| Constant | 0.0002*** | 0.0002*** | ||
| (0.00000) | (0.00001) | |||
| Observations | 336 | 336 | 336 | 336 |
| R2 | 0.093 | 0.001 | 0.041 | 0.036 |
| Adjusted R2 | 0.091 | -0.002 | -0.120 | -0.149 |
| F Statistic | 34.390*** (df = 1; 334) | 0.175 | 12.190*** (df = 1; 287) | 10.510*** (df = 1; 281) |
| Note: | p<0.1; p<0.05; p<0.01 | |||
6.6 Hausman檢定
Hausman test
RE中的\(\alpha_i\)是否與\(BeerTax_{it}\)有關
phtest(fe1,re1)##
## Hausman Test
##
## data: model
## chisq = 18, df = 1, p-value = 2e-05
## alternative hypothesis: one model is inconsistent6.7 固定效果
迴歸模型: \[mrall_{it}=\alpha_i+\beta_1 BeerTax_{it}+\gamma_1 urate_{it}+\epsilon_{it}\]
fatality %>%
plm(mrall~beertax+unrate, data=., method="within",effect = "individual")##
## Model Formula: mrall ~ beertax + unrate
## <environment: 0x7f83dc9e1d08>
##
## Coefficients:
## beertax unrate
## -4.13e-05 -3.00e-06