5 RLM part II

Simplificació mètode del model “únic”

Model únic; aplicable tant amb RLM com GLM

Authors:Compte, J. & Gascón S.

Aquesta secció servirà per conèixer quines variables independents són més importants en una Regresió Lineal Multiple (RLM) amb R, utilitzant el mètode de model únic.

5.1 Carregar les dades

L’exercici és una continuació de l’exercici de RLM(I).

Per a aquest exercici, utilitzarem les dades de l’arxiu “contaminacio.RData”.

Les dades s’han extret del llibre Sokal, R.R. and Rohlf, F.J. (1995) Biometry: The Principles and Practice of Statistics in Biological Research. 3rd Edition, W.H. Freeman and Co., New York. pàg 611-612.

Carreguem les dades a R.

load("contaminacio.RData")

S’ha mesurat la concentració de diòxid de sofre (SO2) en 41 ciutats dels EUA i es vol saber, de les variables que tenen efectes sobre l’SO2, quines tenen més influència. Les variables que s’han estudiat són:
- temperatura (temp)
- número de fàbriques que hi ha a cada ciutat (n_fabr)
- densitat de població (Pobl)
- velocitat del vent (vent)
- precipitació (precp)
- dies de pluja (dies_pluja)

Per contestar aquesta pregunta, es partirà de la RLM realitzada en la sessió anterior de RLM(I).

5.1.1 packages necessaris

Per aquesta sessió es necessiten els següents packages:

library(car)
library(MASS)

Si surt Warning no pasa res, sol ser un avis perquè la versió del package és anterior al nostre R. En general, no és un problema i els packages funcionen bé.

Si surt Loading vol dir que per funcionar el package que volem “activar” cal carregar altres packages, R ho detecta i ho fa automàticament.

5.2 Les variables

Comprovem si les variables s’han carregat bé

summary(contaminacio.data)
##               ciutat        so2              temp           n_fabr      
##  Albany          : 1   Min.   :  8.00   Min.   :43.50   Min.   :  35.0  
##  Albuquerque     : 1   1st Qu.: 13.00   1st Qu.:50.60   1st Qu.: 181.0  
##  Atlanta         : 1   Median : 26.00   Median :54.60   Median : 347.0  
##  Baltimore       : 1   Mean   : 30.05   Mean   :55.76   Mean   : 463.1  
##  Buffalo         : 1   3rd Qu.: 35.00   3rd Qu.:59.30   3rd Qu.: 462.0  
##  Charleston      : 1   Max.   :110.00   Max.   :75.50   Max.   :3344.0  
##  (Other)         :35                                                    
##       Pobl             vent            precp         dies_pluja   
##  Min.   :  71.0   Min.   : 6.000   Min.   : 7.05   Min.   : 36.0  
##  1st Qu.: 299.0   1st Qu.: 8.700   1st Qu.:30.96   1st Qu.:103.0  
##  Median : 515.0   Median : 9.300   Median :38.74   Median :115.0  
##  Mean   : 608.6   Mean   : 9.444   Mean   :36.77   Mean   :113.9  
##  3rd Qu.: 717.0   3rd Qu.:10.600   3rd Qu.:43.11   3rd Qu.:128.0  
##  Max.   :3369.0   Max.   :12.700   Max.   :59.80   Max.   :166.0  
##

Hem de realitzar la RLM de la sessió anterior.

5.3 Fem la Regressió múltiple i simplificació automàtica

Fem l’RLM. No posem la variable Pobl perquè com vam veure en la sessió RLM(I) tenia col·linealitat amb n_fabr.

lnso2_rlm<-lm(log(so2)~dies_pluja+n_fabr+precp+temp+vent, data=contaminacio.data)

Mirem els resultats:

summary(lnso2_rlm)
## 
## Call:
## lm(formula = log(so2) ~ dies_pluja + n_fabr + precp + temp + 
##     vent, data = contaminacio.data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.7864 -0.2563 -0.0516  0.2759  1.1473 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  7.6864628  1.4471647   5.311 6.25e-06 ***
## dies_pluja   0.0003444  0.0050524   0.068 0.946037    
## n_fabr       0.0005550  0.0001331   4.170 0.000191 ***
## precp        0.0194181  0.0112308   1.729 0.092620 .  
## temp        -0.0689735  0.0184040  -3.748 0.000643 ***
## vent        -0.1797441  0.0562091  -3.198 0.002936 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4565 on 35 degrees of freedom
## Multiple R-squared:  0.6304,	Adjusted R-squared:  0.5776 
## F-statistic: 11.94 on 5 and 35 DF,  p-value: 8.74e-07

En el nostre cas, n_fabr, temp i el vent estan relacionades amb el SO2. Peró, dies_pluja i precp no presenten relació (ja que tenen p-valors > 0.05), per tant podem simplificar el model de regressió.

Fem una simplificació automàtica del model utilitzant el mètode backward.

stepb <- stepAIC(lnso2_rlm, direction="backward")
## Start:  AIC=-58.8
## log(so2) ~ dies_pluja + n_fabr + precp + temp + vent
## 
##              Df Sum of Sq     RSS     AIC
## - dies_pluja  1    0.0010  7.2933 -60.791
## <none>                     7.2924 -58.797
## - precp       1    0.6229  7.9152 -57.436
## - vent        1    2.1306  9.4229 -50.287
## - temp        1    2.9264 10.2188 -46.963
## - n_fabr      1    3.6226 10.9149 -44.261
## 
## Step:  AIC=-60.79
## log(so2) ~ n_fabr + precp + temp + vent
## 
##          Df Sum of Sq     RSS     AIC
## <none>                 7.2933 -60.791
## - precp   1    1.8539  9.1472 -53.505
## - vent    1    2.2095  9.5028 -51.941
## - n_fabr  1    3.6457 10.9390 -46.171
## - temp    1    7.3823 14.6757 -34.123

La simplificació ha consistit en eliminar dies_pluja aconseguint passar d’un AIC inicial = -58.8 a un AIC sense dies de pluja = -60.79 . Per tant, s’ha millorat el model, ja que l’AIC és més petit.

Fem, doncs, l’RLM sense dies_pluja. Li posem el nom lnso2_rlm2

lnso2_rlm2<-lm(log(so2)~n_fabr+precp+temp+vent, data=contaminacio.data)

5.4 Característiques del model

  1. La R2 del model final:
summary(lnso2_rlm2) 
## 
## Call:
## lm(formula = log(so2) ~ n_fabr + precp + temp + vent, data = contaminacio.data)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.77450 -0.26074 -0.05387  0.27927  1.14267 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  7.7628404  0.9032385   8.594 3.02e-10 ***
## n_fabr       0.0005556  0.0001310   4.242 0.000148 ***
## precp        0.0200318  0.0066221   3.025 0.004568 ** 
## temp        -0.0699392  0.0115861  -6.036 6.21e-07 ***
## vent        -0.1803936  0.0546244  -3.302 0.002172 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4501 on 36 degrees of freedom
## Multiple R-squared:  0.6303,	Adjusted R-squared:  0.5892 
## F-statistic: 15.35 on 4 and 36 DF,  p-value: 2.053e-07

Adjusted R-squared: 0.5892

5.5 Gràfics de relacions parcials

Obtenir els gràfics de les relacions parcials de cada variable independent (X) amb la variable dependent (ln_so2). Són les relacions de cada X amb la Y deixant la resta de X constants. La comanda que s’utilitza és avPlots on s’ha d’especificar el nom de la RLM i perquè no calgui que pregunti cada vegada que faci un gràfic, posar ask=F.

avPlots(lnso2_rlm2,ask=F)

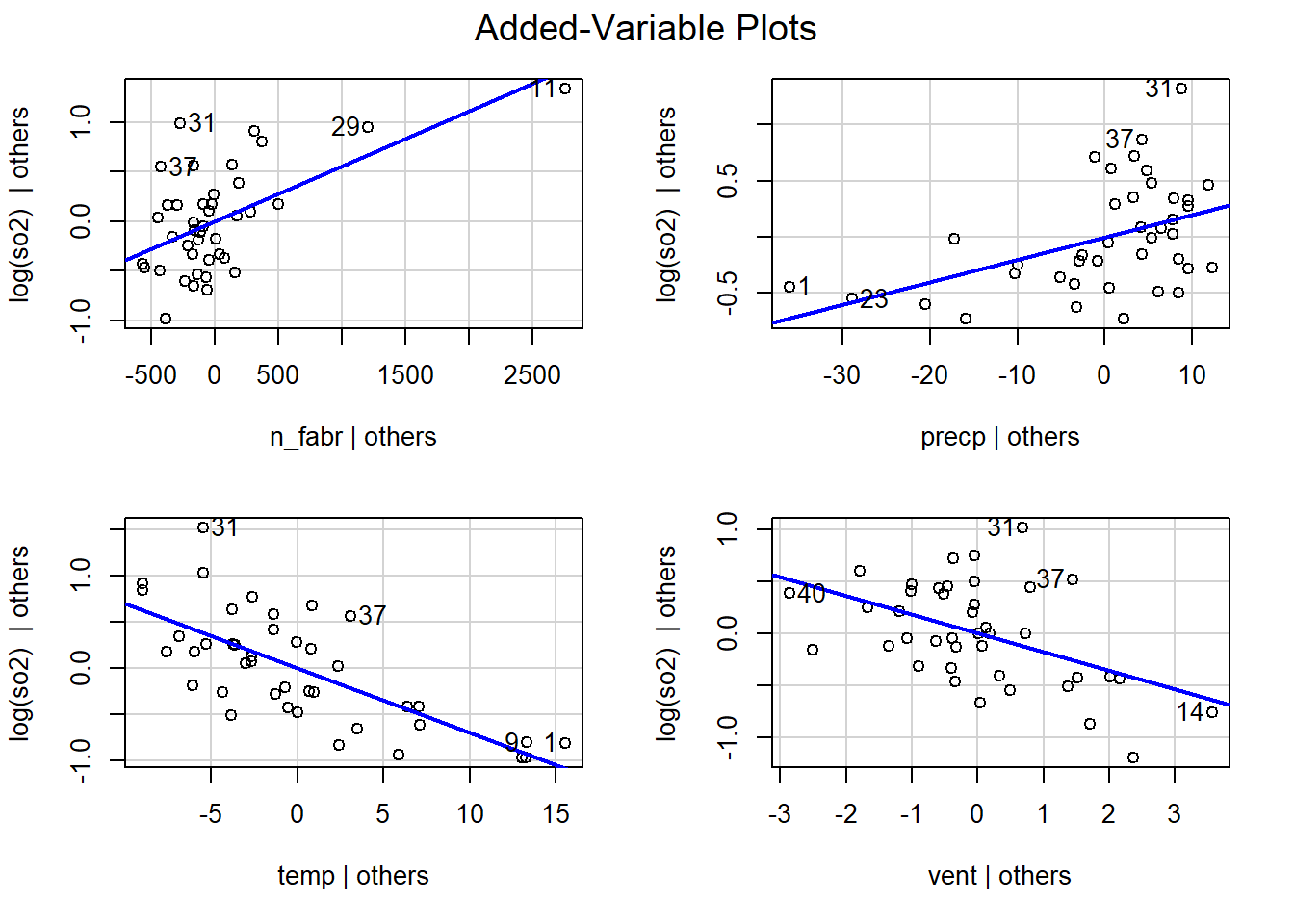
5.6 Com quantificar la influència de variables explicatives quan tenim un únic model

Per saber quina variable X té més influència, no podem comparar directament l’efecte de les variables (és a dir, els seus coeficiets de regressió parcial) ja que tenen diferents unitats. Per aixó s’han d’estandaritzar els coeficients.

Per saber quina variable independent té més influència sobre la variable depenent (SO2), s’han de calcular els coeficients parcials estandaritzats (Beta) amb la següent fórmula:
Beta = coeff * SD(X) / SD(Y)
- coeff: coeficient de regressió parcial (efecte d’una variable “X” sobre la “Y” mantenint les altres variables “X” constants).
- SD: desviació estàndard de “Y” i de la “X” de la que volem el seu coeficient estandarditzat (amb R s’obté escrivint sd.).

Primer s’ha de calcular el coeficient de regressió parcial a cada variable explicativa (X). Per fer-ho s’utilitza la comanda coeff on entre claudàtors s’indica el nom de la variable “x”. També s’ha d’indicar abans de la comanda el nom de l’RLM afegint el símbol de dólar.

  • Coefficent de regressió parcial de n_fabr
coeff_n_fabr <- lnso2_rlm2$coeff["n_fabr"]
coeff_n_fabr
##       n_fabr 
## 0.0005555672

coef–>pendent= 0.0005555672

  • Coefficent de regressió parcial de precp
coeff_precp <- lnso2_rlm2$coeff["precp"]
coeff_precp
##      precp 
## 0.02003175

coef–>pendent=0.02003175

  • Coefficent de regressió parcial de temp
coeff_temp <- lnso2_rlm2$coeff["temp"]
coeff_temp
##        temp 
## -0.06993917

coef–>pendent=-0.06993917

  • Coefficent de regressió parcial de vent
coeff_vent <- lnso2_rlm2$coeff["vent"]
coeff_vent 
##       vent 
## -0.1803936

coef–>pendent=-0.1803936

Ara ja podem calcular la beta per a cada una de les 4 variables explicatives (X) amb la fórmula descrita a dalt:

  • n_fabr:
Beta_n_fabr<- coeff_n_fabr*sd(contaminacio.data$n_fabr)/sd(log(contaminacio.data$so2))
Beta_n_fabr
##    n_fabr 
## 0.4457473

La beta n_fabr= 0.4457473

  • precp
Beta_precp<- coeff_precp*sd(contaminacio.data$precp)/sd(log(contaminacio.data$so2))
Beta_precp
##     precp 
## 0.3357614

La beta precp= 0.3357614

  • temp
Beta_temp<- coeff_temp*sd(contaminacio.data$temp)/sd(log(contaminacio.data$so2))
Beta_temp
##     temp 
## -0.71978

La beta temp= -0.71978

  • vent
Beta_vent<- coeff_vent*sd(contaminacio.data$vent)/sd(log(contaminacio.data$so2))
Beta_vent
##       vent 
## -0.3669641

La beta vent= -0.3669641

A partir d’aquests resultats quina de les 4 variables té més influència sobre el contingut en sofre atmosfèric?
La temperatura (temp) perquè és la variable que té la Beta en valor absolut més elevada.