3 ANCOVA
Anàlisis de la Covariància
Mètode “clàssic” quan la Y segueix una distribució NORMAL
Autors: Antón, M. & Gascón S.
Aquesta secció servirà per veure els diferents passos que s’han de seguir per realitzar una ANCOVA. L’anàlisi de la covariància combina elements de l’ANOVA i la regressió: com a variables explicatives tindrem una variable categòrica (factor amb diferents nivells) i una variable continua.
3.1 Carregar les dades
Per a aquest exercici, utilitzarem les dades de l’arxiu “amfipoda.RData”.
En aquest exemple, s’ha mesurat la velocitat en què mouen les potes (variable vel) dos espècies d’amfípodes (variable sp), i com que la temperatura de l’aigua pot influir en aquesta velocitat i no sha pogut garantir la mateixa temperatura a l’experiment, s’ha tingut la precaució de mesurar també la temperatura de l’aigua cada vegada que es mesurava la velocitat del moviment de les potes del amfípodes (variable temp).
Importem la taula:
I fem una ullada a les dades:
## sp temp vel
## 1 1 10.1 89.0
## 2 1 12.2 94.8
## 3 1 13.5 99.6
## 4 1 11.2 93.8
## 5 1 10.2 91.0
## 6 1 9.8 89.2
## 7 2 14.1 104.5
## 8 2 12.3 103.6
## 9 2 9.5 91.1
## 10 2 11.6 99.6
## 11 2 10.1 99.1
## 12 2 9.4 88.7Comprovem que ha importat les variables de manera correcta amb les funcions summary() i str():
## sp temp vel
## Min. :1.0 Min. : 9.40 Min. : 88.70
## 1st Qu.:1.0 1st Qu.:10.03 1st Qu.: 90.55
## Median :1.5 Median :10.70 Median : 94.30
## Mean :1.5 Mean :11.17 Mean : 95.33
## 3rd Qu.:2.0 3rd Qu.:12.22 3rd Qu.: 99.60
## Max. :2.0 Max. :14.10 Max. :104.50## 'data.frame': 12 obs. of 3 variables:
## $ sp : int 1 1 1 1 1 1 2 2 2 2 ...
## $ temp: num 10.1 12.2 13.5 11.2 10.2 9.8 14.1 12.3 9.5 11.6 ...
## $ vel : num 89 94.8 99.6 93.8 91 ...En aquest cas, l’R no ha considerat l’espècie d’amfípode com un factor, sinò que l’ha considerat una variable quantitativa. Per això, haurem de modificar-la: la columna sp de la matriu amfipoda$sp la passarem a factor amb la funció as.factor().
Si pel contrari el que volguéssem és tranformar una variable de factor a numérica (ha importat una variable numèrica com a factor), podriem fer-lo amb la funció as.numeric().
I comprovem que ara està correcte:
## sp temp vel
## 1:6 Min. : 9.40 Min. : 88.70
## 2:6 1st Qu.:10.03 1st Qu.: 90.55
## Median :10.70 Median : 94.30
## Mean :11.17 Mean : 95.33
## 3rd Qu.:12.22 3rd Qu.: 99.60
## Max. :14.10 Max. :104.50## 'data.frame': 12 obs. of 3 variables:
## $ sp : Factor w/ 2 levels "1","2": 1 1 1 1 1 1 2 2 2 2 ...
## $ temp: num 10.1 12.2 13.5 11.2 10.2 9.8 14.1 12.3 9.5 11.6 ...
## $ vel : num 89 94.8 99.6 93.8 91 ...3.2 Comprovació dels supòsits
Ja tenim la matriu de dades a l’R! Com hem dit, volem comparar si la velocitat de moviment de les potes (variable resposta) és diferent per cada espècie (variable categòrica)… però aquesta velocitat pot estar influenciada per la temperatura de l’aigua (variable continua). Per exemple, una de les espècies pot moure les potes més ràpidament simplement perquè està a una major temperatura, i l’altra les mou més lentament perquè les mesures s’han fet a un ambient més fred (temperatura més baixa). Llavors, s’ha de treure l’efecte de la temperatura a l’anàlisi, i per això fem una ANCOVA, Anàlisi de la Covariància.
El primer pas per fer l’ANCOVA és comprovar que les dades tenen homogeneïtat de pendents (primer supòsit). Si els pendents són homogenis, es pot mirar si hi ha diferències de velocitat per espècie, tenint en compte la relació entre velocitat i temperatura. Si els pendents no són homogenis, llavors no es pot fer la comparativa de mitjanes ajustades. Per mirar si les pendents són homogènies fem el primer pas de l’ANCOVA.
Apliquem la funció lm() (igual que heu utilitzat a l’ANOVA de la primera pràctica), i especifiquem la nostra variable resposta (vel : velocitat de moviment de les potes), i les nostres variables predictores (sp: l’espècie d’amfípode, i temp: la temperatura mesurada). Utilitzem sp:temp per a analitzar la interacció entre aquestes dues variables.
Abans de veure els resultats, haurem de comprovar si els supòsits de l’ANCOVA es compleixen. Per això, els comprovem visualment amb la funció plot().
Primer, l’hem de carregar, i després representarem el nostre model d’ANCOVA ancova_amf1:
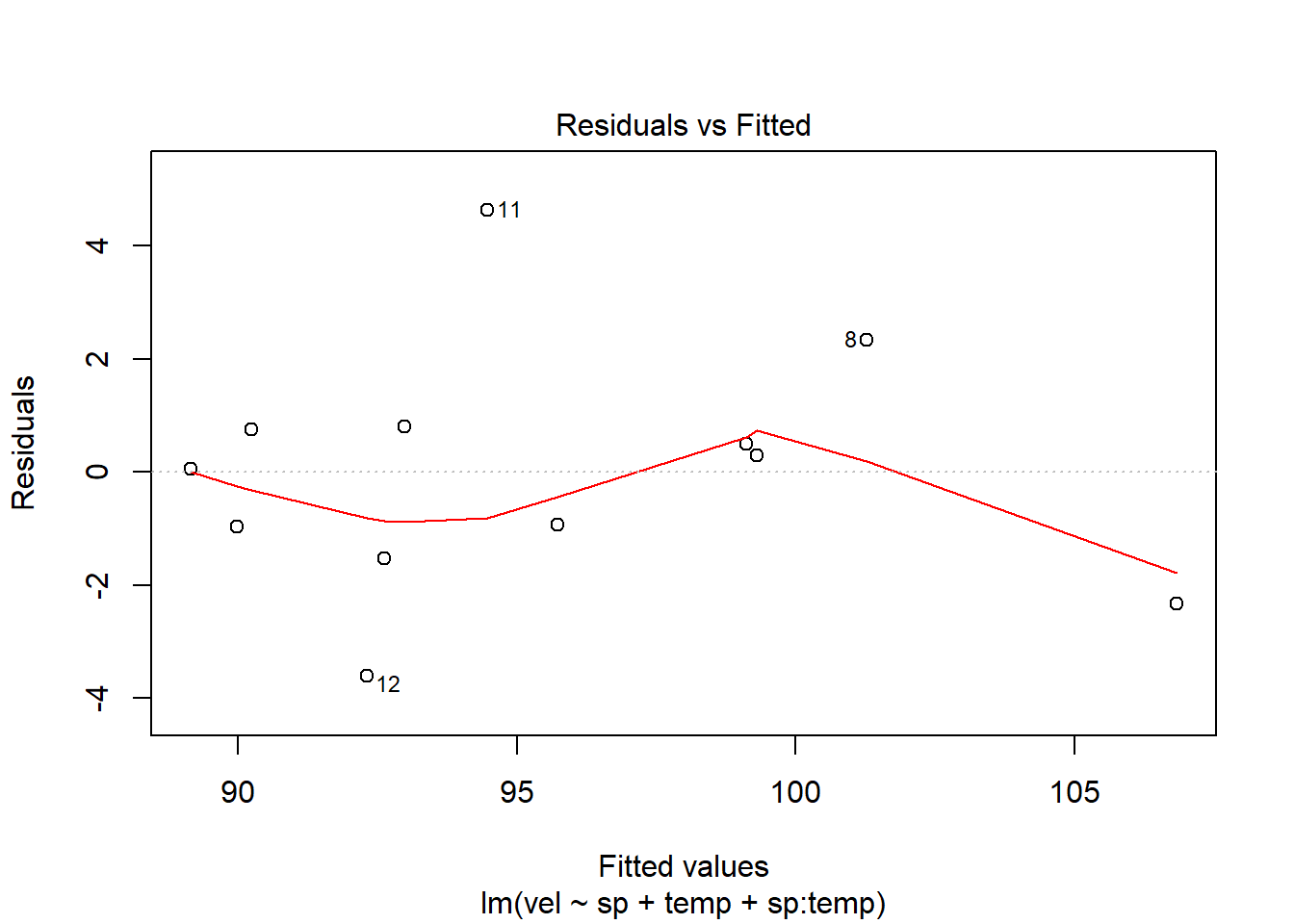
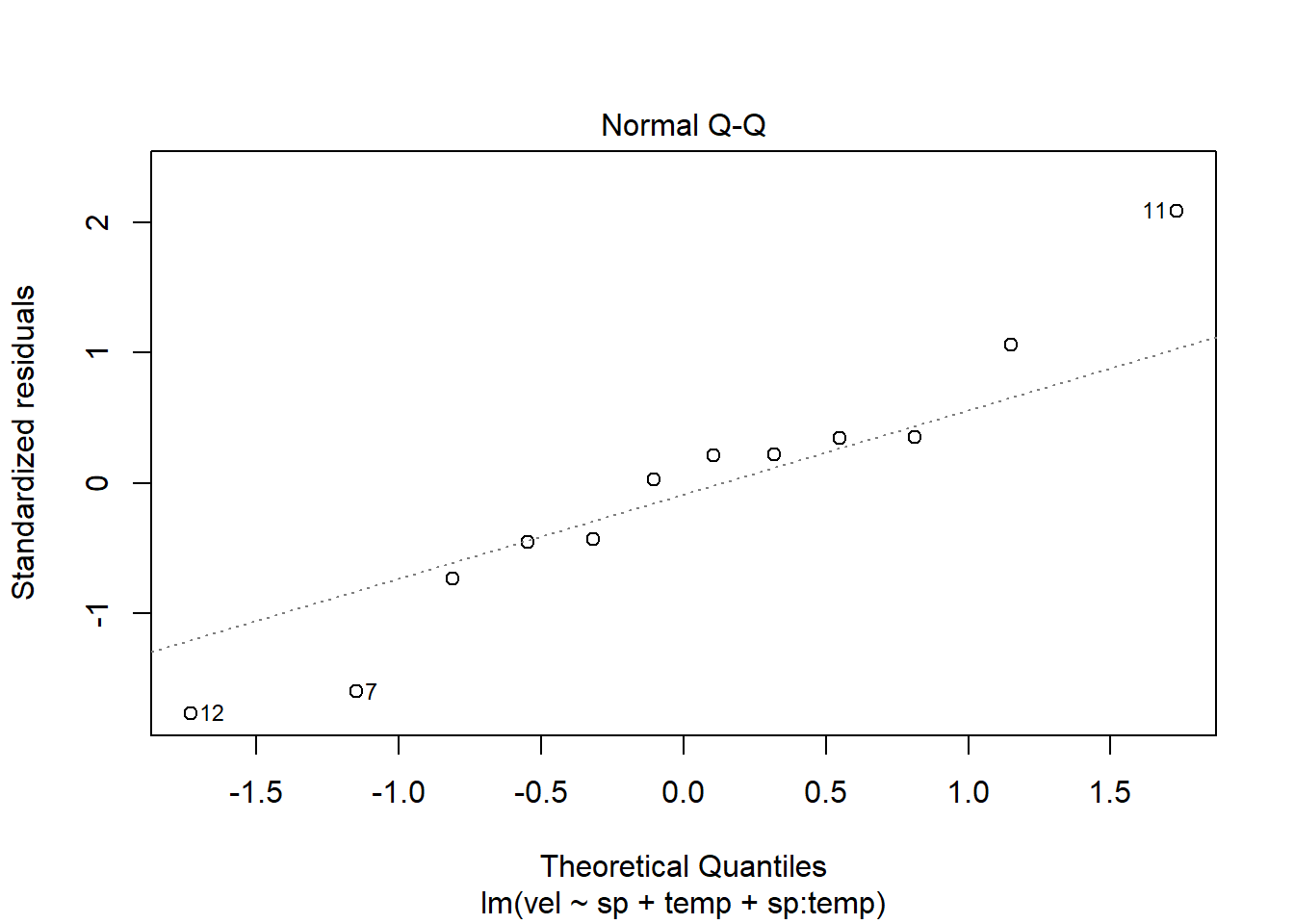
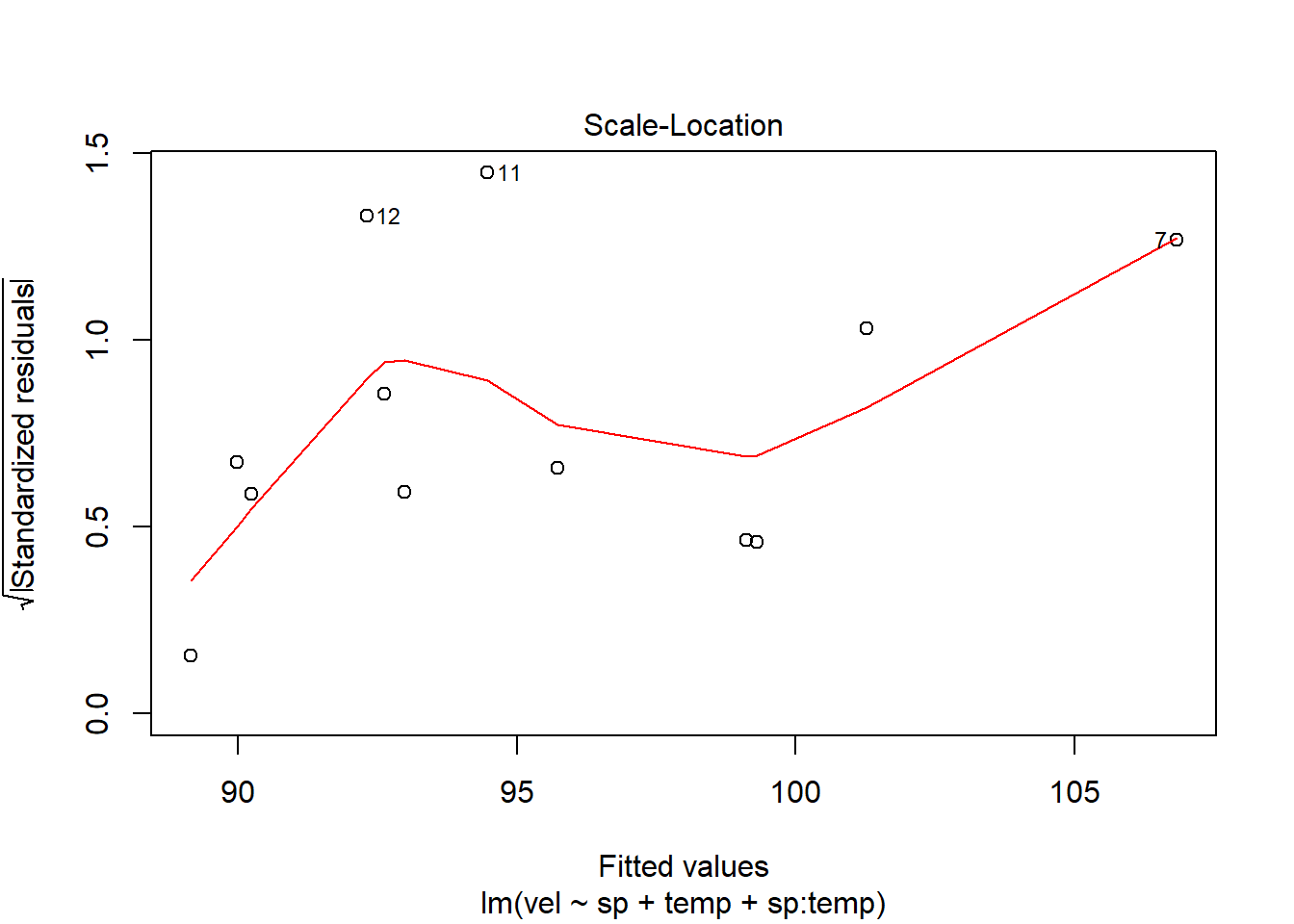
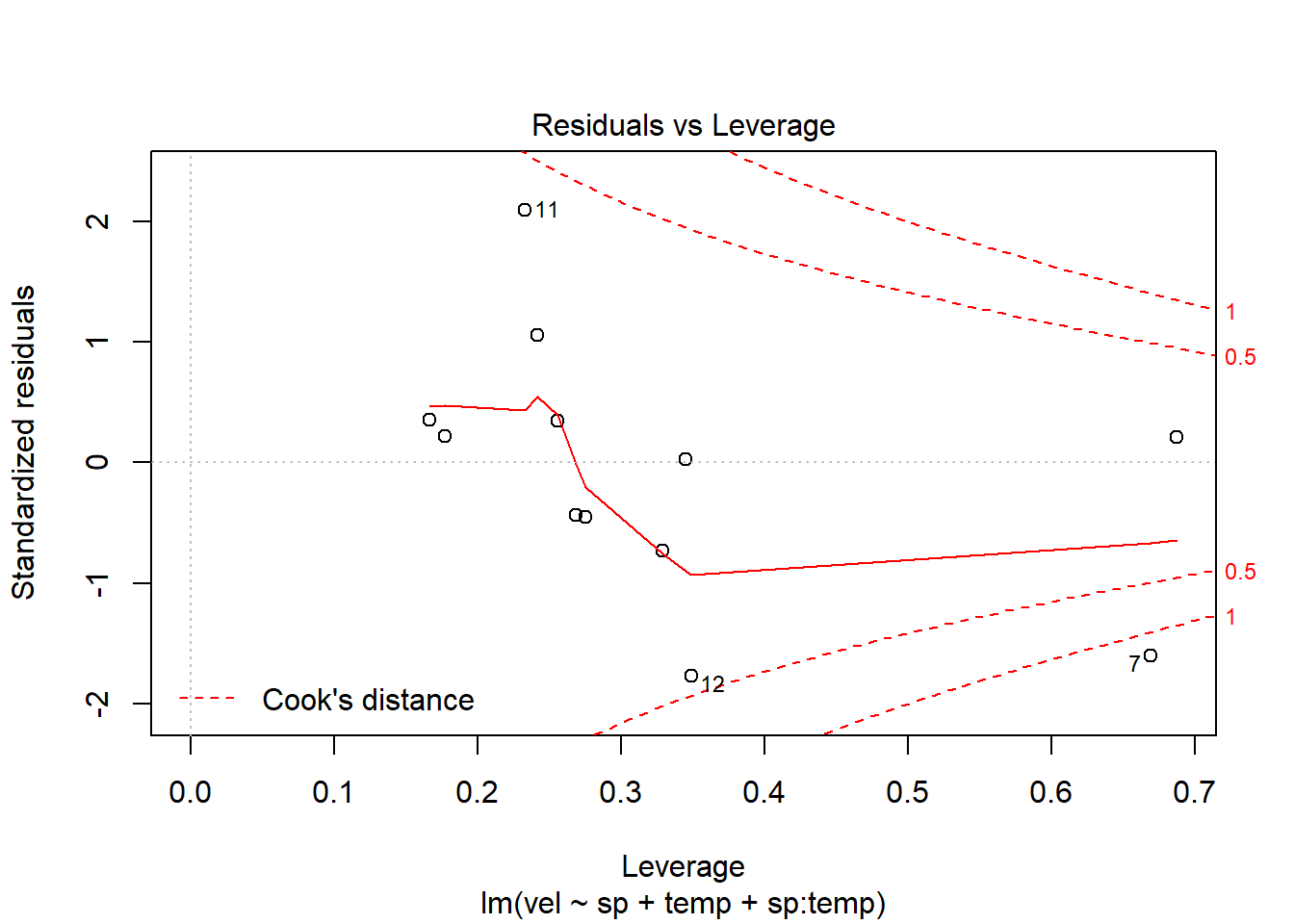
El primer gràfic, representa els valors de residus respecte als valors predits (supòsit d’homogeneïtat de variàncies) i en el següent es representa la distribució dels residus respecte a una distriució Normal (la línia discontinua representa una distribució normal). Com observem, els dos supòsits es compleixen.
Amb la funció summary (ancova_amf1) obtindrem els resultats desglossats de l’ANCOVA, però per obtindre el resultat resumit en forma de taula d’ANOVA, ho fem amb la funció anova().
## Analysis of Variance Table
##
## Response: vel
## Df Sum Sq Mean Sq F value Pr(>F)
## sp 1 71.053 71.053 11.1477 0.0102492 *
## temp 1 241.209 241.209 37.8436 0.0002735 ***
## sp:temp 1 0.774 0.774 0.1215 0.7364515
## Residuals 8 50.991 6.374
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1En aquest primer pas, comprovem si els pendents són homogenis: mirem si la interacció de les variables sp i temp (sp:temp) és significativa. En aquest cas, com el p-valor = 0.73645, ens quedem amb la hipòtesi nul·la (Ho: no hi ha interacció = els pendents són homogenis).
3.3 ANCOVA
Com es compleixen els supòsits de l’ANCOVA, podem continuar per testar si la velocitat del moviment de les potes és diferent en les dos espècies. Per això, passem al segon pas, on anem a comparar les mitjanes ajustades (sense interacció entre les variables).
Comprovem de nou que es compleixen els supòsits amb la mateixa funció d’abans mcheck():
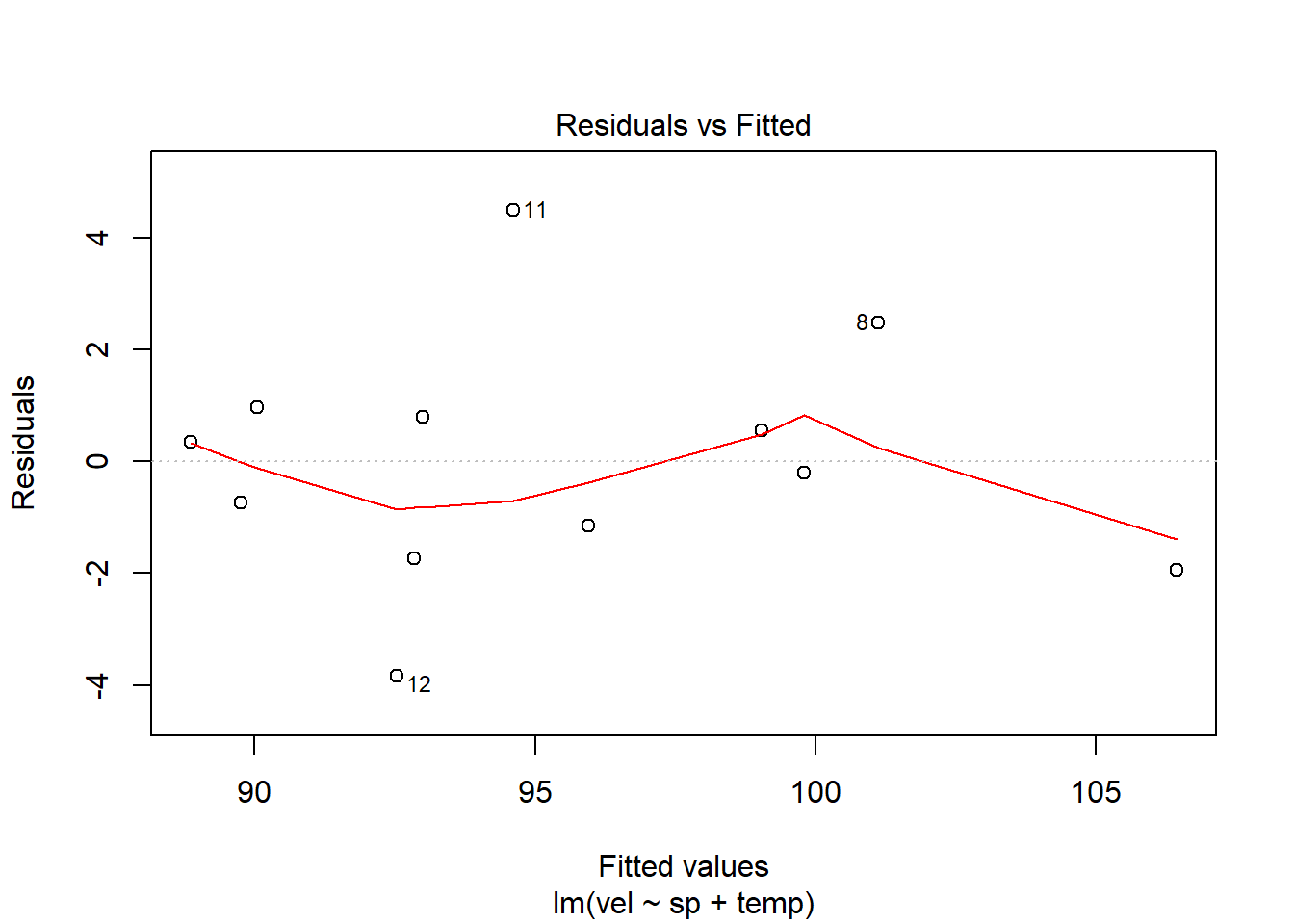
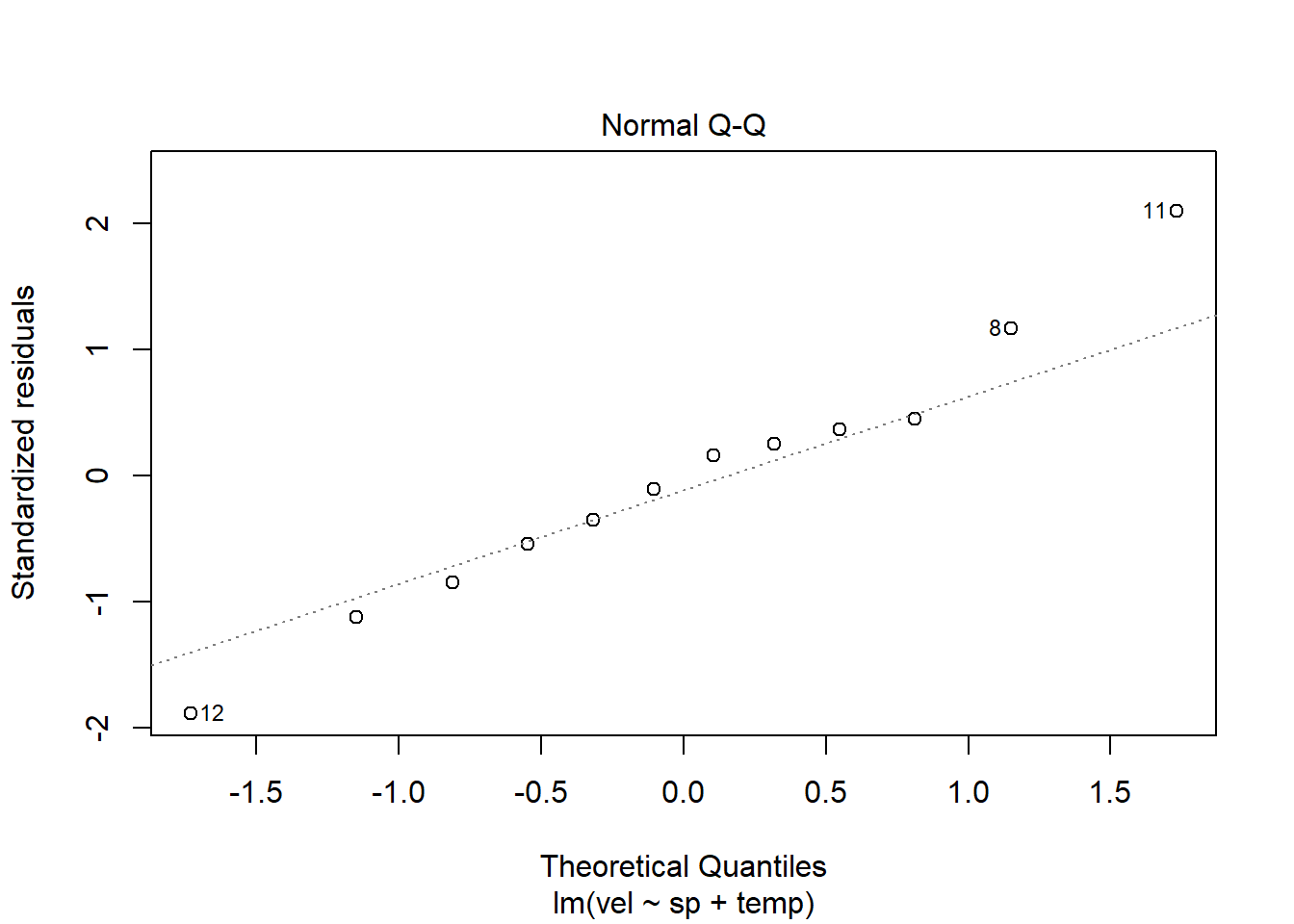
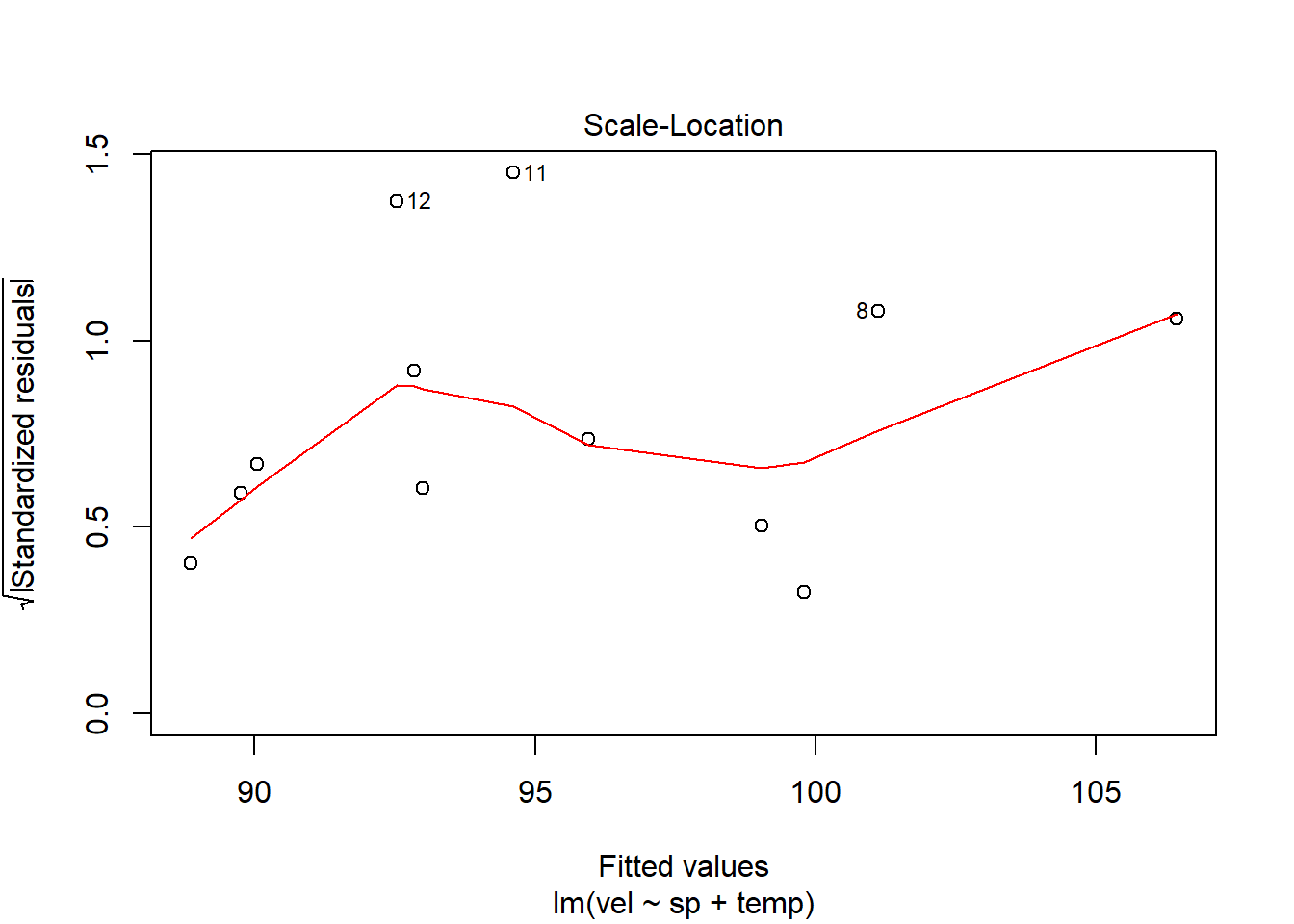
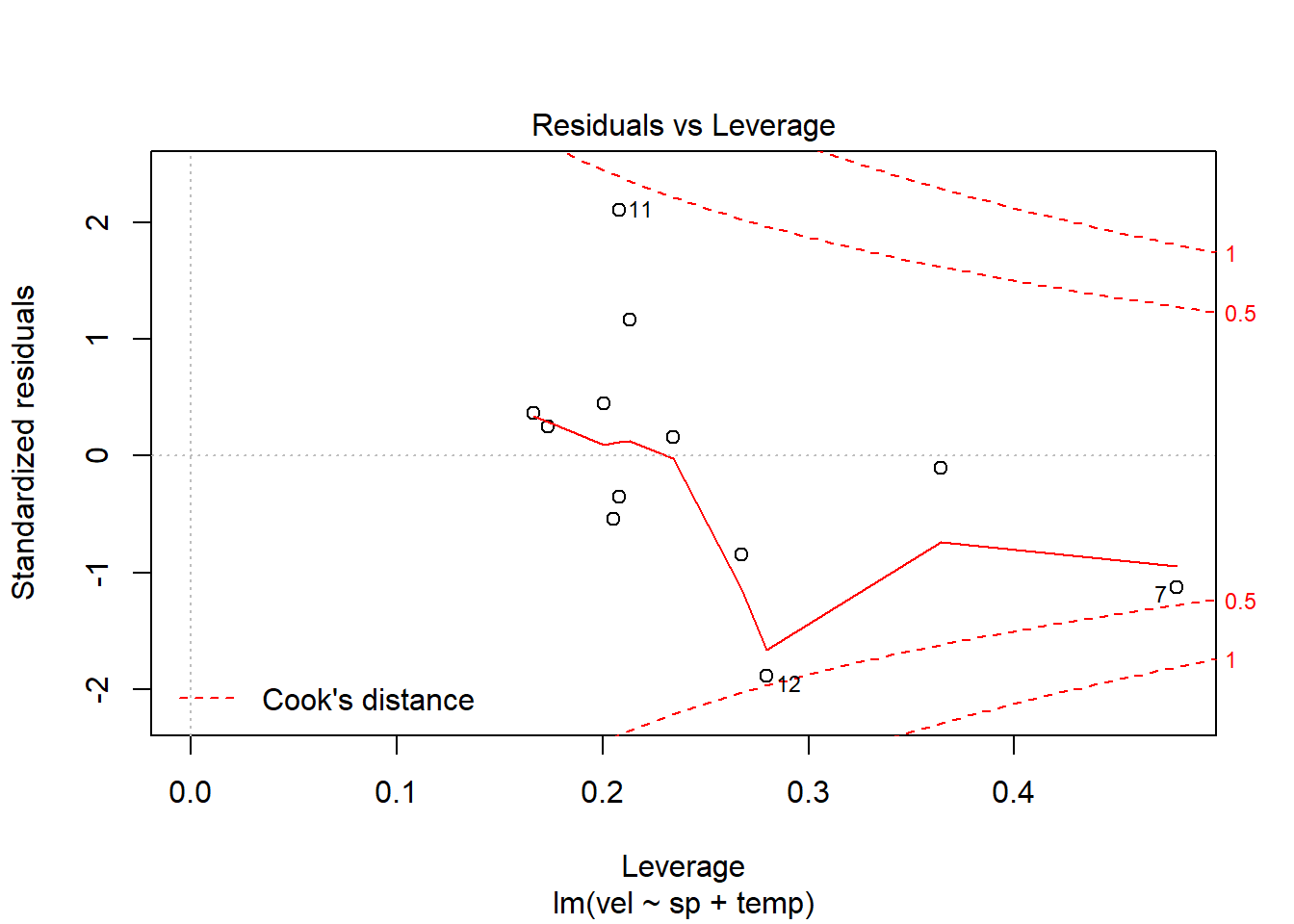
I mirem els resultats
## Analysis of Variance Table
##
## Response: vel
## Df Sum Sq Mean Sq F value Pr(>F)
## sp 1 71.053 71.053 12.354 0.0065693 **
## temp 1 241.209 241.209 41.937 0.0001146 ***
## Residuals 9 51.765 5.752
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1En aquesta taula es mostren:
Df: els graus de llibertat de cada variable i del residus
Sum Sq: la suma de quadrats
Mean Sq: valor de la suma de quadrats dividit pels graus de llibertat
F value: el valor de l’estatístic F per a cada variable
Pr(>F): p-valor corresponent.
Així, podem observar que les mitjanes ajustades mostren que hi ha diferències entre les espècies: p-valor=0.0065693 (és significant), rebutgem la hipòtesi nul·la (Ho: les mitjanes ajustades són iguals).
Igualment, hi ha diferències en la velocitat de les potes amb la temperatura: p-valor=0.0001146, així que rebutgem de nou la hipòtesi nul·la (Ho: no hi ha efecte de la temperatura)
Per tant, podem concloure que la velocitat de moviment de les potes és diferent en les dos espècies, i a més, està influïda per la temperatura.
3.4 Representació gràfica dels resultats
Primer podem respresentar el gràfic amb els punts per cada spècie:
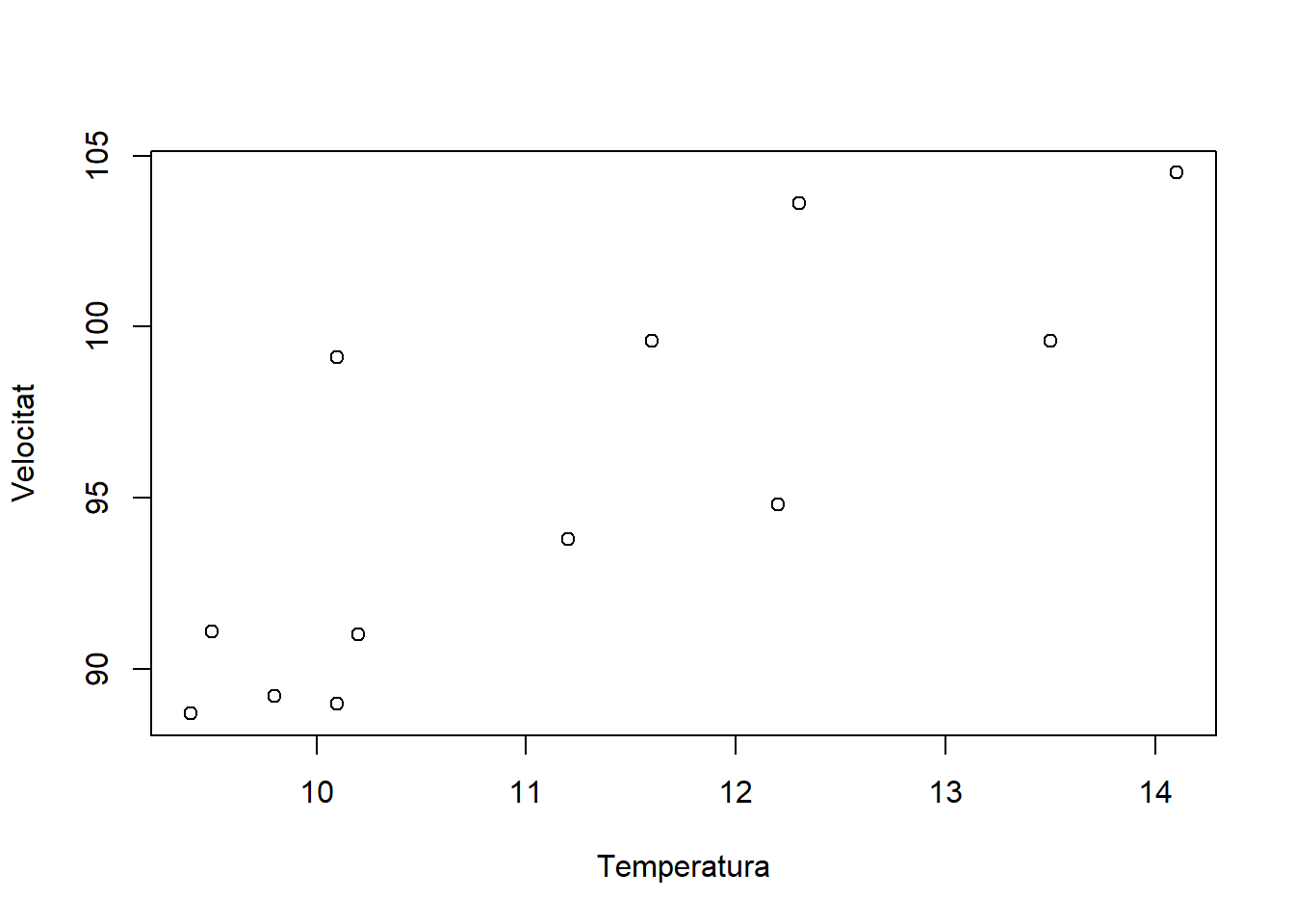
Mitjançant la funció plot(), utilitzem els següents arguments:
- x = amfipoda.data$temp: a l’eix x representarà la temperatura mesurada
- y = amfipoda.data$vel: a l’eix y representarà la velocitat del moviment de les potes
- xlab: titol de l’eix x. Com és text, l’hem de posar entre cometes
- ylab: títol de l’eix y, també entre cometes.
Amb aquesta primera ordre ja ens representa els punts en funció de la temperatura i la velocitat, però quin punt correspon a cada espècie? Per això, anem a especificar que els punts de l’espècie 2 siguen cercles negres. Utilitzem la funció points() amb els següents arguments:
- amfipoda.data$temp[amfipoda.data$sp ==“2”]: els punts de l’eix de temperatura x que corresponen a l’espècie 2 ( amfipoda.data$sp ==“2”)
- amfipoda.data$vel[amfipoda.data$sp ==“2”]: els punts de l’eix de velocitat y que corresponen a l’espècie 2
- pch=16: especifiquem el simbol (cercle negre) que volem per als punts que hem indicat (els de l’espècie 2). Amb l’ajuda ?points o help(points) podeu veure les diferents formes (pch) que es poden utilitzar, així com el seu tamany (cex) o color (col).
plot(x=amfipoda.data$temp,
y=amfipoda.data$vel,
xlab="Temperatura",
ylab="Velocitat")
points(amfipoda.data$temp[amfipoda.data$sp =="2"],
amfipoda.data$vel[amfipoda.data$sp =="2"],
pch=16)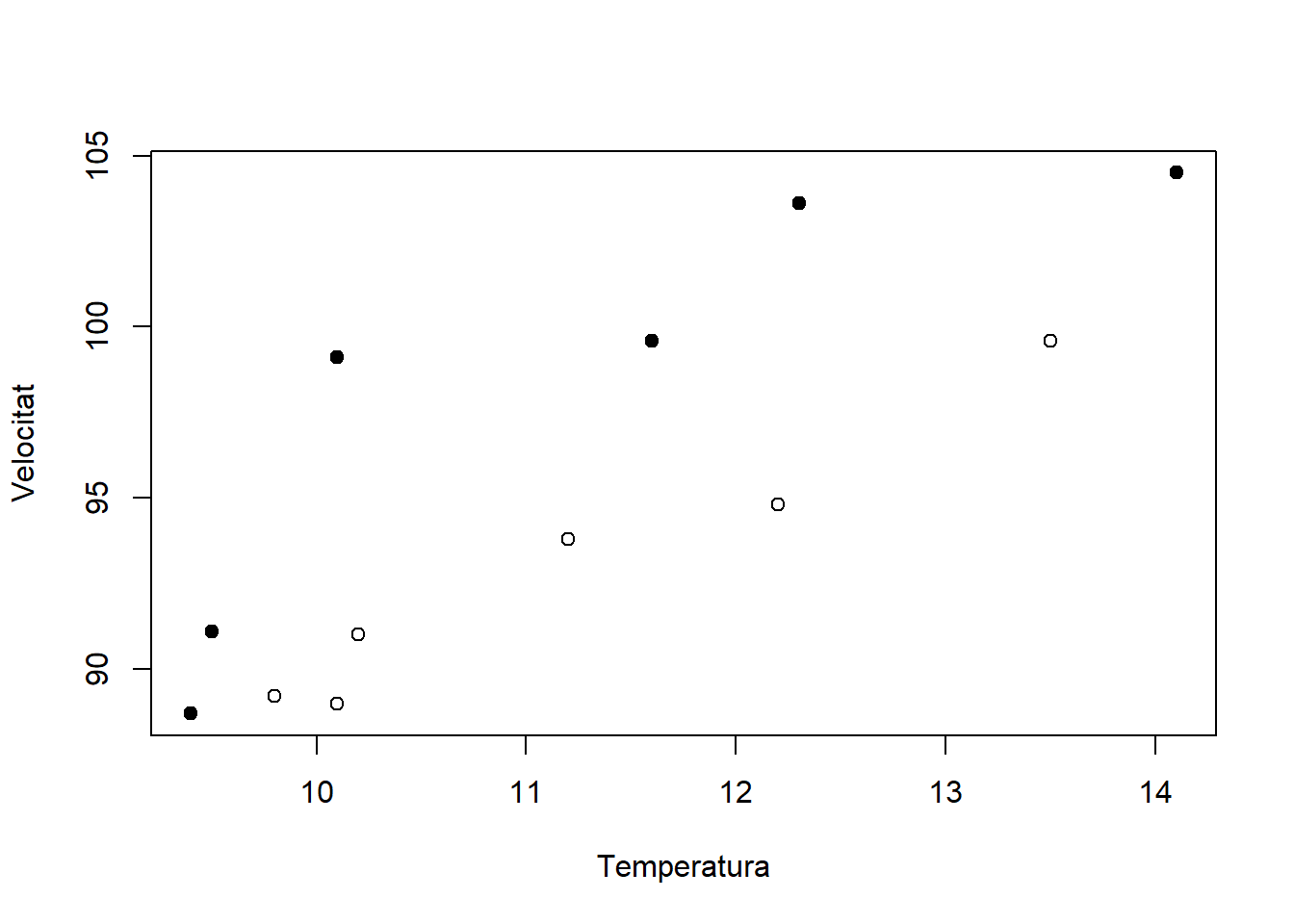
A més, podem afegir les rectes per a cada espècie. Per això, necessitem saber els valors per a representar-les: l’ordenada a l’origen i el pendent. Ho fem amb la comanda coef().
## (Intercept) sp2 temp
## 59.868541 4.866667 2.958041Aquests resultats ens mostren:
Intercept: ordenada a l’origen per a l’espècie 1 (no està especificat però agafa per defecte la primera en ordre alfabètic o numèric)
sp2: és el valor que hem d’afegir a l’intercept per a obtenir l’ordenada a l’origen de l’espècie 2. En aquest cas seria 59.868541 + 4.866667. Aquest valor (positiu) també ens indica és que l’espècie 2 té una velocitat de moviment de les potes major que l’espècie 1 (i com hem vist abans, aquest diferència és significativa). Si fos negatiu, seria a l’inversa, i hauriem de restar aquest valor a l’intercept de l’espècie 1.
temp: ens dóna el valor del pendent de les rectes (ja hem vist abans que els pendents són homogenis, aleshores tenim a soles un valor).
Ara que ja sabem els valors de les rectes, podem afegir-les al gràfic d’abans amb la funció abline(), on hem d’afegir l’ordenada a l’origen, pendent i el tipus de recta.
L’argument lty=2 el fem servir per a dir que la recta de l’espècie 1 siga discontinua. Podeu consultar més tipus de recta a ?par o help(par)
plot(x=amfipoda.data$temp,
y=amfipoda.data$vel,
xlab="Temperatura",
ylab="Velocitat")
points(amfipoda.data$temp[amfipoda.data$sp =="2"],
amfipoda.data$vel[amfipoda.data$sp =="2"],pch=16)
abline(59.868541, 2.958041,lty=2) ##afegim la recta per a l'espècie 1
abline(59.868541 + 4.866667, 2.958041) ##afegim la recta per a l'espècie 2