6 GLM part I
Mètodes lineals Generalitzats (Y Binomial)
Mètode “modern” quan la Y segueix una distribució Binomial
Authors:Compte, J. & Gascón S.
Aquesta secció servirà per introduir l’ús de Models lineals Generalitzats (GLM) per analitzar variables resposta (Y) amb distribució Binomial.
6.1 Packages necessaris
Per aquesta sessió es necessita els següent package:
Si surt Warning no pasa res, sol ser un avis perquè la versió del package és anterior al nostre R. En general, no és un problema i els packages funcionen bé.
6.2 Carregar dades
Per exemplificar l’ús, s’utilitzaran dades d’un exercici extret d’un exemple del llibre Quinn & Keough 2002. Experimental design and data analysis for biologists. Cambridge University Press, Cambridge. pag. 361. Aquest exemple es basa en un estudi realitzat per Polis et al. (1998) Multifactor population limitation: variable spatial and temporal control of spiders on Gulf of California islands. Ecology 79: 490-502. Es tracta d’un estudi sobre aranyes en 19 illes del Golf de California, utilitzarem una part de les seves dades per analitzar la relació que hi ha entre els llangardaixos del gènere Uta (depredadors potencials de les aranyes) i la relació perímetre/àrea de l’illa (mesura d’aport de detritus marins).
6.3 Les variables
Les variables de les que es disposa són:
- ISLAND: Nom de l’illa
- PARATIO: relació del perímetre/àrea
- UTA: presència (P) i absència (A) del llangardaixos
- La variables resposta Y és la presència absència de llangardaixos ( UTA )
- La variables explicativa X és la relació del perimetre/àrea ( PARATIO )
Com que la variable UTA no és numèrica no podem fer una regressió tradicional (RLS) . UTA ès una variable binària, per això utilitzem els GLM distribució binomial.
Primer de tot cal, carregar les dades “polis.RData”.
Comprovem si les variables s’han carregat bé
## ISLAND PARATIO UTA
## Angeldlg: 1 Min. : 0.21 A: 9
## Bahiaan : 1 1st Qu.: 5.86 P:10
## Bahiaas : 1 Median :15.17
## Blanca : 1 Mean :18.74
## Bota : 1 3rd Qu.:23.20
## Cabeza : 1 Max. :63.16
## (Other) :13Per poder fer l’anàlisi necessitem la variable Y numèrica, i tal qual la tenim ara és una variable no numèrica. Per tant, hem de transformar la variable UTA de presència i abscència a una variable numèrica ja que sinó no podrem fer l’anàlisis de regressió.6 Per fer-ho, utilitzarem un package d’R que s’anomena “dplyr”7, molt útil per fer càlculs amb les variables o senzillament modificar l’arxiu de dades (p.e. seleccionant casos o variables, o creant nous arxius fent la mitjana d’algunes coses, etc…)
#en les següents instruccions el que fem és modificar, l'arxiu "polis.data"
polis.data <- polis.data %>%
mutate(PA= recode(UTA,
A = 0,
P = 1))
#al davant de "<-" posem l'arxiu nou (el que contindrà la nova variable), en aquest cas el matexi arxiu "polis.data". A vegades pot interessar crear un arxiu nou, llavors cal posar un nom nou al arxiu
#darrera "<-" posem l'arxiu on hi ha la variable que es vol transfirmar, en aquest cas "polis.data"
#"mutate" per indicar que es vol crear una nova variable, i el nom de la nova variable serà "PA". Llavors indiquem com es crea aquesta variable, que en aquest exemple és una recodificació, per tant "recode", i entre parèntesis especifiquem com cal fer aquesta recodificació. Agafa la variable original "UTA" i pel valors de "A" posa "0" i pel "P" posa "1"Ara comprovem que hagi funcionat com volem.
## 'data.frame': 19 obs. of 4 variables:
## $ ISLAND : Factor w/ 19 levels "Angeldlg","Bahiaan",..: 5 6 7 8 9 10 11 12 14 15 ...
## $ PARATIO: num 15.41 5.63 25.92 15.17 13.04 ...
## $ UTA : Factor w/ 2 levels "A","P": 2 2 2 1 2 1 1 1 1 2 ...
## $ PA : num 1 1 1 0 1 0 0 0 0 1 ...Tenim una nova variable PA que ja és numèrica i només té dos valors 0 i 1.
Perfecte, podem seguir endavant.
6.4 Exploració gràfica
Primer mirem la relació entre les variables gràficament amb la comanda plot. En la comanda indiquem:
- La variable X en primera posició: PARATIO i la base de dades on es troba polis.data separats per el símbol de dòlar.
- La variable Y en segona posició: PA i la base de dades on es troba polis.data separats per el símbol dòlar.
- Opcional: indicar que en el gràfic s’hi vegi el títol dels eixos. Aquesta comanda es posa al final i s’indica el nom de cada variable ylab=“Presence-absence of Uta” i xlab=“Perimeter/area”.
- Opcional: indicar les característiques estètiques de la gràfica com per exemple: marcar les dades en punts negres pch=16.
plot(polis.data$PARATIO,polis.data$PA, ylab="Presence-absence of Uta", xlab="Perimeter/area", pch=16)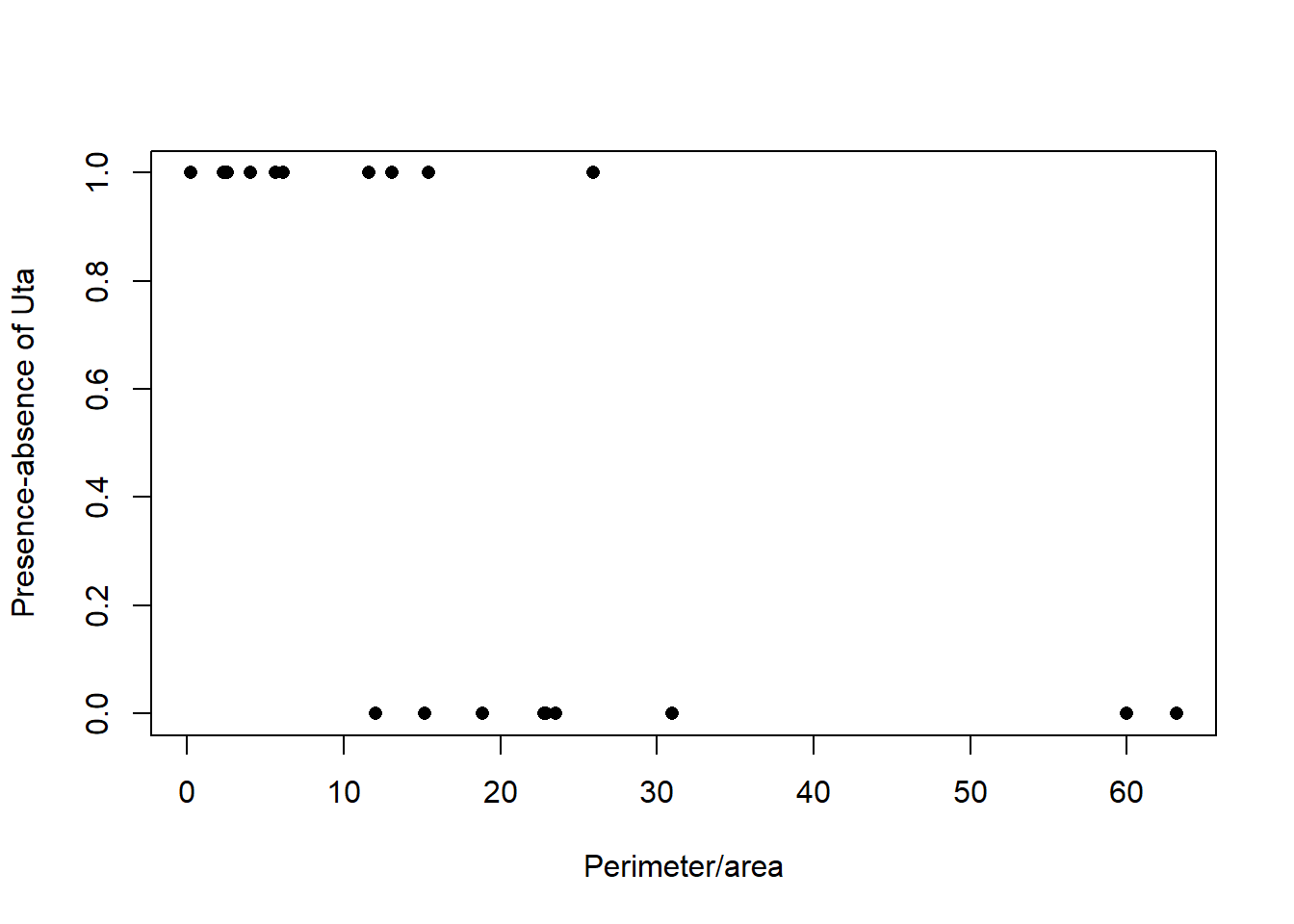
Com es veu al gràfic, la relació de les dades no s’ajusta a una regressió lineal simple sinó a una regressió binomial. Per fer aquest ajustament, utilitzarem GLM.
6.5 Fem el model de regressió amb GLM
Posar un nom a l’anàlisis (ex: uta_glm) i la comanda que utilitza és glm. Despés s’ha d’indicar entre parèntesis:
- La variable resposta (Y) PA i la explicativa (X) PARATIO separades per ~.
- La distribució que volem que s’ajusti amb la comanda family=binomial.
- La base de dades on es troben “data=polis.data”.
Fem un model nul on només tinguem en compte la Y (PA) i no tinguem en compte la X (PARATIO). Després compararem si el model amb la X és millor que el model sense .
Per fer-ho, posem un nom al model nul (ex: uta_glm0) i utilitzem la mateixa comanda que abans, però en el lloc de la variable explicativa (PARATIO), hi posem un 1.
Comprovem, comparant models, si el model que hem ajustat amb el PARATIO és millor que el nul (sense PARATIO). La comanda utlitzada és anova8 on hi indiquem:
- el model nul
- el model que hem fet amb la variable explicativa (PARATIO)
- Que ens faci la comparació, i calculi el p-valor de la chi-square test=“Chisq” .
## Analysis of Deviance Table
##
## Model 1: PA ~ 1
## Model 2: PA ~ PARATIO
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 18 26.287
## 2 17 14.221 1 12.066 0.0005134 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Si ens fixem amb el p-valor de l’anàlisi (p-valor = 0.0005134) aquest surt significatiu. Per tant, el model amb PARATIO és significativament millor que sense (model nul). És a dir, el model amb PARATIO explica millor la distribució de les dades de PA (presència i abscència dels llargandaixos).
6.6 Com detectar problemes “Overdispersion”
Si tenim overdispersion, hi ha més probabilitat de trobar diferències significatives9
Per comprovar si hi ha overdispersion:
- Mirar en els resultats del model la Residual deviance que és la variança no explicada pel model i els graus de llibertat del model.
##
## Call:
## glm(formula = PA ~ PARATIO, family = binomial, data = polis.data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.6067 -0.6382 0.2368 0.4332 2.0986
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 3.6061 1.6953 2.127 0.0334 *
## PARATIO -0.2196 0.1005 -2.184 0.0289 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 26.287 on 18 degrees of freedom
## Residual deviance: 14.221 on 17 degrees of freedom
## AIC: 18.221
##
## Number of Fisher Scoring iterations: 6Residual deviance: 14.221
graus de llibertat: 17
- Calculem el coeficient d’overdispersion: dividint la residual derviance pels graus de llibertat:
## [1] 0.8365294Coeficient d’overdispersion=0.8365294
6.6.1 Hi ha overdispersion?
- Coeficient d’overdispersion < 1 : underdispersion (augmentem l’error tipus II)
- Coeficient d’overdispersion = 1 : correcta
- Coeficient d’overdispersion > 1 : overdispersion (inflem les significacions, augmentem l’error tipus I)
Hi ha una mica d’underdispersion, quan més allunyat és el valor de 1 més gran és el problema (la diferència en el resultat del p-valor pot ser més evident). Per tant, en aquest cas és diferent de 1, però molt poquet, segurament no afecta gaire als p-valors.
Tot i que la underdispersion no és tant greu com la overdispersion, es podria aplicar una correcció com faríem en el cas d’overdispersion. Aquesta correcció no s’aplica per defecte perquè implica canvis col·laterals que a vegades no són desitjables10. Per això només es corregeix si és estrictament necessari.
6.7 Correcció per problemes d’over-underdispersion
La correcció consisteix en especificar a l’R que no utilitzi el valor de 1 com a paràmetre de dispersió, sinó que calculi la dispersió de les dades. Per fer això, cal la mateixa comanda de glm però especificant quasibinomial a la part de la família11. Així s’obté el valor de dispersió de les dades i no aplica 1, que és el que s’aplica per defecte quan no posem el “quasi”. Li donem un altre nom al model perquè no sobreescrigui la informació (p.e.: uta_glm1 ).
Mirem els resultats.
##
## Call:
## glm(formula = PA ~ PARATIO, family = quasibinomial, data = polis.data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.6067 -0.6382 0.2368 0.4332 2.0986
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.60607 1.60999 2.24 0.0388 *
## PARATIO -0.21956 0.09546 -2.30 0.0344 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasibinomial family taken to be 0.9019333)
##
## Null deviance: 26.287 on 18 degrees of freedom
## Residual deviance: 14.221 on 17 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 6Fixeu-vos que ara el Dispersion parameter no és 1, com en el model sense corregir. Això vol dir que ara hem aplicat la correcció i els p-valors ja són els adients.
Si compareu el resultat del model sense i amb la correcció, veureu que els valors dels coeficients (ordenada a l’origen = 3.60607; pendent=-0.21956) no han canviat. Això ja és correcta perquè aquesta correcció només afecta als p-valors, no als coeficients.
La Null deviance representa la variança total de la variable resposta (Y). La Residual deviance és la que queda per explicar un cop hem afegit les variables explicatives (Xs).
Per calcular la variança explicada pel model s’ha d’aplicar la fòrmula següent:
((Deviance null - Devinace residual)/Deviance null) x 100
## [1] 45.90102Variança explicada: 45.90102%
També es pot obtenir fent la següent comanda:
## [1] 45.90197D’aquesta manera no cal picar els valors de deviance, i així evitem problemes de resultats erronis per picar malament els números.
6.8 Es pot millorar el model?
Mirem els gràfics de residus.
Els gràfics de residus d’un GLM s’interpreten igual que els gràfics de residus d’una anàlisis clàssica. Ja que si el GLM està ben especificat i aplicat, transforma les dades perquè tinguin una distribució normal (vegeu lliçó GLM), i per tant, els residus han de ser el màxim de Normals possible, i no presentar problemes d’heterogeneïtat.
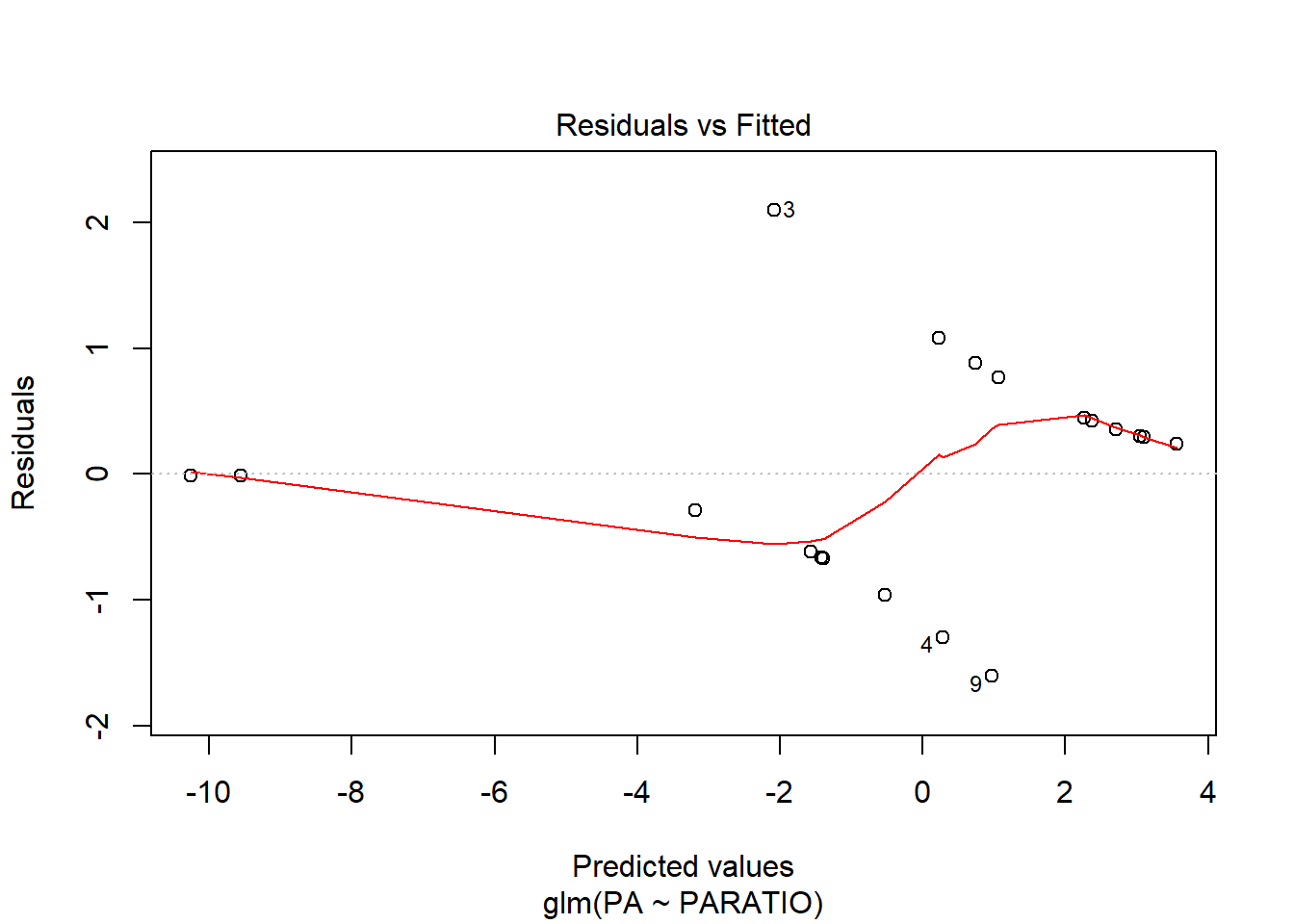
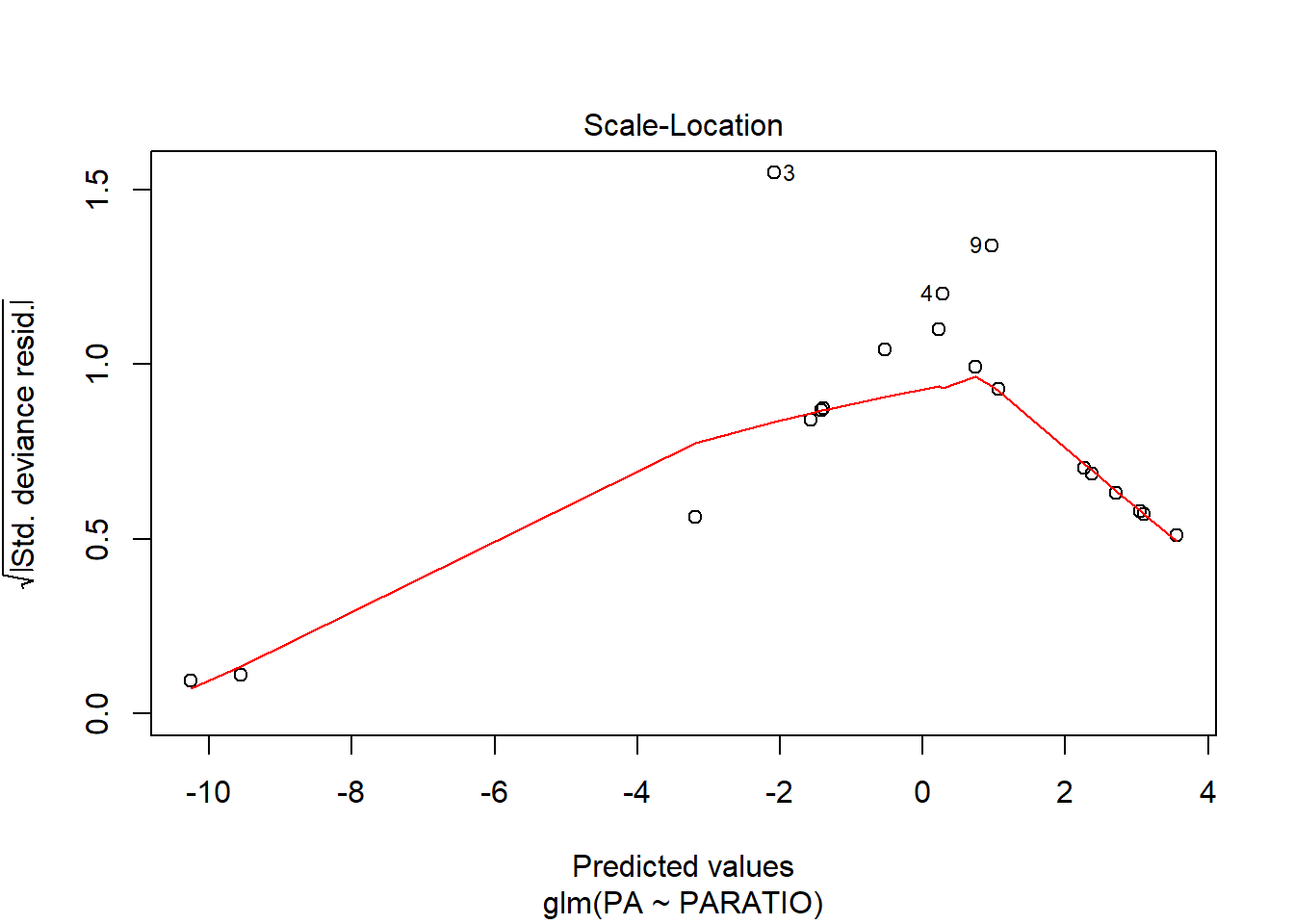
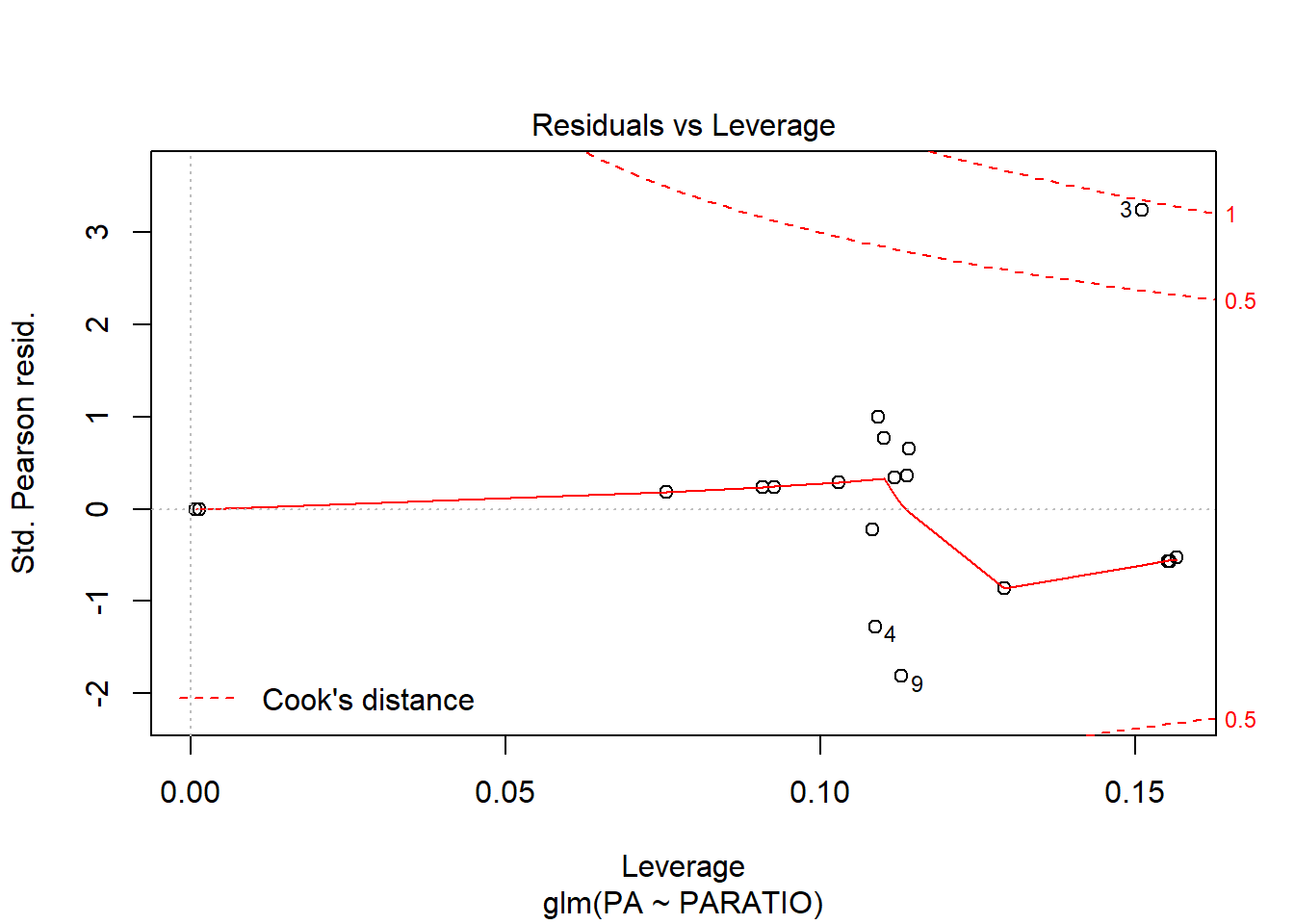
En el gràfic d’homogeneïtat de variàncies, s’observa un patró, ja que els punts estan ordenats en forma d’arc. Ara bé, aquest patró és normal en anàlisis de Ys binomials, ja que la Y només pot pendre 2 valors. El que s’ha de mirar és que els arcs no s’ajuntin més d’un costat que de l’altre. En aquest exemple estan força bé.
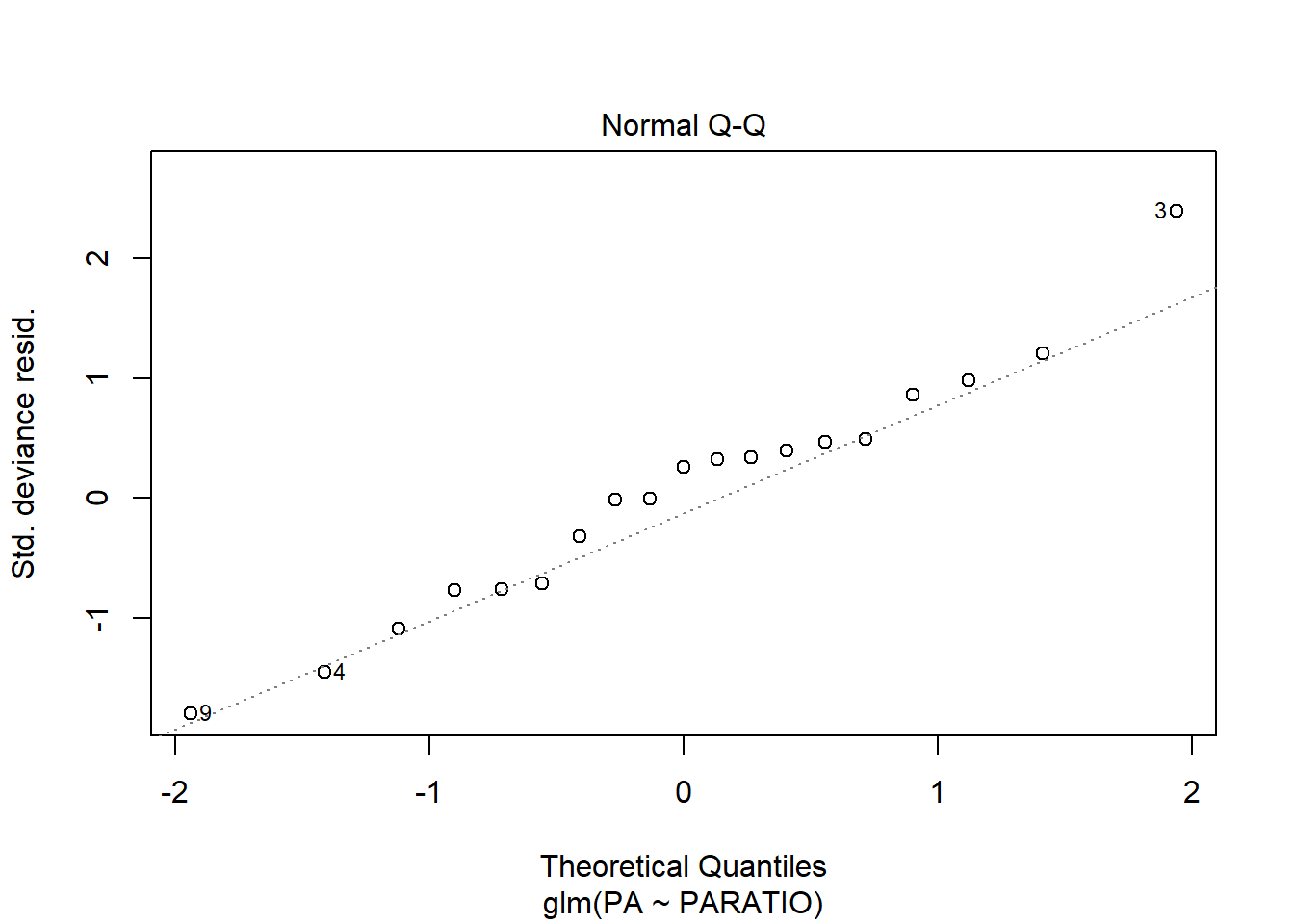
El gràfic de Normalitat també està força bé, i pel que fa la distància de Cook veiem que hi ha un cas que està a punt sobrepassar el límit de 1, però entra dins el marge de seguretat, i per tant no seria un problema.
Així doncs la distribució de residus sembla prou bona, però potser la podem millora transformant les varables12.
Però, potser es pot millorar transformant les variables explicatives Xs. Per saber-ho, fem un histograma de la varaible explicativa (x) PARATIO.
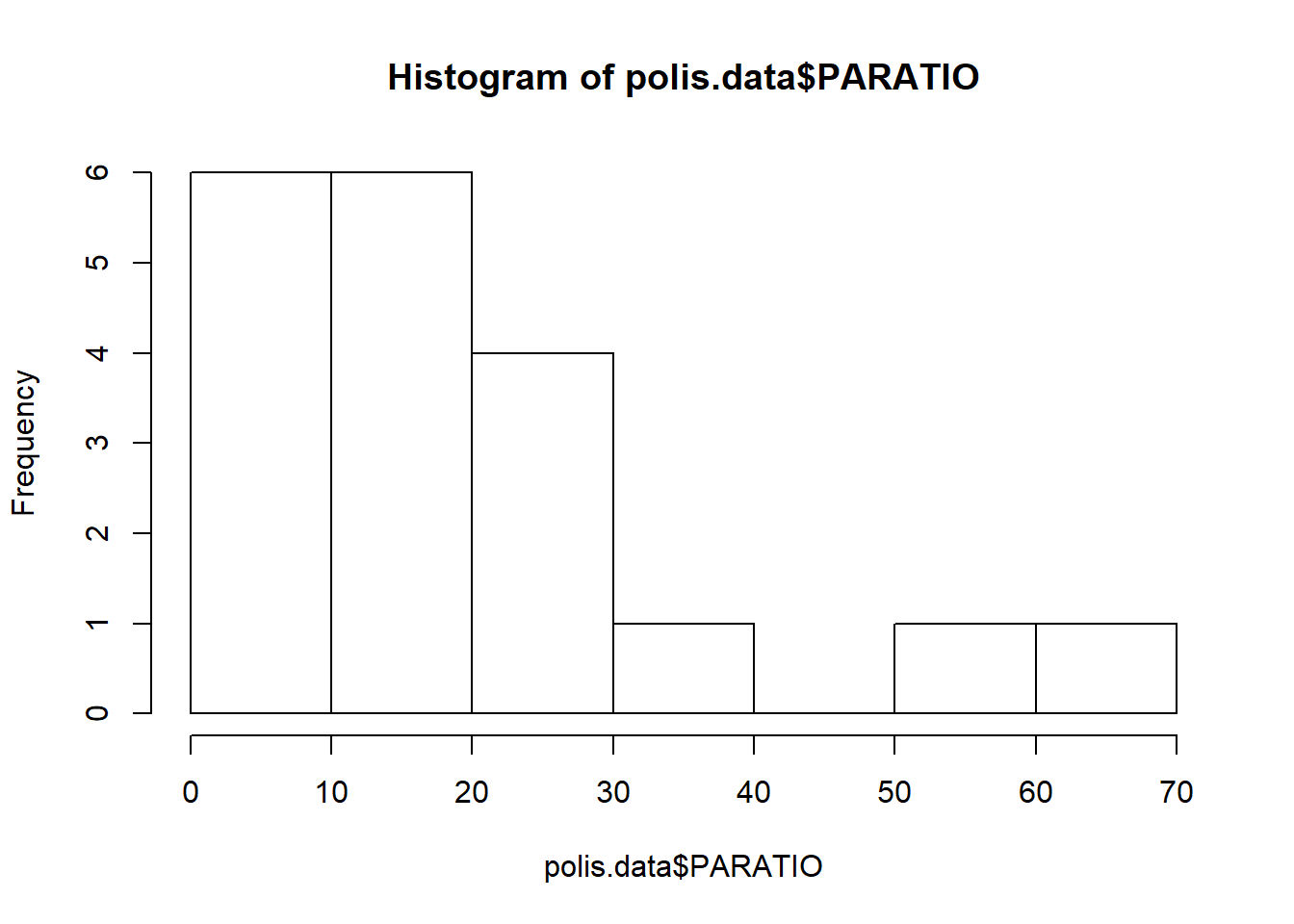
S’observa un biaix a la dreta. Per corregir-ho es pot transformar logarítmicament la PARATIO. Ho podem fer directament indicant en la comanda glm que faci el logaritme ( log) de PARATIO. Al nou model li posem un altre nom com per exemple: uta_glm2.
Mirem els gràfics de residus per veure si són millors que els del model sense transformar la X.
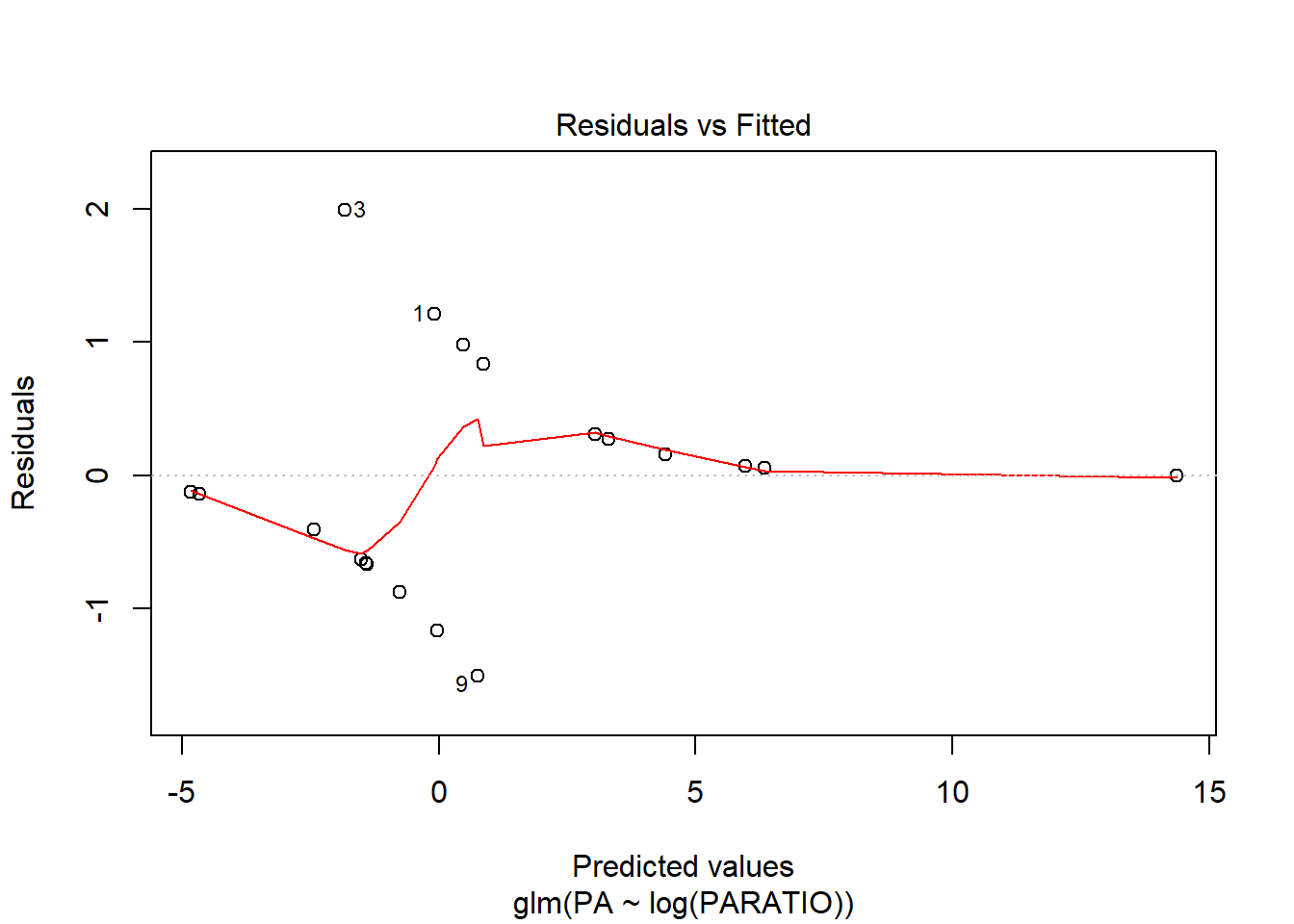
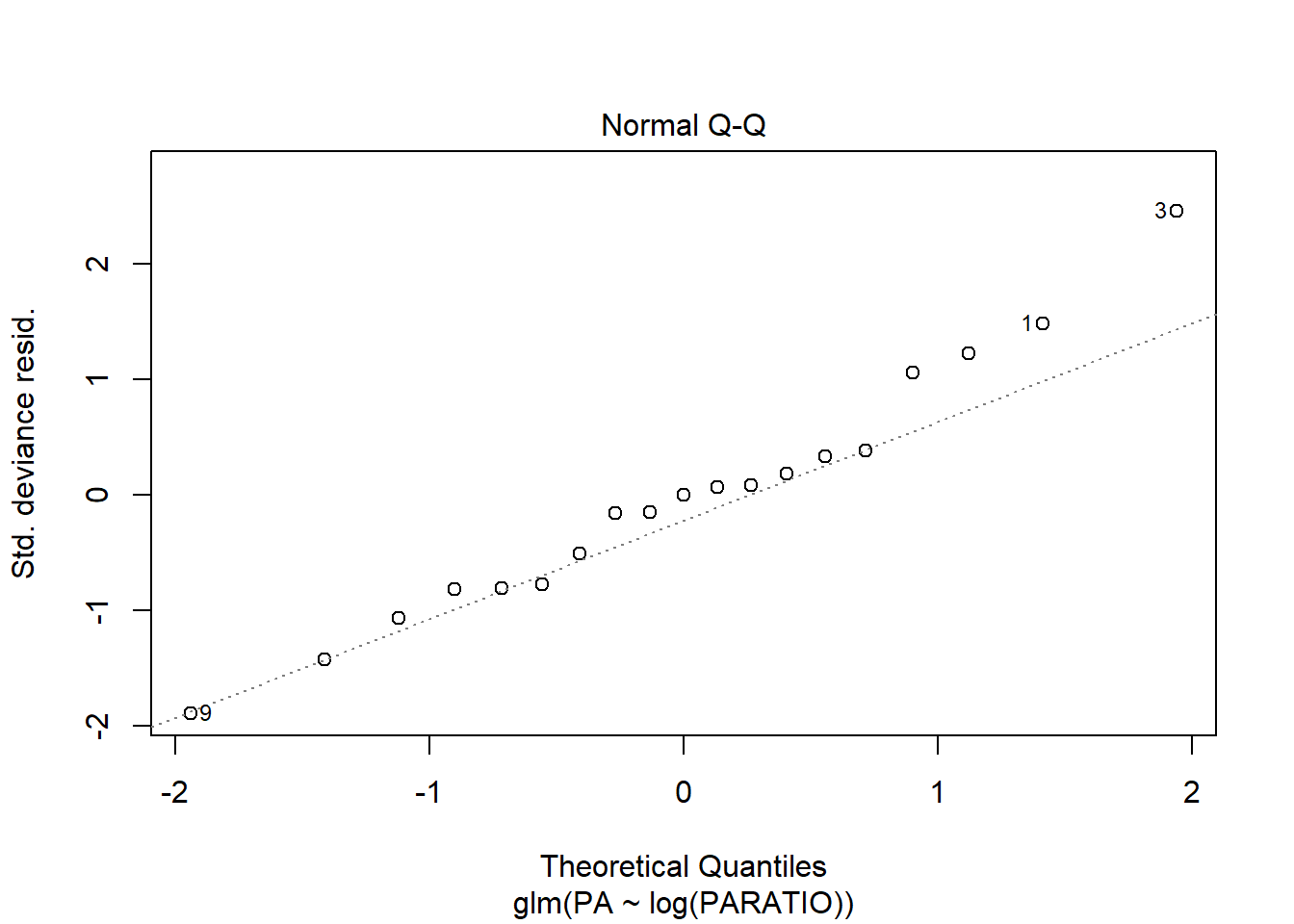
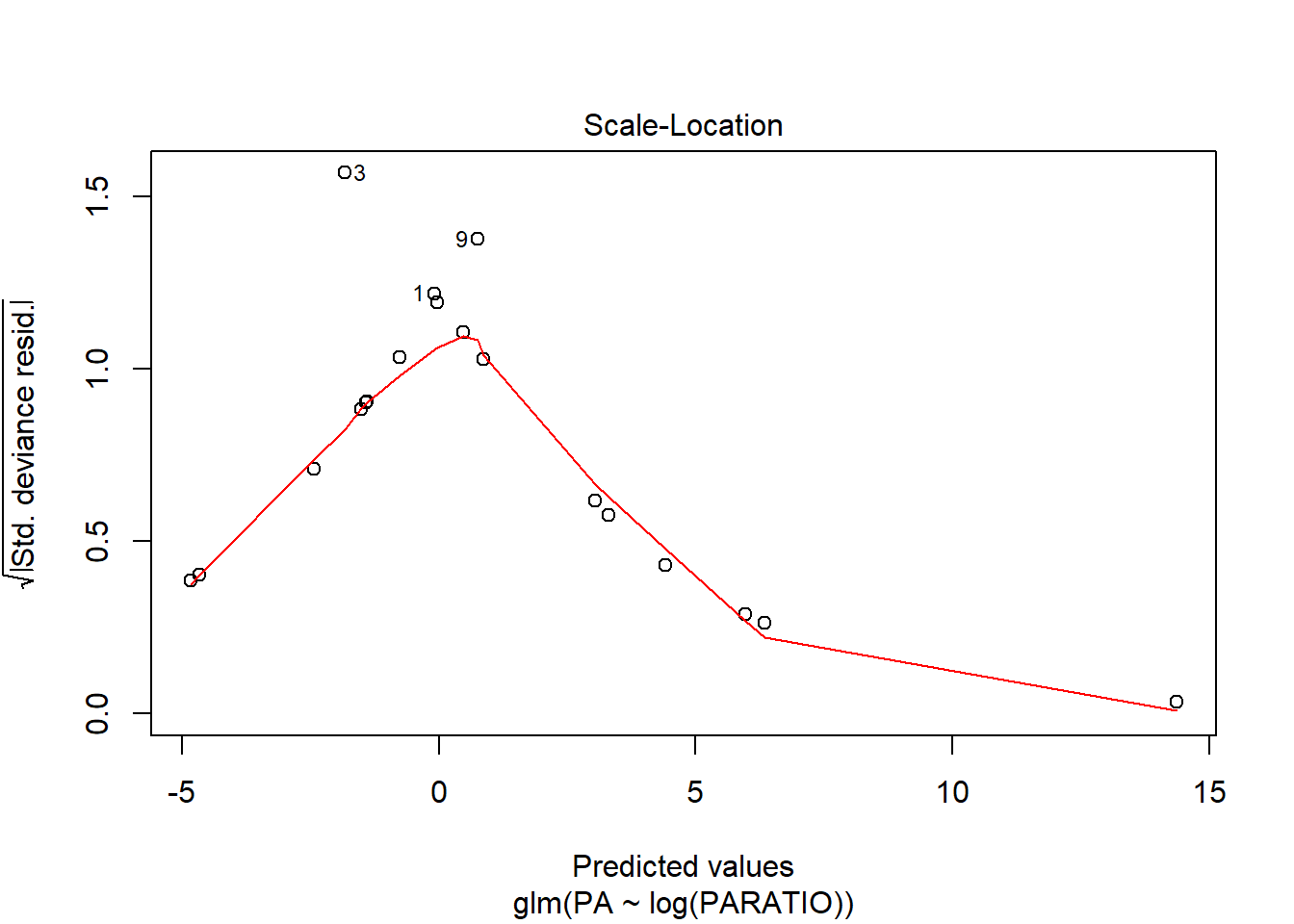
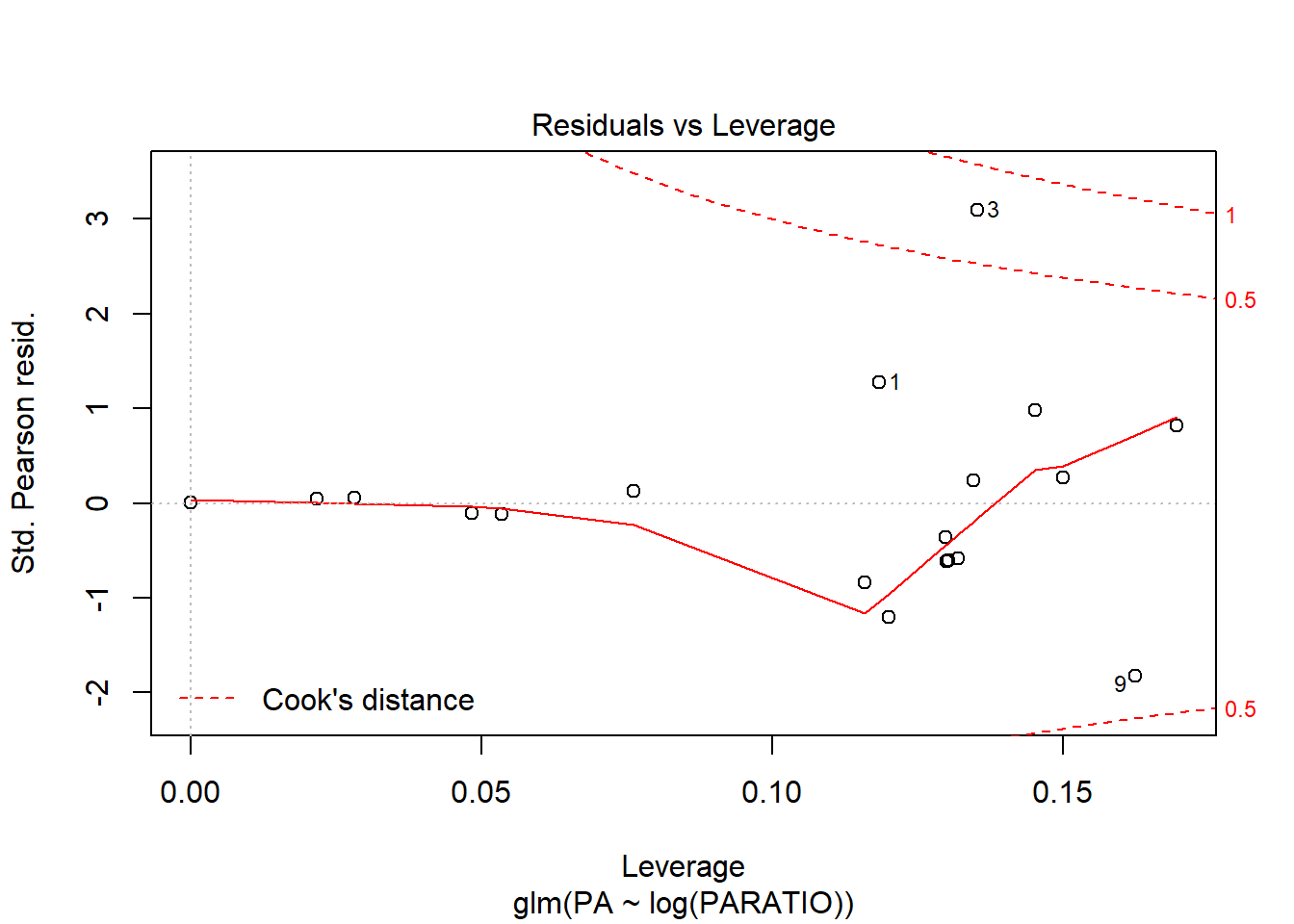
Els canvi és mínim, així que no val la pena fer la transformació. Ens quedem amb el model inicial.
6.9 Representem gràficament la relació
Utlitzarem un script adaptat de http://zoonek2.free.fr/UNIX/48_R/12.html#4
- Dibuixem la relació:
- Indiquem que la variable X és PARATIO.
- Indiquem que la variable Y és PA
- Creem un model glm amb les variables “X” i “Y”. Tornem a utilitzar la comanda glm i indiquem que relacioni la “X” i la “Y” separades per un ~ i la distribució binomial. Li donem un nom nou com per exemple modelplot.
- Fem el gràfic amb la comanda plot on indiquem que utilitzi la y i la x i que posi el noms a aquestes dos variables al gràfic xlab=“Perimeter/area ratio” i ylab=“Presence-Absence of lizards (Uta) on the islands”.
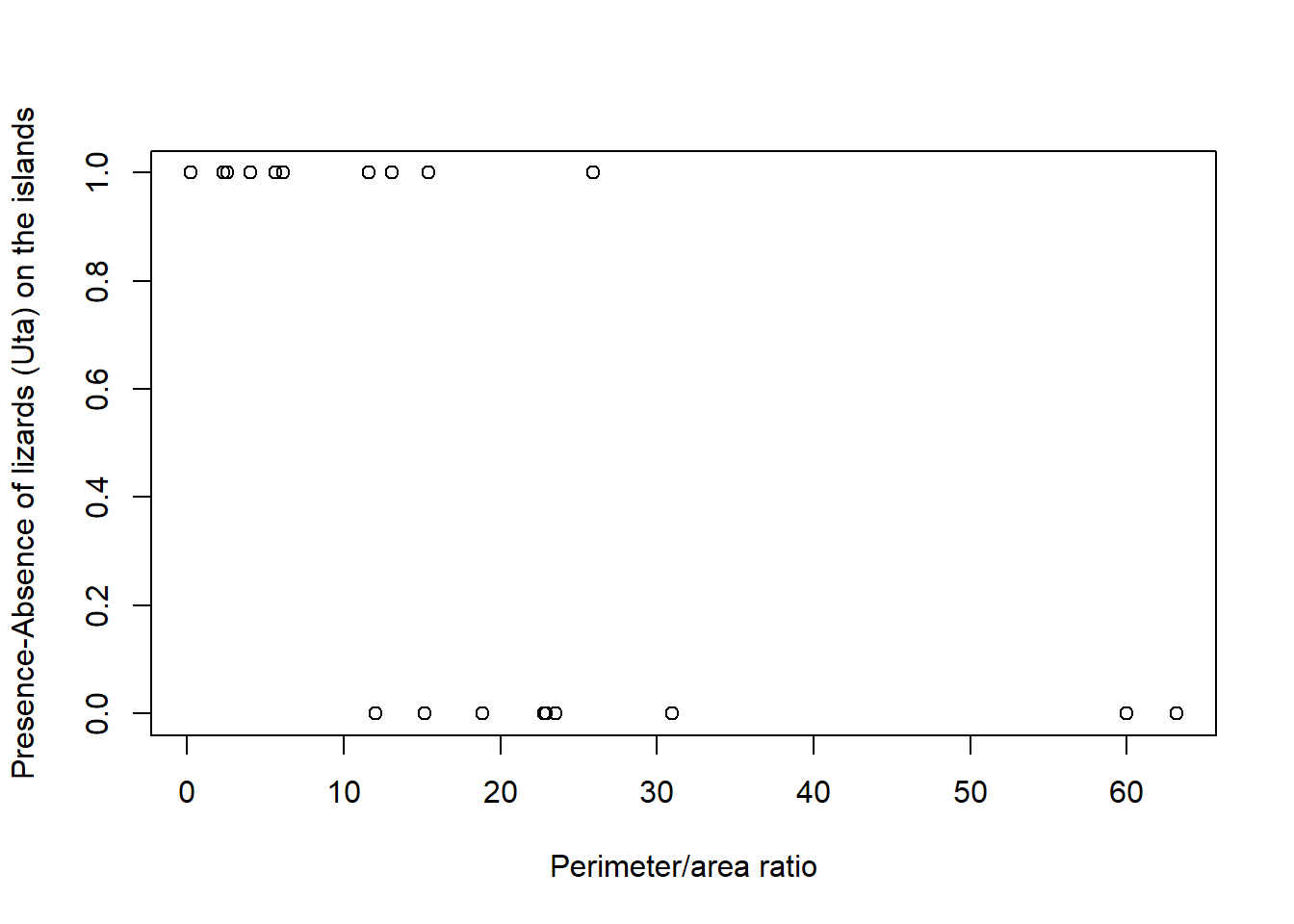
- Dibuixem la línia de l’ajustament binomial. Utilitzem tres comandes:
- Determinem el rang de valors de X ( xx) va fins a 100 amb la comanda seq(min(x), max(x), length=100).
- Determinem que la variable y ( yy) es predigui amb la comanda predict segons el model nou que hem creat modelplot a partir de les dades de la variable x data.frame(x=xx), type=‘response’.
- Dibuixem la linea lines que relaciona les variables x i y (xx,yy).
plot(y~x,xlab="Perimeter/area ratio", ylab="Presence of lizards (Uta) on the islands")
xx <- seq(min(x), max(x), length=100)
yy <- predict(modelplot, data.frame(x=xx), type='response')
lines(xx,yy)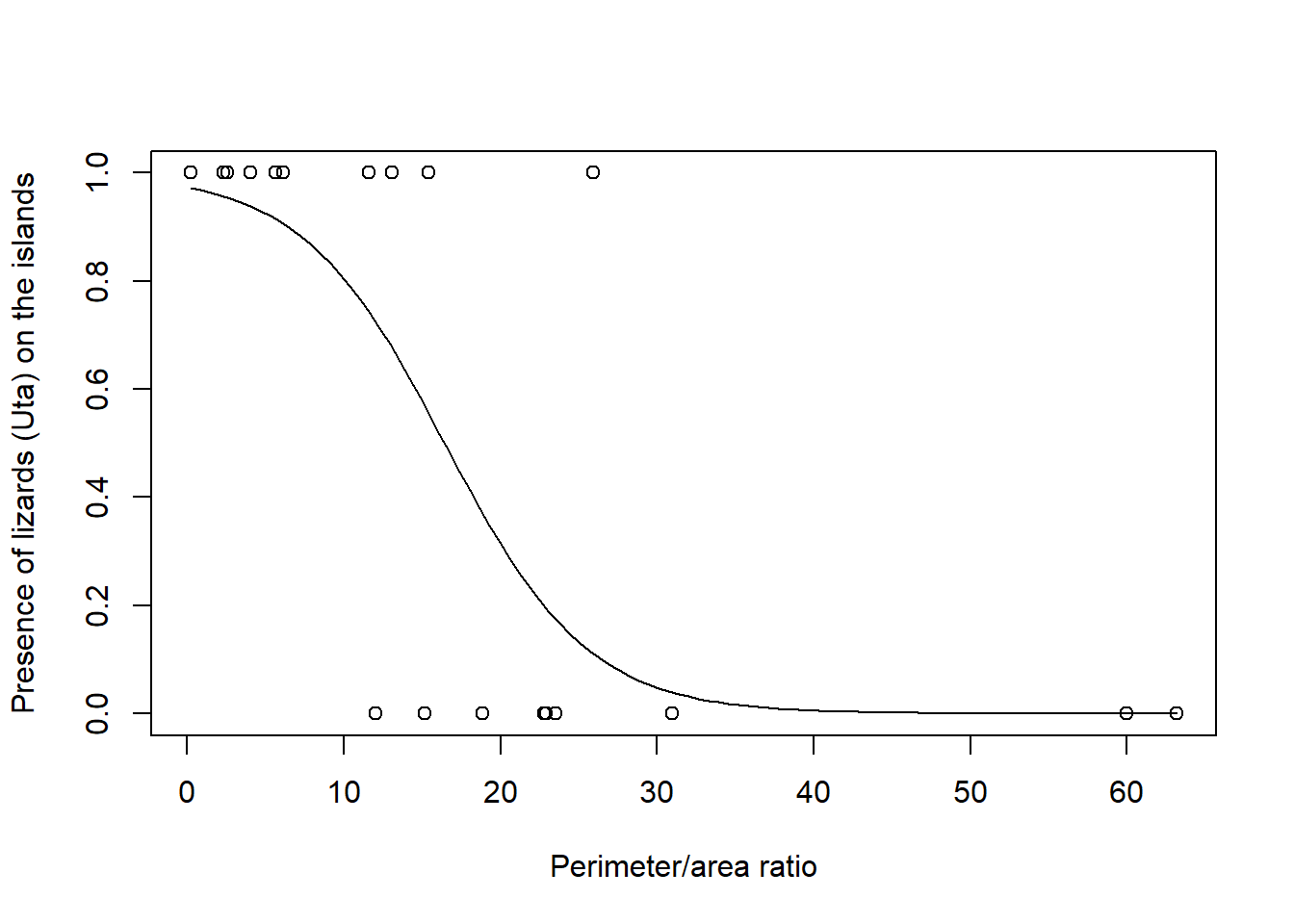
Si mirem el gràfic i el símbol del pendent de la regressió, veiem que la relació és negativa. Per tant, a més PARATIO més probabilitats de NO trobar llangardaixos del gènere Uta.
en aquest cas l’anàlisi que es vol fer és una regressió, per mirar la relació entre 2 variables i quantificar-la, però com que Y no és normal, no podem fer la regressió amb el mètode clàssic i la fem amb un mètode modern (GLM) que permet altres distribucions, com la binomial.↩︎
podeu consultar el cheatsheet per veure un resum de tot el que es pot fer amb aquest package: https://raw.githubusercontent.com/rstudio/cheatsheets/master/data-transformation.pdf↩︎
aquesta anova no vol dir que farà una ANOVA d’un factor, sinò que compararà models, i mirarà si explica més o menys. Si no troba diferències entre models, vol dir que el model amb la variable X és igual de bo explicant variacions de Y que un model sense aquella X, per tant aquella X no aporta res alhora d’explicar la variabilitat de Y (no cal posar-la al model)↩︎
Per defecte, en GLM amb distribucions Binomial i Poisson s’aplica un paràmetre de dispersió=1. Aquest paràmetre de dispersió es clau per calcular correctament els p-valors, d’aquí la seva importància, ja que si tenim problemes d’over o underdispersion el p-valor no estarà correctament calculat (augmentat les probabilitats d’error tipus I o II). Per entendre això, heu de pensar en com funcionen les taules estadístiques per calcular p-valors, normalment especifiqueu, graus de llibertat i tipus de distribució, i podeu trobar el p-valor. Doncs seria com posar malament els graus de llibertat, també us tornaria un p-valor erroni.↩︎
el canvi més rellevant quan s’aplica aquesta correcció és que no es pot calcular l’AIC, i això dificulta la selecció de models automatizada, per exemple via “stepAIC”.↩︎
quasibinomial no és un tipus de família d’error (tipus de distribució de dades), sinó que especificant quasi davant la distribució binomial és la manera de dir a R que calculi la dispersió de les dades i no utilitzi el paràmetre per defecte=1↩︎
Molt important!!! quan s’apliquen GLM NO podeu transformar la Y, ja que quan es fa un GLM ja es transforma la Y, via link (veure lliçó GLM)↩︎