2 Contrastos “Lliures”

Contrastos No Paramètrics

Autors: Muñoz R. & Gascón S.

A la secció anterior hem vist com determinar si existeixen diferències entre les mitjanes d’un seguit de grups (i.e. 2 o 2+ grups) mitjançant la prova de l’ANOVA. No obstant, l’ANOVA té un supòsits que s’han de complir per tal que els resultats i conclusions siguen veritables. Aquesta sessió vos servirà per explorar algunes possibilitats d’anàlisis no-paramètrics amb R quan els supòsits de l’ANOVA no es compleixen. En concret, es veurà com fer anàlisis alternatives a l’ANOVA quan hi ha manca de Normalitat en els residus o Heteroscedasticitat a les variàncies.

2.1 Les dades

Treballarem amb dos exemples diferents:

  1. Dades no publicades de Sokal and Rohlf (1997) on s’analitza l’efecte de diferents tractaments de sucre (Control, 2% glucosa, 2% fructosa, 1% glucosa i 1% fructosa, i 2% sucrosa) sobre la llargada de la bajoca d’uns pèsols. Exemple extret de Logan, M. 2010. Biostatistical Design and Analysis Using R: a practical guide. Wiley-Blackwell.

  2. Dades provinents d’un estudi realitzat amb la finalitat d’avaluar l’estat de la població de gambúsia (Gambusia holbrookii) en 4 basses dels aiguamolls de l’Empordà.

El primer exemple ens durà a una distribució de residus Normal però Heteroscedàstica on aplicarem el test de Welch (oneway.test()) (Taula 1).

Per contra, al segon exemple la distribució de residus resultant és No normal però Homoscedàstica i haurem d’aplicar el test de Kruskal-Wallis (kruskal.test()) (Taula 1).

## Warning: package 'knitr' was built under R version 3.5.3
Table 2.1: Taula 1. Contrastos adequats per a cada tipus de distribució dels residus
Homoscedasticitat Heteroscedasticitat
Normal ANOVA Welch
No normal Kruskal-Wallis -

2.2 Flux general de treball

La mecànica de les anàlisis que es descriuen, és la següent:

  1. Carregar dades.

  2. Visualització i exploració de les dades.

  3. ANOVA amb les dades originals.

  4. Comprovar que els supòsits es compleixen.

Comprovació mitjançant dos plantejaments diferent:

  1. Mitjançant proves estadístiques per a comprovar que existeix Normalitat (Shairo-Wilk) i Homoscedasticitat de variàncies (Levene).

  2. Mitjançant l’estudi dels gràfics de residus.

  1. Si cap dels supòsits no es compleix, transformació de les dades per poder aplicar ANOVA perquè ANOVA és més robusta.

  2. Fer una ANOVA amb les dades transformades.

  3. Comprovar que els supòsits es compleixen.

  4. Si tot i així els supòsits no es compleixen: aplicar test no-paramètric adequat per als supòsits que no es compleixen (i.e. Welch o Kruskal-Wallis).

Alerta! Els exemples triats obliguen a usar algun contrast no-paramètric però al treball amb dades i en el futur podrien complir-se d’entrada, i no caldre fer cap transformació. També podria passar que en transformar les dades es complisquen els supòsits de l’ANOVA per la qual cosa no caldria aplicar cap test no-paramètric.

2.3 Preliminars: instal·lar i carregar paquets amb funcions addicionals

R a més d’esser un llenguatge de programació és una eina d’anàlisi. Això fa que en obrir R mitjançat l’Rstudio tot un seguit de funcions estiga disponible (e.g. summary(), plot(), lm(), etc.). No obstant, ens poden caldre funcions addicionals per a les anàlisis que volem realitzar. Aquestes funcions estan contingudes en el que s’anomena paquets (packages). Hi ha diversos servidors que alberguen paquets però el més important és CRAN.

Una vegada hem decidit quina o quines funcions ens calen per a fer una anàlisi, i a quin paquet estan contingudes, cal instal·lar el paquet. Existeixen diverses formes d’instal·lar un paquet. Una força habitual consisteix a usar la funció install.packages():

install.packages("car")

install.packages("plotrix")

install.packages("FSA")

On “car”, “plotrix” i “dunn.test” són els noms dels paquets que contenen les funcions que usarem en aquesta pràctica. Alerta! El paquets sols cal instal·lar-los una vegada ja que romanen instal·lats a l’ordinador de forma permanent.

Quan instal·leu els paquets veureu coses com ara: “U:/Rafa/Documents/R/win-library/3.6”. Açò indica la ruta on s’emmagatzemen els paquets i variarà en el vostre cas.

És molt important que el nom del paquet vaja entre " " o R tractarà de trobar un objecte al Global Environment de nom “car” o, “plotrix”, o “dunn.test”.

Instal·lar un paquet no implica que les funcions que hi conté estiguen disponibles a la nostra sessió. Cal carregar-les a la sessió cada vegada que les volem usar. Açò alleugereix R en reduir la quantitat d’informació que cal processar a l’inici de la sessió.

Per a carregar un paquet en una sessió de treball s’empra la funció library():

library("car")
## Warning: package 'car' was built under R version 3.5.3
## Loading required package: carData
library("plotrix") # ens permetrà usar la funció std.error()
## Warning: package 'plotrix' was built under R version 3.5.3
library("FSA") # ens permetrà usar la funció dunnTest() al 2n exemple
## Warning: package 'FSA' was built under R version 3.5.3
## ## FSA v0.8.30. See citation('FSA') if used in publication.
## ## Run fishR() for related website and fishR('IFAR') for related book.
## 
## Attaching package: 'FSA'
## The following object is masked from 'package:car':
## 
##     bootCase

  • Si apareix Warning no passa res, sol ser un avís perquè la versió del paquet és anterior a la nostra versió R. En general, no és un problema i els paquets funcionen bé, però poden aparèixer incompatibilitats.

  • Si apareix Loading vol dir que per funcionar el paquet que volem ‘activar’ cal carregar altres paquets. R ho detecta i ho fa automàticament.

Test de Welch: Normalitat i Heteroscedasticitat dels residus

2.3.1 Carregar dades i comprovar que s’ha fet correctament

Com ja ha estat explicat a la sessió anterior, per tal que R trobe l’arxiu a cada sessió cal definir quina és la nostra carpeta (directori) de treball.

Aquesta tasca es fa mitjançant la funció set working directory (setwd()).

setwd("U:/Docència/Girona/AAD - R markdown/Contrastos no-paramètrics/")

En el vostre cas haureu de substituir: “U:/Docència/Girona/AAD - R markdown/Contrastos no-paramètrics/” per la vostra ruta. Alerta! Els símbols / han d’estar orientats cap a la dreta.

Una vegada indicat el directori de treball podem carregar les dades a R.

load("purves.RData")
  1. purves.RData és el nom que li donem a la taula de dades en format R (objecte).
  2. Sobretot les dades han d’estar enmagatzemades en el directori de treball

Una vegada han estat carregades i assignades les dades cal comprovar que no ens hem equivocat. Existeixen diverses formes de saber si les dades han estat carregades correctament. A banda de mirar les característiques de l’objecte a la finestra superior dreta d’RStudio anomenada Global Environment, des de la consola R tenim diverses opcions. En el context d’AAD, la combinació de dim() i summary() és la més recomanable.

dim(purves.dat)
## [1] 50  2
summary(purves.dat)
##       TREAT        LENGTH     
##  Control :10   Min.   :56.00  
##  Fructose:10   1st Qu.:58.00  
##  GlucFruc:10   Median :60.50  
##  Glucose :10   Mean   :61.94  
##  Sucrose :10   3rd Qu.:65.00  
##                Max.   :76.00

Gràcies a la funció dim() podem veure que el data frame (i.e. taula de dades) purves.dat conté 50 línies/dades i dues columnes. Aquestes consisteixen en dues variables (i.e. TREAT i LENGTH). La variable TREAT és una variable/columna categòrica (factor) amb 5 categories o levels i 10 dades per categoria. Per contra la variable/columna LENGTH és una variable continua de mitjana 61.94 i amb mínim 56 i màxim 76.

La funció summary() ens dóna informació sobre el contingut i natura de cada variable. No obstant però, és habitual realitzar una exploració gràfica de cada variable per separat i/o bé de la relació entre variables. Tenint en compte els objectius de la sessió optem per la segona opció. Vos recomanem usar la funció plot() amb les dues variables d’interès per observar la presència d’alguna mena de relació entre les dues.

Gràcies a la funció summary() sabem que la variable TREAT és un factor. Llavors, la funció plot() generarà un seguit de boxplots, un per a cada categoria. Per tal de millorar l’aparença del gràfic, primer podem definir un vector, amb els seus elements anomenats, on assignarem un color per a cada categoria de la variable/columna TREAT. Per a conèixer les categories d’aquesta variable podeu usar la funció levels() com es mostra a continuació. Podeu descarregar un manual amb el nom dels colors més habituals picant aquí: RColor.

levels(purves.dat$TREAT) ## Permet obtindre les diferents categories de la columna 'TREAT' al data frame 'purves.dat'.
## [1] "Control"  "Fructose" "GlucFruc" "Glucose"  "Sucrose"
Colors <- c(Control="dodgerblue",  Glucose="deeppink",  Fructose="seagreen", GlucFruc="yellow", Sucrose="darkblue") # Vector de 5 colors, un per a cadascuna de les categories a la variable/columna 'TREAT' del data frame 'purves.dat'. 

Colors # Vector resultant
##      Control      Glucose     Fructose     GlucFruc      Sucrose 
## "dodgerblue"   "deeppink"   "seagreen"     "yellow"   "darkblue"
str(Colors) # estructura de l'objecte
##  Named chr [1:5] "dodgerblue" "deeppink" "seagreen" "yellow" ...
##  - attr(*, "names")= chr [1:5] "Control" "Glucose" "Fructose" "GlucFruc" ...
plot(x=purves.dat$TREAT, y=purves.dat$LENGTH,
     xlab="Tractament", ylab="Longitud (cm)",
     col=Colors,
     frame=F)

legend("topright",
       legend=levels(purves.dat$TREAT),
       fill=Colors,
       ncol=3,
       bty="n")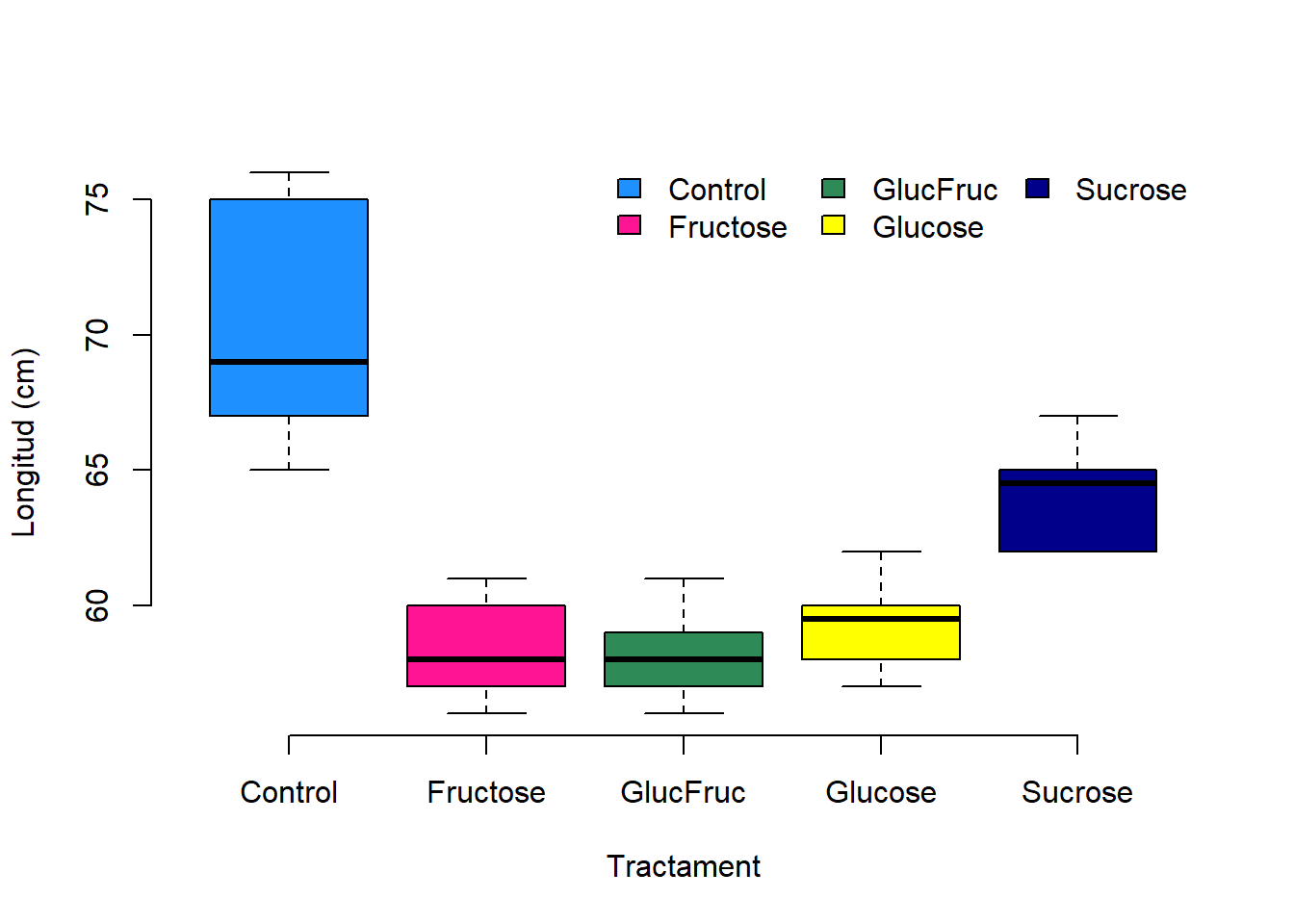
Box plots de les longituds de les bajoques dels pèsols corresponent a cada tractament i control

Figure 2.1: Box plots de les longituds de les bajoques dels pèsols corresponent a cada tractament i control

Pel que fa als arguments:

  1. x és la variable usada a l’eix x.
  2. y és la variable usada a l’eix y.
  3. col determina el color del les caixes.
  4. xlab determina l’etiqueta (label) usat per a l’eix x.
  5. ylab determina l’etiqueta (label) usat per a l’eix y.
  6. frame elimina la caixa que envolta el plot igual que bty=“n”. S’usa quan la variable x és categòrica i es generen boxplots. És un argument merament estètic.

A continuació es mostra un altre exemple de l’ús de la funció legend(). Serveix per a afegir la llegenda a la cantonada superior dreta (“topright”).

Pel que fa als arguments:

  1. “topright” indica la posició.
  2. legend el text/etiquetes. En aquest cas s’ha fet coincidir amb les categories que conté la variable TREAT mitjançant la fórmula “levels(purves.dat$TREAT)”.
  3. fill determina el color dels rectangles. En aquest cas s’ha fet coincidir amb les categories que conté la variable TREAT mitjançant el vector Colors.
  4. ncol determina que la llegenda té tres columnes.
  5. bty elimina la caixa que envolta el plot. És un argument merament estètic.

Podeu mirar altres opcions de la funció legend() picant help(legend).

La figura mostra que les bajoques de control són les més llargues i variables de totes. Mentre que les longituds corresponents als tractaments amb 2% glucosa, 2% fructosa i 1% glucosa i 1% fructosa mostren les menors longituds i són força semblants. Les bajoques del tractament amb un 2% sucrosa mostren longituds intermèdies.

2.3.2 ANOVA i comprovació de supòsits amb dades originals

Seguint el flux general de treball indicat a l’inici del document, primer cal fer una ANOVA amb les dades originals i seguidament comprovar que es compleixen els supòsits: numèricament i gràficament. Alerta! Els supòsits es miren dels residus. Per tant, cal fer primer l’ANOVA, i una vegada feta, comprovar si els seus residus compleixen els supòsits. Com hem vist a la sessió anterior, per tal de realitzar l’anàlisi d’ANOVA utilitzem la funció lm() (linear model):

length_anova <- lm(LENGTH~TREAT, data=purves.dat)

Pel que fa als arguments:

  1. length_anova és l’objecte que contindrà l’anàlisi.
  2. LENGTH és la variable depenent (y).
  3. ~ és el signe que indica la relació o =.
  4. TREAT és la variable independent/explicativa (x).
  5. data=purves.dat indica d’on s’han de extraure les variables (i.e. columnes de dades).

2.3.2.1 Comprovació numèrica dels supòsits amb dades originals

Amb la funció leveneTest() es fa el test de Levene del model d’ANOVA per comprovar que existeix Homoscedasticitat de variàncies. Com a únic argument cal introduir el nom del model de l’ANOVA i la funció extrau els residus del model. Les hipòtesis de l’anàlisi són:

  • Ho: Homoscedasticitat de variàncies
  • Ha: Heteroscedasticitat de variàncies
leveneTest(length_anova) # funció que aplica el test de Levene
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value   Pr(>F)   
## group  4  4.5767 0.003468 **
##       45                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

S’observa un p-valor significatiu, ja que és inferior a 0.05 ( p-valor = 0.003468). Això indica que hi ha evidències suficients com per a rebutjar la hipòtesi nul·la.

Per tant, NO és compleix el supòsit d’Homoscedasticitat de variàncies.

Seguidament cal comprovem el supòsit de Normalitat mitjançant el test de Shapiro-Wilk.

Per tal d’aplicar-lo s’utilitza la funció shapiro.test() i dins el parèntesis el nom del model “length_anova” seguit per “$res” indica a R on ha d’anar a buscar els residus dins el model “length_anova”. Les hipòtesis de l’anàlisi són:

  • Ho: Normalitat
  • Ha: Manca de Normalitat
shapiro.test(length_anova$res)  # funció que aplica el test de Shapiro-Wilk
## 
## 	Shapiro-Wilk normality test
## 
## data:  length_anova$res
## W = 0.96928, p-value = 0.2164

S’observa un p-valor NO significatiu, ja que és superior 0.05 ( p-valor = 0.2164). Això indica que no hi ha evidències suficients com per rebutjar la hipòtesis nul·la.

Per tant, SÍ que es compleix el supòsit de Normalitat.

CONCLUSIONS

Les proves estadístiques indiquen que els residus són:

  • Normals
  • Heteroscedàstics

2.3.2.2 Comprovació gràfica dels supòsits amb dades originals

A la sessió anterior hem definit una funció anomenada mcheck() per comprovar gràficament els supòsits de l’ANOVA. No obstant, en aplicar la funció plot() a un objecte obtingut mitjançant la funció lm(), R ja genera 4 plots de diagnòstic, el que simplifica el procés. Alerta! És molt important que abans d’usar la funció plot() piqueu par(mfrow=c(2, 2)) o sols veureu l’últim plot.

par(mfrow=c(2, 2), bty="n") # paràmetres del plot. mfrow=c(2,2) indica dos plots en una única fila. bty="n" elimina la caixa que envolta el plot. És un argument merament estètic.

plot(length_anova)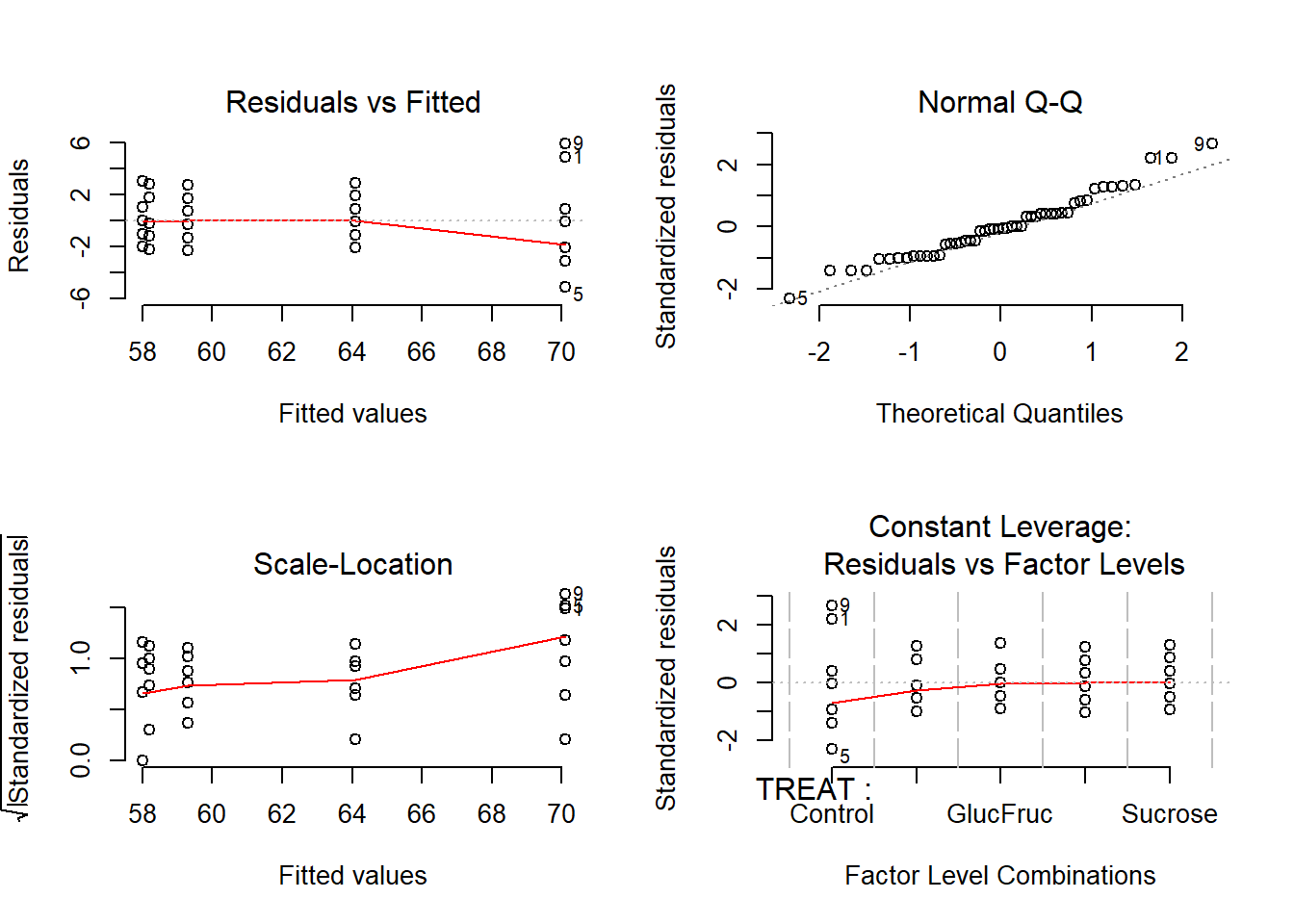
Plots de diagnosi de l'ANOVA amb les longituds de les bajoques de pèsol originals.

Figure 2.2: Plots de diagnosi de l’ANOVA amb les longituds de les bajoques de pèsol originals.

El primer plot mostra els valors calculats (i.e. mitjanes per a cada categoria) i els residus. El segon mostra el Normal Q-Q Plot i permet comprovar si els quantils dels residus s’ajusten als d’una distribució normal amb la mateixa mitjana i distribució estàndard. El tercer, que encara no havíem vist, s’anomena ‘Scale Location Plot’. És molt similar al primer gràfic, però simplifica l’anàlisi de la suposició de l’homoscedasticitat. En principi cal que:

  • La línia roja siga aproximadament horitzontal.
  • L’amplitud del valors al voltant de la línia roja siga aproximadament constant.

L’últim plot és molt semblant al primer però mostra les categories en compte dels valors mitjans calculats per a cada categoria.

Pel que fa a la interpretació dels gràfics, aquests confirmen els resultats obtinguts a la comprovació numèrica dels supòsits. Els gràfics mostren que la categoria Control té una variància superior el que provoca una lleugera tendència a l’Scale Location Plot (cantonada inferior esquerre) ja que la línia roja no és completament horitzontal. Aquesta tendència és indicativa d’heteroscedasticitat. Per contra el Normal Q-Q Plot (cantonada superior dreta) no indica una desviació clara de la distribució de residus respecte de la distribució normal d’igual mitjana i desviació típica.

2.3.2.3 Transformació i comprovació de la transformació

Abans d’aplicar un test no-paramètric sempre mirem de transformar les dades per poder aplicar ANOVA perquè ANOVA és més robusta. Per tal de decidir quina mena de transformació és la més adequada el més habitual és fer un histograma amb la funció hist() i comprovar cap on apareix el biaix.

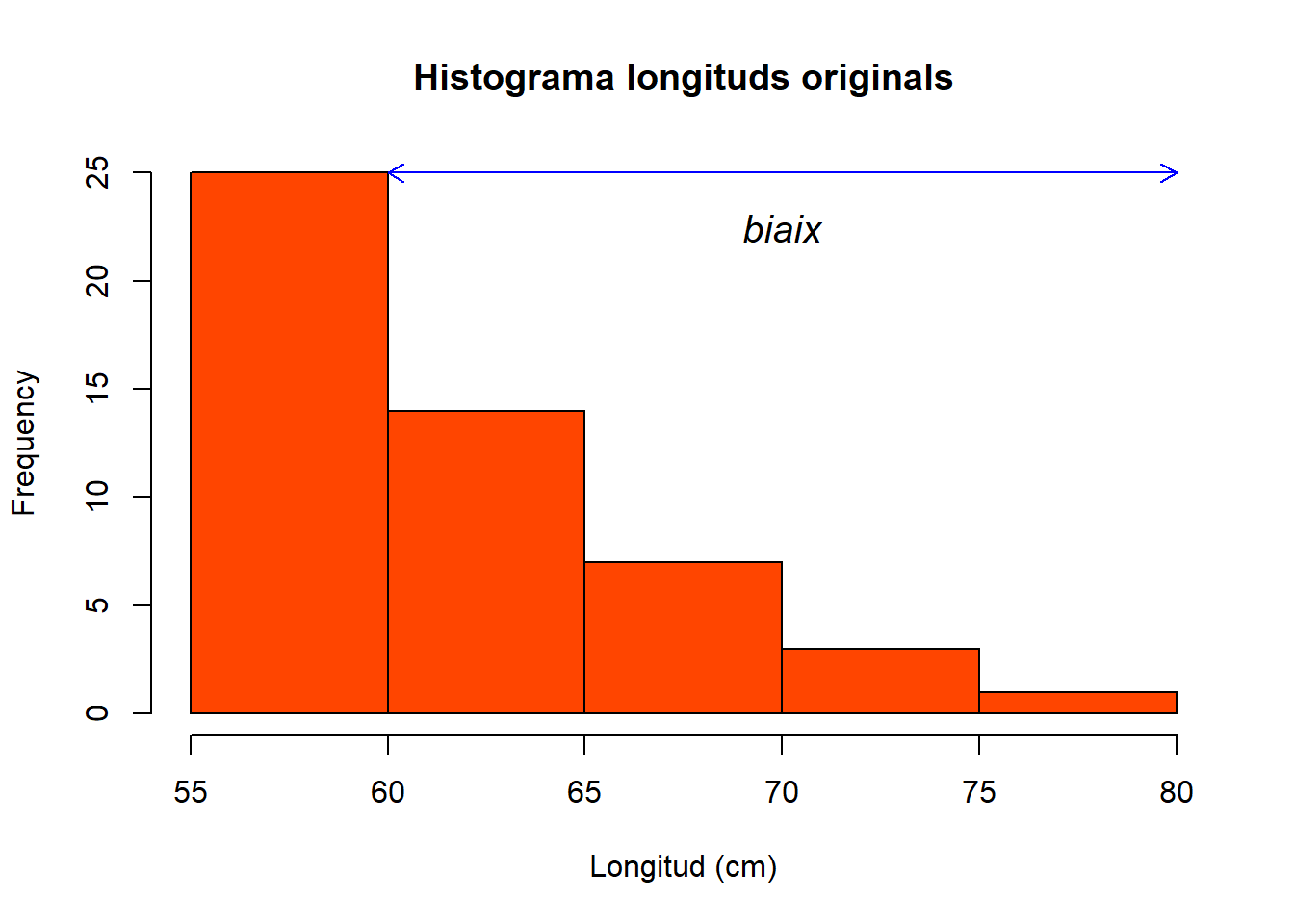
Histograma de les longituds de les bajoques de pèsol

Figure 2.3: Histograma de les longituds de les bajoques de pèsol

A l’histograma podem observar que la distribució està esbiaixada cap a la dreta, per la qual cosa la transformació més adequada és la logarítmica. Per tal d’executar-la podem usar la funció log(). Tot i que podríem substituir la variable (columna) LENGTH al data frame purves.dat és recomanable crear un objecte nou amb un nom informatiu (e.g. length.log) que continga la variable transformada.

length.log <- log(purves.dat$LENGTH)

Com podem veure a les figures següents la log-transformació ha reduït l’esbiaix de la distribució. També podríem utilitzar la funció summary() sobre l’objecte length.log per veure com han canviat els valors. Una vegada realitzada la transformació, podem procedir a realitzar la resta d’anàlisis. Alerta! Cal repetir les anàlisis usant la variable TRANSFORMADA comprovant tots els supòsits de nou i si algun no es compleix, llavors utilitzar el test no-paramètric escaient.

par(mfrow=c(1,2), cex.main=0.95) # 'cex.main' controla la mida del títol.

hist(purves.dat$LENGTH,
     main="Histograma longituds originals",
     xlab="Longitud (cm)",
     col="orangered",
     bty="n") # histograma amb les dades original

hist(length.log, 
     main="Histograma longituds log-transformades",
     xlab="Longitud (cm)",
     col="dodgerblue",
     bty="n") # histograma amb les log-transformades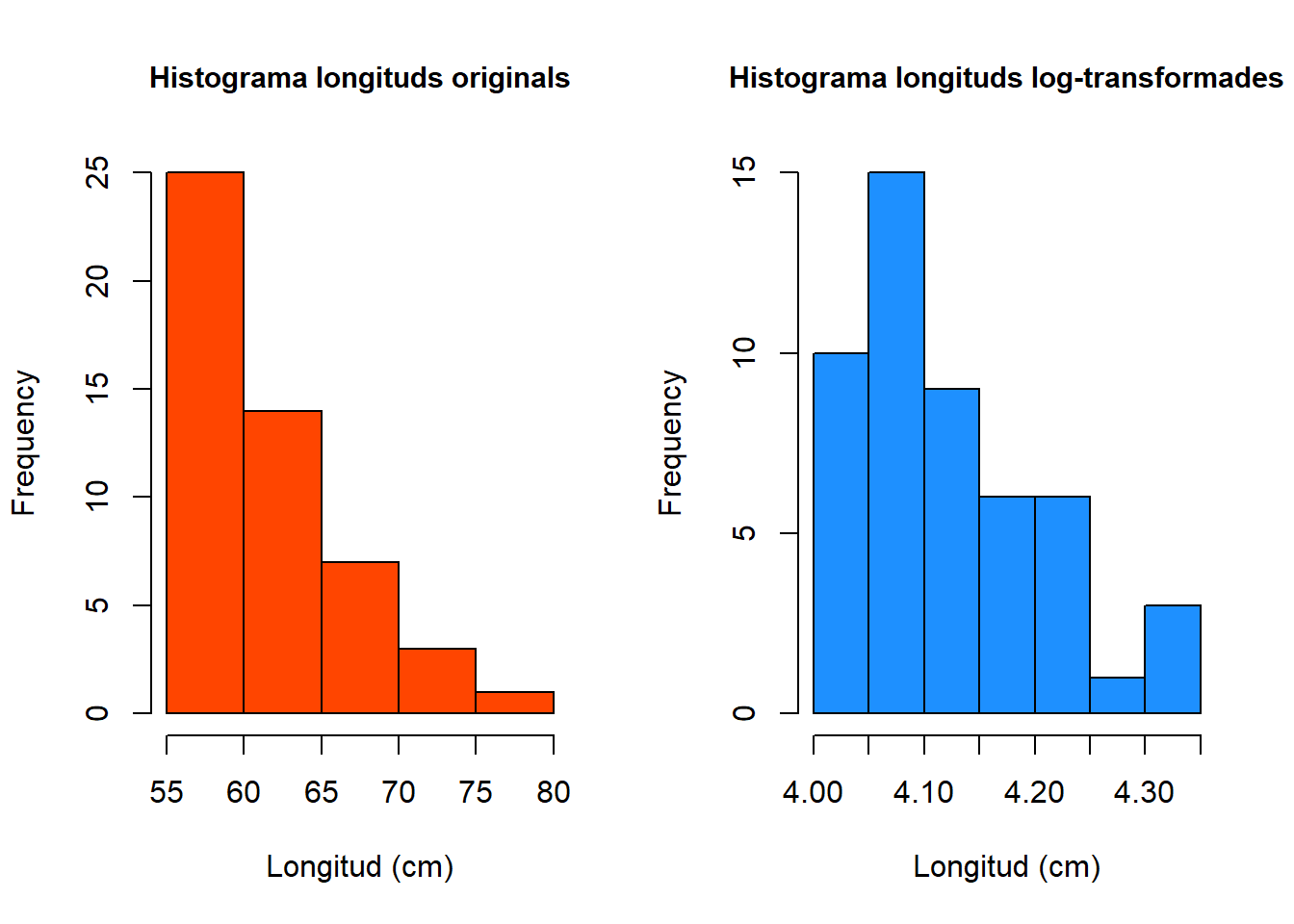
Histograma de les longituds de les bajoques de pèsol original (esquerre). Histograma de les longituds de les bajoques de pèsol log-transformades (dreta).

Figure 2.4: Histograma de les longituds de les bajoques de pèsol original (esquerre). Histograma de les longituds de les bajoques de pèsol log-transformades (dreta).

2.3.2.4 ANOVA amb dades transformades

Seguint el flux general de treball cal fer una ANOVA amb les dades transformades i seguidament comprovar que es compleixen els supòsits: numèricament i gràficament. Tot i que podríem substituir el model de l’ANOVA anomenat length_anova és recomanable crear un objecte nou amb un nom informatiu (e.g. length_anova.log) que continga el model amb les dades log-transformades. Fixeu-vos que a més de canviar el nom de l’objecte també s’ha substituït la variable depenent LENGTH per la variable log-transformada length.log. La resta roman igual. Si no substituïu LENGTH per la variable log-transformada length.log el model resultant serà exactament igual a l’original.

length_anova.log <- lm(length.log~TREAT, data=purves.dat)

Els arguments han estat explicats per al cas anterior.

Per tal de veure que tots dos models són diferents podeu usar summary() i comprovar que certament tots dos difereixen. Alerta! Això no indica que són correctes, sols que han estat obtinguts amb dades diferents.

summary(length_anova)
## 
## Call:
## lm(formula = LENGTH ~ TREAT, data = purves.dat)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -5.100 -1.825 -0.150  0.975  5.900 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    70.1000     0.7386  94.907  < 2e-16 ***
## TREATFructose -11.9000     1.0446 -11.392 7.50e-15 ***
## TREATGlucFruc -12.1000     1.0446 -11.584 4.27e-15 ***
## TREATGlucose  -10.8000     1.0446 -10.339 1.81e-13 ***
## TREATSucrose   -6.0000     1.0446  -5.744 7.48e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.336 on 45 degrees of freedom
## Multiple R-squared:  0.8144,	Adjusted R-squared:  0.7979 
## F-statistic: 49.37 on 4 and 45 DF,  p-value: 6.737e-16
summary(length_anova.log)
## 
## Call:
## lm(formula = length.log ~ TREAT, data = purves.dat)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.074098 -0.027189 -0.002095  0.016593  0.082248 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    4.24849    0.01125 377.677  < 2e-16 ***
## TREATFructose -0.18506    0.01591 -11.633 3.70e-15 ***
## TREATGlucFruc -0.18831    0.01591 -11.837 2.04e-15 ***
## TREATGlucose  -0.16622    0.01591 -10.448 1.29e-13 ***
## TREATSucrose  -0.08839    0.01591  -5.556 1.42e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.03557 on 45 degrees of freedom
## Multiple R-squared:  0.8219,	Adjusted R-squared:  0.8061 
## F-statistic: 51.92 on 4 and 45 DF,  p-value: 2.691e-16

2.3.2.5 Comprovació numèrica dels supòsits amb dades transformades

Apliquem la funció leveneTest() a l’ANOVA fet amb les dades log-transformades (i.e. length_anova.log) per a comprovar que existeix Homoscedasticitat de variàncies. Recordem les hipòtesis de l’anàlisi:

  • Ho: Homoscedasticitat de variàncies
  • Ha: Heteroscedasticitat de variàncies
leveneTest(length_anova.log) # funció que aplica el test de Levene
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value  Pr(>F)  
## group  4  3.2413 0.02026 *
##       45                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

S’observa un p-valor significatiu, ja que és inferior a 0.05 ( p-valor = 0.02026). Això indica que hi ha evidències suficients com per a rebutjar la hipòtesis nul·la.

Per tant, NO és compleix el supòsit d’Homoscedasticitat de variàncies. El que indica que per a aquest supòsit la log-transformació ha estat inútil.

Apliquem la funció shapiro.test() als residus de l’ANOVA fet amb les dades log-transformades (i.e. length_anova.log) per a comprovar que existeix Normalitat. Les hipòtesis d’aquest test són:

  • Ho: Normalitat
  • Ha: Manca de Normalitat
shapiro.test(length_anova.log$res)  # funció que aplica el test de Shapiro-Wilk
## 
## 	Shapiro-Wilk normality test
## 
## data:  length_anova.log$res
## W = 0.97063, p-value = 0.2454

S’observa un p-valor NO significatiu, ja que és superior 0.05 ( p-valor = 0.2454). Això indica que no hi ha evidències suficients com per rebutjar la hipòtesis nul·la.

Per tant, sí que es compleix el supòsit de Normalitat.

CONCLUSIONS per al model amb dades log-transformades

Les proves estadístiques indiquen que des d’un punt de vista numèric els residus continuen essent:

  • Normals
  • Heteroscedàstics

2.3.2.6 Comprovació gràfica dels supòsits amb dades transformades

Comprovem els supòsits mitjançant els gràfics de residus. De nou aquests confirmen els resultats obtinguts a la comprovació numèrica dels supòsits. Els gràfics mostren que la categoria Control té una variància superior. Aquesta continua provocant una lleugera tendència a l’Scale Location Plot (cantonada inferior esquerre) ja que la línia roja continua sense esser horitzontal. Per contra el Normal Q-Q Plot (cantonada superior dreta) no indica una desviació clara de la distribució de residus respecte de la distribució normal d’igual mitjana i desviació estàndard. Així doncs caldrà usar un test no-paramètric.

par(mfrow=c(2, 2), bty="n") # paràmetres del plot. mfrow=c(2,2) indica dos plots en una única fila. bty="n" elimina la caixa que envolta el plot. És un argument merament estètic.

plot(length_anova.log)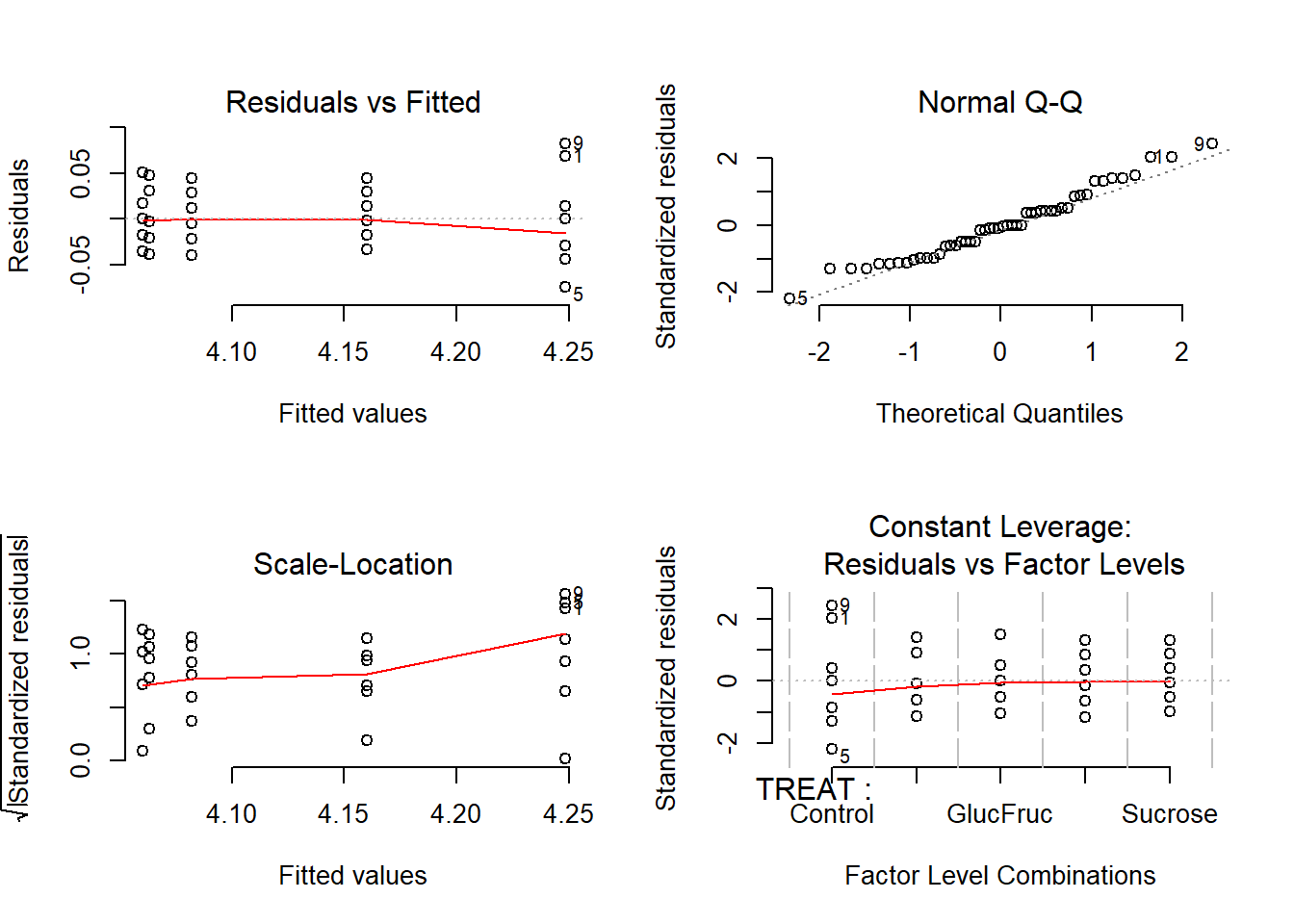
Plots de diagnosi de l'ANOVA amb les longituds de les bajoques de pèsol log-transformades.

Figure 2.5: Plots de diagnosi de l’ANOVA amb les longituds de les bajoques de pèsol log-transformades.

2.3.3 Fem el Test de Welch

Una vegada confirmat que cap transformació no impedeix que els residus siguen Normals però Heteroscedàstics cal trial el contrast no-paramètric més idoni. En aquest cas usarem el test de Welch. El test de Welch és una prova que s’utilitza per comprovar la hipòtesi que dues o més poblacions tenen mitjanes iguals. Aquest contrast és més fiable quan les mostres tenen variacions o mides de mostra desiguals (i.e. Heteroscedasticitat). Alerta! Fixeu-vos que usem les dades originals.

  • Ho: les mitjanes de cada categoria són iguals
  • Ha: almenys una mitjana no és igual a les altres
oneway.test(LENGTH~TREAT, data=purves.dat)  # funció que aplica el test de test de Welch: Normalitat i Heteroscedasticitat dels residus 
## 
## 	One-way analysis of means (not assuming equal variances)
## 
## data:  LENGTH and TREAT
## F = 33.834, num df = 4.0, denom df = 22.2, p-value = 3.77e-09

S’observa un p-valor significatiu, ja que és inferior a 0.05 ( p-valor = 3.77e-09). Això indica que hi ha evidències suficients com per a rebutjar la hipòtesis nul·la. Per tant almenys una mitjana no és igual a les altres.

2.3.4 Proves Post-hoc

El test de Welch ens ha confirmat que almenys una mitjana no és igual a les altres però no ens indica quines són semblants. Per tal de saber quins grups existeixen entre les categories (i.e. tractaments) s’utilitza el què s’anomena proves post hoc. Aquest tipus de proves testen les similituds entre cada parella de categories (i.e. tractaments).

pairwise.t.test(purves.dat$LENGTH, purves.dat$TREAT, pool.sd=F, p.adj="holm")
## 
## 	Pairwise comparisons using t tests with non-pooled SD 
## 
## data:  purves.dat$LENGTH and purves.dat$TREAT 
## 
##          Control Fructose GlucFruc Glucose
## Fructose 9.7e-06 -        -        -      
## GlucFruc 1.2e-05 0.7909   -        -      
## Glucose  2.5e-05 0.3587   0.2214   -      
## Sucrose  0.0035  9.7e-06  1.7e-06  3.5e-05
## 
## P value adjustment method: holm

Els resultats es mostren en una taula amb els p-valors per a cada parella. Com podem observar a la següent taula, on els valors han estat arrodonits fins a 3 posicions decimals, les longituds obtingudes al Control són diferents a la resta. Fructose, GlucFruc, Glucose formen altre grup separat mentre que Sucrose, l’últim tractament, forma el tercer grup de longituds. Tot plegat indicant que si l’objectiu és aconseguir longituds de bajoca menudes, l’ús dels tractaments Fructose, GlucFruc, Glucose és indiferent. Deixar el conreu sense tractament (Control) provocarà un increment en la longitud, mentre que usar el tractament amb Sucrose provocarà que les bajoques tinguen una longitud intermèdia.

Table 2.2: Taula 2. Simplificació dels p-valors obtinguts amb la funció pairwise.t.test()
Control Fructose GlucFruc Glucose
Fructose 0.000 NA NA NA
GlucFruc 0.000 0.791 NA NA
Glucose 0.000 0.359 0.221 NA
Sucrose 0.003 0.000 0.000 0

Tot i que la informació continguda a la taula és suficient per a interpretar els resultats, als informes i articles és habitual mostrar figures com la que apareix a continuació. Aquestes mostren la mitjana i error estàndard al voltant d’aquesta per a cada tractament i amb una lletra el grup al que pertany cada tractament.

Desenvolupar aquesta mena de figures requereix de certs càlculs previs. Mitjançant la funció tapply() podem calcular diversos estadístics de la variable LENGTH per a cadascuna de les categories de la variable TREAT. En el primer cas, Mitjanes, calculem la mitjana mitjançant la funció mean Alerta! no calen parèntesis perquè la funció mean() també és un objecte. Al segon cas calculem l’error estàndard (std.error). Açò ens permetrà afegir les barres d’error mitjançant la funció arrows().

El plot es desenvolupa en tres passes:

  1. Generar el barplot usant la funció barplot().
  2. Afegir les barres d’error usant la funció arrows().
  3. Afegir els grups amb la funció text().
(Mitjanes <- tapply(purves.dat$LENGTH, purves.dat$TREAT, mean))
##  Control Fructose GlucFruc  Glucose  Sucrose 
##     70.1     58.2     58.0     59.3     64.1
(Estandard.errors <- tapply(purves.dat$LENGTH, purves.dat$TREAT, std.error)) # la funció std.error apareix al paquet plotrix 
##   Control  Fructose  GlucFruc   Glucose   Sucrose 
## 1.2600705 0.5925463 0.4472136 0.5174725 0.5666667
par(mfrow=c(1, 1), bty="n")

Barplot <- barplot(Mitjanes,
                   beside = T, # serveix per a que les barres no apareguen amuntegades
                   col = Colors, 
                   xlab = "Tractament", ylab = "Longitud (cm)",
                   ylim = c(0, max(Mitjanes + Estandard.errors)))

arrows(x0 = Barplot, y0 = Mitjanes - Estandard.errors, # Inici de les fletxes
       x1 = Barplot, y1 = Mitjanes + Estandard.errors, # Final de les fletxes
       ang=90, # angle de la fletxa. 90 fa que siguen horitzontals
       code=3, # indica que ha d'haver fletxa a l'inici i al final 
       xpd=T) # xpd=T és necessari per a que les barres d'error no apareguen tallades

text(Barplot, # Posició x on s'afegirà el text
     Mitjanes + Estandard.errors, # Posició y on s'afegirà el text
     labels = c('A','B','B','B','C'), # Text
     pos = 3, # Indica que el text ha d'aparèixer d'alt de les coordenades
     xpd = T) # xpd=T és necessari per a que el text aparega fora de l'àrea del plot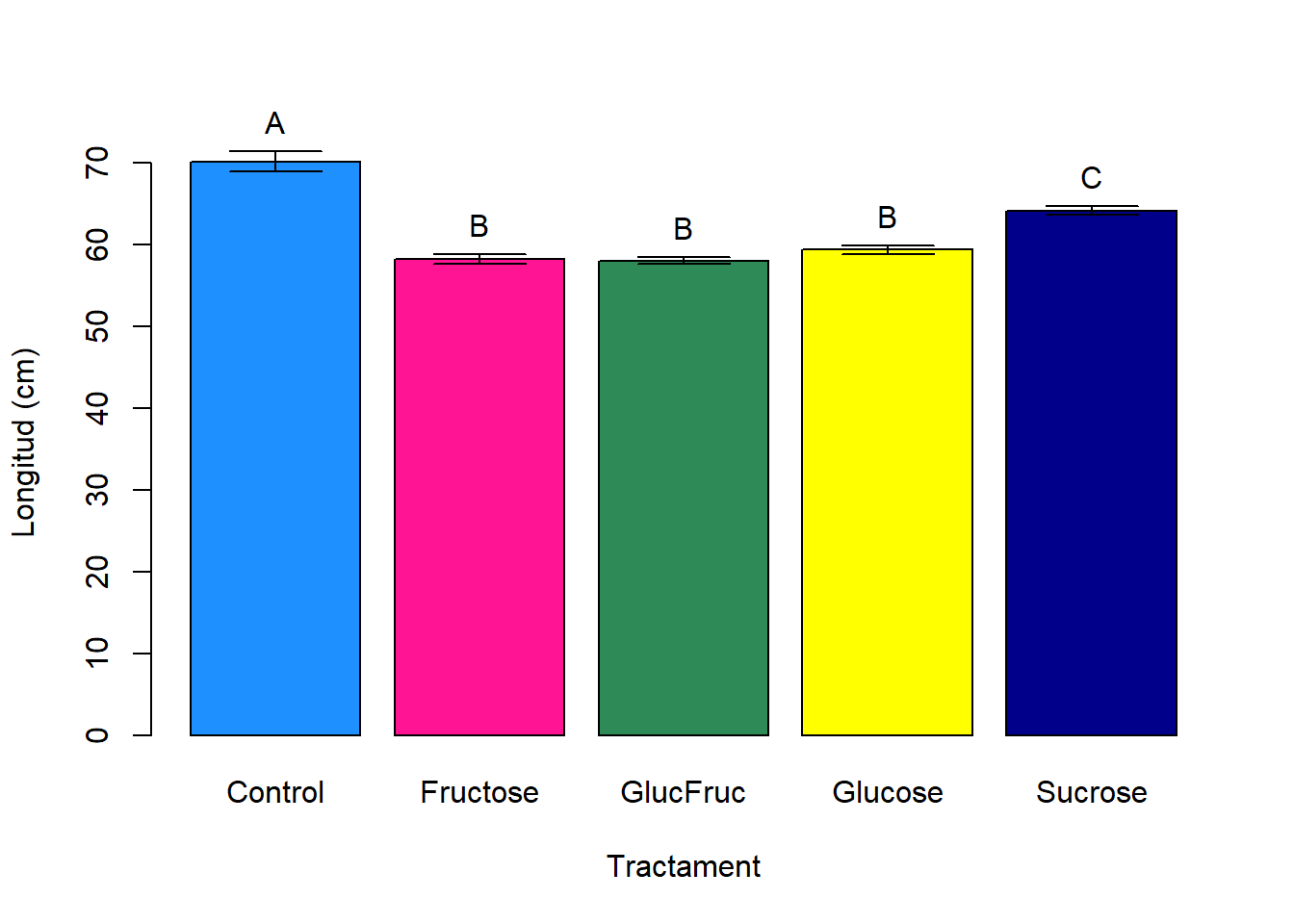
Barplot amb errors estàndards de les longituds de les bajoques y resultats de l'anàlisi post hoc

Figure 2.6: Barplot amb errors estàndards de les longituds de les bajoques y resultats de l’anàlisi post hoc

Pel que fa als arguments, molts han estat explicats en càlculs anteriors. Tanmateix, a banda de les funcions barplot(), arrows() i text(), destaquem:

  1. beside = T serveix per a que les barres no apareguen amuntegades. = T indica que és TRUE (cert).
  2. ylim indica el rang de la figura a l’eix y. Fixeu-vos que mitjançant la funció max() hem calcular el màxim valor que assoleix alguna de les barres d’error (i.e. Mitjanes + Estandard.errors).
  3. xpd = T és necessari per a que el text aparega fora de l’àrea del plot. = T indica que és TRUE (cert).

La resta d’arguments estan explicats com a comentaris al costat de codi. Fixeu-vos que el barplot està assignat a un objecte de nom Barplot que s’usa per a dibuixar les barres d’error mitjançant la funció arrows(). Aquest objecte simplement conté el centre de les barres a l’eix x.

Test de Kruskal-Wallis; Manca de Normalitat i Homoscedasticitat

2.3.5 Carregar dades i comprovar que s’ha fet correctament

Com ja ha estat explicat a la sessió anteriorment, per tal que R trobe l’arxiu a cada sessió cal definir quina és la nostra carpeta (directori) de treball. Aquesta tasca es fa mitjançant la funció set working directory setwd() i sols cal fer-ho una vegada per sessió. El mateix ocorre amb les paquets. Cal carregar-los sols una vegada per sessió. Podeu conèixer el directori de treball picant getwd(). Si esteu fent el segon exemple independentment del primer caldrà doncs que el determineu i que carregueu els paquets necessaris.

setwd("U:/Docència/Girona/AAD - R markdown/Contrastos no-paramètrics/")

Recordeu, en el vostre cas haureu de substituir: “U:/Docència/Girona/AAD - R markdown/Contrastos no-paramètrics/” per la vostra ruta. Alerta! Els símbols / han d’estar orientats cap a la dreta.

Una vegada indicat el directori de treball podem carregar les dades del segon exercici a R.

load("fish.RData")

Els argument han estat explicats a la sessió anterior i a l’exemple anterior en aquesta mateixa sessió.

Una vegada han estat carregades i assignades les dades cal comprovar que no ens hem equivocat. Aplicarem les funcions dim() i summary() al data frame (i.e. taula de dades) fish.dat.

dim(fish.dat)
## [1] 31  2
summary(fish.dat)
##  Bassa      Captures     
##  B1: 8   Min.   :  0.00  
##  B2:10   1st Qu.: 17.00  
##  B3: 5   Median : 74.00  
##  B4: 8   Mean   : 69.03  
##          3rd Qu.:113.00  
##          Max.   :178.00

El data frame (i.e. taula de dades) fish.dat conté 31 línies (casos) i dues columnes (variables). Aquestes consisteixen en dues variables (i.e. Bassa i Captures). La variable Bassa és categòrica (factor) amb 4 categories o levels i un nombre variable de dades per categoria. Per contra la variable Captures és continua de mitjana 69.03 amb mínim de 0 i màxim de 178.

A banda de la funció summary() és recomanable fer una exploració gràfica de les dades. De forma anàloga al que s’ha explicat per a l’exemple 1, utilitzarem la funció plot() per a veure la relació entre les categories (i.e. basses) i els valors de la variable d’interès (i.e. nombre de captures).

De nou anem a utilitzar un vector anomenat per a definir un color per a cadascuna de les basses. Per a quest exemple es mostra una forma alternativa amb igual resultat. Primer es defineix el vector i després amb la funció names() se li assigna com a nom cada categoria. El nom de les categories s’obté usant la funció levels().

Colors <- c("dodgerblue",  "deeppink",  "seagreen", "yellow") # vector amb 4 colors

names(Colors) <- levels(fish.dat$Bassa)

Colors # Vector resultant
##           B1           B2           B3           B4 
## "dodgerblue"   "deeppink"   "seagreen"     "yellow"
str(Colors) # estructura de l'objecte
##  Named chr [1:4] "dodgerblue" "deeppink" "seagreen" "yellow"
##  - attr(*, "names")= chr [1:4] "B1" "B2" "B3" "B4"
plot(x=fish.dat$Bassa, y=fish.dat$Captures,
     xlab="Bassa", ylab="# de captures",
     col=Colors,
     frame=F)

legend("topleft",
       legend=levels(fish.dat$Bassa),
       fill=Colors,
       ncol=4,
       bty="n")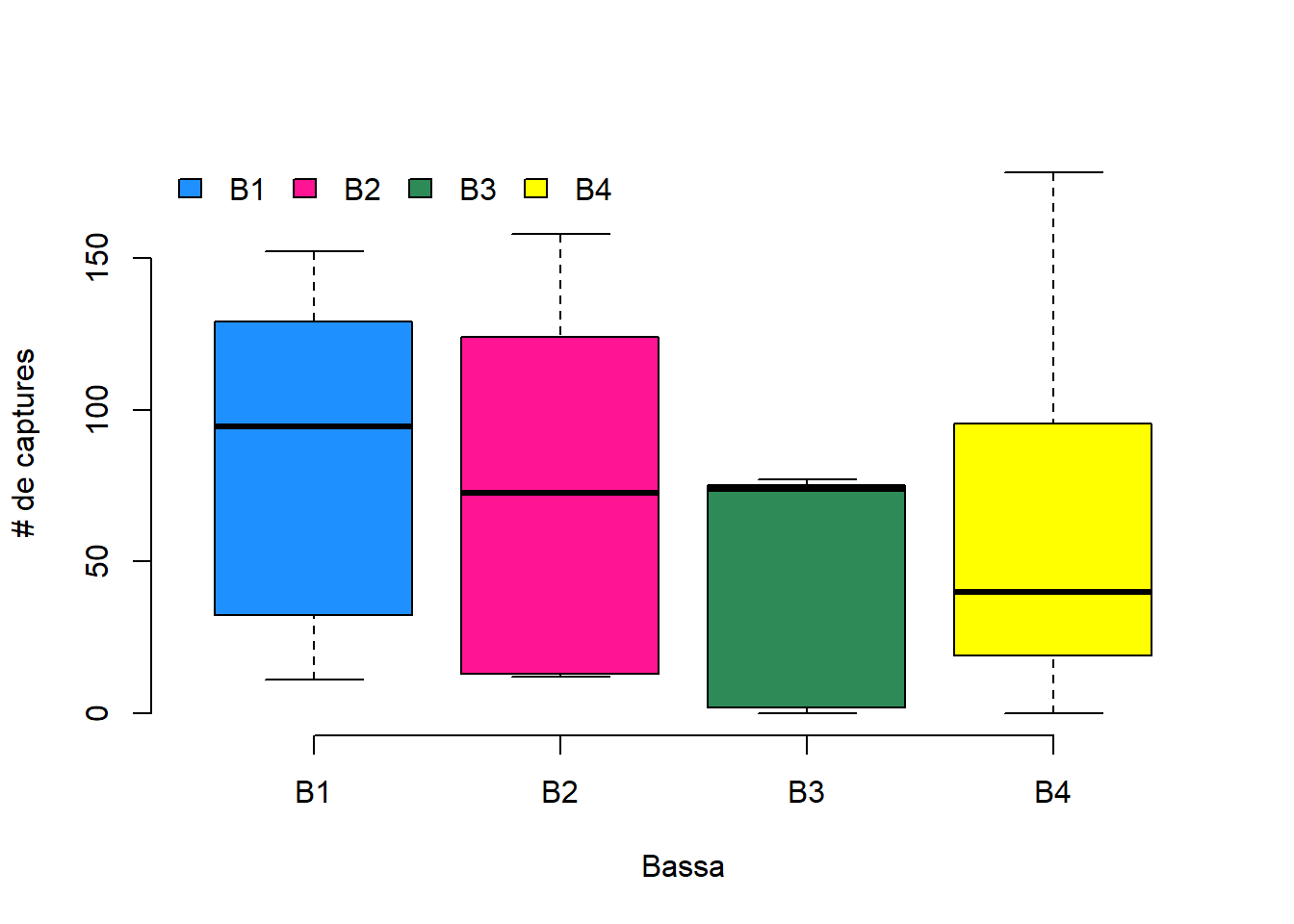
Box plots del nombre de captures per bassa

Figure 2.7: Box plots del nombre de captures per bassa

Els arguments són els mateixos que han estat explicats a l’exemple anterior. Amb la diferència que la llegenda té 4 columnes i està ubicada a la cantonada superior esquerre “topleft”.

La figura mostra que, en general, el nombre de captures és superior a B1, seguit de B2 i B3. A B3, tot i tindre una mitjana de captures similar a B2, no s’ha pogut capturar massa exemplars en algunes campanyes. B4 mostra, de mitjana, un nombre de captures inferior però major variabilitat que la resta.

2.3.6 ANOVA i comprovació de supòsits

Seguint el flux general de treball indicat a l’inici del document, primer cal fer una ANOVA amb les dades originals i seguidament comprovar que es compleixen els supòsits: numèricament i gràficament. Per tal de realitzar l’anàlisi d’ANOVA utilitzem la funció lm() (linear model):

nombre.de.captures_anova <- lm(Captures~Bassa, data=fish.dat)

Els arguments han estat explicats a la primera sessió i a l’exemple anterior d’aquesta sessió.

2.3.6.1 Comprovació numèrica dels supòsits

Per tal de comprovar l’Homoscedasticitat de variàncies dels residus del model de l’ANOVA hi apliquem la funció leveneTest(). Com a únic argument cal introduir el nom del model de l’ANOVA i la funció extrau els residus del model. Recordem les hipòtesis de l’anàlisi:

  • Ho: Homoscedasticitat de variàncies
  • Ha: Heteroscedasticitat de variàncies
leveneTest(nombre.de.captures_anova) # funció que aplica el test de Levene
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  3  0.5321 0.6642
##       27

S’observa un p-valor NO significatiu, ja que és superior a 0.05 ( p-valor = 0.6642). Això indica que no podem rebutjar la hipòtesis nul·la.

Per tant, SÍ es compleix el supòsit d’Homoscedasticitat de variàncies.

Tal i com ha estat explicat a l’exemple anterior, cal que comprovem el supòsit de Normalitat mitjançant el test de Shapiro-Wilk. Les hipòtesis de l’anàlisi són:

  • Ho: Normalitat
  • Ha: Manca de Normalitat
shapiro.test(nombre.de.captures_anova$res)  # funció que aplica el test de Shapiro-Wilk
## 
## 	Shapiro-Wilk normality test
## 
## data:  nombre.de.captures_anova$res
## W = 0.92725, p-value = 0.03691

S’observa que el p-valor és significatiu, ja que és inferior a 0.05 (p-valor = 0.03691). Això indica que hi ha evidències suficients com per rebutjar la hipòtesis nul·la.

Per tant, NO es compleix el supòsit de Normalitat.

CONCLUSIONS

Les proves estadístiques indiquen que els residus són:

  • No Normals
  • Homoscedàstics

2.3.6.2 Comprovació gràfica dels supòsits

Per comprovar gràficament els supòsits de l’ANOVA cal aplicar la funció plot() a nombre.de.captures_anova i R genera 4 plots de diagnòstic. Recordeu que abans cal picar par(mfrow=c(2, 2)) o solament es veurà l’últim gràfic.

Pel que fa a la interpretació dels gràfics, de nou confirmen els resultats obtinguts a la comprovació numèrica dels supòsits. El Normal Q-Q Plot (cantonada superior dreta) indica una desviació clara dels quantils de la distribució de residus respecte de la distribució normal d’igual mitjana i desviació típica. Especialment pel que fa als quantils inferiors. Per contra, l’Scale Location Plot (cantonada inferior esquerre) tot i tindre certes irregularitats no mostra una tendència clara. Així doncs podem considerar que la línia roja és horitzontal. Aquesta manca de tendència és indicativa d’homoscedasticitat.

par(mfrow=c(2, 2), bty="n") # paràmetres del plot. mfrow=c(2,2) indica dos plots en una única fila. bty="n" elimina la caixa que envolta el plot. És un argument merament estètic.

plot(nombre.de.captures_anova)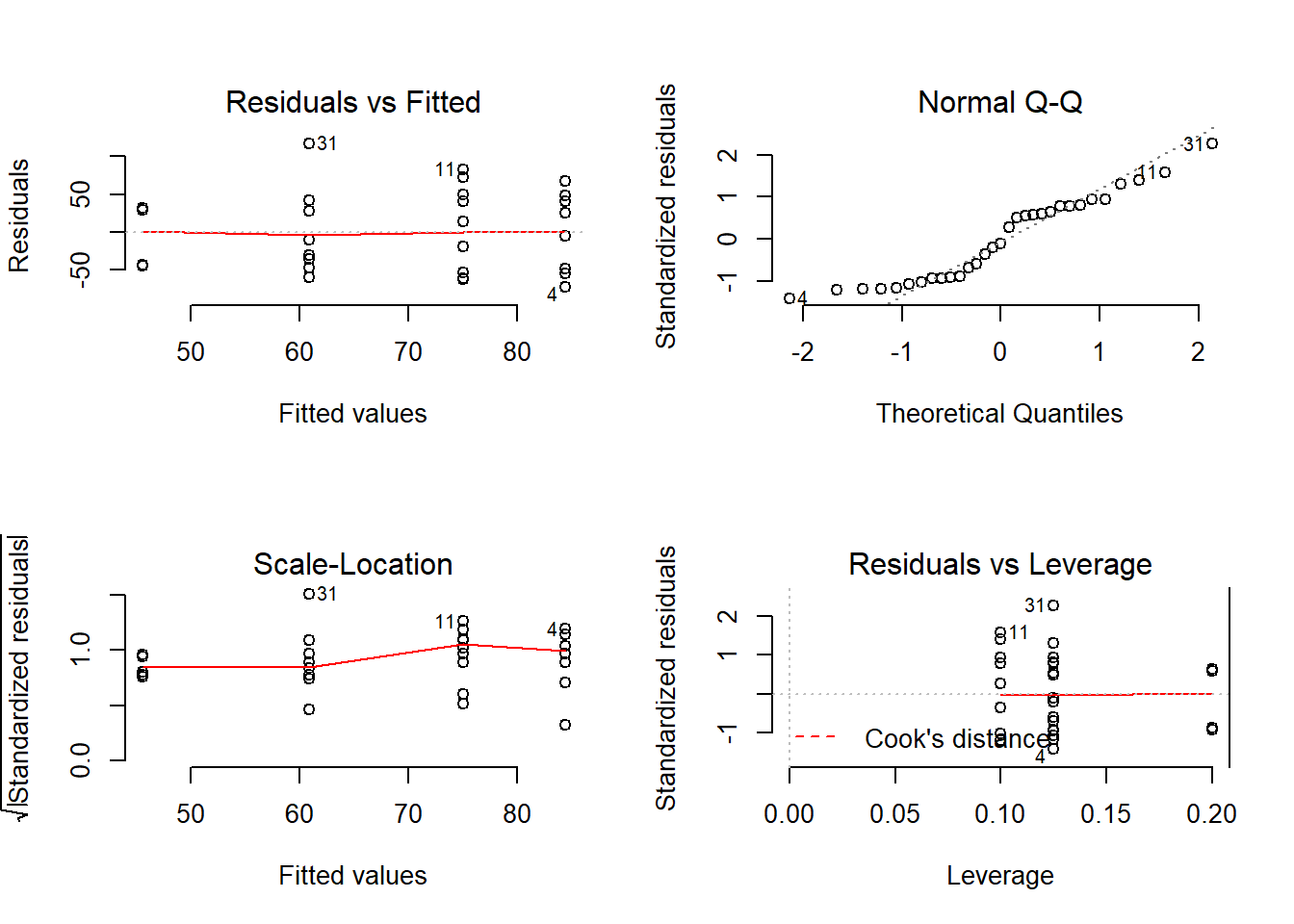
Plots de diagnosi de l'ANOVA amb el # de captures originals.

Figure 2.8: Plots de diagnosi de l’ANOVA amb el # de captures originals.

2.3.6.3 Transformació i comprovació de la transformació

Abans d’aplicar un test no-paramètric cal tractar de complir amb el supòsits de l’ANOVA mitjançant una transformació perquè ANOVA és més robusta. Per tal de decidir quina mena de transformació és la més adequada el més habitual és fer un histograma amb la funció hist() i comprovar cap on apareix el biaix.

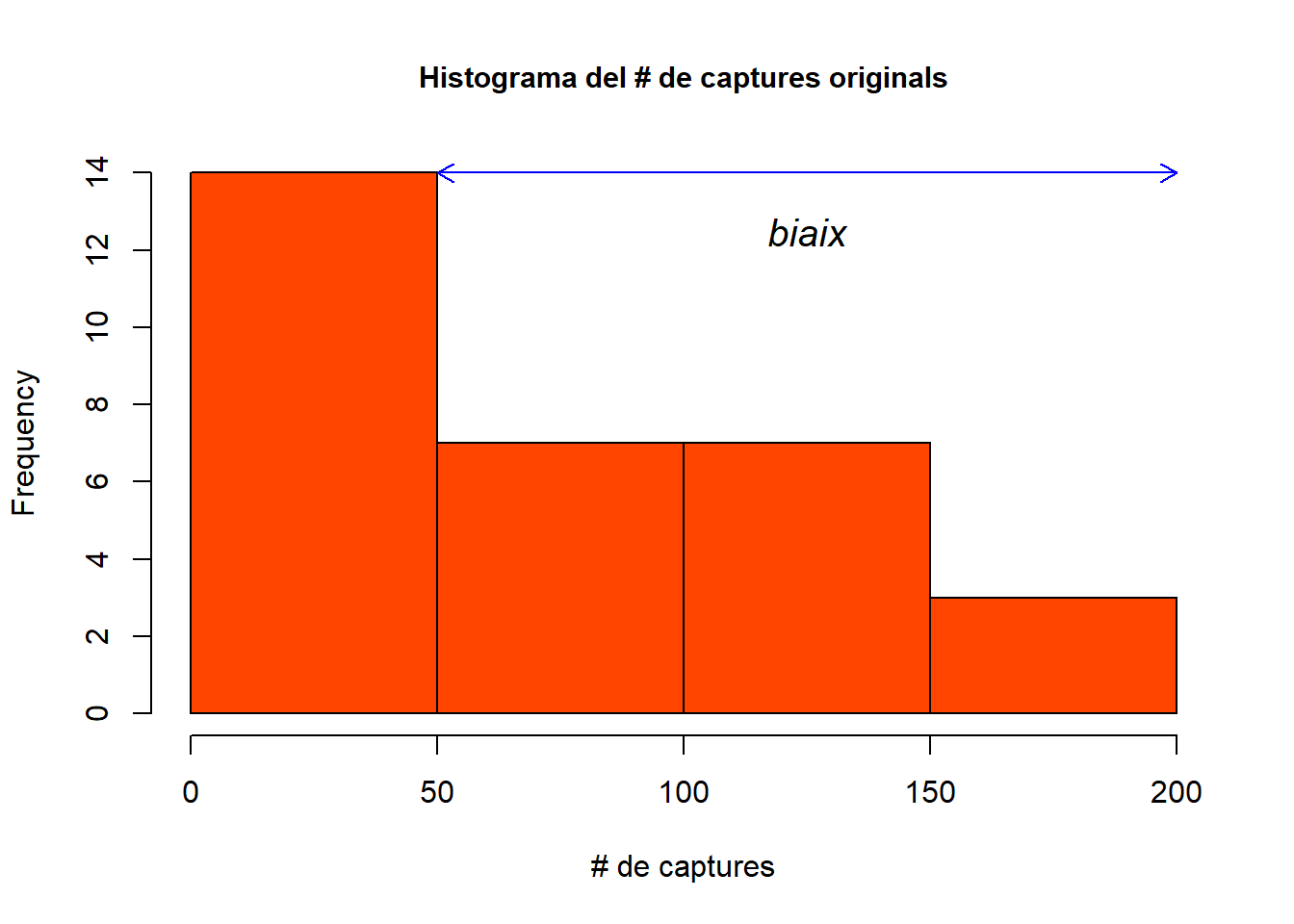
Histograma del # de captures

Figure 2.9: Histograma del # de captures

A l’histograma podem observar que la distribució està esbiaixada cap a la dreta, per la qual cosa la transformació més adequada és la logarítmica. Per tal d’executar-la podem usar la funció log() assignant el resultat a un objecte nou amb un nom informatiu (i.e. n.captures.log) que continga la variable transformada. Alerta! Quan el mínim d’una variable és zero y es vol log-transformar és necessari afegir un petita quantitat perquè el logaritme de zero és una indeterminació. Com que la variable és el nombre de captures, i augment unitat a unitat, el valor que afegirem serà d’1.

n.captures.log <- log(fish.dat$Captures + 1) # Alerta! log + 1 perquè mínim del # de captures és zero.

Com podem veure a les figures següents la log-transformació ha reduït l’esbiaix de la distribució. Ara podem procedir a realitzar la resta d’anàlisis Alerta! Cal repetir les anàlisis usant la variable transformada comprovant tots els supòsits de nou i si algun no es compleix utilitzar el test no-paramètric escaient.

par(mfrow=c(1,2), cex.main=0.95)

hist(fish.dat$Captures,
     main="Histograma del # de captures originals",
     xlab="# de captures",
     col="orangered",
     bty="n") # histograma amb les dades original

hist(n.captures.log, 
     main="Histograma del # de captures log-transformades",
     xlab="# de captures",
     col="dodgerblue",
     bty="n") # histograma amb les log-transformades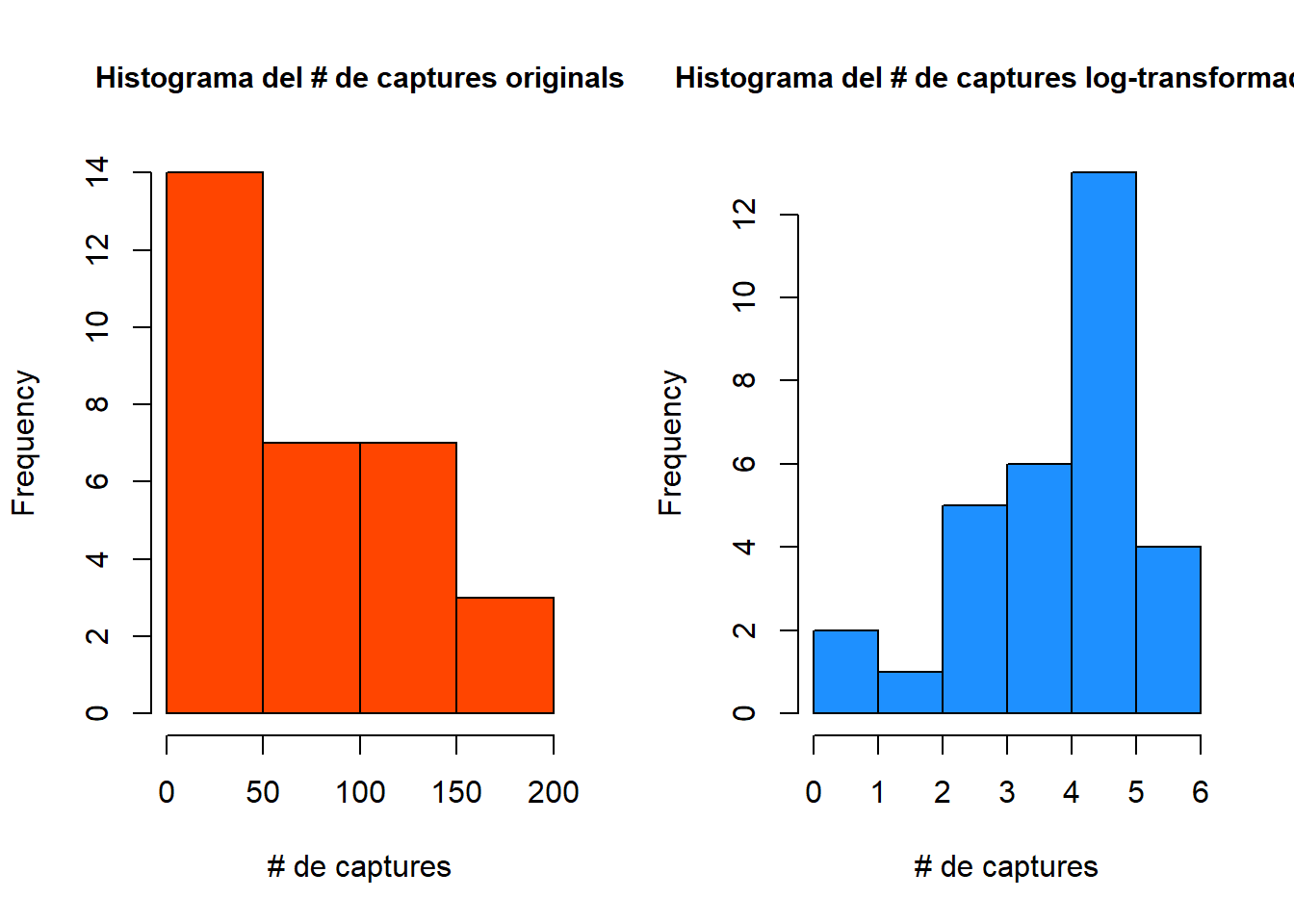
Histograma del # de captures original (esquerre). Histograma del # de captures log-transformades (dreta).

Figure 2.10: Histograma del # de captures original (esquerre). Histograma del # de captures log-transformades (dreta).

2.3.6.4 ANOVA amb dades transformades

Seguint el flux general de treball cal fer una ANOVA amb les dades transformades i seguidament comprovar que es compleixen els supòsits: numèricament i gràficament. De nou podríem substituir el model de l’ANOVA anomenat nombre.de.captures_anova però és recomanable crear un objecte nou amb un nom informatiu (i.e. nombre.de.captures_anova.log) que continga el model amb les dades log-transformades. Fixeu-vos que a més de canviar el nom de l’objecte també s’ha substituït la variable depenent Captures per la variable log-transformada n.captures.log. La resta roman igual. Si no substituïu Captures per la variable log-transformada n.captures.log el model resultant serà exactament igual a l’original.

nombre.de.captures_anova.log <- lm(n.captures.log~Bassa, data=fish.dat)

Els arguments han estat explicats per al cas anterior.

Per tal de veure que tots dos models són diferents podeu usar summary() i comprovar que certament tots dos difereixen. Alerta! Això no indica que són correctes, sols que han estat obtinguts amb dades diferents.

summary(nombre.de.captures_anova)

summary(nombre.de.captures_anova.log)

2.3.6.5 Comprovació numèrica dels supòsits amb dades transformades

Apliquem la funció leveneTest() a l’ANOVA fet amb les dades log-transformades (i.e. nombre.de.captures_anova.log) per a comprovar que existeix Homoscedasticitat en els residus. Recordem les hipòtesis de l’anàlisi:

  • Ho: Homoscedasticitat de variàncies
  • Ha: Heteroscedasticitat de variàncies
leveneTest(nombre.de.captures_anova.log) # funció que aplica el test de Levene
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  3   0.621 0.6075
##       27

S’observa un p-valor NO significatiu, ja que és superior a 0.05 ( p-valor = 0.6075). Això indica que NO hi ha evidències suficients com per a rebutjar la hipòtesis nul·la.

Per tant, és compleix el supòsit d’Homoscedasticitat de variàncies. El que indica que per a aquest supòsit la log-transformació no ha tingut cap efecte.

Apliquem la funció shapiro.test() als residus de l’ANOVA fet amb les dades log-transformades (i.e. nombre.de.captures_anova.log) per a comprovar que existeix Normalitat. Les hipòtesis d’aquest test són:

  • Ho: Normalitat
  • Ha: Manca de Normalitat
shapiro.test(nombre.de.captures_anova.log$res)  # funció que aplica el test de Shapiro-Wilk
## 
## 	Shapiro-Wilk normality test
## 
## data:  nombre.de.captures_anova.log$res
## W = 0.92241, p-value = 0.02737

S’observa un p-valor significatiu, ja que és inferior a 0.05 ( p-valor = 0.02737). Això indica que hi ha evidències suficients com per rebutjar la hipòtesis nul·la.

Per tant, NO es compleix el supòsit de Normalitat.

CONCLUSIONS per al model amb dades log-transformades

Les proves estadístiques indiquen que des d’un punt de vista numèric els residus continuent essent:

  • No Normals
  • Homoscedàstics

2.3.6.6 Comprovació gràfica dels supòsits amb dades transformades

Comprovem els supòsits mitjançant els gràfics de residus. Pel que fa a la manca de normalitat, els gràfics de diagnosi confirmen els resultats obtinguts a la comprovació numèrica dels supòsits. No obstant però l’Scale Location Plot (cantonada inferior esquerre) mostra certa tendència i per tant seria indicatiu d’Heteroscedasticitat dels residus, el què contravé el resultat del de Levene. Com que la transformació no suposa cap millora utilitzarem un test no-paramètric per a comparar el # de captures a cada bassa.

par(mfrow=c(2, 2), bty="n") # paràmetres del plot. mfrow=c(2,2) indica dos plots en una única fila. bty="n" elimina la caixa que envolta el plot. És un argument merament estètic.

plot(nombre.de.captures_anova.log)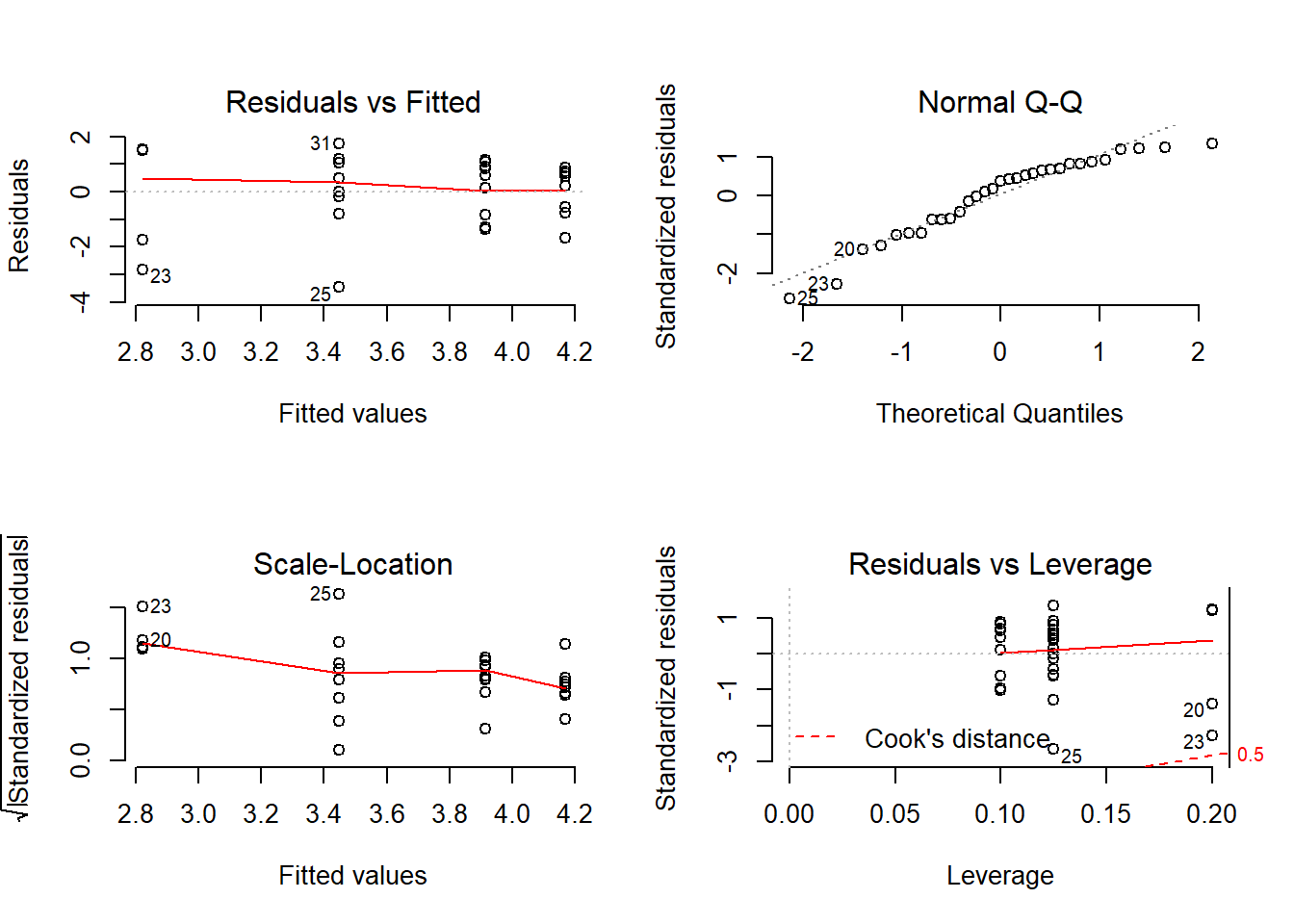
Plots de diagnosi de l'ANOVA amb el # de captures log-transformades.

Figure 2.11: Plots de diagnosi de l’ANOVA amb el # de captures log-transformades.

2.3.7 Fem el Test de Kruscal-Wallis

Una vegada confirmat que cap transformació no impedeix que els residus siguen No Normals però Homoscedàstics cal trial el contrast no-paramètric més idoni. En aquest cas el test de Kruskal-Wallis. El test de Kruskal-Wallis és un mètode no-paramètric per provar si les mostres s’originen a partir de la mateixa distribució. S’utilitza per comparar dues o més mostres independents de mides de mostra iguals o diferents. Les hipòtesis del test són:

  • Ho: no hi ha diferencies entre els valors de cada categoria
  • Ha: els valors d’almenys una categoria difereixen dels d’una altra
kruskal.test(Captures~Bassa, data=fish.dat)  # funció que aplica el test de Kruscal-Wallis: Manca de Normalitat i Homoscedasticitat dels residus
## 
## 	Kruskal-Wallis rank sum test
## 
## data:  Captures by Bassa
## Kruskal-Wallis chi-squared = 2.6109, df = 3, p-value = 0.4556

S’observa un p-valor NO significatiu, ja que és superior a 0.05 ( p-valor = 0.4556). Això indica que no hi ha evidències suficients com per a rebutjar la hipòtesis nul·la: no hi ha diferencies entre els valors de cada categoria. Per tan cal concloure que, en conjunt, no hi ha diferències significatives entre el nombre de captures a les quatre basses.

El test de Kruscal-Wallis ens ha indicat que no hi ha diferències entre els valors de cada categoria.

2.3.8 Proves Post-hoc

Quan aquest test és significatiu indica que els valors d’almenys una categoria difereixen dels d’una altra però no indica quines parelles són semblants i quines diferents. Si haguérem de saber quins grups existeixen entre les categories (i.e. basses) hauríem d’usar el test de Dunn com es mostra a continuació dunnTest(), del package FSA.

dunnTest(Captures~Bassa, method="hs",data=fish.dat) #method="hs", vol dir qe s'ha aplicat la correcció de Holm-Sidak per comparacions múltiples
## Dunn (1964) Kruskal-Wallis multiple comparison
##   p-values adjusted with the Holm-Sidak method.
##   Comparison          Z   P.unadj     P.adj
## 1    B1 - B2  0.4524191 0.6509671 0.6509671
## 2    B1 - B3  1.5250463 0.1272475 0.5580771
## 3    B2 - B3  1.1955121 0.2318870 0.7326221
## 4    B1 - B4  0.9354413 0.3495609 0.8210109
## 5    B2 - B4  0.5336226 0.5936027 0.8348412
## 6    B3 - B4 -0.7046100 0.4810530 0.8602444

Fixeu-vos que cap de les comparacions és significativa té p-valors ajustats (P.adj) inferiors a 0.05. Sobretot, quan es fan proves post-hoc en que es realitzen comparacions múltiples cal corregir el p-valor pel fet de comparar varies vegades la mateixa mitjana.