4 RLM part I

Regressió Lineal Múltiple

Mètode “clàssic” quan la Y segueix una distribució NORMAL

Authors:Gascón S.

Aquesta secció servirà per conèixer com fer una Regresió Lineal Multiple (RLM) amb R utilitzant un mètode “clàssic”.

4.1 Carregar les dades

Les dades per aquest exercici s’han extret del llibre Sokal, R.R. and Rohlf, F.J. (1995) Biometry: The Principles and Practice of Statistics in Biological Research. 3rd Edition, W.H. Freeman and Co., New York. (pàg 611-612), i les trobarem a l’arxiu “contaminacio.RData”.

Carreguem les dades a R.

load("contaminacio.RData")

En aquest estudi es va mesurar la concentració de diòxid de sofre (SO2) en 41 ciutats dels EUA i es volia crear un model per poder predir la concentració de diòxid de sofre (SO2) a partir d’altres variables ambientals.

Aquestes són les variables uqe es van mesurar:

  • temperatura (temp)
  • número de fàbriques que hi ha a cada ciutat (n_fabr)
  • densitat de població (Pobl)
  • velocitat del vent (vent)
  • precipitació (precp)
  • dies de pluja (dies_pluja)

Per contestar aquesta pregunta, es farà una regressió linal múltiple (RLM) mitjançant un mètode “clàssic” ja que a priori esperem que SO2 presenti una distribució Normal.

4.1.1 packages necessaris

Per aquesta sessió es necessiten els següents packages:

library(car)
library(MASS)

Si surt Warning no pasa res, sol ser un avis perquè la versió del package és anterior al nostre R. En general, no és un problema i els packages funcionen bé.

Si surt Loading vol dir que per funcionar el package que volem “activar” cal carregar altres packages, R ho detecta i ho fa automàticament.

4.2 Les variables

Comprovem si les variables s’han carregat bé

summary(contaminacio.data)
##               ciutat        so2              temp           n_fabr      
##  Albany          : 1   Min.   :  8.00   Min.   :43.50   Min.   :  35.0  
##  Albuquerque     : 1   1st Qu.: 13.00   1st Qu.:50.60   1st Qu.: 181.0  
##  Atlanta         : 1   Median : 26.00   Median :54.60   Median : 347.0  
##  Baltimore       : 1   Mean   : 30.05   Mean   :55.76   Mean   : 463.1  
##  Buffalo         : 1   3rd Qu.: 35.00   3rd Qu.:59.30   3rd Qu.: 462.0  
##  Charleston      : 1   Max.   :110.00   Max.   :75.50   Max.   :3344.0  
##  (Other)         :35                                                    
##       Pobl             vent            precp         dies_pluja   
##  Min.   :  71.0   Min.   : 6.000   Min.   : 7.05   Min.   : 36.0  
##  1st Qu.: 299.0   1st Qu.: 8.700   1st Qu.:30.96   1st Qu.:103.0  
##  Median : 515.0   Median : 9.300   Median :38.74   Median :115.0  
##  Mean   : 608.6   Mean   : 9.444   Mean   :36.77   Mean   :113.9  
##  3rd Qu.: 717.0   3rd Qu.:10.600   3rd Qu.:43.11   3rd Qu.:128.0  
##  Max.   :3369.0   Max.   :12.700   Max.   :59.80   Max.   :166.0  
##

4.3 Exploració inicial

Primer realitzarem una exploració inicial de les dades, i una manera ràpida de fer-ho és mitjançant un gràfic.

#utilitzem la funció "scatterplotMatrix" per dibuixar totes les variables alhora.
#a la diagonal principal apareix la distribució de les diferents variables

scatterplotMatrix(~dies_pluja+n_fabr+Pobl+precp+so2+temp+vent, data=contaminacio.data)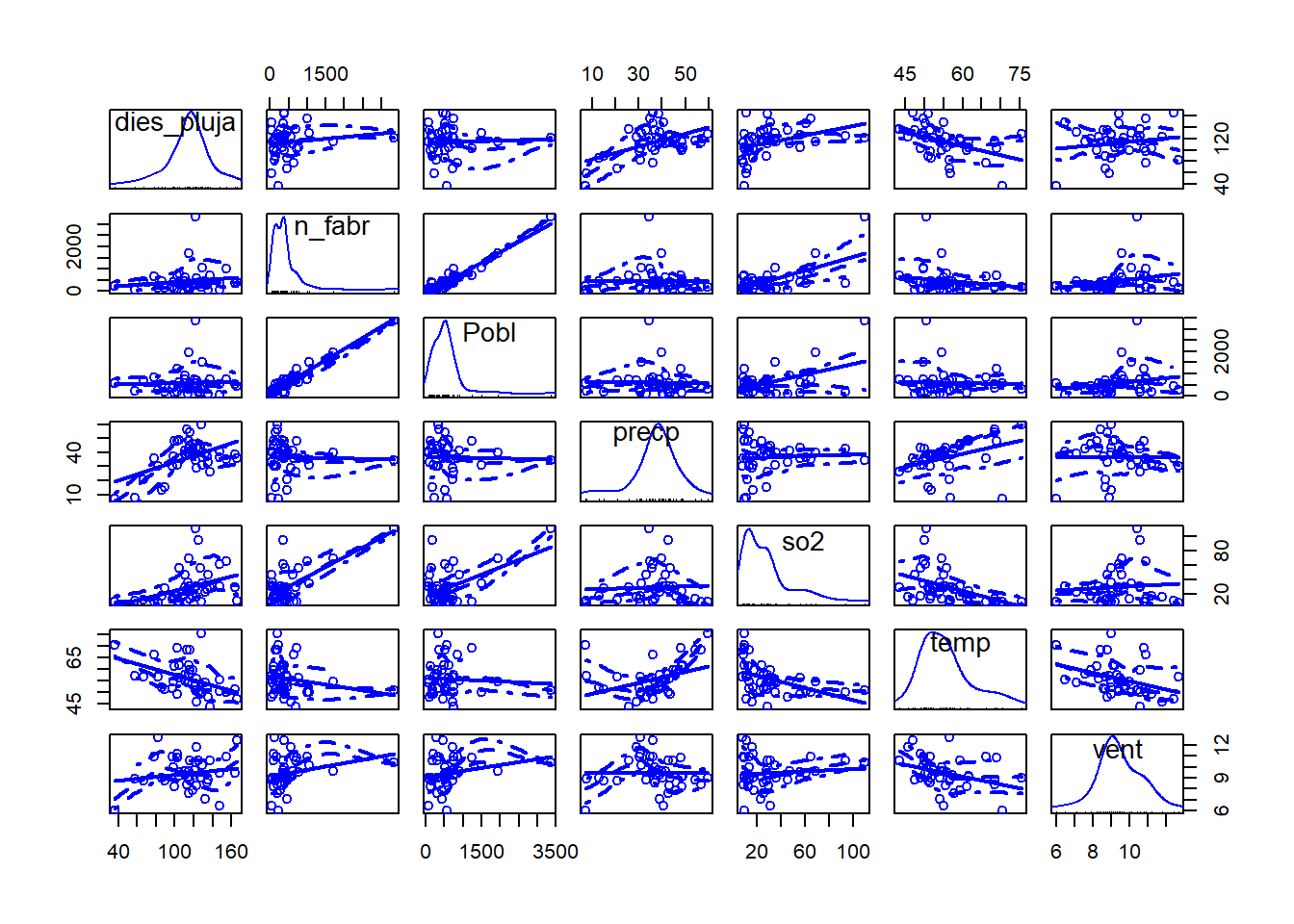

Podem veure com:

  • dies_pluja, precp i vent presenten una distribució en forma de campana i bastant centrada
  • n_fabr, Pobl, so2 i temp presenten una distribució esbiaixada a la dreta.

En principi, mirarem si sense fer cap transformació es pot fer la regressió i es compleixen els supòsits, ja que si és possible, és millor treballar amb les variables sense transformar.

4.4 Com fer una Regressió Lineal Múltiple (RLM) (mètode “clàssic”)

Fem el model de regressió. Per fer-ho utilitzarem la funció lm, ja que és la que permet ajustar models amb el mètode “clàssic”, suposant distribució Normal.

  • La variable resposta Y és so2

  • Les variables explicatives X són: temp,n_fabr,Pobl,vent,precp,dies_pluja

so2_rlm<-lm(so2~temp+n_fabr+Pobl+vent+precp+dies_pluja, data=contaminacio.data)

Molt bé, si no surt cap error, podem passar a comprovar la distribució dels residus.

par(mfrow=c(2,2))#així indiquem a R que volem els gràfics en un panell de 2*2
plot(so2_rlm)

par(mfrow=c(1,1))#indiquem a R que torni a la configuració inicial de gràfic per panell.

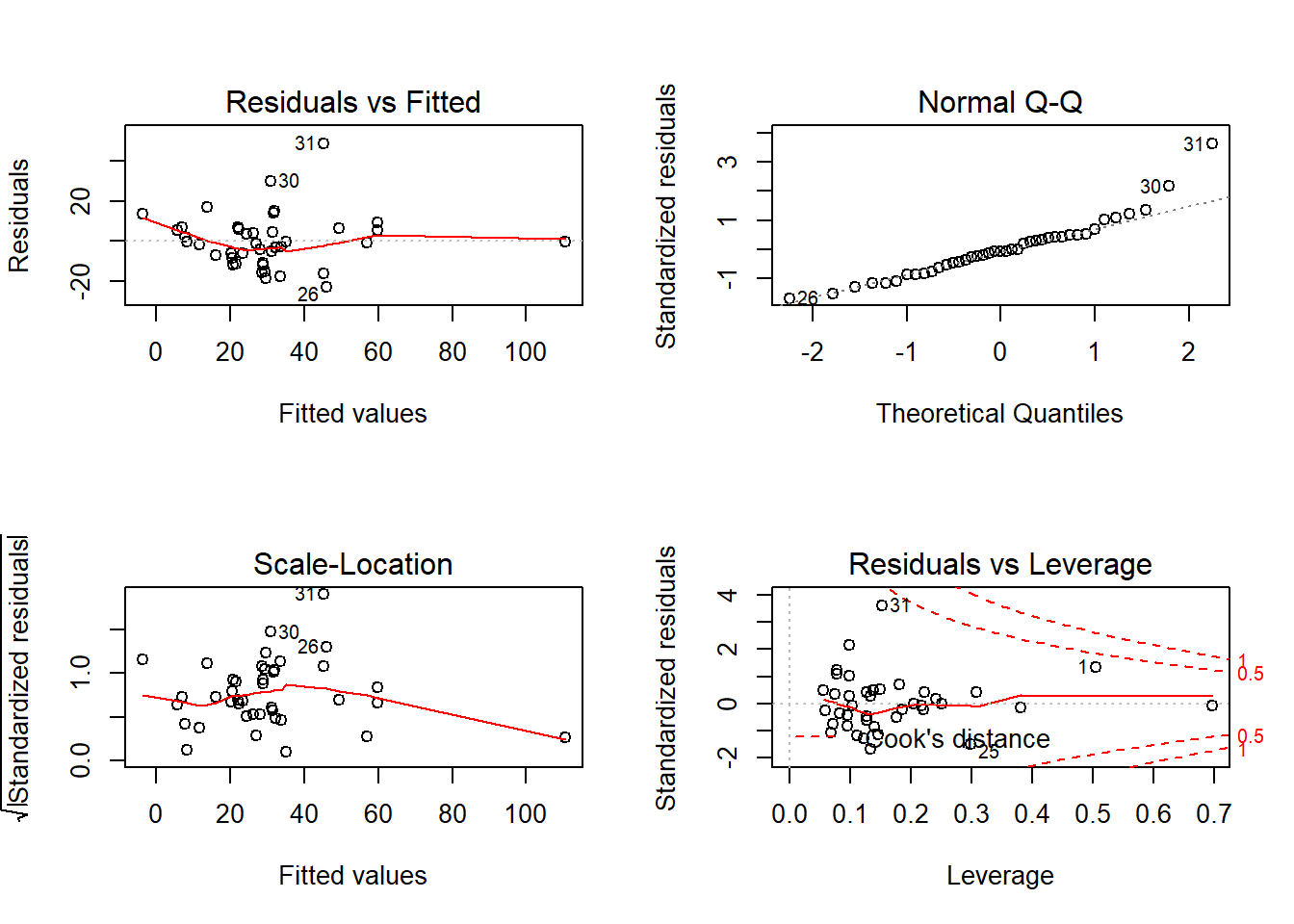
El gràfic corresponent a la homogeneïtat de variàncies és molt millorable. Els punts haurien d’estar dispersos, i en canvi es troben molt junts, en alguns punts i en canvi en d’altres quasi no hi ha punts.

Pel que fa ala Normalitat, en general sembla força correcta i tenim una petita desviació cap al final.

Mirant, la distància de Cook no veiem cap punt que pugui influir massa els resultats, ja que tots es troben dins els límits de 1.

Com podem millorar la distribució de residus?

Per millorar la distribució de residus tenim vàries opcions:

  1. Intentar transformar variables i mirar si millora la distribució dels residus.

  2. Si transformant no millora, llavors potser que un mètode “clàssic” no sigui el més indicat. En aquest cas, mireu com aplicar un mètode “modern” (GLM).

4.5 Transformació de variables

En aquest exemple, podem començar per provar que passaria si transformen la Y. Mirant la distribució del so2 (vegeu gràfic inicial), es veu com hi ha biaix a la dreta, pel que la transformació més indicada seria el logaritme3. Així doncs, farem un nou model, però aquesta vagda posant el logaritme de so2. Això ho podem fer directament en el model de la manera següent:

#canviem el nom al model, i ara serà lnso2_rlm, per indicar que so2 s'ha logaritmitzat
#per dir a R que cal fer el logaritme s'ha d'escriure "log(so2)". Ull!!! si no s'indica el contrari, per defecte al escriure 2log2 en R es calcula el logaritme neperià.

lnso2_rlm<-lm(log(so2)~temp+n_fabr+Pobl+vent+precp+dies_pluja, data=contaminacio.data)

Un cop fet el model tornem a comprovar els supòsits:

par(mfrow=c(2,2))#així indiquem a R que volem els gràfics en un panell de 2*2
plot(lnso2_rlm)

par(mfrow=c(1,1))#indiquem a R que torni a la configuració inicial de gràfic per panell.

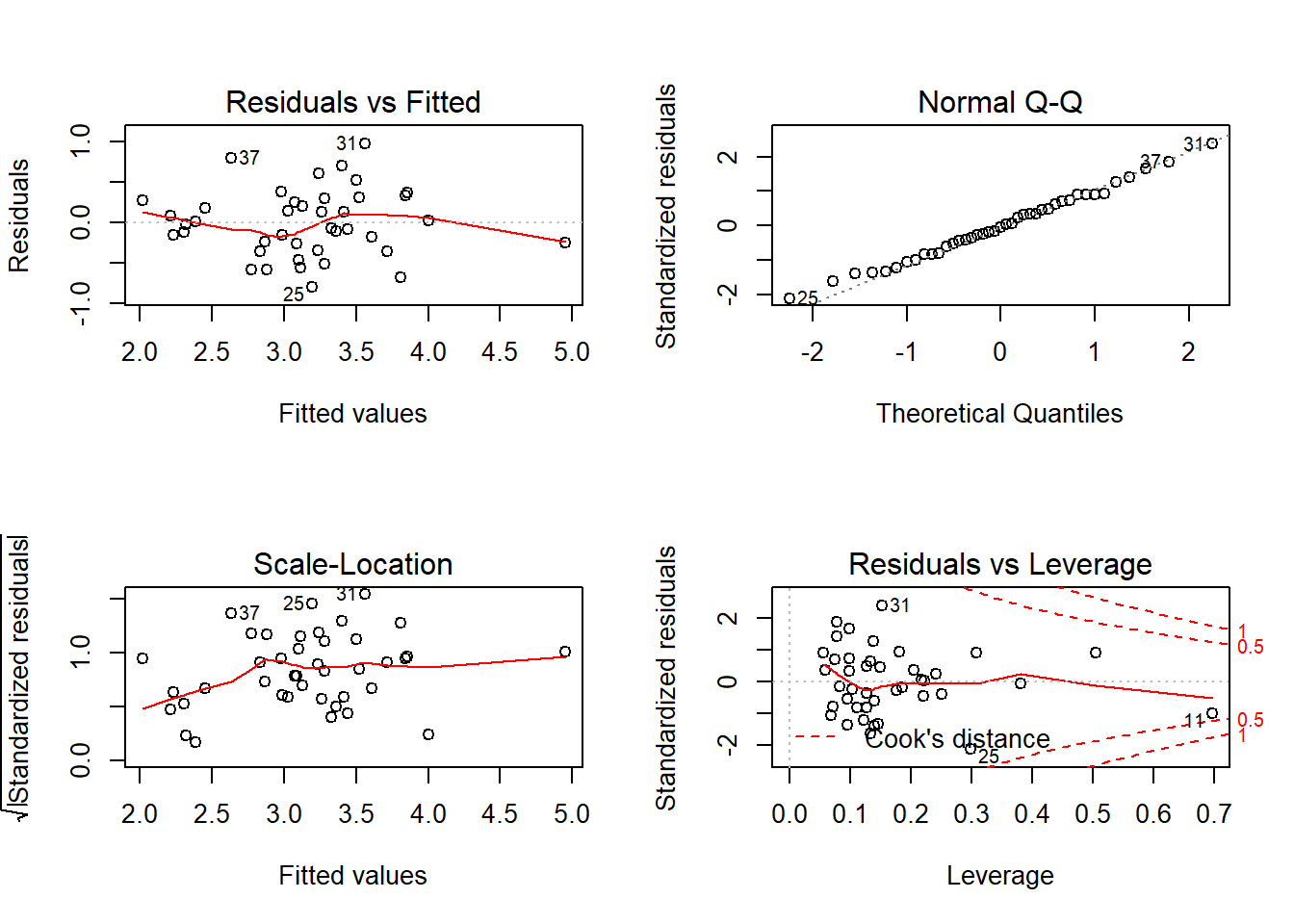
Molt millor!!!! només transformant una variable.

Com a exercici podeu provar si aconseguim millorar la distribució dels residus transformant altres variables (les Xs)

4.6 Control de Col·linealitat

Per controlar que no tinguem problemes de col·linealitat utilitzarem el variance inflation factor (vif) Per calcular el vif és molt fàcil un cop s’ha creat el model, ja que només s’ha d’escriure vif(nom del model)

vif(lnso2_rlm)
##       temp     n_fabr       Pobl       vent      precp dies_pluja 
##   3.763996  14.703652  14.340833   1.255519   3.404921   3.443651

Tenim 2 variables amb valors elevats de vif : n_fabr i Pobl. Això és degut a que estan molt relacionades entre elles. Ho podem comprovar visualment fent un gràfic de correlació

#recordeu que fent aquest gràfic simple, cal especificar el nom de l'arxiu d'R (en aquest cas "contaminacio.data") perquè R sàpiga on buscar les variables

#el símbol de "$" que indica a l'R que seleccioni dins l'arxiu indicat la variable que poseu després del símbol
plot(contaminacio.data$n_fabr,contaminacio.data$Pobl)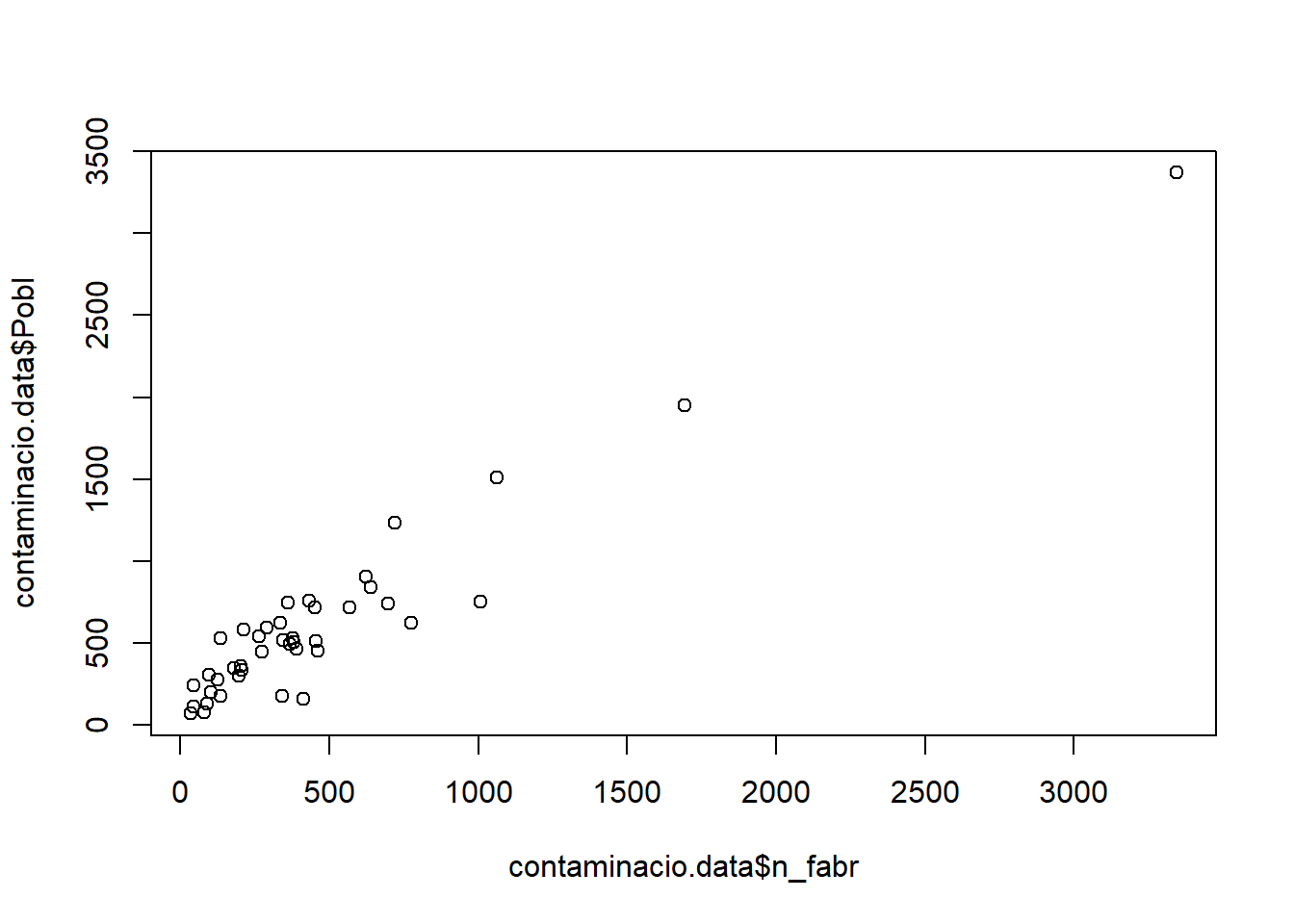

Que prou clar que hi ha relació entre les variables, i per tant això ens provoca un problema de col·linealitat que hem de solucionar.

4.6.1 Solucionar problemes de col·linealitat

La manera per solucionar aquest tipus de problemes és només deixar una de les variables al model. Per escollir quina variable es queda hi ha diferents criteris:

  1. Criteri biològic. A partir dels vostres coneixements, decidiu que té més sentit que es quedi una de les variables.

  2. Deixeu la variable que més es relaciona amb la Y, perquè ajudarà a que el model sigui millor.

En aquest exemple, ambdues variables porten la mateixa informació (stress d’origen antropogènic), per tant utilitzarem el criteri#2.

Mirem la relació entre les variables i el lnso2

cor(contaminacio.data$Pobl,log(contaminacio.data$so2))
## [1] 0.3434499
cor(contaminacio.data$n_fabr,log(contaminacio.data$so2))
## [1] 0.4843335

La correlació és més elevada amb n-fabr, per tant deixem aquesta variable al nostre model i eliminem Pobl

Així, el model queda de la següent manera:

lnso2_rlm1<-lm(log(so2)~temp+n_fabr+vent+precp+dies_pluja, data=contaminacio.data)

Comprovem supòsits

par(mfrow=c(2,2))#així indiquem a R que volem els gràfics en un panell de 2*2
plot(lnso2_rlm1)

par(mfrow=c(1,1))#indiquem a R que torni a la configuració inicial de gràfic per panell.

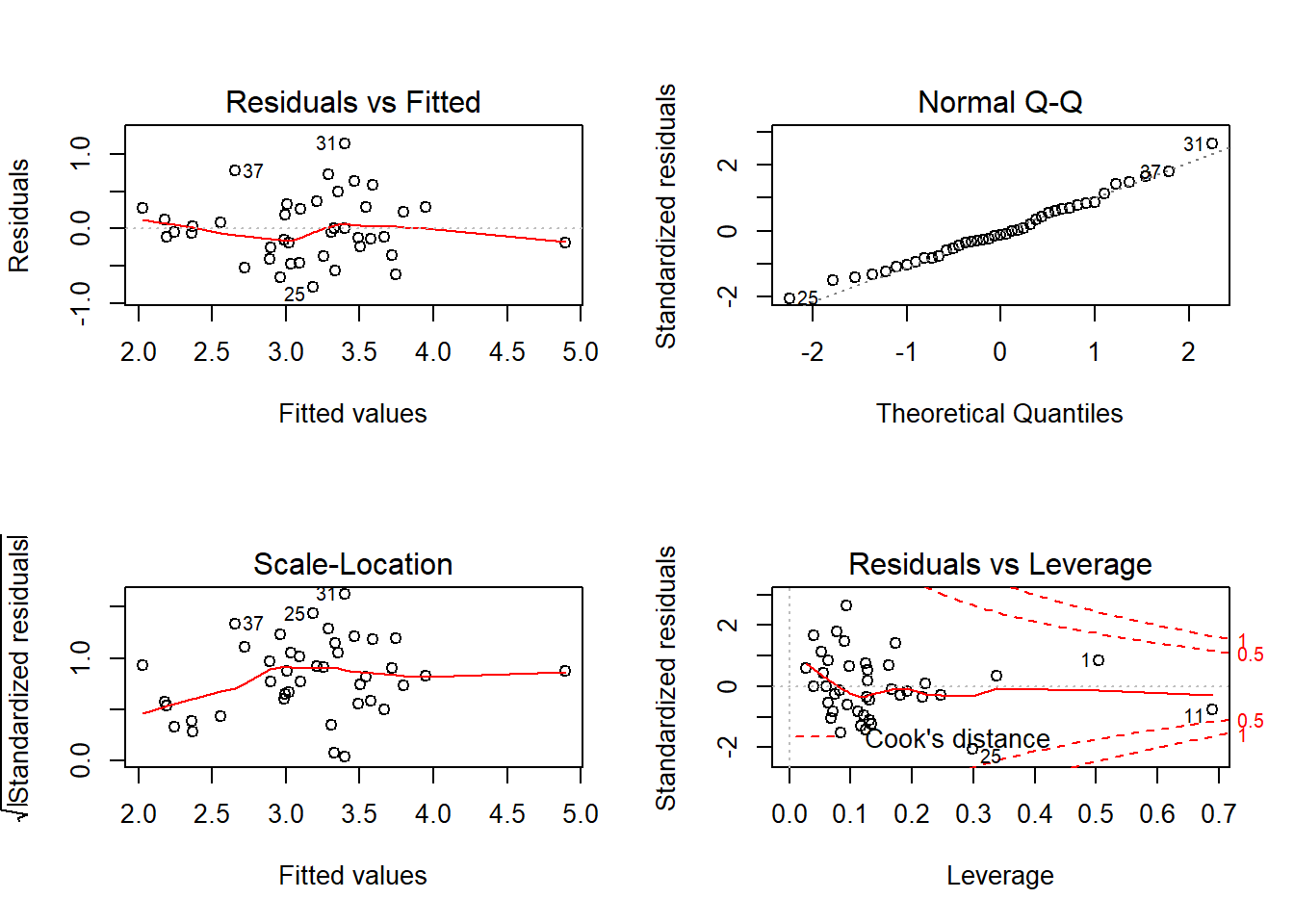
OK!, sembla que tot correcte.

Ara comprovem col·linealitat

vif(lnso2_rlm1)
##       temp     n_fabr       vent      precp dies_pluja 
##   3.396942   1.079793   1.237999   3.355407   3.443162

Tots els valors son inferiors a 5, per tant no hi ha problemes.

Ja podem passar a interpretar els resultats del model.

4.7 Interpretació resultats RLM

Per fer-ho, cal demanar a l’R un resum del nostre model.

summary(lnso2_rlm1)
## 
## Call:
## lm(formula = log(so2) ~ temp + n_fabr + vent + precp + dies_pluja, 
##     data = contaminacio.data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.7864 -0.2563 -0.0516  0.2759  1.1473 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  7.6864628  1.4471647   5.311 6.25e-06 ***
## temp        -0.0689735  0.0184040  -3.748 0.000643 ***
## n_fabr       0.0005550  0.0001331   4.170 0.000191 ***
## vent        -0.1797441  0.0562091  -3.198 0.002936 ** 
## precp        0.0194181  0.0112308   1.729 0.092620 .  
## dies_pluja   0.0003444  0.0050524   0.068 0.946037    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4565 on 35 degrees of freedom
## Multiple R-squared:  0.6304,	Adjusted R-squared:  0.5776 
## F-statistic: 11.94 on 5 and 35 DF,  p-value: 8.74e-07

En aquesta sortida d’R hi ha molta informació.

Comencem pels resultats generals.

4.7.1 El nostre model explica les variacions de Y ?

  • A la pràctica, volem saber si el nostre conjunt de variables explicatives, realment es poden relacionar amb variacions del so2. Per saber-ho, cal mirar el p-valor que surt a baix de tot a la dreta . Si és <0.05 llavors és significatiu i vol dir que tenim prou evidències com per rebutjar la hipòtesis nul·la que una anàlisis de RLM diu que NO HI HA REGRESSIÓ (vindria a ser que el conjunt de variables explicatives que em posat en el model no explica les variacions de la Y). En aquest cas, el nostre valor és inferior a 0.05 (p-valor = 8.74e-07) per tant el model és vàlid.

4.7.2 Ajustament del model

  • Per quantificar quina part de les variacions de Y es poden explicar pel model creat, cal mirar la R2ajustada. Aquest valor el trobem, també a les últimes línies Adjusted R-squared: 0.5776, i això vol dir que amb aquest model podem explicar el 57%4 de la variabilitat del so2.

Anem ara a interpretar els resultats interns

4.7.3 Valors dels coeficients de la regressió

  • Mirant una miqueta més amunt, trobem molts números sota el títol de Coefficients. Allà trobem llistats tots els coeficients del model de regressió, a la columna Estimates els valors dels coeficients, i a la columna Std. Error els seu error estadandard. Així, els valors dels coeficients per aquest model serien:
    • ordenada a l’origen (Intercept)= 7.68
    • coeficients de regressió parcial
      • temp = -0.0689735
      • n_fabr = 0.0005550
      • vent = -0.1797441
      • precp = 0.0194181
      • dies_pluja = 0.0003444

4.7.4 Relació de cada X amb la Y

Els valors sota la columna de Pr(>|t|) son els p-valors dels test de t-student que es fan per cada coeficient (ordenada a l’origen i coeficients de regressió parcials) en que es compara cada coeficient amb 0. La H0: el coeficient és = 0. Llavors si aquest p-valor és <0.05 indica que hi ha evidències suficients com per rebutjar la H0 i acceptar la Ha: el coeficient és diferent de 0. Això a la pràctica vol dir que si per algun coeficient de regressió parcial el p-valor >0.05, aquella variable explicativa no està relacionada amb les variacions de la Y5

  1. Ull!!! la variable que voleu transformar amb logaritme no pot tenir 0, ja que sinó no es pot calcular el logaritme. Si la variable té 0, llavors cal fer log(var+1). tampoc podeu transformar amb logaritme variables que tinguin números negatius↩︎

  2. els valors es donen en tant per u, però multiplicant per 100 es poden passar a %↩︎

  3. és com si tingués un pendent=0, seria una línia horitzontal, i per tant per molt que augmentés o disminuís el valor d’aquella X la Y no canviaria↩︎