7 GLM part II
Mètodes lineals Generalitzats (Y Poisson)
Mètode “modern” quan la Y segueix una distribució Poisson
Authors:Compte, J. & Gascón S.
Aquesta secció servirà per introduir l’ús de Models lineals Generalitzats (GLM) per analitzar variables resposta (Y) amb distribució Poisson.
7.1 Packages necessaris
Per aquesta sessió es necessita els següent package:
Si surt Warning no pasa res, sol ser un avis perquè la versió del package és anterior al nostre R. En general, no és un problema i els packages funcionen bé.
7.2 Carregar dades
Les dades utilitzades són extretes de Zuur et al. (2009) Mixed Effects Models and Extensions in Ecology with R (pag. 101). Es tracta d’un estudi en platges holandeses on es vol conèixer la riquesa de macrofauna segons l’alçada del punt de mostreig respecte el nivell mitjà de la marea. S’han estudiat 45 punts situats a diferents alçades.
7.3 Les variables
Les variables de les que es disposa són:
- Sample: Número de punt de mostreig.
- NAP: Alçada del punt de mostreig respecte el nivell mitjà de la marea.
- richness: Riquesa de macrofauna en un punt concret de mostreig.
- La variables resposta Y és la riquesa d’espècies ( richness )
- La variables explicativa X és l’alçada del punt de mostreig respecte el nivell mitjà de la marea ( NAP )
Com que tenim dos variables continues, la primera idea és fer una regressió lineal simple (RLS) amb le mètode tradicional.
Carreguem les dades de l’arxiu “richness.RData”.
Comprovem si les variables s’han carregat bé
## Sample NAP richness
## Min. : 1 Min. :-1.3360 Min. : 0.000
## 1st Qu.:12 1st Qu.:-0.3750 1st Qu.: 3.000
## Median :23 Median : 0.1670 Median : 4.000
## Mean :23 Mean : 0.3477 Mean : 5.689
## 3rd Qu.:34 3rd Qu.: 1.1170 3rd Qu.: 8.000
## Max. :45 Max. : 2.2550 Max. :22.000Perfecte, tenim 3 variables a l’arxiu i totes numèriques.
7.4 Exploració gràfica
Comprovació gràfica mitjaçant la comanda scatterplot on indiquem les variables a analitzar richness~NAP, i indiquem que ens dibuixi una línia recta de color blau representant la relació lineal reg.line=lm,smooth=F, spread=F, id.method=‘mahal’, id.n = 2 i que ens dibuixi els diagrames de caixa de les dos variables boxplots=‘xy’, span=0.5. Finalment, li hem de dir la base de dades d’on s’extreu data=richness.data.
scatterplot(richness~NAP, reg.line=lm, smooth=F, spread=F, id.method='mahal', id.n = 2, boxplots='xy', span=0.5, data=richness.data)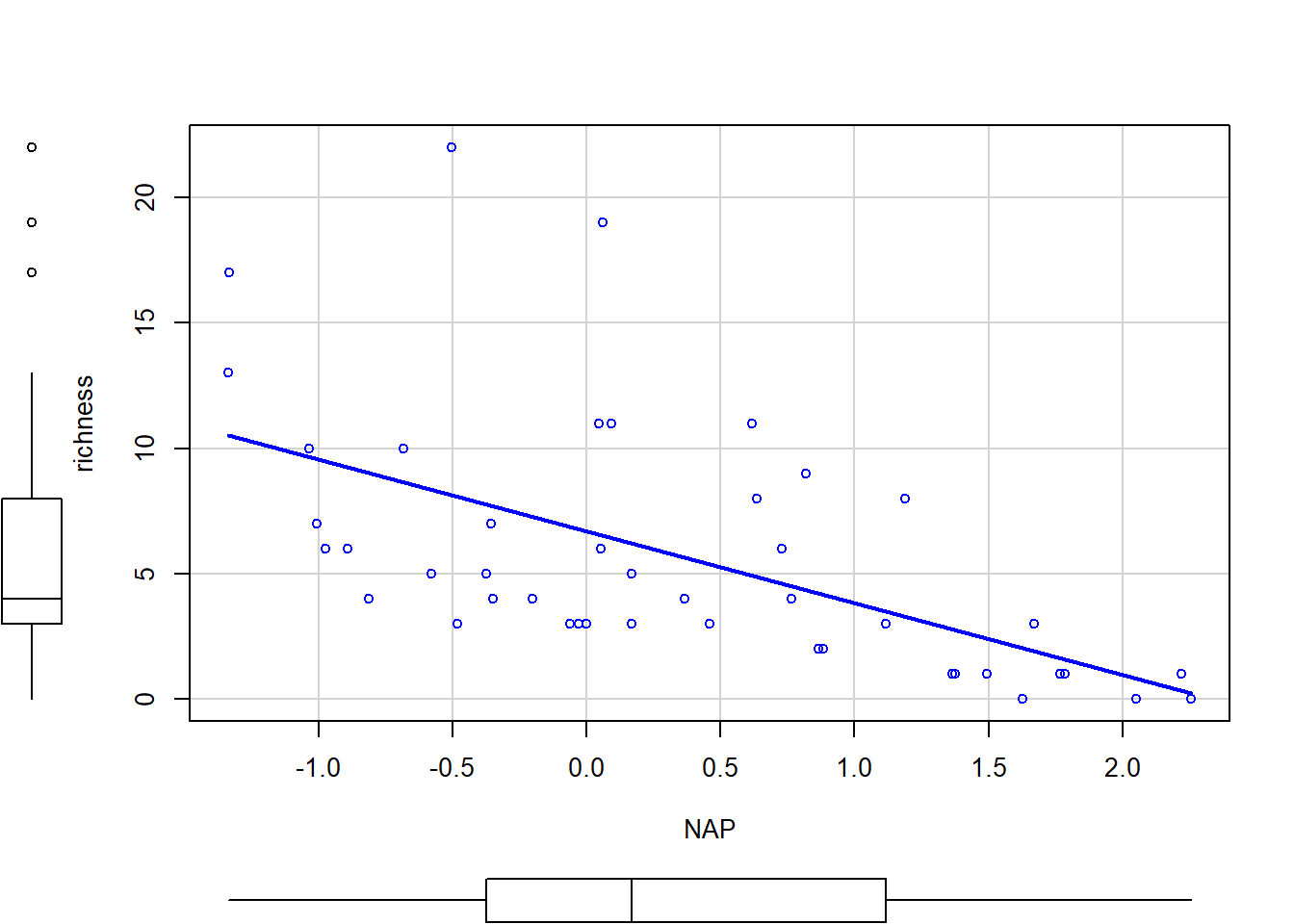
A la gràfica es poden observar diferents aspectes:
- La riquesa té dades anòmales (mirar diagrama de caixa).
- La línia de la RLS no s’acaba d’ajustar a la distribució de les dades. SAlguna valors queden molt allunyats de la predicció (línia blava)
- Fem un RLS amb la comanda lm (mètode clàssic) indicant les variables a analitzar richness~NAP i la base de dades d’on s’extreuen data=richness.data.
Comprovem si la RLS compleix els supòsits de normalitat i homoscedasticitat de forma gràfica amb la comanda plot. Abans, dividim la finestra de les gràfiques en 4 parts amb la comanda par, i indicant que dibuixi dos gràfics a dalt i dos a baix mfrow=c(2,2). Finalment indiquem que torni a unificar la finestra dels gràfics amb la comanda par(mfrow=c(1,1)).
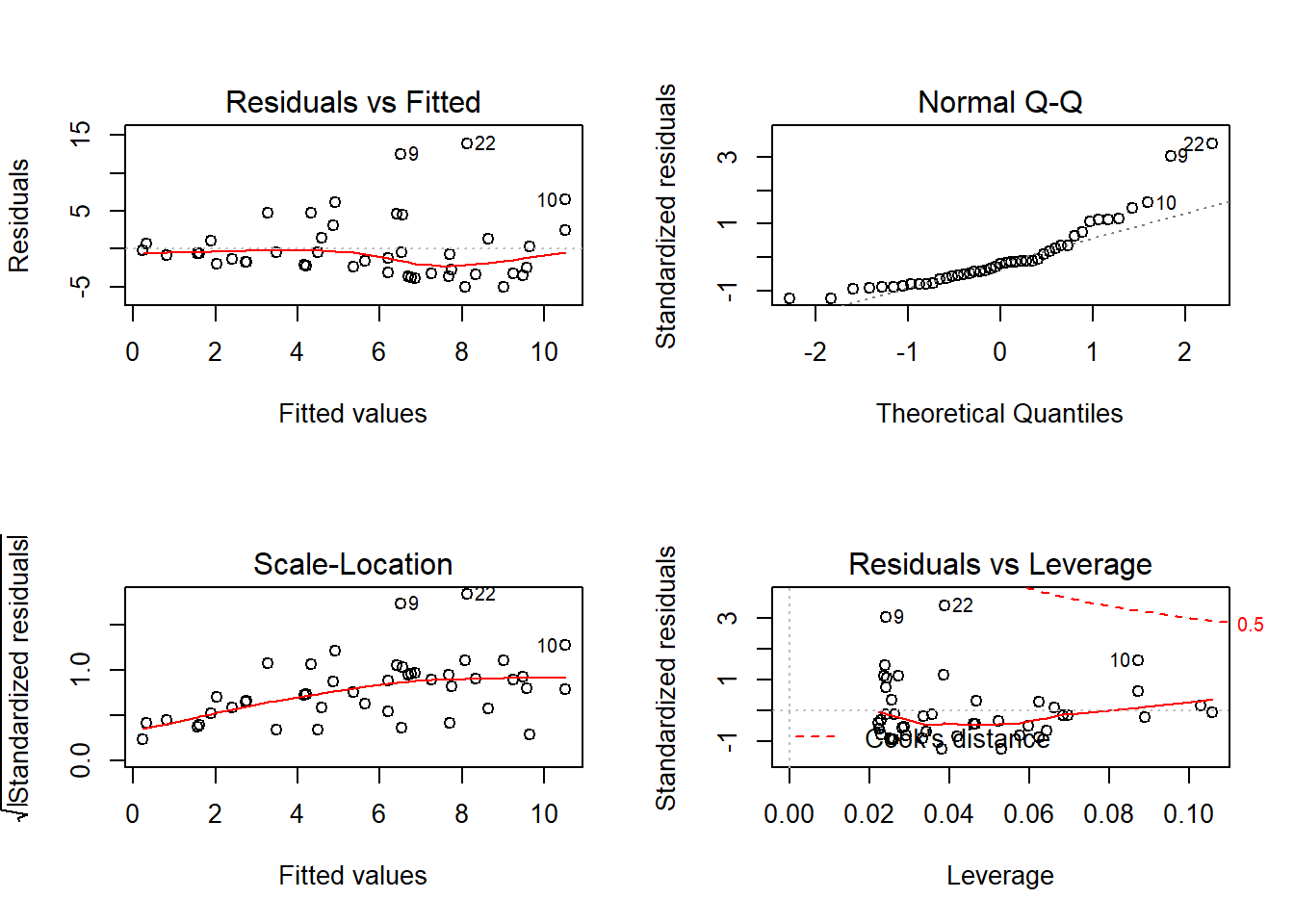
Es pot observar a la gràfica dels residus que hi ha mala distribució. En el gràfic d’homogeneïtat de variàncies es veu un cert patró de ventall, indicant heterogeneïtat, i per la Normalitat també es veu com hi ha punts que s’allunyen de la diagonal.
Per tant, tenim problemes amb els supòsits. Mirant el gràfic anterior, on hi havia els diagrames de caixa es veu com la riquesa està esbiaixada a la dreta, una opció seria repetir l’anàlisi, però amb la riquesa transformada amb logaritme.
Però la riquesa és el típic exemple de variable amb distribució de tipus Poisson, ja que està esbiaixada a la dreta, no té decimals, i no pot agafar valors negatius. Per tant, podem fer la regressió amb un mètode modern GLM, l’avantatge de fer això i no una regressió amb la riquesa transformada és que:
No farà prediccions impossibles. Per exemple, si fem el mètode clàssic utilitzant distribució Normal de Y, els valors que poden agafar les variables amb aquests tipus de distribucions poden ser tan positius com negatius, pel que al fer prediccions també podríem obtenir riqueses negatives.
Quan demanem les prediccions, automàticament ens donarà valors de riquesa. No haurem de transformar el valor per saber a quina riquesa correspon.
7.5 Fem el model de regressió amb GLM
La forma de fer el GLM amb distribució de Poisson és igual que el GLM binomial però especificant que la distribució de les dades segueix Poisson.
Fem el GLM indicant que les dades tenen una distribució de Poisson (especificant a family “poisson”).
Fem un model nul on només tinguem en compte la Y (richness) i no tinguem en compte la X (NAP). Després compararem si el model amb la X és millor que el model sense .
Per fer-ho, posem un nom al model nul (ex: ric_glm0) i utilitzem la mateixa comanda que abans, però en el lloc de la variable explicativa (NAP), hi posem un 1.
Comprovem, comparant models, si el model que hem ajustat amb el NAP és millor que el nul (sense NAP). La comanda utlitzada és anova13 on hi indiquem:
- el model nul
- el model que hem fet amb la variable explicativa (NAP)
- Que ens faci la comparació, i calculi el p-valor de la chi-square test=“Chisq” .
## Analysis of Deviance Table
##
## Model 1: richness ~ 1
## Model 2: richness ~ NAP
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 44 179.75
## 2 43 113.18 1 66.571 3.376e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Si ens fixem amb el p-valor de l’anàlisi (p-valor= 3.376e-16 ***) aquest surt significatiu. Per tant, el model amb NAP és significativament millor que sense (model nul). És a dir, el model amb NAP explica millor la distribució de les dades de riquesa.
7.6 Tenim “Overdispersion”?
##
## Call:
## glm(formula = richness ~ NAP, family = "poisson", data = richness.data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.2029 -1.2432 -0.9199 0.3943 4.3256
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.79100 0.06329 28.297 < 2e-16 ***
## NAP -0.55597 0.07163 -7.762 8.39e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 179.75 on 44 degrees of freedom
## Residual deviance: 113.18 on 43 degrees of freedom
## AIC: 259.18
##
## Number of Fisher Scoring iterations: 5Residual Deviance =113.48
graus de llibertat=43
Càlcul del coeficient:
## [1] 2.632093coeficient= 2.632>1 Per tant, hi ha OVERDISPERSION!!!
7.7 Apliquem la correcció14
##
## Call:
## glm(formula = richness ~ NAP, family = "quasipoisson", data = richness.data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.2029 -1.2432 -0.9199 0.3943 4.3256
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.7910 0.1104 16.218 < 2e-16 ***
## NAP -0.5560 0.1250 -4.448 6.02e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 3.044178)
##
## Null deviance: 179.75 on 44 degrees of freedom
## Residual deviance: 113.18 on 43 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 5Creem un model nul amb la correcció de quasipoissont sense tenir en compte la variable NAP.
Comprovem els supòsits
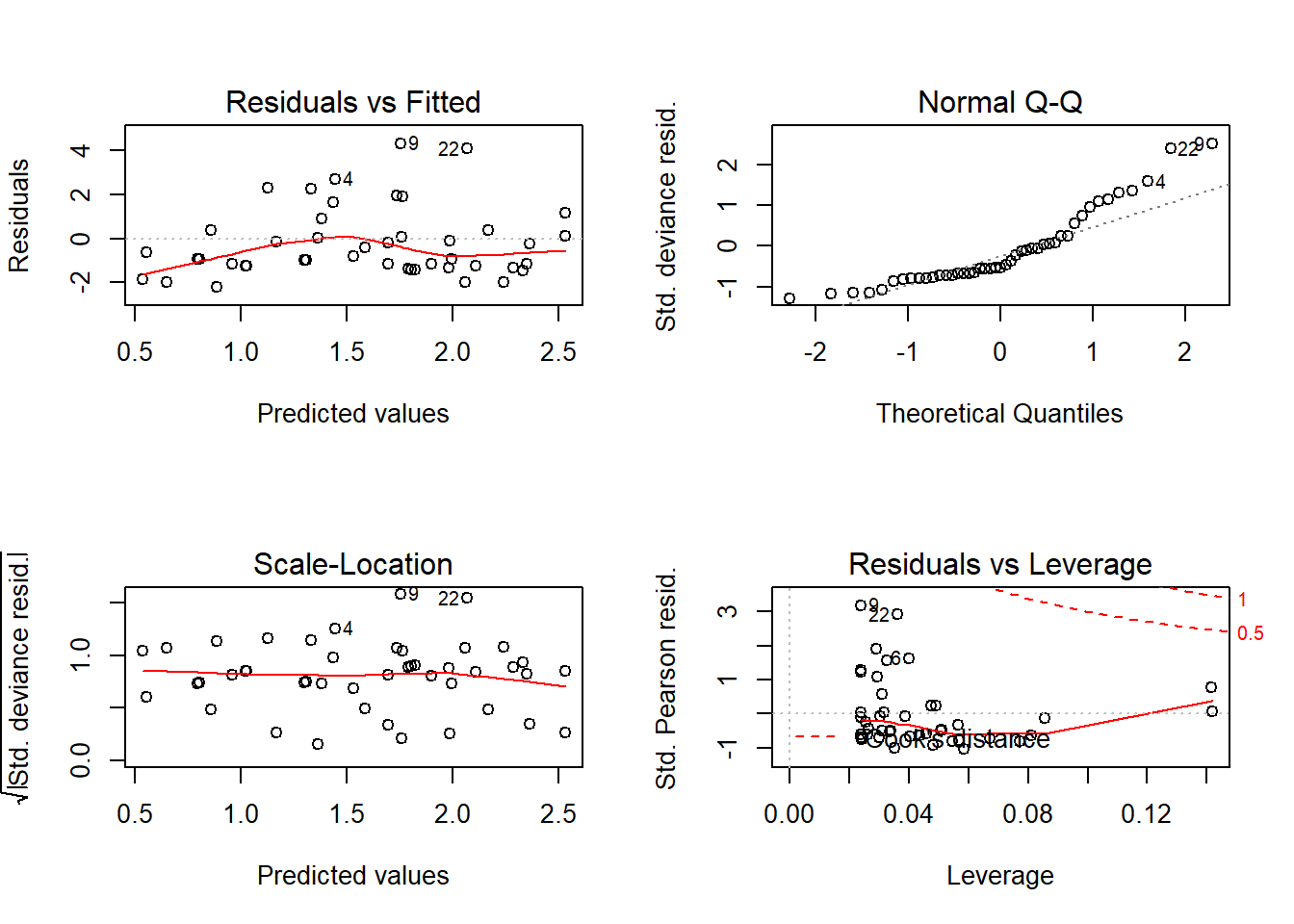
Ja no tenim una distribució de residus tan dolenta, sobretot ha millorat molt el gràfic que mostra si tenim homogeneïtat de variàncies. El de la Normalitat també ha millorat una miqueta. Tot indica que el glm amb la correcció s’ajusta millor a les dades que una RLS.
I comprobem si el nostre model és significativament millor que el nul fent la comparació de models.
anova(ric_qglmo,ric_qglm, test="F")#quan tenim hem aplicat la correcció per over-under dispersion, llavors millor canviar la "Chisq" per "F"(F-Fisher)## Analysis of Deviance Table
##
## Model 1: richness ~ 1
## Model 2: richness ~ NAP
## Resid. Df Resid. Dev Df Deviance F Pr(>F)
## 1 44 179.75
## 2 43 113.18 1 66.571 21.868 2.9e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1El p-valor (p-valor= 2.92e-06 ***) indica que és millor el model amb NAP.
7.8 Calculem la variància explicada pel model
## [1] 0.3703455Resultat: 0.37. Això vol dir que el 37% de la variança és epxlicada pel model.
7.9 Realitzem la gràfica del model:
plot(richness~NAP, pch=16, data=richness.data)#primer fem el gràfic de base
xv<-seq(min(richness.data$NAP),max(richness.data$NAP),0.1)#informem a l'R del mínim i màxim de la X
yv<-predict(ric_qglm,list(NAP=xv),type="response")#demanen la predicció del nostre model per tots els valors de X (xv)
lines(xv,yv)#dibuixem la línia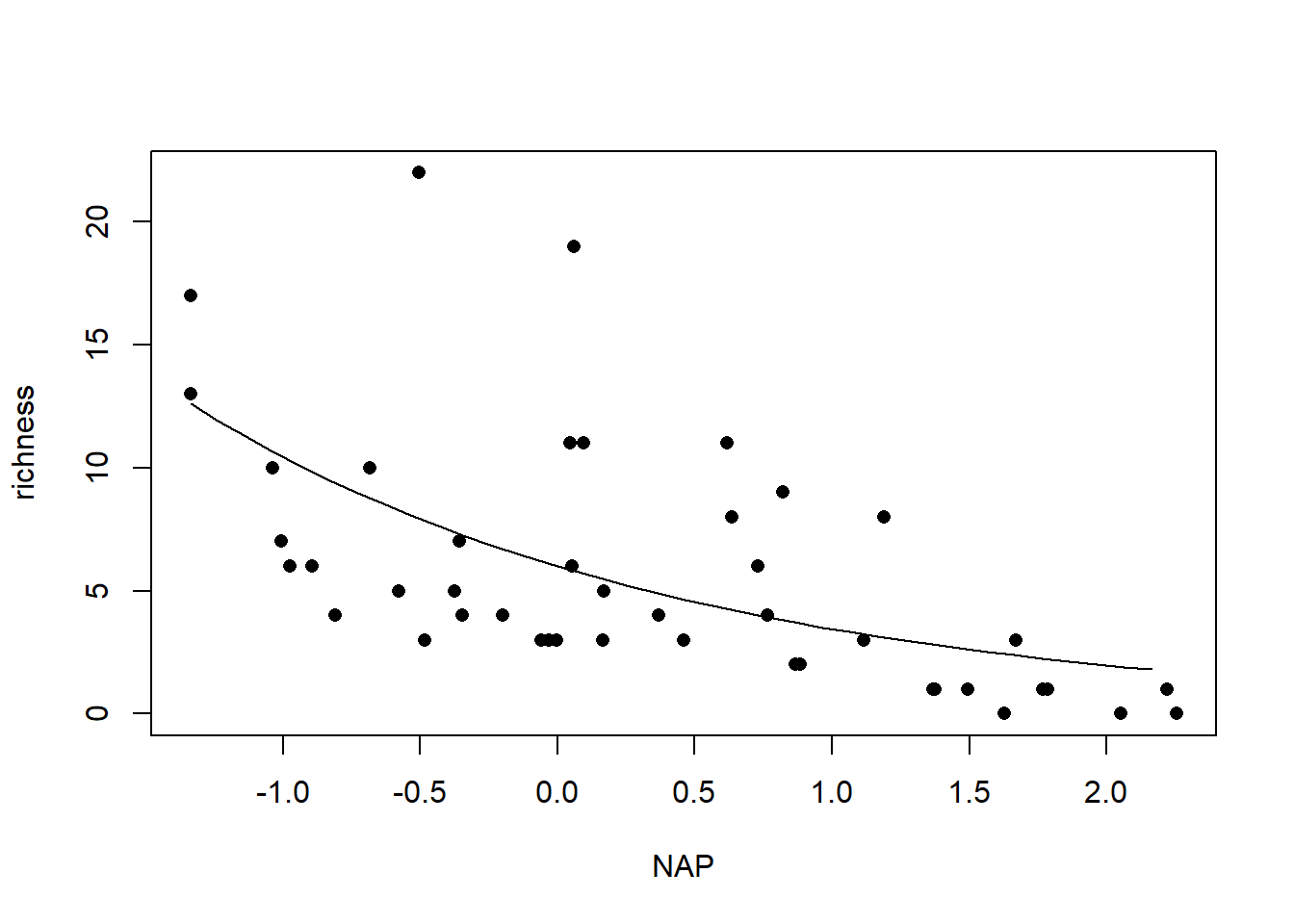
Si mirem els resultats de l’anàlisi i la gràfica del model, podem veure que hi ha una relació negativa entre el NAP i la riquesa de macrofauna.
aquesta anova no vol dir que farà una ANOVA d’un factor, sinò que compararà models, i mirarà si explica més o menys. Si no troba diferències entre models, vol dir que el model amb la variable X és igual de bo explicant variacions de Y que un model sense aquella X, per tant aquella X no aporta res alhora d’explicar la variabilitat de Y (no cal posar-la al model)↩︎
veure GLM Binomial, pels detalls d’aquesta correcció↩︎