8  เมนูเสริมที่น่าสนใจ

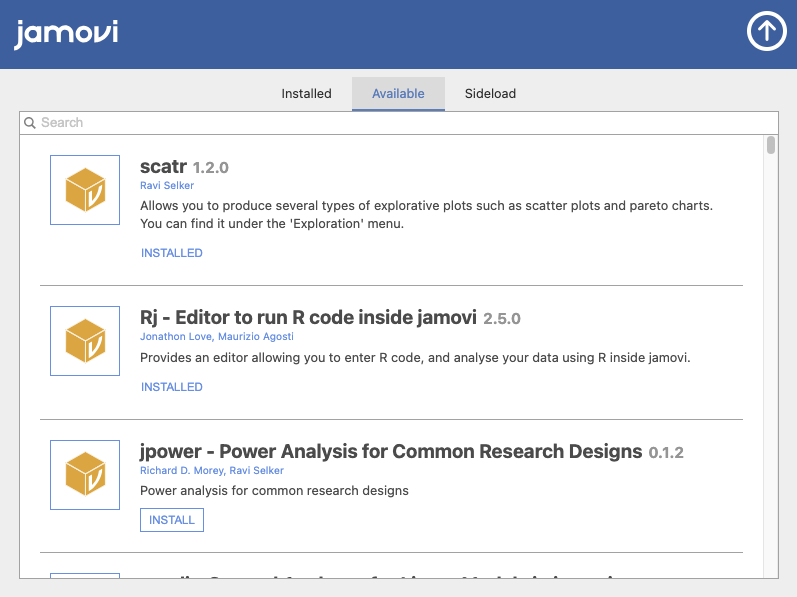
นอกจากเมนูการคำนวณและตัวแบบสถิติแบบมาตราฐานแล้ว โปรแกรม jamovi ยังเปิดโอกาสให้นักพัฒนาโปรแกรมสร้างชุดการทำงานเสริม เพื่อให้ผู้ใช้งานติดตั้งสำหรับการทำงานด้านสถิติอื่นๆ เพิ่มเติมได้ โดย สามารถเลือกการติดตั้งได้จากเมนูเครื่องหมาย + ที่มุมบนด้านขวา

การค้นหาและติดตั้งเมนูเสริม

จะต้องการเชื่อมต่ออินเทอร์เน๊ตก่อนทำการติดตั้งเมนูเสริม

เมื่อกดเข้าไปแล้วจะพบชุดคำส่ังให้ติดตั้งเพิ่มเติมมากมาย

ชุดคำสั่งเสริมต่างๆ

เมนูเสริมที่ผู้เขียนแนะนำ มีดังต่อไปนี้

8.1 surveymv

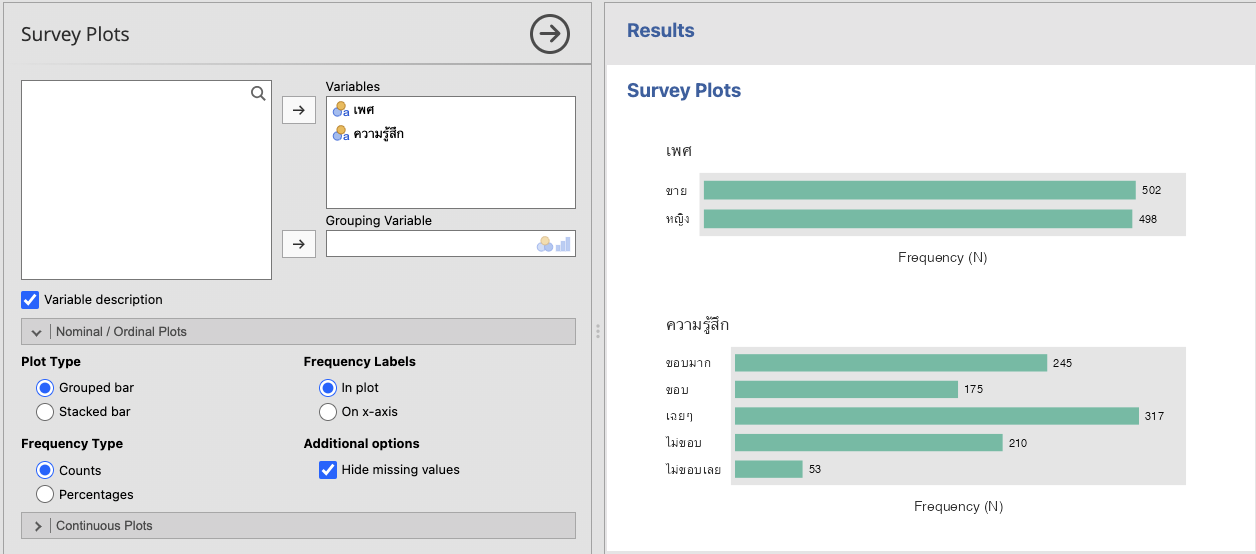
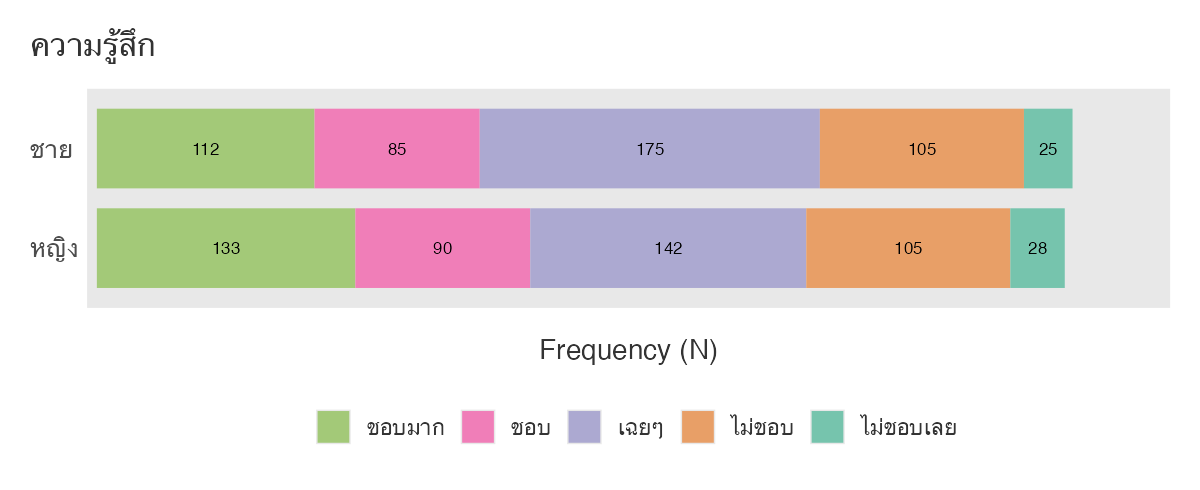
เมนูนี้เหมาะสำหรับการสร้างกราฟแท่งแสดงจำนวน หรือสัดส่วนของตัวแปรแบบกลุ่ม (categorical) ที่มีการวัดแบบ nominal

Show 102550100 entries

Search:

	gender	feeling
1	ชาย	ชอบมาก
2	หญิง	ชอบ
3	ชาย	ชอบมาก
4	ชาย	ไม่ชอบเลย
5	หญิง	เฉยๆ
6	ชาย	เฉยๆ
7	ชาย	ชอบมาก
8	ชาย	ชอบ
9	หญิง	ไม่ชอบ
10	หญิง	ชอบ

Showing 1 to 10 of 1,000 entries

Previous12345…100Next

เมื่อ install แล้วสามารถเรียกใช้งานได้เมนู Explolation แล้วเลือกใช้ Survey PLots

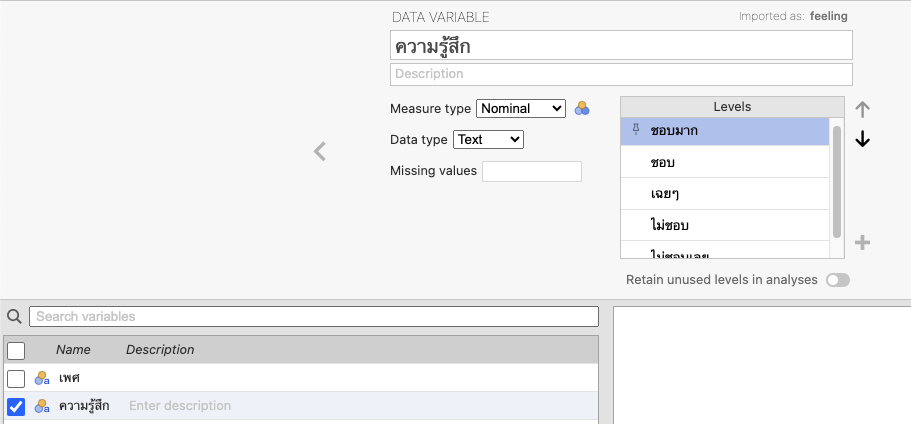
ลองใช้่ข้อมูล question.xlsx เปิดด้วย jamovi แล้วกำหนดระดับดังนี้

1. เปลี่ยนชื่อตัวแปรจาก gender เป็นเพศ และเปลี่ยนชื่อตัวแปรจาก feeling เป็นความรู้สึก
2. และเรียงลำดับความสำคัญดังนี้ ชอบมาก ชอบ เฉย ไม่ชอบ ไม่ชอบเลย

เปลี่ยนชื่อตัวแปรและกำหนดระดับความสำคัญของตัวแปรความรู้สึก

Grouped bar แบบ Counts

Grouped bar แบบ Percentages

Stacked bar แบบ Counts

Stacked bar แบบ Percentages

ผู้เขียนเลือกใช้ theme Hadley และจานสี Dark2

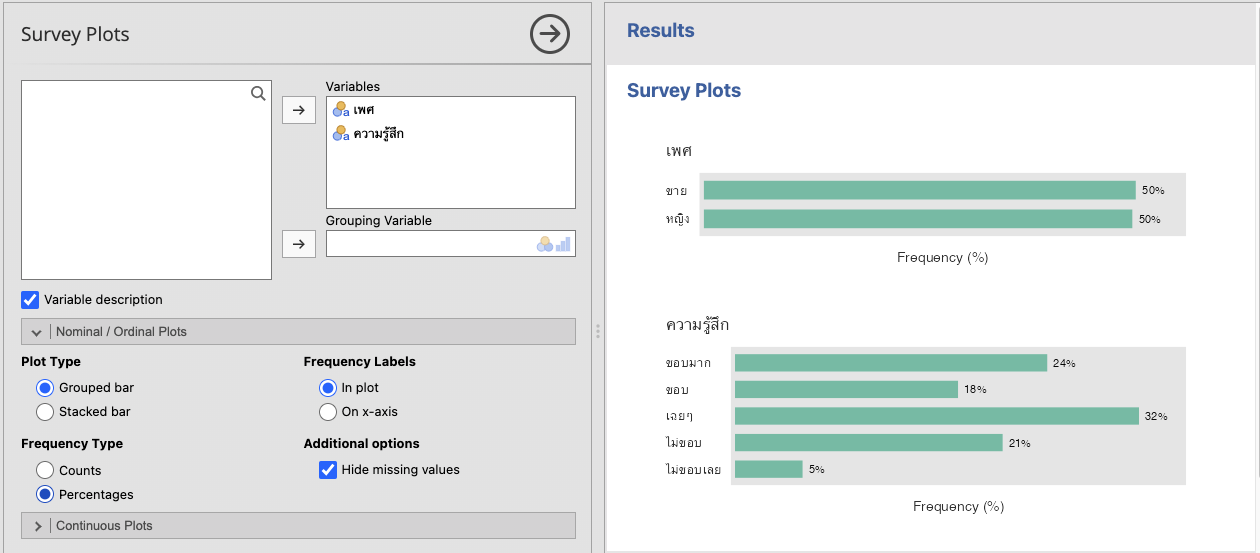
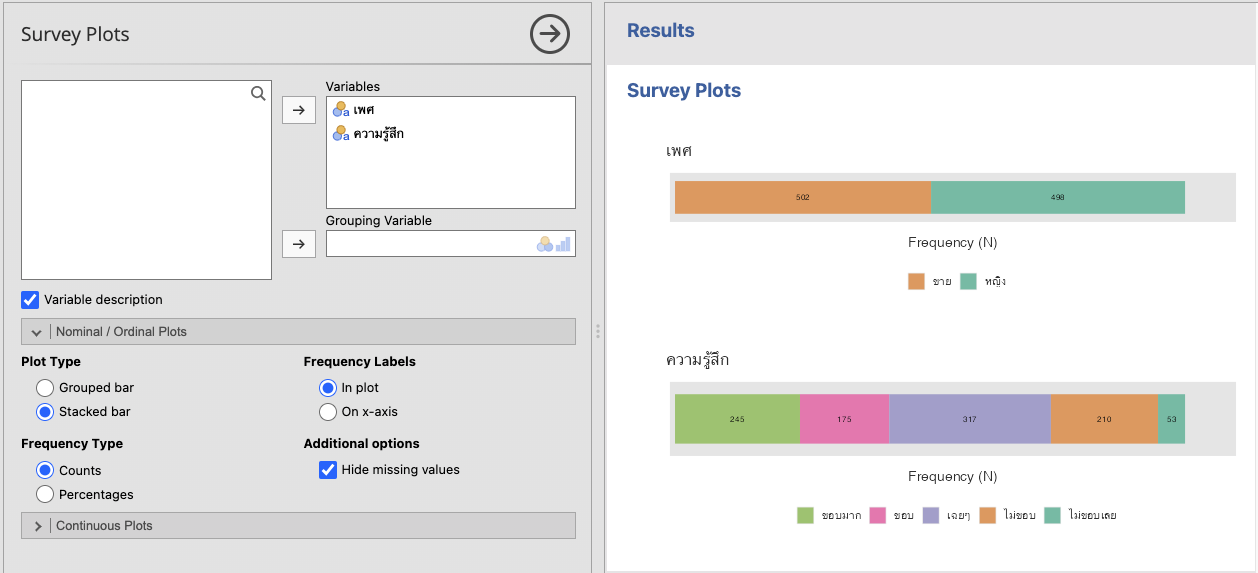
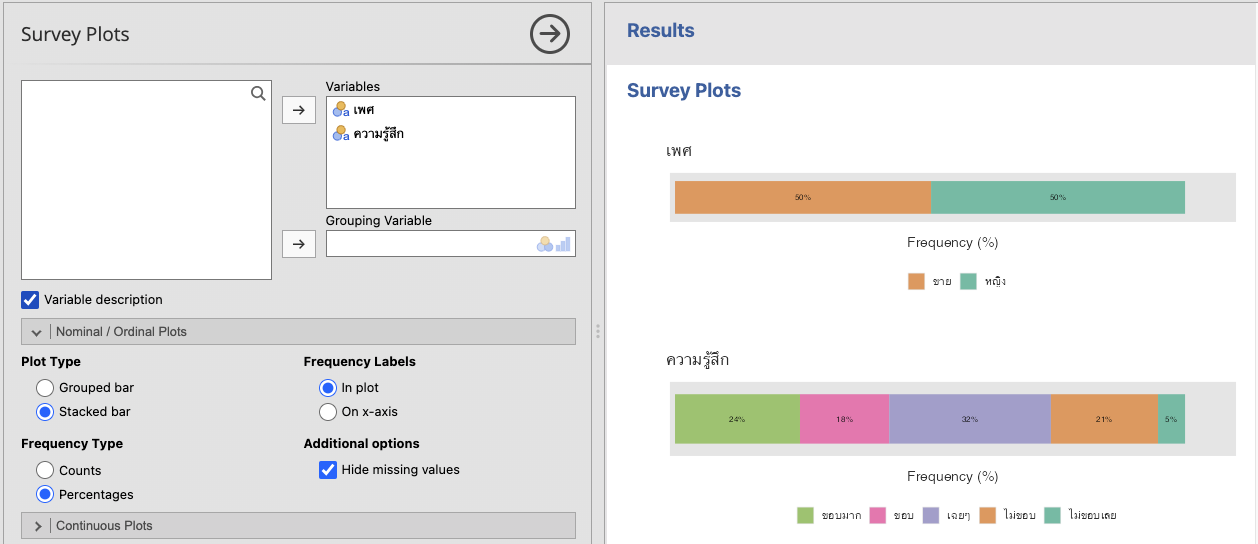
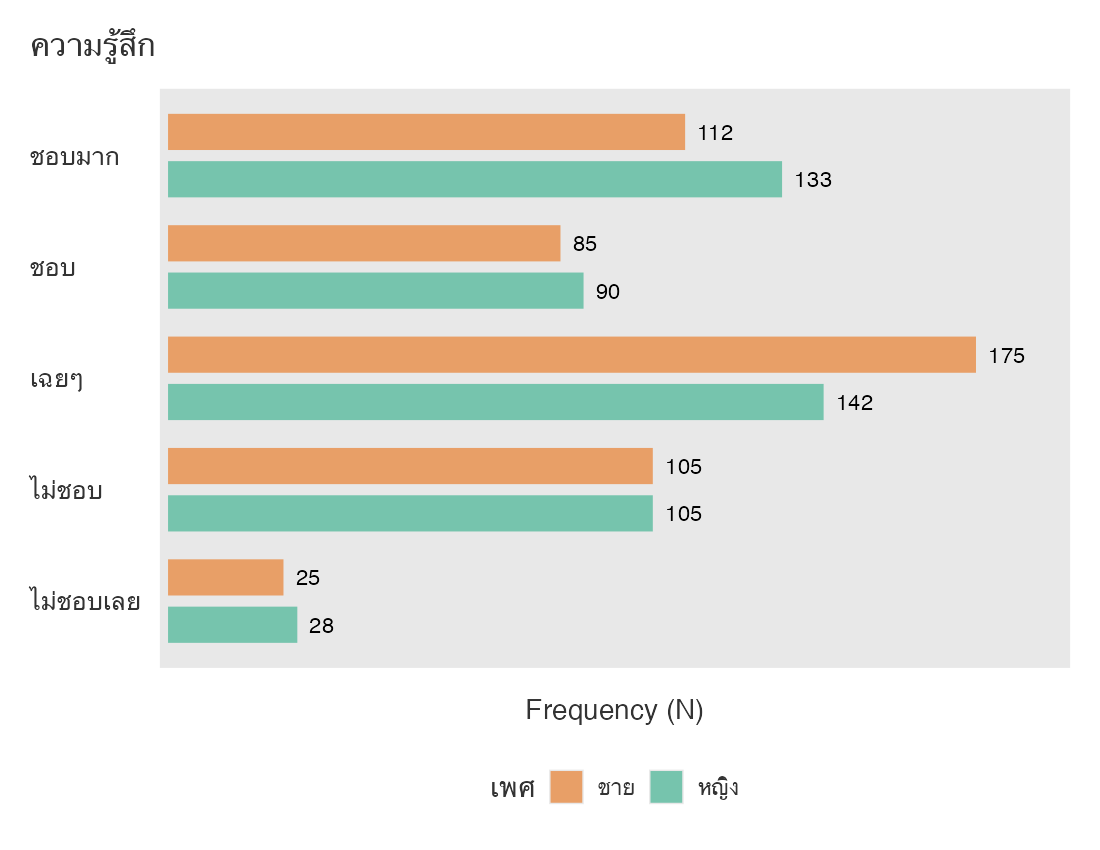
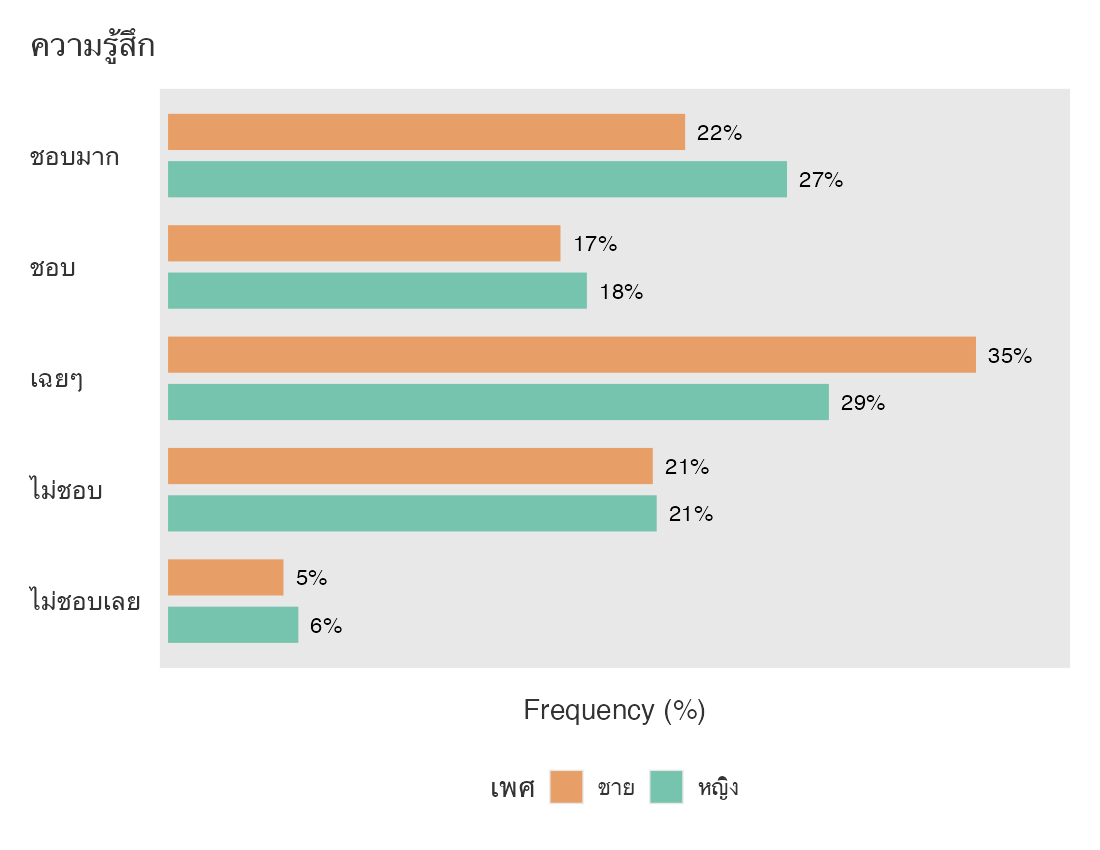
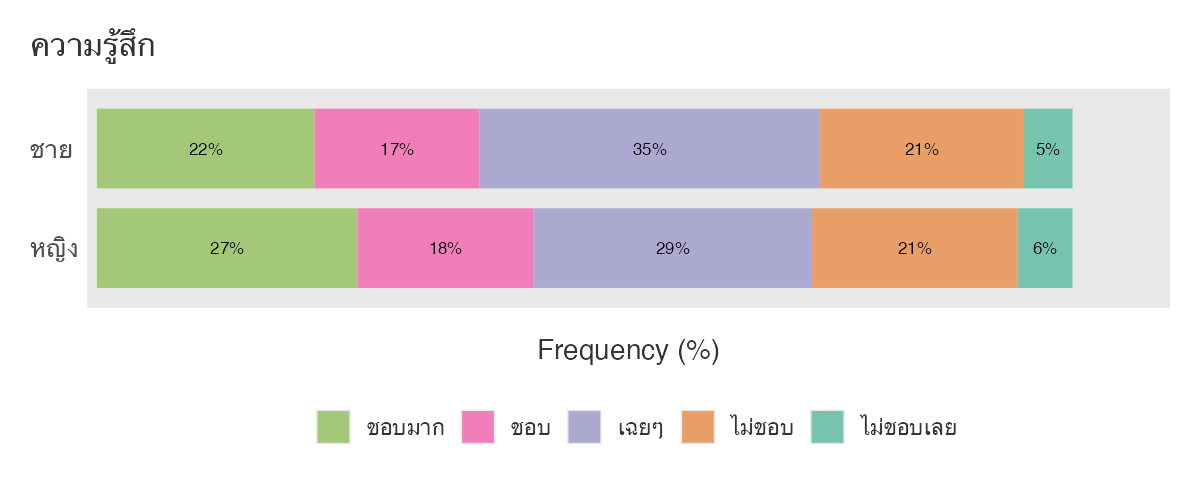
ถ้าพิจารณาความรู้สึกแยกตามเพศจะได้ กราฟต่างๆ ดังนี้

Grouped bar แบบ Counts

Grouped bar แบบ Percentages

Stacked bar แบบ Counts

Stacked bar แบบ Percentages

จะเห็นว่า jamovi ลองรับภาษาไทยได้ดีพอสมควรแล้ว

ต่อไปเป็นจะเป็นเมนูเสริมสำหรับการศึกษาตัวแบบความน่าจะเป็นที่สำคัญทางสถิติ

เมนเสริมที่น่าสนใจ สำหรับการศีกษาสถิิติหรือความน่าจะเป็นที่โปรแกรม jamovi มีอยู่ 2 เมนูและข้อมูลฟรี สำหรับฝึกใช้งาน ที่มาจากชุดคำสั่ง dataset ในโปรแกรมอาร์

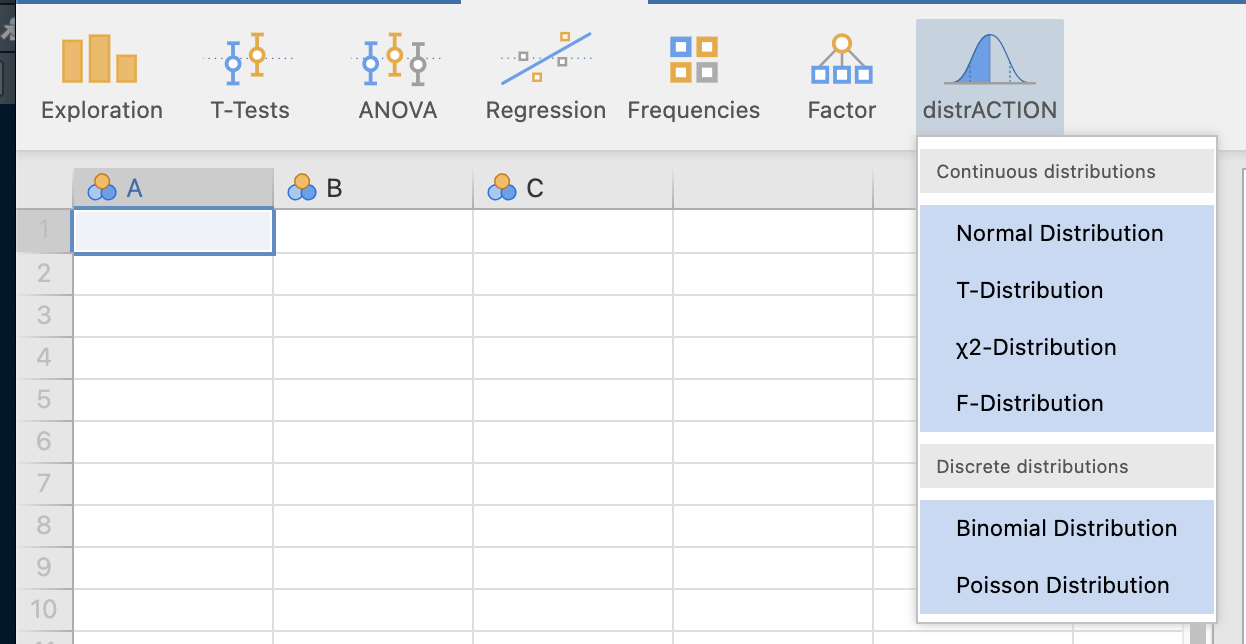
8.2 เมนู distrACTION

เมื่อการติดตั้งแล้ว จะใช้การคำนวณความน่าจะเป็นที่ตัวแปรสุ่ม (random variable) เป็นตัวแปรแบบต่อเนื่อง (continuous) และเป็นจำนวนเต็ม (integer) เมนูจะใช้ในการคำนวณค่าความน่าจะเป็นและค่าควอไทร์ของการแจกแจงความน่าจะเป็น

8.2.1 การแจกแจงแบบปกติ (Normal Distribution)

การแจกแจงแบบปกติ (Normal Distribution) คือการแจกแจงความน่าจะเป็นที่ใช้กันอย่างแพร่หลายในทางสถิติและทฤษฎีความน่าจะเป็น มีลักษณะเป็นกราฟรูประฆังคว่ำ (bell curve) ซึ่งแสดงถึงการกระจายตัวของข้อมูลที่มีลักษณะสมมาตรรอบค่าเฉลี่ย (mean) และลดลงอย่างค่อยเป็นค่อยไปเมื่อห่างจากค่าเฉลี่ย

คุณสมบัติสำคัญของการแจกแจงแบบปกติ ได้แก่:

1. ค่าเฉลี่ย (Mean), ค่ามัธยฐาน (Median), และฐานนิยม (Mode): การแจกแจงแบบปกติจะมีค่าเฉลี่ย ค่ามัธยฐาน และฐานนิยมเท่ากัน และอยู่ตรงกลางของการแจกแจง

2. ความสมมาตร (Symmetry): กราฟของการแจกแจงแบบปกติเป็นสมมาตรซ้าย-ขวา ดังนั้นครึ่งซ้ายและครึ่งขวาของกราฟจะเป็นภาพสะท้อนของกันและกัน

3. ความเบ้ (Skewness): การแจกแจงแบบปกติมีค่า skewness เท่ากับ 0 หมายความว่าไม่มีความเบ้ไปทางซ้ายหรือขวา

4. ความกว้าง (Spread): การแจกแจงแบบปกติมีการกระจายตัวของข้อมูลที่สามารถวัดได้ด้วยส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation, σ) โดยประมาณ 68% ของข้อมูลจะอยู่ภายในระยะ ±1σ จากค่าเฉลี่ย ประมาณ 95% ของข้อมูลจะอยู่ภายในระยะ $\pm 2\sigma$ และประมาณ 99.7% ของข้อมูลจะอยู่ภายในระยะ $\pm 3\sigma$ จากค่าเฉลี่ย (กฎสาม σ หรือ Empirical Rule)

สูตรของฟังก์ชันความหนาแน่นความน่าจะเป็น (Probability Density Function, PDF) ของการแจกแจงแบบปกติ คือ:

$$f(x)={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}},x,\mu \in \mathrm{R},{\sigma }^2>0}$$ ช่วงค่าความจะน่าจะเป็นที่ต้องการ

$$Pr(x_1\le x\le x_2)=F(x_1)-F(x_2)={\int }_{x_1}^{x_2}f(s)ds={\int }_{x_1}^{x_2}\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(s-\mu {)}^2}{2{\sigma }^2}}ds$$

การคำนวณค่าควอไทร์

$$F_X^{-1}(\alpha )=x,\alpha \in (0,1)$$

ที่ $\mu$ คือค่าเฉลี่ย (Mean) และ $\sigma$ คือส่วนเบี่ยงเบนมาตรฐาน (SD)

ถ้า $\mu =0$ และ $\sigma =1$ ก็คือการแจกแจงปกติมาตราฐานนั้นเอง

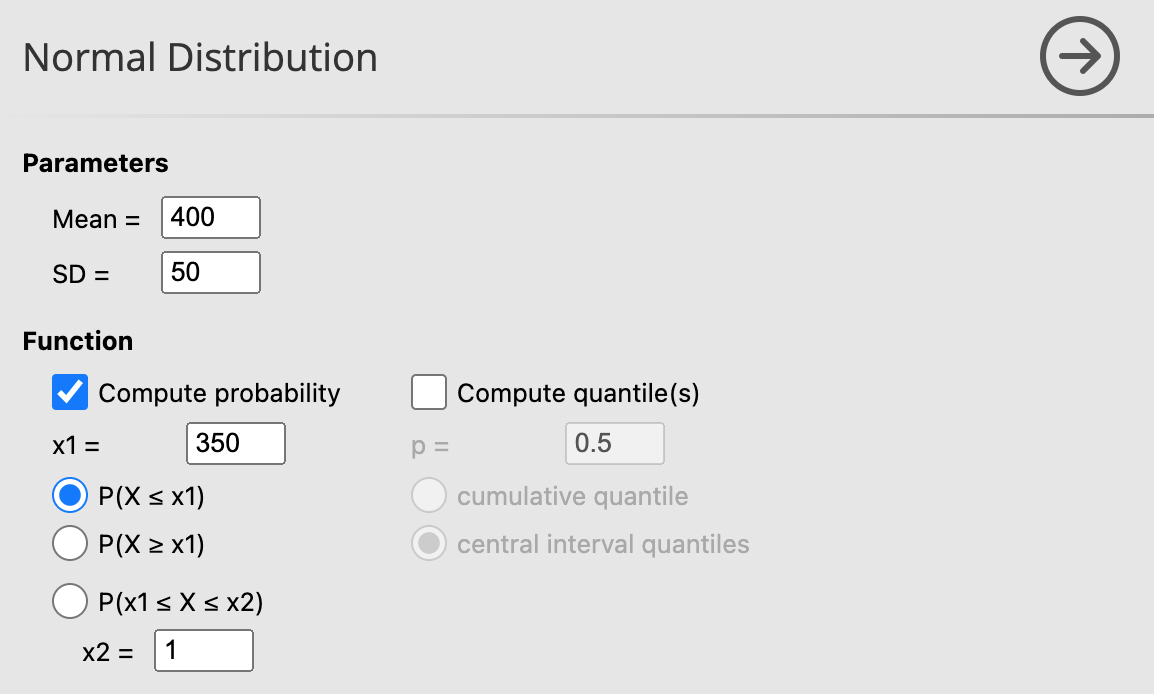
การใช้คำนวณนี้ใน jamovi จะต้องใส่ค่าพารามิเตอร์ Mean และ SD เข้าไปก่อน เพื่อจะสามารถหาค่าความน่าจะเป็นที่ต้องการได้

ตัวอย่าง ถ้าผลผลิตของข้าวเปลือกหอมมะลิไทยมีผลผลิตเฉลี่ยต่อไร่ คือ 400 กิโลกรัม และมีส่วนเบี่ยงเบนมาตราฐานคือ 60

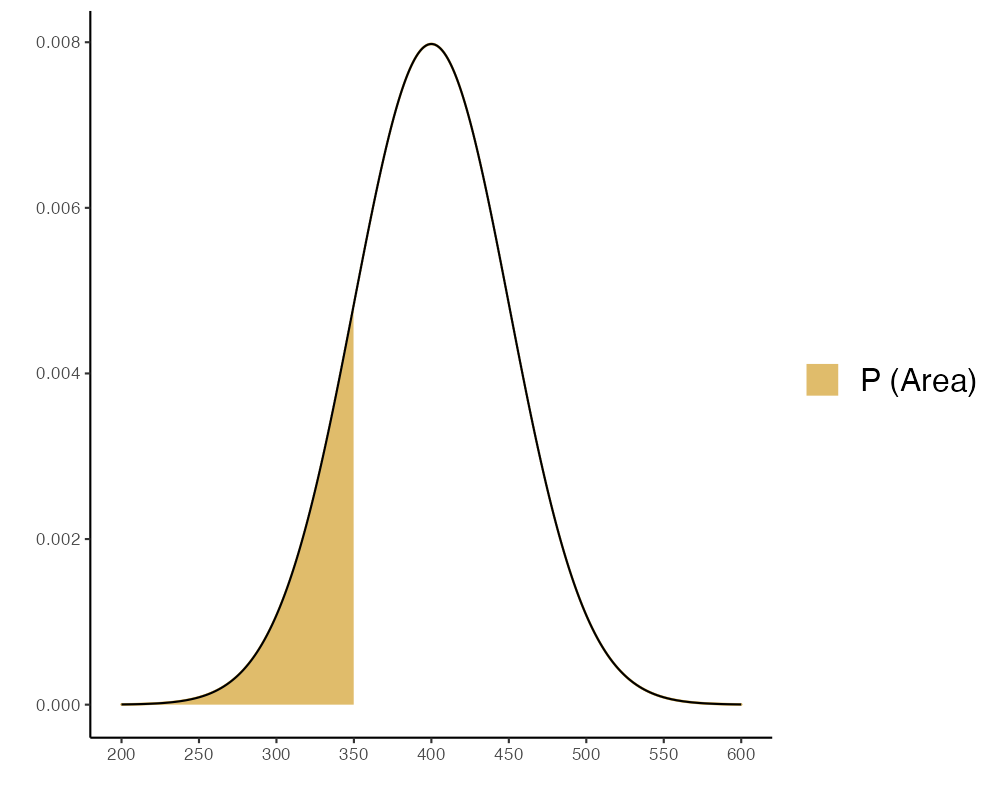
1. ความน่าจะเป็นที่ จะได้ข้าวหอมมะลิน้อยกว่า 350 กก./ไร่

Input values
Parameters	‘Compute probability’
Mean $=400$	$\mathrm{x}1=350$
$SD=50$	Mode: $\mathrm{P}(\mathrm{X}\le \mathrm{x}1)$

Result

Probability = 0.159

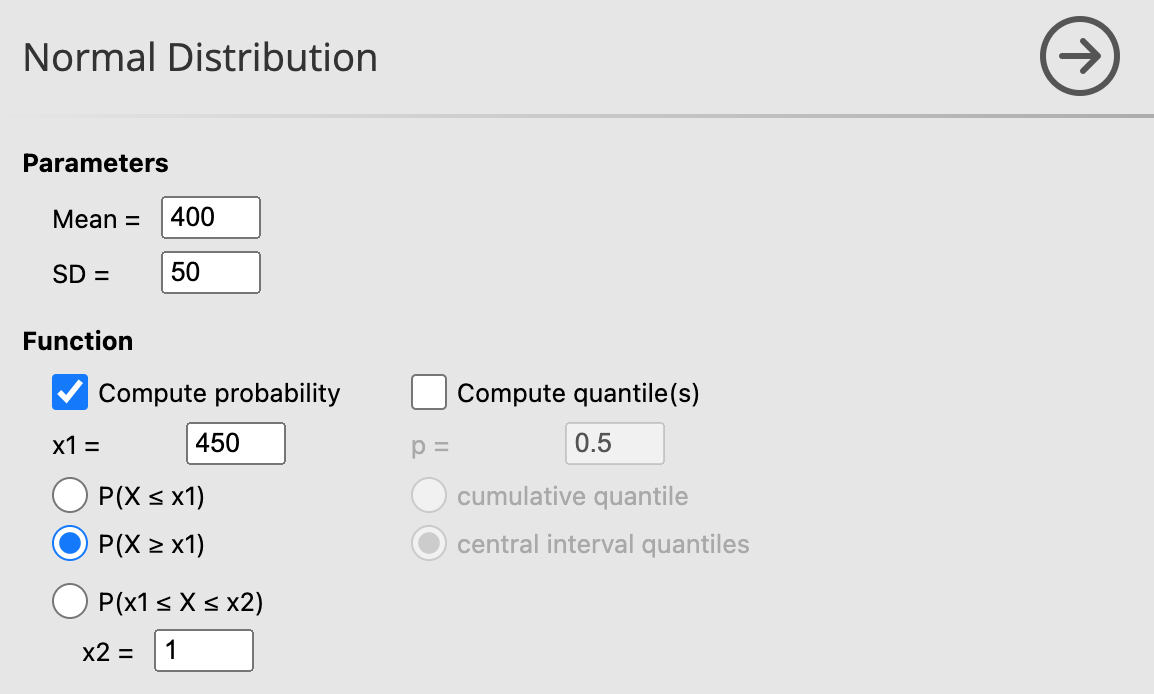
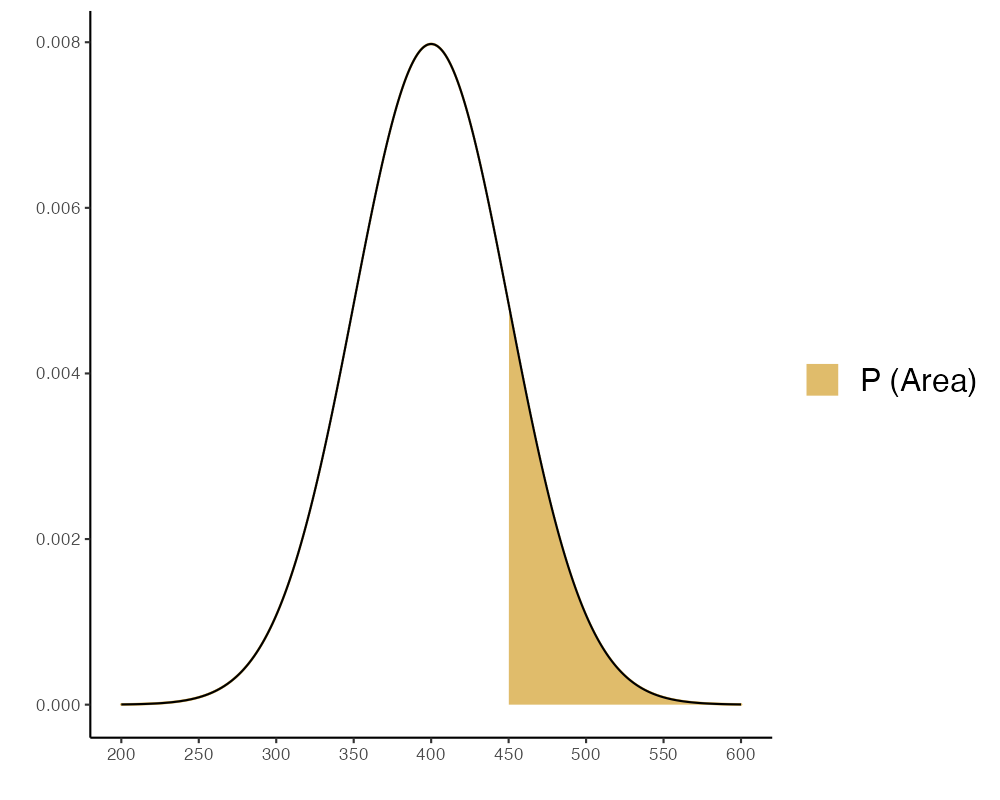
2. ความน่าจะเป็นที่ จะได้ข้าวหอมมะลิมากกว่า 450 กก./ไร่

Input values
Parameters	‘Compute probability’
Mean $=400$	$\mathrm{x}1=450$
$SD=50$	Mode: $\mathrm{P}(\mathrm{X}\ge \mathrm{x}1)$

Result

Probability = 0.159

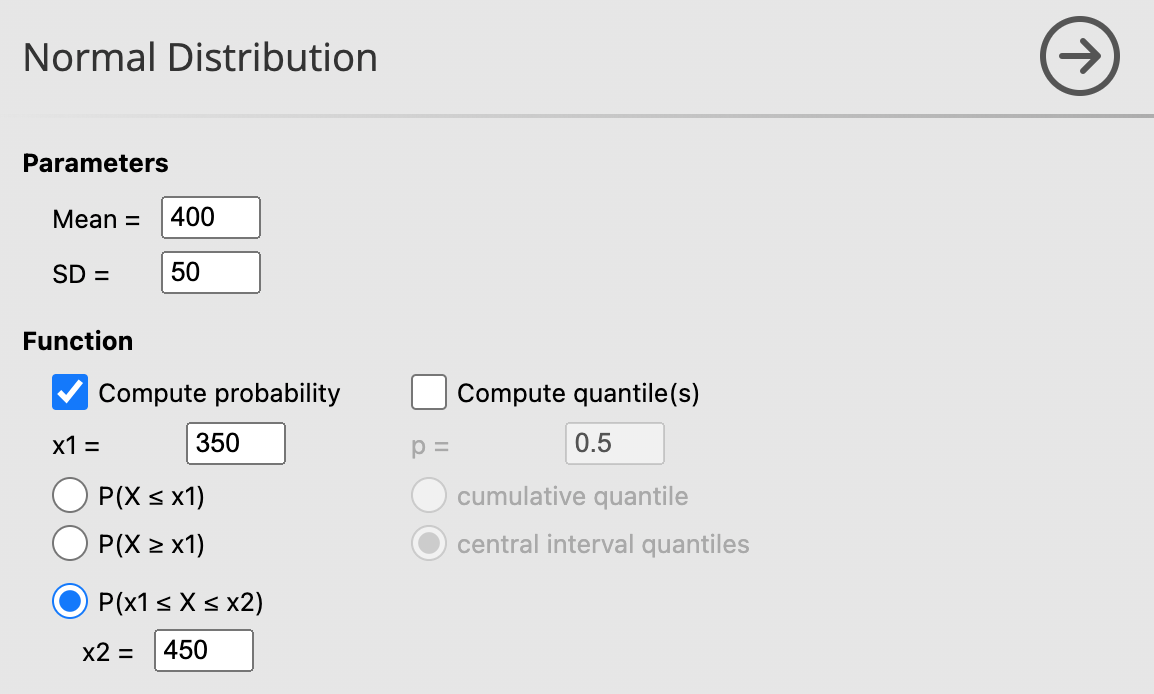
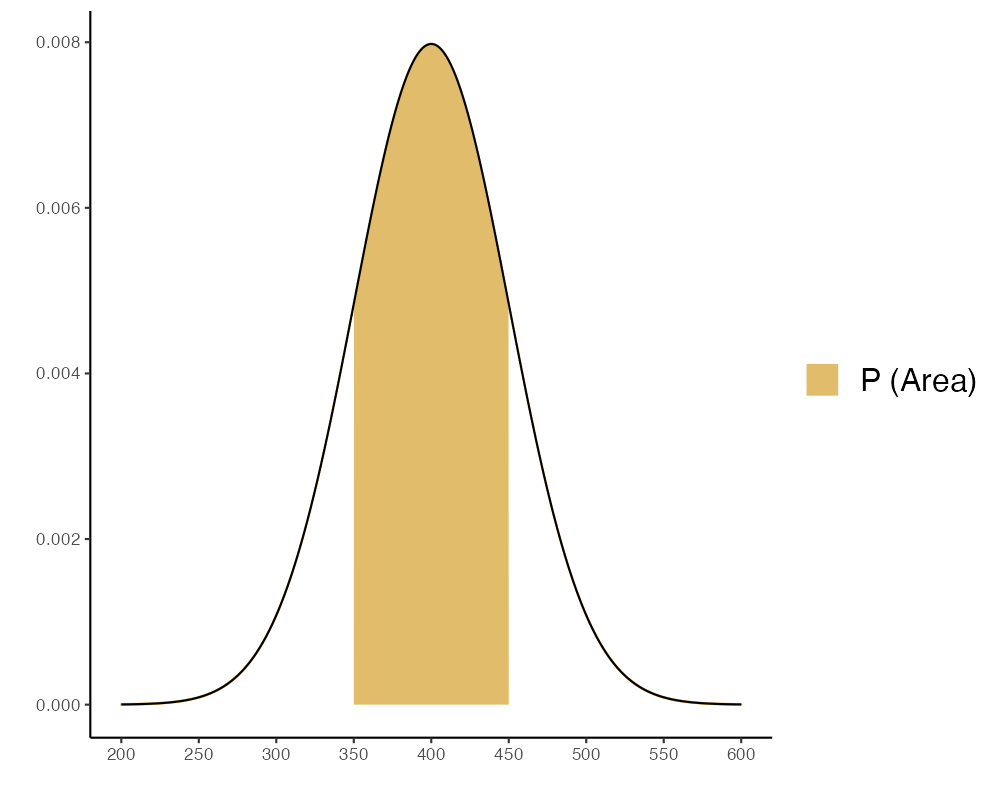
3. ความน่าจะเป็นที่ จะได้ข้าวหอมมะลิมากกว่า 350 กก./ไร่ แต่ไม่เกิน 450 กก./ไร่

Input values
Parameters	‘Compute probability’
Mean $=400$	$x1=350$
$SD=50$	Mode: $x2=450$

Result

Probability = 0.683

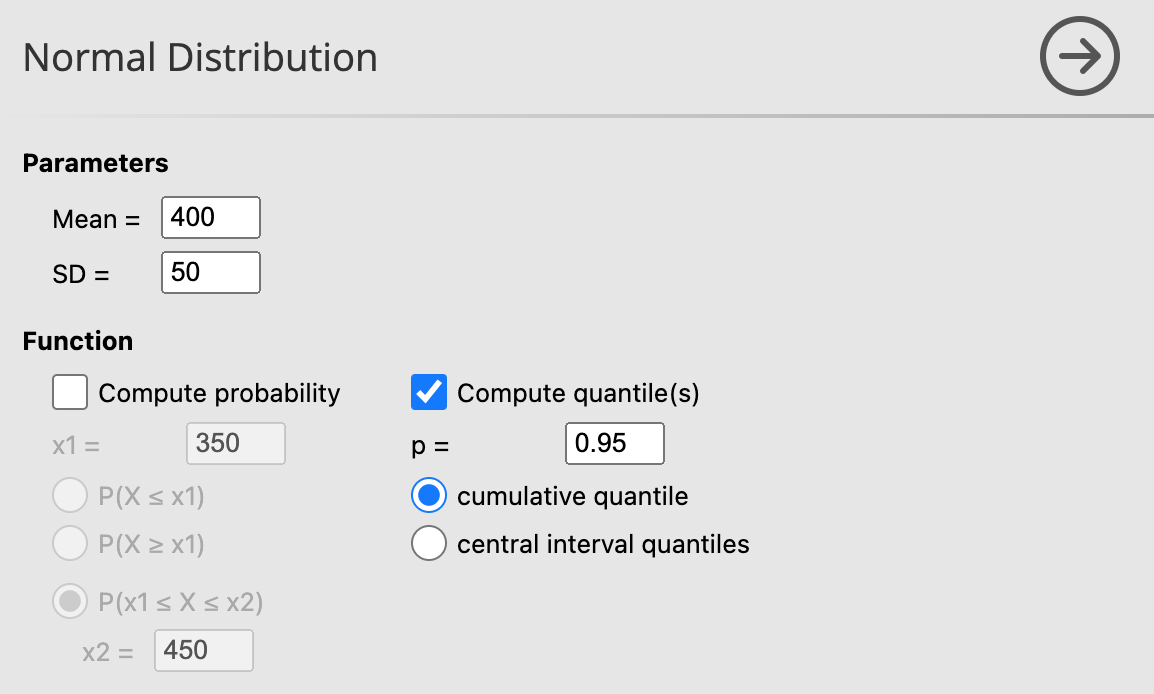
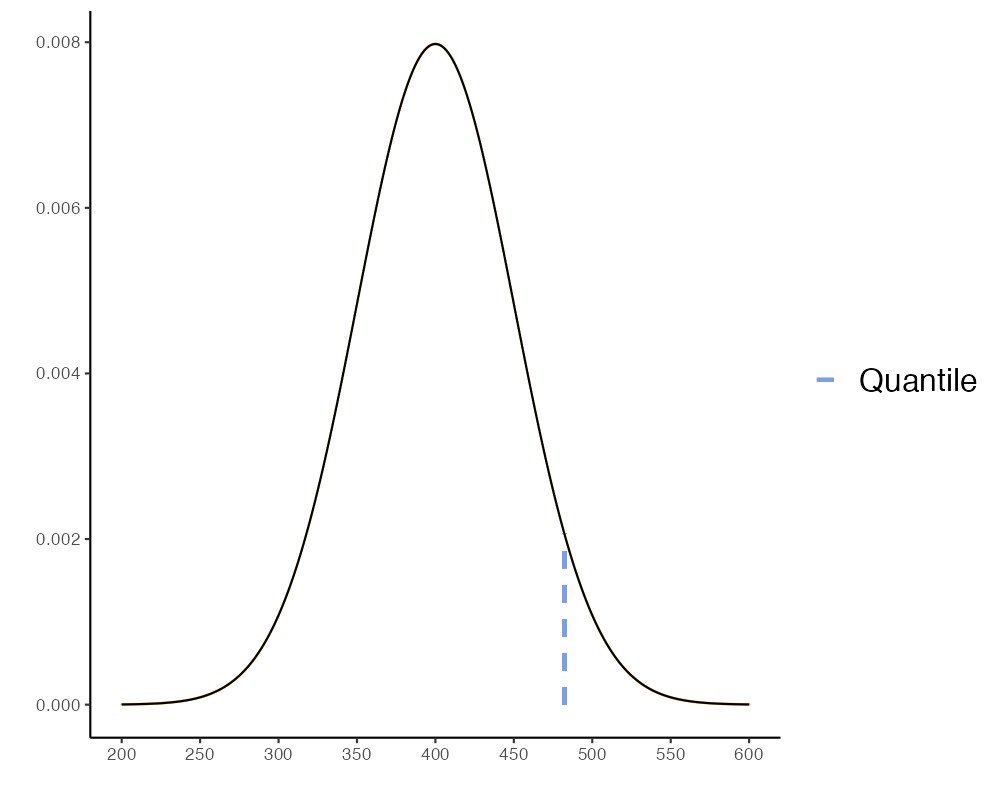
4. ที่ค่าควอไทร์ .95 หรือ 95% จะผลิตข้าวได้สูงสุดเท่าไหร่

Parameters	‘Compute quantile(s)’
Mean $=400$	$p=0.95$
$SD=50$	cumulative mode

Result

Quantile 95 = 482

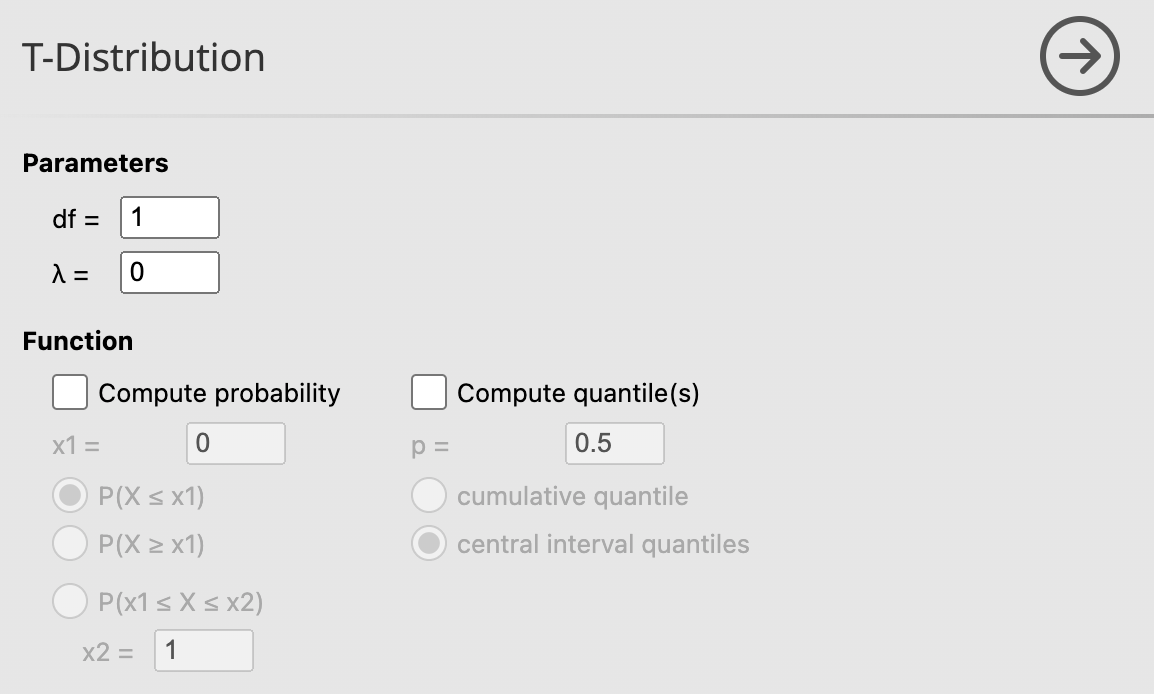
8.2.2 การแจกแจงแบบ t (t-Distribution)

การแจกแจงแบบ t (t-Distribution) หรือที่เรียกว่าการแจกแจงแบบสตูเดนต์ (Student’s t-Distribution) เป็นการแจกแจงทางสถิติที่ใช้ในการประมาณค่าของค่าเฉลี่ยของประชากรเมื่อขนาดของตัวอย่างมีขนาดเล็กหรือเมื่อส่วนเบี่ยงเบนมาตรฐานของประชากรไม่เป็นที่รู้จัก

คุณสมบัติสำคัญของการแจกแจงแบบ t มีดังนี้:

1. รูปแบบ: การแจกแจงแบบ t มีลักษณะคล้ายกับการแจกแจงแบบปกติ แต่จะมีหางที่ยาวกว่า (fatter tails) ซึ่งหมายความว่ามีความน่าจะเป็นที่จะได้ค่าที่อยู่ไกลจากค่าเฉลี่ยมากกว่า

2. อิสระ (Degrees of Freedom): การแจกแจงแบบ t ขึ้นอยู่กับค่าอิสระ (Degrees of Freedom, df) ซึ่งเท่ากับขนาดของตัวอย่างลบด้วยหนึ่ง ((df = n - 1)) การเพิ่มค่าอิสระจะทำให้การแจกแจงแบบ t เข้าใกล้การแจกแจงแบบปกติมากขึ้น

3. การใช้งาน: ใช้ในการทดสอบสมมติฐานสำหรับค่าเฉลี่ยของประชากรโดยเฉพาะในกรณีที่ขนาดตัวอย่างมีขนาดเล็กหรือส่วนเบี่ยงเบนมาตรฐานของประชากรไม่เป็นที่รู้จัก เช่น t-test สำหรับตัวอย่างเดียว (One-sample t-test), t-test สำหรับสองตัวอย่างอิสระ (Independent two-sample t-test), และ t-test สำหรับตัวอย่างคู่ (Paired sample t-test)

ฟังก์ชันความหนาแน่นความน่าจะเป็น (Probability Density Function, PDF) ของการแจกแจงแบบ t คือ:

$$f(t)={\displaystyle \frac{\mathrm{\Gamma }\left(\frac{df+1}{2}\right)}{\sqrt{df\pi }\mathrm{\Gamma }\left(\frac{df}{2}\right)}{(1+\frac{t^2}{df})}^{-\frac{df+1}{2}},df\ge 1,t\in \mathrm{R}}$$

ที่ $\mathrm{\Gamma }$ คือฟังก์ชันแกมมา และ $df$ คือค่าอิสระ

ในโปรแกรม jamovi เป็นการแจกแจง t แบบทั่วไปคือ สามารถกำหนดการแจก t มีความไม่สมมาตรด้วย พารามิเตอร์ $\lambda$ ดังนั้น โดยปกติแล้วค่า พารามิเตอร์ $\lambda =0$ จะเป็นการแจกแจงแบบ t ที่ใช้กันอยู่ทั่วไป

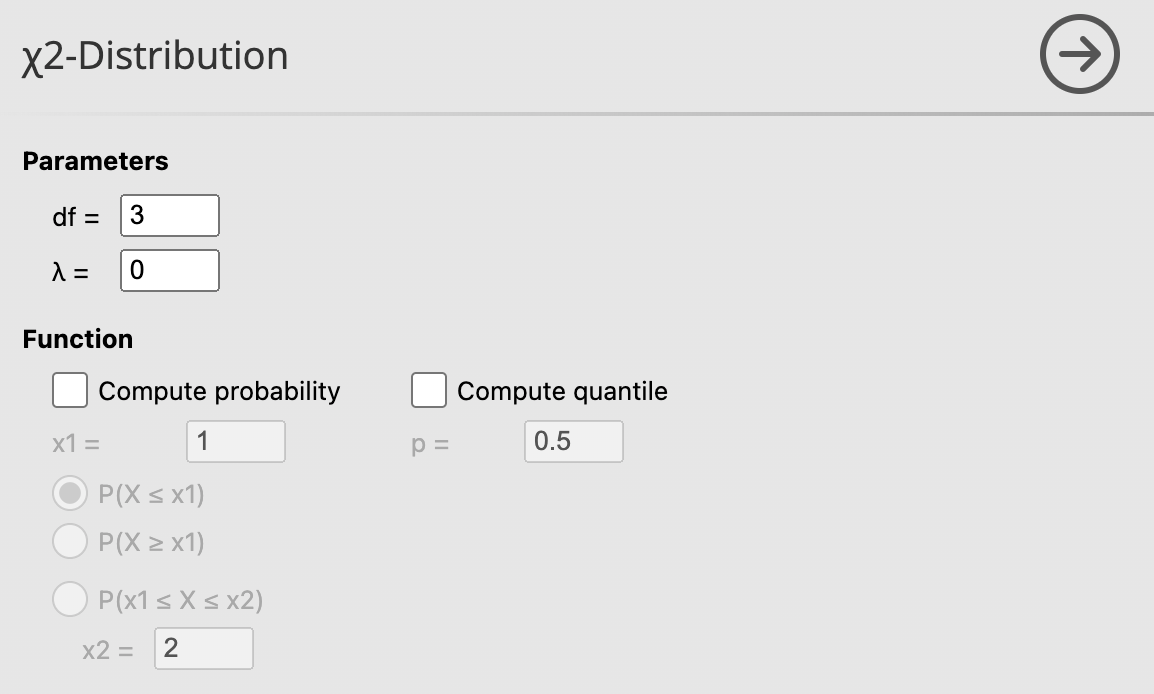
8.2.3 การแจกแจงแบบไคสแควร์ (Chi-Square Distribution

การแจกแจงแบบไคสแควร์ (Chi-Square Distribution) เป็นการแจกแจงทางสถิติที่ใช้กันอย่างแพร่หลายในการทดสอบสมมติฐานเกี่ยวกับการกระจายความถี่และการวิเคราะห์ความแปรปรวน

คุณสมบัติของการแจกแจงแบบไคสแควร์

1. ความไม่สมมาตร: การแจกแจงแบบไคสแควร์มีลักษณะเป็นไม่สมมาตร โดยมีหางขวายาว ลักษณะการไม่สมมาตรจะลดลงเมื่อค่าของอิสระ (degrees of freedom, df) เพิ่มขึ้น และจะเข้าใกล้การแจกแจงแบบปกติมากขึ้นเมื่อ df มีค่าสูง

2. ค่าอิสระ (Degrees of Freedom, df): การแจกแจงแบบไคสแควร์ขึ้นอยู่กับค่า df ซึ่งมักจะเป็นจำนวนเต็มบวก ค่า df มากขึ้นจะทำให้การแจกแจงมีแนวโน้มเข้าใกล้การแจกแจงแบบปกติมากขึ้น

3. ฟังก์ชันความหนาแน่นความน่าจะเป็น (PDF): ฟังก์ชัน PDF ของการแจกแจงแบบไคสแควร์คือ

$$f(x;k)=\frac{1}{2^{k/2}\mathrm{\Gamma }(k/2)}{x}^{(k/2)-1}{e}^{-x/2}\text{for }x>0$$ ที่ $k$ คือค่า df และ $\mathrm{\Gamma }$ คือฟังก์ชันแกมมา

##๒ การใช้งานของการแจกแจงแบบไคสแควร์

1. การทดสอบความเป็นอิสระ (Test of Independence): ใช้ในการทดสอบว่าตัวแปรสองตัวเป็นอิสระหรือไม่ โดยการทดสอบนี้จะใช้กับตารางความถี่ (contingency table)

2. การทดสอบความพอดี (Goodness-of-Fit Test): ใช้ในการทดสอบว่าสัดส่วนของตัวอย่างที่สังเกตได้ตรงกับสัดส่วนที่คาดหวังหรือไม่ เช่น การทดสอบว่าข้อมูลมาจากการแจกแจงแบบปกติหรือไม่

3. การวิเคราะห์ความแปรปรวน (ANOVA): ใช้ในการวิเคราะห์ความแปรปรวนระหว่างกลุ่มและภายในกลุ่ม

4. การประเมินความแปรปรวน (Variance Estimation): ใช้ในการประเมินความแปรปรวนของประชากร

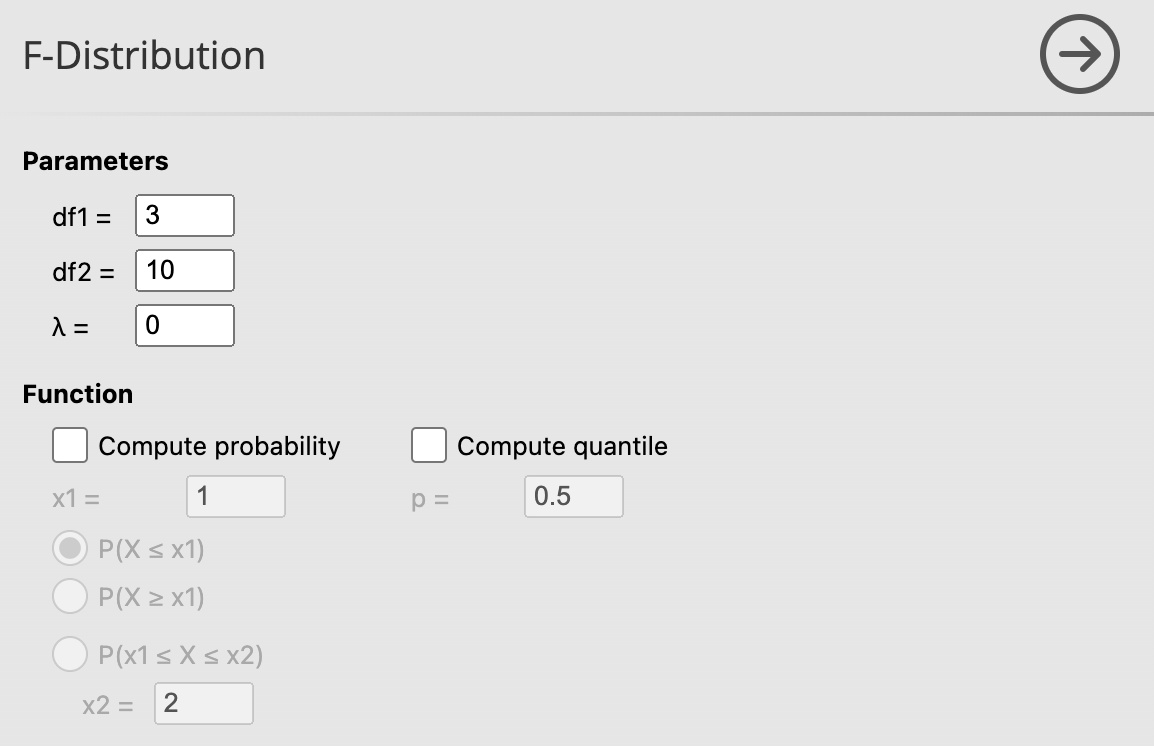
8.2.4 การแจกแจงแบบ F (F-Distribution)

การแจกแจงแบบ F (F-Distribution) เป็นการแจกแจงความน่าจะเป็นที่สำคัญในสถิติ โดยเฉพาะในงานวิเคราะห์ความแปรปรวน (Analysis of Variance, ANOVA) และการทดสอบสมมติฐานที่เกี่ยวข้องกับความแปรปรวนของกลุ่มข้อมูลหลายกลุ่ม

คุณสมบัติของการแจกแจงแบบ F

1. ความไม่สมมาตร: การแจกแจงแบบ F มีลักษณะเป็นไม่สมมาตร และมีค่าตั้งแต่ 0 ถึง $\mathrm{\infty }$ โดยมีหางขวายาว

2. ค่าอิสระ (Degrees of Freedom): การแจกแจงแบบ F ขึ้นอยู่กับค่าอิสระสองค่า ซึ่งได้แก่ $d_1$ และ $d_2$ โดยที่ $d_1$ เป็นค่าอิสระของตัวเศษ (numerator degrees of freedom) และ $d_2$ เป็นค่าอิสระของตัวส่วน (denominator degrees of freedom)

3. ฟังก์ชันความหนาแน่นความน่าจะเป็น (PDF): ฟังก์ชัน PDF ของการแจกแจงแบบ F คือ: $$f(x;d_1,d_2)=\frac{\sqrt{{\left(\frac{d_{1}x}{d_{1}x+d_2}\right)}^{d_1}{(1-\frac{d_{1}x}{d_{1}x+d_2})}^{d_2}}}{xB(\frac{d_1}{2},\frac{d_2}{2})}$$

โดยที่ $B$ คือฟังก์ชันเบตา, $d_1$ คือค่าอิสระของตัวเศษ และ $d_2$ คือค่าอิสระของตัวส่วน

การใช้งานของการแจกแจงแบบ F

1. การวิเคราะห์ความแปรปรวน (ANOVA): ใช้ในการเปรียบเทียบความแปรปรวนระหว่างกลุ่มต่าง ๆ กับความแปรปรวนภายในกลุ่มเดียวกัน เพื่อทดสอบสมมติฐานว่าค่าเฉลี่ยของกลุ่มต่าง ๆ เท่ากันหรือไม่

2. การทดสอบความแปรปรวนร่วม (Analysis of Covariance, ANCOVA): ใช้ในการตรวจสอบผลกระทบของตัวแปรร่วมควบคู่กับตัวแปรอิสระ

3. การทดสอบสมมติฐานเกี่ยวกับความแปรปรวนของสองประชากร: ใช้ในการเปรียบเทียบความแปรปรวนของสองประชากรเพื่อตรวจสอบว่าความแปรปรวนของทั้งสองกลุ่มมีค่าเท่ากันหรือไม่

ตัวอย่างการใช้การแจกแจงแบบ F

สมมติว่าคุณต้องการทดสอบว่าค่าเฉลี่ยของสามกลุ่มตัวอย่างมีค่าเท่ากันหรือไม่ คุณสามารถใช้ ANOVA ซึ่งการทดสอบนี้จะใช้การแจกแจงแบบ F ในการคำนวณค่า p-value

1. กำหนดสมมติฐาน:

   • $H_0$: ค่าเฉลี่ยของทุกกลุ่มเท่ากัน
   • $H_1$: ค่าเฉลี่ยของอย่างน้อยหนึ่งกลุ่มแตกต่างกัน

2. คำนวณสถิติการทดสอบ: คำนวณค่า F-statistic จากความแปรปรวนระหว่างกลุ่ม (MSB, Mean Square Between) และความแปรปรวนภายในกลุ่ม (MSW, Mean Square Within): $$F=\frac{MSB}{MSW}$$

3. เปรียบเทียบกับค่า F ที่วิกฤติ: ใช้ค่าอิสระ $d_1=k-1$ และ $d_2=N-k$ (ที่ $k$ คือจำนวนกลุ่มและ $N$ คือขนาดตัวอย่างรวม) และเปรียบเทียบกับค่า F-critical ที่ระดับนัยสำคัญที่ต้องการ (เช่น 0.05)

ข้อควรระวัง

สำหรับการตัวแปรสุ่มที่เป็นตัวแปรแบบต่อเนื่อง ความน่าจะเป็นของ

$$Pr(X=x)=0$$

ถ้า $x$ มีค่าเป็นจุด ที่ไม่ใช่ช่วง

8.2.5 การแจกแจงแบบทวินาม (Binomial Distribution

การแจกแจงแบบทวินาม (Binomial Distribution) เป็นการแจกแจงความน่าจะเป็นที่ใช้สำหรับการทดลองที่มีผลลัพธ์สองแบบ (เช่น สำเร็จ/ล้มเหลว, ชนะ/แพ้, ผ่าน/ไม่ผ่าน) และมีการทดลองซ้ำ ๆ กันหลายครั้งอย่างอิสระ การแจกแจงแบบทวินามจะบอกความน่าจะเป็นของการได้จำนวนครั้งของผลลัพธ์หนึ่งในจำนวนการทดลองทั้งหมด

คุณสมบัติของการแจกแจงแบบทวินาม

1. การทดลองซ้ำ: การทดลองต้องเป็นแบบซ้ำกันหลายครั้ง (n) และเป็นอิสระจากกัน

2. ผลลัพธ์สองแบบ: แต่ละการทดลองมีผลลัพธ์สองแบบ ซึ่งเรียกว่า “สำเร็จ” และ “ล้มเหลว” โดยความน่าจะเป็นของความสำเร็จคือ $p$ และความน่าจะเป็นของความล้มเหลวคือ $1-p$

3. ความน่าจะเป็นคงที่: ความน่าจะเป็นของการสำเร็จ ($p$) และความล้มเหลว ($1-p$) คงที่ในแต่ละครั้งของการทดลอง

ฟังก์ชันความน่าจะเป็น (Probability Mass Function, PMF)

ฟังก์ชัน PMF ของการแจกแจงแบบทวินามคือ: $$P(X=k)=(\genfrac{}{}{0ex}{}{n}{k})p^k(1-p{)}^{n-k}$$ โดยที่

• $(\genfrac{}{}{0ex}{}{n}{k})$ คือสัมประสิทธิ์ทวินาม (binomial coefficient) ซึ่งคำนวณได้จาก $\frac{n!}{k!(n-k)!}$

• $n$ คือจำนวนครั้งของการทดลอง

• $k$ คือจำนวนครั้งของการสำเร็จ

• $p$ คือความน่าจะเป็นของการสำเร็จในแต่ละครั้งของการทดลอง

ตัวอย่าง

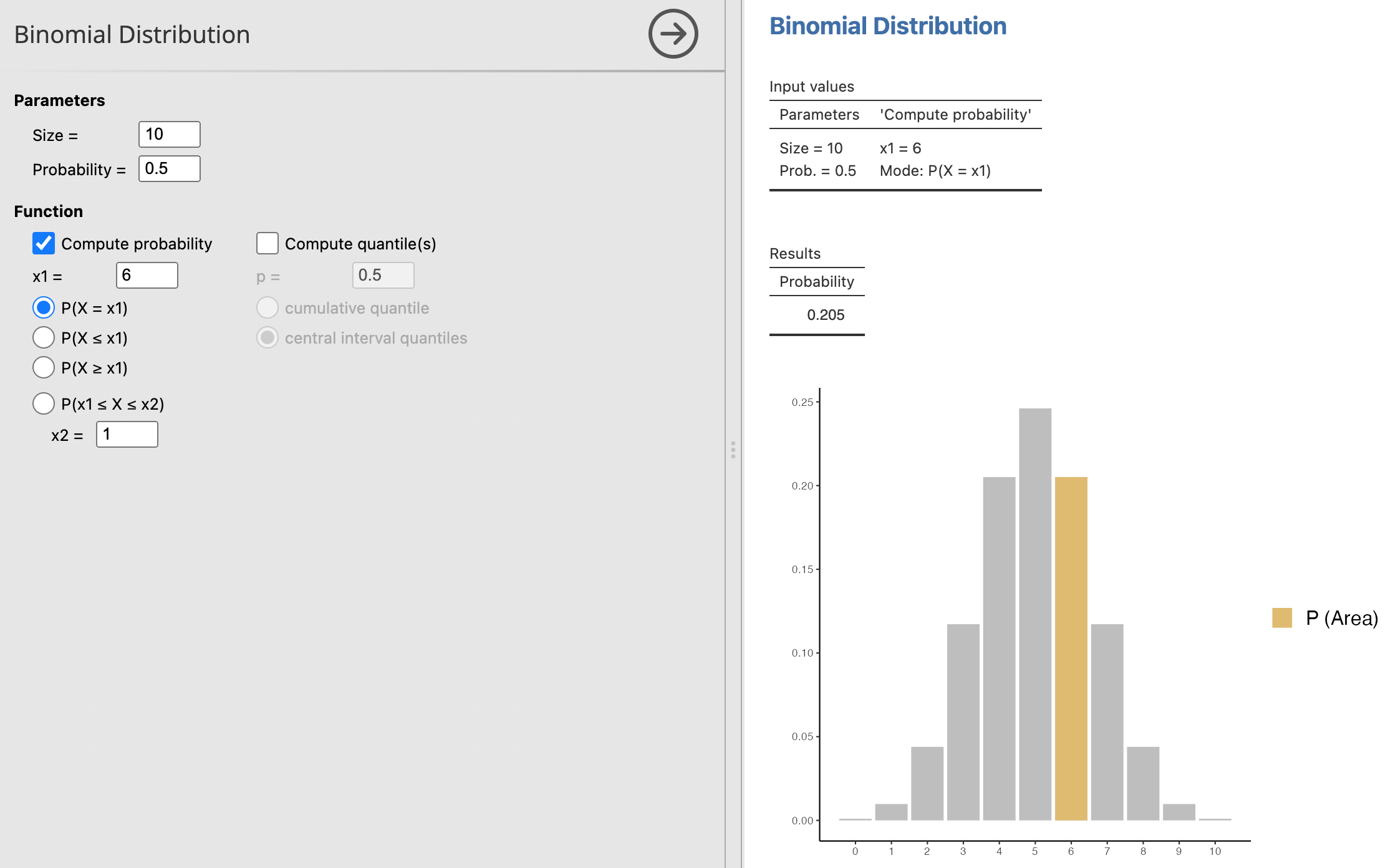
สมมติว่าคุณมีเหรียญที่คุณคาดว่าเป็นเหรียญยุติธรรม (คือมีความน่าจะเป็นของการออกหัวเท่ากับ 0.5) และคุณจะโยนเหรียญนี้ 10 ครั้ง คุณต้องการทราบความน่าจะเป็นของการออกหัว 6 ครั้งจากการโยน 10 ครั้ง

ในกรณีนี้:

• $n=10$

• $k=6$

• $p=0.5$

เราสามารถคำนวณความน่าจะเป็นได้ดังนี้: $$P(X=6)=(\genfrac{}{}{0ex}{}{10}{6})(0.5{)}^6(1-0.5{)}^{10-6}$$ $$=\frac{10!}{6!4!}(0.5{)}^6(0.5{)}^4$$ $$=210\times (0.5{)}^{10}$$ $$=210\times 0.0009765625$$ $$\approx 0.205$$

ดังนั้น ความน่าจะเป็นของการออกหัว 6 ครั้งจากการโยนเหรียญ 10 ครั้งคือประมาณ 0.205 หรือ 20.5%

การคำนวณใน jamovi

8.2.6 การแจกแจงแบบปัวซอง (Poisson Distribution)

การแจกแจงแบบปัวซอง (Poisson Distribution) เป็นการแจกแจงความน่าจะเป็นที่ใช้ในการสร้างแบบจำลองเหตุการณ์ที่เกิดขึ้นอย่างต่อเนื่องในช่วงเวลาหนึ่งหรือพื้นที่หนึ่งโดยไม่ขึ้นกับกัน และมีอัตราเฉลี่ยคงที่

คุณสมบัติของการแจกแจงแบบปัวซอง

1. เหตุการณ์เกิดขึ้นอย่างอิสระ: การเกิดเหตุการณ์หนึ่งไม่ได้ส่งผลต่อการเกิดเหตุการณ์อื่น ๆ

2. เหตุการณ์เกิดขึ้นอย่างสม่ำเสมอ: ความน่าจะเป็นของการเกิดเหตุการณ์ในช่วงเวลาหรือพื้นที่หนึ่ง ๆ เป็นสัดส่วนกับขนาดของช่วงเวลาหรือพื้นที่นั้น ๆ

3. ไม่สามารถเกิดเหตุการณ์พร้อมกันได้: ความน่าจะเป็นของการเกิดเหตุการณ์มากกว่าหนึ่งเหตุการณ์ในช่วงเวลาหรือพื้นที่เล็ก ๆ มากนั้นมีค่าเป็นศูนย์

ฟังก์ชันความน่าจะเป็น (Probability Mass Function, PMF)

ฟังก์ชัน PMF ของการแจกแจงแบบปัวซองคือ: $$P(X=k)=\frac{{\lambda }^k{e}^{-\lambda }}{k!},k=0,1,2,3,\cdots$$ ที่:

• $X$ คือจำนวนครั้งของเหตุการณ์ที่เกิดขึ้น

• $k$ คือจำนวนครั้งของเหตุการณ์ที่เราสนใจ (เช่น จำนวนการโทรเข้ามาที่ศูนย์บริการในหนึ่งชั่วโมง)

• $\lambda$ คือค่าเฉลี่ยของเหตุการณ์ที่เกิดขึ้นต่อช่วงเวลาหรือพื้นที่หน่วย (เช่น ค่าเฉลี่ยของการโทรเข้ามาที่ศูนย์บริการในหนึ่งชั่วโมง)

• $e$ คือค่าคงที่ทางคณิตศาสตร์ (ประมาณ 2.71828)

ตัวอย่าง

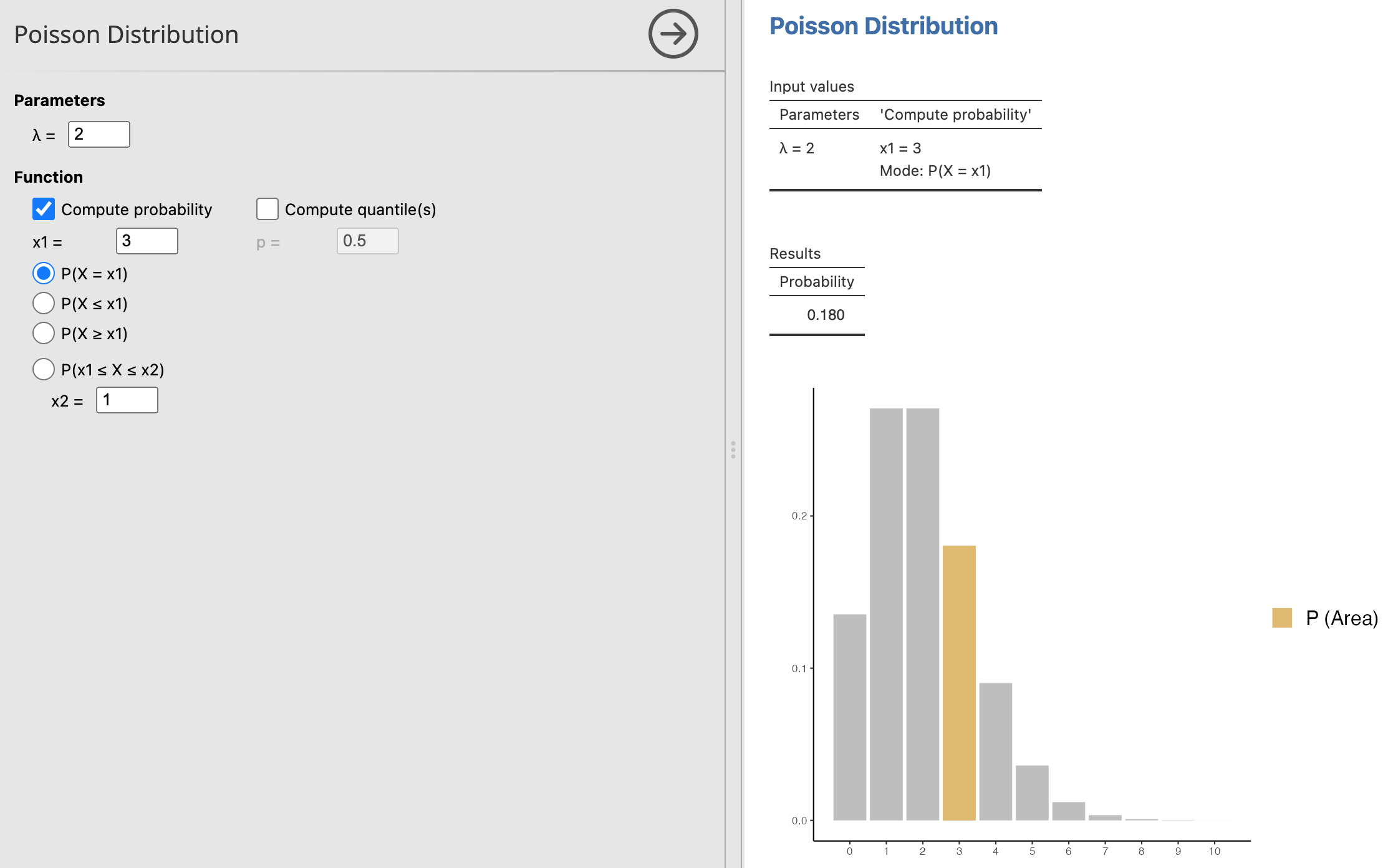
สมมติว่าคุณต้องการทราบความน่าจะเป็นที่ในหนึ่งชั่วโมงจะมีการโทรเข้ามาที่ศูนย์บริการลูกค้า 3 ครั้ง โดยที่ค่าเฉลี่ยของการโทรเข้ามาคือ 2 ครั้งต่อชั่วโมง

ในกรณีนี้:

• $\lambda =2$

• $k=3$

เราสามารถคำนวณความน่าจะเป็นได้ดังนี้:

$$P(X=3)=\frac{2^3{e}^{-2}}{3!}$$

$$=\frac{8\cdot e^{-2}}{6}$$

$$=\frac{8}{6}\cdot e^{-2}$$

$$=\frac{4}{3}\cdot 0.1353$$

$$\approx 0.1804$$

ดังนั้น ความน่าจะเป็นที่ในหนึ่งชั่วโมงจะมีการโทรเข้ามาที่ศูนย์บริการลูกค้า 3 ครั้งคือประมาณ 0.1804 หรือ 18.04%

การคำนวณด้วย jamovi

การใช้งานของการแจกแจงแบบปัวซอง

การแจกแจงแบบปัวซองถูกใช้ในหลากหลายสาขา เช่น:

• การบริหารจัดการทรัพยากร: เช่น การประเมินจำนวนการโทรเข้ามาที่ศูนย์บริการลูกค้าในช่วงเวลาหนึ่ง

• การวิเคราะห์ทางการแพทย์: เช่น การวิเคราะห์จำนวนผู้ป่วยที่มาถึงห้องฉุกเฉินในช่วงเวลาหนึ่ง

• การวิเคราะห์อัตราการเกิดเหตุการณ์: เช่น การวิเคราะห์จำนวนการเกิดอุบัติเหตุในช่วงเวลาหนึ่งหรือพื้นที่หนึ่ง

• การจัดการขนส่งและโลจิสติกส์: เช่น การวิเคราะห์จำนวนยานพาหนะที่ผ่านทางแยกในช่วงเวลาหนึ่ง

การแจกแจงแบบปัวซองเป็นเครื่องมือที่มีประโยชน์ในการวิเคราะห์และประเมินเหตุการณ์ที่เกิดขึ้นต่อเนื่องในช่วงเวลาหรือพื้นที่ โดยเฉพาะเมื่อเหตุการณ์นั้น ๆ มีอัตราเฉลี่ยคงที่

เมื่อทำการติดตั้งเมนูนี้ จะสามารถเลือกนำเข้าข้อมูลมาวิเคราะห์ได้

8.2.7 jReshape สำหรับการเปลี่ยนโครงสร้าง (reshape)

การ Reshape ข้อมูล คืออะไร?

Reshape ข้อมูล คือกระบวนการเปลี่ยนโครงสร้างของข้อมูลจากรูปแบบหนึ่งไปเป็นอีกรูปแบบหนึ่ง เพื่อให้เหมาะสมกับการวิเคราะห์หรือการแสดงผล เช่น เปลี่ยนจาก Wide Format เป็น LongFormat หรือในทางกลับกันก็ได้

รูปแบบของข้อมูลในการ Reshape

1. Wide Format (รูปแบบกว้าง)

   • ข้อมูลถูกจัดให้อยู่ในรูปแบบที่แต่ละตัวแปรมีคอลัมน์ของตัวเอง
     

   • นิยมใช้สำหรับรายงานหรือการแสดงผลแบบตารางหรือใช้สำหรับการวิเคราะห์ด้วยโปรแกรม Excel

ตัวอย่าง

Show 102550100 entries

Search:

	ID	Gender	Math	Science	English
1	1	Male	100	89	97
2	2	Male	84	83	94
3	3	Male	88	91	78
4	4	Male	83	94	98
5	5	Male	72	95	72
6	6	Female	79	96	77
7	7	Female	87	74	95
8	8	Female	91	88	76
9	9	Female	80	96	79
10	10	Female	74	94	78

Showing 1 to 10 of 10 entries

Previous1Next

2. Long Format (รูปแบบยาว)

   • ข้อมูลถูกแปลงให้แต่ละค่าของตัวแปรแยกเป็นแถว
     

   • นิยมใช้สำหรับการวิเคราะห์ข้อมูลด้วยโปรแกรม jamovi JASP หรือ R

ตัวอย่าง

Show 102550100 entries

Search:

	ID	Gender	Subject	Score
1	1	Male	Math	100
2	1	Male	Science	89
3	1	Male	English	97
4	2	Male	Math	84
5	2	Male	Science	83
6	2	Male	English	94
7	3	Male	Math	88
8	3	Male	Science	91
9	3	Male	English	78
10	4	Male	Math	83

Showing 1 to 10 of 30 entries

Previous123Next

โมดูล jeRshape

เนื้อหาส่วนนี้ได้รับทำการเขียนขึ้น หลังจากที่ jamovi ออกโปรแกรมรุ่น 2.6.44 ในหลายๆ กรณีผู้เขียนพบโจทย์เสริมความเข้าใจในวิชาสถิติพื้นฐาน จะแสดงข้อมูลอยู่รูปของ wide format เพื่อให้ง่ายสำหรับการคำนวณด้วยเครื่องคิดเลข หรือโปรแกรม Excel ทำให้นักศึกษาหรือผู้อ่าน จำเป็นต้องจัดข้อมูลให้อยู่ในรูป Long format เพื่อให้สามารถ นำไปวิเคราะห์ต่อด้วย jamovi ได้ ดังนั้นถ้าต้องการใช้ Excel ในการเปลี่ยนจาก wide ไปเป็น Long จำเป็นต้องใช้ Excel ในรุ่นที่สามารถใช้งาน Power Query ได้ จะได้ไม่เสียเวลามากจนเกินไป แล้วก็นำผลที่ได้มาใส่ในโปรแกรม jamovi อีก จึงเป็นการทำงาน 2 ขั้นตอน

Power Query

Power Query เป็นเครื่องมือใน Excel ที่ช่วยในการดึงและแปลงข้อมูลจากแหล่งต่าง ๆ ให้เป็นไปตามความต้องการของผู้ใช้ การรองรับ Power Query ใน Excel บน Windows และ Mac มีความแตกต่างกันดังนี้:

สำหรับ Windows:

• Excel 2010 และ 2013: ผู้ใช้สามารถติดตั้ง Power Query ได้โดยการดาวน์โหลดและติดตั้ง Add-in ที่สอดคล้องกับสถาปัตยกรรมของ Office (32-bit หรือ 64-bit) ที่ใช้งานอยู่

• Excel 2016 และรุ่นใหม่กว่า: Power Query ถูกผนวกรวมอยู่ในแท็บ “Data” ภายใต้กลุ่ม “Get & Transform Data” โดยไม่ต้องติดตั้งเพิ่มเติม

สำหรับ Mac:

• Microsoft 365 Subscription: Power Query มีให้ใช้งานใน Excel สำหรับ Mac ตั้งแต่เวอร์ชัน 16.26 (19052200) เป็นต้นไป โดยสามารถเข้าถึงได้จากคำสั่ง “Get Data” บนแท็บ “Data”

โมดูล jReshape จะทำให้สามารถดำเนินการแปลงข้อมูลแล้วทำวิเคราะห์ต่อไปได้ทันที

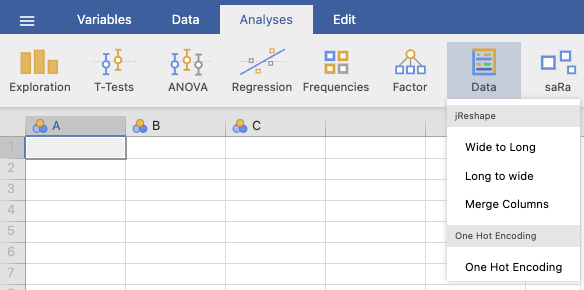
และเมื่อได้ทำการติดตั้งโมดูลนี้แล้วจะพบไอคอนใหม่ ชื่อว่า Data ปรากฏขึ้น

icon ชื่อ Data ของโมดูล jReshape

โดยฟังก์ชันการทำงาน 3 แบบ คือ

1. Wide to Long ทำการแปลงข้อมูลจาก Wide ไปเป็น Long

2. Long to Wide ทำการแปลงข้อมูลจาก Long ไปเป็น Wide

3. Merge Columns ทำการรวม 2 ตาราง โดยที่แต่ละตาราง มีตัวแปร 1 ตัวเหมือนกัน เพื่อทำหน้าที่เป็นตัวเชื่อม

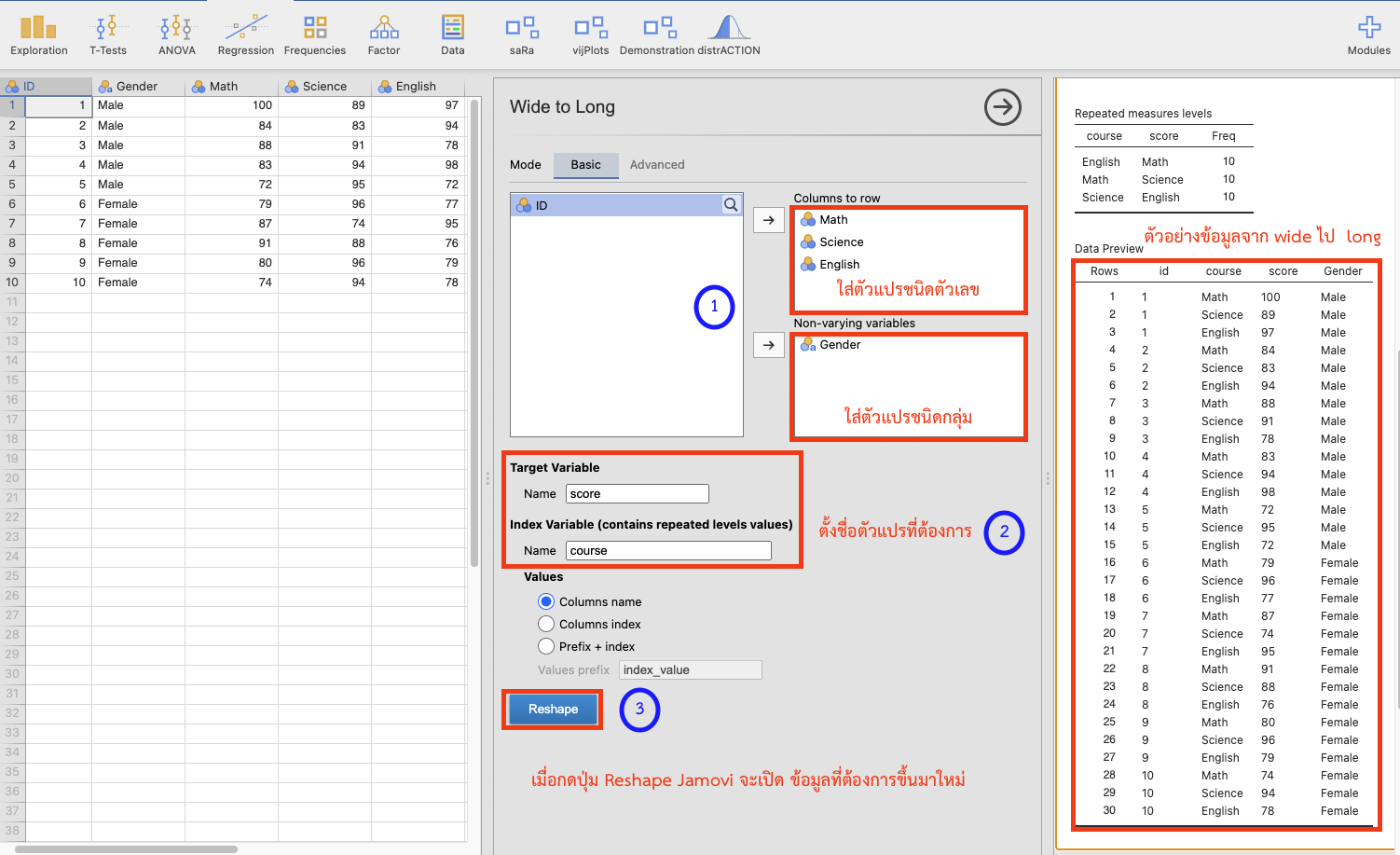
ตัวอย่างการแปลงจาก wide เป็น long ด้วย jamovi

1. Download ข้อมูลจาก googledrive ชื่อ df_wide.xlsx

2. เปิดไฟล์ด้วย jamovi เลือก icon Data $\to$ Wide to Long แล้วทำตามภาพด้านล่าง

ขั้นตอนการแปลง จาก wide เป็น long

3. หลังจากกดปุ้ม Reshape jamovi จะเปิดข้อมูลที่ทำการแปลงแล้วขึ้นมา

ข้อมูลที่ได้หลังจาการแปลง

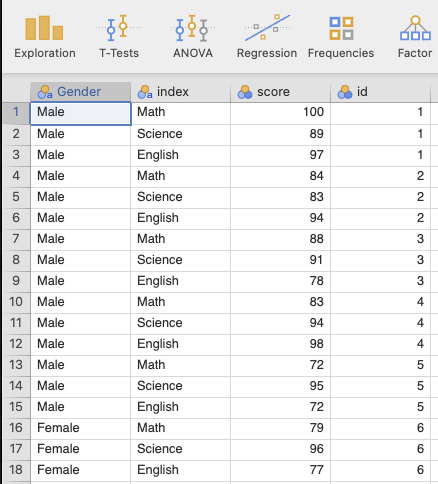
ตัวอย่างการแปลงจาก long เป็น wide ด้วย jamovi

จะผลลัพธ์ที่ได้จาก wide to long ย้อนกลับไป

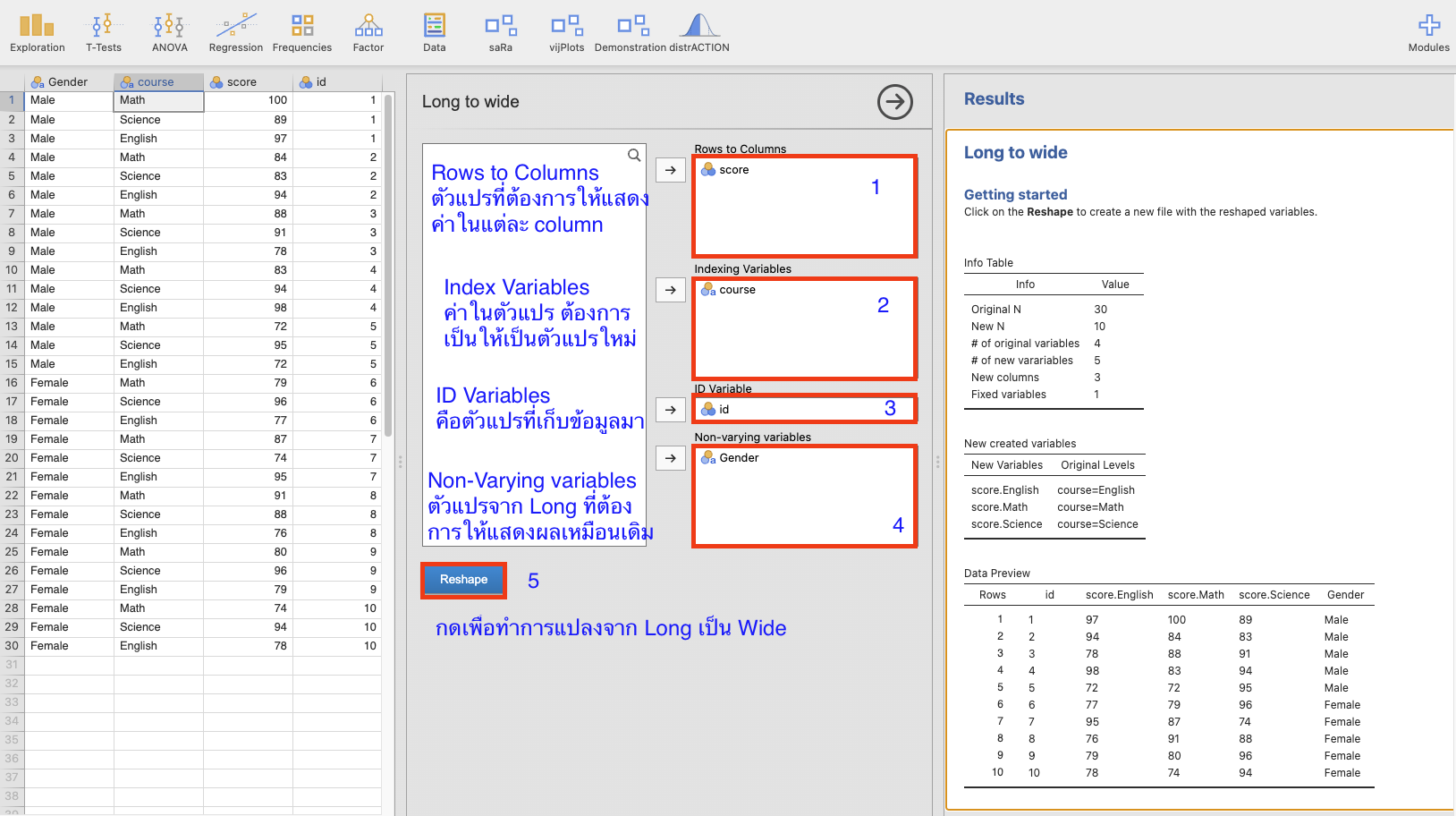
1. เลือก icon Data $\to$ Long to Wide แล้วทำตามภาพด้านล่าง

ขั้นตอนการแปลงจาก Long เป็น Wide

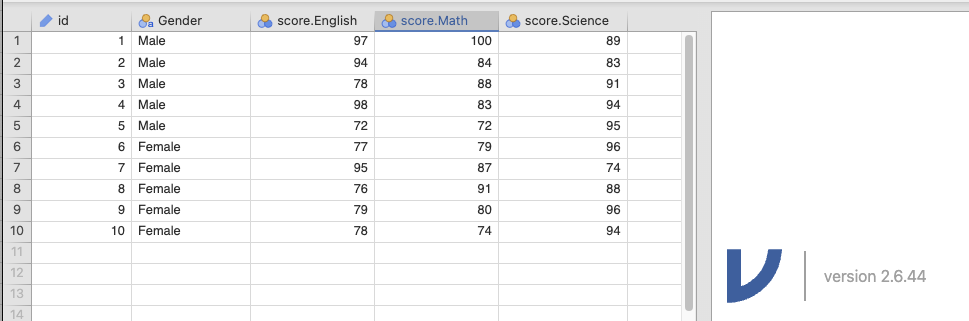
2. กด Reshape เพื่อทำการแปลง jamovi จะเปิด ข้อมูลที่ทำการแปลงแล้วขึ้นมา

ข้อมูลแบบ Long ไป Wide ที่ต้องการ

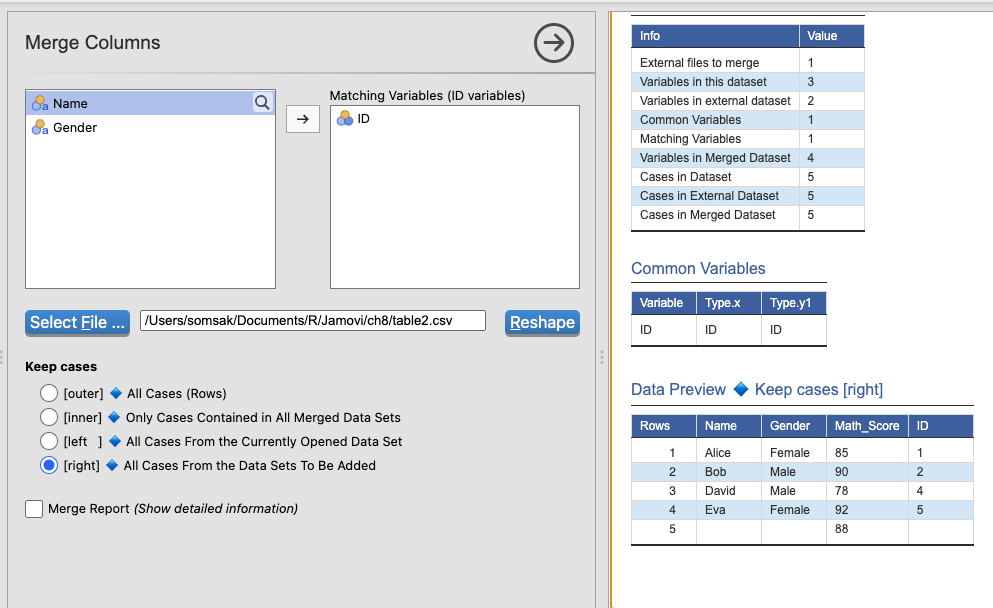
ตัวอย่างการ Merge Columns

Important

การ Merge Columns ก็คือการจาก Join ตารางในภาษา SQL นั่นเอง

การ Join เป็นกระบวนการรวมข้อมูลจากหลายตารางโดยใช้คอลัมน์ที่มีค่าร่วมกัน (Key) ซึ่งช่วยให้เราสามารถรวมข้อมูลจากแหล่งต่างๆ เพื่อการวิเคราะห์ที่สมบูรณ์ยิ่งขึ้น

ข้อมูลตัวอย่าง

Table 1

ID	Name	Gender
1	Alice	Female
2	Bob	Male
3	Charlie	Male
4	David	Male
5	Eva	Female

Table 2

ID	Math_Score
1	85
2	90
4	78
5	92
6	88

Download ข้อมูลจาก googledrive ชื่อ table1.csv และ table2.csv

ตัวอย่างการ Merge Columns ด้วย jReshape โดยใช้ไฟล์ table1.csv และ table2.csv

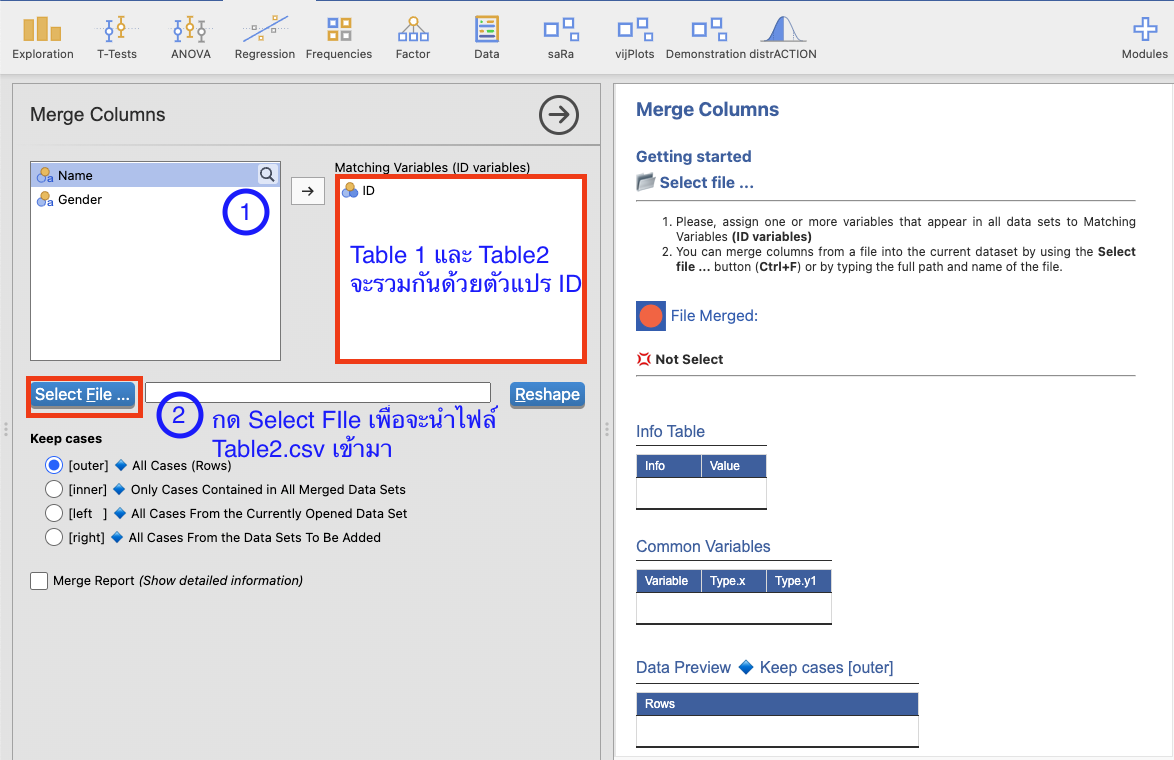
1. เปิดไฟล์ table1.csv ด้วย jamovi $\to$ เลือก icon Data $\to$ `เลือก Merge columns แล้วทำตามดังภาพ

ขั้นตอนการรวม Table1 และ Table2

2. กด Add Files นำไฟล์ Table2.csv เข้ามา แล้วกด Confirm

เมนูการ นำไฟล์เข้ามา

ไฟล์ที่สามารถ นำเข้ามาเข้ารวมด้วย Merge columns ได้

จะต้องเป็นนามสกุลดังต่อไปนี้เท่านั้น (.omv, .omt, .csv, .tsv, .rdata, .rda, .rds, .sav, .zsav, .dta, .sas7bdat, .sd2, .sd7, .xpt, .stx, .stc).

3. เลือกการรวมที่ต้องการ (outter, inner, left, right) แล้วกดปุ่ม `Reshape เพื่อเปิด jamovi ขึ้นมาใหม่พร้อมตารางผ่านการรวมแล้ว

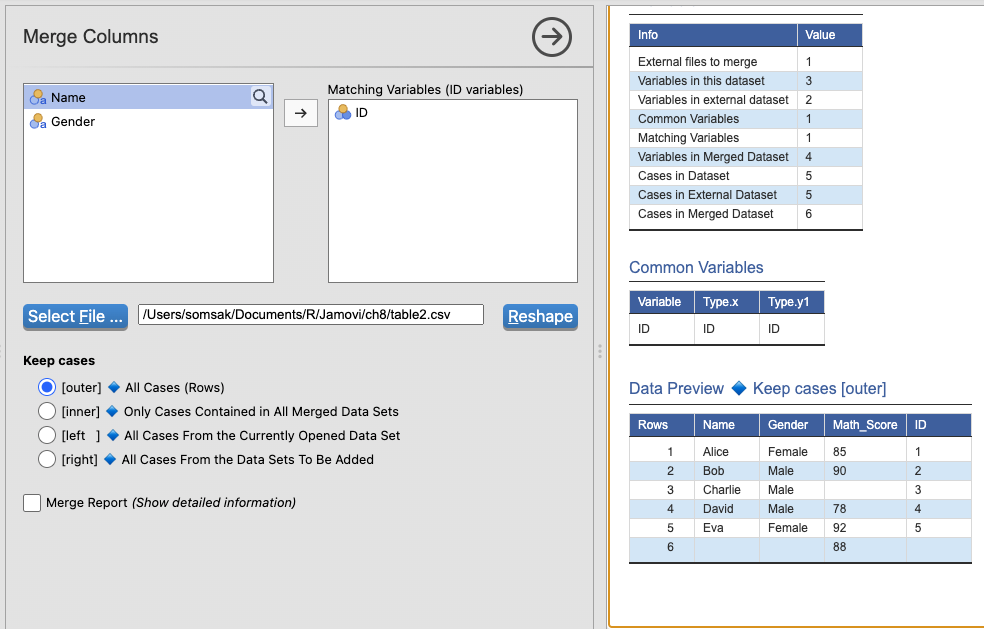
1. เลือก outer → เอาทุกข้อมูลจากทั้งสองตาราง (รวมทุก ID)

   • รวมข้อมูลทั้งหมดจาก ทั้งสองตาราง

   • ถ้าไม่มีข้อมูลในตารางใด → เติม NA

เลือก outer

ID	Name	Gender	Math_Score
1	Alice	Female	85
2	Bob	Male	90
3	Charlie	Male	NA
4	David	Male	78
5	Eva	Female	92
6	NA	NA	88

• สังเกต: ทั้ง ID = 3 และ ID = 6 อยู่ในผลลัพธ์ แต่ค่าที่ไม่มีในอีกตารางจะเป็น NA
  
• เหมาะสำหรับ: เมื่อต้องการเก็บข้อมูลทั้งหมด ไม่ว่าจะอยู่ในตารางใดก็ตาม

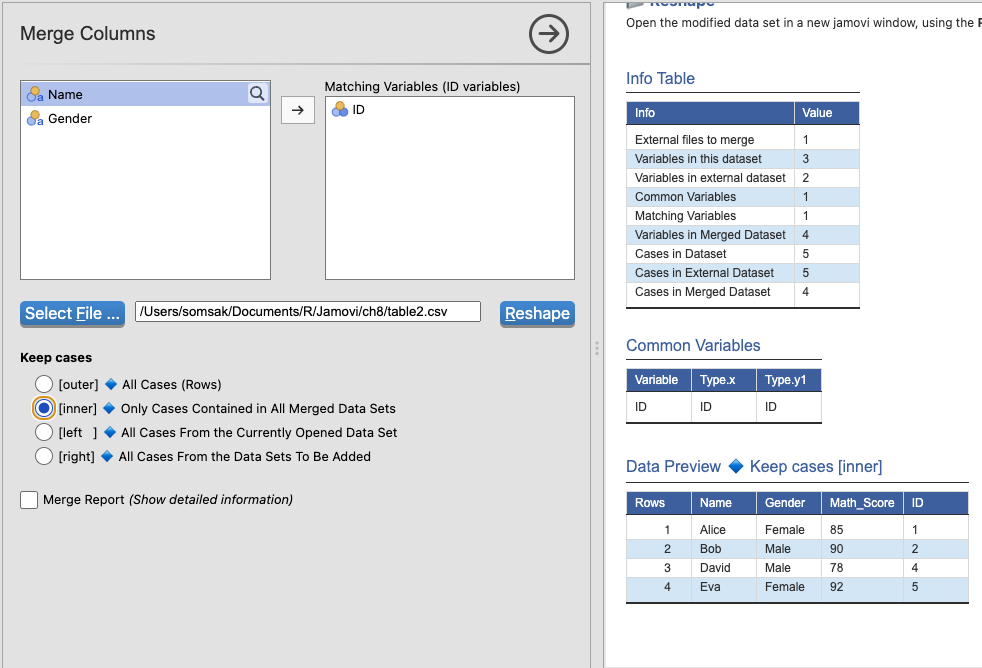
2. เลือก inner → เอาเฉพาะข้อมูลที่ตรงกันในทั้งสองตาราง

   • เก็บเฉพาะแถวที่มีค่าตรงกันในทั้งสองตาราง

   • ถ้าค่าใน ID ของTable2 ไม่มีในTable1 → หายไป

   • ถ้าค่าใน ID ของTable1 ไม่มีในTable2 → หายไป

เลือก inner

ID	Name	Gender	Math_Score
1	Alice	Female	85
2	Bob	Male	90
4	David	Male	78
5	Eva	Female	92

• สังเกต: Charlie (ID = 3) และ ID = 6 ไม่อยู่ในผลลัพธ์ เพราะไม่มีข้อมูลตรงกัน

• เหมาะสำหรับ: เมื่อต้องการเฉพาะข้อมูลที่มีอยู่ทั้งสองตาราง เช่น ต้องการเฉพาะนักเรียนที่มีคะแนนเท่านั้น

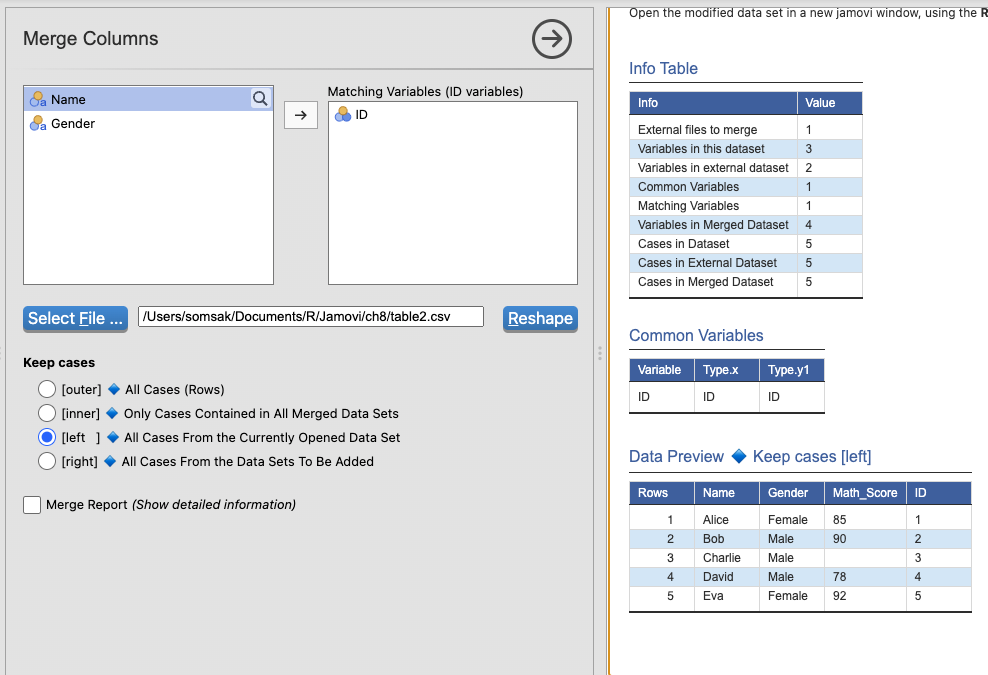
3. เลือก left → เอาข้อมูลทั้งหมดจากTable2 + เติมข้อมูลจากTable1

   • เอาข้อมูลทั้งหมดจาก ตารางหลัก (Table2)

   • ถ้าข้อมูล ในTable1ตรงกับTable2 → เติมข้อมูลเข้าไป

   • ถ้า ไม่มีข้อมูลในTable1 → ได้ค่า NA

เลือก left

ID	Name	Gender	Math_Score
1	Alice	Female	85
2	Bob	Male	90
3	Charlie	Male	NA
4	David	Male	78
5	Eva	Female	92

• สังเกต: Charlie (ID = 3) ไม่มีคะแนน Math เลยได้ NA

• เหมาะสำหรับ: เมื่อเราต้องการเก็บข้อมูลทั้งหมดจากตารางหลัก (เช่น รายชื่อนักเรียนทั้งหมด) แม้ว่าบางคนจะไม่มีคะแนนก็ตาม

4. เลือก right → เอาข้อมูลทั้งหมดจากTable1 + เติมข้อมูลจากTable2

   • เอาข้อมูลทั้งหมดจาก Table1 (ตารางที่เราจะเข้าร่วม)

   • ถ้าข้อมูล ในTable2ตรงกับTable1 → เติมข้อมูลเข้าไป

   • ถ้า ไม่มีข้อมูลในTable2 → ได้ค่า NA

เลือก right

ID	Name	Gender	Math_Score
1	Alice	Female	85
2	Bob	Male	90
4	David	Male	78
5	Eva	Female	92
6	NA	NA	88

• สังเกต: ID = 6 ไม่มีใน students เลยได้ NA ใน Name และ Gender

• เหมาะสำหรับ: เมื่อต้องการเก็บข้อมูลจากตารางคะแนนทั้งหมด แม้ว่าบางคนจะไม่มีข้อมูลนักเรียน

8.3 OneHotEncoding

One-Hot Encoding คืออะไร?

One-Hot Encoding (OHE) เป็นเทคนิคในการแปลงข้อมูลประเภทที่เป็น หมวดหมู่ (Categorical Data) ให้กลายเป็น ข้อมูลตัวเลข เพื่อให้สามารถนำไปใช้กับโมเดลทางสถิติหรือ Machine Learning ได้

ทำไมต้องใช้ One-Hot Encoding? บางอัลกอริธึม เช่น Linear Regression, Logistic Regression, Neural Networks ไม่สามารถทำงานกับ ตัวแปรหมวดหมู่ (Categorical Variables) โดยตรงได้ จำเป็นต้องแปลงข้อมูลเป็นตัวเลขก่อน

วิธีการทำ One-Hot Encoding

1. สร้างคอลัมน์ใหม่ สำหรับแต่ละค่าที่เป็นไปได้ของตัวแปรหมวดหมู่

2. แทนค่าด้วย 1 หรือ 0

   • 1 หมายถึง แถวนี้อยู่ในหมวดหมู่นั้น

   • 0 หมายถึง แถวนี้ ไม่ได้ อยู่ในหมวดหมู่นั้น

ตัวอย่าง One-Hot Encoding

ตัวแปรเดิม (Categorical)

ID	Color
1	Red
2	Green
3	Blue
4	Red
5	Blue

หลังทำ One-Hot Encoding

ID	Red	Green	Blue
1	1	0	0
2	0	1	0
3	0	0	1
4	1	0	0
5	0	0	1

โมดูล OneHotEncoding

เมื่อทำการติดตั้งแล้ว มี icon Data ขึ้นมา เหมือนกับ rReshape

icon ชื่อ Data ของโมดูล One Hot Encoding

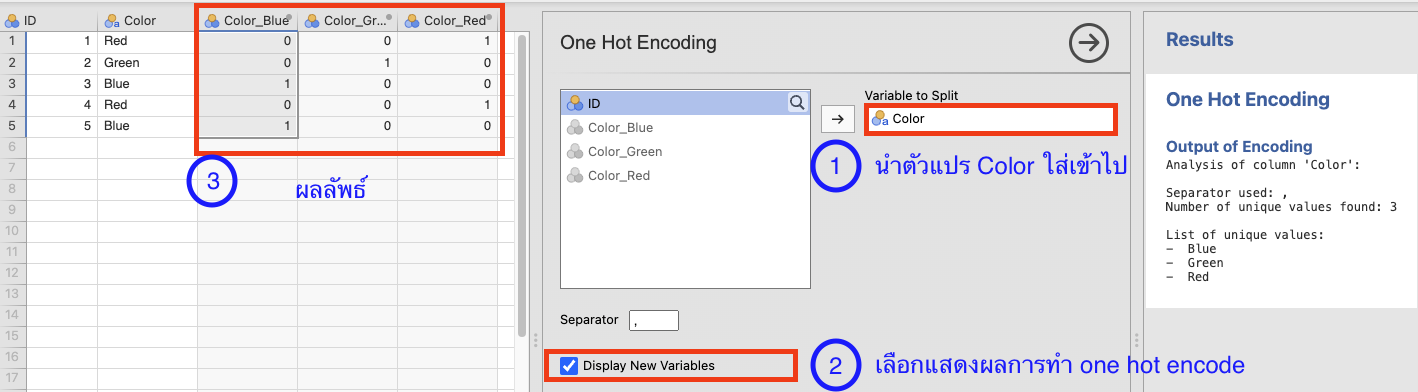
ตัวอย่างการใช้งาน เมนู One hot Encoding

Download ข้อมูลจาก googledrive ชื่อ color.xlsx

1. เปิดไฟล์ color.xlsx ด้วย jamovi $\to$ icon Data $\to$ เลือกเมนู One Hot Encoding แล้วทำตามภาพ

ขั้นตอนการทำ one hot encode