5 เมนู Regression
ผู้อ่านสามารถโหลดข้อมูลได้ google drive นี้
Regression เป็นกระบวนการทางสถิติที่ใช้เพื่อหาความสัมพันธ์ระหว่างตัวแปรต้น (independent variables) กับตัวแปรตาม (dependent variable) และสร้างสมการที่อธิบายความสัมพันธ์นี้ในรูปแบบของสมการเชิงเส้น (linear equation) หรือแบบอื่น ๆ ตามความเหมาะสมของข้อมูล
Regression, มีหลายวิธีและแบบที่สามารถใช้ ตัวอย่างบ่อยที่ใช้ในปฏิบัติมี Linear Regression, Multiple Regression, Classification Regression, และอื่น ๆ
Linear Regression เป็นกรณีที่ทั้งตัวแปรต้นและตัวแปรตามมีความสัมพันธ์เชิงเส้น ซึ่งสามารถแสดงในรูปแบบของสมการเส้นตรงได้:
\[Y = \beta_0 + \beta_1X + \varepsilon\]
\(Y\) คือตัวแปรตาม (dependent variable)
\(X\) คือตัวแปรต้น (independent variable)
\(\beta_0\) คือ intercept (จุดตัดแกน Y เมื่อ \(X = 0\))
\(\beta_1\) คือ slope (ความชันของเส้น)
\(\varepsilon\) คือข้อผิดพลาดที่ไม่สามารถอธิบายได้ในสมการ
Linear Regression จะพยายามปรับค่า \(\beta_0\) และ \(\beta_1\) เพื่อทำให้รูปแบบของเส้นเข้าใกล้ค่าจริงของข้อมูลที่มีอยู่ในสมการ
Multiple Regression ใช้เมื่อมีมากกว่าหนึ่งตัวแปรต้น, และสามารถแสดงได้ในรูปแบบ:
\[Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_kX_k + \varepsilon \]
ในทำนองเดียวกัน, พยายามปรับค่า \(\beta\) เพื่อให้เส้นที่ได้สามารถอธิบายข้อมูลได้อย่างดีที่สุด
Regression มักถูกนำมาใช้ในการทำนาย, การจำแนกประเภทข้อมูล, การทดสอบสมมติฐานเกี่ยวกับความสัมพันธ์, และการวิเคราะห์ตัวแปรที่ส่งผลกระทบต่อตัวแปรอื่น ๆแปรอื่น ๆ
ก่อนที่จะหาค่าพารามิเตอร์ใน Regression ควรต้องพิจารณา correlation เสียก่อน
5.1 เมนู Correlation Matrix
ทางสถิตค่า correlation ที่ได้รับความนิยมมีอยู่ 3 วิธีคือ
5.1.1 Pearson correlation
Pearson correlation coefficient (หรือที่เรียกสั้น ๆ ว่า Pearson correlation) เป็นหนึ่งในวัตถุประสงค์ที่ใช้บ่งบอกถึงความสัมพันธ์เชิงเส้นระหว่างคู่ตัวแปรในชุดข้อมูล. มักใช้เพื่อวัดความสัมพันธ์ที่เป็นเส้นตรงระหว่างตัวแปร
Pearson correlation coefficient (\(r\)) คำนวณโดยใช้สูตร:
\[ r= \frac{\sum{(X_i - \bar{X})(Y_i - \bar{Y})}}{\sqrt{\sum{(X_i - \bar{X})^2} \sum{(Y_i - \bar{Y})^2}}}\]
โดยที่:
\(X_i\) และ \(Y_i\) คือค่าของตัวแปร \(X\) และ \(Y\) ในสมการลำดับที่ \(i\)
\(\bar{X}\) และ \(\bar{Y}\) คือค่าเฉลี่ยของ \(X\) และ \(Y\) ตามลำดับ
\(\sum\) หมายถึงผลรวม
Pearson correlation coefficient มีค่าอยู่ในช่วง \(-1\) ถึง \(1\):
\(1\) แสดงถึงความสัมพันธ์เชิงบวกที่แข็งแกร่ง
\(-1\) แสดงถึงความสัมพันธ์เชิงลบที่แข็งแกร่ง
\(0\) แสดงถึงความสัมพันธ์ที่ไม่มีการเปลี่ยนแปลงร่วมกัน
การใช้ Pearson correlation coefficient มีประโยชน์ในการวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรที่มีการกระจายเป็นรูปกระจายที่เป็นรูปเป็นระบบ (normal distribution) และมีการกระจายเป็นแบบเดียวกัน (homoscedasticity)
5.1.2 Spearman’s Rho
Spearman’s Rank Correlation Coefficient (หรือที่เรียกว่า Spearman’s Rho) เป็นวิธีการทางสถิติที่ใช้วัดความสัมพันธ์ระหว่างคู่ตัวแปรในชุดข้อมูล โดยไม่ขึ้นอยู่กับการกระจายที่เป็นรูปกระจายเป็นรูปเป็นระบบ (normal distribution) หรือการกระจายที่เป็นแบบเดียวกัน (homoscedasticity) ตามที่ Pearson correlation ต้องการ
Spearman’s Rho คำนวณจากค่าลำดับ (rank) ของข้อมูลที่มีอยู่, แทนที่จะใช้ค่าเป็นตัวแปรจริง ขั้นตอนในการคำนวณ Spearman’s Rho คือ:
กำหนดลำดับ (Ranking): กำหนดลำดับ (rank) ให้กับข้อมูลของทั้งคู่ตัวแปร
คำนวณต่างลำดับ (Rank Differences): คำนวณความต่างในลำดับระหว่างคู่ตัวแปรที่ตรงกัน
คำนวณ Spearman’s Rho: ใช้สูตรต่อไปนี้ \[\rho = 1 - \frac{6\sum d_i^2}{n(n^2 - 1)}\] โดยที่ \(d_i\) คือความต่างในลำดับระหว่างคู่ตัวแปรที่ตรงกันแต่ละคู่, และ \(n\) คือขนาดของตัวอย่าง
Spearman’s Rho มีค่าระหว่าง \(-1\) ถึง \(1\):
\(1\) แสดงถึงความสัมพันธ์เชิงบวกที่แข็งแกร่ง
\(-1\) แสดงถึงความสัมพันธ์เชิงลบที่แข็งแกร่ง
\(0\) แสดงถึงความสัมพันธ์ที่ไม่มีการเปลี่ยนแปลงร่วมกัน
Spearman’s Rho มักถูกนำมาใช้ในการวัดความสัมพันธ์ระหว่างตัวแปรที่ไม่มีการกระจายเป็นรูปกระจายที่เป็นรูปเป็นระบบ (non-normally distributed data) หรือที่มีข้อมูลที่มีลำดับแต่ไม่จำเป็นต้องมีตัวเลขที่เป็นตัวแปรจริง (ordinal data)
5.1.3 Kendall’s Tau
Kendall’s Tau (Kendall’s rank correlation coefficient) เป็นวิธีการทางสถิติที่ใช้วัดความสัมพันธ์ระหว่างคู่ตัวแปรในชุดข้อมูล โดยใช้ลำดับ (rank) ของข้อมูลที่มีอยู่. ค่าที่ได้จาก Kendall’s Tau บ่งบอกถึงความสัมพันธ์ระหว่างคู่ตัวแปร โดยค่าของ Tau อยู่ในช่วง \([-1, ~1]\)
ขั้นตอนในการคำนวณ Kendall’s Tau คือ:
กำหนดลำดับ (Ranking): กำหนดลำดับ (rank) ให้กับข้อมูลของทั้งคู่ตัวแปร
นับ Concordant Pairs และ Discordant Pairs:
Concordant Pairs: คู่ของตัวแปรที่ลำดับเดียวกันทั้งสองคู่ (เช่น ลำดับของ A มาก่อน B ทั้งที่ A และ B มีลำดับเดียวกันทั้งสองในตัวอย่าง)
Discordant Pairs: คู่ของตัวแปรที่ลำดับตรงข้ามกันทั้งสองคู่ (เช่น ลำดับของ A มาก่อน B ทั้งที่ B มาก่อน A ทั้งสองในตัวอย่าง)
คำนวณ Tau: \[\tau = \frac{{\text{Concordant Pairs} - \text{Discordant Pairs}}}{{\text{Total Pairs}}}\] โดยที่ Total Pairs คือจำนวนคู่ทั้งหมดของตัวแปรทั้งสอง.
Kendall’s Tau มีค่าที่มี interpretability ดังนี้:
\(\tau = 1\) แสดงถึงความสัมพันธ์ที่แข็งแกร่งทางบวก
\(\tau = -1\) แสดงถึงความสัมพันธ์ที่แข็งแกร่งทางลบ
\(\tau = 0\) แสดงถึงไม่มีความสัมพันธ์ (independent)
Kendall’s Tau มักถูกนำมาใช้ในการวัดความสัมพันธ์ระหว่างตัวแปรที่ไม่มีการกระจายเป็นรูปกระจายที่เป็นรูปเป็นระบบ (non-normally distributed data) และที่มีข้อมูลที่มีลำดับแต่ไม่จำเป็นต้องมีตัวเลขที่เป็นตัวแปรจริง (ordinal data).
5.1.4 Correlation matrix
ค่า Correlation matrix เป็นตารางที่แสดงค่า correlation coefficient ระหว่างตัวแปรทุกคู่ในชุดข้อมูล. Correlation coefficient คือค่าที่บ่งบอกถึงทิศทางและความแรงของความสัมพันธ์ระหว่างคู่ตัวแปร
ใน correlation matrix, ค่า correlation coefficient ระหว่างทุกคู่ตัวแปรถูกจัดเก็บในรูปของตารางที่มีรูปร่างเป็นสี่เหลี่ยม. สามารถใช้สูตร Pearson correlation coefficient หรือสูตรอื่น ๆ ที่เหมาะสมกับลักษณะของข้อมูล. Pearson correlation coefficient เป็นตัวแปรที่ใช้บ่งบอกถึงความสัมพันธ์เชิงเส้นระหว่างตัวแปร โดยมีค่าอยู่ในช่วง [-1, 1] โดยที่:
\(1\) แสดงถึงความสัมพันธ์เชิงบวกที่แข็งแกร่ง
\(-1\) แสดงถึงความสัมพันธ์เชิงลบที่แข็งแกร่ง
\(0\) แสดงถึงความสัมพันธ์ที่ไม่มีการเปลี่ยนแปลงร่วมกัน
ตาราง correlation matrix สามารถให้ข้อมูลเกี่ยวกับโครงสร้างของข้อมูล ว่าตัวแปรไหนมีความสัมพันธ์กับตัวแปรอื่น ๆ บ้าง, และความแรงของความสัมพันธ์นั้น ๆ. Correlation matrix มักถูกใช้ในการทำ Exploratory Data Analysis (EDA) หรือเพื่อการวิเคราะห์รูปแบบความสัมพันธ์ในชุดข้อมูล โปรแกรม jamovi สามารถหาค่า correlation ได้มั้ย 3 วิธี
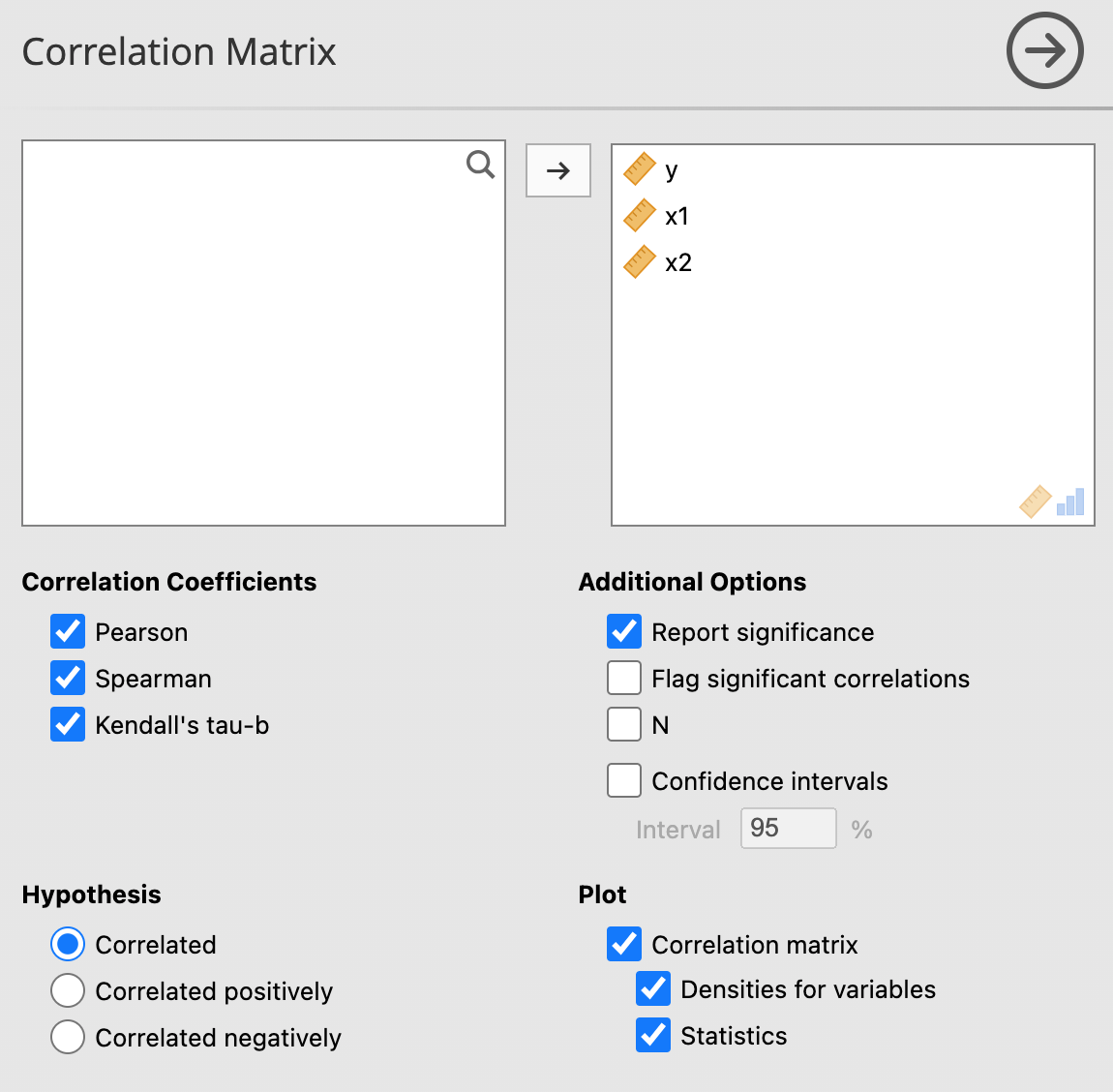
ตัวอย่างการคำนวณ
โดยมีผลการคำนวณออกมาเป็นตารางดังนี้
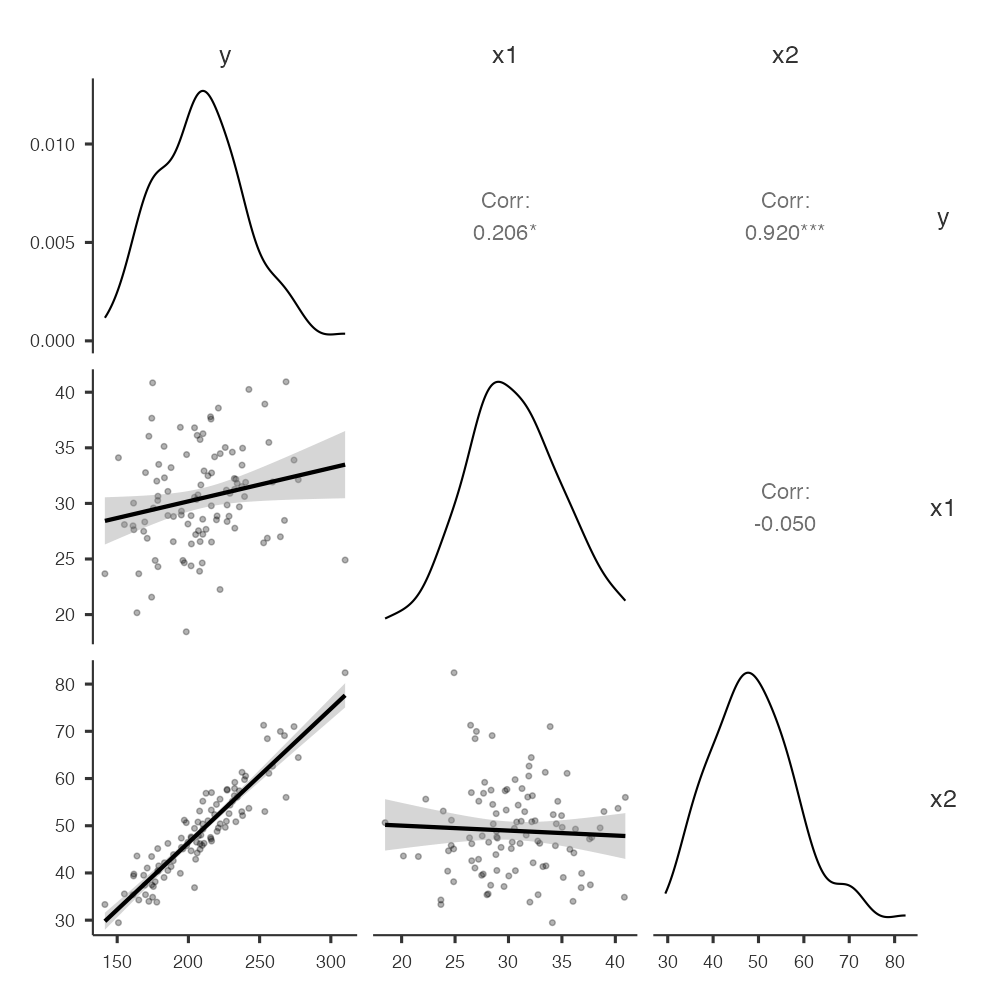
นอกจากยังสามารถสร้างแผนภาพ scatter plot และ histogram ของตัวแปรละตัวได้
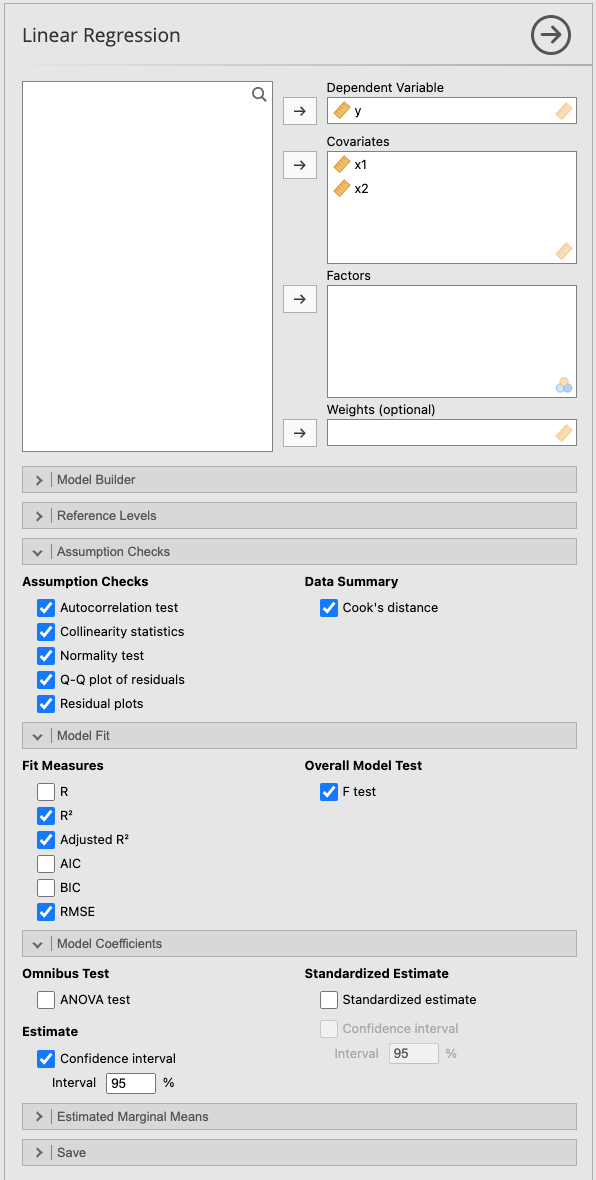
5.2 เมนู Linear Regression
ถัดจากการพิจารณา correlation ก็เป็นการประมาณค่าพารามิเตอร์ และตรวจสมมุติฐานการต่างๆ ของ linear regression
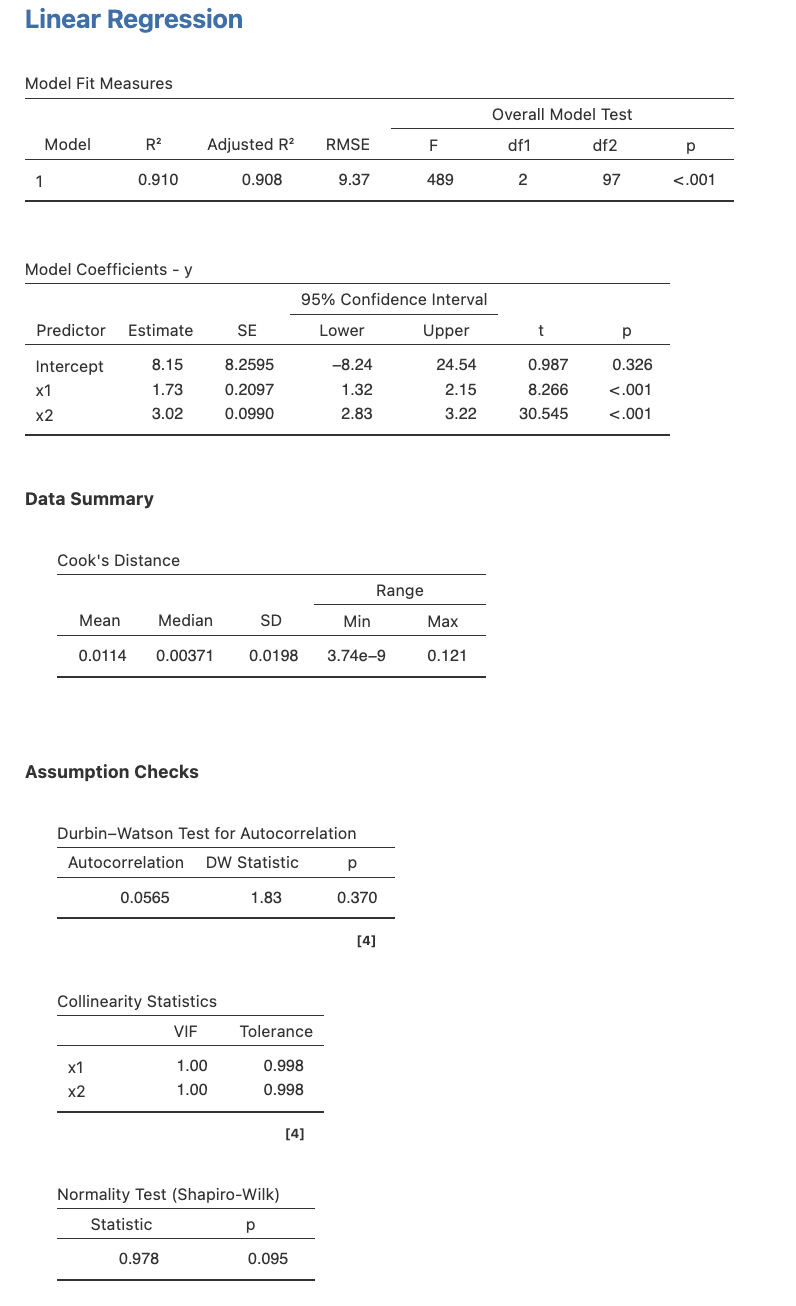
ผลการประมาณค่าพารามิเตอร์และการตรวจสอบสมมุติฐานต่างๆ
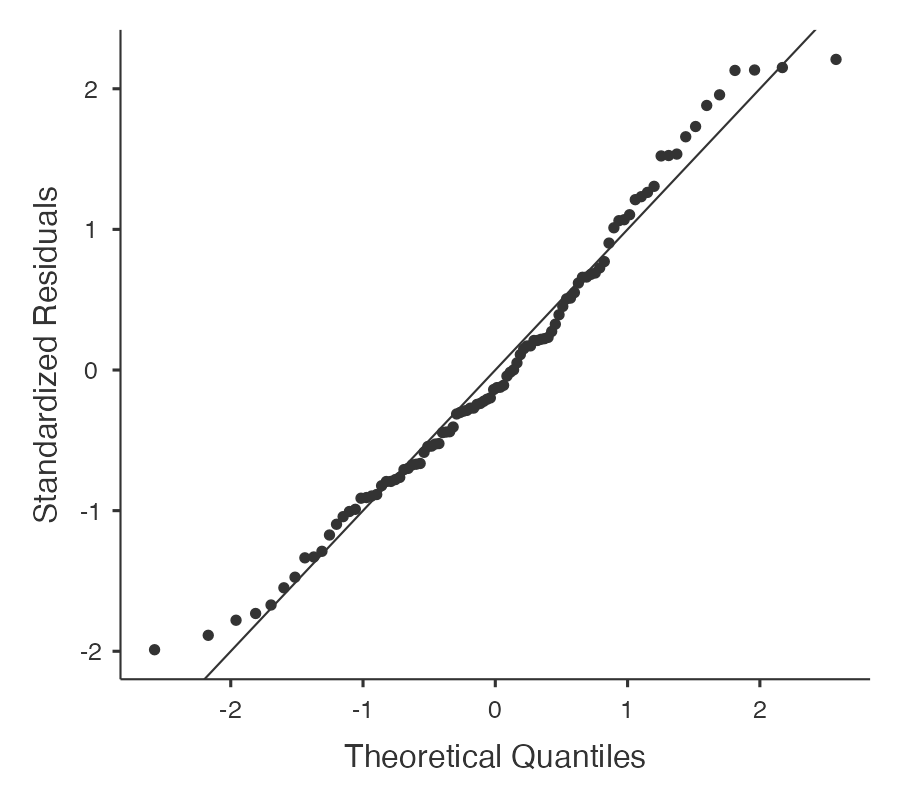
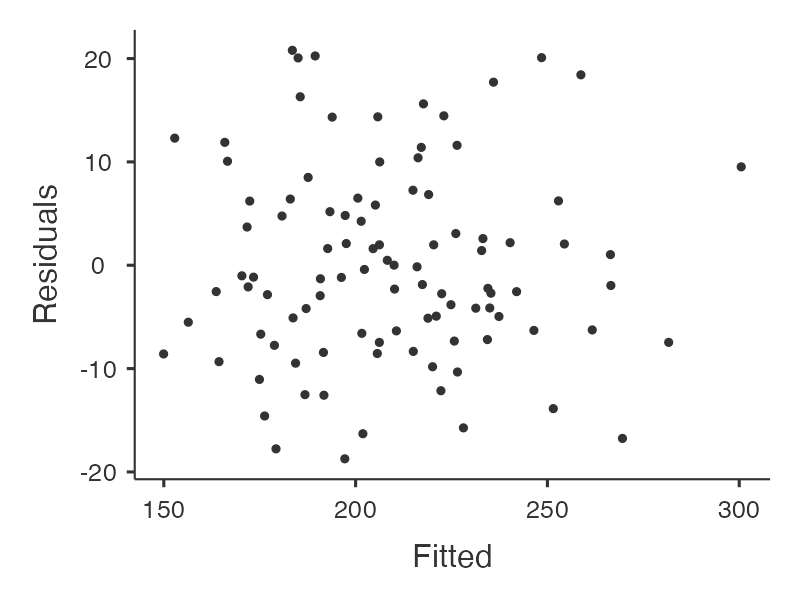
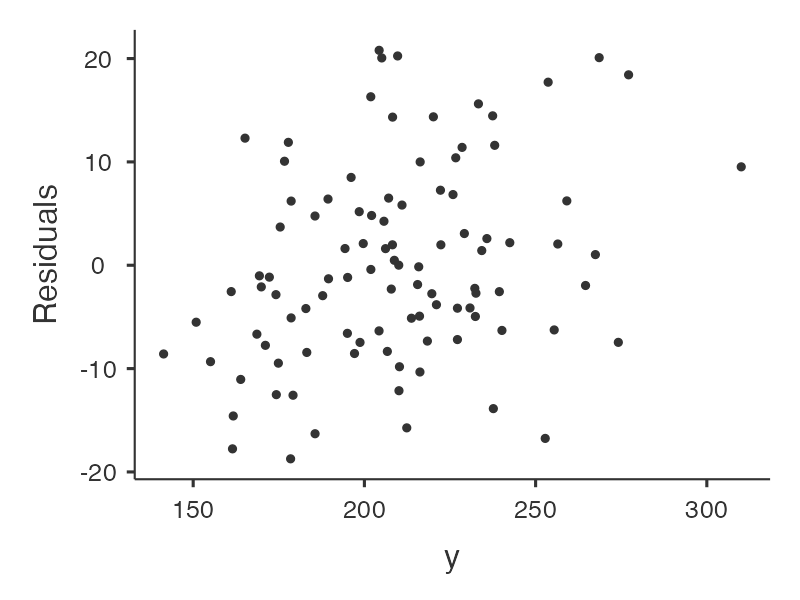
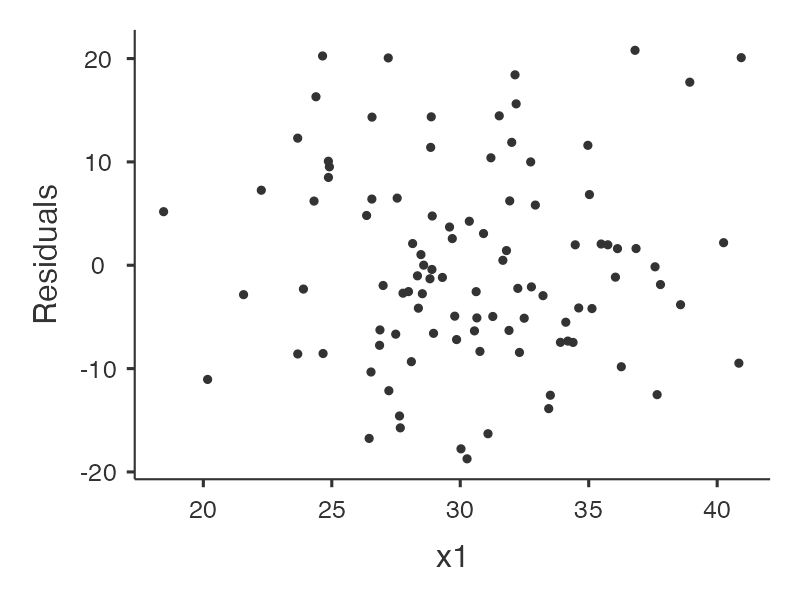
กราฟที่เกี่ยวข้องกับการวิเคราะห์
 |
 |
 |
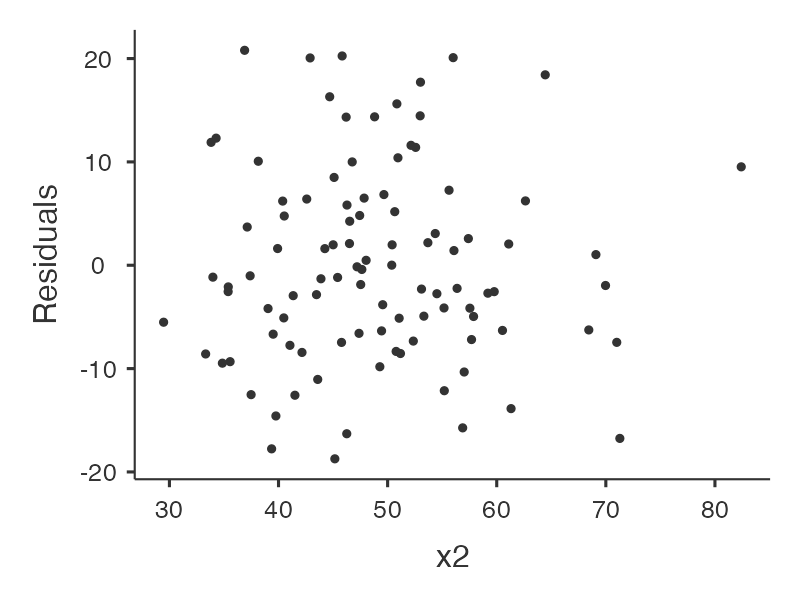 |
5.3 เมนู Logistic Regression
Logistic regression คือ
Logistic Regression เป็นอัลกอริทึมในสถิติและ machine learning ที่ใช้สำหรับการแก้ปัญหาที่เกี่ยวกับการจำแนกประเภท (classification) โดยเฉพาะต่อการจำแนกประเภทที่มีสองหรือมากกว่าสองกลุ่ม (binary or multiclass classification)
โมเดล Logistic Regression ถูกใช้ในการทำนายความน่าจะเป็น (probability) ที่ตัวแปรตามจะอยู่ในหนึ่งในกลุ่มของตัวแปรตามที่กำหนดไว้ล่วงหน้า (class). ฟังก์ชัน Logistic ถูกใช้ในการแปลงผลลัพธ์เป็นความน่าจะเป็นระหว่าง 0 ถึง 1 โดยมีสูตรดังนี้:
\[P(Y=1) = \frac{1}{1 + e^{-(\beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_nX_n)}}\]
ที่: - \(P(Y=1)\) คือความน่าจะเป็นที่ตัวแปรตามจะอยู่ในกลุ่มที่กำหนด (class 1) - \(e\) คือฐานศูนย์ของลอการิทึม (natural logarithm) - \(\beta_0, \beta_1, \beta_2, \cdots, \beta_n\) คือพารามิเตอร์ที่ต้องปรับให้เหมาะสมในขั้นตอนการฝึก (training) ของโมเดล - \(X_1, X_2, \ldots, X_n\) คือค่าของตัวแปรต้น
การปรับค่าพารามิเตอร์ใน Logistic Regression ทำโดยใช้ข้อมูลจริงในการฝึกโมเดล และการใช้เทคนิคการปรับแก้ไข (optimization algorithm) เช่น gradient descent เพื่อทำให้โมเดลมีความแม่นยำในการทำนาย
โมเดล Logistic Regression มักถูกนำมาใช้ในหลายงานเช่น การจำแนกอีเมลเป็นสแปมหรือไม่สแปม, การทำนายการวินิจฉัยของโรค
ตัวอย่างข้อมูล สามารถ download ได้จาก https://stats.oarc.ucla.edu/r/dae/logit-regression/ หรือจะ download จาก googledrive ของหนังสือเล่มนี้ก็ได้
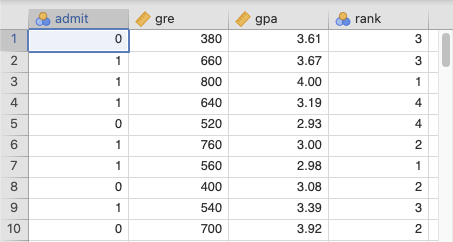
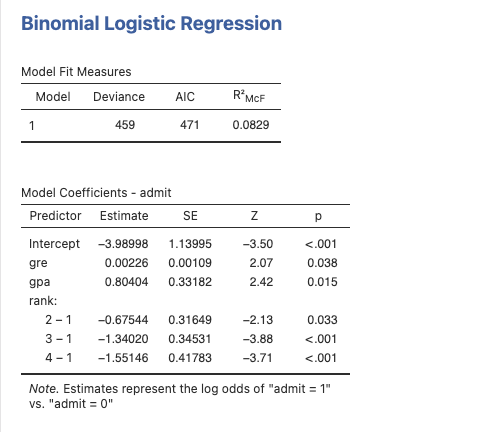
ชุดข้อมูลนี้มีตัวแปรตาม (dependent variable) เป็นแบบ BInary ที่เรียกว่า “admit” ซึ่งเป็นตัวแปรที่ต้องการทำนายหรือจำแนก และมีตัวแปรที่ใช้ในการทำนาย (predictor variables) ทั้งหมด 3 ตัวคือ “gre”, “gpa”, และ “rank”
“gre” และ “gpa” ถูกจัดการเป็นตัวแปรต่อเนื่อง (continuous variables) ซึ่งหมายถึงเป็นตัวเลขที่มีค่าต่อเนื่องกันไป
“rank” เป็นตัวแปรที่มีค่าเป็น 1 ถึง 4 ซึ่งบ่งบอกถึงระดับของสถาบันการศึกษา โดยที่ 1 คือมีชื่อเสียงสูงที่สุดและ 4 คือมีชื่อเสียงต่ำที่สุด
ขั้นที่ 1 นำเข้าข้อมูล และจัดการชนิดของตัวแปรให้เป็นตามรูป
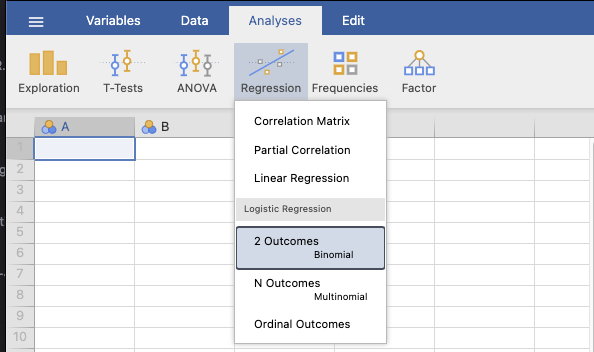
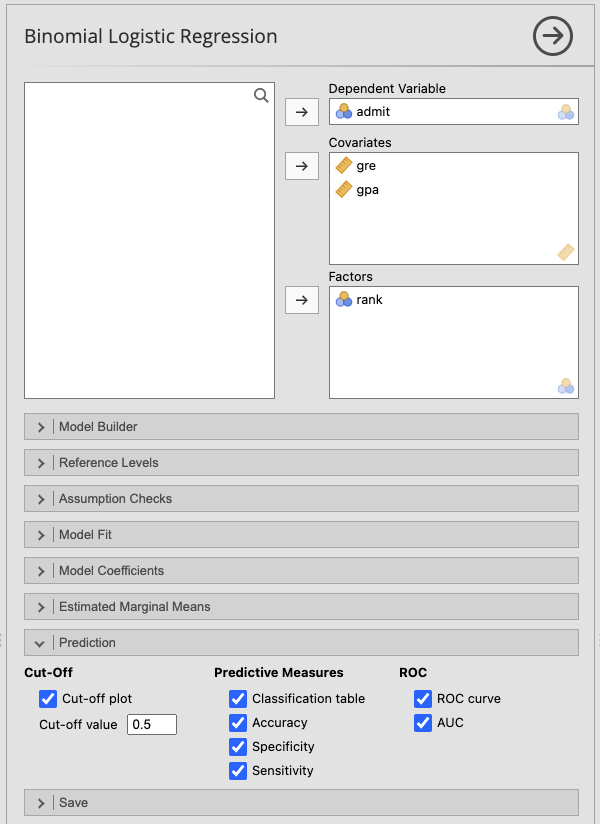
ขั้นที่ 2 เลือกตามภาพ
หมายเหตุ ผู้อ่านสามารถเลือกผลการเคราะห์หรือการคำนวฯต่างๆ ได้ตามต้องการ
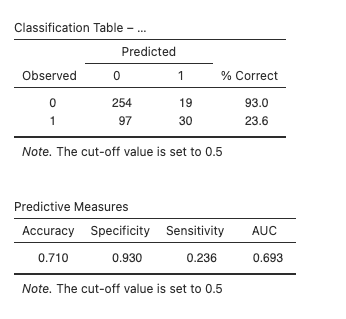
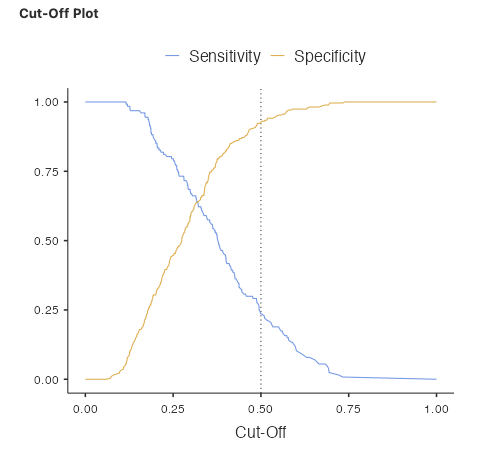
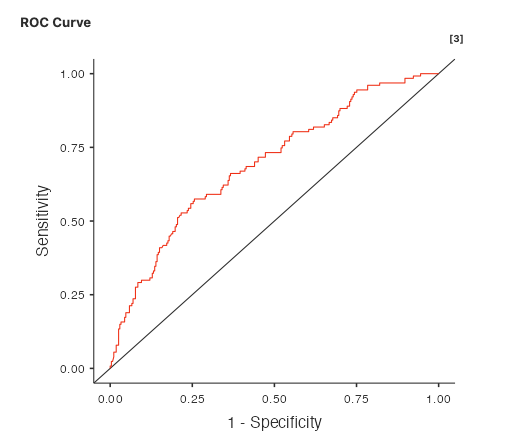
ผลการวิเคราะห์
5.3.1 N outcomes multinomial
Multinomial Regression เป็นอัลกอริทึมที่ใช้ในการจำแนกประเภทหลาย ๆ ประเภท (multiclass classification) หรือการทำนายตัวแปรตามที่มีมากกว่าสองกลุ่ม ซึ่งแตกต่างจาก Binary Logistic Regression ที่ใช้ในการจำแนกเพียงสองกลุ่ม
ใน Multinomial Regression, ตัวแปรตาม (dependent variable) เป็นแบบไม่ต่อเนื่องและมีมากกว่าสองกลุ่ม โดยที่แต่ละกลุ่มไม่มีลำดับที่เหมาะสม เช่น ประเภทของสินค้าที่ลูกค้าเลือกซื้อ (A, B, C) หรือประเภทของรถยนต์ที่ลูกค้าเลือก (Compact, Sedan, SUV)
สมการที่ใช้ใน Multinomial Regression สามารถเขียนได้เป็น:
\[P(Y = k | X) = \frac{e^{\beta_{k0} + \beta_{k1}X_1 + \beta_{k2}X_2 + \ldots + \beta_{kp}X_p}}{\sum_{j=1}^{K} e^{\beta_{j0} + \beta_{j1}X_1 + \beta_{j2}X_2 + \ldots + \beta_{jp}X_p}}\]
ที่: - \(P(Y = k | X)\) คือความน่าจะเป็นที่ตัวแปรตามจะอยู่ในกลุ่ม \(k\) - \(K\) คือจำนวนกลุ่มทั้งหมด - \(X\) คือตัวแปรต้น - \(\beta_{k0}, \beta_{k1}, \ldots, \beta_{kp}\) คือพารามิเตอร์ที่ต้องปรับในการฝึกโมเดลสำหรับกลุ่ม (k) - \(e\) คือฐานศูนย์ของลอการิทึม (natural logarithm)
การฝึก Multinomial Regression จะทำโดยการปรับพารามิเตอร์ทั้งหมดในขั้นตอนการฝึกโมเดลในกระบวนการทำนาย และใช้ฟังก์ชันการสูญเสีย (loss function) เช่น Cross-Entropy Loss ในการวัดความคลาดเคลื่อนระหว่างค่าทำนายและค่าจริง
ตัวอย่าง ใช้ข้อมูลชื่อ multinomial.xlsx ที่มีมาจาก
[https://stats.oarc.ucla.edu/r/dae/multinomial-logistic-regression/](https://stats.oarc.ucla.edu/r/dae/multinomial-logistic-regression/)
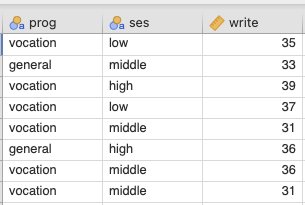
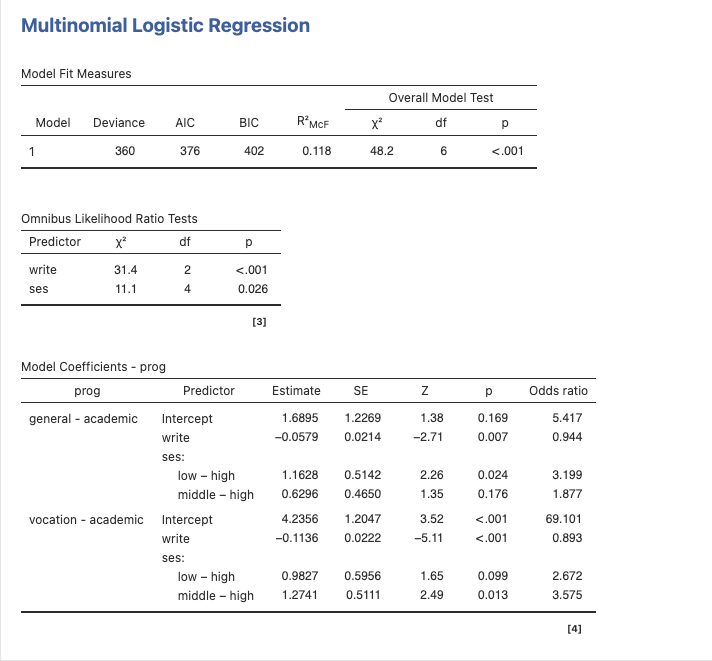
นักเรียนที่เข้ามัธยมศึกษาตัดสินใจเลือกโปรแกรมการเรียนที่เข้าร่วม ระหว่างโปรแกรมทั่วไป, โปรแกรมวิชาชีพ, และ โปรแกรมวิชาการ ตัวเลือกของพวกเขาอาจถูกจำลองโดยใช้คะแนนเขียนและสถานะเศรษฐกิจสังคมของพวกเขา
การทำนายการเลือกโปรแกรมของนักเรียนจะใช้ตัวแปรคะแนนเขียนและสถานะเศรษฐกิจสังคม (SES) เป็นตัวทำนาย
ในบริบทนี้, “คะแนนเขียน” น่าจะเป็นการวัดทักษะในการเขียนของนักเรียน และ “สถานะเศรษฐกิจสังคม (SES)” คือตัวบ่งชี้ทางเศรษฐกิจสังคม ทั้งสองตัวแปรนี้ถูกใช้เป็นตัวทำนายเพื่อทราบถึงหรือทำนายการเลือกโปรแกรมที่นักเรียนจะทำ
เพื่อทำนายนี้, จะใช้โมเดลทำนาย multinomial regression, ที่จะช่วยในการสร้างความเข้าใจหรือทำนายถึงการเลือกโปรแกรมของนักเรียนโดยใช้คะแนนเขียนและสถานะเศรษฐกิจสังคม
ชุดข้อมูลนี้ประกอบด้วยตัวแปรตาม (outcome variable) คือ “prog” ซึ่งเป็นประเภทของโปรแกรมการเรียน และตัวแปรทำนาย (predictor variables) คือ “ses” และ “write”
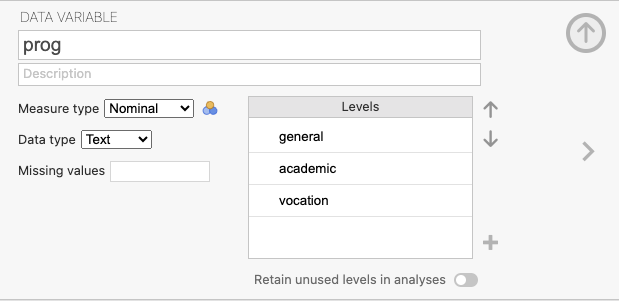
- “prog”: เป็นตัวแปรที่เราสนใจทำนายหรือวิเคราะห์ และมีประเภทของโปรแกรมการเรียน
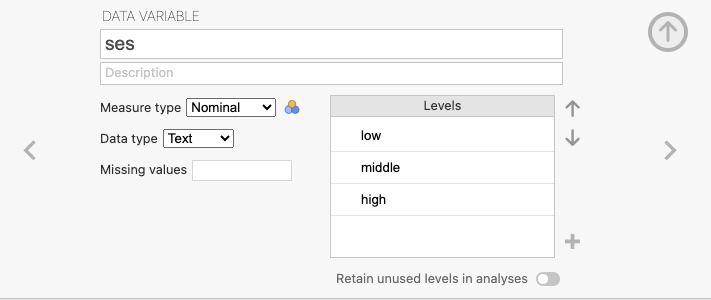
- “ses”: เป็นตัวแปรทำนายที่เป็นแบบหมวดหมู่ที่มี 3 ระดับ (three-level categorical variable) แทนสถานะทางเศรษฐกิจสังคม (social economic status)
- “write”: เป็นตัวแปรทำนายที่เป็นตัวเลขต่อเนื่อง (continuous variable) แทนคะแนนการเขียน
ขั้นที่ 1 โหลดข้อมูล multinomial.xlsx เข้า jamovi และแปรข้อมูลดังนี้
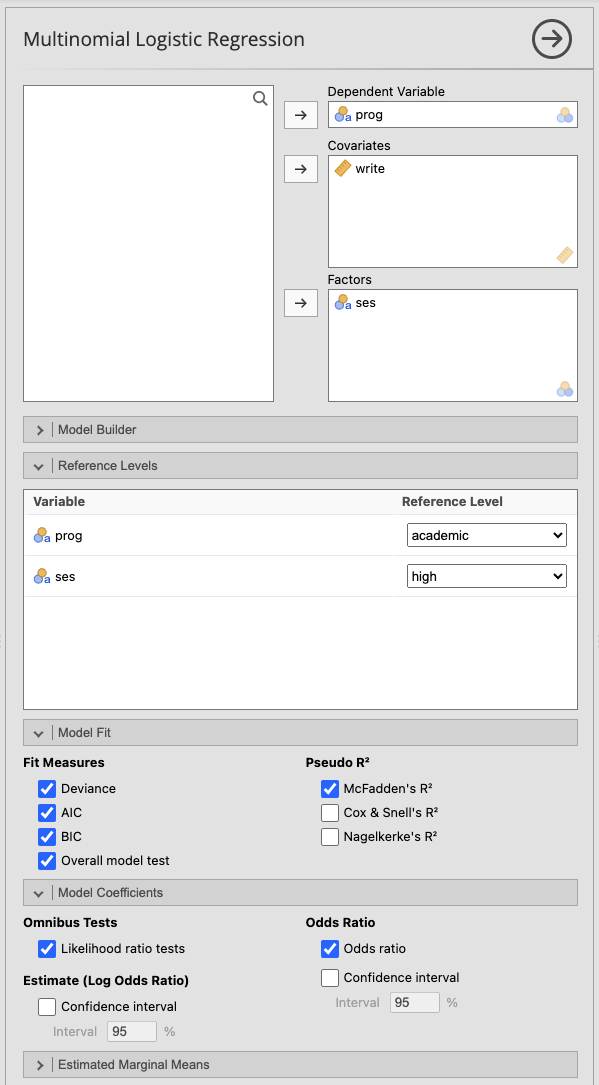
เมนู N outcome และผลลัพธ์
5.3.2 ORDINAL LOGISTIC REGRESSION
Ordinal Logistic Regression เป็นแบบจำลองทางสถิติที่ใช้ในการทำนายหรือวิเคราะห์ตัวแปรตาม (dependent variable) ที่มีลำดับหรือลำดับมีความหนาแน่นอยู่ระหว่างกลุ่มหลาย ๆ กลุ่ม ซึ่งเหมาะสำหรับข้อมูลที่มีลำดับหรือขั้นตอนคุณภาพ เช่น ระดับการคุ้มครองทางสังคม, ระดับความพึงพอใจ, หรือระดับการศึกษา
ใน Ordinal Logistic Regression, ตัวแปรตามมีลำดับหรือเป็น Ordinal ซึ่งแปลว่ามีระดับหรือลำดับที่มีความหมายเช่น “น้อย”, “ปานกลาง”, “มาก” หรือ “แย่”, “พอใช้,”ดี“,”ดีมาก” และอาจจะมีการตั้งค่าเลขที่สองเท่ากัน, แต่ห่างกันในทางคุณภาพ
Ordinary Logistic Regression จะปรับพารามิเตอร์ของสมการเพื่อให้การเปลี่ยนแปลงในตัวแปรต้มสัมพันธ์กับความน่าจะเป็นในการตัดสินใจหรือกลุ่มที่ต่ำกว่า
สมการ Ordinal Logistic Regression สามารถเขียนได้เป็น:
\[\text{logit}(P(Y \leq j)) = \alpha_j - \beta_1X_1 - \beta_2X_2 - \ldots - \beta_pX_p\]
ที่:
\(P(Y \leq j)\) คือความน่าจะเป็นที่ตัวแปรตามจะอยู่ในกลุ่ม \(j\) หรือน้อยกว่าหรือเท่ากับ \(j\)
\(\alpha_j\) คือค่าคงที่สำหรับกลุ่ม (j)
\(\beta_1, \beta_2, \ldots, \beta_p\) คือพารามิเตอร์ที่ต้องปรับในการฝึกโมเดลสำหรับตัวแปรต้น \(X_1, X_2, \ldots, X_p\)
การปรับทำโดยใช้การสร้างความเข้าใจเกี่ยวกับลำดับของตัวแปรตามและตัวแปรตามที่เกี่ยวข้อง
ตัวอย่างข้อมูล “dat.xlsx”
ปัจจัยที่มีผลต่อการตัดสินใจว่าจะสมัครเข้าศึกษาโทหรือไม่(apply) นักศึกษาชั้นปีที่สามถูกถามว่าพวกเขาไม่น่าจะสมัคร (unlikely), มีโอกาสสมัครเล็กน้อย(likely)หรือมีโอกาสสมัครสูง(very likely)เข้าศึกษาโท. ดังนั้น, ตัวแปรตามที่เป็นผลลัพธ์มีสามหมวดหมู่. ข้อมูลเกี่ยวกับสถานะการศึกษาของพ่อแม่(pared), ว่าสถาบันการศึกษาในระดับปริญญาตรีเป็นของรัฐ(public)หรือเป็นของเอกชน(private), และเกรดเฉลี่ยปัจจุบันของนักศึกษาก็ถูกเก็บรวบรวม(gpa)
นักวิจัยมีเหตุผลเพื่อเชื่อว่า “ระยะห่าง”(distance) ระหว่างจุดทั้งสามนี้ไม่เท่ากัน. ตัวอย่างเช่น, “ระยะห่าง”(distance) ระหว่าง “ไม่น่าจะสมัคร”(unlikely) และ “มีโอกาสสมัครเล็กน้อย”(likely) อาจจะสั้นกว่า “ระยะห่าง”(distance) ระหว่าง “มีโอกาสสมัครเล็กน้อย”(likely) และ “มีโอกาสสมัครสูง”(very likely)
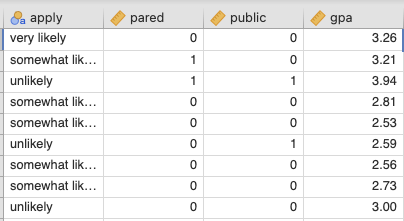
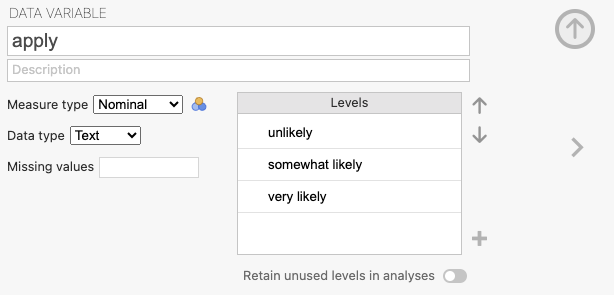
ขั้นที่ 1 โหลดข้อมูลเข้า jamovi และแปลงข้อมูล
ชุดข้อมูลที่สมมตินี้มีตัวแปร outcome ที่มีระดับสามระดับชื่อ apply โดยมีระดับ “unlikely”, “somewhat likely”, และ “very likely” ตามลำดับ. เราจะใช้ตัวแปรนี้เป็นตัวแปรตาม (outcome variable)
นอกจากนี้, มีตัวแปรทำนาย (predictor variables) ทั้งหมด 3 ตัว ได้แก่:
pared: เป็นตัวแปรแบบ 0/1 ที่ระบุว่าอย่างน้อยหนึ่งคู่ของพ่อแม่มีปริญญาโทหรือไม่
public: เป็นตัวแปรแบบ 0/1 โดยที่ 1 แทนสถานศึกษาระดับปริญญาตรีเป็นสาธารณะ และ 0 แทนสถานศึกษาเป็นส่วนตัว
gpa: เป็นเกรดเฉลี่ยของนักศึกษา
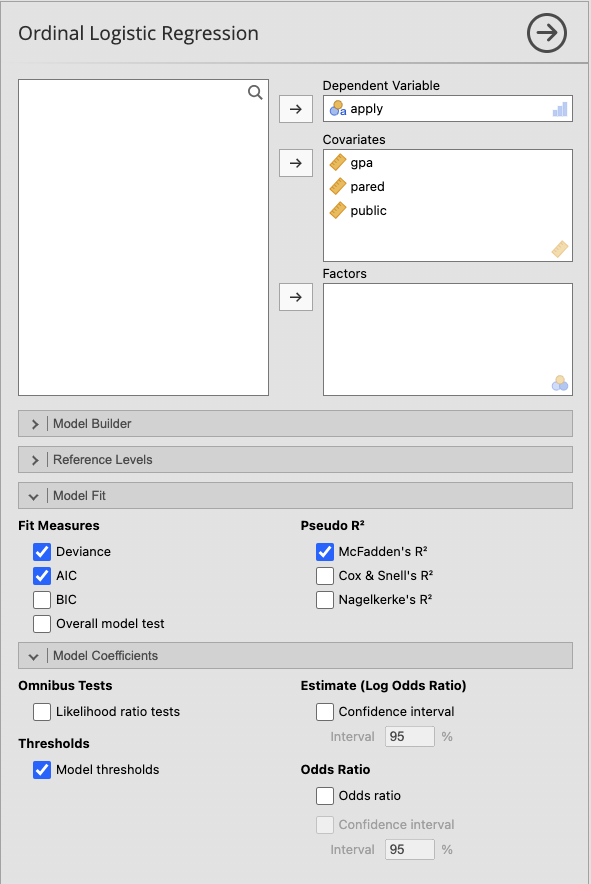
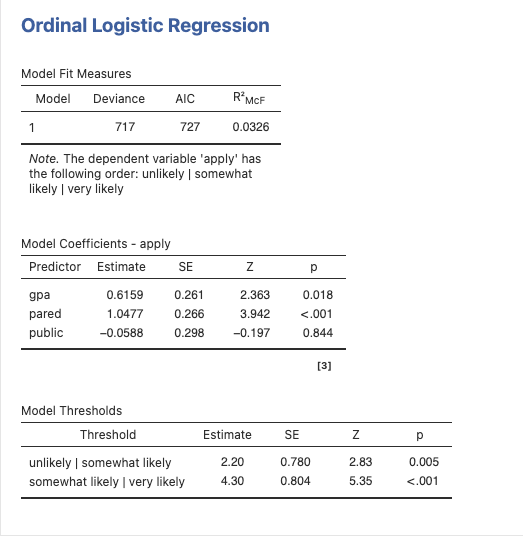
เมนู Ordinal Logistic regression
ผลการวิเคราะห์