| group | value |
|---|---|
| Group 1 | 10 |
| Group 1 | 12 |
| Group 1 | 14 |
| Group 1 | 15 |
| Group 1 | 11 |
| Group 1 | 13 |
| Group 1 | 16 |
| Group 1 | 18 |
| Group 1 | 19 |
| Group 1 | 17 |
| Group 2 | 8 |
| Group 2 | 9 |
| Group 2 | 11 |
| Group 2 | 10 |
| Group 2 | 12 |
| Group 2 | 10 |
| Group 2 | 13 |
| Group 2 | 14 |
| Group 2 | 15 |
| Group 2 | 12 |
3 เมนู T-Test
ผู้อ่านสามารถโหลดข้อมูลได้ google drive นี้
เมนูคือการทดสอบสมมุติของข้อมูลด้วย T-test ซึ่งเลือกได้ 3 แบบ คือ
Independent Sample T-Test
Paired Sample T-Test
One Sample T-Test
Independent Sample T-Test
Independent Sample T-Test เป็นวิธีทางสถิติที่ใช้เพื่อตรวจสอบความแตกต่างของค่าเฉลี่ยระหว่างกลุ่มที่อิสระ (independent groups) ซึ่งมีการวัดแต่ละกลุ่มโดยอิสระจากกัน หรือกล่าวได้ง่ายคือ กลุ่มหนึ่งไม่มีผลกระทบต่อกลุ่มอีกกลุ่มหนึ่งในการทดลอง
ทดสอบ T-Test สามารถนำมาใช้เพื่อตรวจสอบว่ามีความแตกต่างทางสถิติที่สำคัญ (statistically significant) ของค่าเฉลี่ยระหว่างกลุ่มทั้งสองหรือไม่ โดยพิจารณาค่า t-statistic และ p-value
ขั้นตอนในการดำเนินการ Independent Sample T-Test ได้แก่:
กำหนดสมมติฐาน (Hypothesis Setting): กำหนดสมมติฐานเกี่ยวกับความแตกต่างของค่าเฉลี่ยระหว่างกลุ่มทั้งสอง
สมมติฐานหลัก (Null Hypothesis, \(H_0\)): ค่าเฉลี่ยของกลุ่มทั้งสองเท่ากัน (ไม่มีความแตกต่าง).
สมมติฐานรอง (Alternative Hypothesis, \(H_1\)): ค่าเฉลี่ยของกลุ่มทั้งสองมีความแตกต่าง.
Collect Data: รวบรวมข้อมูลจากกลุ่มที่อิสระทั้งสอง และแบ่งข้อมูลเป็น 2 กลุ่ม
คำนวณ T-Statistic: ใช้ข้อมูลที่ได้รับเพื่อคำนวณค่า t-statistic ที่จำเป็น
คำนวณ P-Value: คำนวณค่า p-value เพื่อให้เราทราบถึงความน่าจะเป็นที่จะพบค่า t-statistic ที่ได้ โดยบรรจุค่าทางสถิติทั้งหมดที่เกิดขึ้น (หรือมีความแตกต่าง) และคำนวณพื้นที่ใต้ curve ของการแจกแจง t-distribution ที่อยู่ทางด้านท้ายของกราฟ
ตัดสินใจ: ตัดสินใจว่าจะปฏิเสธสมมติฐานต้นทางหรือไม่ โดยใช้ระดับนัยสำคัญ (significance level) ที่กำหนดไว้ (เช่น 0.05)
ถ้า p-value น้อยกว่าระดับนัยสำคัญที่กำหนดไว้, เราจะปฏิเสธสมมติฐานต้นทางและสรุปว่ามีความแตกต่างทางสถิติที่สำคัญระหว่างกลุ่มทั้งสอง ถ้า p-value มากกว่าระดับนัยสำคัญที่กำหนดไว้, เราจะไม่ปฏิเสธสมมติฐานต้นทางและสรุปว่าไม่มีหลักฐานในการแสดงถึงความแตกต่างทางสถิติ
วิธีการคำนวณ
สูตรการคำนวณ Independent Sample T-Test สำหรับคำนวณค่า t-statistic และ p-value จะแบ่งเป็นขั้นตอนต่าง ๆ ดังนี้:
คำนวณ Mean (ค่าเฉลี่ย):
- คำนวณค่าเฉลี่ย (mean) ของกลุ่มทั้งหมด และค่าเฉลี่ยของแต่ละกลุ่ม
คำนวณ Variance (ความแปรปรวน):
- คำนวณความแปรปรวน (variance) ของแต่ละกลุ่ม
คำนวณ Standard Error (ค่าคลาดเคลื่อนมาตรฐาน):
- ใช้ค่าเฉลี่ยและความแปรปรวนเพื่อคำนวณ standard error สำหรับแต่ละกลุ่ม
คำนวณ t-Statistic:
- ใช้ค่าเฉลี่ยของแต่ละกลุ่ม, ค่าคลาดเคลื่อนมาตรฐาน, และขนาดของกลุ่ม (sample size) เพื่อคำนวณ t-statistic ด้วยสูตร:
\[t = \frac{{\bar{X}_1 - \bar{X}_2}}{{\sqrt{\frac{{s_1^2}}{{n_1}} + \frac{{s_2^2}}{{n_2}}}}}\]
โดยที่
\(\bar{X}_1,~\bar{X}_2\) คือค่าเฉลี่ยของกลุ่มที่ 1 และกลุ่มที่ 2 ตามลำดับ, ( \(s_1^2,~s_2^2\) ) คือความแปรปรวนของกลุ่มที่ 1 และกลุ่มที่ 2 ตามลำดับ, และ ( \(n_1,~n_2\) ) คือขนาดของกลุ่มที่ 1 และกลุ่มที่ 2 ตามลำดับ.
คำนวณ Degrees of Freedom (องศาเสรี):
- ใช้ขนาดของกลุ่มทั้งสองเพื่อคำนวณ degrees of freedom ด้วยสูตร: \(df = n_1 + n_2 - 2\)
คำนวณ p-Value:
- ใช้ t-statistic และ degrees of freedom เพื่อคำนวณ p-value จากการดูค่า t ที่ได้ในตาราง t-distribution
นอกจากนี้, เรายังต้องกำหนดระดับนัยสำคัญ (significance level) ที่จะใช้ในการตัดสินใจว่าจะปฏิเสธหรือไม่ปฏิเสธสมมติฐานต้นทาง. ตัวอย่างระดับนัยสำคัญที่ใช้บ่อยคือ 0.05 ถ้า p-value น้อยกว่าระดับนัยสำคัญที่กำหนด, เราจะปฏิเสธสมมติฐานต้นทางและสรุปว่ามีความแตกต่างทางสถิติ
ตัวอย่างการคำนวณ
นี่คือตัวอย่างข้อมูลสำหรับการทดสอบ Independent Sample T-Test:
กลุ่มที่ 1 (Group 1): [ 10, 12, 14, 15, 11, 13, 16, 18, 19, 17 ]
กลุ่มที่ 2 (Group 2): [ 8, 9, 11, 10, 12, 10, 13, 14, 15, 12 ]
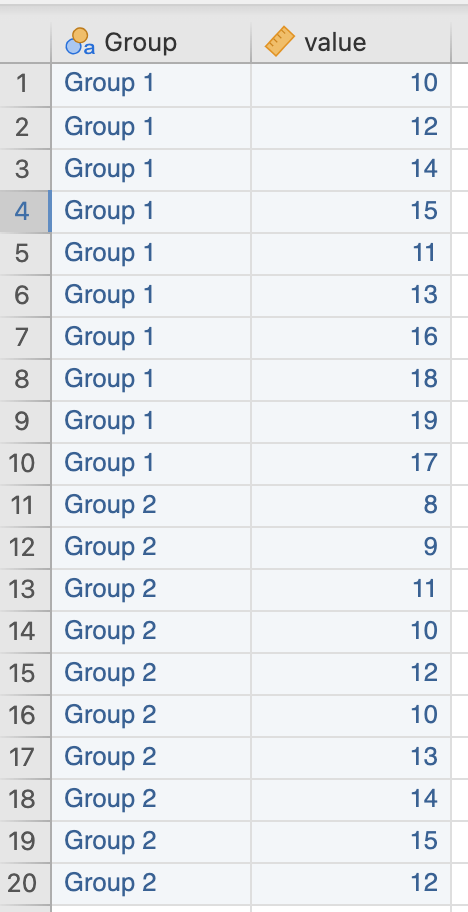
จะต้องสร้างตารางข้อมูลที่ถูกต้องเพื่อนำไปใส่โปรแกรม jamovi คือ
เมื่อนำไปใส่ jamovi และเลือกประเภทข้อมูลให้ถูกต้องจะได้
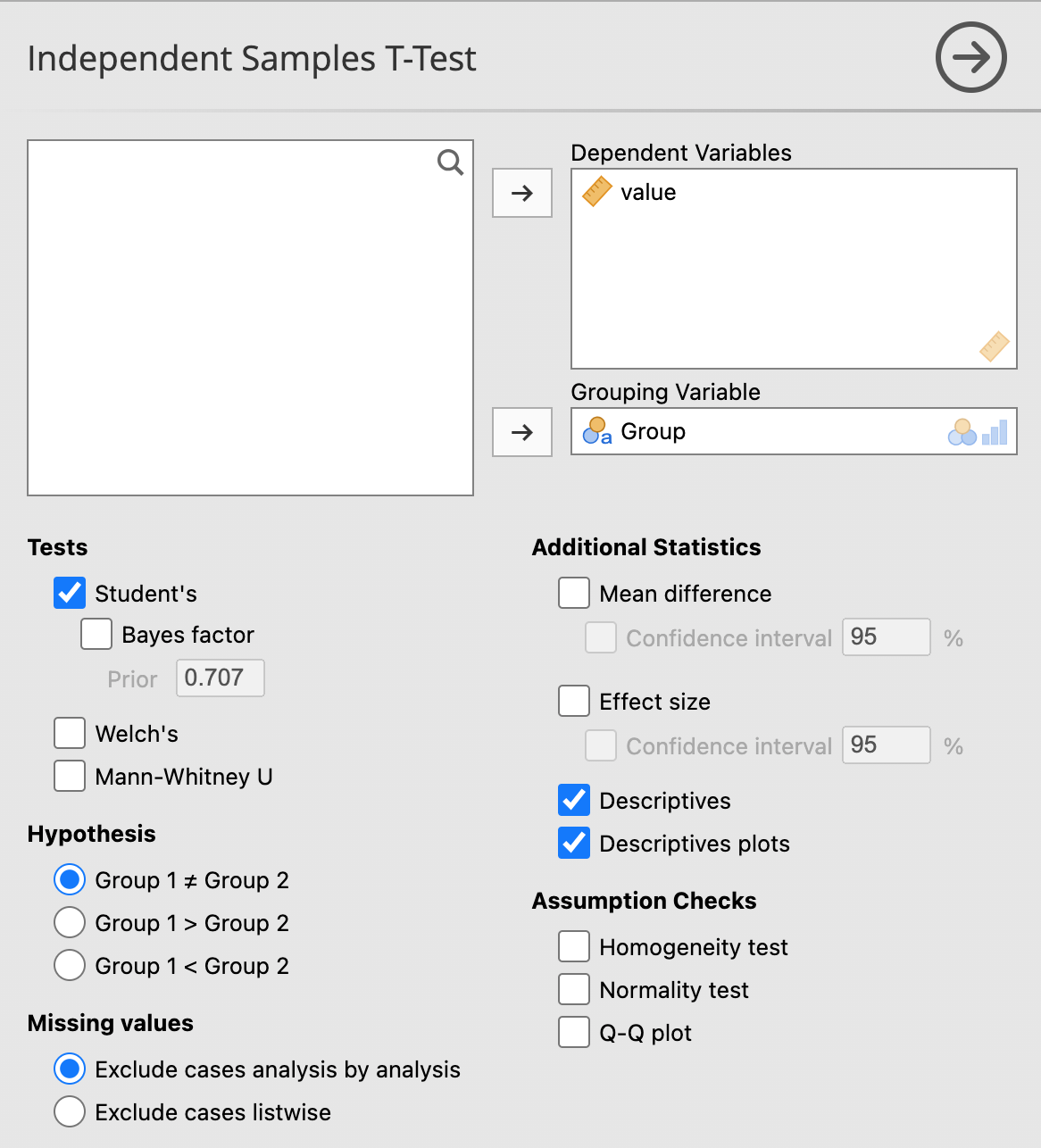
และเมื่อเลือกเมนู Independent Sample T-Test ตามภาพ
ผู้ใช้งานสามารถเลือกการทดสอบที่ต้อง และการตรวจสอบสมมุติฐานของข้อมูล การคำนวณค่าค่าเฉลี่ยและความแปรปรวนของตัวอย่าง กราฟแสดงความแตกต่างของค่าเฉลี่ยและช่วงความเชื่อมั่นได้
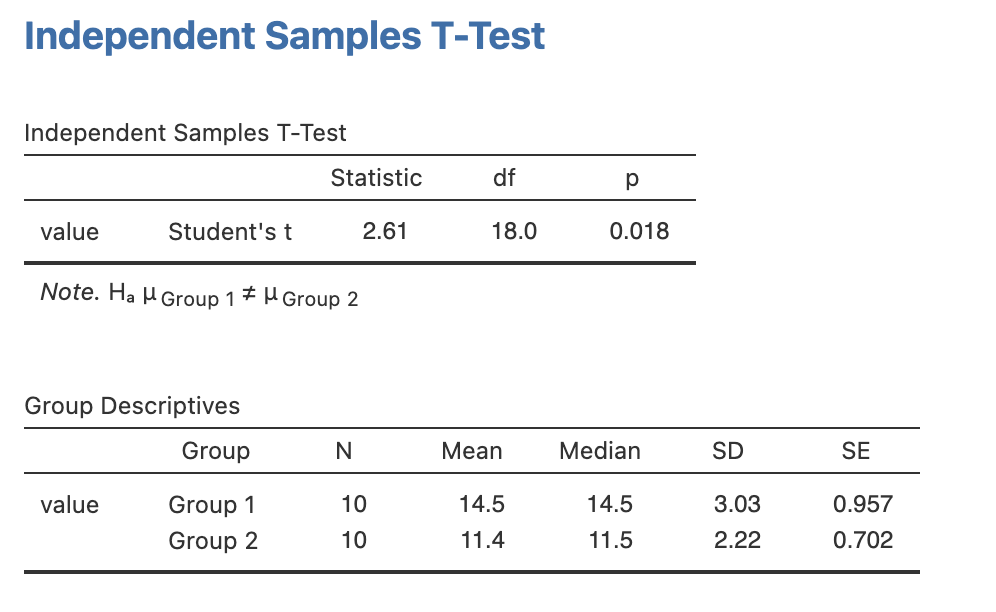
จากผลการทดสอบ Independent Sample T-Test พบที่ระดับนัยยะสำคัญ 0.05 ค่าเฉลี่ยระหว่าง group 1 และ group 2 มีความแตกต่างกันอย่างมีนัยยะสำคัญยิ่ง ก็คือการยอมรับสมมุติฐานรองนั่นเอง
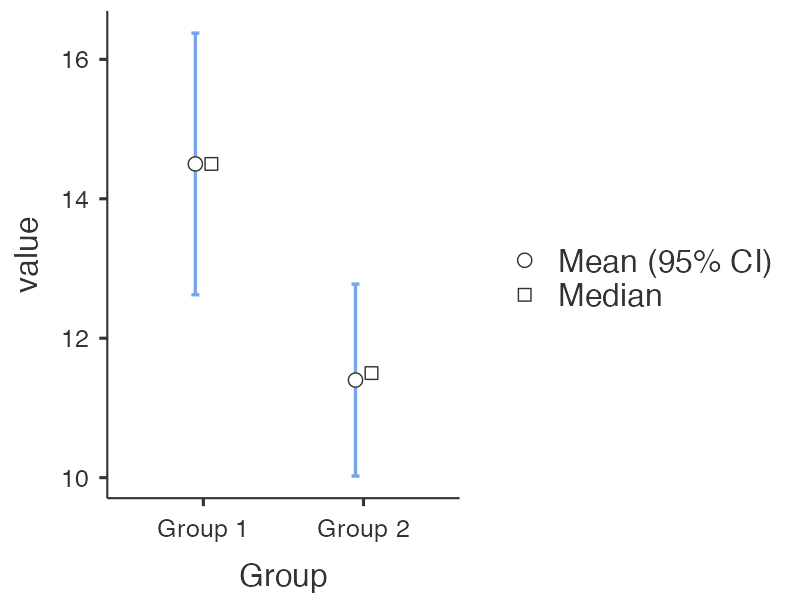
และสามารถแสดงได้โดยกราฟ
3.1 Paired Sample T-Test
Paired Sample T-Test เป็นวิธีทางสถิติที่ใช้เพื่อตรวจสอบความแตกต่างของค่าเฉลี่ยระหว่างคู่ของกลุ่มที่มีความเกี่ยวข้อง (paired or matched groups) คู่ของตัวอย่างนี้หมายถึงการที่มีการวัดข้อมูลในกลุ่มที่หนึ่งและกลุ่มที่สองจากสมาชิกที่เหมือนกันหรือจากวัดตัวแปรเดียวกันในหนึ่งขณะที่เปลี่ยนแปลงเงื่อนไข
วิธีการดำเนินการ Paired Sample T-Test มีขั้นตอนหลัก ๆ ดังนี้:
กำหนดสมมติฐาน (Hypothesis Setting): กำหนดสมมติฐานเกี่ยวกับความแตกต่างของค่าเฉลี่ยระหว่างคู่ของกลุ่ม
สมมติฐานหลัก (Null Hypothesis, \(H_0\)): ค่าเฉลี่ยของคู่ของกลุ่มเท่ากัน (ไม่มีความแตกต่าง)
สมมติฐานรอง (Alternative Hypothesis, \(H_1\)): ค่าเฉลี่ยของคู่ของกลุ่มมีความแตกต่าง
Collect Data: รวบรวมข้อมูลจากคู่ของกลุ่มที่มีความเกี่ยวข้อง
คำนวณ Mean Difference (ความแตกต่างของค่าเฉลี่ย):
- คำนวณค่าเฉลี่ยของความแตกต่างระหว่างคู่ของกลุ่ม
คำนวณ Standard Deviation of Differences (ส่วนเบี่ยงเบนของความแตกต่าง):
- คำนวณส่วนเบี่ยงเบนของความแตกต่างระหว่างคู่ของกลุ่ม.
คำนวณ t-Statistic:
- ใช้ค่าเฉลี่ยของความแตกต่างระหว่างคู่ของกลุ่มและส่วนเบี่ยงเบนของความแตกต่างเพื่อคำนวณ t-statistic ด้วยสูตร:
\[t = \frac{{\bar{D}}}{{SD / \sqrt{n}}}\]
โดยที่ \(\bar{D}\) คือค่าเฉลี่ยของความแตกต่าง, \(SD\) คือส่วนเบี่ยงเบนของความแตกต่าง, และ \(n\) คือขนาดของกลุ่มคู่ของ
คำนวณ Degrees of Freedom (องศาเสรี):
- ใช้ขนาดของกลุ่มคู่ของเพื่อคำนวณ degrees of freedom ด้วยสูตร: \(df = n - 1\)
คำนวณ p-Value:
- ใช้ t-statistic และ degrees of freedom เพื่อคำนวณ p-value จากการดูค่า t ที่ได้ในตาราง t-distribution.
ตัดสินใจ:
- ตัดสินใจว่าจะปฏิเสธหรือไม่ปฏิเสธสมมติฐานต้นทาง, โดยใช้ระดับนัยสำคัญที่กำหนดไว้ (เช่น 0.05)
ตัวอย่างการคำนวณ
ข้อมูลจากกลุ่มที่ 1 (ก่อนทำการรักษา): [ 15, 18, 20, 22, 25, 17, 19, 21, 23, 16 ]
ข้อมูลจากกลุ่มที่ 2 (หลังทำการรักษา): [ 13, 16, 18, 20, 21, 19, 22, 24, 26, 17 ]
ต่อไปนี้คือขั้นตอนการคำนวณ:
กำหนดสมมติฐาน:
\(H_0\): ค่าเฉลี่ยของความแตกต่างระหว่างกลุ่มที่ 1 และ 2 เท่ากัน (ไม่มีความแตกต่าง)
\(H_1\): ค่าเฉลี่ยของความแตกต่างระหว่างกลุ่มที่ 1 และ 2 มีความแตกต่าง (มีความแตกต่าง)
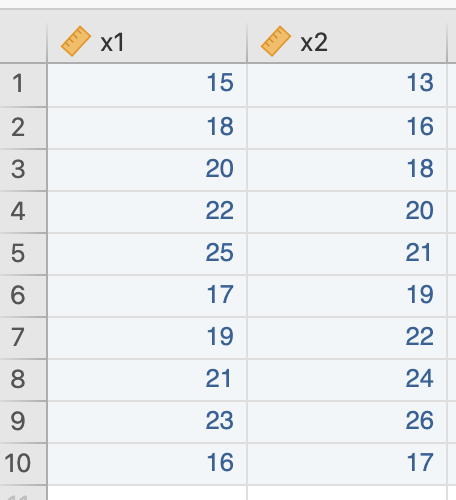
นำข้อมูลใส่ตารางให้ถูกต้อง
| x1 | x2 |
|---|---|
| 15 | 13 |
| 18 | 16 |
| 20 | 18 |
| 22 | 20 |
| 25 | 21 |
| 17 | 19 |
| 19 | 22 |
| 21 | 24 |
| 23 | 26 |
| 16 | 17 |
- นำตารางเข้าวิเคราะห์ด้วย jamovi
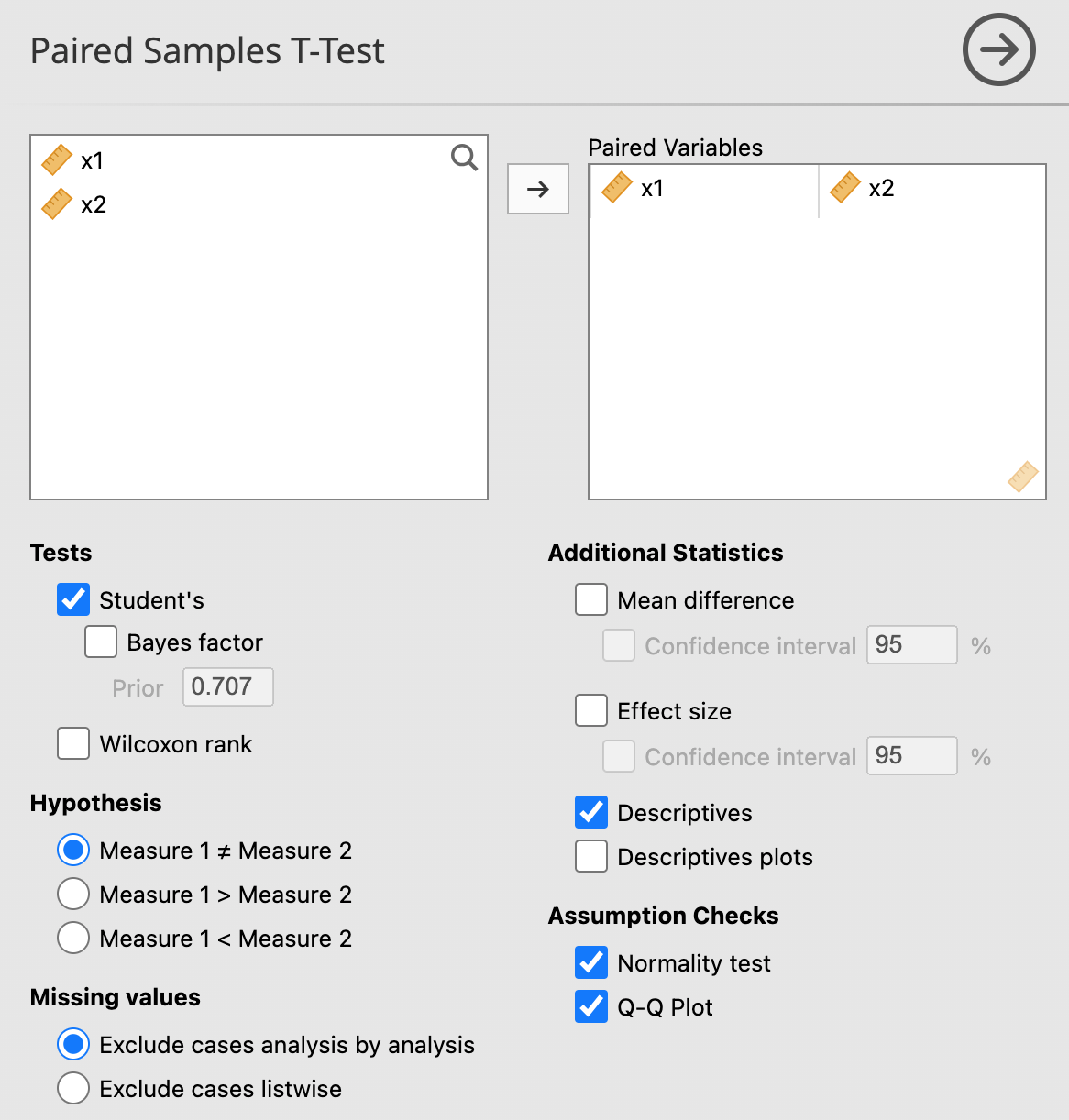
ทำการวิเคราะห์ด้วยเมนู Analyse และเลือก Paired Sample T-Test จะได้ดังภาพข้างล่าง
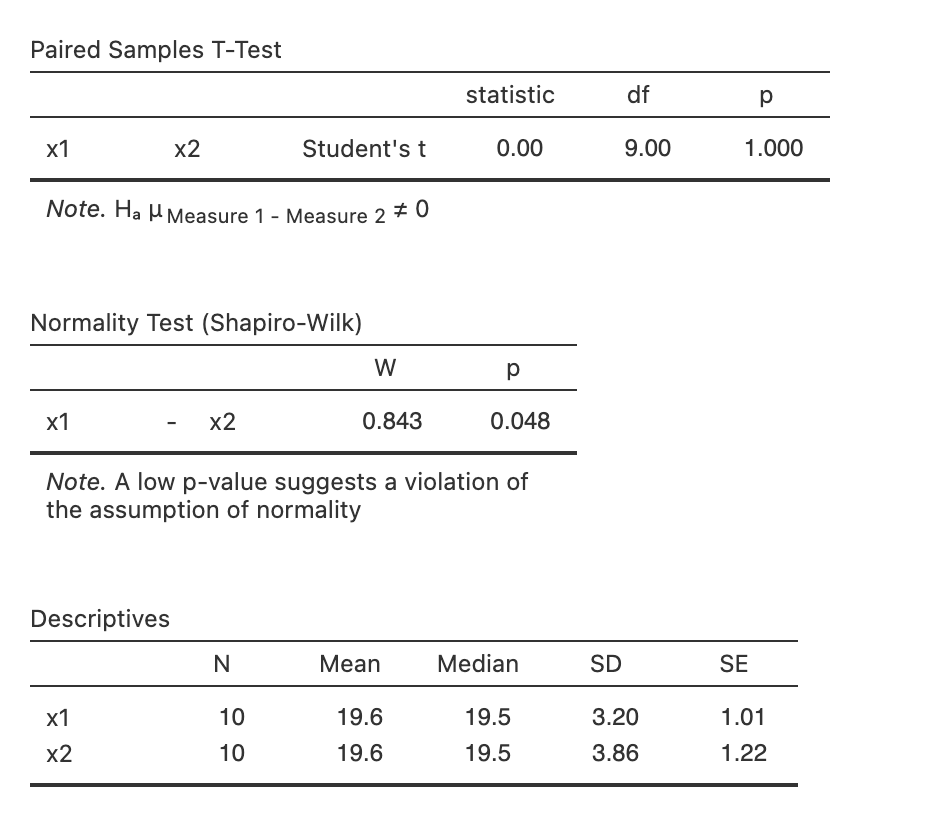
ผลการทดสอบที่ได้
จากตาราง Paired Sample T-Test พบว่าค่าเฉลี่ยนของทั้งสองกลุ่มไม่ต่างกัน ด้วยค่า P-value เข้าใกล้ 1 นั่นก็คือการยอมรับสมมุติฐานหลักนั่นเอง
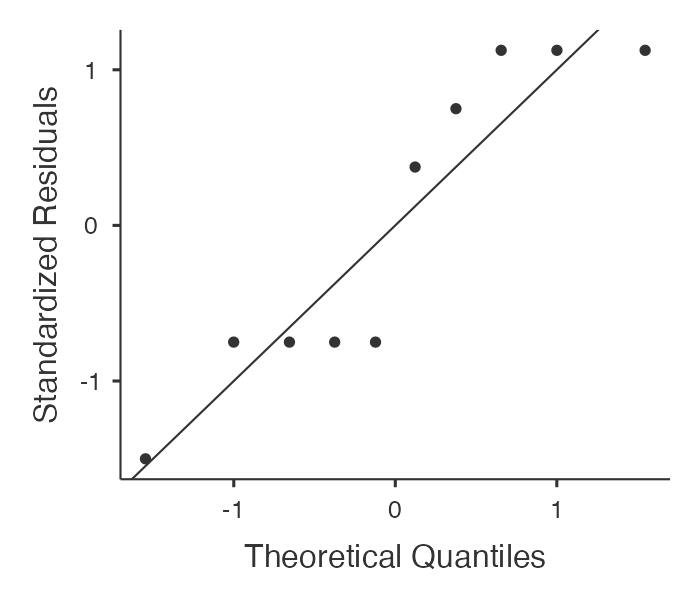
จากตาราง Normality Test (Shapiro Wilk) ยอมรับผลต่างของค่าเฉลี่ยไม่ใช่การแจกแจงแบบปกติ ด้วยค่า P-value เท่ากับ .048 น้อยกว่า .05
จากตาราง Descriptives แสดงว่าสถิติพรรณาของตัวแปร \(x_1\) และ ตัวแปร \(x_2\)
3.2 One Sample T-Test
One Sample T-Test เป็นวิธีทางสถิติที่ใช้เพื่อตรวจสอบว่าค่าเฉลี่ยของกลุ่มหนึ่งมีความแตกต่างจากค่าที่คาดหวังหรือไม่ โดยใช้การทดสอบ t-statistic. วิธีนี้มักถูกใช้เมื่อคุณมีข้อมูลจากกลุ่มเดียวและต้องการตรวจสอบว่าค่าเฉลี่ยของกลุ่มนี้มีความแตกต่างจากค่าที่คาดหวัง (hypothesized mean) หรือไม่?
ขั้นตอนในการดำเนินการ One Sample T-Test ประกอบด้วย:
กำหนดสมมติฐาน (Hypothesis Setting):
สมมติฐานหลัก (Null Hypothesis, \(H_0\)): ค่าเฉลี่ยของกลุ่มเท่ากับค่าที่คาดหวัง
สมมติฐานรอง (Alternative Hypothesis, \(H_1\)):ค่าเฉลี่ยของกลุ่มมีความแตกต่างจากค่าที่คาดหวัง
Collect Data: รวบรวมข้อมูลจากกลุ่มที่ต้องการทดสอบ
คำนวณ Mean (ค่าเฉลี่ย):
- คำนวณค่าเฉลี่ยของกลุ่มที่ต้องการทดสอบ
คำนวณ Standard Deviation (ส่วนเบี่ยงเบนมาตรฐาน):
- คำนวณส่วนเบี่ยงเบนมาตรฐานของกลุ่มที่ต้องการทดสอบ
คำนวณ t-Statistic:
- ใช้ค่าเฉลี่ยของกลุ่ม, ค่าที่คาดหวัง, ส่วนเบี่ยงเบนมาตรฐาน, และขนาดของกลุ่ม (sample size) เพื่อคำนวณ t-statistic ด้วยสูตร:
\[ t = \frac{{\bar{X} - \mu}}{{SD / \sqrt{n}}} \]
โดยที่ \(\bar{X}\) คือค่าเฉลี่ยของกลุ่ม, \(\mu\) คือค่าที่คาดหวัง, \(SD\) คือส่วนเบี่ยงเบนมาตรฐานของกลุ่ม, และ \(n\) คือขนาดของกลุ่ม.
คำนวณ Degrees of Freedom (องศาเสรี):
- ใช้ขนาดของกลุ่มเพื่อคำนวณ degrees of freedom ด้วยสูตร: \(df = n - 1\)
คำนวณ p-Value:
- ใช้ t-statistic และ degrees of freedom เพื่อคำนวณ p-value จากการดูค่า t ที่ได้ในตาราง t-distribution
ตัดสินใจ:
- ตัดสินใจว่าจะปฏิเสธหรือไม่ปฏิเสธสมมติฐานต้นทาง, โดยใช้ระดับนัยสำคัญที่กำหนดไว้ (เช่น 0.05)
ถ้า p-value น้อยกว่าระดับนัยสำคัญที่กำหนด, เราจะปฏิเสธสมมติฐานต้นทางและสรุปว่ามีความแตกต่างทางสถิติ. ถ้า p-value มากกว่าระดับนัยสำคัญที่กำหนด, เราจะไม่ปฏิเสธสมมติฐานต้นทางและสรุปว่าไม่มีหลักฐานในการแสดงถึงความแตกต่างทางสถิติ.
ตัวอย่างการคำนวณOne Sample T-Test ด้วยตัวอย่างข้อมูลดังนี้
ข้อมูล:
\[ X = [18,~22,~25,~19,~21,~23,~16,~20,~24,~17] \] ขั้นที่ 1 ตั้งสมมมุติฐาน
สมมติฐาน:
$ H_0: = 20$ (ค่าเฉลี่ยของกลุ่มเท่ากับ 20)
$ H_1: $ (ค่าเฉลี่ยของกลุ่มไม่เท่ากับ 20)
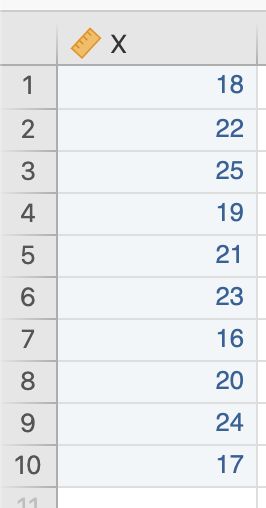
ขั้นที่ 2 สร้างตารางข้อมูลให้ถูกต้องเพื่อนำไปใส่ในโปรแกรม jamovi
| X |
|---|
| 18 |
| 22 |
| 25 |
| 19 |
| 21 |
| 23 |
| 16 |
| 20 |
| 24 |
| 17 |
ขั้นที่ 3 ใส่ตารางข้อมูลลงไปใน jamovi
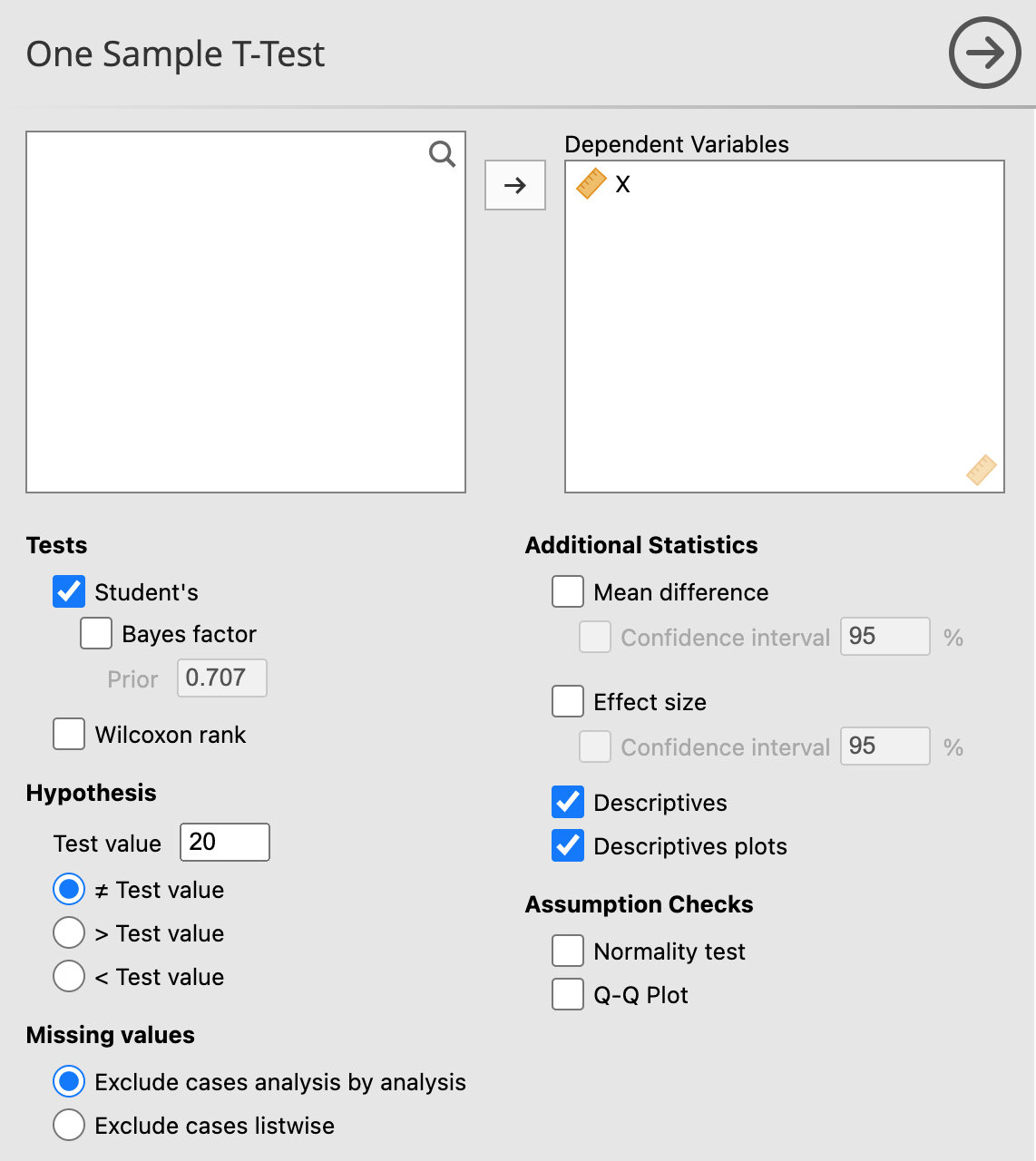
ขั้นที่ 4 เลือกเมนู One Sample T-Test และเลือกและกรอกตัวเลขตามภาพจะได้
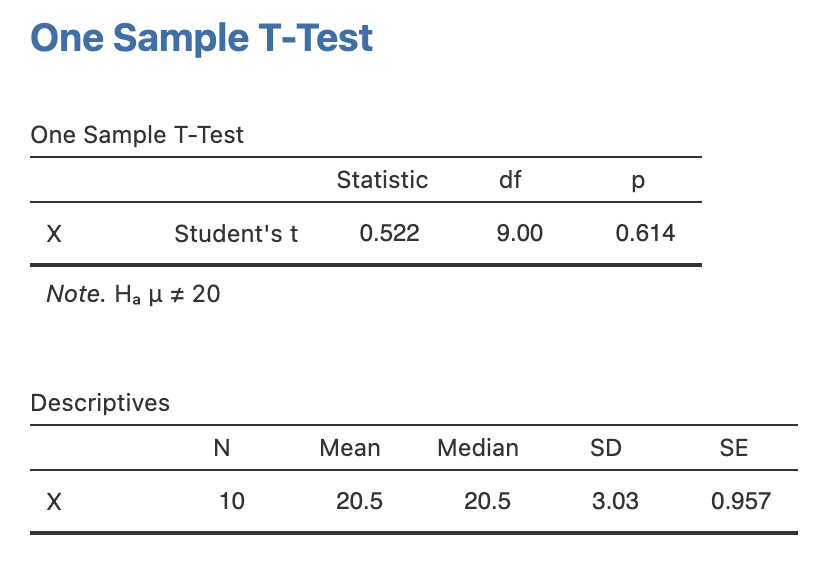
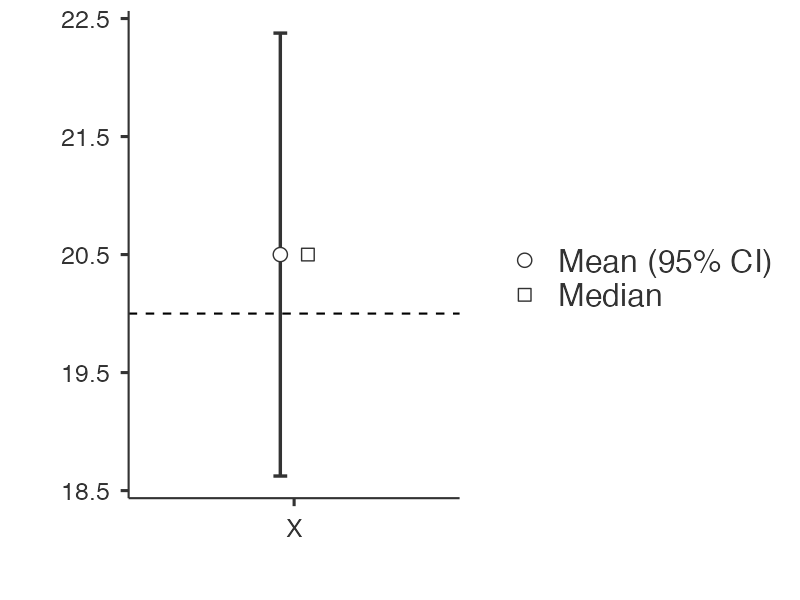
ผลลัพธ์การคำนวณ
จากตาราง One Sample T-Test พบว่าการยอมรับสมมุติที่บอกว่า ค่าเฉลี่ยของข้อมูลชุดนี้มีค่าเท่ากับ 20 เนื่องจากมีค่า P-value มากกว่า 0.05 นั้นคือยอมรับสมมุติฐานหลัก
ตาราง Descriptive เป็นการแสดงว่าสถิติพรรณาของตัวแปร \(X\)