6  เมนู Frequencies

ผู้อ่านสามารถโหลดข้อมูลได้ google drive นี้

เมนู Frequencies

6.1 One Sample Propotion Tests

One Sample Proportion Test เป็นวิธีการทางสถิติที่ใช้ในการทดสอบว่าสัดส่วนของความสำเร็จในการเกิดขึ้นของเหตุการณ์หนึ่ง ๆ ในกลุ่มหนึ่งมีค่าเท่ากับค่าที่กำหนดหรือไม่ ในทางปฏิบัติแล้ว มักจะใช้ในการทดสอบสัดส่วนของการเป็นโรค หรือการเป็นสิ่งที่ต้องการในกลุ่มของประชากรหนึ่ง ๆ

วิธีการนี้ใช้การทดสอบสมมติฐานว่าสัดส่วนของสิ่งที่สนใจในกลุ่มนั้นมีค่าเท่ากับค่าที่ระบุ (ซึ่งเรียกว่าค่าสัดส่วนที่กำหนด) หรือไม่ โดยใช้ข้อมูลจากกลุ่มที่สนใจและสร้างสมมติฐานเกี่ยวกับค่าพารามิเตอร์ของประชากร และทดสอบสมมติฐานนั้นด้วยการใช้สถิติทดสอบที่เหมาะสม เช่น Z-test หรือ t-test ตามกรณีการทดสอบ

วิธีการนี้มักจะใช้ในการตรวจสอบว่าสัดส่วนของกลุ่มหนึ่งมีค่าเท่ากับค่าที่คาดหวังหรือไม่ เช่น การทดสอบว่าสัดส่วนของผู้ป่วยที่หายจากโรคหลังได้รับการรักษามีค่าเท่ากับ 80% หรือไม่ หรือการทดสอบว่าสัดส่วนของผู้บริโภคที่มีความพึงพอใจในผลิตภัณฑ์หนึ่ง ๆ มีค่าเท่ากับ 70% หรือไม่ การทดสอบนี้ช่วยให้เราสามารถทำสรุปเกี่ยวกับสัดส่วนในประชากรรวมได้อย่างมั่นใจได้มากขึ้นโดยใช้ข้อมูลตัวอย่างจำนวนจำกัดที่มีอยู่ในกรณีนั้น ๆ อย่างไรก็ตาม เราต้องระมัดระวังในการใช้และการทำอ้างอิงตามผลการทดสอบนี้เนื่องจากมีข้อจำกัดและเงื่อนไขในการใช้งานที่ต้องคำนึงถึงด้วย

6.1.1 2 Outcomes: Binomial test

นั่นมาแสดงตัวอย่างการใช้ One Sample Proportion Test ในการทดสอบสมมติฐานว่าสัดส่วนของการเป็นโรคซึ่งมีการรักษาแล้วหายมีค่าเท่ากับ 0.8 ในประชากรทั่วไปหรือไม่ โดยมีข้อมูลตัวอย่างจากการสำรวจผู้ป่วย 200 คนที่ได้รับการรักษาและหายจากโรค 150 คน และต้องการทดสอบสมมติฐานด้วยระดับนัยสำคัญ \(\alpha= 0.05\)

1. กำหนดสมมติฐาน:
   • \(H_0\) (สมมติฐานปลอม): สัดส่วนของการหายจากโรคหลังได้รับการรักษามีค่าเท่ากับ 0.8
   • \(H_1\) (สมมติฐานที่จะทดสอบ): สัดส่วนของการหายจากโรคหลังได้รับการรักษาไม่ได้มีค่าเท่ากับ 0.8
2. คำนวณสถิติทดสอบ:
   • สูตรสำหรับคำนวณสถิติทดสอบคือ:\(Z = \frac{(p - p_0)}{\sqrt{\frac{p_0(1-p_0)}{n}}}\)
   • ที่ \(p\) คือ สัดส่วนของการหายจากโรคในตัวอย่าง, \(p_0\) คือ สัดส่วนที่กำหนดในสมมติฐานปลอม, และ \(n\) คือ ขนาดของตัวอย่าง
   • จากข้อมูลที่กำหนดไว้: \(p = \frac{150}{200} = 0.75\), \(p_0= 0.8\), \(n = 200\)
   • นำข้อมูลนี้มาคำนวณจะได้ \(Z\)
3. ตัดสินใจ:
   • ใช้ค่า \(Z\) ที่คำนวณได้ มาเปรียบเทียบกับค่าคริทิคอลที่มีความสำคัญทางสถิติ \(Z\_{\alpha/2}\) ที่มีค่า สำหรับ \(\alpha = 0.05\) จะได้ประมาณ 1.96
   • ถ้า \(Z\) ที่คำนวณได้มากกว่า 1.96 หรือน้อยกว่า -1.96 จะปฏิเสธสมมติฐานปลอม \(H_0\), มีข้อความว่า สัดส่วนของการหายจากโรคหลังได้รับการรักษาไม่ได้มีค่าเท่ากับ 0.8
   • ถ้า \(Z\) ที่คำนวณได้ไม่เกิน 1.96 และไม่น้อยกว่า -1.96 จะไม่ปฏิเสธสมมติฐานปลอม \(H_0\), มีข้อความว่า สัดส่วนของการหายจากโรคหลังได้รับการรักษามีค่าเท่ากับ 0.8

ลองมาคำนวณสถิติทดสอบ $ Z $:

\[Z = \frac{(0.75 - 0.8)}{\sqrt{\frac{0.8(1-0.8)}{200}}}\approx -1.768\]

จะเห็นได้ว่าค่า \(Z\) ที่คำนวณได้ (-1.768) ไม่มากกว่า 1.96 และไม่น้อยกว่า -1.96 ดังนั้น เราจะไม่ปฏิเสธสมมติฐานปลอม \(H_0\) นั่นคือ สัดส่วนของการหายจากโรคหลังได้รับการรักษามีค่าเท่ากับ 0.8 ที่ระดับนัยสำคัญ 0.05 และสรุปได้ว่าไม่มีข้อมูลเพียงพอที่จะสนับสนุนการปฏิเสธสมมติฐานปลอมดังกล่าว.

sample_data
   fail success 
     50     150 

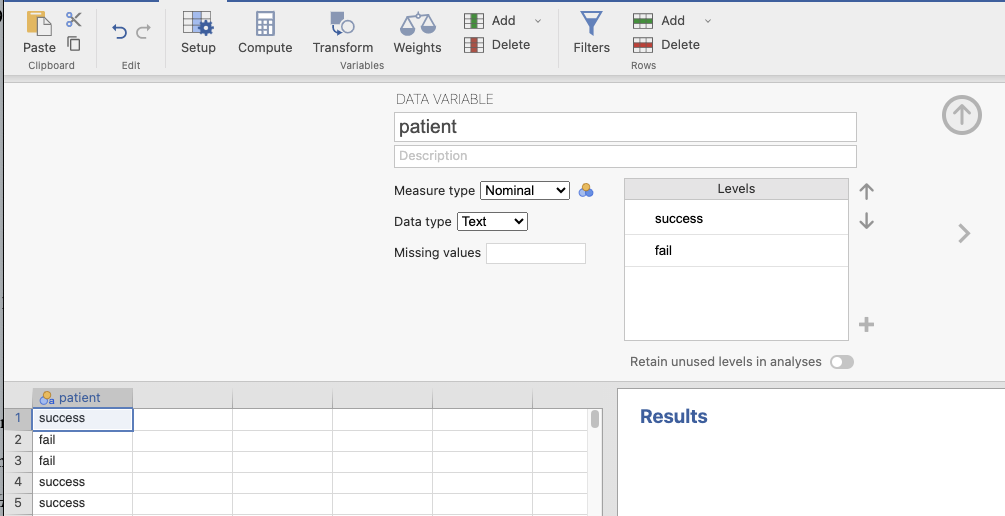
ขั้นที่ 1 นำข้อมูล one_sample_prop_test.xlsx เข้าสู่โปรแกรม Jamovi และกำหนดค่าดังนี้

จัดลำดับข้อมูล

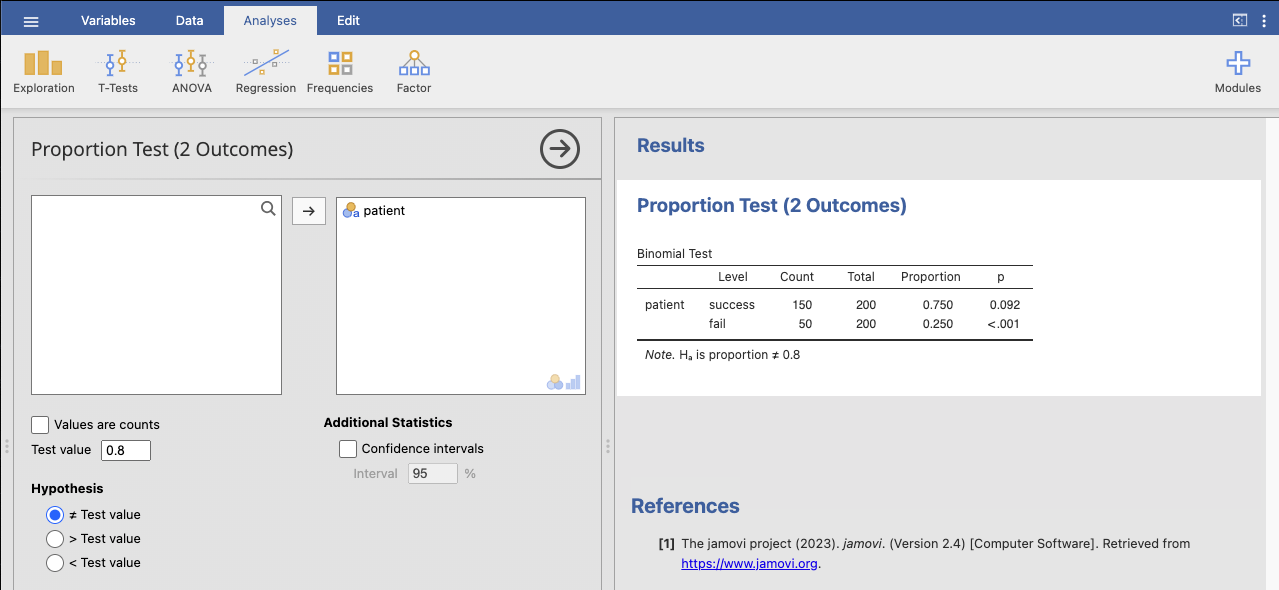
ขั้นที่2 เลือกเมนู Analyses \(\rightarrow\) Frequencies \(\rightarrow\) 2 Outcomes Binomial test และกำหนด

ค่าตามภาพ จะได้ผลลัพธ์ดังนี้

ทางซ้าย: การกำหนดค่า ทางขวา: ผลลัพธ์

6.1.2 N outcomes: \(\chi^2\) goodness of fit

Goodness of Fit Test (การทดสอบความเหมาะสมของข้อมูล) เป็นวิธีการทางสถิติที่ใช้ในการตรวจสอบว่าข้อมูลที่มีอยู่สอดคล้องกับการกระจายที่กำหนดหรือไม่ โดยส่วนใหญ่จะใช้กับข้อมูลที่แบ่งออกเป็นกลุ่มหรือคลาสต่าง ๆ เพื่อดูว่าความถี่ของข้อมูลในแต่ละกลุ่มมีความสอดคล้องกับการคาดการณ์หรือไม่

การทดสอบความเหมาะสมด้วย Goodness of Fit Test มักใช้ทำนายหรือตรวจสอบว่าค่าที่เรามีอยู่มาจากการกระจายที่รู้จักหรือไม่ ตัวอย่างเช่น การทดสอบว่าความถี่ของการโหวตในการเลือกตั้งสามารถเป็นไปตามการกระจายของคาดการณ์หรือไม่ หรือการทดสอบว่าส่วนแบ่งของผู้ติดเชื้อโรคในประชากรมีความเหมาะสมกับอัตราส่วนที่คาดหวังหรือไม่

วิธีการทดสอบสมมติฐานในการทดสอบความเหมาะสมนี้ มักจะใช้ Chi-Square Test (ทดสอบความสัมพันธ์ของตารางความถี่) โดยทดสอบว่าความถี่ที่ม observed มีความแตกต่างกับความถี่ที่คาดหวังหรือไม่ การทดสอบนี้ใช้วิธีการเปรียบเทียบค่าที่มาจากการสร้างตารางความถี่จริง ๆ กับค่าที่คาดหวัง โดยใช้สถิติจากการกระจายของที่เฉพาะจำนวนระดับความอิสระที่มีในตารางนั้น ๆ การทดสอบนี้มักใช้ในการทดสอบความเหมาะสมของการเข้ากันได้กับการกระจายที่คาดหวังในการสำรวจปรากฎการณ์ในข้อมูล ถ้าค่าสถิติที่คำนวณได้มากกว่าค่าวิกฤติที่กำหนดล่วงหน้า ซึ่งมักเป็นค่าที่มีการจำกัดในการอนุมานที่ระดับนัยสำคัญที่ 5% จะทำให้ปฏิเสธสมมติฐานว่าข้อมูลไม่เหมาะสมกับการกระจายที่คาดหวัง

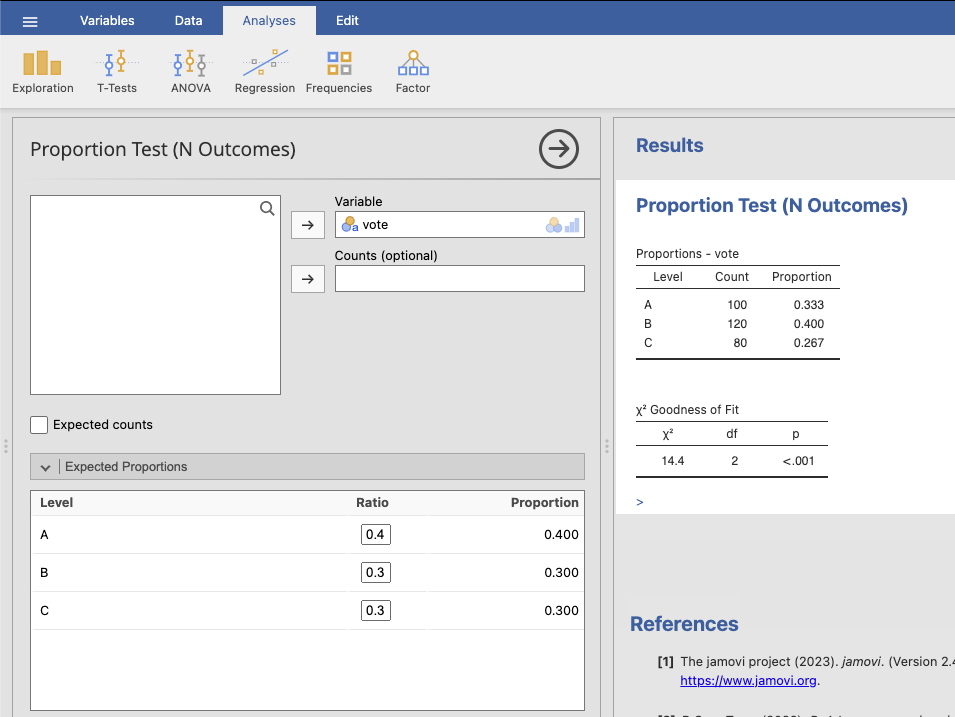
สมมติว่าเรามีข้อมูลตัวอย่างเกี่ยวกับการโหวตในการเลือกตั้ง โดยมีคาดการณ์ว่าสัดส่วนของการโหวตสำหรับพรรค A, B, และ C คือ 0.4, 0.3, และ 0.3 ตามลำดับ และเราได้รับข้อมูลตัวอย่างจากผู้โหวต 300 คน และพบว่าจำนวนผู้โหวตสำหรับแต่ละพรรคเป็นดังนี้:

• พรรค A: 100 คน
• พรรค B: 120 คน
• พรรค C: 80 คน

เราจะทดสอบว่าการโหวตมีความเหมาะสมกับคาดการณ์หรือไม่

1. คำนวณคาดการณ์สัดส่วนของการโหวตสำหรับแต่ละพรรค:

\[\text{Expected counts} = \text{สัดส่วนที่คาดหวัง} \times \text{จำนวนตัวอย่างทั้งหมด}\]

\(\text{Expected count for A} = 0.4 \times 300 = 120\)

\(\text{Expected count for B} = 0.3 \times 300 = 90\)

\(\text{Expected count for C} = 0.3 \times 300 = 90\)

2. ทำการคำนวณค่าสถิติทดสอบ Chi-Square:

\[\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}\]

โดยที่ $ O_i $ คือจำนวนที่สังเกตเจอจริง, $ E_i $ คือจำนวนที่คาดหวัง

\(\chi^2 = \frac{(100 - 120)^2}{120} + \frac{(120 - 90)^2}{90} + \frac{(80 - 90)^2}{90}\)

\(\chi^2 ≈ 14.444\)

3. คำนวณดีกรีเสรีของ Chi-Square Test:

\(df = (\text{จำนวนกลุ่ม} - 1) = (3 - 1) = 2\)

4. ดัดแปลงค่า p-value:

จากการคำนวณได้ \(\chi^2 ≈ 14.444\) ที่ดีกรีเสรี \(df = 2\) ดังนั้น ค่า p-value จะได้จากการค้นหาค่าที่มากกว่า 14.444 ในการทดสอบ Chi-Square Distribution ที่มีดีกรีเสรี 2

5. สรุปผล:

ถ้าค่า p-value มีค่าน้อยกว่าระดับนัยสำคัญที่กำหนด (เช่น 0.05) เราจะปฏิเสธสมมติฐานว่าข้อมูลไม่เหมาะสมกับคาดการณ์ที่กำหนดไว้ ในที่นี้เราควรจะปฏิเสธสมมติฐานว่าการโหวตไม่เหมาะสมกับคาดการณ์ที่กำหนดไว้

การคำนนวณด้วย Jamovi

ขั้นที่ 1 นำเข้าไฟล์ chi2_test.xlsx เข้าสู่ Jamovi

เนื่องจากข้อมูลเรียงลำดับตามตัวอักษร A B C จึงไม่ต้องเปลี่ยนแปลงข้อมูล

ขั้นที่ 2 ขั้นที่2 เลือกเมนู Analyses \(\rightarrow\) Frequencies \(\rightarrow\) N Outcomes \(\chi^2\) test และกำหนดค่าตามภาพ จะได้ผลลัพธ์ดังนี้

ทางซ้าย: การกำหนดค่าเพื่อทดสอบ ทางขวา: ผลการทดสอบ

6.1.3 Independent Samples Chi-Square Test of Association

เป็นการทดสอบความสัมพันธ์ระหว่างตัวแปรสองตัวที่เป็นแบบจำนวนนับ (categorical variables) โดยมีการจัดกลุ่มข้อมูลเป็นตารางความถี่ (contingency table) ซึ่งใช้วิธีการทดสอบความสัมพันธ์โดยใช้ค่าสถิติที่เรียกว่า Chi-Square (χ²)

โดยทั่วไปแล้ว Independent Samples Chi-Square Test of Association ใช้สำหรับทดสอบว่ามีความสัมพันธ์ระหว่างตัวแปรสองตัวที่เป็นแบบจำนวนนับหรือไม่ ซึ่งตัวแปรสองตัวนี้สามารถแบ่งออกเป็นกลุ่มหรือชนิดต่าง ๆ ได้ เช่น การทดสอบความสัมพันธ์ระหว่าง:

• การสูบบุหรี่ (สูบ/ไม่สูบ) และโรคมะเร็งปอด (มี/ไม่มี)
• การลงคะแนนเพศและความคิดเห็นเกี่ยวกับประเภทของหนังสือ
• การชนิดของยา (A, B, C) และการหายขาดของโรค

การทดสอบด้วย Chi-Square Test of Association จะทำการสร้างตารางความถี่ (contingency table) ขึ้นมาจากข้อมูลตัวอย่าง แล้วทำการเปรียบเทียบความแตกต่างระหว่างค่าที่สังเกตเจอจริง ๆ กับค่าที่คาดหวัง หากมีความแตกต่างมากนัก จะสรุปได้ว่ามีความสัมพันธ์ระหว่างตัวแปรสองตัวที่เราสนใจ

ค่าสถิติที่ได้จาก Chi-Square Test จะใช้ในการคำนวณหาค่า p-value เพื่อทำการตัดสินใจว่าจะปฏิเสธหรือยอมรับสมมติฐานที่ตั้งไว้ว่าไม่มีความสัมพันธ์ โดยระดับนัยสำคัญที่มักใช้คือ 0.05 ซึ่งหาก p-value น้อยกว่าระดับนัยสำคัญจะสรุปได้ว่ามีความสัมพันธ์ระหว่างตัวแปรสองตัวที่เราสนใจ ในทางกลับกัน หาก p-value มากกว่าระดับนัยสำคัญจะไม่มีหรือมีความสัมพันธ์น้อยมาก หรือไม่สามารถปฏิเสธสมมติฐานนั้นได้

เราจะคำนวณค่าสถิติทดสอบ Chi-Square และค่า p-value ได้ดังนี้

1. กำหนดตารางความถี่ (contingency table) จากข้อมูลที่ให้มา:

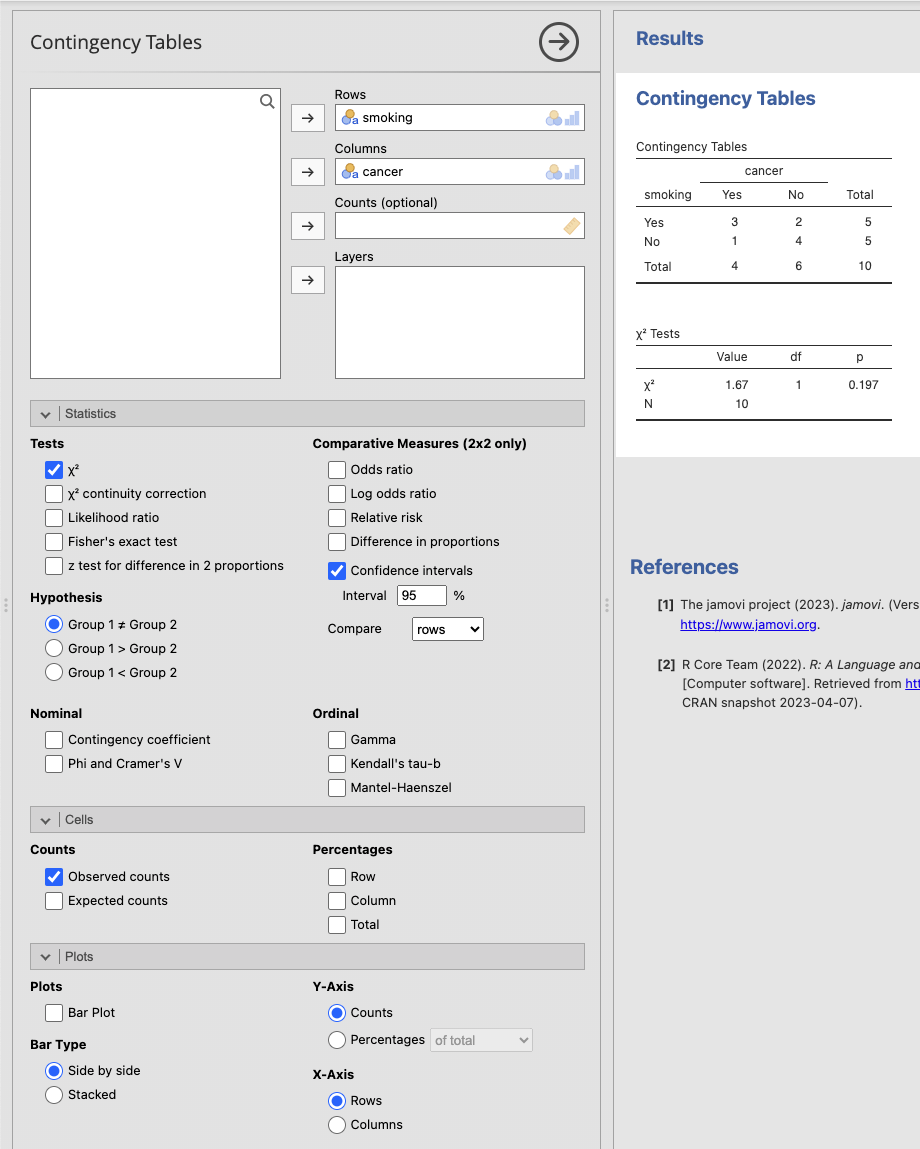
       cancer
smoking Yes No
    Yes   3  2
    No    1  4

2. คำนวณค่าคาดหวัง (expected frequencies) สำหรับแต่ละเซลล์ในตารางความถี่:

\[\text{Expected frequency} = \frac{\text{row total} \times \text{column total}}{\text{grand total}}\]

สำหรับตารางความถี่ข้างต้น:

• สำหรับเซลล์ (Yes, Yes):

  • คาดหวัง = \(\frac{(3 + 2) \times (3 + 1)}{(3 + 2 + 1 + 4)} = \frac{5 \times 4}{10} = 2\)

• สำหรับเซลล์ (Yes, No):

  • คาดหวัง = \(\frac{(3 + 2) \times (2 + 4)}{(3 + 2 + 1 + 4)} = \frac{5 \times 6}{10} = 3\)

• สำหรับเซลล์ (No, Yes):

  • คาดหวัง = \(\frac{(1 + 4) \times (3 + 1)}{(3 + 2 + 1 + 4)} = \frac{5 \times 6}{10} = 2\)

• สำหรับเซลล์ (No, No):

  • คาดหวัง = \(\frac{(1 + 4) \times (2 + 4)}{(3 + 2 + 1 + 4)} = \frac{5 \times 8}{10} = 4\)

3. คำนวณค่าสถิติทดสอบ Chi-Square:

\[\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}\]

โดยที่ \(O_i\) คือจำนวนที่สังเกตเจอจริง, \(E_i\) คือจำนวนที่คาดหวัง

สำหรับตารางความถี่ข้างต้น:

• สำหรับเซลล์ (Yes, Yes):

  • \(\chi^2 = \frac{(3 - 2)^2}{2} = \frac{1}{2} = 0.5\)

• สำหรับเซลล์ (Yes, No):

  • \(\chi^2 = \frac{(2 - 3)^2}{3} = \frac{1}{3} = 0.3333\)

• สำหรับเซลล์ (No, Yes):

  • \(\chi^2 = \frac{(1 - 2)^2}{2} = \frac{1}{2} = 0.5\)

• สำหรับเซลล์ (No, No):

  • \(\chi^2 = \frac{(4 - 3)^2}{3} = \frac{1}{3} = 0.333\)

ดังนั้นค่าสถิติทดสอบ Chi-Square คือ:

\(\chi^2 = 0.5 + 0.333 + 0.5 + 0.333 = 1.667\)

4. คำนวณดีกรีเสรี (degrees of freedom):

\(df = (r - 1)(c - 1)\)

โดยที่ \(r\) คือจำนวนแถวและ \(c\) คือจำนวนคอลัมน์ในตารางความถี่ สำหรับตารางความถี่ข้างต้น:

• \(r = 2\) (มีแถว 2 แถว)

• \(c = 2\) (มีคอลัมน์ 2 คอลัมน์)

ดังนั้น \(df = (2 - 1)(2 - 1) = 1\)

5. หาค่า p-value:

\(\text{p-value} = 0.197\)

ค่า p-value มากกว่าระดับนัยสำคัญที่ 0.05 ดังนั้นเราไม่สามารถปฏิเสธสมมติฐานได้ แสดงว่าไม่มีความสัมพันธ์ทางสถิติระหว่างการสูบบุหรี่และการเกิดโรคมะเร็งปอดที่ระดับนัยสำคัญ 0.05

การคำนวณด้วย Jamovi

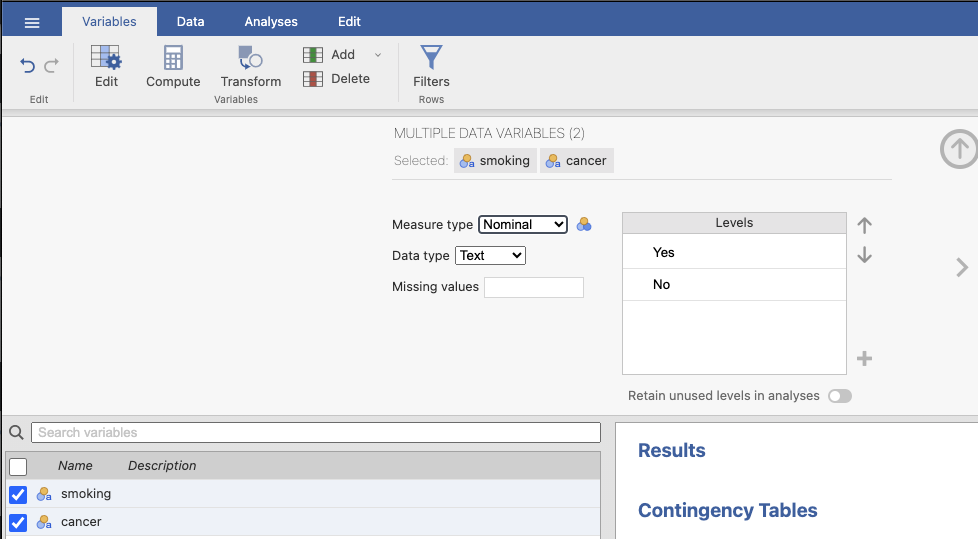
ขั้นที่ 1 นำข้อมูล asso_test.xlsx เข้า Jamovi และเรียงลำดับตัวแปรทั้งสองดังนี้

ขั้นที่ 2 กำหนดการคำนวณที่ต้องการ

ทางซ้าย: กำหนดค่าที่ต้องการ ทางขวา: ผลการทดสอบ

6.1.4 Paired Samples McNemar Test

McNemar Test เป็นการทดสอบสมมติฐานว่ามีความแตกต่างในการจำแนกกลุ่มของตัวแปรตามคู่ในการทดสอบสมมติฐานของเปอร์ซอน McNemar ซึ่งมักใช้กับข้อมูลที่เป็นตัวอย่างที่จับคู่กัน เช่น การวัดผลการรักษาของโรคก่อนและหลังการให้ยาเดียวกัน หรือการวัดผลของการทดสอบที่ทำซ้ำซ้อนกัน

ขั้นตอนการดำเนิน McNemar Test มีดังนี้: 1. สร้างตารางความถี่ 2x2 ที่แสดงความสัมพันธ์ระหว่างตัวแปรตามคู่ที่จับคู่กัน โดยมีรายละเอียดดังนี้:

	ไม่พบอาการ	พบอาการ
ไม่ใช่ก่อนการรักษา	\(a\)	\(b\)
ใช่ก่อนการรักษา	\(c\)	\(d\)

2. คำนวณค่า McNemar Test statistic โดยใช้สมการ:

\[\chi^2_{\text{McNemar}} = \frac{(b - c)^2}{b + c}\]

3. คำนวณหา p-value จากการประมาณค่าของค่าที่ได้จากการทดสอบสมมติฐานแบบทีมีการแจกแจงปกติ (normal distribution) หรือจากการใช้การจำลองบวกเบี่ยง (simulation).

4. สรุปผลการทดสอบโดยพิจารณาค่า p-value ว่าเป็นค่าน้อยกว่าระดับนัยสำคัญที่กำหนดหรือไม่ (โดยทั่วไปจะใช้ระดับนัยสำคัญ 0.05) เพื่อตัดสินใจว่าจะปฏิเสธหรือยอมรับสมมติฐานว่ามีความแตกต่างในการจำแนกกลุ่มของตัวแปรตามคู่ที่จับคู่กันหรือไม่

McNemar Test มักใช้ในกรณีที่ข้อมูลมีลักษณะที่เป็นตัวอย่างที่จับคู่กัน เช่น การทดสอบการรักษาโรคก่อนและหลังการให้ยาเดียวกัน หรือการทดสอบที่มีการทำซ้ำซ้อนกัน เพื่อทดสอบว่ามีการเปลี่ยนแปลงหรือไม่ในตัวแปรที่สนใจหลังจากการกระทำใด

ตัวอย่างข้อมูลและการทำ McNemar Test

สมมติว่าเรามีข้อมูลตัวอย่างเกี่ยวกับผลการทดสอบโรคในกลุ่มของผู้ป่วย ก่อนและหลังการให้ยาเดียวกัน และต้องการทดสอบว่ามีความแตกต่างในผลการทดสอบระหว่างก่อนและหลังการให้ยาหรือไม่ ข้อมูลสามารถแสดงได้ดังนี้:

        test
drug     Positive Negative
  before       10        5
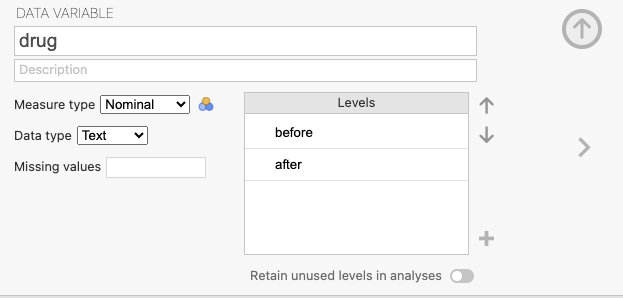
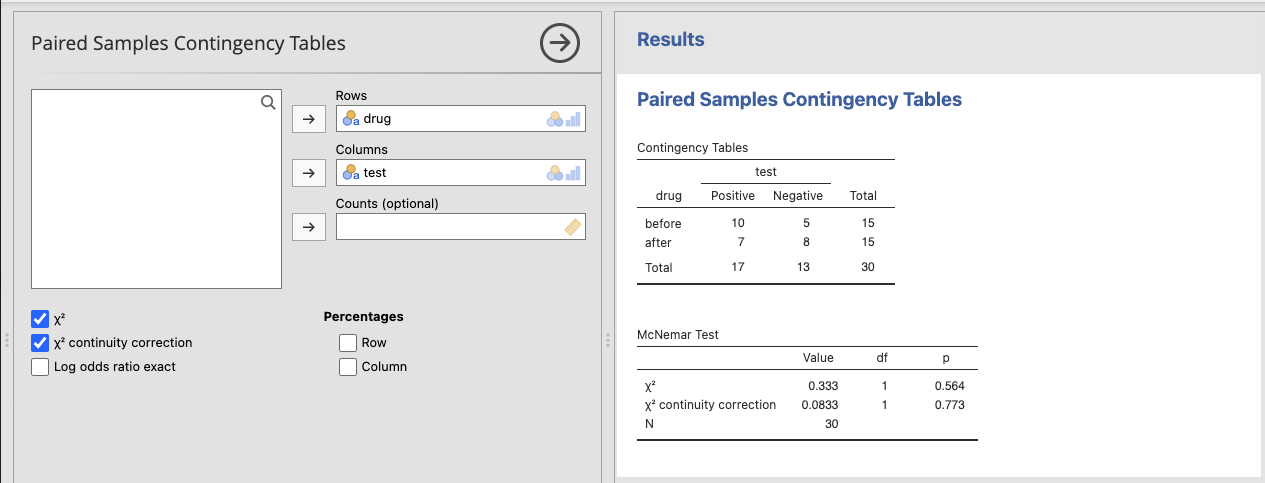
  after         7        8

ขั้นที่ 1 นำไฟล์ mcnemar.xlsx เข้าสู่ ๋Jamovi จัดการข้อมูลตามภาพ

ขั้นที่ 2 เลือกเมนู Paired Sample Mcnemar test