2  เมนู Exploration

ผู้อ่านสามารถโหลดข้อมูลได้ google drive นี้

การคำนวณสถิติพรรณา และการสร้างตารางแจกแจงความถี่ และภาพนิทัศน์แบบต่างๆ เช่นแผนภาพการกระจาย (histogram) กราฟความหนาแน่น (density plot) กราฟกล่อง (box plot) กราฟไวโอลิน (violin plot) กราฟแท่ง(bar plot) และกราฟคิวคิว (QQ plot) โดยผู้ใช้งานเลือกสถิติที่ต้องการแสดงค่า และกราฟที่สนใจได้ด้วยตนเอง

Descriptives

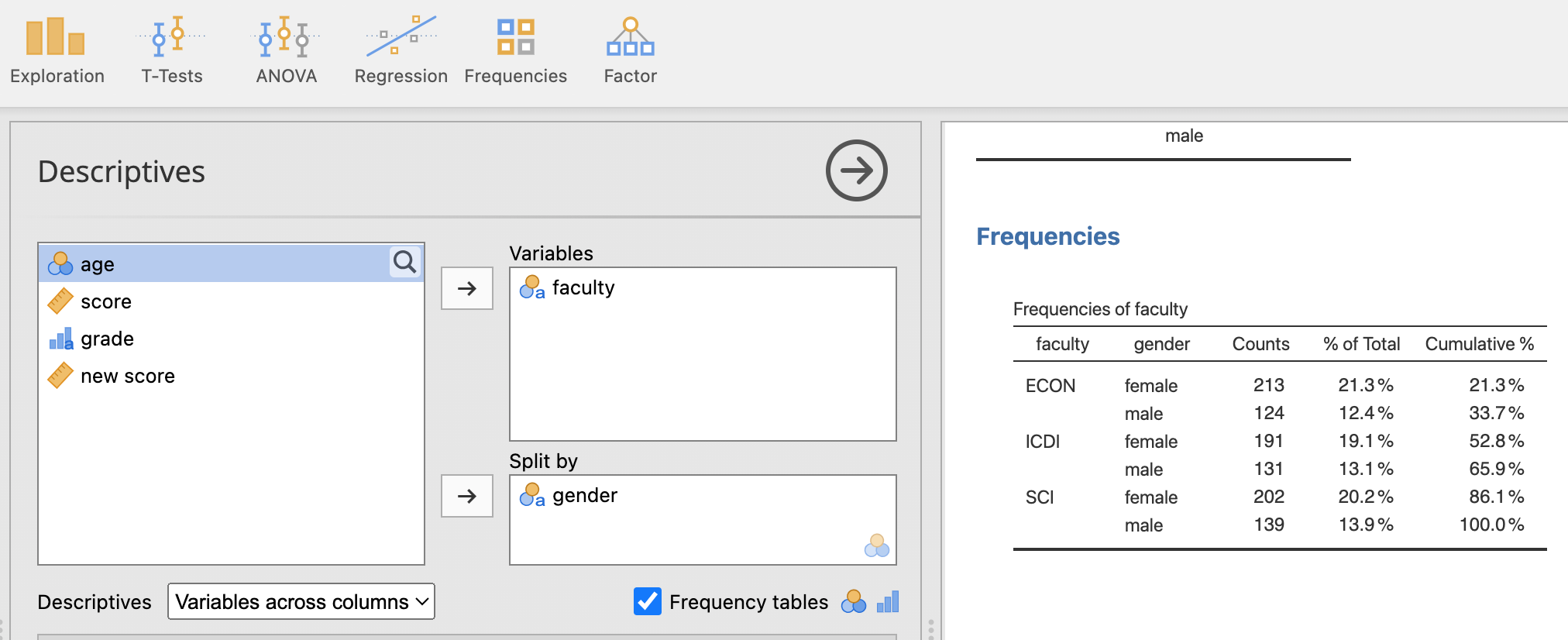
เช่น ต้องการนับจำนวนนศ.ในแต่ละคณะและแยกตามเพศ ทำได้โดยสร้างตารางแจกแจงความถี่ดังภาพ

ตารางแจกแจงควมถี่ของตัวแปร faculty แยกตามตัวแปร gender

เพียงแค่ลากตัวแปรที่ต้องการไปใส่ยัง variables และ split by และต้องไปไม่ลืมใส่เครื่องหมายในช่อง Frequency Table จะได้ตารางแจกแจงความถี่ทางชวา โดยที่ตารางนี้สามารถคัดไปวางยังโปรแกรม MS-word หรือ Writer ใน Libre office ได้ทันทีและยังสามารถแก้ข้อความภายหลังได้

Note

• ช่อง Variable จะใช่ตัวแปรประเภทใดก็ได้และกี่ตัวก็ได้ จะเป็นการคำนวณหลัก

• ช่อง Split by จะใส่ได้เฉพาะตัวแปรแบบ nominal หรือ ordinal เท่านั้น โดยใส่ตัวแปรได้สูงสุดสองตัวเท่านั้น

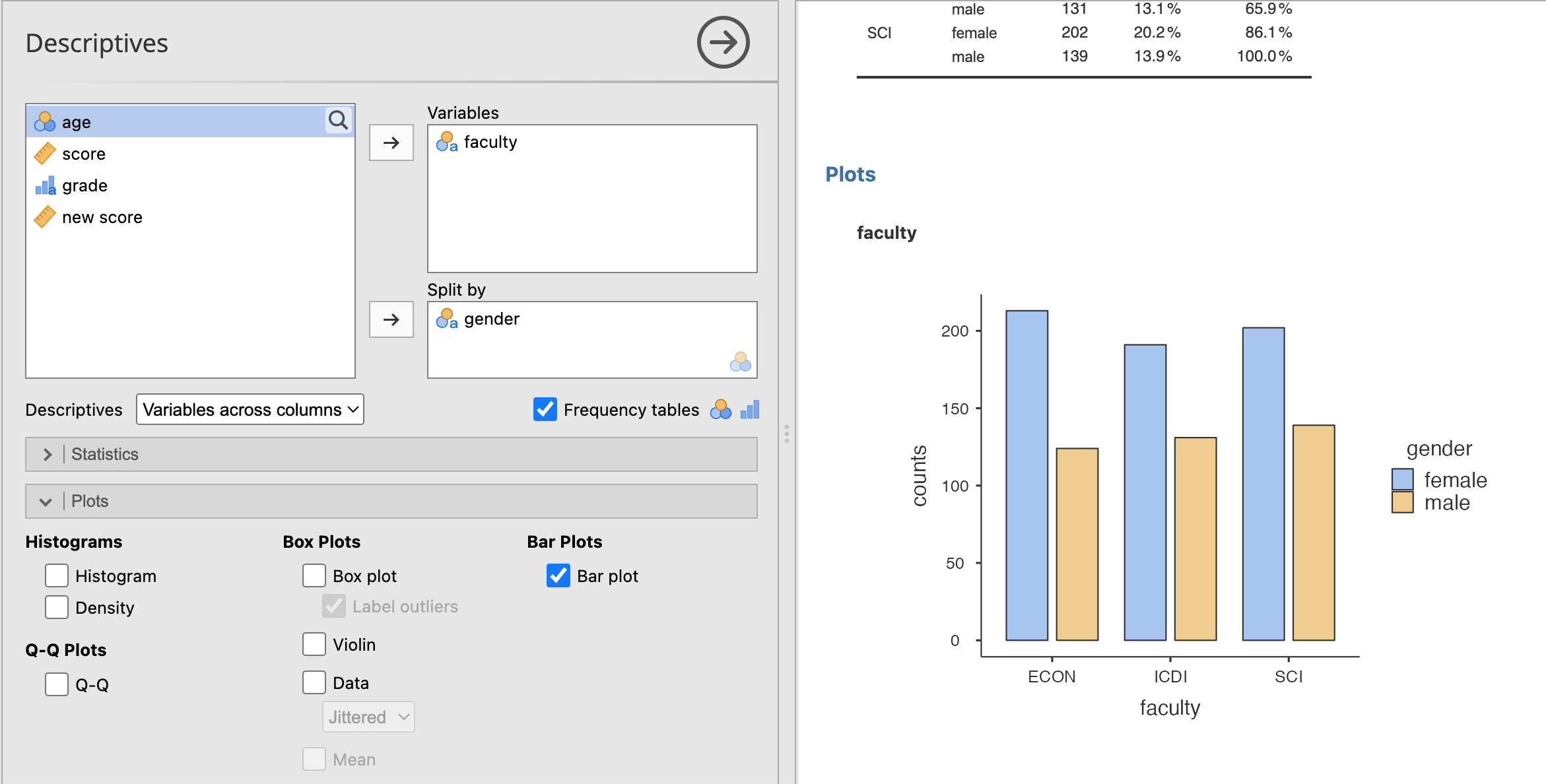
และข้อมูลชนิดสามารถสร้างกราฟแท่งได้เท่านั้น

กราฟแท่ง

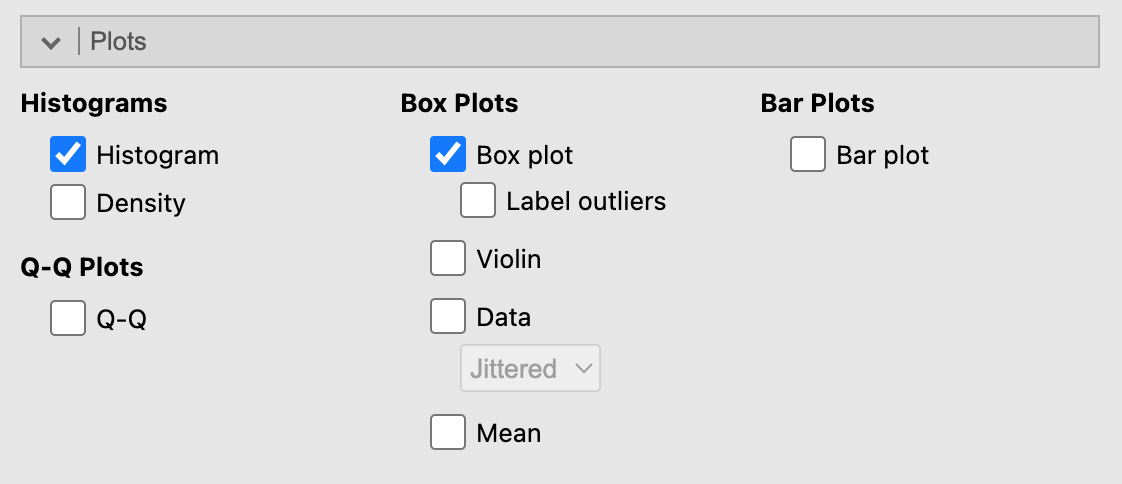
โดยเลือกจากเมนู Plots

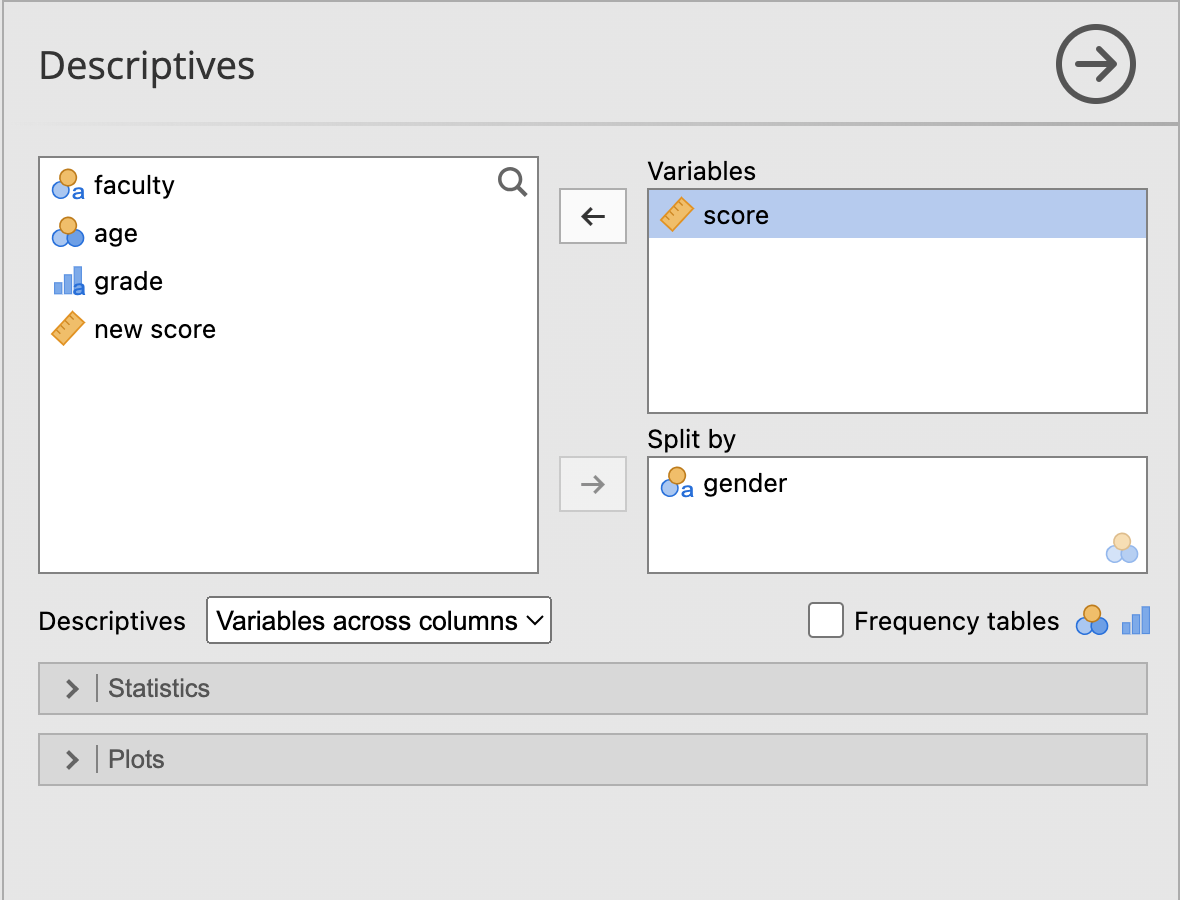
ในกรณีที่ใส่ตัวแปรที่เป็นเลขในช่อง  Variable จะเป็นคำนวณค่าทางสถิติต่างๆ เช่น ค่าเฉลี่ย (mean) ความแปรปรวน (variance) และอื่นๆ เช่นสถิติพรรณาของตัวแปร score แยกตามเพศ จะได้

ขั้นที่ 1 เลือกตัวแปรที่ต้องการ

ขั้นที่ 2 เลือกค่าสถิติที่ต้องการแสดงในตาราง

ขั้นที่ 3 เลือกกราฟที่ต้องการแสดง (เลือกหรือไม่ก็ได้)

ผลลัพธ์ที่ได้คือ

	gender	score
N	female	606
	male	394
Missing	female	0
	male	0
Mean	female	65.9
	male	64.9
Median	female	66.5
	male	65.0
Variance	female	209
	male	210
Minimum	female	40.5
	male	40.5
Maximum	female	90.0
	male	90.0

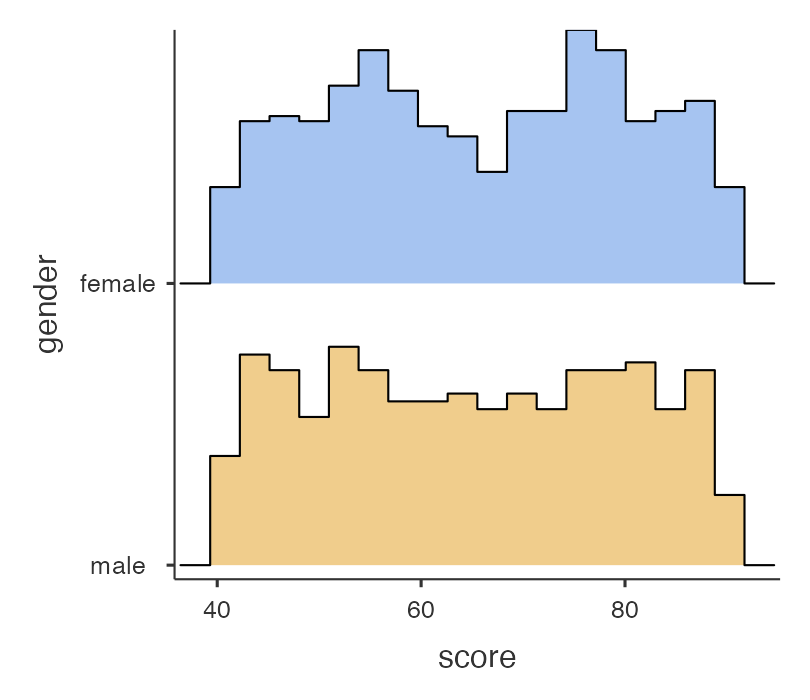
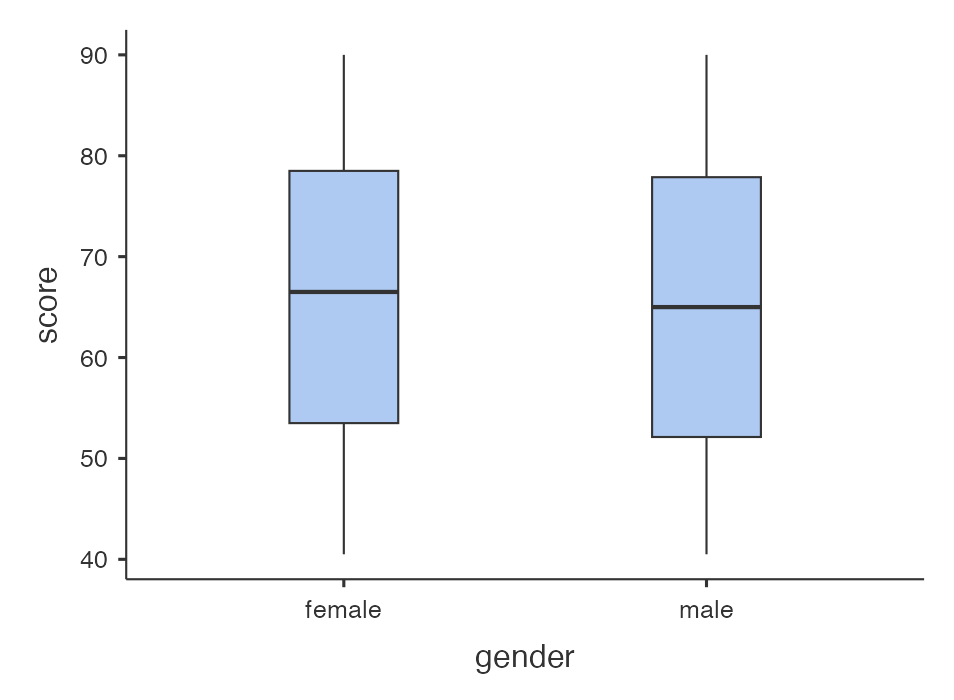
และกราฟที่ได้

กราฟ histogram และ box plot

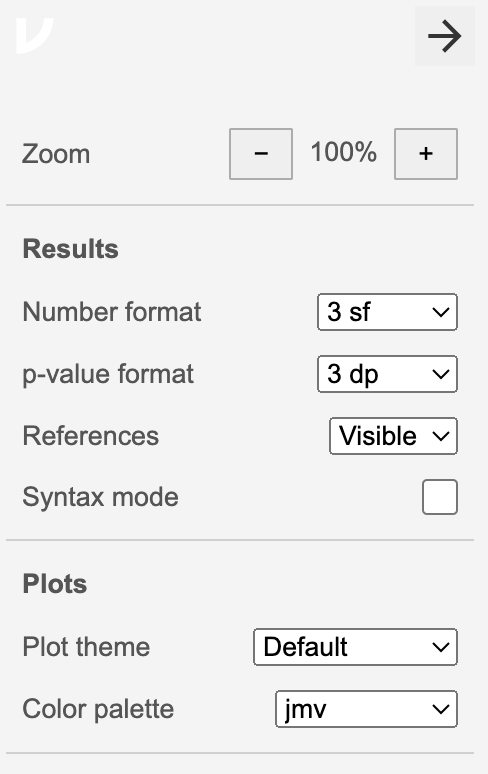
หมายเหตุ การแสดงผลของเลขทศนิยมและชุดสีเลือกได้สำหรับกราฟให้เลือกเมนู Analyse และกดเครื่อง \(\vdots\)

เมนูปรับแต่งการแสดงผล

ช่อง Results เป็นการเลิอกการแสดงผล และช่อง Plots เป็นการเลือกจานสีและชุดสี

2.1 ตัววัดสถิติที่ควรทราบ

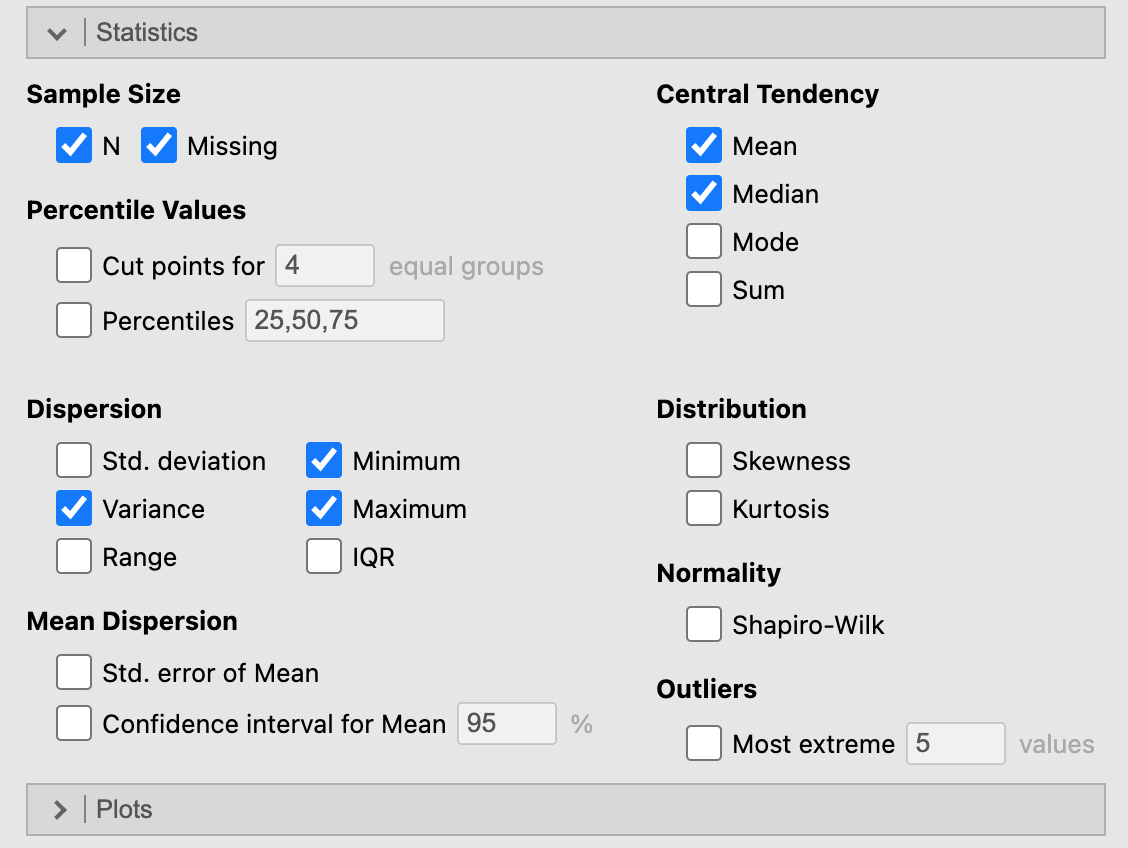
2.1.1 ขนาดตัวอย่าง (Sample Size)

• N จำนวนข้อมูลทั้งหมดของตัวแปรที่พิจารณา

• Missing จำนวนข้อมูลที่สูญหายของตัวแปรที่พิจารณา

2.1.2 Central Tendency

Central tendency (คือ) คุณลักษณะหรือค่าที่ใช้เพื่อแทนความเฉลี่ยหรือค่าที่ตัวอย่างข้อมูลมีแนวโน้มที่เกินการกระจายหรือค่าที่ตัวอย่างมุ่งหมายที่จะเลื่อนไป ค่าที่ใช้ใน central tendency

• ค่าเฉลี่ย (mean) ที่คำนวณจากผลบวกของข้อมูลทั้งหมดหารด้วยจำนวนข้อมูลทั้งหมด

• ค่ามัธยฐาน (median) ที่เป็นค่าที่ตัดกลางของข้อมูลเมื่อเรียงลำดับจากน้อยไปหามาก

• ค่าฐานซ้าย/ฐานขวา (mode) ซึ่งเป็นค่าที่มีความถี่สูงสุดในชุดข้อมูล

  การใช้ central tendency ช่วยให้เราสามารถทำความเข้าใจรูปแบบหรือลักษณะที่สำคัญของข้อมูลได้ง่ายขึ้นโดยไม่ต้องพึ่งพาการดูข้อมูลทุกจุดแต่ละจุดอย่างละเอียด

2.1.3 การกระจาย (Dispersion)

Dispersion ในทางสถิติหมายถึง การกระจายของข้อมูลหรือความแตกต่างระหว่างค่าข้อมูลแต่ละค่าในชุดข้อมูล เราใช้ dispersion เพื่อวัดความแปรปรวนหรือการกระจายของข้อมูลว่าข้อมูลมีการกระจายอย่างไรจากค่ากลาง เช่น ค่าเฉลี่ย หรือค่ามัธยฐาน ซึ่ง dispersion ช่วยให้เราเข้าใจถึงความแตกต่างระหว่างข้อมูลในชุดข้อมูลต่างๆ และมีวิธีการวัด dispersion หลายวิธี เช่น

• ค่าเบี่ยงเบนมาตรฐาน (Standard Deviation): วัดความแตกต่างระหว่างค่าข้อมูลแต่ละค่ากับค่าเฉลี่ยของชุดข้อมูล

• การระดับของการกระจาย (Range): วัดความต่างระหว่างค่าข้อมูลที่มากที่สุดและน้อยที่สุดในชุดข้อมูล

• ค่าสมมาตร (Variance): เป็นค่าเบี่ยงเบนมาตรฐานยกกำลังสอง แสดงถึงการกระจายของข้อมูล

• range: เป็นผลต่างระหว่างค่าสูงสุดและค่าต่ำสุดของข้อมูล

การเข้าใจ dispersion ช่วยให้เราเข้าใจถึงความหลากหลายและการกระจายของข้อมูลที่ซับซ้อนมากขึ้นในชุดข้อมูลโดยรวม ซึ่งมีผลต่อการวิเคราะห์และการตีความข้อมูลในการศึกษาหรืองานวิจัยต่างๆ อย่างสำคัญ

2.1.4 การกระจาย (Distribution)

Distribution ในทางสถิติหมายถึง รูปแบบหรือลักษณะการกระจายของข้อมูลภายในชุดข้อมูลที่กำลังพิจารณา การแจกแจงนี้บ่งบอกถึงว่าข้อมูลมีการกระจายอย่างไร โดยทั่วไปเราจะเกณฑ์การวัดว่า การกระจายมีความแตกต่างจาก การแจกแจงแบบปรกติหรือไม่ ตัวสถิติที่ใช้วัดคือ

• ความเบ้ (Skewness) เป็นค่าทางสถิติที่ใช้ในการวัดรูปแบบการกระจายของข้อมูลในชุดข้อมูล โดยเฉพาะการแปลงการกระจายแบบปกติ ความเบ้บ่งบอกถึงการเอียงของการกระจายข้อมูลไปทางด้านใดของกราฟการแจกแจง ซึ่งสามารถแบ่งได้เป็น 3 ประเภทหลัก ได้แก่

  • บวก (Positive skewness): เมื่อมีการเอียงของข้อมูลไปทางด้านขวาของกราฟ หรือมีค่าข้อมูลที่มากกว่าค่าเฉลี่ยมากขึ้น ซึ่งทำให้ทำนายว่าค่าสูงๆ มักจะเกิดขึ้นบ่อยขึ้น

  • ลบ (Negative skewness): เมื่อมีการเอียงของข้อมูลไปทางด้านซ้ายของกราฟ หรือมีค่าข้อมูลที่น้อยกว่าค่าเฉลี่ยมากขึ้น ซึ่งทำให้ทำนายว่าค่าต่ำๆ มักจะเกิดขึ้นบ่อยขึ้น

  • ไม่มีเบ้ (Zero skewness): เมื่อข้อมูลกระจายแบบสมมาตร ไม่มีการเอียงไปทางซ้ายหรือขวาของกราฟการแจกแจง

  ความเบ้มักถูกใช้เพื่อให้เราเข้าใจถึงลักษณะการกระจายของข้อมูล โดยค่าเบ้ที่มากขึ้นแสดงถึงการกระจายที่มีการเอียงมากขึ้น ในขณะที่ค่าเบ้ที่น้อยแสดงถึงการกระจายที่น้อยลง

• ความโด่ง (Kurtosis)

  ความโด่ง (Kurtosis) ในทางสถิติหมายถึง การวัดรูปร่างหรือลักษณะของการแจกแจงข้อมูลเมื่อเปรียบเทียบกับการแจกแจงปกติ (Normal distribution) หรือกระจายปกติ ความโด่งบ่งบอกถึงการกระจายของข้อมูลที่มีการเสียแต่ละด้าน เช่น การมี “ยอด” ที่สูงหรือต่ำกว่าปกติ ซึ่งสามารถแยกเป็น Positive kurtosis และ Negative kurtosis ได้ดังนี้

  • Positive Kurtosis: หมายถึงการมี “ยอด” ที่สูงกว่าปกติ เป็นสัญญาณว่าข้อมูลมีการกระจายส่วนใหญ่ไปที่แถบความเข้มของข้อมูลมากกว่า ซึ่งหมายถึงการมีความสูงของค่าข้อมูลที่มากกว่าปกติ

  • Negative Kurtosis: หมายถึงการมี “ยอด” ที่ต่ำกว่าปกติ เป็นสัญญาณว่าข้อมูลมีการกระจายไปที่แถบความเข้มของข้อมูลน้อยกว่าปกติ ซึ่งหมายถึงการมีความสูงของค่าข้อมูลที่น้อยกว่าปกติ

  ความโด่งมักถูกใช้เป็นหนึ่งในวิธีการประเมินว่าข้อมูลมีความแปรปรวนหรือการกระจายอย่างไร เนื่องจากมันช่วยให้เราเข้าใจถึงลักษณะของการกระจายข้อมูลอย่างเป็นระบบและลึกซึ้งขึ้น

2.1.5 ความปกติ (Normality)

Normality (ความปกติ) ในทางสถิติหมายถึง การกระจายของข้อมูลที่มีลักษณะเป็นรูปกระจายปกติ (Normal distribution) หรือเรียกอีกชื่อว่าการแจกแจงปกติ (Gaussian distribution) ความปกติเป็นสถานะที่ข้อมูลมีการกระจายเป็นรูปกระจายที่เป็นแบบกรวยและมีลักษณะที่เป็นรูปโค้งบนกราฟหรือแผนภูมิที่เรียกว่า Bell curve โดยที่ค่ากลางของข้อมูลอยู่ตรงกลางของกราฟ และค่าข้อมูลมีการกระจายอย่างสม่ำเสมอทั้งสองด้านของค่ากลาง

• Shapiro-Wilk test เป็นทดสอบสถิติที่ใช้ในการตรวจสอบว่าข้อมูลมีการแจกแจงปกติ (normally distributed) หรือไม่ โดยทดสอบสมมติฐานที่ว่าข้อมูลถูกสุ่มมาจากการแจกแจงปกติ เริ่มต้นด้วยการคำนวณสถิติทดสอบ Shapiro-Wilk ซึ่งมีข้อดีที่สามารถใช้กับข้อมูลจำนวนมากได้ และมีความไวสูงในการตรวจสอบความปกติของข้อมูล โดยสถิติทดสอบนี้จะให้ค่า p-value เพื่อใช้ในการตีความผลลัพธ์ว่าข้อมูลมีการแจกแจงปกติหรือไม่ ถ้า p-value น้อยกว่าระดับนัยสำคัญที่กำหนด (เช่น 0.05) แสดงว่ามีหลักฐานทางสถิติในการปฏิเสธสมมติฐานว่าข้อมูลมีการแจกแจงปกติ หรือกล่าวอีกนัยหนึ่ง ข้อมูลไม่มีการแจกแจงปกติ

Shapiro-Wilk test เหมาะสำหรับข้อมูลที่มีขนาดไม่เยอะมากและมีความแปรปรวนไม่สูงมาก และมักนิยมใช้ในการตรวจสอบความปกติของข้อมูลก่อนที่จะทำการวิเคราะห์สถิติที่ต้องการด้วยวิธีอื่นๆ เช่น t-test หรือ ANOVA การใช้ Shapiro-Wilk test ช่วยให้ผู้วิจัยหรือผู้ที่ทำการวิเคราะห์ข้อมูลสามารถรับรู้ถึงความเหมาะสมในการใช้วิธีการวิเคราะห์สถิติที่มีข้อกำหนดเกี่ยวกับการแจกแจงของข้อมูลได้ดีขึ้น