4  เมนู ANOVA

ผู้อ่านสามารถโหลดข้อมูลได้ google drive นี้

เมนูการทดสอบสมมุติฐานด้วยการแจกแจง F distribution โดยมีการรูปแบบการทดสอบได้ดังนี้

เมนู ANOVA

เมนู ANOVA

  1. One-Way ANOVA

  2. ANOVA

  3. Repeated Measures ANOVA

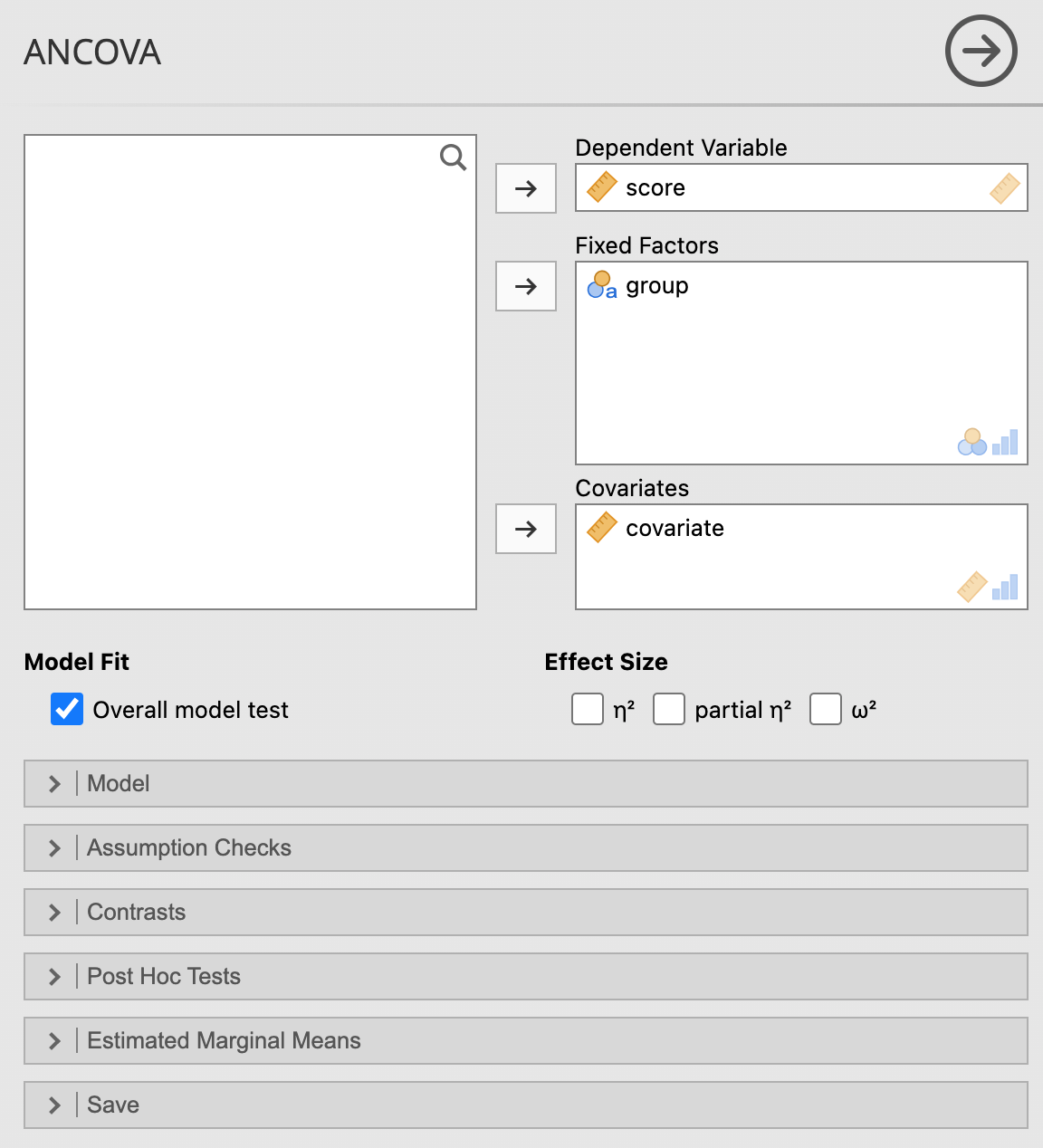
  4. ANCOVA

  5. MANCOVA

4.1 One-Way ANOVA

“One-Way ANOVA” หรือ “Analysis of Variance” เป็นวิธีการทางสถิติที่ใช้เพื่อทดสอบว่ามีความแตกต่างระหว่างค่าเฉลี่ยของกลุ่มหลาย ๆ กลุ่มซึ่งมีต่อตัวแปรตาม (dependent variable) ที่วัดขึ้นมาจากกลุ่มต่าง ๆ นี้ วิธีการนี้มีชื่อเสียงในการใช้กับการทดสอบความแตกต่างในค่าเฉลี่ยของกลุ่มและมีการใช้งานแพร่หลายในการวิเคราะห์ข้อมูลที่เป็นปริมาณ (quantitative data)

สำหรับการวิเคราะห์ One-Way ANOVA ที่มี \(k\) กลุ่ม สมการเชิงเส้นของ ANOVA สามารถเขียนได้เป็น: \[ Y_{i j}=\mu+\tau_i+\varepsilon_{i j} \]

โดยที่:

  • \(Y_{i j}\) คือค่าของตัวแปรตามสำหรับการสังเกตครั้งที่ \(j\) ในกลุ่มที่ \(i\)

  • \(\mu\) คือค่าเฉลี่ยของประชากรทั้งหมด (grand mean)

  • \(\tau_i\) คือผลกระทบของกลุ่มที่ \(i\) (group effect)

  • \(\epsilon_{i j}\) คือข้อผิดพลาด (error term) ที่เกี่ยวข้องกับการสังเกตครั้งที่ \(j\) ในกลุ่มที่ \(i\) \(i\)

ถ้าสังเกตุสมการเชิิงเส้นให้ดี ก็สมการถดถอยที่มีตัวแปรอิสระ 1 ตัวที่เป็นตัวแปรแบบ ืnominal นั้นเอง โดยที่ตัวแปรจะถูกเขียนในรูปของตัวแปรดัมมี่(dummy)

\[Y =a+bX+\varepsilon\]

มุมมองแบบง่าย ๆ สามารถอธิบายกระบวนการ One-Way ANOVA ได้ดังนี้:

  1. กำหนด Null Hypothesis (\(H_0\)): มีความแตกต่างในค่าเฉลี่ยของกลุ่มทั้งหมด (ไม่มีความแตกต่างระหว่างกลุ่ม)

  2. กำหนด Alternative Hypothesis (\(H_1\)): มีความแตกต่างในค่าเฉลี่ยของอย่างน้อยหนึ่งกลุ่ม

  3. ทำการวิเคราะห์: ทำการคำนวณ ANOVA ซึ่งจะให้ผลลัพธ์ F-statistic

  4. ตัดสินใจ: ถ้าค่า p-value น้อยกว่าระดับนัยสำคัญที่กำหนด (โดยทั่วไปใช้ 0.05), เราจะปฏิเสธ Null Hypothesis และสรุปว่ามีความแตกต่างในค่าเฉลี่ยของกลุ่ม

One-Way ANOVA ใช้เพื่อทดสอบว่ามีความแตกต่างระหว่างค่าเฉลี่ยของกลุ่มที่ต่างกันหรือไม่ โดยใช้ F-statistic และ p-value เป็นตัวชี้วัดทางสถิติ

ตัวอย่างการคำนวณ พิจารณาตัวอย่างโดยใช้ข้อมูลเชิงปริมาณ (quantitative data) ที่มี 3 กลุ่ม (Group A, Group B, Group C).

สมมติว่าเรามีข้อมูลคะแนนทดสอบ (ข้อมูลจำลอง) ดังนี้:

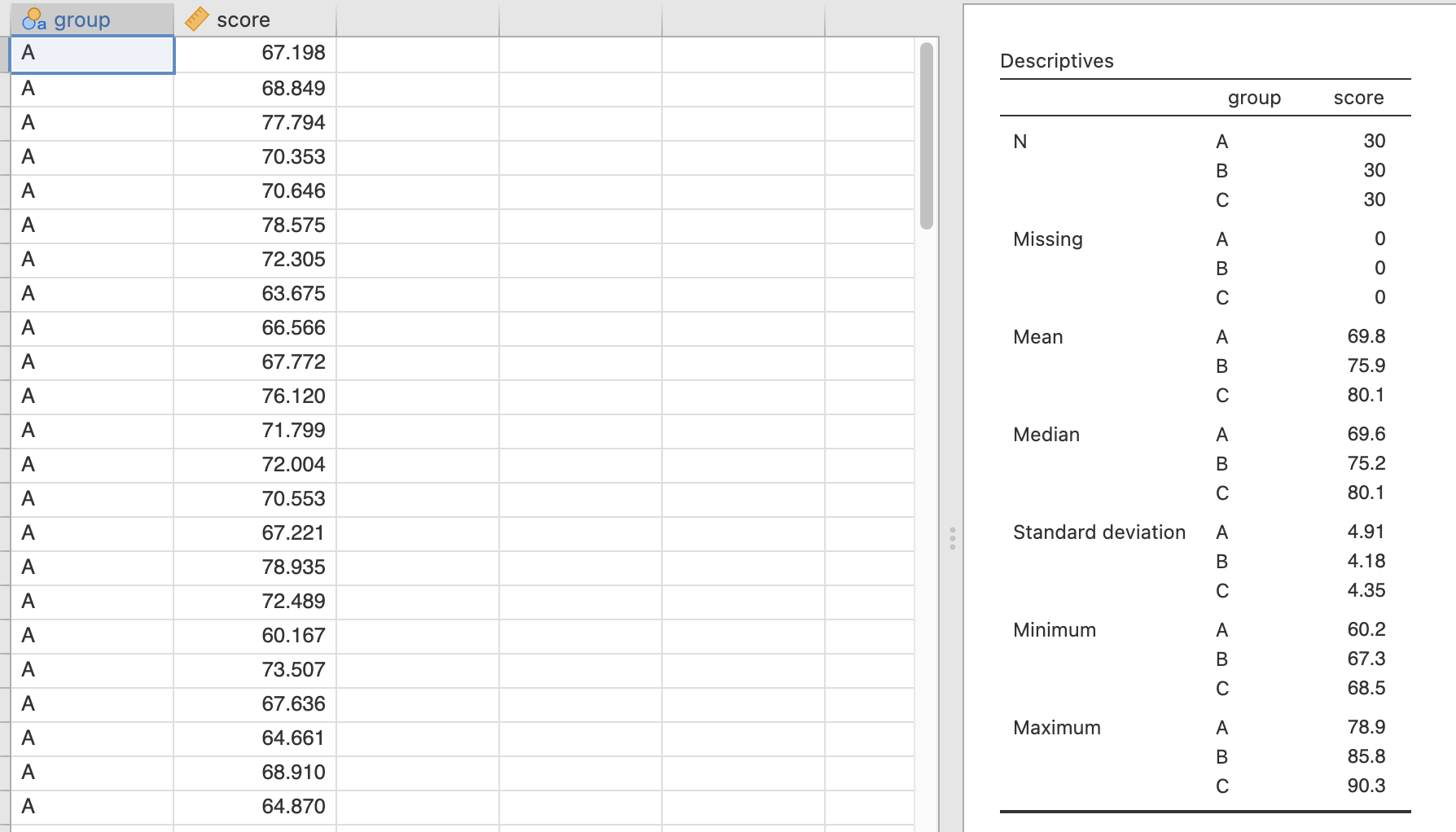
เมื่อนำข้อมูลชุดนี้เข้า Jamovi และแสดงค่าสถิติเชิงพรรณาจะได้

นำเข้าข้อมูลแล้วแสดงค่าสถิติเชิงพรรณา

นำเข้าข้อมูลแล้วแสดงค่าสถิติเชิงพรรณา

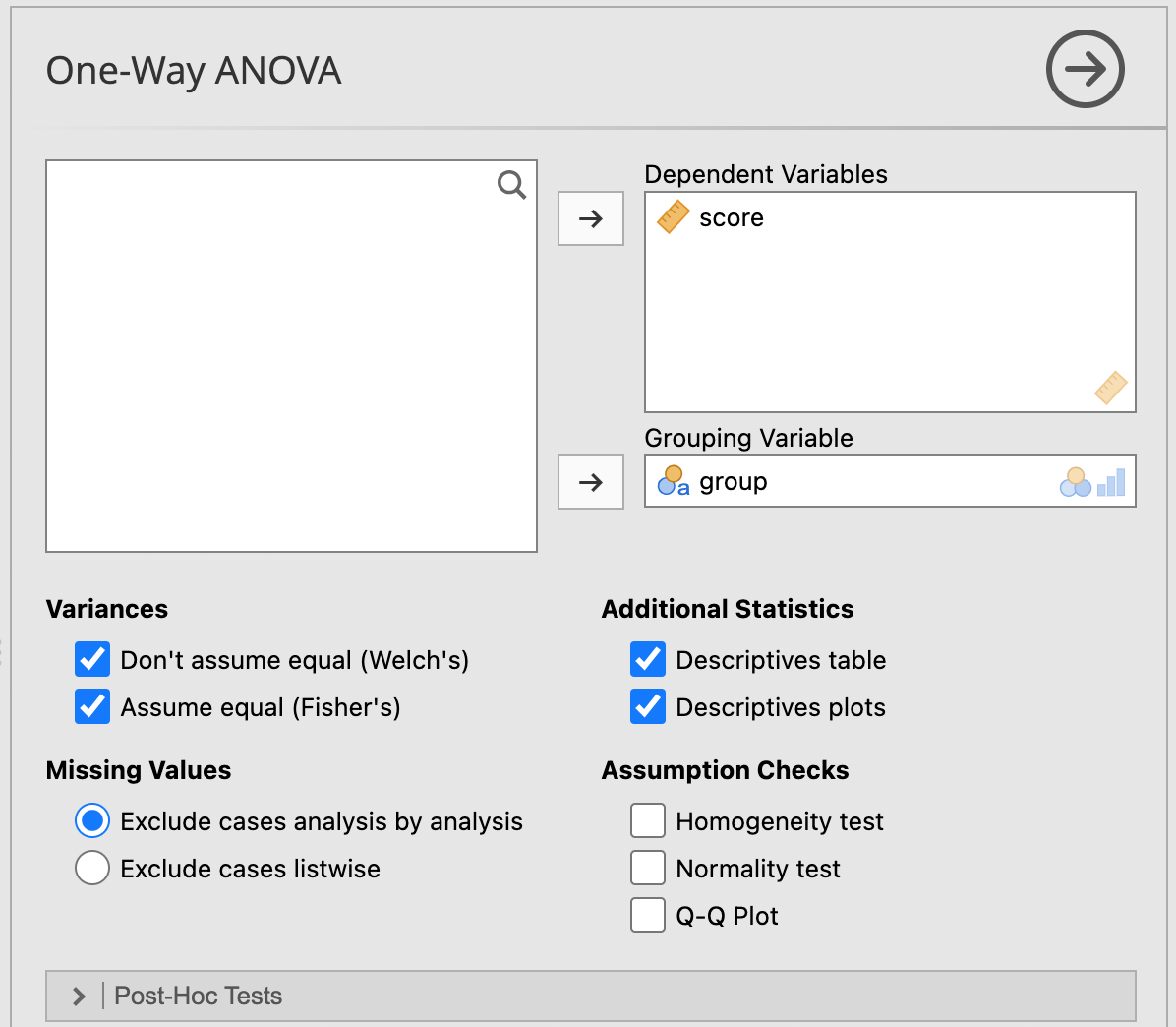
และเมื่อนำข้อมูลไปใส่ในเมนู ANOVA ตามภาพด้านล่าง

เลือกข้อตามภาพ

เลือกข้อตามภาพ

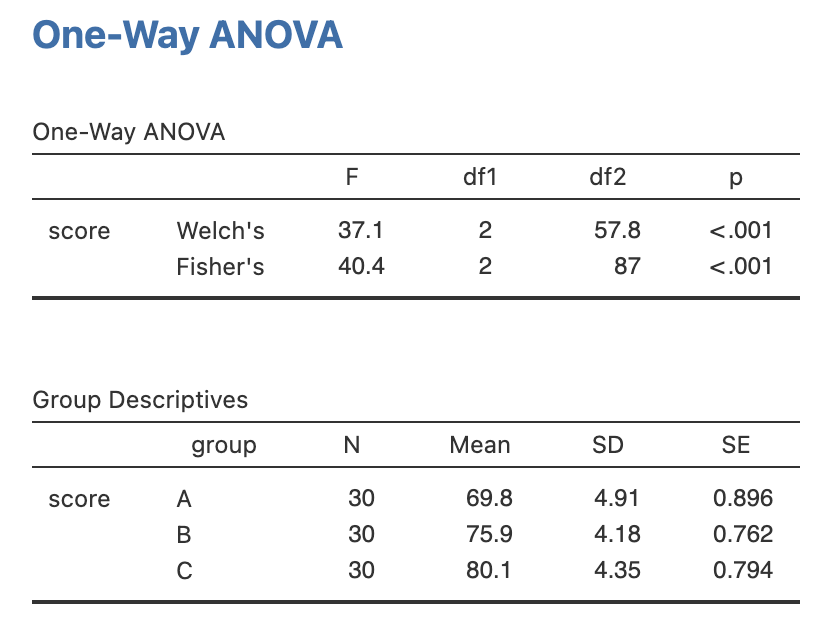
จะได้ผลลัพธ์ คือ

ผลการทดสอบสมมุติฐาน และสถิติเชิงพรรณา

ผลการทดสอบสมมุติฐาน และสถิติเชิงพรรณา

จากรูปการทดสอบ One-Way ANOVA ด้วยวิธีการของ Welch (สมมุติฐานคือความแปรปรวนของข้อมูลในแต่ละกลุ่มไม่เท่ากัน) พบว่ายอมรับสมมุติฐานรองที่ ค่าเฉลี่ยแต่ละกลุ่มมีความแตกต่างกันอย่างน้อย 1 กลุ่มด้วยค่า P-value น้อยกว่า 0.001

จากรูปการทดสอบ One-Way ANOVA ด้วยวิธีการของ Fisher (สมมุติฐานคือความแปรปรวนของข้อมูลในแต่ละกลุ่มเท่ากัน) พบว่ายอมรับสมมุติฐานรองที่ ค่าเฉลี่ยแต่ละกลุ่มมีความแตกต่างกันอย่างน้อย 1 กลุ่มด้วยค่า P-value น้อยกว่า 0.001

ตาราง Group Descriptives เป็นการแสดงสถิติเชิงพรรณา ผู้ใช้งานสามารถทดสอบสมมุติฐานอื่นๆ เพิ่มเติมจากเมนู One-Way ANOVA

4.2 ANCOVA

ANCOVA (Analysis of Covariance) เป็นวิธีการทางสถิติที่ใช้เพื่อวิเคราะห์ความแตกต่างในค่าเฉลี่ยของกลุ่มที่มีต่อตัวแปรตาม (dependent variable) โดยคำนึงถึงตัวแปรตัวเสริม (covariate) ที่มีอิทธิพลต่อตัวแปรตาม

ANCOVA นำเอากระบวนการที่ใช้ในการทดสอบ ANOVA มาเพิ่มเติมด้วยตัวแปรตัวเสริม ทำให้สามารถควบคุมการแปรผัน (variation) ที่เป็นผลมาจากตัวแปรตัวเสริมได้, และทำให้การทดสอบความแตกต่างระหว่างกลุ่มมีประสิทธิภาพมากขึ้น

ขั้นตอนการทำ ANCOVA มีลักษณะคล้ายกับ ANOVA แต่มีการเพิ่มเติมดังนี้

  1. กำหนด Null Hypothesis (\(H_0\)): ค่าเฉลี่ยของทุกกลุ่มเท่ากันหมด (ไม่มีความแตกต่าง) หรือความแตกต่างในค่าเฉลี่ยขึ้นอยู่กับตัวแปรตัวเสริม (covariate)

  2. กำหนด Alternative Hypothesis (\(H_1\)): มีความแตกต่างอย่างน้อยหนึ่งกลุ่มโดยคำนึงถึงตัวแปรตัวเสริม

  3. ทำ ANCOVA: ทำ ANCOVA โดยคำนึงถึงตัวแปรตัวเสริม, หลังจากนั้นทำการทดสอบว่าความแตกต่างระหว่างกลุ่มมีความสัมพันธ์กับตัวแปรตัวเสริมหรือไม่

  4. ตัดสินใจ: ถ้า p-value น้อยกว่าระดับนัยสำคัญที่กำหนด (โดยทั่วไปใช้ 0.05), เราจะปฏิเสธ Null Hypothesis และสรุปว่ามีความแตกต่างระหว่างกลุ่ม

การทดสอบ ANCOVA เป็นที่นิยมในการวิเคราะห์ข้อมูลที่มีตัวแปรตัวเสริมที่มีผลต่อตัวแปรตาม, และมีประโยชน์ในการควบคุมตัวแปรตัวเสริมที่อาจส่งผลกระทบต่อตัวแปรตาม

ตัวอย่างการคำนวณ

เราสร้างข้อมูลคะแนนทดสอบจากกลุ่ม A, B, และ C แล้วสร้างตัวแปรตัวเสริม covariate.

เมื่อนำข้อมูลนี้ใส่ Jamovi และเลือกเมนู ANCOVA ตามภาพ

ตัวอย่างการใส่ข้อมูลลงไปเมนู ANCOVA

ตัวอย่างการใส่ข้อมูลลงไปเมนู ANCOVA

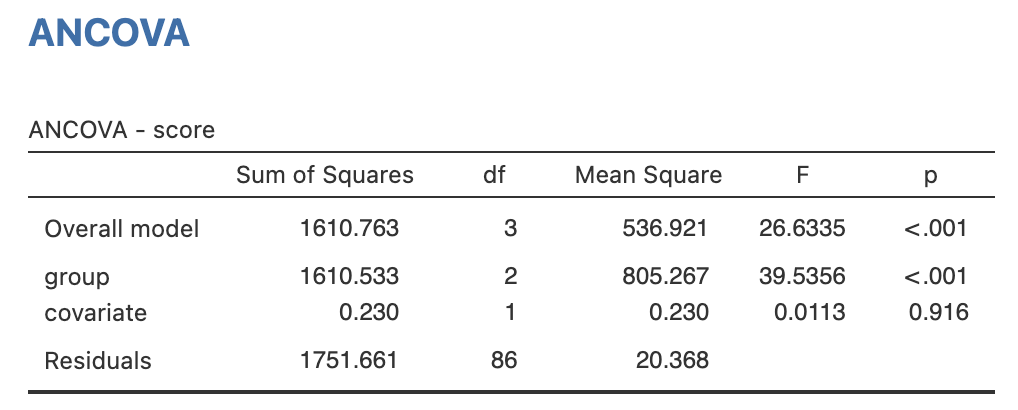
ผลจากการทดสอบสมมุติฐานสรุปได้ว่า

ผลการทดสอบสมมุติฐาน

ผลการทดสอบสมมุติฐาน

จากตาราง สรุปได้ว่าคะแนนเฉลี่ยแต่ละกลุ่มมีความแตกต่างกันอย่างน้อย 1 กล่มที่ระดับ P-value น้อยกว่า 0.001

บทนี้ยังเสร็จยังไม่เสร็จสมบูรณ์ รายละเอียดเชิงทฤษฎีเยอะ