14.1 Full-factorial between-subjects ANOVA
There are many types of ANOVAs that depend on the type of data you are analyzing. In fact, there are so many types of ANOVAs that there are entire books explaining differences between one type and another. For this book, we’ll cover just one type of ANOVAs called full-factorial, between-subjects ANOVAs. These are the simplest types of ANOVAs which are used to analyze a standard experimental design. In a full-factorial, between-subjects ANOVA, participants (aka, source of data) are randomly assigned to a unique combination of factors – where a combination of factors means a specific experimental condition. For example, consider a psychology study comparing the effects of caffeine on cognitive performance. The study could have two independent variables: drink type (soda vs. coffee vs. energy drink), and drink dose (.25l, .5l, 1l). In a full-factorial design, each participant in the study would be randomly assigned to one drink type and one drink dose condition. In this design, there would be 3 x 3 = 9 conditions.
For the rest of this chapter, I will refer to full-factorial between-subjects ANOVAs as `standard’ ANOVAs
14.1.1 What does ANOVA stand for?
ANOVA stands for “Analysis of variance.” At first glance, this sounds like a strange name to give to a test that you use to find differences in means, not differences in variances. However, ANOVA actually uses variances to determine whether or not there are ‘real’ differences in the means of groups. Specifically, it looks at how variable data are within groups and compares that to the variability of data between groups. If the between-group variance is large compared to the within group variance, the ANOVA will conclude that the groups do differ in their means. If the between-group variance is small compared to the within group variance, the ANOVA will conclude that the groups are all the same. See Figure~ for a visual depiction of an ANOVA.
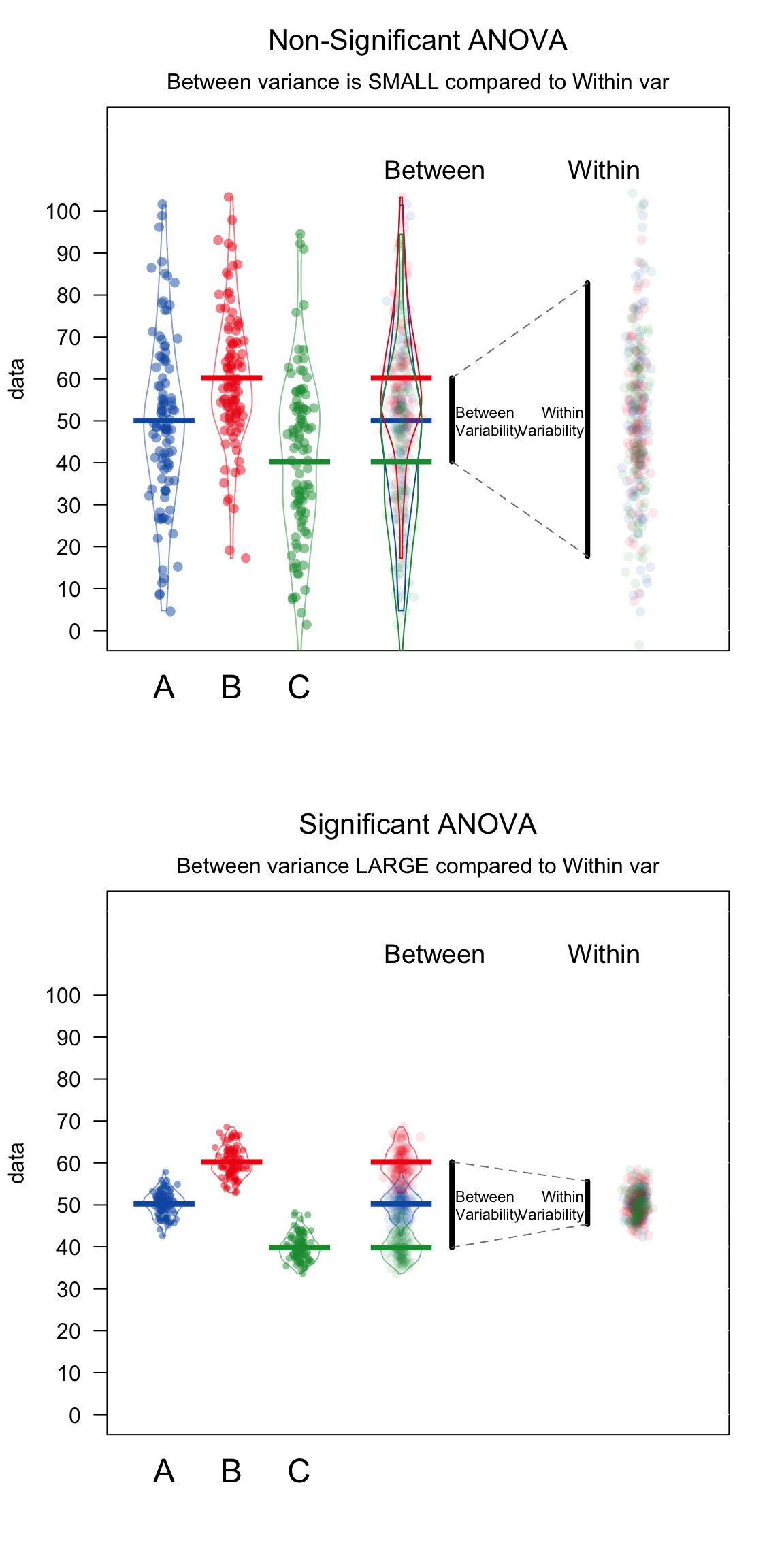
Figure 14.2: How ANOVAs work. ANOVA compares the variability between groups (i.e.; the differences in the group means) to the variability within groups (i.e.; how much individuals generally differ from each other). If the variability between groups is small compared to the variability between groups, ANOVA will return a non-significant result – suggesting that the groups are not really different. If the variability between groups is large compared to the variability within groups, ANOVA will return a significant result – indicating that the groups are really different.