Chapter 3 The Missing Data Indicator
Rubin (Rubin (1987)) proposed that variables with missing data can be divided in a part that is observed and a part that is missing. The observed and missing data can be coded by a 1 and 0 respectively. This dichotomous coding variable is called the missing data indicator variable. Figure 3.1 shows the missing data indicator variable for the observed and missing data in the Tampa scale variable. This indicator variable is now a single variable because there is missing data in only the Tampa scale variable. When more variables contain missing data, multiple indicator variables can be generated, one for each variable that contains missing data.
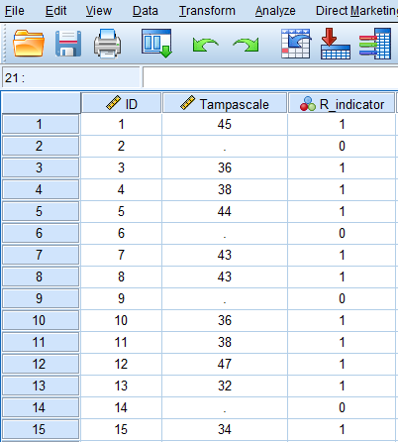
Figure 3.1: The missing data in the Tampa scale variable coded according to the missing data indicator variable.
Using the missing data indicator variable implies that missing values (or the probability of missing values) can be described by a statistical model. This model may consist of variables that have a relationship with the probability of missing data, in this case the indicator variable. A logistic regression model can be used to describe the relationship of variables with the probability of missing data in the Tampa scale variable.
3.0.1 Missing data Mechanisms
By evaluating the missing data patterns, we get insight in the location of the missing values. With respect to the missing data mechanism we are interested in the underlying reasons for the missing values and the relationships between variables with and without missing data. In 1976, Donald Rubin introduced a typology for missing data that distincts between random and non-random missing data situations, which are called Missing Completely At Random, Missing At Random and Missing Not At Random and abbreviated as MCAR, MAR and MNAR respectively (Rubin (1976)).
The key idea behind Rubin’s missing data mechanisms is that the probability of missing data in a variable may or may not be related to the values of other measured variables in the dataset. With probability we loosely mean the likelihood of a missing value to occur, i.e. if a variable has a lot of missing data, the probability of missing data in that variable is high. This probability can be related to other measured or not-measured variables. For example, when mostly older people have missing values, the probability for missing data is related to age. Moreover, the missing data mechanisms also assume a certain relationship (or correlation) between observed variables and variables with missing values in the dataset.
3.0.2 Missing Completely At Random
Data are Missing Completely At Random (MCAR) when the probability that a value is missing, is unrelated to the value of other observed (or unobserved) variables, and unrelated to values of the missing data variable itself. An MCAR example could be that, low back pain patients had to come to a research center to determine their level of disability by performing some physical tests and some of these patients were unable to leave their home, due to the flu. There is no assumed relationship between having the flu and scores on the disability variable which makes that this data is MCAR.
An MCAR missing data situation for the disability variable is visualized in the MCAR column in Figure 2.7 below. Note that in real live we do not know the completely observed data, but for educational reasons, the completely observed values of the disability variable are displayed as well. We can observe that in the MCAR situation an equal number of lower and higher values of the disability variable are missing (in total 4 disability scores are missing, 2 for lower and 2 for higher values). Also, the missing data in the disability variable do not seem to be related to the values of another variable like pain; an equal number of disability values is missing for patients with low pain scores as well as for patients with higher pain scores.
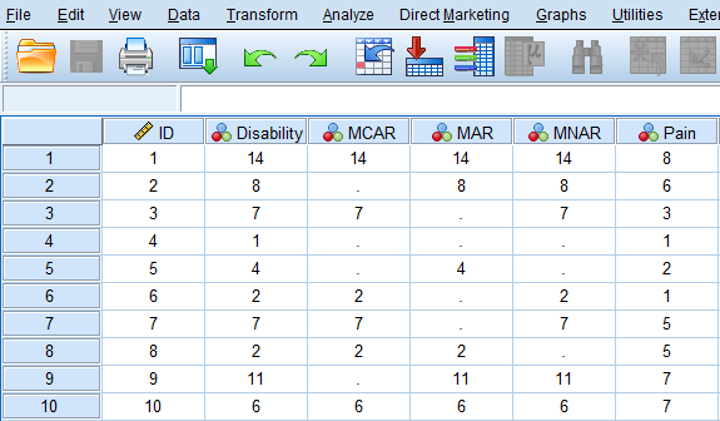
Figure 3.2: Examples of MCAR, MAR and MNAR data.
3.0.3 Missing At Random
Data are Missing At Random (MAR) when the probability that a value for a variable is missing is related to other observed values in the dataset but not to the variable itself. An example of MAR data is presented in the MAR column of Figure 3.2. Now 4 disability scores are missing for pain scores that are ≤ 5. In other words the probability of missing data in the disability variable is higher for patients with lower pain scores. However, MAR also assumes that within the category of pain scores with values ≤ 5, the disability scores are MCAR, because disability scores are randomly missing for lower and higher values within that category. As a consequence, means and standard deviations do not differ between the observed and missing data for the disability variable. An explanation could be that patients with lower pain scores that were assessed by questionnaires that were filled in at home were less likely to visit the research center to determine their level of disability because they thought that information about their level of disability was not of interest anymore.
3.0.4 Missing Not At Random
The data are MNAR when the probability of missing data in a variable is related to the scores of that variable itself, e.g. mostly high or low scores are missing. In low back pain patients, MNAR data can occur when patients with the highest scores on the disability variable have missing disability values. This is shown in the MNAR column of Figure 3.2. An explanation could be that these patients were not able to visit the research center due to their high level of disability.
MNAR missing data can also occur indirectly through the relationship of the variable with missing data with another variable that is not available in the dataset. For example, it could also be that patients with a high level of disability also have a high fear of moving their back, and for that reason will not visit the research center. In case of a positive relationship between disability and fear of movement, the highest values on the disability variable are than missing. If fear of movement is not measured in the study, the missing data in the disability variable is called MNAR.
The difference with MAR is that with MNAR, the missing data problem cannot be handled by using a technique as Multiple Imputation. However, as with MAR data, MNAR data can also not be verified because for that information about the missing values is needed.
3.0.5 The meaning of data being MAR
In a MAR missing data situation, missing values can be explained by other (observed) variables, like in the example of the disability and pain variables above. Further, it was stated that within the category of pain scores ≤ 5 the disability scores are MCAR. This means that the mean difference of disability between persons with low pain scores and high pain scores is the same between the observed and missing data. This is illustrated by using the mean disability values in the tables below.
In the tables the means of the disability variables are presented for the subgroups of patients with pain scores ≤ 5 and > 5. There is MAR missing data in the disability variable in the subgroup of patients with pain scores ≤ 5. The consequence is that the means are equal between the groups with complete and missing data, i.e 9.26 and 9.23 respectively. Consequently this also accounts for the mean difference of disability between patients with complete and missing data, i.e 5.3 and 5.2 respectively.
|
|
However, it is not possible to test this assumption, because for that you need information of the missing values and in real-life, that is not possible. In general, excluding MAR data leads to biased parameter estimates and false results for your statistical tests. A missing data method that works well with MAR data is Multiple Imputation (Chapter 4).
3.0.6 Auxiliary Variables
The MAR assumption can be made more plausible by including additional variables in the imputation model (Baraldi and Enders (2010)). Therefore, it is advised, to include extra variables that have a relationship with the missing data rate in other variables, i.e. have a relationship with the probability of missing data or that have a relationship (correlated) with the variables that contain the missing values (Collins, Schafer, and Kam (2001)). These additional variables can help dealing with missing data as well and are called auxiliary variables.
3.1 Missing Data evaluation
The performance of missing data methods depends on the underlying missing data mechanism. As previously descirbed, the difference between the MCAR and not-MCAR mechanisms depend on the relationship between the probability for missing data and the observed variables. If this relationship cannot be detected we assume that the data is MCAR. If there is some kind of relationship, the missing data may be MAR or MNAR. In practice we study and measure outcomes and independent variables that are related to each other. This makes the MAR assumption mostly an accepted “working” missing data assumption in practice.
It is important to think about the most plausible reasons for the data being missing. For example, when cognitive scores are assessed during data collection and these are mostly not filled out by people that have decreased cognitive functions, the missing data can be assumed to be MNAR. Statistical tests can also be used to get an idea about the missing data mechanism. In these statistical tests, the non-responders (i.e., participants with missing observations), can be compared to the responders on several characteristics. By doing this, we can test whether the missing data mechanism is likely to be MCAR or not-MCAR. There are several possibilities to compare the non-responders with the responders groups, for example using t-tests or Chi-square tests, logistic regressions with the missing data indicator as the outcome, or Little’s MCAR test (Little (1988)).
Researchers need to be aware that the assumptions that underlie an independent t-test, logistic regression, and Chi-square test apply to these missing data mechanism procedures as well. This means that the residuals are assumed to be normally distributed and that the tests rely on a decent sample size.
3.1.1 Missing data Evaluation in SPSS
3.1.1.1 Descriptive Statistics
Descriptive information of variables can be obtained via the following options of the Missing Value Analysis (MVA) module in the SPSS menu:
Analyze -> Missing Value Analysis…
Transfer all variables in the correct Quantitative and Categorical variables window and then click
Descriptives option -> Univariate statistics -> Continue.
The following table will appear in the SPSS Output window.
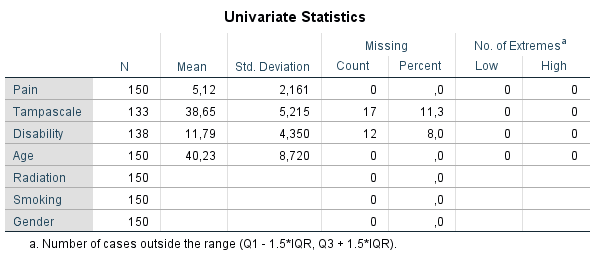
Figure 3.3: Univariate descriptive statistics of variables with and without missing data.
Under the column N, the information of all cases in the dataset are displayed. Further, for all continuous variables information about the Mean and Standard deviation are displayed. No descriptive information is given for categorical variables. Under the column Missing we get the number and percentage of missing values in each variable and under the column No. of Extremes we get information of cases that fall outside a range, which is specified under the table. These descriptive information of variables with missing data provide a quick overview of the amount of missing data in each variable. However, it does not provide us information about the relationship between variables with complete and missing data and therefore does not give us an idea about the potential missing data mechanism. Methods as T-tests, regression or Little’s MCAR test, discussed in the next section, can better be used for that purpose.
3.1.1.2 T-test procedure
For the t-test procedure, SPSS first separates cases with complete and missing values by creating an indicator variable of variables that ontain missing values. This can be all type of variables. Then, group means of other (only continuous) variables are compared by using the indicator variable as group variable within the t-test procedure. You can apply his procedure by following:
Analyze -> Missing Value Analysis… -> Descriptives -> click “t-tests with groups formed by indicator variables” and “include probabilities in table” -> Continue -> OK (Figure 2.15).
Figure 3.4: The T-test procedure as part of the Missing Value Analysis menu
SPSS will produce the following table.
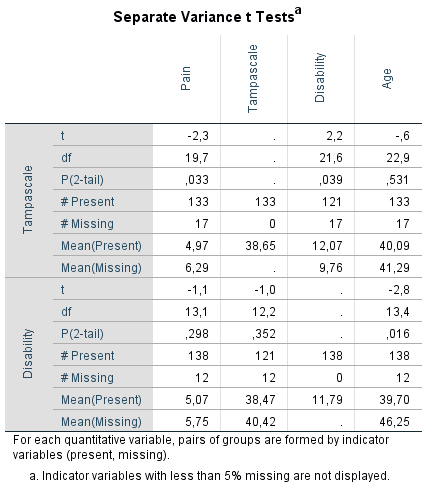
Figure 3.5: Output table of the t-test procedure.
On the left side of the output table the names of the variables with missing values are presented which are the Tampa scale and Disability variables. Of these variables, indicator variables are defined which are used to compare group means of other variables, that can be tested for significance using independent t-tests. The results of these t-tests are shown in the table according to the information in separate rows on the left side with the t-value (t), degrees of freedom (df), P-value (P(2-tail)), numbers of observed and missing cases (# Present and # Missing) and means of observed and missing cases (Mean(Present) and Mean(Missing)) presented. The variables for which the indicator groups are compared, are listed in the columns of the table and are the Pain, Tampa scale, Disability and Age variables. For the Tampa scale variable that contain missing values, only the observed mean is presented, because for the missing cases the values are missing. Note that in the row of the Tampa scale variable the means of the Disability variable can still be compared between the observed and missing cases, because they do not miss values for exactly the same cases. Figure 3.5 shows that patients that have observed values on the Tampa scale variable (row Mean(Present)) differ significantly from patients with missing values on the Tampa scale variable (row Mean(Missing)) on Pain (P(2-tail = 0.033) and Disability (P(2-tail = 0.039). When we look at the means of the Pain variable, we see that the mean of patients with missing values on the Tampa scale variable is higher compared to the mean of patients with observed scores. This means that there is a higher probability of missing data on the Tampa scale variable for patients with higher pain scores. If Tampa scale and Pain scores are correlated, the missing values on the Tampa scale variable can also be explained by the Pain score variable. This is also the case for the Age variable, however, the t-test is not significant. For the Disability variable, it is the other way around. We see more missing data on the Tampa scale variable for lower Disability scores.
In the Missing Value Analysis and subsequently the descriptives option, another possiblity is to select “Crosstabulations of categorical and indicator variables”. In that case a table is displayed to compare the percentage of present and missing data for categorical variables related to the indicator variable similarly defined as explained above. An example can be found in Figure 3.6 that prodces SPSS when a missing data indicator variable is used for the Radiation variable, where for 11 cases data is missing.
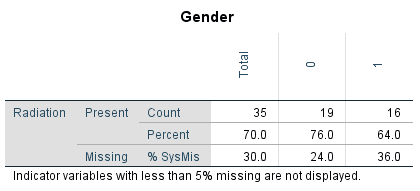
Figure 3.6: Output table of the Crosstabulations procedure.
You see in the table that Radiation values are more frequently missing for males (coded as 1 on the Gender variable) than for females (coded as 0). Note that for these tables, the Chi-square tests and p-values are not performed. These have to be obtained via the usual Crosstabs function, using a self-generated missing data indicator variable.
3.1.1.3 Logistic Regression Analysis
With logistic regression analysis, we can evaluate if the probability of missing data is related to other variables in the data (Ridout (1991)). For this procedure, we first generate an indicator variable that separates the subjects with missing values from the participants with observed values. This indicator variable can be used as the dependent variable in a logistic regression analysis. A backward regression can be used to determine the strongest predictors of missing data. The output for the logistic regression with the Tampa scale variable as the indicator outcome variable is presented in the table below:
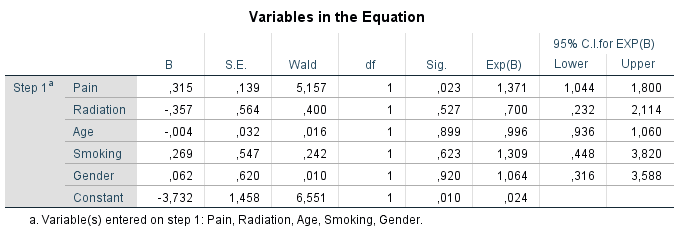
Figure 3.7: Logistic regression analysis with variable that contain missing data as the outcome variable.
The variable Pain is significantly related to the missing data indicator variable of the Tampa scale variable, which indicates that the probability for missing data in the Tampa scale variable can be explained by the Pain variable. The positive coefficient of 0.315 indicates that the probability of missing data on the Tampa scale variable is higher for higher Pain scores. The other variables do not show a significant relationship with missing data on the Tampa scale variable. This logistic regression analysis procedure can be repeated for each variable with missing values in the dataset.
3.1.1.4 Little’s MCAR test in SPSS
Another possibility is to use a test that was developed by Roderick Little: Little’s MCAR test. This test is based on differences between the observed and estimated means in each missing data pattern. This test is developed for continuous data. We use it for the data in Figure 2.1. The test can be applied via:
Analyze -> Missing Value Analysis…-> select the continuous variables -> Select EM in the Estimation group -> OK

Figure 3.8: EM selection in the Missing Value Analysis menu.
The following table that is called EM Means can be found in the output window of SPSS. Under the table the result of Little’s MCAR test is displayed (tables that provide information of univariate statistics and a summary of estimated means and standard deviations are also provided. Further, tables that are called EM Covariances and EM Correlations are also generated, but they provide the same results for Little’s MCAR test as under the EM Means table. These tables are not shown)

Figure 3.9: Output tables with information of Little’s MCAR test.
3.1.2 Missing data Evaluation in R
3.1.2.1 Little’s MCAR test in R
Little´s MCAR test is available in the BaylorEdPsych package as the LittleMCAR function. To apply the test, we select only the continuous variables. We use it for the same dataset as in the previous paragraph. The p-value for the test is not-siginificant, indicating that the missings seem to be compeletely at random.
library(haven)
dataset <- read_sav("data/CH2 example.sav")
library(BaylorEdPsych)
LittleMCAR(dataset[,c("Pain", "Tampascale","Disability", "GA")])## this could take a while## $chi.square
## [1] 0.7537406
##
## $df
## [1] 3
##
## $p.value
## [1] 0.8604966
##
## $missing.patterns
## [1] 2
##
## $amount.missing
## Pain Tampascale Disability GA
## Number Missing 0 0 0 5.0
## Percent Missing 0 0 0 0.1
##
## $data
## $data$DataSet1
## Pain Tampascale Disability GA
## 1 9 45 20 8
## 2 6 43 10 36
## 3 1 36 1 8
## 5 6 44 14 8
## 6 7 43 11 29
## 8 6 43 11 34
## 9 2 37 11 8
## 10 4 36 3 38
## 11 5 38 16 8
## 12 9 47 14 8
## 13 0 32 3 42
## 14 6 38 12 8
## 15 3 34 13 39
## 17 3 35 11 26
## 18 1 31 1 8
## 19 2 31 7 8
## 20 4 32 9 28
## 22 5 39 12 8
## 23 4 34 8 8
## 24 8 47 13 8
## 25 5 36 6 35
## 26 5 38 16 8
## 27 9 48 23 8
## 28 3 36 3 36
## 30 6 37 16 40
## 31 10 43 21 8
## 32 4 37 8 39
## 33 10 42 20 8
## 34 2 37 3 37
## 35 6 43 12 8
## 36 3 38 7 8
## 37 8 47 8 35
## 38 3 38 6 8
## 39 3 39 8 33
## 40 7 44 15 8
## 41 7 45 10 32
## 42 6 40 12 8
## 43 7 40 16 8
## 44 1 35 2 34
## 45 9 41 19 8
## 46 5 41 17 38
## 47 6 43 11 41
## 48 3 39 9 33
## 49 2 33 6 8
## 50 8 44 19 32
##
## $data$DataSet2
## Pain Tampascale Disability GA
## 4 5 38 14 NA
## 7 8 43 18 NA
## 16 6 42 8 NA
## 21 5 39 13 NA
## 29 2 36 9 NAOf course T-tests and Regression analyses can also be conducted in R. For this the user can use a script file and some coding.
References
Baraldi, A. N., and C. K. Enders. 2010. “An introduction to modern missing data analyses.” J Sch Psychol 48 (1): 5–37.
Collins, L. M., J. L. Schafer, and C. M. Kam. 2001. “A Comparison of Inclusive and Restrictive Strategies in Modern Missing Data Procedures.” Psychological Methods 6 (3): 330–51.
Little, R. J. A. 1988. “A Test of Missing Completely at Random for Multivariate Data with Missing Values.” Journal of the American Statistical Association 83 (404): 1198–1202.
Ridout, M S. 1991. “Testing for Random Dropouts in Repeated Measurement Data.” Biometrics 47 (4): 1617–9; discussion 1619–21.
Rubin, D. B. 1976. “Inference and Missing Data.” Biometrika 63 (3): 581–90.
Rubin, D. 1987. Multiple Imputation for Nonresponse in Surveys. Wiley.