BLOQUE 6: Análisis dinámicos

Clase 1: Introducción a las ecuaciones en diferencias

¿Para qué son necesarios estos modelos?

Por primera vez vamos a tratar de una manera explícita la variable tiempo en los modelos. La idea de que un modelo sea dinámico (es decir, que incluya la variable tiempo) es para que seamos capaces de introducir los conceptos de tendencia o ciclos en el comportamiento de las variables. Y en Economía es clave, puesto que la tendencia y el ciclo son comportamientos muy apreciables en casi todas las variables económicas y sociales.

Entonces, estos modelos podrán ser muy útiles para tratar de predecir. PREDECIR! El objetivo de la ciencia. Casi nada.

Una idea inicial

Seguro que te has encontrado muchas veces en redes sociales pruebas como esta:

Sigue la secuencia: \[ 2,4,3,... \]

y, por supuesto, uno puede pensar que hay muchas opciones para continuarla. Una manera de trabajar en cualquier problema es establecer un modelo por hipótesis. Una vez tienes el modelo, lo ajustas a los datos y, si funciona con la información que tienes, tratas de PREDECIR, que es de lo que se trata con este ejercicio.

Vamos a imaginar que el valor siguiente de la serie depende del anterior. Por ejemplo, para “formalizar” algo las cosas, vamos a decir que la serie de números se llamará \(x\) y el subíndice indicará el número de orden de los valores. Entonces, tenemos: \[ x_{0}=2,x_{1}=4,x_{2}=3 \]

y nos gustaría saber \(x_{3},x_{4},...,\) etc.

Nuestra hipótesis va a ser que el valor “nuevo” dependerá del anterior. Para empezar por un modelo sencillo, elijamos una ecuación lineal:

\[ x_{nuevo}=ax_{viejo}+b \]

De esta forma, tendremos que

\[ \begin{cases} x_{1}=ax_{0}+b\\ x_{2}=ax_{1}+b \end{cases} \]

y sustituyendo los valores que conocemos:

\[ \begin{cases} 4=a2+b\\ 3=a4+b \end{cases} \]

lo cual nos queda un sistema (compatible determinado) donde \(a=-1/2\) y \(b=5\). Como estos parámetros hacen que el sistema sea compatible con los datos, diremos que tenemos un modelo que explica nuestros datos disponibles. Lo podemos, entonces, usar para generalizar el comportamiento de esta serie de datos:

\[ x_{t+1}=-\frac{1}{2}x_{t}+5 \]

Donde \(t=0,1,2,3,....\) Por lo que, si tratamos de predecir por dónde irá la serie, sabiendo que \(x_{2}=3,\)

\[ x_{4}=-\frac{1}{2}x_{3}+5\Rightarrow x_{4}=-\frac{3}{2}+5=3.5 \]

Otro ejemplo: una hucha

Vamos a imaginar que en nuestra cuenta corriente ingresamos todas las semanas 10 euros. Entonces, la variable “tiempo” serán las semanas y la semana “inicial” la llamaremos “semana cero”. Entonces, nuestra cuenta tendrá esta pinta:

t	ingreso	saldo
0	10	10
1	10	20
2	10	30
…	…	…
T	10	\((T-1)\times 10\)

si queremos escribir estas operaciones contables utilizando una ecuación, esta podría ser :

\[ x_{t+1}=x_{t}+10 \]

Es decir, \(x\) es la cantidad de dinero. Esta ecuación se puede leer como:

El dinero que tendré la semana que viene \(x_{t+1}\) es igual al dinero que tengo esta sema \(x_{t}\) más el dinero que introduzco en la cuenta: \(10.\)

La pregunta que surge ahora, por lo tanto, es ¿cuánto dinero tendrás en una semana \(t\) cualquiera? Para verlo, vamos a echar cuentas empezando desde \(t=0.\)

t	Ecuación
0	\(x_{0}\)
1	\(x_{1}=x_{0}+10\)
2	\(x_{2}=x_{1}+10\)	\(x_{2}=x_{0}+10+10\)
…	…	…
T		\(x_{T}=x_{T-1}+10\)

Si te das cuenta, podemos “inferir” una ley de comportamiento:

\[ x(T)=x_{0}+10T \]

con esta sencilla ecuación, podemos obtener el valor de nuestros ahorros para cualquier momento de tiempo \(T\).

Las ecuaciones en diferencias

Estas ecuaciones que hemos introducido se conocen como “ecuaciones en diferencias finitas lineales de orden 1” o ecuaciones en diferencias de orden 1, para abreviar. Son del tipo :

\[ x_{t+1}=ax_{t}+b \]

o también, equivalentemente

\[ x_{t}=ax_{t-1}+b \]

A esta ecuaci?n la llamaremos una ecuación en diferencias lineal de orden 1. Lo de “las diferencias” tiene su origen en la inclusión de \(x_{t+1}\) y \(x_{t}\) en la ecuación (estamos calculando, en realidad, lo que ocurre al sufrir el paso del tiempo, es decir, la diferencia entre el periodo \(t+1\) y el periodo \(t\), o el periodo \(t\) y el \(t-1\).

Resolver una ecuación en diferencias implica buscar una función del tiempo que da, a cada valor de \(t\) un valor para \(x\)

Por otro lado, estaremos muy interesados en analizar de manera cualitativa la ecuación correspondiente. Para ello, deberemos definir un concepto necesario que es el “equilibrio” de una ecuación. Este valor va a ser una referencia de la tendencia de la secuencia a largo plazo.

Definición del equilibrio

Llamamos equilibrio \(x^{*}\) de una ecuación en diferencias al valor de la solución a largo plazo. Para ello, sustituímos \(x_{t+1}=x^{*}\) y \(x_{t}=x^{*}\) en la ecuación y obtenemos:

\[ x^{*}=ax^{*}+b \]

donde

\[ x^{*}=\frac{b}{(1-a)} \]

Nota que, para que haya equilibrio, \(a\neq1.\)

Entonces, el equilibrio es un valor constante, de referencia, al que la variable va a tender a largo plazo si el modelo es estable. Si no es estable, la variable “pasará por el equilibrio” pero nunca se quedará en él. Esto lo iremos viendo en diferentes modelos.

Resolución de ecuaciones en diferencias lineales de orden 1

Vamos a ver cómo resolver las ecuaciones del tipo \[ x_{t+1}=ax_{t}+b \]

en sus diferentes versiones de interés.

Caso 1: \(a\neq1\),\(b=0\)

En este caso, tenemos una ecuación lineal de primer orden y homogénea (se llama homogéneo porque \(b=0\)). Vamos a resolver como hicimos en el caso de la hucha. Para ello, suponemos que tenemos un valor “inicial” es decir, conocemos \(x_{0}.\)

\[ x_{1}=ax_{0} \]

\[ x_{2}=ax_{1}=a\left(ax_{0}\right)=a^{2}x_{0} \]

\[ x_{3}=ax_{2}=a\left(a^{2}x_{0}\right)=a^{3}x_{0} \]

Entonces, si seguimos iterando, para cualquier \(t\), obtendremos

\[ x_{t}=a^{t}x_{0} \]

Nota que el equilibrio de esta ecuación es \(x^*=0\)

caso 2 \(a\neq1\),\(b\neq0\)

Esta ecuación no es homogénea, ya que \(b\neq0:\)

\[ x_{t+1}=ax_{t}+b \]

Para resolver esta ecuación, vamos a definir primeramente su equilibrio.

\[ x^{*}=\frac{b}{(1-a)} \]

La solución de esta ecuación es fácil obtenerla así (como una resta del cole), donde calculamos la diferencia de la ecuación habitual menos una solución particular de esta (ya que el equilibrio es un valor que resuelve la ecuación):

	\(x_{t+1}=\)	\(ax_{t}\)	\(+b\)
\(\color{red}-\)	\(x^{*}=\)	\(ax^{*}\)	\(+b\)

	\(x_{t+1}-x^{*}=\)	\(a\left(x_{t}-x^{*}\right)\)	\(+0\)

Por un momento, nos desaparece la \(b\) y la solución es muy sencilla, puesto que si llamamos \(y_{t}=x_{t}-x^{*}\), entonces,\(y_{t+1}=x_{t+1}-x^{*}\) y la ecuación se convierte en

\[ y_{t+1}=ay_{t} \]

Esta ya la sabes resolver: \[ y_{t}=a^{t}y_{0} \]

De tal manera que, deshaciendo el cambio:

\[ x_{t}-x^{*}=a^{t}\left(x_{0}-x^{*}\right) \]

llegamos también a \[ x_{t}=x^{*}+a^{t}\left(x_{0}-x^{*}\right) \]

Si te das cuenta, esta ecuación responde al modelo inicial de la serie “del test de inteligencia” \[ x_{t+1}=-\frac{1}{2}x_{t}+5 \]

por lo que la solución de esta ecuación es:

\[ x_{t}=3.33+(-\frac{1}{2})^{t}\left(2-3.33\right) \]

Como ves, la ventaja fundamental de tener la solución es que, de forma sencilla, podríamos saber cuánto vale la serie si \(t\) es igual a cualquier número, por ejemplo, ¿Cuánto vale \(x_{105}\)?

caso 3 \(a=1\),\(b\neq0\)

En este particular caso, tenemos

\[ x_{t+1}=x_{t}+b \]

Para resolver esta ecuación, debemos notar que no tenemos equilibrio. Es, de hecho, el caso general del modelo “de la hucha”

\[ x_{1}=x_{0}+b \]

en el siguiente periodo,

\[ x_{2}=x_{1}+b \]

pero de antes, sabemos que

\[ x_{2}=x_{0}+b+b=x_{0}+2b \]

si seguimos iterando, llegamos a la conclusión de que

\[ x_{t}=x_{0}+bt \]

Extra: la resolución en Excel

Los modelos de ecuaciones en diferencias pueden resolverse en Excel de forma muy sencilla. Esto puede servirte para comprobar si lo has resuelto bien. Vamos a ver un ejemplo:

\[ x_{t+1}=0.5x_{t}+3 \]

con \(x_{0}=5\) (valor inicial).

De acuerdo con la teoría, el equilibrio es \(x^{*}=\frac{3}{(1-0.5)}=6\). Entonces, la solución de nuestra ecuación en diferencias:

\[ x_{t}=6+0.5^{t}(x_{0}-6) \]

FIG1.Ejemplo de cómo escribirlo en Excel

En esta pantalla, lo que hemos hecho es escribir esta ecuación \[ x_{t+1}=0.5x_{t}+3 \] y resolverla mediante Excel.

A continuación, vamos a escribir en Excel la solución que obtuvimos:

FIG2.Ejemplo de cómo escribirlo en Excel

\[ x_{t}=6-0.5^{t} \]

debería dar el mismo resultado.

¿cuál es, entonces, la ventaja de usar esta ecuación \(x_{t}=6-0.5^{t}\) versus usar \(x_{t+1}=0.5x_{t}+3\)? Si te das cuenta, en Excel tardas lo mismo. Pero si tienes que hacer un cálculo a mano, y te pido cuál es el valor que toma \(x\) en el momento 100?. Si usas la ecuaci?n de la solución, lo tienes en un segundo: \[ x_{100}=6-0.5^{100} \]

Sin embargo, con la ecuación inicial, tendrás

\[ x_{100}=0.5x_{99}+3 \]

Y necesitas saber cuánto vale \(x_{99}.\) Pero \(x_{99}\) depende de \(x_{98}\)y así sucesivamente.

CLASE 2: La convergencia al equilibrio: análisis cualitativo

Uno de los intereses de estudiar estas ecuaciones es tratar de hacer predicciones que, en este caso, tengan algún sentido económico. ¿Qué tipos de predicciones nos interesan?

¿Qué ocurrirá con mi variable dentro de 3 periodos?

¿Qué pasará a largo plazo con esta?

¿Sufrirá fluctuaciones o tendrá un comportamiento monótono?

Ejercicio

Resuelve, utilizando Excel, las siguientes ecuaciones en diferencias y comenta cuáles de ellas convergen al equilibrio y qué criterio satisfacen. Resuelve para \(x_{0}=5\) y para \(t=1,2,....,20\) y haz el gráfico correspondiente

\[ x_{t}=0.5x_{t-1}+3 \]

\[ x_{t}=-0.5x_{t-1}+3 \]

\[ x_{t}=1.5x_{t-1}+3 \]

\[ x_{t}=-1.5x_{t-1}+3 \]

\[ x_{t}=0.5x_{t-1} \]

\[ x_{t}=-0.5x_{t-1} \]

\[ x_{t}=1.5x_{t-1} \]

\[ x_{t}=-1.5x_{t-1} \]

sol

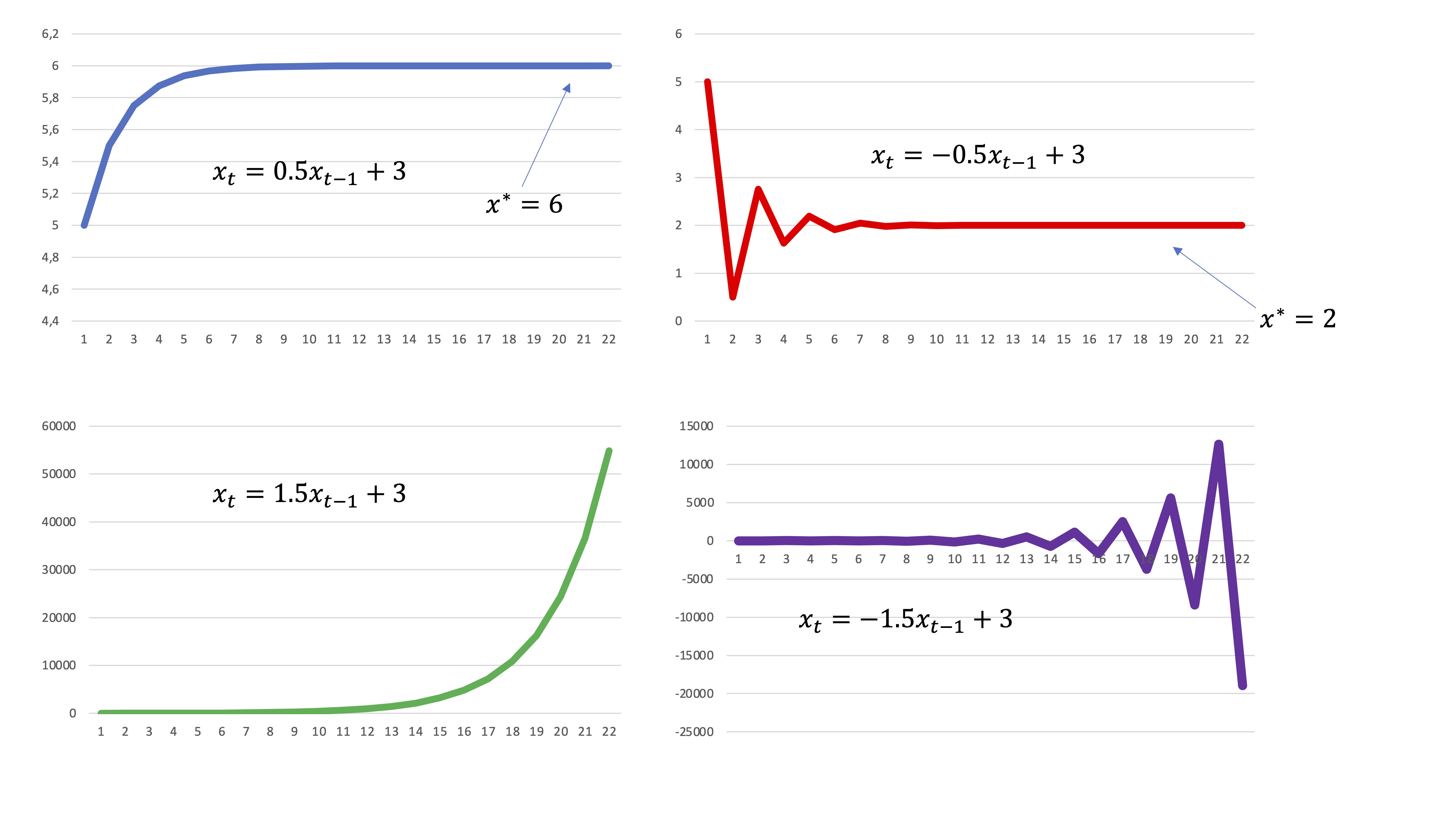
FIG1.

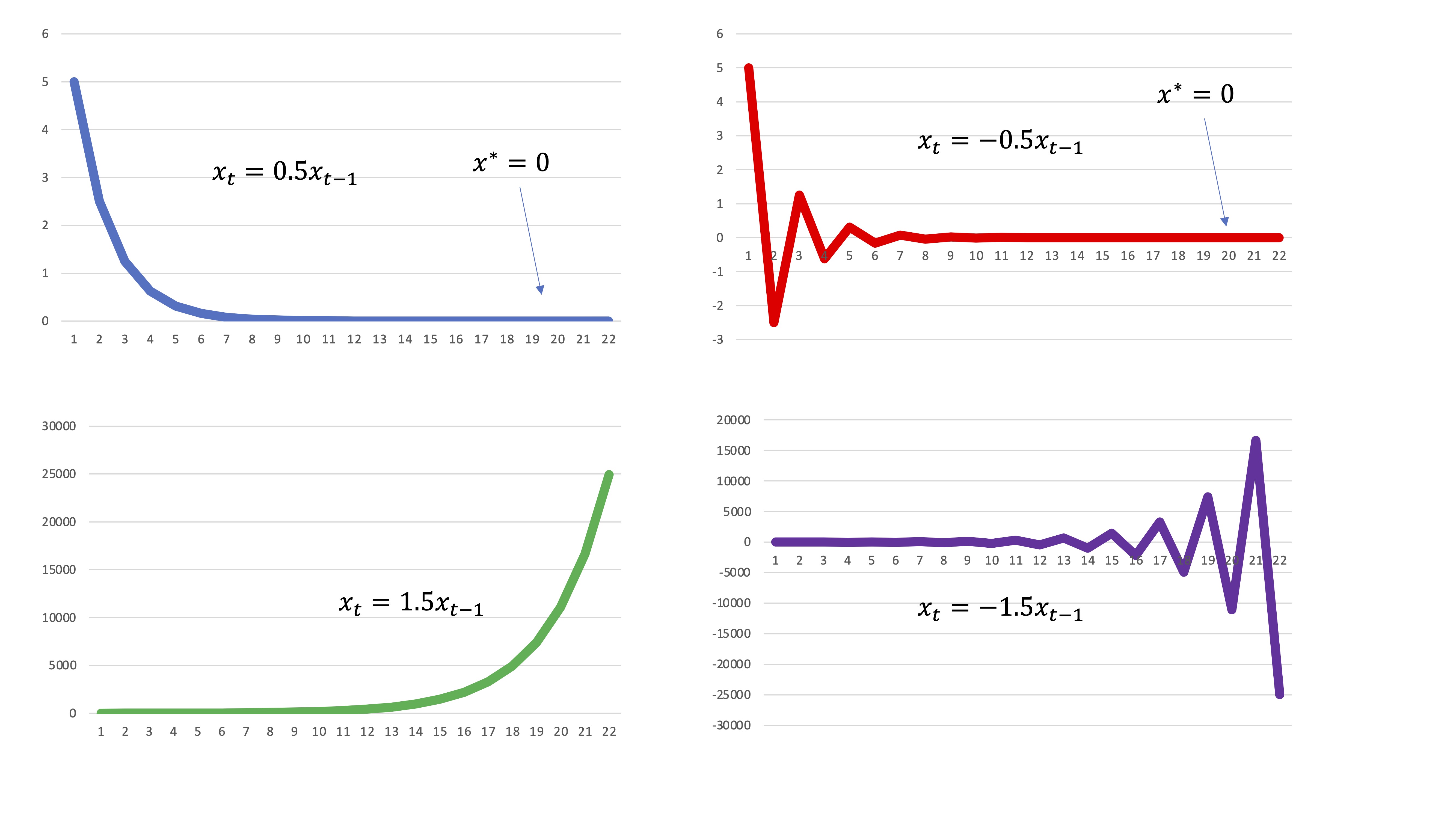
FIG2.

A la primera pregunta responderemos usando la solución general de la ecuación (ya sabes hacerlo). Sin embargo, a las otras dos preguntas, responderemos analizando los parámetros. Hacer esto se llama “analizar cualitativamente” la ecuación en diferencias. Con los gráficos que has hecho anteriormente en Excel, te resultará sencillo pensar sobre ello.

Caso 1

\[ x_{t+1}=ax_{t} \]

Equilibrio: \(x^{*}=0\)

Solución general: \(x_{t}=a^{t}x_{0}\)

si \(t\rightarrow\infty\)?

Entonces,

si \(\left|a\right|<1\), es asintóticamente estable (converge al equilibrio, que es cero) y si \(\left|a\right|>1\), es asintóticamente inestable (diverge del equilibrio)

Caso 2 \[ x_{t+1}=ax_{t}+b \]

equilibrio: \(x^{*}=\frac{b}{1-a}\)

solución general: \(x_{t}=x^{*}+a^{t}\left(x_{0}-x^{*}\right)\)

si \(t\rightarrow\infty\)?

Entonces,

si \(\left|a\right|<1\), es asintóticamente estable (converge al equilibrio, que es \(x^{*}=\frac{b}{1-a}\)) y si \(\left|a\right|>1\), es asintóticamente inestable (diverge del equilibrio)

Pero, una cosa, mira qué ocurre si \(a<0\). En cualquiera de estas dos fórmulas de la solución general

\[ \begin{cases} x_{t}=a^{t}x_{0}\\ x_{t}=x^{*}+a^{t}\left(x_{0}-x^{*}\right) \end{cases} \]

cuando \(a\) (negativo) lo eleves a potencia par, el resultado será positivo mientras que si lo elevas a potencia impar, será negativo (por ejemplo, \(x_{\text{1}}=-0.5x_{0},x_{2}=0.25x_{0},x_{3}=-0.125x_{0},\)etc… Entonces, si el parámetro es negativo, la solución de la ecuación decimos que presenta ciclos. Estos ciclos pueden ser convergentes (al equilibrio) o divergentes. Lo has podido comprobar con las soluciones hechas en Excel, en la FIG1 y la FIG2

Clase 3: Ecuaciones en diferencias de segundo orden

Vamos a “complicar” algo más nuestro modelo. Vamos a permitir que ahora haya un retardo temporal más en la ecuación en diferencias. Por ejemplo:

Una homogénea de segundo orden

\[ x_{t}+a_{1}x_{t-1}+a_{2}x_{t-2}=0, \]

recuerda que puede escribirse también así: \[ x_{t+2}+a_{1}x_{t+1}+a_{2}x_{t}=0. \]

Una no homogénea:

\[ x_{t}+a_{1}x_{t-1}+a_{2}x_{t-2}=b, \]

\[ x_{t+2}+a_{1}x_{t+1}+a_{2}x_{t}=b \]

Una no homogénea cuyo término independiente es una función de \(t\) (llamada no autónoma)

\[ x_{t}+a_{1}x_{t-1}+a_{2}x_{t-2}=b^{t+2}, \] o también \[ x_{t+2}+a_{1}x_{t+1}+a_{2}x_{t}=b^{t} \]

Como ves, volvemos a tener homogéneas y no homogéneas. En el caso de las no homogéneas, podemos tener términos independientes que sean constantes (lo que llamamos una ecuación autónoma) mientras que podemos tener términos independientes que sean una función de \(t\) (en la tabla tienes un ejemplo de los muchos que podrían ponerse). No quiere decir que en el caso de primer orden no puedas tener ecuaciones no autónomas, simplemente, si sabes resolverlas en el caso de segundo orden, no tendrás ningún problema en resolver las de primer orden.

Solución de la homogénea

La solución de la ecuación homogénea pasa por la obtención del polinomio característico. Como hemos visto antes, las soluciones de estas ecuaciones tienen la pinta \(x_{t}=r^{t}x_{0}\). Si sutituímos convenientemente,

\[ x_{t+2}+a_{1}x_{t+1}+a_{2}x_{t}=0\Rightarrow r^{t}x_{0}+a_{1}r^{t+1}x_{0}+a_{2}r^{t+2}x_{0}=0 \]

Entonces, para que esto sea solución, sacando factor común: \[ r^{t}(r^{2}+a_{1}r+a_{2})=0 \]

De aquí, obtenemos lo que conocemos como la ecuación característica, si \(r\neq0\):

\[ (r^{2}+a_{1}r+a_{2})=0 \]

De esta ecuación, obtenemos sus raíces (en este curso, sólo trabajaremos con raíces reales).

Caso 1: raíces reales distintas

La solución de la homogénea será del tipo

\[ x_{t}=A(r_{1})^{t}+B(r_{2})^{t} \]

donde \(r_1,r_2\) son las raíces de la ecuación característica. Deberás buscar el valor de \(A\),\(B\) utilizando-para ello- información de \(x_0\) y de \(x_1\).

Caso 2: raíces reales dobles

En este caso, la solución de la homogénea, será

\[ x_{t}=(A+Bt)r^{t} \]

donde \(r\) es la raíz doble de la ecuación característica. Deberás buscar el valor de \(A\),\(B\) utilizando-para ello- información de \(x_0\) y de \(x_1\).

Estabilidad de las ecuaciones en diferencias de orden 2

La ecuación en diferencias convergerá al equilibrio (si lo tiene) o será estable si y sólo si:

Entonces,

Las raíces de la ecuación característica son AMBAS en valor absoluto menores que uno. En cualquier otro caso, diremos que la ecuación es inestable

Caso 3: Solución general=solución homogénea + solución particular

Hay un resultado muy útil en el caso de las ecuaciones en diferencias lineales (las que estudiamos este curso). La solución general es igual a la suma de la solución de la correspondiente ecuación homogénea más una solución particular. Es decir:

\[ x_{t}=x_{t}^{h}+x_{t}^{p} \]

Una solucón particular es una función (o constante) que forme parte de \(x_{t}\).

En el caso de la ecuación autónoma, tenemos un punto claro que resuelve, de forma particular, la ecuación: el equilibrio. En este caso, el equilibrio será el valor de \(x^{*}\) tal que

\[ x^{*}+a_{1}x^{*}+a_{2}x^{*}=b\Rightarrow x^{*}=\frac{b}{(1+a_{1}+a_{2})} \]

Para que este equilibrio exista, nota que \(a_{1}+a_{2}\neq-1\).

Esta es, entonces, una solución particular. Si queremos resolver la ecuación en diferencias sólo tenemos que resolver la homogénea y, a continuación, sumarle el equilibrio.

Ejemplo: Resuelve \[ x_{t}=5x_{t-1}-6x_{t-2}+10 \]

La homogénea consiste en: \(x_{t}-5x_{t-1}+6x_{t-2}=0\)

La ecuación característica \(r^{2}-5r+6=0\) donde \(r_{1}=3,r_{2}=2\)

La solución de la homogénea es, entonces \(x_{t}^{h}=A3^{t}+B2^{t}\)

Por otro lado, tenemos que calcular una particular. Como es autónoma y con equilibrio, este equilibrio es una solución particular:

\(x^{*}=\frac{10}{(1-5+6)}=5\)

La solución general será: \[ x_{t}=A3^{t}+B2^{t}+5 \]

PREGUNTA: ¿Es estable?

RESPUESTA: No, las raíces de la ecuación característica son, en valor absoluto, mayores que uno.

Es posible obtener el valor de \(A\) y \(B\) si nos facilitan el valor de \(x_{0}\)y \(x_{1}.\) ¿Cuál será la solución general si \(x_{0}=10,x_{1}=12\)?

\[ x_{0}=A3^{0}+B2^{0}+5=10\Rightarrow A+B=5 \]

\[ x_{1}=A3^{1}+B2^{1}+5=12\Rightarrow3A+2B=7 \]

Si resuelves el sistema, obtendrás: \[ x_{t}=-3\times3^{t}+8\times2^{t}+5 \]

como solución general.

Ecuación autónoma sin equilibrio

En este otro caso:

\[ x_{t}+2x_{t-1}-3x_{t-2}=16 \]

Nota que \(a_{1}+a_{2}=-1\), por lo que no tenemos equilibrio. En ese caso, debemos buscar otra forma de resolverla. Vamos a proponer una solución particular que tenga esta pinta:

\[ x_{t}=Ct, \] tiene sentido. Al no tener equilibrio, esperamos que la trayectoria tenga una tendencia creciente. De tal forma que tendremos que buscar cuánto vale \(C\). Para ello, nota que \(x_{t-1}=C(t-1)\) y que \(x_{t-2}=C(t-2)\). Ahora, sustituyendo en la ecuación:

\[ Ct+2C(t-1)-3C(t-2)=16 \]

Donde obtenemos que \[ 4C=16\Rightarrow C=4 \]

por lo que \[ x_{t}=4t \]

es, entonces, una solución particular. Si queremos resolver la ecuación en diferencias sólo tenemos que resolver la homogénea y, a continuación, sumarle la particular:

La homogénea consiste en: \(x_{t}+2x_{t-1}-3x_{t-2}=0\)

La ecuación característica \(r^{2}+2r-3=0\) donde \(r_{1}=-3,r_{2}=1\)

La solución de la homogénea es, entonces \(x_{t}^{h}=A(-3)^{t}+B\)

Por otro lado, ya tenemos la particular. Entonces, la solución general será

\[ x_{t}=A(-3)^{t}+B+4t \]

¿Es estable?

RESPUESTA: No, las raíces de la ecuación característica son, en valor absoluto, mayores (o iguales) que uno.

En el caso de la ecuación no autónoma, el término independiente dependerá de \(t\) Por ejemplo:

\[ x_{t}-5x_{t-1}+6x_{t-2}=4^{t}+3 \]

Ahora, una solución particular no puede ser el equilibrio, puesto que esta ecuación no tiene (mira que \(4^{t}\) no es un valor constante y un equilibrio ha de serlo). Si te das cuenta, \(x_{t}-5x_{t-1}+6x_{t-2}=4^{t}+3\) nos está diciendo que, operando con las \(x\), debemos llegar a esta solución \(4^{t}+3\). Lo que se hace es suponer que la solución particular es de esta forma: \(x_{t}^{p}=C4^{t}+D\) y buscamos los valores de \(C\)y \(D\) para que se satisfaga la ecuación y que, por tanto, sea una solución particular. En este caso,

\[ x_{t}=C4^{t}+D \]

\[ x_{t-1}=C4^{t-1}+D \]

\[ x_{t-2}=C4^{t-2}+D \]

Sustituyendo en nuestra ecuación,

\[ C4^{t}+D-5(C4^{t-1}+D)+6(C4^{t-2}+D)=4^{t}+3 \]

sacando factor común: \[ C4^{t}(-5\times 4^{-1}+6\times4^{-2})+D-5D+6D=4^{t}+3 \]

Es decir,

\[ C4^{t}\times\frac{-7}{8}+2D=4^{t}+3 \]

Para que se satisfaga esta igualdad, \[ C=\frac{-8}{7},D=\frac{3}{2} \]

¡Ya tenemos la solución particular! \[ x_{t}=\frac{-8}{7}4^{t}+\frac{3}{2} \]

Si queremos resolver la ecuación en diferencias sólo tenemos que resolver la homogénea y, a continuación, sumarle la particular:

Ejemplo: Resuelve

\[ x_{t}=5x_{t-1}-6x_{t-2} \]

La homogénea consiste en: \(x_{t+2}-5x_{t+1}+6x_{t}{\color{red}=0}\)

La ecuación característica \(r^{2}-5r+6=0\) donde \(r_{1}=3,r_{2}=2\)

La solución de la homogénea es, entonces \(x_{t}^{h}=A3^{t}+B2^{t}\)

Por otro lado, tenemos que calcular una particular. La solución anterior es una particular

\(x_{t}=\frac{-8}{7}4^{t}+\frac{3}{2}\)

La solución general será: \[ x_{t}=A3^{t}+B2^{t}+\frac{-8}{7}4^{t}+\frac{3}{2} \]

Es posible obtener el valor de \(A\) y \(B\) si nos facilitan el valor de \(x_{0}\)y \(x_{1}.\) ¿Cuál será la solución general si \(x_{0}=10,x_{1}=12\)?

¿Qué funciones usar para las no autónomas?

En definitiva, si tu ecuación es de este estilo:

\[ x_{t}+a_{1}x_{t-1}+a_{2}x_{t-2}=b^{t} \]

Prueba con \(x_{t}=Cb^{t}\)

Si es de este estilo

\[ x_{t}+a_{1}x_{t-1}+a_{2}x_{t-2}=b_{1}^{t}+b_{2}, \]

prueba con \(x_{t}=Cb^{t}+D\)

Si es un polinomio:

\[ x_{t}+a_{1}x_{t-1}+a_{2}x_{t-2}=b_{1}t^{2}+b_{2} \]

prueba con \(x_{t}=Cb_{1}t^{2}+Db_{1}t+E\) (con polinomios es aconsejable introducir todas las potencias aunque no aparezcan explícitamente).

NOTA: si una de las raíces coincide con \(b\), entonces debes probar con \(x_{t}=C\times t\times b^{t}\).

Clase 4: Ecuaciones Diferenciales (I)

Ya pudimos ver en la parte 1 de este tema que podíamos considerar el tiempo como una variable discreta, esto es, una sucesión de números naturales \[ t=\{0,1,2,3,4,5....\} \]

o una variable continua, de tal forma que \[ t\in [0,10] \]

indica cualquier momento en el tiempo desde el momento \(0\) hasta el mmomento \(10\) (por ejemplo, \(t=1,387)\), algo que cuando se considera el tiempo como una variable discreta, no puede ocurrir.

Ecuaciones diferenciales de primer orden

Si una función \(x\), depende del tiempo (es decir, \(x(t)\)), donde esa función puedes pensar que sea la cotización bursátil que, a cada momento \(t\) nos proporciona un valor del mercado, podemos analizar cómo cambia ante incrementos “marginales” de la variable tiempo. Es decir, usaremos la derivada:

\[ \frac{\mathrm{d}x}{\mathrm{d}t} \]

La derivada nos dice: “el incremento de la variable \(x\) si el tiempo aumenta una pizca. Por cierto, como la \(x\) en nuestros modelos sólo depende del tiempo, puedes poner la derivada como \(x'\) , y hay una notación muy utilizada para hablar de la derivada de una función que depende del tiempo:

\[ \dot{x} \]

sí, con un puntito.

Bueno, recuerda que nuestro objetivo va a ser partir de una ecuación diferencial (lineal) de este estilo:

\[\begin{equation} x'=ax+b\label{eq:EDO} \end{equation}\]

y ser capaces de obtener la solución, que es la función \(x(t):\)

Resolver una ecuación diferencial implica buscar una función del tiempo que da, a cada valor de \(t\) un valor para \(x\).

Por otro lado, no olvides que un primer resultado que ya calculábamos en las ecuaciones en diferencias es el equilibrio. El equilibrio vuelve a ser, en este caso, la idea de un valor de \(x\) para el cual la derivada es cero, es decir, para el cual la función es constante

Equilibrio:

Llamamos equilibrio \(x^{*}\) de una ecuación diferencial a un valor constante que satisface la ecuación. Para ello, hacemos que \(x'=0\) en la ecuación \[ x'=ax+b, \] entonces \[ 0=ax^{*}+b \]

donde

\[ x^{*}=\frac{-b}{a} \]

Nota que, para que haya equilibrio, \(a\neq0\) y que, en este caso, siempre será así para poder tener la ecuación diferencial lineal.

Entonces, el equilibrio es un valor constante, de referencia al que la variable va a tender a largo plazo si el modelo es estable. Si no es estable, la variable pasará por el equilibrio pero nunca se quedará en él.

Recuerda

Equilibrio	Ecuación Diferencial	Ecuación en diferencias
\(x^*=\)	\(\frac{-b}{a}\)	\(\frac{b}{1-a}\)

Resolución de las ecuaciones diferenciales de orden 1.

Vamos a ver cómo resolver las ecuaciones (diferenciales de primer orden) del tipo \[ x'=ax+b \]

en sus diferentes versiones de interés.

Caso 1: \(a\neq0\),\(b=0\)

En este caso, tenemos una ecuación diferencial lineal de primer orden y homogénea (recuerda, porque \(b=0).\) Vamos a resolverla utilizando: EL TEOREMA FUNDAMENTAL DEL CÁLCULO!

\[ \frac{\mathrm{d}x}{\mathrm{d}t}=ax \]

Como ves, utilizo la notación con \(\mathrm{d}x,\mathrm{d}t\), porque me va a resultar más cómodo. Para empezar, dejo en un lado todo lo que tenga que ver con las \(x\) y, en el otro, lo que tenga que ver con las \(t\), entonces: \[ \frac{\mathrm{d}x}{x}=a\mathrm{d}t \]

Ahora, para librarme de las “diferenciales”, ya que quiero una solución para \(x\), utilizo el Teorema Fundamental del Cálculo que dice:

\[ \int\frac{\mathrm{d}x}{x}=a\mathrm{\int d}t \]

de lo que obtengo:

\[ \ln(x)=at+C \]

(recuerda poner la constante de integración). Como quiero una solución para la \(x\), debo deshacer el logaritmo. Uso la exponencial:

\[\begin{equation} e^{\ln(x)}=e^{at+C} \end{equation}\]

de donde,

\[ x=e^{at}e^{C} \]

ya tengo la solucuión:

\[\begin{equation} x(t)=e^{at}A,\label{eq:homog_orden1} \end{equation}\]

donde \(A\) es una constante cualquiera. Si conozco el valor inicial, por ejemplo, sé que \(x(0)=x_{0}\), pues lo utilizo para obtener lo que vale \(A\):

\[ x(0)=e^{a\times0}A=x_{0}\Rightarrow A=x_{0}, \]

por lo que tenemos

\[ x(t)=e^{at}x_{0}, \] que es la solución que estábamos buscando.

caso 2 \(a\neq0\),\(b\neq0\)

Esta ecuación no es homogénea: decimos que es autónoma cuando \(b\neq0:\)

\[ \frac{\mathrm{d}x}{\mathrm{d}t}=ax+b \]

Para resolver esta ecuación, vamos a definir primeramente su equilibrio. \[ x^{*}=\frac{-b}{a}, \]

que ya sabemos que el equilibrio es un valor de \(x\) que satisface la ecuación. Ahora, usemos el principio ya conocido de que la solución general de la ecuación será la suma de la solución de la homogénea más la particular. La homogánea ya la tenemos resuelta de antes, es decir, \[ x^{h}(t)=e^{at}A. \]

La solución general será la suma de ambas, por tanto \[ x(t)=e^{at}A-\frac{b}{a} \]

Ahora bien, si tenemos que \(x(0)=x_{0}\), entonces,

\[ x(0)=e^{a\times0}A-\frac{b}{a}=x_{0}\Rightarrow A=x_{0}+\frac{b}{a} \]

Enchufando el valor obtenido

\[ x(t)=e^{at}\left[x_{0}+\frac{b}{a}\right]-\frac{b}{a}, \] reescribimos la solución como \[ x(t)=x^{*}+e^{at}\left[x_{0}-x^{*}\right]. \]

Si te das cuenta, se parece a la solución de la análoga en diferencias!

Mira

	Ecuación Diferencial	Ecuación en diferencias
Ecuación	\(x'=ax\)	\(x_{t}=ax_{t-1}\)
Solución	\(x(t)=e^{at}x_{0}.\)	\(x(t)=e^{at}x_{0}\)
Ecuación	\(x'=ax+b\)	\(x_{t}=ax_{t-1}+b\)
Solución	\(x(t)=x^{}+e^{at}\left[x_{0}-x^{}\right]\)	\(x_{t}=x^{}+a^{t}\left[x_{0}-x^{}\right]\)

La convergencia al equilibrio: análisis cualitativo

De la misma manera que estudiábamos la tendencia a largo plazo en el caso de las ecuaciones en diferencias, hacemos lo mismo con las ecuaciones diferenciales. Sin embargo, hay una buena noticia: ¡Es más fácil! ¿y eso por qué? Como ya sabes, analizar a largo plazo consiste en ver qué ocurre con la ecuación si \(t\rightarrow\infty\). En el caso de la solución, \(x(t)=x^{*}+e^{at}\left[x_{0}-x^{*}\right]\), como tenemos una exponencial, sólo hay dos posibilidades: si \(a>0\), entonces \(\lim_{t\rightarrow\infty}e^{at}=\infty\) y, si \(a<0\), entonces, \(\lim_{t\rightarrow\infty}e^{-at}=0\). De esta forma, si el parámetro es positivo, sabemos que no convergeremos al equilibrio mientras que, si el parámetro es negativo, sí.

Clase 5: Ecuaciones diferenciales de segundo orden

Vamos a “complicar” algo más nuestro modelo. Vamos a permitir que ahora aparezca la segunda derivada en la ecuación diferencial, teniendo ecuaciones diferenciales lineales de segundo orden Ecuación homogénea

\[ x''+a_{1}x'+a_{2}x=0 \]

Ecuación no homogénea (autónoma)

\[ x''+a_{1}x'+a_{2}=b \]

Ecuación no homogénea (no autónoma)

\[ x''+a_{1}x'+a_{2}x=be^{t} \]

Solución de la homogénea

La solución de la ecuación homogénea pasa por la obtención del polinomio característico. Como hemos visto antes, las soluciones de estas ecuaciones de primer orden tienen la pinta \(x(t)=e^{rt}x_{0}\). Si sutituímos convenientemente,

\[ x''+a_{1}x'+a_{2}x=0\Rightarrow r^{2}e^{rt}x_{0}+a_{1}re^{rt}x_{0}+a_{2}e^{rt}x_{0}=0 \]

Entonces, para que esto sea solución: \[ e^{rt}x_{0}(r^{2}+a_{1}r+a_{2})=0 \]

De aquí, obtenemos lo que conocemos como la ecuación característica, puesto que hay que resolver, si \(r\neq0\)

\[ (r^{2}+a_{1}r+a_{2})=0 \]

De esta ecuación, obtenemos sus raíces (en este curso, sólo trabajaremos con raíces reales).

Raíces reales distintas

La solución de la homogénea será del tipo

\[ x(t)=Ae^{r_{1}t}+Be^{r_{2}t} \]

Raíces reales dobles

En este caso, la solución de la homogénea, será

\[ x(t)=(A+Bt)e^{rt} \]

Solución general=solución homogénea + solución particular

Volvemos a necesitar este resultado para poder resolver ecuaciones NO homogéneas.

\[ x_{t}=x_{t}^{h}+x_{t}^{p}, \]

veamos los diferentes casos.

Caso 1: autónoma

\[ x''+a_{1}x'+a_{2}=b \]

Para obtener el equilibrio, hacemos \(x''=x'=0\)

Con equilibrio

En el caso de la ecuación autónoma, tenemos un punto claro que resuelve, de forma particular, la ecuación: el equilibrio. En este caso, el equilibrio será el valor de \(x^{*}\) tal que

\[ a_{2}x^{*}={\color{red}b}\Rightarrow x^{*}=\frac{b}{a_{2}} \]

Para que este equilibrio exista, nota que \(a_{2}\neq0\).

Esta es, entonces, una solución particular. Si queremos resolver la ecuación diferencial, sólo tenemos que resolver la homogénea y, a continuación, sumarle el equilibrio.

Ejemplo: Resuelve

\[ x''=5x'-6x+10 \]

La homogénea consiste en: \(x''-5x'+6x=0}\)

La ecuación característica \(r^{2}-5r+6=0\) donde \(r_{1}=3,r_{2}=2\)

La solución de la homogénea es, entonces \(x_{t}^{h}=Ae^{3t}+Be^{2t}\)

Por otro lado, tenemos que calcular una particular. Como es autónoma, el equilibrio-si existe- es una solución particular:

\(x^{*}=\frac{10}{6}=\frac{5}{3}\)

La solución general será: \[ x(t)=Ae^{3t}+Be^{2t}+\frac{5}{3} \]

Es posible obtener el valor de \(A\) y \(B\) si nos facilitan el valor de \(x(0)\) y \(x'(0).\) ¿Cuál será la solución general si \(x(0)=\frac{5}{3},x'(0)=1\)?

Entonces, \[ x(0)=A+B+\frac{5}{3}=\frac{5}{3}\Rightarrow A+B=0 \]

por otro lado, necesitamos hacer la derivada de \(x(t):\)

\[ x'=3Ae^{3t}+2Be^{2t} \]

Ahora la evaluamos en 0,

\[ x'(0)=3A+2B=1 \]

Si resuelves el sistema, obtendrás: \[ x(t)=e^{3t}-e^{2t}+\frac{5}{3} \]

como solución general.

Caso 2: Ecuación No autónoma

En el caso de la ecuación no autónoma, el término independiente dependerá de \(t.\) Por ejemplo:

\[ x''=5x'-6x+e^{-2t}+10 \]

Ahora, una solución particular no puede ser el equilibrio, puesto que esta ecuación no tiene (mira que \(e^{-2t}\) no es un valor constante y un equilibrio ha de serlo). Utilizamos el método de los coeficientes indeterminados. Este método funciona en casos muy sencillos (como los que aquí abordaremos) y se basa en tratar de averiguar qué pinta tiene la solución de la ecuación diferencial. Si te das cuenta, \(x''-5x'+6x=e^{-2t}\), nos está diciendo que, operando con las \(x\), debemos llegar a esta solución \(e^{-2t}\). Lo que se hace es suponer que la solución particular es de esta forma: \(x_{t}^{p}=Ce^{-2t}\) y buscamos el valor de \(C\) para que se satisfaga la ecuación y que, por tanto, sea una solución particular. En este caso,

\[ x^{'p}=Ce^{-2t} \]

de donde \({x}^{'p}=-2Ce^{-2t}\) y donde \({x}^{''p}=4Ce^{-2t}.\) Por lo que, sustituyendo:

\[ 4Ce^{-2t}+10Ce^{-2t}+6Ce^{-2t}=e^{-2t} \]

\[ 20Ce^{-2t}=e^{-2t}\Rightarrow C=\frac{1}{20}. \]

Si queremos resolver la ecuaci?n completa, sólo tenemos que resolver la homogénea y, a continuación, sumarle la particular:

Como ya tenemos la homogénea del caso anterior

\[ x(t)=Ae^{3t}+Be^{2t}+\frac{1}{20}e^{-2t} \]

Ideas:¿Qué funciones utilizar para la particular en no autónomas?

En definitiva, si tu ecuación es de este estilo:

\[ x''+a_{1}x'+a_{2}x=be^{t} \]

Prueba con \(x(t)=Cbe^{t}\)

SI es de este estilo

\[ x''+a_{1}x'+a_{2}x=b_{1}e^{t}+b_{2}, \]

prueba con \(x(t)=Cb_{1}e^{t}+D\)

Si es un polinomio:

\[ x''+a_{1}x'+a_{2}x=b_{1}t^{2}+b_{2} \]

prueba con \(x(t)=Cb_{1}t^{2}+Db_{1}t+E\) (con polinomios es aconsejable introducir todas las potencias aunque no aparezcan explícitamente).

NOTA: si una de las raíces coincide con \(b\), entonces debes probar con \(x(t)=C\mathbf{t}e^{t}\).

Ejercicios Resueltos para Practicar

El precio de un bien sigue la siguiente ecuación diferencial

\[ P'=-6P+270 \]

Obtén la ecuación del precio para todo \(t\) y di hacia dónde converge a largo plazo.

solución

Al ser una ED linear de primer orden. Su equilibrio es \(P^{*}=\frac{270}{6}=45\) y su solución: \[ P(t)=45+e^{-6t}\left(P_{0}-45\right) \]

como vemos, \(\lim_{t\rightarrow\infty}P=45\) , ya que el término \(e^{-6t}\rightarrow0\) cuando \(t\rightarrow\infty.\)

Se sabe que el número de aficionados al fútbol varía en función de los aficionados que haya en cada instante de tiempo, ya que los aficionados actuales captan a nuevos aficionados entre sus amigos, de modo que lo que varía el número de aficionados en cada momento (medido en horas) es igual al 0.1% del número de aficionados que haya en cada momento. Sabiendo que actualmente existen 20 millones de seguidores de fútbol español, ¿cuántas horas tendrán que pasar para que se triplique el número de seguidores? ¿Y si el número de seguidores fuera de 30 millones?

solución

Sea \(A\) el número de aficionados, y sea \(A(t)\) la función que describe los aficionados que hay en un momento \(t\) de tiempo. En el texto se dice que los aficionados evolucionan de la siguiente manera:

\[ \frac{\mathrm{d}A}{\mathrm{d}t}=0.001A \]

La solución de esta ecuación es \[\begin{equation} A(t)=e^{0.001t}A_{0} \end{equation}\]

En este caso, incluyendo la condición inicial: \[\begin{equation} A(t)=e^{0.001t}20 \end{equation}\]

Para saber en qué momento se triplicarán (\(A(t)=60)\) debemos despejar \(t\):

\[ 60=e^{0.001t}20\Rightarrow3=e^{0.001t}\Rightarrow1.098=0.001t\rightarrow t=1098 \]

Sean las funciones de demanda y de oferta de un modelo de ajuste de precios dinámico: \(Q_{d}=4-2P(t)+5\frac{dP}{dt},Q_{s}=-6+3P(t)\). Asimismo, se sabe que la variación del precio en cada instante t es igual al 60% del exceso de la demanda (hipótesis walrasiana). Obtener:

La trayectoria temporal del precio para las condiciones iniciales \(P(0) = 8\).

¿Cuál es la tendencia del precio para un periodo de tiempo suficientemente largo? ?Podr?a decirse que el modelo es dinámicamente estable? Justificar la respuesta.

solución

Tal y como se especifica en el modelo \[ P'=0.60(D-S) \]

es decir,

\[ P'=0.60(4-2P+5P'+6-3P), \]

entonces

\[ P'=6-3P+3P' \] y, por tanto, \[ -2P'=6-3P\Rightarrow P'=-3+\frac{3}{2}P \]

La trayectoria temporal del precio será la solución a la ecuación diferencial de primer orden presentada, es decir,

\[ P(t)=2+e^{\frac{3}{2}t}\left(P_{0}-2\right) \]

El precio de equilibrio intertemporal es el que se obtiene al hacer \(0=-3+\frac{3}{2}P\Rightarrow P=2\). El de mercado perfecto es el de igualar la oferta y la demanda con \(P'=0\), que sale también 2.

Sin embargo, a largo plazo, este mercado no es dinámicamente estable, ya que para \(t\rightarrow\infty\), entonces \(P(t)\rightarrow\infty\).