BLOQUE 2: herramientas de cálculo diferencial

En este bloque se empezará recordando (y contextualizando) la derivada. Una técnica de cálculo diferencial que lleváis, por lo menos, dos años usando y que-sin embargo- os cuesta definir y entender su porqué. Una vez esté claro, vamos a llevarla lejos, viendo la de usos que tiene.

Entonces, será el momento de extender toda esta artillería a funciones de más variables (en general, 2).

Clase 1: el concepto de función en \(1\) y \(n\) variables

Este vídeo introductorio puede ayudarte a entender los conceptos.

Una función es una regla (llamada, generalmente, \(f,g,h,....\)) que asigna a los valores de un conjunto llamado dominio un único valor de un conjunto llamado imagen. En este curso trabajaremos, en general con funciones \(\mathscr{\mathbb{R}}^{n}\rightarrow\mathbb{R}\), indicando que el dominio es un conjunto \(n-\) dimensional de números reales (muy a menudo \(n=1,2\)) y \(\mathbb{R}\) es la, famosísima, recta real.

Asegúrate que entiendes qué significan \(\mathbb{R}^{2}\) y \(\mathbb{R}^{3}\)

¿Te convence el vídeo?

En este curso trabajaremos, en general, con los números reales \(n\) dimensionales, lo que ya constituye un avance frente a lo que has aprendido en cursos pasados.

[ IMAGE_ALT ]

Ejemplo de una función de una variable: Sea la función \[ f(x)=\frac{1}{x-1} \] Como ves, el dominio son todos los valores reales salvo el 1, puesto que la función, cuando el denominador vale 0, no está definida; y lo escribimos así \[ D=\left\{ x\in\mathbb{R}|x\neq1\right\} \] El recorrido (o rango, o imagen) son los posibles valores que puede tomar la \(y.\) En este caso, será todo \(\mathbb{R}\) salvo el valor 0.

Puedes usar Geogebra para hacer los gráficos de muchas de las funciones que se presentarán en este curso. Por ejemplo, aquí representamos la función anterior:

FIG1. La función real de variable real de la Anotación 1 ¿sabrías hacerla a mano?.

Si tenemos \(n\) variables, que es lo nuevo de este curso, la idea será similar: necesitamos una regla que le asigne un único output a un conjunto de \(n\) variables input.

Función de n variables: Una función de variables se define como \[ y=f(x_{1},x_{2},...,x_{n}) \]

\(y\)	\(x_{1},...,x_{n}\)
endógena	exógenas
explicada	explicativas
dependiente	independientes

Y necesitamos \(n\) variables porque los modelos que estudiarás en Ciencias Sociales suelen basarse en un conjunto amplio de factores que explican un hecho. Entonces:

Decimos que \(f\,:\,D\subset\mathbb{R}^{n}\rightarrow\mathbb{R}\) si la regla o función \(f\) asigna a cada valor del dominio \(D\) (que es un subconjunto de los numeros reales \(n\) dimensionales) un valor real. En este texto usaremos, generalmente, funciones de dos variables, es decir:

\[ y=f\left(x_{1},x_{2}\right), \]

donde \(f\,:\,D\subset\mathbb{R}^{2}\rightarrow\mathbb{R}.\)

Pero, por supuesto, podríamos tener una función de \(n\) variables

\[ y=f\left(x_{1},x_{2},...,x_{n}\right), \]

donde \(f\,:\,D\subset\mathbb{R}^{n}\rightarrow\mathbb{R}.\)

Ejemplo: piensa sobre las funciones aparecen en el vídeo: \[ ResultadosPISA=f(gasto) \] es una función \(\mathbb{R\rightarrow R}\), por otro lado, \[ IMC=\frac{peso}{altura^{2}} \] es una función \(\mathbb{R}^{2}\rightarrow\mathbb{R}\), mientras que la última función

\[ M=C_{0}\frac{\left(1+\frac{i}{m}\right)^{n\times m}\left(\frac{i}{m}\right)}{\left(1+\frac{i}{m}\right)^{n\times m}-1} \]

es \(\mathbb{R}^{4}\rightarrow\mathbb{R}\). Asegúrte de que entiendes lo que esto significa, de acuerdo con lo que se dice en el vídeo.

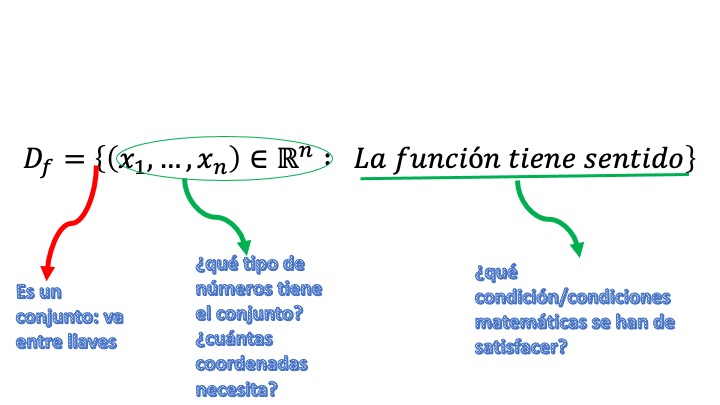
[ IMAGE_ALT ]

El dominio de una función es el conjunto de valores de la(s) variable(s) independientes para los que la función está definida y tiene sentido.

-Si la función es \(f\::\:\mathscr{\mathbb{R}}\rightarrow\mathbb{R},\) (por ejemplo, \(y=f(x))\) el dominio se puede escribir como \(D=\left\{ x\in\mathbb{R}\::\:f\;\mathrm{est\acute{a}\:definida}\right\}\).

Lo que estás diciendo es que _el dominio consiste en valores de la variable \(x\), tales que pertenecen al conjunto de los números reales, siempre que la función tenga sentido matemático. Donde pone f está definida, deberás poner tú qué condiciones debe cumplir para que lo esté. Por ejemplo, \(y=ln(x+1)\), \(D=\left\{ x\in\mathbb{R}\::\:x>-1\right\}\).

-Si la función es \(f\::\:\mathscr{\mathbb{R}}^{2}\rightarrow\mathbb{R}\), (por ejemplo, \(y=f(x_{1},x_{2}))\), el domino se escribe como \(D=\left\{ (x_{1},x_{2})\in{\mathbb{R}^{2}}\::\:f\;\mathrm{está\:definida}\right\}\). Por ejemplo, \(y=ln(x_{1}+x_{2})\), \(D=\left\{ (x_{1},x_{2})\in\mathbb{R}^{2}\::\:x_{1}>-x_{2}\right\}\).

Fíjate cómo indicamos \(\mathbb{R}^{2}\) como el conjunto donde vamos a buscar los valores para las variables independientes.

Si la función con la que estás trabajando tiene sentido económico, físico, biológico,… es conveniente que pienses sobre posibles restricciones adicionales en el dominio, indicando que usarás dicha restricción.

Puedes llamarlo Dominio Natural o Económico (por ejemplo, si la función de demanda de un bien depende de dos precios, \(y=-2x_{1}+3x_{2}\), entonces \(D_{N}=\left\{ (x_{1},x_{2})\in\mathbb{R}^{2}\::\:x_{1},x_{2}>0\right\}\), mientras que \(D=\left\{ (x_{1},x_{2})\in\mathbb{R}^{2}\right\}\), puesto que no existen los precios negativos (dominio natural) pero la función tendría sentido matemático para cualquier valor real de las variables exógenas.

En el vídeo anterior aparece otra función de dos variables muy famosa, que conoces, y que -a lo mejor- no te habías parado a pensar en que lo era: el índice de masa corporal.

FIG 2. Este es el IMC que te encuentras en la farmacia. En los ejercicios trabajaremos sobre él.

El índice de masa corporal (IMC) es una función que tiene su dominio en dos dimensiones (el par \((p,a)\)) y cuya imagen es un único valor real (el valor del índice para cada individuo). Es decir, \(f\::D\subset\mathbb{R}^{2}\rightarrow\mathbb{R}:\)

\[\begin{equation} IMC=\frac{p}{a^{2}} \tag{1.1} \end{equation}\]

En este caso, la función se puede escribir de esta forma:

\[ IMC=f(p,a) \]

Si te das cuenta, la variable output o endógena es el IMC, mientras que \(p,a\) son los inputs o exógenas de la función. Pertenecen a valores en \(\mathbb{R}^{2}\). ¿Pero cualquier para en \(\mathbb{R}^{2}\) será válido? Por ejemplo, valdrá decir que el peso de un individuo es -15 kg y su altura -1,75 metros?

¿Cuál será el dominio? En principio, si analizamos la función de una manera fría sin saber qué es \(p\) ni \(a\), tenemos que pensar qué valores de la función harían que no esté correctamente definida. En este caso, si \(a=0\), el IMC no estará definido, puesto que no podemos dividir por cero. Por lo que el dominio de la función será:

\[ D=\left\{ \left(p,a\right)\in\mathbb{R}^{2}|a\neq0\right\} \]

(que se lee: el dominio de la función es el conjunto de todos los valores reales en dos dimensiones de \(p\) y \(a\) tales que \(a\neq0\))

Sin embargo, este dominio parece no tener sentido. ¿Puede ser el peso de un individuo -8 kilogramos en el planeta Tierra tal y como están las cosas? ¡NO! Por ello, definimos el dominio natural de una función que será aquel que tenga sentido económico, de una manera amplia (por económico también entendemos social, psicológico, biológico, etc…). En nuestro caso, dado que el peso y la altura son siempre valores positivos, el domino natural:

\[ D_{N}=\left\{ \left(p,a\right)\in\mathbb{R}^{2}|p>0,a>0\right\} \]

Por tanto, el dominio, al final, es el subconjunto de los números reales \(n\)-dimensionales (en este caso, \(n\)=2) para los cuales la función tiene sentido. El rango (recorrido o imagen) lo buscaremos en el conjunto: \(\mathbb{R}\)). La imagen es el resultado de aplicarle la expresión de la función al conjunto de \(n\) valores cualesquiera que pertenezcan al dominio.

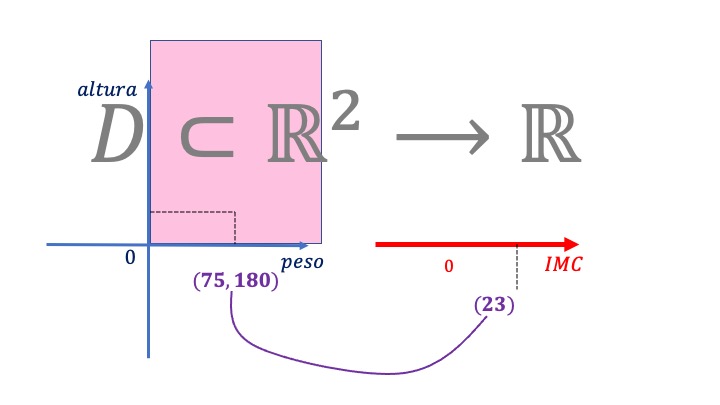
FIG3 Esta es la idea esquemática del IMC. El dominio está en dos dimensiones, mientras que la imagen en una dimensión.

1.3.1 ¿Para qué necesitamos las funciones?

Como se apunta en el vídeo, en general las funciones son una herramienta muy natural para poder expresar un comportamiento humano, económico, social, sanitario, etc… Permiten dotar de lógica a un modelo con el objetivo de poder obtener predicciones. Piensa que uno de los grandes fines de la ciencia es ser capaces de poder decir qué va a ocurrir y, además, disponer de herramientas para optimizar resultados. Puedes hacer esta lectura breve que, como verás, tiene mucho de actual

https://theconversation.com/covid-19-pandemia-de-modelos-matematicos-136212

Ejercicio 1

Piensa, o busca por internet, en contextos en los que creas que se usan modelos matemáticos basados en funciones. Propón alguno en clase.

Ejercicio 2

En el siguiente gráfico aparecen varias curvas en el plano. Identifica cuáles se corresponden con funciones de la forma \(y=f(x)\), cuáles se corresponden con funciones de la forma \(x=f(y)\) y si, mediante alguna modificación (al dominio), se puede extraer alguna función de donde, en principio, no la hay.

Gráfico para el Ejercicio 2

Ejercicio 3

En los siguientes diagramas se proponen diferentes posibles funciones. El sentido de la flecha indica cuál es el dominio y cuál el conjunto imagen (\(dominio\rightarrow imagen)\). Discute si son o no funciones y bajo qué condiciones (por ejemplo, una restricción en el dominio) pueden serlo:

Gráfico para el Ejercicio 3

Ejercicio 4

Halla el dominio y la imagen de las siguientes funciones:

\(h(t)=\frac{1}{3}t^{3}+t^{2}+1\)
\(f(x)=\sqrt{10-2x}\)

solución \(D_{f}=\left\{x\in\mathbb{R}\::\:x\leq5\right\}\), \(Im_{f}=[0,\infty)\)

\(y(k)=\frac{2k-1}{k^{2}-k}\)
\(j(x)=\sqrt{9-x^{2}}\)
\(g(p)=\left(\frac{p-1}{\left(p-2\right)\left(p-3\right)}\right)^{1/2}\)

Ejercicio 5

Sea \(W(q)\) la función definida por

\[ W(q)=\frac{3q+6}{q-2} \]

Calcula su dominio

Muestra que el 5 pertenece al conjunto imagen de la función ¿Está también el 3 en dicho conjunto?

Ejercicio 6

Halla el dominio de las siguientes funciones definidas en \(\mathbb{R}^{2}\rightarrow\mathbb{R}\)

\(f(x,y)=x-3y\)
\(g(x,y)=\ln(x-3y)\)

solución \(D_{g}=\left\{ (x,y)\in\mathbb{R}^{2}\::\:x-3y>0\right\}\)

\(h(x,y)=x+4y^{2}\)
\(i(x,y)=\frac{x}{y-2}\)
\(j(x,y)=4(x-1)^{2}+9(y-2)^{2}\)
\(k(x,y)=(x-1)^{1/2}(y-2)\)
\(l(x,y)=\ln y+x\)
\(m(x,y)=\ln(y+e^{-x})\)

Ejercicio 7

La función \(x(p,q)=\frac{20-p+q}{p}\) representa la demanda \(x\) de un bien, dado su precio \(p\) y el precio de otro bien, \(q\). Halla su dominio natural (o económico) y dibuja los puntos \((p,q)\) del dominio natural (o económico) para los que la demanda es mayor o igual a 3 unidades.

-Indicación para la segunda parte: deberás resolver \(\frac{20-p+q}{p}\geq3\) y dibujar la desigualdad que encuentres. Puedes comprobarlo con Geogebra

Ejercicio resuelto

Imagina una función \(f\), cuyo dominio está conformado por el peso y la altura de un individuo y la imagen es el IMC del individuo y, además, toma los siguientes valores:

0, si el individuo está en su peso
1, si el individuo está en una situación de sobrepeso
-1, si el individuo tiene un IMC por debajo de lo normal.

Explica cómo sería el dominio e imagen de la función. Razona si es una función definida como \(f\::\mathbb{R}^{2}\rightarrow\mathbb{R}\). En caso de no serlo, especifica de manera adecuada la función. Busca, además, una manera sensata de dar el resultado para un individuo cuyo peso son 68 kilogramos y su altura es 1.80 metros.

solución:

la función no es del tipo \(f\::\mathbb{R}^{2}\rightarrow\mathbb{R}\) sino de este otro \(f\::\mathbb{R}_{++}^{2}\rightarrow\mathbb{R}^{2}\), ¡ojo! esto no quiere decir que tenga dos imágenes en un mismo conjunto. Tiene una imagen en el conjunto IMC y otro en el conjunto \(\left\{ 0,1,-1\right\}\) que evalúa su resultado. La función es tal que \[ D=\left\{ (p,a)\in\mathbb{R}_{++}^{2}\right\} \]

\[ Im=\left\{ (IMC,y)\in\mathbb{R}^{2}\::\:IMC>0,y=\left\{ -1,0,1\right\} \right\} \] De tal forma que \(f(68,1.80)=(20.98,0)\).

Ejercicio 8

Expresa el dominio natural de la siguiente función de la que se habla en el vídeo 1, encontrada en Ponferrada (León). Para ello, vuelve al vídeo, mira los detalles de cada variable y piensa en qué conjunto está bien definido.

\[ M=C_{0}\frac{\left(1+\frac{i}{m}\right)^{n\times m}\left(\frac{i}{m}\right)}{\left(1+\frac{i}{m}\right)^{n\times m}-1} \]

Recuerda los conjuntos de números que conocemos:

Naturales: para contar. \(\mathbb{N}=\{0,1,2,3,....\}\)

Enteros: una ampliación de los naturales \(\mathbb{Z}=\left\{....,-3,-2,-1,0,1,2,3,....\right\}\)

Racionales: \(\mathbb{Q}=\left\{\frac{p}{q},p\in\mathbb{Z},q\in\mathbb{Z}\setminus\left\{ 0\right\} \right\}\)

Irracionales \(\mathbb{I}=\left\{e,\pi,\sqrt{2},...\right\}\)

Reales \(\mathbb{R}=\mathbb{N}\cup\mathbb{Z}\cup\mathbb{Q}\cup\mathbb{I}\)

Clase 2: las curvas de nivel (isocuantas, isoutiliad, etc…)

Presta atención al siguiente enunciado:

Una empresa fabrica un producto combinando dos factores productivos, capital (K) y trabajo (L), según la función de producción:

\[ Q(K,L)=4K^{2}+2L. \]

Dibujar la isocuanta de producción Q = 100 unidades.
Dibujar la isocuanta de producción Q = 256 unidades.

Nos piden que dibujemos la isocuanta. Esta palabra significa iso=igual cuanta=cantidad, esto es, nos están piendo que dibujemos la combinación de \(K,L\) para la que producimos 100 unidades. Para hacer esto, nos damos cuenta de que la función tiene su dominio natural (o económico) en los pares de \((K,L)\in\mathbb{R}^{2}\) para los cuales \(K,L>0\), es decir, de todo \(\mathbb{R}^{2}\), sólo nos quedamos con el primer cuadrante (sin incluir capital o trabajo igual a cero).

FIG1

Como ves en la FIG1, en la parte azul estamos representando las posibles combinaciones de \(K,L\) que admite nuestra función de producción. Ahora bien, nos piden sólo las combinaciones de \(K,L\) que nos proporcionen 100 unidades de producto. Para obtener esto, tendremos que sustituir \(Q\) por 100 en la función: \[ 100=4K^{2}+2L. \]

Como ves, dejamos de tener una función en dos variables (que se dibuja en 3D) a tener una función de una variable. Si despejas \(L\) (que es fácil), tendrás:

\[ L=50-2K^{2} \]

que, como ves, es una parábola (con las ramas hacia abajo) que toma valor \(L=50\) cuando \(K=0\) y que corta al eje \("K"\) en \(\pm5\) (haz las cuentas con lo que sabes de la ESO/Bachillerato para comprobarlo).

FIG2

Esta curva, FIG2, te proporciona todas esas cantidades de \(K,L\) con que producir 100 unidades de producto. Sin embargo, deberemos <> de aquellos valores de \(K,L\) que no pertenecen al dominio (es decir, en la FIG2, hemos hecho desaparecer la parte de la parábola para la que o \(K\leq0\) o \(Lleq 0\)). Y esta es la <>. Podemos dibujar aquella que nos proporciona 256 unidades. Se trabaja de la misma manera

\[ 256=4K^{2}+2L. \] despejando: \[ L=128-2K^{2} \] seguiremos teniendo una parábola que, ahora, corta al eje \(L\) en 128 y que corta al eje \(K\) en \(\pm8\)

FIG3

Las isocuantas o las curvas de isoutilidad, o de isocostes, etc… son todas familias de lo que se conoce como curvas de nivel.

Son una nueva herramienta de análisis visual que, aunque no lo creas, llevas mucho tiempo viéndolas hasta por la televisión. Mira el siguiente vídeo para familiarizarte con las curvas de nivel

Como ya vimos, es complicado tratar de dibujar funciones en 3D. Pero tiene que haber alguna manera de que entendamos los aspectos más importantes de una función sin que nos cueste mucho esfuero. ¡La hay! Es una técnica de representación que se utiliza en muchos contextos. Las curvas de nivel. ¿Recuerdas haberlas visto?

FIG7 Todas las noches en tu TV.

Efectivamente, en “El Tiempo’’ siempre las ponen. Esas curvas unen coordenadas del planeta Tierra que tienen la misma presión atmosférica. ¡Espera un momento! vamos a volver a los datos del IMC. Si te fijas, pesar 75 kilos y medir 1.75 te da el mismo IMC que si pesas 80 kilos y mides 1.80, es decir, un IMC de 25. Por lo tanto, podemos buscar esos valores de peso y altura que te dan el mismo IMC

FIG8 Curvas de nivel de la función IMC generadas por ordenador: en el vídeo te explicamos de dónde vienen.

Pues ya podemos definir una curva de nivel. Consiste en los puntos del dominio que nos proporcionan un valor, \(C\in\ Im(f)\) (es decir, constante y que pertenezca a la imagen de la función) o lo que es lo mismo

\[ Nivel=\left\{ \left(x_{1},x_{2}\right)\in D\::\:f(x_{1},x_{2})=C\right\} \]

De esta forma, dando diferentes valores a \(C\) podemos esbozar el comportamiento de nuestra función. Por ejemplo, si damos valor \(C=20\), en el ejemplo del IMC, tendremos que

\[ 20=\frac{p}{a^{2}}\Rightarrow p=20a^{2} \]

si te fijas, \(p=20a^{2}\) es una parábola (es como si tuvieras \(y=20x^{2}\)) por eso, las curvas de nivel de la figura 8 tienen esa pinta de curva.

FIG8 Curvas de nivel de la función IMC, remarcando la de nivel 20 y el sentido de crecimiento de la función.

Una vez dibujas la curva de nivel 20, puedes darte cuenta enseguida de que si aumentas el valor de \(C\), en este caso la parábola se irá haciendo cada vez más estrecha (claro, \(p=25a^{2}\) te devuelve un valor mayor para \(p\) por cada \(a\), comparada con \(p=20a^{2})\). De esta forma, ya puedes dibujar unas flechas que indiquen hacia dónde crece la función (es decir, hacia dónde tiene mayor nivel).

Ejercicio 1

Dibuja 3 curvas de nivel de cada función e indica con una flecha el sentido hacia el que crece.

\(f(x,y)=x+2y\)

\(h(x,y)=2x^{2}+y\)

\(j(x,y)=y-\sqrt{x}\)

\(l(x,y)=y-\ln(x)\)

\(m(x,y)=(x-2)y\)

\(n(x,y)=(x+1)^{2}+(y+3)^{2}\)

Las curvas de nivel van a ser una herramienta que estaremos utilizando constantemente. Deberías practicar mucho con ellas y entender perfectamente las claves de estas.

Clase 3: La derivada en funciones de una variable

Este vídeo puede ser de utilidad:

El concepto de derivada está muy relacionado con la idea de la tasa de variación media de una función.

La tasa de variación media: Imaginemos que un virus provoca una cantidad de contagios (en miles) que viene dada por la siguiente función \[ y=x^{2} \] donde \(x\) es el tiempo medido en meses ¿te suena esta historia?. Su gráfica será la siguiente:

FIG1 Gráfica con una supuesta evolución del virus.

De tal forma que, si estamos en el mes 1, hay mil contagiados y si estamos en el mes 4 hay 16 mil contagiados (como se puede ver en la FIG1). Ahora bien, si queremos resumir la información, podemos hacer lo siguiente: cogemos los dos puntos que conocemos \((x_{0},y_{0})=(1,1)\), \((x_{1},y_{1})=(4,16)\) y podemos hacer la cuenta de cuántos contagiados promedio hay por mes: lo que llamaremos la tasa de variación media: \[ TVM=\frac{16-1}{4-1}=5 \] podemos, entonces, decir que se han contagiado, en promedio 5000 individuos cada mes. Si te das cuenta, esa tasa de variación media se calcula igual que ¡la pendiente de una recta! En realidad, estamos calculando la pendiente de una recta secante a la curva anterior (es decir, \(y=1+5(x-1)\Rightarrow y=-4+5x\)

FIG2 Esta es justo la secante: prueba a hacerlo tú en Geogebra.

Comprueba, ahora, que puedes hacer muchas más secantes. ¡Todas las que quieras!

FIG3 Más secantes a la curva \(y=x^2\).

la particularidad de estas secantes es que vamos cogiendo, cada vez, puntos más cercanos al \((x_{0},y_{0})=(1,1).\) Según nos acercamos a ese punto (que lo hemos elegido como referencia, de la misma manera que podríamos haber elegido otro cualquiera) ¿qué pinta tiene la secante?

La tasa de variación instantánea: Pues lo has averiguado. La secante se acaba convirtiendo en una tangente. De hecho, la pendiente de la tangente podemos encontrarla. Como ves, en la FIG13, para definir la tangente tenemos que acercarnos todo lo posible al punto \((x_{0},y_{0}).\) La forma que tenemos, en Matemáticas, de escribir eso es con un límite. Diremos que la pendiente de la recta tangente a la función en el punto \((x_{0},y_{0})\) es \[ \lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x} \]

Fíjate: usamos el límite para decir que nos movemos muy poquito (un pelín, ligeramente, etc…) de \(x_{0}\). Para no llamar a esto la pendiente de la recta tangente a la función en el punto \((x_{0},y_{0})\), que es muy largo, lo llamamos DERIVADA y lo escribimos como \(y',f',\frac{\mathrm{d}y}{\mathrm{d}x}\) entre otras notaciones, de tal forma que:

\[ f'(x_{0})=\lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow0}\frac{f(x_{0}+\triangle x)-f(x_{0})}{\triangle x} \]

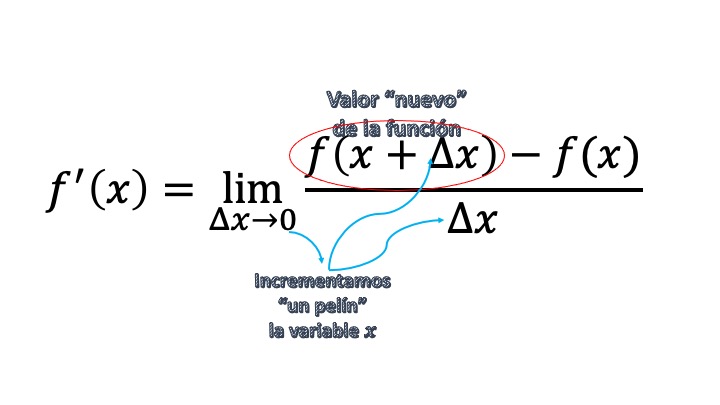
FIG4 Destripamos la fórmula.

Esta definición de derivada, en realidad, nos permitirá obtener la reglas de derivación habituales (que están en cualquier libro y te pedimos que rescates)

Repasa

Por tu cuenta las derivadas de las funciones principales, así como las derivadas de funciones compuestas que se resuelven mediante la regla de la cadena. Esto se da por sabido.

Ejercicio 1

Calcula las sifuientes derivadas (dejando el resultado lo más simplificado posible)

1: \(f(x)=\sqrt{2x}-\frac{2}{x^{2}}+\sqrt{3}\),
2: \(f(x)=(3x^2-x+2)/x\)
3: \(f(x)=\sqrt{\frac{2}{x}}-e^{3}\)
4: \(f(x)=\frac{1}{(2\sqrt{x})}\)
5: \(f(x)=a^2e^{\sqrt{ax}}+3cos(2x^2-\sqrt{a})\)
6: \(f(a)=a^2e^{\sqrt{ax}}+3cos(2x^2-\sqrt{a})\) MirA lA diferenciA :)
7: \(f(x)=ln{\sqrt{(x^2+1)/(x^2-1)}}\) (a lo mejor te interesa aplicar las propiedades del logaritmo)

Interpretación de la derivada en Economía

Con lo que sabemos hasta ahora, vamos a pensar:

Si estoy en el punto (1,1) y la derivada de la función es \(f'(x)=2x,\) entonces, la ecuación de la recta tangente a ese punto será:

\[ y=y_{0}+f'(x_{0})(x-x_{0}) \]

En este caso, \(f'(1)=2,\) por lo que \[ y=1+2(x-1)\Rightarrow y=-1+2x \]

Puedes ver en la FIG4 que, efectivamente, es la recta tangente al punto (1,1)

FIG4 Aquí se ve claramente, usando GEOGEBRA que esa recta es la tangente a la curva en el punto deseado.

Si te das cuenta, en el entorno del punto (1,1) la curva y la recta se parecen mucho. No ocurría así con las otras secantes trazadas, ¿verdad?. Vamos a aprovechar que en el entorno del punto (1,1) la recta tangente se “parece” a la función y diremos que será una aproximación de la curva en el entorno de ese punto. Es decir:

\[ \left.f(x)\right|_{x_{0}}\simeq y_{0}+f'(x_{0})(x-x_{0}) \]

y leemos como que la función en el entorno del punto \(x_{0}\) (así es cómo se interpreta \(\left.f(x)\right|_{x_{0}})\) es aproximadamente igual a la recta tangente. Ahora bien, como \(y=f(x),\) podemos reescribir la ecuación anterior como \[ y\simeq y_{0}+f'(x_{0})(x-x_{0}) \] y, si pasamos restando \(y_{0},\) entonces

\[ y-y_{0}\simeq f'(x_{0})(x-x_{0}) \]

Como ya has visto, podemos escribir \(\triangle y=(y-y_{0})\), \(\triangle x=(x-x_{0})\) y, por tanto, tendremos que \[ \triangle y\simeq f'(x_{0})\triangle x \] de tal forma que podemos decir que, si \(\triangle x=1,\) entonces

\[ \triangle y\simeq f'(x_{0}) \]

es decir:

la derivada es el incremento aproximado de la \(y\) si aumentamos \(x\) en una unidad.

Nota, por favor, que se introduce claramente el adjetivo aproximado. A esto, además, se lo conoce como la tasa de variación instantánea para diferenciarla de la anterior, que llamábamos tasa de variación media. El adjetivo instantánea aquí implica incrementar “muy poquito” la \(x\).

Siempre que queramos analizar cómo cambia una variable cuando modificamos otra , el cálculo diferencial es imprescindible. En Economía es estándar añadir el adjetivo “marginal” a la interpretación de una derivada (como ya habrás visto en Teoría Económica). Si \(f(x)\) denota la producción de un bien, su derivada \(f'(x)\)- que representa el incremento de la producción ante un incremento pequeño (marginal) del input- se interpreta directamente como la productividad marginal. Otra de las expresiones que se utiliza para la derivada es el concepto de ritmo de variación puesto que nos permite analizar si el cambio que se produce en \(f(x)\) es o no grande al aumentar \(x\).

Ejercicio 3

Sea \(C(x)=a_2x^2+a_1x+a_0\), con \(a_0,a_1,a_2>0\), la función de costes de una empresa. El bien producido se vende a un precio \(p>0\) por unidad, luego los ingresos serían \(R(x)=px\). El beneficio obtenido, si produjese \(x\) unidades de bien sería \(\Pi(x)=R(x)-C(x)\)

Halla las funciones de ingreso, coste y beneficio marginal

Determina el valor de \(x\) para que el beneficio marginal sea nulo

Sea \(x=s(p)\), el resultado obtenido en el apartado anterior, calcula el ritmo de variación de \(x\) si modificamos el precio en 1 unidad.

Clase 4: la elasticidad a través del cálculo diferencial

El concepto de la elasticidad bien merece una semana: va a ser de los más manejados a lo largo del grado. En muchas disciplinas recurrirán a él (marketing, macroeconomía, microeconomía)….y es el concepto sobre el que más dudáis.

Quizás, este vídeo te ayude a entender mejor la idea: haz click en la imagen

Por tanto, la elasticidad nos ayuda a entender ``cambios’’ (s?, otra vez la idea del principio: cambios, cambios, cambios) porcentuales de la función cuando la variable input también cambia un un tanto por ciento. Por ejemplo, en la función

\[\begin{equation} y=f(x),\tag{1.2} \end{equation}\]

nos interesa analizar el cambio porcentual de la variable \(y\) ante un incremento porcentual de la variable \(x\) y escribamos la aproximación lineal de (1.2)

\[ \triangle y\simeq f'(x)\triangle x \]

vamos ahora a jugar un poco. Haremos cambios en la ecuación, pero para llegar a otra expresión en tantos por ciento para ambas variables. Para ello, dividamos en ambos lados por \(y\)

\[ \frac{\triangle y}{y}\simeq f'(x)\frac{1}{y}\triangle x, \]

ahora dividamos en ambos lados por \(x\)

\[\begin{equation} \frac{\triangle y}{y}\frac{1}{x}\simeq f'(x)\frac{1}{y}\frac{\triangle x}{x},\tag{1.3} \end{equation}\]

como quiero que me quede en la izquierda de la ecuación (1.3) el cambio porcentual en la \(y\), paso la \(x\) a la derecha:

\[ \frac{\triangle y}{y}\simeq f'(x)\frac{x}{y}\frac{\triangle x}{x}, \]

multiplico por 100 en ambos lados

\[ \left(\frac{\triangle y}{y}\right)\times100\simeq f'(x)\frac{x}{y}\left(\frac{\triangle x}{x}\right)\times100, \]

y obtengo

\[\begin{equation} \Delta\%y\simeq{f'(x)\frac{x}{y}}\Delta\%x, \end{equation}\]

donde \(\Delta\%y\) y \(\Delta\%x\) se leen como cambio porcentual de la y y cambio porcentual de la x . Por otro lado, \({f'(x)\frac{x}{y}}\) es la elasticidad. La interpretación, por lo tanto, es clara:

OJO, la elasticidad!

si hacemos que \(\Delta\%x=1\), estamos incrementando la variable \(x\) en un 1%. Entonces, si llamamos \(\epsilon_{y,x}\) a la elasticidad de la variable \(y\) con respecto a la \(x\)

Entonces, \(\epsilon_{y,x}=f'(x)\frac{x}{y}\)

este valor indica el incremento porcentual aproximado de la \(y\) ante cambios en un 1% de la variable \(x\).

Ejemplo

Si la demanda de un bien sigue la función \(y(p)=\frac{2}{p^{2}}\), la elasticidad-precio (\(\epsilon_{y,p}\)) será:

\[ \epsilon_{y,p}=\frac{-4}{p^{3}}\frac{p}{y(p)} \]

Como ves, este resultado es una función. Dependerá del valor del precio actual. De tal forma que si, por ejemplo, en estos momentos, el precio es \(p=1\),la elasticidad será

\[ \epsilon_{y,p}=\frac{-4}{1}\frac{1}{2}=-2 \]

OJO, interpretamos una elasticidad!

si incremento el precio en un 1%, la demanda caerá -aproximadamente- en un 2%. ¡No olvides que la elasticidad es un concepto porcentual! ¡Por favor!

Clase 5: Las derivadas en funciones de \(n\) variables.

Una vez hemos repasado los conceptos más importantes de derivación, es el momento de hablar de cómo aplicamos esta idea en funciones de dos (o más variables). Introducimos la derivada parcial, que es otro contenido nuevo en este curso.

Primeramente, vamos a intentar practicar este nuevo tipo de derivada para, posteriormente, indagar en su significado.

Una derivada parcial de la función \(f(x_1 ,...,x_n)\) consiste en derivar la función con respecto a la variable \(x_i\) haciendo que el resto de variables (es decir, \(x_{-i}\)) permanezcan constantes. Es decir, si sabes derivar en una variable, esto no te va a costar

Las derivadas parciales solemos denotarlas con el símbolo \(\partial\), como verás a continuación de manera intuitiva

Empezamos con una función sencilla, de dos variables.

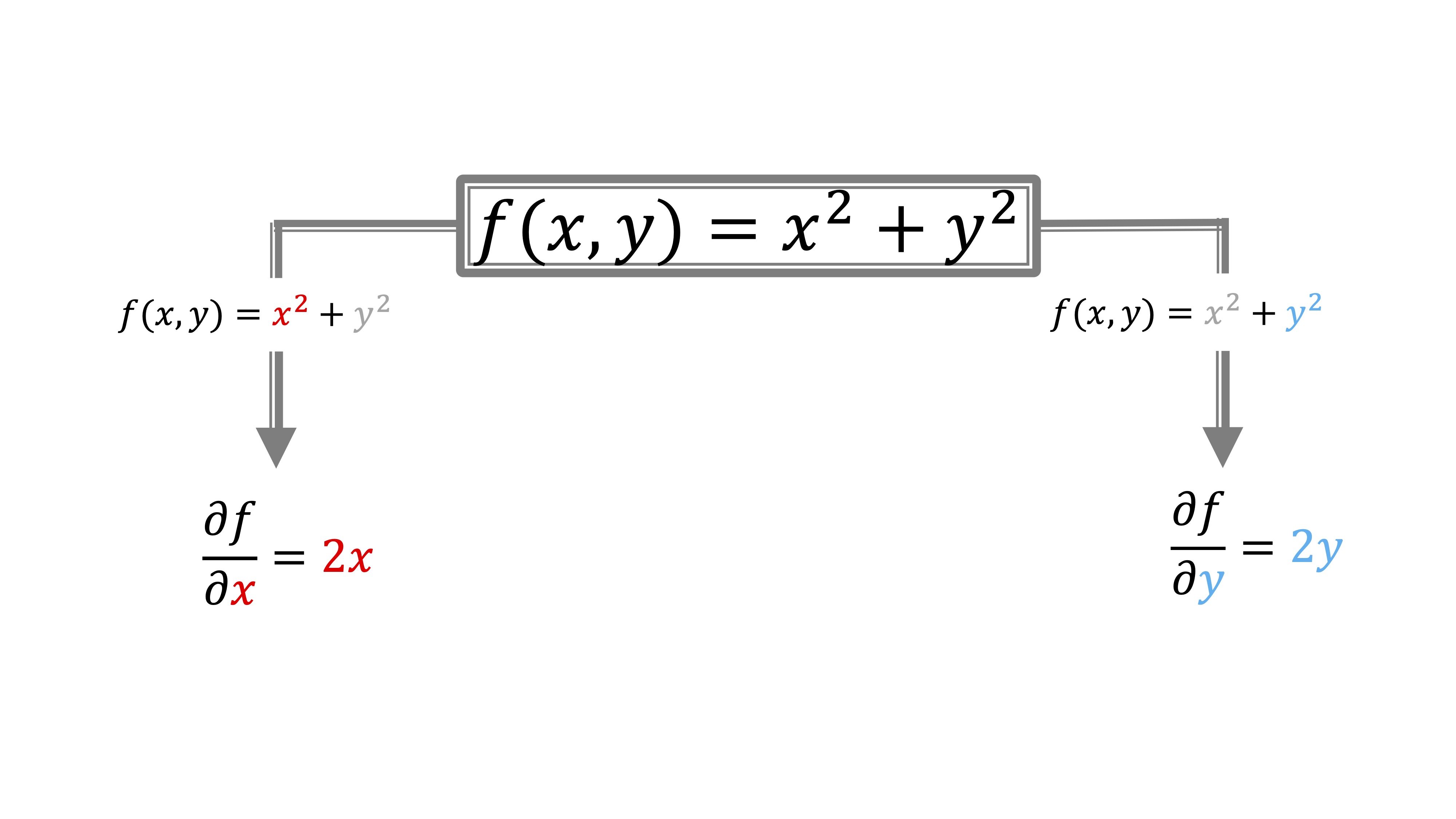
FIG1 Las derivadas parciales de la función \(f(x,y)=x^2+y^2\)

Como ves, cuando derivamos con respecto de \(x\), y lo escribimios así: \(\frac{\partial{f}}{\partial{x}}\) lo que estamos haciendo es convertir a la \(y\) en una constante y operar en consecuencia con las reglas de derivación. De igual manera, cuando derivamos con respecto de \(y\). Como ves, te pongo en color rojo la \(x\) cuando es variable y en gris cuando es constante: con la \(y\), lo mismo, pero en azul.

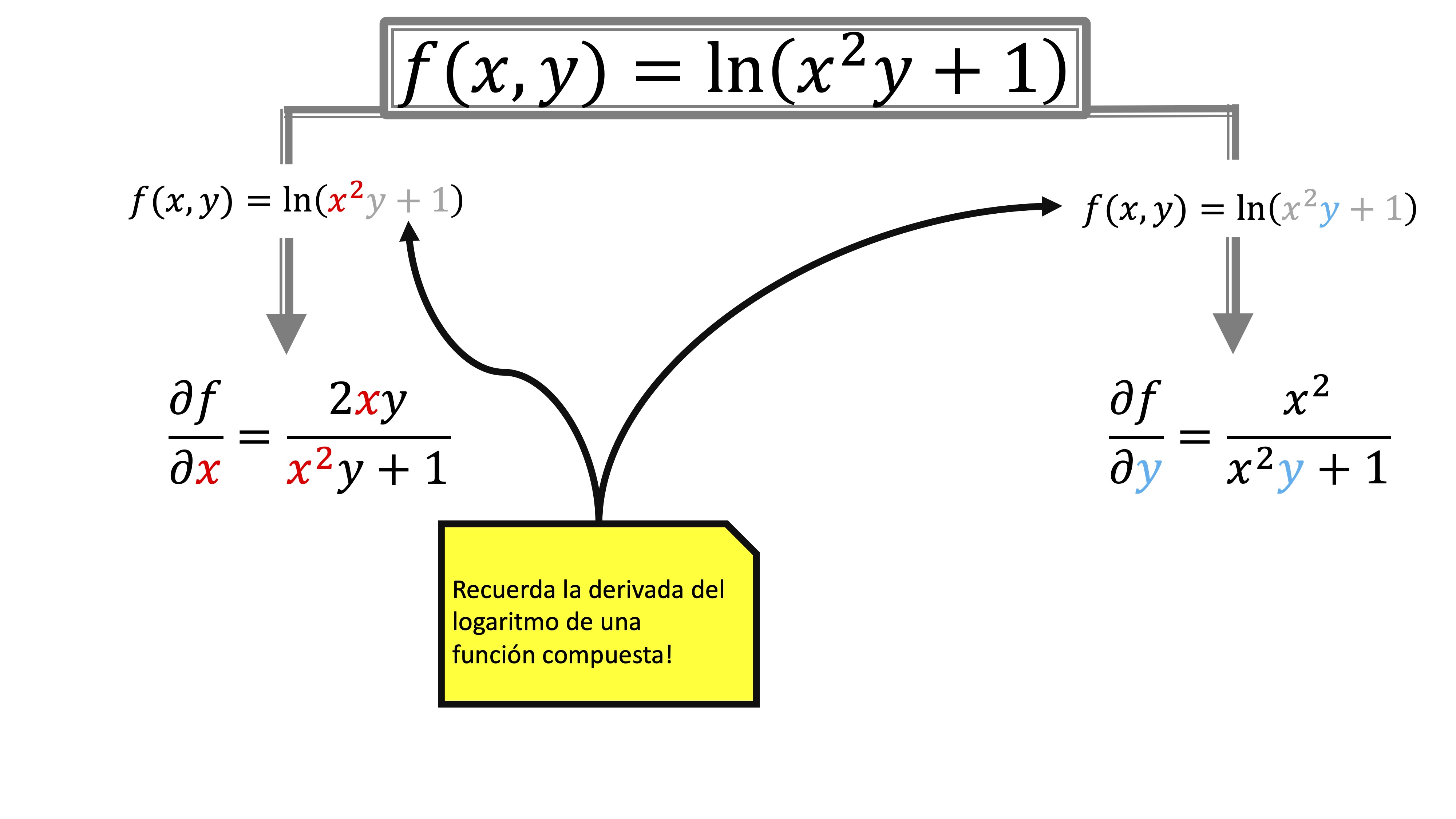
FIG2 Las derivadas parciales de la función \(f(x,y)=ln(x^2y+1)\)

Ahora se complica la cosa: en la FIG2 tenemos una composición de funciones: por un lado, el logaritmo, y por el otro \(x^2y+1\). Aquí, para derivar, tienes que hacer lo mismo que en una variable. Recuerda, por si acaso, cómo es la derivada del logaritmo de una función.

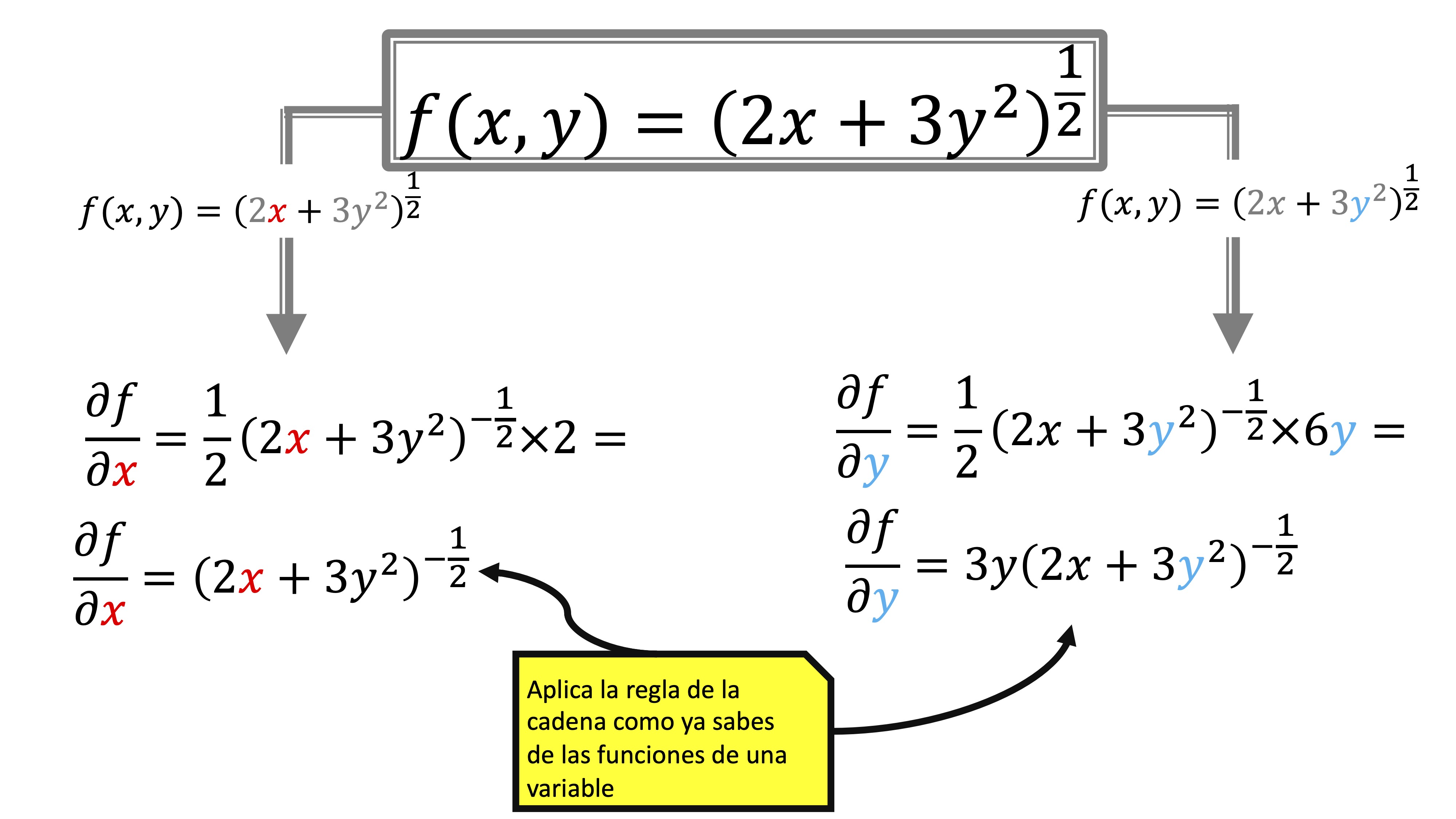FIG3 Las derivadas parciales de la función f(x,y)=(2x+3y^2)^(1/2) Y finalmente, en FIG3 tienes el último ejemplo: como verás es similar a lo que ya hemos dicho.

Ejercicios resueltos:

haz las siguientes derivadas parciales

\(f(x_{1},x_{2})=x_{1}+6x_{2}^{2}\)
- \(\frac{\partial f}{\partial x_{1}}=1\)
- \(\frac{\partial f}{\partial x_{2}}=12x_{2}\)
\(g(x_{1},x_{2})=\left(x_{1}+6x_{2}^{2}\right)^{2}\) (ten en cuenta la aplicación de la regla de la cadena)
- \(\frac{\partial g}{\partial x_{1}}=2\left(x_{1}+6x_{2}^{2}\right)\)
- \(\frac{\partial g}{\partial x_{2}}=24x_{2}\left(x_{1}+6x_{2}^{2}\right)\)
\(h(x_{1},x_{2})=Ax_{1}^{1/3}x_{2}^{2}\)
- \(\frac{\partial h}{\partial x_{1}}=\frac{A}{3}x_{1}^{-2/3}x_{2}^{2}\)
- \(\frac{\partial h}{\partial x_{2}}=2Ax_{1}^{1/3}x_{2}\)

Para entender la idea de la derivada parcial, vamos a empezar a trabjar de manera intuitiva con la función, ya famosa, “paraboloide de revolución” (mira el vídeo 2, si no la recuerdas)

\[ y=x_{1}^{2}+x_{2}^{2} \]

que ya dibujamos en 3D e hicimos sus curvas de nivel en la clase 1 y 2. En el gráfico siguiente, la FIG 1, mostramos algunas curvas de nivel

FIG1 Curvas de nivel de la función \(y=x_1^2+x_2^2\)

Como puedes ver, sobre las curvas de nivel hemos puesto una flecha (un vector) que indica que nos movemos una unidad en el eje de las abscisas y 0 unidades en las ordenadas. Es decir, incrementamos la variable \(x_{1}\) en una unidad y no tocamos la variable \(x_{2}.\) De hecho, tenemos que \(f(0,0)=0,\)y \(f(1,0)=1.\) Podemos decir, por ejemplo, que el incremento \(\triangle f=f(1,0)-f(0,0)=1.\) Escrito de otra forma ese incremento: \(f(x_{1}^{0}+\triangle x_{1},x_{2}^{0})-f(x_{1}^{0},x_{2}^{0})\). Fíjate que podríamos hacer cálculos similares a los que hicimos con una sola variable. Podríamos, por tanto, calcular la tasa de variación media de la función, ante el cambio que ha sufrido \(x_{1}.\) De esta forma:

\[ TVM_{x_{1}}=\frac{f(x_{1}^{0}+\triangle x_{1},x_{2}^{0})-f(x_{1}^{0},x_{2}^{0})}{\triangle x_{1}} \]

la cual nos dice el cambio promedio de la función al incrementar \(x_{1}\) y dejando \(x_{2}\) constante (lo que se conoce como ceteris paribus ). Ahora bien, ¿qué pasaría si, de nuevo, hacemos \(x_{1}\) tan pequeño como queramos dejando \(x_{2}\) quieto?

FIG2 tratamos de analizar qué pasará en la función si incrementamos \(x_1\) “una migaja”.

Como vemos, nos encontraremos en una curva de nivel, marcada en azul en la FIG2, que tiene un valor de la función mucho más pequeño que el de antes. De esta manera, podemos calcular, al igual que con una sola variable, la tasa de variación instantánea:

\[ TV{\color{red}I}_{x_{1}}=\lim_{\triangle x_{1}\rightarrow0}\frac{f(x_{1}^{0}+\triangle x_{1},x_{2}^{0})-f(x_{1}^{0},x_{2}^{0})}{\triangle x_{1}} \]

que se va a llamar derivada parcial . Como ves, nos permitirá analizar el impacto que tiene un incremento pequeño de \(x_{1}\), haciendo que \(x_{2}\) no varíe. La derivada parcial tiene su propia notación:

Sea la función \(f\left(x_{1},x_{2},...,x_{n}\right)\), la derivada parcial de la función con respecto a \(x_{i}\) (donde \(i\) es cualqueira de los posibles inputs): \[ \frac{\partial f}{\partial x_{i}} \] o, también, \[ f_{x_{i}}' \]

En el caso de una función con dos inputs, se concreta en

\[ \frac{\partial f}{\partial x_{1}}=\underset{\triangle x_{1}\rightarrow0}{\lim}\frac{f(x_{1}+\triangle x_{1},x_{2})-f(x_{1},x_{2})}{\triangle x_1} \]

\[ \frac{\partial f}{\partial x_{2}}=\underset{\triangle x_{2}\rightarrow0}{\lim}\frac{f(x_{1},x_{2}+\triangle x_{2})-f(x_{1},x_{2})}{\triangle x_2} \]

De ahí que, efectivamente, derivar de manera parcial consista en dejar constantes todas las variables con respecto a la que no se derive y utilizar las reglas de derivación habituales con la variable \(i\)-ésima. Destripamos, un momento, la fórmula de la derivada parcial

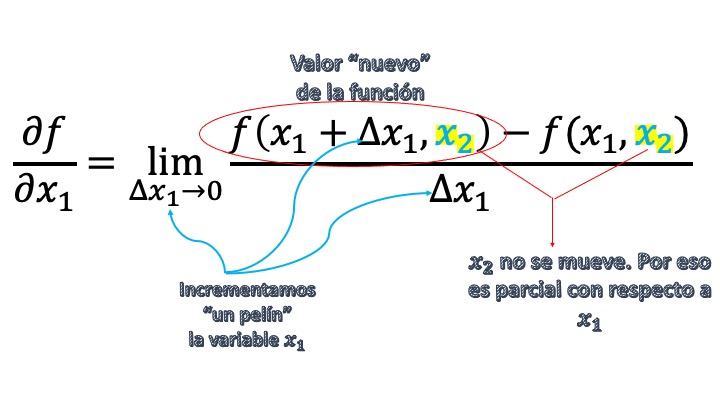
FIG3 …por si se entiende mejor.

Seguro que entiendes que, en el caso de \(x_{2}\) podríamos realizar el mismo análisis visual pero, en este caso, cambiando la orientación del vector \(\overrightarrow{v}.\)

FIG4 Lo mismo, pero en la dirección del otro eje coordenado.

Clase 7: Más sobre derivadas parciales

Ejercicio para calentar

Calcula las derivadas parciales de las siguientes funciones

1: \(f(m,n)=me^{2m-n}\)

2: \(f(x,y)=\frac{xe^{2y+1}}{1+3x}+(y+3)\sqrt{x^{2}+\ln y}\)

3: \(f(p,q)=\ln\left(\frac{p^{2}}{p+q}\right)\)

4: \(f(x,y,z)=xe^{z}\left(\frac{y+x}{z^{2}+1}\right)\)

5: \(f(a,b)=\frac{a}{a+b}+\sin(2a)\)

y ahora, el objetivo es entender la interpretación de una derivada parcial. Para ello, volveremos- de nuevo- a hablar de la relación entre la tasa de variación media y la(s) derivada(s) parciales de una función. Hasta ahora, lo que hemos hecho es aprender las técnicas para obtener derivadas parciales de funciones que son, a su vez, funciones (salvo que derivemos una función lineal). Ahora vamos a ver cómo, evaluándolas en un punto, obtenemos un significado con interpretación económica.

Para seguir entendiendo la idea, veamos el caso del índice de masa corporal, recordemos \(IMC=\frac{p}{a^{2}}\), de tal forma que \(p\) es el peso en kilogramos y \(a\) es la altura en metros del individuo. Ahora vamos a imaginarnos a un individuo que mide 1.65 metros y pesa 70 kilos (por lo que su IMC es 25.71). La idea de la derivada parcial es la siguiente (FIG1)

Si no variamos la altura (es decir, nos quedamos en \(a=1.65\)) podemos analizar cómo se modifica el IMC al ir variando el peso. Por ejemplo ¿y si pasamos de pesar 65 kilos a 70?

Vamos a calcular, primeramente, la varaición del IMC, es decir \(\Delta IMC\), para ello:

\[ \Delta IMC=IMC(70,1.65)-IMC(65,1.65)=25.71-23.87=1.84, \]

es decir, un individuo que pasa de \((65,1.65)\) a \((70,1.65)\), incrementa su IMC en 1.84 puntos. Ahora vamos a analizar la variación promedio, es decir, por cada kilo que aumenta, cuánto aumenta su IMC:

\[ \frac{\Delta IMC}{\Delta p}=\frac{IMC(p+\triangle p, a)-IMC(p,a)}{\triangle p}=\frac{1.84}{5}=0.37 \]

es decir, en promedio, por cada kilo que engorda nuestro individuo, su IMC sube 0.37 unidades.

Por otro lado, como vimos, la derivada consiste en calcular la tasa anterior cuando \(\Delta p\rightarrow 0\). Esto, en realidad, es difícil de interpretar. Nuestra imaginación no entiende muy bien qué quiere decir que el incremento del peso se acerque todo lo que queramos a cero, pero que nunca sea cero. Sin embargo, lo traduciremos como “cuánto cambia el IMC si incrementamos ligeramente el peso”.

FIG1 La idea de derivar el IMC con respecto al peso (dejo fija la estatura en un valor: en este caso 1.65), y me muevo por el eje del peso (de 65 a 70 kilos, en este caso).

la derivada parcial será \[ \frac{\partial IMC}{\partial p}=\frac{1}{a^{2}} \] que, evaluada en el punto en el que está el individuo

\[ \frac{\partial IMC}{\partial p}(65,1.65)=\frac{1}{1.65^{2}}=0.36 \]

En este caso, como ves, la derivada parcial se parece bastante a la tasa de variación media. Esto ocurre porque el cambio que ha sufrido la función (en este caso, aumentar 5 kilos) no parece ser muy grande. Esto nos lleva a decir que, si \(\Delta p\) es lo suficientemente pequeño, entonces:

\[ \frac{\Delta IMC}{\Delta p}\approx \frac{\partial IMC}{\partial p}(65,1.65) \]

De esta forma, podemos también decir que

\[ \Delta IMC\approx \frac{\partial IMC}{\partial p}(65,1.65)\Delta p \]

y, por ejemplo, es normal en economía atribuir como “pequeño” un incremento unitario en la variable independiente (trabajadores, precios, capital, etc…). En este caso, parece sensato, y entonces,haciendo \(\Delta p=1\)

\[ \Delta IMC\approx \frac{\partial IMC}{\partial p}(65,1.65)=0.36 \] y, por tanto, diremos que el incremento aproximado del IMC, ante cambios en una unidad del peso,manteniendo la altura constante, cuando el individuo está en el punto \((65,1.65)\) es de 0.36 unidades.

Sin embargo, no siempre es cierto que un incremento unitario en la variable independiente nos asegure que es “pequeño” y que, por tanto, podemos interpretar así la derivada

FIG2 Ahora, la idea de la derivada parcial del IMC con respecto a la estatura, dejando fijo el peso en un valor arbitrario.

Imaginemos un individuo que pesa \(70\) kilos y mide \(1.65\). Su IMC ya sabemos que es \(25.71\). Si fuera capaz de crecer un metro, mediría \(2.65\) y, manteniendo el peso constante, su IMC sería \(9.96\), por lo que

\[ \Delta IMC=IMC(70,2.65)-IMC(70,1.65)=9.96-25.71=-15,75, \]

es decir, el IMC se reduce en 15.75 unidades. Si calculamos la tasa de variación media \[ \frac{\Delta IMC}{\Delta a}=\frac{IMC(p, a+\triangle a)-IMC(p,a)}{\triangle a}=\frac{-15.75}{1}=-15.75, \] como es obvio, por cada metro que crece, el IMC cae -en este caso- 15.75 unidades. Si hacemos la derivada parcial y la evaluamos en el punto

\[ \frac{\partial IMC}{\partial a}=\frac{-2p}{a^{3}}, \] es decir

\[ \frac{\partial IMC}{\partial a}(70,1.65)=-31.16, \]

como ves, la derivada parcial y la tasa de variación media ya no se parecen. La derivada parcial está sobreestimando la verdadera variación. En este caso, si quisiéramos usar la derivada parcial, volveríamos a este resultado:

\[ \Delta IMC\approx \frac{\partial IMC}{\partial a}(70,1.65)\Delta a \]

donde \(\Delta a\) deberá ser mucho más pequeño que la unidad. Por ejemplo, si el individuo creciera cinco centímetros, tendríamos que

\[ \Delta IMC\approx \frac{\partial IMC}{\partial a}(70,1.65)\times 0.05=-31.16\times 0.05=-1.55 \]

es decir, el IMC se reduciría-aproximadamente-en 1.55 unidades si manteniendo el peso constante, el individuo pasa de 1.65 a 1.70. Utilizando la variación real obtendríamos:

\[ \Delta IMC=IMC(70,1.70)-IMC(70,1.65)=24.22-25.71=-1.49 \] que, como ves, ahora sí que se parece a la derivada.

Entonces:

El incremento de la función (\(\Delta IMC\), en este caso) nos da la variación exacta de la función ante cambios en una de sus variables independientes

La derivada parcial nos da la variación aproximada de la función, ante cambios “pequeños” en un input dejando el resto constantes.

En Economía, muchas veces, un cambio pequeño suele ser una unidad, pero no siempre.

Las derivadas parciales se utilizan, por ejemplo, para analizar cambios marginales en funciones (productividad marginal de los factores, coste marginal, etc…)

Puedes ver este vídeo de Maths & GO que te explica, con ayuda del inefable Homer Simpson, la idea de derivada parcial.

Ejercicio

Cuando se producen \(x\) unidades del bien \(X\) e \(y\) unidades del bien \(Y\) se incurre en unos costes dados por la función \(C(x,y)=8\sqrt{x^2+3y}\). Actualmente, \(x_0=2\) e \(y_0=4\).

Calcula los costes marginales (derivadas parciales) en cualquier punto y en el punto \((x_0,y_0)\) e interpreta su signo
¿Cuál es, aproximadamente, la variación en el coste si \(x\) se incrementa una décima?
¿Cuál es, aproximadamente, la variación en el coste si \(y\) se incrementa un 10%?

Clase 8 El gradiente y la derivada direccional

Ahora nos preguntamos ¿y si un individuo todavía está en edad de crecer y se pone a dieta? Entonces, no sólo avanzará en la dirección que marcan el eje \(x\) o el eje \(y\), sino que podrá tomar una dirección cualquiera que tendrá que determinarse, de nuevo, con un vector

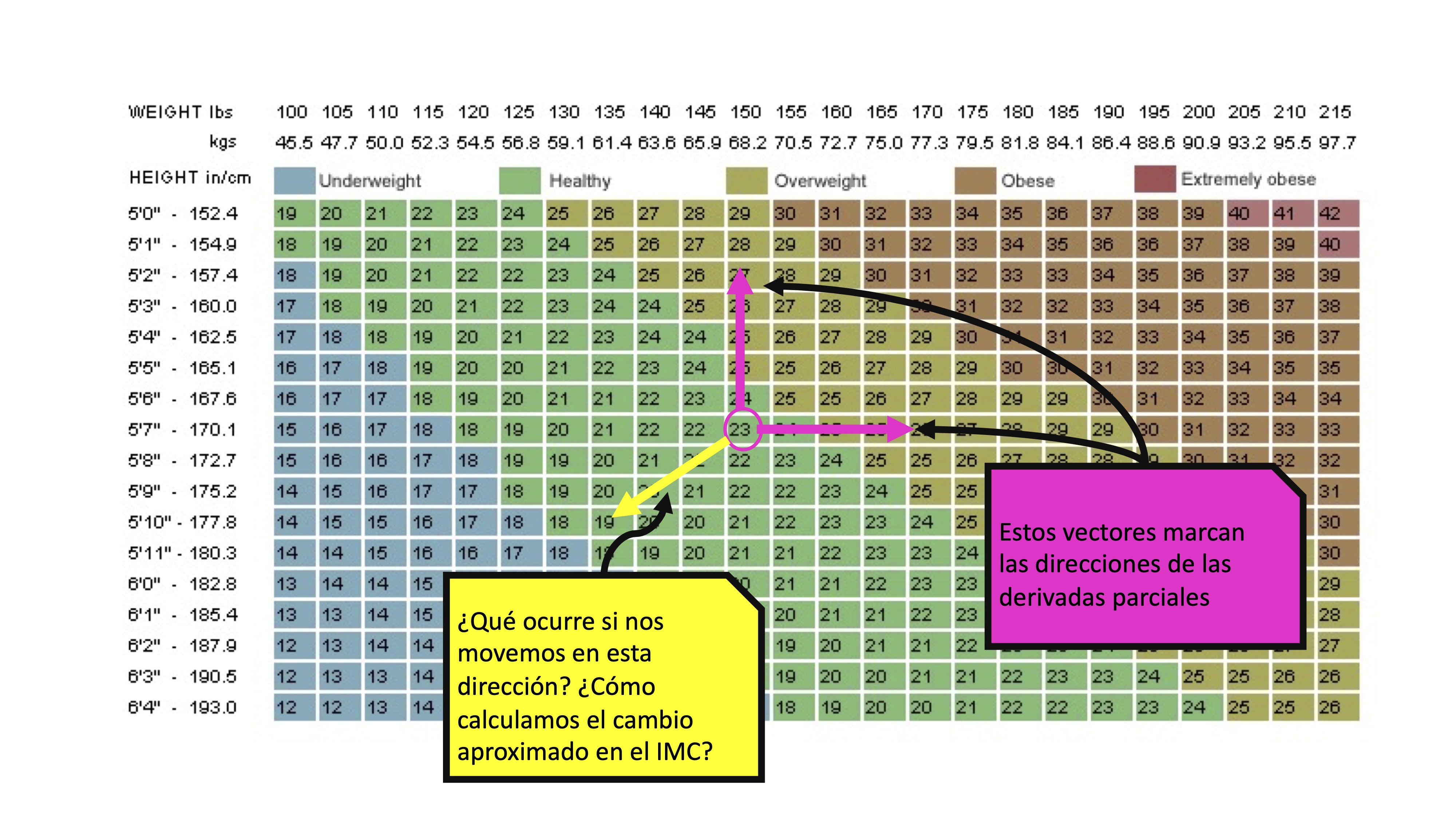FIG1 Tomamos una dirección en la que adelgazamos y crecemos Fíjate que, en la FIG1, El individuo pesa 68.2 y mide 170.1 (tiene, por tanto, un IMC de 23). Si crece hasta llegar a los 177.8 y adelgada hasta pesar 61.4, el vector que modela ese desplazamiento será: \(\vec{v}=(\Delta peso,\Delta altura)=(-6.8,-7.7)\), ya que es el cambio que ha sufrido en ambas variables.

Un caso más general de derivada, por tanto, es la derivada direccional. Esta derivada trata de evaluar el incremento de la función (en nuestro caso \(f(x_1,x_2)\)) cuando los incrementos de \(x_1,x_2\) se producen en cualquier dirección. Marcaremos la dirección utilizando “vectores”, de tal forma que si el vector de incrementos de ambas variables es \(\overrightarrow{v}=(v_1, v_2)\), la derivada direccional (que se marcará como \(D_\overrightarrow{v}f\)) será, simplemente

\[ D_\overrightarrow{v}f=\frac{\partial f}{\partial x_1} v_1 + \frac{\partial f}{\partial x_2} v_2 \]

La derivada direccional nos permitirá analizar si la función crece o decrece, en el entorno de un punto, siguiendo la dirección de un vector concreto. Esto, además, lo podemos usar para aproximar la variación de la función en el entorno de un punto ante incrementos- pequeños- de las variables explicativas.

Es habitual usar vectores que tengan norma 1, es decir, dividiendo por la raíz cudrada de la suma de cuadrados de sus componentes, aunque en este curso, tal y como está orientado, no es necesario normalizar los vectores.

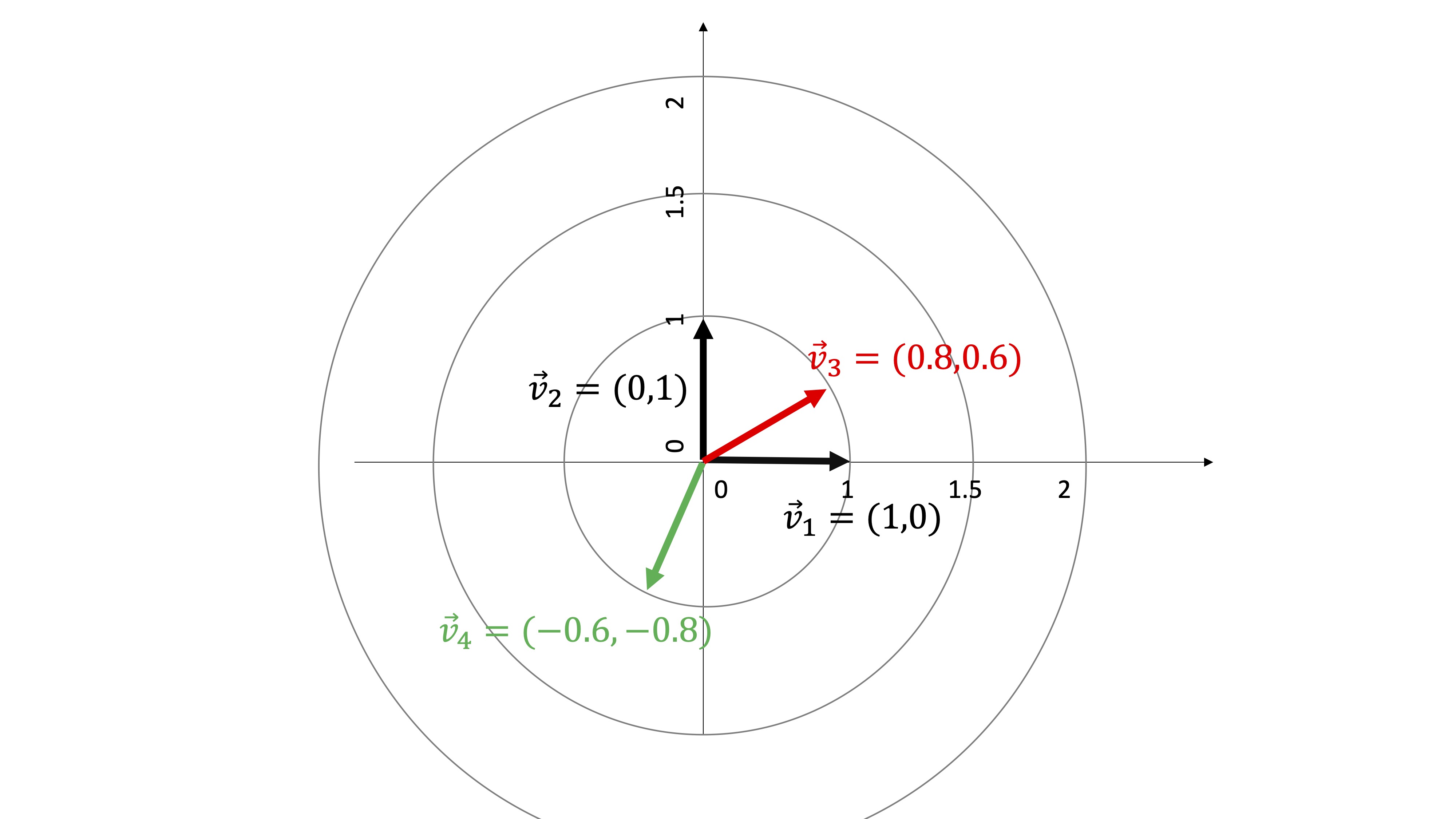
FIG2 Vectores con norma 1 que modelan la derivada direccional

Fíjate, en este caso, todos los vectores tienen norma 1. Entonces, veamos las siguientes derivadas direccionales:

\(D_\overrightarrow{v_1}f=(\frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2})\cdot(1,0)=\frac{\partial f}{\partial x_1}\) Es la derivada parcial con respecto a \(x_1\)

\(D_\overrightarrow{v_2}f=(\frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2})\cdot(0,1)=\frac{\partial f}{\partial x_2}\) Es la derivada parcial con respecto a \(x_1\)

y (4) \(D_\overrightarrow{v_3}f=(\frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2})\cdot(0.8,0.6)=0.8\times\frac{\partial f}{\partial x_1}+0.6\times\frac{\partial f}{\partial x_2}\) y nos indica el ritmo de variación de la función en la dirección del vector \(\vec{v_3}\). Del mismo modo que \(D_\overrightarrow{v_4}f=(\frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2})\cdot(-0.6,-0.8)=-0.6\times\frac{\partial f}{\partial x_1}-0.8\times\frac{\partial f}{\partial x_2}\) y nos indica el ritmo de variación de la función en la dirección del vector \(\vec{v_4}\).

Ejercicio Con los datos de Homer Simpson, obtén los siguientes resultados:

La derivada parcial del IMC con respecto al peso y la altura. Interpreta su significado

La derivada direccional si decide avanzar en la dirección “por cada kilo que engordo crezco un centímetro”. Interpreta el resultado

¿Y si fuera en sentido contrario, es decir, por cada kilo que adelgazo decrezco un centímetro? (no olvides que es un dibujo animado: puede crecer y decrecer como quiera)

Propiedad importante del gradiente

Vamos a tratar de entender las propiedades interesantes del gradiente, y muy útiles en optimización, con un ejemplo. Analicemos una función sencilla:

\[ f(x,y)=ln(4x-y) \]

Supongamos que estamos en el punto inicial \(x_{0},y_{0}=(1,3)\). Vamos a calcular el vector gradiente de la función:

\[ \nabla f(x,y)=\left[\frac{4}{4x-y},\frac{-1}{4x-y}\right] \]

que, evaluado en el punto \((1,3)\),

\[ \nabla f(x_{0},y_{0})=\left[4,-1\right] \]

¿Recuerdas qué información nos daba un vector? En este caso, al tener dos coordenadas, nos está marcando en qué dirección nos movemos. Por ejemplo, el vector (4,-1) nos dice que andemos siempre 4 pasos en dirección eje \(x\) (es decir, a la derecha) y menos 1 pasos (es decir, hacia abajo) en dirección eje \(y\). Si lo dibujamos, estamos recorriendo esta dirección:

FIG5. El mismo vector en \(\mathbb{R}^{2}\).

Nota que los vectores marcan la misma dirección, da igual que empecemos del (0,0). Es decir, donde empieces da igual, que es lo mismo que decir que el punto de aplicación del vector no es importante. Todos esos vectores son, en definitiva, el (4,-1).

Bueno, ya tenemos pillada la idea de para qué nos sirve un vector (por lo menos, para nosotros). Ahora vamos a por el siguiente argumento. Pinta las curvas de nivel de la función del ejemplo. Para ello:

\[ C=ln(4x-y)\Rightarrow e^{C}=4x-y \]

FIG6. las curvas de nivel para diferentes valores de c.

Como ves en la FIG2, la función crece según nos vamos en sentido sureste. ¿Se puede mejorar esta descripción?. Ahora nos preguntamos ¿cuál de estas flechas (sí, sí, vectores) es la que permite avanzar hacia el siguiente valor mayor de la función de forma más rápida? Mira estos candidatos. ¿Qué flecha (vector) te parece el mejor?

FIG7. ¡La verde!

estarás de acuerdo conmigo que el mejor candidato es el verde. Esa es la forma más rápida que encontramos para avanzar al siguiente punto de la función. Pues fíjate, ese vector es proporcional a otro que ya hemos dibujado antes:

FIG8. ¿De qué vector es proporcional?

¡Del gradiente! En efecto. De hecho, esto nos permite enunciar una propiedad (que no demostramos) sobre el gradiente:

El gradiente marca la dirección de máximo crecimiento/decrecimiento de la función

¿En qué consiste buscar la dirección de máximo crecimiento/decrecimiento de la función?

Necesitamos,en este caso, encontrar el vector de desplazamientos \((\Delta x,\Delta y)\). Que me permita crecer/decrecer lo más rápido a partir de un punto dado \(x_0,y_0\).

Ya sabemos que el cambio en la función se puede escribir, de forma aproximada como:

\[ \triangle f\approx\frac{\partial f(x_{0},y_{0})}{\partial x}\triangle x+\frac{\partial f(x_{0},y_{0})}{\partial y}\triangle y \]

Entonces, vemos que:

La dirección de máximo crecimiento es aquella en la que el ángulo entre el gradiente y el vector de incrementos es nulo (es decir, son el mismo vector). Esto quiere decir que \(\triangle x,\triangle y\) se han de mover proporcionales al vector gradiente.
La dirección de mayor decrecimiento es la contaria (es decir, formando 180 grados respecto a la curva de nivel)
Hay direcciones en las que no varía: si el vector de incrementos es perpendicular al vector gradiente.

Ejercicio 4 Considera la función \(B(p,Q)=(p-3)Q\). Dibuja la curva de nivel de la función que contiene al punto \((7,8)\). ¿Qué relación existe entre la curva de nivel y el vector gradiente de \(B\) en el punto \((7,8)\)? ¿qué indica dicho gradiente?

Ejercicio 5

Sea \(f(x,y)=1+x-2y+0.5x^2+3y^2-2xy\), ¿qué relación deben satisfacer las variaciones \((\Delta x, \Delta y)\) de las variables para que partiendo del punto \((0,1)\) se aumente la función lo más rápidamente posible?

Ejercicio 5 Sea \(\Pi(r,w)=100\frac{r+w}{rw}\) la función de beneficios de una empresa (donde \(r\) es el precio del capital y \(w\) es el salario) 1) Calcula el vector gradiente de la función de beneficios en el punto (2,1) 2) Obtén el plano tangente a la función en ese punto y dibuja la función y dicho plano. ¿En qué entorno la aproximación parece aceptable? 3) ¿En qué proporción se deben incrementar precio de capital y salario para que el beneficio crezca lo más rápido posible?