Apéndice: repaso de gráficas de funciones
Funciones polinómicas
Parábola. \(y=ax^2+bx+c\). Tenemos dos casos
\(a<0\) con forma: \({\color{red}\cap}\)
\(a>0\) con forma: \({\color{teal}\cup}\)
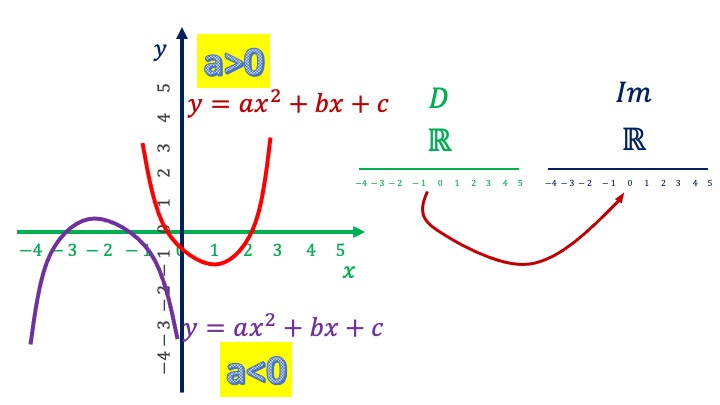
Las parábolas
Recuerda
- vértices: \(x=\frac{-b}{2a}\) \(y=f(\frac{-b}{2a})\).
- corte con el eje de las \(x\) : \(\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\)
- corte con el eje de la \(y\), hacemos \(x=0\) y obtenemos el valor correspondiente.
cúbicas. \(y=a+bx+cx^{2}+dx^{3}\). Tenemos dos casos
\(d<0\) con forma: \({\cup\cap}\)
\(d>0\) con forma: \({\cap\cup}\)
Las cúbicas
Más adelante, cuando veamos aplicaciones de las derivadas, veremos cómo dibujarlas con mayor precisión. Es cierto que el dibujo de gráficas polinomiales se va complicando con el grado del polinomio y es necesario conocer más herramientas de cálculo para hacerlo adecuadamente.
Potenciales . Funciones del tipo \(f(x)=x^{n}\). Con diferentes tipos de valores para \(n\). Mira los pies de cada una de las imágenes para identificarlas
\(n\) par y positivo , \(n=\left\{ 2,4,6,....\right\}\)
\(n\) impar y positivo , \(n=\left\{ 3,5,7,....\right\}\)
\(n\) par y negativo , \(n=\{-2,-4,...\}\)
\(n\) impar y negativo \(n=\{-1,-3.-5...\}\)
\(n\) positivo y racional
En este vídeo puedes repasar ideas de estas funciones polinómicas que te hemos presentado
Ejercicio 3
Sea la función \(f(x)=ax^2+bx+c\). Sabiendo que los puntos \((1,-3)\), \((0,-6)\), \((3,15)\), son puntos de su gráfica: calcula los valores de \(a,b,c\)
Ejercicio 4
Dibuja las gráficas de \(f(x)=x^2\), \(g(x)=(x-2)^2\), \(h(x)=x^2+3\) ¿Cómo se relacionan dichas gráficas?
Ejercicio 5
Una forma muy cómoda de escribir una parábola es así: \(y=(x-2)(x-8)\) ¿Por qué? ¡ya nos da las raíces de la ecuación de segundo grado!. Dibújala.
Ejercicio 6
Escribe de forma simplificada y, posteriormente, dibuja las siguientes funciones potenciales
\(f(a)=(((a^{1/2})^{2/3})^{3/4})^{4/5}\)
\(g(x)=(((3x)^{-1})^{-2}(2x^{-2})^{-1})/x^{-3}\)
Logaritmo y exponencial
El logaritmo -en base \(a\)- es una función tal que
\[ log_{a}y=x\Longleftrightarrow a^{x}=y \]
Esta relación indica, además, que la función inversa al logaritmo es la función exponencial (y viceversa): \[ y=a^{x} \]
Donde \(a>0\).
Es muy común el uso del logaritmo en base \(e\), es decir, el logaritmo neperiano. De tal forma que
\[ \ln y=x\Longleftrightarrow e^{x}=y \]
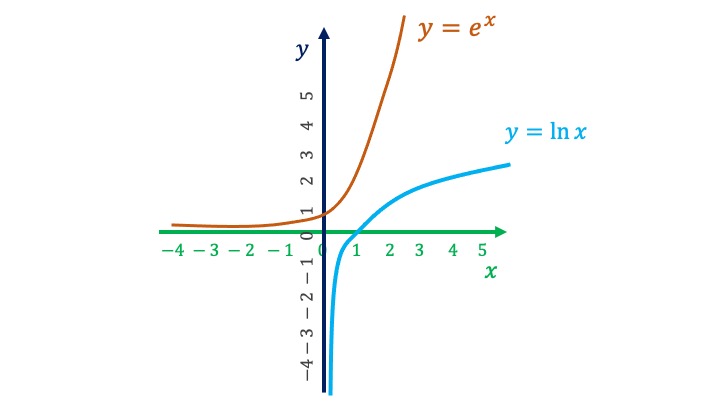
En esta figura se puede ver la propiedad de que ambas funciones son inversas
Ejercicio 7
Recupera las propiedades del logaritmo y de la exponencial. Haz una lista con ellas y tenla siempre a mano.
Ejercicio 8
Una libreta de ahorros con un capital inicial de \(600\) euros, produce un \(3\)% de interés anual
Escribe una función que represente el capital que se obtendrá en el año \(t\) y responde
- a: ¿Cuánto tiempo tendrá que pasar para que reciba \(655.63\) euros?
- b: ¿Qué ocurre con el capital si \(t\) se vuelve “muy grande”?
Ejercicio 9
Después de desactivar una bomba, el agente especial 00.0 regresa a casa y se entera de que su mejor amigo “Siggy”, ha sido asesinado. La policía dice que el cuerpo fue encontrado a la 1 de la madrugada del jueves, en un frigorífico a 10ºF. También le dijeron que la temperatura del cadáver, cuando lo encontraron, era de 40ºF. Se sabe que la temperatura de un cuerpo, después de muerto, sigue la función
\[ T=T_{a}+(98.6-T_a)(0.97)^t \]
Donde \(T_a\) es la temperatura del aire que rodea el cuerpo y \(t\) son las horas. El agente sabe que el asesinato fue cometido o por Ernest Stabros o por André Scélérat. Si el primero estuvo en la cárcel hasta el miércoles y el segundo fue visto en Las Vegas desde el mediodía del miércoles hasta el viernes: ¿quién cometió el crimen?
pista:necesitas obtener \(t\) para los datos de los que dispones
Ejercicio 10
Demuestra las siguientes igualdades
- a: \(ln(x)-x=ln(x/e^{x})\)
- b: \(ln (x) - ln(y) + ln(z) =ln(xz/y)\)
- c: \(3 +2ln(x)=ln(e^{3}x^2)\)
Simplifica las expresiones siguientes
- a: \(e^{lnx}-ln{e^x}\)
- b: \(ln(x^4 e^{-x})\)
- c: \(e^{ln{x^2}-2ln{x}}\)
Uno de sus usos es simplificar las unidades y escalas de medida. Por ejemplo, mira esta información de El País sobre los datos del Coronavirus:
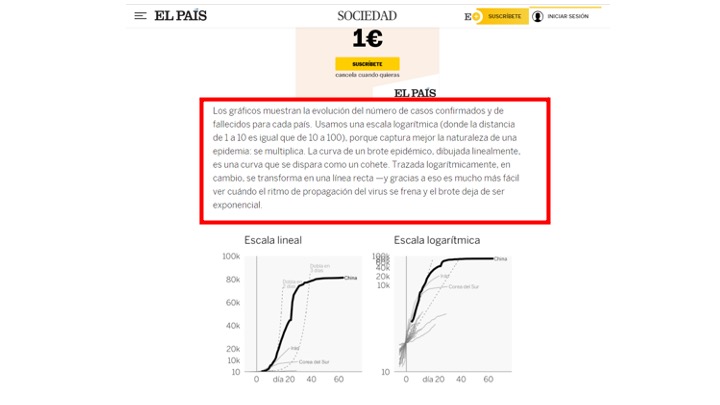
¡el logaritmo sale en la prensa!
Lo que viene a decir este recorte de prensa es que si el virus avanza siguiendo una función exponencial como esta \(f(x)=ae^{bx}\), con \(a,b\in \mathbb{R}\), si se introduce la transformación logarítmica a los datos, esta debería convertirse en una recta. Mira cómo:
\[ y=ae^{bx} \]
\[ \ln y=\ln a+\ln e^{bx} \]
\[ \ln y=\ln a+bx \]
\[ \ln y=a^{*}+bx, \]
En este vídeo tienes un buen resumen de la función logaritmo y la exponencial
Cónicas
Las cónicas esenciales que necesitaremos este año van a ser las circunferencias y las elipses. Ambas son curvas que se dibujan en el plano (en \(\mathbb{R}^2\)) pero que, como ves, no constituyen una función (sabrías por qué?) ¿Ves? Este es un ejemplo, de tantos, de una “fórmula” que no es una función.
circunferencia . Su expresión canónica es \((x-x_{0})^2+(y-y_{0})^2=r^2\), de tal forma que \((x_{0},y_{0})\) es el punto central de la circunferencia. La ecuación dice que todos los puntos equidistan de ella a la misma distancia, llamada \(r\) o radio. Por lo tanto, dibujar una circunferencia con esta expresión es muy sencillo: tienes tanto el centro como el radio. No tiene pérdida.
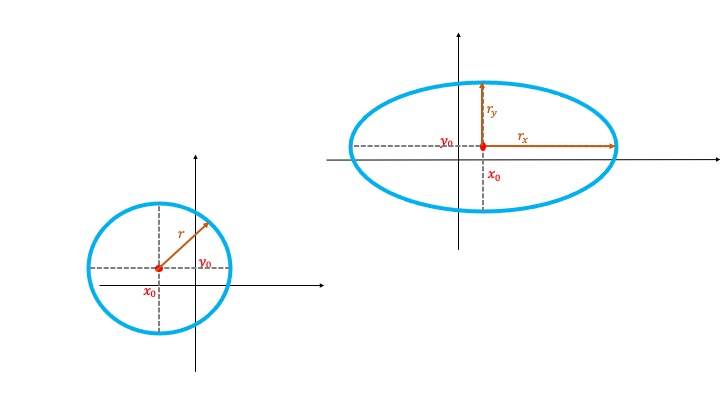
La circunferencia y la elipse
elipse . Su expresión canónica es \(\frac{(x-x_{0})^2}{r_x^2}+\frac{(y-y_{0})^2}{r_y^2}=1\), de tal forma que \((x_{0},y_{0})\) es el punto central de la elipse. Como ya sabes, una elipse es una circunferencia “achatada”. Para dibujarla, necesitas de nuevo conocer su centro y, en el denominador de la expresión \((x-x_{0})^2\) te encontrarás con el cuadrado del semieje mayor (es decir, \(r_x\)), mientras que en el denominador de \((y-y_{0})^2\) te encontrarás con el cuadrado del semieje menor (es decir, \(r_y\)). Con esa información puedes dibujarla como en la figura. Es importante que notes que *la ecuación debe estar igualada a 1. Si no, deberás dividir en ambos lados por el mismo valor.
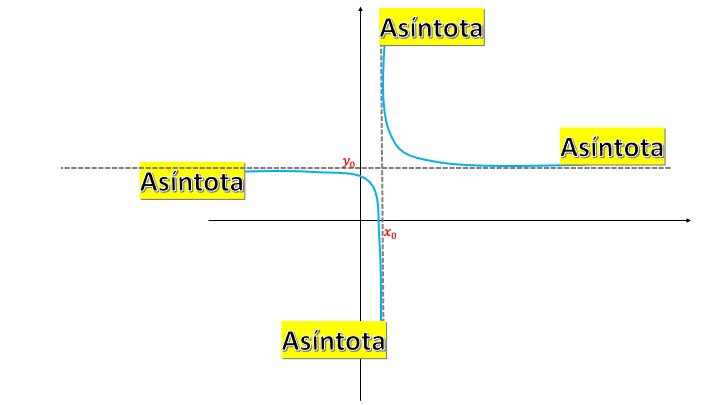
La hipérbola equilátera
hipérbola equilátera . Finalmente, otra de las cónicas de interés. Esta sí es una función cuya expresión es \((x-x_0)(y-y_0)=K\), donde \(K\) es una constante. Tiene, como asíntotas, las rectas \(x=x_0\) e \(y=y_0\). Y se sitúa en el primer y tercer cuadrante si \(K>0\) y en el segundo y cuarto si \(K<0\)
En este vídeo tienes un buen resumen de las cónicas. Además, hay ejercicios resueltos que te ayudarán a practicar.
- Ojo, todas estas gráficas no sólo son relevantes para esta parte del curso, sino que las necesitaremos de nuevo para dibujar curvas de nivel y, además, en Matemáticas II.


