BLOQUE 3: Introducción a la Optimización
Clase 1 (magistral): La optimización en una variable (I)
Un problema de optimización en una variable, se puede plantear como un problema de maximización o minimización como sigue
\[ \max_{x\in D}f(x) \]
\[ \min_{x\in D}f(x) \]
es decir, lo que queremos escribir es
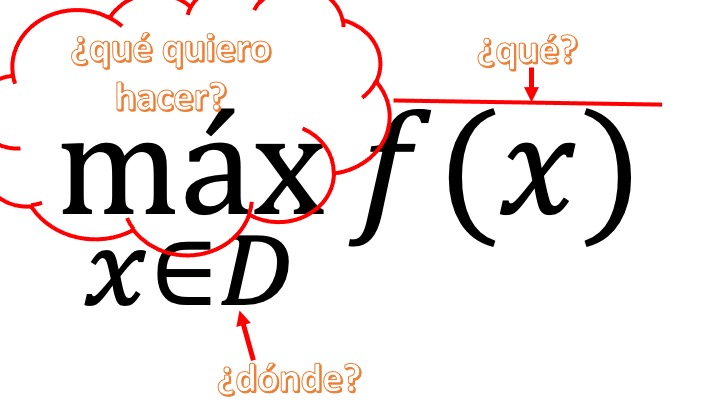
FIG 1 Un problema general
- primero: ¿qué quiero hacer: maximizar o minimizar? Si no lo sé, puedo poner “\(opt\)” en su lugar (que querrá decir: quiero “optimizar”)
- segundo: ¿qué quiero optimizar? generalmente, una función. En esta clase, además, funciones de una variable
- tercero: ¿dónde busco los valores de \(x\) que optimizan mi función? Pues, como parece lógico en el dominio de la función. Cuando sea así, y el dominio sea \(\mathbb{R}\), diremos que la optimización es “libre”. Si buscamos el óptimo en un intervalo, (por ejemplo, el dominio es \(3<x<5\)) entonces la optimización con la que trabajaremos será restingida
1.3.2 Optimización libre para funciones \(\mathbb{R}\rightarrow\mathbb{R}\)
En la búsqueda de los máximos o mínimos que hemos enunciado previamente, nos podemos encontrar con distintas posibilidades. Lo analizamos para mínimos pero sería igual para máximos (cambiando la orientación de las desigualdades). Mira esta FIG2
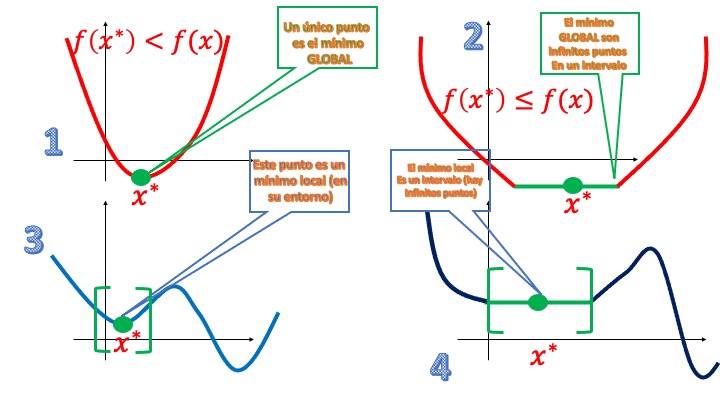
FIG 2 Diferentes tipos de mínimos
1: Un punto \(x^*\) es un mínimo global estricto de \(f\) si \(f(x^*)<f(x)\) para todo \(x\in\mathbb{R}\). Fíjate bien: de todos los posibles valores de \(x\) en la recta real hay sólo uno que es el que proporciona el menor valor de la función
2: Un punto \(x^*\) es un mínimo global de \(f\) si \(f(x^*)\leq f(x)\) para todo \(x\in\mathbb{R}\). Fíjate bien: de todos los posibles valores de \(x\) en la recta real hay un intervalo de ellos (todos iguales a \(x^*\)) que proporcionan el menor valor de la función*
3: Un punto \(x^*\) es un mínimo local estricto de \(f\) si \(f(x^*)<f(x)\) para todo \(x\in B(x^*)\), donde \(B(x^*)\) es un entorno del punto. Fíjate bien: en el entorno de \(x^*\), este resulta ser el que da el menor valor de la función. Pero es local puesto que hay otro mínimo (local) que da un valor de la función aun menor*
4: Un punto \(x^*\) es un mínimo local de \(f\) si \(f(x^*)\leq f(x)\) para todo \(x\in B(x^*)\), donde \(B(x^*)\) es un entorno del punto. Fíjate bien: en el entorno del intervalo que contiene a \(x^*\), dicho intervalo resulta ser el que da el menor valor de la función. Pero es local puesto que hay otro mínimo (local) que da un valor de la función aun menor*
Vamos a intentar descubrir, de manera intuitiva, todas las condiciones que necesitamos para asegurarnos en qué situación estamos. Necesitaremos recuperar, eso sí, algo que ya vimos en las aplicaciones de las derivadas en funciones de una variable
Punto Crítico o condición necesaria de primer orden
Una función \(f\) diferenciable tendrá un punto crítico \(x^*\in \mathbb{R}\) si \(f'(x^*)=0\) o \(f'(x^*)\) no existe.
Es decir, los puntos que buscamos han de satisfacer esa condición (por eso decimos que es NECESARIA). Luego deberemos clasificarlos.
Ejemplo 1 Busca los puntos críticos de \(f(x)=2-x^4-2x^2\) y de \(g(x)=e^{x^4}\)
- En el primer caso, \(f'(x)=-4x^3-4x\). Igualando a cero, tenemos \(4x^3+4x=0\), de donde sacamos el único punto crítico, que es \(x^*=0\).
- En el segundo caso, \(g'(x)=e^{x^4}(4x^3)\) Si igualamos a cero esta derivada, de nuevo obtenemos que el único punto crítico es \(x^*=0\)
Ahora bien, ¿qué tipo de puntos críticos son? ¿Son máximos, mínimos, puntos de inflexión? Para ello, deberemos aprender lo que conoceremos como condición de segundo orden
Condición necesaria de segundo orden: óptimos locales
un punto \(x^*\in \mathbb{R}\) que satisface \(f'(x^*)=0\)
- Mínimo local si \(f''(x^*)\geq 0\)
- Máximo local si \(f''(x^*)\leq 0\)
Esta condición se conoce como CONDICIÓN NECESARIA DE SEGUNDO ORDEN de óptimo local. Cuando \(f''(x^*)= 0\) podremos estar en mínimo, máximo o punto de inflexión, como ya sabes.
La condición necesaria de segundo orden nos permite clasificar los puntos críticos. Por ahora, como sólo tenemos en cuenta el valor del punto crítico, el análisis se realiza en un entorno del punto, de tal forma que sólo podemos hacer un análisis local (de ahí que no podamos todavía decir nada de la globalidad)
Ejemplo 2 Pensemos, entonces, sobre las funciones del Ejemplo 1.
- Obtenemos la segunda derivada \(f''(x)=-12x^2-4\). Particularizando en el punto crítico \(f''(0)=-4\). Por tanto, sabemos que es un máximo local
- En el segundo caso, \(g''(x)=e^{x^4}(4x^3)^2+12x^2e^{x^4}\) evaluando en el punto crítico \(f''(0)=0\) por lo que cumple la condición tanto de máximo, de mínimo local o de punto de inflexión.
Nota Estas condiciones pueden hacerse “necesarias y suficientes” simplemente restringiendo la condición de máximo local si \(f''(x^*)< 0\) o mínimo local si \(f''(x^*)> 0\).
Si queremos analizar la posible globalidad del punto crítico, entonces deberemos echar mano de un teorema importante.
Local-Global
Una función \(f\), diferenciable:
- convexa en todo su dominio: los mínimos locales son globales
- cóncava en todo su dominio: los máximos locales son globales
Recuerda que una función es convexa en todo su dominio si, para todo \(x\in D\) la derivada segunda es mayor o igual a cero y es cóncava en todo su dominio si, para todo \(x\in D\) la derivada segunda es menor o igual a cero.
Aplicando el teorema local-global a las funciones anteriores, podemos ver
- En el primer caso, \(f''(x)=-12x^2-4\) siempre es NEGATIVA, es decir, para cualquier \(x\), la segunda derivada es estrictamente menor que cero. Entonces, sabemos que la función es estrictamente cóncava. Por el teorema local-global, el punto crítico \(x^*=0\) es automáticamente máximo global.
- En el segundo caso, \(g''(x)=e^{x^4}(4x^3)^2+12x^2e^{x^4}\) siempre es MAYOR O IGUAL A CERO Es una función convexa y, por tanto, el punto crítico \(x^*=0\) es un mínimo global.
Estas condiciones- junto con el Teorema Local-Global- te ayudarán a tomar las decisiones correspondientes. En esencia, usamos las condiciones necesarias para discriminar si un punto puede ser un punto óptimo, mientras que las suficientes nos ayudan a clasificarlos (aunque con limitaciones, ya que no cumplir una condición suficiente no te asegura nada, aunque cumplirla sí). Vamos con ejemplos
Ejemplo 3
Utilicemos lo aprendido para clasificar los puntos críticos de \(f(x)=x^3\), \(g(x)=3x^5-5x^3\), \(h(x)=\sqrt(x)+2ln(x)\), \(i(x)=\frac{1}{1+x^2}\)
| Derivada primera | Derivada segunda | ¿Cumple Local Global? |
|---|---|---|
| \(f'(x)=3x^2\) | \(f''(x)=6x\) | NO |
| \(g'(x)=15x^4-15x^2\) | \(g''(x)=60x^3-30x\) | NO |
| \(h'(x)=\frac{-1}{2\sqrt(x)}+\frac{2}{x}\) | \(NA\) | \(NA\) |
| \(i'(x)=\frac{-2x}{(1+x^2)^2}\) | \(i''(x)=\frac{6x^2-2}{(1+x^2)^3}\) | \(NO\) |
Vamos caso a caso
- el 1) El punto crítico es, únicamente, \(x^*=0\). La derivada segunda, como vemos, cambia de signo según \(x\), por lo que no satisface el teorema local-global (que exigiría un único signo para todo \(x\)). Si nos fijamos, \(f''(0)=0\), que podría ser máximo como mínimo local.Ahora bien, como no se cumple el teorema local-global, debemos pensar algo más: si nos fijamos, la derivada segunda cambia de signo a la izquierda y derecha del punto crítico. Recuerda que esa característica es la de PUNTO DE INFLEXIÓN. Ya está clasificado.
- el 2) tenemos 3 puntos críticos: \(x^*_1=0\), \(x^*_2=1\), \(x^*_3=-1\). Como vemos, el teorema local-global no aplica, puesto que la derivada segunda cambia de signo según el valor de \(x\) y, por tanto, no es ni cóncava ni convexa. Si evaluamos la derivada segunda en cada uno de los puntos (para poder clasificarlos como locales), tendremos \(f''(0)=0\) por lo que puede ser máximo o mínimo o punto de inflexión, \(f''(1)=30\), por lo que es un mínimo local y \(f''(-1)=-30\) por o que es un máximo local. No podemos saber si son globales, puesto que no se satisface el teorema local-global. Una idea que podemos hacer es ver su gráfica. Si no la tienes disponible, puedes pensar si la función puede obtener mejores y peores máximos y mínimos. Coge la calculadora: sabemos que en \(x=1\) tenemos un mínimo (local). Ahí la función vale \(g(1)=-2\). Si fuera un mínimo global, seríamos incapaces de encontrar un valor para \(g\) menor que \(-2\) para cualquier otro \(x\). Pero fíjate: \(g=3x^5-5x^3\). Puedes encontrar, seguro, valores para \(x\) que hagan que \(g\) sea menor que \(-2\). Por ejemplo, si \(x=-3\), \(g(-3)=-594\). Eso es así porque, si te fijas, si \(x\rightarrow -\infty\), entonces, \(g\rightarrow -\infty\). Verás que pasa lo mismo con \(x=-1\) es un máximo local. \(x=0\) es un punto de inflexión, ya que la derivada segunda cambia de signo a la derecha e izquierda de \(x=0\). Este ha costado, puesto que si no se cumple el Teorema Local-Global, todo es más tedioso.
- el 3), como ves, la derivada primera no existe cuando \(x^*=0\): pero \(x=0\) no es un punto del dominio, por lo que esta función no tiene punto crítico: es siempre creciente.
- el 4) tiene un único punto crítico: \(x^*=0\). No se cumple el teorema local-global porque la derivada segunda cambia con el valor de \(x\). Sin embargo, \(i''(0)=-2\), por lo que es un máximo local estricto. Para saber si es global, deberemos pensar si hay valores de \(x\) que hagan que esta función pueda tomar valores mayores que \(i(0)=1\). Para ello, deberás pensar sobre la función \(i=\frac{1}{1+x^2}\). Si te das cuenta, cuanto mayor/menor sea \(x\), esta función se va acercando a cero, por lo que el máximo que hemos encontrado es global.
Dominio de la función objetivo definido en un intervalo cerrado: no necesitamos la segunda derivada
En el caso en el que se defina que el dominio de la función en el que interesa buscar el óptimo es en un intervalo cerrado, se han de analizar los puntos siguientes:
\(x\in[a,b]\)
- los puntos donde la derivada de la función se anula o no existe
- los extremos del intervalo
Cuando el dominio se define en un intervalo cerrado y acotado, decimos que este está definido en un conjunto compacto. El Teorema de Weierstrass asegura que, entonces, si la función objetivo es continua, el problema tendrá mínimo y máximo globales. Para saber cuáles son sólo hay que hacer una tabla con los valores de la función de los puntos anteriores.
Veamos un ejemplo:
Ejemplo 1 Busca los óptimos de la función \(f(x)=x^{2/3}(5-2x)\) si \(x\in[-1,2]\)
solución Al estar definida la función en un intervalo cerrado, sabemos que deberemos analizar el valor que toma la función en los extremos del intervalo. Además, deberemos obtener los puntos críticos de esta. Tenemos que
\[ f'(x)=\frac{10}{3}x^{-1/3}(1-x) \]
Donde podemos ver que, si \(x^*=1\), la derivada se anula y si \(x=0\) la derivada no existe (ya que la raíz cúbica está en el denominador). Entonces, dado que el intervalo de la \(x\) es cerrado, podemos hacer una tabla de valores para conocer qué \(x\) proporciona el mayor valor a la función y el menor
| Valor \(x^*\) | \(f(x^*)\) | ¿Qué tipo de punto es? |
|---|---|---|
| \(x=-1\) | \(7\) | Máximo GLOBAL |
| \(x=0\) | \(0\) | Mínimo GLOBAL |
| \(x=1\) | \(3\) | |
| \(x=2\) | \(1.59\) |
Dominio de la función objetivo definido en un intervalo abierto
Si la función se define en un intervalo abierto, entonces esta no toma valores en los extremos del intervalo, por lo que ya no son puntos que debamos contemplar (aunque sí qué ocurre con la función cuando se acerca a esos puntos)
\(x\in(a,b)\)
- los puntos donde la derivada de la función se anula o no existe
- El límite de la función cuando se acerca a \(a\) y a \(b\)
Ahora ya no aplica el Teorema de Weierstrass, puesto que el intervalo donde está definida la \(x\) no es cerrado. Veamos un ejemplo:
Ejemplo 2 Busca los óptimos de la función \(f(x)=x^{2/3}(5-2x)\) si \(x\in(-1,2)\)
solución Ya conocemos los puntos críticos. Utilicemos la derivada segunda (siempre que sea posible) para caracterizarlos:
\[ f''(x)=\frac{-10}{9}x^{-4/3}(1-x)-\frac{-10}{3}x^{-1/3} \]
Donde podemos ver que, si \(x^*=1\), la segunda derivada es negativa (por lo que es un máximo local) y en \(x=0\), obviamente, la segunda derivada no existe. Sin embargo, la primera derivada es es negativa cuando \(x<0\) y positiva cuando \(x>0\). Entonces, sabemos que es un mínimo local. Estudiamos estos puntos, así como lo que ocurre con la función si esta se acerca a los extremos
| Valor \(x^*\) | \(f(x^*)\) | ¿Qué tipo de punto es? |
|---|---|---|
| $x $ | \(f(x)\rightarrow 7\) | NADA |
| \(x=0\) | \(0\) | Mínimo global |
| \(x=1\) | \(3\) | Máximo local |
| \(x=\rightarrow 2\) | \(f(x)\rightarrow 1.59\) | NADA |
**vemos que \(x=1\) es un máximo local (puesto que cuando nos acercamos a \(x=-1\), la función es mayor que \(3\)).Sin embargo, en dicho intervalo \(x=0\) pasa a ser el mínimo GLOBAL.
¿Cómo trabajar de forma razonable?
Te recomendamos:
Primero busca los puntos criticos (condición necesaria de primer orden)
Analiza el intervalo donde se define la variable (es cerrado?) Si es cerrado, utiliza el Teorema de Weierstrass: no necesitas analizar las segundas derivadas, puedes encontrar directamente el (los) máximos y mínimos GLOBALES.
Si el intervalo no es cerrado, piensa si satisfaces, mediante la derivada segunda, el teorema local-global (si es así, decide si es un problema de maximización o minimización globales)
Después clasifica cada punto crítico con la derivada segunda (condiciones necesarias/suficientes de segundo orden)
Como ves, esto no es sólo seguir una receta: también se necesita algo de ARTE.
Esto se resume en dos vídeos:
- En este se definen las condiciones necesarias y suficientes de óptimo
- En este se hace un repaso a cómo enfocar un problema de optimización
Proyecto: el almacén Una óptica compra 600 gafas de sol de un modelo al año. El coste de cada envío son 50 euros. El coste de almacenamiento es de 1 euro por par y año. Cada par cuesta, al vendedor, 20 euros. Supongamos que se venden a un ritmo \(a\) constante en el tiempo (días) y que el envío llega cuando se acaban las existencias del envío anterior. ¿Cuántas gafas tiene que pedir por lote para minimizar el coste?
- Llamaremos \(x\) a las unidades almacenadas y a \(t\) al tiempo en días. En promedio, en el almacén hay \(x/2\) gafas. ¿Por qué? Porque el inventario empieza siempre en \(x\) gafas y acaba en \(0\). El promedio es \(x/2\).
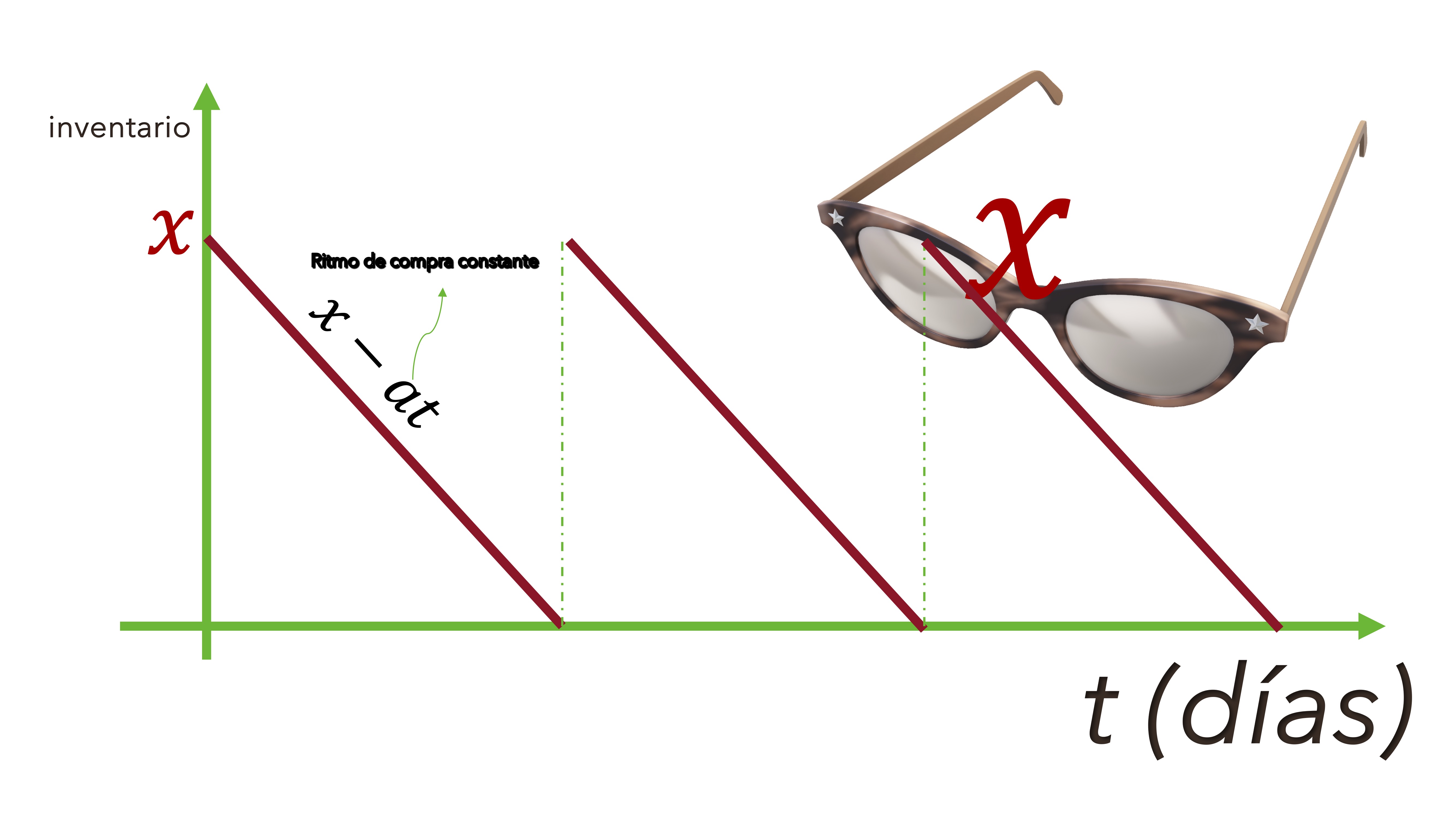
FIG 3 Esquema del almacén
- El coste medio de almacenar en cada ciclo será \(C_{A}=1 euro \times \frac{x}{2}\), \(C_{A}=\frac{x}{2}\).
- ¿Cuánto cuestan los envíos? son 50 euros por el total de envíos. Ese total serán las 600 gafas entre el número de gafas por envío. Es decir, \(C_{E}=50\times \frac{600}{x}\)
- ¿Cuál es el coste total de las gafas? \(C_{G}=20\times 600=12000\) es el coste fijo del empresario.
La suma de todos esos costes nos proporciona el total:
\[ C_{T}=\frac{x}{2}+\frac{30000}{x}+12000 \] date cuenta, por otro lado, que el coste lo deberemos minimizar atendiendo a que \(x\in (0,600]\). El intervalo está abierto por la izquierda y cerrado por la derecha.
*¿Cómo resolvemos el problema utilizando la guía?
¿Cómo trabajar de forma razonable?
Te recomendamos:
Primero busca los puntos criticos. Si hacemos la derivada primera, tenemos que \(f'(x)=0.5-\frac{30000}{x^2}\). Esta no existe si \(x=0\) pero ese punto no está en el dominio. Por otro lado, esta se anula (es decir, \(0.5-\frac{30000}{x^2}=0\)) si \(x=245\) o \(x=-245\). Nos quedamos con \(x=245\), que es el que está en el dominio.
Analiza el intervalo donde se define la variable (es cerrado?) Si es cerrado, utiliza el Teorema de Weierstrass. El intervalo, como hemos dicho no es cerrado por la izquierda, por lo que no satisface dicho teorema.
Si el intervalo no es cerrado, piensa si satisfaces, mediante la derivada segunda, el teorema local-global La derivada segunda es \(f''(x)=\frac{600}{x^3}\). En el dominio de \(x\) esta derivada será siempre positiva. Entonces, esta función es convexa en dicho tramo y el mínimo local pasa automáticamente a ser global.
Otra forma de proceder es analizando los puntos críticos como locales y luego pensar en su globalidad. En ese caso, no es necesario que analices la convexidad/concavidad de la función objetivo: es algo más laborioso. Puedes analizar el valor de la función objetivo en los puntos críticos para, posteriormente, ver cuánto vale la función objetivo en \(x=600\), que es donde está cerrado y a qué valor se acerca la función objetivo si \(x\) se acerca a cero (nunca puede valer \(0\)), En ese caso, es fácil ver que el coste se va a infinito y que cuando \(x=600\) el coste es mayor que en el punto crítico. Por eso, decimos que es un mínimo global.
Ya sabemos que la política óptima consiste en elegir \(x=245\) con un coste de 12245 euros.
Clase 2: Optimización libre en funciones \(\mathbb{R^2}\rightarrow\mathbb{R}\)
Planteamiento del problema
Nuestro objetivo es, ahora, buscar el óptimo en una función de dos variables sin restricciones en dichas variables. Escribiremos el problema como:
\[ \underset{(x,y)\in\mathbb{R}^{2}}{opt}f(x,y) \]
Si la función objetivo es diferenciable (tiene derivadas parciales primeras y segundas continuas), podremos utilizar las herramientas de cálculo diferencial aprendidas en el BLOQUE 2 para poder resolver de manera eficiente el problema.
Condiciones NECESARIAS de Primer orden
¿Para qué sirven?
- Nos permiten encontrar puntos críticos que podrán ser: máximos, mínimos o puntos de silla.
- Al ser necesarias: excluyen como candidatos a óptimo a aquellos puntos que nunca podrán serlo, pero incluirán puntos que luego no serán óptimos
- Están basadas en la información que proporciona el gradiente.
Si \(f(x,y)\) es diferenciable y el punto \((x^{*},y^{*})\) es un óptimo, verifica que
- \(\nabla f(x^*,y^*)=(0,0)\)
Esta condición se conoce como CONDICIÓN NECESARIA DE PRIMER ORDEN de óptimo local. Es análoga al caso con una variable.
Esta condición (que, para abreviar, se suele denotar como CPO), nos permitirá obtener un conjunto de puntos críticos que serán los candidatos a óptimo del problema. Tendremos tres posibles puntos: máximos, mínimos o puntos de silla. Como ves en la FIG 1, es fácil caracterizar de manera visual estos puntos:
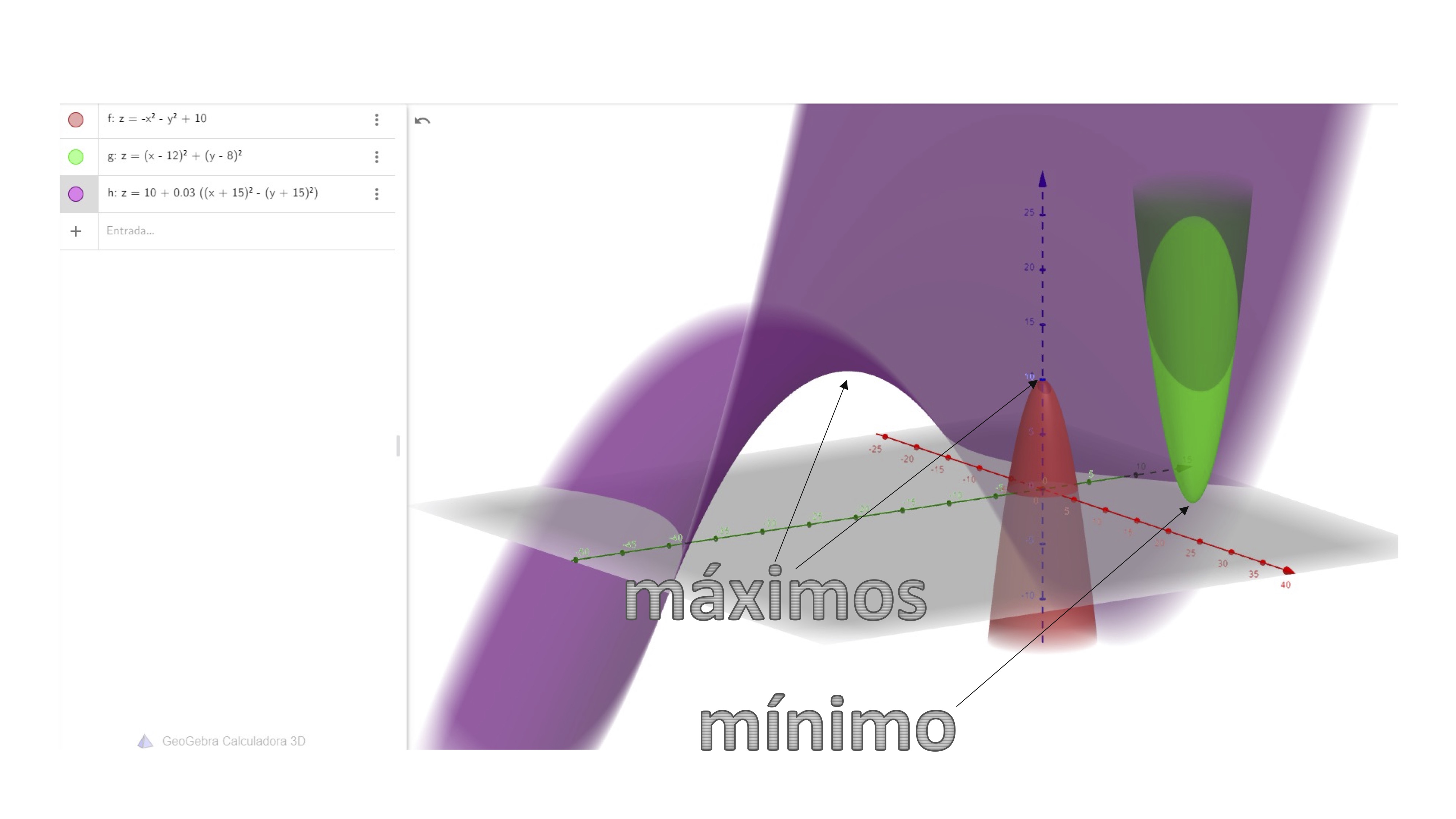
FIG 1 La función roja tiene un máximo y la verde un mínimo… La morada parece que tiene un máximo (local), ¿no?
Pero algo pasa con la función morada. Vamos a girar el dibujo, como verás en la FIG2:
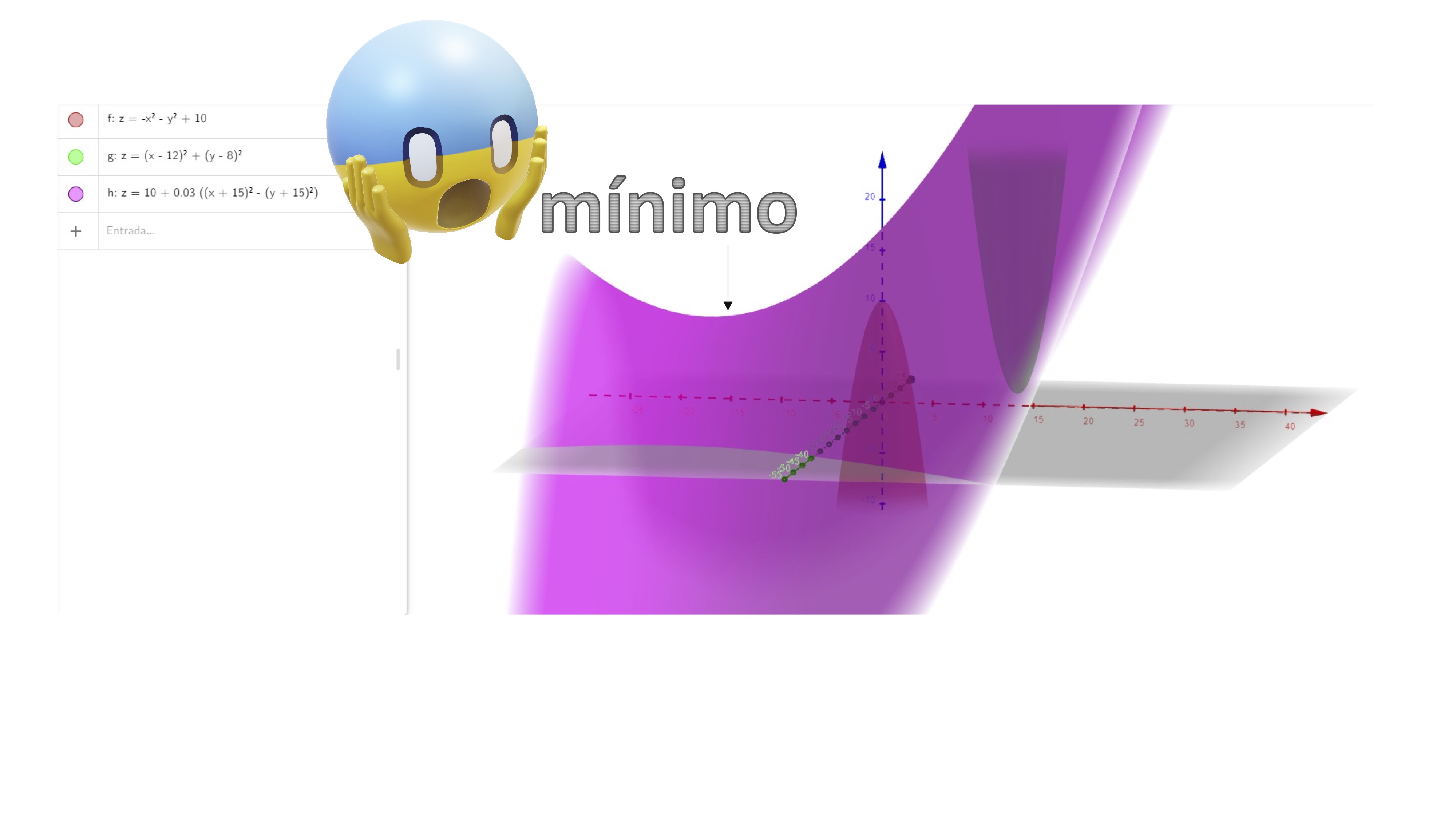
FIG 2 Fíjate, si la giras, entonces paree un mínimo local, arggg!
Ah, parece que la función morada tiene un punto de silla.
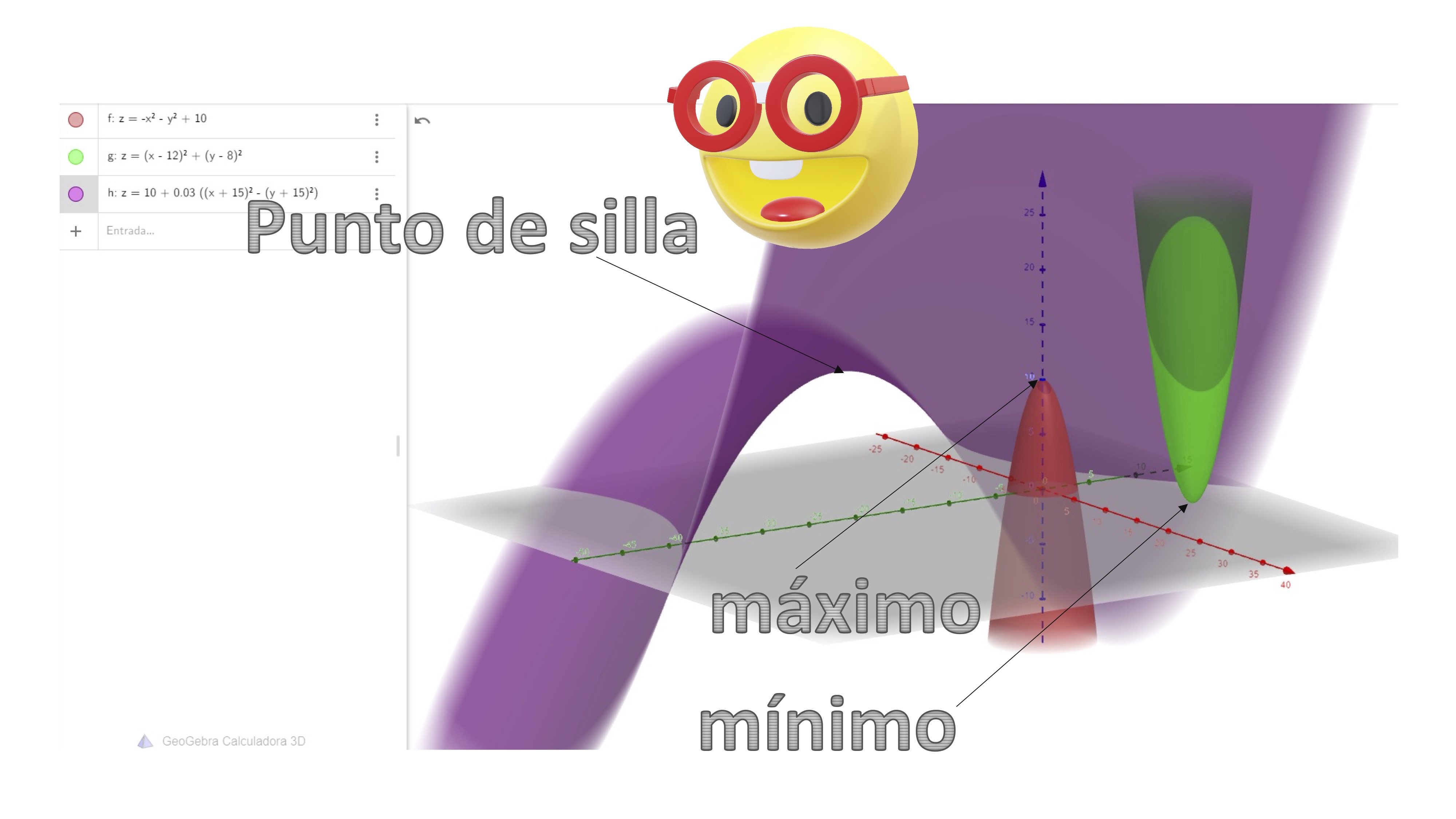
FIG 3 ¡Es un punto de silla!
Es decir, definimos como:
- Máximo local: en un entorno, es el punto (o conjunto de puntos) que proporcionan mayor valor a la función
- Mínimo local: en un entorno, es el punto (o conjunto de puntos) que proporcionan menor valor a la función
- Punto de silla: en un entorno, es el punto (o conjunto de puntos) que proporcionan menor valor a la función (en una posible dirección) y mayor valor a la función (en otra posible dirección).
Ejercicio resuelto
Calcular los mínimos, máximos (locales) y puntos de silla de la función de dos variables:
\[ f(x,y)=x^{3}+y^{3}+2x^{2}+4y^{2}+6 \]
Entonces, aplicamos:
- Condiciones necesarias de primer orden: \[ \nabla f(x,y)=(0,0), \]
es decir, obtenemos el sistema:
\[ \begin{cases} 3x^{2}+4x=0\\ 3y^{2}+8y=0 \end{cases} \]
Lo resolvemos:
\[ \begin{cases} x(3x+4)=0\Rightarrow x=0,x=\frac{-4}{3}\\ y(3y+8)=0\Rightarrow y=0,y=\frac{-8}{3} \end{cases} \]
Donde la solución son los siguientes cuatro puntos
\[ A(0,0),B\left(-\frac{4}{3},0\right),C\left(0,-\frac{8}{3}\right),D\left(-\frac{4}{3},-\frac{8}{3}\right) \]
¿Cómo clasificamos estos puntos? Necesitamos más condiciones
Condiciones NECESARIAS de segundo orden
¿Para qué las usaremos?
- Sirven para caracterizar (es decir, etiquetar) los puntos críticos como “máximos locales”, “mínimos locales” o “puntos de silla”, sin decir nada sobre la globalidad.
- No identifica mínimos/máximos estrictos.
- De nuevo, al ser condiciones necesarias de óptimo, habrá puntos que las satisfagan y que sean puntos de silla (es decir, NADA a efectos de optimizar).
Pero la novedad es que: ahora utilizamos la información del Hessiano (es decir, las derivadas segundas)
Si \(f(x,y)\) es diferenciable y tiene, además, derivadas parciales segundas continuas en \(\mathbb{R}^{2}\), se verifica que:
- \(\nabla f(x^*,y^*)=(0,0)\)
| Tipo | Primer Orden | Segundo Orden |
|---|---|---|
| máximo local | \(\nabla f(x^*,y^*)=(0,0)\) | \(Hf(x^*,y^*)\) semi definida negativa |
| mínimo local | \(\nabla f(x^*,y^*)=(0,0)\) | \(Hf(x^*,y^*)\) semi definida positiva |
| punto de silla | \(\nabla f(x^*,y^*)=(0,0)\) | \(Hf(x^*,y^*)\) Indefinida |
Y definimos,
Una matriz \(2\times2\) \(A=\left[\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right]\)
es semidefinida negativa si \(a_{11}\leq0\) y \(\left|A\right|\geq0\). Es semidefinida positiva si \(a_{11}\geq0\) y \(\left|A\right|\geq0\). Es indefinida si \(\left|A\right|=0.\) En este caso, también hay otra forma cómoda de clasificar los puntos atendiendo a los “autovalores’’ de la matriz. Los autovalores, \(\lambda_{1},\lambda_{2}\) resuelven esta ecuación:
\[ \left|\left[\begin{array}{cc} a_{11}-\lambda & a_{12}\\ a_{21} & a_{22}-\lambda \end{array}\right]\right|=0\Rightarrow\lambda^{2}-(a_{11}+a_{22})\lambda+\left|A\right|=0 \]
y, mediante el criterio de los autovalores, podemos decir que
| Tipo | Primer Orden | Segundo Orden |
|---|---|---|
| máximo local | \(\nabla f(x^*,y^*)=(0,0)\) | \(\lambda_{1},\lambda_{2}\geq0\) |
| mínimo local | \(\nabla f(x^*,y^*)=(0,0)\) | \(\lambda_{1},\lambda_{2}\leq0\) |
| punto de silla | \(\nabla f(x^*,y^*)=(0,0)\) | \(\lambda_{1}\neq0\),\(\lambda_{2}\neq0\) y de distinto signo. |
Si \(\lambda_{1}=0\), ¡estamos en problemas!: la información disponible no nos va a permitir caracterizar los puntos críticos. No siempre hay una respuesta clara. Luego, veremos ejemplos.
Condiciones SUFICIENTES de segundo orden
- Sirven para caracterizar (es decir, etiquetar) los óptimos locales, sin decir nada sobre la globalidad.
- La novedad es que permite asegurar si estos son estrictos.
Si \(f(x,y)\) es diferenciable y tiene, además, derivadas parciales segundas continuas en \(\mathbb{R}^{2}\), se verifica que:
| Tipo | Primer Orden | Segundo Orden |
|---|---|---|
| máximo local | \(\nabla f(x^*,y^*)=(0,0)\) | \(Hf(x^*,y^*)\) Definida negativa |
| mínimo local | \(\nabla f(x^*,y^*)=(0,0)\) | \(Hf(x^*,y^*)\) Definida positiva |
| punto de silla | \(\nabla f(x^*,y^*)=(0,0)\) | \(Hf(x^*,y^*)\) Indefinida |
OJO, es una condición suficiente
Si un punto no la cumple, no quiere decir que no pueda ser un óptimo.
Definición:
Una matriz \(2\times2\)
\(A=\left[\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right]\)
es definida negativa si \(a_{11}<0\) y \(\left|A\right|>0\). Es definida positiva si \(a_{11}>0\) y \(\left|A\right|>0\). Es indefinida si \(\left|A\right|=0.\)
En este caso, también hay otra forma cómoda de clasificar los puntos atendiendo a los “autovalores” de la matriz. Los autovalores, \(\lambda_{1},\lambda_{2}\) resuelven esta ecuación: \[ \left|\left[\begin{array}{cc} a_{11}-\lambda & a_{12}\\ a_{21} & a_{22}-\lambda \end{array}\right]\right|=0\Rightarrow\lambda^{2}-(a_{11}+a_{22})\lambda+\left|A\right|=0 \]
| Tipo | Primer Orden | Segundo Orden |
|---|---|---|
| máximo local | \(\nabla f(x^*,y^*)=(0,0)\) | \(\lambda_{1},\lambda_{2}>0\) |
| mínimo local | \(\nabla f(x^*,y^*)=(0,0)\) | \(\lambda_{1},\lambda_{2}<0\) |
| punto de silla | \(\nabla f(x^*,y^*)=(0,0)\) | \(\lambda_{1}\neq0\),\(\lambda_{2}\neq0\) y de distinto signo. |
Volvamos al ejemplo resuelto
Del ejemplo anterior, con puntos críticos \[ A(0,0),B\left(-\frac{4}{3},0\right),C\left(0,-\frac{8}{3}\right),D\left(-\frac{4}{3},-\frac{8}{3}\right) \],
las derivadas parciales segundas son
\[ \frac{\partial^{2}f}{\partial x^{2}}=6x+4 \]
\[ \frac{\partial^{2}f}{\partial y^{2}}=6y+8 \]
\[ \frac{\partial^{2}f}{\partial x\partial y}=\frac{\partial^{2}f}{\partial y\partial x}=0 \]
que nos proporcionan una matriz Hessiana:
\[ Hf(x,y)=\left(\begin{array}{cc} 6x+4 & 0\\ 0 & 6y+8 \end{array}\right) \]
y la vamos a analizar para cada punto:
| Punto | Hessiana | Tipo |
|---|---|---|
| \(A(0,0)\) | \(Hf(0,0) = \begin{bmatrix} 4 & 0\\ 0 & 8 \end{bmatrix}\) | Definida Positiva (mínimo local estricto) |
| \(B\left(-\frac{4}{3},0\right)\) | \(Hf(\frac{-4}{3},0)=\begin{bmatrix} -4 & 0\\ 0 & 8 \end{bmatrix}\) | Indefinida & Punto de silla |
| \(C\left(0,-\frac{8}{3}\right)\) | \(Hf(0,\frac{-8}{3})=\begin{bmatrix} 4 & 0\\ 0 & -8 \end{bmatrix}\) | Indefinida & Punto de silla |
| \(D\left(-\frac{4}{3},-\frac{8}{3}\right)\) | \(Hf(\frac{-4}{3},\frac{-8}{3})=\begin{bmatrix} -8 & 0\\ 0 & -8 \end{bmatrix}\) | Definida negativa & Máximo Local Estricto |
Ejercicio utiliza el criterio de los autovalores para clasificar la matriz.
Óptimos Globales: el teorema local-global
Hasta ahora sólo hemos presentado condiciones de óptimo local, ya que las técnicas anteriores están basadas en analizar la Hessiana de la función en el entorno de los puntos candidatos. El Teorema Local-Global afirma:
Teorema Local Global en un problema de optimización libre en dos variables
Si la función objetivo \(f(x,y)\) es diferenciable y:
- convexa, los mínimos locales son globales.
- cóncava, los máximos locales son globales.
Recuerda ¿Cómo sabemos si una función es convexa o cóncava? Debemos analizar la Hessiana. Si es Semidefinida positiva para todo punto, entonces, la función será convexa y si es semidefinida negativa será cóncava. Además, si es Definida positiva, entonces es estrictamente convexa implicando que sólo hay un m?nimo global y, viceversa si es Definida negativa.
Ejemplo : ¿Es convexa \(f(x,y)=x^{2}+y^{2}\)?
En el dibujo se ve claramente, pero vamos a verlo analíticamente \[ \Delta f(x,y)=\left[2x,2y\right] \]
Por lo que la Hessiana ser? \[ Hf(x,y)=\left[\begin{array}{cc} 2 & 0\\ 0 & 2 \end{array}\right] \]
como ves, es Definida positiva para cualquier valor de \((x,y)\). Entonces, es estrictamente convexa y-por tanto- el candidato a mínimo local sabemos que será, automáticamente, global.
Ejemplo donde todo falla clasifica el punto \((0,0)\) en el siguiente problema de minimización
\[ \min f(x,y)=x^{3}-3xy^{2} \]
Primero debemos asegurar que sea un punto crítico, es decir, que cumple la condión necesaria de primer orden
\[ \nabla f(x,y)=\left[3x^{2}-3y^{2},-6xy\right] \]
como vemos, \(\nabla f(0,0)=\left[3\times0^{2}-3\times0^{2},6\times0\times0\right]=[0,0]:\) cumple la condición necesaria de primer orden. Obtengamos la Hessiana \[ Hf(x,y)=\left[\begin{array}{cc} 6x & -6y\\ -6y & 6x \end{array}\right] \]
Evaluando la Hessiana en el (0,0), tenemos \[ Hf(0,0)=\left[\begin{array}{cc} 0 & 0\\ 0 & 0 \end{array}\right] \]
Como vemos, respecto a las condiciones necesarias de segundo orden, no sabemos si es máximo, mínimo o punto de silla. El test no es concluyente.
Además, no satisfacemos el teorema local global. Aquí tendremos que utilizar algo la imaginación y deberemos analizar qué ocurre en el entorno del punto crítico (0,0)
\[ f(x,0)=x^{3} \]
como vemos, si \(x>0\), la función (en el entorno de \((0,0)\)) toma valores positivos y si \(x<0\), valores negativos. Es decir, que si nos acercamos por la izquierda, en el eje de las \(x\) estamos ante un máximo y, si nos acercamos por la derecha, ante un mínimo. Entonces, debe ser un punto de silla.
De nuevo, puedes consultar este contenido en dos vídeos
- En este se definen las condiciones necesarias y suficientes de óptimo
- En este se hace un repaso a cómo enfocar un problema de optimización
Clase 3: Introducción a la optimización restringida en funciones \(\mathbb{R^2}\rightarrow\mathbb{R}\)
Vamos a resolver, gráficamente, el problema siguiente:
\[ \min_{x,y}x^{2}+y^{2} \]
sujeto a :
\[ x+2y=10 \]
Como ves, incorporamos una restricción: los puntos \((x,y)\) que minimizan la función objetivo han de satisfacer la ecuación \(x+2y=10\). Vamos a intentar resolverlo gráficamente, siguiendo unos pasos concretos.
- Esboza las curvas de nivel de la función objetivo
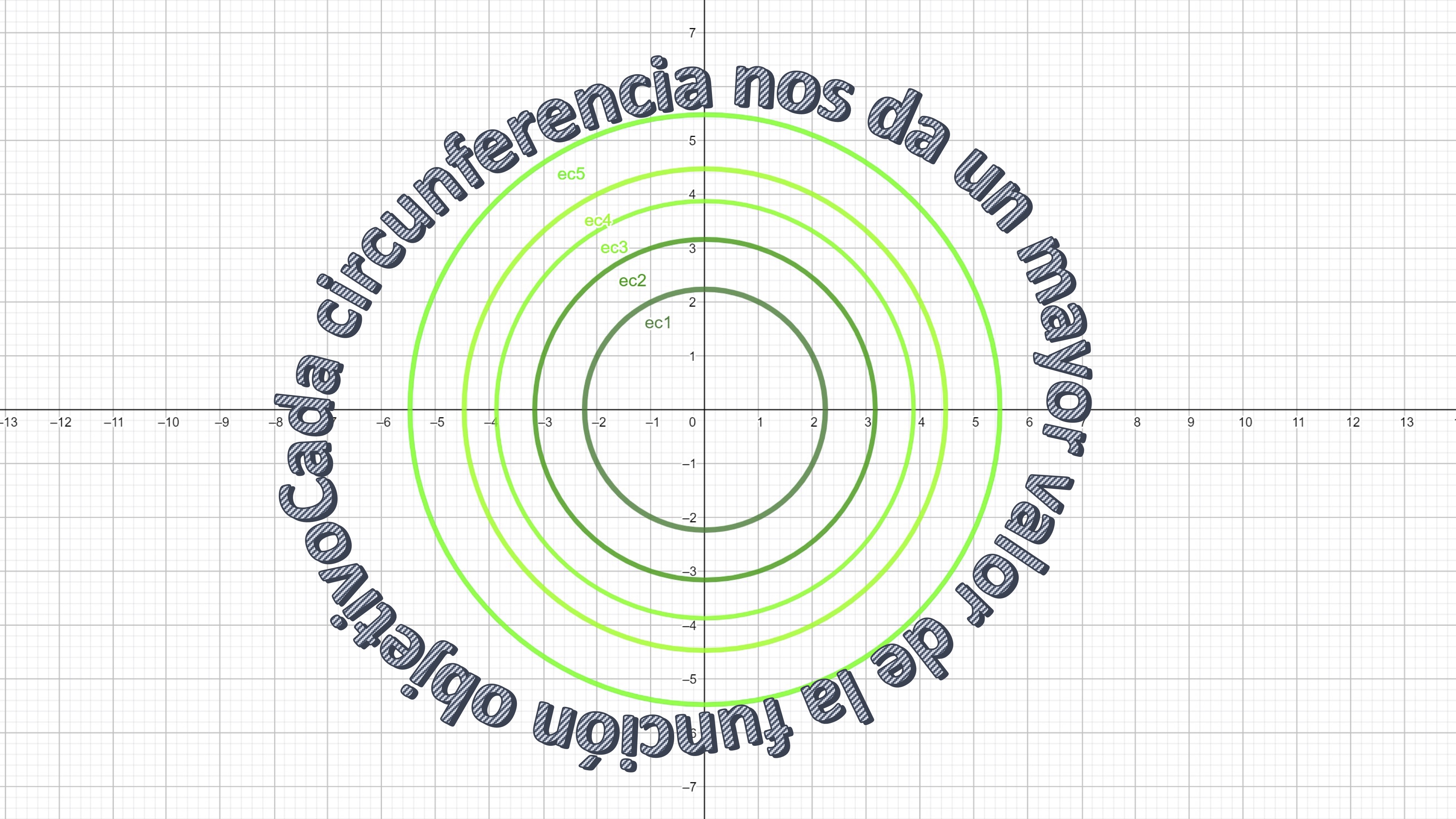
FIG 1 Estas curvas de nivel ya las conoces, ¿no?
- Incluye la restricción \((x+2y=10)\) sobre el mismo gráfico
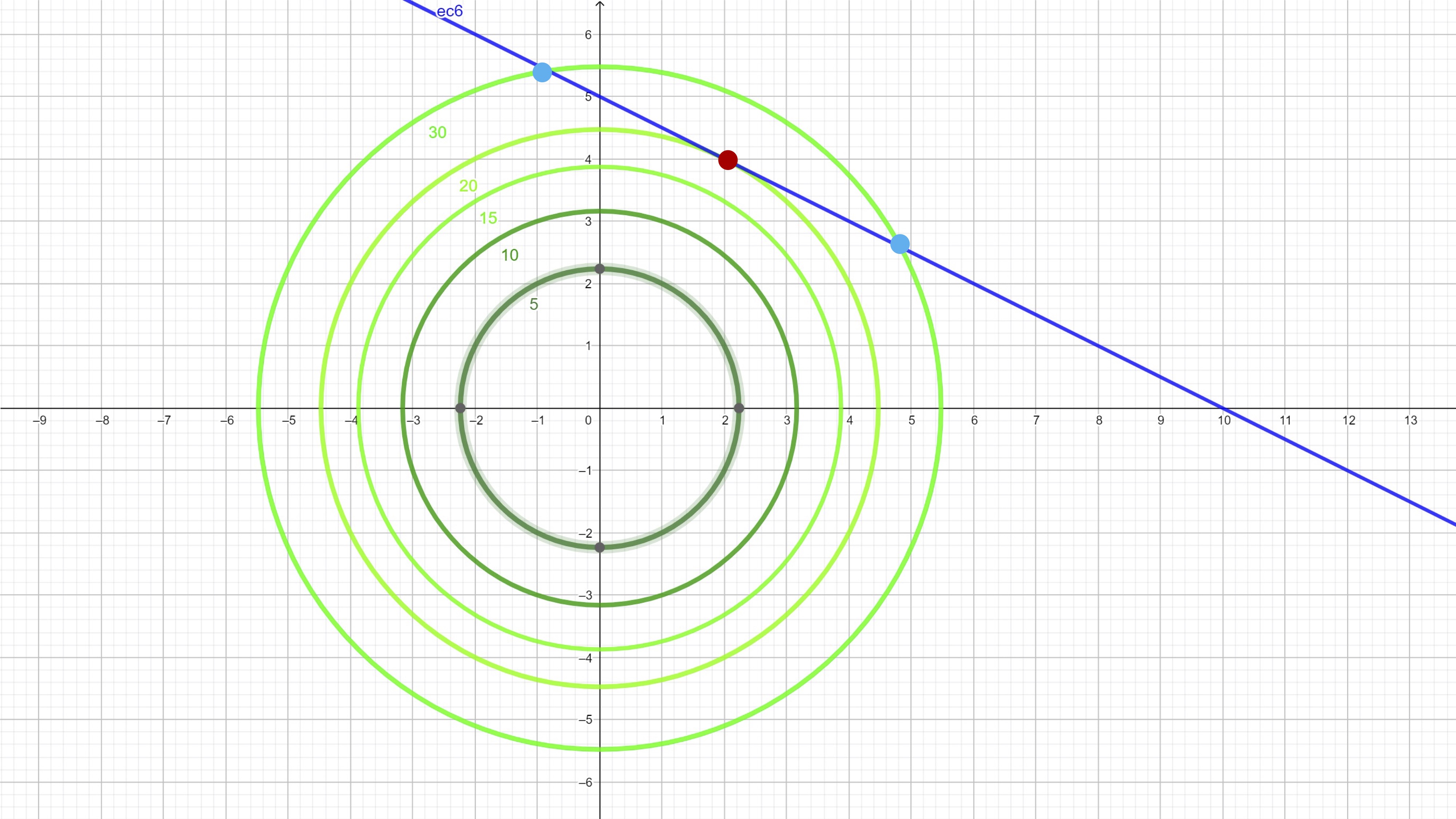
FIG 2 Incluimos, además, tres puntos de interés
Como ves, hemos marcado tres puntos: los de color azul son factibles (puesto que satisfacen la restricción) pero dan un valor de la función objetivo de 30. Sin embargo, el punto rojo es factible y da un valor de la función objetivo de 20. ¿Hay algún punto factible (es decir, que esté contenido en la recta) que dé un valor menor de la función objetivo? ¡No! Por lo tanto, hemos encontrado el mínimo (global) del problema. Está en el punto \(x^{*}=2,y^{*}=4\).
Vamos a seguir analizando la figura. Ahora, calculemos el gradiente de la función objetivo
\[ \nabla f(x,y)=\left[2x,2y\right] \]
y vamos a dibujarlo en el punto que nos da el mínimo del problema (\(x^{*},y^{*})=(2,4)).\) El gradiente resulta ser \[ \nabla f(2,4)=\left[4,8\right] \]
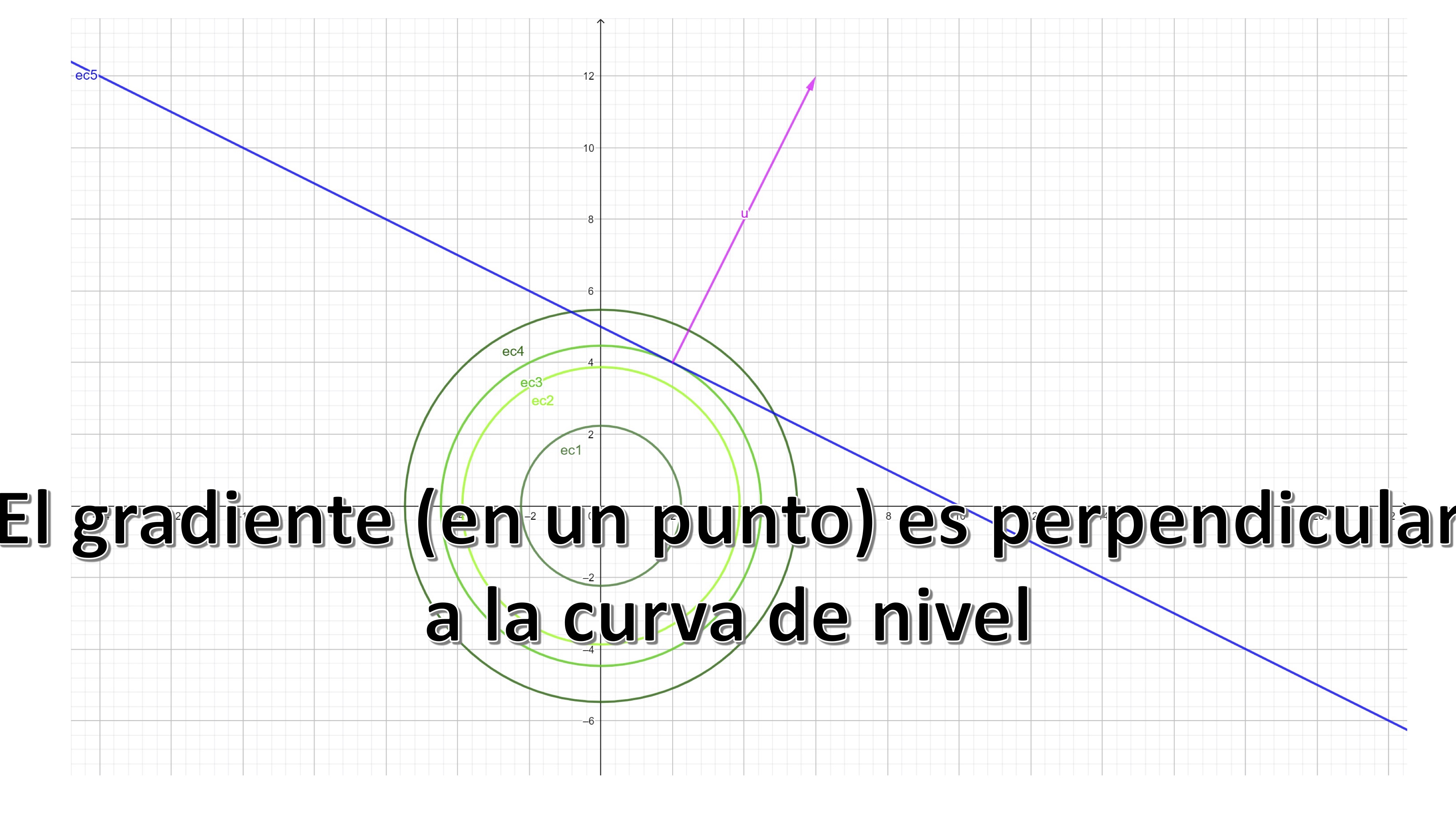
FIG 3 recuerda que el gradiente, en un punto, es perpendicular a la curva de nivel en dicho punto
Ahora, por otro lado, obtengamos el vector gradiente de la restricción \(g(x,y)=x+2y\): \[ \nabla g(x,y)=\left[1,2\right] \] lo dibujamos, igualmente, y obtenemos:
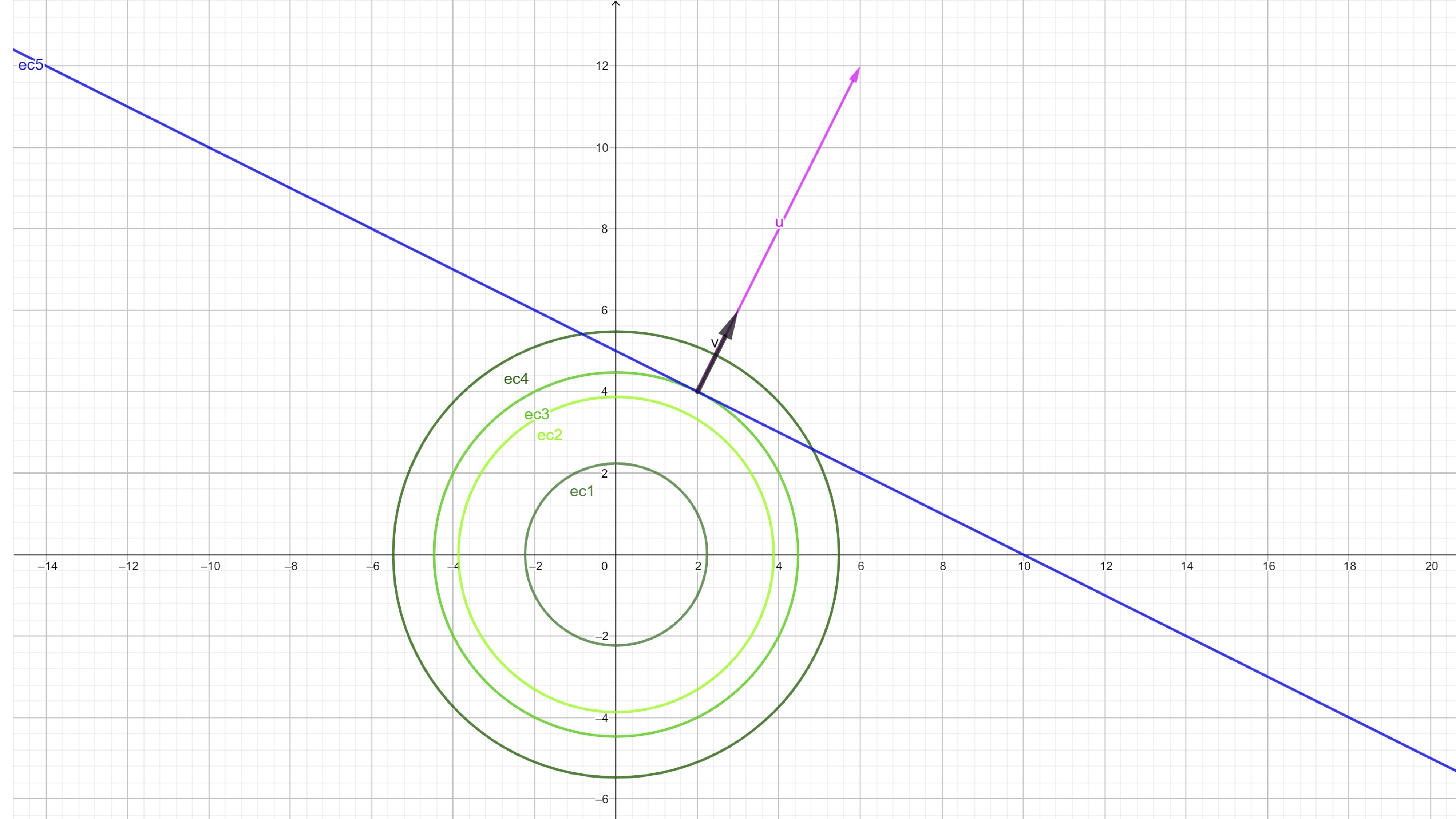
FIG 4 Ambos vectores son “proporcionales”
Como ves, son proporcionales. Pensemos: ¿podría pasar esto mismo entre otro par de vectores que satisfagan la restricción? Puedes tratar de verlo gráficamente: ¡imposible! Entonces, en el punto donde se obtiene el mínimo global ambos vectores son proporcionales, es decir, existe un \(\lambda\) tal que:
\[ \nabla f(x^{*},y^{*})=\lambda\nabla g(x^{*},y^{*}) \]
de tal forma, además, que se satisface la



