BLOQUE 4: Ampliación de Optimización

• En este bloque, profundizaremos en el planteamiento y resolución de problemas de optimización relevantes en Economía.
• Nos prepararemos para discutir, dado el problema, si este tiene solución y qué tipo esperar
• Además, insistiremos en la resolución gráfica como un modo de obtener ideas potentes del problema sin hacer mucho esfuerzo analítico.

Referencias de interés

• Stewart, J. (2009). Calculus: Concepts and contexts. Cengage Learning.
• STEWART, James; CLEGG, Daniel K.; WATSON, Saleem. Calculus: early transcendentals. Cengage Learning, 2020.
• SYDSAETER, Knut; HAMMOND, Peter. Matemáticas para el análisis económico. Pearson Educación, 1996.
• SIMON, Carl P., et al. Mathematics for economists. New York: Norton, 1994.
• SMITH, Robert T.; MINTON, Roland B.; RAFHI, Ziad AT. Cálculo de varias variables: trascendentes tempranas. McGraw-Hill Interamericana, 2019.

Clase 1: Repaso de Ideas Importantes de Cálculo

Como ya sabes de Matemátcas 1, estamos trabajando con funciones en dos variables. Recuerda que \(f:\:\mathbb{R}^{2}\rightarrow\mathbb{R}\) es una función cuyo dominio está contenido en el conjunto de los reales en dos dimensiones (\(\mathbb{R}^{2})\) y la imagen son los reales (\(\mathbb{R})\), de tal forma que su gráfica es tridimensional. Por ejemplo, la función \[ f(x,y)=2x+y-3, \]

representa un plano en \(\mathbb{R}^{3}:\)

FIG1 Así se representa la función \(f(x,y)=2x+y-3\).

Ejercicio Propuesto

Representa en geogebra las siguientes funciones en 3D

1. \(f(x,y)=e^{2x-y}\)

2. \(f(x,y)=(x-1)^{2}+(y+2)^{2}\)

3. \(f(x,y)=4(x+1)^{2}+(y+1)^{2}\)

4. \(f(x,y)=xy\)

Generalmente, es complicado dibujar funciones en 3D a no ser que tengamos a mano Geogebra. Recuerda que una manera de estudiar las características más importantes de una función en 3D es mediante sus curvas de nivel. Para ello, lo que tenemos es que fijar valores de la imagen (de tal forma que nos deshacemos de una variable) y despejar una variable (de las dos que quedan) en función de la otra. Por ejemplo, de la función

\[ z=2x+y-3, \]

fijamos valores de \(z,\)como por ejemplo \(z=\{-1,0,2\}\)

\[ -1=2x+y-3,\:\:\:0=2x+y-3,\:\:\:2=2x+y-3 \]

y despejamos la \(y\) en función de la \(x\), y obtenemos:

\[ y=2-2x,\:\:\:y=3-2x,\:\:\:y=5-2x \]

como ves, se corresponden con rectas paralelas con pendientes negativas

FIG2 Algunas curvas de nivel de la función, con la flecha indicando hacia dónde crece

OJO, repasa!

En la clase 5 del BLOQUE 1 puedes repasar la idea de curvas de nivel y ver un vídeo explicativo.

Ejercicio resuelto

Esboza las curvas de nivel de las siguientes funciones, explicando qué objetos en 2D (funciones, cónicas, etc…) representan:

1. \(f(x,y)=(x-1)^{2}+(y+2)^{2}\)\(\rightarrow\) Circunferencia centrada en el punto \((1,-2)\)

2. \(f(x,y)=4(x+1)^{2}+(y+1)^{2}\)\(\rightarrow\) Elipse centrada en el punto \((-1,-1)\)

3. \(f(x,y)=xy\)\(\rightarrow\) Hipérbola

4. \(f(x,y)=e^{2x-y}\)\(\rightarrow\) Son rectas con pendiente positiva

Por otra parte, debemos recordar las propiedades fundamentales del gradiente de una función. Para ello, las mostraremos con ejemplos claros. Sea la función en dos variables \(f\::\:\mathbb{R}^{2}\rightarrow\mathbb{R}\), definiremos el gradiente como el vector \(\nabla f\) que tiene por componentes las derivadas parciales de la función \(f\), es decir

\[ \nabla f(x,y)=\left[\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right]. \]

El gradiente, recordemos, es clave para resolver problemas de optimización. Entre sus propiedades, se encuentran

• Es perpendicular a cada curva de nivel en cada punto (FIG4)

• marca la dirección con dos sentidos: el de crecimiento y el de decrecimiento más rápidos. (FIG5)

Es decir, que si te mueves en el sentido del gradiente (\(\nabla f(x,y))\) sabes que vas a alcanzar lo antes posible niveles de la función mayores. Si eliges el sentido negativo (\(-\nabla f(x,y)\)) te moverás lo antes posible hacia valores más pequeños de la función. Esto tiene, claramente, una relación con maximizar/minimizar una función \(f(x,y)\)

FIG4 propiedades del gradiente (1)

FIG5 propiedades del gradiente (2)

Entenderás, entonces, que el gradiente de una función tendrá que estar presente en la resolución de problemas de optimización. Repasa el bloque 3, donde tienes la teoría de optimización que deberías conocer hasta ahora.

OJO, repasa!

En clase se resolverá el problema de optimización con restricciones de igualdad del examen de Matemáticas I.

Clase 2: Planteamiento de problemas de optimización con restricciones de desigualdad

En general, nos interesará plantear problemas donde, ante un conjunto de opciones posibles, seamos capaces de ver qué es lo mejor y lo peor. A eso se le llama: optimizar . En matemáticas, plantearemos problemas de optimización como el que se representa en este problema 1:

Problema 1

\[\begin{equation} \mathrm{opt}f(x,y) \end{equation}\]

sujeto a \[ (x,y)\in X \]

Donde \(f(x,y)\) es la función objetivo (que queremos optimizar) y \(X\) se conoce como el conjunto factible: es decir, es el lugar donde buscamos los valores de \((x,y)\) para poder resolver nuestro problema de optimización. En este curso, asumiremos que \(X\subseteq\mathbb{R}^{2}\), esto es, que las opciones factibles serán pares de números reales en dos dimensiones y que, además, estas serán un subconjutno de dicho espacio. En la FIG 1, mostramos el gráfico en 3D de una función objetivo representada sobre un conjunto de soluciones factibles \(X\) formado por un cuadrado.

FIG1 Representamos la función \(f(x,y)=\ln(1+x^{2}+y^{2})-x^{2}\), con \(X=\left\{ (x,y)\in\mathbb{R}^{2}:-3\leq x\leq3,-1\leq y\leq4\right\}\)

Por otro lado, si nuestro objetivo es maximizar o minimizar, reformularemos el problema 1: deberemos escribir \(\max/\min\) según corresponda.

Recuerda que nuestro objetivo será buscar óptimos globales: es decir, los mejores/peores de todos los candidatos a máximos y mínimos de la función objetivo. En la FIG2, representamos el máximo y mínimo globales de la función \(f(x,y)=\ln(1+x^{2}+y^{2})-x^{2}\), para los valores \((x,y)\in X\), así como los máximos y mínimos locales. Recuerda que los métodos generales de búsqueda de óptimos suelen encontrar puntos críticos locales que, posteriormente, deberemos analizar para saber cuáles de ellos son globales.

FIG2 Representamos la función \(f(x,y)=\ln(1+x^{2}+y^{2})-x^{2}\), con \(X=\left\{ (x,y)\in\mathbb{R}^{2}:-3\leq x\leq3,-1\leq y\leq4\right\}\)

De manera general, en este capítulo vamos a trabajar con conjuntos factibles \(X\) conformados por desigualdades como proponemos en el problema 2

Problema 2

\[\begin{equation} \mathrm{opt}f(x,y) \end{equation}\]

sujeto a \[\begin{equation} \begin{cases} g_{1}(x,y)\leq k_{1}\\ ...\\ g_{m}(x,y)\leq k_{m} \end{cases}\label{eq:rest} \end{equation}\]

Donde, como novedad, las funciones \(g_{i}(x,y)\), para \(i=1,...m\) son las restricciones de desigualdad que conforman el conjunto de soluciones factibles. Utilizaremos, como convenio, desigualdades del tipo menor o igual.

En Economía hay multitud de ejemplos de interés. Aquí pensamos sobre unos cuantos:

• P1.Maximizar la utilidad \((U)\) que le reporta a un individuo la compra de dos bienes \((x,y)\) sujeto a una restricción presupuestaria:

\[ \max U(x,y) \] \[ p_{x}x+p_{y}y\leq R, \] donde \(p_{x},p_{y}\) son los precios de los bienes, \(R\) es la renta y \(U\::\mathbb{R}_{++}^{2}\rightarrow\mathbb{R}_{+}\)

• P2.Elegir cuánto capital \((k)\) y trabajadores \((L)\) contratar para minimizar el coste si se quiere producir, como mínimo \(u\) unidades de producto:

\[ \min C(K,L) \] \[ f(k,L)\geq u, \]

donde \(C\) es una función de coste, tal que \(C\::\mathbb{R}_{++}^{2}\rightarrow\mathbb{R}_{+}\) y \(f\) una función de producción \(f\::\mathbb{R}_{++}^{2}\rightarrow\mathbb{R}_{+}\).

• P3. Elegir niveles de publicidad en redes sociales \((x)\) y televisión \((y)\) así como el precio \((p)\) que maximizan el beneficio de una empresa, sujeto a cierta restricción (por ejemplo, el gasto en ambos medios ha de ser menor que 5 M de euros) y el precio debe estar entre 2 y 5 euros:

\[ \max pV(p,x,y)-(x+y) \] \[ x+y\leq5, \] \[ 2\leq p\leq5, \]

donde \(V\) son las ventas del producto asociadas al precio y gastos en publicidad, tal que \(V\::\mathbb{R}_{+++}^{3}\rightarrow\mathbb{R}_{+}\)

---

Ejercicio Resuelto

Discute si los ejemplos propuestos anteriormente, encajan con el problema de optimización con restricciones de desigualdad que se ha enunciado al principio de la clase.

• P1.Encaja perfectamente, puesto que consiste en un problema de maximización con una restricción de desigualdad del tipo “menor o igual que”
• P2.No, habría que escribir \(-f(k,L)\leq-u\), para tener una desigualdad del tipo pedido.
• P3.Habría que escribir dos desigualdades \(\begin{cases} -p\leq-2\\ p\leq5 \end{cases}\)

NOTA: Es importante reescribir siempre las desigualdades de esta forma, puesto que todos los procedimientos analíticos que vamos a usar dependen de que las restricciones están escritas con ese sentido de desigualdad: “\(\leq\)”.

---

Ejercicio 2

Realiza los planteamientos de los problemas del curso 6-10.

Clase 3: Método de Karush-Khun-Tucker

Condiciones necesarias de óptimo

Una vez visto todo lo anterior, vamos a enuncuar un algoritmo que nos va a permitir buscar los puntos críticos en un problema de optimización con restricciones de desigualdad.

OJO, repasa!

Un punto crítico es aquel punto que puede ser un máximo, mínimo o punto de silla.

El método de KKT parte del planteamiento de un programa matemático con desigualdades (recuerda que en este sentido: \(\leq\), si no has de cambiarlas convenientemente)

\[ \mathrm{opt}f(x,y) \]

sujeto a

\[ \begin{cases} g_{1}(x,y)\leq k_{1}\\ ...\\ g_{m}(x,y)\leq k_{m} \end{cases} \]

Nota: en estos apuntes consideraremos que se cumple la condición de regularidad que requiere que los gradientes de \(g_{i}(x,y),\:i=1,...,m\) son linealmente independientes.

Construimos la función lagrangiana tal que:

\[ \mathcal{L}(x,y,\lambda_{1},...,\lambda_{m})={ \color{red}{f(x,y)}-{\color{green}{ \lambda_{1}\left(g_{1}(x,y)-k_{1}\right)}}-...-{{\color{green}{ \lambda_{m}\left(g_{m}(x,y)-k_{m}\right)}}}} \]

de forma que tenemos en una sola función el objetivo y las restricciones. Esto ya lo has hecho en optimización con restricciones de igualdad.

Las condiciones de KKT indican que existen \(\lambda_{1},...,\lambda_{m}\in\mathbb{R}\) tales que satisfacen

concepto	para máximo	para mínimo
derivadas parciales	\[ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \frac{\partial\mathcal{L}}{\partial x}=0, \frac{\partial\mathcal{L}}{\partial y}=0 \]
holgura complementaria	\[ \begin{cases} \lambda_{1}[g_{1}(x,y)- k_{1}]=0\\ ...\\ \lambda_{m}[g_k(x,y)-k_{m}]=0 \end{cases} \]
multiplicadores	\(\lambda_{1},...,\lambda_{m}\geq0\)	\(\lambda_{1},...,\lambda_{m}\leq0\)
Factibilidad	\[ \begin{cases} g_{1}(x,y)\leq k_{1}\\ ...\\ g_{m}(x,y)\leq k_{m} \end{cases} \]

Estas condiciones, necesarias, nos permitirán obtener el conjunto de puntos críticos \((x,y,\lambda_{1},...,\lambda_{m})\) candidatos a óptimo.

• Las condiciones de Holgura Complementaria se os suelen atragantar. Presta atención al ejemplo y ¡usa la lógica!
• La condición sobre los multiplicadores nos da mucha información. Si obentemos que son de signo contrario, enseguida descartamos ese punto crítico porque no la satisface
• La factibilidad implica que, una vez tengas candidatos a óptimo, has de verificar que satisfacen todas las restricciones (las ecuaciones anteriores no lo aseguran). Si no, se descarta ese punto.

Nota: en estas notas, no se tendrán en cuenta las condiciones de no negatividad (\(x,y>0\) o \(x,y\geq0\)). Estas se verificarán sobre la marcha, pero no se incluirán en el lagrangiano.

---

Ejercicio fácil Trata de resolver el problema #5 de la hoja de ejercicios del curso.

Ejemplo más complicado

Sea el problema de optimización

\[ \mathrm{opt}\:f(x,y)=x^{2}+y \] sujeto a

\[ \frac{x^{2}}{4}+\frac{y^{2}}{9}\leq1 \]

• Escribimos el lagrangiano:

\[ \mathcal{L}(x,y,\lambda_{1},...,\lambda_{m})=x^{2}+y-\lambda\left(\frac{x^{2}}{4}+\frac{y^{2}}{9}-1\right) \]

• Obtenemos las derivadas parciales e igualamos a cero \[ \frac{\partial\mathcal{L}}{\partial x}=0\Rightarrow2x-\frac{x\lambda}{2}=0 \] \[ \frac{\partial\mathcal{L}}{\partial y}=0\Rightarrow1-\frac{2y\lambda}{9}=0 \]

• Escribimos las condiciones de holgura complementaria \[ \lambda\left(\frac{x^{2}}{4}+\frac{y^{2}}{9}-1\right)=0 \]

En realidad, puedes verlo como tener que resolver este sistema de ecuaciones

\[\begin{equation} KKT\begin{cases} x\left(2-\frac{\lambda}{2}\right)=0 & (1)\\ 1-\frac{2y\lambda}{9}=0 & (2)\\ \lambda\left(\frac{x^{2}}{4}+\frac{y^{2}}{9}-1\right)=0 & (3) \end{cases} \end{equation}\]

Como el sistema es no lineal, te aconsejamos que sistematices la búsqueda de soluciones, por ejemplo, haciendo un árbol como sigue:

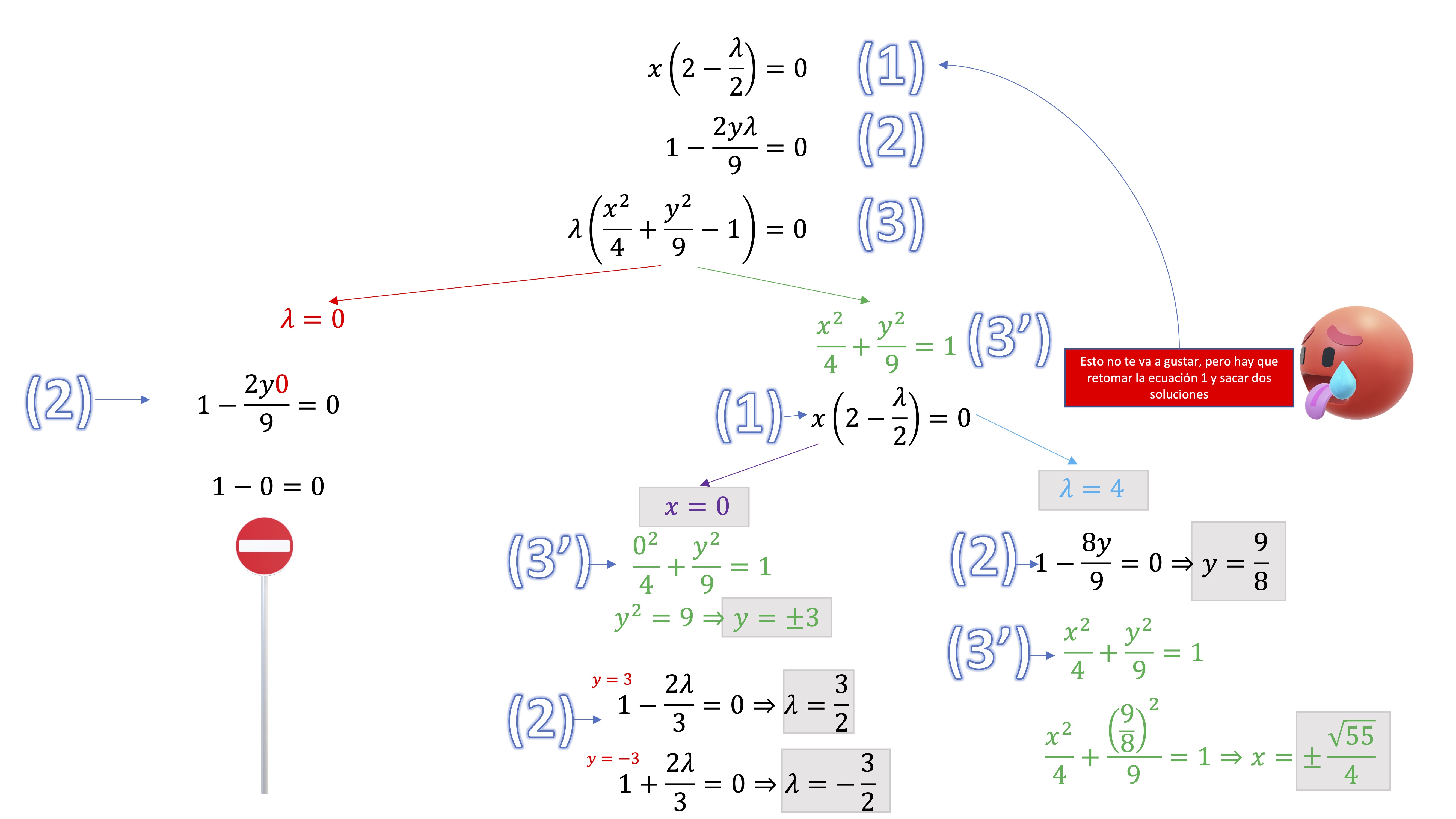
FIG1 Árbol de soluciones

---

• Clasifica las soluciones obtenidas utilizando las condiciones necesarias.

Punto	1	2	3	4
\(x^*\)	0	0	\(\sqrt{55}/4\)	\(-\sqrt{55}/4\)
\(y^*\)	3	-3	\(9/8\)	\(9/8\)
\(\lambda^*\)	3/2	-3/2	\(4\)	\(4\)

Los puntos 1,3,4 cumplen con la condición de Kuhn Tucker para máximo y el punto 2 con la condición para mínimo.

Para saber más: ¿De dónde vienen las condiciones de Kuhn y Tucker? Esto no hace falta que lo mires, sólo si te pica la curiosidad.

---

Vamos a entender, de manera gráfica, las particularidades de las condiciones de Karush-Kuhn- Tucker Recordemos, eso sí, brevemente, la potente idea que está detrás del lagrangiano. Supongamos que queremos resolver un problema de minimización, tal que

\[\begin{equation} \min f(x,y) \end{equation}\]

En ese caso, una condición necesaria para la búsqueda del mínimo consistía en

\[ \frac{\partial f}{\partial x}=0,\frac{\partial f}{\partial y}=0\Rightarrow\nabla f(x,y)=(0,0) \]

Es decir, un candidato a mínimo ha de cumplir que el gradiente se anule en dicho punto. En la FIG 2 podemos intuir de dónde procede dicha condición:

FIG2 problema no restringido

Empezamos en cualquier punto \(A\) y yendo en el sentido negativo del gradiente-recuerda lo que vimos en la CLASE 1- para minimizar una función, debemos ir en el sentido negativo del gradiente. Vamos descendiendo lo más rápidamente posible por la función hasta que llegamos al punto donde es imposible descender más. Ese punto con coordenadas \((x^{*},y^{*})\) es aquel en el que el gradiente es el \((0,0)\). Claro, si el gradiente es distinto del (0,0), eso querrá decir que podemos seguir decreciendo en esa dirección, por lo que debemos buscar un punto donde ya no decrezcamos más. Esto en lo que se refiere a buscar un mínimo sin tener ninguna restricción.

Ahora, recuerda que si restringías la función a un conjunto de puntos, como en el caso siguiente

\[\begin{equation} \min f(x,y) \end{equation}\]

sujeto a

\[ g(x,y)=k, \]

estarás en una situación como esta, donde la curva roja es la restricción \(g(x,y)=k\)

FIG3 el punto \(C\) es el mejor

FIG4 ¿Cómo llegamos al punto \(C\) con lo que sabemos de cálculo?

Los puntos \(A\) y \(B\) son puntos de corte de la curva de nivel con la restricción. Ambos puntos son factibles (están contenidos en la restricción) pero no proporcionan los menores valores posibles de la función objetivo (el punto \(A\) proporciona valor 30, mientras que el punto \(B\) proporciona valor 40). Si nos movemos a lo largo de la curva de nivel, llegaremos al punto \(C\). Este es un punto de tangencia entre la curva de nivel (de valor 20) y la restricción. Es el mejor, puesto que no puedes encontrar otro punto que, satisfaciendo la restricción, proporcione un menor valor de la función objetivo. Dadas las propiedades del vector gradiente que repasamos en la clase 1, sabemos que este será perpendicular a la curva de nivel en el punto \(C\). Además, el punto \(C\) es común también para la restricción, cuyo gradiente (\(\nabla g)\) será perpendicular a dicha restricción. De esta forma, y como ves en la FIG 4, tanto el gradiente de la curva de nivel como el de la restricción deberán apuntar en la misma dirección (al estar en un punto de tangencia, es decir, común) de tal manera que serán proporcionales, esto es:

\[\begin{equation} \nabla f(x,y)=\lambda\nabla g(x,y) \end{equation}\]

Nota que, en este caso, el gradiente de la función objetivo \(\nabla f\) y el de la restricción \(\nabla g\) están en la misma dirección pero tienen sentidos opuestos (lo que hará que \(\lambda<0)\).

Lagrange probó que esa condición de tangencia se puede alcanzar mediante la funciún lagrangiana \(\mathcal{L}\::\:\mathbb{R}^{3}\rightarrow\mathbb{R}\) definida como \[ \mathcal{L}(x,y,\lambda)=f(x,y)-\lambda g(x,y), \] que, posteriormente, recuperaremos.

Las condiciones de KKT: solución de tangencia versus solución interior

Ha llegado el momento de entender cuáles son las condiciones necesarias que nos van a permitir buscar puntos críticos cuando estemos en problemas con restricciones de desigualdad.

Supongamos que queremos resolver un problema de minimización, tal que

\[\begin{equation} \min f(x,y) \end{equation}\]

sujeto a \[ g(x,y)\leq k \]

como supondrás, dependerá de la función \(f(x,y)\) y de dónde esté ubicada la restricción, podemos tener dos tipos de mínimos básicamente:

FIG5 solución interior vs solución de tangencia

• solución interior

En el caso primero, el de la solución interior, vemos que la función decrece según nos vamos acercando al centro de la elipse. En este caso, si te das cuenta, la restricción nos permite que el punto óptimo que buscamos consista en trabajar como si no tuviéramos la restricción (es decir, el óptimo se encuentra en un punto que satisface \(g(x,y)<k)\). Y, vía el lagrangiano, tendríamos que

\[\begin{equation} \mathcal{L}(x,y,\lambda_{1},...,\lambda_{m})={ {\color{red}f(x,y)}-{\color{green}{ \lambda\left(g(x,y)-k\right)}}} \end{equation}\]

pero, como en este caso la restricción es como si no estuviera, sabemos que la condición necesaria de óptimo deberá ser \(\frac{\partial f}{\partial x}=0,\frac{\partial f}{\partial y}=0\). Para que eso ocurra en la ecuación anterior, tendrá que ocurrir que \(\lambda=0\).

IDEA: si la solución es interior, esto implica que \(\lambda=0.\) En Economía: si un recurso, disponible en cantidad limitada (es decir, donde opera una restricción), no se utiliza en el óptimo de modo en que se agote, su limitación no representa ningún papel en el problema. Sin embargo, hasta que no se resuelve el problema, no sabemos si la solución es interior o no.

• solución de tangencia

En el segundo caso, la solución óptima se encontrará justo en la restricción \(g(x,y)=k\). Aquí volvemos a recuperar la idea de Lagrange que hemos repasado antes, por lo que tendremos que los gradientes de la función objetivo y de la restricción han de ser proporcionales:

FIG6 solución de tangencia

que implicará, por tanto, que cuando busquemos soluciones que son puntos de tangencia, \(\lambda\neq0\) (en este caso, como vemos, al buscar un mínimo, \(\lambda<0\)).

• Holgura complementaria

Visto lo anterior, debemos entonces estudiar dos posibilidades de interés para buscar puntos críticos que están relacionadas con el valor del multiplicador, \(\lambda=0\) (solución interior) y \(g(x,y)=k\Rightarrow\lambda\neq0\) (punto de tangencia). Una manera práctica de escribir ambas condiciones a la vez será

\[ \lambda\left[g(x,y)-k\right]=0, \]

por lo que,

\[\begin{cases} \lambda=0 & g(x,y)\neq k\\ \lambda\neq0 & g(x,y)=k \end{cases}\]

lo que se conoce como HOLGURA COMPLEMENTARIA. Se suele decir, en el argot, que si \(\lambda=0\) no saturamos la restricción, o que esta no está activa.

• Signo del multiplicador

Si buscamos un óptimo mediante la condición de tangencia, ha de cumplirse \(\nabla f(x,y)=\lambda\nabla g(x,y)\), donde nos queda por determinar el signo (y el valor, claro) de \(\lambda\). Si buscamos un máximo (en una condición de tangencia), el gradiente de la función objetivo y de la restricción serán, ambos, proporcionales (por lo que \(\lambda>0)\). En caso de que busquemos un mínimo, el gradiente de la restricción sigue apuntando al mismo sentido pero será ahora el de la función objetivo el que vaya en sentido contrario. Esto implicará que \(\lambda<0\)

FIG7 el signo del multiplicador

Por otro lado, si la solución es interior ya sabemos que \(\lambda=0\). De esta forma, ya tenemos condición necesaria para máximo respecto al multiplicador: \(\lambda\geq0\) y, por supuesto, para mínimo: \(\lambda\leq0\).

---

Clase 4: Caracterización de puntos críticos

Teorema de Weierstrass

Una manera de poder obtener rápidamente los óptimos GLOBALES de un problema de optimización con restricciones (de desigualdad, en este caso) es analizar el conjunto de soluciones factibles. Para ello, deberás saber dibujarlos (los que se te proponen en este curso no son especialmente complicados). Deberás entonces, ser capaz de encontrar aquellos que sean cerrados y acotados. Vamos a definir, visualmente, lo que es un conjunto cerrado y acotado (es decir, compacto). Piensa que un conjunto es cerrado si incluye su frontera (en nuestro caso, deberá aparecer el signo de “=” en todas las restricciones y es acotado si puedes abarcarlo, mentalmente, con un círculo finito)

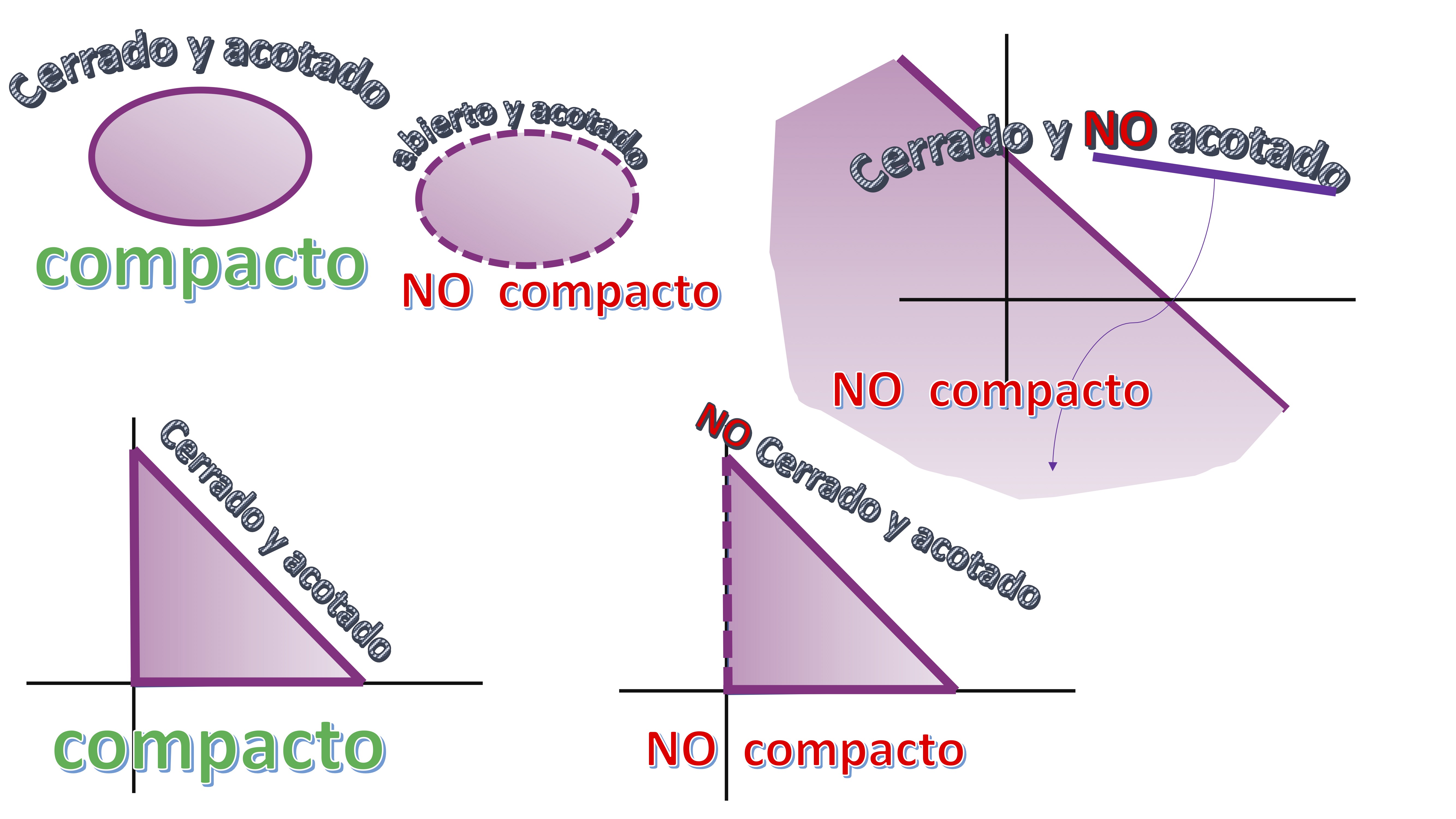
FIG1 conjuntos compactos vs no compactos

hay un resultado muy celebrado justo cuando estás trabajando con conjuntos compactos (cerrados+acotados), el Teorema de Weierstrass:

Teorema de Weierstrass Si la función objetivo es continua en el conjunto de soluciones factibles y el conjunto de soluciones factibles es compacto, el problema tiene tanto máximo(s) como mínimo(s) globales

---

Este es un famoso teorema de Existencia. No te dice cómo obtener los máximos/mínimos globales, pero sí que te asegura que estos existen bajo dichas condiciones.

Habitualmente Las funciones objetivos con las que trabajas son continuas, por lo que sólo tienes que verificar que el conjunto factible sea compacto

• Ejemplo: analiza si tienes óptimos globales en el problema de la clase #3 y di cuáles son:

recuerda:

\[ \mathrm{opt}\:f(x,y)=x^{2}+y \] sujeto a

\[ \frac{x^{2}}{4}+\frac{y^{2}}{9}\leq1 \]

Analizamos el conjunto de soluciones factibles. Es una elipse, como puedes recordar del curso anterior (o de bachillerato)

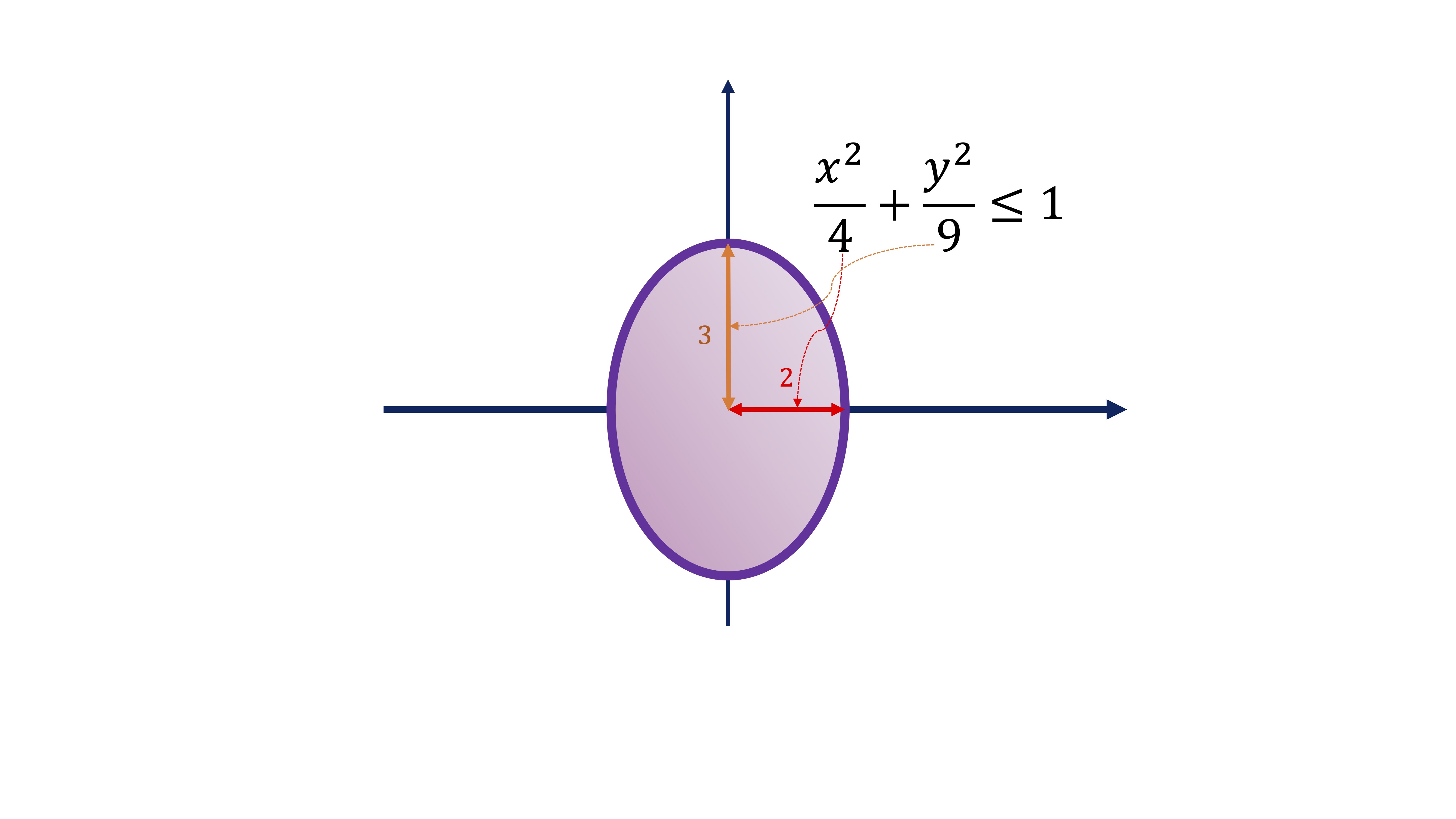como es cerrada (la frontera está incluida) y acotada (no se desparrama ek conjunto) entonces es COMPACTO. Esto implica que tenemos máximo(s) y mínimo(s) globales.

-¿Cómo los encontramos? Muy fácil, vamos a la tabla de clasificación de los puntos críticos

Punto	1	2	3	4
\(x^*\)	0	0	\(\sqrt{55}/4\)	\(-\sqrt{55}/4\)
\(y^*\)	3	-3	\(9/8\)	\(9/8\)
\(\lambda^*\)	3/2	-3/2	\(4\)	\(4\)

y añadimos una fila más, donde ponemos el valor de la función objetivo \(f(x,y)=x^2+y\) para cada uno de esos puntos:

Punto	1	2	3	4
\(x^*\)	0	0	\(\sqrt{55}/4\)	\(-\sqrt{55}/4\)
\(y^*\)	3	-3	\(9/8\)	\(9/8\)
\(\lambda^*\)	3/2	-3/2	\(4\)	\(4\)
\(f(x^*,y^*)\)	\(3\)	\(-3\)	\(73/16\)	\(73/16\)

Por lo que tenemos que :

• Mínimo global: es el punto \((x,y)=(0,-3)\)
• Máximos globales: los puntos \((x,y)=(\sqrt{55}/4,9/8)\) y \((x,y)=(-\sqrt{55}/4,9/8)\)

---

consejo!

Cuando tengas un problema de optimización, lo mejor que puedes hacer es analizar primeramente si verificas Weierstrass.

Otro resultado: Teorema “local-Global”

Además del Teorema de Weierstrass, utilizaremos otro resultado de interés para buscar puntos globales. En este caso, son condiciones suficientes de máximp-mínimo global:

Teorema Local GLOBAL Si el conjunto de soluciones factibles es convexo y la función objetivo es: >- Cóncava: los candidatos a máximo, son máximo globales >- Convexa: los candidatos a mínimo, son minimo globales

Fíjate que, en este caso, no estás ante un teorema de existencia. Una condición suficiente te dice que, si la satisfaces, los puntos críticos podrán ser clasificados como máximos o mínimos globales. Si no la satisfaces, entonces no puedes decir nada.

Con este resultado tendremos que analizar cuándo una función objetivo es cóncava o convexa y cuándo un conjunto de soluciones factibles es convexo (cuidado, no existen los conjuntos cóncavos).

En el caso de dos variables, diremos que una función \(f:\:\mathbb{R}^{2}\rightarrow\mathbb{R}\) es convexa si al aproximarla mediante planos tangentes en el entorno de un punto \((x^{*},y^{*})\), estos planos siempre aproximan por defecto (es decir, quedan por debajo). Al revés, ocurrirá cuando queramos definir una función cóncava: mira la FIG3:

FIG3 Funciones cóncavas o convexas

Podemos utilizar, dado que las funciones con las que trabajaremos se comportarán adecuadamente, los siguientes criterios de clasificación:

• FUNCIÓN ESTRICTAMENTE CONVEXA

Si \(f\in\mathcal{C}^{2}\), será estrictamente convexa en el conjunto \(X\), si \[ \frac{\partial^{2}f}{\partial x^{2}}>0,\left|Hf(x,y)\right|>0 \]

para todo \((x,y)\in X.\) En ese caso, se dirá que \(Hf(x,y)\) es DEFINIDA POSITIVA

• FUNCIÓN ESTRICTAMENTE CÓNCAVA

Si \(f\in\mathcal{C}^{2}\), será estrictamente cóncava en el conjunto \(X\), si \[ \frac{\partial^{2}f}{\partial x^{2}}<0,\left|Hf(x,y)\right|>0 \]

para todo \((x,y)\in X.\) En ese caso, se dirá que \(Hf(x,y)\) es DEFINIDA NEGATIVA

• FUNCIÓN CONVEXA

Si \(f\in\mathcal{C}^{2}\), será convexa en el conjunto \(X\), si

\[ \frac{\partial^{2}f}{\partial x^{2}}{\color{red}\geq}0,{\left|Hf(x,y)\right|=0} \]

para todo \((x,y)\in X.\) En ese caso, se dirá que \(Hf(x,y)\) es SEMIDEFINIDA POSITIVA

• FUNCIÓN CÓNCAVA

Si \(f\in\mathcal{C}^{2}\), será cóncava en el conjunto \(X\), si \[ \frac{\partial^{2}f}{\partial x^{2}}{\color{red}\leq}0,{\left|Hf(x,y)\right|=0} \]

para todo \((x,y)\in X.\) En ese caso, se dirá que \(Hf(x,y)\) es SEMIDEFINIDA NEGATIVA

Ejercicio Resuelto

Comprueba si son cóncavas o convexas las siguientes funciones

1. \(f(x,y)=-x^{2}-y^{2}\)
2. \(f(x,y)=x^{4}+y^{4}\)
3. \(f(x,y)=x^{2}+y^{2}+2xy\)
4. \(f(x,y)=xy\)
5. \(f(x,y)=y-x^{2}\)
6. \(f(x,y)=2\ln x+\ln y\)

Para ello, necesitamos calcular la Hessiana y clasificarla:

1. \(Hf(x,y)=\left[\begin{array}{cc} -2 & 0\\ 0 & -2 \end{array}\right]\) que cumple con la condición para ser estrictamente cóncava. Además, independientemente del valor de \(x,y\in\mathbb{R}^{2}\). Es decir, es estrictamente cóncava en todo su dominio (que es \(\mathbb{R}^{2}\))

2. \(Hf(x,y)=\left[\begin{array}{cc} 12x^{2} & 0\\ 0 & 12y^{2} \end{array}\right]\) cumple con la condición para ser convexa. Si \(x\neq0\) e \(y\neq0\) será DEFINIDA POSITIVA Si Si \(x=0\) o \(y=0\) será SEMIDEFINIDA POSITIVA (por lo que no sabemos, con este criterio, si esta funci?n es convexa o estrictamente convexa). Puedes hacer un dibujo en Geogebra y decidirlo. Para ello, fíjate en el entorno de \((x,y)=(0,0)\).

3. \(Hf(x,y)=\left[\begin{array}{cc} 2 & 2\\ 2 & 2 \end{array}\right]\) como ves, es SEMIDEFINIDA POSITIVA, para cualquier valor de \(x,y\in\mathbb{R}^{2}\). Esto indica que es convexa (pero no estrictamente).

4. \(Hf(x,y)=\left[\begin{array}{cc} 0 & 1\\ 1 & 0 \end{array}\right]\) Esta no cumple ninguno de los criterios anteriores. Decimos que la matriz Hessiana es INDEFINIDA y, por lo tanto, no es ni cóncava ni convexa

5. \(Hf(x,y)=\left[\begin{array}{cc} -2 & 0\\ 0 & 0 \end{array}\right]\) Esta es SEMIDEFINIDA negativa. Entonces, sabemos que es cóncava (no estricta)

6. \(Hf(x,y)=\left[\begin{array}{cc} -\frac{2}{x^{2}} & 0\\ 0 & -\frac{1}{y^{2}} \end{array}\right]\) Esta es DEFINIDA negativa. La función es estrictamente cónvava

Otro resultado sobre convexidad que nos interesa es el relacionado con conjuntos. En nuestro caso, necesitaremos ser capaces de analizar los conjuntos factibles.

Conjunto convexo

Diremos que un conjunto es convexo si dados dos puntos cualesquiera del conjunto, el segmento que los une está también dentro del conjunto

De hecho, para identificar si un conjunto es o no convexo deberás esbozarlo y, a continuación, ver si cumple con la definición que hemos subrayado. En la siguiente FIG 4, podemos ver la idea: en los conjuntos convexos, eliges dos puntos cualesquiera del conjunto, trazas un segmento imaginario y dicho segmento “no se sale” del conjunto. Eso no pasa con los conjuntos no convexos.

FIG4 Conjuntos convexos vs no convexos

Ejemplos de conjuntos convexos que vamos a utilizar habitualmente:

• El espacio\(\mathbb{R}^{2}\)

• El conjunto de soluciones de un sistema lineal de ecuaciones (caso muy concreto de conjunto factible en nuestro caso)

-Intersecciones de conjuntos convexos (ojo, no la unión). Mira este ejemplo gráfico.

FIG5 Conjuntos convexos vs no convexos

Ejercicio Propuesto 6

Analiza qué tipo de programa matemático tenemos de acuerdo con la convexidad de este.

• \(\mathrm{opt}\:2x+y,\;s.a\:xy\geq1,x,y\geq0\)
• \(\mathrm{opt}\:(x-1)^{2}+(y-1)^{2},\;s.a\:2x+y\leq10,x,y\geq0\)
• \(\mathrm{opt}\:y-x^{2},\;s.a\:x+y\leq1,x,y\geq0\)
• \(\mathrm{opt}\:x+y,\;s.a\:2x+2y\leq10,x,y\geq0\)

Habitualmente Los conjuntos con los que vas a trabajar son convexos (semiplanos, circunferencias, elipses, etc…)

Clase 5 El método de Khun-Tucker en Excel. Interpretación del multiplicador

Vamos a ver cómo, de forma sencilla, podemos obtener la solución (de ótimo global) utilizando la herramienta solver de Excel. Esta herramienta te la tienes que descargar de archivo-opciones en el caso de que tengas Windows y en herramientas en el caso de que tengas Apple.

FIG1 Entonces, vas a complementos y de ahí eliges “solver”. Dale a “ir” y volverás a tener que elegir”solver”. Aceptas, y ya lo tienes

Ahora vamos a trabajar con el Problema de la clase 2 usando Excel. Empieza declarando quiénes son tus variables, la función objetivo y, por supuesto, las restricciones. Hazlo así:

FIG2: así se escribe el problema

como ves, lo usas para estructurar tu problema. Debes introducir qué celda es la función beneficio, qué quieres hacer con ella (max-min), qué celdas modificarás para obtener ese objetivo y con qué restricciones cuentas.

FIG3: así se especifica

si pulsas a “resolver”, obtendrás esta pantalla. No te olvides de pedirle el informe de sensibilidad:

FIG4: así se especifica

Una vez pides ese informe, puedes analizar cuál es el óptimo (global) que encuentra Excel y el multiplicador. Eso sí, Excel no analiza por ti si el óptimo es o no global. Él te da la mejor solución. De ti depende saber si estamos en el caso global analizando los teoremas de condiciones suficientes que te hemos contado!

FIG5: El resultado

La interpretación del multiplicador de Lagrange

Finalmente, a lo largo de estos días has preguntado: ¿para qué calculamos los multiplicadores?

• RESPUESTA 1: recuerda que nos ayudan a identificar si un candidato a solución lo es para máximo o para mínimo
• RESPUESTA 2: ¡¡es que tiene un significado económico interesante!!

Imagina que estás ante este problema: \[ \max x^{2}\times y^{2}-x-y \]

s.a

\[ x+y\leq10 \]

\[ x,y>0 \]

Quieres analizar, por otro lado, qué ocurriría si estas fueran tus restricciones

\[ x+y\leq{\color{red}1\color{red}1} \]

\[ x,y>0 \]

Vamos a calcular el óptimo de ambos problemas usando Excel:

FIG5: ¿Cómo cambia el resultado?

Si reescribimos el problema de forma genérica como \[ \max x^{2}\times y^{2}-x-y \]

s.a

\[ x+y\leq{\color{lime}k} \]

\[ x,y>0 \]

Si te fijas, tras cambiar \(k\) en una unidad (\(\triangle k=1)\) el beneficio pasa de ser 615 unidades a 904. La diferencia es 289. Esa diferencia es el beneficio que podrías ganar, si produces de forma óptima, al incrementar una unidad tus recursos. A eso se le llama “precio sombra”. Imagina que incrementar en una unidad tu recurso implica que debes ampliar tu empresa y el coste de ampliarla es 1000 euros. Entonces, como ampliar la empresa y producir de forma óptima sólo te va a reportar 289 euros más, no te sale a cuenta. Es, por tanto, la cifra máxima que estarías dispuesto a pagar si haces las mejoras necesarias para aumentar tus recursos. Pues bien, en vez de resolver el problema dos veces, te vamos a enseñar una manera de calcular, aproximadamente, tu precio sombra. Resulta que el incremento del beneficio en el óptimo (o de tu función objetivo) se puede obtener como \[ \triangle f\simeq\lambda\triangle k \]

Resulta que usando cálculo diferencial, podemos aproximar el valor que esperamos que se incremente la función objetivo. En nuestro caso, \[ \lambda=249 \]

(obtenido de la salida de Excel). Entonces, como \(\triangle k=1\), esperaríamos:

\[ \triangle f\simeq249 \]

De tal forma que, aproximadamente, ese es el incremento de la función objetivo en el óptimo ante un incremento del recurso. Para que esta aproximación sea buena (y, por lo tanto, no tengas que resolver el problema para cada valor de \(k\)), \(\Delta k\rightarrow0.\)