Chapter 9 Sets, Inequalities and Functions

In the first semester we have been generating sequences of numbers, for instance, using the Newton-Raphson method for solving non-linear equations (Chapter 2) , or using the rectangle rule for integration (Chapter 3). In this section we will say what real numbers are as limits of these sequences, where we will need to formally define limit. Once we know what real numbers are we will discuss ordering of these numbers with $<,>,=$ and the arithmetic of inequalities. The notes here are based on the book An Introduction to Mathematical Analysi by my old lecturer at Manchester John Reade. This book can be found for free at http://www.mathstudio.co.uk/sequences.htm.

9.1 Sets

This section is a revision of set notation. Suppose $S$ is a set of objects (need not be numbers).

1. Membership: We denote membership of the set $s$ is a member of $S$, by $s \in S$. If $s$ is not a member we write $s \not \in S$. For example $S=\{$Toyota, Ford, Renault, Peugeot$\}$ a set of brands of car. Then Ford $\in S$, but Mercedes $\not \in S$. For a numerical example, let $S=\{x:0 \le x \le 1\}$. Then $0.5 \in S$, but $1.5 \not \in S$. We have introduced the notation $S=\{s:P(s)$ is true$\}$.

2. Relations and operations: We have the following ways of operating with sets:

   • Subset: If $S$ and $T$ are sets, $S \subset T$ ($S$ is a subset of $T$) if $s \in S$ implies $s \in T$. Another way of writing this is to use the universal quantifier ‘for all’. Using this we can write $\forall x \in S, s \in T$;
   • Union: If $S$ and $T$ are sets, $S \cup T = \{s:s \in S \; {\rm or} \; s \in T\}$;
   • Intersection: If $S$ and $T$ are sets, $S \cap T = \{s:s \in S \; {\rm and} \; s \in T\}$;
   • Set difference: If $S$ and $T$ are sets, $S \backslash T = \{s \in S:s \not \in T\}$.
   • Cardinality or size: If a set is finite, then the number of elements in the set is called its cardinality or size. We denote the cardinality of a set $A$ using $|A|$. This idea can be expanded to sets such as ${\mathbb Z}$ or even ${\mathbb R}$, but this will not be covered in this module.

In addition to the universal quantifier we have the existential quantifier $\exists$. We use this to say that at least one element of a set exists which satisfies some property. For instance $\exists s \in {\mathbb N}$ such that $s > 0$.

This is a nice Youtube video which discusses elementary set thoery.

9.2 Ordered sets

The sets ${\mathbb N}, {\mathbb Z}, {\mathbb Q}, {\mathbb R}$ all satisfy the following ordering axioms. We use the sign $<$ (less than) for the ordering. Let $S$ denote one of these sets.

• Trichotomy (total order): If $s,t \in S$ either $s<t$, $t<s$ or $s=t$;
• Transitivity: If $s,t,u \in S$, $s<t$ and $t<u$, then $s<u$;
• Compatability: If $s,t,u \in S$ and $s<t$ then $s+u<t+u$;
  1. if $0<u$ then $su<tu$,
  2. and (ii) if $u<0$ then $tu<su$.

We use the sign $>$ than for convenience: $s<t$ means that $t>s$. We use the signs $s \le t$ and $s \ge t$ to mean $s$ is less than or equal to $t$ and $s$ is greater than or equal to $t$ respectively.

We also have the following field axioms which you will immediately see are needed for us to do a lot of the arithmetic calculutions and algebra we have become accustomed to. Let us use the notation ${\mathbb F}$ to refer to any sets which satisfy these axioms.

• Additive identity: $\exists \; 0 \in {\mathbb F}$ such that $0+s=s+0=s \; \forall \; s \in {\mathbb F}$;
• Additive inverse: $\forall \; s \in {\mathbb F} \; \exists -s \in {\mathbb F}$ such that $s+(-s)=(-s)+s=0$;
• Additive associativity: If $s,t,u \in {\mathbb F}$ the $(s+t)+u = s+(t+u)$;
• Additive commutativity: If $s,t \in {\mathbb F}$ then $s+t = t+s$;
• Multiplicative identity: $\exists \; 1 \in {\mathbb F}$ such that $1 \cdot s=s \cdot 1=s \; \forall \; s \in {\mathbb F}$;
• Multiplicative inverse: $\forall \; s \not = 0 \in {\mathbb F} \; \exists s^{-1} \in {\mathbb F}$ such that $s^{-1} \cdot s=s \cdot s^{-1}=1$;
• Multiplicative associativity: If $s,t,u \in {\mathbb F}$ then $s \cdot (t \cdot u) = (s \cdot t) \cdot u$;
• Multiplicative commutativity: If $s,t \in {\mathbb F}$ then $s \cdot t = t \cdot s$;
• Distributivity: If $s,t,u \in {\mathbb F}$ then $s \cdot (t + u) = s \cdot t+s \cdot u$;
• $0 \neq 1$.

In this video Tom will explain about these rules, and use them to prove some other results.

Definition 9.1 (Open and closed intervals) We denote by $[a,b] \subset {\mathbb F}$ the set $\{x:a \le x \le b\}$ and we refer to it as the closed interval a b. The set $\{x:a<x<b\}$ is called the open interval a b. The closed interval contains its end points, and the open interval does not contain either end point. The set $(a,b]=\{x:a<x\le b\}$ is neither open nor closed. The notion of open and closed sets become more important as you develop your mathematical knowledge, and will be used in topics such as Topology and Complex Analysis. The ideas generalise into higher dimensions.

Example 9.1 Solve the following inequality for $x \in {\mathbb F}$: $$x+4<2x+6.$$

Solution: Adding -4 to both sides (compatibility) we have $$x<2x+2.$$ Adding $-2x$ to both sides (compatibility) then gives $$-x<2.$$ Multiplying both sides by -1 ((ii) in multiplicative part of compatibility) gives $$x>-2.$$ We can check this by trying e.g. $x=-1$ as this is part of our solution set. $$-1+4=3<4=2(-1)+6.$$

Here is video on solving linear inequalities.

Proposition 9.1 Let $x, a \in {\mathbb F}$ with $a>0$. Then $x^2<a^2$ if and only if $-a < x < a$.

Proof: We will break the proof into a number of steps. First we will show that if $-a < x < a$ then $x^2<a^2$. We will do this by splitting into three cases:

• If $x=0$ then the proposition is trivial.
• If $0<x<a$ then by the compatability law (multiplying by $a$) $0<ax<a^2$, and (multiplying by $x$) $0<x^2<ax$. Hence $0 < x^2 < ax < a^2$ and $x^2 < a^2$ by the transitive law.

• If $-a<x<0$ then by the compatability law (multiplying by $-a$) $0<-ax<a^2$ and (multiplying by $x$ which we recall is negative) $0<x^2<-ax$. Hence $0 < x^2 < -ax < a^2$ and $x^2 < a^2$ by the transitive law.

  Now we need to show that if $x \not \in (-a,a)$ then $x^2 \not < a^2$. This will then show that if $x^2 < a^2$ then $-a < x < a$. This style of proof is .

  A very similar argument shows that if $x>a$ then $x^2>a^2$, and if $x<-a$ then $x^2>a^2$. This shows that if $x \not \in (-a,a)$ then $x^2 \not < a^2$ by the trichotomy law.

  Of course, the result is obvious from the picture above, but we need to learn how to justify the obvious rigorously from our axioms.

Example 9.2 Solve the equation $x^2-6x+5<0$ for $x \in {\mathbb F}$.

Solution: We will use a very useful technique called completing the square. We write $$x^2-6x+5 = x^2-6x+9-4 = (x-3)^2-4.$$ Hence $$(x-3)^2-4 < 0,$$ so that $$(x-3)^2<4.$$ Using Proposition 9.3 we see that $$-2<x-3<2$$ and adding 3 to both sides we get our final result $1<x<5$. We check this by putting $x=2$ and seeing that $4-12+5<0$. Alternatively, if we put $x=6$ we have $36-36+5>0$ and if $x=0$, $0-0+5>0$

In this video they solve the quadrtic inequality by factorising the quadratic. This is a good idea if the quadratic factorises easily, otherwise the completing the square method might be better.

Example 9.3 Prove that for $a,b \in {\mathbb F}$ $$\left ( {a+b \over 2} \right )^2 \ge ab.$$ This equation is called the arithmetic -geometric mean inequality.

Solution: Since $(a-b)^2>0$,

$$\begin{eqnarray*} \left ( {a+b \over 2} \right )^2 & \ge & \left ( {a+b \over 2} \right )^2 - \left ( {a-b \over 2} \right )^2 \\ & = & \left ( {a^2\over 4} + {b^2\over 4} + {ab\over 2}\right ) - \left ( {a^2\over 4} + {b^2\over 4} - {ab\over 2}\right ) & = & ab. \end{eqnarray*}$$

9.2.1 Test yourself

9.3 The Modulus Function and Triangle Inequalities

One of the most important functions in analysis is

Definition 9.2 (Modulus, Absolute Value or Distance Function) Here is a picture of it:

The modulus function is defined by $$|x| = \left \{ \begin{array}{cc} x, & x \ge 0, \\ -x, & x < 0. \end{array} \right.$$

Here is a picture of it:

Remark. If $a,b \in {\mathbb F}$ the number $|a-b|$ is the distance between $a$ and $b$ in ${\mathbb F}$. For example if $a=-2$ and $b=3$, $|-2-3|=|-5|=5$ which is the distance between $-2$ and $3$. Also, the distance function is symmetric, i.e. $|a-b|=|b-a|$, $|3-(-2)|=|5|=5$. Also $|x|=\sqrt{x^2}$ if we interpret this as the positive square root. Thus $$|xy|=\sqrt{x^2 y^2}=\sqrt{x^2} \sqrt{y^2} = |x||y|. \tag{9.1}$$

Theorem 9.1 (Triangle Inequality) For all $x,y \in {\mathbb F}$ $$|x+y|\le |x|+|y|.$$

Proof: Squaring the left hand side of the equation above

$$\begin{eqnarray*} (|x+y|)^2 & = & (x+y)^2 \\ & = & x^2+y^2+2xy \\ & \le & |x|^2+|y|^2+2|x||y| \\ & = & (|x|+|y|)^2. \end{eqnarray*}$$

Using Proposition~9.1 we arrive at the desired result.

Corollary 9.1 (Reverse Triangle Inequality) For all $x,y \in {\mathbb F}$ $$|x-y|\ge ||x|-|y||.$$

Proof: Since $x=(x-y)+y$ we have, using the triangle inequality, $$|x| \le |x-y|+|y|,$$ so that $$|x|-|y| \le |x-y|.$$ On the other hand $y=(y-x)+x$, so again using the triangle inequality, we have $$|y| \le |y-x|+|x|=|x-y|+|x|,$$ since $|y-x|=|x-y|$. Therefore $$|y|-|x| \le |x-y|.$$ If $|x| \ge |y|$, $||x|-|y||=|x|-|y|$ and if $|y| \ge |x|$, $||x|-|y||=|y|-|x|$. Thus $$||x|-|y|| \le |x-y|.$$

Here is a video about the triangle inequality.

Test yourself

This second video talks about the inequality in two dimensions and gives the inequality its name. Enjoy the music.

9.3.1 Test yourself

9.4 Bounds on Sets of Numbers

In this section we talk about bounded sets. Not only is this useful in its own right, but it also gives us the machinery we need to use to define the real numbers.

Definition 9.3 (Bounds on sets) Let $S \subset {\mathbb F}$. Then $M \in {\mathbb F}$ is an upper bound for $S$ if $s \le M$ $\forall s \in S$. Similarly $m \in {\mathbb F}$ is a lower bound for $S$ if $s \ge m$ $\forall s \in S$. We say $S$ is bounded above if it has an upper bound and is bounded below if it has a lower bound. If $S$ it is bounded above and below it is bounded.

Example 9.4 Both 1 and 2 are upper bounds for the set $S=[0,1]$. Similarly -1 and 0 are lower bounds for $S=(0,1)$. We can see that both of these sets are bounded. However, the set $\{ x \in {\mathbb F}: x>0 \}$ is not bounded.

Definition 9.4 (Maximum and Minimum) We say that $M$ is the maximum of $S$ if $M \in S$ and $x<M$ if $x \in S$ and $x \neq M$. We denote this $\max (S)$. Similarly we call $m$ the minimum if $m \in S$ and $m<x$ if $x \in S$ and $x \neq m$. We denote this $\min (S)$.

Example 9.5 Let $S=[0,1]$. Then $\max(S)=1$ and $\min(S)=0$. On the other hand the set $(0,1)$ does not have a maximum or a minimum for suppose $x$ is the minumum. Then $x>0$. Hence $0<x/2<x$ and $x/2 \in S$.

Theorem 9.2 Every finite set in ${\mathbb F}$ has a maximum and a minimum.

Proof: We prove this by induction on the size of the set. So let us assume that all sets with $n$ points have a maximum and a minimum, and let $S=\{x_1,x_2,\cdots,x_{n+1}\}$. Let $T=\{x_1,x_2,\cdots,x_n\}$. Then, using the inductive hypothesis, because $T$ is finite and of size $n$, it has a maximum $M=\max(T)$ and a minimum $m=\min(T)$. Now, by the trichotomy axiom, either $x_{n+1}>M$ or $x_{n+1}\le M$. In the former case $\max(S)=x_{n+1}$, and in the latter case $\max(S)=M$. Hence $S$ has a maximum. The argument for $\min(S)$ is similar. To begin the induction it is clear that if $S=\{x_1\}$ has only one element then $\max(S)=\min(S)=x_1$.

Definition 9.5 (Least Upper Bound and Greatest Lower Bound) If a set $S$ is bounded above then the smallest upper bound for the set is called the of $S$, $\sup(S)$, or the ${\rm lub} \, (S)$. If the set is bounded below then the largest lower bound for the set is called the of $S$, $\inf(S)$, or the greatest lower bound ${\rm glb} \, S$. If $\sup(S) \in S$ then $\sup(S)=\max(S)$. Similarly in $\inf(S) \in S$ then $\inf(S)=\min(S)$.

Example 9.6 Let $S=(3,4] \cup [5,6]$. Then $\sup(S)=\max(S)=6$, and $\inf(S)=3$. $S$ does not possess a minimum.

Here is a video about bounds on sets.

9.4.1 Test yourself

9.5 The Uper Bound Axiom and Real Numbers

There are a number of ways one could introduce an axiom which would can specify the real numbers. We will add one more axiom to all of the field axioms we listed in Section~9.1

The Upper Bound Axiom: Every non-empty subset of ${\mathbb R}$ which is bounded above has a supremum in ${\mathbb R}$.

Remark. It is helpful to think about how this distinguishes the real numbers from the rational numbers ${\mathbb Q}$. For consider the sequence of numbers $S=\{1,1.4,1.41,\cdots,\}$, the terms in the decimal expansion for $\sqrt{2}$. Then this set is bounded above by 2 say, but it does not have a supremum in ${\mathbb Q}$. This axiom is telling us that if we allow ourselves to use the bigger set of real numbers then the supremum exists. What this is doing is filling out the continuum of numbers. With ${\mathbb Q}$ we have some holes. With ${\mathbb R}$ we do not. This is a reason why this is also called the completness axiom.

Theorem 9.3 $\sqrt{2}$ is a real number.

Proof: In order to prove this we need to show that there is a number $M$ such that $M^2=2$ and $M$ is the supremum of some set of real numbers.

Let $S=\{x: x^2<2\}$. Then $S$ is bounded above and therefore has a supremum $M$. We will now show that $M^2=2$. For suppose $M^2<2$ and consider the number $M+{1 \over n}$ where $n$ is a positive integer. Then

$$\begin{eqnarray*} \left (M+{1 \over n} \right )^2 & = & M^2+{2M \over n} + {1 \over n^2} \\ & \le & M^2+{2M \over n} + {1 \over n} \\ & = & M^2+{2M+1 \over n}. \end{eqnarray*}$$

Since $M^2<2$, if $${2M+1 \over n} < 2-M^2,$$ i.e.  $$n > {2M+1 \over 2-M^2},$$ then $$\left (M+{1 \over n} \right )^2 < 2,$$ which means that $M+{1 \over n} \in S$ and so $M$ is not the supremum. This is a contradiction, so that $M^2 \ge 2$.

On the other hand, suppose $M^2>2$. In the same spirit as above we now consider the number $M-{1 \over n}$. Then

$$\begin{eqnarray*} \left (M-{1 \over n} \right )^2 & = & M^2-{2M \over n} + {1 \over n^2} \\ & \ge & M^2-{2M \over n}. \end{eqnarray*}$$

Since $M^2>2$, if $${2M \over n} < M^2-2,$$ i.e.  $$n > {2M \over M^2-2},$$ then $$\left (M-{1 \over n} \right )^2 > 2,$$ which means that $M-{1 \over n} \not \in S$ and so $M-{1 \over n}$ is an upper bound, but it is less than $M$. This is a contradiction, so that $M^2 \le 2$.

Hence $M^2=2$.

The following video talks about the completeness axiom, which we have called the upper bound axiom.

9.6 Functions

In this section we look at the definition of functions, their composition and the inverse of a function.

Definition 9.6 (Domain and range of function) The domain of a function $f$, ${\rm dom}\,(f)$, is the set on which the function is defined. The range of $f$, ${\rm ran}\,(f)=\{f(x):x \in {\rm dom}\,(f)\}$.

Example 9.7

• The domain for $f(x)=\sqrt{x}$, ${\rm dom}\,(f)=[0,\infty)$. Then ${\rm ran}\,(f)=[0,\infty)$.
• If $g(x)=x^2$, then ${\rm dom}\,(g)={\mathbb R}$ and ${\rm ran}\,(g)=[0,\infty)$.
• If $h(x)=1/|x|$, then ${\rm dom}\,(h)={\mathbb R}/\{0\}$ and ${\rm ran}\,(h)=(0,\infty)$

Definition 9.7 (Composition of functions) If $f$ and $g$ are functions with ${\rm ran}\,(f) \subset {\rm dom}\,(g)$, then the composition of $f$ and $g$, $g \circ f:{\rm dom},(f) \rightarrow {\rm ran},(g)$ is defined by $$g \circ f (x) = g(f(x)).$$

Example 9.8 Let $f(x)=|x|$ and $g(x)=x-1$. Then ${\rm ran}\,(f) = [0,\infty) \subset {\mathbb R}={\rm dom}\,(g)$. Hence $g \circ f(x)=|x|-1$. Also ${\rm ran}\,(g) = {\mathbb R} = {\rm dom}\,(f)$, so we see that $f \circ g(x)=|x-1|$. Note that composition is not , i.e. $f \circ g \neq g \circ f$ in all cases (sometimes it might).

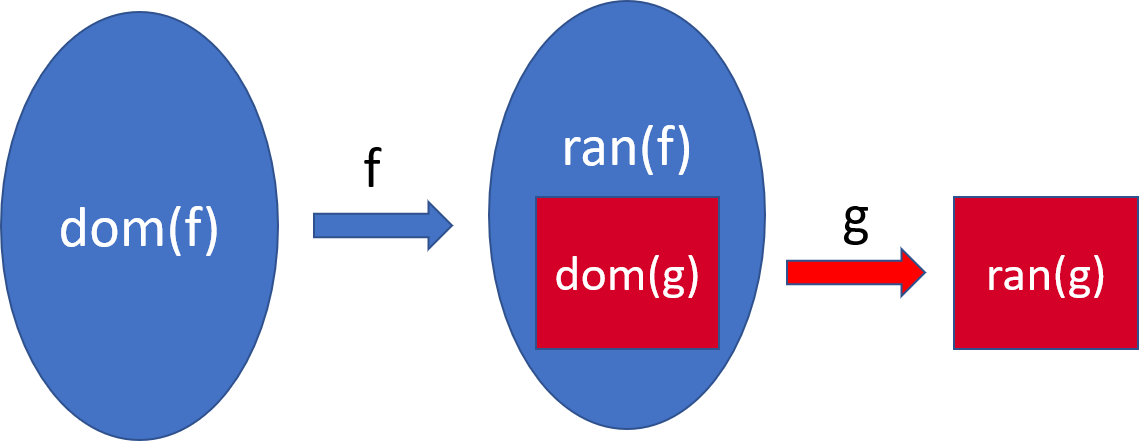
In order to construct inverses of functions i.e. to come back from where we have gone, we need for the inverse function to know where to go back to, so one point in the range cannot come from two different points in the domain. This property of functions is defined below.

Definition 9.8 (One to One) Let $f$ be a function defined on a set $E$. Then $f$ is one to one if $f(x_1) = f(x_2) \in {\rm ran}\,(f)$ implies $x_1 = x_2 \in E$.

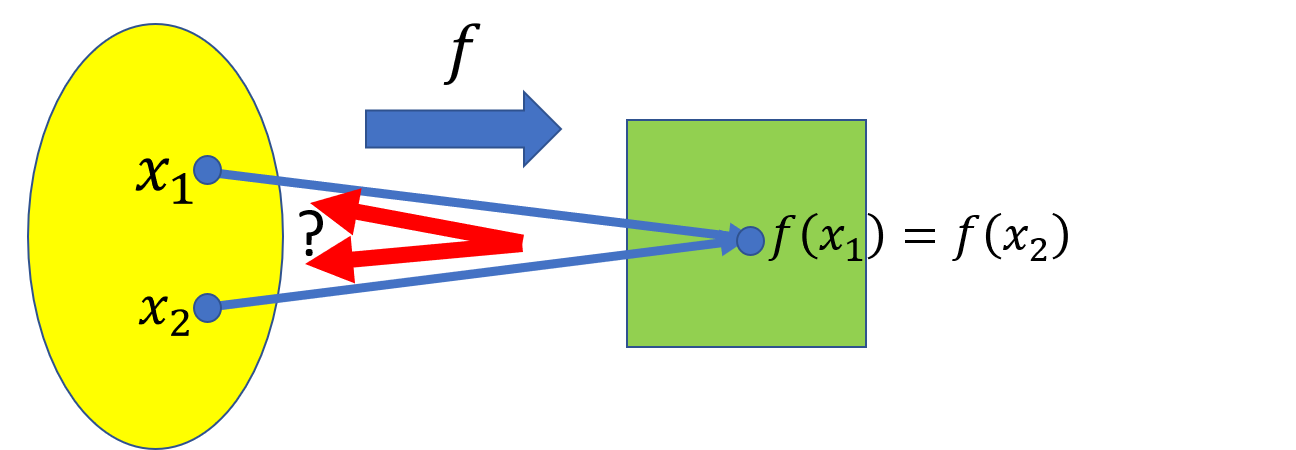
Example 9.9 The function $f(x)=x^3$ is one to one, since $x_1^3 = x_2^3$ implies $$x_1^3-x_2^3=(x_1-x_2)(x_1^2+x_1x_2+x_2^2)=0.$$ Now, $x_1^2+x_1x_2+x_2^2=(x_1+x_2/2)^2+3x_2^2/4>0$. Hence $x_x-x_2=0$ which means $x_1 = x_2$.

On the other hand $f(x)=x^2$ is not one to one as $(-1)^2=1^2$.

Here is a nice video about one to one functions.

Theorem 9.4 (Inverse Function Theorem) If $f$ is one to one there exists a unique inverse function which we denote by $f^{-1} : {\rm ran}\,(f) \rightarrow {\rm dom}\, (f)$ such that $$f^{-1} \circ f(x) = x, \quad \forall x \in {\rm dom}\, (f), \quad f \circ f^{-1} (y) = y, \forall y \in {\rm ran}\, (f).$$

Example 9.10 Let $f(x)={3x+2 \over x-7}$. Find the inverse function of $f$.

Let $y=f(x)$, i.e. $$y = {3x+2 \over x-7}.$$ Cross multpilying we have $$(x-7)y = 3x+2.$$ Getting the the $x$’s on one side we have $$x(y-3) = 7y+2.$$ Dividing gives $$x={7y+2 \over y-3}.$$ The inverse function is $g(y)={7y+2 \over y-3}$.

Remark. Note that $f^{-1}(x) \neq 1/f(x)$ in general. For instance, if $f(x)=x$, then $f^{-1}(x)=x$, whereas $1/f(x)=1/x$. If $f(x)=1/x$, then $f^{-1}(x)=1/x$.

9.7 Challenge yourself

1. Prove that $$|a+b+c| \le |a|+|b|+|c|.$$
2. Can you use the upper bound axiom to prove that any set with a lower bound has an infimum (a greatest lower bound)?
3. Show that $\max\{|a|,|b|\} \le (a^2+b^2)^{1/2} \le |a|+|b|$.
4. Can you prove that $3^{1/2}$ and $2^{1/3}$ are real numbers?
5. Prove the Inverse Function Theorem~9.4.