Chapter 3 Differentiation

3.1 Introduction

In this chapter we will introduce the idea of differentiation. Of course, you have been able to differentiate for a couple of years now, so we will not focus on the mechanics of differentiation, but rather on the ideas behind it, so that you can use these ideas flexibly in any problem you may be required to solve. The main reason we want to differentiate is to find the rate of change of something. If that something is the rate of change of height with distance, then we are finding the gradient. This is useful for understanding how steep roads are for instance. If we want to find out the rate at which distance changes with time then we are computing the speed of something.

The main idea is that if I am very small then all slopes look like straight lines. To the ant all roads look flat. In order to make the slope look flat I just have to look close enough. This is the idea of the limit. For a straight line we know how to calculate the gradient:

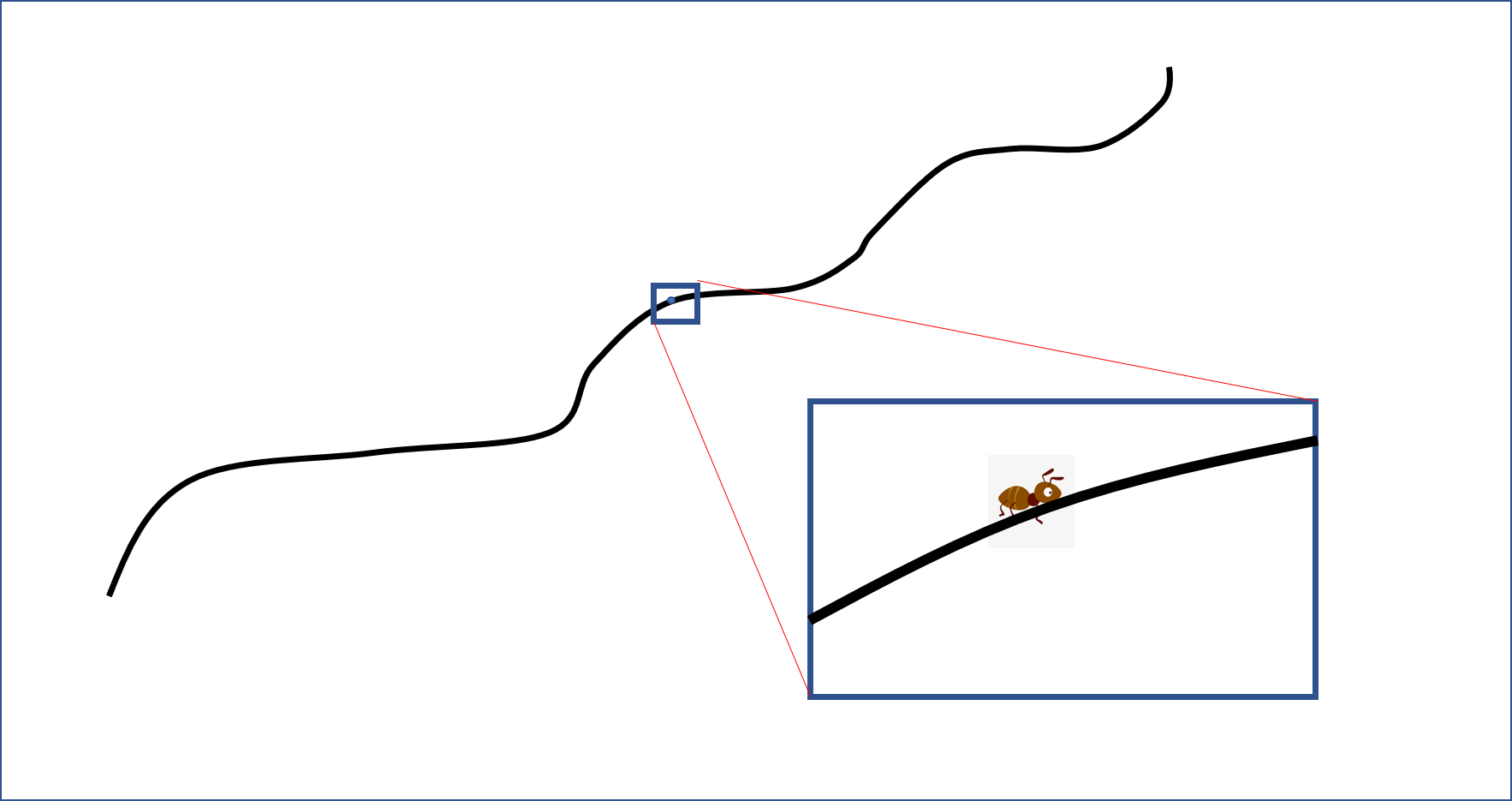
ant

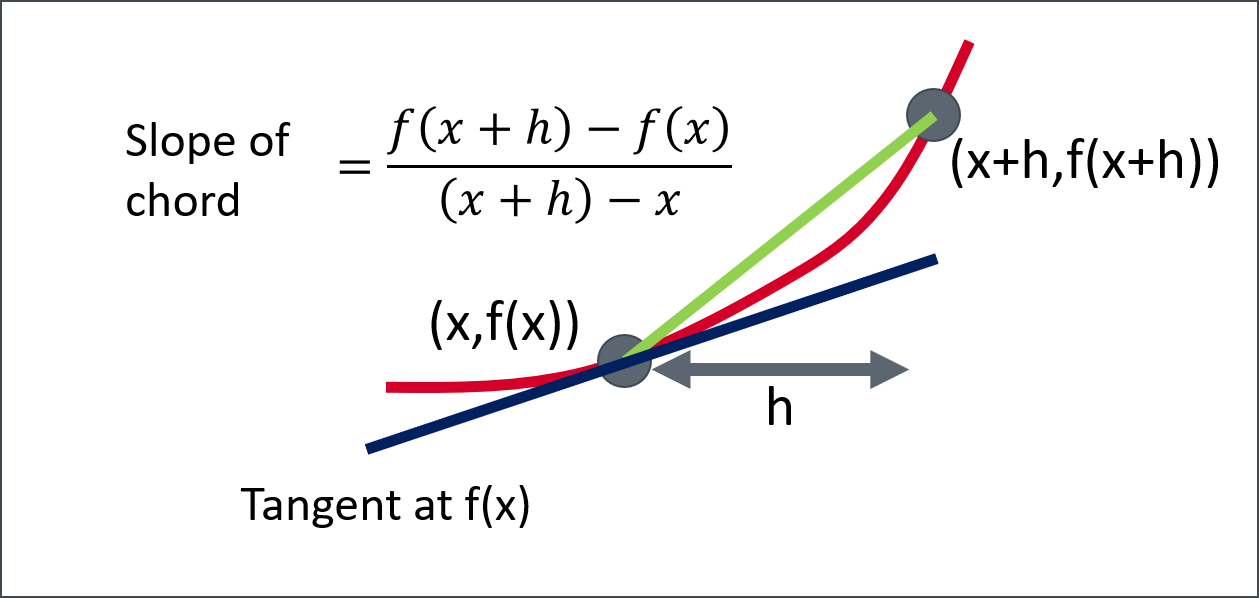
Key idea: the derivative is calculated by considering such a small change in the independent variable \(x\) that the dependent variable \(y\) depends linearly on \(x\) in that time interval. Another way of thinking about this is to say that the function is represented by its tangent (is a straight line). More formally we define this as a limit.

Example 3.1 Find the derivative of \(f(x)=x^2\) at the point \(x=2\). To do this we compute \[ \lim_{h \rightarrow 0} {f(2+h)-f(2) \over h} = \lim_{h \rightarrow 0}{(2+h)^2-2^2 \over h} = \lim_{h \rightarrow 0}{4+4h+h^2-4 \over h} = \lim_{h \rightarrow 0} (4+h) = 4. \] We call this dofferentiation from first principles.
Here is a video about differentiation that you might find interesting:

3.1.1 The cultural heritage of mathematics

3.1.2 Test yourself

3.2 Newton’s method for solving non-linear equations

Solution of non-linear equations is one of the most important applications of mathematics. These are used to optimise complicated processes. The set up of the equation is usually of the form \(f(x)=0\) in some interval \([a,b]\) where we know that \(f(a)f(b)<0\) (i.e. the sign of the function changes in the interval).

Root of a equation
In order to be sure that there is number at the point where the graph crosses the axis we must assume:
  • The real axis is a continuum;
  • The function is continuous (cannot suddenly jump);
  • The Intermediate Value Theorem holds.

We will not deal with these issues here, but these will be looked at more carefully next semester. However, you should be aware that we are assuming things when we solve equations.

Example 3.2 We want to construct a box whose base length is 3 times the base width. The material used to build the top and bottom cost \(10\) pounds per square metre and the material used to build the sides cost \(6\) pounds per square metre. If the box must have a volume of \(5 {\rm m}^3\) determine the dimensions that will minimize the cost to build the box.

The box is made up of a base and a lid, plus four sides. Two of the sides are length times height and two are width times height. If \(w\) is the width, \(l\) is the length and \(h\) is the height, we have \(l=3w\). The volume is \(lwh=5\), so that \(h=5/(lw)=5/(3w^2)\). Hence the cost of the box \[ C(w)=2lw \times 10 + 2lh \times 6 + 2 wh \times 6 = 60w^2+{80 \over w}. \] To find when this is a minimum we must differentiate and solve \[ C'(w)=120w-{80 \over w^2}=0. \]

We will get back to solving this later.

Newton’s method finds the root of a nonlinear equation (like \(x^2-2=0\)) by pretending that the function is a straight line (if we are ant it is true), and finding the root of the linear equation. This gives a better guess than before. Then we repeat this, in other words, iterate.

The following image is from (https://www.math24.net/newtons-method/) and you can get a number of examples there to practice. In the image you can see the first guess \(x_0\). Then we construct the (green) tangent at \((x_0,f(x_0))\). The interesection of this line with the \(x\)-axis is \(x_1\). We then construct the (red) tangent at \((x_1,f(x_1))\). The intersection of this line with the \(x\)-axis is \(x_2\). Rinse and repeat. YOu can see we get closer and closer to the intersection of the function with the \(x\)-axis.

Newton’s Method

Here is a webpage where you can see this iteration process happening, and try to solve your own equations.

(https://www.intmath.com/applications-differentiation/newtons-method-interactive.php)

In order to implement the idea we need to work out the equation of the tangent line to a curve at a point.

For Newton’s method we find where the tangent cuts the \(x\)-axis and use this as a next guess. Hence we solve \[ y=f(a)+(x-a)f'(a)=0, \] so that \[ x=a-{f(a) \over f'(a)}. \]

Thus we have the equation for Newton’s iteration \[ x_{n+1}=x_n-{f(x_n) \over f'(x_n)}. \tag{3.1} \]

To implement Newton’s Method we:
  1. Choose a starting guess \(x_0\) and a tolerance \(\epsilon\). The tolerance is the number which tells us what error we are happy with;
  2. Iterate \[ x_{n+1}=x_n-{f(x_n) \over f'(x_n)}; \]
  3. Stop if either \(|f(x_{n+1})|<\epsilon\) or \(|x_{n+1}-x_n|<\epsilon\) (the choice is yours).

Here are some animations demonstrating Newton’s method

(http://mathfaculty.fullerton.edu/mathews/a2001/Animations/RootFinding/NewtonMethod/NewtonMethod.html)

Example 3.3 Find the cube root of 9.

To do this we need to solve the equation \(x^3-9=0\). We will use Newton’s iteration . We have \[ f'(x)=3x^2. \] Hence the iteration is \[ x_{n+1}=x_n-{x_n^3-9 \over 3x_n^2}. \] Let us start with \(x_0=2\) because we know that this is the cube root of 8, which is not far away. Then \[\begin{eqnarray*} x_1 & = & x_0-{x_0^3-9 \over 3x_0^2} = 2-{-1 \over 12} = 2.080088888888889.\\ x_2 & = & x_1-{x_1^3-9 \over 3x_1^2} = 2.080083823064241.\\ x_3 & = & x_2-{x_2^3-9 \over 3x_2^2} = 2.080083823051904.\\ x_4 & = & x_3-{x_3^3-9 \over 3x_3^2} = 2.080083823051904. \end{eqnarray*}\]

Here is some R code which does the heavy lifting for you in this iteration. Of course you can change the code to solve any equation you like.

fun = function(x){
  x^3-9
}

dfun=function(x){
  3*x^2
}

options(digits=12) # Print answers to 12 digits

epsilon <- 10^{-10} # Terminate the iteration when the difference is less than epsilon

xold <- 2 # Starting point

xnew <- xold-fun(xold)/dfun(xold) # first Newton iteration

print(xnew) # write the answer to the screen
## [1] 2.08333333333
while (abs(xnew-xold) > epsilon){
  
  xold <- xnew # use the new point for the next iteration
  
  xnew<-xold-fun(xold)/dfun(xold) # Newton iteration
  
  print(xnew) # write the answer to the screen with 12 decimal places
}
## [1] 2.08008888889
## [1] 2.08008382306
## [1] 2.08008382305
cat("Solution is", xnew) # print answer with a comment in front of it
## Solution is 2.08008382305
Remark. The sequence above is another example of a Cauchy sequence as the distance between consecutive numbers in the sequence is getting smaller and smaller. How much smaller are the errors getting? One of the questions we will return to is how to prove what we observe here.
Example 3.4 Adapt the code above to solve the equation from Example 3.2.


3.2.1 Test yourself

Now check that you understand Newton iteration.







3.3 Properties of the derivative

You are all accustomed to all of the standard properties of the derivative, so we are not going to prove any of these here. You did them in A level. Here is a webpage with all of the appropriate properties.

Here are the properties you need for the moment.

Theorem 3.2 (Properties of differentiation) Let \(f\) and \(g\) be differentiable functions. Then if \(\alpha, \beta \in {\mathbb R}\), \(\alpha f+\beta g\) and \(fg\), are differentiable, and \(f/g\) is at all points \(x\) with \(g(x) \neq 0\). Furthermore,

  • \((\alpha f+\beta g)'=\alpha f'+ \beta g'\);
  • \((fg)'=f'g+fg'\);
  • \((f/g)' = (f'g-fg')/g^2\) at all points \(x\) where \(g(x) \neq 0\);
  • \((f(g))'= f'(g) g'\) (chain rule).

3.4 The fundamental theorem of calculus

The reason that you were shown integration from first principles first is that it is a process independent of differentiation. It is often taught as antidifferentiation, but the fact that this is true is one of the great theorems of mathematics. This explains the conundrum presented to you in your induction pack

Why is the derivative of the area of a circle its circumference?

Here is a picture to explain.

Two circles

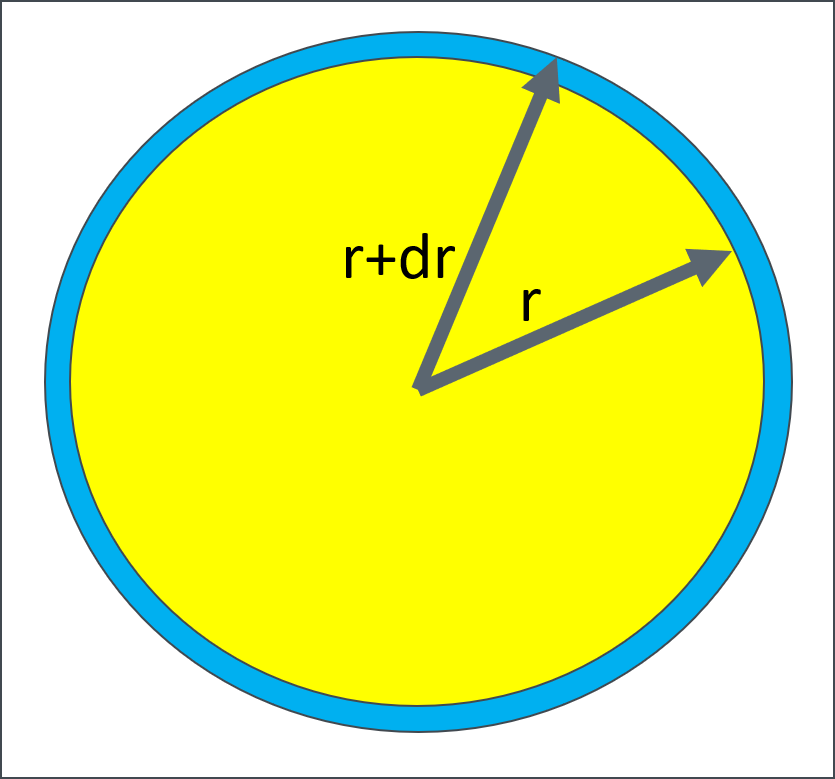
In the picture let \(A(r)\) be the area of a circle of radius \(r\). Then underneath the yellow circle is a blue circle of radius \(r+dr\) with area \(A(r+dr)\). The difference between these two areas can be unwrapped into a rectangle of length \(c(r)\), the circumference of the circle of radius \(r\), and \(dr\) the extra width of the larger circle. Hence \[ {A(r+dr)-A(r)} \approx c(r) dr, \] so that \[ c(r) = {A(r+dr)-A(r) \over dr}, \] which gets to be a better approximation as \(dr \rightarrow 0\).

We are going to use the idea of integral as the area under a curve. So suppose \[ F(x) = \int_a^x f(t) dt. \]

Fundamental theorem of calculus 1

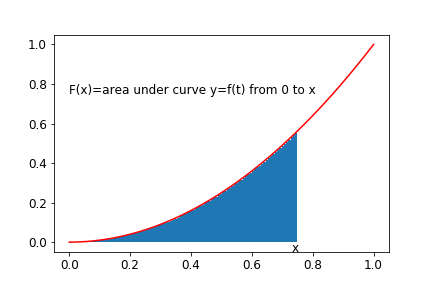
Then \[ F(x+h) = \int_a^x f(t) dt; \] see the figure below.

Fundamental theorem of calculus 2

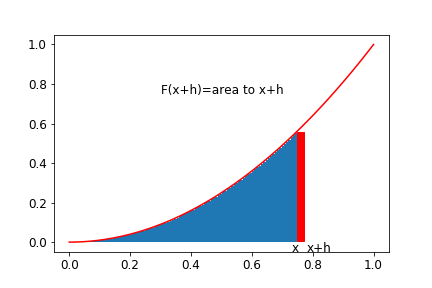
The difference in the areas is the red rectangle which has height \(f(x)\) and width \(h\). Hence \[ F(x+h)-F(x) \approx h f(x), \] so that \[ {F(x+h)-F(x) \over h} \approx f(x). \] As \(h\), the width of the red rectangle , gets smaller the rectangle gets to be a better and better approximation to the actual area under the curve. Thus \[ \lim_{h \rightarrow 0} {F(x+h)-F(x) \over h} \approx f(x). \]

Theorem 3.3 (The fundamental theorem of calculus) Let \(a \in {\mathbb R}\) and \(x>a\). Let \[ F(x)= \int_a^x f(t) dt. \] Then \(F'(x)=f(x)\).

This is not a formal proof, but gives the idea of the proof. If you do not understand the idea, then you will never be able to understand the formal proof. Mathematical analysis is the tool by which we justify all the arm waving arguments I made above. We call this being rigorous.

3.4.1 Test yourself

Check that you understand the fundamental theorem of calculus with these examples.







3.5 Properties of integration

Now that we know that integration is the inverse operation to differentiation, we can use the rules of differentiation to make rules for integration.

Theorem 3.4 (Properties of integration) Let \(f\) and \(g\) be differentiable functions. Then if \(\alpha, \beta \in {\mathbb R}\),

  • \(\int (\alpha f+\beta g) =\alpha \int f + \beta \int g\);
  • \(\int f'g = fg-\int fg'\) (integration by parts);
  • \(\int f(g(x))g'(x) dx = \int f(y) dy\), where \(y=g(x)\) (integration by substitution).

3.6 Challenge yourself

  1. Compute the derivative of \(f(x)=x^n\) from first principles.
  2. Which functions can you differentiate from first principles. For instance try to differentiate \(\exp(x), \log(x), \sin(x), \cos(x)\) for instance and see what you would need to know in order to do this. We will look at this more closely next semester.
  3. Look on line to find out how the error when using Newton’s Method behaves. If at the current estimate you have one digit correct, how many iterations will it take to get 10 digits correct?
  4. What could go wrong with Newton’s Method. Can you think of a way of getting around the problems?
  5. Can you think of a method where you approximate the function with a quadratic instead of a straight line. Can you try this out?
  6. What is the history of calculus in Chinese mathematics?
  7. Explain why you think that if \(F'(x)=f(x)\), then \[ \int_a^b f(x) dx = F(b)-F(a). \]