3 Block Relaxation
3.1 Introduction
The history of block relaxation methods is complicated, because many special cases were proposed before the general idea became clear. I make no claim here to be even remotely complete, but I will try to mention at least most of the general papers that were important along the way.
It makes sense to distinguish the coordinate descent methods from the more general block methods. Coordinate descent methods have the major advantage that they lead to one-dimensional optimization problems, which are generally much easier to handle than multidimensional ones.
We start our history with iterative methods for linear systems. Even there the history is complicated, but it has been ably reviewed by, among others, Forsythe (1953), Young (1990), Saad and Van der Vorst (2000), Benzi (2009), and Axelsson (2010). The origins are in 19th century German mathematics, starting perhaps with a letter from Gauss to his student Gerling on December 26, 1823. See Forsythe (1950) for a translation. To quote Gauss: “I recommend this method to you for imitation. You will hardly ever again eliminate directly, at least not when you have more than 2 unknowns. The indirect procedure can be done while half asleep, or while thinking about other things.” For discussion of subsequent contributions by Jacobi (1845), Seidel (1874), Von Mises and Pollackzek-Geiringer (1929), we refer to the excellent historical overviews mentioned before, and to the monumental textbooks by Varga (1962) and Young (1971).
The next step in our history is the quadratic programming method proposed by Hildreth (1957). Coordinate descent is applied to the dual program, which is a simple quadratic problem with non-negativity constraints, originating from the Lagrange multipliers for the primal problem. Because the constraints are separable in the dual problem the technique can easily handle a large numbers of inequality constraints and can easily be parallelized. Hildreth already considered the non-cyclic greedy and random versions of coordinate descent. A nice historical overview of Hildreth’s method and its various extensions is in Dax (2003).
Coordinate relaxation for convex functions, not necessarily quadratic, was introduced by D’Esopo (1959). in an important paper, followed by influential papers of Schechter (1962), Schechter (1968), Schechter (1970). The D’Esopo paper actually has an early version of Zangwill’s general convergence theory, applied to functions that are convex in each variable separably are are minimized under separable bound constraints.
Ortega and Rheinboldt (1967), Ortega and Rheinboldt (1970b), Elkin (1968), Céa (1968), Céa (1970), Céa and Glowinski (1973), Auslender (1970), Auslender (1971), Martinet and Auslender (1974) Many of these papers present the method as a nonlinear generalization of the Gauss-Seidel method of solving a system of linear equations.
Modern papers on block-relaxation are by Abatzoglou and O’Donnell (1982) and by Bezdek et al. (1987).
So many more now Spall (2012), Beck and Tetruashvili (1913), Saha and Tewari (2013), Wright (2015)
In Statistics .. Statistical applications to mixed linear models, with the parameters describing the mean structure collected in one block and the parameters describing the dispersion collected in the second block, are in Oberhofer and Kmenta (1974). Applications to exponential family likelihood functions, cycling over the canonical parameters, are in Jensen, Johansen, and Lauritzen (1991). Applications in lasso etc.
3.2 Definition
Block relaxation methods are fixed point methods. A brief general introduction to fixed point methods, with some of the terminology we will use, is in the fixed point section 15.5 of the background chapter.
Let us thus consider the following general situation. We minimize a real-valued function \(f\) defined on the product-set \(\mathcal{X}=\mathcal{X}_1\otimes\mathcal{X}_2\otimes\cdots\otimes\mathcal{X}_p,\) where \(\mathcal{X}_s\subseteq\mathbb{R}^{n_s}.\)
In order to minimize \(f\) over \(\mathcal{X}\) we use the following iterative algorithm. \[ \begin{matrix} \text{Starter:}&\text{Start with } x^{(0)}\in\mathcal{X}.\\ \hline \text{Step k.1:}&x^{(k+1)}_1\in\underset{x_1\in\mathcal{X}_1}{\mathrm{argmin}} \ f(x_1,x^{(k)}_2,\cdots,x^{(k)}_p). \\ \text{Step k.2:}&x^{(k+1)}_2\in\underset{x_2\in\mathcal{X}_2}{\mathrm{argmin}} \ f(x^{(k+1)}_1,x_2,x^{(k)}_3,\cdots, x^{(k)}_p). \\ \cdots&\cdots\\ \text{Step k.p:}&x^{(k+1)}_p\in\underset{x_p\in\mathcal{X}_p}{\mathrm{argmin}} \ f(x^{(k+1)}_1,\cdots,x^{(k+1)}_{p-1}, x_p).\\ \hline \text{Motor:}&k\leftarrow k+1 \text{ and go to } k.1 \\ \hline \end{matrix} \]
Observe that we assume that the minima in the substeps exist, but they need not be unique. The \(\mathrm{argmin}\)’s are point-to-set maps, although in many cases they map to singletons. In actual computations we will always have to make a selection from the \(\mathrm{argmin}\).
We set \(x^{(k)}:=(x^{(k)}_1,\cdots,x^{(k)}_p),\) and \(f^{(k)}:=f(x^{(k)}).\) The map \(\mathcal{A}\) that is the composition of the \(p\) substeps on an iteration satisfies \(x^{(k+1)}\in\mathcal{A}(x^{(k)})\). We call it the iteration map (or the algorithmic map or update map). If \(\mathcal{A}(x)\) is a singleton for all \(x\in\mathcal{X}\), then we can write \(x^{(k+1)}=\mathcal{A}(x^{(k)})\) without danger of confusion, and call \(\mathcal{A}\) the iteration function.
If \(\mathcal{A}\) is differentiable on \(\mathcal{X}\) then we introduce some extra terminology and notation. The matrix \(\mathcal{M}(x):=\mathcal{DA}(x)\) of partial derivatives is called the Iteration Jacobian and its spectral radius \(\rho(x):=\rho(\mathcal{DA}(x))\), the eigenvalue of maximum modulus, is called the Iteration Spectral Radius or simply the Iteration Rate. Note that for a linear iteration \(x^{(k+1)}=Ax^{(k)}+b\) we have \(\mathcal{M}(x)=A\) and \(\rho(x)=\rho(A)\).
The function blockRelax() in Code Segment 1 is a reasonable general R function for unrestricted block relation in which each \(\mathcal{X}_s\) is all of \(\mathbb{R}^{n_s}\). The arguments are the function to be minimized, the initial estimate, and the block structure. Both the initial estimate and the block structure are of length \(n=\sum n_s\), and block structure is indicated by two elements having the same integer value if and only if they are in the same block. Each of the subproblems is solved by a call to the optim() function in R.
3.3 First Examples
Our first examples of block relaxation are linear least squares examples. There are obviously historical reasons to choose linear least squares, and in a sense they provide the simplest examples that allow us to illustrate various important calculations and results.
3.3.1 Two-block Least Squares
Suppose we have a linear least squares problems with two sets of predictors \(A_1\) and \(A_2,\) and outcome vector \(b\). Matrices \(A_1\) and \(A_2\) are \(m\times n_1\) and \(m\times n_2\), and the vector of regressions coefficients \(x=(x_1\mid x_2)\) is of length \(n=n_1+n_2.\) Without loss of generality we assume \(n_1\leq n_2\).
Minimizing \(f(x)=(b-A_1x_1-A_2x_2)'(b-A_1x_1-A_2x_2)\) is then conveniently done by block relaxation, alternating the two steps \begin{align*} x_1^{(k+1)}&=A_1^+(b-A_2x_2^{(k)}),\\ x_2^{(k+1)}&=A_2^+(b-A_1x_1^{(k+1)}). \end{align*}Here \(A_1^+\) and \(A_2^+\) are Moore-Penrose inverses.
Define \begin{align*} c&:=A_1^+b,\\ d&:=A_2^+b,\\ R&:=A_1^+A_2^{\ },\\ S&:=A_2^+A_1^{\ }. \end{align*} Then the iterations are \begin{align*} x_1^{(k+1)}&=c-Rx_2^{(k)},\\ x_2^{(k+1)}&=d-Sx_1^{(k+1)}. \end{align*} A solution \((\hat x_1,\hat x_2)\) of the least squares problem satisfies \begin{align*} \hat x_1&=c-R\hat x_2,\\ \hat x_2&=d-S\hat x_1, \end{align*} and thus \begin{align*} (x_1^{(k+1)}-\hat x_1)&=R(x_2^{(k)}-\hat x_2),\\ (x_2^{(k+1)}-\hat x_2)&=S(x_1^{(k+1)}-\hat x_1), \end{align*} and \begin{align*} (x_2^{(k+1)}-\hat x_2)&=SR(x_2^{(k)}-\hat x_2),\\ (x_1^{(k+1)}-\hat x_1)&=RS(x_1^{(k)}-\hat x_1). \end{align*} The matrices \(SR=A_2^+A_1^{\ }A_1^+A_2^{\ }\) and \(RS=A_1^+A_2^{\ }A_2^+A_1^{\ }\) have the same eigenvalues \(\lambda_s\), equal to \(\rho_s^2\), the squares of the canonical correlations of \(A_1\) and \(A_2\). Consequently \(0\leq\lambda_s\leq 1\) for all \(s\). Specifically there exists a non-singular \(K\) of order \(n_1\) and a non-singular \(L\) of order \(n_2\) such that \begin{align*} K'A_1'A_1^{\ }K&=I_1,\\ L'A_2'A_2^{\ }L&=I_2,\\ K'A_1'A_2^{\ }L&=D. \end{align*}Here \(I_1\) and \(I_2\) are diagonal, with the \(n_1\) and \(n_2\) leading diagonal elements equal to one and all other elements zero. \(D\) is a matrix with the non-zero canonical correlations in non-increasing order along the diagonal and zeroes everywhere else. This implies \(R=KDL^{-1}\) and \(S=LD'K^{-1}\), and consequently \(RS=KDD'K^{-1}\) and \(SR=LD'DL^{-1}\).
Let us look at the convergence speed of the \(x_1^{(k)}\). The results for \(x_2^{(k)}\) will be basically the same. Define \[ \delta^{(k)}\mathop{=}\limits^{\Delta}K^{-1}(x_1^{(k)}-\hat x_1^{\ }) \] It follows, using \(RS=KDD'K^{-1}\), that \(\delta^{(k)}=\Lambda^k\delta^{(0)}\), with the squared canonical correlations on the diagonal of \(\Lambda=DD'.\) If \(\lambda_+:=\max_i\lambda_i>0\) and \(\mathcal{I}=\left\{i\mid\lambda_i=\lambda_+\right\}\) then \[ \frac{\delta^{(k)}_i}{\lambda_+^k}\rightarrow\begin{cases} \delta^{(0)}_i&\text{ if }i\in\mathcal{I},\\ 0&\text{ otherwise} \end{cases} \] and thus \[ \frac{\|\delta^{(k+1)}\|}{\|\delta^{(k)}\|}\rightarrow\lambda^+. \] This implies \[ \frac{\|x_1^{(k)}-\hat x_1^{\ }\|}{\lambda^k}\rightarrow\|\sum_{i\in\mathcal{I}}\delta_i^{(0)}k_i^{\ }\| \] where the \(k_i\) are columns of \(K\). In turn this implies \[ \frac{\|x_1^{(k+1)}-\hat x_1^{\ }\|}{\|x_1^{(k)}-\hat x_1^{\ }\|}\rightarrow\lambda. \]
3.3.2 Multiple-block Least Squares
Now suppose there are multiple blocks. We minimize the loss function \begin{equation} f(x)=\mathbf{SSQ}(b-\sum_{j=1}^m A_jx_j). \end{equation}Block relaxation in this case is Gauss-Seidel iteration.
The update formula for the Gauss-Seidel method is \[ \beta_j^{(k+1)}=X_j'\left(y-\sum_{\ell=1}^{j-1}X_\ell^{\ }\beta_\ell^{(k+1)}-\sum_{\ell=j+1}^{m}X_\ell^{\ }\beta_\ell^{(k)}\right). \] Define \(C_L\) to be the block triangular matrix with the blocks \(X_j'X_\ell^{\ }\) with \(j>\ell\) of \(C\) below the diagonal, and \(C_U\) the block triangular matrix with the upper diagonal blocks \(X_j'X_\ell^{\ }\) with \(j<\ell\). Thus \(C_L+C_U+I=C\) and \(C_L=C_U'\). Now \[ \beta^{(k+1)}=X'y-C_L\beta^{(k+1)}-C_U\beta^{(k)}, \] and thus \[ \beta^{(k+1)}=(I+C_L)^{-1}X'y-(I+C_L)^{-1}C_U\beta^{(k)}. \] The least squares estimate \(\hat\beta\) satisfies \[ \hat\beta=(I+C_L)^{-1}X'y-(I+C_L)^{-1}C_U\hat\beta, \] and thus \[ \beta^{(k+1)}-\hat\beta=-(I+C_L)^{-1}C_U(\beta^{(k)}-\hat\beta), \] or \[ \beta^{(k)}-\hat\beta=\left[-(I+C_L)^{-1}C_U\right]^k(\beta^{(0)}-\hat\beta). \]
Code in Code Segment 2.
3.4 Generalized Block Relaxation
In some cases, even the supposedly simple minimizations within blocks may not have very simple solutions. In that case, we often use generalized block relaxation, which is defined by \(p\) maps \(\mathcal{A}_s\) mapping \(\mathcal{X}\) into (subsets of) \(\mathcal{X}\). We have \[ \mathcal{A}_s(x)\in\{x_1\}\otimes\cdots\otimes\{x_{s-1}\}\otimes\mathcal{F}_s(x)\otimes\{x_{s+1}\}\otimes\cdots\otimes\{x_p\}, \] where \(z\in\mathcal{F}_s(x\)$ implies \[ f(x_1,\cdots,x_{s-1},z,x_{s+1},\cdots,x_p)\leq f(x_1,\cdots,x_{s-1},x_s,x_{s+1},\cdots,x_p). \]
In ordinary block relaxation \[ \mathcal{F}_s(x)=\mathop{\mathbf{argmin}}\limits_{z\in\mathcal{X}_s} f(x_1,\cdots,x_{s-1},z,x_{s+1},\cdots,x_p), \] but in generalized block relaxation we could update \(x_s\) by taking one or more steps of a stable and convergent iterative algorithm for minimizing \(f(x_1,\cdots,x_{s-1},z,x_{s+1},\cdots,x_p)\) over \(z\in\mathcal{X}_s\).
3.4.1 Rasch Model
In the item analysis model proposed by Rasch, we observe a binary \(n\times m\) matrix \(Y=\{y_{ij}\}\). The (unconditional) log-likelihood is \[ \mathcal{L}(x,z)=\sum_{i=1}^n\sum_{j=1}^m y_{ij}\log\pi_{ij}(x,z)+(1-y_{ij})\log(1-\pi_{ij}(x,z)), \] with \[ \pi_{ij}(x,z)=\frac{\exp(x_i+z_j)}{1+\exp(x_i+z_j)}. \]
The negative log-likelihood can be written as \[ f(x,z)=\sum_{i=1}^n\sum_{j=1}^m\log\{1+\exp(x_i+z_j)\} -\sum_{i=1}^n y_{i\star}x_i-\sum_{j=1}^m y_{\star j}z_j, \] where \(\star\) indicates summation over an index. The stationary equations have the elegant form \begin{align*} \pi_{i\star}(x,z)&=y_{i\star}\\ \pi_{\star j}(x,z)&=y_{\star j}. \end{align*}The standard algorithm for the unconditional maximum likelihood problem (Wainer, Morgan, and Gustafsson (1980)) cycles through these two blocks of equations, using Newton’s method at each substep. In this case Newton’s method turns out to be \[ x_i^{(k+1)}=x_i^{(k)}-\frac{\pi_{i\star}(x^{(k)},z^{(k)})-y_{i\star}} {\sum_{j=1}^m{\pi_{ij}(x^{(k)},z^{(k)})(1-\pi_{ij}(x^{(k)},z^{(k)}))}}, \] and similarly for \(z_j^{(k+1)}.\)
3.4.2 Nonlinear Least Squares
Consider the problem of minimizing \[ \sum_{i=1}^n (y_i-\sum_{j=1}^m \phi_j(x_i,\theta)\beta_j)^2, \] with the \(\phi_j\) known nonlinear functions.
Again the parameters separate naturally into two blocks \(\beta\) and \(\theta\), and finding the optimal \(\beta\) for given \(\theta\) is again linear regression.
The best way of finding the optimal \(\theta\) for given \(\beta\) will typically depend on a more precise analysis of the problem, but one obvious alternative is to linearize the \(\phi_j\) and apply Gauss-Newton.
3.5 Block Order
If there are more than two blocks, we can move through them in different ways. In analogy with linear methods such as Gauss-Seidel and Gauss-Jacobi, we distinguish cyclic and free-steering methods. We could select the block, for instance, that seems most in need of improvement. This is the greedy choice. We can pivot through the blocks in order, and start again when all blocks have been visited. Or we could go back in the reverse order after arriving at the last block. We can even choose blocks in random order, or use some other chaotic strategy.
We emphasize, however, that the methods we consider are all of the Gauss-Seidel type, i.e. as soon as we upgrade a block we use the new values in subsequent computations. We do not consider Gauss-Jordan type strategies, in which all blocks are updated independently, and then all blocks are replaced simultaneously. The latter strategy leads to fewer computations per cycle, but it will generally violate the monotonicity requirement for the loss function values.
We now give a formalization of these generalizations, due to Fiorot and Huard (1979) Suppose \(\Delta_s\) are \(p\) point-to-set mappings of \(\Omega\) into \(\mathcal{P}(\Omega),\) the set of all subsets of \(\Omega.\) We suppose that \(\omega\in\Delta_s(\omega)\) for all \(s=1,\cdots,p.\) Also define \[ \Gamma_s(\omega)\mathop{=}\limits^{\Delta}\hbox{argmin} \{\psi(\overline\omega)\mid\overline\omega\in\Delta_s(\omega)\}. \] There are now two versions of the generalized block-relaxation method which are interesting.
In the free-steering version we set \[ \omega^{(k+1)}\in\cup_{s=1}^p\Gamma_s(\omega^{(k)}). \] This means that we select, from the \(p\) subsets defining the possible updates, one single update before we go to the next cycle of updates.
In the cyclic method we set \[ \omega^{(k+1)}\in\otimes_{s=1}^p\Gamma_s(\omega^{(k)}). \] In a little bit more detail this means \begin{align*} \omega^{(k,0)}&=\omega^{(k)},\\ \omega^{(k,1)}&\in\Gamma_s(\omega^{(k,0)}),\\ \cdots&\in\cdots,\\ \omega^{(k,p)}&\in\Gamma_s(\omega^{(k,p-1)}),\\ \omega^{(k+1)}&=\omega^{(k,p)}. \end{align*}Since \(\omega\in\Delta_s(\omega),\) we see that, for both methods, if \(\xi\in\Gamma(\omega)\) then \(\psi(\xi)\leq\psi(\omega).\) This implies that Theorem continues to apply to this generalized block relaxation method.
A simple example of the \(\Delta_s\) is the following. Suppose the \(G_s\) are arbitrary mappings defined on \(\Omega.\) They need not even be real-valued. Then we can set \[ \Delta_s(\omega)\mathop{=}\limits^{\Delta}\{\xi\in\Omega\mid G_s(\xi)=G_s(\omega)\}. \] Obviously \(\omega\in\Delta_s(\omega)\) for this choice of \(\Delta_s.\)
There are some interesting special cases. If \(G_s\) projects on a subspace of \(\Omega,\) then \(\Delta(\omega)\) is the set of all \(\xi\) which project into the same point as \(\omega.\) By defining the subspaces using blocks of coordinates, we recover the usual block-relaxation method discussed in the previous section. In a statistical context, in combination with the EM algorithm, functional constraints of the form \[ G_s(\overline\omega)=G_s(\omega) \] were used by Meng and Rubin (1993). They call the resulting algorithm the ECM algorithm.
3.5.1 Projecting Blocks
3.6 Rate of Convergence
3.6.1 LU-form
In block relaxation methods, including generalized block methods, we update \(x=(x_1,\cdots,x_n)\) to \(y=(y_1,\cdots,y_n)\) by the rule \[ y_s=F_s(y_1,\cdots,y_{s-1},x_s,x_{s+1},\cdots,x_n). \] Differentiation gives \[ \mathcal{D}_ty_s= \sum_{u<s}(\mathcal{D}_uF_s)(\mathcal{D}_ty_u)+ \begin{cases}0&\text{ if }t<s,\\ \mathcal{D}_tF_s&\text{ if }t\geq s. \end{cases}.\tag{1} \] It should be emphasized that in many cases of interest in \(F_s\) does not depend on \(x_s,\) so that \(\mathcal{D}_sF_s=0\) for all \(s\). It is also important to realize that the derivatives, which we write without arguments in this section, are generally evaluated at points of the form \((y_1,\cdots,y_{s-1},x_s,\cdots,x_p)\). At fixed points, however, \(x_s=y_s\) for all \(s\), and we can just write \(\mathcal{D}_ty_s\) without ambiguity. And for our purposes the derivatives at fixed points are the interesting ones.
Now define \[ \mathcal{M}\mathop{=}\limits^{\Delta} \begin{bmatrix} \mathcal{D}_1y_1&\mathcal{D}_2y_1&\cdots&\mathcal{D}_ny_1\\ \mathcal{D}_1y_2&\mathcal{D}_2y_2&\cdots&\mathcal{D}_ny_2\\ \vdots&\vdots&\ddots&\vdots\\ \mathcal{D}_1y_n&\mathcal{D}_2y_n&\cdots&\mathcal{D}_ny_n\\ \end{bmatrix}, \] and \[ \mathcal{N}\mathop{=}\limits^{\Delta} \begin{bmatrix} \mathcal{D}_1F_1&\mathcal{D}_2F_1&\cdots&\mathcal{D}_nF_1\\ \mathcal{D}_1F_2&\mathcal{D}_2F_2&\cdots&\mathcal{D}_nF_2\\ \vdots&\vdots&\ddots&\vdots\\ \mathcal{D}_1F_n&\mathcal{D}_2F_n&\cdots&\mathcal{D}_nF_n\\ \end{bmatrix}. \] Also \[ \mathcal{N}_L\mathop{=}\limits^{\Delta} \begin{bmatrix} 0&0&\cdots&0\\ \mathcal{D}_1F_2&0&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ \mathcal{D}_1F_n&\mathcal{D}_2F_n&\cdots&0\\ \end{bmatrix}, \] and \[ \mathcal{N}_U\mathop{=}\limits^{\Delta} \begin{bmatrix} \mathcal{D}_1F_1&\mathcal{D}_2F_1&\cdots&\mathcal{D}_nF_1\\ 0&\mathcal{D}_2F_2&\cdots&\mathcal{D}_nF_2\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&\mathcal{D}_nF_n\\ \end{bmatrix}, \] so that \(\mathcal{N}=\mathcal{N}_U+\mathcal{N}_L\). From \((1)\) \[ \mathcal{M}=\mathcal{N}_L\mathcal{M}+\mathcal{N}_U, \] or \[ \mathcal{M}=(I-\mathcal{N}_L)^{-1}\mathcal{N}_U. \] This is the Lower-Upper or LU form of the derivative of the algorithmic map.
For two blocks \(\mathcal{M}\) is equal to \[ \begin{bmatrix} \mathcal{D}_1F_1&\mathcal{D}_2F_1\\ (\mathcal{D}_1F_2)(\mathcal{D}_1F_1)&(\mathcal{D}_1F_2)(\mathcal{D}_2F_1)+\mathcal{D}_2F_2 \end{bmatrix}, \] and if \(\mathcal{D}_1F_1=0\) and \(\mathcal{D}_2F_2=0\) this is \[ \begin{bmatrix} 0&\mathcal{D}_2F_1\\ 0&(\mathcal{D}_1F_2)(\mathcal{D}_2F_1) \end{bmatrix}. \] Thus the non-zero eigenvalues are the eigenvalues of \((\mathcal{D}_1F_2)(\mathcal{D}_2F_1)\).
3.6.2 Product Form
There is another way to derive the formulas from the previous section. We use the fact that the algorithmic map \(\mathcal{A}\) is a composition of the form \[ \mathcal{A}(x)=\mathcal{A}_p(\mathcal{A}_{p-1}(\cdots(\mathcal{A}_1(x))), \] where each \(\mathcal{A}_s\) leaves all blocks, except block \(s\), intact, and changes only the variables in block \(s\), Thus \[ \mathcal{A}_s(x)= \begin{bmatrix} x_1\\\vdots\\x_{s-1}\\F_s(x_1,\cdots,x_p)\\x_{s+1}\\\vdots\\x_{p} \end{bmatrix}. \]
Blocks \((u,v)\) of the matrix of partials is (surpressing the dependence on \(x\) again for the time being) \[ \{\mathcal{DA}_s\}_{uv}\mathop{=}\limits^{\Delta} \begin{cases} \mathcal{D}_vF_u&\text{ if }u=s,\\ I&\text{ if }u=v\not= p,\\ 0&\text{otherwise}. \end{cases} \] Again, in many cases of interest we have \(\{\mathcal{DA}\}_{uv}=0\) if \(u=v=s\).
Now clearly, from the chain rule, \[ \mathcal{M}=\mathcal{DA}=\mathcal{DA}_p\mathcal{DA}_{p-1}\cdots\mathcal{DA}_1 \] This is the product form of the derivative of the algorithmic map.
For two blocks, and zero diagonal blocks, we have, as in the previous section, \[ \mathcal{M}=\mathcal{DA}_2\mathcal{DA}_1=\begin{bmatrix} I&0\\ \mathcal{D}_1F_2&0 \end{bmatrix} \begin{bmatrix} 0&\mathcal{D}_2F_1\\ 0&I \end{bmatrix}= \begin{bmatrix} 0&\mathcal{D}_2F_1\\ 0&\mathcal{D}_1F_2\mathcal{D}_2F_1 \end{bmatrix}. \] Thus the non-zero eigenvalues of \(\mathcal{M}\) are the non-zero eigenvalues of \(\mathcal{D}_1F_2\mathcal{D}_2F_1\).
In the general cases with \(p\) blocks computing eigenvalues of \(\mathcal{M}\) we can use the result that the spectrum of \(A_pA_{p-1}\cdots A_1\) is related in a straightforward fashion to the spectrum of the cyclic matrix \[ \Gamma(A_1,\cdots,A_p)\mathop{=}\limits^{\Delta}\begin{bmatrix} 0&0&\cdots&0&A_p\\ A_1&0&\cdots&0&0\\ 0&A_2&\cdots&0&0\\ \vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&\cdots&A_{p-1}&0 \end{bmatrix}. \] In fact if \(\lambda\) is an eigenvalue of \(\Gamma(A_1,\cdots,A_p)\) then \(\lambda^p\) is an eigenvalue of \(A_pA_{p-1}\cdots A_1\), and if \(\mu\) is a eigenvalue of \(A_pA_{p-1}\cdots A_1\) then the \(p\) solutions of \(\lambda^p=\mu\) are eigenvalues of \(\Gamma(A_1,\cdots,A_p)\).
3.6.3 Block Optimization Methods
The results in the previous two sections were for general block modification methods. We now specialize to block relaxation methods for unconstrained differentiable optimization problems. The rate of convergence of block relaxation algorithms depends on the block structure, and on the matrix of second derivatives of the function \(f\) we are minimizing.
The functions \(F_s\) that update block \(s\) are defined implicitly by \[ \mathcal{D}_sf(x_1,x_2,\cdots,x_p)=0. \] From the implicit function theorem \[ \mathcal{D}_tF_s(x)=-[\mathcal{D}_{ss}f(x)]^{-1}\mathcal{D}_{st}f(x). \] If we use this in the LU-form \(\mathcal{M}=(I-B_L)^{-1}B_U\) we find \[ \mathcal{M}(x)=- \begin{bmatrix} \mathcal{D}_{11}f(x)&0&\cdots&0\\ \mathcal{D}_{21}f(x)&\mathcal{D}_{22}f(x)&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ \mathcal{D}_{p1}f(x)&\mathcal{D}_{p2}f(x)&\cdots&\mathcal{D}_{pp}f(x)\\ \end{bmatrix}^{-1} \begin{bmatrix} 0&\mathcal{D}_{12}f(x)&\cdots&\mathcal{D}_{1p}f(x)\\ 0&0&\cdots&\mathcal{D}_{2p}f(x)\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&0\\ \end{bmatrix}, \]
If there are only two blocks the result simplifies to
\begin{multline*} \mathcal{M}(x)=- \begin{bmatrix} [\mathcal{D}_{11}f(x)]^{-1}&0\\ -[\mathcal{D}_{22}f(x)]^{-1}\mathcal{D}_{21}f(x)^{}[\mathcal{D}_{11}f(x)]^{-1}& [\mathcal{D}_{22}f(x)]^{-1} \end{bmatrix} \begin{bmatrix} 0&\mathcal{D}_{12}f(x)\\ 0&0 \end{bmatrix}=\\ \begin{bmatrix} 0&-[\mathcal{D}_{11}f(x)]^{-1}\mathcal{D}_{12}f(x)^{}\\ 0&[\mathcal{D}_{22}f(x)]^{-1}\mathcal{D}_{21}f^{}(x)[\mathcal{D}_{11}f(x)]^{-1}\mathcal{D}_{12}f(x)^{} \end{bmatrix} \end{multline*}Thus, in a local minimum, where the matrix of second derivatives is non-negative definite, we find that the largest eigenvalue of \(\mathcal{M}(x)\) is like the largest squared canonical correlation \(\rho\) of two sets of variables, and is consequently less than or equal to one.
We also see that a sufficient condition for local convergence to a stationary point of the algorithm is that \(\rho<1.\) This is always true for an isolated local minimum, because there the matrix of second derivatives is positive definite. If \(\mathcal{D}^2f(x)\) is singular at the solution \(x\), we find a canonical correlation equal to \(+1,\) and we do not have guaranteed linear convergence.
For the product form we find that \[ \mathcal{DA}_s(x)=I-E_s[\mathcal{D}_{ss}f(x)]^{-1}E_s'\mathcal{D}^2f(x), \] where \(E_s\) has blocks of zeroes, except for block \(s\), which is the identity. Thus \[ \mathcal{M}(x)=\{I-E_s[\mathcal{D}_{ss}f(x)]^{-1}E_s'\mathcal{D}^2f(x)\}\times\cdots\times \{I-E_1[\mathcal{D}_{11}f(x)]^{-1}E_1'\mathcal{D}^2f(x)\}. \] It follows that \(\mathcal{M}(x)z=z\) for all \(z\) such that \(\mathcal{D}^2f(x)z=0\). Thus \(\rho(\mathcal{M}(z))=1\) whenever \(\mathcal{D}^2f(x)\) is singular.
For two blocks \[ \mathcal{M}(x)=\begin{bmatrix} I&0\\-[\mathcal{D}_{22}f(x)]^{-1}\mathcal{D}_{21}f(x)&0 \end{bmatrix}\begin{bmatrix} 0&-[\mathcal{D}_{11}f(x)]^{-1}\mathcal{D}_{12}f(x)\\0&I, \end{bmatrix} \] which gives the same result as obtained from the LU-form.
The code in blockRate.R in Code Segment 3 computes \(\mathcal{M}(x)\) in one of four ways. We can use the analytical form of the Hessian or compute it numerically, and we can use the LU-form or the product form. If we compute the Hessian numerically we give the function we are minimizing as an argument, if we use the Hessian analytically we pass a function for evaluating it at \(x\).
3.6.4 Block Newton Methods
In block Newton methods we update using \[ y_s=x_s-[\mathcal{D}_{ss}f(y_1,\cdots,y_{s-1},x_s,\dots,x_p)]^{-1}\mathcal{D}_{s}f(y_1,\cdots,y_{s-1},x_s,\dots,x_p) \] It follows that at a point \(x\) where the derivatives vanish we have \[ \mathcal{D}_tF_s(x)=\delta^{st}I-[\mathcal{D}_{ss}f(x)]^{-1}\mathcal{D}_{st}f(x) \] and in particular \(\mathcal{D}_sF_s(x)=0\). The iteration matrix \(\mathcal{M}(x)\) is the same as the one in section 3.6.3, and consequently the convergence rate is the same as well. We will again have the same rate if we make more than one Newton step in each block update.
Of course the single-step block Newton method does not guarantee decrease of the loss function, and consequently needs to be safeguarded in some way.
3.6.5 Constrained Problems
Similar calculations can also be carried out in the case of constrained optimization, i.e. when the subproblems optimize over differentiable manifolds and/or convex sets. We then use the implicit function calculations on the Langrangean or Kuhn-Tucker conditions, which makes them a bit more complicated, but essentially the same. In the manifold case, for example, it suffices to replace the matrices \(\mathcal{D}_{pq}\) by the matrices \(H_p'\mathcal{D}_{pq}H_{q},\) where the matrices \(H_p\) contain a local linear coordinate system for \(\Omega_p\) near the solution.In this note we look at the special case in which \(f\) is differentiable, and the \(\mathcal{X}_s\) are of the form \[ \mathcal{X}_s=\{x\in\mathbb{R}^{n_s}\mid G_s(x)=0\} \] for some differentiable vector-valued \(G_s\).
The algorithm shows that the update \(y_s\) of block \(s\) is defined implicitly in terms of \(y_1,\cdots,y_{s-1}\) and \(x_{s+1},\cdots,x_p\) by the equations \[ \mathbf{D}_sf(y_1,\cdots,y_s,x_{s+1},\cdots,x_p)-\mathbf{D}G_s(y_s)\lambda_s=0, \] and \[ G_s(y_s)=0. \] The equations also implicitly define the vector \(\lambda_s\) of Lagrange multipliers.
Let us differentiate this again with respect to \(x\). Define \begin{align*} H_{sr}&=\mathcal{D}_{sr}^2f,\\ U_{sr}&=\mathcal{D}_{r}y_s,\\ V_{sr}&=\mathcal{D}_{r}\lambda_s, \end{align*}as well as \[ W_s(\lambda)=\sum_{r=1} \lambda_r\mathcal{D}^2g_{sr} \] and \[ E_s=\mathcal{D}G_s. \] From the first set of equations we find for all \(r>1\) \[ \begin{bmatrix} H_{11}-W_1(\lambda)& -E_1\\ E_1 &0 \end{bmatrix} \begin{bmatrix} U_{1r}\\ V_{1r} \end{bmatrix} = \begin{bmatrix}-H_{1r}\\ 0 \end{bmatrix}. \] which can easily be solved for \(U_{1r}\) and \(V_{1r}\).
3.7 Additional Examples
3.7.1 Canonical Correlation
Canonical Correlation is a matrix problem in which the notion of blocks of variables is especially natural. The problem can be formulated in various ways, but we prefer a least squares formulation. We want to minimize \[\sigma(A,B)\mathop{=}\limits^{\Delta}\mathbf{tr }\ (XA-ZB)'(XA-ZB)\] over \(A\) and \(B.\) In order to avoid boring complications which merely lead to more elaborate notations we again suppose that \(X'X=I\) and \(Z'Z=I\).
Note that this problem is basically a multivariate version of the block least squares problem with \(Y=0\) in the previous example. There are some crucial differences, however. The fact that \(Y=0\) means that \(A=B=0\) trivially minimizes \(\sigma\). Thus we need to impose some normalization condition such as \(A'A=I\) and/or \(B'B=I\) to exclude this trivial solution. Nevertheless, in our analysis we shall initially proceed without actually using normalization.
Start with \(A^{(0)}\). To find the optimal \(B^{(k)}\) for given \(A^{(k)}\) we compute \(R'A^{(k)}=B^{(k)},\) and then we update \(A\) with \(RB^{(k)}=A^{(k+1)},\) where \(R\mathop{=}\limits^{\Delta}X'Z\), as before. Thus \(A^{(k+1)}=R'RA^{(k)}\) and \(A^{(k)}=(R'R)^kA^{(0)}\). Clearly \(A^{(k)}\rightarrow 0\) if \(R'R\lesssim I\), which implies convergence to the correct, but trivial, solution \(A=B=0\).
Suppose \(R'R=K\Lambda K'\) is the eigen-decomposition and define \(\Delta^{(k)}\mathop{=}\limits^{\Delta}K'A^{(k)}\), so that \(\Delta^{(k)}=\Lambda^k\Delta^{(0)}.\) As in the previous example \[ \frac{\|\Delta^{(k)}\|}{\lambda_+^k}\rightarrow\|\tilde\Delta^{(0)}\|, \] where \(\tilde\Delta^{(0)}\) consists of the columns corresponding with the dominant eigenvalue. Again \[ \frac{\|\Delta^{(k+1)}\|}{\|\Delta^{(k)}\|}\rightarrow\lambda_+. \]
Now consider \[\Xi^{(k)}=A^{(k)}((A^{(k)})'A^{(k)})^{-\frac12}=\Lambda^k\Delta_0(\Delta_0'\Lambda^{2k}\Delta_0)^{-\frac12}\]
3.7.2 Low Rank Approximation
Given an \(n\times m\) matrix \(X\) we want to minimize \[ \sigma(A,B)=\text{tr }(X-AB')'(X-AB') \] over the \(n\times p\) matrices \(A\) and the \(m\times p\) matrices \(B\). In other words, we find the projection of \(X\), in the Frobenius norm, on the set of matrices of rank less than or equal to \(p\).
The block relaxation iterations are \begin{align*} B^{(k+1)}&=X'A^{(k)}((A^{(k)})'A^{(k)})^{-1}\\ A^{(k+1)}&=XB^{(k+1)}((B^{(k+1)})'B^{(k+1)})^{-1}, \end{align*}or \[ A^{(k+1)}=\left[XX'A^{(k)}((A^{(k)})'XX'A^{(k)})^{-1} (A^{(k)})'\right]A^{(k)}. \]
\[ A^{(k)}(B^{(k+1)})'=P_A^{(k)}X, \] \[ A^{(k+1)}(B^{(k+1)})'=XP_B^{(k+1)}, \]
It follows that \((A^{(k)})'(A^{(k+1)}-A^{(k)})=0\) and, thus, for all \(k\) \[ \|A^{(k+1)}-A^{(k)}\|^2=\|A^{(k+1)}\|^2-\|A^{(k)}\|^2\geq 0. \] Thus \(||A^{(k)}||^2\) increases to a limit less than or equal to the upper bound \(\alpha\). Also \[ \sum_{i=1}^k \|A^{(i+1)}-A^{(i)}\|^2=\|A^{(k+1)}\|^2-\|A^{(0)}\|^2\leq\alpha-\|A^{(0)}\|^2, \] and consequently \(\|A^{(i+1)}-A^{(i)}\|\) converges to zero.
Now suppose \(\tilde A^{(k)}=A^{(k)}S\), with \(S\) nonsingular. Then \(\tilde B^{(k+1)}=B^{(k+1)}S^{-t}\), and thus \[ \tilde A^{(k)}(\tilde B^{(k+1)})'=A^{(k)} (B^{(k+1)})'. \] In addition \(\tilde A^{(k+1)}=A^{(k+1)}S\), and thus \[ \tilde A^{(k+1)}(\tilde B^{(k+1)})'=A^{(k+1)} (B^{(k+1)})'. \]
Alternative \begin{align*} B^+&=X'A,\\ A^+&=XB^+((B^+)'B^+)^{-1}=XX'A(A'XX'A)^{-1}, \end{align*}\begin{align*} B^+&=X'A(A'XX'A)^{-\frac12},\\ A^+&=XB^+=XX'A(A'XX'A)^{-\frac12}, \end{align*}\[ A^+(B^+)'=X\{X'A(A'XX'A)^{-1}A'X\} \]
3.7.3 Optimal Scaling with LINEALS
Suppose we have \(m\) categorical variables, where variable \(j\) has \(k_j\) categories. Also suppose \(C_{j\ell}\) are the \(k_j\times k_\ell\) cross tables and \(D_j\) are the diagonal matrices with univariate marginals. Both the \(C_{jl}\) and the \(D_j\) are normalized so they add up to one.
A quantification of variable \(j\) is a \(k_j\) element vector \(y_j\), normalized by \(e'D_jy_j=0\) and \(y_j'D_j^{\ }y_j^{\ }=1\). If we replace the categories of a variable by the corresponding elements of the quantification vector then the correlation between quantified variables \(j\) and \(\ell\) is \[ \rho_{j\ell}(y_1,\cdots,y_m)\mathop{=}\limits^{\Delta}y_j'C_{j\ell}^{\ }y_\ell^{\ }. \] Of course \(\rho_{j\ell}(y_1,\cdots,y_m)=\rho_{\ell j}(y_1,\cdots,y_m)\) for all \(j\) and \(\ell\), and \(\rho_{jj}(y_1,\cdots,y_m)=1\) for all \(j\).
The correlation ratio between variables \(j\) and \(\ell\) is \[ \eta^2_{j\ell}(y_1,\cdots,y_m)\mathop{=}\limits^{\Delta}y_j'C_{jl}^{\ }D_\ell^{-1}C_{\ell j}^{\ }y_j^{\ }. \] In general \(\eta^2_{j\ell}(y_1,\cdots,y_m)\not=\eta^2_{\ell j}(y_1,\cdots,y_m)\), but still \(\eta^2_{jj}(y_1,\cdots,y_m)=1\).
Statistical theory, and the Cauchy-Schwartz inequality, tell us that \begin{align*} \rho_{j\ell}^2(y_1,\cdots,y_m)&\leq \eta_{j\ell}^2(y_1,\cdots,y_m),\\ \rho_{j\ell}^2(y_1,\cdots,y_m)&\leq\eta_{\ell j}^2(y_1,\cdots,y_m), \end{align*} with equality if and only if \begin{align*} C_{\ell j}y_j&=\rho_{j\ell}(y_1,\cdots,y_m)D_\ell y_\ell,\\ C_{j\ell}y_\ell&=\rho_{j\ell}(y_1,\cdots,y_m)D_j y_j, \end{align*}i.e. if and only if the regressions between the quantified variables are both linear.
De Leeuw (1988) has suggested to find standardized quantifications in such a way that the loss function \[
f(y_1,\cdots,y_m)\sum_{j=1}^m\sum_{\ell=1}^m(\eta_{j\ell}^2(y_1,\cdots,y_m)-\rho_{j\ell}^2(y_1,\cdots,y_m))
\] is minimized. Thus we try to find quantifications of the variables that linearize all bivariate regressions. A block relaxation method to do just this is implemented in the lineals function of the R package aspect (Mair and De Leeuw (2010)). In lineals there is the additional option of requiring that the elements of the \(y_j\) are increasing or decreasing.
If we change quantification \(y_j\) while keeping all \(y_\ell\) with \(\ell\not= j\) at their current values, then we have to minimize \[ y_j'\left\{\sum_{\ell\not= j}C_{jl}^{\ }\left[D_\ell^{-1}-y_\ell^{\ }y_\ell'\right]C_{\ell j}^{\ }\right\}y_j^{\ }\tag{1} \] over all \(y_j\) with \(e'D_jy_j=0\) and \(y_j'D_j^{\ }y_j^{\ }=1\). Thus each step in the cycle amounts to finding the eigenvector corresponding with the smallest eigenvalue of the matrix in \(\text{(1)}\).
3.7.4 Multinormal Maximum Likelihood
The negative log-likelihood for a multinormal random sample is \[ f(\theta,\xi)=n\log\mathbf{det}(\Sigma(\theta))+\sum_{i=1}^n (x_i-\mu(\xi))'\Sigma^{-1}(\theta)(x_i-\mu(\xi)). \] The vector of means \(\mu\) depends on the parameters \(\xi\) and the matrix of covariances \(\Sigma\) depends on \(\theta\). We assume the two sets of parameters are separated, in the sense that they do not overlap.
Oberhofer and Kmenta (1974) study this case in detail and give a proof of convergence, which is actually the expected special case of Zangwill’s theorem.
Suppose we have a normal GLM of the form \[ \underline{y}\sim\mathcal{N}[X\beta,\sum_{s=1}^p\theta_s\Sigma_s] \] where the \(\Sigma_s\) are known symmetric matrices. We have to estimate both \(\beta\) and \(\theta,\) perhaps under the constraint that \(\sum_{s=1}^p\theta_s\Sigma_s\) is positive semi-definite.
This can be done, in many case, by block relaxation. Finding the optimal \(\beta\) for given \(\theta\) is just weighted linear regression. Finding the optimal \(\theta\) for given \(\beta\) is more complicated, but the problem has been studied in detail by Anderson and others.
For further reference, we give the derivatives of the log-likelihood function for this problem. \[ \frac{\partial\mathcal{L}}{\partial\theta_s}= \text{tr }\Sigma^{-1}\Sigma_s -\text{tr }\Sigma^{-1}\Sigma_s\Sigma^{-1}S. \] \[ \frac{\partial^2\mathcal{L}}{\partial\theta_s\partial\theta_t}= \text{tr }\Sigma^{-1}\Sigma_s\Sigma^{-1}\Sigma_t\Sigma^{-1}S+ \text{tr }\Sigma^{-1}\Sigma_t\Sigma^{-1}\Sigma_s\Sigma^{-1}S- \text{tr }\Sigma^{-1}\Sigma_s\Sigma^{-1}\Sigma_t. \] Taking expected values in Equation gives \[ \mathbf{E}\left\{\frac{\partial^2\mathcal{L}}{\partial\theta_s\partial\theta_t}\right\}= \text{tr }\Sigma^{-1}\Sigma_s\Sigma^{-1}\Sigma_t. \]
3.7.5 Array Multinormals
3.7.6 Rasch Model
The Rasch example has a rather simple structure for the second derivatives of the negative log-likelihood \(f\) defined in section @(blockrelaxation:generalizedblockrelaxation:raschmodel).
The elements of \(\mathcal{D}_{12}f(x)\) are equal to \(\pi_{ij}(x)(1-\pi_{ij}(x))\), while \(\mathcal{D}_{11}f(x)\) is a diagonal matrix with the row sums of \(\mathcal{D}_{12}f(x),\) and \(\mathcal{D}_{22}f(x)\) is a diagonal matrix with the column sums.
This means that computing the eigenvalues of \[ [\mathcal{D}_{11}f(x)]^{-1}\mathcal{D}_{12}f(x)[\mathcal{D}_{22}f(x)]^{-1}\mathcal{D}_{21}f(x) \] amounts, in this case, to a correspondence analysis of the matrix with elements \(\pi_{ij}(x)(1-\pi_{ij}(x))\).The speed of convergence will depend on the maximum correlation, i.e. on the degree in which the off-diagonal matrix \(\mathcal{D}_{12}f(x)\) deviates from independence.
3.8 Some Counterexamples
3.8.1 Convergence to a Saddle
Convergence, even it occurs, does not need to be towards a minimum. Consider \[ f(x,y)=\frac16 y^3-\frac12y^2x+\frac12yx^2-x^2+2x. \] Perspective and contour plots of this function are in figures 3.1 and 3.2.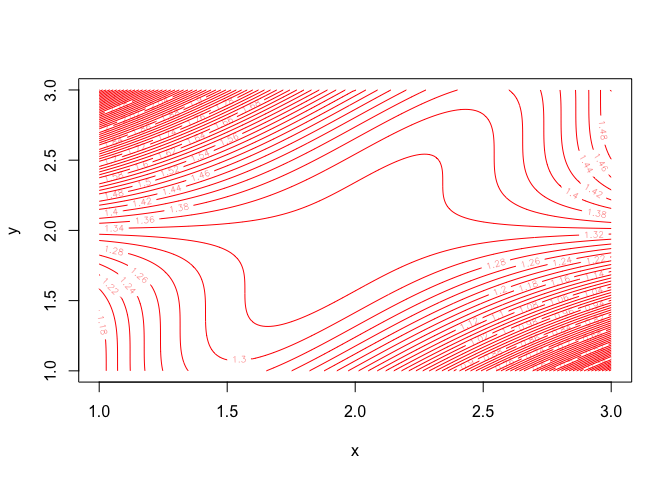
Figure 3.1: Contour Plot Bivariate Cubic
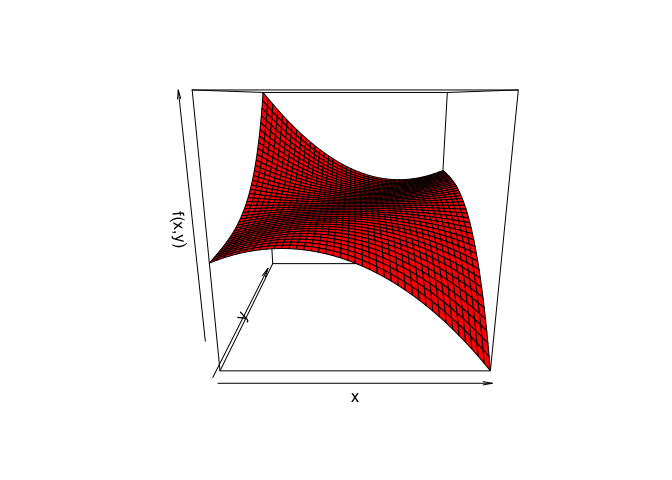
Figure 3.2: Perspective Plot Bivariate Cubic
The derivatives are \begin{align*} \mathcal{D}_1f(x,y)&=(y-2)(x-\frac12(y+2)),\\ \mathcal{D}_2f(x,y)&=\frac12(x-y)^2, \end{align*} and \[ \mathcal{D}^2f(x,y)=\begin{bmatrix} y-2&x-y\\ x-y&y-x \end{bmatrix}. \] Start with \(y^{(0)}>2\). Minimizing over \(x\) for given \(y^{(k)}\) gives \[ x^{(k)}=\frac12(y^{(k)}+2), \] and minimizing over \(y\) for given \(x^{(k)}\) gives \[ y^{(k+1)}=x^{(k)}. \] It follows that \begin{align*} x^{(k+1)}-2&=\frac12(x^{(k)}-2),\\ y^{(k+1)}-2&=\frac12(y^{(k)}-2). \end{align*}
Thus both \(x^{(k)}\) and \(y^{(k)}\) decrease to two with linear convergence rate \(\frac12\). The function \(f\) has a saddle point at \((2,2)\), and \[ \mathcal{D}^2f(2,2)= \begin{bmatrix}0&0\\0&0\end{bmatrix}. \]
3.8.2 Convergence to Incorrect Solutions
Convergence needs not be towards a minimum, even if the function is convex. This example is an elaboration of the one in Abatzoglou and O’Donnell (1982).
Let \[ f(a,b)=\max_{x\in [0,1]}\mid x^2-bx-a\mid. \] To compute \(\min f(a,b)\) we do the usual Chebyshev calculations. If \(h(x)\mathop{=}\limits^{\Delta}bx+a\) and \(g(x)\mathop{=}\limits^{\Delta}x^2-h(x)\) we must have \(g(0)=\epsilon\), \(g(y)=-\epsilon\) for some \(0<y<1\) and \(g(1)=\epsilon\). Moreover \(g'(y)=0\). Thus \begin{align*} -a&=\epsilon,\\ y^2-by-a&=-\epsilon,\\ 1-b-a&=\epsilon,\\ 2y-b&=0. \end{align*}The solution is \(b=1\), \(y=\frac12\), \(a=-\frac18\), and \(\epsilon=\frac18\). Thus the best linear Chebyshev approximation to \(x^2\) on the unit interval is \(x-\frac{1}{8},\) which has function value \(f(-\frac18,1)=\frac18\),
Now use coordinate decent. Start with \(b^{(0)}=0.\) Then \[ a^{(0)}=\mathop{\mathbf{argmin}}\limits_{a} f(a,0)=\frac12. \] and \[ b^{(1)}=\mathop{\mathbf{argmin}}\limits_{b}f(\frac12,b)=0. \] Thus \(b^{(1)}=b^{(0)}\), and we have convergence after a single cycle to a point \((a,b)=(\frac12,0)\) for which \(f(\frac12,0)=\frac12\).This example can be analyzed in more in detail. First we compute the best constant (zero degree polynomial) approximation to \(h(x)\mathop{=}\limits^{\Delta}x^2-bx\). The function \(h\) is a convex quadratic with roots at zero and \(b\), with a mimimum equal to \(-\frac14 b^2\) at \(x=\frac12 b\).
We start with the simple rule that the best constant approximation is the average of the maximum and the minimum on the interval. We will redo the calculations later on, using a different and more general approach.
Case A: If \(b\leq 0\) then \(h\) is non-negative and increasing in the unit interval, and thus \(\mathop{\mathbf{argmin}}\limits_{a} f(a,b)=\frac12(h(0)+h(1))=\frac12(1-b)\).
Case B: If \(0\leq b\leq 1\) then \(h\) attains its minimum at \(\frac12 b\) in the unit interval, and its maximum at one, thus \[\mathop{\mathbf{argmin}}\limits_{a} f(a,b)=\frac12(h(\frac12 b)+h(1))=-\frac18 b^2-\frac12 b +\frac12\].
Case C: If \(1\leq b\leq 2\) then \(h\) still attains its minimum at \(\frac12 b\) in the unit interval, but now the maximum is at zero, and thus \(\mathop{\mathbf{argmin}}\limits_{a} f(a,b)=\frac12(h(\frac12 b)+h(0))=-\frac18 b^2\).
Case D: If \(b\geq 2\) then \(h\) is non-positive and decreasing in the unit interval, and thus again \(\mathop{\mathbf{argmin}}\limits_{a} f(a,b)=\frac12(h(0)+h(1))=\frac12(1-b)\).
We can derive the same results, and more, by using a more general approach. First \[ f(a,b)= \max\left\{\max_{0\leq x\leq 1}(x^2-a-bx),-\min_{0\leq x\leq 1}(x^2-a-bx)\right\}. \] Since \(x^2-a-bx\) is convex, we see \[ f(a,b)= \max\left\{-a,1-a-b,-\min_{0\leq x\leq 1}(x^2-a-bx)\right\}. \] Now \(x^2-a-bx\) has a minimum at \(x=\frac12 b\) equal to \(-a-\frac14 b^2\). This is the minimum over the closed interval if \(0\leq b\leq 2\), otherwise the minimum occurs at one of the boundaries. Thus \[ \min_{0\leq x\leq 1}(x^2-a-bx)=\begin{cases} -a-\frac14 b^2&\text{ if }0\leq b\leq 2,\\ \min(-a,1-a-b)&\text{ otherwise},\end{cases} \] and \[ f(a,b)=\begin{cases} \max\{1-a-b,a+\frac14 b^2\}&\text{ if }0\leq b\leq 1,\\ \max\{-a,a+\frac14 b^2\}&\text{ if }1\leq b\leq 2,\\ \max\{|a|,|1-a-b|\}&\text{ otherwise}.\end{cases} \] It follows that \[ \mathop{\mathbf{argmin}}\limits_{a} f(a,b)=\begin{cases} \frac12-\frac12 b-\frac18b^2&\text{ if }0\leq b\leq 1,\\ -\frac18 b^2&\text{ if }1\leq b\leq 2,\\ \frac12(1-b)&\text{ otherwise}.\end{cases} \] It is more complicated to compute \(\mathop{\mathbf{argmin}}\limits_{b} f(a,b)\), because the corresponding Chebyshev approximation problem does not satisfy the Haar condition, and the solution may not be unique.
We make the necessary calculations, starting from the left. Define \(g_1(b)\mathop{=}\limits^{\Delta}\max\{|a|,|1-a-b|\}\). For \(b\leq 0\) we have \(f(a,b)=g_1(b)\). Define \(b_-\mathop{=}\limits^{\Delta}(1-a)-|a|\) and \(b_+\mathop{=}\limits^{\Delta}(1-a)+|a|\). Then \[ g_1(b)= \begin{cases} (1-a)-b&\text{ if }b\leq b_-,\\ |a|&\text{ if }b_1<b<b+,\\ b-(1-a)&\text{ if }b\geq b_+. \end{cases} \] Note that \(b_+>0\) for all \(a\). If \(b_-<0\) then \(g_1\) has a minimum equal to \(-b_-\) for all \(b\) in \([b_-,0]\). Now \(b_-<0\) if and only if \(a>\frac12\). Thus for \(a>\frac12\) we have \[ \mathbf{Arg}\mathop{\mathbf{min}}\limits_{b}f(a,b)=[(1-a)-|a|,0]. \]
Switch to \(g_2(b)\mathop{=}\limits^{\Delta}\max\{1-a-b,a+\frac14 b^2\}\). For \(0\leq b\leq 1\) we have \(f(a,b)=g_2(b)\). We have \(1-a-b>a+\frac14 b^2\) if and only if \(\frac14 b^2+b+(2a-1)<0\). The discriminant of this quadratic is \(2(1-a)\), which means that if \(a>1\) we have \(g_2(b)=a+\frac14 b^2\) everywhere. If \(a<1\) define \(b_-\) and \(b_+\) as the two roots \(-2\pm 2\sqrt{2(1-a)}\) of the quadratic. Now \[ g_2(b)= \begin{cases} 1-a-b&\text{ if }b_-\leq b\leq b_+,\\ a+\frac14 b^2&\text{ otherwise}. \end{cases} \] Clearly \(b_-<0\). If \(a>\frac12\) then also \(b_+<0\) and thus \(g_2(b)=a+\frac14 b^2\) on \([0,1]\). If \(0<b_+<1\) then \(g_2\) has a minimum at \(b_+\). Thus if \(-\frac18<a<\frac12\) we have \[ \mathop{\mathbf{argmin}}\limits_{b} f(a,b)=2+2\sqrt{2(1-a)}. \]
Next \(g_3(b)\mathop{=}\limits^{\Delta}\max\{-a,a+\frac14 b^2\}\), which is equal to \(f(a,b)\) for \(1\le b\leq 2\). If \(a>0\) then \(g_3(b)=a+\frac14 b^2\) everywhere. If \(a<0\) define \(b_-\) and \(b_+\) as \(\pm\sqrt{-8a}\). Then \[ g_3(b)= \begin{cases} -a&\text{ if }b_-\leq b\leq b_+,\\ a+\frac14 b^2&\text{ otherwise}. \end{cases} \] If \(1<b_+<2\) then we have a minimum of \(g_3\) at \(b_+\). Thus if \(-\frac12<a<-\frac18\) we find \[ \mathop{\mathbf{argmin}}\limits_{b} f(a,b)=\sqrt{-8a}. \]
And finally we get back to \(g_1\) again at the right hand side of the real line. We have a minimum if \(b_+>2\), i.e. \(a<-\frac12\). In that case \[ \mathbf{Arg}\mathop{\mathbf{min}}\limits_{b} f(a,b)=[2,(1-a)+|a|] \]
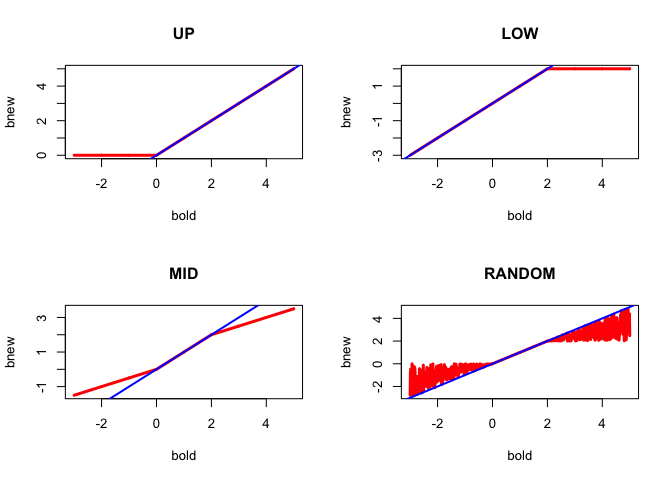
So, in summary, \[ \mathbf{Arg}\mathop{\mathbf{min}}\limits_{b} f(a,b)=\begin{cases} [(1-a)-|a|,0]&\text{ if }a>\frac12,\\ \{2+2\sqrt{2(1-a)}\}&\text{ if }-\frac18<a<\frac12,\\ \{\sqrt{-8a}\}&\text{ if }-\frac12<a<-\frac18,\\ [2,(1-a)+|a|]&\text{ if }a<-\frac12. \end{cases} \] We now have enough information to write a simple coordinate descent algorithm. Of course such an algorithm would have to include a rule to select from the set of minimizers if the minimers are not unique. In ourR implementation in ccd.R we allow for different rules. If the minimizers are an interval, we always choose the smallest point, or always to largest point, or always the midpoint, or a uniform draw from the interval. We shall see in our example that these different options have a large influence on the approximation the algorithm converges too, in fact even on what the algorithm considers to be desirable points.
We give the function that transforms \[b^{(k)}\] into \[b^{(k+1)}\] with the four different selection rules in Figure 1.
The function is in red, the line \(b^{(k+1)}=b^{(k)}\) in blue. Thus over most of the region of interest the algorithm does not change the slope, which means it converges in a single iteration to an incorrect solution. It needs more iterations only for the midpoint and random selection rules if started outside \([0,2].\)
3.8.3 Non-convergence and Cycling
Coordinate descent may not converge at all, even if the function is differentiable.
There is a nice example, due to Powell (1973). It is somewhat surprising that Powell does not indicate what the source of the problem is, using Zangwill’s convergence theory. The reason seems to be that the mathematical programming community has decided, at an early stage, that linearly convergent algorithms are not interesting and/or useful. The recent developments in statistical computing suggest that this is simply not true.
Powell’s example involves three variables, and the function \[ \psi(\omega)=\frac{1}{2}\omega'A\omega+\hbox{dist}^2(\omega,\mathcal{K}), \] where \[ a_{ij}=\begin{cases} -1& \text{if $i\not=j$,}\\ 0& \text{if $i=j$,} \end{cases} \] and where \(\mathcal{K}\) is the cube \[ \mathcal{K}=\{\omega\mid -1\leq\omega_i\leq +1\}, \]
The derivatives are \[ \mathcal{D}\psi=A\omega+2(\omega-\mathcal{P}_\mathcal{K}(\omega)). \] In the interior of the cube \(\mathcal{D}\psi=A\omega,\) which means that the only stationary point in the interior is the saddle point at \(\omega=0.\) In general at a stationary point we have \((A+2\mathcal{I})\omega=\mathcal{P}_\mathcal{K}(\omega)),\) which means that we must have \(u'\mathcal{P}_\mathcal{K}(\omega))=0.\) The only points where the derivatives vanish are saddle points. Thus the only place where there can be minima is on the surface of the cube.
Also for \(x=y=z=t>1\) we see that \(\psi(x,y,z)=-3t^2+3(t-1)^2= 3-6t,\) which is unbounded. For \(x=y=t>1\) and \(z=-t\) we find \[ \psi(x,y,z)=-t^2+3(t-1)^2=2t^2-6t+3. \] This has its minimum \(-1.5\) at \(t=1.5\) and it has a root at \(t=\frac{1}{2}(3+\sqrt{12})=4.9641.\)
Let us apply coordinate descent. A search along the x-axis finds the optimum at \(+1+\frac{1}{2}(y+z)\) if \(y+z>0\) and at \(-1+\frac{1}{2}(y+z)\) if \(y+z<0\). If \(y+z=0\) the minimizer is any point in \([-1,+1]\).
This guarantees that the partial derivative with respect to \(x\) is zero. The other updates are given by symmetry. Thus, if we start from \[ (-1-\epsilon,1+{\frac{1}{2}}\epsilon,-1-{\frac{1}{4}}\epsilon), \] with \(\epsilon\) some small positive number, then we generate the following sequence. \[ \begin{bmatrix} (+1+\frac{1}{8}\epsilon, &+1+\frac{1}{2}\epsilon,&-1-\frac{1}{4}\epsilon)\\ (+1+\frac{1}{8}\epsilon, &-1-\frac{1}{16}\epsilon,&-1-\frac{1}{4}\epsilon)\\ (+1+\frac{1}{8}\epsilon, &-1-\frac{1}{16}\epsilon,&+1+\frac{1}{32}\epsilon)\\ (-1-\frac{1}{64}\epsilon,&-1-\frac{1}{16}\epsilon,&+1+\frac{1}{32}\epsilon)\\ (-1-\frac{1}{64}\epsilon,&+1+\frac{1}{128}\epsilon,&+1+\frac{1}{32}\epsilon)\\ (-1-\frac{1}{64}\epsilon,&+1+\frac{1}{128}\epsilon,&-1-\frac{1}{256}\epsilon) \end{bmatrix} \]
But the sixth point is of the same form as the starting point, with \(\epsilon\) replaced by \(\frac{\epsilon}{64}.\) Thus the algorithm will cycle around six edges of the cube. At these edges the gradient of the function is bounded away from zero, in fact two of the partials are zero, the others are \(\pm 2.\) The function value is \(+1.\) The other two edges of the cube, i.e. \((+1,+1,+1)\) and \((-1,-1,-1)\) are the ones we are looking for, because there the function value is \(-3,\) the global minimum. At these two points all three partials are \(\pm 2.\)
Powell gives some additional examples which show the same sort of cycling behaviour, but are somewhat smoother.
3.8.4 Sublinear Convergence
Convergence can be sublinear.
\begin{align*} \psi(\omega,\xi)&=(\omega-\xi)^2+\omega^4,\notag \\ \mathcal{D}_1\psi(\omega,\xi)&=2(\omega-\xi)+4\omega^3,\notag\\ \mathcal{D}_2\psi(\omega,\xi)&=-2(\omega-\xi),\notag\\ \mathcal{D}_{11}\psi(\omega,\xi)&=2+12\omega^2,\notag\\ \mathcal{D}_{12}\psi(\omega,\xi)&=-2,\notag\\ \mathcal{D}_{22}\psi(\omega,\xi)&=2.\notag \end{align*}It follows that coordinate descent updates \(\omega^{(k)}\) by solving the cubic \(\omega-\omega^{(k)}+2\omega^3=0.\) The sequence converges to zero, and by l’Hopitål’s rule \[ \lim_{k\rightarrow\infty}{\frac{\omega^{(k+1)}}{\omega^{(k)}}}=1. \] This leads to very slow convergence. The reason is that the matrix of second derivatives of \(\psi\) is singular at the origin.