Capitolo 4 Presentazione dei risultati
Il seguente capitolo è organizzato con lo scopo di mostrare in sequenza cronologica, analisi e risultati personali ottenuti durante lo svolgimento del lavoro di tesi, comprendente la fase previa di tirocinio. Pertanto l’articolazione dello scritto sarà data da otto sottoparagrafi riguardanti l’acquisizione di dati geomeccanici raccolti durante la fase di tirocinio nel periodo compreso tra Agosto 2020 e Novembre 2020), l’acquisizione dei dati di pioggia e le analisi pluviometriche, analisi di contenuto idrico sotterraneo, dati di spessore e del grado delle coperture di alterazione ottenuti durante l’attività di rilevamento di campo effettuato nel Maggio 2021, calcolo di parametri necessari alla creazione di Ietogramma e Idrogramma di progetto richiesti dal software IDRA2D-DF, ed in ultimo, i risultati di suscettibilità all’innesco ed invasione ottenuti con i modelli scelti e già precedentemente trattati.
4.1 Resoconto dell’attività di tirocinio
I lavori sul cantiere hanno previsto un programma di indagine geognostica consistente nell’esecuzione di sondaggi geotecnici (indagini stratigrafiche e piezometriche, indagini di laboratorio (eseguite dalla ditta committente) e di sito sulle terre e misurazioni inclinometriche) (indagini sismiche MASW di 3 e sondaggi stendimenti, e Tomografie geofisici Elettriche in 4 stendimenti). Tale campagna è stata richiesta dalla ditta committente C.I.G.I.T Geotecnica al fine di caratterizzare al meglio le geometrie, i rapporti e le strutture presenti nel sottosuolo e di realizzare un modello geologico del terreno.

Figure 4.1: georeferenziazione Mappa Topografica Calabria e della Carta del Reticolo idrografico su Google Earth; geolocalizzazione del sito
La campagna di indagini geognostiche si avvia con i 4 sondaggi verticali a carotaggio continuo, effettuati con la sonda meccanica Comacchio MC900P con carotiere da 101 mm e spinti fino alla profondità massima di 24 m. Sono quindi state prelevate le carote e posizionate nelle apposite cassette catalogatrici. Sono stati prelevati inoltre alcuni campioni indistirbuti sui quali sono state eseguite le analisi commissionate presso il laboratorio della società incaricata. Per ogni sondaggio sono state redatte le stratigrafie che mostrano come i materiali prevalenti nel sottosuolo siano per lo più grossolani (materiali di disfacimento) con una ridotta quantità di matrice limoso-argillosa, per cui i terreni interessati dai fenomeni franosi possono essere classificati come ad elevata permeabilità. I sondaggi S2 ed S4 sono stati poi attrezzati a contenere tubi inclinometrici (Figg.4.2 - 4.3) mediante sonda prodotta dalla SISGEO di MASATE (MI) Mod.0S242SV3000G, collegata ad una centralina di acquisizione dati mod. Archimede.
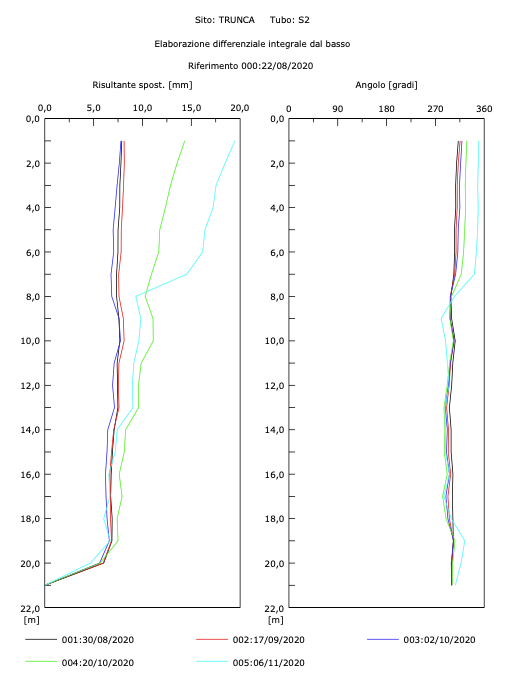
Figure 4.2: verticale inclinometrica S2
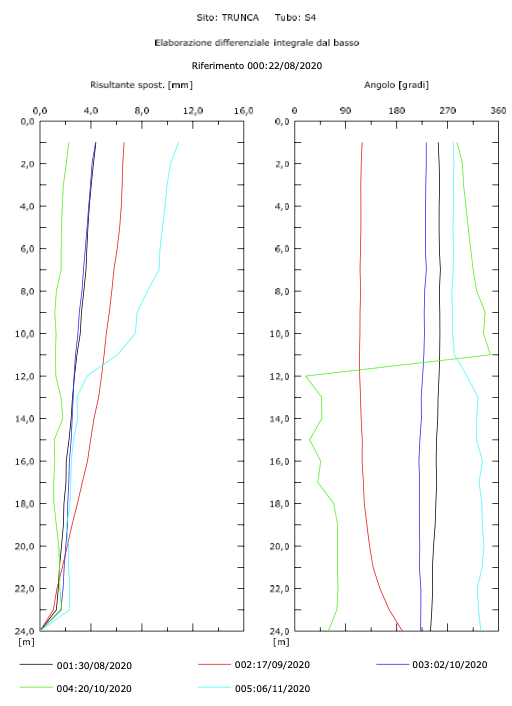
Figure 4.3: verticale inclinometrica S4
L’analisi inclinometrica ha permesso di constatare un movimento franoso costantemente attivo di tipo scorrimento rotazionale e con probabile superfice di scorrimento s circa 25 m di profondità; per ottenere questi risultati è stato però possibile utilizzare un solo inclinometro in quanto l’altro è stato danneggiato dal traffico veicolare, per cui non può essere preso in considerazione.
Il sondaggio S1 è stato attrezzato per installare una tubazione piezometrica a tubo aperto per monitorare il livello della falda freatica nel periodo di tempo richiesto dal monitoraggio.
Il sondaggio S3 è stato ritombato con un riempimento costituito da una miscela di cemento e bentonite.
La campagna corrente è stata anche caratterizzata dall’esecuzione di 15 prove SPT con punta conica, maglio di 63,5 Kg, volata di 760 mm e infissione massima di 30 cm. Analizzando i risultati complessivi delle prove penetrometriche si è dedotto che i litotipi perforati si comportano come materiali ad addensamento crescente con la profondità.
Le prove di laboratorio effettuate per parametrizzare geomeccanicamente i terreni sono state scelte appositamente a seconda dei litotipi per misurare il contenuto d’acqua naturale, il peso di volume, il peso specifico, la porosità, l’indice dei vuoti, i parametri di resistenza al taglio (attraverso prove di taglio tipo CD) e sono state effettuate anche analisi granulometriche (Fig. 4.4).
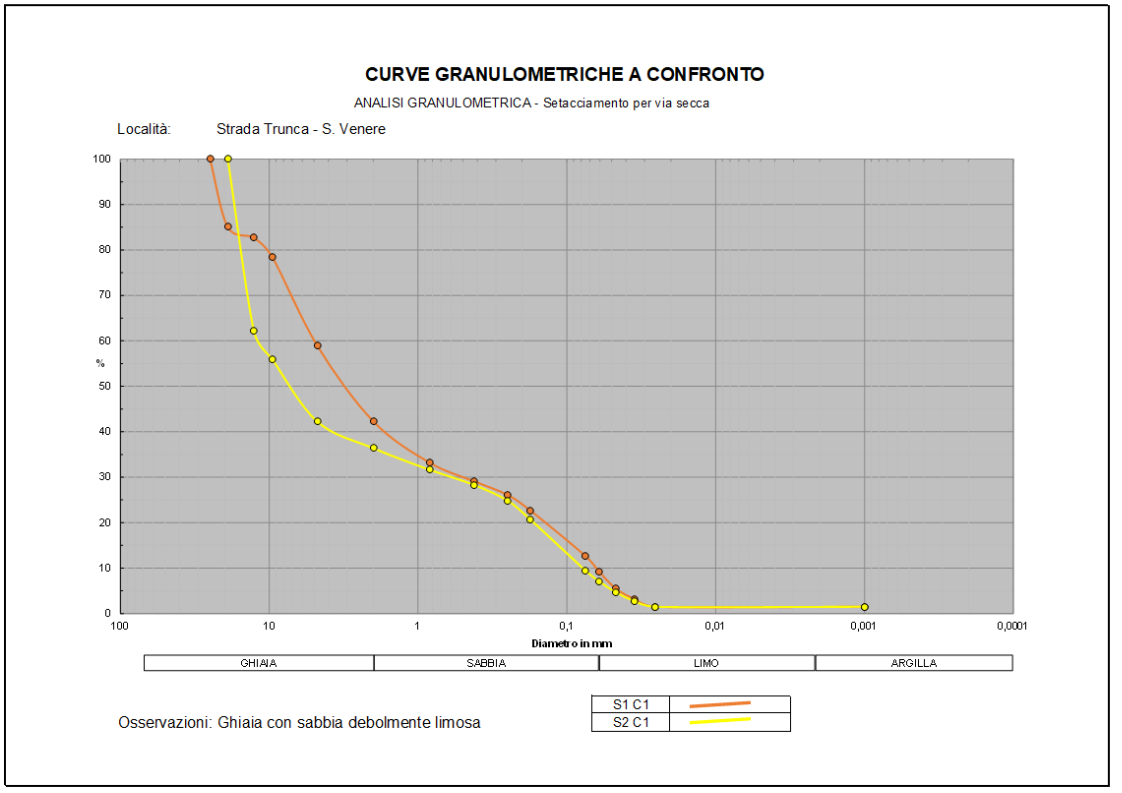
Figure 4.4: curve di analisi granulometrica
Alla campagna geotecnica è seguita la campagna geofisica.
Durante la fase di indagine sismica, per il rilievo della velocità del moto del suolo sono stati utilizzati geofoni con frequenza di oscillazione di 4.5 Hz che, attraverso la configurazione adottata nell’applicativo di acquisizione, sono stati spinti anche fino a frequenze di 10 Hz. Lo stendimento è stato realizzato con 24 geofoni verticali posti a distanza intergeofonica di 2 m al fine di ottenere il maggior dettaglio possibile. Per l’elaborazione dei dati di campagna abbiamo utilizzato il software Geogiga Surface Plus ed il Front End, adatti per l’analisi delle onde di Raileigh. Tali software sono serviti alla produzione dei profili di velocità delle onde di taglio Vs necessarie alla caratterizzazione geotecnica. In questo modo i terreni sono stati classificati secondo la categoria di sottosuolo B, ovvero caratterizzato da rocce tenere e depositi di terreni a grana grossa molto addensati caratterizzati da un miglioramento delle proprietà meccaniche con la profondità e con valori di velocità equivalente compresi tra 360 e 800 m/s.
Durante la fase di indagine geoelettrica è stata applicata una metodologia multielettrodo utilizzando come elettrodi picchetti in alluminio, infissi nel terreno e collegati tramite cavi elettrici multipolari e box di espansione all’unità di acquisizione dati; quest’ultima era costituita da un georesistivimetro modello MAE A6000-ES multielettrodo. Sono stati utilizzati 32 elettrodi posizionandoli ad una distanza costante di 3 metri tra loro per quanto riguarda gli stendimenti TM1, TM2, TM4, per una lunghezza totale dello stendimento di 93m; lungo la TM3 la distanza tra gli elettrodi era di 2 metri. Sono state effettuate 465 misure in modalità dipolo-dipolo ed i dati acquisiti sono stati elaborati con il software Zondres 2D con elaborazione a 40 iterazioni. E’ risultato quindi un profilo medio di resistività e, dall’interpretazione di questo, si possono individuare 2 orizzonti principali (Fig.(fig:f405)):
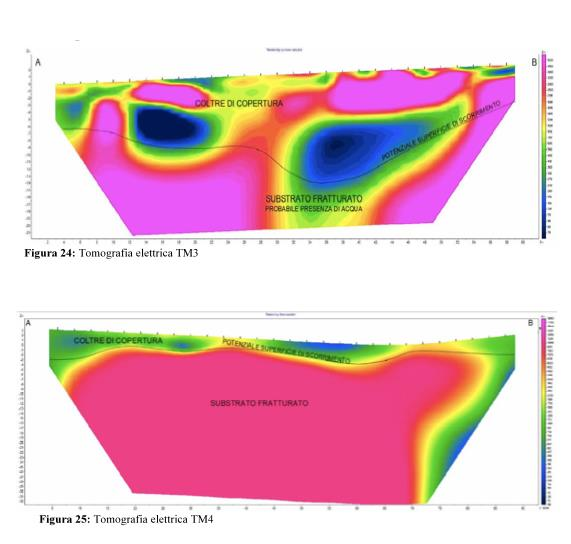
Figure 4.5: suddivisione in layer ottenuta dalla tomografia
- Il più superficiale caratterizzato da litotipi per lo più sciolti che comprendono anche la porzione rocciosa maggiormente alterata e fratturata;
- il più profondo, caratterizzato dalla presenza di basamento cristallino fratturato all’interno del quale è presente acqua di falda.
Il contatto tra i due orizzonti si può presumibilmente ricondurre ad una superficie di scorrimento della coltre di copertura superficiale sul basamento fratturato.
La campagna di indagini è quindi terminata caratterizzando i terreni interessati dalla frana nel seguente modo (Tab. 4.1):
|
|
- Granulometria media: Ghiaia con sabbia debolmente limosa
- Categoria di sottosuolo: B; depositi di terreni a grana grossa molto addensati o terreni a grana fine molto consistenti caratterizzati da un miglioramento delle proprietà meccaniche con la profondità e da valori di velocità equivalente compresi tra 360 e 800 m/s
Alla luce dei modelli interpretativi di sottosuolo elaborati grazie alle indagini geofisiche e alla luce dei dati inclinometrici, stratigrafici e piezometrici risultati dalle indagini geotecniche, si è identificata l’area in esame come assolutamente instabile. Come si evince dalle immagini 4.2-4.3, le verticali inclinometriche non seguono lo stesso trend di spostamento, quindi il cinematismo complessivo dell’area risulta mutevole nel tempo in termini di direzioni e di entità di spostamento a seguito di fattori climatici e/o cause esterne di diverso tipo che hanno potuto incidere momentaneamente sul moto gravitativo della massa di terreno che risulta collassata. Uno dei fattori è sicuramente rappresentato dalla morfologia; l’area di versante che collega l’abitato di Trunca con quello di Santa Venere si trova infatti sulla sua parte più esterna ed esposta rasentando la verticalità e che ha subito più volte fenomeni di dissesto di notevole importanza e che, nonostante questo, è ancora in assenza di qualsiasi opera o tipo di stabilizzazione; risulta quindi maggiormente sensibile a qualunque fattore di disturbo esterno che si riflette sul corpo di frana.
Le fessure di trazione, sulla sede stradale sono ancora aperte e beanti e possono essere state veicolo di una grande quantità di infiltrazione di acqua piovana e aver inciso perciò sulla direzione della massa. Di seguito si allega la cartografia del corpo di frana mobilitato (Figg. 4.1-4.2) e studiato durante il tirocinio e le sezioni geologiche legate alle tracce A-A’ e B-B’ (figg. 4.2-4.3) eseguite nell’ambito di tesi Magistrale all’Università di Napoli Federico II dalla studentessa Erica Postorino.
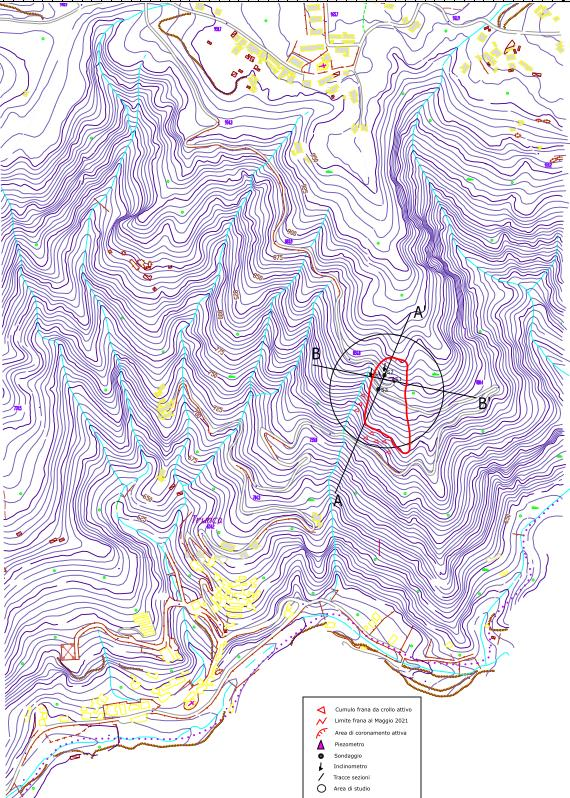
Figure 4.6: cartografia dell’area in frana studiata durante il tirocinio. scala 1:5.000
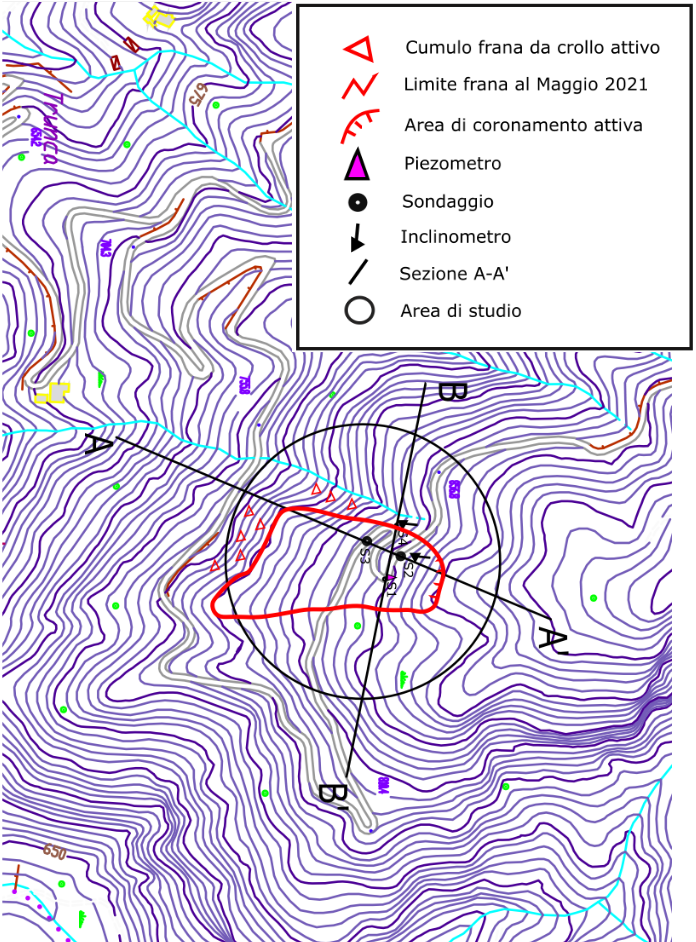
Figure 4.7: dettaglio dell’area e della leggenda
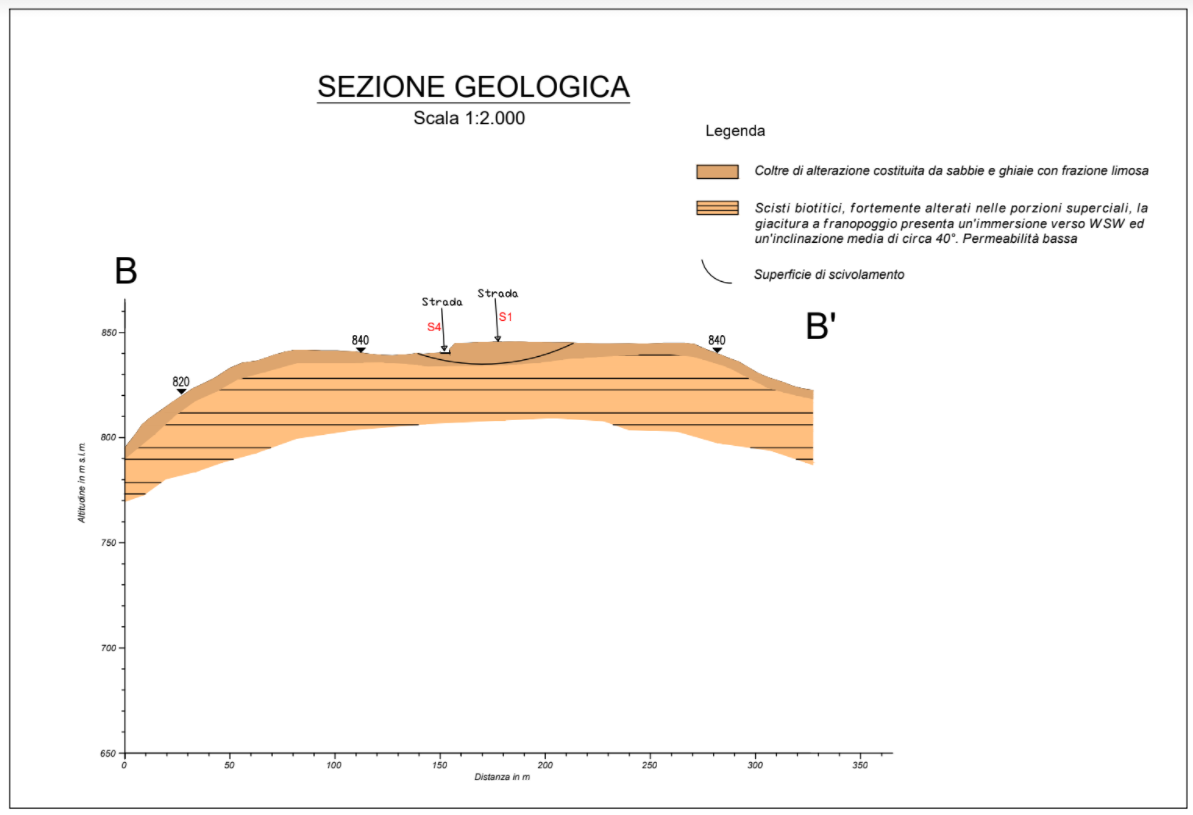
Figure 4.8: sezione geologica A-A’
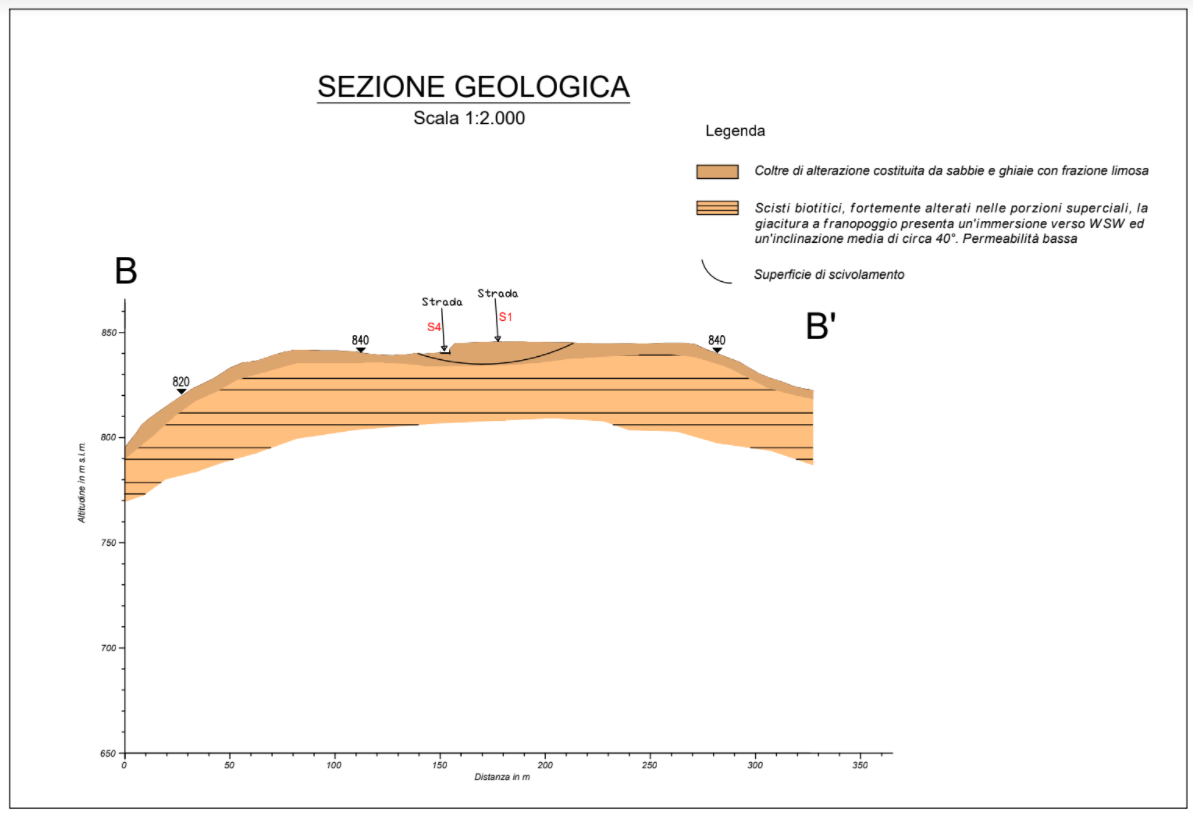
Figure 4.9: sezione geologica B-B’
4.2 Analisi sui dati di pioggia
L’assetto generale di piovosità della regione si riflette nell’area di studio, accomodando le ipotesi secondo le quali, la frana di Trunca-Santa Venere possa essere stata scatenata dalle intense piogge concentrate tra i mesi di Ottobre e Dicembre. Per verificarlo si è fatto ricorso ai dati pluviometrici storici, ai quali si è acceduto tramite il sito ARPACAL, previa richiesta di libero accesso. Il sito in questione (http://www.cfd.calabria.it/index.php) mette anche a disposizione un portale webgis che ha permesso, tra le varie sue funzionalità, di individuare le 3 stazioni pluviometriche più vicine all’area di sito. Le stazioni in questione (in ordine da monte verso valle: Cardeto-Liddu, Motta San Giovanni-Allai, Reggio Calabria- Rosario) (Fig. 4.4) sono posizionate all’interno del bacino idrografico del torrente Valanidi, raccogliendo quindi dati che, in mancanza di stazionamenti prettamente relativi al bacino di competenza del sito in frana, sono risultati utili all’analisi.
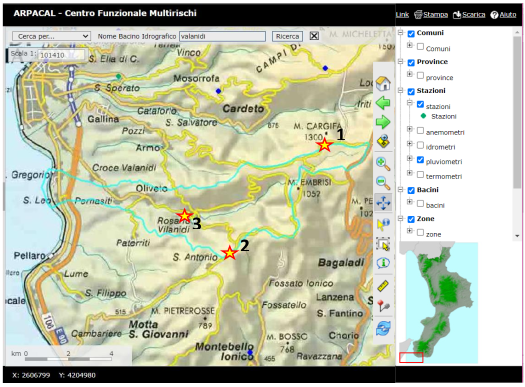
Figure 4.10: finestra del webgis ARPACAL con evidenza sul bacino idrografico del Valanidi e sulle tre stazioni pluviometriche interessate
I record di dati per ogni stazione utilizzata constano rispettivamente di 10 anni (2010-2020), 6 anni (2015-2020) e 10 anni (2010-2020) quindi, secondo un’analisi incrociata di questi, è stata utilizzata la serie 2015-2020, per un totale di 6 anni. In base ai dati sopracitati sono stati costruiti alcuni istogrammi che inquadrano per ogni anno e per ogni stazione pluviometrica, in quale mese siano caduti più mm di pioggia (Figg. 4.4-4.5-4.6), e, più in dettaglio, quali e quante settimane per ogni anno hanno definito un picco pluviometrico (Figg. da 4.7-4.16). Rispetto alla totalità dei dati analizzati, ogni stazione considera anche la precipitazione nevosa che riguarda il 21% per Cardeto-Liddu, lo 0.04% per Motta San Giovanni-Allai, e lo 0.14% per Reggio Calabria-Rosario; percentuali che risultano in accordo con le posizioni topografiche dei pluviometri considerati, ovvero, nello stesso ordine, a monte del bacino idrografico, nel mezzo, e in ultimo quasi alla quota dell’alveo. La frana in questione è parte di un ciclo di riattivazioni di cui si ha conoscenza dal 2003 e che ha avuto sicuramente seguito nel Novembre 2015, nel Novembre 2018 e nel Novembre 2019, anno durante il quale è stata fatta richiesta di cantiere al comune di Reggio Calabria. Osservando gli istogrammi è in effetti evidente come il 2015 sia stato maggiormente piovoso durante l’intero arco di tempo, e come durante il mese di Ottobre 2018 siano probabilmente avvenuti eventi pluviometrici più intensi del solito, associati ad una certa continuità anche nel mese di Novembre; durante il 2019 invece il picco di piovosità si riscontra a Novembre. Il 2016, 2017 e 2020, sono stati anni generalmente meno piovosi, e non hanno infatti scatenato alcuna riattivazione.
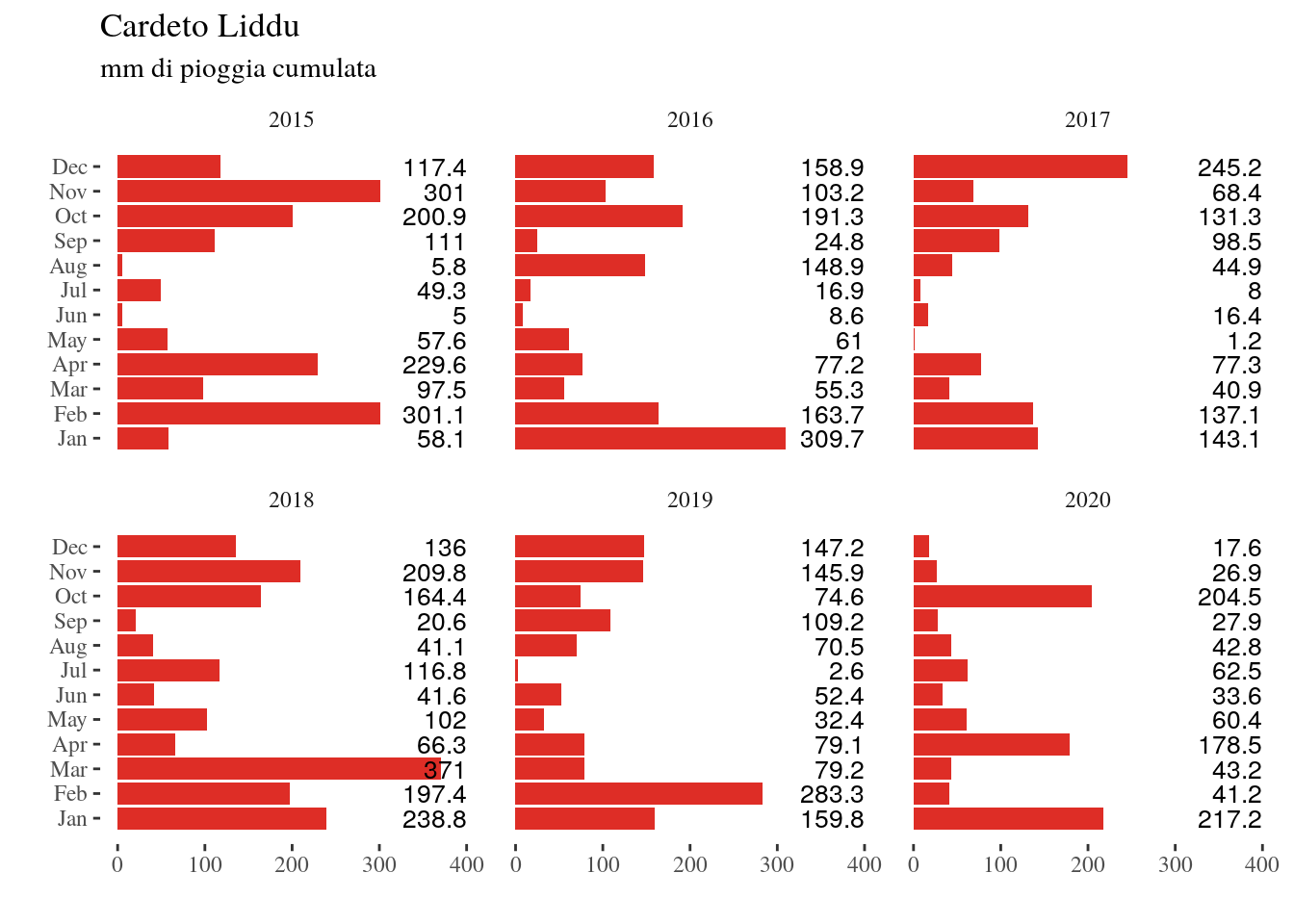
Figure 4.11: mm di pioggia Cardeto-Liddu per gli anni 2015-2020
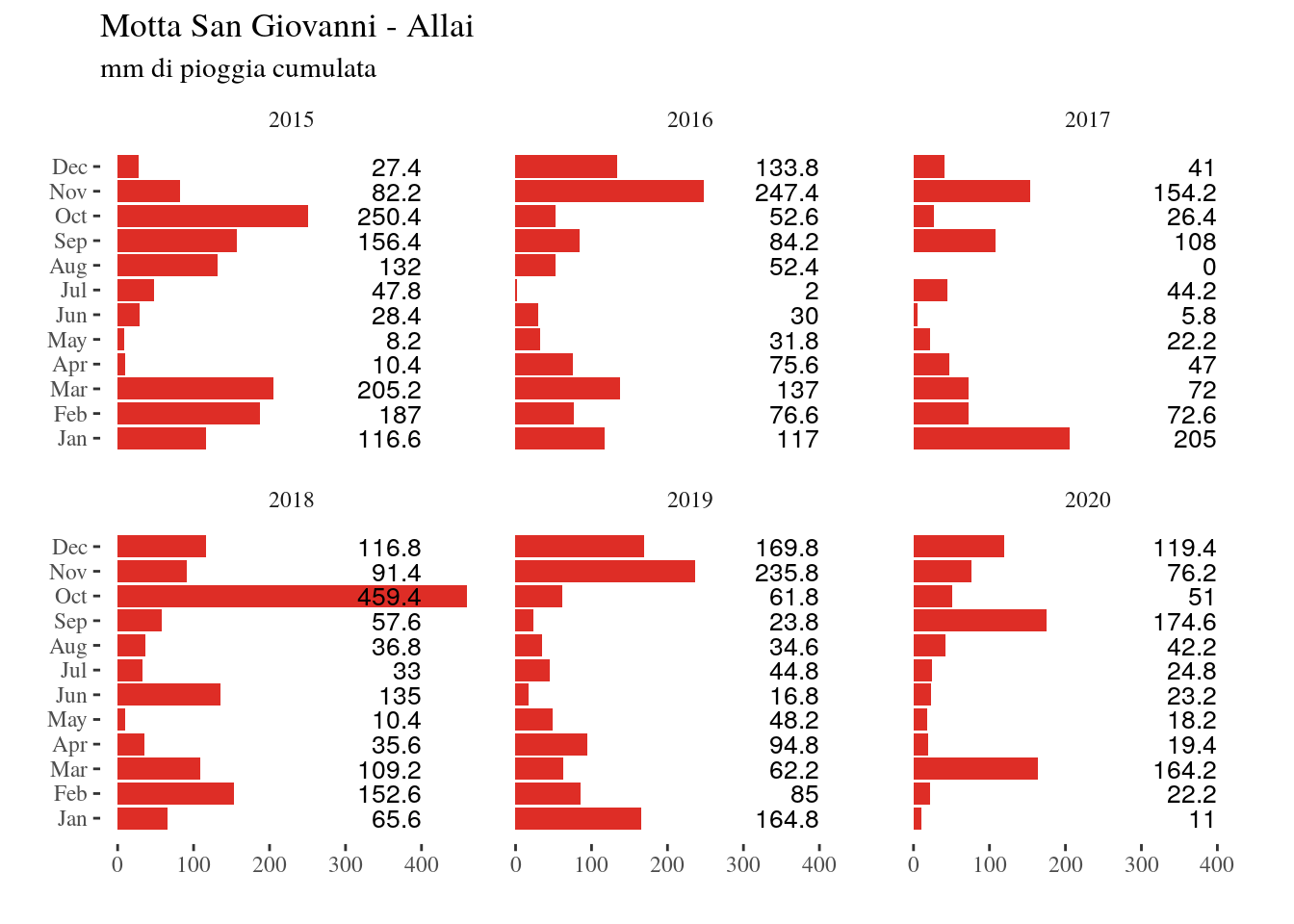
Figure 4.12: mm di pioggia Motta San Giovanni-Allai per gli anni 2015-2020
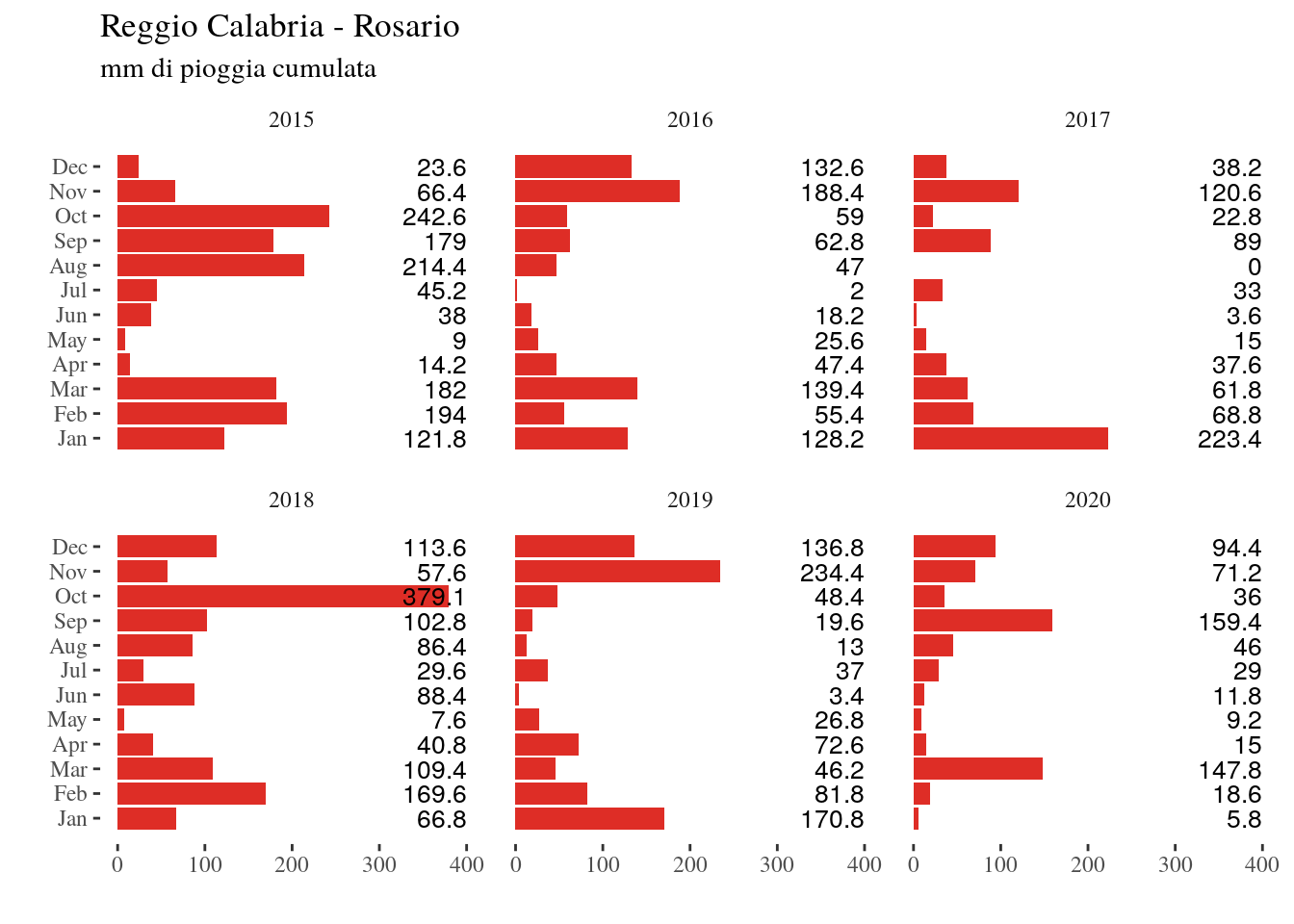
Figure 4.13: mm di pioggia Reggio Calabria-Rosario per gli anni 2015-2020
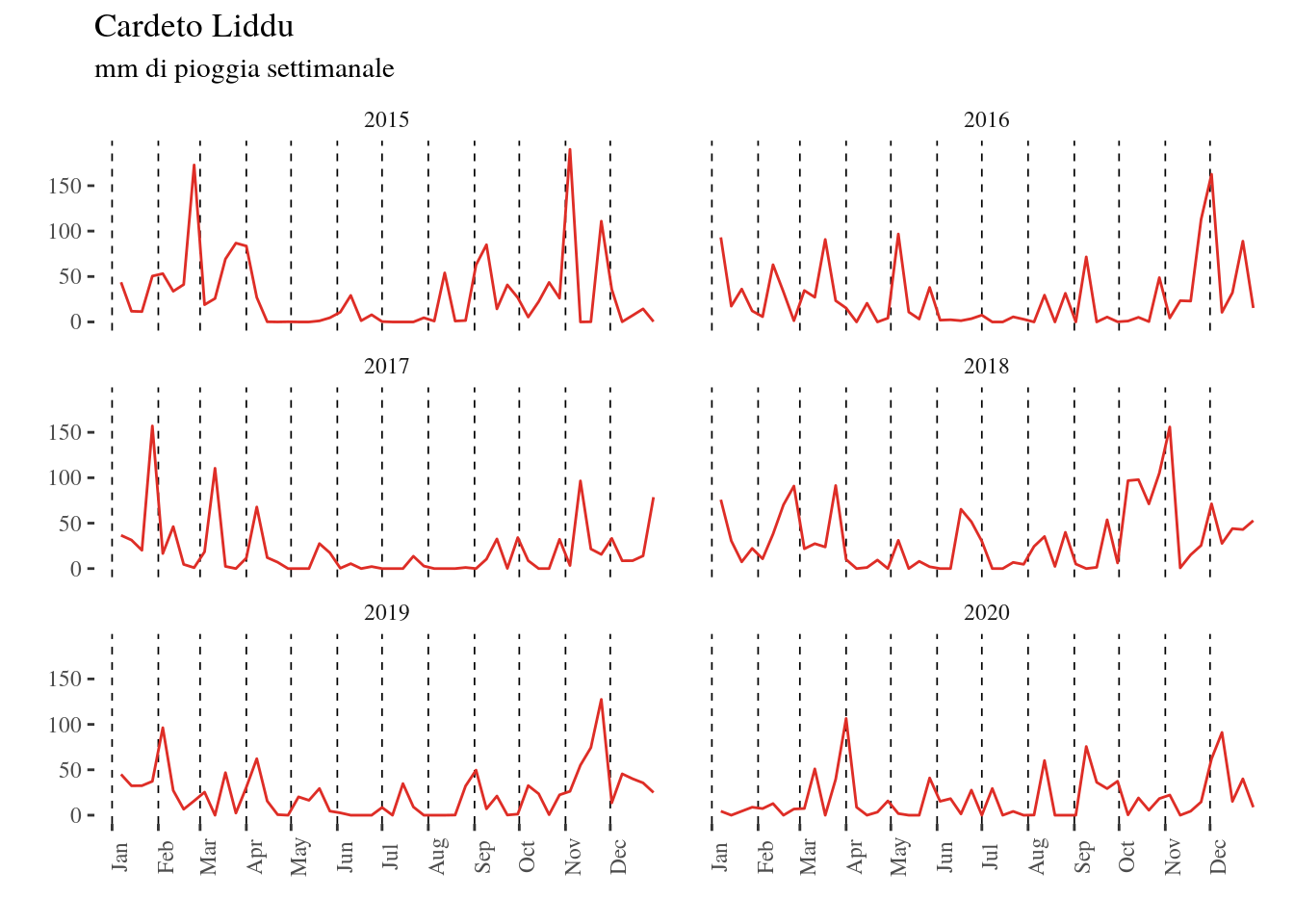
Figure 4.14: grafici pluviometrici settimanali Cardeto-Liddu per gli anni 2015-2020
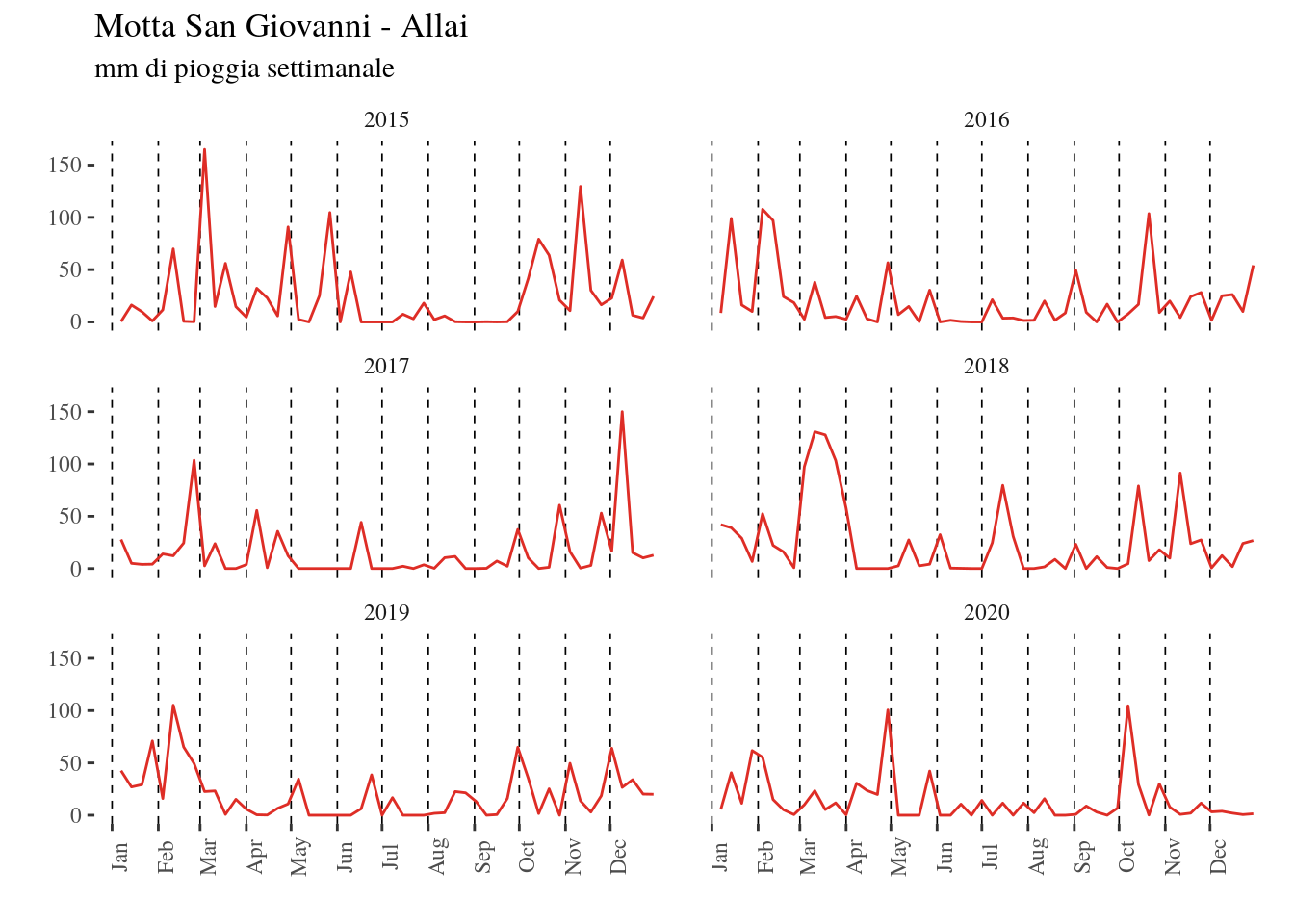
Figure 4.15: grafici pluviometrici settimanali Motta San Giovanni-Allai per gli anni 2015-2020
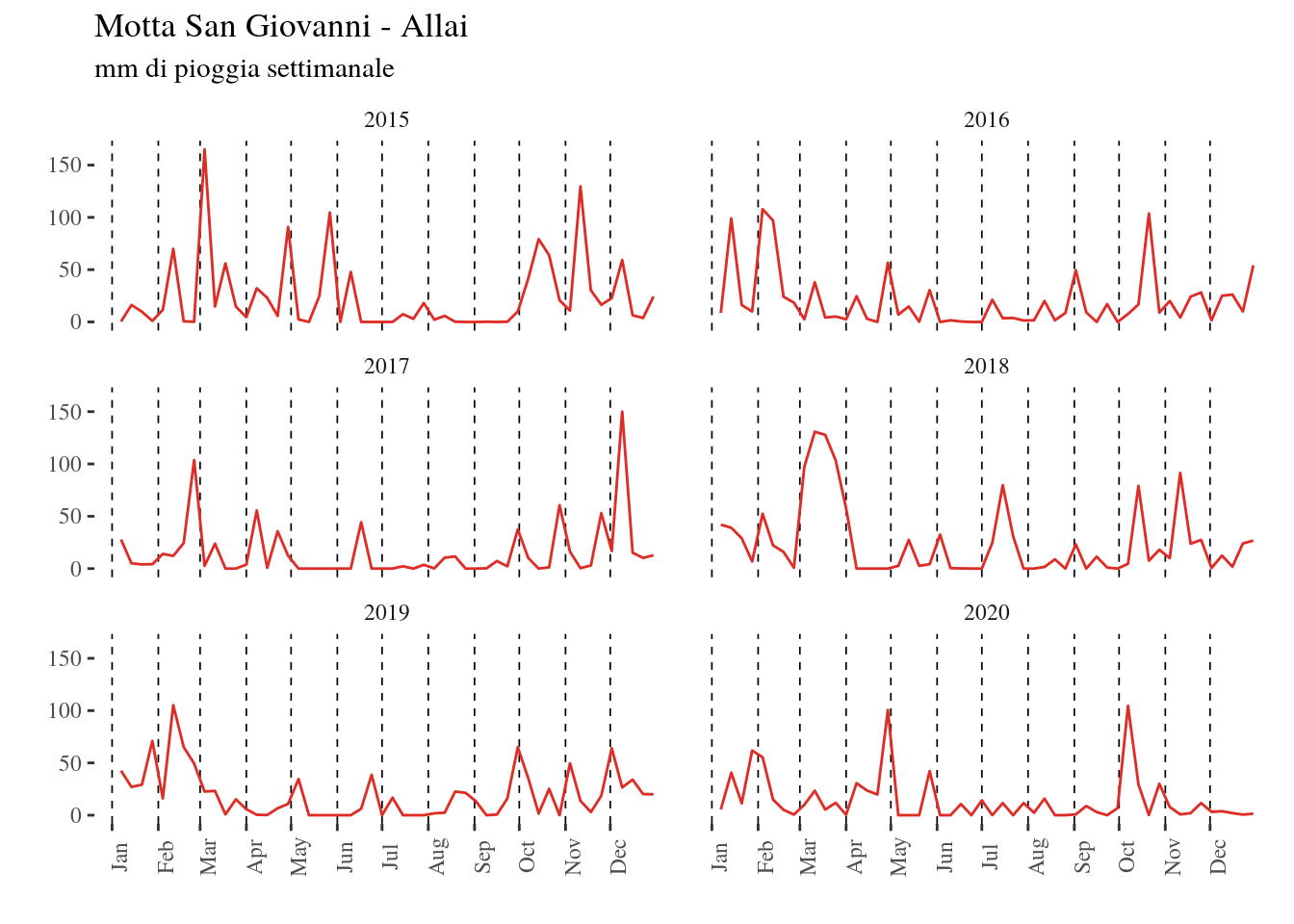
Figure 4.16: grafici pluviometrici settimanali Reggio Calabria.Rosario per gli anni 2015-2020
4.3 Analisi sul bilancio idrologico
Un’ulteriore analisi sul bacino può riguardare la stima del contenuto idrico sotterraneo che, in casi di pioggia intensa può facilitare l’innesco di fenomeni franosi. Per determinare le riserve idriche sotterranee e quindi i volumi d’acqua sotterranei disponibili, è necessario prima effettuare un calcolo del bilancio idrico dell’intero dominio idrogeologico, ovvero della fiumara Valanidi, in quanto all’interno del bacino idrografico di progetto non ricade alcuna stazione di misura. Considerando la struttura geologico-strutturale profonda ed in particolare la presenza di un basamento roccioso cristallino-metamorfico, profondamente diaclasato e fratturato da cui scaturisce una circolazione idrodinamica rilevante ancorché difficilmente individuabile, non potendo definire gli spartiacque sotterranei che definiscono forma, dimensione ed orientamento dei bacini idrografici sotterranei, generalmente diversi da quelli superficiali, nelle considerazioni e nei calcoli seguenti si farà riferimento all’estensione del solo bacino imbrifero (superficiale) delimitato come da cartografia in figura (Fig. ??).
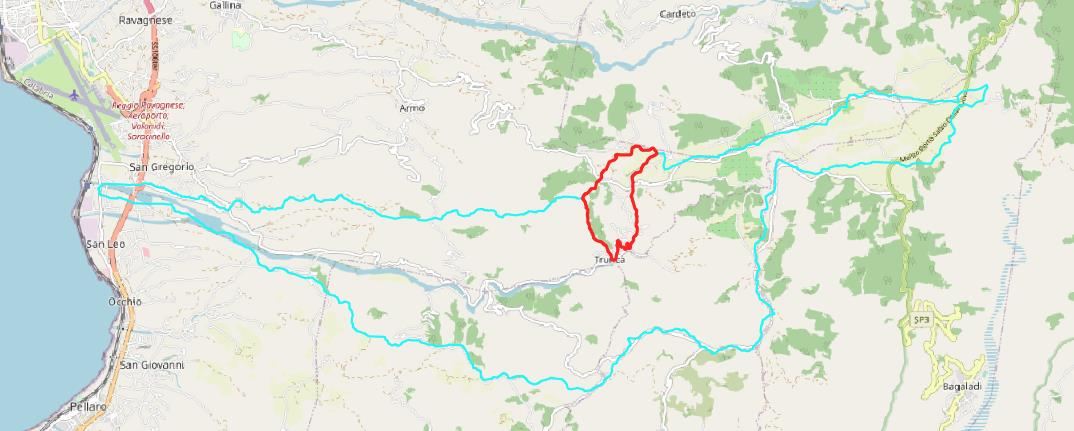
Figure 4.17: Bacino idrografico Valanidi estratto con procedure Qgis
Il calcolo del bilancio idrologico viene effettuato attraverso la definizione analitica di alcuni parametri presenti nella seguente espressione del ciclo idrologico:
\[ P = ET + R + I \]
dove: \[ \begin{array}{l} P = quantitativi\ d’acqua\ di\ precipitazione\ (in\ mm/anno);\\ E T = quantitativi\ d’acqua\ di\ evapotraspirazione\ reale\ (in\ mm/anno);\\ R = quantitativi\ di\ acqua\ di\ ruscellamento\ superficiale\ (in mm/anno);\\ I = quantitativi\ d’acqua\ di\ infiltrazione\ efficace\ (in\ mm/anno). \end{array} \]
Questa relazione traduce l’ipotesi che la quantità d’acqua che affluisce sul bacino si divida in 3 parti: quella che si infiltra nel sottosuolo, quella che torna all’atmosfera per evaporazione e quella che defluisce nei corpi idrici superficiali. In considerazione del fatto che il suddetto calcolo è tanto più preciso e veritiero quanto più frequenti sono le misure dei dati di base e quanto più lungo è il periodo di riferimento, condizioni difficilmente eseguibili, si precisa che si tratta di una valutazione approssimativa dei volumi che costituiscono la risorsa idrica profonda, probabilmente sottostimata, vista anche l’esclusione all’interno dell’espressione di alcuni parametri (neve, condensazione dell’umidità atmosferica…).
Le precipitazioni (P) vengono misurate utilizzando i dati forniti dalle stazioni metereologiche. Come anticipato nel paragrafo 4.2 “Analisi sui dati di pioggia”, all’interno del bacino idrografico considerato solo le stazioni di Reggio Calabria- Rosario e Cardetu Liddu, utilizzate in precedenza per l’analisi pluviometrica, vantano un record di 10 anni, utile per definire una media precipitazione annua, per cui sono state utilizzate per questo tipo di analisi unicamente le suddette stazioni.

|
||

|
Per cui, il parametro \(P\) dell’equazione risulta \(1317.45 mm\) annui. Per valutare l’evapotraspirazione (\(ET\) ) viene comunemente utilizzata la seguente formula (Turc):
\[ ET = \frac{P}{\sqrt{\left( 0.9 + \frac{P^2}{L^2} \right)}} \qquad \text{con} \quad L=300+25T+0.05T^3 \]
dove: \[ \begin{array}{l} P = totale\ precipitazioni\ annue\ in\ mm \\ 0.9 = fattore\ dipendente\ dalla\ temperatura\ media\ annua\ Tm \\ T = temperatura\ media\ annuale\ dell’aria\ in\ gradi\ Celsius\\ \qquad alla\ quota\ media\ dell’area\ di\ interesse \end{array} \]
Dai dati provenienti dalle suddette stazioni pubblicati sul sito ARPACAL si ha che pressappoco la temperatura media è la seguente:
| Rosario..RC. | Cardetu.Liddu | Media.annua |
|---|---|---|
| 16,6° | 11,4° | 14,0° |
Per cui si ha che \(ET = 684,82 mm/anno\).
Per quanto riguarda la stima del deflusso superficiale (\(R\)), esso dipende da dalla permeabilità dei terreni affioranti, dall’acclività e della vegetazione. Attraverso una serie di valutazioni effettuate su diversi studi in letteratura all’interno dei bacini imbriferi della Calabria meridionale è stato possibile ottenere e stimare un valore medio pari al 25% delle acque che giungono al suolo. Per cui si ha che \(R = 329,362 mm/anno\).
Per determinare le risorse idriche sotterranee è necessario quantificare l’acqua d’infiltrazione efficace (\(I\)) per cui la suddetta espressione del ciclo idrologico diventa:
\[ I=P-(ET+R)\] Per cui \(I = 303.268\) mm/anno.
Considerando che il bacino imbrifero del Valanidi ha una superficie di circa 80 Km2, allora le risorse idriche sotterranee ammontano ad una quantità di circa 24.262.563 m3 all’anno. Di conseguenza, conoscendo l’estensione del bacino di competenza del progetto (circa 1 km2), possiamo stimare che la quantità di materiale idrico sotterraneo è di circa 303.268 m3 all’interno di coltri di copertura da alterazione variabili da medio-grossolane a fini. Questo fattore, unitamente ai picchi di pioggia settimanali, può effettivamente favorire lo scatenarsi di un evento franoso.
4.4 Rilevamento di campo
La stima della pericolosità è funzione delle caratteristiche fisiche e di franosità del territorio indagato e del dettaglio che si intende raggiungere a livello di zonazione; di conseguenza, i procedimenti adottati per tale stima sono particolarmente diversificati nell’ambito della letteratura. La scelta dei fattori predisponenti da considerare, avviene tenendo conto dei fattori di franosità di maggiore influenza, delle caratteristiche fisiografiche del territorio, della tipologia dei fenomeni franosi maggiormente ricorrenti (fenomeni a cinematica lenta), della disponibilità degli enti governativi di cedere dati, e dal modello di analisi che si vuole utilizzare. Nelle aree in cui sono presenti rocce cristalline, la stabilità dei versanti, e più in generale la loro dinamica evolutiva, risulta fortemente condizionata dagli spessori di roccia attaccati dai processi di alterazione e dall’intensità raggiunta dagli stessi. Anche ad una sommaria analisi del territorio infatti, emerge con chiarezza l’elevata concentrazione di fenomeni di instabilità sia nelle coltri regolitiche (più o meno spesse) sia più in profondità negli ammassi alterati e degradati.
4.4.1 Carta degli spessori
Per la creazione di questa carta l’attività di rilevamento è consistita nella misurazione dello spessore verticale delle coltri di copertura impostate sulla roccia non ancora alterata tramite fioretti telescopici. E’ stata riscontrata una grande variabilità (tra 0 e 20 m) dovuta al fatto che generalmente le coltri sono state spostate dai numerosi eventi di frana e lasciate accumulare nelle zone di interbacino. Per redigere questo tipo di carta è stato creato sulla piattaforma Qgis un nuovo shape file puntuale georeferenziato (Fig. ??) che identificasse i vari spessori misurati in ogni stop effettuato durante il rilevamento, per poi essere interpolati.
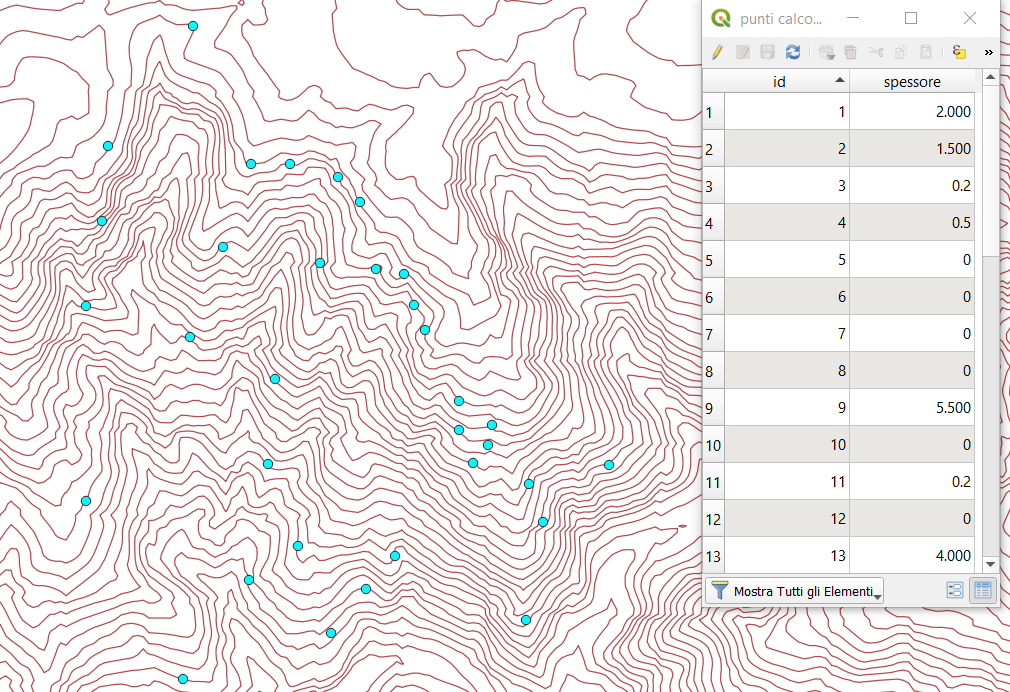
Figure 4.18: shape file puntuale con valori di spessore delle coperture analizzate
Il file in questione è stato interpolato con metodo IDW (Inverse Distance Weighted) con il quale i punti campione vengono pesati durante l’interpolazione in modo che l’influenza di ogni punto rispetto agli altri diminuisca in base alla distanza dal punto ignoto che si vuole creare. Il peso viene assegnato attraverso un coefficiente che controlla come l’influenza del peso diminuisca all’aumentare della distanza dal nuovo punto, quindi maggiore è il coefficiente minore sarà l’effetto che i punti distanti dal punto ignoto avranno durante il processo di interpolazione. All’aumentare del coefficiente, il valore del punto sconosciuto si avvicina al valore del punto osservato più vicino. L’interpolazione IDW ha mostrato come output un file raster (Fig. ??) che può essere considerato come carta degli spessori delle coperture di alterazione.
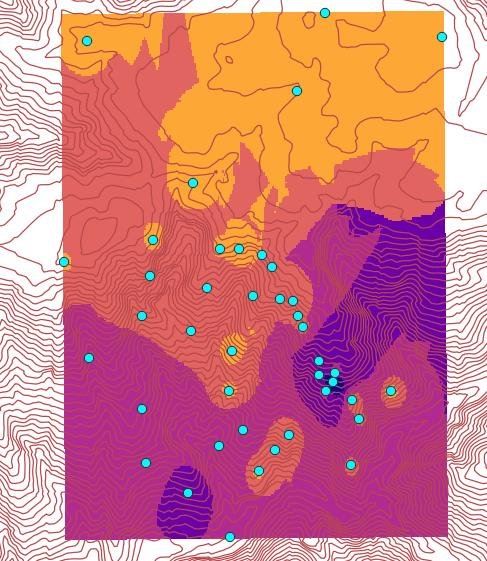
Figure 4.19: shape file puntuale con valori di spessore delle coperture analizzate
Questa carta, ritagliata secondo il bacino idrografico di progetto, è risultata necessaria per definire il layer del bottom delle coperture, ottenuto sottraendo la carta delle coperture al DEM, e del bottom del substrato roccioso, considerato teoricamente parallelo al bottom delle coperture e quindi ottenuto sottraendone uno spessore generico di 20m.
4.4.2 Carta dello stato di alterazione
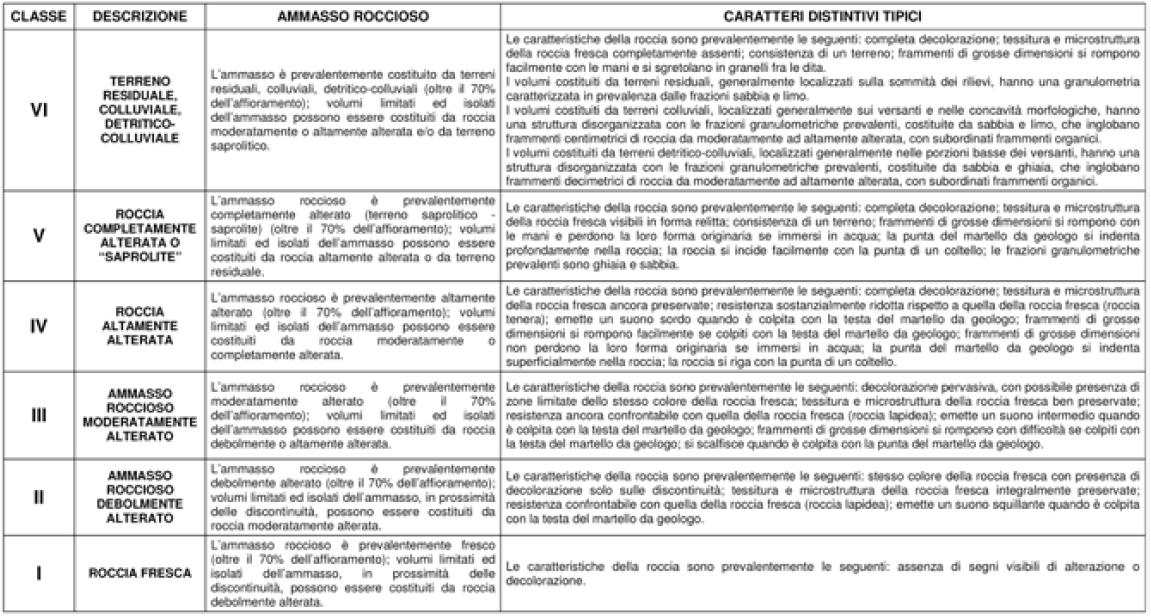
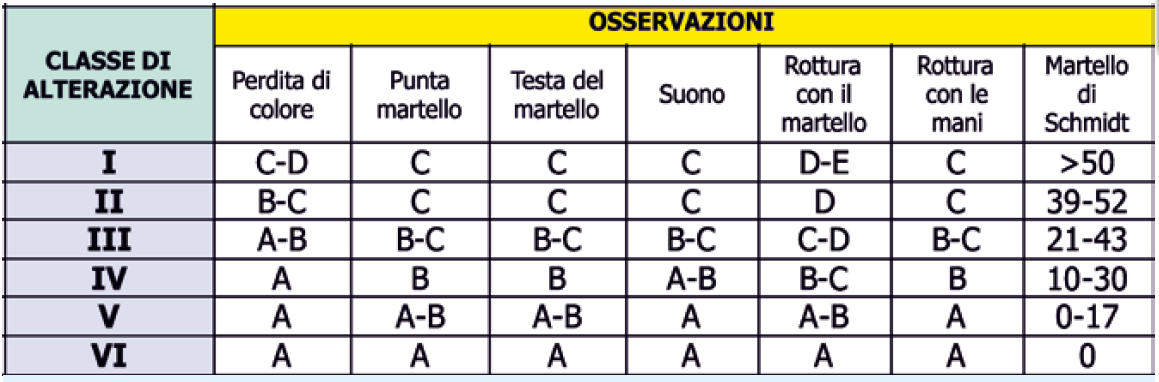
Il rilievo delle condizioni di weathering di un ammasso roccioso richiede come premessa la definizione di una procedura che consenta di distinguere i diversi stadi di alterazione. Nella letteratura tecnico-scientifica sono reperibili numerose proposte di classificazione del grado di alterazione delle rocce cristalline (Dearman, 1978; I.A.E.G. Commission, 1981; Cascini et al., 1992; Gullà & Matano, 1997; Le Pera et al., 2001;…), che utilizzano criteri generali differenti: analisi visiva di alcune caratteristiche geologiche, stima di proprietà meccaniche tramite alcuni test, considerazione dei fattori geo-litologici e geomeccanici ecc. La procedura assunta in questo caso come riferimento prevede, con l’osservazione di caratteri geologici (tessitura, decolorazione, compatteza, granulometria) e con la valutazione di semplici test correlabili alla resistenza meccanica della roccia attraverso il martello di Schmidt, la distinzione di sei classi di alterazione (di seguito descritte anche in tabella 4.5: classe VI (terreni residuali e/o colluviali), classe V (roccia completamente alterata o saprolite), classe IV (roccia altamente alterata), classe III (roccia moderatamente alterata), classe II (roccia debolmente alterata) e classe I (roccia fresca).
|
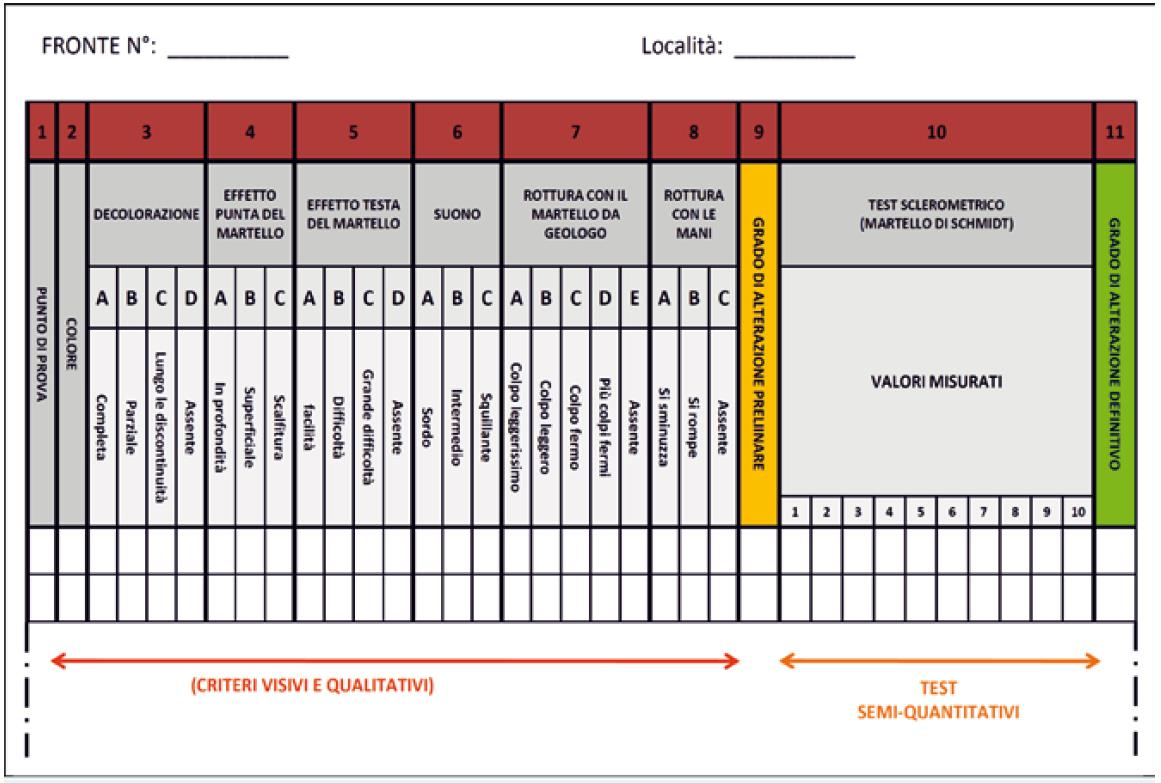
Durante l’attività di rilevamento, per ogni stop sono state effettuate le misure e le osservazioni; per la raccolta di questi e la scelta riguardante l’attribuzione dei pesi relativi, si utilizza la scheda mostrata di seguito (Tab. 4.6).
|
Per ogni punto di controllo (da indicare nella prima colonna, bisogna indicare il colore della roccia e riferendosi a quello della roccia fresca, il livello di decolorazione (colonne 2 e 3): (A) completa, (B) parzialmente decolorata, (C) decolorata solo lungo le discontinuità, (D) non decolorata. Per le ulteriori osservazioni, la procedura prevede l’utilizzo del martello da geologo e del martello di Schmidt; colpendo l’affioramento con il martello si valuta l’effetto della sua punta sulla superficie della roccia (colonna 4) osservando se si indenta facilmente in profondità, se si indenta solo superficialmente o se provoca solo scalfiture; utilizzando invece la testa del martello si rilevano le modalità con cui si staccano i frammenti di roccia dalla parete, e si valuta il suono emesso dalla roccia quando viene colpita (colonne 5-6). Utilizzando un campione di roccia prelevato dall’affioramento, se ne valuta la difficoltà di rottura con la testa del martello (colonna 7), mentre nella colonna 8, la facilità di rottura manuale. Ultimato questo tipo di osservazione, si procede all’esame complessivo dei risultati e alla relativa classificazione preliminare del grado di alterazione (colonna 9) riferendosi alle indicazioni riassunte in tabella. La verifica e la classificazione definitiva sono condotte sulla scorta dei valori di rimbalzo dati dal martello di schmidt (colonna 10) che consente di valutare un indice di resistenza della roccia in base al rimbalzo di un pistoncino metallico che percuote la roccia stessa. In particolare devono essere eseguite 10 misure in ogni punto di controllo con il martello disposto ortogonalmente alla superficie della roccia, che deve essere pulita e regolare. Il valore assegnato a qul punto sarà dato della media degli otto valori ottenuti scartando il più alto ed il più basso dei dieci misurati. Questo valore di rimbalzo è correlabile mediante un abaco con la resistenza a compressione semplice o compressione uniassiale, in funzione della densità della roccia e dell’inclinazione del martello rispetto alla superficie indagata (Hoek & Bray, 1981). Anche per l’assegnazione del grado di alterazione definitivo si rimanda, come riferimento generale, agli intervalli dei valori di rimbalzo del martello di Schmidt proposti in tabella (Tab 4.7) per le sei classi di alterazione considerate.
|
Il quadro conoscitivo così definito può poi essere ulteriormente integrato caratterizzando i campioni rappresentativi prelevati in ogni punto di controllo attraverso prove geotecniche (granulometria, resistenza a rottura) e analisi petrografiche; mentre ulteriori indicazioni circa l’andamento in profondità del profilo di alterazione potrebbero essere ottenute tramite ausilio di indagini geofisiche condotte con metodi geoelettrici e sismici.
Nel presente studio, il rilievo del grado di alterazione a scala di bacino ha
permesso la delimitazione preliminare di aree identificabili con 4 classi di
alterazione, ovvero classe VI (terreni residuali, colluviali e detritico-colluviali),
classe V (roccia completamente alterata o terreno saprolitico), classe IV (roccia altamente alterata) e classe III (roccia moderatamente alterata). Le classi di
alterazione I e II non sono state rilevate in affioramento. Le rocce appartenenti
alla classe III (Fig. ??) si presentano alla scala dell’ammasso, con una
decolorazione pressocchè completa e variabile dal grigio-biancastro al grigio-
verdastro, tranne che nei nuclei dei prismi rocciosi individuati dai vari sistemi di
discontinuità presenti, dove si riconoscono i toni originari del marrone e
dell’arancione. Le rocce altamente alterate (classe IV) sono completamente
decolorate e presentano un’elevata degradazione fisico-meccanica; presentano
un colore variabile dal grigio al beije al rosato e al rossastro. In questa classe,
nonostante l’alterazione molto spinta, sono ancora conservati i caratteri tessiturali
e le superfici di discontinuità sono distinguibili (Fig. ??). Le rocce
completamente alterate o saprolite, della classe V (Fig. ?? in alto) si presentano
come una roccia decolorata e completamente disgregata che ha assunto la
consistenza di un terreno, ma nella quale sono ancora riconoscibili qualche
discontinuità allo strato relitto e nelle quali risulta parzialmente preservata la
tessitura originaria; il colore di questi affioramenti risulta generalmente marrone,
ma è comunque leggermente variabile sui toni del grigio. Nell’ambito dei terreni
residuali e dei depositi detritico-colluviali (classe VI) sono state raggruppate le
rocce sciolte a granulometria variabile, di colore dal marrone al marrone-
giallastro/rossastro e nelle quali è stata completamente distrutta la tessitura
originaria. Gli affioramenti che sono stati ascritti a questa classe sono
principalmente depositi colluviali, che quindi non presentano alcuna traccia
dell’originaria tessitura, e in cui solo raramente si riconoscono allineamenti sub-orizzontali di piccoli ciottoli a spigoli vivi (Figg. @ref(fig:f430 in basso-??.
Nell’ambito di
tali terreni sono stati quindi considerati anche i depositi detritici di frana e di
versante in generale, caratterizzati da una matrice a granulometria medio-
grossolana inglobante blocchi di roccia con grado di alterazione riferibile alle
classi IV e V.

Figure 4.20: affioramenti ascrivibili alla III classe di alterazione

Figure 4.21: affioramenti ascrivibili alla IV classe di alterazione

Figure 4.22: in alto affioramenti ascrivibili alla V classe di alterazione; in basso affioramenti ascrivibili alla VI classe

Figure 4.23: affioramenti ascrivibili alla VI classe di alterazione
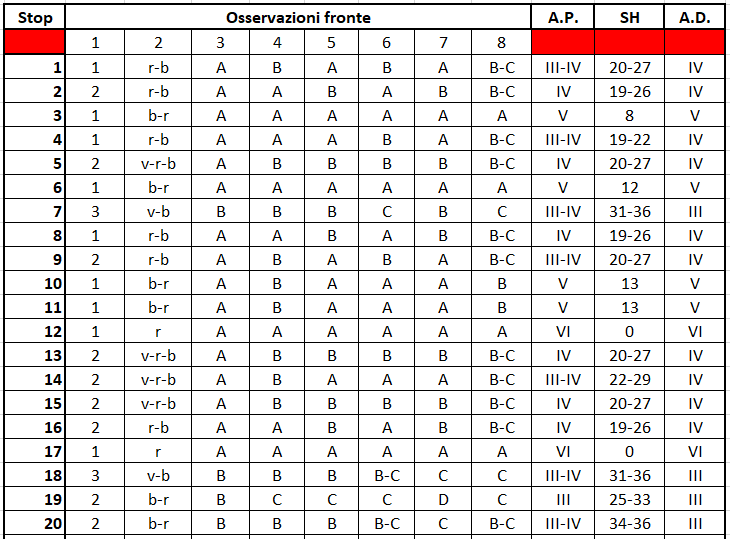
L’assegnazione della classe di alterazione ai punti di controllo è stata ottenuta invece in via definitiva dall’analisi complessiva dei valori di rimbalzo del martello di Schmidt. Gli intervalli di variazione dei rimbalzi del martello possono essere assunti come rappresentativi dei materiali attribuiti alle classi di alterazione presenti nell’area di studio. In particolare abbiamo rilevato valori variabili da 37 a 45 per le rocce di classe III, da 12 a 34 per la classe IV e da 0 a 22 per la classe V; i terreni di classe VI non forniscono valori di rimbalzo. Considerando complessivamente gli intervalli di vaiazione delle classi di alterazione delle rocce cristalline in generale, si osserva che nella classe III varia da 21 a 43, nella IV da 9 a 31, e nella V da 0 a 18. Le differenze riscontrate tra i valori di letteratura e quelli misurati sugli affioramenti dell’area esaminata dipendono dal fatto che i passaggi da una classe ad un’altra sono graduali, come anche testimoniato dalla parziale alternanza tra le classi in alcuni siti. L’analisi delle osservazioni e delle misure condotte, seguite dall’attribuzione definitiva del grado di alterazione è presente nella tabella 4.8. A seguito di queste elaborazioni, la suddivisione in classi è stata utilizzata per creare la carta del grado di alterazione dell’area. Con le stesse modalità utilizzate per la carta degli spessori, è stato aggiunto il campo “classe” allo shape file puntuale che descrive i luoghi di stop, ed è stato applicato il metodo di interpolazione IDW che ha mostrato, come risultato, un file raster che può essere considerato come carta dei gradi di alterazione (Fig. 4.17).
|
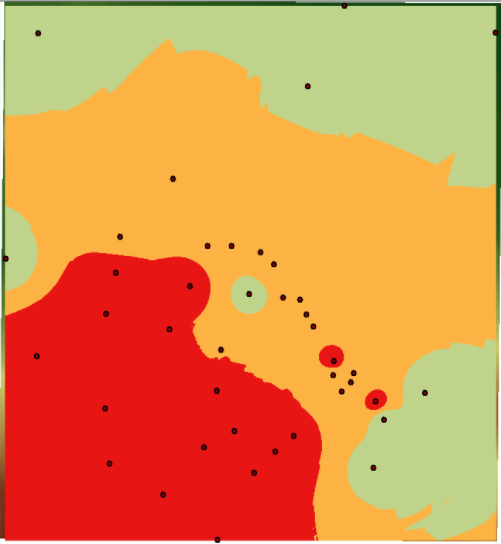
Figure 4.24: carta del grado di alterazione
4.5 Calcolo delle linee segnalatrici di possibilità pluviometrica
Le linee segnalatrici di possibilità pluviometrica o LSPP, sono curve che esplicano la relazione esistente tra le altezze massime di precipitazione e le durate delle stesse che si possono verificare in una determinata area e per un assegnato valore del tempo di ritorno, ossia l’intervallo di tempo intercorrente tra il verificarsi di due eventi successivi di uguale intensità.
Tali curve sono rappresentate tramite una funzione elementare del tipo:
\[\begin{equation} H=f(t) \tag{4.1} \end{equation}\]
In Italia si utilizzano espressioni esponenziali monomie derivanti dalla legge a due parametri di Massari,
\[\begin{equation} H=at^n \tag{4.2} \end{equation}\]
Dove:
\(H\) è l’altezza espressa in mm, \(t\) la durata della pioggia espressa in ore, \(a\) è il
parametro caratteristico della stazione presa in considerazione che dipende dal
tempo di ritorno, ed \(n\) il parametro caratteristico della stazione presa in
considerazione, definito sempre minore di uno, in quanto all’aumentare della
durata l’intensità deve diminuire.
La scelta della distribuzione di probabilità che
meglio si adatta alla popolazione delle altezze di precipitazione di determinata
durata, di cui è noto un certo campione, consente di stimare l’altezza di
precipitazione avente una determinata probabilità di verificarsi.
Per effettuare un’ analisi di questo tipo, è stata prima effettuata un’analisi incrociata dei dati di pioggia appartenenti alle tre stazioni già precedentemente utilizzate, ovvero Cardeto-Liddu, Motta San Giovanni-Allai e Reggio Calabria- Rosario, in modo da ottenere una media di precipitazioni in mm distribuite su 1h, 3h, 6h, 12h e 24h dell’area più in generale, per l’intervallo temporale 2002-2017 (Tab. 4.9).
| Anno | Max 1 h | Max 3 h | Max 6 h | Max 12 h | Max 24 h |
|---|---|---|---|---|---|
| 2002 | 25.6 | 42.4 | 61.4 | 90.0 | 99.0 |
| 2003 | 33.0 | 57.4 | 67.6 | 68.0 | 97.4 |
| 2004 | 27.2 | 38.2 | 54.8 | 64.0 | 68.2 |
| 2005 | 48.6 | 59.2 | 64.6 | 64.6 | 79.2 |
| 2007 | 18.8 | 30.0 | 38.6 | 40.0 | 56.2 |
| 2008 | 24.6 | 44.6 | 50.2 | 57.0 | 62.8 |
| 2009 | 26.6 | 44.6 | 76.8 | 98.8 | 109.8 |
| 2011 | 31.6 | 44.2 | 79.0 | 92.6 | 95.6 |
| 2012 | 23.0 | 27.0 | 43.6 | 68.6 | 103.2 |
| 2013 | 43.8 | 69.4 | 74.2 | 75.6 | 76.2 |
| 2014 | 33.2 | 42.6 | 74.0 | 112.8 | 137.2 |
| 2015 | 35.8 | 62.6 | 73.4 | 87.0 | 119.8 |
| 2016 | 21.6 | 48.0 | 69.0 | 97.8 | 103.8 |
| 2017 | 38.6 | 41.8 | 65.4 | 106.8 | 144.0 |
I parametri vengono stimati mediante il metodo dei momenti, che si basa sull’ ipotesi che i momenti teorici della distribuzione della variabile casuale siano uguali alle stime campionarie calcolate in base alle osservazioni disponibili, i passi in cui si articola la procedura sono:
- calcolo dei momenti campionari della serie di osservazioni
- considerazione delle relazioni teoriche che legano i momenti della distribuzione ai parametri della stessa.
Sulla base di tali relazioni si stimano i parametri incogniti con il presupposto di uguagliare i momenti teorici a quelli campionari. I momenti teorici di primo e secondo ordine, sono rappresentati dalla media \((\mu)\) e lo scarto quadratico \((\sigma)\), rispettivamente calcolati tramite le formule:
\[\begin{equation} \mu = \frac{\sum_{i=1}^{n}x_i}{n} \tag{4.3} \end{equation}\]
\[\begin{equation} \sigma = \frac{\sqrt{\sum_{i=1}^{n}(x_i-\mu)^2}}{n} \tag{4.4} \end{equation}\]
A questo punto sono stati ricavati dai momenti teorici i parametri \(a\) ed \(u\) tramite le formule: \[\begin{equation} \alpha = \frac{\sqrt{\sigma \mu}}{\pi} \tag{4.5} \end{equation}\]
\[\begin{equation} u = \sigma - (0.5772 \alpha) \tag{4.6} \end{equation}\]
Calcolati i sopracitati parametri è possibile quindi trovare i quantili di precipitazione per gli assegnati tempi di ritorno (\(TR\)), che nel caso in questione è stato posto uguale ad 1 anno, mediante la relazione:
\[\begin{equation} H = u + \alpha \left\{-ln \left[ln \left(\frac{TR}{TR+1}\right)\right]\right\} \tag{4.7} \end{equation}\]
La relazione (4.7) esprime la frequenza mediata di accadimento degli eventi e la lega al tempo di ritorno. I valori di h ottenuti insieme a tutti i parametri calcolati sono espressi in maniera sintetica nella tabella (Tab. 4.10 di seguito allegata.
| Risultati | 1h | 3h | 6h | 12h | 24h |
|---|---|---|---|---|---|
| \(\mu\) | 30.857140 | 46.571430 | 63.757140 | 80.257140 | 96.60000 |
| \(\alpha\) | 2.637556 | 4.958625 | 7.785094 | 10.773580 | 13.58384 |
| \(\sigma\) | 2.222834 | 5.205497 | 9.372559 | 14.259210 | 18.83335 |
| \(u\) | 0.700437 | 2.343379 | 4.879003 | 8.040701 | 10.99275 |
| \(H\) | 3.576800 | 6.673800 | 11.697900 | 18.697980 | 22.69870 |
Una volta calcolate le piogge per i diversi tempi di ritorno al fine di calcolare i parametri dell’equazione di Massari espressa in termini di equazione lineare del tipo:
\[\begin{equation} y = mx+q \tag{4.8} \end{equation}\]
\[\begin{equation} y = t log(n) + log(a) \tag{4.9} \end{equation}\]
I parametri espressi in forma logaritmica sono riportati in Tabella (1.1) ed espressi graficamente nella Figura 4.18.
| log tempo | 0.000000 | 0.477121 | 0.778151 | 1.079181 | 1.380211 |
| log H | 0.553495 | 0.824373 | 1.068108 | 1.271795 | 1.356001 |
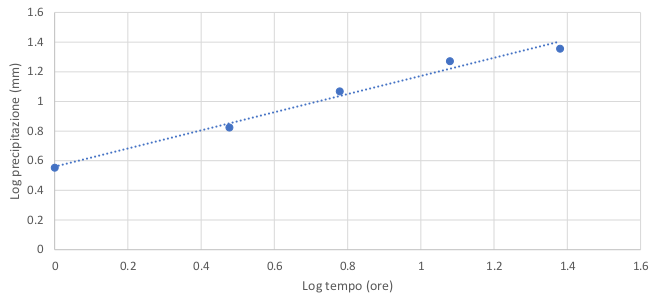
Figure 4.25: rappresentazione grafica della relazione logaritmica tra \(t\) ed \(H\) con annessa retta di regressione lineare
Servendosi dei parametri così calcolati ,sono stati individuati gli elementi della retta di regressione rappresentante la LSPP per quel tempo di ritorno espresso dall’equazione (??); tramite le formule (4.10) e (4.11):
\[\begin{equation} log(n) = \frac{\sum p^2 \sum t - \sum p \sum p t}{N \sum p^2 -\left(p \right)^2} \tag{4.10} \end{equation}\]
\[\begin{equation} log(a) = \frac{N \sum p t - \sum p \sum t}{N \sum p^2 -\left(p \right)^2} \tag{4.11} \end{equation}\]
Dove, \(p\) rappresenta il logaritmo delle precipitazioni (espresso in mm) e \(t\) il logaritmo del tempo (espresso in ore).
I risultati ottenuti sono riportati nella tabella seguente (Tab. 4.12):
| \(log(n)\) | -0.890190 |
| \(log(a)\) | 1.609380 |
| \(n\) | 0.128768 |
| \(a\) | 40.679890 |
Calcolati quindi i parametri della LSPP, sono stati graficati plottando il tempo in
ore e l’altezza di precipitazione in mm presenti nell’equazione di Massari espressa
nella forma più classica (eq (4.2)):
\[
H= a t^n
\]
da cui si ottiene il grafico espresso in fiura 4.19.
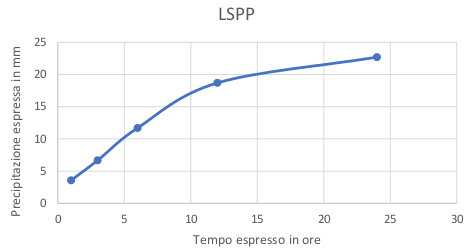
Figure 4.26: rappresentazione grafica della LSPP di progetto
Calcolate le linee di possibilità pluviometrica, grazie ad un applicativo in Adb Toolbox è possibile calcolare lo Ietogramma di progetto necessario alla simulazione andando ad inserire i parametri della curva precedentemente espressi.
4.6 Calcolo di CN, del ritardo e del deflusso di base con il metodo SCS
Per il corretto allestimento delle diverse simulazioni in IDRA2D-DF, è necessario costruire un Idrogramma di progetto e, tra le diverse metodologie messe a disposizione dall’applicativo, si è scelto di utilizzare il metodo SCS 1972, spesso indicato come Soil Conservation Service (SCS) o anche Curve Number (CN). (National Engineering Handbook, Sez. 4: Hydrology (NEH-4) 1993). Tale metodo ha lo scopo di studiare la risposta idrologica di un bacino in termini di deflusso superficiale o di pioggia netta. Si usa questa procedura per trasformare la pioggia totale che ricade in un bacino per una certa durata calcolata mediante la linea segnalatrice di probabilità pluviometrica LSPP, servendosi di analisi statistiche di serie dei massimi annuali, descrivendo la distribuzione di probabilità delle piogge giornaliere massime annue in deflusso superficiale, andando a stimare ed escludere le perdite iniziali quali infiltrazioni, evapotraspirazioni etc…Questo modello tende a stimare i valori sia in funzione dello spazio che del tempo ed è basato sulla semplificazione concettuale del processo idrologico. La sua formulazione deriva dall’equazione di bilancio fra i valori cumulati nel tempo dei principali termini dell’afflusso e del deflusso. L’ipotesi alla base del modello è che durante l’intero evento preso in considerazione il rapporto tra perdite per infiltrazione e il deflusso superficiale resti invariato. L’equazione alla base di tale processo è: \[\begin{equation} \frac{F}{S} = \frac{Q}{P-I_a} \tag{4.12} \end{equation}\]
Dove con \(F\) si indicano le perdite effettive generate durante l’evento espresse in mm, con \(S\) la massima capacità di ritenzione idrica del suolo espressa in mm, \(Q\) rappresenta la pioggia netta cumulata espressa in mm, \(P\) la pioggia lorda cumulata espressa in mm, e \(I_a\) le perdite iniziali dovute all’intercettazione, all’infiltrazione e alla saturazione delle depressioni superficiali, sempre espresse in mm. Assumendo che
\[\begin{equation} F = P-Q \tag{4.13} \end{equation}\]
da cui si ricava che:
\[\begin{equation} P_e = (P-I_a)\frac{F}{S} \tag{4.14} \end{equation}\]
Allora le perdite effettive saranno:
\[\begin{equation} F = P - I_a - P_e \tag{4.15} \end{equation}\]
Da questo si ricava che:
\[\begin{equation} P_e = \frac{P-I_a^2}{P-I_a+S} \tag{4.16} \end{equation}\]
Svolgendo i calcoli si ricava che la pioggia netta \(P_e\) è della stessa entità del deflusso superficiale \(Q\), quindi uguagliando \(P_e\) e \(Q\) si ottiene:
\[\begin{equation} Q = P_e = \frac{P-I_a^2}{P-I_a+S} \tag{4.17} \end{equation}\]
L’equazione ha significato nel caso in cui il valore di \(P\) sia maggiore dell’assorbimento iniziale \(I_a\) , mentre \(Q\) assume valore nullo e quindi l’equazione perde di significato nel caso contrario.
Nell’equazione viene preso in considerazione il parametro \(S\), una grandezza che esprime il grado di saturazione del terreno; tale parametro, così come l’assorbimento iniziale \(I_a\), sono definiti e valutati tramite \(CN\), attraverso le relazioni:
\[\begin{equation} S=S_0\left(\frac{100}{CN}-1\right) \tag{4.18} \end{equation}\]
\[\begin{equation} I_a = \delta S \tag{4.19} \end{equation}\]
dove \(S_0\) è un fattore di scala che dipende dall’unità di misura adottata e che per valori di \(S\), \(F\), \(P\) misurati in mm, è pari a 254 mm e \(\delta\) è un coefficiente di proporzionalità universalmente accettato pari a 0,2 nel caso di misure in mm.
\(CN\) esprime la relazione esistente tra pioggia cumulata e pioggia netta in funzione della sua variazione e dipende dalla litologia del terreno, dal tipo di copertura ricavabile tramite le condizioni di uso del suolo, da condizioni iniziali di umidità del suolo antecedenti l’evento preso in considerazione, e dalla stagionalità della copertura vegetazionale. Il parametro \(CN\) è un numero adimensionale che varia tra 100 per corpi idrici e suoli completamente impermeabili e circa 30 per suoli permeabili con elevati tassi di infiltrazione; per valori di \(CN\) approssimabili a poche unità o comunque inferiori a 30 si può assimilare quella superficie ad una superficie perfetta, ovvero capace di assorbire e trattene percentuali molto elevate di acqua rispetto al totale delle precipitazioni. Con valori di \(CN\) uguali o prossimi a 100, siamo in presenza di terreni o superfici impermeabili dove la precipitazione si trasforma interamente, o quasi, in deflusso.
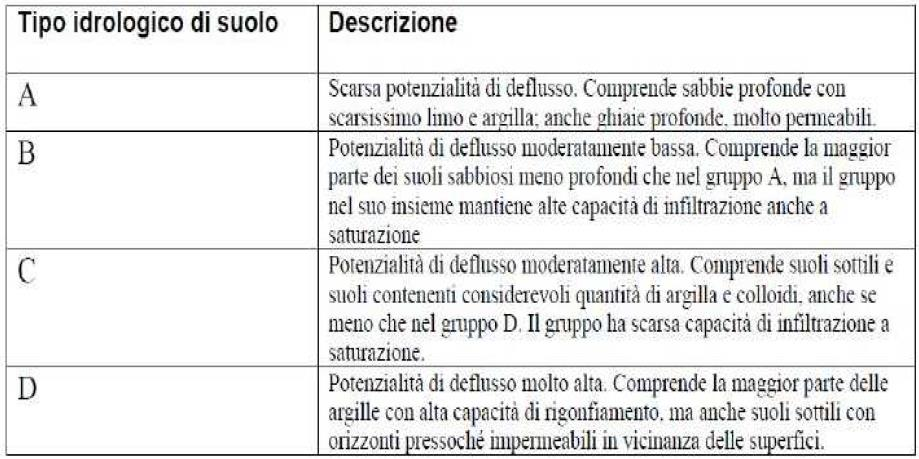
Per la stima corretta del \(CN\) ci si serve di una serie di tabelle relazionali e di alcune formule di correlazione. Innanzitutto bisogna individuare la classe di suolo in base alla capacità di assorbimento dello stesso servendosi della tabella (Tab. 4.13 riportata, fornita dal Natural Resources Conservation Service (NRCS) americano:
|
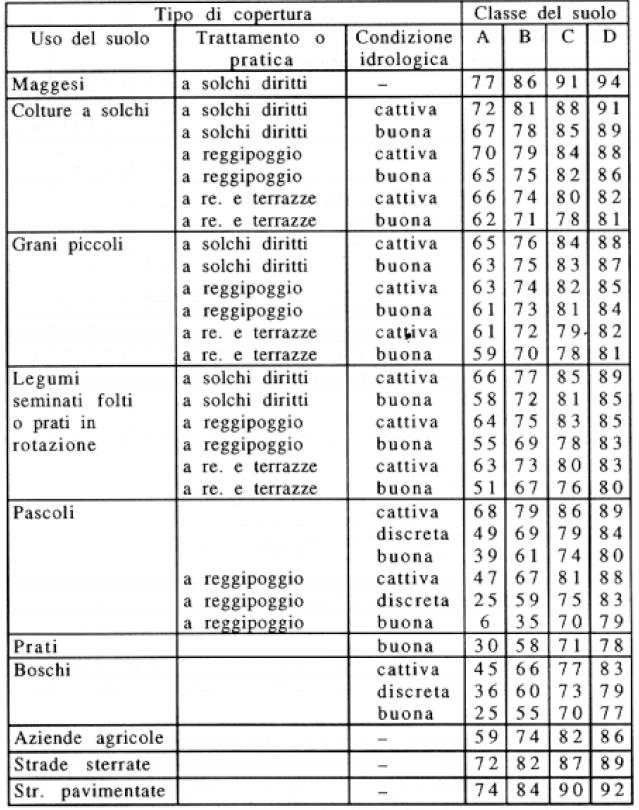
Determinata la classe del suolo in base alla capacità di assorbimento, e nota la classe di uso suolo, è possibile definire la classe di appartenenza del terreno e quindi stimare un primo valore del Curve Number, servendosi della tabella di seguito riportata (Tab. 4.14 nella versione tradotta in italiano, anche questa fornita dal NRCS americano.
|
Tale stima è valida per aree a copertura e permeabilità uniformi, mentre, per essere valida ai fini di un’applicazione a scala di bacino va applicata la formula di Mancini e Rosso (1989), che consiste nella stima del Curve Number per singole aree con caratteristiche omogenee, nella somma delle stesse ed il relativo \(CN\) applicando l’equazione:
\[\begin{equation} CN_{tot} = \frac{\sum CN_i A_i}{A_{tot}} \tag{4.20} \end{equation}\]
Dove \(CN_{tot}\) rappresenta il valore del Curve Number dell’intero bacino; \(CN_i\), il valore di \(CN\) della \(i\)-esima zona omogenea; \(A_i\) l’area della \(i\)-esima zona omogenea, e \(A_{tot}\) l’area totale del bacino. A questo punto è di fondamentale importanza per una corretta stima del \(CN\), andare a valutare le condizioni di saturazione del terreno. Per una precipitazione di uguale entità ed intensità le diverse condizioni del terreno andranno ad influenzare la risposta del bacino e la portata al colmo. In particolare, si vanno a valutare le condizioni di umidità del terreno antecedenti l’inizio dell’evento (AMC, Antecedent Moisture Condition). L’SCS individua tre classi, AMC I, AMC II e AMCIII, in relazione al valore assunto dall’altezza di pioggia caduta nei 5 giorni precedenti l’evento meteorico. L’attribuzione della classe AMC si basa sui criteri riportati nella tabella allegata (Tab. 4.15):

|
Nel caso in cui le condizioni antecedenti l’evento siano molto umide (AMC III), o molto asciutte (AMC I), si possono stimare i relativi valori di \(CN\) dalla tabella ed ascriverli ad una condizione media di umidità (classe II) tramite le relazioni seguenti:
\[\begin{equation} CN(I) = \frac{4.2CN(II)}{10-0.058CN(II)} \tag{4.21} \end{equation}\]
\[\begin{equation} CN(III) = \frac{23CN(II)}{10+0.13CN(II)} \tag{4.22} \end{equation}\]
Per quanto riguarda l’area oggetto di questa tesi, si può ritenere quasi completamente ricoperta di boschi, riservando una quantità pari a circa il 30% dell’intero bacino idrografico alla presenza di strade asfaltate e/o sterrate. Per questo motivo è stato stimato un \(CN\) pari a 75. Un ulteriore passaggio, fondamentale per la creazione dell’Idrogramma di progetto attraverso il software, si riferisce alla valutazione del tempo di ritardo o lag time del bacino. Il lag time è definibile come la distanza temporale tra il baricentro dell’idrogramma di piena superficiale filtrato, quindi senza andare a considerare le portate di base che sarebbero defluite nel corso d’acqua in assenza dell’evento che ha innescato la piena, e il baricentro del pluviogramma netto (Fig. 4.20).
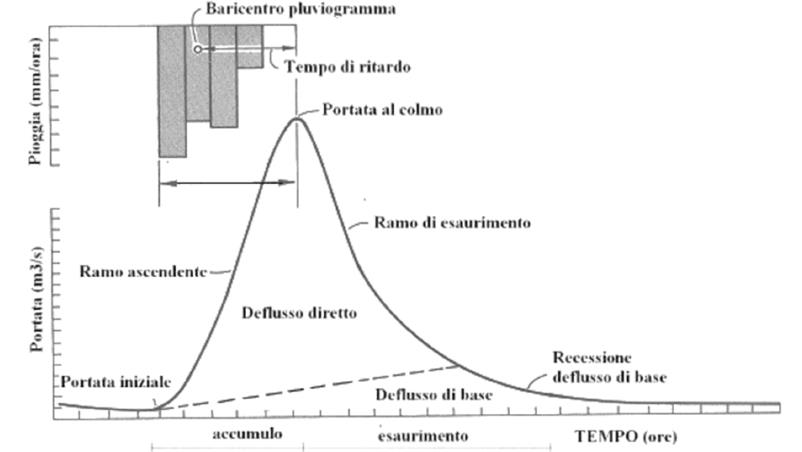
Figure 4.27: rappresentazione grafica della LSPP di progetto
Per la stima del tempo di ritardo del bacino può essere utilizzata la formula di Mockus (SCS, 1972):
\[\begin{equation} t_1 = 0.342\frac{L^{0.8}}{s^{0.5}}\left(\frac{1000}{CN}-9 \right)^{0.7} \tag{4.23} \end{equation}\]
Dove con \(s\) si indica pendenza del bacino espressa in %, e con \(L\) la lunghezza dell’asta principale espressa in Km. Sapendo che i parametri di s ed L per l’area in esame sono rispettivamente pari a 46.6% e 2.2 Km, il tempo di ritardo misurato per questo progetto risulta di 0.2h. Attraverso il calcolo di \(CN\) e conoscendo il tempo di lag, si può fare una stima anche del deflusso di base, in gran parte dovuto allo scorrimento sotterraneo e pertanto di solito caratterizzato da tempi molto lunghi.; si può infatti manifestare anche mesi o anni dopo il termine delle precipitazioni che lo hanno originato in quanto l’acqua può accumularsi nelle falde sotterranee anche in grandi quantità. L’entità dei tempi di risposta è legata certamente alle dimensioni degli acquiferi ed alla natura delle formazioni geologiche. L’indice \(Q\) del deflusso di base si stima tramite la formula:
\[\begin{equation} Q=C\frac{Ah}{3.6t_c} \tag{4.24} \end{equation}\]
Con \(A\) che esprime l’area di studio in km2, \(t_c\) il tempo di corrivazione e \(C\) il rapporto tra pioggia efficace e totale. Per il calcolo del tempo di corrivazione utilizziamo la formula di Pezzoli
\[\begin{equation} t_c= 0.05\frac{L}{\sqrt{p}} \tag{4.25} \end{equation}\]
Dove \(p\) rappresenta la pendenza media dell’alveo. Il parametro \(C\) invece è rappresentato dalla formula seguente
\[\begin{equation} C = \frac{(h-I_a)^2}{h-I_a+S} \tag{4.26} \end{equation}\]
Con \[\begin{equation} I_a= 0.05S \tag{4.27} \end{equation}\]
\[\begin{equation} S=254\left(\frac{100}{CN}-1 \right) \tag{4.28} \end{equation}\]
Sulla base di queste formule, il valore di \(Q\), assieme a tutti gli altri parametri relativi, è mostrato nella tabella seguente (Tab. 4.15)
| parametri | valori |
|---|---|
| \(A\) | 1.18km\(^2\) |
| \(h\) | 23 mm |
| \(L\) | 2.2 Km |
| \(p\) | 37.6° |
| \(CN\) | 75 |
| \(t_c\) | 0.014h |
| \(S\) | 84.6667 |
| \(I_a\) | 4.23333 |
| \(C\) | 3.40497 |
| \(Q\) | 1430.94 |
4.7 Risultati di suscettibilità all’innesco con Scoops3D
I dati geomeccanici, i layer relativi al bottom delle coperture e al bottom del substrato, il DEM del bacino idrografico considerato e le relative misure di volume massimo e minimo mobilitato, sono state utilizzate per lanciare il programma Scoops3D ed ottenere risultati relativi alla mappa di suscettibilità all’innesco derivabile dal valore del fattore di stabilità media per ogni cella considerata nell’area. Il livello di falda è stato parametrizzato considerandolo a 2 m, 4 m, 6 m ed 8 m rispetto al piano campagna, per valutare l’influenza delle fluttuazioni del livello piezometrico sulla distribuzione del fattore di stabilità. Di seguito sono presentate le carte di distribuzione di FS in relazione al livello variabile di falda.
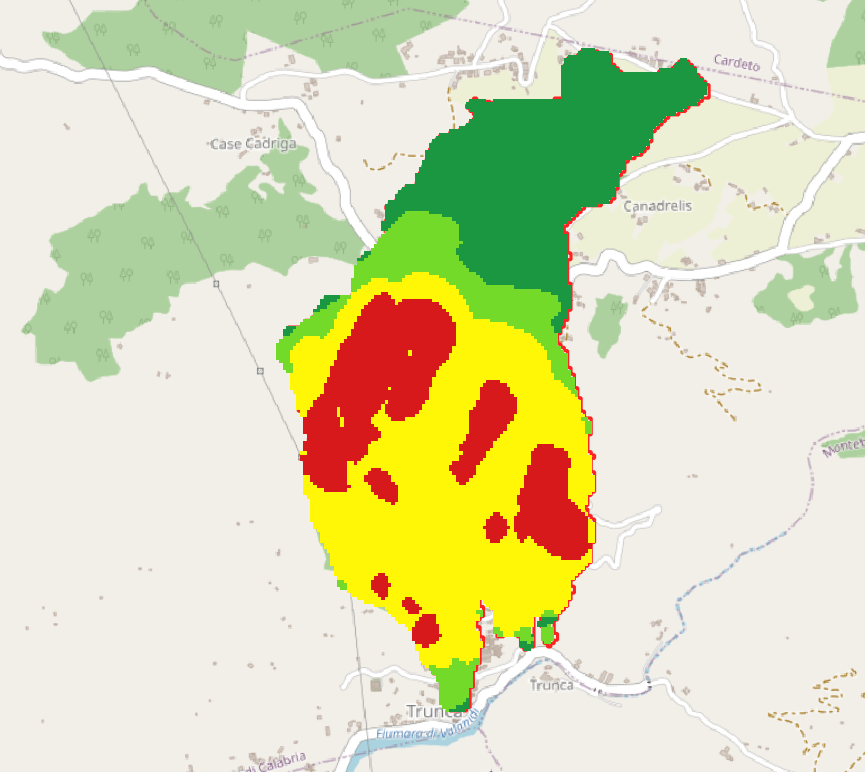
Figure 4.28: carta FS con falda a -2m dal piano campagna
4.8 Risultati di suscettibilità all’invasione con IDRA2D-DF
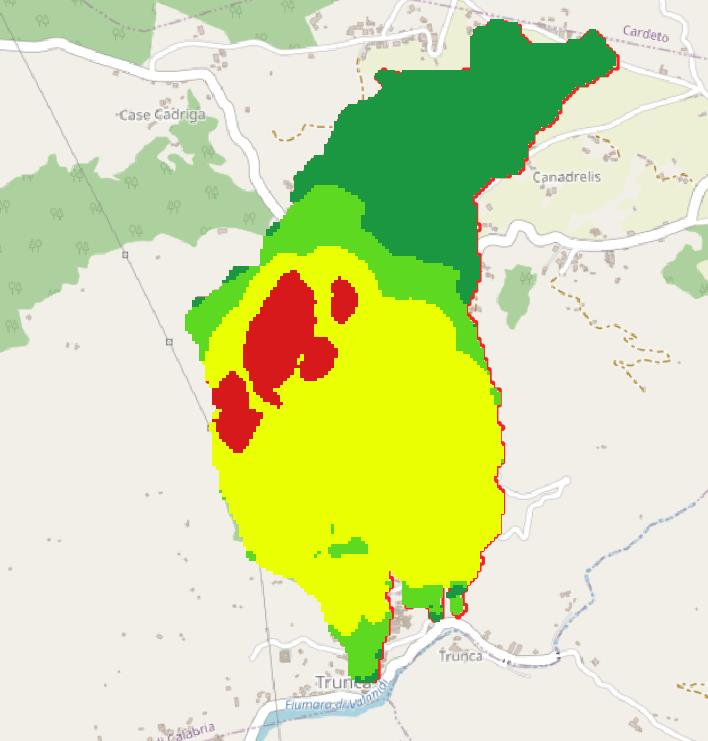
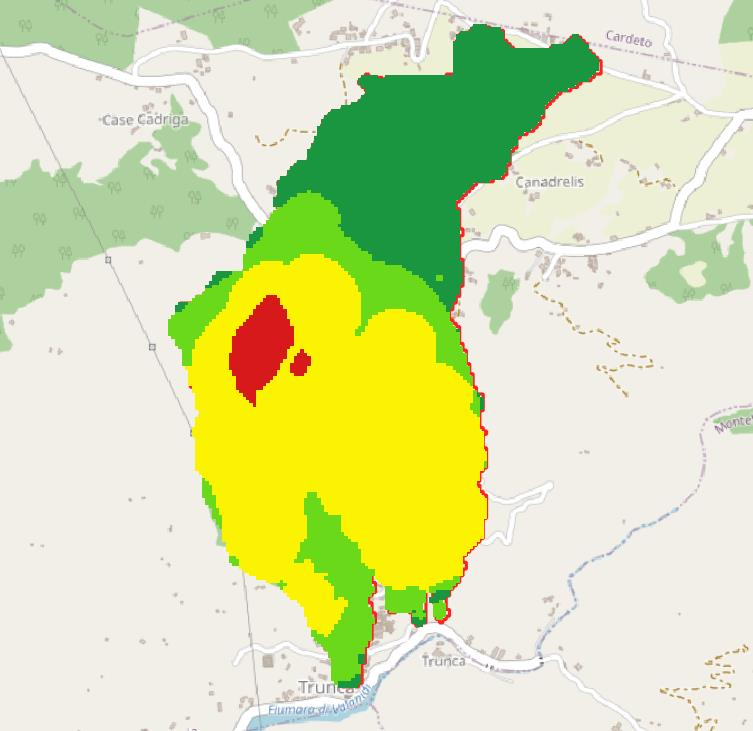
Figure 4.29: carta FS; in alto falda a -4 m, in basso falda a -6m dal piano campagna
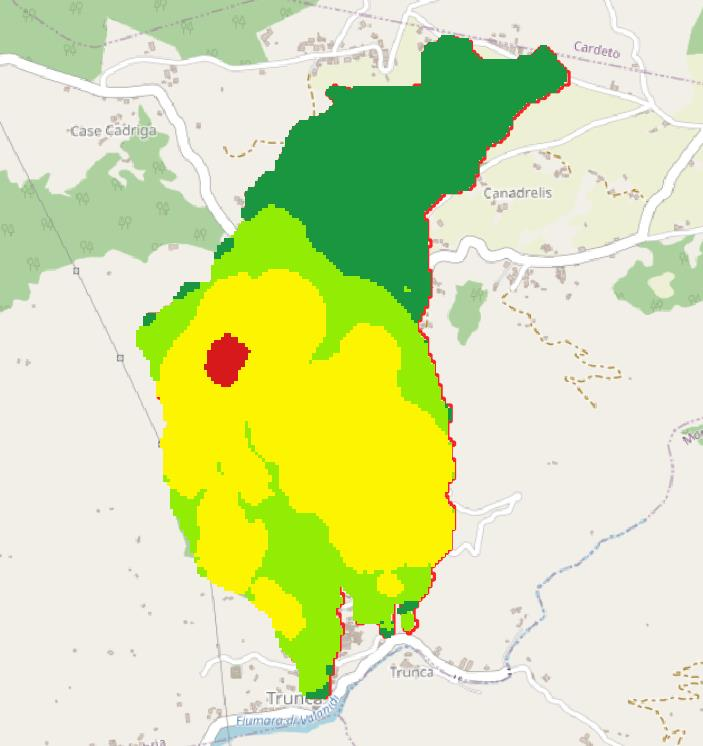
Figure 4.30: carta FS con falda a -8 m dal piano campagna