Capitolo 2 Concetto di suscettibilità

Quando si parla di dissesto idrogeologico non si può non tenere conto che il problema rientra nel più ampio contesto di riferimento dell’analisi del rischio e della valutazione della pericolosità, concetti per i quali è sempre meglio fornire un’adeguata definizione.

Il rischio si definisce come

\[\begin{equation} R = H\cdot V\cdot E \tag{2.1} \end{equation}\]

dove \(H (Hazard)\) rappresenta la pericolosità ovvero la probabilità che un evento potenzialmente distruttivo, di determinata intensità, si verifichi in una determinata zona in un determinato periodo di tempo;

con \(V\) si intende la vulnerabilità, cioè il grado di perdita prodotto su un certo elemento o gruppo di elementi esposti al rischio risultante dal verificarsi di un fenomeno naturale di una data intensità;

con \(E\) si considera l’esposizione, cioè il valore esposto dalla zona.

Il principale contributo della ricerca e della modellistica è centrato nel calcolo e nella definizione del fattore \(H\). la valutazione della pericolosità segue un approccio basato sulla regola delle cinque \(W+H\), ovvero sei domande tramite le cui riposte si potrà ottenere un quadro completo ed esaustivo della situazione:

• When: bisogna stimare quando è avvenuto questo evento, e potenzialmente quando potrebbe ripetersi
• What: bisogna avere un quadro chiaro e preciso del fenomeno che si sta indagando che può rappresentare un rischio
• Where: bisogna individuare l’area interessata o potenzialmente interessata da un determinato evento
• Who: bisogna stimare quali sono gli elementi potenzialmente esposti al rischio
• Why: bisogna stimare la possibilità di formulare ipotesi circa la possibilità che uno stesso evento vada a coinvolgere aree con simile caratteristiche
• How: bisogna stimare la magnitudo o l’intensità dell’evento

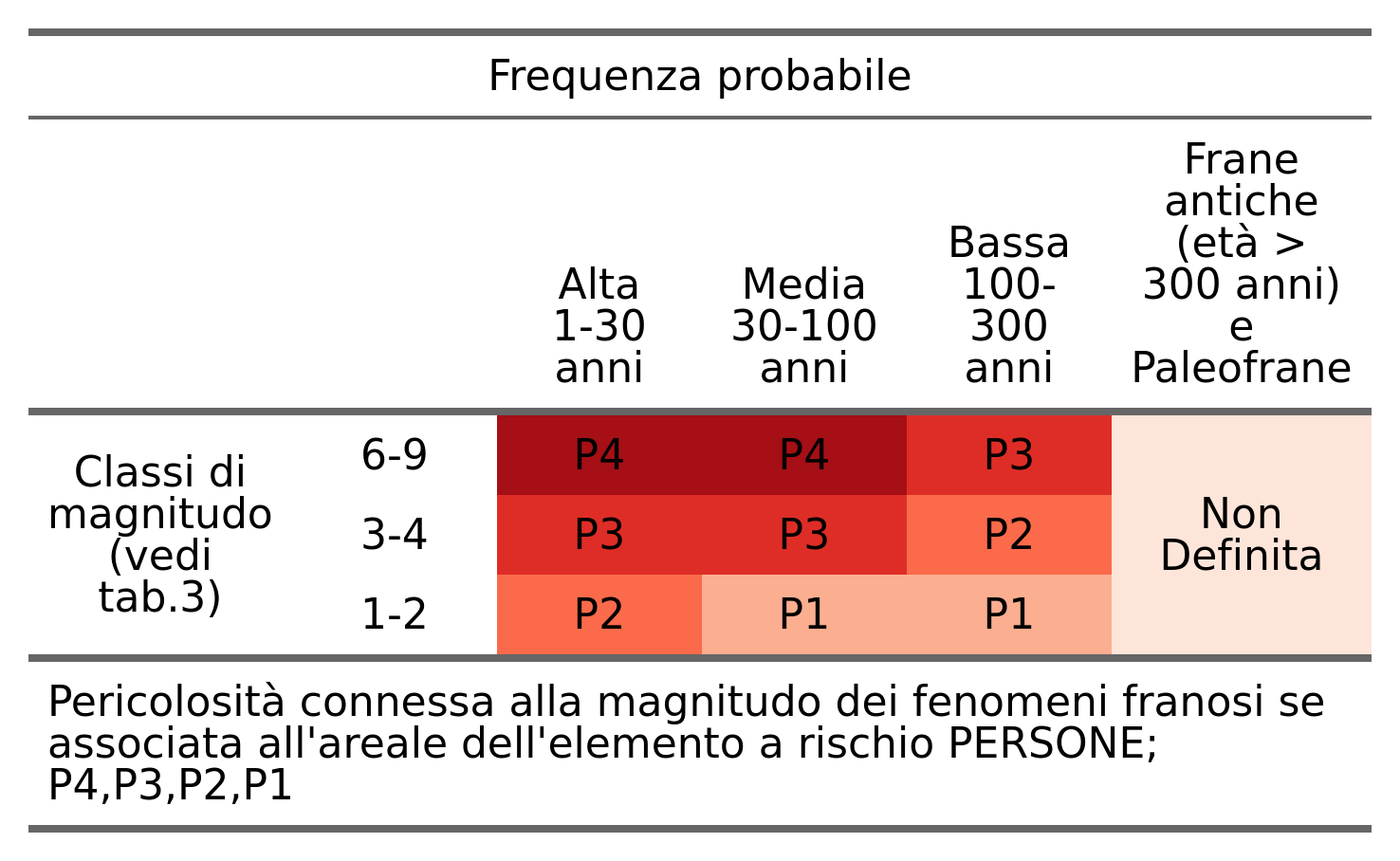
Rispondendo a queste domande, nella formulazione dell’ipotesi di pericolosità si va a quantificare il parametro dell’Hazard in funzione delle due variabili di Frequenza (\(F\)) ed Intensità (\(I\)) attraverso l’equazione (2.2):

\[\begin{equation} H = f(F, I) \tag{2.2} \end{equation}\]

Table 2.1: classi di magnitudo (intensità) associati alla frequenza per lo studio dell’Hazard

La ricerca della pericolosità associata alle frane si può dividere in due componenti: la previsione temporale e la previsione spaziale; la prima si basa sull’osservazione della frequenza di avvenimento dei fenomeni franosi; si tratta, quindi, della risposta alla domanda Quando un fenomeno franoso potrebbe accadere. Per arrivare a definire questa tendenza al franamento ci si deve basare essenzialmente su tre tipologie di metodi:

1. determinazione dei tempi di ritorno mediante la consultazione delle foto aeree o delle ortofoto che comprendono il territorio in esame;
2. utilizzo dell’interferometria RADAR satellitare, che fornisce informazioni più precise e dettagliate rispetto alle foto aeree riguardo al movimento dei fenomeni franosi;
3. studio bibliografico degli afflussi meteorici che rappresentano le precipitazioni che si sono verificate nell’arco degli anni sul territorio.

La previsione spaziale invece, meglio conosciuta come suscettibilità, è volta alla localizzazione sul territorio delle aree più propense al dissesto e quindi alla realizzazione di carte di pericolosità relativa, con ripercussioni e applicazioni sia nel campo della pianificazione territoriale che in ambito di Protezione Civile.

La suscettibilità da frana può essere definita come la propensione di una determinata area all’innesco di movimenti di massa in relazione alle caratteristiche intrinseche dei terreni di copertura e del substrato, delle caratteristiche morfologiche, ed alla maggiore esposizione nei confronti degli agenti climatici. La suscettibilità non considera la ricorrenza temporale, né la dimensione delle frane. In termini matematici, la suscettibilità da frana è comunemente espressa come la probabilità d’occorrenza spaziale di un dissesto, dato un insieme di condizioni territoriali e ambientali. La zonazione della suscettibilità da frana suddivide e classifica un territorio sulla base della propensione che lo stesso ha di produrre frane. Le mappe di suscettibilità da frana sono quindi propedeutiche alla zonazione della pericolosità e del rischio, e possono essere strumenti utili alla pianificazione ed alla gestione territoriale. L’analisi di suscettibilità richiede alcune assunzioni di base (Guzzetti et al., 1999):

1. Ogni evento franoso lascia sul terreno delle tracce caratteristiche che sono riconoscibili e mappabili attraverso rilievi sul campo o da remoto;
2. I meccanismi di innesco di un qualsiasi fenomeno franoso obbediscono a leggi fisiche, quindi la raccolta dei fattori di instabilità consente la definizione dei modelli di suscettibilità;
3. I dissesti futuri si verificheranno sotto le stesse condizioni che hanno causato i dissesti passati;
4. E’ possibile determinare la probabilità spaziale e temporale dei dissesti attraverso l’analisi dei fattori geologico-ambientali.

Quindi, un dato territorio può essere classificato in accordo ai diversi gradi di probabilità di essere soggetto a una determinata tipologia di dissesto.

2.1 Metodi d’analisi della suscettibilità da frana

L’estrema varietà dei fenomeni franosi, delle loro cause, e dei loro possibili effetti, rende difficile definire una metodologia universale per identificare e mappare una frana o per definirne la suscettibilità e il rischio. Esiste una letteratura specializzata, prodotto dell’esperienza acquisita da esperti del settore in numerose aree in tutto il mondo, che mostra la varietà di strategie, di applicazioni e la possibilità di combinazione tra diversi metodi e tecniche. In particolare, per la mappatura della suscettibilità, esistono diversi criteri di approccio, funzione degli scopi e della scala di analisi.

In generale, questi criteri sono raggruppabili in tre grandi famiglie: modelli euristici; metodi statistici; modelli deterministici (Guzzetti et al., 1999; van Westen et al., 2003; Brenning, 2005; van Westen et al., 2008; Cascini, 2008; Constantin et al., 2011; Neuhäuser et al., 2012; Reid et al., 2015; Chen et al., 2018):

1. I metodi Euristici sono approcci empirici qualitativi o quantitativi, in parte legati alla soggettività di chi produce il modello. La soggettività in sé non è necessariamente un aspetto negativo, specialmente se è basata sull’opinione di un “esperto”. Il successo dipende quindi dal grado di conoscenza che l’operatore possiede del territorio in studio e dei processi morfologici. Inizialmente “l’esperto” individua i fattori che favoriscono, condizionano e determinano i dissesti. Ogni fattore viene suddiviso in classi, ad ognuna delle quali viene attribuito un peso che ne esprime la maggiore o minore propensione al dissesto. Al fine di valutare correttamente l’influenza relativa di ogni classe, se si dispone di un catalogo dei dissesti, può risultare utile analizzare la frequenza degli eventi nelle singole classi di ogni fattore per calibrare il modello. La carta di suscettibilità viene ottenuta sovrapponendo le mappe relative ad ogni fattore. Ogni unità di territorio di questa mappa risulterà caratterizzata da un indice di suscettibilità il cui valore è uguale alla somma dei pesi di ogni classe. È possibile assegnare anche un peso ad ogni fattore, per esprimerne l’influenza relativa. In questo caso il peso di ogni classe viene moltiplicato per il peso del fattore di appartenenza. Una mappa di suscettibilità euristica quindi si basa su rilievi di campagna e/o fotointerpretazione (Canuti et al., 1979; Cardinali et al., 2002) i cui risultati sono poi interpretati secondo i criteri dettati dall’esperienza, elaborando i dati (variabili indipendenti) in modi non formalizzabili. Questo metodo ha il difetto di essere soggettivo e fortemente legato alla presenza e alla qualità (non scontate) di dati di campagna; d’altra parte può prendere in considerazione particolarità e disomogeneità difficilmente modellabili. Può di conseguenza capitare che la mappa di suscettibilità prodotta non rispecchi la distribuzione delle frane, così come rilevabile attraverso indagini geomorfologiche. È possibile correggere il modello attraverso aggiustamenti successivi tramite confronto con un catalogo dei dissesti.

2. I metodi deterministici si basano sulla comprensione e sulla modellazione delle leggi fisiche che governano l’innesco e lo sviluppo delle instabilità. Questi modelli prevedono il calcolo del fattore di sicurezza per ogni unità di mappa, al fine di mapparne la distribuzione spaziale. Il fattore di sicurezza è definito come il rapporto tra forze resistenti e forze agenti lungo la superficie di rottura potenziale. Valori maggiori dell’unità indicano stabilità del pendio, viceversa valori inferiori identificano condizioni di instabilità. I parametri che possono essere presi in considerazione con l’approccio deterministico sono: lo stress normale, l’angolo di attrito del materiale, la coesione, la pressione neutra, lo spessore del suolo, l’accelerazione sismica, i carichi esterni, etc. Inoltre, in relazione alla tipologia di dissesto, si possono associare modelli di infiltrazione delle piogge e modelli idrogeologici complessi dando vita ai modelli fisicamente basati (Montgomery & Dietrich, 1994; Godt et al., 2008). Questo tipo di approccio ha trovato negli anni larga diffusione in ambito informatico attraverso lo sviluppo di differenti software atti all’elaborazione di mappe di suscettibilità, tra cui SHALSTAB (Montgomery e Dietrich,1994), TRIGRS (Baum er al.,2002) e Scoops3D (Reid et al., 2015), utilizzato nel presente lavoro di tesi con lo scopo di studiare la suscettibilità all’innesco dell’area in esame.

3. Della categoria dei metodi Statistici fanno parte le regressioni mono o multivariate, le reti neurali e l’indicizzazione delle cause. Tutti questi metodi si basano su una banca dati di calibrazione dove si conoscono i valori delle variabili indipendenti (input e parametri) e la corrispondente variabile dipendente (output). Gli algoritmi contenuti in questi metodi ricercano le relazioni e i coefficienti ottimali che legano le variabili indipendenti a quella dipendente. Sono questi i metodi più adatti all’analisi in aree molto vaste. Attraverso i metodi statistici è possibile valutare quantitativamente e oggettivamente l’incidenza di ciascun parametro sul verificarsi di un evento franoso noto. I pesi sono calcolati con relazioni, diverse per ogni metodo, che considerano il rapporto spaziale tra l’area occupata da ogni classe e l’area in frana nella stessa classe. Esistono due sottogruppi principali: metodi bivariati (Constantin et al., 2011, Chen et al., 2018) e metodi multivariati. I metodi bivariati considerano i fattori geologico-ambientali come variabili indipendenti nel favorire i dissesti. Tutti i fattori sono correlati con la variabile dipendente (catalogo dei dissesti) e attraverso l’incrocio di ogni fattore con la mappa dei dissesti se ne calcolala quantitativamente la relazione. Successivamente si utilizzano diversi metodi per determinare il peso di ogni tematismo elaborato e concorrente all’attivazione della frana, come il metodo del Weight of evidence e del Fraquency ratio (Spielgelhalter, 1986; Bonham-Carter et al., 1989, Neuhaser et al., 2012). Con i metodi multivariati è invece possibile calcolare anche il contributo relativo dei singoli parametri. Si considera infatti l’influenza reciproca dei fattori e si realizzano modelli in cui tutte le variabili agiscono contemporaneamente sulla suscettibilità. Le tecniche statistiche multivariate più usate sono quelle della regressione lineare multipla, dell’analisi discriminante e della regressione logistica (Guzzetti et al., 2006; Akgun and Turk, 2011).

Per ognuno di questi modelli d’analisi esistono numerosi metodi applicazione, molti dei quali si sono sviluppati in tempi recenti conseguentemente al diffondersi dell’uso di sistemi informatici territoriali (GIS) (Umar et al., 2014; Chen et al., 2017; Buecchi et al., 2019; Di Napoli et al., 2020).

2.1.1 Scala di applicazione

La scala di analisi per la valutazione della suscettibilità è innanzitutto connessa agli scopi che si propone la stessa analisi e al dettaglio che essi richiedono. La scelta della scala però può anche rappresentare una restrizione per la scelta del metodo di analisi e all’atto di reperire i dati; può risultare infatti privo di significato applicare metodologie di “base” su scale dettagliate o, viceversa, metodi “sofisticati” su aree molto estese, per cui la risoluzione e la qualità dei dati devono essere adeguate alla scala di analisi (Cascini, 2008; van Westen et al., 2008) (Tabella 2.2). In accordo con Cascini (2008), le scale per la valutazione della suscettibilità possono essere classificate in:

Table 2.2: Metodi, livelli e tipologie di zonazione a scale differenti. : applicabile; (): potenzialmente applicabile; [*]: sconsigliato e non usato comunemente. Modificato da Cascini (2008)

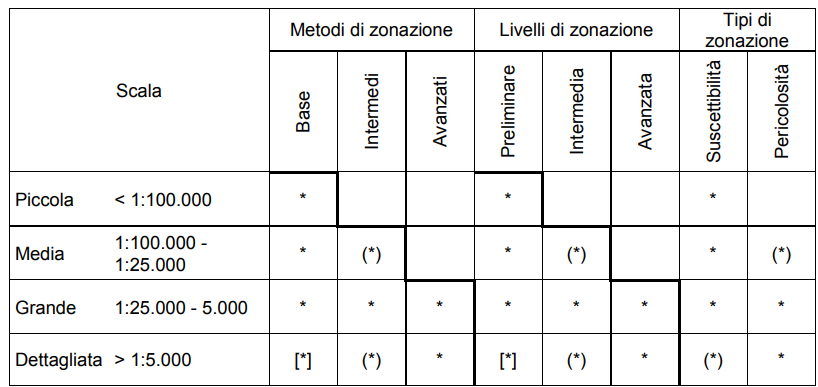
• Piccola scala ( < 1:100.000 ), solitamente usata per analisi di suscettibilità su scala nazionale o regionale con estensioni dell’ordine di 10⁴ km² e più. Lo studio a queste scale permette solo applicazione di metodologie di base, spesso di tipo qualitativo, che consentono valutazioni di carattere esclusivamente generale. Può essere utile per l’individuazione delle porzioni di territorio sulle quali approfondire le indagini.

• Media scala ( 1:100.000 – 1:25.000 ) indicata per estensioni da 103 a 104 km2. Anche questo tipo di scala può essere usata in studi preliminari per l’individuazione di aree con problematiche specifiche che necessitano un approfondimento con un elevato dettaglio.

• Grande scala ( 1:25.000 – 1:5.000 ) a questa scala è già possibile applicare metodologie quantitative per l’analisi e la zonazione del territorio in classi di suscettibilità con dettaglio sufficiente da poter essere base per interventi di pianificazione territoriale ed urbanistica. L’estensione superficiale è solitamente compresa tra 10 e 103 km2.

• Scala di dettaglio ( > 1:5000 ) per estensioni non superiori alla decina di km². A questa scala è possibile l’applicazione di procedure sofisticate per valutazione della suscettibilità (es. metodi deterministici) e, conseguentemente, il grado di confidenza nella classificazione del territorio risulta molto elevato. Il dettaglio del prodotto consente il passaggio al piano del rischio, considerando nell’analisi anche gli elementi vulnerabili e il loro valore. Mappe del rischio così prodotte sono validi strumenti per pianificazioni a livello urbano e perimetrazione delle aree a rischio.

2.1.2 Unità di mappa

Per elaborare una mappa di suscettibilità è necessario suddividere il territorio in esame in unità di mappa, ovvero porzioni caratterizzate da uniformità dei caratteri geologico-ambientali. Ogni unità di mappa sarà quindi caratterizzata da una combinazione di fattori differente da quelle immediatamente adiacenti. Esistono differenti criteri di suddivisione in unità di mappa (Guzzetti et al., 1999). Tra quelli più in uso ricordiamo:

1. Griglia di Celle. Le “celle” sono il risultato della suddivisione del territorio attraverso una griglia a maglia regolare, solitamente quadrata. Ad ogni cella è assegnato un valore numerico che descrive la variazione nello spazio di una determinata caratteristica. Questo tipo di suddivisione è molto usato quando si dispone di informazioni in formato raster. Il limite della griglia di celle consiste nel non essere in grado di approssimare con precisione il limite continuo di un oggetto (limite geologico, unità geomorfologica, etc.), se la dimensione delle celle è maggiore del grado di definizione dell’oggetto stesso.

2. Unità di Terreno; si basano sulla distinzione delle caratteristiche geomorfologiche e geologiche. Tali unità sono caratterizzate quindi da uniformità di processi, di forme o di materiali. Un limite di questa classificazione consiste nella soggettività della distinzione tra i processi o tra le forme del rilievo o ancora può essere rappresentato dalla contemporanea presenza su una stessa area di più processi morfologici.

3. Unique-Condition Units (UCU); sono unità che derivano dalla sovrapposizione delle mappe tematiche di ogni fattore geologico-ambientale che ha influenza sui dissesti. Ogni fattore deve essere suddiviso in un numero finito di classi omogenee e l’intersezione dei limiti delle mappe di tutti i fattori disegnerà la mappa delle UCU. Ogni unità è caratterizzata da un’esclusiva combinazione di fattori che descrivono una particolare condizione dal punto di vista geologico-ambientale. Questo tipo di suddivisione è molto usata quando si dispone di rappresentazioni tematiche in formato vettoriale, in quanto la sovrapposizione di queste risulta molto speditiva mediante elaborazione con sistemi GIS.

4. Unità Idrologiche; Il reticolo di drenaggio e le linee di spartiacque possono rappresentare i limiti di unità idrologiche o idrogeologiche. In questi casi parametri morfometrici e idrologici possono essere considerati fattori predisponenti nella valutazione della suscettibilità. Questo tipo di suddivisione è molto usata (Guzzetti et al,. 2006a; Coelho-Netto et al., 2007; Rossi et al., 2010) poiché, in generale, i processi morfologici che interessano un versante, e quindi l’unità di mappa, possono essere legittimamente considerati omogenei. Tale criterio di suddivisione può essere migliorato prendendo in considerazione i tipi litologici o le classi di uso del suolo.

5. Unità Politico-amministrative. Talvolta, per rispondere all’esigenza di effettuare analisi di suscettibilità su aree molto vaste (scala regionale o nazionale) come unità di mappa possono essere presi in considerazione i confini politico-amministrativi. Può esistere una reale corrispondenza tra questi limiti e quelli geografici e fisiografici di un territorio, ma nella maggior parte dei casi questo tipo di suddivisione rappresenta comunque un limite per l’analisi di suscettibilità.

La scelta del tipo di unità di mappa dipende dal metodo e dalla scala di elaborazione, dalla tipologia di dissesto da investigare e anche dal tipo e dalla qualità dei dati di cui si dispone.

2.2 Modelli utilizzati

Nell’intento di effettuare un’analisi caratterizzata da una certa accuratezza, è stato suddiviso il processo di generazione della mappa di suscettibilità in due stadi, che individuano la fase di innesco e la fase di invasione dei fenomeni franosi. Le mappe di suscettibilità all’innesco identificheranno le aree che più probabilmente potrebbero portare allo scatenarsi di eventi dannosi, mentre le mappe di suscettibilità all’invasione individueranno le aree che più probabilmente potrebbero risultare invase dagli eventi analizzati.

2.2.1 Suscettibilità all’innesco: Scoops3D

Per questa cartografia, è stato utilizzato il software Scoops3D, sviluppato in Fortran 90 dalla U.S. Geological Survey, ramo scientifico del Ministero dell’Interno americano con l’obiettivo di analizzare la stabilità dei versanti mediante modelli tridimensionali utilizzando come base un modello digitale di elevazione del terreno. Scoops3D fornisce diverse opzioni di ricerca sistematica in un intero DEM. Nella ricerca ogni cella del DEM è inclusa in più potenziali frane, quindi il software calcola diverse superfici di rottura potenziali e quella con il fattore di sicurezza (FS) più basso viene registrata e fornita come output per quella singola cella e, partendo da questi valori, ricava il potenziale minimo di stabilità per l’intero DEM; Inoltre calcola il volume massimo della frana generatasi a partire da quella cella e per quel valore registrato di FS. Scoops3D lavora assumendo una superficie di rottura costante, di tipo circolare; questo fattore potrebbe costituire una limitazione per il software ma, il criterio di base della funzionalità del programma prevede la suddivisione del versante in conci che effettivamente permettono di suddividere la superficie di rottura in archi abbastanza piccoli da poter essere ridotti a segmenti, comportando di conseguenza una riduzione delle problematiche geometriche relative alle superfici circolari, seppur semplificando anche l’azione delle forze agenti interconcio normali e di taglio. Bisogna inoltre ricordare che già di per sé, i modelli di rottura all’equilibrio limite, prevedono una semplificazione nel meccanismo di rottura assunto come contemporaneo su tutta la superficie e non progressivo, affidando di conseguenza un valore univoco di FS per ogni superficie di rottura individuata.
Il software in questione prevede l’utilizzo di due modelli geotecnici per la determinazione del fattore di stabilità su superfici di rottura circolari:

1. Metodo di Fellenius (Fellenius, 1936)

\[\begin{equation} FS = \frac{\sum_{i=1}^{n}R_i\left\{ c_iA_i + \left[ \frac{cos^2\alpha_i}{cos \varepsilon_i}\left(W_i - k_{eq}W_itg\alpha_i\right)-u_iA_i \right] tg \varphi_i\right\} }{\sum_{i=1}^{n}W_i\left(R_i sen \alpha_i + k_{eq} e_i \right)} \tag{2.3} \end{equation}\]

2. Metodo di Bishop Semplificato (Bishop, 1955)

\[\begin{equation} FS = \frac{\sum_{i=1}^{n}R_i\left[ c_iA_i + \left(W_i - u_iA_{h_i}\right)tg\varphi_i\right]/m_{\alpha_i} }{\sum_{i=1}^{n}W_i\left(R_i sen \alpha_i + k_{eq} e_i \right)} \tag{2.4} \end{equation}\]

Il modello di Bishop semplificato presenta un processo iterativo indirizzato alla convergenza del valore di FS secondo più ripetizioni della stessa formula matematica, allungando talvolta anche notevolmente il processo di elaborazione dei dati, ma fornendo un valore del fattore di stabilità molto accurato a differenza del metodo di Fellenius che generalmente tende a calcolare un fattore FS più conservativo (ovvero più basso) rispetto ad altri metodi, come dimostrato in diversi studi (Ugai, 1988; Lam e Fredlund, 1993; Cheng e Yip, 2007). i risultati forniti da Scoops3D possono facilmente essere importati in un sistema di informazione geografica (GIS) o in altri software di visualizzazione.

La schermata di partenza del software si presenta come in figura 2.1, suddividendo in blocchi i passaggi utili all’inserimento dei dati di input.

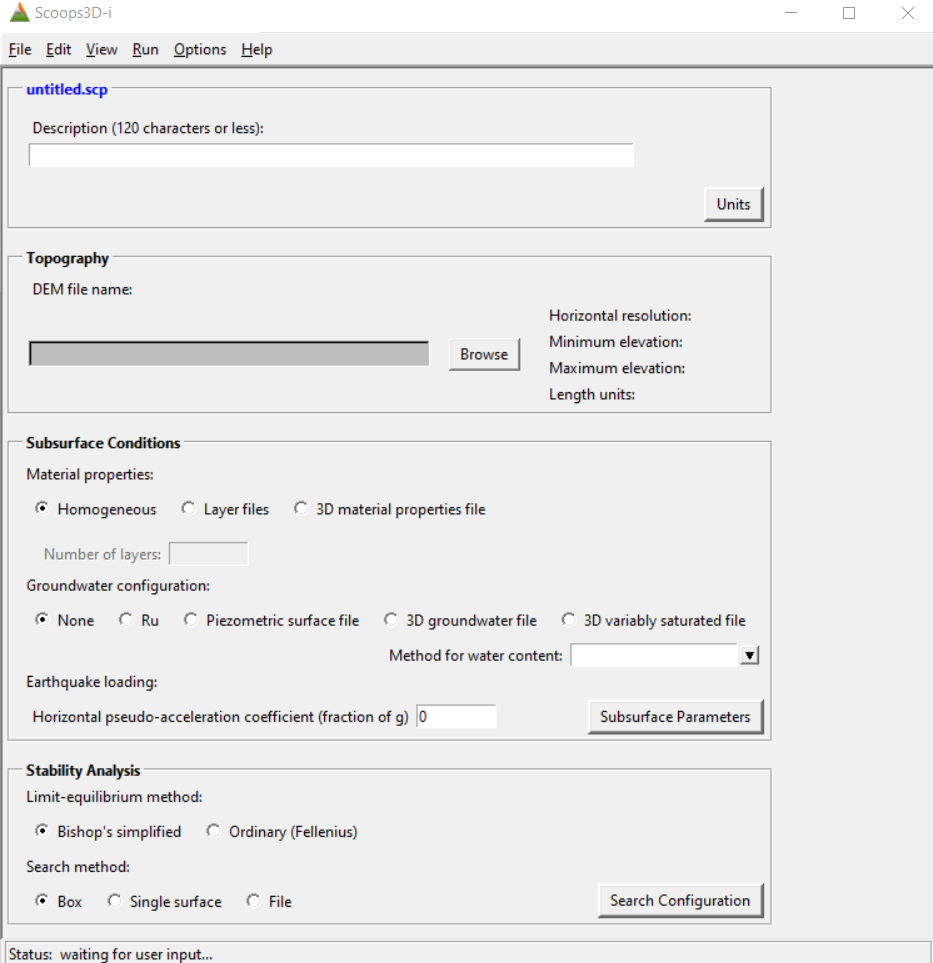
Figure 2.1: schermata iniziale del software Scoops3D

• Untitled.scp: Il primo blocco serve ad inserire una descrizione del progetto, ovvero a rinominarlo, e a definire le unità di misura del progetto (Fig.2.2); le unità di misura sono da definire prima di inserire qualsiasi file di input in quanto il sistema non può riconoscere automaticamente le unità di misura utilizzate, né effettuare conversioni. Le unità scelte per il progetto Innesco_Trunca sono quelle del sistema metrico decimale.

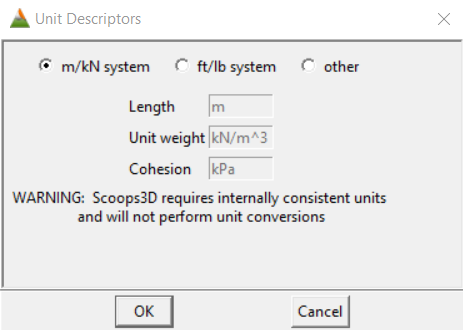
Figure 2.2: schermata di impostazione delle unità di misura

• Il blocco Topography della schermata iniziale del software prevede la definizione di una topografia di base inserendo il file DEM dell’area in formato .asc; automaticamente il programma ne mostrerà i valori di risoluzione ed elevazione (Fig. 2.3)

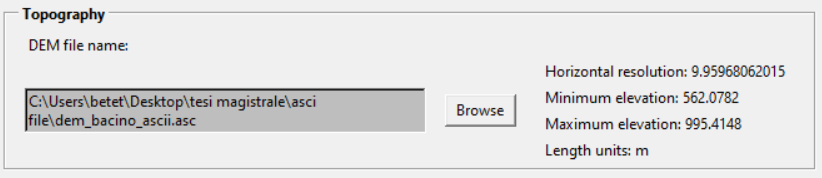
Figure 2.3: schermata di impostazione delle unità di misura

• In Subsurface Conditions si forniscono i parametri geotecnici e idraulici dell’area; questa operazione può differire a seconda della conformazione del sottosuolo. Nella sottocategoria Materials si definisce il terreno come omogeneo (opzione Homogeneous) oppure eterogeneo; un terreno eterogeneo può essere analizzato attraverso l’opzione Layer files che permette di definire il numero di strati in esame e di inserire come dato di input la suddetta suddivisione secondo layer in file ascii, oppure attraverso l’opzione 3D Material properties file inserendo un file testuale ASCII, costruito a partire dal file topografico, in cui per ogni coordinata x, y e z si abbinano i valori geomeccanici necessari. Nella sottocategoria Groundwater configuration si analizzano i dati idraulici di falda; le scelte possibili sono:
  1. non inserire alcun dato di falda (opzione None)
  2. considerare il rapporto della pressione di poro (opzione Ru)
  3. inserire un file ascii riguardante il livello di superficie piezometrica (opzione Piezometric subsurface file)
  4. inserire un file 3D del contenuto d’acqua sotterraneo costruito nello stesso modo del file 3D delle caratteristiche del materiale precedentemente descritto (opzione 3D Groundwater file)
  5. inserire un file 3D del contenuto d’acqua sotterraneo variabile che considera, diversamente dal precedente, le pressioni di poro non omogenee secondo uno schema (definibile dall’opzione Method for water content) fornito tramite file 3D o tramite i parametri delle curve delle proprietà suolo-acqua di van Genuchten o di Fredlund e Xing.

L’ultima sottocategoria del blocco, Earthquake loading, riguarda i valori di carico aggiuntivo dovuto ai terremoti.

Per questo progetto verrà definito il sottosuolo come eterogeneo e costituito di due strati (coltri di copertura e substrato roccioso) e verrà utilizzata l’opzione c. sopra descritta per definire le caratteristiche idrauliche del corpo di falda. Come visibile dalla figura (Fig. 2.4), sono richiesti i dati di coesione, angolo d’attrito interno e peso di volume medio e saturo per i due strati del sottosuolo, oltre che il file .asc che caratterizza il livello della falda; le caratteristiche geomeccaniche del layer 1 sono pervenute dall’attività di tirocinio, mentre quelle del layer 2 provengono dalla letteratura e vengono inserite nel software con valori leggermente maggiorati. Inoltre si è deciso di non fornire i coefficienti di pseudo-accelerazione orizzontale (keq).

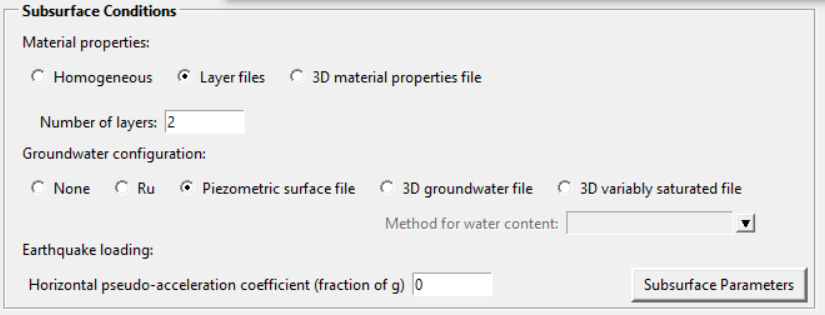
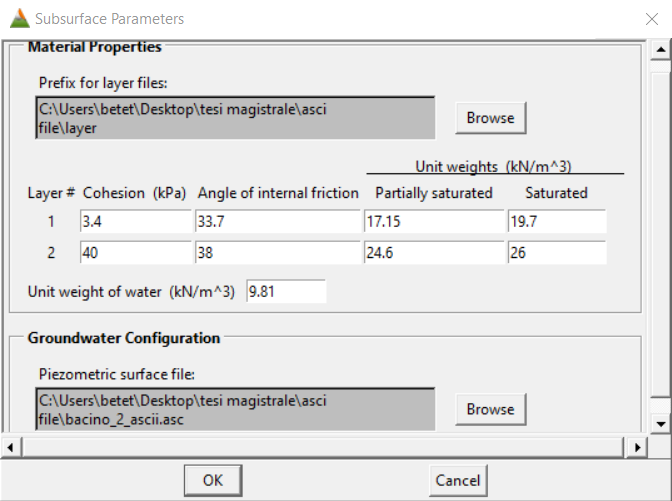
Figure 2.4: in alto blocco subsurface conditions; in basso schermata subsurface parameters con inserimento di dati piezometrici

• In ultimo, Stability Analysis permette di specificare quale modello si vuole utilizzare per l’analisi del versante e per permettere all’utente di aggiungere delle restrizioni alla ricerca della superficie di rottura con il minimo valore di stabilità. In particolare, la prima scelta da effettuare riguarda il metodo di elaborazione dei dati e, per il presente progetto, è stato scelto di utilizzare il metodo di Bishop Semplificato. Il Search Method riguarda l’area di ricerca; una ricerca di tipo Box riguarda un volume di area di studio coincidente con il volume fornito tramite il DEM, una ricerca di tipo Single surface interessa un’unica superficie di rottura definita dall’utente, mentre File è una ricerca volumetrica (come in Box) ma i cui limiti del volume sono definiti, in un file apposito, dall’utente. La schermata d’apertura di Search Configuration (Fig. 2.5) permette di caratterizzare l’area in frana scegliendo dimensioni massime e minime del corpo ipotizzato, sia considerato come volume di materiale franato che come superficie di scorrimento, direzione/i dello scorrimento e dimensioni verticali e orizzontali della cella. Con l’opzione Advanced, se la ricerca effettuata è di tipo Single Surface, nelle configurazioni verrà specificato se si vuole utilizzare una superficie precedentemente calcolata dal software o se la si vuole inserire tramite file, mentre, se l’opzione scelta fosse, come in questo caso, Box oppure File si può scegliere un approccio di tipo Simple search, preferita in questo studio, oppure fine to coarse search.

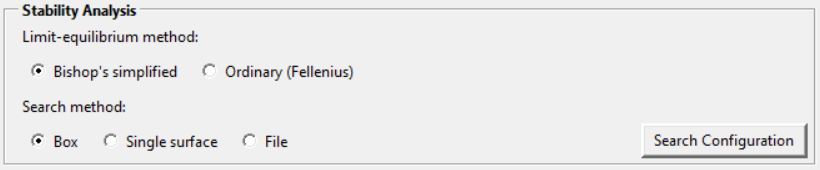
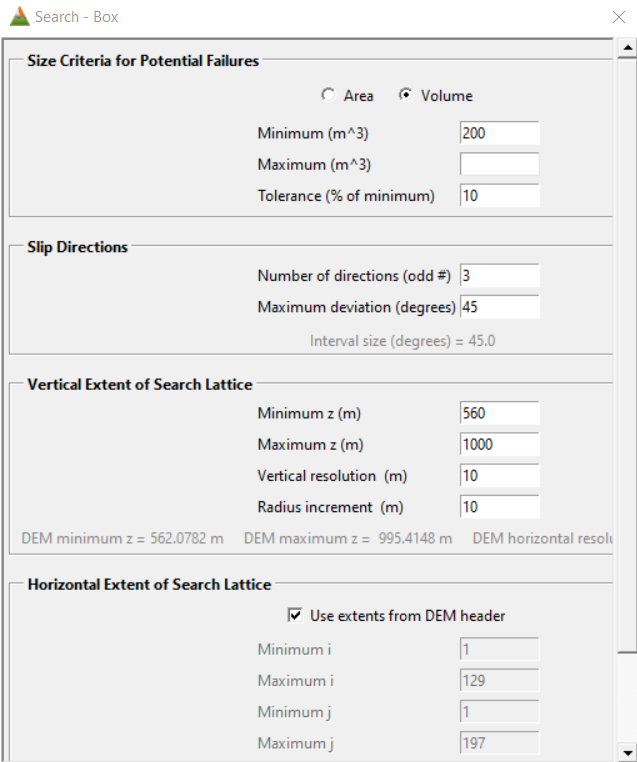
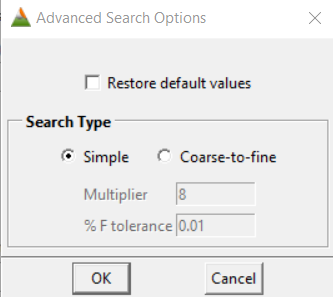
Figure 2.5: Blocco Analisi di Stabilità, definizione del metodo d’analisi, inserimento dati superficie di distacco e risoluzione, opzioni avanzate di ricerca

Inseriti tutti i dati di input e definite le impostazioni di ricerca di progetto, dalla command tool del programma è possibile monitorare i progressi della processazione in quanto si rendono visibili il nome del file input, il nodo di ricerca, il numero di iterazioni eseguite durante la ricerca, la percentuale di completamento di ogni iterazione di ricerca, il numero di superfici di prova analizzate e, al completamento, i file di output creati. Il progetto in questione è stato realizzato ipotizzando il livello di falda a -2,-4,-6 e -8 m dalla superficie del piano campagna, per cui sono state create complessivamente 4 cartelle di output, ognuna relativa ad una delle ipotesi sulla posizione della falda.

Il software restituisce diversi file di output: Il primo che viene fornito alla fine dell’elaborazione è sempre accompagnato dal suffisso _fos3d_out.asc. e contiene una griglia formato ASCII nella quale ad ogni cella viene assegnato il valore di fattore di sicurezza più basso calcolato per quella cella con il metodo richiesto dall’utente. Un’altra mappa prodotta è quella dei volumi (o aree a seconda delle impostazioni precedenti) mobilitati dalla superficie di scorrimento con il minimo fattore di stabilità per ogni singola cella; in questo caso il suffisso è _fosvol_out.asc. L’ultimo file griglia fornito presenta il suffisso slope_out.asc ed è un file ASCII contenente una mappa delle pendenze per ogni cella calcolata a partire dal DEM fornito in Input.

Oltre a questi tre file griglia, sono forniti anche tre file testuali, il primo dei quali, definito dal suffisso out.txt, è un file contenente i dati inseriti in input che descrive il valore minimo del Fattore di Sicurezza dell’area. Il secondo file testuale, _spheres_out.okc, contiene i parametri associati al Fattore di Sicurezza minimo per ogni cella e l’ultimo file, con suffisso _errors_out.txt, è un log contenente eventuali errori riscontrati nella processione delle informazioni.

Di seguito si allega una tabella riassuntiva dei principali output (Tab.2.3)

Table 2.3: descrizione file output Scoops3D

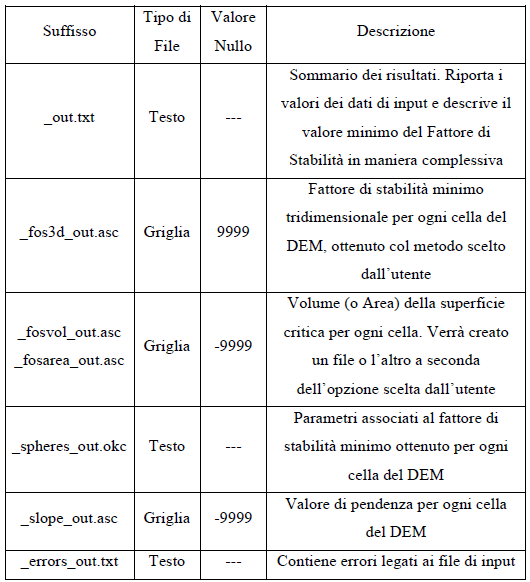
2.2.2 Suscettibilità all’invasione: AdB-Toolbox

AdB-Toolbox è un applicativo GIS open source che può essere utilizzato per visualizzare ed elaborare dataset spaziali. L’applicativo è stato sviluppato nell’ambito del Geoportale Nazionale e ulteriormente integrato di funzionalità specifiche nell’ambito del progetto Sistema Cartografico Cooperante (SCC), del Piano Straordinario di Telerilevamento Ambientale (PST-A), della sua estensione, ed ulteriormente evoluto all’interno del presente progetto PON Sicurezza per il Monitoraggio dell’Impatto Ambientale dovuto a Reati Ambientali (PON-MIADRA).

AdB-Toolbox, basato su tecnologie e librerie di tipo open source è pertanto uno strumento standard, aperto, espandibile, e consultabile da diverse categorie di utenza per analisi di diverso livello di complessità. Per istituire un quadro per la valutazione e la gestione dei rischi di alluvioni volto a ridurre le conseguenze negative per la salute umana, l’ambiente, il patrimonio culturale e le attività economiche connesse con le alluvioni all’interno del territorio nazionale, è stato aggiunto ad AdBToolBox un innovativo strumento di analisi, che riguarda il calcolo bidimensionale sulle piane alluvionali e sulle colate detritiche, identificabile come IDRA2D, suddiviso in funzionalità H ed funzionalità DF. L’utilizzo di uno strumento di propagazione bidimensionale di tale tipo è legata alla necessità di confrontare, anche in termini quantitativi e non solo qualitativi, le variazioni di estensione di una colata con quella esistente nel PAI (Piano stralcio per l’Assetto Idrogeologico), di definire una nuova mappatura della potenziale estensione della stessa laddove se ne venisse a creare la necessità, o ancora di studiare l’effetto post-operam di una struttura di progetto o di un intervento idraulico di miglioramento dei deflussi. Per la parte relative alle piene alluvionali, l’applicativo IDRA2D_H consente l’individuazione delle aree allagabili, delle velocità di flusso, delle altezze dei tiranti, delle direzioni di flusso, dei profili longitudinali, delle sezioni trasversali, nonché la simulazione video dell’evoluzione della piena. Per la parte relativa alle colate detritiche, l’applicativo IDRA2D_DF consente di simulare la modalità di evoluzione di una colata detritica, di costruire il profilo del corpo detritico e la rappresentazione del modello digitale del terreno post-evento.

IDRA2D_H quindi offre un fattivo contributo alla stesura delle mappe di pericolosità da alluvione e alla determinazione dei parametri principali che caratterizzano i fenomeni alluvionali, mentre IDRA2D_DF implementa funzionalità di modellazione bidimensionale delle colate detritiche monofasiche. La combinazione dei due software garantirà output relativi a mappe raster e vettoriali sia di erosione che di deposizione, oltre ad un confronto/interrogazione delle stesse mappe/profili, assieme a vari output detti di secondo livello, che riguardano il setting morfologico post evento.

Questo strumento quindi risulta ottimale per un’analisi di suscettibilità all’invasione in quanto si pone l’obiettivo di generare una griglia di propagazione della colata detritica al fine di permettere all’utente successive valutazioni inerenti le potenziali conseguenze negative, di future colate, riguardo la salvaguardia dell’ambiente, del patrimonio culturale, delle attività economiche e, non in ultimo, della salute umana, rendendo quindi più precisa la creazione di mappe di rischio. Per avviare l’estensione IDRA2D Debris Flow è necessario cliccare sull’apposita icona plugin presente nella toolbar di AdB-ToolBox. All’avvio viene visualizzata la finestra di dialogo iniziale che contiene gli strumenti per la gestione dei progetti (Fig.2.6). Una volta avviata l’estensione IDRA2D-DF, è necessario impostare il workspace ovvero la cartella dove saranno salvati tutti i progetti; successivamente bisogna creare il progetto dall’opzione Nuovo Progetto e rinominarlo.

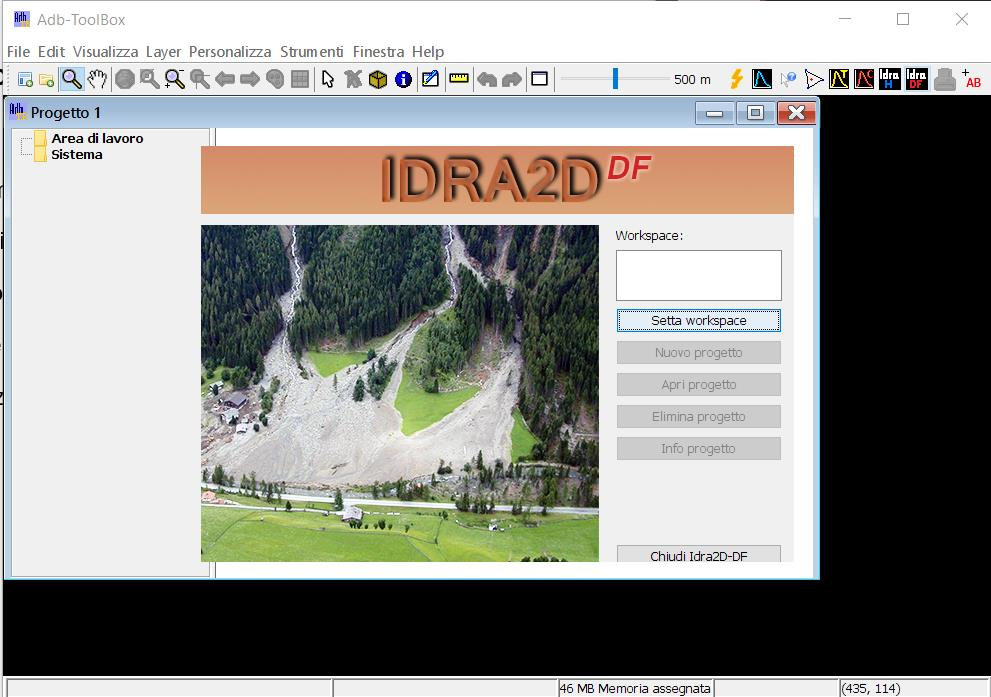
Figure 2.6: schermata di lancio IDRA2D-DF

La creazione di un nuovo progetto implica la formazione all’interno del workspace della struttura cartelle del progetto stesso (Fig.2.7) e la visualizzazione della finestra principale di modellazione che contiene tutti gli strumenti necessari per la modellazione bidimensionale e si presenta suddivisa in sei schede: geometrie, condizioni a contorno, colate detritiche, parametri, output e output colate.

Figure 2.7: creazione percorso cartelle automatico

La disposizione delle schede nella finestra rispetta l’ordine con cui l’utente deve eseguire le operazioni necessarie alla modellazione idraulica dall’impostazione dei dati in input (scheda geometrie) alla produzione dei dati di output (schede output e output colate) passando per il settaggio di eventuali condizioni o parametri necessari a caratterizzare il processo (schede: contorno, colate e parametri). Nelle varie finestre, i comandi relativi alle azioni che devono obbligatoriamente essere effettuate per poter visualizzare una simulazione sono evidenziati in blu.

• Geometrie: in questa scheda (Fig. 2.8) si inseriscono i dati di input relativi proprio alle geometrie, per cui i passaggi obbligati prevedono prima l’importazione del DEM e poi la sua aggregazione. Con il comando importazione DEM è possibile selezionare uno o più file in formato .flt, anche da differenti posizioni, e copiarli nella cartella di progetto 01_Geometry/01_InputDEM. Si procede con lo strumento aggregazione DEM che prevede un ricampionamento, se necessario, delle celle a risoluzione inferiore, e l’unione tra i DEM, nel caso in cui ne sia stato selezionato più d’uno gestendo eventuali aree di sovrapposizione. Per ricampionare i DEM ad una risoluzione inferiore sono presenti quattro metodi di aggregazione:

  1. Min: il valore della cella di output viene dato dal valore più basso presente tra le celle che è stato necessario aggregare.
  2. Max: il valore della cella di output viene dato dal valore più alto presente tra le celle che è stato necessario aggregare.
  3. Mean: il valore della cella di output deriva dalla media dei valori delle celle che è stato necessario aggregare.
  4. Sum: il valore della cella di output deriva dalla somma dei valori delle celle che è stato necessario aggregare.

  Ottenuto il raster aggregato è possibile effettuare diverse operazioni non obbligatorie come il ricondizionamento secondo raster del reticolo idrografico (opzione Ricond.DEM:raster), l’inserimento di file batimetrici di singoli punti o di polilinee quotate (opzione Batimetria da punti o Batimetria da sezioni), l’importazione dell’asta fluviale principale del bacino attraverso l’opzione Thalweg oppure una sua digitalizzazione utilizzando Digitalizza thalweg, la creazione ed estrazione di sezioni trasversali al corso d’acqua con lo strumento Estrai sezioni > Crea nuove sezioni, il calcolo dei profili idrometrici con Inters.Thalweg/sez, e fin anche l’importazione di eventuali immagini dell’area oggetto di analisi (Inserimento foto). L’ultimo passaggio obbligatorio di questa scheda del programma è la scelta del DEM per la modellizzazione, ovvero quello da utilizzare nella simulazione, per poter validare le geometrie.

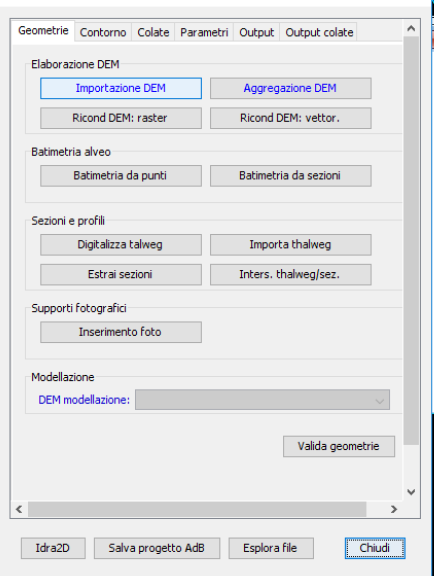
Figure 2.8: scheda geometrie

• Contorno: la seconda serie di input da inserire in IDRA2D-DF è quella relativa alle condizioni al contorno. In questo caso i passaggi obbligatori si riferiscono ad un maggiore numero di dati (Fig. 2.8)

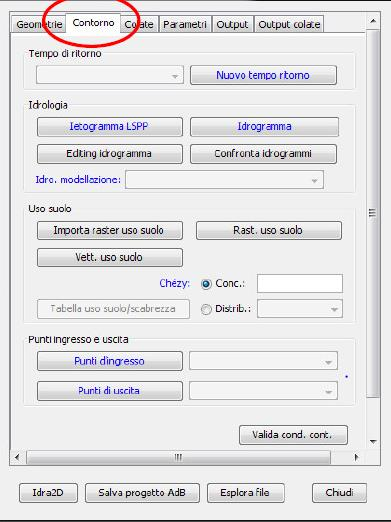
Figure 2.9: scheda contorno

Innanzitutto deve essere inserito il tempo di ritorno, calcolato o ipotizzato, attraverso l’opzione Nuovo tempo di ritorno; la frana in questione prevede un tempo di riattivazione medio di un ciclo stagionale quindi è stato impostato un tempo di ritorno di 1 anno (TR_1). Automaticamente sono state create dal software le cartelle necessarie al salvataggio delle condizioni a contorno per il tempo di ritorno scelto. Si procede con l’inserimento e analisi di dati idraulici, creando innanzitutto uno ietogramma sintetico (Ietorgamma LSPP), ovvero un grafico che rappresenta l’andamento nel tempo dell’intensità di precipitazione (da considerarsi in realtà sempre un’intensità media, calcolata su intervalli di tempo di una certa durata); per costruirlo bisogna discretizzare la durata totale delle piogge in intervalli di durata idonea \(t\), per i quali si misura l’altezza di pioggia \(h\). Il legame funzionale tra l’altezza di pioggia \(h(t)\) e durata \(t\) è solitamente espresso dalla relazione monomia

\[\begin{equation} h(t) = a t^n \tag{2.5} \end{equation}\]

dove i parametri \(a\) ed \(n\) sono caratteristici della stazione e rappresentano rispettivamente l’altezza di precipitazione relativa alla durata di un’ora e la pendenza della retta che rappresenta la suddetta relazione in un cartogramma probabilistico dove,

\[\begin{equation} log(h) = n log(t)+log(a) \tag{2.6} \end{equation}\]

Con “Ietogramma di progetto” si intende un evento pluviometrico generato sinteticamente con l’obiettivo di pervenire ad un corretto dimensionamento o alla verifica della rete di drenaggio. IDRA2D-DF permette, a partire dai parametri \(a\) ed \(n\) e dalla durata \(t\), di calcolare l’altezza di pioggia \(h\) utilizzando ((2.5)); il grafico sarà generato in base al passo in minuti e alla forma scelta tra le opzioni possibili. Il file creato sarà salvato automaticamente nella cartella 02_Boundary/05_ReturnPeriods/TR_1/01_Hyetographs. Il passo successivo prevede la creazione dell’idrogramma di piena. Il software permette, da uno ietogramma, di calcolare un idrogramma unitario SCS, unitario triangolare, unitario hortoniano triangolare, unitario di Nash e unitario geomorfologico; per la valutazione della precipitazione efficace che alimenta il deflusso superficiale, è permesso scegliere tra due distinte procedure, ovvero, applicare un coefficiente di deflusso costante oppure ricorrere al metodo del Curve Number. Per il progetto in questione è stato scelto di utilizzare il metodo del Curve Number, anche detto SCS perché proposto dal Soil Conservation Service (1972); questo si basa sulla completa validità dell’ipotesi che il rapporto tra il volume di deflusso \(V\) e la precipitazione netta \(P_n\) sia pari a quello esistente tra il volume idrico effettivamente immagazzinato nel suolo \(W\) ed il valore massimo della capacità di invaso del suolo \(S\) secondo la relazione:

\[ \frac{V}{P_n}=\frac{W}{S} \]

La precipitazione netta \(P_n\) si ottiene detraendo alla precipitazione totale \(P\), le perdite iniziali \(Ia\), dovute sia all’immagazzinamento superficiale del suolo, sia all’intercettazione operata dalla copertura vegetale, sia all’infiltrazione che ai vari fenomeni che si verificano prima del ruscellamento superficiale.

Le perdite iniziali vengono assunte proporzionali alla capacità massima di invaso del suolo \(S\) secondo la legge:

\[ Ia = \lambda S \]

Assumendo \(\lambda\) pari a \(0.2\) si ottiene

\[ V = \frac{(P - 0.2S)^2}{P + 0.8S} \]

La stima della massima capacità di invaso del suolo \(S\) viene effettuata con buona approssimazione, salvo la necessità di calibrazione del coefficiente di proporzionalità \(I\) per tener conto delle differenti condizioni geomorfologiche e geoclimatiche tramite la formula:

\[S = 25.4\left(\frac{1000}{CN}-10\right)\]

Il parametro \(CN\), definito appunto Curve Number, assume valori compresi tra 0 (assenza di deflusso superficiale) e 100 (assenza di perdite idrologiche con trasformazione totale della precipitazione in deflusso superficiale) e rappresenta quindi l’attitudine del bacino esaminato a produrre deflusso. Per la stima di \(CN\) è necessaria quindi una determinazione preliminare della classe idrologica del suolo all’interno dei quattro gruppi (A,B,C e D) individuati dall’USDA-SCS in ragione della capacità di formazione del deflusso del suolo dovuta alla rispettiva capacità di infiltrazione. Il software inoltre consente di modificare l’idrogramma generato impostando un fattore di moltiplicazione, divisione, addizione o sottrazione, anche applicabili direttamente sui singoli valori di tempo e portata.

Il prossimo passaggio obbligatorio è scegliere l’idrogramma da insierire nella modellazione per avviare la simulazione. Inseriti il tempo di ritorno e le caratteristiche idrologiche, il programma permette di inserire, in maniera facoltativa, file raster o vettoriali riguardanti l’uso del suolo, e in maniera obbligatoria un parametro riguardante la scabrezza secondo la formula empirica di Chèzy, sviluppata per calcolare la velocità di un fluido in un condotto, sia in pressione che a pelo libero; questa impostazione può essere definita da un parametro concentrato (un valore di scabrezza per tutta la superficie di simulazione, oppure distribuito, un valore di scabrezza per ogni uso del suolo. Nell’ultimo caso è quindi necessario che nel progetto sia presente un layer raster dell’uso del suolo. I valori ammessi variano da 1 a 3 su ghiaione e da 3 a 6 per deflusso canalizzato. In ultimo è necessario definire i punti di ingresso per l’idrogramma (inlets) e i punti di uscita per l’onda di piena (outlets), attraverso le apposite opzioni dell’ultima categoria in finestra, per poi validare le condizioni a contorno - Colate: quest’interfaccia (Fig. 2.10) garantisce all’utente la possibilità di impostare i parametri di calcolo per le colate detritiche che verranno utilizzati durante la simulazione. Nel caso in cui si voglia simulare un evento di colata su fondo erodibile, deve essere tenuta in considerazione l’evoluzione dello stesso, valutando quindi possibili erosioni e conseguenti depositi. Un modello semplice è quello proposto da Egashira e Ashida, i quali suppongono il tasso di erosione-deposito funzione dell’angolo di pendenza del fondo \(\vartheta\) e dell’angolo di equilibrio \(\vartheta_e\), moltiplicati per una costante empirica e per la velocità media

\[ \begin{cases} Erosione = Ku\frac{tan\vartheta}{1+tan\vartheta tan\vartheta_e}\\ \\ Deposito = KU\frac{tan\vartheta_e}{1+tan\vartheta tan\vartheta_e} \end{cases} \]

Dove, \(KU\) è il coefficiente empirico assunto da Egashira e Ashida, spesso uguale ad \(1\) e \(\vartheta_e\) è l’angolo di equilibrio per cui una volta raggiunta tale inclinazione da parte del letto del canale, erosione e deposito cesseranno. Secondo questo metodo le misure da attribuire alle voci indicate nella scheda, sono semi-standardizzate e riportate di seguito in tabella 2.4.

Table 2.4: misure da attribuire alle voci della scheda colate secondo il metodo di Egashira

Parametro	Unità di misura	Descrizione
Coefficiente di deposizione alla soglia angolare		Coefficiente moltiplicatore della costante di Egashira (deposito) per angoli inferiori all’angolo limite inferiore per colate. Valore consigliato: 5. Si consiglia di eseguire un’analisi di sensibilità su tale parametro in relazione alla legge di Egashira.
Angolo limite inferiore	gradi	Angolo al di sotto del quale si ha deposito di grandi quantità di sedimenti. Valori consigliati: per ghiaione 20°, per canale 5-6°. Si consiglia di eseguire un’analisi di sensibilità su tale parametro.
Coefficiente Egashira di erosione		Costante per legge di Egashira (erosione). Valore consigliato: 1. Si consiglia di eseguire un’analisi di sensibilità su tale parametro in relazione alla legge di Egashira.
Coefficiente Egashira di deposito		Costante per legge di Egashira (deposito). Valore consigliato: 1. Si consiglia di eseguire un’analisi di sensibilità su tale parametro în relazione alla legge di Egashira.
Velocità superiore di deposito	metri/secondo	Limite di velocità per la legge di Egashira (deposito). Valore di deposito consigliato: 1 m/s. Si consiglia di eseguire un’analisi di sensibilità su tale parametro in relazione alla legge di Egashira.
Velocità inferiore di erosione	metri/secondo	Limite di velocità per la legge di Egashira (erosione). Valore consigliato: 2 m/s. Si consiglia di eseguire un’analisi di sensibilità su tale parametro in relazione alla legge di Egashira.
Angolo superiore di deposito	gradi	Angolo limite per deposito per legge di Egashira. Valore consigliato: 14° per canale e fino a 30° per ghiaione. Si consiglia di eseguire un’analisi di sensibilità su tale parametro in relazione alla legge di Egashira.
Angolo inferiore di erosione	gradi	Angolo limite per erosione per legge di Egashira. Valore consigliato: 16° per canale e fino a 35° per ghiaione. Si consiglia di eseguire un’analisi di sensibiltà su tale parametro in relazione alla legge di Egashira.
Tirante minimo per erosione e depositi	metri	Profondità minima per cui vengono calcolate deposito ed erosione. Valore consigliato: 0.1 m

Il pannello Parametri distribuiti si attiva solo se è stata settata precedentemente la scabrezza distribuita nella scheda precedente. Anche in questa fase è stato verificato che i parametri settati per le colate fossero validi attraverso l’opzione valida parametri.

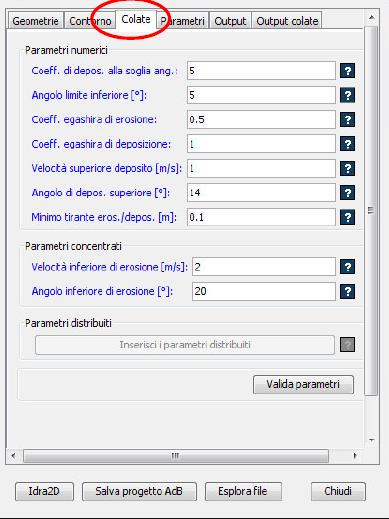
Figure 2.10: scheda colate

• Parametri: per avviare la simulazione è necessario impostare i parametri di calcolo nell’apposita scheda (Fig. 2.11); Per la descrizione dettagliata dei parametri si rimanda al Manuale utente. Attraverso lo strumento Gestore simulazione, scegliendo l’opzione obbligatoria Nuova simulazione e digitando il nome della nuova cartella, è possibile salvare tutti gli output della simulazione. Anche in quest’ultima scheda è necessario validare i parametri per poi avviare la simulazione scegliendo Simula.

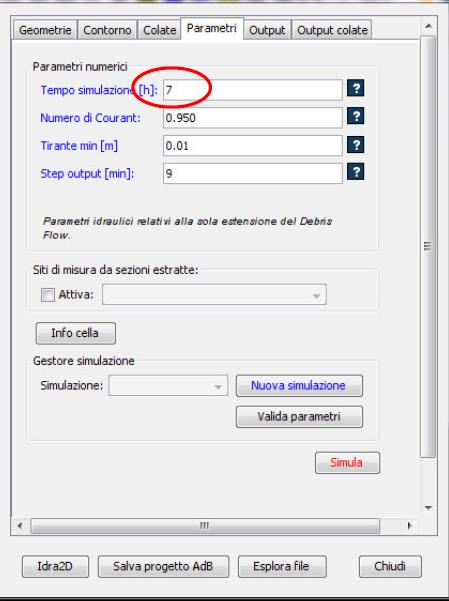
Figure 2.11: scheda parametri

• Le schede Output e Output colate mostrano i vari file output restituiti dal programma dividendoli in livelli (Fig. 2.12). Tra gli output di primo livello troviamo una stima del tempo di calcolo dell’intera simulazione assieme al log, alla possibilità di confrontare simulazioni diverse e di interrogare il file raster. Le mappe vere e proprie fanno parte degli output di secondo livello; tra queste, le più utili sono la mappa di esondazione massima e quella di velocità critica. I profili/idrogrammi rientrano tra gli output di terzo livello.

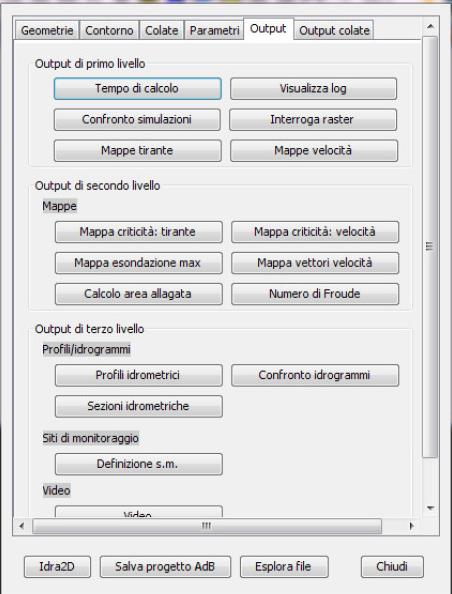
Figure 2.12: scheda output

2.3 Conoscenze Pregresse

La scelta dei metodi utilizzati per eseguire il presente lavoro alla scala del bacino idrografico di Trunca, in provincia di Reggio Calabria, è stata fatta su base bibliografica, esaminando studi già elaborati in altre aree del mondo e resi pubblici durante il quinto convegno mondiale sugli eventi franosi. Il WLF5 2020, paragonando finemente la condizione pandemica mondiale, del quale rischio non si aveva percezione, all’approccio di preparazione ai rischi naturali, ha ospitato una sessione sulle frane e sulla valutazione dei pericoli presso siti designati dall’UNESCO come siti naturali del patrimonio mondiale, riserve della biosfera e geoparchi globali, con lo scopo di valutare gli impatti delle frane sul nostro comune patrimonio culturale e naturale, e di offrire un’opportunità di generare consapevolezza pubblica e sviluppo delle capacità per la riduzione dei disastri da frana. Di seguito si inquadrano quindi alcune tra le più rappresentative applicazioni dei modelli Scoops3D e IDRA2D_DF.

Tra le applicazioni di Scoops3D, le più recenti derivano dagli studi di Predizione della stabilità spazio-temporale relativa ai limiti di pioggia di frane superficiali utilizzando TRIGRS e Scoops3D (J. He, H.Qiu, F.Qu, S.Hu et ali, 2021), Miglioramento della predizione spaziale delle frane con analisi di pendio 3D (N. Palazzolo, J.Peres et ali, 2021), Verica tridimensionale della stabilità sismica del pendio con applicazioni di Scoops3D e GIS; caso di studio in Atsuma, Hokkaido (S. Zhang, F.Wang, 2019) e Utilizzo di Scoops3D e GIS per la verifica tridimensionale della stabilità di un pendio: caso di studio in Sapa, Vietnam (V. H. Hoang, H.D. Pham, G. Sato, 2020).

Il primo studio citato, applica i modelli 1D (TRIGRS) e 3D (Scoops) all’evento di frana verificatosi in gruppo il 21 luglio 2013 (976 frane poco profonde) nel bacino del Niangniangba, in Cina. J. He et ali hanno calcolato la prevalenza nel tempo utilizzando il modello TRIGRS sulla base di dati pratici sulle precipitazioni e previsto la stabilità della frana superficiale utilizzando il modello Scoops3D in base alla superficie piezometrica risultante. Abbiamo confrontato le distribuzioni spaziali di stabilità di frana dei due modelli in condizioni iniziali e di saturazione con il catalogo delle frane. Il tasso di successo delle frane previsto dal modello 3D è superiore del 4,20% rispetto al modello 1D. La previsione, secondo lo studio, risulta infatti più efficace utilizzando il modello 3D per le frane superficiali in quanto si perimetra più dettagliamente la regione instabile, mentre utilizzando modello 1D si rischia una previsione eccessiva nella regione stabile in quanto probabilmente si utilizzano dati geologici meno dettagliati. Entrambi i modelli sono stati proposti dall’U.S. Geological Survey (USGS) e richiedono entrambi la definizione di una serie di parametri geometrici e numerici che possono avere un impatto significativo sulle loro prestazioni. A questo scopo è stato eseguito uno studio di calibrazione di tali parametri attraverso un’ottimizzazioni multi-obiettivo basata su algoritmi genetici per massimizzare le prestazioni di prevedibilità del modello in termini statistici. L’area di applicazione è stata quella di un bacino idrografico dell’oltrepò pavese (Italia) in cui le aree di frana innescate sono state accuratamente monitorate durante una piovosità estrema del 27-28 Aprile 2009. (Miglioramento della predizione spaziale delle frane con analisi di pendio 3D, N. Palazzolo, J.Peres et ali, 2021). L’ottimizzazione del modello è stata rilevata dalla creazione di un codice MATLAB in grado di ridurre al minimo i False Positive Rates (FPR) e all’unità i True Positive Rates (TPR) in modo da distinguere al meglio le zone stabili da quelle instabili, definendo un FS tra 0.5 e 1.2 per la presenza di frane ed un FS fino a 2.5 nel caso di assenza di frane.

Un’ulteriore area indagata è stata quella colpita dal terremoto di Hokkaido, Est Iburi del 6 Settembre 2018 (Mw 6.6) che ha innescato migliaia di eventi franosi impostati in depositi piroclastici da caduta; le frane hanno quindi provocato ingenti danni alle strutture e diverse vittime. L’area ha continuato a subire diverse scosse di assestamento e quindi la regione di Iburi si caratterizza come ad alta probabilità di accadimenti sismici in futuro. Scoops3D è stato considerato in questa circostanza un metodo efficace per valutare la stabilità sismica dei pendii e di grande importanza per la conseguente prevenzione e mitigazione dei disastri (Verica tridimensionale della stabilità sismica del pendio con applicazioni di Scoops3D e GIS; caso di studio in Atsuma, Hokkaido, S. Zhang, F.Wang, 2019). Scoops3D infatti può includere l’effetto del terremoto applicando un carico sismico orizzontale alla potenziale massa scorrevole in un’analisi pseudo-statica (Reid et al. 2015), quindi, nel caso di studio citato, applicando diversi coefficienti di pseudo accelerazione orizzontale nel programma, sono state ottenute le mappe del fattore di sicurezza delle quali è stata poi valutato il risultato di un coefficiente di pseudo accelerazione orizzontale compreso tra \(1/2\) e \(2/3\) di Peak horizontal Ground Acceleration (PHGA) per la valutazione della stabilità sismica dei pendii nei depositi piroclastici da caduta. Lo studio è servito per la corretta previsione degli eventi di frana successivi che hanno interessato le adiacenti località di Tomisato e di Yoshinova. Per continuare quindi a valutare le capacità di predizione del modello, un successivo studio nell’area di Sapa, Lao Cai in Vietnam, ha effettuato una back analisys dell’evento di frana verificatosi il 5 Agosto 2019 a seguito di uno storico evento temporalesco. I risultati hanno mostrato una moderata accuratezza nel confronto tra la cicatrice di frana effettiva e quella prevista dal modello per cui, Scoops3 rende possibile anche diverse simulazioni basate su futuri possibili cambiamenti delle condizioni topografiche.

l’applicativo IDRA2D_DF di AdB-ToolBox è stato invece utilizzato per elaborazioni idrologiche, geomorfologiche ed idrauliche operate per lo studio idrologico ed idraulico dei bacini idrografici che possono interessare centri abitati. Un esempio è relativo allo studio del bacino dell’abitato di San Giovanni Rotondo, in Puglia, al fine di rappresentare gli scenari di pericolosità idrulica che possono derivare in caso di piogge alluvionali (Studio idrologico e idraulico dei bacini idrografici dell’abitato di San Giovanni Rotondo, Dott. Leonardo Di Maggio, 2015), oppure nel caso studio del conoide di deiezione ubicato nella provincia autonoma di Bolzano lungo la SS51 che collega la città di Dobbiaco al Lago di Landro (IDRA2D-Hydraulic-Debris Flow Case study, Ministero dell’Ambiente e della tutela del Territorio e del Mare, 2018). Questi tipi di studi hanno consentito di valutare meglio gli aspetti connessi alle portate massime attese e allo sviluppo di scenari di inondazione e allagamento degli abitati nelle zone urbane e periurbane.

2.4 Metodi di validazione

I risultati di un modello devono essere confrontati con una realtà, che può essere rappresentata da un’interpretazione di dati sperimentali o dai risultati di un altro modello. Si definisce Previsione il risultato del modello (il termine implica una valutazione temporale, ma si può applicare anche all’analisi di suscettibilità, che ha come risultato l’indicazione delle aree soggette alle future frane) e Osservazione la mappa della realtà con cui si vuole confrontare il modello: il rapporto tra Previsione e Osservazione può essere analizzato con una Tabella di Contingenza.

Le tabelle di contingenza sono tabelle utilizzate in statistica per rappresentare e analizzare le relazioni tra due o più variabili. In esse si riportano le numerosità congiunte delle variabili. Il caso più semplice è quello delle tabelle tetracoriche, in cui ciascuna delle due variabili assume solo due possibili valori. Nel nostro caso le due variabili sono Previsione e Osservazione e i due valori che ognuna di queste può assumere sono Stabile e Instabile. Ottengo così risultati

True Positive (aree in frana in classe di pericolosità),

False Positive (aree non in frana in classe di pericolosità),

True Negative (aree non in frana in classe non di pericolosità),

False Negative (aree in frana in classe di non pericolosità).

Si definisce Sensitività o Sensibilità (\(Se\)) la percentuale di esempi in frana correttamente classificati, espressa dalla formula

\[ Se = \frac{VP}{VP+FN} \]

e Specificità (\(Sp\)) la percentuale di casi non in frana correttamente classificati, espressa dalla formula

\[ Sp\frac{VN}{VN+FP} \]

Vale la pena sottolineare l’importanza di considerare entrambi i valori (\(Se\) ed \(Sp\)) per avere un quadro comprensibile del funzionamento del modello: non ha senso dire “il modello prevede l’80% delle frane” senza specificare quanti sono i casi in cui la previsione non è corretta. Sia Se che Sp dipendono dalla scelta dei parametri del modello e solo la loro analisi congiunta permette di valutare i risultati. Il problema di base che genera incertezza nell’interpretazione dei risultati di classificazione di un modello risiede nel fatto che nella maggioranza dei casi esiste una zona di sovrapposizione fra le distribuzioni dei risultati, che generalmente sono valori continui. Infatti, se le due classi risultassero perfettamente separate (fig. 2.13), sarebbe molto semplice individuare il valore soglia ottimale da utilizzare per discriminarle con assoluta precisione. Nella realtà, invece, si verifica sempre una sovrapposizione più o meno ampia delle due distribuzioni (fig. 2.13), ed è perciò impossibile individuare sull’asse delle ascisse un valore soglia che consenta una classificazione ottimale tale da azzerare i falsi positivi ed i falsi negativi.

La scelta del valore soglia non può essere dettata soltanto da considerazioni di ordine probabilistico volte a minimizzare la proporzione di classificazioni errate, poiché in diversi ambiti, tra cui l’analisi di suscettibilità, gli errori commessi nella classificazione di casi positivi e negativi possono avere valenze differenti. Classificare come suscettibile a franare un’area che non lo è, ha sicuramente meno conseguenze negative che non definire sicura un’area che ha buone probabilità di franare. L’obiettivo della classificazione è dunque quello di minimizzare i falsi negativi, e di ottenere un’alta sensitività. Per selezionare il valore soglia in grado di ottimizzare una classificazione, è necessario osservare come variano le misure di prestazione al variare di questa soglia.

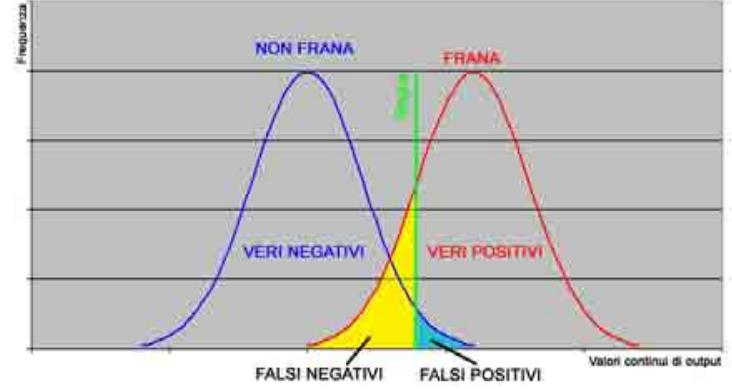
Figure 2.13: Distribuzione dei valori in uscita da un ipotetico modello nelle classi frana-non frana con individuazione del valore soglia; in alto senza zona di sovrapposizione tra le classi, in basso con sovrapposizione tra le classi

Tra i criteri di validazione più utilizzati c’è quello dell’analisi della curva ROC (Receiver Operating Characteristic), secondo cui si valuta la capacità di discernere i dati realistici dai meno realistici calcolandone l’area sottesa, ovvero AUC (Area Under Curve). Il valore di AUC equivale alla probabilità che il risultato del metodo utilizzato sia riuscito quindi molti analisti concordano nel dare a ROC il significato di probabilità che una nuova entità sia classificata correttamente dal modello. Nel grafico di ROC Sensitività e Specificità vengono calcolati per valori soglia differenti, nello specifico per tutti i valori soglia possibili, per poi riportare in ascissa i valori \((1-Sp)\), e in ordinata i corrispondenti valori di \(Se\), evidenziando quindi l’andamento dei casi positivi correttamente individuati (\(Se\)) rispetto ai falsi positivi \((1-Sp)\). L’unione dei punti ottenuti riportando nel piano cartesiano ciascuna coppia \((Se ; 1-Sp)\) per diversi valori di soglia, genera una curva spezzata con andamento a scaletta. Per interpolazione, è possibile eliminare la scalettatura (smoothing) ed ottenere la curva di ROC, che rappresenta una stima basata sui parametri del data set sperimentale. La curva ROC passerà per i punti \((0,0)\) e \((1,1)\) ed ha come condizione limite la retta bisettrice del quadrante che rappresenta la Linea di non beneficio (Chance line) sotto la quale l’AUC è pari 0,5. La ROC idealmente dovrebbe tendere ad una curva limite che renda l’AUC pari ad 1, rappresentando il modello perfetto (fig. 2.14). È immediato osservare come i due parametri siano inversamente correlati e quindi come l’adozione di una soglia che offre un’elevata \(Se\) comporta una perdita di \(Sp\) e viceversa, ma la curva permette di individuare la soglia migliore da utilizzare al fine di ottenere il compromesso desiderato tra la percentuale sovrastimata di aree in frana ed i falsi negativi che si è disposti a tollerare. Come regola generale, si può affermare che il punto sulla curva ROC più vicino all’angolo superiore sinistro rappresenta il

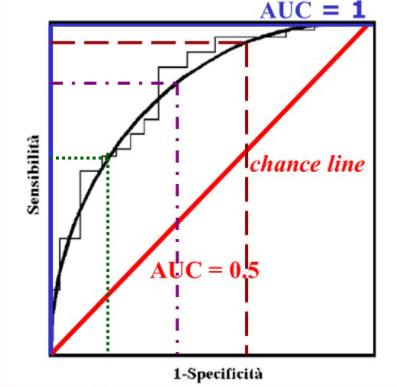
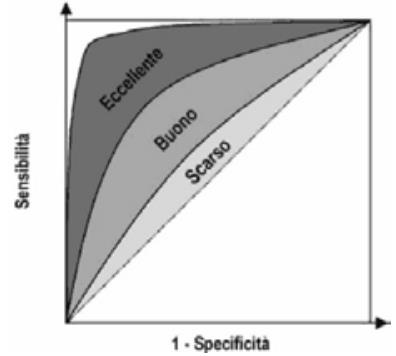
Figure 2.14: a sinistra Costruzione e limitazioni della curva di ROC; a destra risoluzione del modello d’analisi applicato a seconda di AUC

miglior compromesso fra sensitività e specificità, e che quindi sia da preferire il valore soglia ad esso associato. Tuttavia, in condizioni ottimali, la procedura di selezione del valore soglia consiste in un percorso decisionale molto più complesso. L’area sottesa dalla curva di ROC, è una misura della qualità della discriminazione tra le classi e dell’accuratezza del classificatore. Risulta quasi sempre necessario testare la capacità discriminante del test, ovvero se l’area sotto la curva eccede significativamente il suo valore atteso di 0.5. Tale procedura corrisponde a verificare se la proporzione dei veri positivi è superiore a quella dei falsi positivi. La capacità del classificatore di distinguere e separare le due classi è visualizzata nella pendenza del primo tratto della curva. Più questa è alta, infatti, più la sensitività sarà alta a parità di specificità (fig. 2.14).