12 Hypothesis testing
Statistical inference usually falls into one of two frameworks: parameter estimation and hypothesis testing. As introduced in sections 2.6 and 5.1, a hypothesis testing framework involves two complementary hypothesis, which are commonly called the null hypothesis (\(H_0\)) and the alternative hypothesis (\(H_a\)). The alternative hypothesis usually represents what we are seeking evidence for. If the data collected provides “strong” evidence in favor of the alternative hypothesis, we reject \(H_0\) in favor of \(H_a\). In the absence of such evidence, the null hypothesis is not rejected and is seen as possibly true.
A hypothesis testing procedure or hypothesis test is a rule that specifies how a sample estimate is used to make the decision to reject or not reject \(H_0\).
It is comon to use p-values (probability values) and a significance level (usually denoted \(\alpha\)) to make the decision to reject or not reject \(H_0\). For example, in section 2.6, the Malaria vaccine study showed a difference in proportions (of infected individuals in the control and treatment groups) of 64.3%. We then estimated via simulation that the probability of observing a difference of at least 64.3% under the assumption that \(H_0\) was true is 0.02 (2%). Considering that any probability below 5% would be “small enough” to reject \(H_0\), we then rejected \(H_0\) and concluded that there was strong evidence in favor of \(H_a\). In this example, the p-value is 0.02 and the cuttof value of 0.05 is the significance level.
Choosing a signifficance level for a test is important in many contexts, and the traditional level is \(\alpha = 0.05.\) However, it is appropriate to adjust the signifficance level based on the application (as long as the adjustment is done before running the test, and not after a p-value has been calculated.)
The p-value is the probability of observing data at least as favorable to the alternative hypothesis as our current data set, if the null hypothesis were true. The p-value is usually found by comparing a test statistic to the null distribution of the test statistic. The null distribution of a test statistic is the distribution of all possible values of the test statistic under the assumption that the null hypothesis is true.
In what follows, we discuss hypothesis testing procedures that rely on the Central Limit Theorem (CLT).
12.1 Hypothesis testing for \(\mu\)
In this subsection, we describe the procedure to test hypotheses of the type:
\(H_0:\) \(\mu = a\)
\(H_a:\) \(\mu \neq a\)
That is, hypotheses for a population mean. The hypotheses above are “two-sided”, that is, the alternative hypothesis accounts for both \(\mu<a\) and \(\mu>a\). We may also test “one-sided” hypotheses, for example,
\(H_0:\) \(\mu = a\)
\(H_a:\) \(\mu > a.\)
To perform a hypothesis test for \(\mu\) using the CLT, we calculate \[Z = \frac{\overline{X}-a}{S/\sqrt{n}}.\] The denominator is the approximate standard deviation of \(\overline{X}\), which is also called the standard error of \(\overline{X}.\) Under \(H_0\), for large enough \(n\) (usually \(n\geq 30\) suffices), the distribution of \(Z\) is approximately \(N(0,1).\) That is, the null distribution of \(Z\) is a standard normal distribution. The p-value is then the probability that, under the null hypothesis, one would observe a test statistic \(Z\) at least as large (in absolute value) as the one obtained from the data. Like in the case for confidence intervals, if \(n\) is not as large (usually between 10 and 30), the t-distribution may be used instead of the normal, if the population distribution can be reasonably considered to be normal. In general, it is common to use a t-distribution with \(n-1\) degrees of freedom to model the sample mean when the sample size is \(n,\) even if \(n\geq 30.\) This is because when we have more observations, the degrees of freedom will be larger and the t-distribution will look more like the standard normal distribution; when the degrees of freedom are about 30 or more, the t-distribution is nearly indistinguishable from the normal distribution.
Example 12.1 Is the typical US runner getting faster or slower over time? We consider this question in the context of the Cherry Blossom Race, which is a 10-mile race in Washington, DC each spring. The average time for all runners who finished the Cherry Blossom Race in 2006 was 93.29 minutes (93 minutes and about 17 seconds). We want to determine using data from 100 participants in the 2017 Cherry Blossom Race whether runners in this race are getting faster or slower, versus the other possibility that there has been no change. The competing hypotheses are:
\(H_0\): The average 10-mile run time was the same for 2006 and 2017. That is, \(\mu = 93.29\) minutes.
\(H_a\): The average 10-mile run time for 2017 was different than that of 2006. That is, \(\mu\neq 93.29\) minutes.
The sample mean and sample standard deviation of the sample of 100 runners are 97.32 and 16.98 minutes, respectively. The data come from a simple random sample of all participants, so the observations are independent. The sample is large enough for the use of the CLT. The test statistic is
\[Z = \frac{\overline{X} - \mu_0}{S/\sqrt{n}} = \frac{97.32 - 93.29}{16.98/\sqrt{100}} = 2.37.\]
The \(p\)-value is then the probability that we observe a test statistic \(Z\) at least as large (in abslute value) as 2.37, under the assumption that \(H_0\) is true. By the CLT, the null distribution of the test statistic \(Z\) is approximately \(N(0,1)\). So the p-value is the area of the tails highlighted below
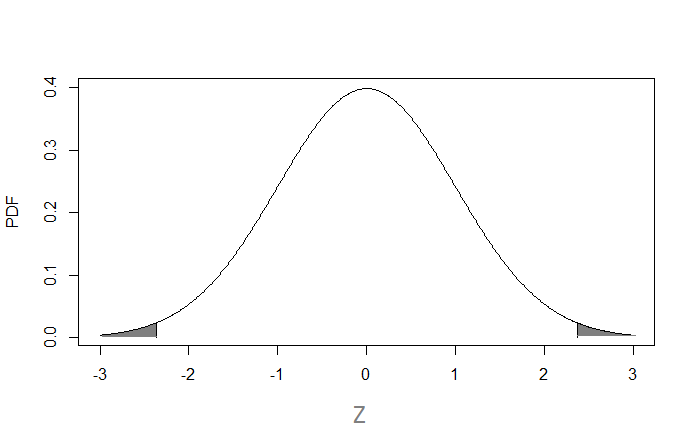
The calculation of the p-value can be done with the \(pnorm\) function. The area to the right of 2.37 is
## [1] 0.008894043The area to the left of -2.37 is
## [1] 0.008894043It should be no surprise that they are the same, given the symmetry if the PDF of the normal distribution. Therefore it is only necessary to calculate one of the areas, and then multiply it by 2 (for a two-sided test). In the case of a one-sided test, the p-value is the area of only one of the tails.
In this example, since we are running a two-sided test, the p-value is
## [1] 0.01778809The p-value can be interpreted as follows:
Under the assumption that the null hypothesis is true (that is, under the assumption that the average 10-mile run time for 2017 was 93.27 minutes), the probability of observing a test statistic \(Z\) at least as large (in absolute value) as the one obtained from the sample is 0.0178. At a significance level of \(\alpha=0.05,\) this p-value indicates that it’s unlikely to oberve a sample average like the one in the curent sample, if the null hypothesis was true. Therefore, we reject the null hypothesis in favor of the alternative. We would then say that this sample provided reasonable evidence against the null hypothesis (and in favor of the alternative).
Notice that since the sample size was large enough, using a t-distribution would result in a similar p-value and conclusion:
## [1] 0.01972642When using a t-distribution, we name the test statistic “T” instead of “Z”, but they are calculated in the same manner.
12.2 Hypothesis testing for \(\mu_1 - \mu_2\)
In this subsection, we describe the procedure to test hypotheses of the type:
\(H_0:\) \(\mu_1 - \mu_2 = 0\)
\(H_a:\) \(\mu_1 - \mu_2 \neq 0\)
That is, hypotheses for the difference between two population means. Again, we can have one-sided hypotheses instead of two-sided ones. The value 0 can be replaced with a non-zero one, but the most common choice is 0 because it is more common to be interested in whether two population means are equal.
To perform a hypothesis test for \(\mu_1 - \mu_2\) using the CLT, we calculate \[Z = \frac{\overline{X}_1-\overline{X}_2}{\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}}.\]
The denominator is the approximate standard deviation of \(\overline{X}_1 - \overline{X}_2.\) For large enough \(n_1\) and \(n_2\) (usually \(n_1, n_2 \geq 30\) suffices), the null distribution of \(Z\) is approximately a standard normal distribution. The p-value is then the probability that, under the null hypothesis, one would observe a test statistic \(Z\) at least as large (in absolute value) as the one obtained from the data. If one of \(n_1\) or \(n_2\) is not as large (usually between 10 and 30), the t-distribution may be used instead of the normal (with the degrees of freedom given by equation (11.1)), if the population distribution of both groups can be reasonably considered to be normal.
Example 12.2 Prices of diamonds are determined by what is known as the 4 Cs: cut, clarity, color, and carat weight. The prices of diamonds go up as the carat weight increases, but the increase is not smooth. For example, the difference between the size of a 0.99 carat diamond and a 1 carat diamond is undetectable to the naked human eye, but the price of a 1 carat diamond tends to be much higher than the price of a 0.99 diamond. Emma collected two random samples of diamonds, 0.99 carats and 1 carat, each sample of size 43, and compare the average prices of the diamonds. In order to be able to compare equivalent units, we first divide the price for each diamond by 100 times its weight in carats. That is, for a 0.99 carat diamond, we divide the price by 99. For a 1 carat diamond, we divide the price by 100. The sample statistics are shown below. Here we construct a hypothesis test to evaluate if there is a difference between the average standardized prices of 0.99 and 1 carat diamonds.
| 0.99 carats | 1 carat | |
|---|---|---|
| Mean | $44.51 | $56.81 |
| SD | $13.32 | $16.13 |
| n | 43 | 43 |
The hypotheses we are testing are:
\(H_0\): \(\mu_1 - \mu_2 = 0\)
\(H_a\): \(\mu_1 - \mu_2 \neq 0,\)
where \(\mu_1\) is the (population) average standardized prices of 0.99 carat diamonds and \(\mu_2\) is the (population) average standardized prices of 1 carat diamonds.
The test statistic is
\[Z = \frac{44.51-56.81}{\sqrt{\frac{13.32^2}{43}+\frac{16.13^2}{43}}} = -3.8557\]
Since both \(n_1\) and \(n_2\) are large enough, under \(H_0\), \(Z \approx N(0,1)\) and the p-value can be calculated as
## [1] 0.0001153989The small p-value supports the alternative hypothesis. That is, the difference between the average standardized prices of 0.99 and 1 carat diamonds is statistically significant.
If \(n_1\) or \(n_2\) are not large enough and if the data for both groups could come from a normal distribution (no extreme skew is present), the t distribution should be used to find the p-value. That is, \[\mbox{p-value} = 2\times pt(-|T|, df) = 2\times (1-pt(|T|,df)),\] where \[df = \frac{\left(\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}\right)^2}{\frac{\left(\frac{S_1^2}{n_1}\right)^2}{n_1-1}+\frac{\left(\frac{S_2^2}{n_2}\right)^2}{n_2-1}}.\]
In the previous example, if using the t distribution, \(df=81.1\) and the p-value would be 0.00023, as shown in the calculations below.
S1 <- 13.32
S2 <- 16.13
n1 <- 43
n2 <- 43
df <- (S1^2/n1 + S2^2/n2)^2/((S1^2/n1)^2/(n1-1) + (S2^2/n2)^2/(n2-1)); df## [1] 81.09966## [1] 0.000230116412.3 Hypothesis testing for proportions
Hypothesis tests can also be carried out for one-sample or two-sample proportions. For example, suppose that in example 11.2, we suspect that the proportion of borrowers who have at least one bankruptcy on their record is greater than 10%. So instead of finding a confidence interval for \(p\), we could carry out a hypothesis test, with the following null and alternative hypotheses:
\(H_0\): \(p = 0.1\)
\(H_a\): \(p > 0.1,\)
where \(p\) is the (population) proportion of borrowers who have at least one bankruptcy on their record. To check the success-failure condition in a hypothesis test, we use \(p_0\) instead of \(\hat{p}\) (for a confidence interval, we use \(\hat{p}\), since there are no hypotheses):
## [1] 1000## [1] 9000Since both values are greater than 10, we pass the condition. The standard error is also calculated using \(p_0\) instead of \(\hat{p}\). The test statistic is
\[Z = \frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} = \frac{0.1215-0.1}{\sqrt{\frac{0.1(1-0.1)}{10000}}} = 7.1667.\]
The p-value can be calculated as
## [1] 3.841372e-13Notice that we didn’t multiply the one-tail probability by two, like we did in the previous examples. This is because this is a one-sided test (the alternative hypothesis only accounts for \(p>0.1\)). Two-sided alternative hypotheses are more common, and in those cases, the probability above should be multiplied by 2.
Now let’s turn to an example of a hypothesis test for the difference between two proportions. From the loans dataset, suppose that we are interested in knowing whether the proportion of borrowers who have been bankrupt is different for those who had a joint application and those who had an individual one. We addressed this question in example 11.4 using a confidence interval for the difference between two proportions. We call the (population) proportion for these two groups \(p_1\) and \(p_2\). Let us conduct a hypothesis test for the following hypotheses:
\(H_0\): \(p_1 - p_2 = 0\)
\(H_a\): \(p_1 - p_2 \neq 0.\)
We first check the success-failure condition:
## [1] 1046.115## [1] 7458.885## [1] 157.36## [1] 1247.64All values are greater than 10, so we can proceed to use the CLT. Next we find the test statistic, using a pooled proportion, \(\hat{p}\), in the calculation of the standard error. This is because the null hypothesis says that \(p_1=p_2.\) The pooled proportion is calculated as the total number of successes in both groups divided by the sum of the sample sizes in both groups. In the current example, \[\hat{p} = \frac{1048+167}{8505+1405} = 0.1226.\] This gives
\[Z = \frac{\hat{p}_1 - \hat{p}_2}{\sqrt{\frac{\hat{p}(1-\hat{p})}{n_1} + \frac{\hat{p}(1-\hat{p})}{n_2}}} = \frac{0.123 - 0.112}{\sqrt{\frac{0.1226(1-0.1226)}{8505} + \frac{0.1226(1-0.1226)}{1405}}} = 1.165\]
## [1] 1.164628The p-value is then calculated using pnorm:
## [1] 0.2441697Since the p-value is not small enough, we do not reject the null hypothesis, that is, we did not find strong evidence that proportion of borrowers who have been bankrupt is different for those who had a joint application and those who had an individual one.
12.4 Hypotheses testing for \(\hat{b}\)
In section 11.5, we discussed the sampling distribution of the slope and intercept of a Least Squares regression line, \(\hat{b}\) and \(\hat{a}\). We saw that under assumptions A1 (the errors are independent) and A2 (the errors are normally distributed with mean 0 and constant variance \(\sigma^2,)\) the distributions of \(\hat{b}\) and \(\hat{a}\) are given by:
\[\hat{b} \sim N\left(b, \frac{\sigma}{\sqrt{\sum(X_i-\overline{X})^2}}\right)\quad \mbox{and}\] \[\hat{a} \sim N\left(a, \sigma\sqrt{\frac{1}{n}+\frac{\overline{X}}{\sum(X_i-\overline{X})^2}}\right).\]
Here \(b\) and \(a\) are the population values for the slope and intercept. Suppose now that we would like to test the following hypotheses:
\(H_0: b = 0\)
\(H_a: b \neq 0\)
Recall that a non-zero slope is indicative of an existing relationship between the explanatory and the response variable.
Under the null hypothesis, the distribution of \(\hat{b}\) is
\[\hat{b} \sim N\left(0, \frac{\sigma}{\sqrt{\sum(X_i-\overline{X})^2}}\right).\]
Since we usually don’t have access to \(\sigma^2\), we use the MSE as an estimate for \(\sigma^2.\) The MSE was defined in section 3.4.1 and is given by \(MSE = SSE/(n-2).\) When using this estimate, the t distribution should be used instead of the normal distribution. That is,
\[\frac{\hat{b}-0}{SE(\hat{b})} \sim t_{n-2},\] where \[SE(\hat{b}) \approx \sqrt{\frac{MSE}{\sum(X_i-\overline{X})^2}}.\]
This allows us to compute the test statistic for the hypothesis test: \[\begin{eqnarray} T = \frac{\hat{b}}{SE(\hat{b})}. \end{eqnarray}\] Then the p-value for the hypothesis test is the probability of observing this T statistic or more extreme, under the null hypothesis, that is, \[p-value = 2*pt(-|T|, df) = 2*(1-pt(|T|, df)),\] where \(df = n-2.\) Such calculation is demonstraded in the following example.
Example 12.3 Suppose that we would like to find the significance of the slope of the line that describes the relationship between interest_rate and debt_to_income in the loans dataset, introduced in chapter 4. Let’s begin by finding the LS model for these variables:
##
## Call:
## lm(formula = interest_rate ~ debt_to_income, data = loans)
##
## Residuals:
## Min 1Q Median 3Q Max
## -21.7391 -3.7203 -0.7945 2.7351 18.6274
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 11.511445 0.080732 142.59 <2e-16 ***
## debt_to_income 0.047183 0.003302 14.29 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.948 on 9974 degrees of freedom
## (24 observations deleted due to missingness)
## Multiple R-squared: 0.02007, Adjusted R-squared: 0.01997
## F-statistic: 204.2 on 1 and 9974 DF, p-value: < 2.2e-16R calculates \(SE(\hat{b})\), which is given in the second column of the summary output. In this example, \(SE(\hat{b})=0.0033.\) The summary output also has the degrees of freedom, which this case is 9974. The test statistic is then \[T = \frac{\hat{b}}{SE(\hat{b})} = \frac{0.047183}{0.003302} = 14.29,\] which gives the p-value: \[p-value = 2*(1-pt(14.29, 9974)) \approx 0.\] Since the p-value is less than the significance level \(\alpha=0.05,\) we can reject the null hypothesis and conclude that there is strong evidence that the slope of the line is not zero. In this case, the data sugests that there is a positive association between debt_to_income and interest_rate.
A hypothesis test for the intercept can be carried out in a similar way; however, such test is of much less interest than the one for the slope, as it is often the case that the intercept is not interpretable.
The calculations for hypothesis testing described above are reasonable if assumptions A1 and A2 are met. We check for these assumptions through the diagnostic plots discussed in section 5.2.
12.5 Hypothesis test for other parameters
As you may have noticed, hypothesis tests (HTs) are built by first stating two complementary hypotheses (null and alternative). We then calculate the probability that one would observe a sample at least as favorable to the alternative hypothesis as the current sample, if the null hypothesis was true. This sequence of steps can be taken for conducting tests about several population parameters (for example, means, proportions, standard deviations, slopes of regression lines, etc). Notice that the key to the development of such tests was gaining an understanding of the null distribution of an estimator, that is, the sampling distribution of an estimator under the assumption that \(H_0\) was true.
12.6 Statistical significance versus practical significance
When the sample size becomes larger, point estimates become more precise and any real differences in the sample estimate and null value become easier to detect and recognize. Even a very small difference would likely be detected if we took a large enough sample. In such cases, we still say the difference is statistically significant, but it is not practically significant. For example, an online experiment might identify that placing additional ads on a movie review website statistically significantly increases viewership of a TV show by 0.001%, but this increase might not have any practical value. Therefore, it is important to interpret the practical implications of a result and not simply rely on statistical significance as the “final” result.