11 Confidence intervals
In the last chapter, we discussed sampling distributions of estimators, and in this chapter, we use sampling distributions to construct confidence intervals for population parameters. This is one of the most used ways to perform statistical inference on parameters of interest.
In sections 2.6 and 5.1, we have mentioned a threshold of 0.05 for p-values when performing hypothesis tests. This cutoff value is referred to as the significance level of a test and is usually denoted by \(\alpha\). For confidence intervals, we use a confidence level instead of a significance level, which is usually \(1-\alpha\). For example, \(\alpha = 0.05\) implies a confidence level of \(0.95\) (95%).
Definition 11.1 A \((1-\alpha)\) confidence interval (CI) for a population parameter \(\theta\) is a random interval \([L, U]\) such that \([L, U]\) calculated from a given future sample will cover \(\theta\) with probability \(1-\alpha\). That is, \(P(L\leq \theta \leq U)=1-\alpha.\) In other words, a proportion \(1-\alpha\) of random samples of fixed size will produce a confidence interval that contain \(\theta\).
We call the interval \([L,U]\) random for the same reason we call estimators random variables; different samples will produce different intervals. The population parameter is a fixed number, not a random variable, but because confidence intervals are random intervals, sometimes they will not capture the population parameter and that’s why we need to quantify our confidence that we captured it.
In what follows, we develop ways of constructing confidence intervals for common population parameters of interest.
11.1 Confidence interval for \(\mu\)
The goal in this subsetion is to construct a \((1-\alpha)\) confidence interval for the population mean \(\mu\), using a random sample of the population.
Theorem 11.1 (Confidence interval for one mean) Consider an iid sample \(X_1, X_2, \dots, X_n\) with \(E(X_i) = \mu\) and \(Var(X_i) = \sigma^2\). Then the endpoints of a \((1-\alpha)\) CI for \(\mu\) are given by \[ \overline{X}\pm c\times \frac{S}{\sqrt{n}}, \quad \mbox{where } c = qnorm(1-\alpha/2). \] That is, the \((1-\alpha)\) CI is: \[ \left[\overline{X} - c\times \frac{S}{\sqrt{n}}, \overline{X} + c\times \frac{S}{\sqrt{n}}\right], \quad \mbox{where } c = qnorm(1-\alpha/2). \] The value \(c\) is called the critical value for the confidence interval and it’s related to the confidence level \(1-\alpha\). The quantity \(c\times \frac{S}{\sqrt{n}}\) is called the margin of error of the confidence interval.
Proof. For large enough \(n\) (usually \(n\geq 30\) suffices), the Central Limit Theorem says that \(\frac{\overline{X}-\mu}{\sigma/\sqrt{n}} \approx N(0,1).\) We can begin the construction of the confidence interval by using the symmetry of the normal PDF to find \(c\) such that \(P\left(-c\leq \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\leq c\right) = 1-\alpha.\) This is equivalent to finding \(c\) such that \(P(\frac{\overline{X}-\mu}{\sigma/\sqrt{n}} \leq c) = 1-\alpha/2\) (see figure below with the \(N(0,1)\) PDF.) Therefore, \(c\) is the inverse CDF of the standard normal distribution evaluated at \(1-\alpha/2.\) Using R’s notation, this is \(qnorm(1-\alpha/2).\) Notice that we omit the values 0 and 1 in the input of qnorm. This is because in the absence of the parameters of the normal distribution, R uses the standard normal parameters, 0 and 1. Finally, with some algebra, one can show that the statement
\[P\left(-c\leq \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\leq c\right) = 1-\alpha\] is equivalent to
\[P\left(\overline{X}-c\frac{\sigma}{\sqrt{n}} \leq \mu \leq \overline{X}+c\frac{\sigma}{\sqrt{n}}\right) = 1-\alpha.\]
In practice, we usually don’t have access to \(\sigma\), so we use the estimator \(S\) in its place. For large enough \(n\), this substitution is appropriate and yields reliable confidence intervals.
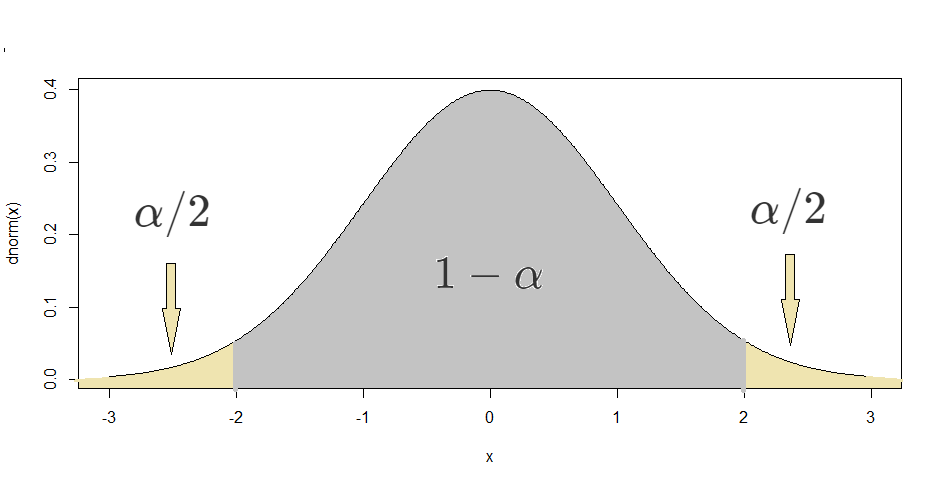
The following example illustrates how to find a confidence interval from a sample.
Example 11.1 Suppose that we would like to estimate the average interest rate given to borrowers by per-to-peer lenders by providing a 95% confidence interval. We can use the loans dataset introduced in chapter 4 as a representative sample of such borrowers. The best estimate for the average interest rate is the sample mean for interest rate, which is
## [1] 12.42752That is, \(\overline{X} = 12.43\)%. The sample standard deviation of interest_rate is
## [1] 5.001105That is, \(S = 5.001\)%. The sample size for interest_rate is \(n=10000\). Finally, for a 95% CI, \(\alpha = 0.05\) and therefore the critical value \(c\) is
## [1] 1.959964Now we have the information we need to construct a 95% confidence interval for the average interest rate:
\[ \overline{X}\pm c\times \frac{S}{\sqrt{n}} = 12.43 \pm 1.96\times\frac{5.001}{\sqrt{10000}} = 12.43\pm 0.098 = [12.332, 12.528]. \]
So we can say that we are 95% confident that the average interest rate given to borrowers by per-to-peer lenders is between 12.332% and 12.528%. Notice that this is a very “tight” confidence interval. This is because the sample size is large enough for a high precision. If instead of 10000 we had sample of 50 borrowers, the interval would be wider (try recalculating the interval for different values of \(n\) and different confidence levels.)
One question that you may have made at this point is “what if my sample is not large enough?” In this case, we can’t rely on the Central Limit Theorem and need to have some information about the population distribution. It turns out that if the population distribution is normal, then the distribution of \(\frac{\overline{X}-\mu}{S/\sqrt{n}}\) follows a t distribution with \(n-1\) degrees of freedom25 In that case, we calculate the CI in the way described in theorem 11.1 with the critical value being calculated with the t distribution instead of the normal. That is, \(c = qt(1-\alpha/2, n-1).\) One can also use the t distribution to calculate \(c\) even when \(n\) is large enough. This is because the t distribution approaches the standard normal as the degrees of freedom increase.
Let’s re-calculate the critical calue \(c\) from example 11.1 using the t distribution:
## [1] 1.960201In this case, because \(n\) is so large, we get the same critical value using qnorm or qt.
11.2 Confidence interval for \(p\)
The following is a version of theorem 11.1 when the \(X_i\)’s take only the values 0 and 1.
Theorem 11.2 (Confidence interval for one proportion) Consider an iid sample \(X_1, X_2, \dots, X_n\) of 0s and 1s with \(E(X_i) = p\) and \(Var(X_i) = p(1-p)\). Then the endpoints of a \((1-\alpha)\) CI for \(p\) are given by \[ \hat{p}\pm c\times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}, \quad \mbox{where } c = qnorm(1-\alpha/2). \] That is, the \((1-\alpha)\) CI is: \[ \left[\hat{p} - c\times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}, \hat{p} + c\times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\right], \quad \mbox{where } c = qnorm(1-\alpha/2). \]
The confidence interval for \(p\) is a reasonable estimate if the success-failure condition is met, that is, if \(np\geq 10\) and \(n(1-p)\geq 10.\) Since we don’t have access to \(p\), we use \(\hat{p}\) to check the success-failure condition. This allows us to calculate confidence intervals for proportions, as described in the following example.
Example 11.2 Suppose that now we would like to estimate the proportion of borrowers in peer-to-peer lending programs who have at least one bankruptcy on their record. We would like to provide a 99% confidence interval for such proportion. We use the loans dataset as a sample of borrowers. The best estimate for the population26 proportion is the sample proportion. Since bankruptcy is recorded with 0s and 1s, the sample proportion is calculated as
## [1] 0.1215That is, \(\hat{p}=0.1215\). Let us check the success-failure condition for \(n=10000\) and \(\hat{p}=0.1215.\)
## [1] 1215## [1] 8785Both values are greater than 10, so we can use the CLT and proceed with the confidence interval computation. The critical value \(c\) is
## [1] 2.575829Therefore, the 99% CI for \(p\) is given by \[ \hat{p}\pm c\times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} = 0.1215 \pm 2.576\times \sqrt{\frac{0.1215(1-0.1215)}{10000}} = 0.1215 \pm 0.0084 = [0.1131, 0.1299]. \]
That is, we can say that we are 99% confident that the proportion of borrowers from peer-to-peer lending programs who have been bankrupt is between 11.31% and 12.99%.
If the success-failure condition is not met, then one can use simulations to find a confidence interval for \(p\).
11.3 Confidence interval for \(\mu_1 - \mu_2\)
Sometimes we may be interested in estimating the difference between the means of two groups, for example, the difference in interest rate between borrowers who have been bankrupt and those who haven’t. We denote the means of the populations for these two groups by \(\mu_1\) and \(\mu_2\). The best estimate for \(\mu_1 - \mu_2\) is \(\overline{X}_1 - \overline{X}_2\). However, the Central Limit Theorem gives the approximate sampling distribution of one sample mean, not the difference between two sample means. Thankfully, we can still obtain the sampling distribution of \(\overline{X}_1 - \overline{X}_2\) by using a fact about normal distributions:
Fact: The sum of two normally distributed random variables is also normal.27
Denote by \(\sigma_1\) and \(\sigma_2\) the (population) standard deviations of both groups and by \(n_1\) and \(n_2\) the sample sizes of the two groups. The fact stated above implies that, for large enough \(n_1\) and \(n_2\), \(\overline{X}_1 - \overline{X}_2\) is approximately normal. Now we just need to find \(E(\overline{X}_1 - \overline{X}_2)\) and \(Var(\overline{X}_1 - \overline{X}_2)\) in order to find a confidence interval for \(\mu_1-\mu_2\):
\[ E(\overline{X}_1 - \overline{X}_2) = E(\overline{X}_1) - E(\overline{X}_2) = \mu_1 - \mu_2. \] \[ Var(\overline{X}_1 - \overline{X}_2) = Var(\overline{X}_1) + 2 Cov(\overline{X}_1, \overline{X}_2) + (-1)^2 Var(\overline{X}_2) = \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}. \]
Here we used the assumption that the data was collected independently for both groups, which implies that \(Cov(\overline{X}_1, \overline{X}_2) = 0.\)
The calculations above give us the approximate sampling distribution of \(\overline{X}_1 - \overline{X}_2\) for large enough \(n_1\) and \(n_2\) (usually \(n_1 \geq 30\) and \(n_2 \geq 30\) suffices):
\[ \overline{X}_1 - \overline{X}_2 \approx N\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}\right). \]
This gives the following result:
Theorem 11.3 (Confidence interval for the difference between two means) Consider iid samples of the same variable for two different groups. Then the endpoints of a \((1-\alpha)\) CI for \(\mu_1 - \mu_2\) are given by \[ \overline{X}_1 - \overline{X}_2 \pm c\times \sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}, \quad \mbox{where } c = qnorm(1-\alpha/2). \] That is, the \((1-\alpha)\) CI is: \[ \left[\overline{X}_1 - \overline{X}_2 - c\times \sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}, \overline{X}_1 + \overline{X}_2 + c\times \sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}\right], \quad \mbox{where } c = qnorm(1-\alpha/2). \]
If \(n_1\) or \(n_2\) are not large enough and if the data for both groups could come from a normal distribution (no extreme skew is present), the t distribution should be used to find the critical value. That is, \[c = qt(1-\alpha/2, df),\] where
\[\begin{equation} df = \frac{\left(\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}\right)^2}{\frac{\left(\frac{S_1^2}{n_1}\right)^2}{n_1-1}+\frac{\left(\frac{S_2^2}{n_2}\right)^2}{n_2-1}}. \tag{11.1} \end{equation}\]
One can also use the t distribution to calculate \(c\) even when \(n_1\) and \(n_2\) are large enough. This is because the t distribution approaches the standard normal as the degrees of freedom increase.
Example 11.3 Suppose that we want to estimate the difference in interest rate between borrowers who have been bankrupt and those who haven’t. We will provide a 95% CI for this difference. First we find \(\overline{X}_1\), \(\overline{X}_2\), \(S_1\), \(S_2\), \(n_1\), and \(n_2\) using R’s tapply function (see section 3.3.1 for an introduction to tapply):
## 0 1
## 12.33800 13.07479## 0 1
## 5.018019 4.829929## 0 1
## 8785 1215That is, the interest_rate sample average, standard deviation, and size for the non-bankrupt group are \(\overline{X}_1 = 12.33\)%, \(S_1 = 5.018\)%, and \(n_1 = 8785\), while for the bankrupt group these quantities are \(\overline{X}_2 = 13.07\)%, \(S_2 = 4.830\)%, and \(n_2 = 1215\). The critical value for a 95% CI is 1.96. Now we are ready to calculate the confidence interval:
\[\begin{eqnarray} \overline{X}_1 - \overline{X}_2 \pm c\times \sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}} &=& 12.338 - 13.075 \pm 1.96\sqrt{\frac{5.018^2}{8785} + \frac{4.830^2}{1215}} \\ &=& -0.737 \pm 0.291 = [-1.028, -0.445] \end{eqnarray}\]
This means that we are 95% confident that the difference between the interest rates for those who have been bankrupt and those who haven’t is between -1.028% and -0.445%. Since 0 is not included in this interval, then this is statistical evidence that the average interest rate for the two groups is not the same. We would then say that there is a statistically significant difference between the two groups.
Let’s re-calculate the critical value \(c\) from example 11.3 using the t distribution:
S1 <- 5.018019
S2 <- 4.829929
n1 <- 8785
n2 <- 1215
df <- (S1^2/n1 + S2^2/n2)^2/((S1^2/n1)^2/(n1-1) + (S2^2/n2)^2/(n2-1))
qt(1-0.05/2, df)## [1] 1.961449In this case, because \(n_1\) and \(n_2\) are so large, we get the same critical value using qnorm or qt.
11.4 Confidence interval for \(p_1 - p_2\)
In a rationale similar to the one presented in section 11.3, we can also calculate confidence intervals for the difference between two proportions. This is summarized in the theorem below.
Theorem 11.4 (Confidence interval for the difference between two proportions) Consider iid samples of the same variable for two different groups. Then the endpoints of a \((1-\alpha)\) CI for \(p_1 - p_2\) are given by \[ \hat{p}_1 - \hat{p}_2 \pm c\times \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1} + \frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}, \quad \mbox{where } c = qnorm(1-\alpha/2). \] That is, the \((1-\alpha)\) CI is: \[ \left[\hat{p}_1 - \hat{p}_2 - c\times \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1} + \frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}, \hat{p}_1 - \hat{p}_2 + c\times \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1} + \frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}\right]. \]
The confidence interval for \(p_1-p_2\) is a reasonable estimate if the success-failure condition is met, that is, if \(n_1p_1\geq 10\), \(n_2p_2\geq 10\), \(n_1(1-p_1)\geq 10\) and \(n_2(1-p_2)\geq 10\). Since we don’t have access to \(p_1\) and \(p_2\), we use \(\hat{p}_1\) and \(\hat{p}_2\) to check the success-failure condition. This allows us to calculate confidence intervals for the difference between two proportions, as described in the following example.
Example 11.4 Suppose that we are interested in knowing whether the proportion of borrowers who have been bankrupt is different for those who had a joint application and those who had an individual one. We can call the (population) proportion for these two groups \(p_1\) and \(p_2\). We will find a 99% confidence interval for \(p_1-p_2\). To find the sample proportions \(\hat{p}_1\) and \(\hat{p}_2\), we use the function table in R:
##
## 0 1
## individual 7457 1048
## joint 1328 167So the sample proportion of individual applications who have been bankrupt is \(\hat{p}_1 = \frac{1048}{7457+1048} = 0.123\), and the sample proportion of joint applications who have been bankrupt is \(\hat{p}_2 = \frac{167}{1328+167} = 0.112.\) The denominators in these calculations are \(n_1\) and \(n_2\). The critical value for a 99% CI is \(qnorm(1-0.01/2) = 2.576.\) Then the 99% CI is:
\[\begin{eqnarray} & &\hat{p}_1 - \hat{p}_2 \pm c\times \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1} + \frac{\hat{p}_2(1-\hat{p}_2)}{n_2}} \\ &=& 0.123 - 0.112 \pm 2.576\times \sqrt{\frac{0.123(1-0.123)}{8505} + \frac{0.112(1-0.112)}{1495}} \\ &=& 0.011 \pm 0.023 = [-0.012, 0.034]. \end{eqnarray}\]
So we are 99% confident that the difference between the proportion of individual and joint applications who have been bankrupt is between -0.012 and 0.034. Since 0 is within the interval, then it’s plausible that the population difference is 0. In that case, we say that there is not a statistically significant difference (at the significance level of \(\alpha=0.01\)) between the two proportions.
If the success-failure condition is not met, then one can find a confidence interval through simulation.
11.5 Confidence interval for \(\hat{b}\)
In the previous sections, we have constructed confidence intervals by finding an approximate sampling distribution for an estimator of a population parameter. The approximate distributions came from the Central Limit Theorem. In this section, we discuss the sampling distribution of the slope of a Least Squares regression line, \(\hat{b}\). Recall that, in section 5.2, we introduced regression diagnostics, which are conditions that should be checked when using a LS regression for statistical inference. If these conditions are met, the sampling distribution of the slopes and intercept of a LS regression are known, which allows us to find confidence intervals for the regression parameters. We focus the discussions in this section on models with only one predictor, but this theory can also be extended to more than one predictor.
Consider a linear model in which the goal is to predict a variable \(Y\) based on values of a variable \(X.\) That is, consider the model
\[Y = a + bX + \epsilon, \]
where \(\epsilon\) is the error of the model. For LS regression, \(X\), \(a\), and \(b\) are seen as constants, while and the error \(\epsilon\) and \(Y\) are seen as random variables. The values \(a\) and \(b\) are the population values for the intercept and slope that describe the relationship between \(Y\) and \(X.\)
Consider a sample of values of two variables, \((X_1, Y_1),\) \((X_2, Y_2),\) \(\dots,\) \((X_n, Y_n),\) and suppose that we want to predict \(Y_i\) using \(X_i.\) Then we can write
\[Y_i = a + bX_i + \epsilon_i, \quad i=1, 2, \dots, n,\] where \(a\) and \(b\) are the population values of the intercept and slope of the line. If we use the LS estimates \(\hat{a}\) and \(\hat{b}\) in the place of \(a\) and \(b,\) then we have \[\hat{Y}_i = \hat{a} + \hat{b}X_i + \hat{e}_i, \quad i=1, 2, \dots, n,\]
where \(\hat{e}_i = Y_i - \hat{Y}_i\) is the residual for observation \(i.\) The estimates \(\hat{a}\) and \(\hat{b}\) are given in theorem 3.1. In order to do statistical inference for LS regression, we need to gain an understanding of the sampling distributions of \(\hat{a}\) and \(\hat{b}.\) This is possible under a few assumptions about the distribution of the error of the model.
Under the framework described above, consider the following assumptions:
A1) The errors \(\epsilon_i\) are independent;
A2) The errors \(\epsilon_i\) are normally distributed with \(E(\epsilon_i) = 0\) and constant variance \(Var(\epsilon_i) = \sigma^2.\) That is, \(\epsilon_i \sim N(0,\sigma).\)
Under assumptions A1 and A2, the distributions of \(\hat{a}\) and \(\hat{b}\) are given by:
\[\hat{b} \sim N\left(b, \frac{\sigma}{\sqrt{\sum(X_i-\overline{X})^2}}\right)\quad \mbox{and}\] \[\hat{a} \sim N\left(a, \sigma\sqrt{\frac{1}{n}+\frac{\overline{X}}{\sum(X_i-\overline{X})^2}}\right).\]
That is, both estimators (slope and intercept) are unbiased and normally distributed. Since we usually don’t have access to \(\sigma^2\), we use the MSE as an estimate for \(\sigma^2.\) The MSE was defined in section 3.4.1 and is given by \(MSE = SSE/(n-2).\) When using this estimate, the t distribution should be used instead of the normal distribution. That is,
\[\frac{\hat{b}-b}{SE(\hat{b})} \sim t_{n-2}\quad \mbox{and} \quad \frac{\hat{a}-a}{SE(\hat{a})} \sim t_{n-2},\] where \[SE(\hat{b}) = \sqrt{\frac{MSE}{\sum(X_i-\overline{X})^2}}\quad\mbox{and}\] \[SE(\hat{a}) = \sqrt{MSE\left[\frac{1}{n}+\frac{\overline{X}}{\sum(X_i-\overline{X})^2}\right ]}.\] This allows us to compute confidence intervals for \(b\) and \(a\) as follows: \[\begin{eqnarray} \mbox{CI for } b:& &\hat{b} \pm c\times SE(\hat{b})\\ \mbox{CI for } a:& &\hat{a} \pm c\times SE(\hat{a}) \end{eqnarray}\]
Such calculation is demonstraded in the following example.
Example 11.5 Suppose that we would like to find a confidence interval for the slope of the line that describes the relationship between interest_rate and debt_to_income in the loans dataset, introduced in chapter 4. Let’s begin by finding the LS model for these variables:
##
## Call:
## lm(formula = interest_rate ~ debt_to_income, data = loans)
##
## Residuals:
## Min 1Q Median 3Q Max
## -21.7391 -3.7203 -0.7945 2.7351 18.6274
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 11.511445 0.080732 142.59 <2e-16 ***
## debt_to_income 0.047183 0.003302 14.29 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.948 on 9974 degrees of freedom
## (24 observations deleted due to missingness)
## Multiple R-squared: 0.02007, Adjusted R-squared: 0.01997
## F-statistic: 204.2 on 1 and 9974 DF, p-value: < 2.2e-16Thankfully, R calculates \(SE(\hat{b})\) and \(SE(\hat{a})\), which are given in the second column of the summary output. In this example, \[SE(\hat{b})=0.0033\quad\mbox{and}\quad SE(\hat{a})=0.0807.\] For a 95% confidence interval, the critical value is \(c=qt(1-0.05/2, df),\) where \(df=n-2\). The summary output also has the degrees of freedom, which this case is 9974. This gives the following critical value:
## [1] 1.960202Therefore, a 95% confidence interval for \(b\) is
\[\hat{b}\pm c\times SE(\hat{b}) = 0.0472\pm 1.9602\times 0.0033 = [0.0407, 0.0537].\]
The confidence interval tells us that, with 95% confidence, the population slope \(b\) is between 0.0407 and 0.0537.
A confidence interval for the intercept can be calculated in a similar way; however, such interval is of much less interest than the one for the slope, as it is often the case that the intercept is not interpretable.
The calculations for confidence intervals described above are reasonable if assumptions A1 and A2 are met. We check for these assumptions through the diagnostic plots discussed in section 5.2.