| Categoría del dolor | Frecuencia | Frecuencia relativa | Frecuencia acumulada | Frecuencia relativa acumulada |
|---|---|---|---|---|
| Severo | 4 | 0.70 | 60 | 1.00 |
| Moderado | 8 | 0.13 | 56 | 0.93 |
| Leve | 17 | 0.28 | 48 | 0.80 |
| Ninguno | 31 | 0.52 | 31 | 0.52 |
9 Estadística descriptiva
- Autor: Edsaúl Emilio Pérez Guerrero
- Afiliación: Universidad de Guadalajara
- mail: edsaul.perezg@academicos.udg.mx
- Última actualización: 2024-09-11
9.1 Introducción
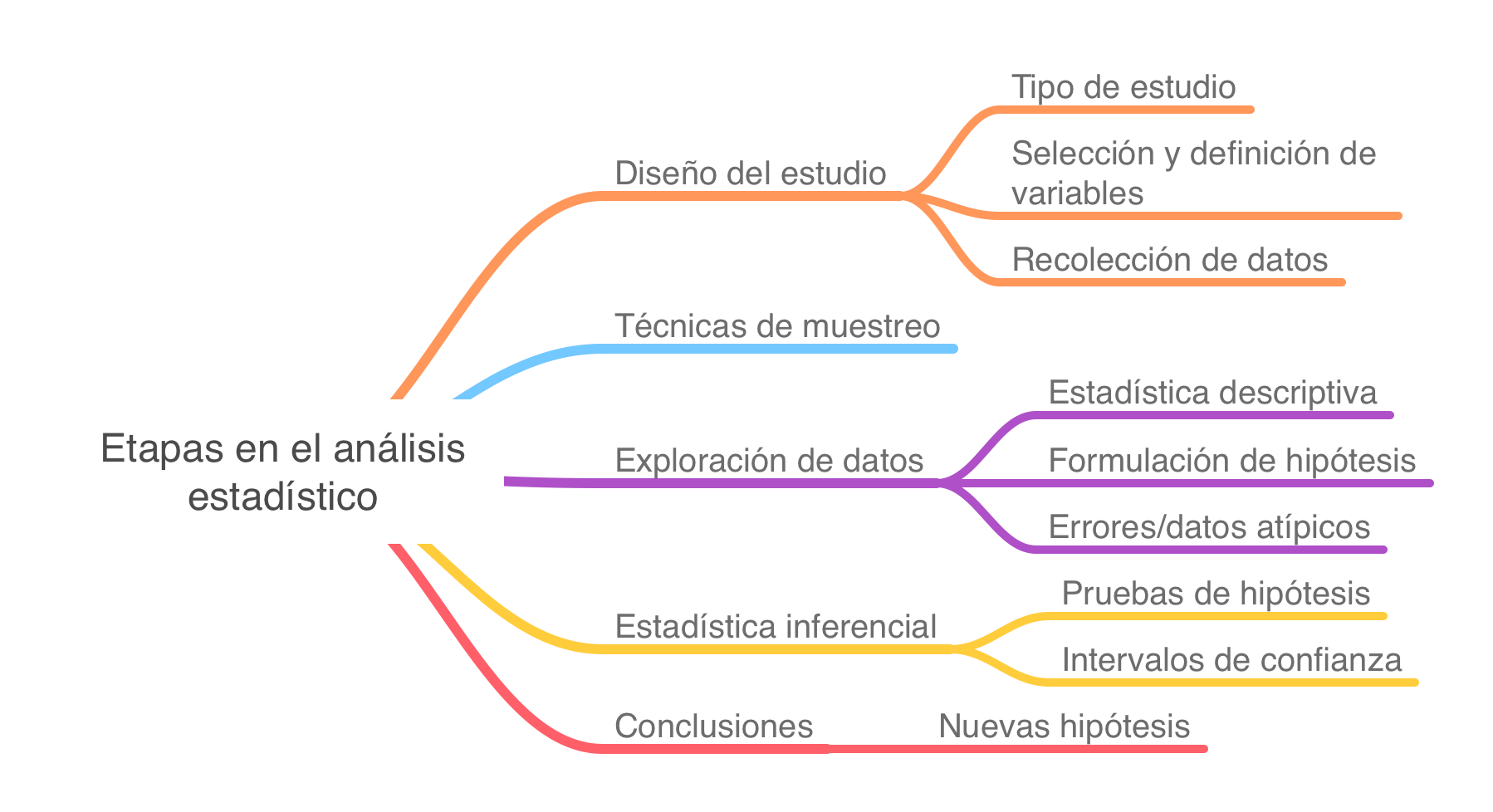
La estadística descriptiva tiene por misión resumir la información que proporciona un conjunto de datos y de las variables. Consiste en presentar y resumir los datos, para ello, empleamos tablas, estimación de estadísticos y gráficos. Lo primero que se debe hacer en el análisis de datos es dar a conocer y presentar nuestros datos. Ver figura Figura 9.1
9.2 Estadística descriptiva para variables cualitativas
La estadística descriptiva en variables cualitativas es extremadamente sencilla. Básicamente consiste en presentar los datos en forma de conteos o frecuencias y en proporciones o porcentajes. Las frecuencias proporcionan una rápida visión del comportamiento de los datos.
La tabla Tabla 9.1 muestra un ejemplo de la descripción de variables cualitativas en un grupo de pacientes en los que les fue evaluado el dolor después de una cirugía por apendicitis.
Existen algunas medidas que podemos utilizar para presentar más ampliamente nuestros datos:
Frecuencia (conteos)
Frecuencia relativa (proporción)
Frecuencia acumulada
Frecuencia relativa
Describiremos cada una de estas medidas a continuación:
Frecuencia absoluta La frecuencia absoluta (fa):es el número de veces que se ha observado dicha modalidad. Son los conteos que podemos hacer a las categorías de las variable cualitativas
\[\sum{fa=n}\]
Frecuencia relativa (proporciones): La frecuencia relativa (fr): Es la frecuencia absoluta dividida entre el número de casos. Se puede expresar como proporción o como porcentaje
\[\sum{fr=\frac{fa}{n}}\]
Frecuencia acumulada: La frecuencia acumulada es el resultado que se obtiene de la suma sucesiva de las frecuencias absolutas o relativas, cuando se realiza de menor a mayor según sus valores. En la frecuencia acumulada, los datos se pueden ir sumando en orden ascendente o descendente
Ejemplo 9.1 En un servicio de Traumatología, con objeto de realizar una correcta planificación, interesa conocer la localización de la patología principal de los pacientes atendidos en urgencia, para lo cual se estudia una muestra de 186 elegida entre los pacientes atendidos durante los últimos 6 meses. La variable de interés es la zona afectada. Es una variable cualitativa dividida en 5 modalidades: rodilla, cadera, tobillo, cráneo y otras
Al final del estudio se obtuvo que en los 6 meses se atendieron 30 problemas relacionados con rodilla, 28 con cadera, 41 con tobillo, 34 cráneo y 53 otras.
Obtenga la frecuencia absoluta, frecuencia relativa, % y frecuencia acumulada
| Zona afectada | fa | fr(n) | fr(%) | fa acumulada |
|---|---|---|---|---|
| Rodilla | 30 | 0.161 | 16.1 | 30 |
| Cadera | 28 | 0.151 | 15.1 | 58 |
| Tobillo | 41 | 0.220 | 22.0 | 99 |
| Cráneo | 34 | 0.183 | 18.3 | 133 |
| Otras | 53 | 0.285 | 28.5 | 196 |
| Total | 186 | 1.000 | 100.0 | – |
9.2.1 ¿Cómo obtener una tabla de frecuencias con R?
En R se utilizan, las siguientes funciones:
table()permite conocer las frecuencias de un objeto, incluso si los tipos de datos no son cualitativos.prop.table()permite obtener las proporciones de un objeto. Es necesario que el objeto sea un tablaaddmargins()permite obtener las frecuencias acumuladas de un determinado objeto. Es necesario que el objeto sea una matriz.cumsum()realiza la suma acumulativa de las frecuencias de un objeto.
No olvide que puede consultar la ayuda de cada una de las funciones utilizando la función help().
Ejemplo 9.2 Partiremos de un objeto llamado grados
set.seed(346598) # Sembrando la semilla
grados <- sample(LETTERS[1:4], 1000, TRUE)Con el código anterior creamos un objeto con 1000 datos de las letras de la A a la D con remplazo. Ahora podemos visualizar y contar cuantos grados (letras) hay
table(grados)# Permite visualizar el conteo de los gradosgrados
A B C D
245 247 239 269 Ahora, podemos ver la proporción de cada uno de los grados con la función prop.table().
# Se requiere un objeto que sea una tabla
prop.table(table(grados)) # Permite conocer las proporciones de cada uno de los gradosgrados
A B C D
0.245 0.247 0.239 0.269 Para obtener los porcentajes, podemos multiplicar nuestra tabla con las proporciones por 100.
prop.table(table(grados))*100# Se multiplica por 100grados
A B C D
24.5 24.7 23.9 26.9 Para obtener las frecuencias acumuladas podemos utilizar la función cumsum.
cumsum(table(grados)) A B C D
245 492 731 1000 Ejemplo 9.3 Si se parte de la creación de un objeto a partir de una tabla, puede utilizar el siguiente código
x <- table(grados)
table(x) # Conteosx
239 245 247 269
1 1 1 1 prop.table(x) # Proporciones, Se requiere un objeto que sea una tablagrados
A B C D
0.245 0.247 0.239 0.269 prop.table(x)*100 # Porcentajesgrados
A B C D
24.5 24.7 23.9 26.9 cumsum(x) # Frecuencias acumuladas A B C D
245 492 731 1000 Ejemplo 9.4 Puede crear varios objetos y posteriormente organizarlos en forma de tabla para obtener de una forma más organizada, en este ejemplo, se presentará primero el código y después se explicará más adelante.
data_freq <-
data.frame(
Freq =as.numeric(x),
Freq_Rela = as.numeric(prop.table(x)),
Freq_Acum = as.numeric(cumsum(x)),
Freq_Rela_Acum = as.numeric (cumsum(prop.table(x))))
rownames(data_freq) <- LETTERS[1:4]
data_freq Freq Freq_Rela Freq_Acum Freq_Rela_Acum
A 245 0.245 245 0.245
B 247 0.247 492 0.492
C 239 0.239 731 0.731
D 269 0.269 1000 1.000Explicación del código . El código de forma general, permitió la creación de un objeto data_freq que contiene una tabla de frecuencias con los conteos (objeto Freq), la frecuencia relativa (objeto Freq_Rela), la frecuencia acumulada (objeto Freq_Acum) y la frecuencia relativa acumulada (objeto Freq_Rela_Acum). Este objeto tomó los datos del x que creamos en el ejemplo Ejemplo 9.3. Para que los datos pudieran ser organizados de forma adecuada en un tabla, es necesario hacer la coerción a valores numéricos de los objetos.
En el código se utilizó la función data.frame(), la cual permite crea marcos de datos cuando es alimentada por objetos y los organiza en columnas. (puede revisar el siguiente enlace. Finalmente la función rownames permite cambiar los nombres del Dataframe, en este caso por las primeras cuatro letras del abecedario (igual que los grados).
Note como en este código no ordena explícitamente los datos, pero al estar utilizando la primeras cuatro letras del abecedario, los datos se ordenan mediante el alfabeto. Si quiere ordenar los datos deberá utilizar la función sort.
La tabla de frecuencias también puede crearse con el siguiente código, en el que creo una nueva columna con los nombres de la tabla Nombres=names(x)
data_freq <-
data.frame(
Nombres= names(x),
Freq =as.numeric(x),
Freq_Rela = as.numeric(prop.table(x)),
Freq_Acum = as.numeric(cumsum(x)),
Freq_Rela_Acum = as.numeric (cumsum(prop.table(x))))
print(data_freq) Ejercicio 9.1 Crear un script con la resolución del ejercicio anterior.
Ejercicio 9.2 Utilizando la base de datos Cushings de la librería MASS cree una tabla de frecuencias para la variable Type.
Ejercicio 9.3 Utilizando la base de datos Cushings de la librería birthwt cree una tabla de frecuencias para la variable race.
9.3 Gráficos utilizados para la exploración de variables cualitativas
Existen diferentes gráficos que nos permiten representar las variables entre ellos se incluyen:
- Gráficos de barras, función
barplot - Gráficos de sectores, función
pie - Gráficos de mosaicos, función
mosaicplot
Aunque una descripción detallada de la elaboración de gráficos se abordará en el capítulo XXX, en este, se realizará una descripción rápida de ellos.
9.3.1 Graficos de barras
Un gráfico de barras es una herramienta útil para representar la frecuencia o proporción de diferentes categorías de una variable cualitativa. Son útiles para representar y comparar conteos, frecuencias, y porcentajes de variables cualitativas
Por ejemplo se utiliza si tenemos datos como el tipo de enfermedad, la clasificación de severidad de una enfermedad, el grupo sanguíneo de pacientes, etc.
Utilizando el objeto grados podemos crear un gráfico de barras con el siguiente código:
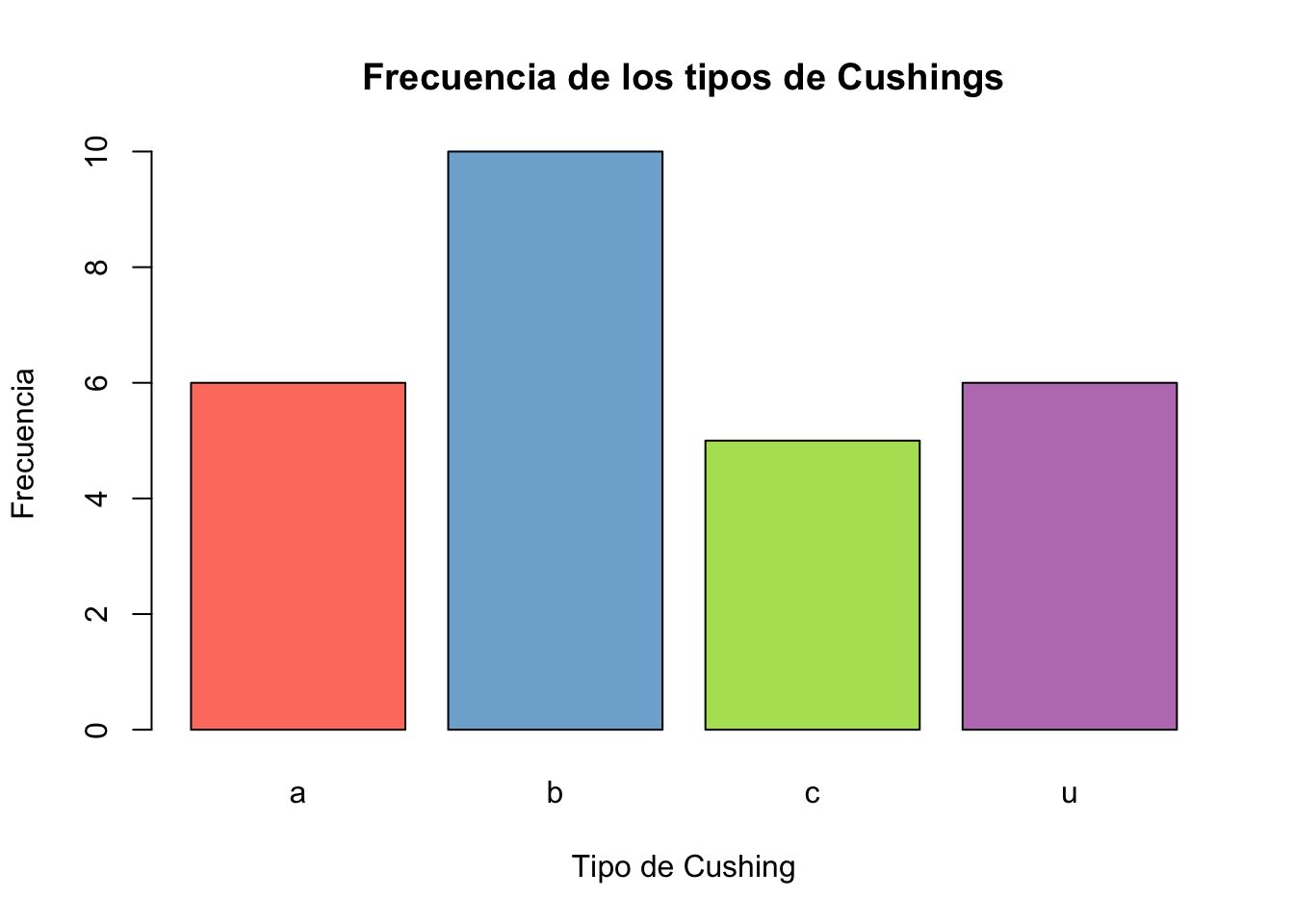
barplot(table(grados), col = c(1:4),
main = "Mi primer gráficos de barras")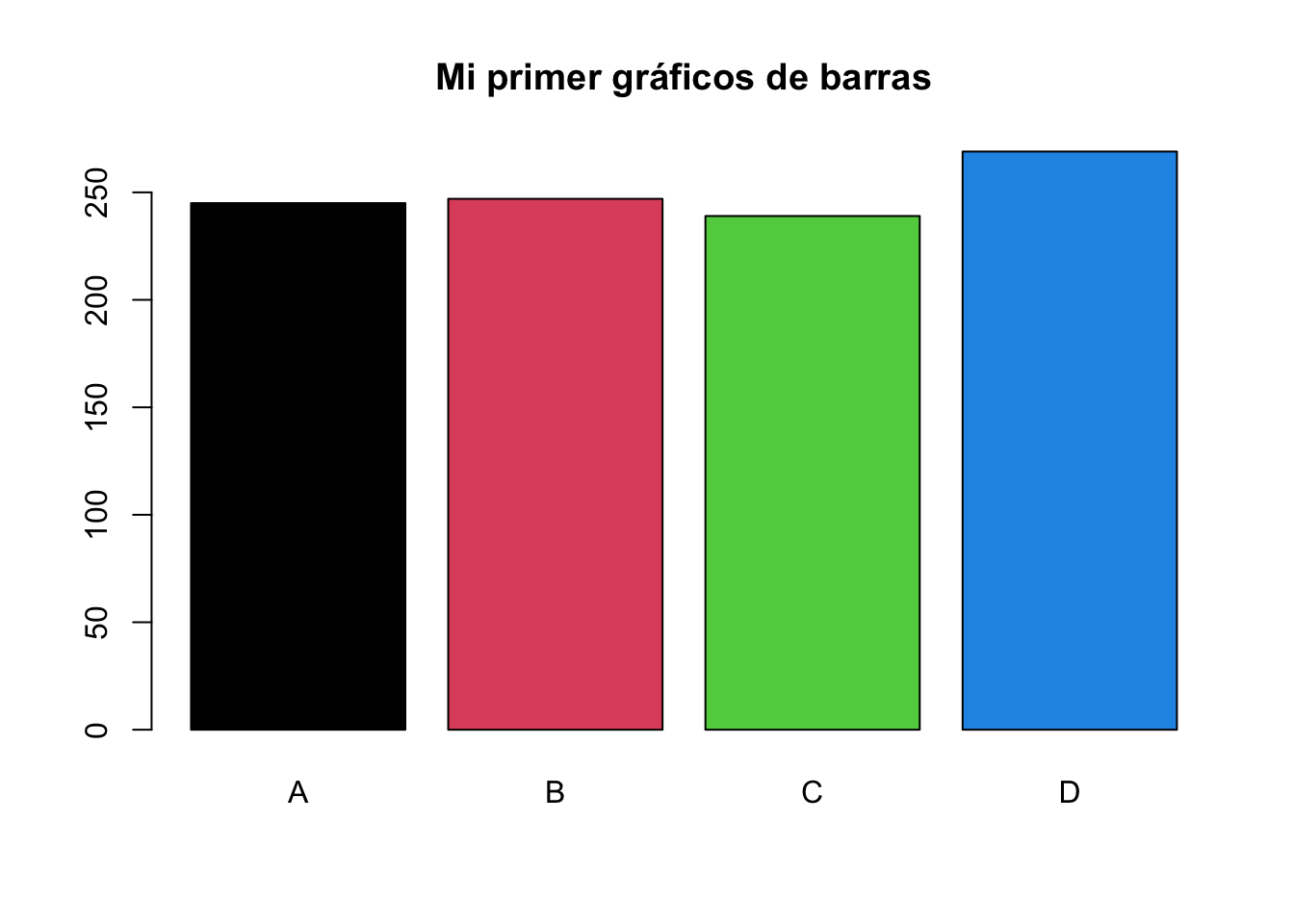
Tome en cuenta que la función barplot necesita ser alimentada con conteos, que en este caso, fueron obtenidos de la función table explicada en la sección anterior ¿Cómo obtener una tabla de frecuencias con R?. Utilizamos los colores del 1 al 4 con el argumento col y agregamos un título con el argumento main. Tome en cuenta que los títulos van entrecomillados.
Puede aprender sobre los colore en R en el manual de la universidad de Columbia que contiene algunos de los colores que puede ser utilizados en R. Usted puede aumentar esta gama de colores mediante la instalación de librerías con paletas de colores
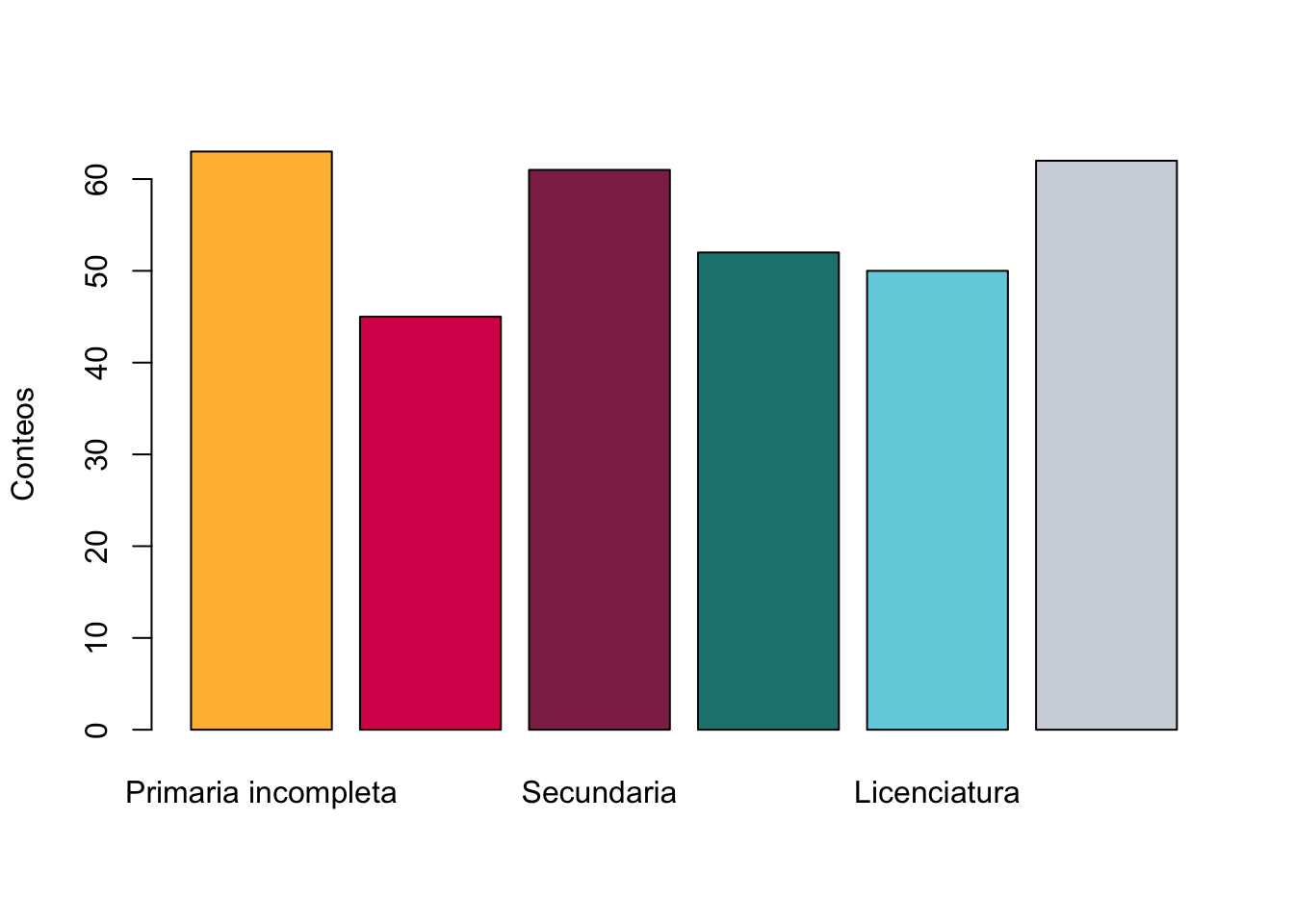
El siguiente código muestra como cambiar los colores del gráfico de barras utilizando el código en lugar de números o nombres de estos.
barplot(table(grados),
main="Gráfico de barras para grados",
xlab= "Grados",
ylab= "Conteos",
col=c("#d0dccb", "#d7c7be", "#b3c5ba", "#88c3b5"))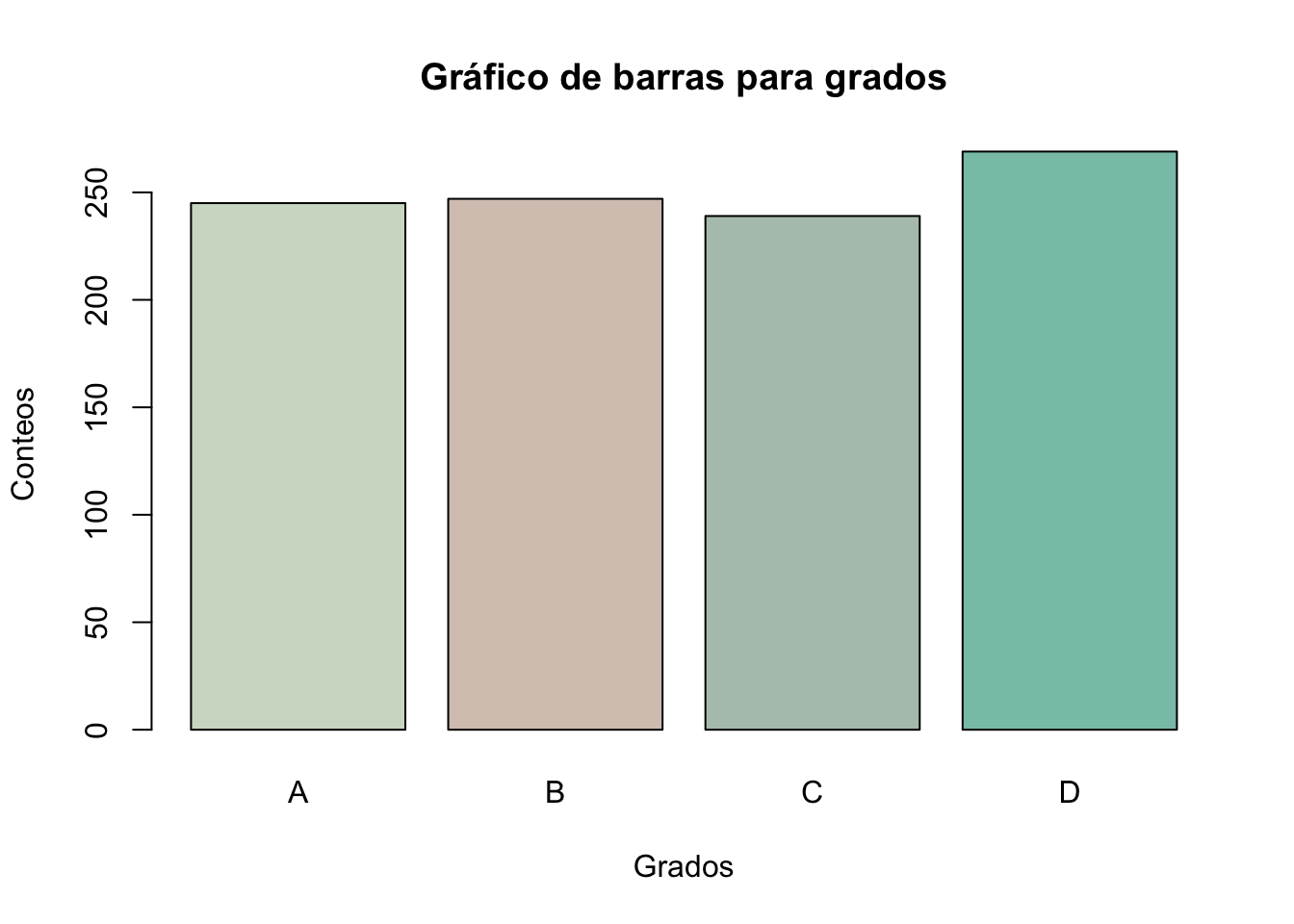
9.3.2 Gráficos de sectores
Los gráficos de sectores ayudan a representar proporciones de una variable cualititiva en un circunferencia. Representa las categorías de una variables mediante proporciones. Para estimar la proporción de cada una de las categorías se utiliza la siguiente formula:
\[\alpha_i= \frac{360}{N} n_i\] Donde \(n_i\) es la frecuencia absoluta y \(N\) el total de las observaciones de la muestra. El 360 estará siempre en la fórmula y no variará porque es necesario para que el diagrama de sectores tenga una forma circular.
El gráfico de sectores, también conocido como gráfico circular o gráfico de pastel, es una representación visual utilizada para mostrar la proporción o distribución de diferentes categorías dentro de un conjunto de datos. Cada categoría se representa como un sector circular en el gráfico, y el tamaño de cada sector es proporcional a la frecuencia o proporción de esa categoría en relación con el total
Vamos realizar un diagrama de sectores del objeto grados con el siguiente código:
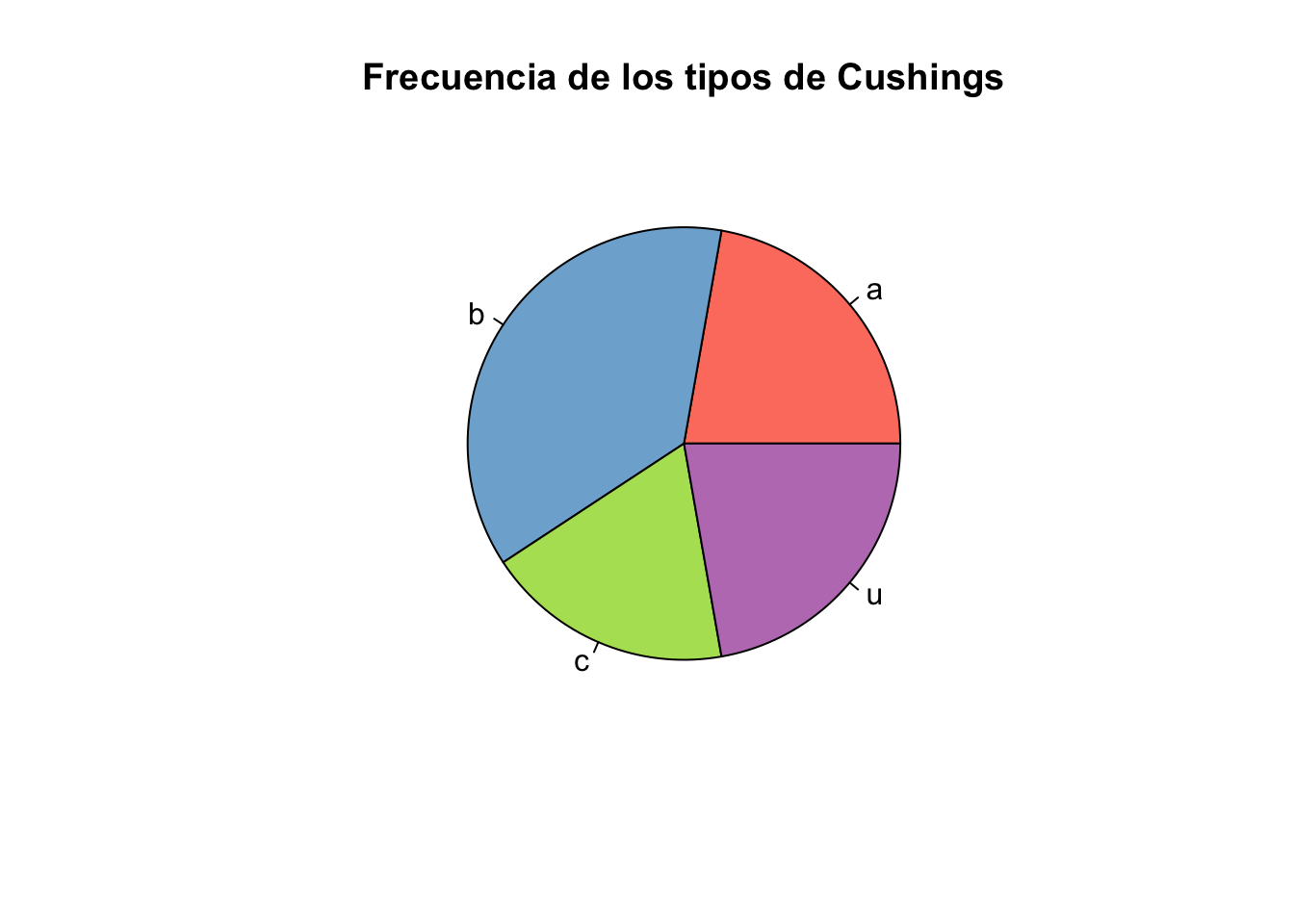
pie(table(grados), main="Mi primer gráfico de sectores")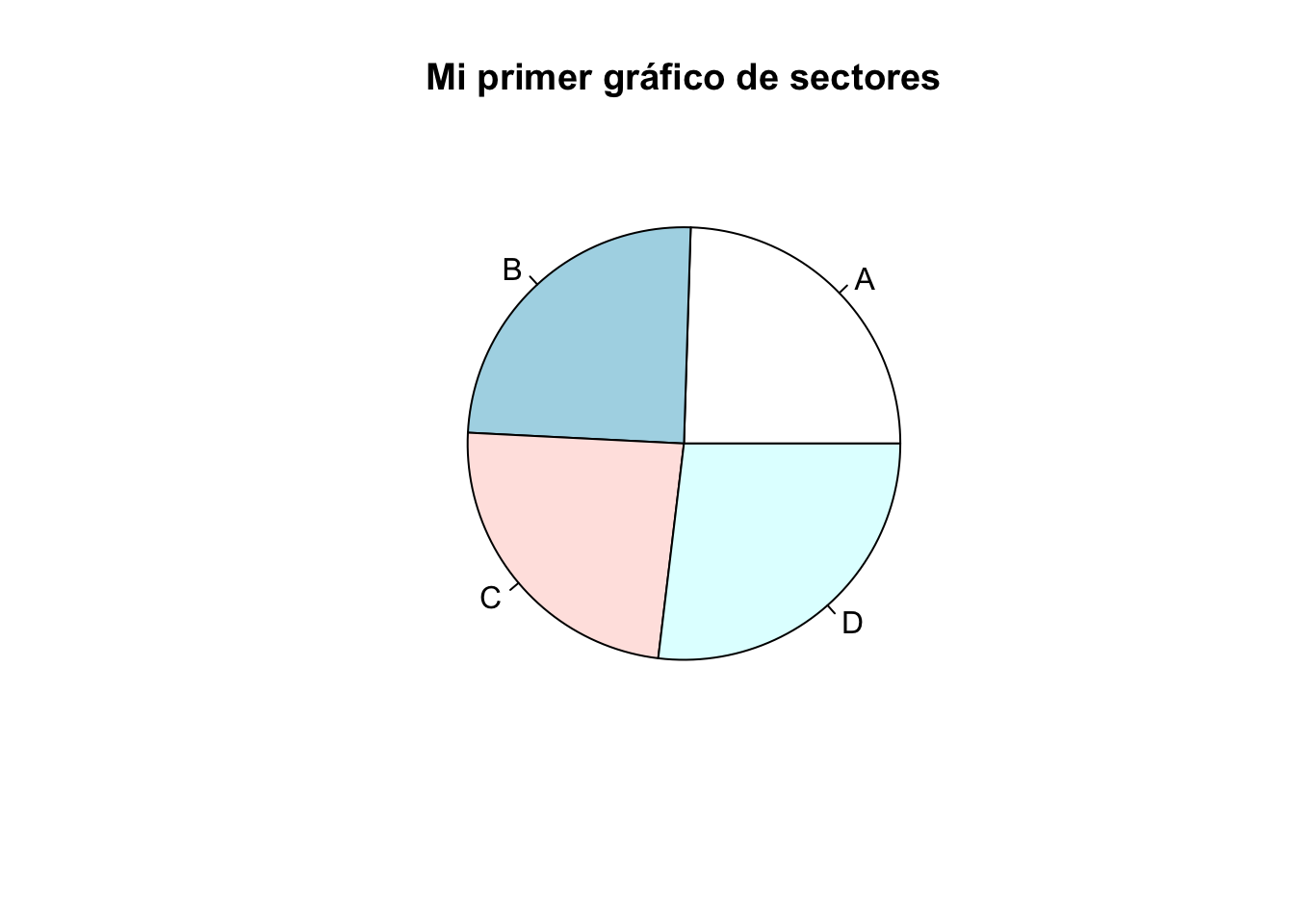
Note como de nuevo utilizamos de nueva cuenta la función table para obtener los conteos de las categorías.
Ejercicio 9.4 Utilizando la base de datos Cushings de la librería MASS cree un gráfico de barras y otro de sectores para la variable Type
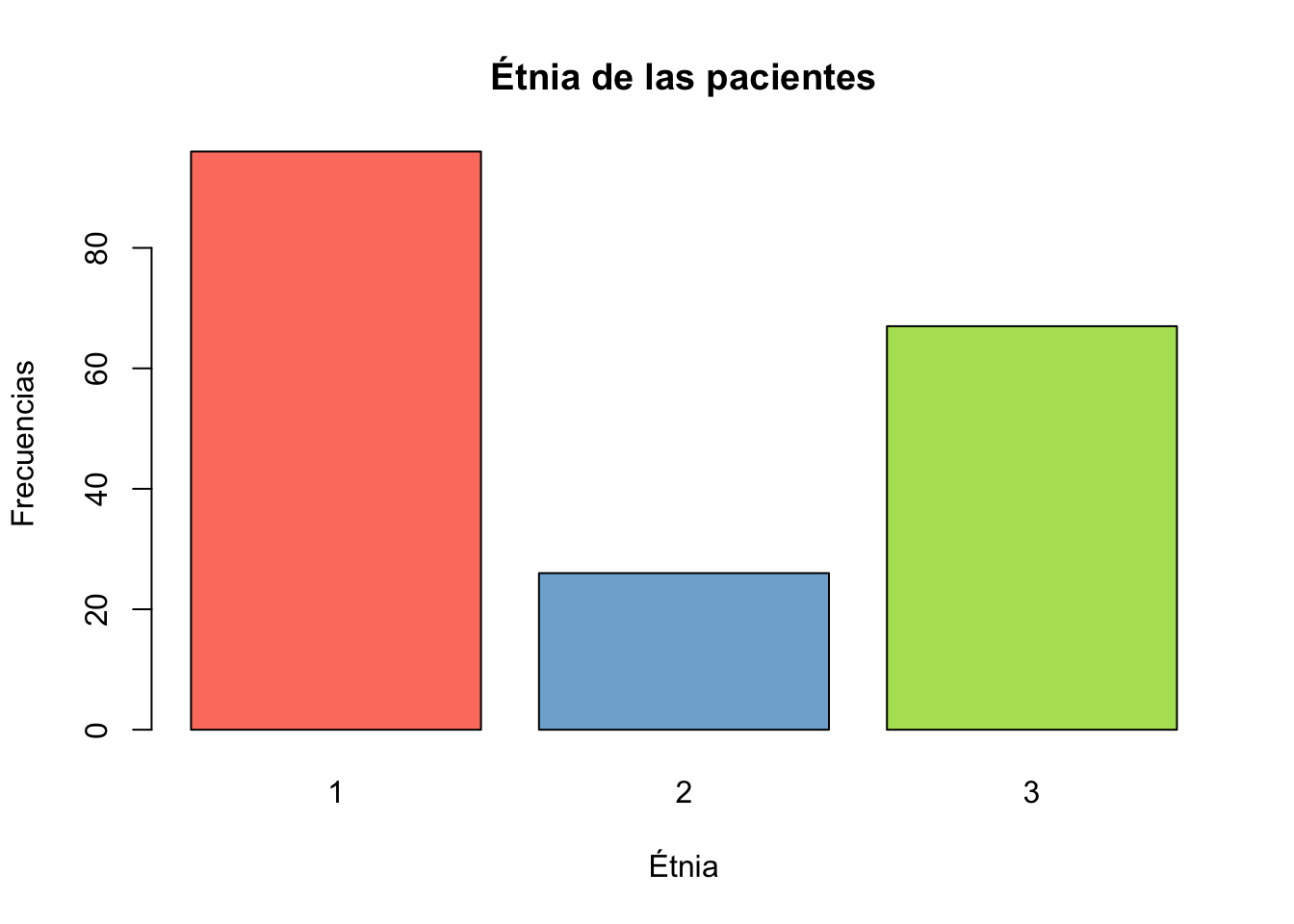
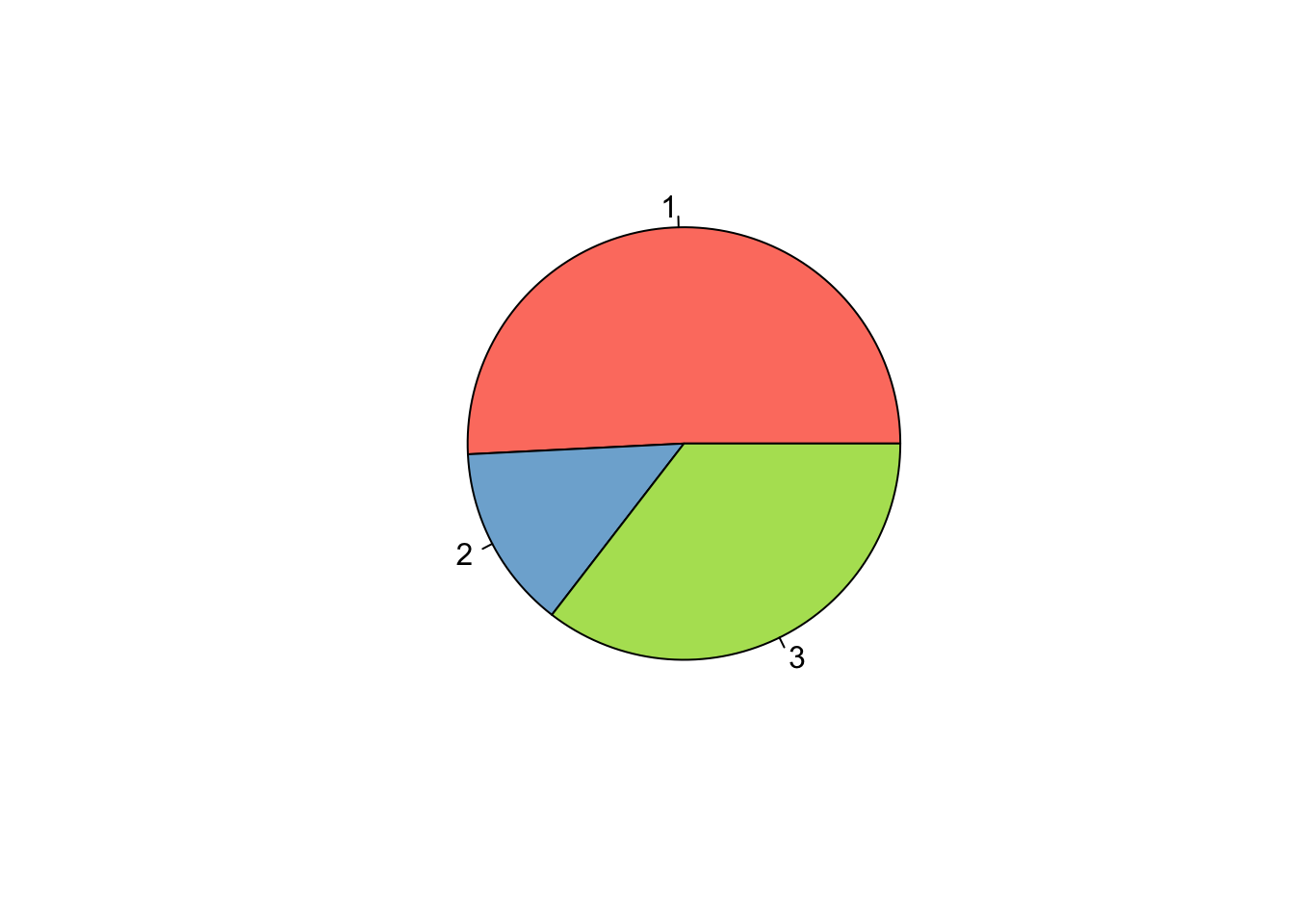
Ejercicio 9.5 Utilizando la base de datos birthwt de la librería MASS cree gráfico de barras y otro de sectores para la variable race.
9.3.3 Gráficos de mosaicos
Es otra forma de representar datos categóricos, sobre todo cuando los datos provienen de una tabla cruzada. Se podría decir que el gráfico de mosaicos es un gráfico de barras segmentado. Aunque revisaremos más a detalle los conceptos de tabla de cruzadas y tablas de contingencia en el capítulo XXXX, realizaremos una descripción sencilla de las mismas. Las tablas cruzadas permiten analizar la relación entre dos variables y permiten conocer valores cumplen con determinada característica al representar los datos en filas y columnas. Para explicar más ampliamente utilizaremos un ejemplo: imagine que estamos interesados cuantas de las madres que fuman tuvieron bebés con bajo al nacer. Para ello utilizamos la base de datos birthwt de la librería MASS. Para ello, utilizamos el siguiente código:
low age lwt race smoke ptl ht ui ftv bwt
85 0 19 182 2 0 0 0 1 0 2523
86 0 33 155 3 0 0 0 0 3 2551
87 0 20 105 1 1 0 0 0 1 2557
88 0 21 108 1 1 0 0 1 2 2594
89 0 18 107 1 1 0 0 1 0 2600
91 0 21 124 3 0 0 0 0 0 2622Si requiere recordar las variables de la base birthwt y su significado puede utilizar help("birthwt")
Si queremos conocer cuantos pacientes fuman y de forma separada cuantos recién nacidos presentaron bajo peso al nacer podemos emplear el siguiente código:
table(smoke)smoke
0 1
115 74 table(low)low
0 1
130 59 Las anteriores son solo tablas de frecuencias, no una tabla de contingencia. Se pueden crear tablas de contingencia con la función table ingresando dos variables.
table(smoke, low)# smoke queda en la filas y low en las columnas low
smoke 0 1
0 86 29
1 44 30table(low, smoke)# low queda en las filas y smoke en las columnas smoke
low 0 1
0 86 44
1 29 30¿Y si quisiéramos proporciones?
table(smoke, race)/100 race
smoke 1 2 3
0 0.44 0.16 0.55
1 0.52 0.10 0.12table(race, smoke)/100 smoke
race 0 1
1 0.44 0.52
2 0.16 0.10
3 0.55 0.12El resultado anterior también se puede hacer utilizando la función prop.table. Con esta función podemos obtener tablas de contingencia con proporciones
prop.table(table(smoke, race)) race
smoke 1 2 3
0 0.23280423 0.08465608 0.29100529
1 0.27513228 0.05291005 0.06349206prop.table(table(race, smoke)) smoke
race 0 1
1 0.23280423 0.27513228
2 0.08465608 0.05291005
3 0.29100529 0.06349206Se puede calcular las proporciones por columnas o por filas, cambiando un argumento. Se utiliza 1 para filas y 2 para columnas.
prop.table(table(smoke, race),1)#Proporciones por fila race
smoke 1 2 3
0 0.3826087 0.1391304 0.4782609
1 0.7027027 0.1351351 0.1621622prop.table(table(race, smoke),2)# Proporciones por columna smoke
race 0 1
1 0.3826087 0.7027027
2 0.1391304 0.1351351
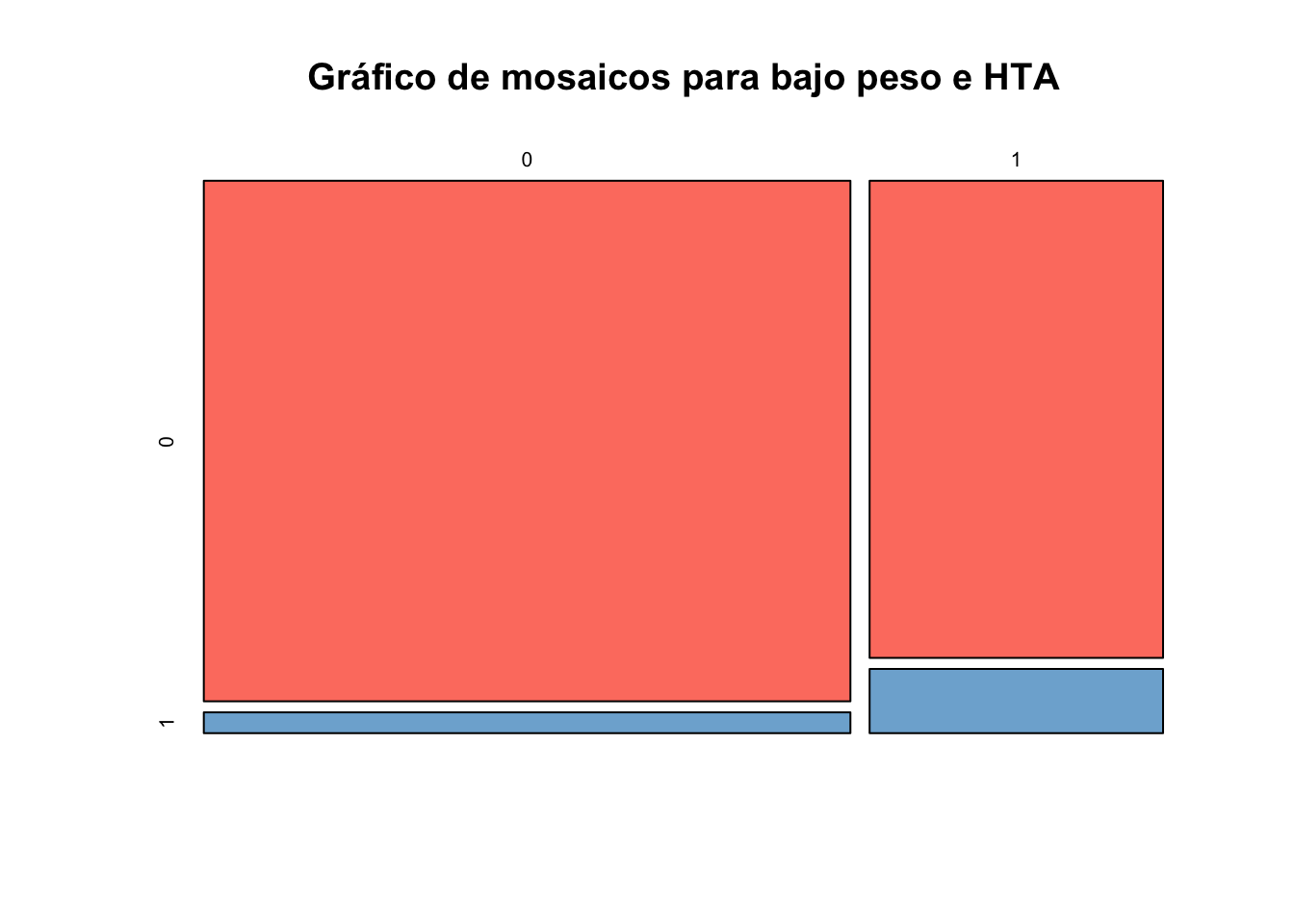
3 0.4782609 0.1621622Ahora para realizar el gráfico de mosaico utilizamos el siguiente código:
mosaicplot(table(smoke, race), col=3:6, main= "Mi primer gráfico de mosaico")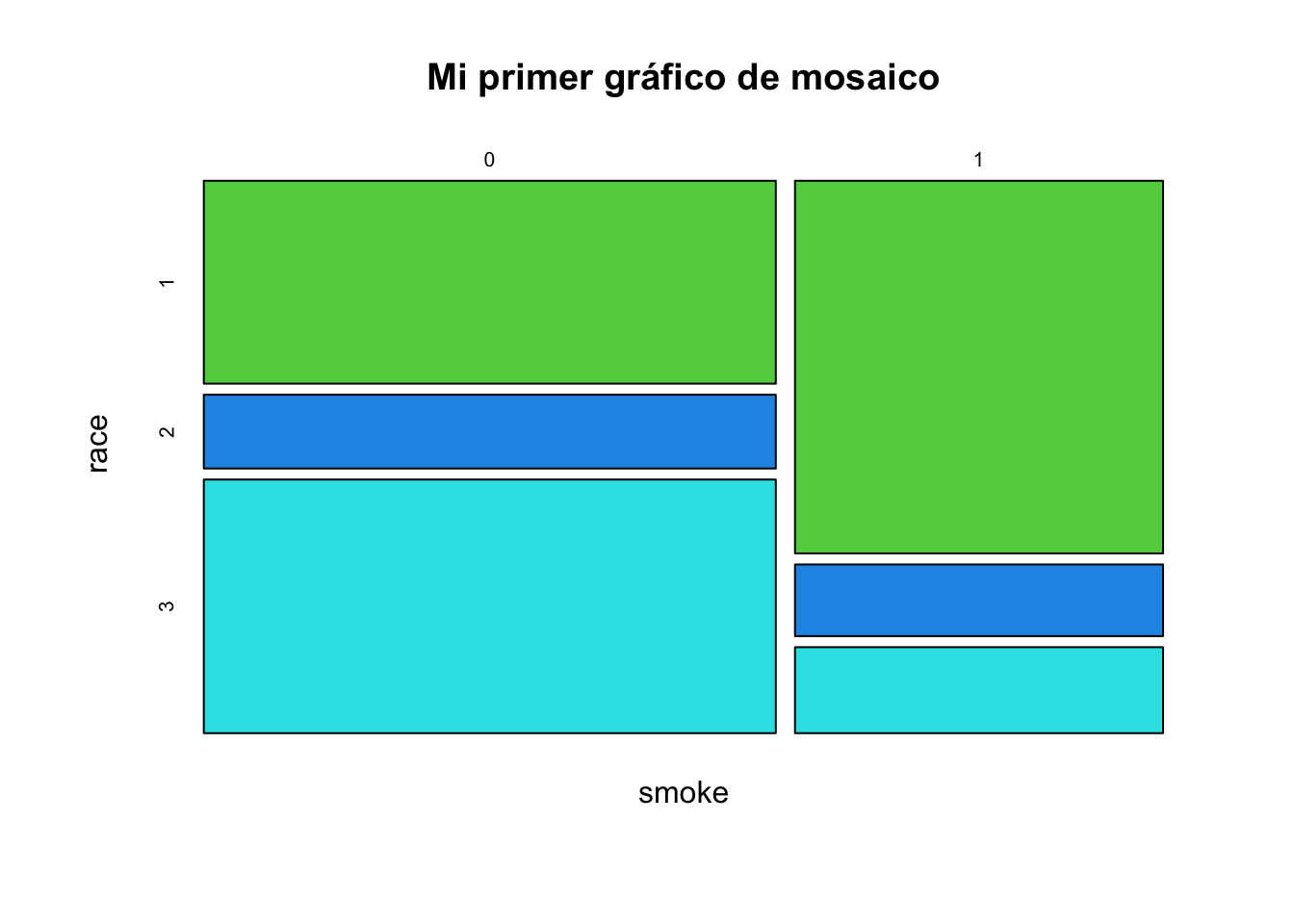
En esta ocasión seleccionamos los colores del 3 al 6. Note como el gráfico nos permite identificar rápidamente las proporciones de cada una de las categorías.
Ejercicio 9.6 Utilizando la base de datos birthwt de la librería birthwt cree gráfico de mosaico con las proporciones de las variables low y ht. Realice una interpretación de su gráfico
9.4 La Función cut
En ocasiones, es de nuestro interés fracciones o segmentar una variable de cuantitativa para poder obtener categorías de la misma. Por ejemplo, supongamos que es de nuestro interés conocer cuantos pacientes presentan una edad de 0 a 10 años, de 11 a 20 años y de 21 a 35 años. Para ello utilizamos la función cut que permite precisamente fraccionar o cortar un a variable de tipo cuantitativo. Esta función tiene la siguiente estructura:
cut(x, breaks, labels = NULL,
include.lowest = FALSE, right = TRUE, dig.lab = 3,
ordered_result = FALSE, …)- x: vector numérico
- breaks: puntos de corte, debe ser mayor a 2
- labels: etiquetas de cada categoría
- right: indica hacía donde debe cerrarse el intervalo ]. El valor predeterminado es el izquierdo ( ], es decir no incluirá el número del lado izquierdo pero si el del lado derecho.
Para resolver los siguientes ejemplos y entender como funciona cut, vamos a crear un vector numérico de datos ficticios que contendrán las edades de 800 pacientes. El código para crear este vector es el siguiente:
# Creando un vector
x <- (1:40)
# Mismos criterios de probabilidad, sembrando la misma semilla
set.seed(1234)
# Obteniendo una muestra
edad <- sample(x, size = 800, replace = T)Del código anterior conviene explicar lo siguiente: - 1) se creó un vector x con una secuencia de números del 1 al 40 - 2) se utilizó la función set.seed para que los número aleatorios se muevan bajo ciertos parámetro y que a pesar de esta aleatoriedad podemos tener todos los mismo resultados. R crear número aleatorios siguiendo un algoritmo, en este caso con la función set.seed podemos definir bajo que parámetros se mueve este algoritmo. Puede revisar más detalles de esta función en: https://www.statology.org/set-seed-in-r/ y en https://r-coder.com/set-seed-r/ - 3) se creó un objeto llamado edad utilizando el objeto x se creo una muestra con reemplazo de 800 datos
Vamos a resolver un ejemplo:
Ejemplo 9.5 Utilizando el objeto edad realice cortes de manera que pueda identificar cuantos pacientes tienen una edad menor o igual a 10, de 11 a 30 años incluyendo el 30 y el resto de los pacientes. No cambie las etiquetas de los niveles. Nombre este nuevo objeto como edad1, pida los conteos de los niveles utilizando la función table, realice una gráfica de barras con esta nueva variable.
El código para resolver este ejercicios es el siguiente:
edad1 <- cut(x = edad, breaks = c(0, 10, 30, Inf),
right=T)
table(edad1)edad1
(0,10] (10,30] (30,Inf]
170 410 220 table(edad1==30)
FALSE
800 Se crearon 4 cortes del objeto edad, el primero va del 0 al 10 sin incluir el 0 pero incluyendo el 10, el segundo corte va del 10 al 30 sin incluir el 10 e incluyendo el 30, el último corte va del 30 (sin incluirlo) al infinito. Utilizar Inf simplifica la selección del número más grande y es muy recomendado cuando no se conoce el número mayor. Aunque más adelante se explicará la construcción de gráficas en mayor detalle en capñitulos posteriores, puede utilizar el siguiente código para construir una gráfica:
barplot(table(edad1))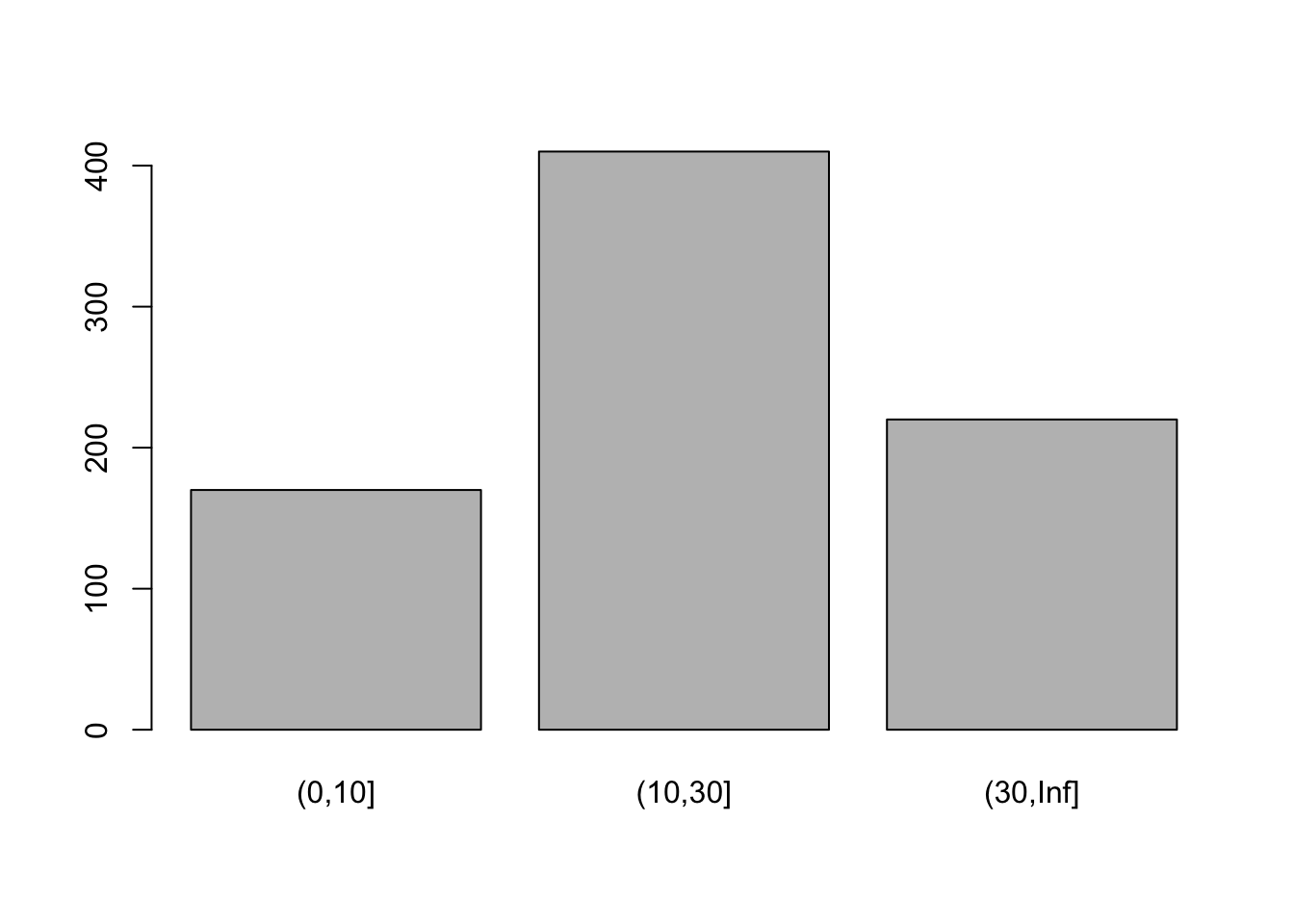
Ejemplo 9.6 Cree una nuevo objeto llamado edad2 que contenga los mismo cortes del ejercicio anterior pero cambie el argumento right = F. Describa que es lo que pasa
edad2 <- cut(x = edad, breaks = c(0, 10, 30, Inf),
right=F)
table(edad2)edad2
[0,10) [10,30) [30,Inf)
154 406 240 table(edad2==30)
FALSE
800 barplot(table(edad2))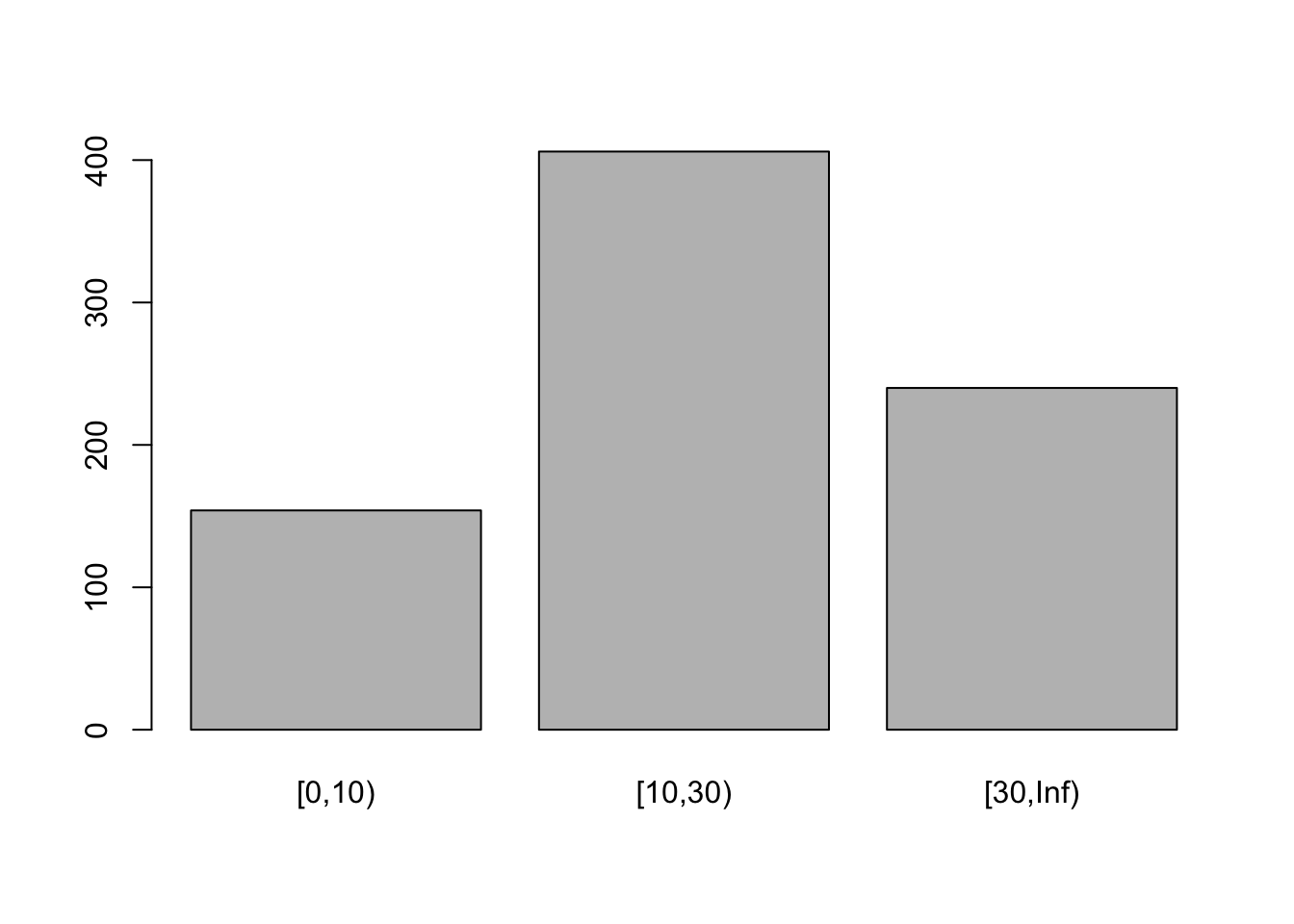
Ejemplo 9.7 Utilizando la función cut Cambie las etiquetas de los niveles edad1 y edad2 por: “Grupo edad 1”, “Grupo de edad 2”, “Grupo de edad 3”. Para ello utilize el argumento labels
edad1 <- as.factor(cut(x = edad, breaks = c(0, 10, 30, Inf),
labels = c("Grupo edad 1", "Grupo de edad 2", "Grupo de edad 3" ),
right=T))
table(edad1)edad1
Grupo edad 1 Grupo de edad 2 Grupo de edad 3
170 410 220 levels(edad1)# Visualizar los niveles de un factor[1] "Grupo edad 1" "Grupo de edad 2" "Grupo de edad 3"9.5 Creación de variables dentro de un data frame
Es común que sea de nuestro interés incluir la variable que recientemente en un data frame, por ejemplo, la variable que recientemente creamos utilizando la función cut. Para ello, podemos utilizar el símbolo $ que en el caso de que la variable no se encuentre dentro nuestro data frame (mega objeto) la crea. Por ejemplo:
base_datos$nueva_variableUtilizando la base de datos `Pima.tr2` de la librería `MASS` corte la variable `age` de acuerdo con los siguiente criterios:
- Mujeres menores a 24 años
- Mujeres de 24 a 33 pero menores de 33
- Mujeres de 33 a 49
- Mujeres de 50 a 72
Además:
- Cree un nuevo objeto dentro la base `Pima.tr2` y nómbrelo como `edad_factor`
- Cambie las etiquetas de `edad_factor` por la etiqueta que más le convenga
- Obtenga un conteo de los niveles del objeto `edad_factor`
- Cree un gráfico de barras de `edad_factor`Resolución al ejemplo Ejemplo 9.10).
library(MASS) # Cargar librería
data("Pima.tr2") # Llamar base de datos
Pima.tr2$edad_factor <- cut(Pima.tr2$age,
breaks = c(0, 24, 33, 50, 73),
labels = c("Edad 1", "Edad 2",
"Edad 3", "Edad 4"),
right = F) # Crear cortes
# El código anterior permitió crear una nueva variables dentro de Pima.tr2
table(Pima.tr2$edad_factor) # Conteos de la nueva variable
Edad 1 Edad 2 Edad 3 Edad 4
65 120 79 36 Si utiliza el código View(Pima.tr2) podrá visualizar su nueva variable.
También, podemos comprobar que nuestros cortes hayan sido correctos. Puede utilizar el siguiente código:
# Comprobamos Edad 1
table(Pima.tr2$age<24)
FALSE TRUE
235 65 # Comprobamos Edad 2
table(Pima.tr2$age>=24&Pima.tr2$age<33)
FALSE TRUE
180 120 Finalmente podemos crear una gráfica para visualizar nuestra nueva variable:
barplot(table(Pima.tr2$edad_factor))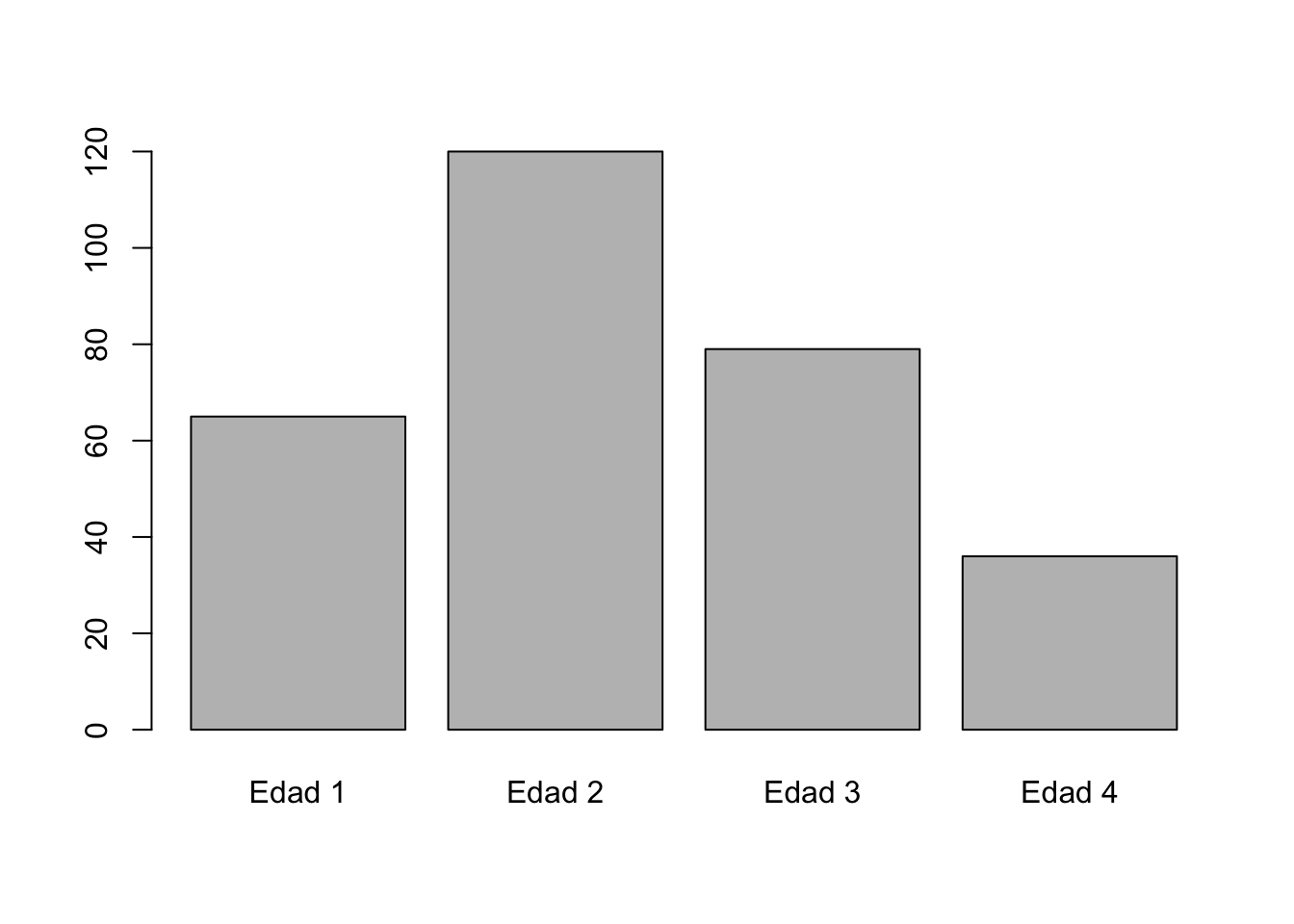
9.5.1 Ejercicios para la función cut
Resuelva el siguiente ejercicio de práctica.
Ejercicio 9.7 Utilizando la base de datos Pima.tr2 de la librería MASS, realice cortes de la variable BMI para clasificar a las pacientes según los criterios de la OMS descritos en la siguiente tabla:
| Clasificación | IMC (kg/m2) | Riesgo Asociado a la salud |
|---|---|---|
| Normo Peso | 18.5 − 24.9 | Promedio |
| Sobrepeso o Pre Obeso | 25 - 29.9 | AUMENTADO |
| Obesidad Grado I o moderada | 30 − 34.9 | AUMENTO MODERADO |
| Obesidad Grado II o severa | 35 - 39.9 | AUMENTO SEVERO |
| Obesidad Grado III o mórbida | ≥ 40 | AUMENTO MUY SEVERO |
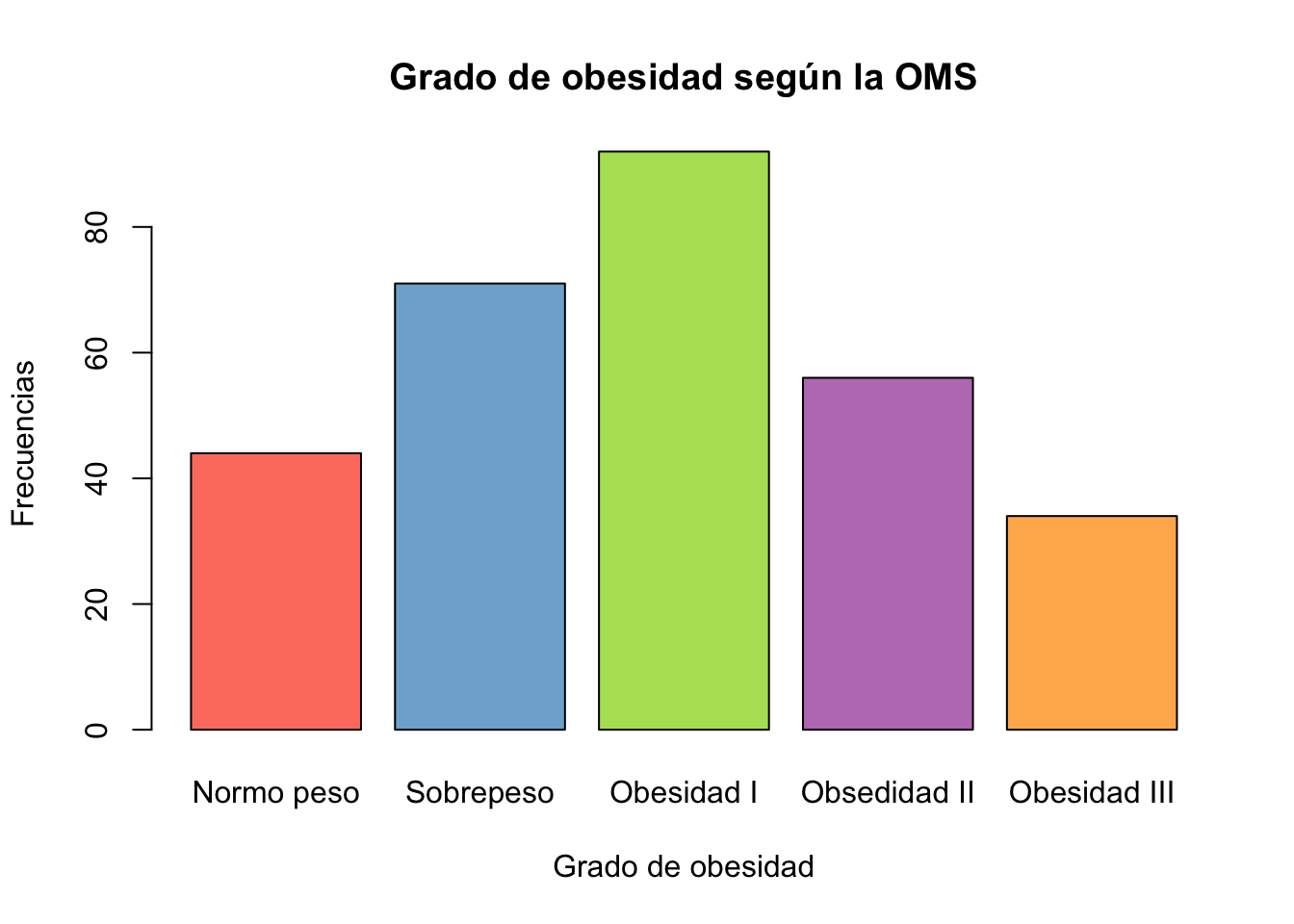
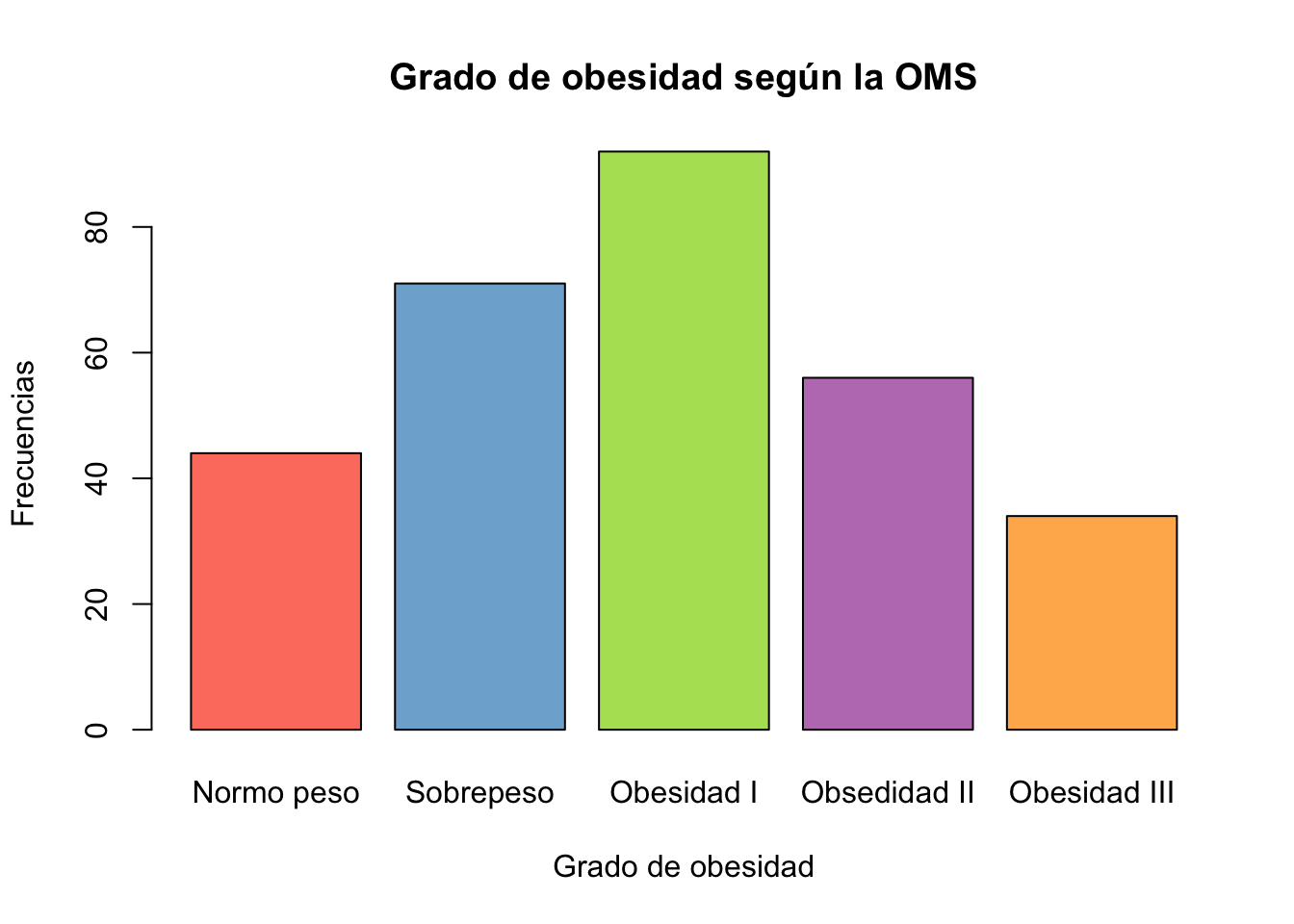
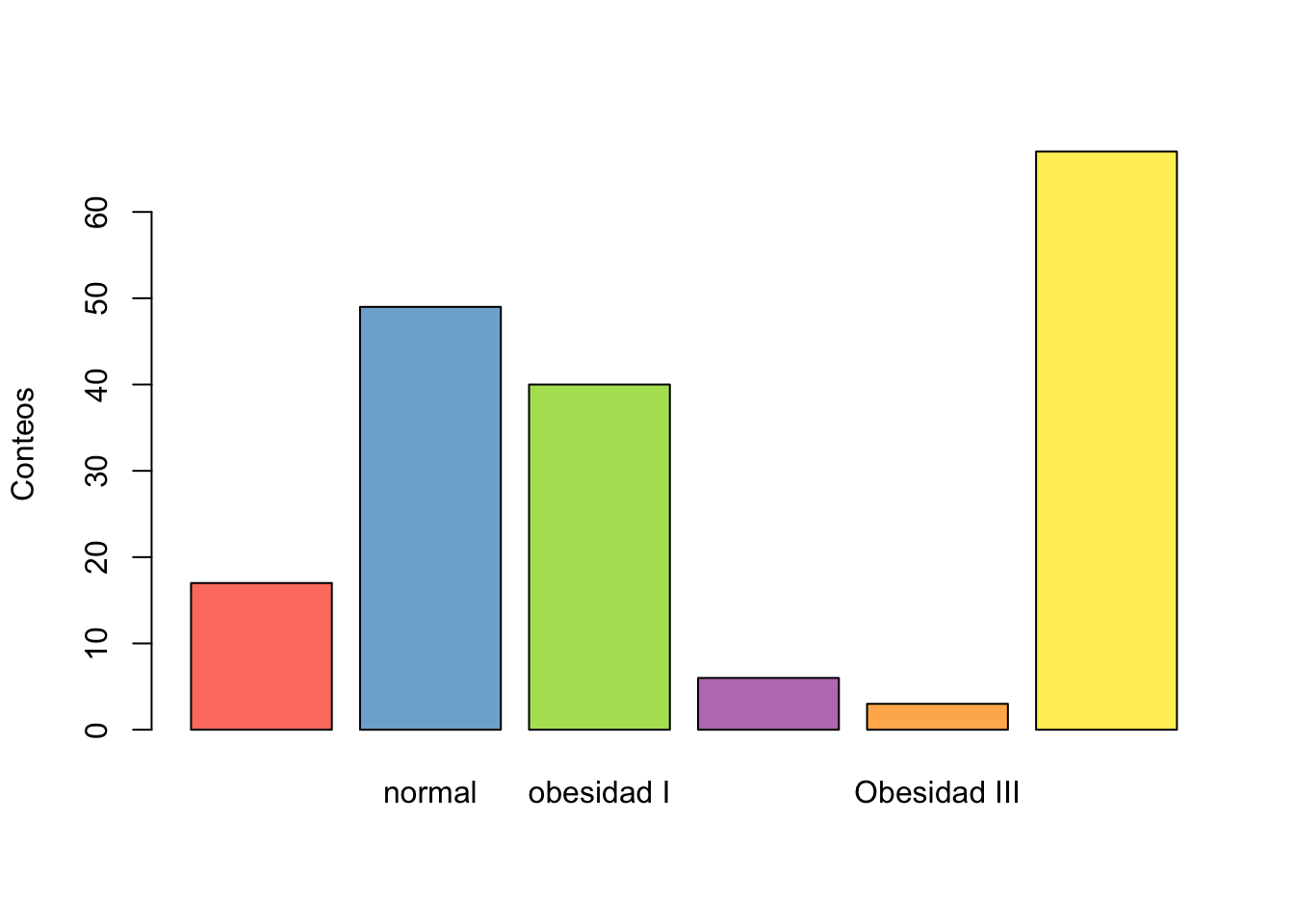
Incluya la nueva variable en la base datos y cree un gráfico de barras
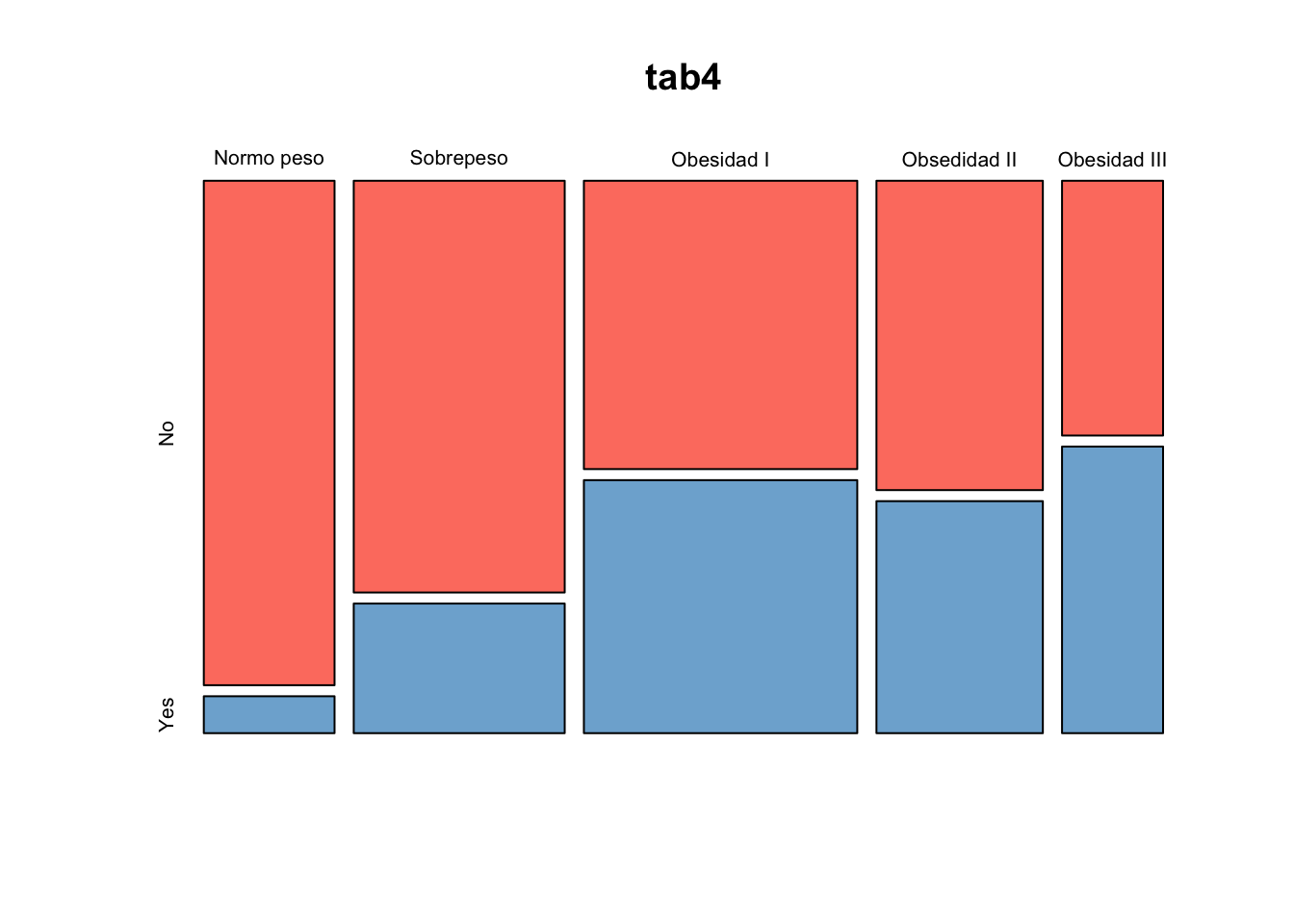
Ejercicio 9.8 Cree una gráfica de barras de las variable que creo en el ejercicio anterior y una gráfica de mosaico que agrupe la nueva variable y el diagnóstico de diabetes en la pacientes
Ejercicio 9.9 El siguiente código crea una variable edades que contiene datos aleatorios para las edades de un grupo de pacientes.
set.seed(123) # Para reproducibilidad, sembrando una semilla
edades <- sample(18:80, 200, replace = TRUE)Utilizando esa variable cree una variable ordinal que contenga los siguiente niveles: - [18,30), - [30,40), - [40,50), - [50,60), - [60,70) - [70,80).
Cambie la etiquetas y realice lo siguiente:
- Cree una tabla de frecuencias
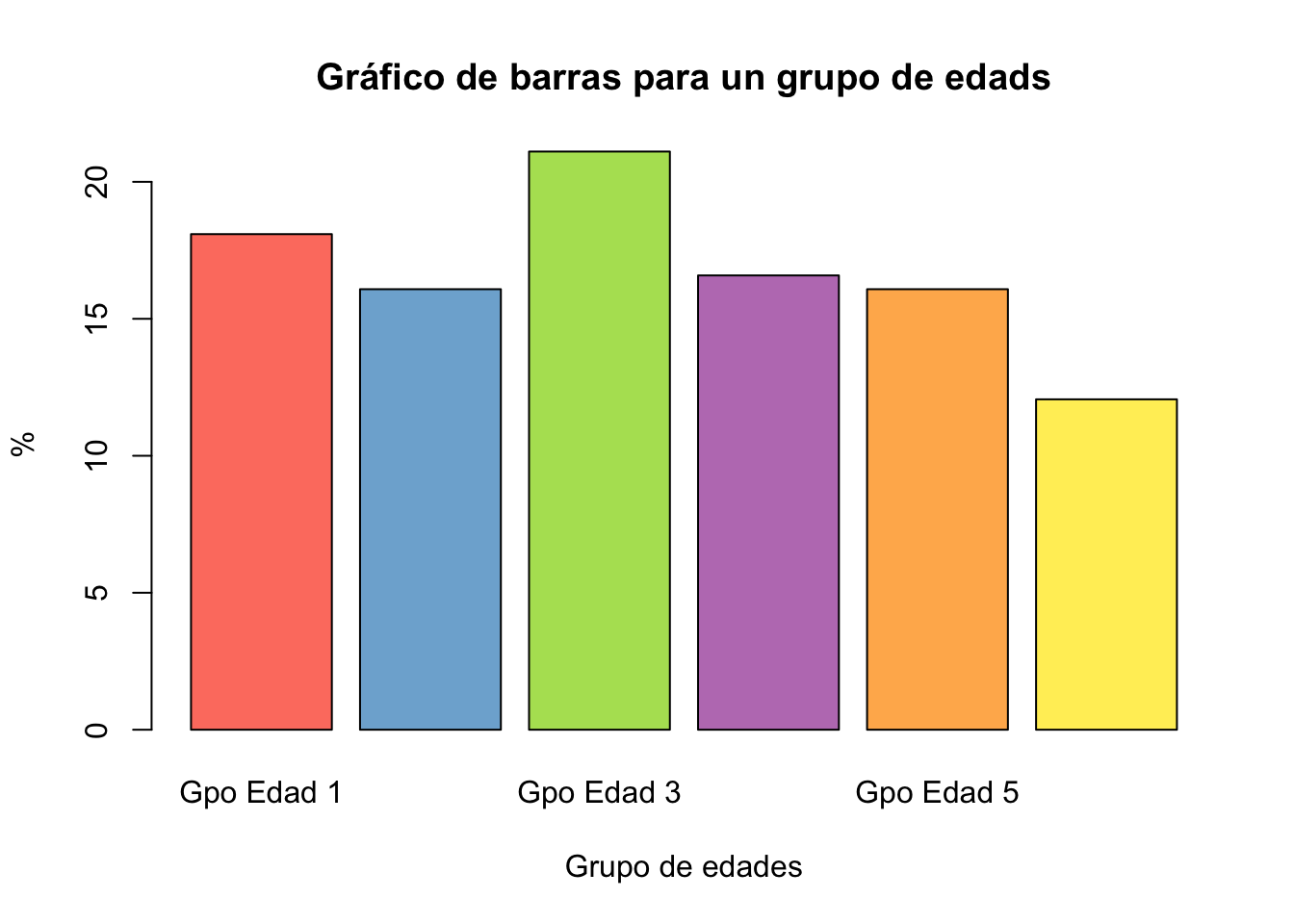
- Cree un gráfico de barras en el que el eje de las “y” sean porcentajes
- Cree un gráfico de sectores y utilice una paletas de colores que le permita combinar los colores de su gráfico. Puede apoyarse de internet
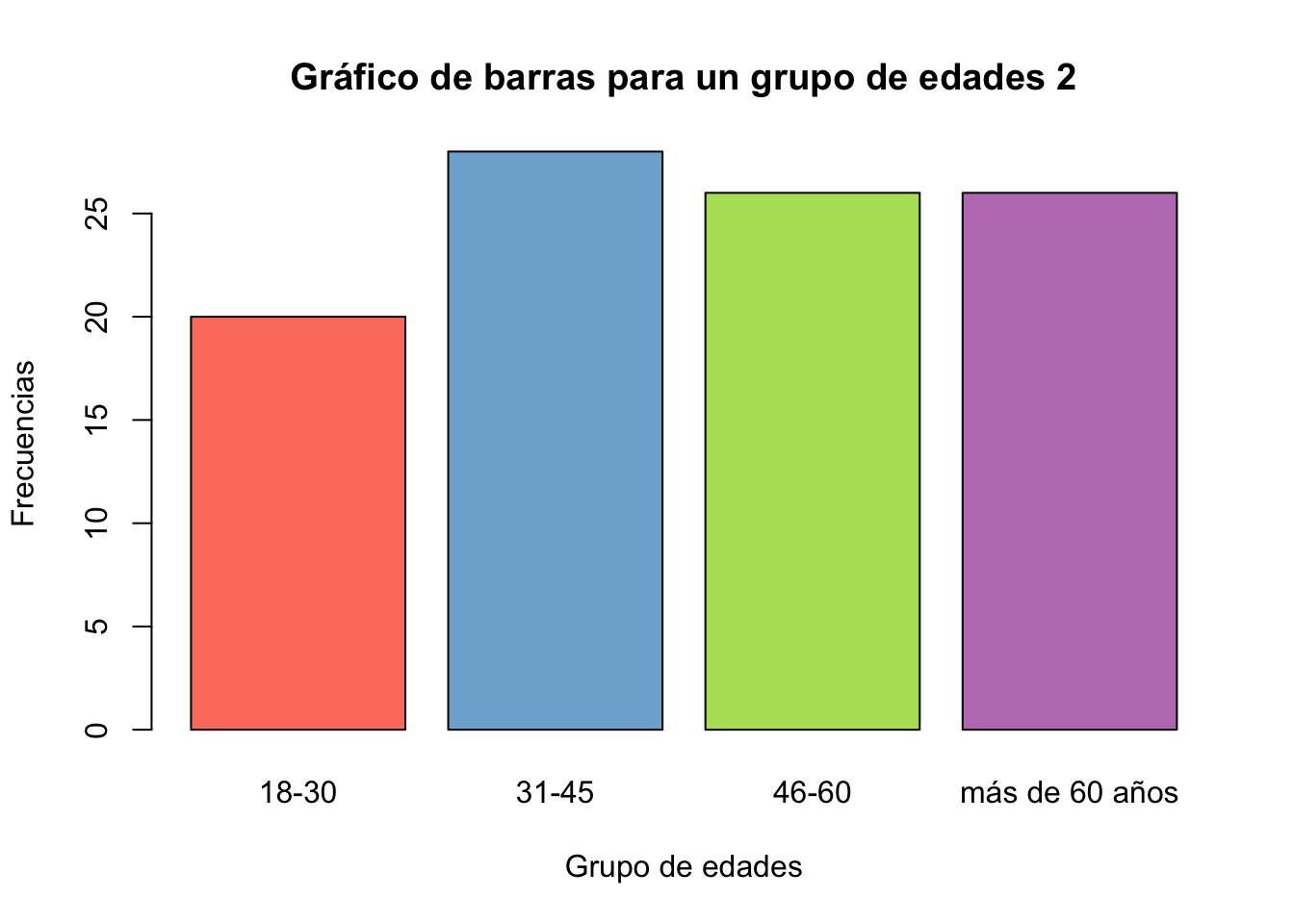
Ejercicio 9.10 En un estudio sobre la prevalencia de una enfermedad crónica en una población, se recopiló la edad de 100 pacientes.
- Genera un vector de 100 edades aleatorias entre 18 y 80 años. Utiliza la función
sample - Utiliza la función
cutpara categorizar estas edades en los siguientes grupos: 18-30, 31-45, 46-60, y más de 60 años. Asegurase de cambiar las etiquetas - Crea una tabla de frecuencias para mostrar cuántos pacientes caen en cada grupo de edad.
- Cree un gráfico de barras con barras diferentes para cada categoría, cambie los títulos de los ejes y el título del gráfico
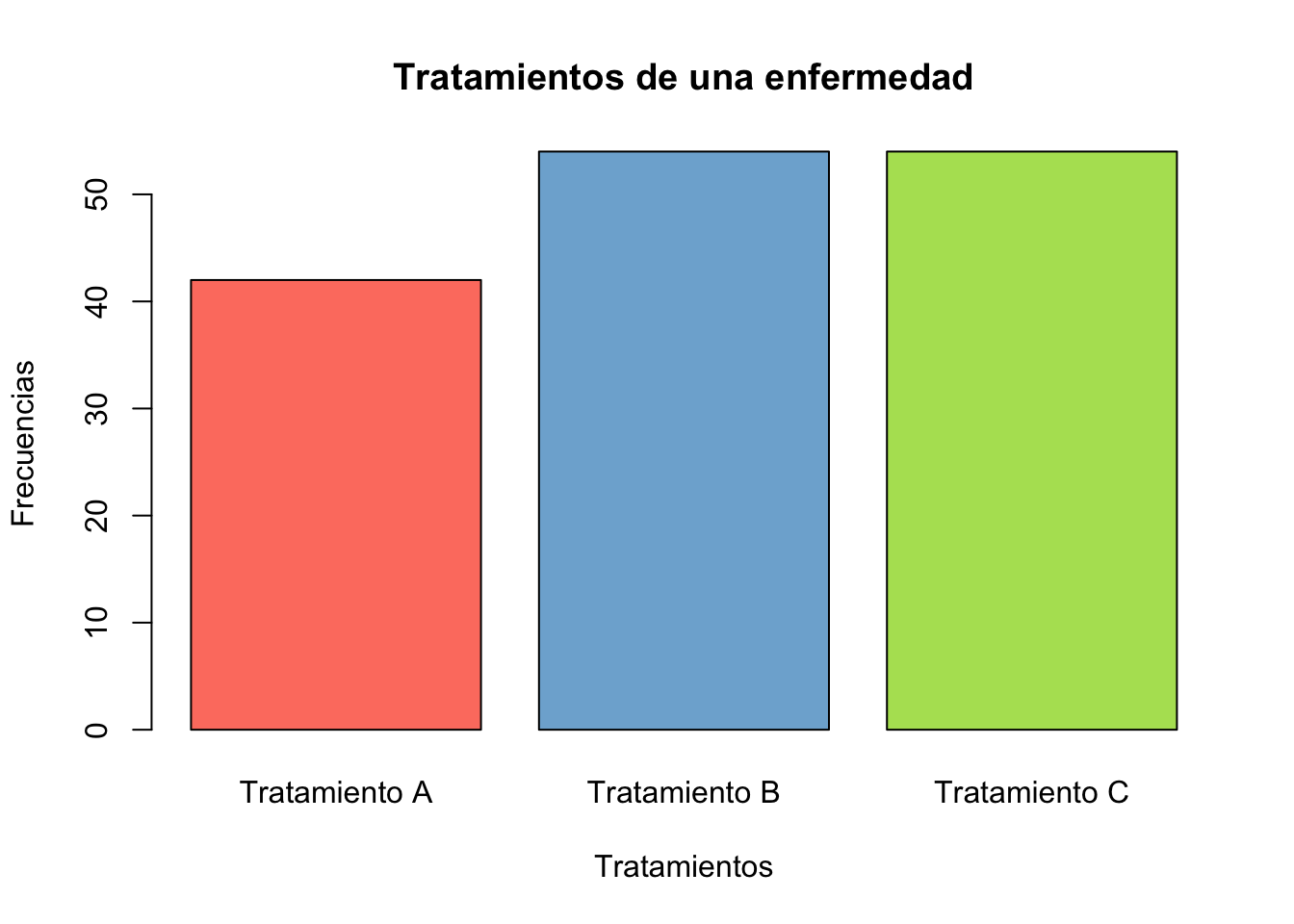
Ejercicio 9.11 Se tiene un conjunto de datos que incluye el tipo de tratamiento recibido por pacientes con una enfermedad específica: Tratamiento A, Tratamiento B, o Tratamiento C.
- Crea un vector que represente el tipo de tratamiento recibido por 150 pacientes, asegurándote de que los tratamientos estén distribuidos de manera no uniforme.
- Utiliza la función
tablepara obtener la frecuencia de cada tipo de tratamiento. - Emplee
barplotpara crear un gráfico de barras que muestre visualmente estas frecuencias. Cambie los títulos de los ejes y el título del gráfico
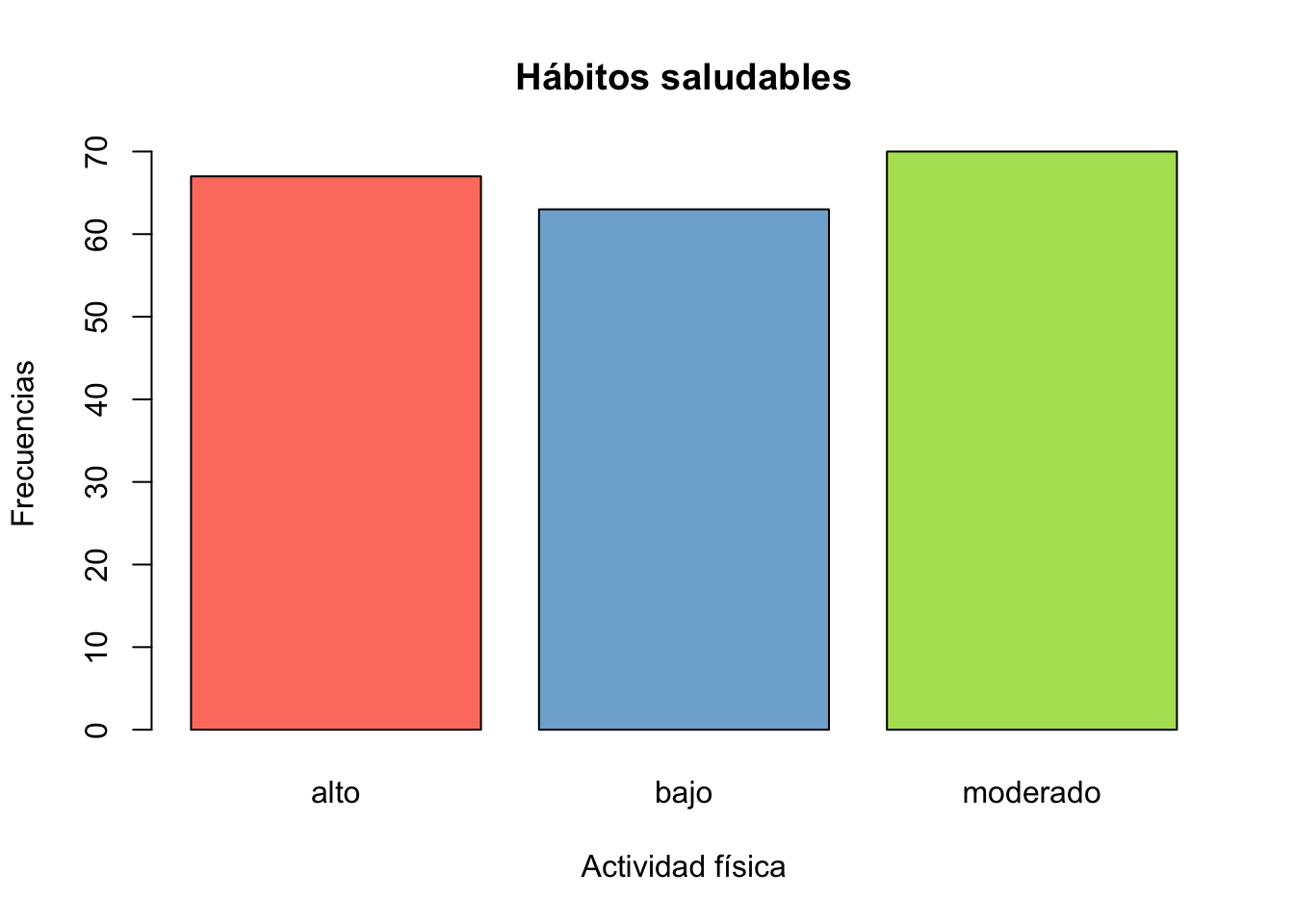
Ejercicio 9.12 En un estudio sobre hábitos de vida saludables, se encuestó a personas sobre su nivel de actividad física: bajo, moderado, o alto.
- Genere un vector que simule las respuestas de 200 personas sobre su nivel de actividad física.
- Calcule la frecuencia de cada nivel de actividad utilizando table.
- Use
prop.tablepara convertir estas frecuencias en proporciones. - Cree un gráfico de pastel (pie) para representar estas proporciones.
Ejercicio 9.13 Observe el gráfico de pastel proporcionado. Responde las siguientes preguntas: a) ¿Qué tipo de dieta es la más común entre los pacientes? a) ¿Cuál es la proporción de pacientes que siguen una dieta balanceada? a) Discute cómo los resultados podrían influir en las recomendaciones nutricionales para pacientes con diabetes tipo 2.
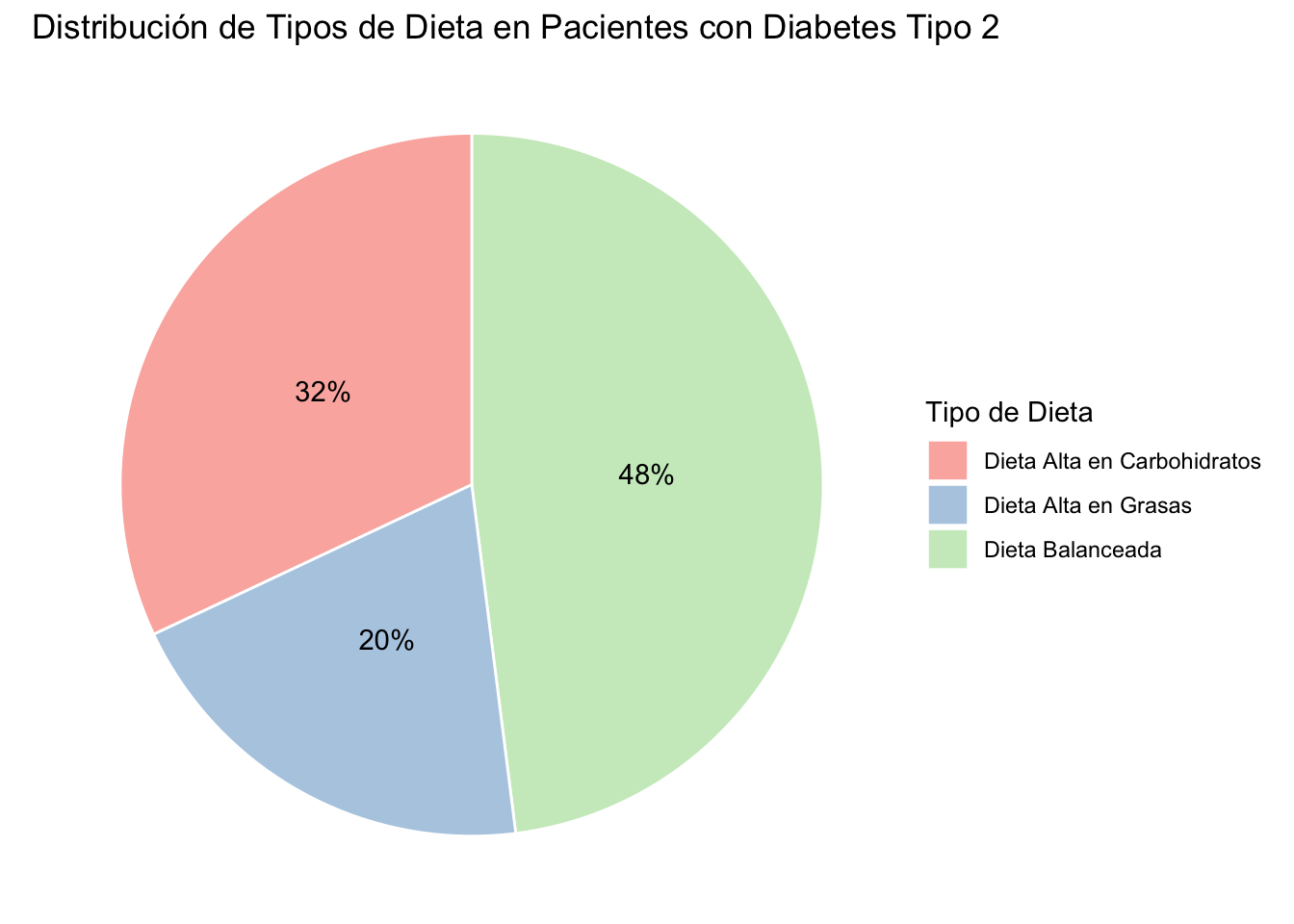
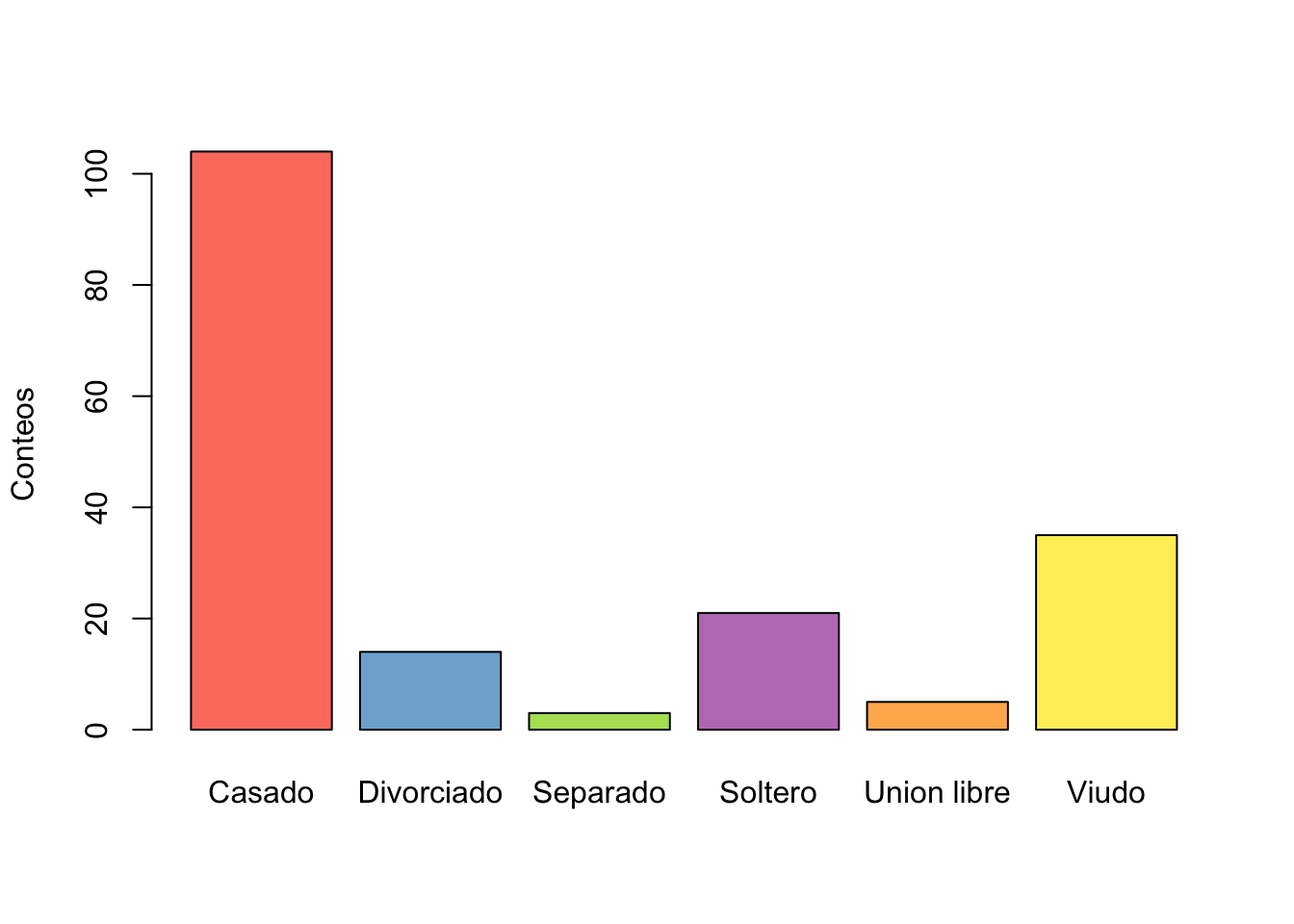
Ejercicio 9.14 Utilice la base de datos Base Descriptivo Cualitativos para realizar una tabla de frecuencias y un gráfico de barras de las siguientes variables
- CIVIL
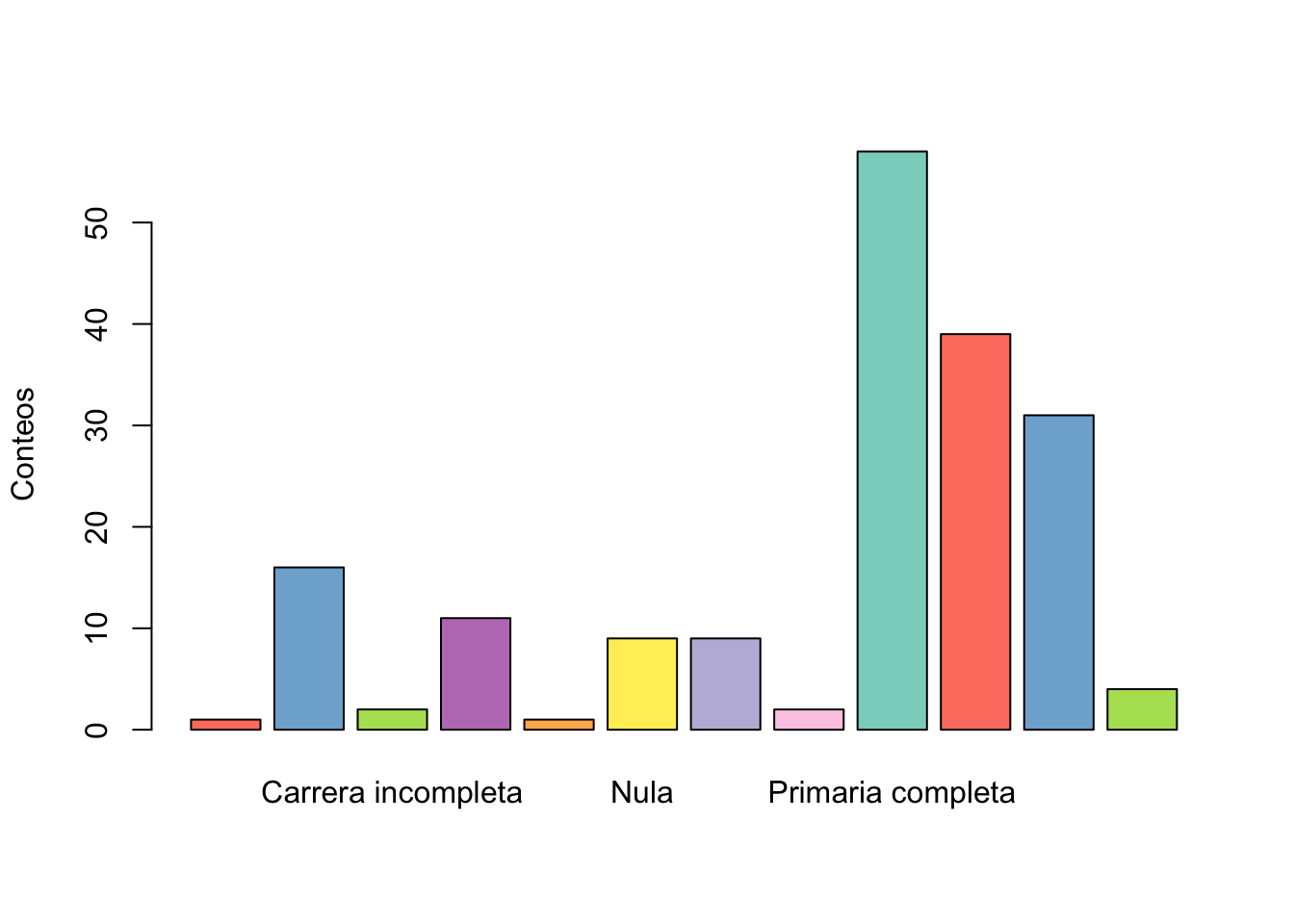
- ESCOLARIDAD
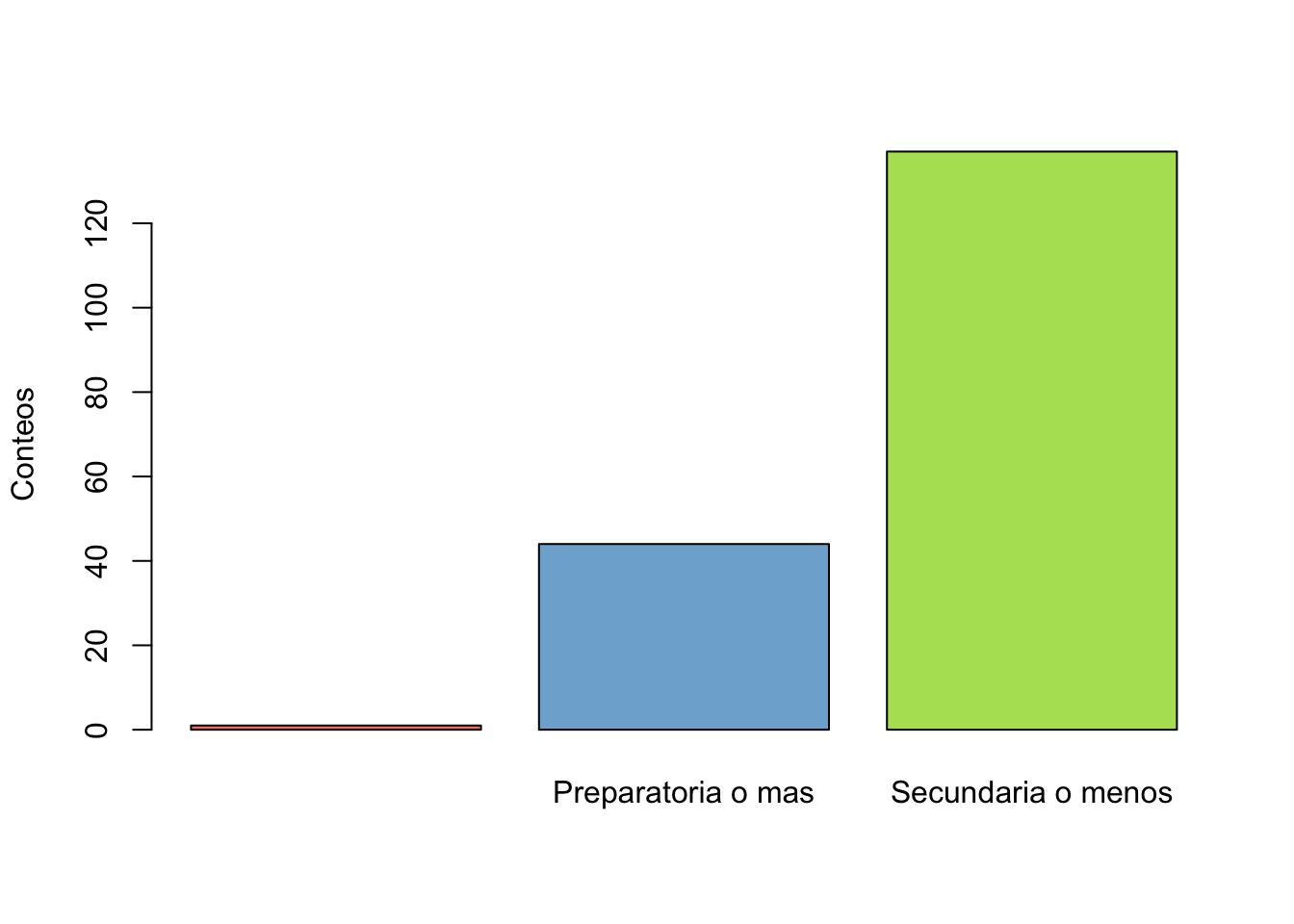
- GDO_ESCOLARIDAD
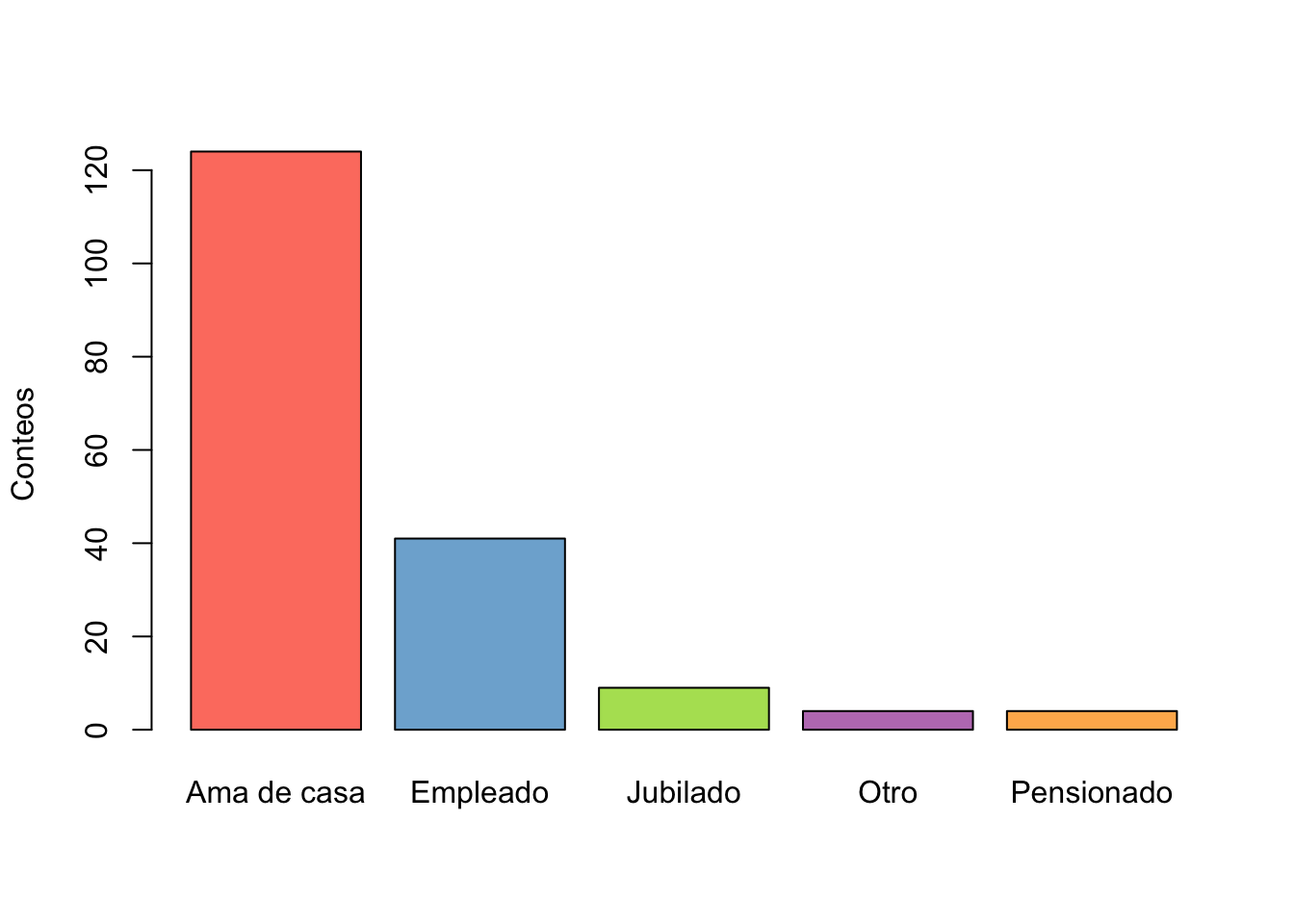
- OCUPACION
- GDO_IMC
9.6 Aspectos teóricos estadísitica descriptiva de las variables cauntitativas
La presentación, descripción y presentación se puede realizar mediante gráficas, medidas de tendencia central y medidas de dispersión. Además se pueden incluir otras medidas que reflejan la posición de los datos cuando estos son ordenados. Comenzaremos la descripción de esta sección con las medidas de tendencia central, seguida de las medidas de dispersión para finalizar con las medidas de dispersión. La siguiente figura Figura 9.2 muestra una visión general sobre la estadística de descriptiva de las variables cuantitativas.
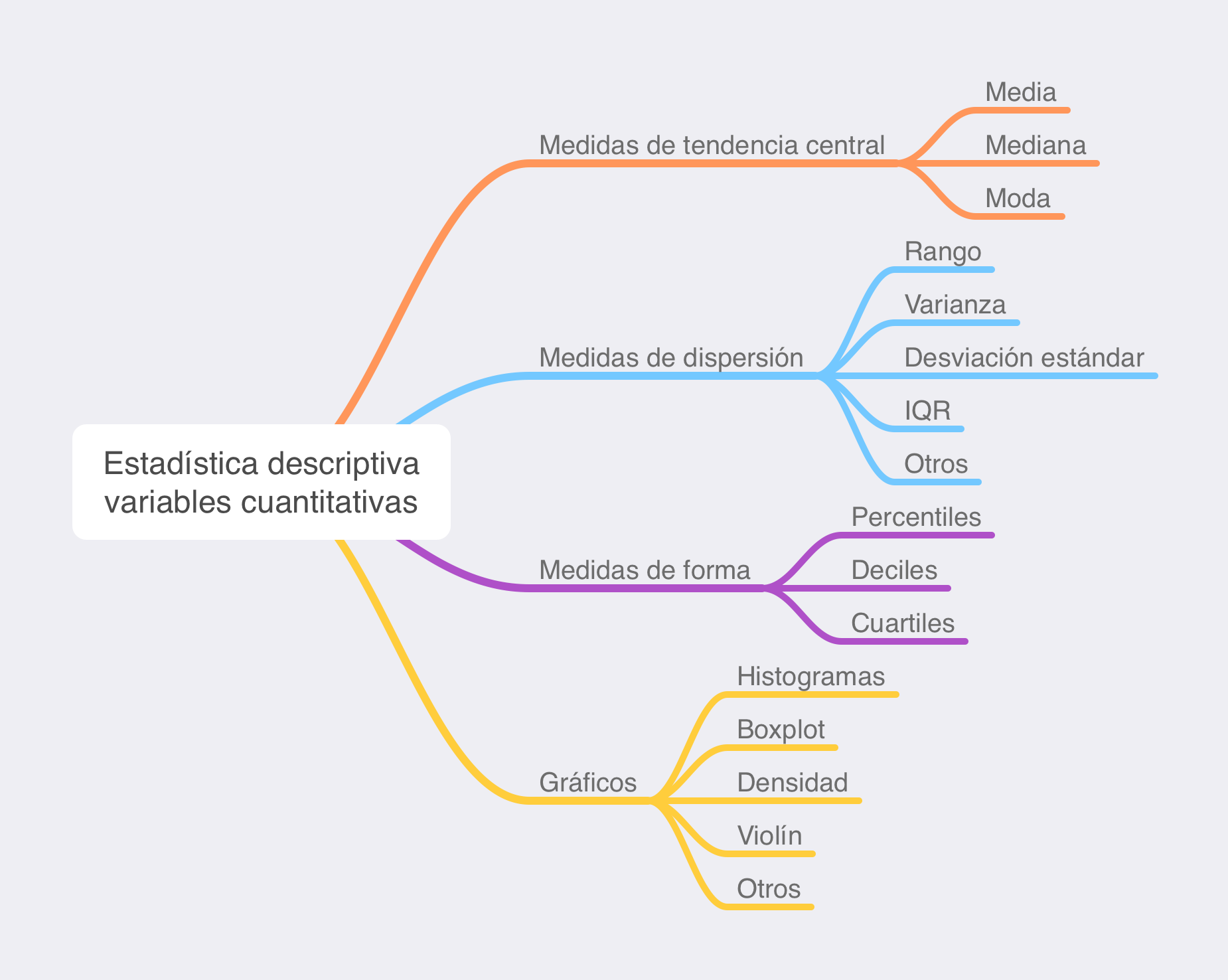
9.6.1 Medidas de tendencia central
9.6.1.1 Media aritimética
Se refiere al valor que tendría cada elemento de la serie de datos si todos tuvieran el mismo valor. Entre otras características presenta las siguientes:
- Es el parámetro de centralización más utilizado, su valor es el centro aritmético de los datos
- Se suele emplear el símbolo \(\mu\) para la media poblacional
- Se emplea \(\bar{x}\) muestral
La formula para estimar la media aritmética es la siguiente:
\[\bar{x}=\displaystyle\sum_{i=1}^n \frac{x_i}{n}\] Donde: \({x_i}\) es el i-ésimo dato; si la suma es desde \(i\) es igual a 1 hasta \(n\)
La media aritmética presenta la desventaja de que es un valor muy susceptible a los valore extremos y que cuanto estos están presentes, la media pudiere no reflejar la realidad. Las propiedades de la medias son:
Unicidad. Para un conjunto determinado de datos, sólo existe una media aritmética.
Simplicidad. La media aritmética es fácil de comprender y calcular.
Todos los valores en la serie de datos se utilizan para su cálculo. Por ello, los valores extremos pueden sesgar el resultado.
Para estimar la media en R utilice la función mean()
9.6.1.2 Mediana
Otra medida de centralización es la mediana. Esta medida refleja el valor central de un conjunto con \(n\) ordenados de mayor a menor. La mediana es el valor que divide al conjunto de datos en dos partes iguales. Su estimación es bastante sencillas, sin embargo, es distinta cuando se trabaja con \(n\) datos impares y cuando se trabaja con \(n\) datos pares.
- Cuando se trabaja con una \(n\) impar la formula es la siguiente:
- \(M= \frac{X(n+1)}{2}\)
- Si \(n\) es par, al mediana es la media aritmética de los dos valores centrales:
- \(M=\frac{{X_{\frac{n}{2}}}+{X_{\frac{n}{2}+1}}}{2}\)
Por ejemplo para el siguiente conjunto de datos: 2, 4, 6, 8, 9, 11, 12, 13, 14, 20, la mediana es 10. Si ordenamos los datos de menor a mayor, notaremos que al tratarse de un número par, los dos valores del centro serán 9 y 11. Por tanto, 10 corresponde al promedio de 9 y 11.
En cambio, si el número de datos del conjunto de valores es impar, simplemente debemos de seleccionar el valor del centro. En el siguiente conjunto de datos, la mediana también es 10. No te como se agregó un valor más.
Datos ordenados: 2, 4, 6, 8, 9, 10, 12, 13, 14, 20. El valor central es el 10.
La mediana posee las siguientes características:
Única.
Simple.
Los valores extremos no le afectan como a la media.
Divide al grupo de valores en dos partes iguales, cada una con el 50% de las observaciones
Desprecia información, porque sólo considera los valores de 1 o 2 observaciones.
Cuando dos o más grupos se unen en uno solo, no es posible calcularla a partir de la mediana de cada grupo.
En R puede utilizar la función median() para estimar la mediana.
9.6.1.3 Moda
Otro valor de centralización es la moda. Este valor refleja al dato o valor que más se repite en un conjunto de datos \(n\). Es una medida que no es muy utilizada en ciencias de la salud, con excepción de algunos casos. Pueden presentarse una moda absoluta y una moda relativa:
- La moda absoluta es el valor que más veces se repite
- La moda relativa es le valor que sin ser el que más veces se repite, se repite más veces que el resto de los datos.
Algunos conjuntos de datos, pueden presentar más de una moda. En el caso de que presenten dos, nos referiremos a ellos como bimodales. También se utiliza los términos trimodales etc.
En el paquete base de R no existe ninguna función para estimar la moda pero la función table le podría ayudar facilmente a conocer caul es el dato que más se repite en un conjunto de datos.
9.6.2 Medidas de dispersión
Estas medidas ofrecen información sobre el grado de variabilidad de una variable. Además, indican si una variable tiene datos más dispersos (variación) que otra. Junto con las medidas de tendencia central y dispersión son las medidas que se utilizan para presentar una variable cuantitativa.
Las importantes son: - Rango - Varianza - Desviación estándar - Coeficiente de variación
9.6.2.1 Rango
- Es la diferencia entre el valor máximo y el valor mínimo de los datos observados.
- Aporta información sobre el recorrido de una variable
- Puede ser engañosa con datos extremos
- Nunca se debe evaluar solo, se necesitan de otras medidas de dispersión
Suponga que es de su interés conocer que tanto varían ciertas presiones arteriales de un grupo de pacientes. Las presiones sistólicas son: 120, 135, 160, 100, 155, 115, 165, 125, 130. Una manera de medir la variabilidad es mediante el rango, que se estima de la siguiente forma:
- \(Máximo=165\)
- \(Mínimo=100\)
- \(Rango= 165-100=65\)
En R utilice la función range()
9.6.2.2 Varianza y Desviación estándar
Una buena medida de dispersión, sería tomar como referencia que tanto los valores se desvían de la media (centro). Por lo tanto, se podría restar la media a cada uno de los valores de nuestro conjunto de datos. Sin embargo, está acción tendría como consecuencia que algunos de los valores calculados sean negativos; y con ello, se anularía el efecto de los valores positivos con los negativos. Para lidiar con este problema, una vez que se haya restado la media a cada uno de los valores, se podrían elevar al cuadrado y con ello, tener siempre valores positivos.
La varianza es la medida que estima el promedio de las diferencias cuadráticas de los datos respecto a la media. Sus unidades son las de los datos al cuadrado, por ejemplo, si medimos las estaturas en \(cm\) de un grupo de niños, la varianza tendrá unidades de \(cm^2\). Para reprensentar la varianza población se utiliza \(\sigma^2\), mientras que para la varianza muestral se utiliza \(s^2\).
La formula para estimar la varianza de una población es:
\[\sigma^2 = \displaystyle\sum_{i=1}^{n}\frac{(x_i - \bar{x})^2} {n}\]
Cuando se utiliza como estimador población se utiliza \(n-1\): \[s^2 = \displaystyle\sum_{i=1}^{n}\frac{(x_i - \bar{x})^2} {n-1}\] Una medida más fácil de manejar, dado que no implica datos al cuadrado, es la desviación estándar. La cual es la raíz cuadrada de la varianza. La desviación estándar poblacional está dada por:
\[\sigma=\sqrt{\displaystyle\sum_{i=1}^{n}\frac{(x_i - \mu)^2} {N}}\] La desviación estándar indica que tanto se desvían los datos en promedio con respecto a la media de ese conjunto de datos. A diferencia de la varianza, la desviación estándar no tiene unidades.
Mientras mayor sea la desviación estándar, mayor será la dispersión de los datos
No olvidar que:
La varianza y la desviación estándar son mayores o iguales a cero
A mayor dispersión de los datos mayor varianza y mayor desviación estándar
En R utilice la funciones var() y sd() para estimar la varianza y la desviación estándar respectivamente.
9.6.2.3 Coeficiente de variación
Es una medida de dispersión sin unidades y es el cociente de la desviación estándar respecto a la media, multiplicado por 100 \(CV=\frac{S}{\bar{X}} 100\). Permite la comparación de datos en distintas unidades y en distintas poblaciones o muestras.
No existe una función en el paquete base de R para la estimación del coeficiente de variación, sin embargo, su estimación es sencilla si combinamos la función mean y sd. También puede crear una función con el siguiente código:
CV<-function(x){
(sd(x)/mean(x))*100
}En el capitulo XXX se abordará la construcción básica de funciones en R.
9.6.2.4 Error estándar
El error estándar, es una medida que se utiliza para conocer que tanto varían un estadístico de una muestra a otra. El error estándar tiende a disminuir cuando aumenta el tamaño de la(s) muestra(s). Se puede establecer por lo tanto que cuanto menor sea el error estándar, más representativa será la muestra de la población en su conjunto.
El error estándar es una medida de la precisión de la estimación de la media de una población a partir de una muestra de datos. Se calcula como la desviación estándar de la distribución de las medias muestrales de todas las posibles muestras de tamaño \(n\) extraídas de la población.
Si la variablidad de las medias muestrales se mide por su desviación estándar, las formulas para el error estándar serían:
\[SE=\frac{\sigma}{\sqrt{N}}\]
\[SE=\frac{S}{\sqrt{n}}\]
El error estándar no disminuye en relación directamente proporcional con el tamaño de la muestra. Ya que tomamos la raíz cuadrada de \(n\) y el valor propio de \(n\). Por ejemplo, es necesario aumentar cuatro veces el tamaño de muestra \(n\) para reducir el error estándar a la mitad.
El error estándar también puede ser calculado para otros estadísticos.
9.6.3 Medidas de posición
Las medidas de posición son aquella que permiten, una vez ordenados los datos de menor a mayor, ubicar donde se encuentra el 10%, 20%, 50% etc. de los datos. Estos datos, a demnas de la posición, nos permiten conocer la dispersión del conjunto de datos. El término \(n-\)tiles se refiere a \(n\) grupos en los que será divido el conjunto de datos. Solemos llamarle cuarteliles a los datos que me permiten dividir en 4 partes iguales a todo mi conjunto de datos, mientras que nos referimos a deciles cuando me permiten dividir el conjunto de datos en 10 partes iguales.
9.6.3.1 Cuartiles
Dividen al conjunto de datos en cuatro partes iguales, en cada una de ella hay 25% de los datos
| 25% | \(Q_1\) | 25% | \(Q_2\) | 25% | \(Q_3\) | 25% |
|---|
9.6.3.2 Deciles
Se consideran como medidas de dispersión o de posición, las cuales dividen un conjunto de datos en 10 partes iguales en cuanto al número de datos.
| 10% | 10% | 10% | 10% | 10% | 10% | 10% | 10% | 10% | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(D_1\) | \(D_2\) | \(D_3\) | \(D_4\) | \(D_5\) | \(D_6\) | \(D_7\) | \(D_8\) | \(D9\) | |||||||||
| 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% |
9.6.3.3 ¿Cómo calcularlos?
Hay muchas formas de calcularlos:
\(P(n +1)\) es la que utilizan normalmente los programas estadísticos - Donde: - \(P=\) al percentil que se desea calcular divido entre 100 - \(n=\) es el número de datos
La función quantile() en R cuenta con 9 algoritmos para estimar los \(n\)-tiles. En este compendio no cambiaremos el argumento type y utilizaremos el argumento predefinido. Puede encontrar más información sobre como R calcula los \(n\)-tiles utilizando la función de ayuda: help("quantile")
9.6.4 Funciones empleadas en la estadística descriptiva para variables cuantitativas
Los aspectos teóricos de las estadística descriptiva para las variable cuantitativas ya fue explicado en la sección anterior. En esta sección, solo abordaremos ejemplos de como realizar la estimación de medidas de centralización y tendencia central utilizando R
Existen diversas funciones para obtener estadísticos que nos permiten resumir datos cuantitativos. Las más comunes son:
mean(). Función que devuelve la media de un vector numéricomedian()Devuelve la mediana de una conjunto de datossd()Devuelve la desviación estándar de un vector numéricovar()Devuelve la varianza de un vector numéricoquantile()Devuelve los percentiles indicados.IQR()Devuelve el rango intercuantil de un vector de datos numérico.summaryDevuelve un resumen de cualquier tipo de variable, en el caso de variable cuantitativas devuelve valores mínimo, máximo, mediana y media.mindevuelve el valor mínimo de conjunto de datosmaxdevuelve el valor máximo de un conjunto de datos
El siguiente, es un ejemplo de como estimar la estadística descriptiva para variables cuantitivas utilizando R base.
Ejemplo 9.8 Para la resolución de estos ejercicios vamos a utilizar la base de datos de Pima.tr de la librería MASS. El primer paso por lo tanto es llamar a la librería y luego a los datos.
library(MASS)
data(Pima.tr)En esta ocasión no vamos a utilizar la función attach y vamos a trabajar todas las funciones con el símbolo de $ para poder acceder a los objetos contenidos en nuestro mega objeto (data frame).
Vamos a calcular algunas medidas de tendencia central y algunas de dispersión para la variable age.
mean(x=Pima.tr$age, rm.na=T)[1] 32.11Note como empleamos dos argumentos en la función mean. Todas las funciones requiere argumentos, en este caso utilizamos uno llamado x y otro rm.na. El primero hace alusión a un vector numérico y el segundo hace alusión a la omisión de los valroes perdidos (NA). En R podemos omitir declarar los argumentos siempre y cuando estén en el orden correcto. Por ejemplo, el código anterior, se podría simplificar:
mean(Pima.tr$age, rm.na=T)[1] 32.11Note como omitimos declarar el valor de x, sin embargo, no podemos omitir declarar el argumento na.rm ya que no es el segundo argumento asignado a la función y R no sabrá que hacer. El siguiente código daría un error:
mean(Pima.tr$age, T)Ahora con una explicación más avanzada del uso de la funciones, podemos estimar el resto de los estadísticos:
median(Pima.tr$age)# Para estimar la mediama[1] 28sd(Pima.tr$age)# Para estimar la desviación estándar[1] 10.97544var(Pima.tr$age)# Para estimar la varianza[1] 120.4602IQR(Pima.tr$age)# Para estimar el rango intercuartil[1] 16.25quantile(Pima.tr$age)# Para estimar los cuartiles 0% 25% 50% 75% 100%
21.00 23.00 28.00 39.25 63.00 quantile(Pima.tr$age, c(0.1,0.2, 0.4, 0.9))# Para estimar los percentiles 10, 20, 40 y 90 10% 20% 40% 90%
21.0 23.0 26.0 49.1 min(Pima.tr$age)# Para estimar el valor mínimo[1] 21max(Pima.tr$age)# Para estimar el valor máximo[1] 63summary(Pima.tr$age)# Para hacer un resumen numérico más general Min. 1st Qu. Median Mean 3rd Qu. Max.
21.00 23.00 28.00 32.11 39.25 63.00 9.6.4.1 Funciones de otras librerías
9.6.4.1.1 La Función describe de la librería pshych
La función describe() del paquete psych en R es una herramienta muy útil para obtener un resumen detallado de las estadísticas descriptivas de un conjunto de datos, especialmente cuando se trabaja con múltiples variables.
La función describe() proporciona una amplia gama de estadísticas descriptivas para cada variable en el conjunto de datos, incluyendo medidas de tendencia central, dispersión, forma de la distribución y otros estadísticos descriptivos relevantes.
Algunos de los estadísticos descriptivos que la función describe() proporciona para cada variable incluyen:
- Media y mediana: Representan medidas de tendencia central.
- Desviación estándar y rango: Indican la dispersión de los datos.
- Valores mínimos y máximos: El rango de los datos.
- Curtosis y asimetría: Describen la forma de la distribución de los datos.
- Moda: El valor más común en la distribución.
- Cuántiles: Proporcionan información sobre la distribución de los datos en diferentes percentiles.
- Además de estas medidas básicas, describe() también puede proporcionar otras estadísticas descriptivas más detalladas, como los valores atípicos, el coeficiente de variación, la entropía y la cantidad de datos faltantes.
Ejemplo 9.9
install.packages("psych")psych::describe(edades) vars n mean sd median trimmed mad min max range skew kurtosis se
X1 1 200 48.51 16.85 47.5 48.33 22.24 18 80 62 0.07 -1.11 1.19# La utilización de los cuatro puntos permite acceder a las
# funciones de un librería sin llamarla9.6.4.1.2 La función ds_tidy_stats() de la librería descriptr
La función ds_tidy_stats() de la librería descriptr en R es una herramienta útil para calcular estadísticas descriptivas de un conjunto de datos y presentar los resultados en un formato “tidy”, que es un formato tabular organizado donde cada fila representa una observación y cada columna representa una variable o una medida descriptiva. En el capitulo XXX se describe más a detalle el funcionamiento de los pipes, de momento puede copiar y pegar el código del ejemplo Ejemplo 9.10
Ejemplo 9.10
install.packages("descriptr")# Instalar libreríalibrary(MASS)
data(Pima.tr)
# La función necesita un data frame
Pima.tr |>
descriptr::ds_tidy_stats(glu)# A tibble: 1 × 16
vars min max mean t_mean median mode range variance stdev skew
<chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
1 glu 56 199 124. 123. 120. 100 143 1003. 31.7 0.456
# ℹ 5 more variables: kurtosis <dbl>, coeff_var <dbl>, q1 <dbl>, q3 <dbl>,
# iqrange <dbl>9.6.5 Ejercicios para estadística descriptiva con variables cuantitivas.
Ejercicio 9.15 Utilizando la base de datos Pima.tr de la librería MASS. Responda las siguientes preguntas:
¿Cuál es el percentil 25 para la variable glu?
Ejercicio 9.16 ¿Cuál es valor mínimo y máximo para la la variable bmi?
Ejercicio 9.17 Utilizando la función summary describa la variable bp
Ejercicio 9.18 ¿Cuál es la edad promedio aquellos pacientes con diabetes (type==“Yes”)?
Ejercicio 9.19 ¿Cuál es la valor de la mediana para la glucosa de las pacientes sin diabetes?
Ejercicio 9.20 Utilice la función summary pero está vez aplicada a todo el data frame (summary(Pima.tr)) y describa que es lo que pasa.
9.7 Gráficos utilizados para la exploración de variables cuantitativas
Para la exploración de variables cuantitativas se pueden utilizar entre otros los siguientes gráficos:
- Histograma
- Gráfico de densidad
- Boxplot
- Gráficos de violin
9.7.1 Histograma
Los histogramas se utilizan comúnmente para visualizar variables de tipo numérico. Hasta cierto punto, un histograma es similar a un gráfico de barras después de que los valores de la variables se agrupan en un número finito de intervalos de clase. En el que, para cada intervalo, la altura de la barra corresponde a la frecuencia de observaciones en ese intervalo.
Los histogramas se crean con la función hist(). Al establecer el argumento freq = FALSE, la gráfica devuelve densidades de probabilidad en lugar de frecuencias.
El siguiente código puede ser utilizado para la creación de un histograma de las edades de las pacientes de las base de datos Pimi.tr
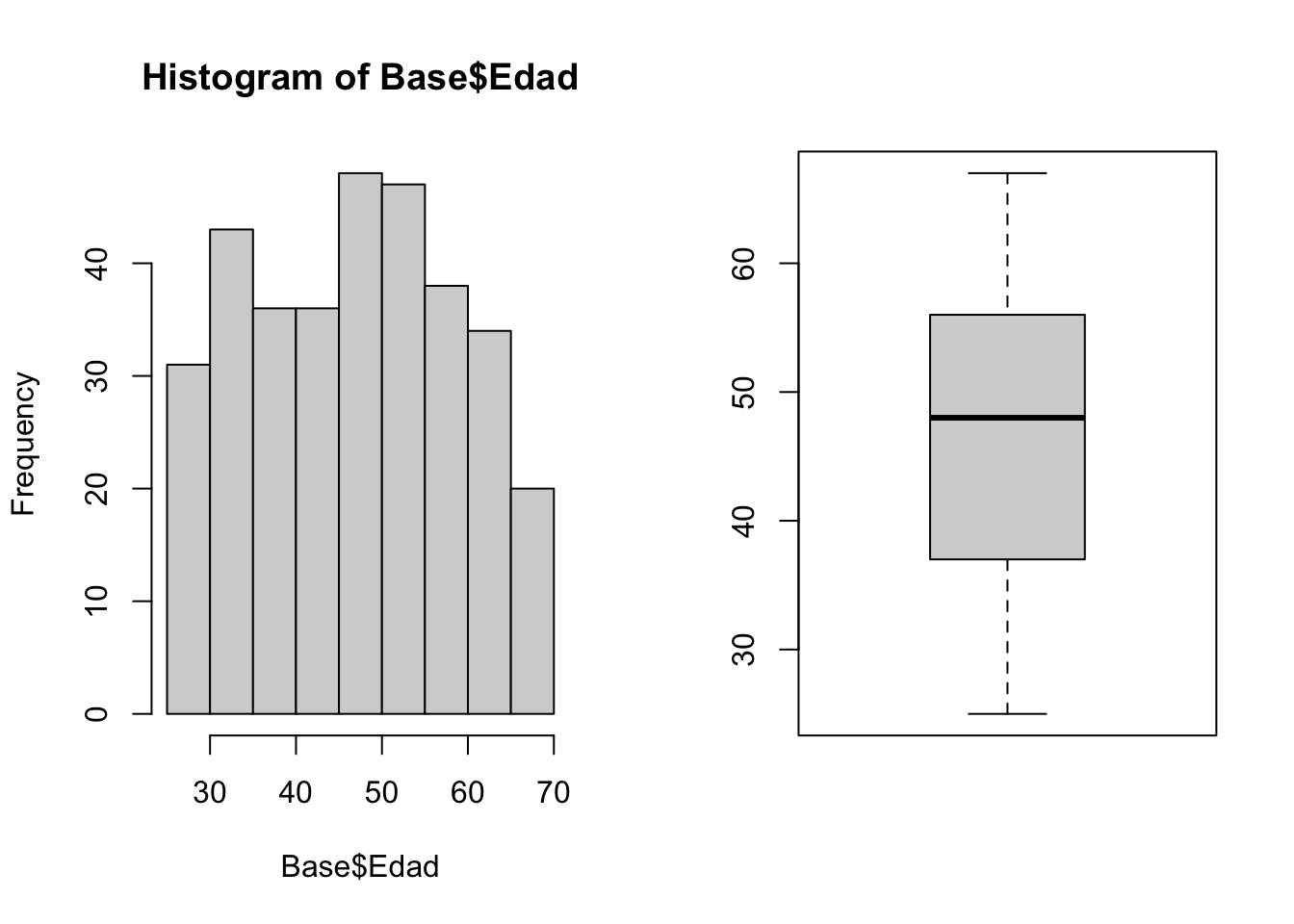
hist(Pima.tr$age)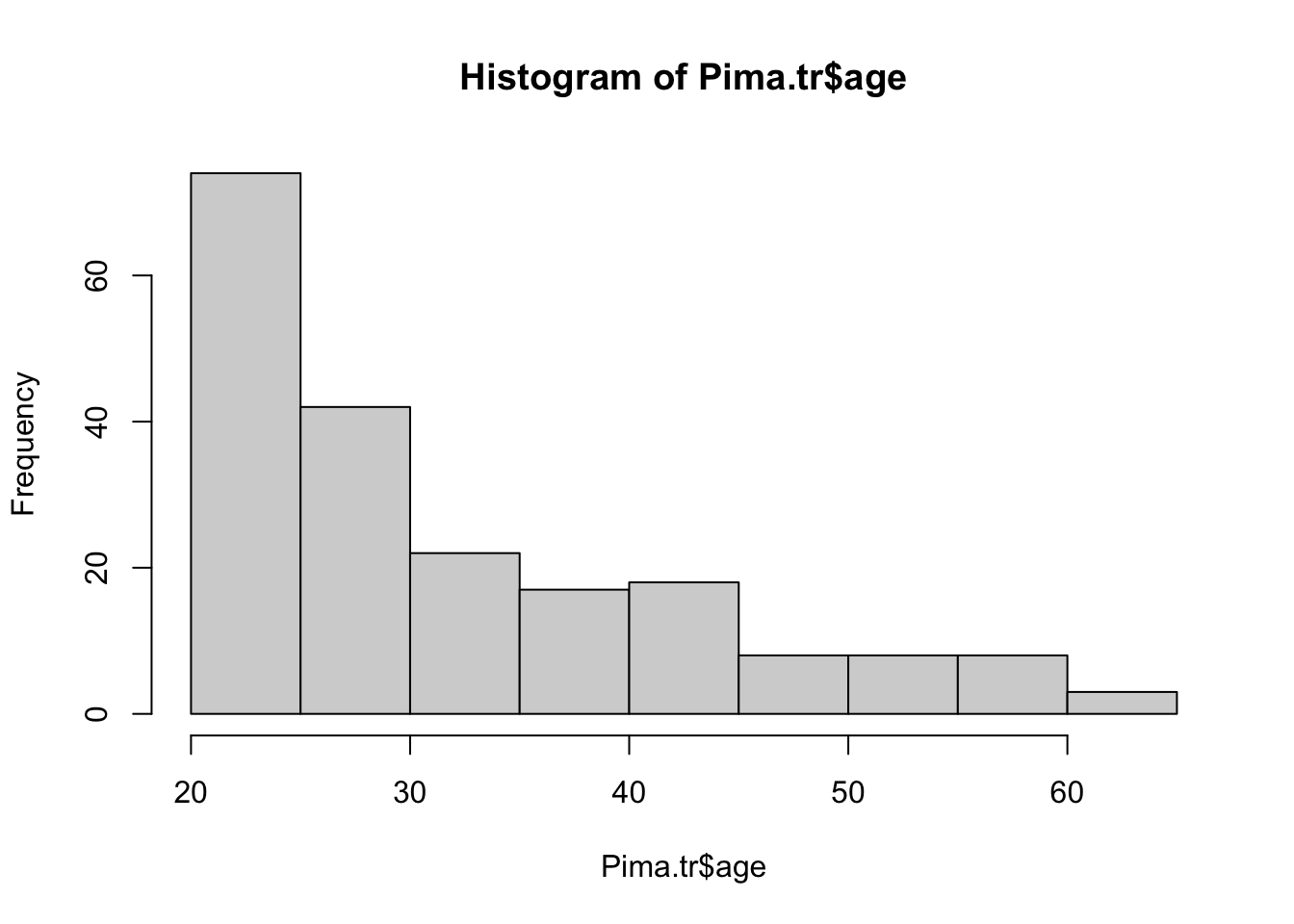
Con el freq = FALSE podemos obtener las densidades
hist(Pima.tr$age, freq = F)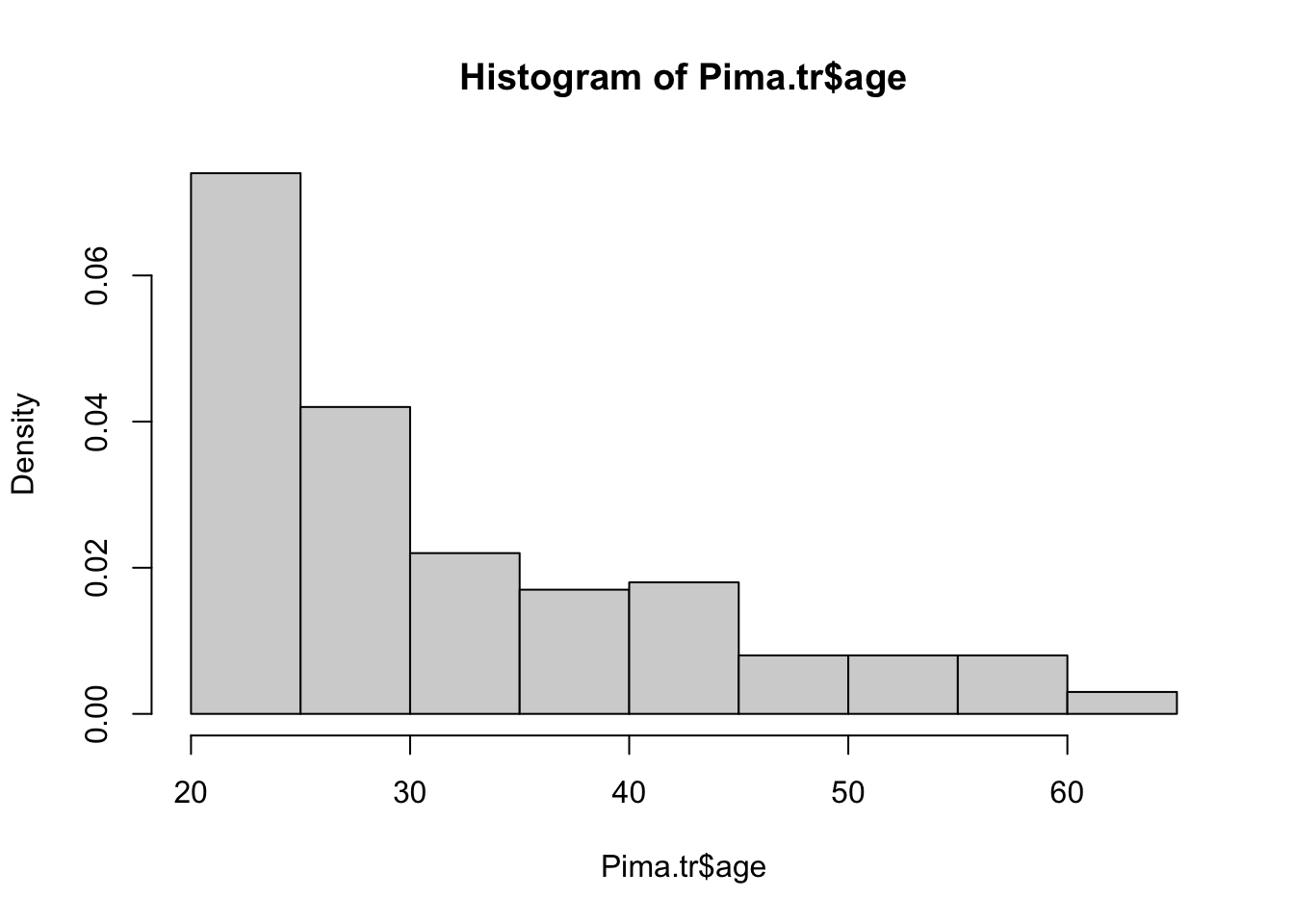
El argumento breaks nos permite cambiar los intervalos de clase por el número que estableszcamos
hist(Pima.tr$age, breaks = 20) #Histograma con 20 intervalos de clase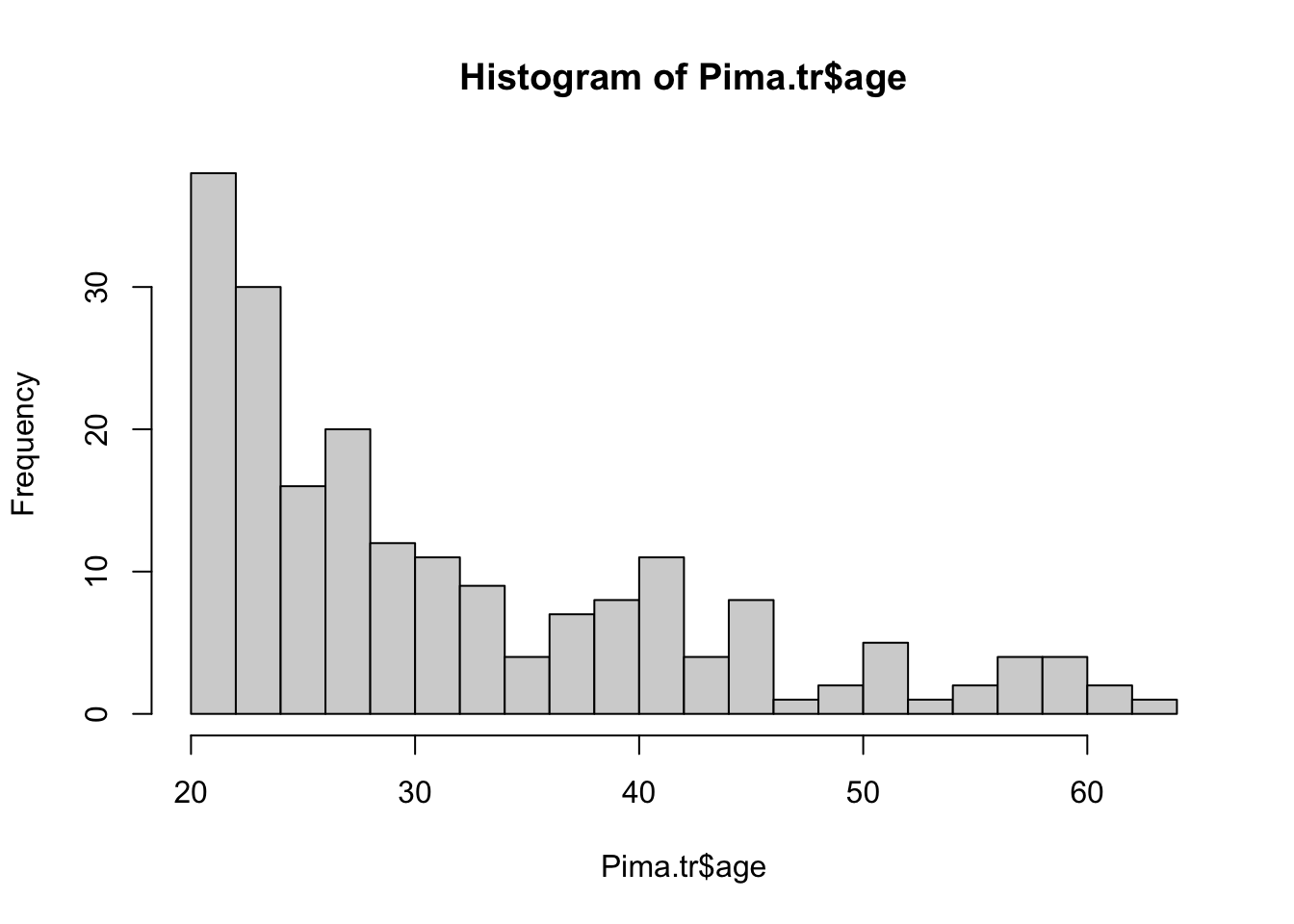
Podemos cambiar el título, para ellos utilizamos el argumento main y entre comillas podemos declarar el título que nos convenga.
hist(Pima.tr$age, breaks = 20, main = "Mi primer histograma")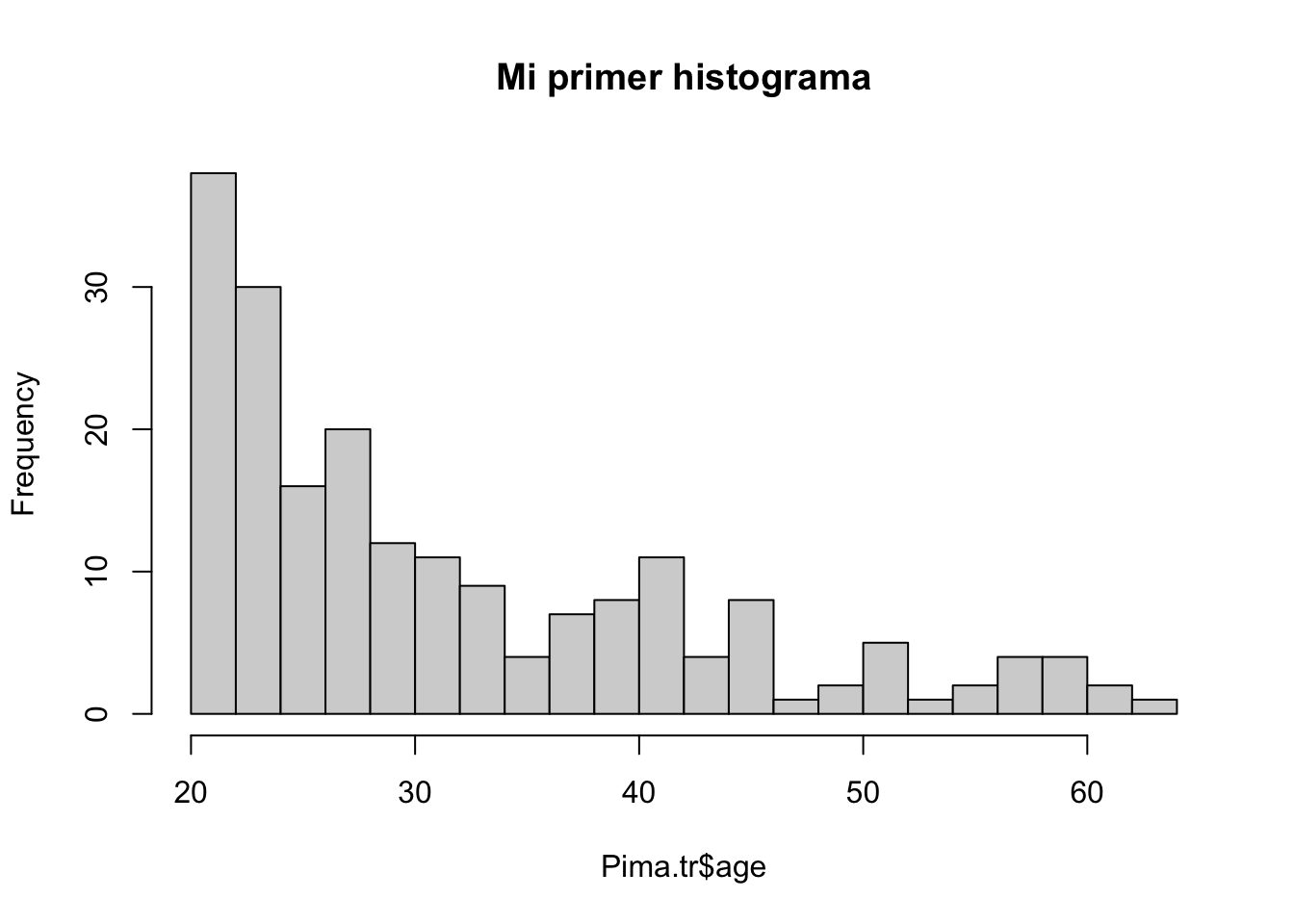
También, con los argumentos ylab y xlab podemos cambiar los nombres de los ejes “y” y “x” respectivamente.
hist(Pima.tr$age, breaks = 20, main = "Mi primer histograma",
ylab = "Frecuencias", xlab= "Intervalos de clase para la edad")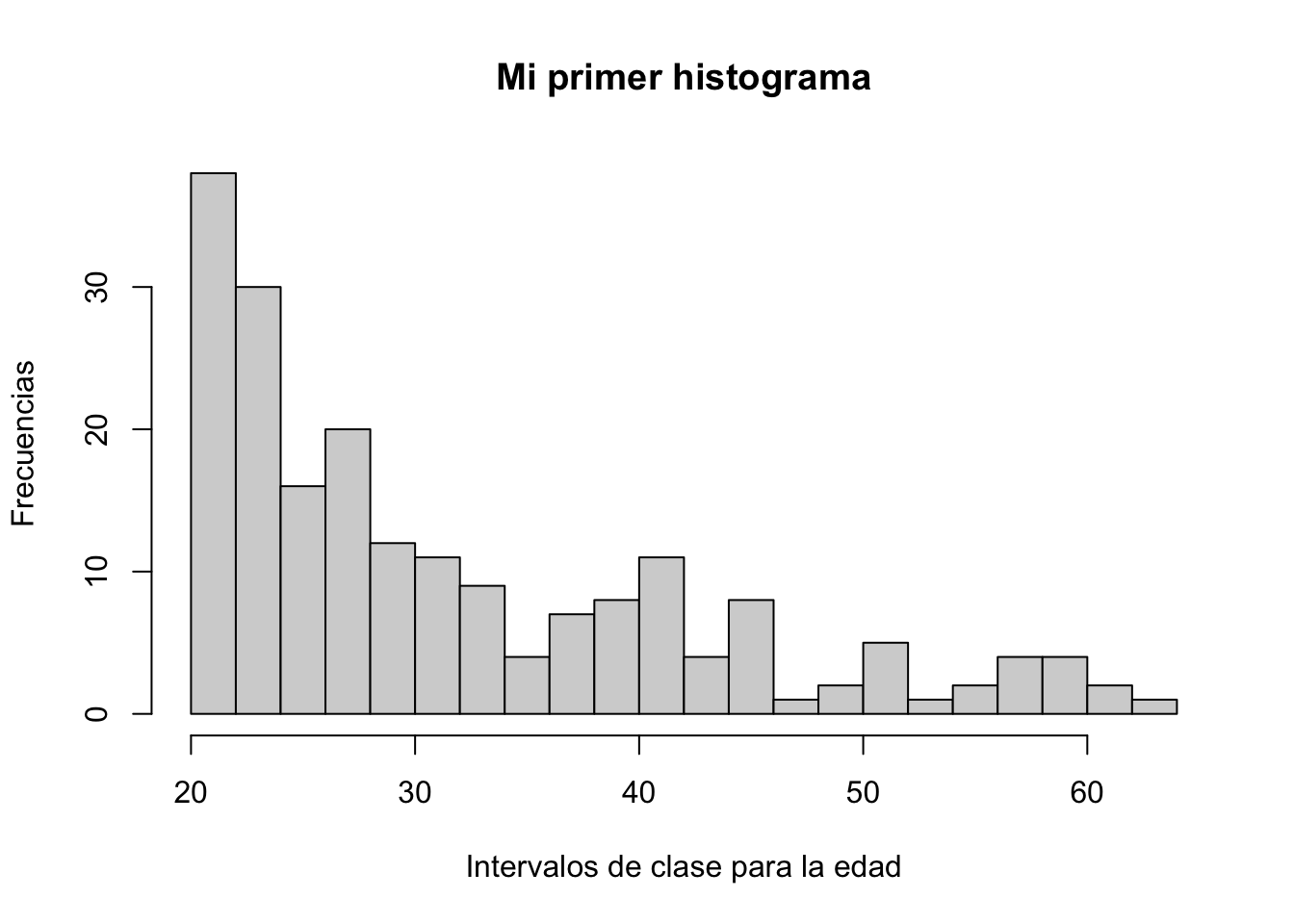
También puede cambiar el color de las barras, por ejemplo, podemos cambiarla por el color “cyan4” utilizando el argumento col
hist(Pima.tr$age, breaks = 20, main = "Mi primer histograma",
ylab = "Frecuencias", xlab= "Intervalos de clase para la edad",
col = "cyan4")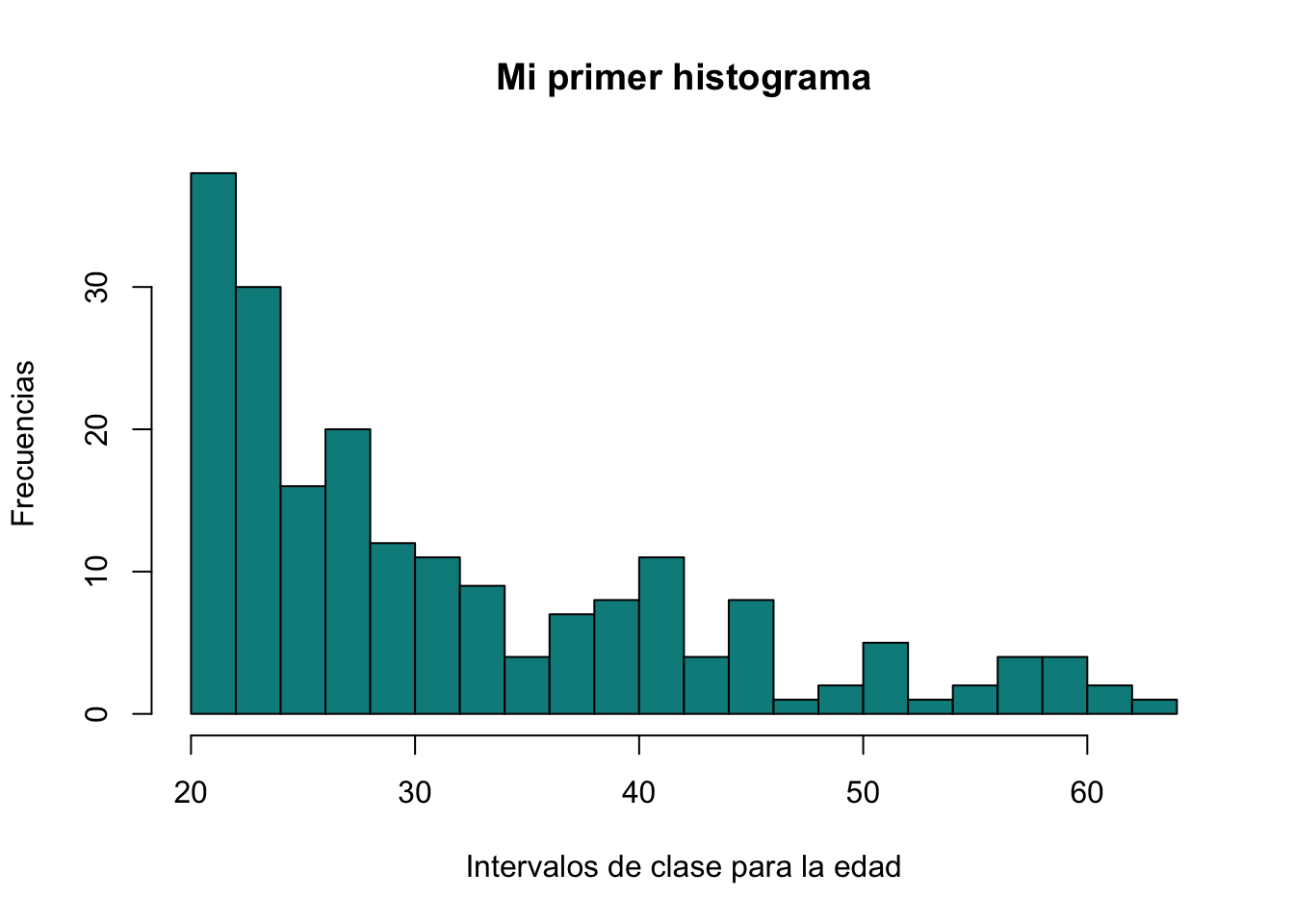
La universidad de Columbia desarrolló un manual que contiene algunos de los colores que puede ser utilizados en R. Usted puede aumentar esta gama de colores mediante la instalación de librerías con paletas de colores
La forma de los histogramas se ve fuertemente afectada por la cantidad de intervalos de clase utilizados, por lo que a veces es útil trazar un gráfico de densidad en su lugar. En R, podemos crear un gráfico de densidad usando la función de density().
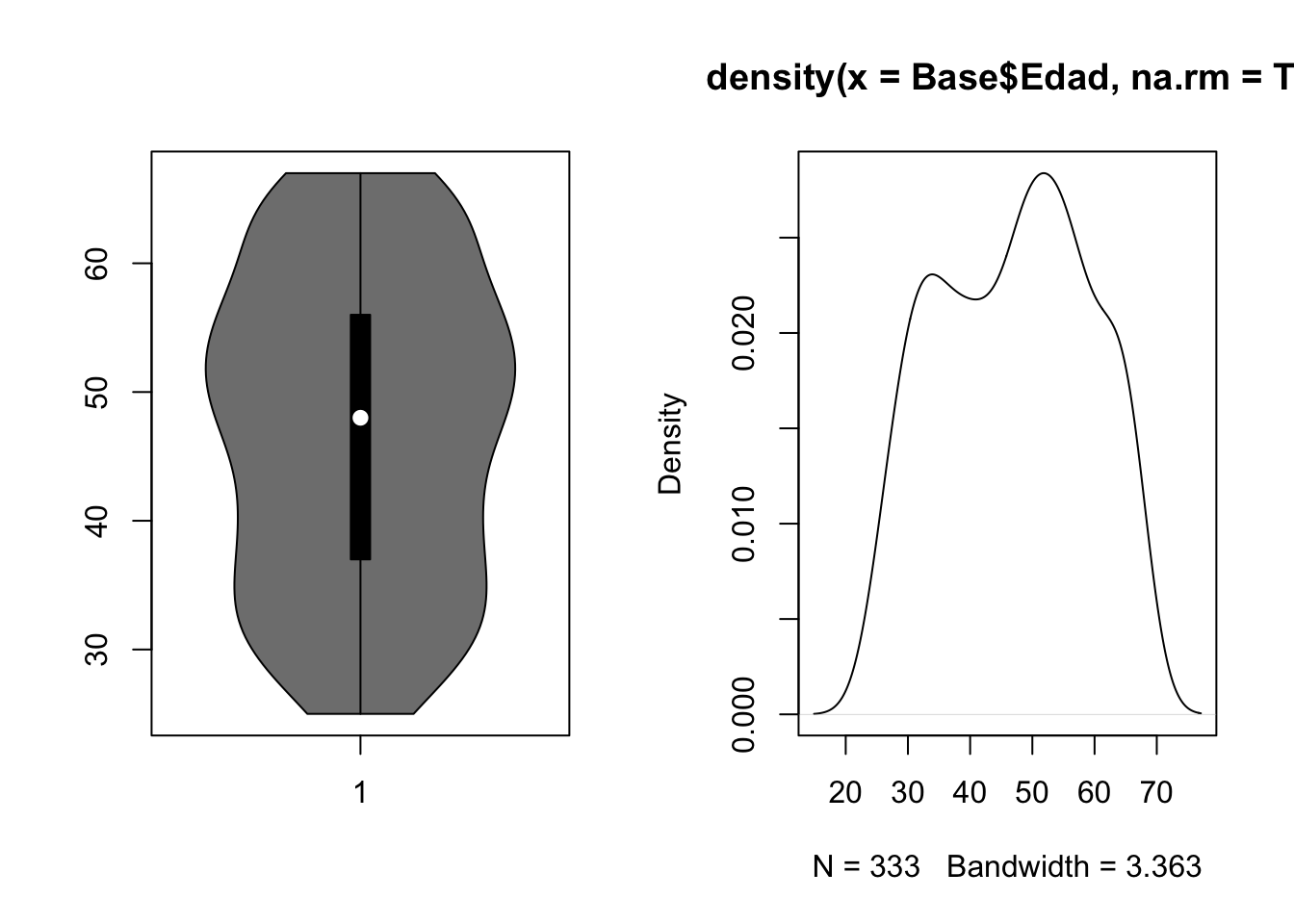
plot(density(Pima.tr$age), main = "Mi primer gráfico de densidad",
ylab = "Frecuencias", xlab= "Intervalos de clase para la edad", col = "cyan4")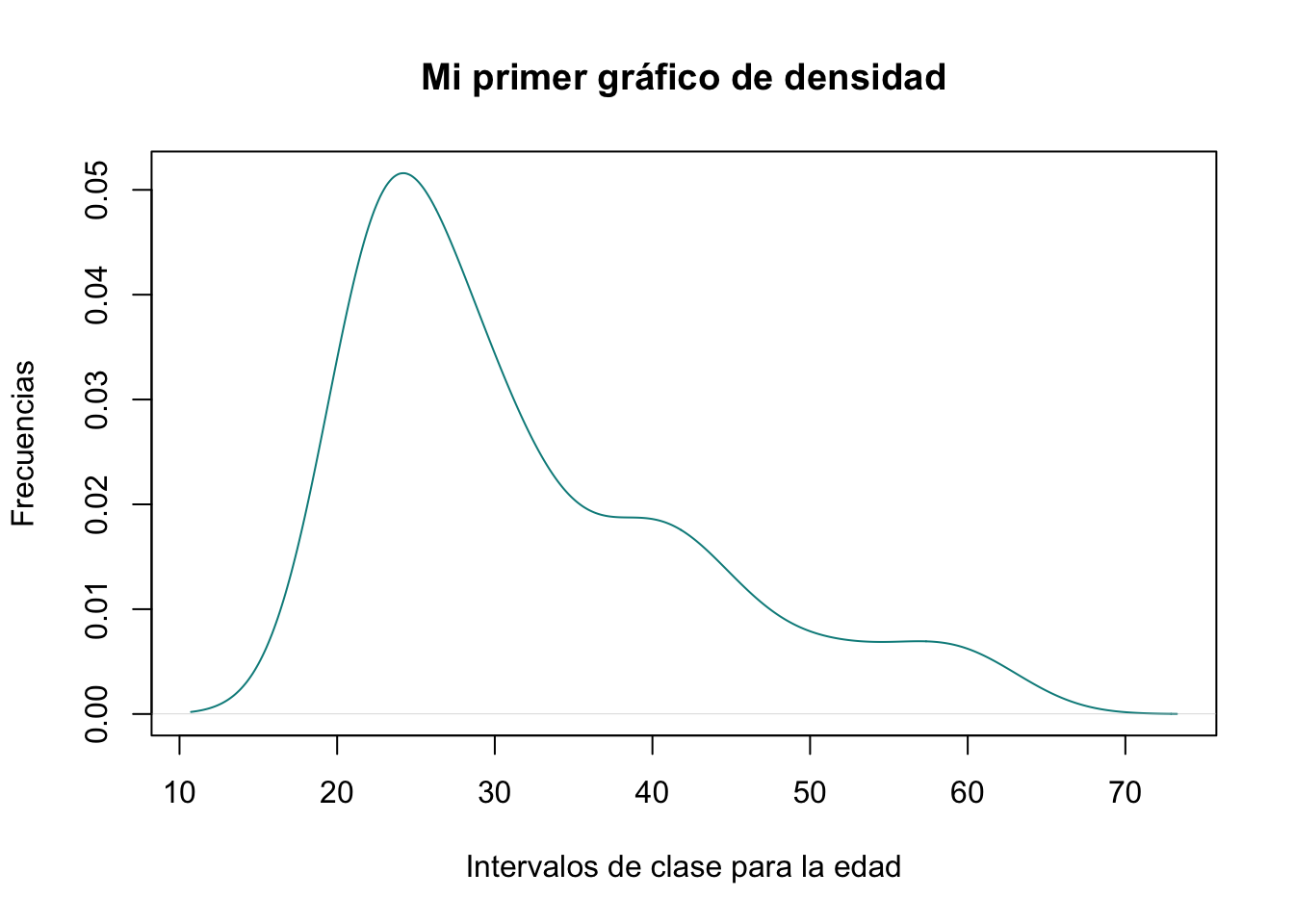
Este código merece algunas aclaraciones. La primera es que se utilizó la función plot, esta función es un función de “orden superior” en el que R tratará de graficar lo más ideal para los datos con las que fue alimentada. Por ejemplo, la podríamos utilizar para graficar un boxplot si la alimentamos con los argumentos correctos. Segundo, note como los argumentos para modficar los aspectos estéticos de las gráfica, se encuentran aplicados a la función plot y no a la función de densidad.
La función plot dada su complejidad merece que se dedique un apartado especial a ella @ref(Funcion-Plot))
9.7.2 Ejercicios para la creación de Histogramas
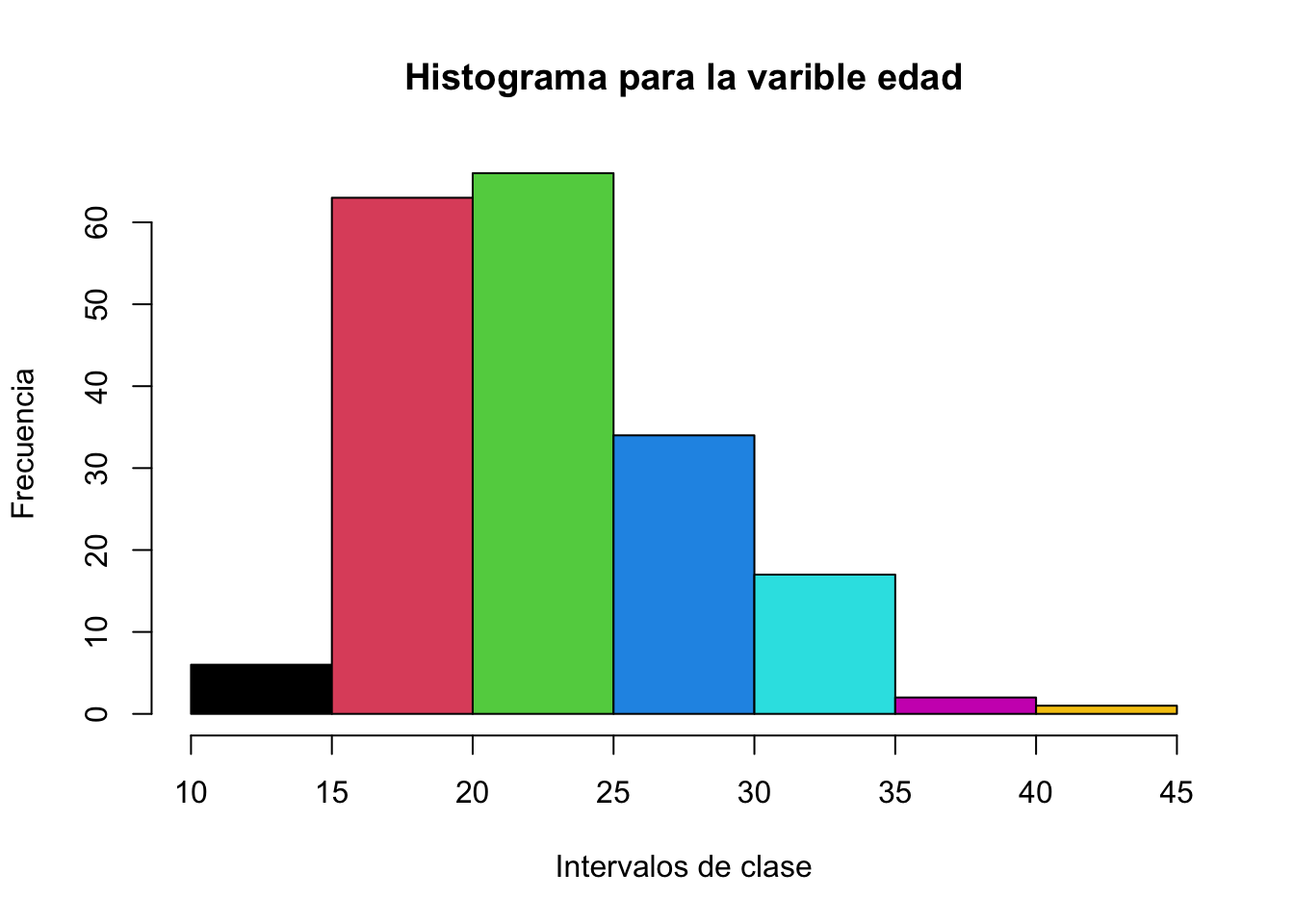
Ejercicio 9.21 Utilizando la base de datos base de datos birtwht realice un histograma con 10 intervalos de clase para la variable age. Cambie el color de las barras, agregue un título y rótulos en los ejes.
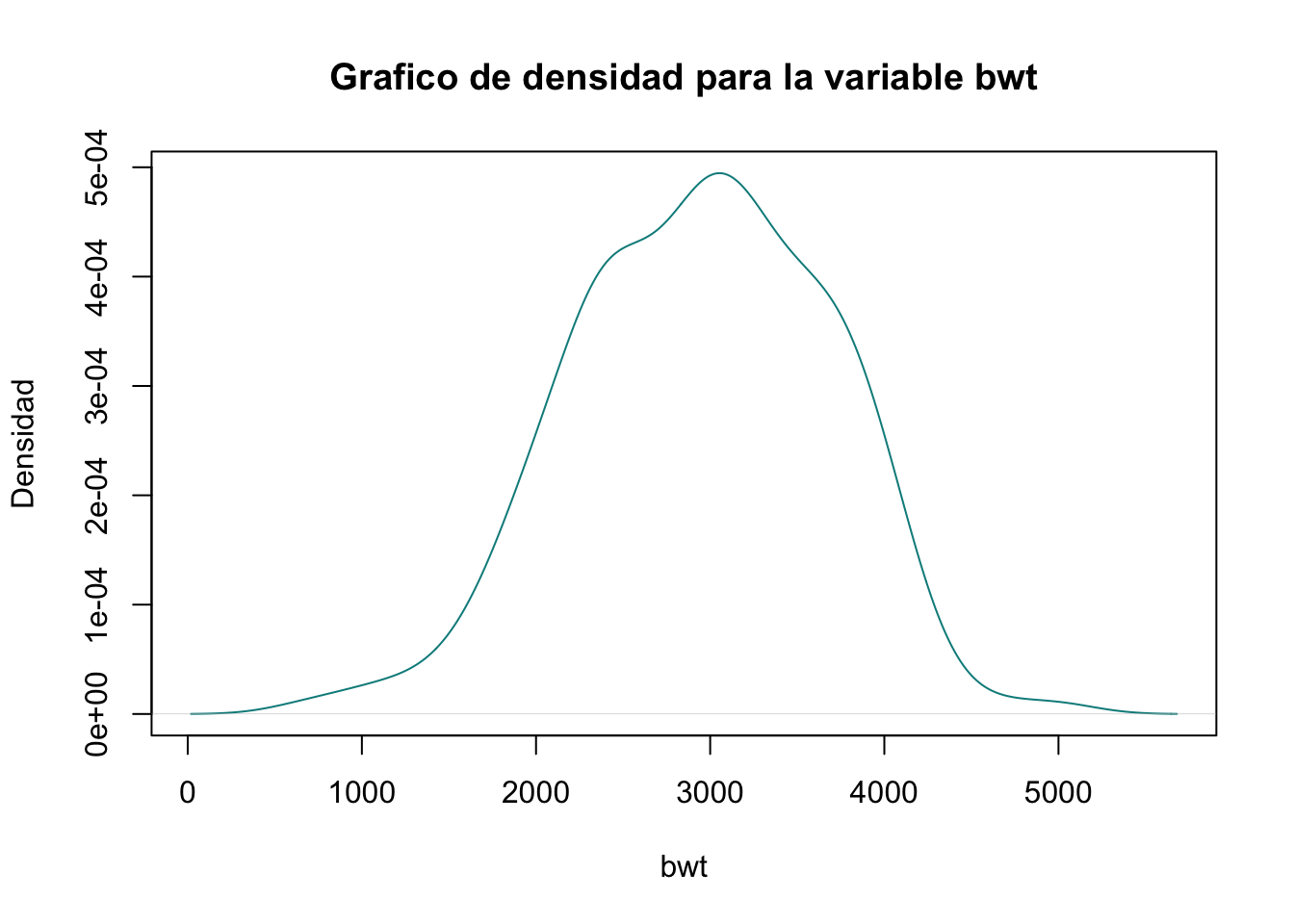
Ejercicio 9.22 Realice una gráfico de densidad para la variable bwt. Cambie el color de las barras, agregue un título y rótulos en los ejes.
9.7.3 Boxplot
Ya hemos utilizado al función boxplot con anterioridad en el apartado @ref(Intro-Funciones). La función boxplot contiene los siguientes tiene ciertas peculiaridades que iremos desglosando.
Para realizar un boxplot de las edades de las pacientes de la base de datos Pima.tr puede utilizar el siguiente código:
boxplot(Pima.tr$age, main="Grafico de caja y bigótes para las edades
de las pacientes de Pima", ylab="Edad (años)", col="cyan4")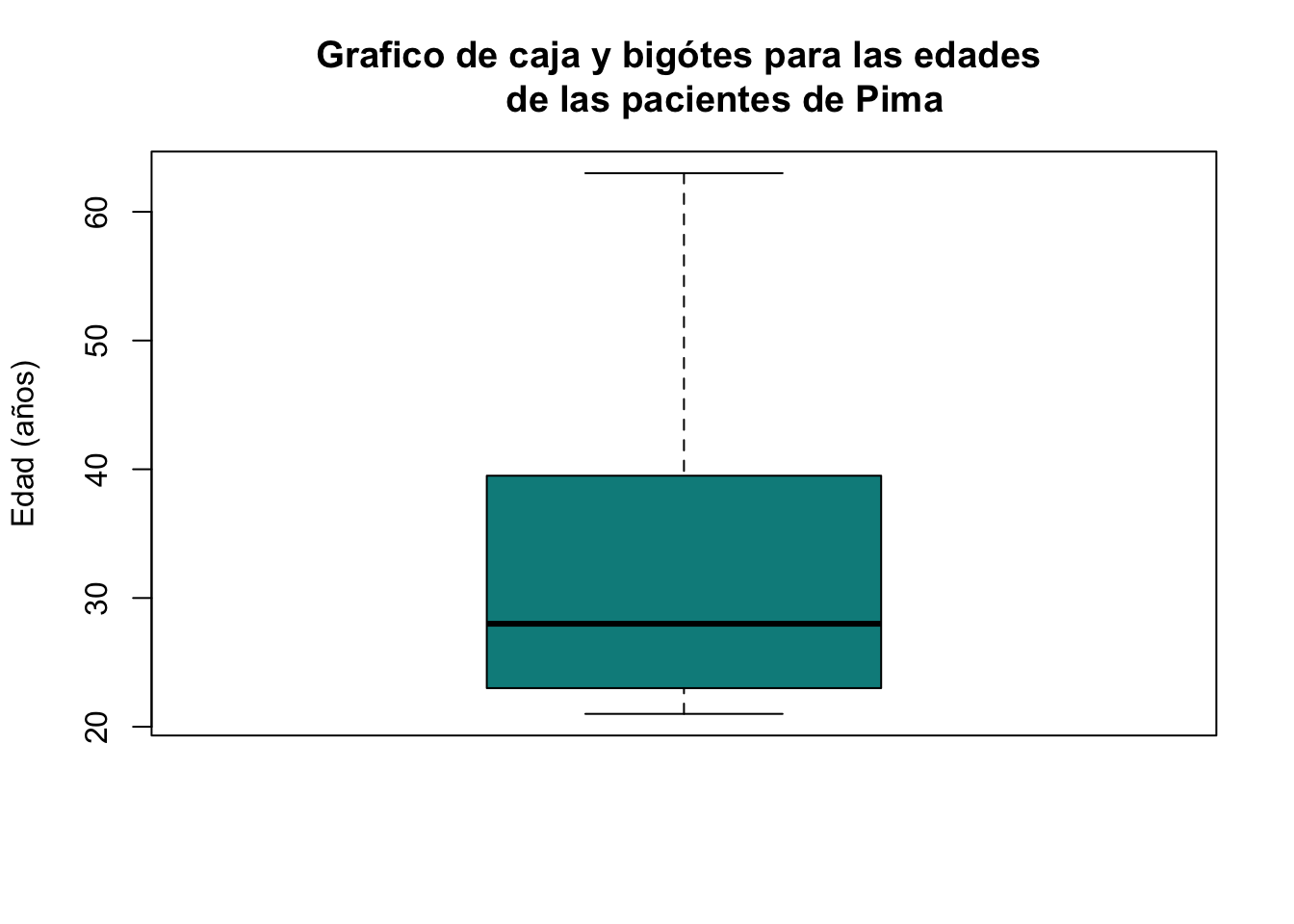
#Note como hay un enter el titulo que se ve reflejado en la gráficaTambién podemos cambiar el color del contorno de la caja con el argumento border.
boxplot(Pima.tr$age, main="Grafico de caja y bigótes para las edades
de las pacientes de Pima", ylab="Edad (años)", col="steelblue",
border="#E69F00")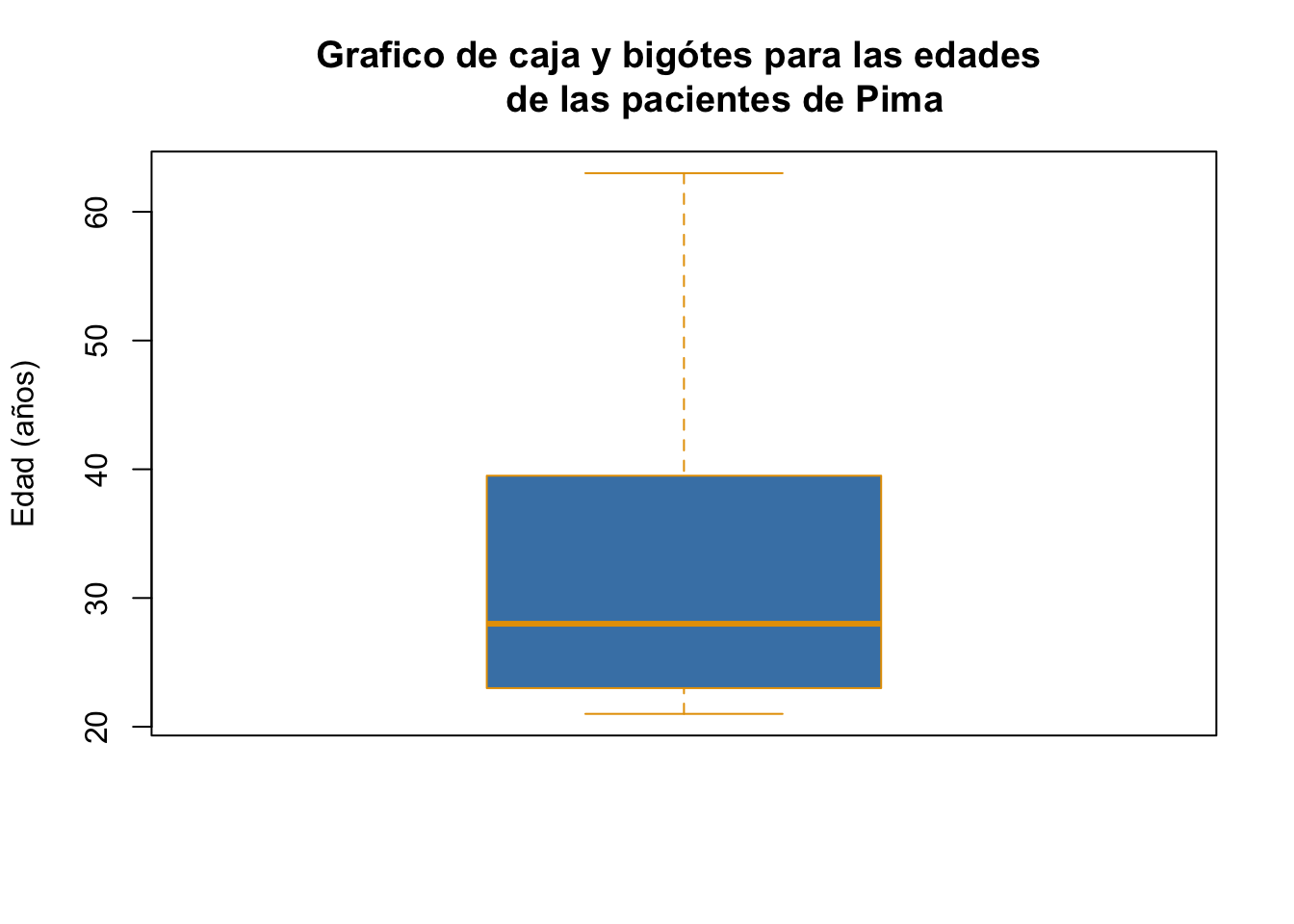
Note como ahora nos referimos a los colores con un código que comienza por un símbolo de # . Puede encontrar mayor información de los colores aquí
En algunas ocasiones es de nuestro interés tener una gráfica de forma horizontal. Para ello, utilizamos el argumento horizontal
boxplot(Pima.tr$age, main="Grafico de caja y bigótes para las edades
de las pacientes de Pima", ylab="Edad (años)", col="steelblue",
border="#E69F00", horizontal = T)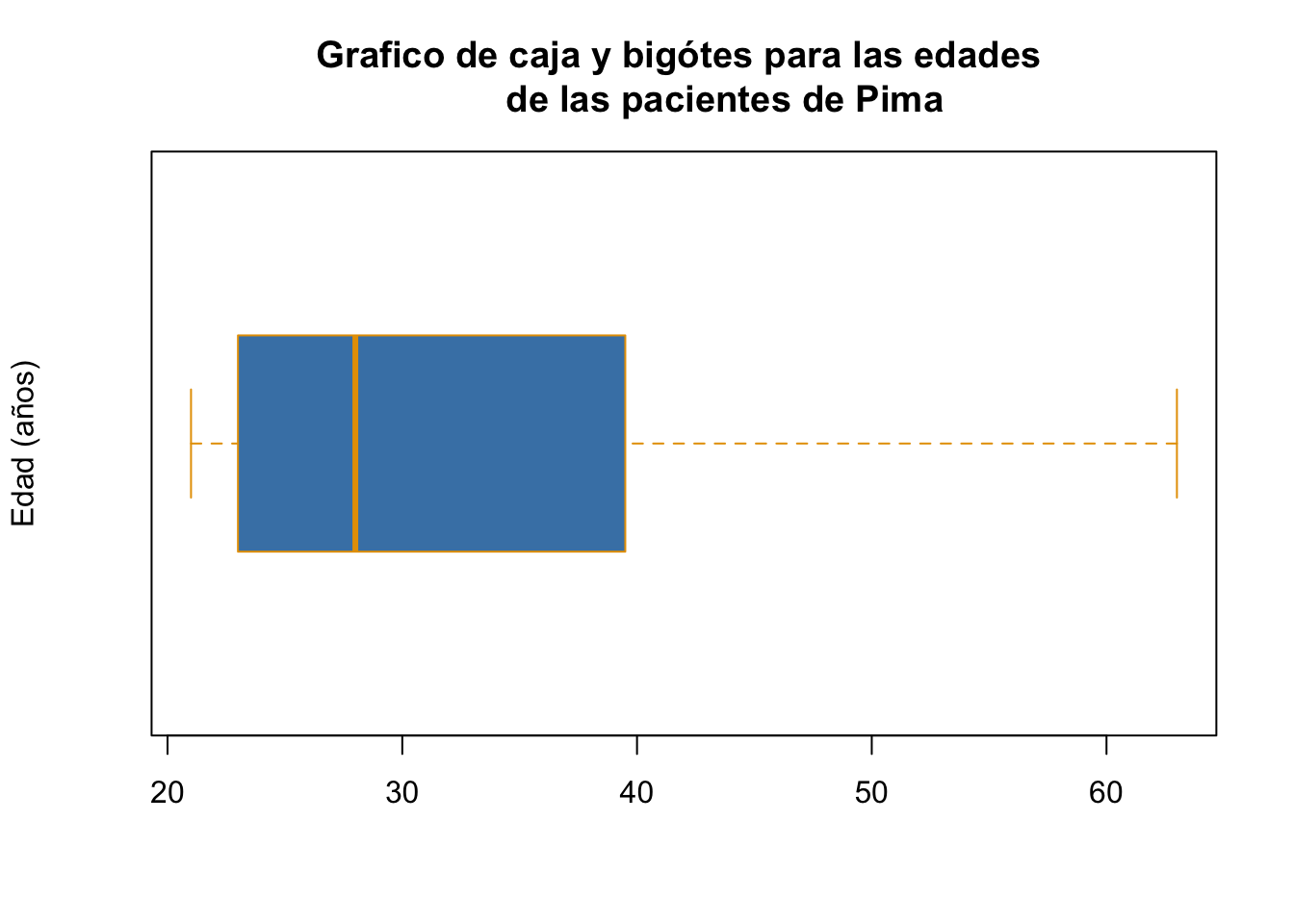
Note que las funciones por defecto tienen predefinidos algunos argumentos, en este caso el argumento horizontal se encuentra predefinido como FALSE
9.7.3.1 Boxplot por grupos
¿Que pasaría si queremos graficar en un boxplot las edades de las pacientes de Pima.tr y agruparlas de acuerdo con la presencia de diabetes?. Para ello, podemos emplear el siguiente código (que después explicaré)
boxplot(Pima.tr$age~Pima.tr$type, main="Comparación de las edades entre las pacientes
con DM vs mujeres sin DM", ylab="Edad (años)", col = c("#999999", "#E69F00"))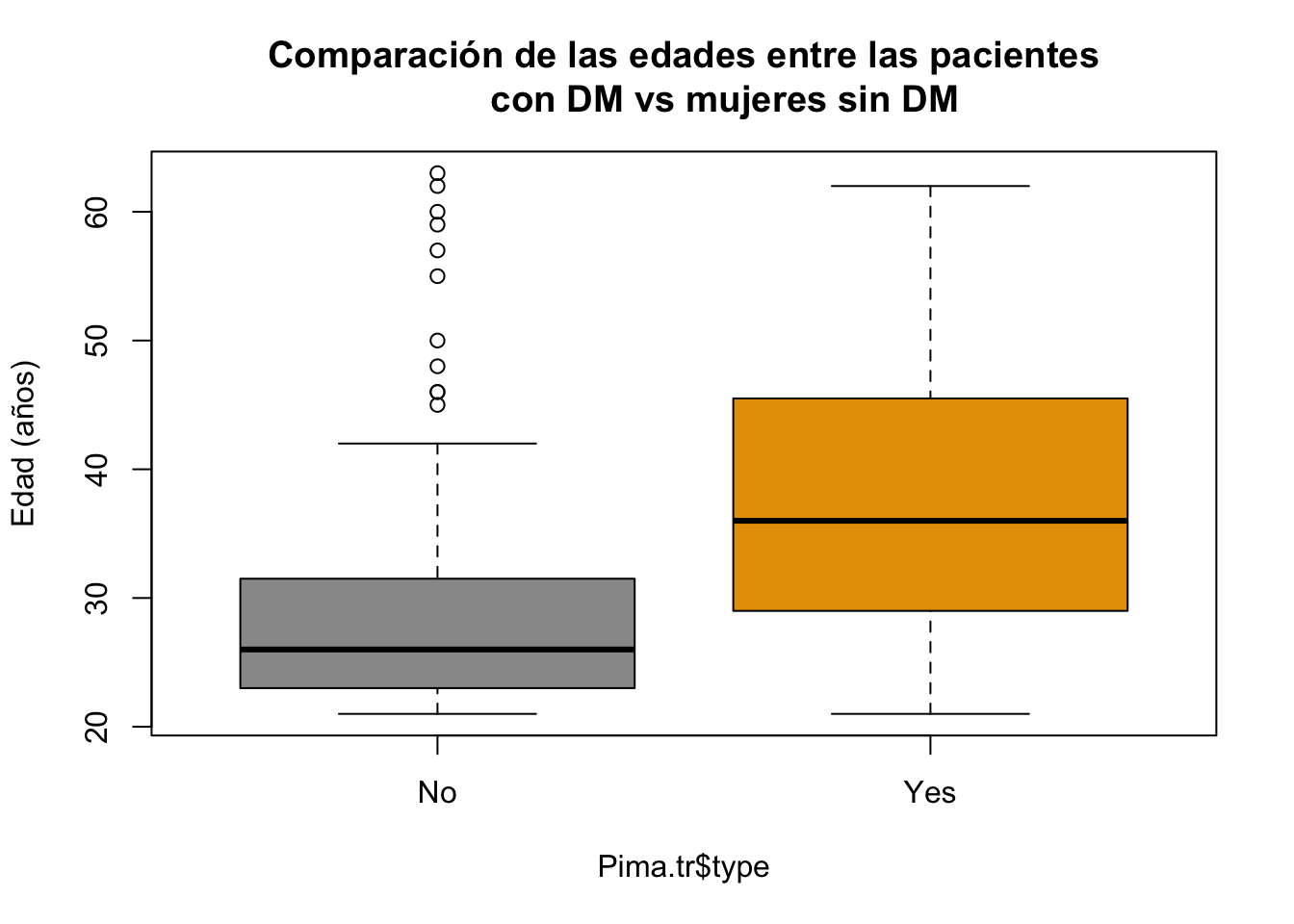
La principal peculiaridad del código es: Pima.tr$age~Pima.tr$type. Esta estrategia se conoce como formula, que se lee como la edad agrupada portype. En este caso el símbolo ~ significa agrupación.
Ahora podemos saber si hay una relación entre la edad y el número de embarazos
boxplot(Pima.tr$age~Pima.tr$npreg, main="Edad de acuerdo con el número de embarazos",
ylab = "Edad (años)", xlab="Número de embarazos")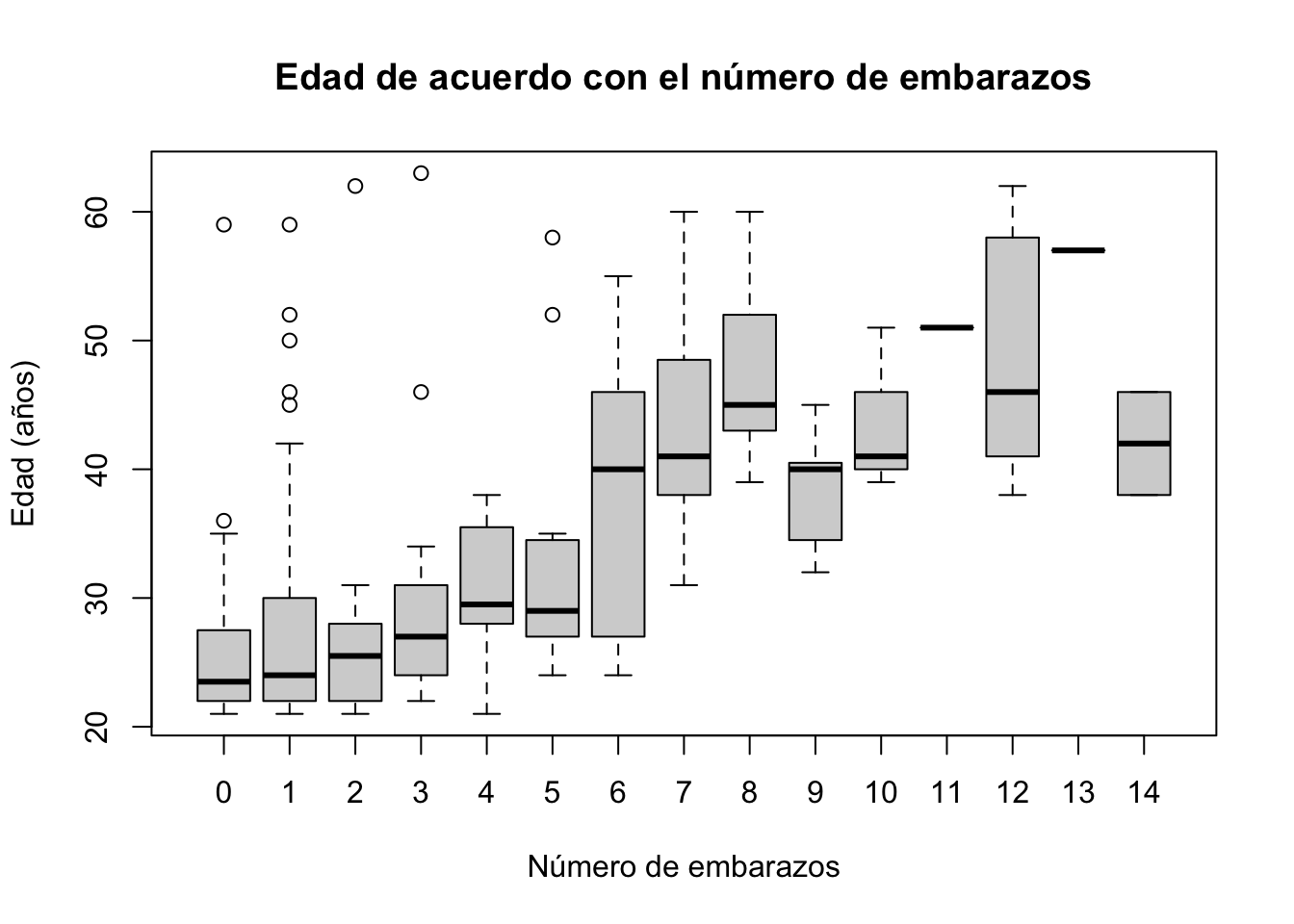
Las agrupaciones pueden ser mas complejas y tener dos variables de agrupación. Utilicemos el data frame birwth para explicarlo mejor.
Supongamos que queremos realizar una gráfica el peso del bebé al nacer (bwt) agrupado por el antecedente de tabaquismo en el embarazo (smoke) y la historia de hipertensión (ht). Podemos emplear el siguiente código:
boxplot(bwt~smoke*ht, data = birthwt, main="Peso del recién nacido",
col = c("white", "steelblue"), frame = FALSE)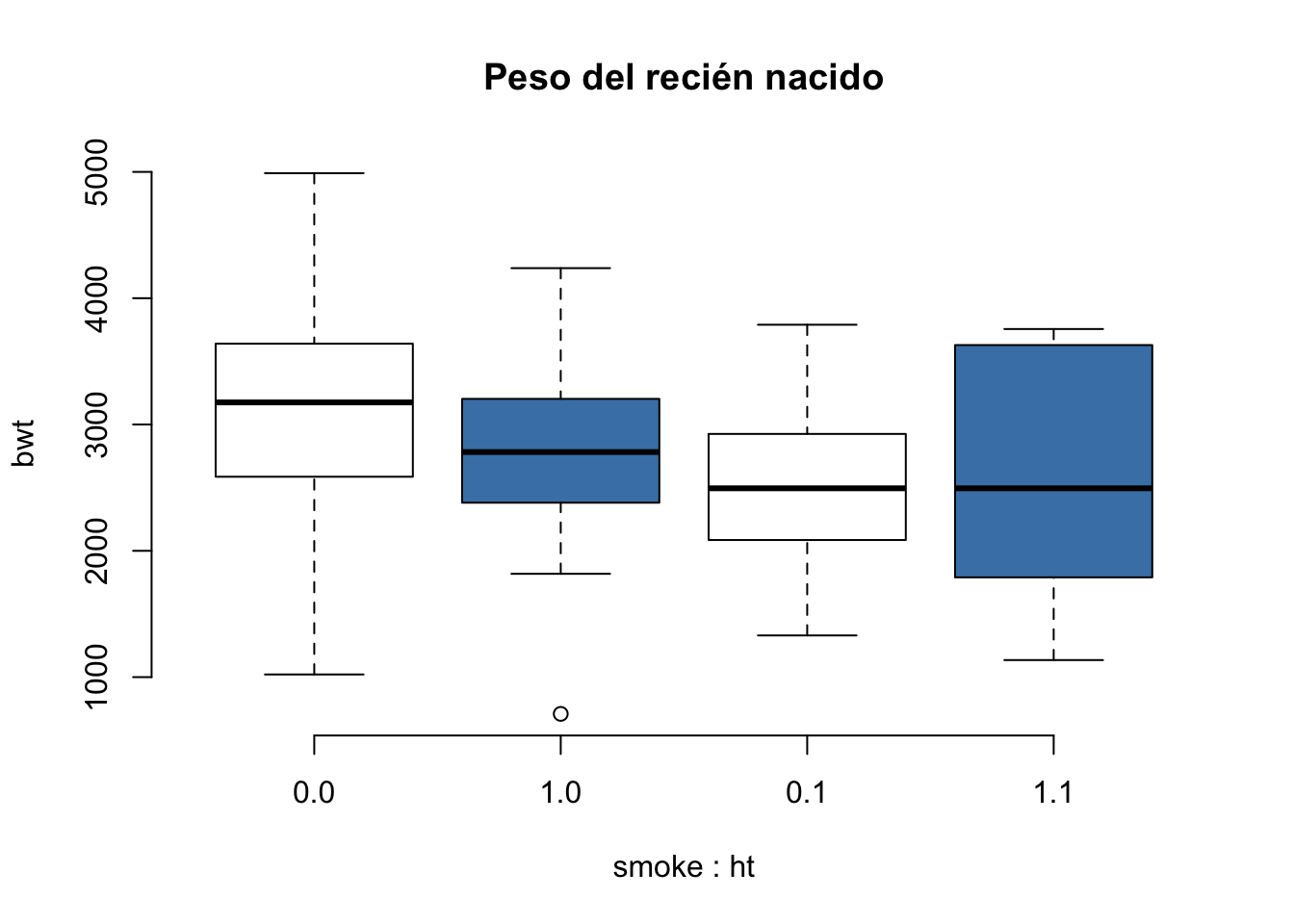
La sección de código bwt~smoke*ht indica el peso del recién nacido agrupado por el antecedente de tabaquismo y de hipertensión del madre. Con el argumento data podemos indicar de puede R obtner los datos y por tanto no es necesario utilizar el símbolo $.
9.7.4 Ejercicios para boxplot
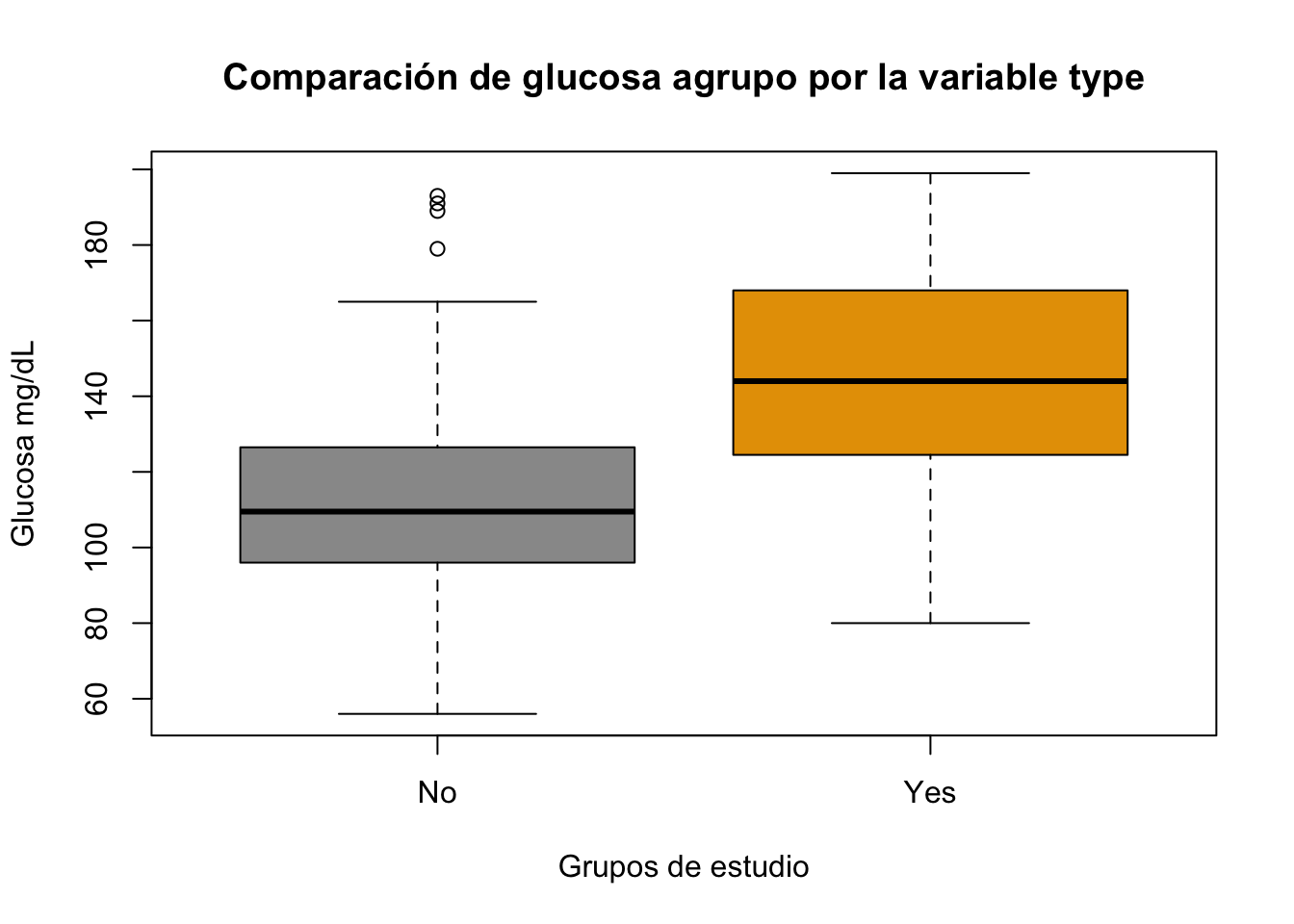
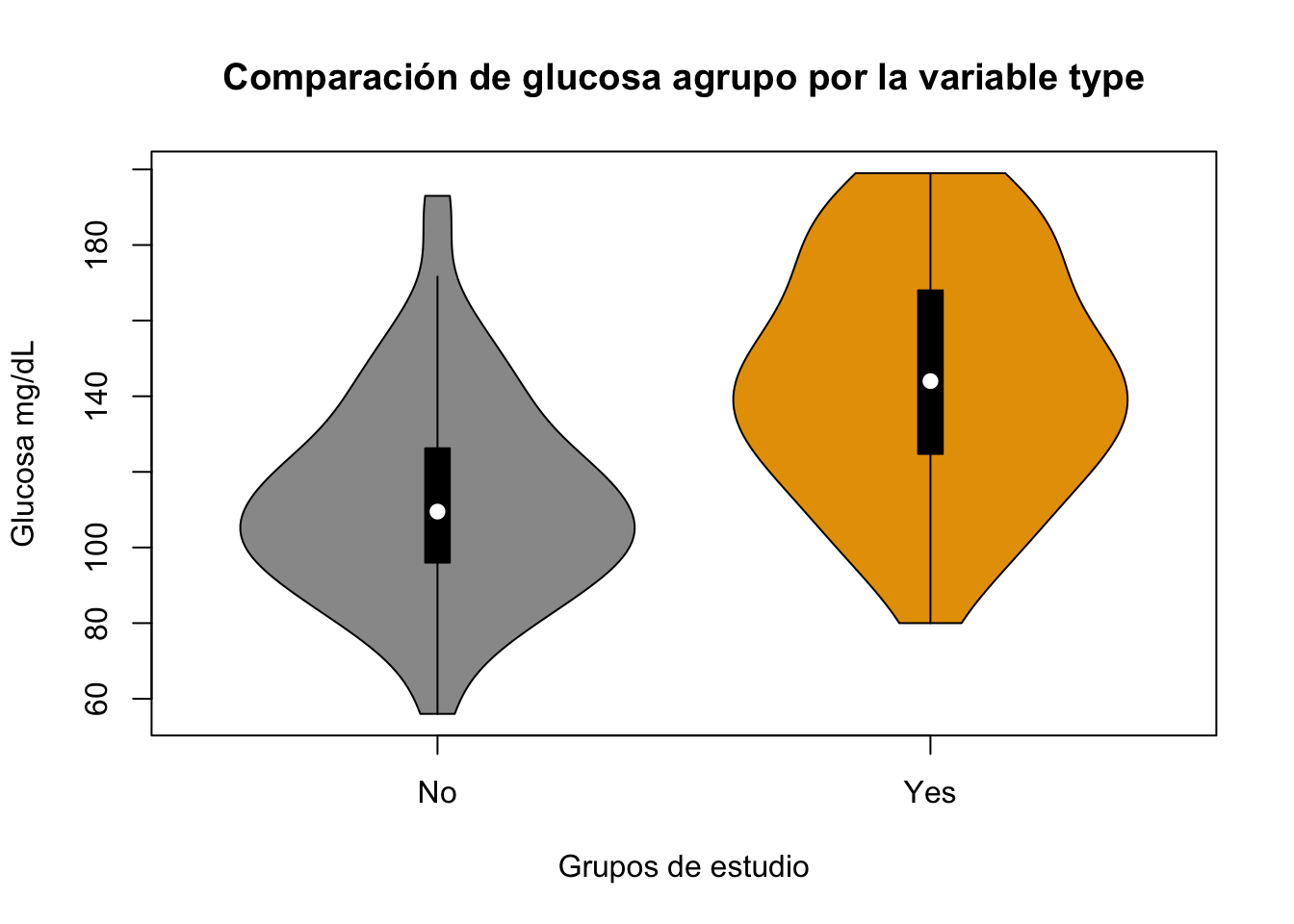
Ejercicio 9.23 Realice un boxplot para la variable glu agrupada por la variable type. Utilice la base Pima.tr. Cambie colores y agregue títulos
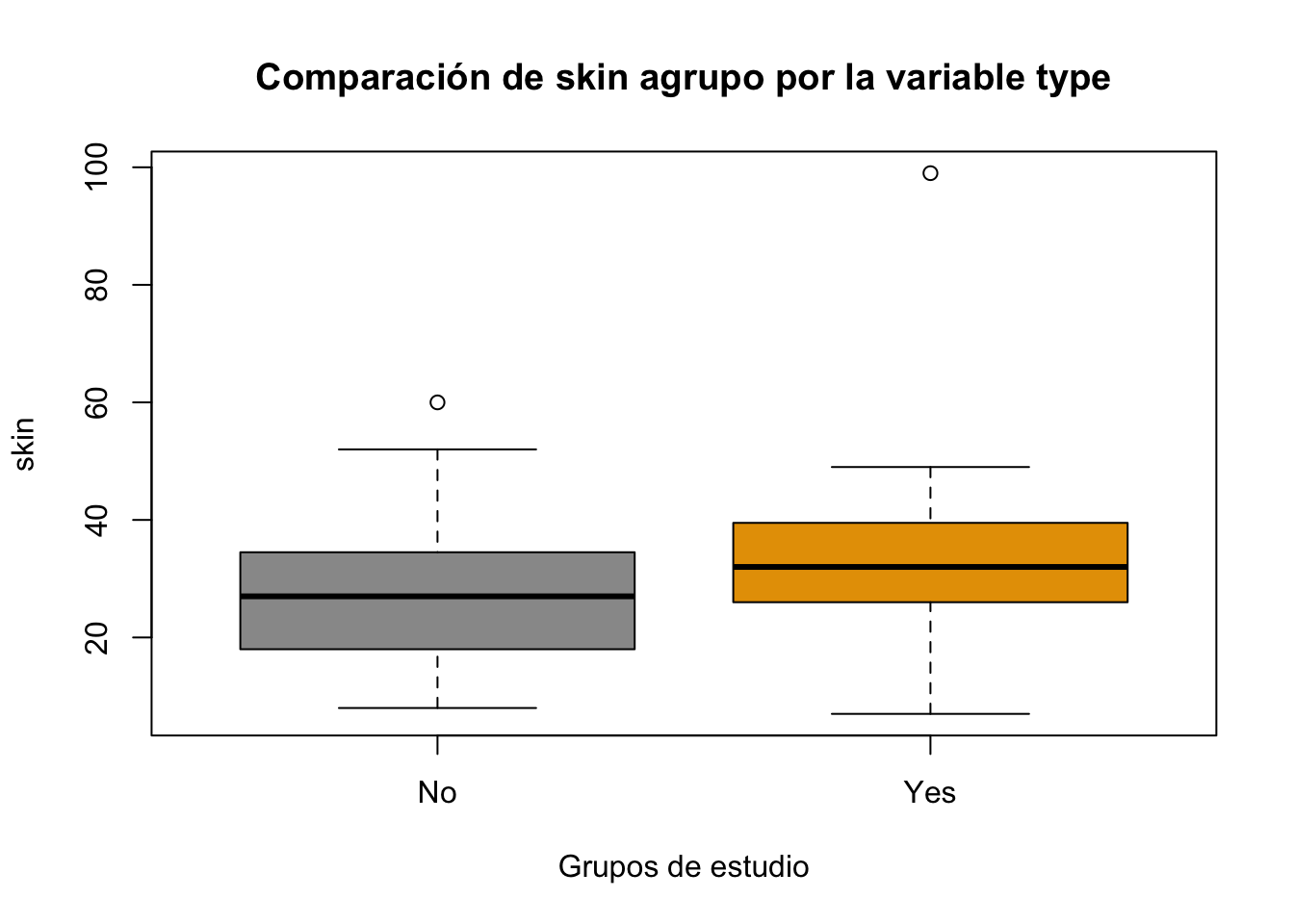
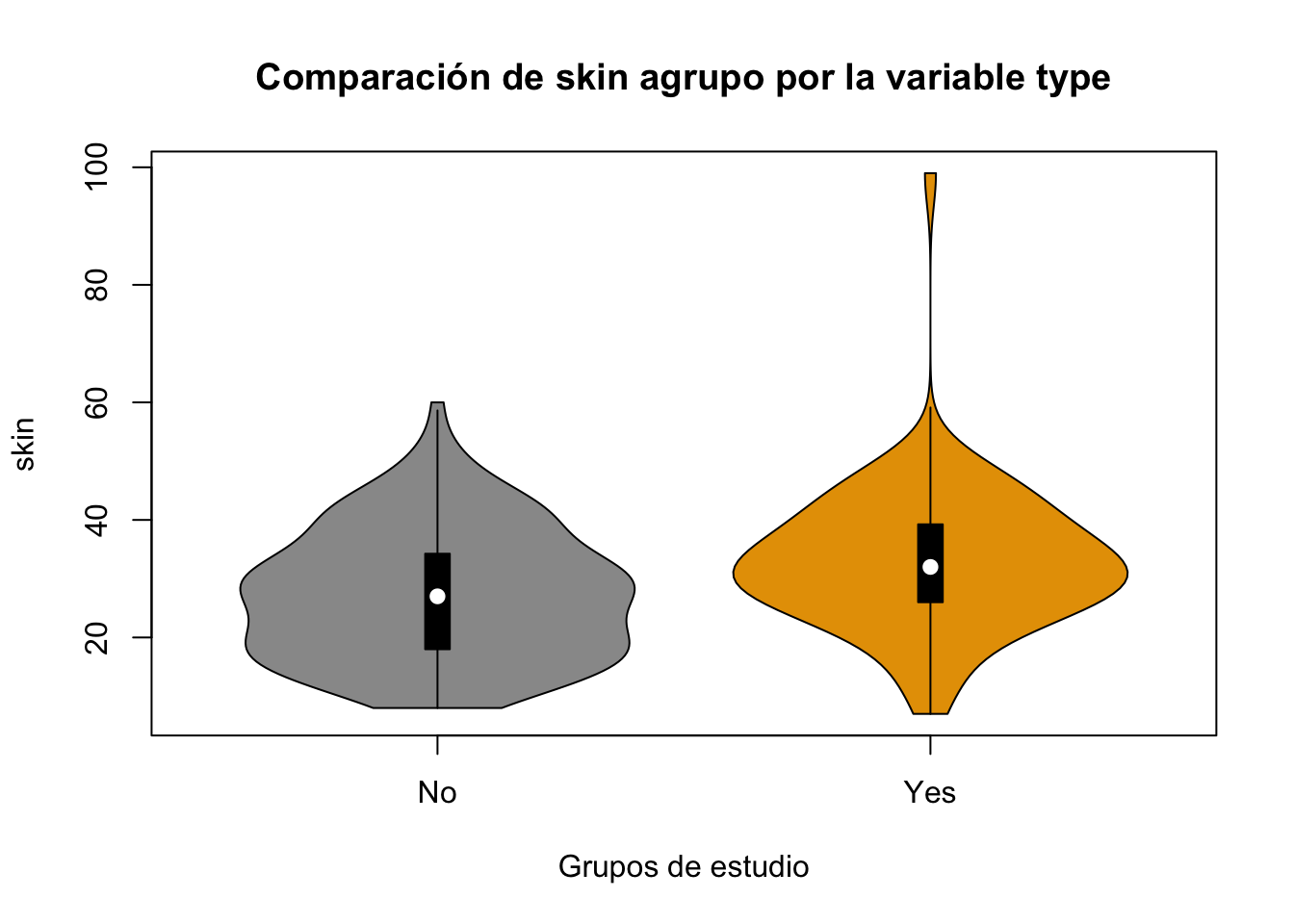
Ejercicio 9.24 Realice un boxplot para la variable skin agrupada por la variable type. Utilice la base Pima.tr. Cambie colores y agregue títulos
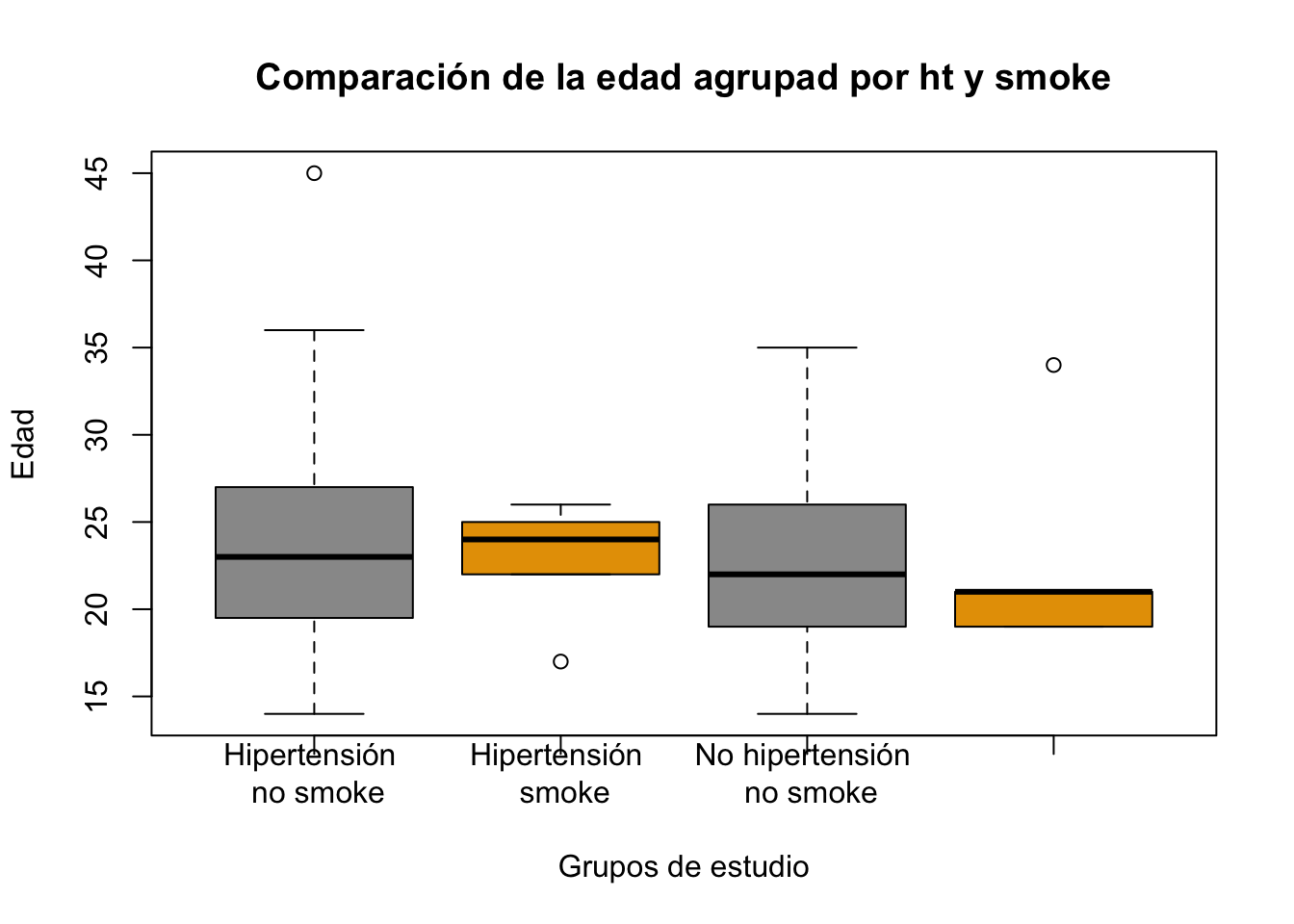
::: {.Exercise #exr-814}} Utilizando la base birthwt realice un boxplot en el que agrupe la edad de la madre (age) de acuerdo al antecedente de hipertension (ht) y el antecedente de tabaquismo de la madre (smoke) :::
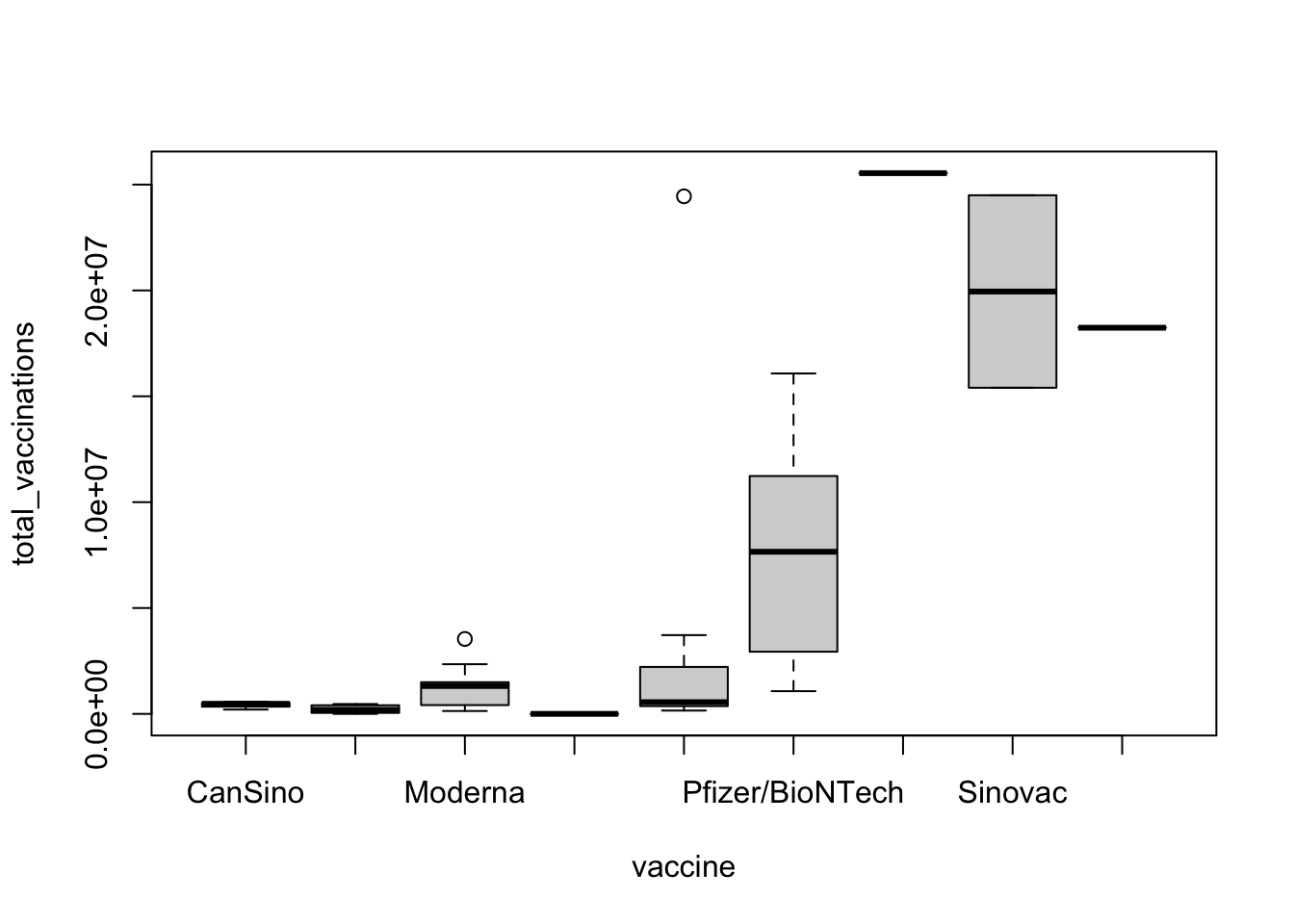
Ejercicio 9.25 Utilizando la base de datos vacunacion seleccione las primeras 50 filas para realizar un boxplot del total de pacientes total_vaccinations vacunados agrupado por el tipo de vacuna vaccine. ¿Tiene sentido hacer esta gráfica?
9.7.5 Gráficos de violín
Existe una alternativa a los boxplot que permite una apreciación de mayor calidad de la distribución de los datos ubicando para ello un núcleos. Estos gráficos se conocen como gráficos de violín, o violín plots.
Un gráfico de densidad es una representación visual de la distribución de una variable cuantitativa. A diferencia de un histograma, que utiliza barras para representar la frecuencia de observaciones en intervalos de valores, un gráfico de densidad utiliza una curva suavizada para mostrar la densidad de probabilidad de los datos en diferentes valores de la variable.
La librería vioplot contiene la función vioplot que requiere de un vector numérico o de una formula par alimentarse. Procedemos a instalar y a cargar la librería.
install.packages("vioplot")library("vioplot")Repetimos la misma gráfica del punto anterior pero esta vez utilizando la función vioplot
vioplot(birthwt$lwt~birthwt$race, ylab="Peso de la madre", xlab = "Raza")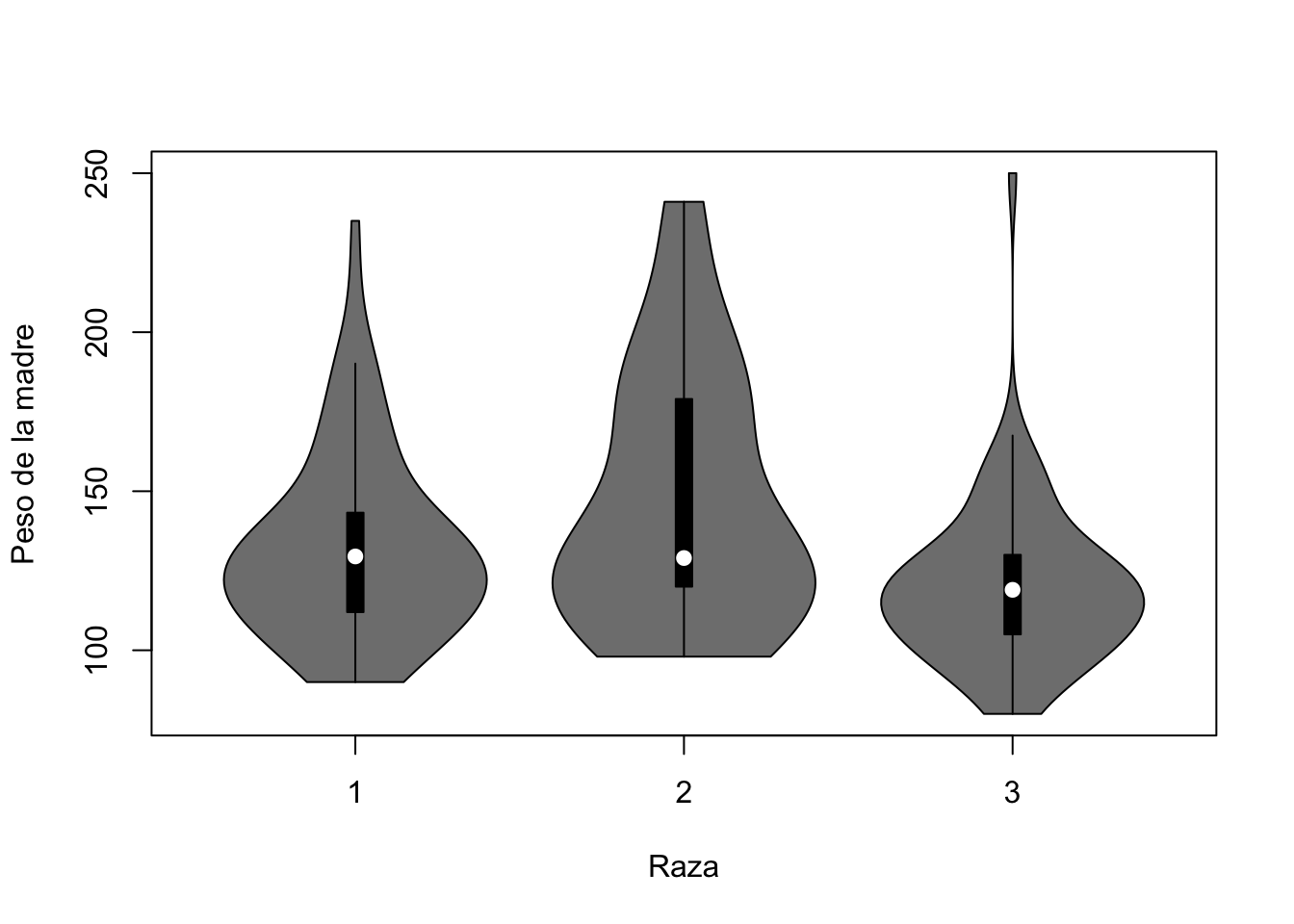
Puede encontrar más información sobre estás gráficas en (https://r-coder.com/violin-plot-en-r/)
9.7.6 Ejercicios para gráficos de violín
Ejercicio 9.26 Realice un gráfico de violin para la variable glu agrupada por la variable type. Utilice la base Pima.tr. Cambie colores y agregue títulos
Ejercicio 9.27 Realice un gráfico de violin para la variable skin agrupada por la variable type. Utilice la base Pima.tr. Cambie colores y agregue títulos
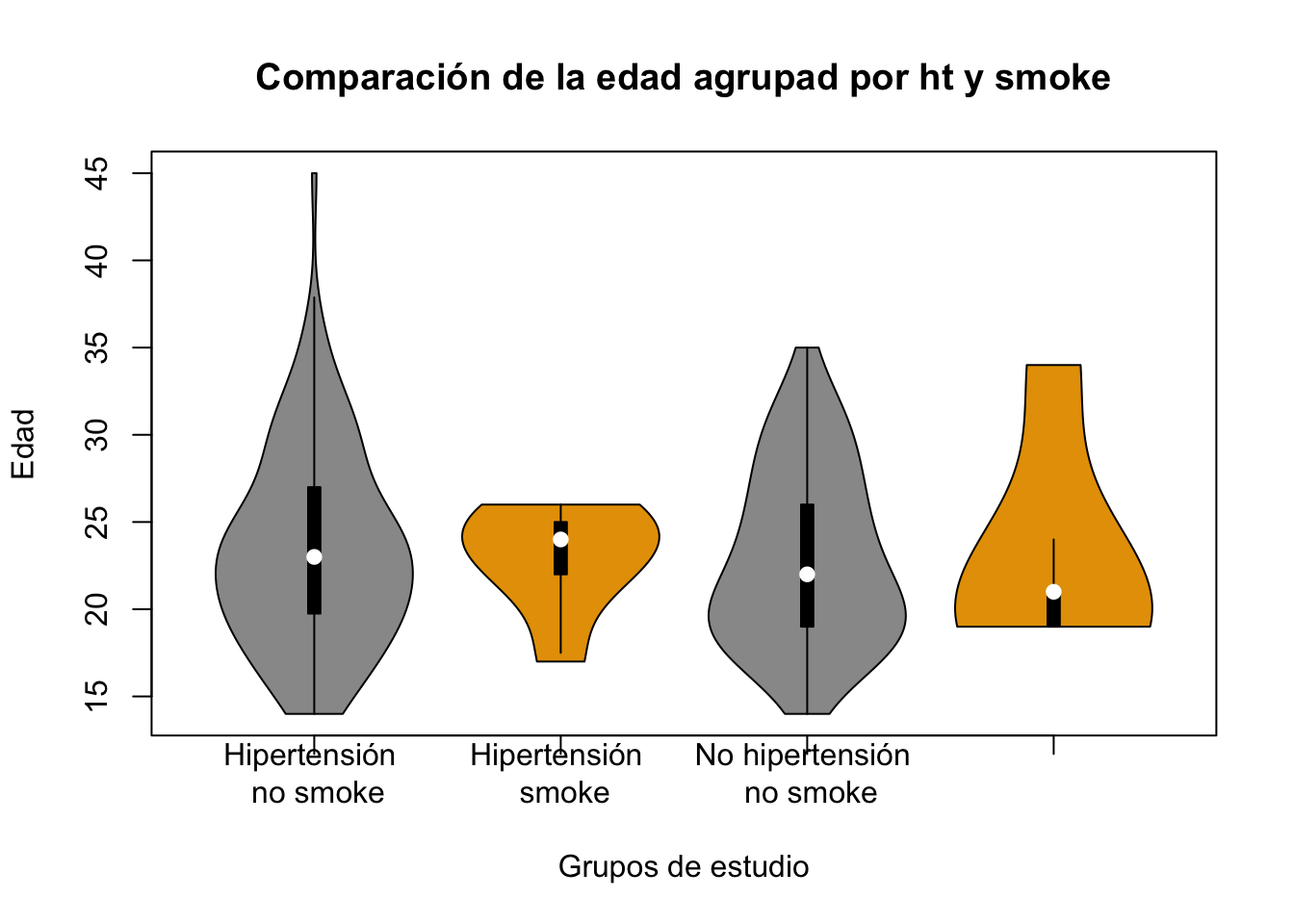
Ejercicio 9.28 Utilizando la base birthwt realice un gráfico de violin en el que agrupe la edad de la madre (age) de acuerdo al antecedente de hipertension (ht) y el antecedente de tabaquismo de la madre (smoke)
Ejercicio 9.29 Supongamos que tienes datos sobre la concentración de una proteína en muestras de sangre de dos grupos diferentes de pacientes, uno con una enfermedad (Grupo 1) y otro sin la enfermedad (Grupo 2). Los datos son ficticios.
Datos:
Grupo 1 (con enfermedad): 20, 22, 21, 23, 19, 24, 25, 18 Grupo 2 (sin enfermedad): 15, 14, 16, 15, 17, 15, 14, 16
- Utiliza R para calcular la media, la desviación estándar y el coeficiente de variación para cada grupo.
- Interpreta los coeficientes de variación en el contexto del estudio.
- ¿Qué grupo muestra mayor consistencia en las concentraciones de proteína?
- ¿Cómo podrías explicar esto en términos de la variabilidad asociada con la enfermedad?
Ejercicio 9.30 Imagine que es un investigador analizando los resultados de dos tratamientos diferentes para una enfermedad. Los resultados representan la mejora en la condición de los pacientes después de recibir cada tratamiento. El objetivo es entender cuál tratamiento es más efectivo y consistente.
Datos:
Tratamiento A: 8, 10, 12, 14, 16 Tratamiento B: 10, 11, 12, 13, 14
Con los datos anteriores responda y calcule lo siguiente:
- Calcula la media, la varianza y la desviación estándar para cada conjunto de datos utilizando R.
- Compara los resultados obtenidos para ambos tratamientos.
- Interpreta los resultados en términos de efectividad y consistencia del tratamiento.
- ¿Qué tratamiento muestra una mayor mejora promedio en la condición de los pacientes?
- ¿Cuál de los tratamientos presenta una mayor variabilidad en los resultados?
- ¿Cómo afecta la variabilidad de los resultados a la interpretación de la efectividad del tratamiento?
Recuerde que:
Media: Indica el valor promedio de los resultados para cada tratamiento. Un valor más alto sugiere una mayor mejora promedio. Varianza: Muestra cuán dispersos están los datos respecto a la media. Una varianza mayor indica una mayor dispersión de los resultados. Desviación Estándar: Es la raíz cuadrada de la varianza y proporciona una medida de dispersión en las mismas unidades que los datos. Facilita la interpretación de la variabilidad de los datos.
Ejercicio 9.31 Continuando con el ejemplo anterior, supongamos que desea analizar más a fondo la consistencia de los resultados de dos tratamientos diferentes para una enfermedad, utilizando el IQR para entender mejor la dispersión de los datos sin la influencia de valores atípicos.
Datos:
Tratamiento A: 8, 10, 12, 14, 16, 18, 20 Tratamiento B: 9, 11, 11, 12, 13, 14, 15
Estime y calcule:
- Calcula el primer cuartil (Q1), el tercer cuartil (Q3) y el rango intercuartílico (IQR) para cada conjunto de datos utilizando R.
- Crea un gráfico de cajas (boxplot) para visualizar la distribución de los resultados de ambos tratamientos, destacando el IQR. a.Interpreta los resultados, enfocándote en la dispersión de los datos y la presencia de valores atípicos.
Ejercicio 9.32 La base de datos “Base Descriptivos.rds” contiene las características de 350 pacientes que acudieron a un hospital de segundo nivel en Guadalajara Jalisco para realizarse una cirugía menor en un periodo de 2018 a 2020. La base de datos proviene de un estudio cuyo objetivo fue conocer las características de los pacientes que se sometieron a cirugía en este hospital. La encuesta para recabar la información fue realizada después de la cirugía, por lo que también podrá encontrar unas variables relacionadas con la percepción del dolor.
La base contiene las siguientes variables:
- ID: Variable de indexación con números consecutivos de los casos.
- Edad: Contiene la edad de los pacientes en años, con valores que van de 25 a 67 años.
- Peso: Representa el peso de los pacientes en kilogramos, con valores que van de 55 a 110 kg.
- Talla: Indica la estatura de los pacientes en centímetros, con valores que van de 152 a 202 cm.
- Género: Variable categórica que indica el género del paciente como “Hombre” o “Mujer”.
- Escolaridad: Variable categórica con 6 niveles que representan el último grado de escolaridad alcanzado por el paciente. Los niveles son: Primaria incompleta, Primaria completa, Secundaria, Preparatoria, Licenciatura, y Posgrado.
- Gdo_Escolaridad: Variable categórica con 2 niveles: “Secundaria o menos” y “Preparatorio o más”, creada en base a la variable de Escolaridad.
- Ocupación: Variable categórica que describe la ocupación del paciente. Los niveles son: Desempleado, Trabajador, Jubilado, Ama de casa y Empresario.
- Trabajador: Variable categórica con dos niveles: “Trabajador” y “No trabajador”, creada en base a la variable de Ocupación.
- Alcohol: Variable categórica que indica si el paciente consume alcohol (“Sí”) o no (“No”).
- Tabaquismo: Variable categórica que indica si el paciente es fumador (“Sí”), no fumador (“No”) o exfumador (“Exfumador”).
- Toxicomanía: Variable categórica que indica si el paciente ha consumido drogas ilícitas (“Sí”) o lo niega (“Negado”).
- Sedentarismo: Variable categórica que indica si el paciente tiene un estilo de vida sedentario (“Sí”) o no (“No”).
- HAS: Variable categórica que indica si el paciente tiene hipertensión arterial sistémica (“Sí”) o no (“No”).
- DM: Variable categórica que indica si el paciente tiene diabetes mellitus (“Sí”) o no (“No”).
- Proteínas_Orina: Variable cuantitativa que muestra la concentración de proteínas en la orina, con valores que van de 0 a 2.5.
- Biomarcador: Variable cuantitativa que muestra la concentración de un biomarcador en particular, con valores que van de 0 a 120.
- Glucosa: Variable cuantitativa que muestra los niveles de glucosa en sangre, con una distribución normal y valores que van de 80 a 230.
- Embarazos: Variable cuantitativa discreta que indica el número de embarazos que ha tenido el paciente, con valores que van de 0 a 9.
- Dolor: Variable categórica que describe el nivel de dolor experimentado por el paciente. Los niveles son: “Mucho”, “Poco” y “Nada”.
- Escala_Dolor: Variable cuantitativa discreta que representa la intensidad del dolor en una escala de 0 a 10.
Para importar su base a R, descargue la base en este enlace y guardela en su carpeta de bases, después utilice el siguiente código:
Base <- readRDS("Bases/Base Descripitivos.rds")
Con esta base resuelva lo siguiente:
- Cree una nueva variable con el IMC de los pacientes
- Categorice este variable de acuerdo con los criterios de la OMS para obesidad
- Utilizando la variable Edad, cree una nueva variable en la que agrupe a los pacientes por década. Es decir, de 20 a 30, 31 a 40 etc.
- Identifique todas las variables cualitativas de la base de datos (incluidas las que creo) y realice una tabla de frecuencias y gráfico de barras para cada una de ellas. Su gráfico deberá de tener un título, colores y nombres en los ejes de las “y” y de las “x”.
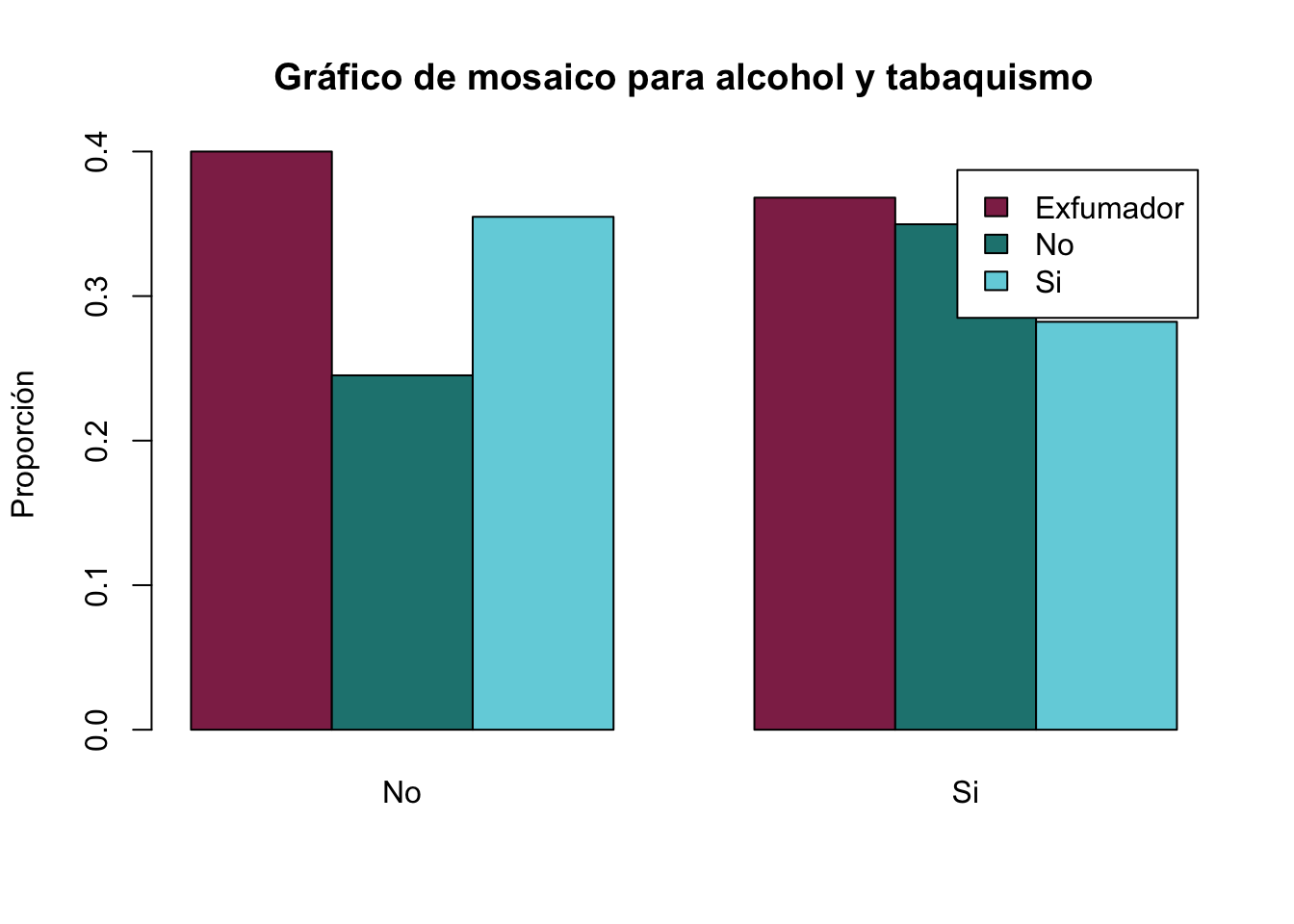
- Realice un gráfico de Mosaico para las variables HAS y DM (en conjunto). Interprete este gráfico
- Realice un gráfico de barras donde agrupe para las variables Alcohol y Tabaquismo. El eje de las “y” deberá de estar en proporciones.
- Identifique todas las variables cuantitativas de la base de datos y estime los siguientes estadísticos:
- Media
- Mediana
- Rango
- Desviación estándar
- IQR
- Coeficiente de variación
- Varianza
- Percentil 0.25, 0.50,0.75
- Mínimo
- Máximo
- Identifique todas las variables cuantitativas de la base de datos y realice los siguientes gráficos, en dónde deberá de cambiar los colores, títulos y nombres de los ejes:
- Histograma
- Boxplot
- Violín
- Densidad
- Realice un gráfico de violín y otro de boxplot para la variable edad agrupando entre:
- Los pacientes que fuman no fuman y que son exfumadores
- Pacientes con hipertensión y sin hipertensión
- Interprete sus gráficos
- Realice un gráfico de boxplot y otro de violín para las variables peso y talla agrupando por la variable creada que divide a los pacientes con décadas. Interprete estos gráficos.