4 Chapter 4: Supervised Learning

Image source

4.1 Introduction

• Sometimes, you know the ‘labels’ of the subjects, or objects under study.
  • These may be biological features, as in the penguins and crabs data
  • These may be clinical outcomes, such as lived or died.
• In a classification problem, we want to be able to make good predictions of the subject labels using the available feature set.
  • This is distinctly different from cluster label assignment, say in model-based clustering
    • Here, we don’t know the labels, and just want to make an assignment that separates homogeneous groups.
  • We can borrow some of the notions of similarity that we developed in cluster analysis to exploit similarity to classify observations.

4.1.1 Training vs. Test data

• Typical classification problems involve a training set of data, in which a model is fit that attempts to capture enough of the structure in the features of the process so that new observations from a test (or withheld) data set may be classified.
  • For some of our discussion, we will not have a test set; the data as a whole will be used to build the model, and the predictions for each observation form the ‘test’ much as in regression modeling.
  • However, just as in regression, this is likely to be overfitting to a specific dataset, if there are new samples or simply new observations expected, or if predictive (rather than descriptive) modeling is the goal
    • The goal of description is non-trivial, and sometimes leads to insights in and of itself.
      
    • Procedures to prevent overfitting will be discussed subsequently.

4.2 K-Nearest Neighbor (K-NN) Classification

• Imagine a dataset in which you have the labels of ALL observations except for one. What would be a good guess as to the label of the remaining observation?
  • Answer: the label of the nearest neighbor, which would be the observation with the minimum distance to the new point.
  • As we discussed in the case of clustering, there are many choices for distance, but we often use the Euclidean distance, with properly rescaled variables (often called features in this context).

4.2.1 K-NN Illustration with penguins data

• Visualized in 2-D.
  • Observation 68 is surrounded by a blue triangle to indicate that we (pretend we) don’t know its label, and then we take wider and wider radius circles until we ‘hit’ the nearest neighbor.
    • The circle would be a hyper-sphere in 3-D space
    • Note: it looks like we might assign the ‘blue’ observation to the red group, but that point is actually ‘black’.

Code

plot(penguins[,c(3,4)],col=penguins$species,cex=.8,pch=16)
#possible points: 60  68  76 
points(penguins[68,c(3,4)],pch=2,col=4,cex=1)
points(penguins[68,c(3,4)],pch=1,col=4,cex=8.6)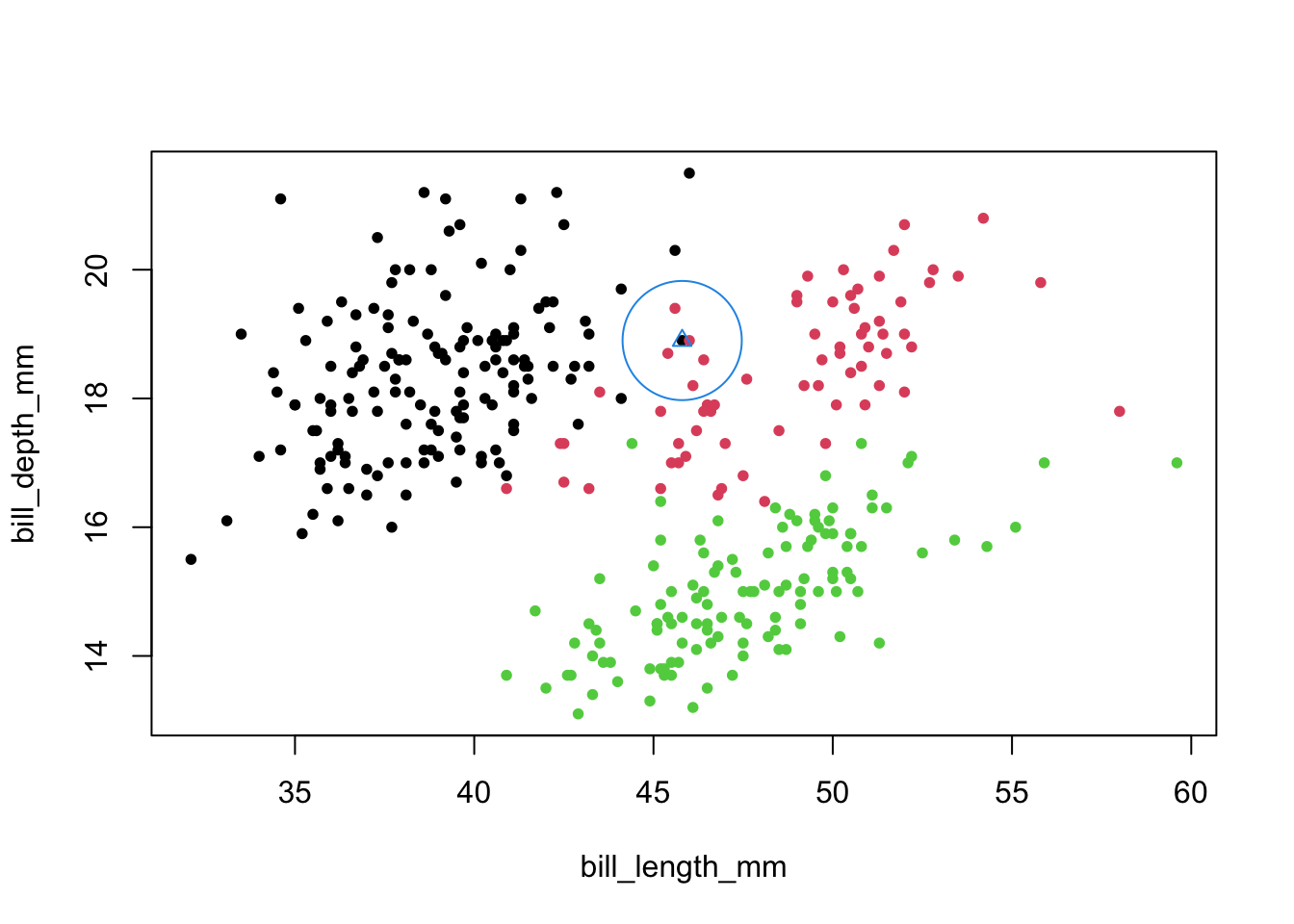

• We repeat this idea on the whole dataset, looking for the nearest neighbor and assigning the ‘new’ observation its group.
  • 1. The newly assigned label is the outer circle.

Code

newLabel <- class::knn.cv(penguins[,3:5],cl=penguins$species,k=1)
plot(penguins[,c(3,4)],col=penguins$species,pch=16,cex=.8)
points(penguins[,c(3,4)],pch=1,col=as.numeric(newLabel),cex=1.1)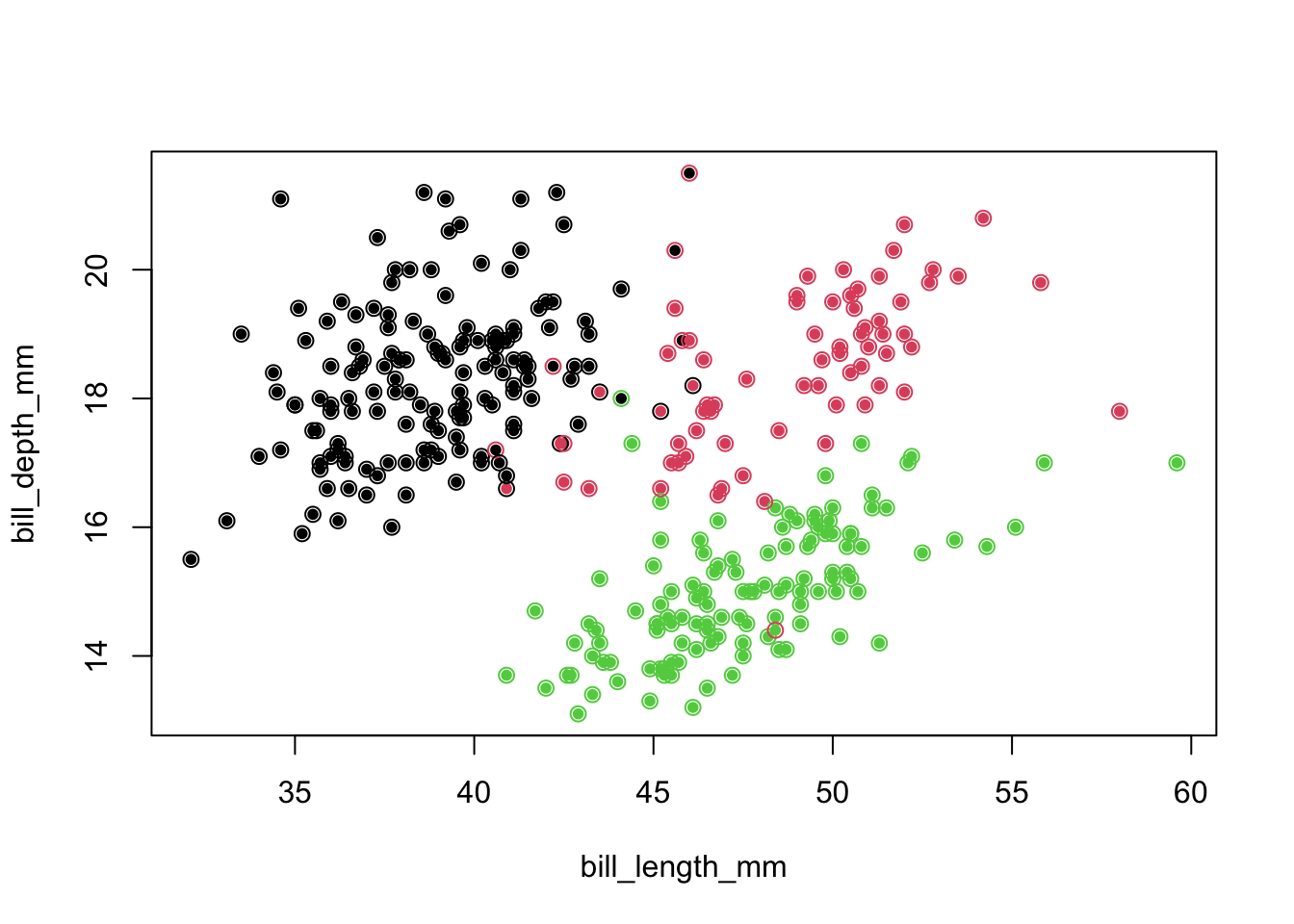

4.2.2 Confusion matrix

• We assess the ‘success’ of this approach to classification with a confusion matrix
  • This is a crosstab of truth to assigned labels
    • Note: we include all species, even though some are easy to classify, for completeness

Code

table(penguins$species,newLabel)

##            newLabel
##             Adelie Chinstrap Gentoo
##   Adelie       140         5      1
##   Chinstrap      5        63      0
##   Gentoo         0         1    118

• - We assigned twelve observations incorrectly.

4.2.3 Exercise 1

Question link

4.2.4 K-NN with \(K>1\)

• One can take the nearest neighbor idea a bit further, with \(K>1\)
  • We look at 5, or 7 nearest neighbors and take the majority vote for the label
    • The use of odd \(K\) tends to remove ‘ties’.
  • There are principled ways to choose \(K\) (e.g., cross-validation), which we discuss in subsequent handouts.

Code

newLabel5 <- knn.cv(penguins[,3:5],cl=penguins$species,k=5)
newLabel7 <- knn.cv(penguins[,3:5],cl=penguins$species,k=7)

Code

par(mfrow=c(1,2))
plot(penguins[,c(3,4)],col=penguins$species,pch=16,cex=.8,main='knn; k=5')
points(penguins[,c(3,4)],pch=1,col=as.numeric(newLabel5),cex=1.1)
plot(penguins[,c(3,4)],col=penguins$species,pch=16,cex=.8,main='knn; k=7')
points(penguins[,c(3,4)],pch=1,col=as.numeric(newLabel7),cex=1.1)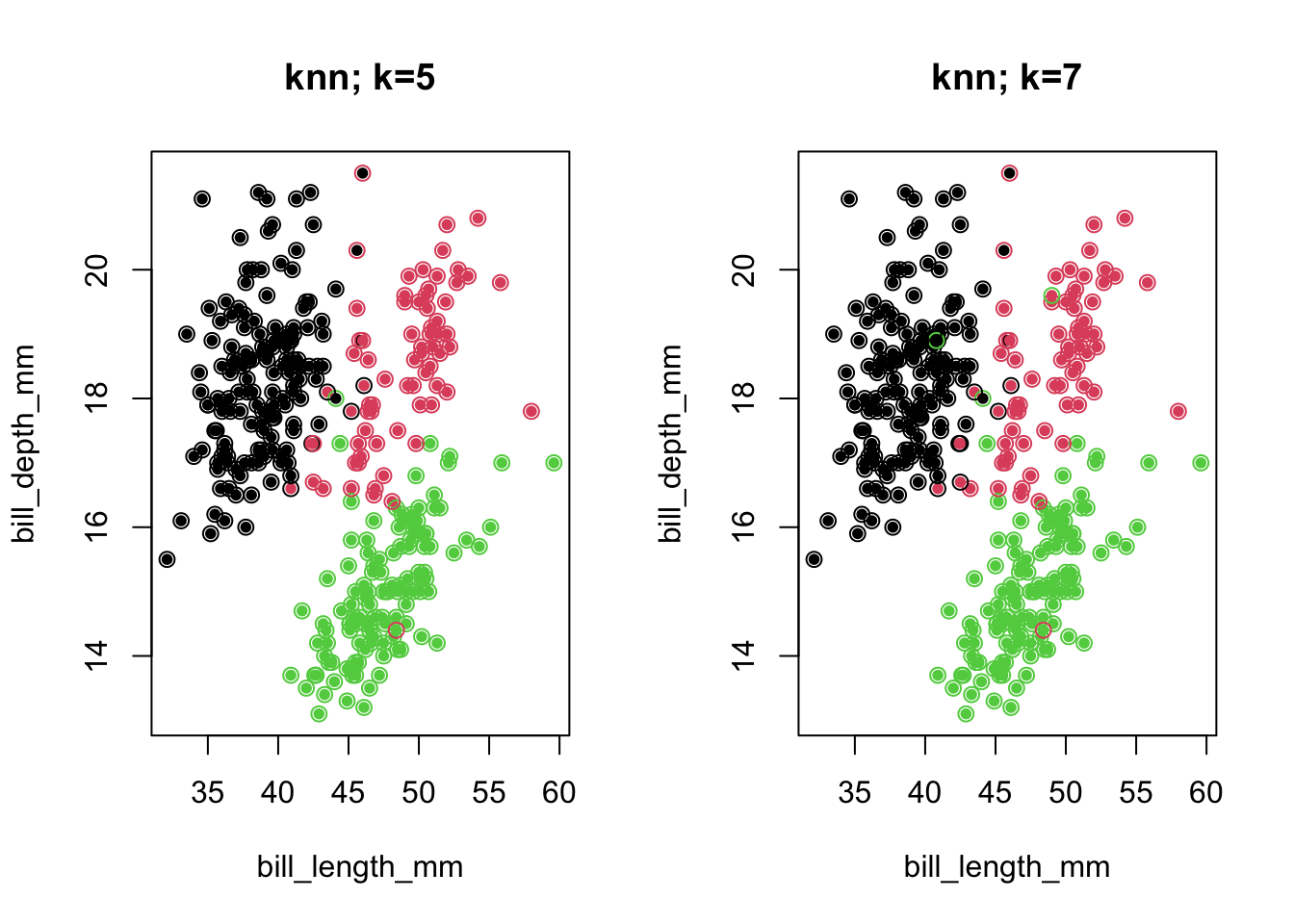

4.2.5 Confusion matrices

Code

table(penguins$species,newLabel5)

##            newLabel5
##             Adelie Chinstrap Gentoo
##   Adelie       142         3      1
##   Chinstrap      5        63      0
##   Gentoo         0         1    118

Code

table(penguins$species,newLabel7)

##            newLabel7
##             Adelie Chinstrap Gentoo
##   Adelie       141         3      2
##   Chinstrap      7        60      1
##   Gentoo         0         1    118

• Note that the overall success rate for 7 NN was worse than for 5 NN!
  • We merely did a better job with one species at the expense of another
• What might we have done differently in terms of the feature metric (knowing that nearest neighbor is defined by Euclidean distance)?
  • Perhaps standardize to prevent one feature from dominating?
    • You can try it: classification could be worse!
  • Would replacing features with a full set of PCs from a PCA have changed anything?
    • No, because (a full) PCA preserves distances.

4.3 Projection-based methods

• Many classification methods produce a lower-dimensional projection of the information contained in the feature set and use these new components to guide the assignment of observations to groups.
  • Logistic regression example: we try to predict sex from the five features given in the crabs data.
    • One logistic regression model is: \({\mathop{\rm logit}\nolimits} (\Pr (sex = Male)) = {b_0} + {b_1}{\rm{FL + }}{b_2}{\rm{RW + }}{b_3}{\rm{CL + }}{b_4}{\rm{CW + }}{b_5}{\rm{BD}}\)
    • We can use the inverse logit function \(\frac{{{e^{\hat y}}}}{{1 + {e^{\hat y}}}}\) to convert any predictions \(\hat{y}\), which will be in logit ‘units’ to probabilities.

4.3.1 Example

• After fitting this model, we get the following prediction equation, for the logit: \({\rm{\hat y = 24.6 - 6.2FL - 20.0RW + 9.7CL - 0.6CW + 2.9BD}}\)
  • \(\frac{{{e^{\hat y}}}}{{1 + {e^{\hat y}}}}\) will yield predicted probabilities in the range 0 to 1 as we require.
• These values for the 200 crabs are mostly near 0 or 1
  • In other words, they classify with a fair amount of certainty
  • But in the cases in which they are closer to 0.5, we have a good chance of misclassification.
    
  • Below is a plot that reveals correct and incorrect classification.
    • It is a ‘superimposed’ set of the classification probabilities.

Code

crabs <- read.dta("./Datasets/crabs.dta")
inv.logit <- function(x) exp(x)/(1+exp(x))
logit.fit1 = glm(I(sex=="Male")~FL+RW+CL+CW+BD,data=crabs,family='binomial')
probMale <- inv.logit(predict(logit.fit1))
df <- data.frame(sex=crabs$sex,prob=probMale)
gg <- ggplot(df, aes(x=prob, color=sex)) + geom_histogram(fill="white", alpha=0.5, position="identity") + labs(x="Prob(Male)",y='Frequency')

Code

gg

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.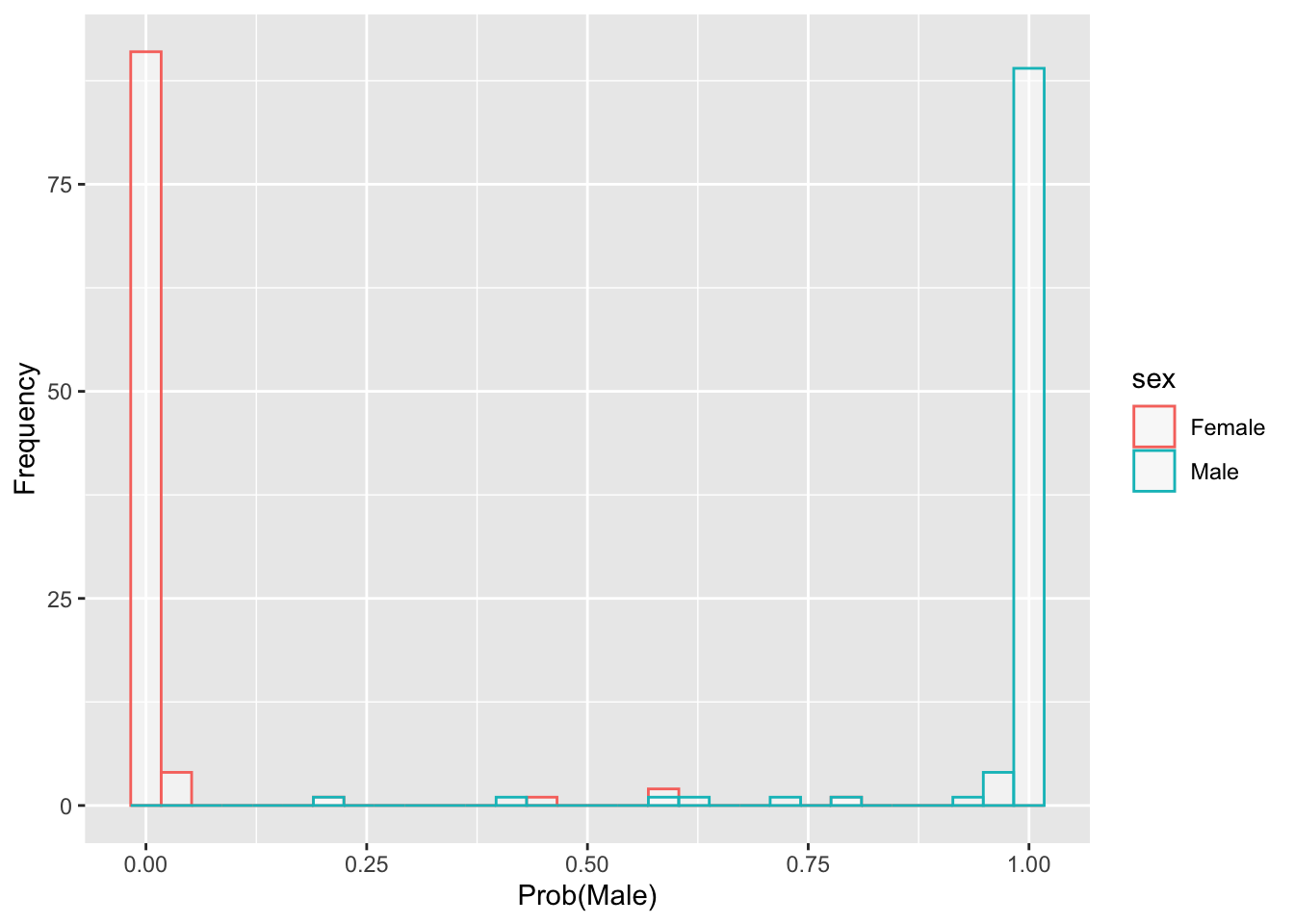

4.3.2 Exercise 2

Question link

• If we used a more complex functional form for the logistic model, we might predict even more accurately.
• Notice that this is a one-dimensional projection from five-dimensional feature set (FL, RW, CL, CW, BD) to a single value in the range (0,1).

4.4 Multinomial Logistic Regression example

• We try to predict species (Adelie, Chinstrap, Gentoo), from the three features given in the penguins data.
  • The multinomial logistic regression model (2 formulas) is:

\[ \begin{array}{l} \log (\Pr (species = Ch)/\Pr (species = Ad)) = \\ {b_{01}} + {b_{11}}{\rm{BL + }}{b_{21}}{\rm{BD + }}{b_{31}}{\rm{FL}} \\ \\ \log (\Pr (species = Ge)/\Pr (species = Ad)) = \\ {b_{02}} + {b_{12}}{\rm{BL + }}{b_{22}}{\rm{BD + }}{b_{32}}{\rm{FL}} \end{array} \]

• • We chose ‘Adelie’ as the reference group because it was listed first in alphabetical order.
• There can be challenges with the model fits
  • Logit models don’t handle perfect or near perfect prediction very well.
    
  • When one group is completely separated from the other, regression coefficients tend toward \(\pm\infty\) and standard errors are unreliable.
• One workaround in data of this type is to remove the Adelie from the analysis and do binary logistic regression.
  • You get about the same results, but it is more stable.
• Another approach involves Bayesian methods, which keep the estimates away from perfect prediction (see glmBayes, chapter 1).
• Nevertheless, we visualize the predictions from the multinomial logit models:

4.4.1 MNlogit example

Code

multinom.fit <- nnet::multinom(species~bill_length_mm+bill_depth_mm+ flipper_length_mm,data=penguins)

## # weights:  15 (8 variable)
## initial  value 365.837892 
## iter  10 value 13.577492
## iter  20 value 8.807802
## iter  30 value 7.830394
## iter  40 value 7.645109
## iter  50 value 7.639216
## final  value 7.637947 
## converged

Code

preds <- predict(multinom.fit,type='probs')
df <- reshape2::melt(data.frame(preds,TrueSpecies=penguins$species))

## Using TrueSpecies as id variables

Code

gg<-ggplot(df, aes(x=value, color=TrueSpecies)) + geom_histogram(fill="white", alpha=0.5, position="dodge") + labs(x='Prob(facet species)',y='Frequency') + facet_grid(variable~"Facet")

Code

gg

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.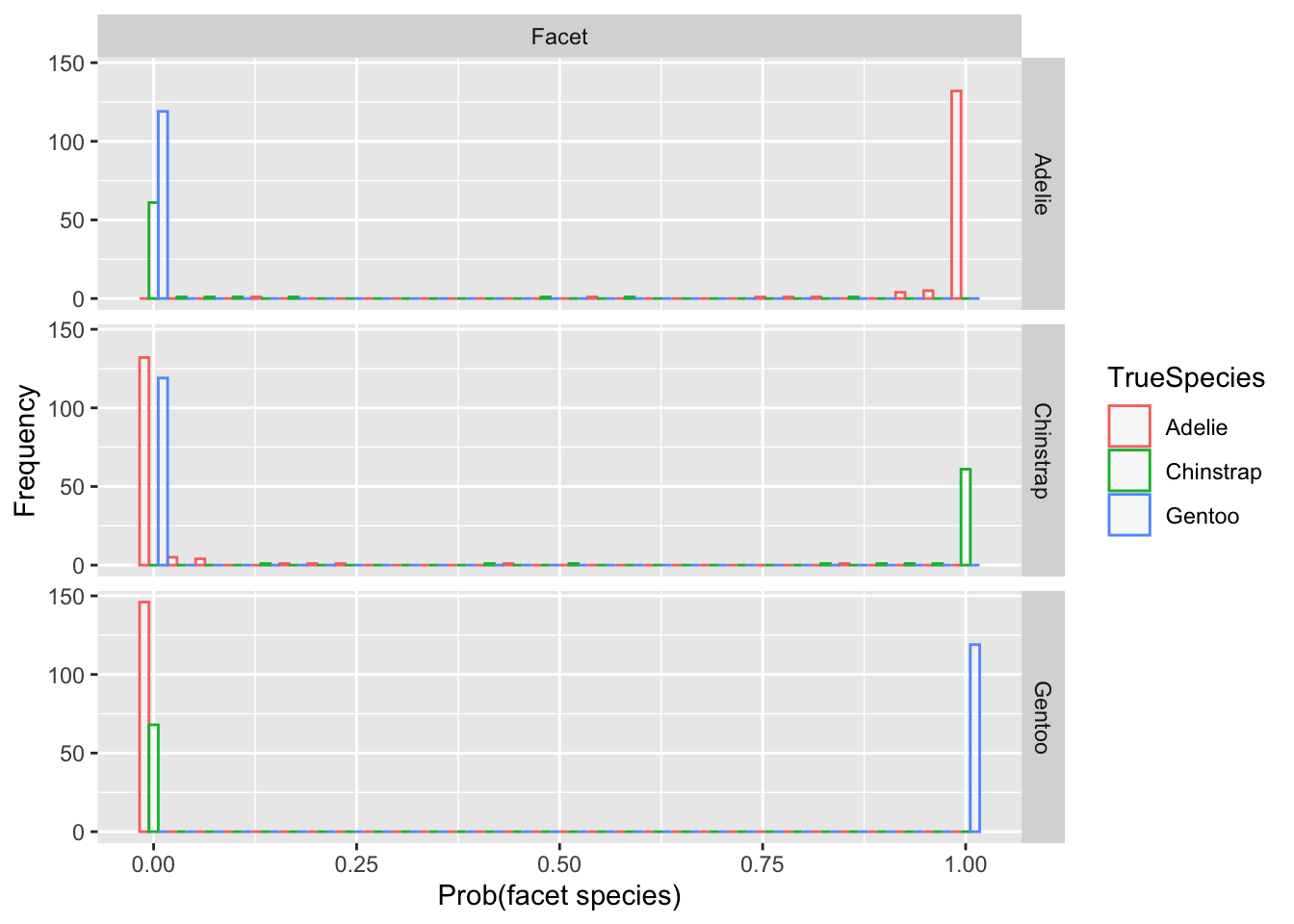

• Note how the Pr(Facet) is near 1 for nearly all blue points in the Gentoo facet.
  • Similarly for the other facet rows, which are predictions for the probability of the species labeled on that row.
• There are only a few points (red or green) for which there is some ambiguity.

4.5 Discriminant function as a projection

• Above, we conceptualized logistic regression as a projection onto the probability space 0-1.
  
• When we are only discriminating between two groups, the closer the projection is to 1, the more likely the observation belongs to the non-reference (‘event’) group.
• We can write down a formal approach to projecting so as to maximize discriminatory power
  • Let \(Z = {a_1}{X_1} + {a_2}{X_2} + \ldots + {a_p}{X_p}\) assuming \(p\) predictor or feature variables.
  • We want coefficients \({a_1},{a_2}, \ldots ,{a_p}\) such that the distributions of \(Z\) for each group are ‘maximally’ separated.
• One of the most direct ways to do this is to come up with a projection \(Z\), then run an ANOVA on \(Z\) using the known groupings.
  • Then try different projections until you find coefficients that maximize the F-statistic in the ANOVA.

4.5.1 Example: penguins data

• Using only two features, bill length and bill depth, we will try three different projections
  • These \(Z_1\), \(Z_2\), \(Z_3\) are to be ‘tested’:

\[ \begin{array}{l} Z_1 = +0.4 BL - 1.0 BD \\ Z_2 = +0.3 BL - 0.9 BD \\ Z_3 = +0.352 BL - 0.904 BD \end{array} \]

• Which of these three is best?
  • Here are densities resulting from the projections:

Code

z1 = 0.4*penguins$bill_length_mm - 1.0*penguins$bill_depth_mm 
z2 = 0.3*penguins$bill_length_mm - 0.9*penguins$bill_depth_mm 
z3 = 0.352*penguins$bill_length_mm  - 0.904*penguins$bill_depth_mm 

Code

plot(density(c(z1,z2,z3)),type='n',ylim=c(0,.5),xlab='Z1',main='Density of Projection')
by(penguins,penguins$species,function(x,a1,a2) lines(density(a1*x$bill_length_mm+a2*x$bill_depth_mm),col=x$species),a1=0.4,a2=-1.0)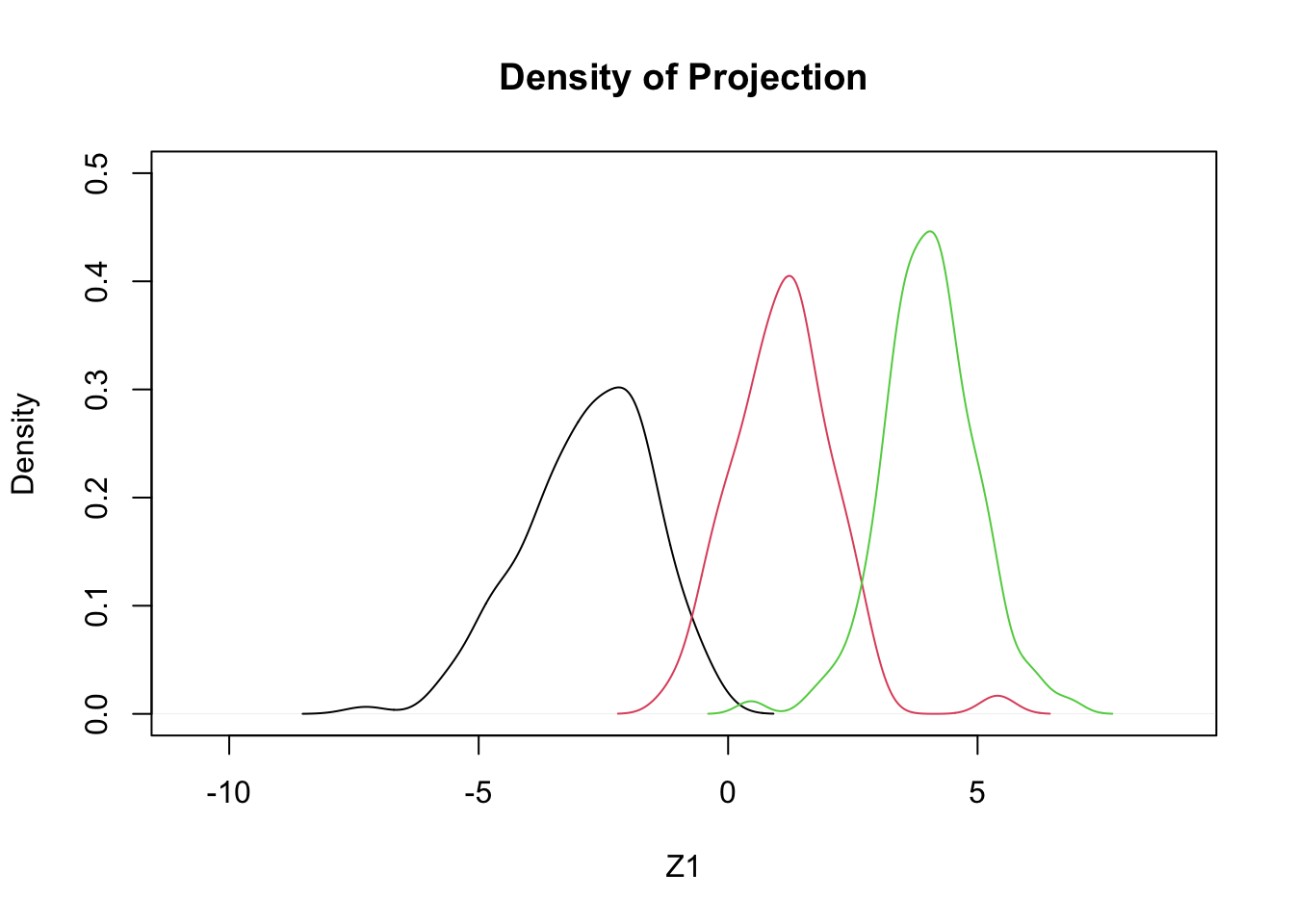

## penguins$species: Adelie
## NULL
## ------------------------------------------------------------ 
## penguins$species: Chinstrap
## NULL
## ------------------------------------------------------------ 
## penguins$species: Gentoo
## NULL

Code

plot(density(c(z1,z2,z3)),type='n',ylim=c(0,.5),xlab='Z2',main='Density of Projection')
by(penguins,penguins$species,function(x,a1,a2) lines(density(a1*x$bill_length_mm+a2*x$bill_depth_mm),col=x$species),a1=0.3,a2=-0.9)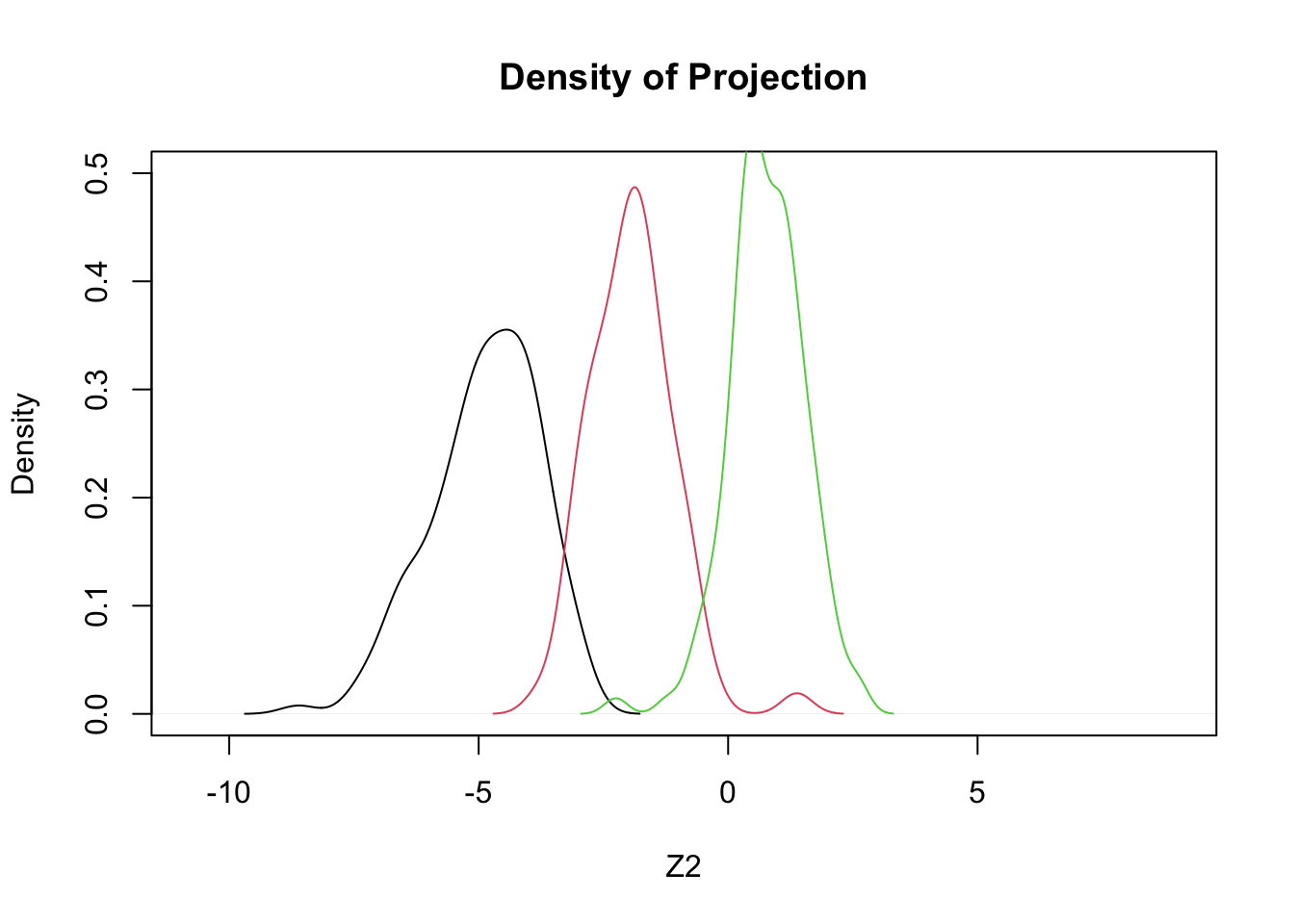

## penguins$species: Adelie
## NULL
## ------------------------------------------------------------ 
## penguins$species: Chinstrap
## NULL
## ------------------------------------------------------------ 
## penguins$species: Gentoo
## NULL

Code

plot(density(c(z1,z2,z3)),type='n',ylim=c(0,.5),xlab='Z3',main='Density of Projection')
by(penguins,penguins$species,function(x,a1,a2) lines(density(a1*x$bill_length_mm+a2*x$bill_depth_mm),col=x$species),a1=0.352,a2=-0.904)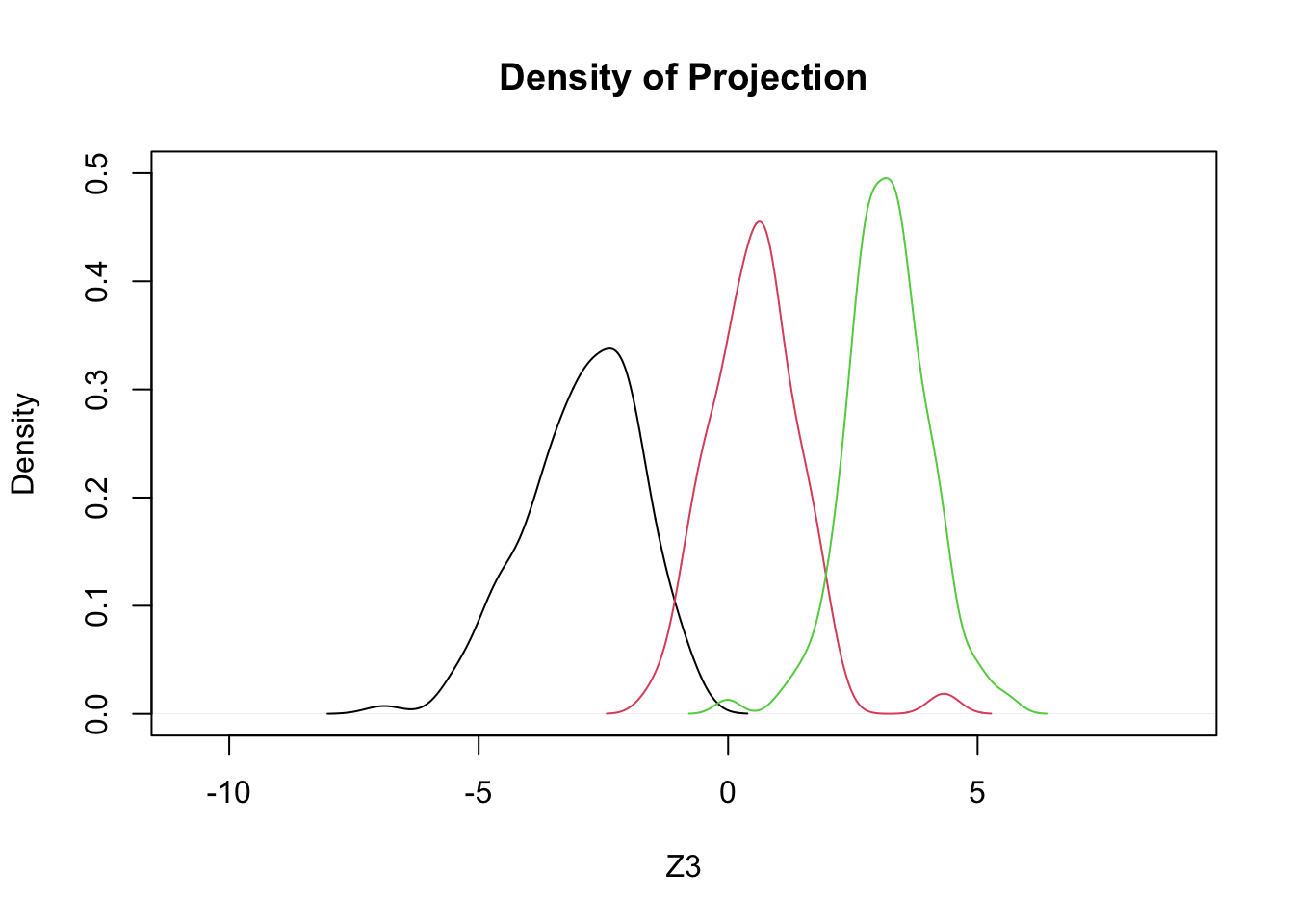

## penguins$species: Adelie
## NULL
## ------------------------------------------------------------ 
## penguins$species: Chinstrap
## NULL
## ------------------------------------------------------------ 
## penguins$species: Gentoo
## NULL

4.5.2 Exercise 3

Question link

• It’s hard to see much difference in the above plots, but clearly the last two indicate better separation.

4.6 Comparison via ANOVA

Code

summary(aov(cbind(z1,z2,z3)~penguins$species))

##  Response z1 :
##                   Df  Sum Sq Mean Sq F value    Pr(>F)    
## penguins$species   2 3114.37 1557.19  1236.3 < 2.2e-16 ***
## Residuals        330  415.64    1.26                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##  Response z2 :
##                   Df  Sum Sq Mean Sq F value    Pr(>F)    
## penguins$species   2 2093.48 1046.74  1214.7 < 2.2e-16 ***
## Residuals        330  284.37    0.86                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##  Response z3 :
##                   Df  Sum Sq Mean Sq F value    Pr(>F)    
## penguins$species   2 2472.73  1236.4  1236.9 < 2.2e-16 ***
## Residuals        330  329.85     1.0                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Suggests that \(Z_3\) is (barely) the best of these 3}.

4.6.1 Notes

• The point in choosing the coefficients that maximize the F-value is that this maximizes the ratio of between groups to within groups variation.
  • This is maximal separation as compared to the homogeneity within groups
  • Recall one definition of C(g)=(\(\Sigma\) msb)/(\(\Sigma\) msw).
    • In the projection approach described above, we are trying to find a linear combination of our features that maximizes msb/msw.
      
    • The summation is removed, because we have projected down to a single value through the transformation.

4.6.2 Geometric View: The two-group case

• Z is the ‘projection’ - a line containing the linear combination of features that maximally separates the two groups.
  
• Line L is defined by the two points of intersection of the two ellipses and represents a boundary between the two groups
  • This is the ‘cutoff’ point to the left of which we would predict membership in one group, and to the right the other.

4.6.3 Exercise 4

Question link

4.7 Discriminant analysis (details)

• Recall the definition of B and W:

\[ B=\sum\limits_{m=1}^{g}{n_m}(\bar{\mathbf{x}}_m - \bar{\mathbf{x}})(\bar{\mathbf{x}}_m-\bar{\mathbf{x}})' \] \[ W=\sum\limits_{m=1}^{g}\sum\limits_{l=1}^{n_m}(\mathbf{x}_{ml}-\bar{\mathbf{x}}_m)(\mathbf{x}_{ml}-\bar{\mathbf{x}}_m)' \] and let \({\bf{a}} = ({a_1},{a_2}, \ldots ,{a_p})'\),

• \(B\) and \(W\) are \(p\times p\) matrices, and as such they can be pre- and post-multiplied by a vector of length, \(1\times p\) and \(p\times 1\), respectively.
• It turns out that finding the vector a that maximizes the discriminant criterion \(\lambda = \frac{{{\bf{a'Ba}}}}{{{\bf{a'Wa}}}}\) (under some assumptions) provides us with the optimal weights to project our feature set into one dimension (\(Z = {a_1}{X_1} + {a_2}{X_2} + \ldots + {a_p}{X_p}\)) with maximal separation.
  • Side note: the linear combination defining \(Z\) can be written \(Z = {\bf{a'X}}\), where \({\bf{X}} = ({X_1},{X_2}, \ldots ,{X_p})\).
    • This is a new coordinate space, analogous to PCA-space.

4.7.1 Notes

• There are slightly different definitions of the discriminant criterion, involving sample vs. population divisors for the degrees of freedom (i.e., n vs. n-1).
  • We will ignore this detail.
• With only two groups, there can be only one linear composite (projection) and one discriminate criterion.
• With more than two groups, however, there will be more than one linear composite and, hence, more than one ratio \(\lambda\).
  • In particular, the number of linear composites and associated ratios, \(\lambda\), equals the number of predictor variables \(p\), or the number of groups minus one \((m-1)\), whichever is smaller.
• To identify a set of projections, they are generated sequentially, so that the second one is constrained to be uncorrelated with the first, and so forth.
  • Just as in a principal components analysis.
• With m=3 and p=5, for example, there will be two distinct linear composites and therefore two corresponding ratios, \(\lambda_1\) and \(\lambda_2\).
  • The amount each linear composite will separate the groups is given in decreasing order by its respective \(\lambda\) (i.e., \(\lambda_1 > \lambda_2\)).
    • So the first linear composite (or dimension) creates the greatest separation among the groups and the next linear composite (or dimension) creates the next greatest separation.

4.7.2 Discriminant function as classifier

• As suggested by the geometric representation above, projection to a line allows us to choose a cut point (a value on the line), location above or below which determines group membership.
• This can be extended to more than two groups using the following procedure (we will assume three groups for the discussion):

1. Form the projections: \[{Z_1} = {a_{11}}{X_1} + {a_{21}}{X_2} + \ldots + {a_{p1}}{X_p}\] and \[{Z_2} = {a_{12}}{X_1} + {a_{22}}{X_2} + \ldots + {a_{p2}}{X_p}\]
   • These are determined by maximizing \(\lambda = \frac{{{\bf{a'Ba}}}}{{{\bf{a'Wa}}}}\) sequentially, under the constraint that \(Z_1\) and \(Z_2\) are uncorrelated.
2. Compute the means of these projections, \(Z_1\), \(Z_2\) within each known group, let us label the mean pair for the \(g^{th}\) group \(({\bar Z_{1g}},{\bar Z_{2g}})\).
   • These are centroids of the groups in the projection space.
3. For any observation, \[({X_1},{X_2}, \ldots ,{X_p})\] compute \(Z_1\) and \(Z_2\) and then compute the squared Euclidean distance between \(Z_1\) and \(Z_2\) from each of the group means contained in \(({\bar Z_{1g}},{\bar Z_{2g}})\); that is, \({d_g} = {({Z_1} - {\bar Z_{1g}})^2} + {({Z_2} - {\bar Z_{2g}})^2}\).
   • With \(m\) groups, there will be \(m\) distances, \[({d_1},{d_2}, \ldots ,{d_m})\].
4. Assign the observation to the group to which it is closest.

4.7.3 Example I: penguins data – discriminate between Chinstrap and Gentoo

• Use R’s lda function in the MASS library.
• We subset, removing the Adelie species using the subset option (subset works when the data are a dataframe, but it can be finicky).
• We show the basic result, along with a classification table.
• Properly managed, the classification table will not suffer from label switching - why?

Code

penguins.lda <-MASS::lda(species ~bill_length_mm+bill_depth_mm+flipper_length_mm, data=penguins,na.action="na.omit", CV=FALSE,subset=species!="Adelie") 
print(penguins.lda)

## Call:
## lda(species ~ bill_length_mm + bill_depth_mm + flipper_length_mm, 
##     data = penguins, CV = FALSE, subset = species != "Adelie", 
##     na.action = "na.omit")
## 
## Prior probabilities of groups:
## Chinstrap    Gentoo 
## 0.3636364 0.6363636 
## 
## Group means:
##           bill_length_mm bill_depth_mm flipper_length_mm
## Chinstrap       48.83382      18.42059          195.8235
## Gentoo          47.56807      14.99664          217.2353
## 
## Coefficients of linear discriminants:
##                           LD1
## bill_length_mm     0.02052193
## bill_depth_mm     -1.18982389
## flipper_length_mm  0.17401721

Code

xtabs(~predict(penguins.lda)$class+penguins$species[penguins$species!="Adelie"])

##                            penguins$species[penguins$species != "Adelie"]
## predict(penguins.lda)$class Adelie Chinstrap Gentoo
##                   Adelie         0         0      0
##                   Chinstrap      0        68      0
##                   Gentoo         0         0    119

4.7.4 Exercise 5

Question link

4.7.5 Notes

• So \(Z=-0.02BL-1.19BD+0.17FL\) (it’s called LD1 by the function lda).
  • R computes these scores for you (and shifts the mean to 0 by subtracting a constant, in this case 18.11 - derived independently).
• Next are the densities of the scores, colored by group.
  • NOTE: they are WELL-SEPARATED!

Code

subdat <- subset(penguins,species!="Adelie")
penguins.scores <- predict(penguins.lda)$x
plot(density(penguins.scores,bw=.5),col=8,ylim=c(0,.24))
dns.s <- density(penguins.scores[subdat$species=="Chinstrap"])
dns.c <- density(penguins.scores[subdat$species=="Gentoo"])
lines(dns.s$x,dns.s$y/2,col=2) #rescaling to sum to one, once combined
lines(dns.c$x,dns.c$y/2,col=3) #rescaling to sum to one, once combined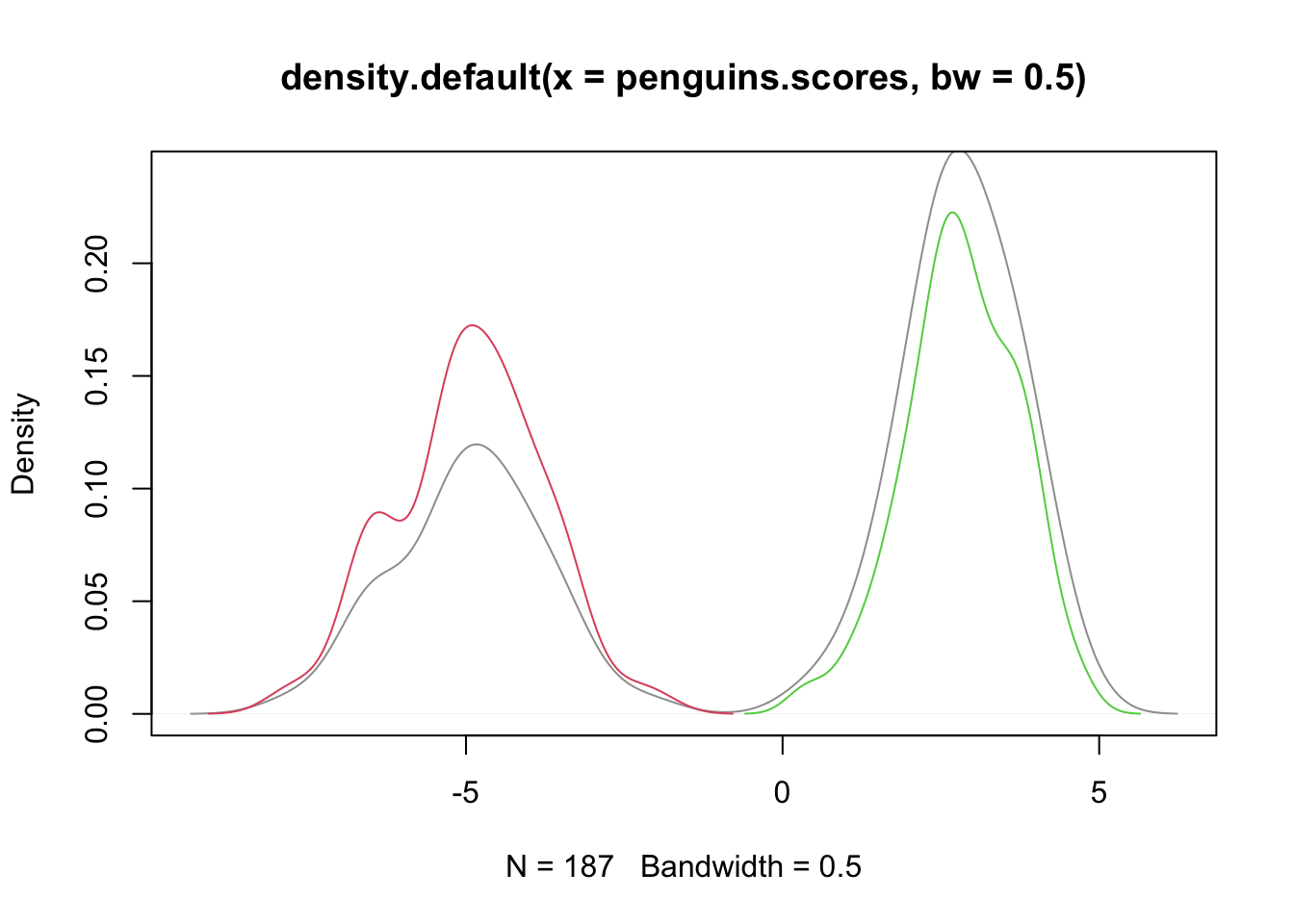

4.7.6 Assumptions

• These methods do require some assumptions (listed below), and some are testable.
  1. The observations are independent of each other.
  2. The observations on the continuous predictor (feature) variables follow a multivariate normal distribution in each group.
     • There are several tests and diagnostics for (univariate) normality, e.g., Shapiro-Wilks
  3. The population covariance matrices for the p continuous variables in each group are equal.
• More About Assumption (3):
  • In the two-group case with one continuous measure, assumption (3) is analogous to the t-test’s homogeneity of variance assumption.
    • With more than one continuous variable, not only are there variances to consider, but also covariances between all pairs of the \(p\) variables.
    • A test for the equality of two or more covariance matrices that is based on the familiar F statistic is due to Box (1949), and is referred to as Box’s M test.
      
    • It tends to be a bit overly sensitive (rejects too often).
  • Failure to meet assumption (3) is common (and there are some alternative approaches in this case), but one implication is that ‘model selection’ techniques will be less reliable.
    
  • This matters because if we are building a discriminating tool step-wise (add one projection after the other, if justified), we will rely on tests of significance that require assumption (3).
    
  • For this discussion, we do not pursue step-wise approaches.
• We might first ask, ‘Is there evidence of separate groups?’ (otherwise, why proceed with an LDA?)
  • Wilks’ Lambda is one test of significance for the equality of group centroids.
  • Wilks’ lambda, \(\Lambda\), is a general statistic for testing the significance of K group centroids (represented by multivariate \(\mu\)) differences. The hypotheses are:

\[\begin{array}{l} {H_0}:\underline {{\mu _1}} = \underline {{\mu _2}} = \underline {{\mu _3}} = ... = \underline {{\mu _K}} \\ {H_1}:not\;\;{H_0} \end{array}\]

• The statistic is defined as the ratio of two determinants (W, B, T defined as before):

\[ \Lambda = \frac{{\left| W \right|}}{{\left| {\rm{T}} \right|}} = \frac{{\left| W \right|}}{{\left| {B + W} \right|}} \]

• The smaller \(\Lambda\), the greater the between-group variability relative to the within-group variability, and the greater the separation between groups.
  • When K=2 or 3, or p=1 or 2, a function of \(\Lambda\) is distributed exactly as F.
  • In all other cases, the distribution of \(\Lambda\) under H0 must be approximated.

4.8 Example: penguins data - all three species

Code

penguins.lda3 <-MASS::lda(species ~bill_length_mm+bill_depth_mm+flipper_length_mm, data=penguins,na.action="na.omit", CV=FALSE) 
penguins.lda3

## Call:
## lda(species ~ bill_length_mm + bill_depth_mm + flipper_length_mm, 
##     data = penguins, CV = FALSE, na.action = "na.omit")
## 
## Prior probabilities of groups:
##    Adelie Chinstrap    Gentoo 
## 0.4384384 0.2042042 0.3573574 
## 
## Group means:
##           bill_length_mm bill_depth_mm flipper_length_mm
## Adelie          38.82397      18.34726          190.1027
## Chinstrap       48.83382      18.42059          195.8235
## Gentoo          47.56807      14.99664          217.2353
## 
## Coefficients of linear discriminants:
##                          LD1         LD2
## bill_length_mm     0.1700022 -0.37676677
## bill_depth_mm     -0.9373808 -0.04268019
## flipper_length_mm  0.1191061  0.10195863
## 
## Proportion of trace:
##    LD1    LD2 
## 0.8915 0.1085

4.8.1 Exercise 6

Question link

4.8.2 Notes

• This yields two projections, named LD1 and LD2, above.
  • We called them \(Z_1\) and \(Z_2\) in our derivation.
• The ‘proportion of trace’ given represents the extent to which each projection explains the differences between groups.
  • Analogous to eigenvalues in PCA.
• Most (99%) of the discrimination occurs in the first function.
  • The LD1 coefficients suggest that the contrast between bill depth and the remaining two is of importance (look at signs).
  • If we wish to compute the \(\lambda = \frac{{{\bf{a'Ba}}}}{{{\bf{a'Wa}}}}\) associated with each projection, we need the \(B\) and \(W\) matrices. - These are a by-product of running a MANOVA on the predictor set over the given groups.
    - Since we need to do this to compute Wilk’s Lambda (a different Lambda), we do this now.

Code

manova.fit <- manova(as.matrix(penguins[,3:5])~penguins$species)
summary(manova.fit,test="Wilks")

##                   Df    Wilks approx F num Df den Df    Pr(>F)    
## penguins$species   2 0.029328    529.1      6    656 < 2.2e-16 ***
## Residuals        330                                              
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Code

#lambdas associated with each LD projection:
B<-summary(manova.fit)$SS[[1]]
W<-summary(manova.fit)$SS[[2]]
B.xprod <- t(penguins.lda3$scaling)%*%B%*%penguins.lda3$scaling
W.xprod <- t(penguins.lda3$scaling)%*%W%*%penguins.lda3$scaling
lambdas <- diag(B.xprod/W.xprod)
lambdas

##       LD1       LD2 
## 12.512768  1.523362

• • Wilks’ Lambda, \(\lambda\), is highly significant
    • The \(\lambda\)s associated with each projection are 12.5 and 1.5S.

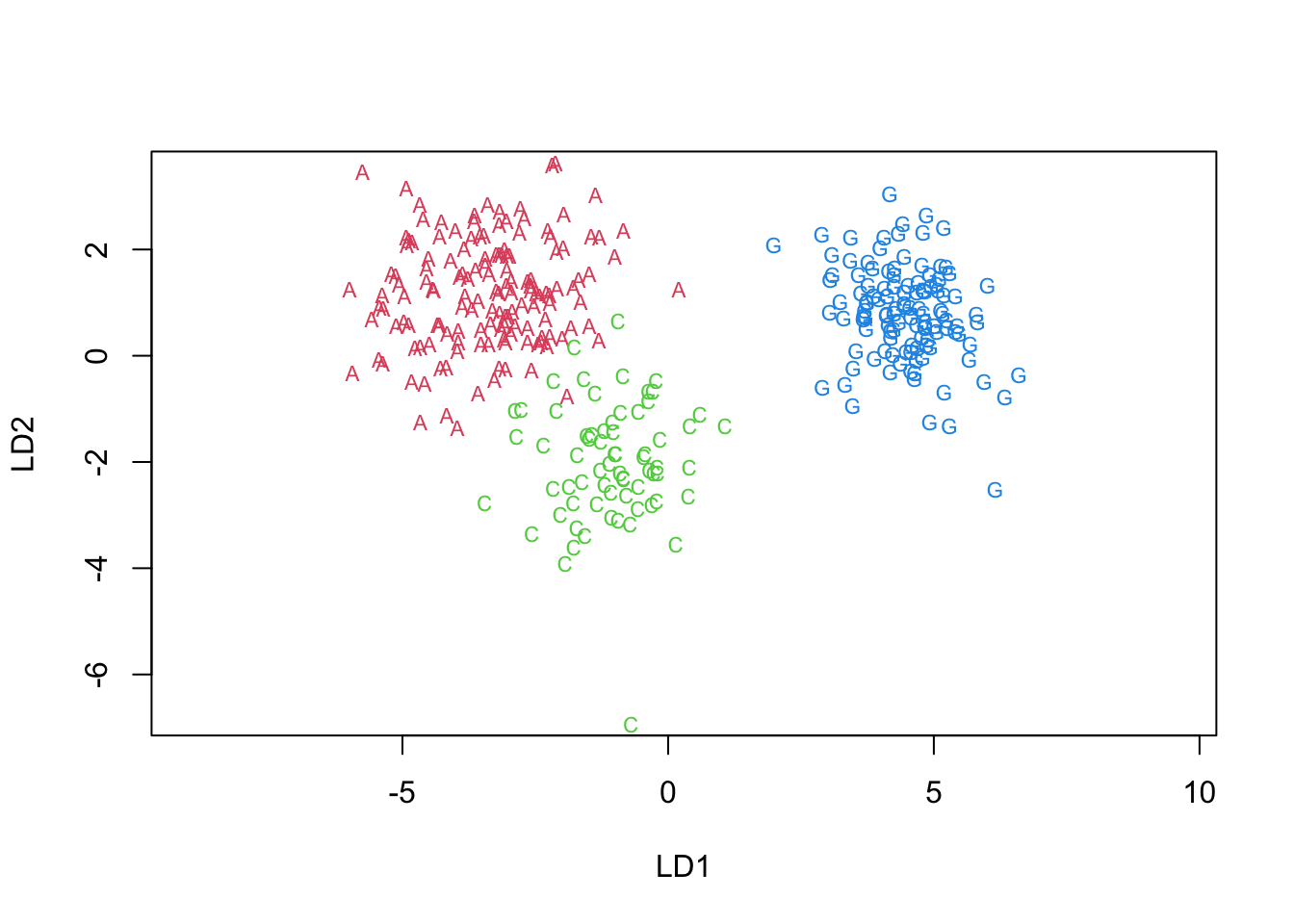
4.8.3 Examine LD1xLD2 space

• We can show the densities of the scores (projections) for each species in 1 and 2 dimensions.
  • We use some manual and some built-in approaches to plotting decision boundaries
• First, we show the LD1 projection, then LD2 and lastly the LD1xLD2 coordinate plane.

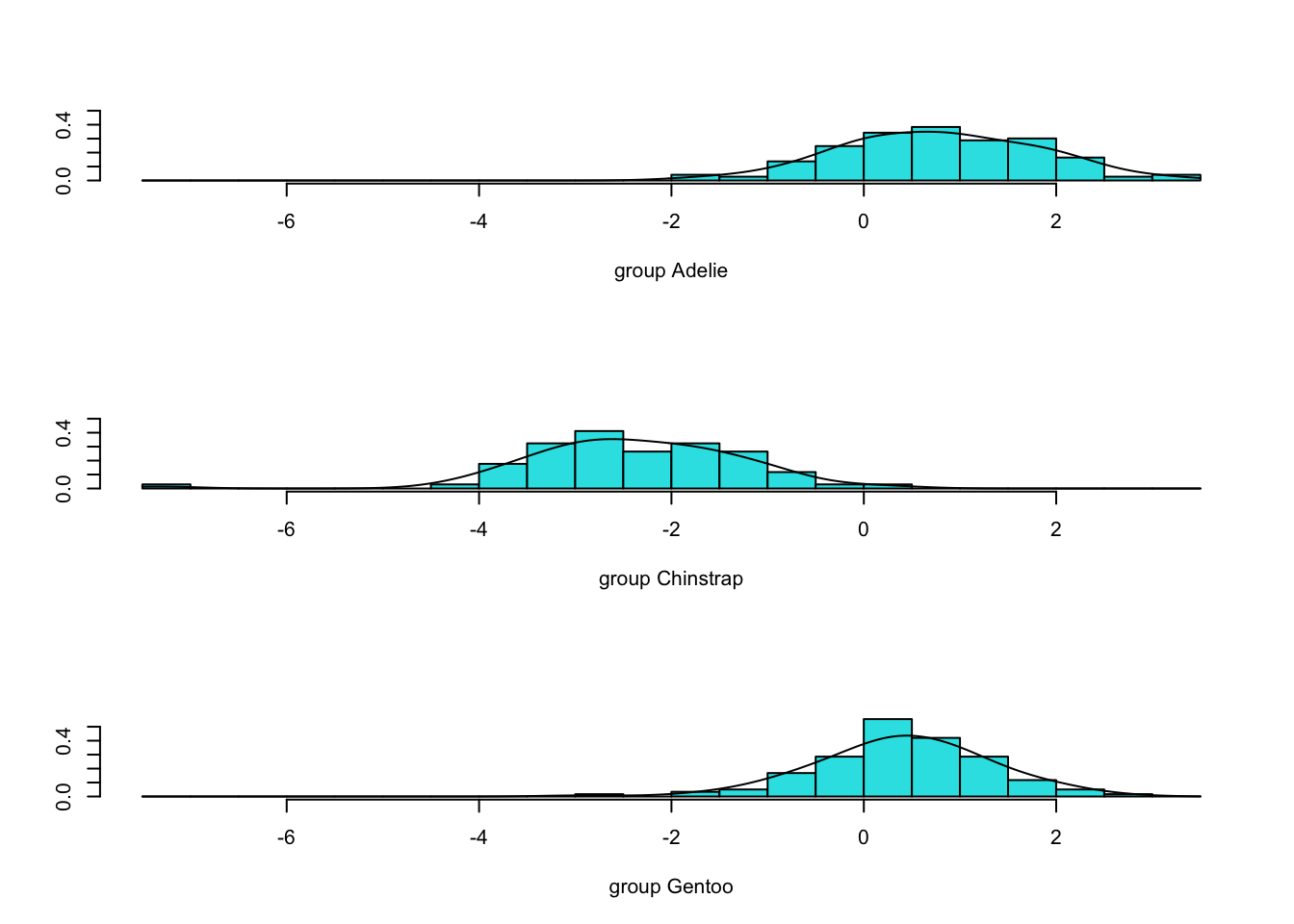
4.8.4 LD1

Code

#the Z1 & Z2 projections are computed and saved with this command.
penguins.LDs <- predict(penguins.lda3)$x
#show 1-D discrimination (LD1):
plot(penguins.lda3,dimen=1)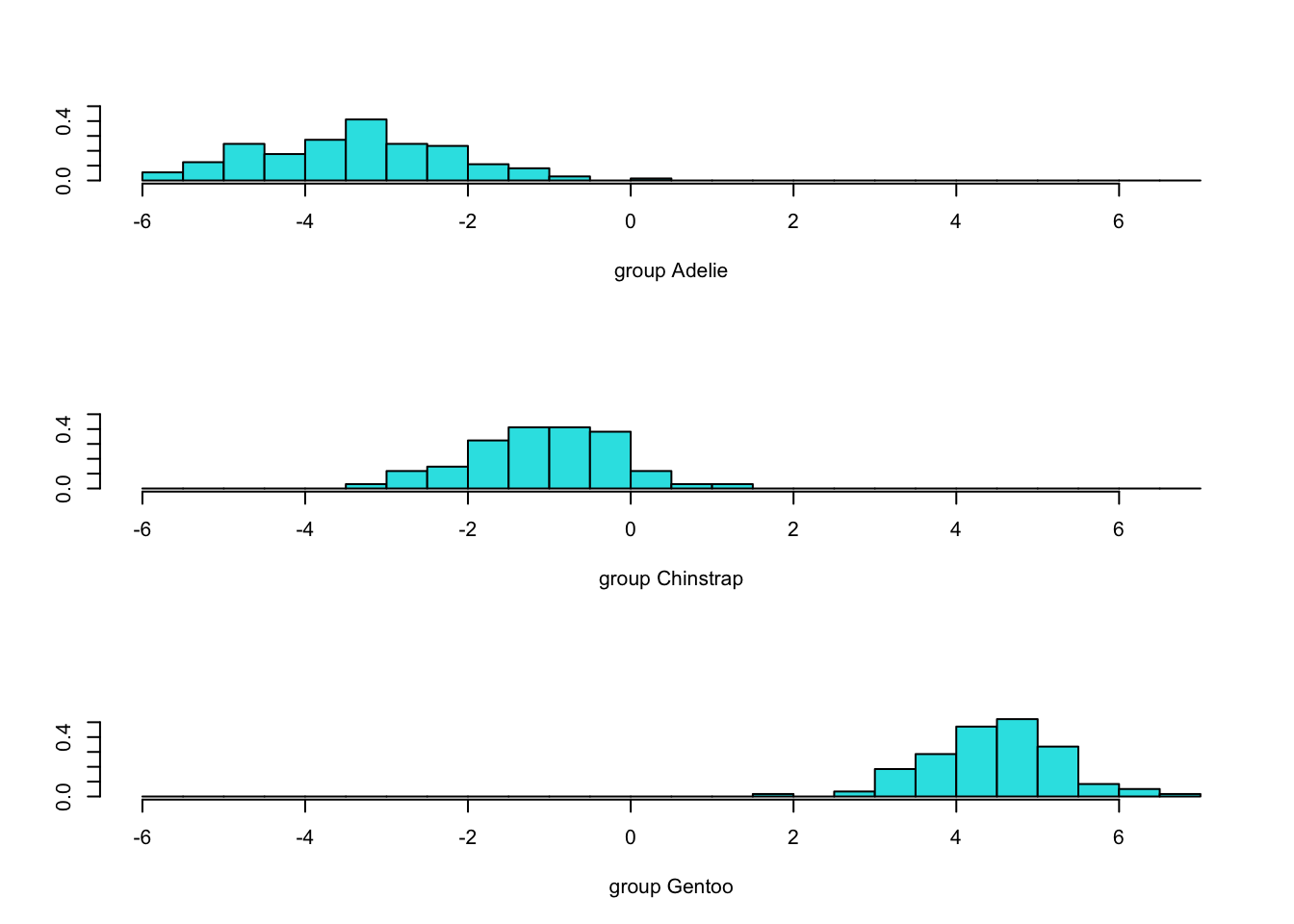

4.8.5 Exercise 7

Question link

4.8.6 LD2

Code

#show 1-D discrimination (LD2):
ldahist(penguins.LDs[,2],penguins$species,type='both')

4.8.7 LD1 x LD2

• Note: LD1 clearly sets Gentoo apart; LD2 may have some discrimination between Chinstrap and the other two, but the 2-D discrimination (next) is more revealing and separating.

Code

plot(penguins.lda3,abbrev=T,col=(2:4)[penguins$species])

4.9 Territorial map

• A territorial map is used to delineate which portions of the 2-D discriminant function space ‘belongs’ to which group.
  • Really, it’s a map of which values are predicted to be in which group.
  • The group centroids are given as reference.
  • The default functions to produce these maps do so for the ORIGINAL feature set
    • What would happen if you tried to use those features DIRECTLY and used a line as boundary between pairs of groups?
      
  • With some custom R coding, we can also produce this map for the LD1 and LD2 space, so we give these after the default map.

Code

klaR::partimat(species ~bill_length_mm+bill_depth_mm+flipper_length_mm, data=penguins,method="lda",gs=c("a","c","g")[penguins$species])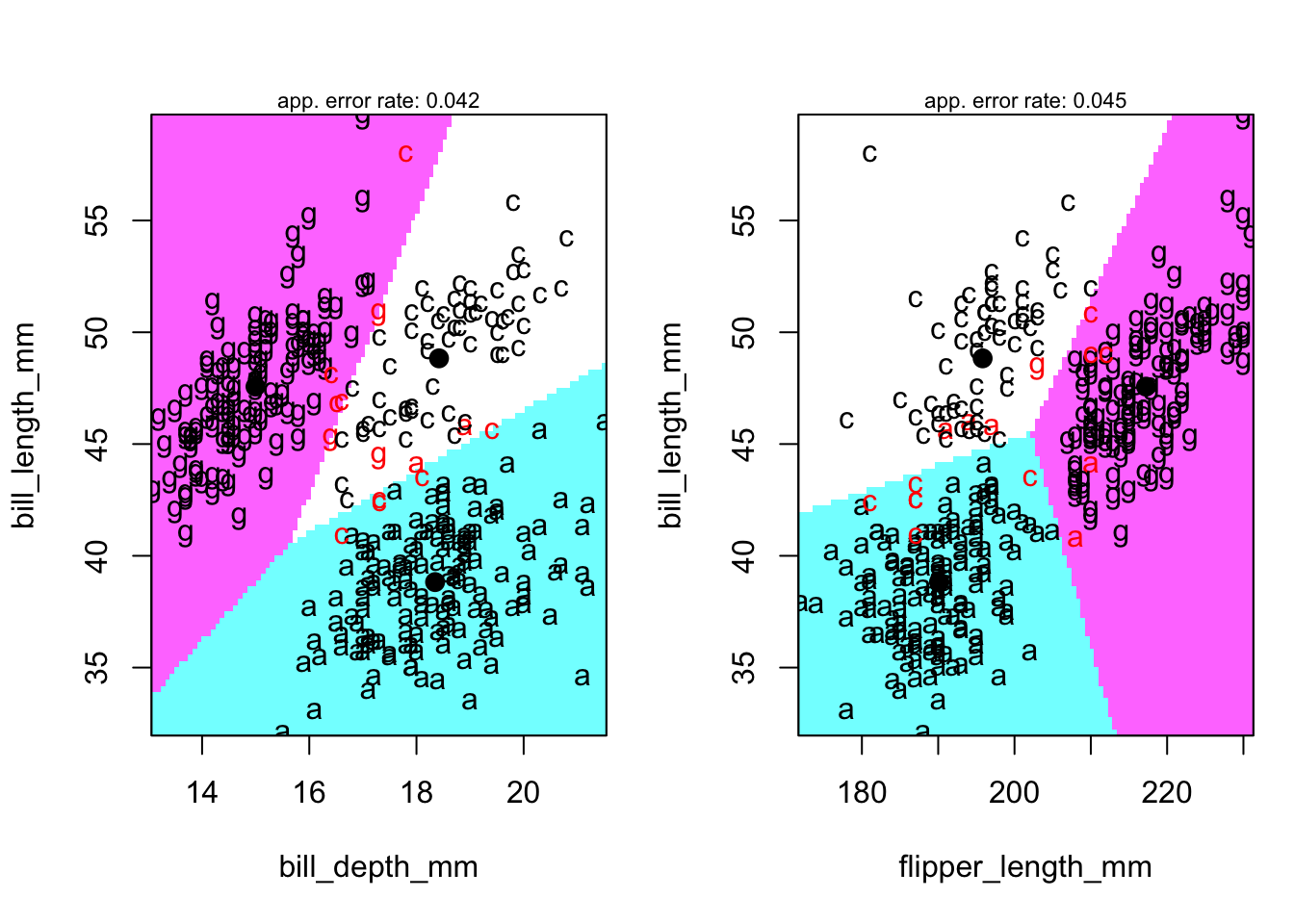

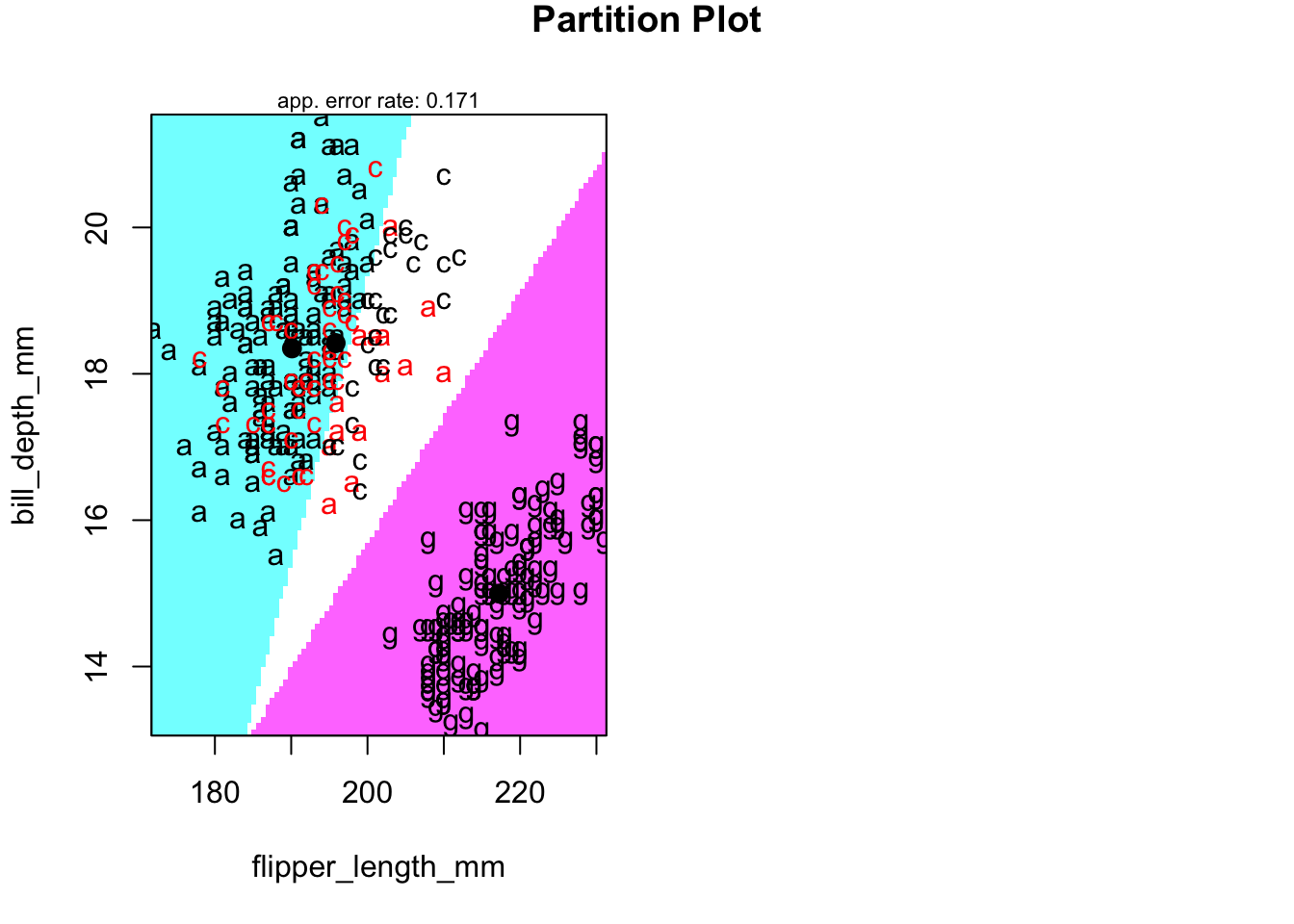
4.9.1 Territorial map in LD-space

Code

newpenguins <- data.frame(cbind(penguins,predict(penguins.lda3)$x))
klaR::partimat(species ~LD2+LD1, data=newpenguins,method="lda",gs=c("a","c","g")[penguins$species])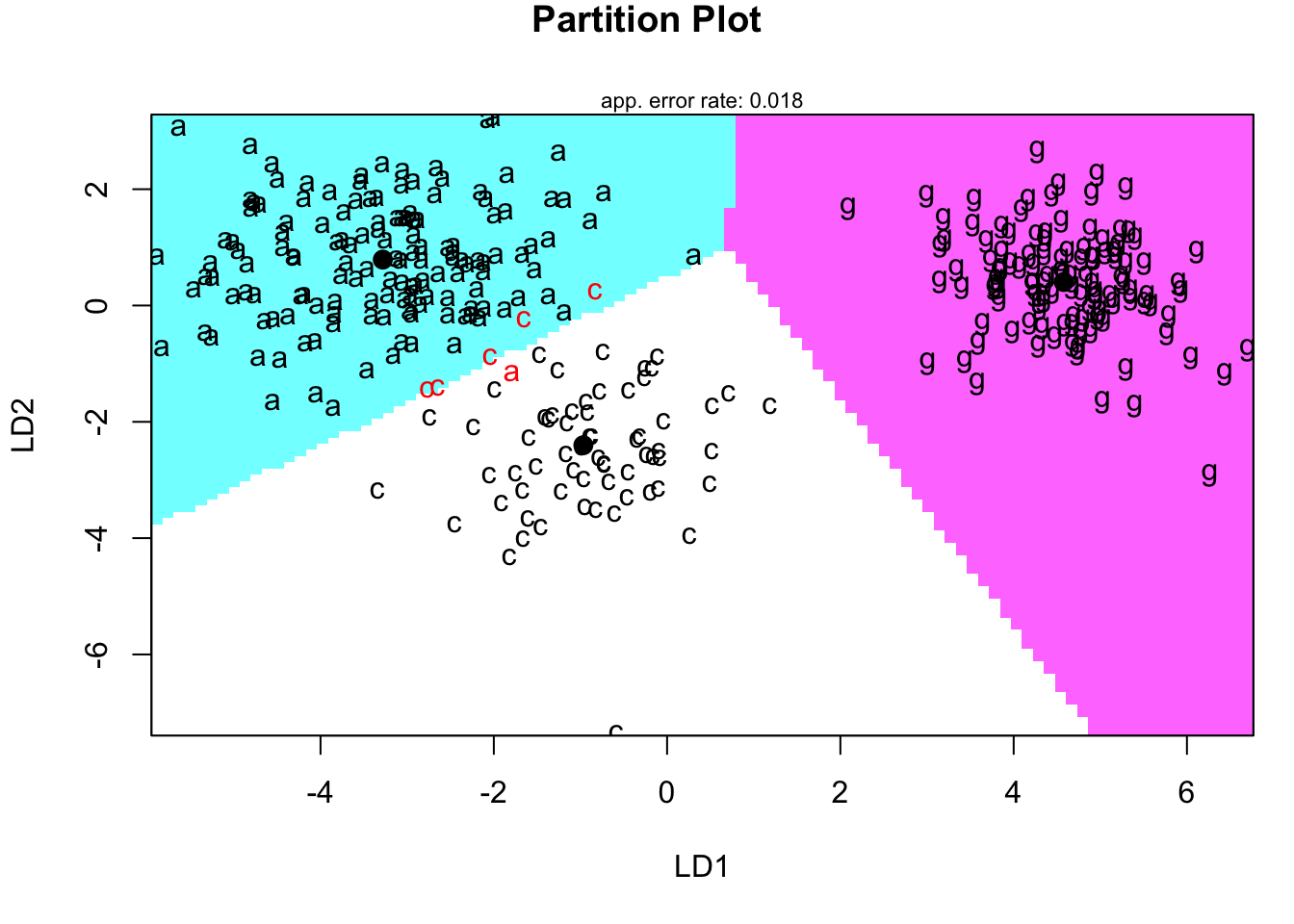 

4.9.2 Exercise 8

Question link

4.9.3 Test of assumption

• For completeness, returning to an assumption of a DFA, we examine the homogeneity of covariance across the groups using Box’s M test.

Code

heplots::boxM(penguins[,3:5],penguins$species)

## 
##  Box's M-test for Homogeneity of Covariance Matrices
## 
## data:  penguins[, 3:5]
## Chi-Sq (approx.) = 58.149, df = 12, p-value = 4.899e-08

• • The p-value suggests ‘reject’ the homogeneity assumption.
    • This matters much more when out of sample prediction is a goal.
      
    • We ignore it here.

4.9.4 Confusion matrix

• The summary table below tells us how many observations we classified correctly:

Code

xtabs(~predict(penguins.lda3)$class+penguins$species)

##                             penguins$species
## predict(penguins.lda3)$class Adelie Chinstrap Gentoo
##                    Adelie       145         5      0
##                    Chinstrap      1        63      0
##                    Gentoo         0         0    119

• - Notice that three observations that are misclassified using LDA.
    - You can see them in the prior plot.

• Note: we could use a ‘leave one out’ approach to classification as well.
  • We will explore this idea further in the next set of notes.

4.10 Lab

• MLE RShiny link

• Lab 4 link

4.11 Appendix

4.11.1 Comparison of model accuracy

• In this section, we will use both unsupervised and supervised learning models to predict outcome values and compare them all together. Here, we will use built-in penguins dataset in R.

Code

# import penguin dataset
data("penguins")
# selecting complete cases only
penguins<- penguins[complete.cases(penguins),] %>%
  mutate(island = as.numeric(island),
         sex = as.numeric(sex))
head(penguins)

## # A tibble: 6 × 8
##   species island bill_length_mm bill_depth_mm flipper_leng…¹ body_…²   sex  year
##   <fct>    <dbl>          <dbl>         <dbl>          <int>   <int> <dbl> <int>
## 1 Adelie       3           39.1          18.7            181    3750     2  2007
## 2 Adelie       3           39.5          17.4            186    3800     1  2007
## 3 Adelie       3           40.3          18              195    3250     1  2007
## 4 Adelie       3           36.7          19.3            193    3450     1  2007
## 5 Adelie       3           39.3          20.6            190    3650     2  2007
## 6 Adelie       3           38.9          17.8            181    3625     1  2007
## # … with abbreviated variable names ¹​flipper_length_mm, ²​body_mass_g

• Next, lets set up the models that we are going to use.

Code

library(class)
library(caret)
library(MASS)
library(ROCR)
library(pROC)
library(ggrepel)
library(factoextra)
library(ggpubr)

# 1. Unsupervised learning method
  # K-means clustering 
kmean_pred <-kmeans(penguins[,-1], centers = 3)$cluster

  # Hierarchical clustering method
hclust_model <- cutree(hclust(dist(penguins[,-1],method="manhattan"),method="ward.D2"), k = 3)

# 2. Supervised learning 
  # K-Nearest Neighbor (KNN) method
knn_model <- knn(penguins[,-1],penguins[,-1],cl=penguins$species,k=3)

  # Linear Discriminant Analysis (LDA) method
lda_model <-MASS::lda(species ~ island + bill_length_mm + bill_depth_mm + flipper_length_mm + body_mass_g+sex+year, data=penguins, CV=FALSE) 

• For unsupervised learning methods, visualization of clusters can be helpful. We usefviz_cluster function from factoextra library to do it.

Code

# kmean clustering
kmean_viz <- fviz_cluster(kmeans(penguins[,-1], centers = 3), penguins[, -1],
   palette = "Set2", ggtheme = theme_minimal(), main = "Kmeans clustering")

# hierarchical clustering
hclust_viz <- fviz_cluster(list(data = penguins[, -1], palette = "Set2",
                  cluster = hclust_model), ggtheme = theme_minimal(), main = "Hierarchical clustering")

two_figures <- ggarrange(kmean_viz, hclust_viz,ncol = 2, nrow = 1)
two_figures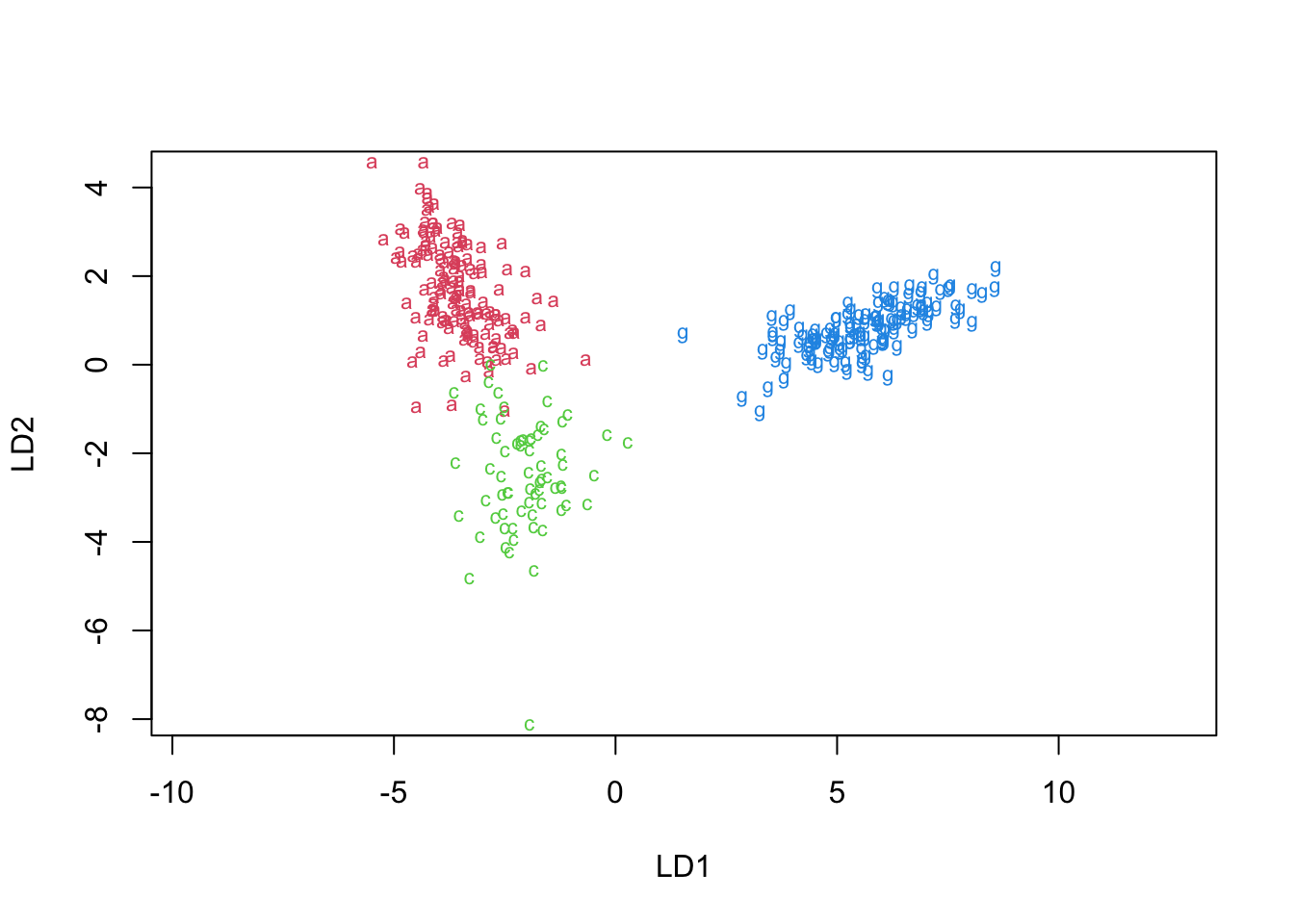

• In addition to the setting, having a helper function is useful. Here, we create a helper function to compute the accuracy of the model.

Code

check_perf <- function(model,type){
  if (type=="unsuper"){
  acc <- confusionMatrix(data=model, 
                reference=factor(as.numeric(penguins$species)))$overall[[1]]    
  } else{
  acc <- confusionMatrix(data=model, 
                reference=factor(penguins$species))$overall[[1]]      
  }
  auc <- auc( multiclass.roc( as.numeric(model), 
                     as.numeric(penguins$species)) )[1]
  list(round(acc,4),round(auc,4) )
}

• Finally, we will gather all information and visualize all predictions by different machine learning models.

Code

data.frame(method = c("kmean","hclust","knn","lda"),
           accuracy = c(check_perf( factor(kmean_pred),"unsuper")[[1]],
                        check_perf( factor(hclust_model),"unsuper")[[1]],
                        check_perf( factor(knn_model),"super")[[1]],
                        check_perf( factor(predict(lda_model)$class),"super")[[1]]),
           auc = c(check_perf( factor(kmean_pred),"unsuper")[[2]],
                        check_perf( factor(hclust_model),"unsuper")[[2]],
                        check_perf( factor(knn_model),"super")[[2]],
                        check_perf( factor(predict(lda_model)$class),"super")[[2]])
           ) %>%  melt(id=c("method")) %>% 
  ggplot(aes(x=method, y=value, color=variable)) +
  geom_line(aes(group=variable)) + geom_point(size=2) + theme_classic() +
  geom_text_repel(aes(label=round(value,2)), position="dodge") +
  labs(title="Comparison of prediction - accuracy and AUC score")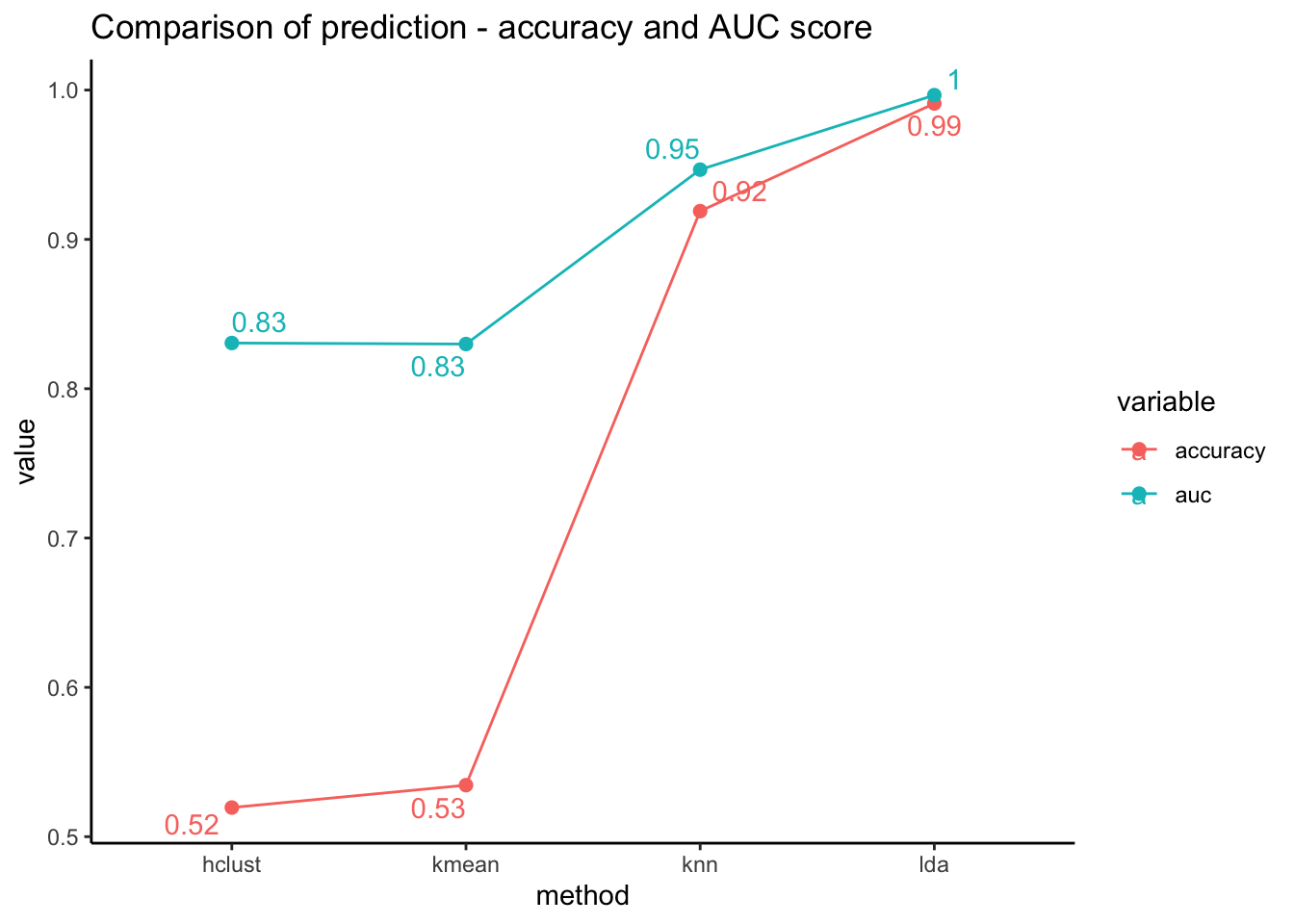

• Plot above shows that the supervised learning methods (both knn and lda) performed better than the unsupervised learning methods. (hierarchical clustering and k means clustering methods)

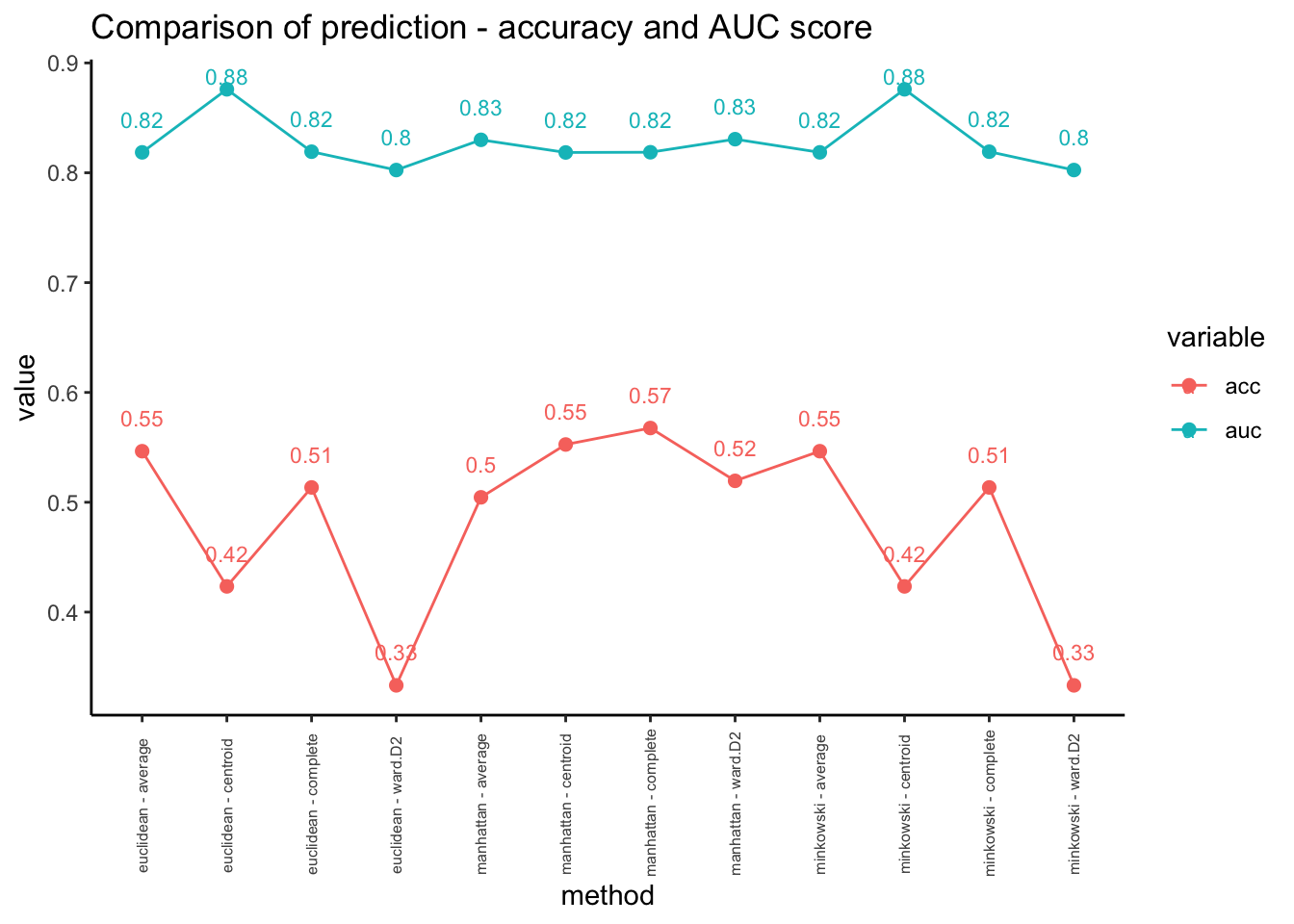
  • In this case, we can try different parameters to improve the performance. Here, we will change distance measures and linkages for hierarchical clustering methods.

Code

# using different distance measures and linkages
distances <- c("euclidean","manhattan","minkowski")
linkage <-c("ward.D2","complete","average","centroid")
data_unsuper <- data.frame(matrix(ncol = 3, nrow = 0))
colnames(data_unsuper)<-c("method","acc","auc")
for (distance in distances){
  for (link in linkage){
    hclust_model <- cutree(hclust(dist(penguins[,-1],method=distance),method=link), k=3)
    method = paste(distance,"-",link)
    acc = check_perf(factor(hclust_model),"unsuper")[[1]]
    auc = check_perf( factor(hclust_model),"unsuper")[[2]]
    data_unsuper = rbind(data_unsuper, cbind(method,acc,auc))
  }
}

# visualization
data_unsuper %>% 
  mutate(acc = as.numeric(acc), auc = as.numeric(auc)) %>%
  melt(id=c("method")) %>%
  ggplot(aes(x=method, y=value, color=variable)) +
  geom_line(aes(group=variable)) + geom_point(size=2) + theme_classic() +
  geom_text_repel(aes(label=round(value,2)), nudge_y=0.03, size=3, ) +
  labs(title="Comparison of prediction - accuracy and AUC score") +
  theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=0.3, size=6))