Rozdział 3 Zmienne losowe
Zmienna losowa to matematyczna formalizacja wielkości, której wartość zależy od przypadku.
Często wyróżnia się zmienne losowe dyskretne (skokowe) i ciągłe. Zmienne ciągłe mogą przyjmować dowolną wartość w określonym przedziale (na przykład od zera do nieskończoności), zaś zmienne skokowe mogą przyjmować wartości oddalone od siebie na osi liczbowej (na przykład tylko nieujemne liczby całkowite) i nic pomiędzy.
3.1 Rozkład prawdopodobieństwa
Rozkład prawdopodobieństwa to miara zmiennej losowej umożliwiająca określenie prawdopodobieństw poszczególnych wartości tej zmiennej. Rozkłady prawdopodobieństwa można przedstawić w formie tabeli albo w formie funkcji. Forma tabelaryczna przydaje się, jeżeli zmienna losowa jest dyskretna i ma niewiele możliwych wartości.
Przykład rozkładu prawdopodobieństwa zmiennej X, oznaczającej np. liczbę orłów w dwóch rzutach symetryczną monetą:
| \(x\) | \(p(x)\) |
|---|---|
| 0 | 0,25 |
| 1 | 0,50 |
| 2 | 0,25 |
3.2 Wartość oczekiwana
Wartość oczekiwana (ang. expected value) to średnia zmiennej losowej o danym rozkładzie prawdopodobieństwa. Zamiast terminu “wartość oczekiwana” używa się podobno1 także pojęcia “nadzieja matematyczna”.
Dla zmiennej losowej dyskretnej o skończonej liczbie wartości \(m\) (indeksowanych od \(x_1\) do \(x_m\)) wartość oczekiwaną można wyznaczyć następującym wzorem:
\[\begin{equation} \mu=E(X)=\sum_{i=1}^m x_i p(x_i) \tag{3.1} \end{equation}\]
Analogicznie, jeżeli liczba wartości przyjmowanych przez dyskretną zmienną losową jest nieskończona, wzór ma taką postać:
\[\begin{equation} \mu=E(X)=\sum_{i=1}^\infty x_i p(x_i) \tag{3.2} \end{equation}\]
W uproszczeniu zapisujemy to w ten sposób:
\[\begin{equation} \mu=E(X)=\sum x p(x) \tag{3.3} \end{equation}\]
Dla zmiennej losowej ciągłej wzór przyjmuje następującą postać:
\[\begin{equation} \mu=E(X)=\int_{-\infty}^{\infty} x f(x) dx \tag{3.4} \end{equation}\]
W uproszczonym zapisie będziemy pomijać granice całkowania:
\[\begin{equation} \mu=E(X)=\int x f(x) dx \tag{3.5} \end{equation}\]
3.3 Wariancja i odchylenie standardowe
Wariancję zmiennej losowej oznaczamy przez \(V(X)\) albo \(\sigma^2_X\) (lub po prostu \(\sigma^2\)). Spotyka się również symbol \(D^2(X)\). Wyznaczamy ją za pomocą wzoru:
\[\begin{equation} \sigma^2=V(X)=E[(X-\mu)^2] = E[X^2]-(E[X])^2 \tag{3.6} \end{equation}\]
Dla zmiennych dyskretnych:
\[\begin{equation} \sigma^2=E[(X-\mu)^2]=\sum (x-\mu)^2 p(x) = \sum x^2 p(x)-\mu^2 \tag{3.7} \end{equation}\]
Dla zmiennych ciągłych:
\[\begin{equation} \sigma^2=E[(X-\mu)^2]=\int (x-\mu)^2 f(x) dx = \int x^2 f(x) dx-\mu^2 \tag{3.8} \end{equation}\]
Odchylenie standardowe zmiennej losowej (oznaczane przez \(\sigma\), \(\sigma_X\), \(D(X)\) lub \(SD(X)\)) to pierwiastek z wariancji:
\[\begin{equation} \sigma=\sqrt{\sigma^2} \tag{3.9} \end{equation}\]
Odchylenie standardowe przez \(\sigma\), \(\sigma_X\), \(D(X)\) lub \(SD(X)\).
3.4 Kowariancja i korelacja
Kowariancję między zmiennymi losowymi X i Y możemy wyznaczyć na podstawie następującej formuły:
\[\begin{equation} cov(X,Y) = \sigma_{XY}=E[\left(X-E(X)\right)(Y-E(Y))] \tag{3.10} \end{equation}\]
Dla zmiennych dyskretnych:
\[\begin{equation} cov(X,Y) = \sigma_{XY}=\sum_i\left(x_i-E(X)\right)(y_i-E(Y))P(X=x_i \land Y=y_i) \tag{3.11} \end{equation}\]
Kowariancja pokazuje współzmienność dwóch zmiennych losowych.
Korelację można uznać za wystandaryzowaną kowariancję:
\[\begin{equation} cor(X, Y) = \rho_{XY}=\frac{\sigma_{XY}}{\sigma_X \sigma_Y} \tag{3.10} \end{equation}\]
Korelacja przyjmuje wartości od -1 do 1, może więc służyć do porównywania siły współzależności pomiędzy różnymi parami zmiennych losowych.
3.5 Dyskretna zmienna losowa - szablon
Dyskretna zmienna losowa - kalkulator – arkusz Google
Dyskretna zmienna losowa - kalkulator – szablon w Excelu: Dyskretna_zmienna_losowa.xlsx
3.6 Rozkład normalny
Popularnym przykładem ciągłej zmiennej losowej jest rozkład normalny. Wzór na gęstość prawdopodobieństwa (którego nie zamierzamy używać wprost) to:
\[ f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}}\:\:\:\:\:\:\: x \in \left(-\infty, \infty \right) \] Rozkład normalny ma dwa parametry: parametr położenia - średnią (wartość oczekiwaną) \(\mu\) i parametr skali - odchylenie standardowe \(\sigma\). Jeżeli zmienna losowa X ma rozkład normalny o tych parametrach zapisujemy to najczęściej w następujący sposób:
\[ X \sim N(\mu, \sigma^2 ) \]
W praktyce wykorzystuje się przede wszystkim całkę, czyli pole pod krzywą gęstości rozkładu normalnego. Do tego celu najwygodniej wykorzystać tablice lub szablon (3.8)
3.7 Rozkład logarytmiczno-normalny
Jeżeli zmienna \(X\) ma rozkład normalny z wartością oczekiwaną \(\nu\) i wariancją \(\sigma^2\), to zmienna \(Y=e^{X}\) ma rozkład logarytmiczno-normalny (inaczej logarytmicznie normalny, log-normalny), z wartością oczekiwaną
\[ E(Y) = e^{\nu + {\sigma^2}/{2}} \] i wariancją:
\[ V(Y) = (e^{\sigma^2} - 1)e^{2\nu+\sigma^2}\]
Rozkład log-normalny jest wykorzystywany w modelach, w których zakłada się multiplikatywne zmiany cen (zob. 4.1, 4.3, 4.4).
3.8 Rozkład normalny - szablon
Kalkulator dla rozkładu normalnego – arkusz Google
Kalkulator dla rozkładu normalnego – szablon w Excelu: Kalkulator_rozkladu_normalnego.xlsx
3.9 Ćwiczenia
Zadanie 3.1 (Luenberger 2003) Rzucamy dwiema kośćmi do gry i mnożymy otrzymane wyniki: w ten sposób powstaje zmienna \(z\). Jaka jest wartość oczekiwana i wariancja zmiennej losowej \(z\)? (Wskazówka: rzuty koścmi należy traktować jako zdarzenia niezależne.)
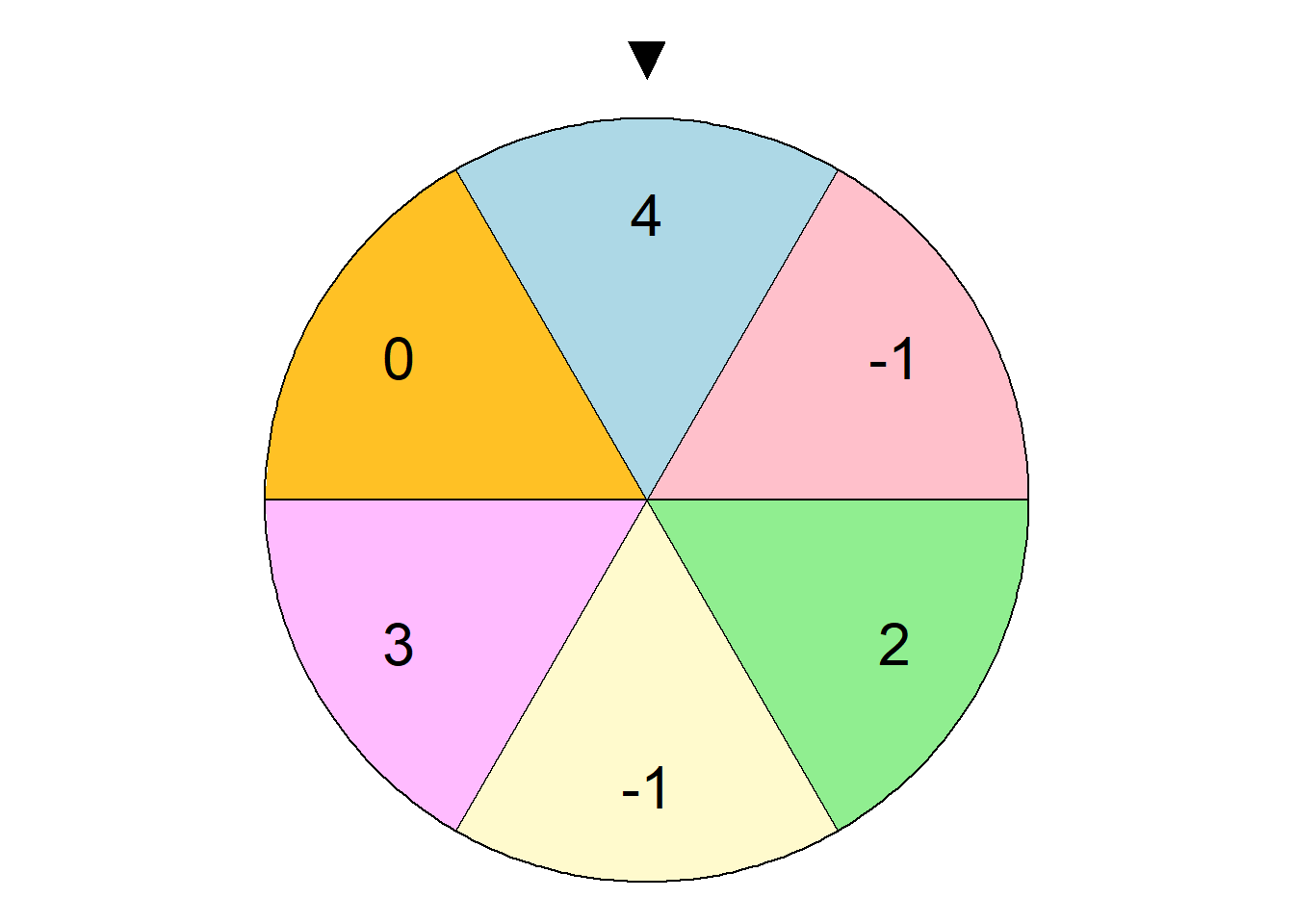
Zadanie 3.2 (Luenberger 2003) Koło fortuny Gracz płaci 1 USD za uczestnictwo w grze “koło fortuny”, w której uzyskana wypłata zależy od tego, na którą część koła wskaże po jego zatrzymaniu czarny trójkąt.
Jaka jest wartość oczekiwana, wariancja i odchylenie standardowe wypłaty w tej grze?
Jaka jest wartość oczekiwana, wariancja i odchylenie standardowe zysku w tej grze?
Jaka jest wartość oczekiwana, wariancja i odchylenie standardowe prostej stopy zwrotu netto w tej grze?
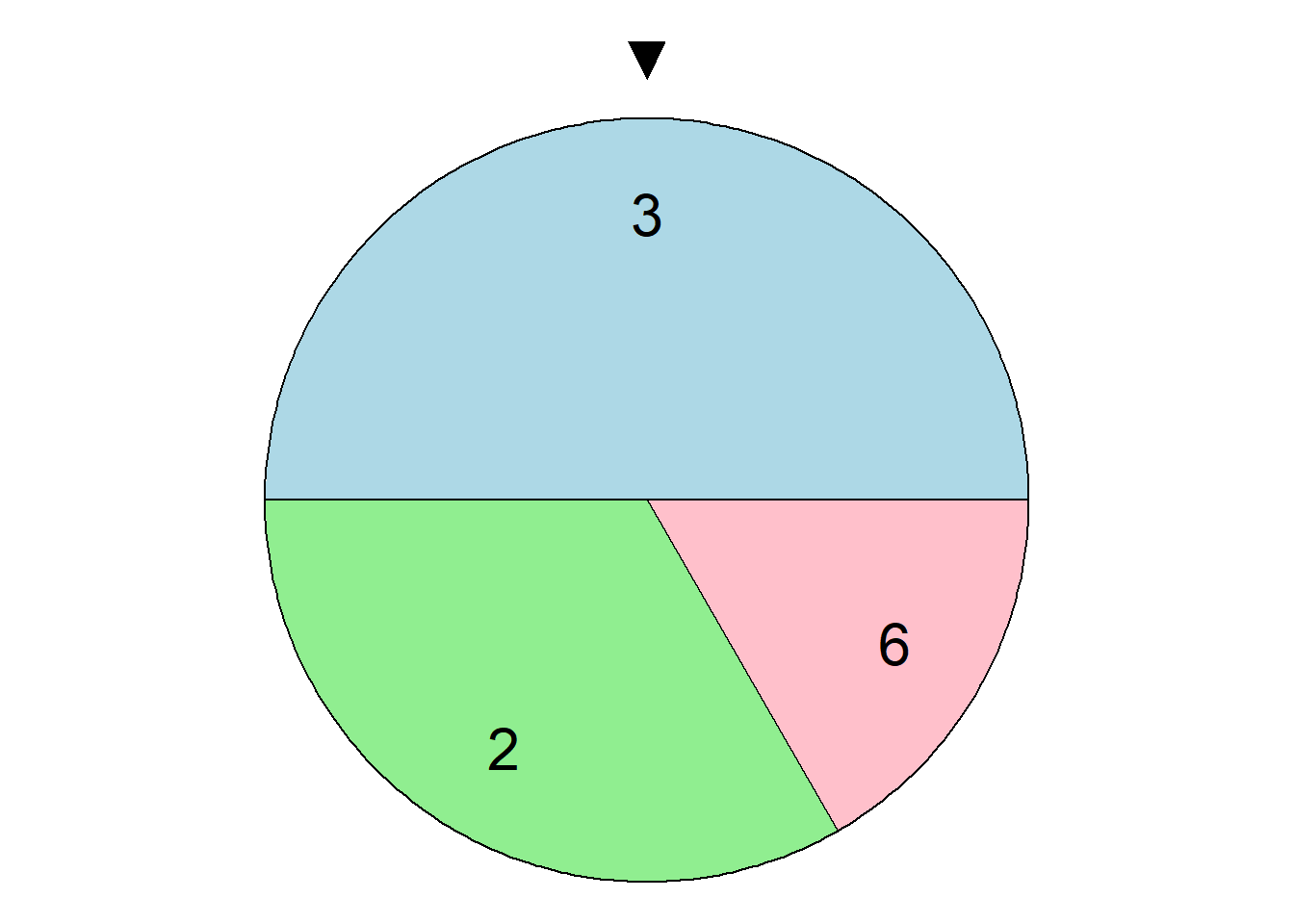
Zadanie 3.3 (Luenberger 2003) Ruletka W grze przypominającej ruletkę uczestnik może postawić pewną kwotę na wybrany wycinek koła. Jeżeli po zatrzymaniu koła czarny trójkąt wskaże obstawiony wycinek, gracz otrzymuje wypłatę w wysokości wielokrotności obstawionej kwoty zgodnie z liczbami zapisanymi na planszy.
Jaka jest wartość oczekiwana, wariancja i odchylenie standardowe wypłaty w tej grze, jeżeli gracz dysponuje stawką 1 USD i:
gracz obstawi trójkę?
gracz obstawi szóstkę?
gracz obstawi dwójkę?
gracz postawi 0,5 USD na trójkę i 0,5 USD na szóstkę?
gracz postawi 0,7 USD na trójkę, 0,2 USD na szóstkę i 0,1 USD na dwójkę?
Ile wynoszą kowariancja i korelacja pomiędzy:
wypłatami dla trójki (1 USD na trójkę) i dla szóstki (1 USD na szóstkę)?
wypłatami dla dwójki i dla szóstki?
wypłatami dla dwójki i dla trójki?
Zadanie 3.4 Na podstawie Ruppert and Matteson (2015). Dzienne zwroty z akcji ZZZ są niezależne i mają rozkład normalny ze średnią 0,001 i odchyleniem standardowym 0,015. Załóżmy, że kupujemy te akcje za 1000 USD. Jakie jest prawdopodobieństwo, że po jednym dniu handlowym inwestycja będzie warta mniej niż 990 USD?
Zadanie 3.5 (Ruppert and Matteson 2015) Roczne logarytmiczne zwroty akcji spółki PRS mają rozkład normalny ze średnią równą 0,1 i odchyleniem standardowym równym 0,2. Dzisiejszy kurs akcji spółki PRS to 100 USD. Jakie jest prawdopodobieństwo, że za rok kurs będzie wynosił 110 USD lub więcej?
Literatura
Szczerze mówiąc, nigdy nie słyszałem, żeby ktokolwiek nazywał wartość oczekiwaną “nadzieją matematyczną”. Z jednym wyjątkiem: kiedy jakiś podręcznik po raz pierwszy mówi o wartości oczekiwanej, wspomina, tak jak ten skrypt, że synonimem tego terminu jest “nadzieja matematyczna.↩︎