Rozdział 5 Analiza średniej-wariancji
Na wykresie 5.1 pokazano statystyki rocznych stóp zwrotu na rynku amerykańskim w latach 1920-2015 skorygowanych o wskaźnik cen – na osi \(x\) jest odchylenie standardowe, a na osi \(y\) średnia stopa zwrotu. Dane historyczne pokazują, że wyższym stopom zwrotu towarzyszy – co do zasady – większa ich zmienność.
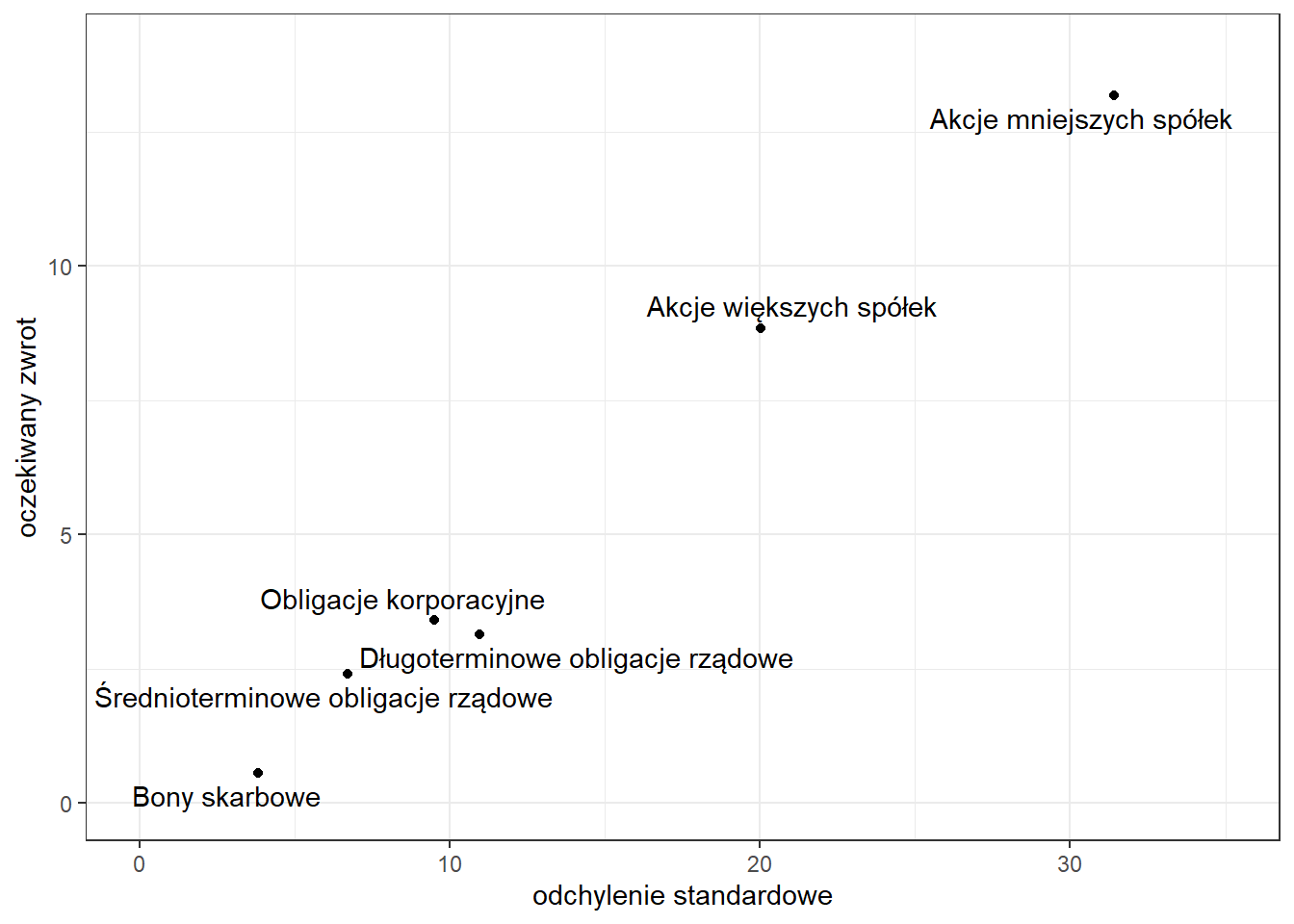
Rysunek 5.1: Historyczne, skorygowane o inflację, stopy zwrotu i odchylenie standardowe grup aktywów amerykańskich w latach 1920-2015 na podstawie danych z raportu SBBI
W tym rozdziale przyjmiemy, że inwestorzy kierują się rozkładami prawdopodobieństwa przyszłych stóp zwrotu dla danego okresu utrzymywania aktywów (holding period). Zakładamy również, że inwestorom do podejmowania decyzji wystarcza znajomość dwóch parametrów tych rozkładów: wartości oczekiwanej i wariancji.
Znajomość wariancji oznacza oczywiście jednocześnie znajomość odchylenia standardowego, stąd na wykresach takich jak 5.1 zwykle przedstawia się odchylenie standardowe na osi \(x\) i wartość oczekiwaną na osi \(y\).
5.1 Dominacja w znaczeniu średniej-wariancji
Każde aktywo lub portfel, dla którego znana jest wariancja (prostych) stóp zwrotu i ich wartość oczekiwana, może zostać przedstawione jako punkt na wykresie.
Zgodnie z teorią portfelową (opartą na analizie średniej-wariancji) inwestor chce:
ograniczać ryzyko i zwiększać oczekiwany zwrot,
przy tym samym oczekiwanym zwrocie ponosić jak najniższe ryzyko,
przy tym samym ryzyku osiągać jak najwyższy zwrot.
Jeżeli aktywo X ma w porównaniu z aktywem Y wyższy zwrot przy tym samym ryzyku lub niższe ryzyko przy tym samym lub wyższym zwrocie, mówimy, że aktywo X dominuje na aktywem Y.
Na rysunku 5.2 aktywa D, E, F i G dominują nad aktywem B. Jeżeli rozważamy tylko portfele A, B, C, to stwierdzamy, że żaden z nich nad żadnym innym nie dominuje, ani nie jest zdominowany. Jeżeli inwestorzy wybierają pomiędzy tymi trzema portfelami, to czy wybiorą A, B czy C zależy tylko i wyłącznie od preferencji dotyczących “apetytu na ryzyko” (czyli na ile są w stanie przyjąć większe ryzyko w zamian za wyższą oczekiwaną stopę zwrotu).
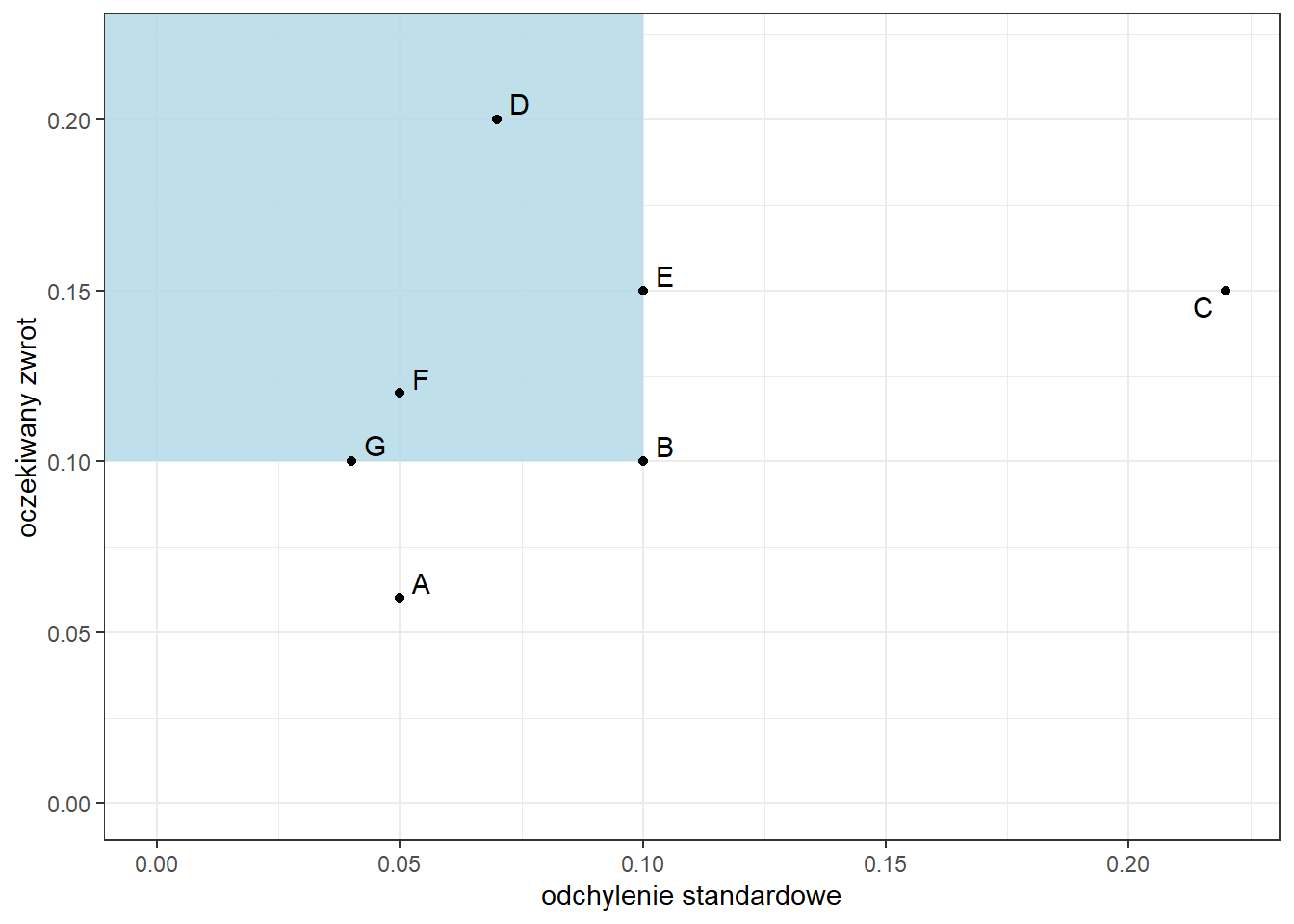
Rysunek 5.2: Portfele D, E, F i G dominują nad portfelem B
5.2 Portfel składający się z dwóch aktywów
Jeżeli mamy dwa aktywa o oczekiwanym zwrocie \(E(R_1)\) i \(E(R_2)\) i odchyleniach standardowych odpowiednio \(\sigma_1\) i \(\sigma_2\), zaś korelacja pomiędzy nimi wynosi \(\rho_{12}\), to portfel zbudowany z tych aktywów będzie miał następującą oczekiwaną stopę zwrotu \(E(R_p)\):
\[\begin{equation} E(R_p) = w_1 E(R_1) + w_2 E(R_2), \tag{5.1} \end{equation}\]
gdzie \(w_1\) to udział aktywa \(1\) w portfelu, a \(w_2=1-w_1\) to udział aktywa \(2\).
Wariancja portfela będzie wynosić:
\[\begin{equation} \begin{split} \sigma^2_p & = w_1^2 \sigma_1^2 + w_2^2 \sigma_2^2 + 2 w_1 w_2 \rho_{12} \sigma_1 \sigma_2 \\ & = w_1^2 \sigma_{11} + w_2^2 \sigma_{22} + 2 w_1 w_2 \sigma_{12}, \end{split} \tag{5.2} \end{equation}\]
gdzie \(\sigma_{12}\) to kowariancja pomiędzy stopami zwrotu aktywa \(1\) i aktywa \(2\)
\[\begin{equation} \sigma_{12}= \rho_{12} \sigma_1 \sigma_2, \tag{5.3} \end{equation}\]
a \(\sigma_{ii}\) to inny sposób zapisu wariancji (\(\sigma^2_i\)).
Odchylenie standardowe stopy zwrotu portfela to będzie oczywiście pierwiastek z wariancji.
\[\begin{equation} \sigma_p = \sqrt{\sigma_p^2} \tag{5.4} \end{equation}\]
Szczególnym przypadkiem portfela składającego się z dwóch aktywów jest sytuacja, kiedy jedno z aktywów jest aktywem wolnym od ryzyka. Oczekiwany zwrot aktywa wolnego od ryzyka wynosi \(R_f\) – jest to stopa wolna od ryzyka, a wariancja i odchylenie standardowe wynoszą zero (\(\sigma_f = 0\)).
W takiej sytuacji wartość oczekiwana to:
\[\begin{equation} E(R_p) = w_1 E(R_1) + (1-w_1) R_f = R_f + w_1\left(E(R_1) - R_f\right). \tag{5.5} \end{equation}\]
Wariancja to:
\[\begin{equation} \sigma^2_p = w_1^2 \sigma_1^2, \tag{5.6} \end{equation}\]
a odchylenie standardowe to:
\[\begin{equation} \sigma_p = w_1 \sigma_1. \tag{5.7} \end{equation}\]
5.3 Portfel składający się z większej liczby komponentów
Dla trzech aktywów wartość oczekiwana wygląda następująco:
\[\begin{equation} E(R_p) = w_1 E(R_1) + w_2 E(R_2) + w_3 E(R_3) = \sum_{i=1}^3 w_i E(R_i), \tag{5.8} \end{equation}\]
zaś wariancję możemy wyznaczyć za pomocą formuły:
\[\begin{equation} \begin{split}\sigma^2_p & = w_1^2 \sigma_1^2 + w_2^2 \sigma_2^2 + w_3^2 \sigma_3^2 + \\ & \:\:\:\: + 2 w_1 w_2 \rho_{12} \sigma_1 \sigma_2 + 2 w_1 w_2 \rho_{23} \sigma_3 \sigma_3 + 2 w_1 w_2 \rho_{13} \sigma_1 \sigma_3 = \\ & = w_1^2 \sigma_1^2 + w_2^2 \sigma_2^2 + w_3^2 \sigma_3^2 +\\ & \:\:\:\: + 2 w_1 w_2 \sigma_{12} + 2 w_2 w_3 \sigma_{23} + 2 w_1 w_3 \sigma_{13} =\\ & = \sum_{i, j = 1}^{3}w_i w_j \sigma_{ij}. \end{split} \tag{5.9} \end{equation}\]
Dla większej liczby aktywów (\(n\) komponentów portfela) wzory są analogiczne:
\[\begin{equation} E(R_p) = \sum_{i=1}^3 w_i E(R_i) \tag{5.10} \end{equation}\]
\[\begin{equation} \sigma^2_p = \sum_{i, j = 1}^{n}w_i w_j \sigma_{ij}. \tag{5.11} \end{equation}\]
5.4 Dywersyfikacja
Załóżmy, że tworzymy portfel składający się tylko z aktywów ryzykownych. Wariancja stopy zwrotu każdego aktywa jest taka sama i wynosi \(\sigma^2\), a korelacja dla każdej pary aktywów wynosi \(\rho\ge 0\). Jaką wariancję i odchylenie standardowe będzie miał portfel składający się \(n\) aktywów, z których każde będzie miało taką samą wagę \(w=1/n\)?
Skorzystamy z wzoru (5.11). W tym przypadku będzie miał on postać.
\[\begin{equation} \sigma^2_p = \sum_{i, j = 1}^{n}\frac{1}{n^2} \sigma_{ij}. \tag{5.12} \end{equation}\]
W \(n\) przypadkach \(i=j\), i wtedy \(\sigma_{ij}\) to wariancja. Dla pozostałych \(n^2-n\) składników sumy mamy do czynienia z kowariancją i wynosi ona ((5.3)) \(\sigma_{ij} = \sigma^2 \rho\).
Stąd:
\[\begin{equation} \begin{split} \sigma^2_p & = \frac{n \sigma^2 + (n^2-n)\sigma^2\rho}{n^2} = \\ & = \frac{\sigma^2}{n} + \left(1-\frac{1}{n}\right) \sigma^2 \rho \end{split} \tag{5.13} \end{equation}\]
Gdy \(n\) dąży do nieskończoności, granicą \(\sigma^2_p\) jest \(\sigma^2\rho\):
\[\begin{equation} \lim_{n \to \infty} \sigma_p = \sqrt{\sigma^2 \rho} = \sigma \sqrt{\rho} \tag{5.14} \end{equation}\]
5.5 Portfele dwuskładnikowe
Załóżmy, że mamy dwa aktywa i łączymy je w portfele. W takiej sytuacji wszystkie możliwe kombinacje tych aktywów znajdą się na wykresie ma jednej krzywej.
Jeżeli nie będziemy dopuszczać krótkiej sprzedaży, wszystkie krzywe będą leżały na wycinku krzywej łączącej punkty A i B. Punkty A i B oznaczają portfele składające się w 100% z jednego z aktywów.
“Wybrzuszenie” krzywej będzie zależeć od wartości korelacji.
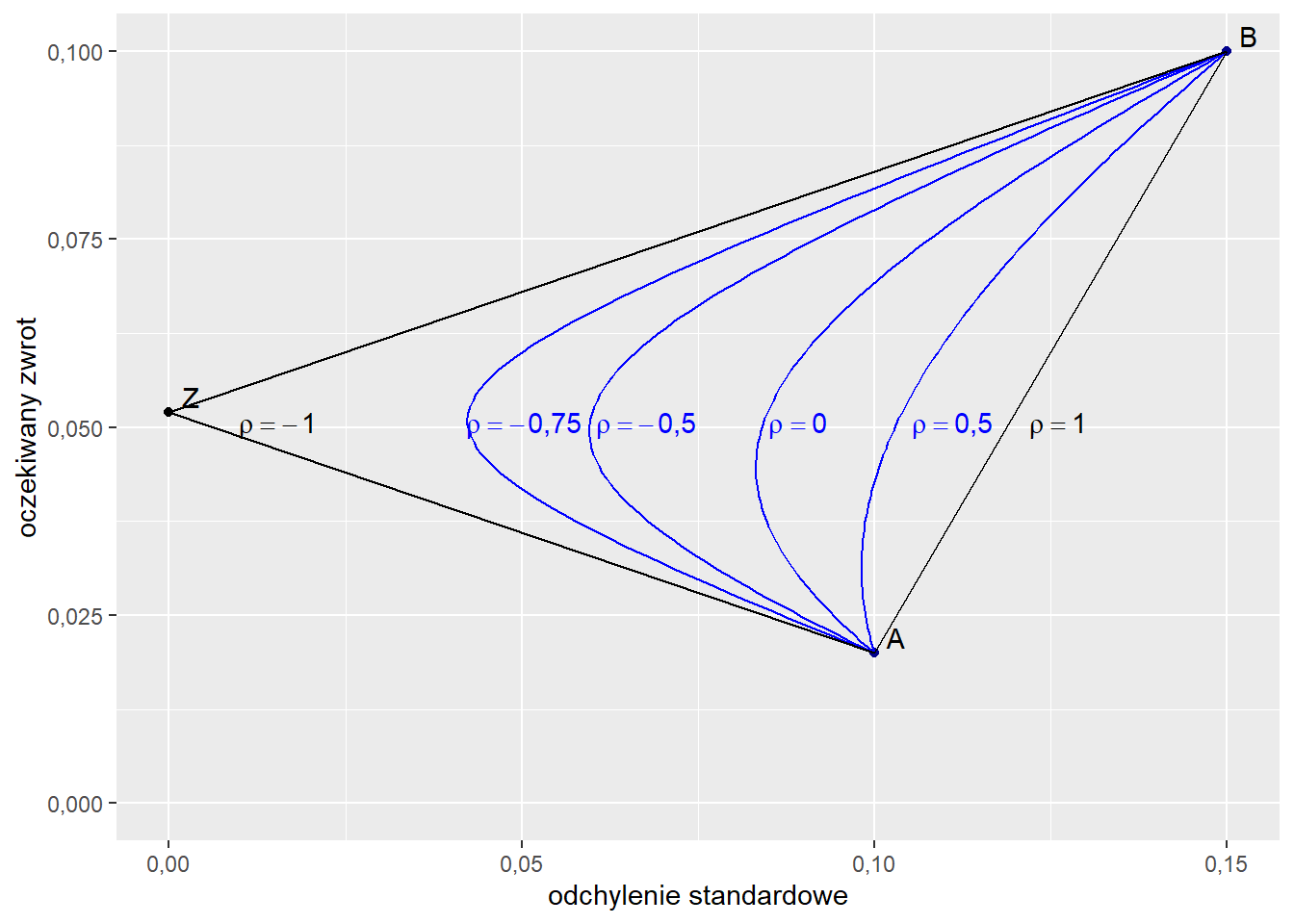
Rysunek 5.3: Krzywe pokazują parametry portfeli złożonych z aktywów A i B. W zależności od poziomu korelacji krzywa jest bardziej lub mniej ‘wybrzuszona’.
Wszystkie “wybrzuszone” wycinki krzywej będą znajdować się wewnątrz trójkąta wyznaczonego przez punkty A, B i Z. Punkt Z to portfel o zerowej wariancji możliwy do osiągnięcia, jeżeli korelacja \(\rho_{AB}\) wynosi -1. Oczekiwany zwrot w tym punkcie to:
\(E(R_Z) = \left(\sigma_AE(R_B)+\sigma_BE(R_A)\right)/(\sigma_A+\sigma_B)\)
Jeżeli dopuścimy krótką sprzedaż krzywe przedstawiające kombinacje portfeli wydłużą się.
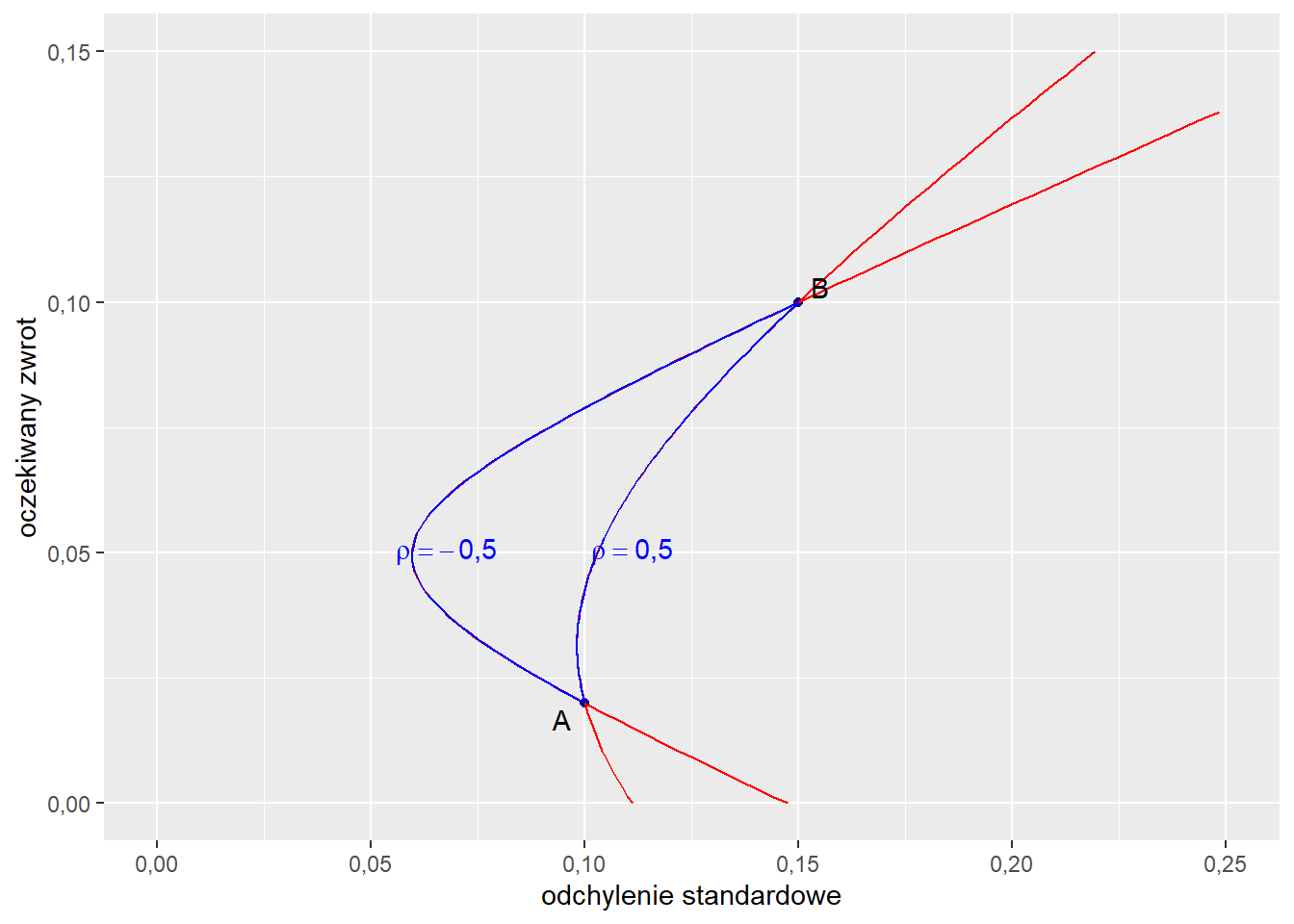
Rysunek 5.4: Kombinacje dwóch portfeli w przypadku braku krótkiej sprzedaży (krzywe niebieskie) i dopuszczalności krótkiej sprzedaży (krzywe czerwone).
Skład portfela minimalnej wariancji można (przy ewentualnym założeniu dopuszczalności krótkiej sprzedaży) wyznaczyć za pomocą prostych metod analizy matematycznej (vide ćwiczenie 5.3).
5.6 Portfele o trzech lub większej liczbie składników
W przypadku większej liczby portfeli powstaje zbiór możliwości inwestycyjnych - portfele nie leżą już zwykle na jednej krzywej.
Przykład na poniższym wykresie.
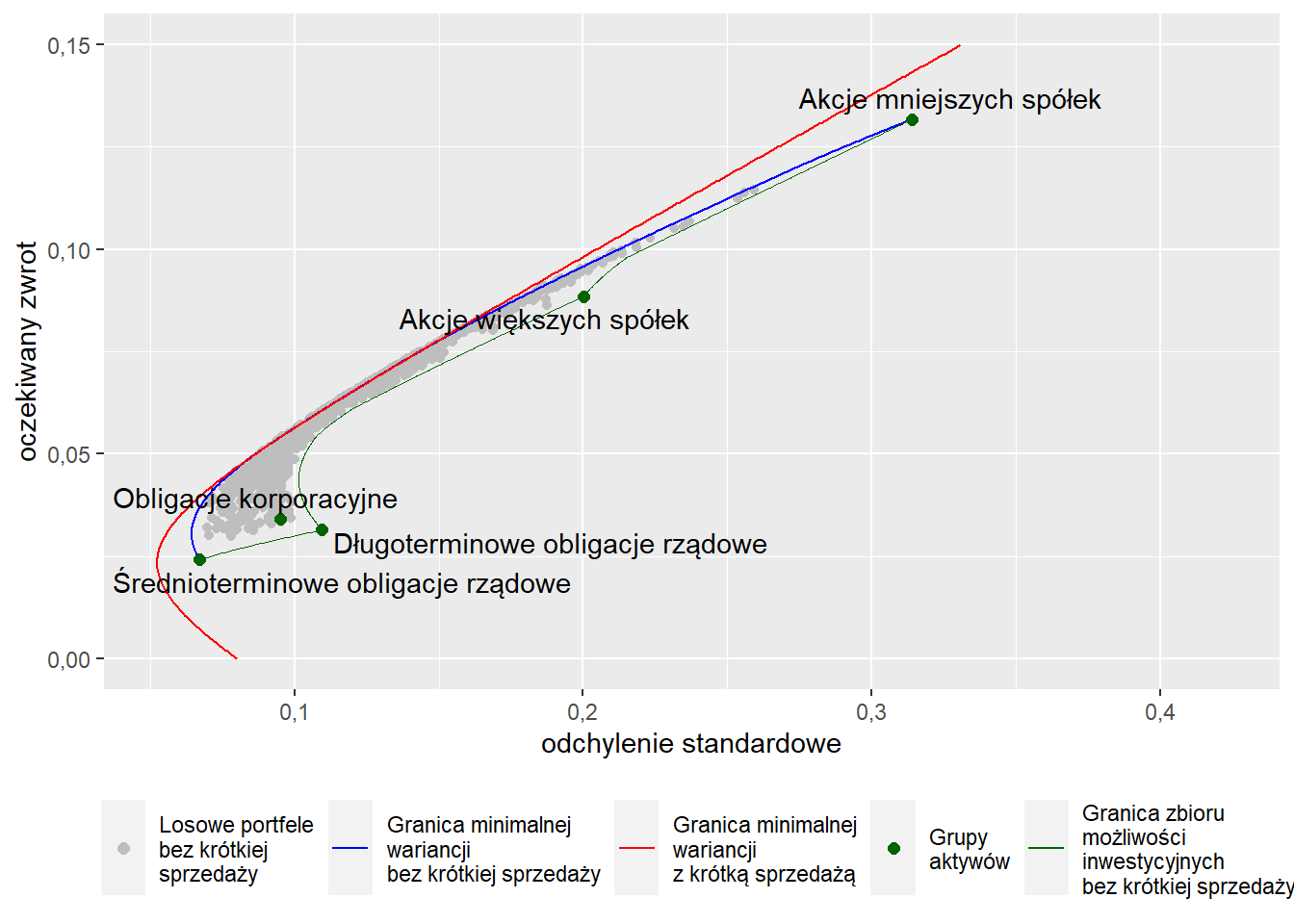
Rysunek 5.5: Losowe portfele złożone z aktywów opisanych na wykresie
Granica minimalnej wariancji to taki zestaw portfeli, które dla zadanego oczekiwanego zwrotu mają najniższą wariancję. Na wykresie zaznaczono dwie granice minimalnej wariancji - jedną w sytuacji, kiedy krótka sprzedaż jest niedopuszczalna, drugą w sytuacji możliwości krótkiej sprzedaży (wagi ujemne).
Globalny portfel minimalnej wariancji to portfel zawierający aktywa ryzykowne skonstruowany w ten sposób, żeby jego wariancja była najmniejsza.
Portfele efektywne to takie portfele, nad którymi nie dominuje żaden inny portfel. Granica efektywna to ta część granicy minimalnej wariancji, która zawiera portfele efektywne.
5.7 Współczynnik Sharpe’a i portfel styczny
Jeżeli jedno z aktywów jest aktywem wolnym od ryzyka granica efektywna staje się linią prostą.
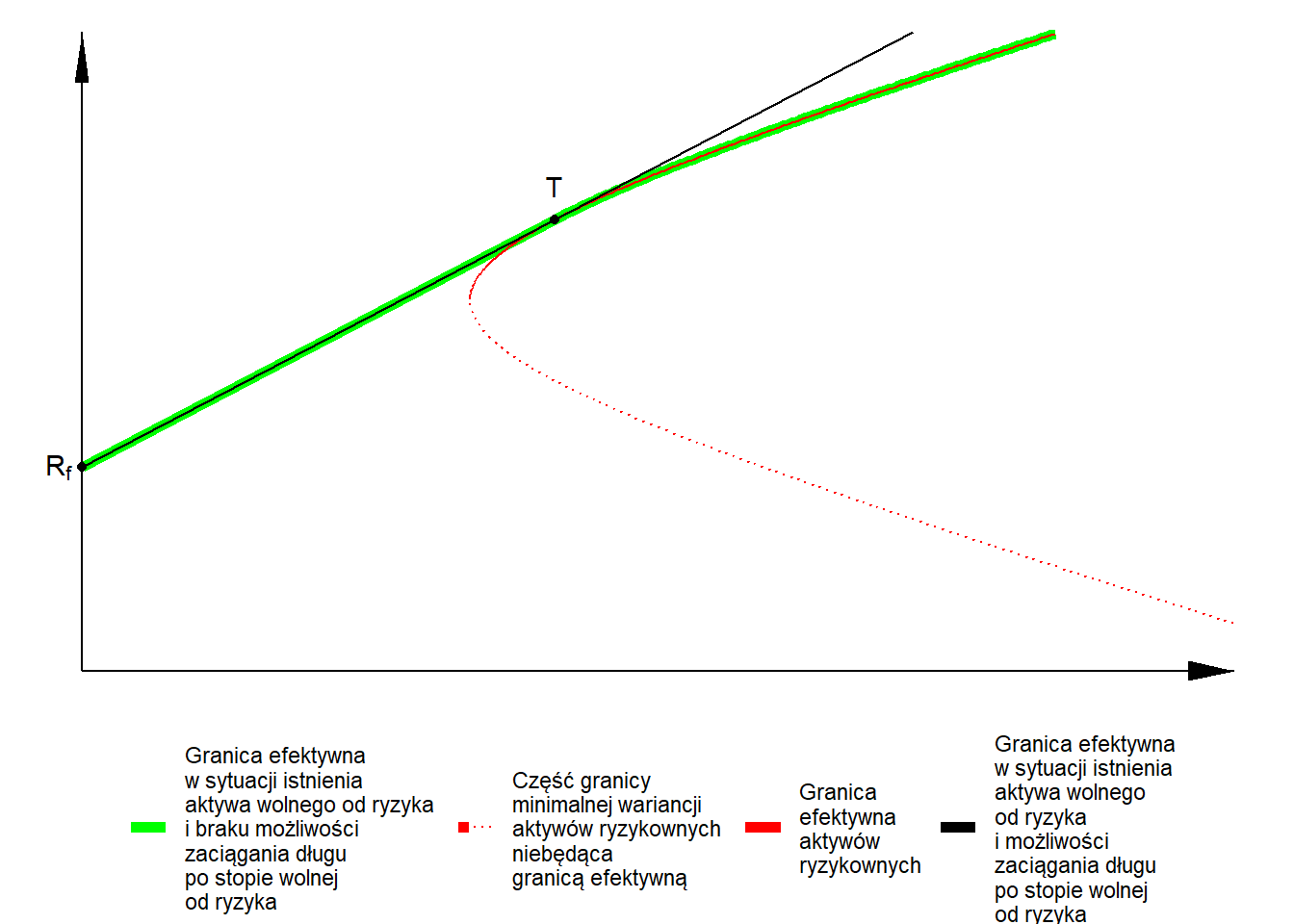
Rysunek 5.6: Granica efektywna bez aktywa wolnego od ryzyka i z tym aktywem
Portfel styczny T to portfel ryzykowny, który leży na linii stycznej do granicy efektywnej aktywów ryzykownych przebiegającej przez punkt oznaczający aktywo wolne od ryzyka.
Innymi słowy: portfel styczny to ten z portfeli efektywnych, którego współczynnik Sharpe’a ex ante jest najwyższy.
Współczynnik Sharpe’a ex ante danego portfela/aktywa \(A\) określamy wzorem:
\[ \text{Sharpe } ex\: ante = \frac{E(R_A)-R_f}{\sigma_A} \]
gdzie \(R_A\) to stopa zwrotu aktywa A, \(\sigma_A\) to jego przewidywane ryzyko mierzone odchyleniem standardowym, \(R_f\) to stopa wolna od ryzyka.
Geometrycznie współczynnik Sharpe’a to współczynnik nachylenia (kierunkowy) linii łączącej punkt reprezentujący aktywo wolne od ryzyka z danym portfelem/aktywem.
5.8 Ćwiczenia
Zadanie 5.1 (Ruppert and Matteson 2015) Załóżmy, że mamy dwa ryzykowne aktywa, \(A\) i \(B\) z oczekiwanym zwrotem równym odpowiednio \(2{,}3\%\) i \(4{,}5\%\). Załóżmy również, że odchylenia standardowe stóp zwrotu wynoszą odpowiednio \(\sqrt{6}\%\) i \(\sqrt{11}\%\), a korelacja pomiędzy stopami zwrotu wynosi 0,17.
Jaki portfel składający się z A i B osiąga oczekiwany zwrot w wysokości 3%?
Jakie portfele składające się z A i B mają ryzyko (odchylenie standardowe) równe \(\sqrt{5{,}5}\%\)? Który z nich ma najwyższą oczekiwaną stopę zwrotu?
Zadanie 5.2 (Luenberger 2003) Współczynnik korelacji \(\rho\) dwóch aktywów A i B wynosi 0,1. Inne dane na ich temat pokazano w tabeli. Uwaga: \(\rho=\sigma_{AB}/(\sigma_A \sigma_B)\).
| Aktywa | \(E(R)\) | \(\sigma\) |
|---|---|---|
| A | 10,0% | 15% |
| B | 18,0% | 30% |
Wyznacz udziały \(w_A\) dla A oraz \(w_B=(1-w_A)\) dla B, które definiują portfel złożony z A i B o najmniejszym możliwym odchyleniu standardowym.
Ile wynosi wartość najmniejszego możliwego do osiągnięcia odchylenia standardowego portfela złożonego z A i B?
Jaka jest oczekiwana stopa zwrotu z tego portfela?
Zadanie 5.3 (Luenberger 2003) Dostępne są dwie akcje. Ich oczekiwane stopy zwrotu wynoszą odpowiednio \(R_1\) i \(R_2\). Wariancje i kowariancje tych stóp zwrotu są równe \(\sigma_1^2\), \(\sigma_2^2\) oraz \(\sigma_{12}\). Jaką część kapitału powinno się zainwestować w poszczególne akcje, aby całkowita wariancja stopy zwrotu z portfela była najmniejsza? Jaka jest oczekiwana stopa zwrotu z tego portfela? Podpowiedź: potrzebna jest minimalizacja funkcji \(f(w)\), gdzie \(w\) to waga jednego z aktywów (np. aktywa 1).
Zadanie 5.4 (Luenberger 2003) Załóżmy, że istnieją dokładnie trzy rodzaje aktywów ryzykownych. Macierz kowariancji oraz oczekiwane stopy zwrotu są następujące:
\[\mathbf{\Sigma} = \left[ {\begin{array}{ccc} 2 & 1 & 0\\ 1 & 2 & 1\\ 0 & 1 & 2\\ \end{array} } \right],\:\:\:\:E(\mathbf{R}) = \left[ {\begin{array}{c} 0{,}4\\ 0{,}8\\ 0{,}8\\ \end{array} } \right]\]
Znajdź portfel o minimalnej wariancji przy założeniu dopuszczalności krótkiej sprzedaży.
Znajdź portfel o minimalnej wariancji przy założeniu braku krótkiej sprzedaży.
Znajdź portfel efektywny składający się aktywów ryzykownych, jeżeli istnieje aktywo wolne od ryzyka o stopie \(r_f\) równej \(0{,}2\).
Zadanie 5.5 Na rynku istnieją aktywa ryzykowne. Ich zwroty mają równe odchylenia standardowe \(\sigma=0{,}15\). Korelacje pomiędzy każdą parą wynoszą \(\rho=0{,}3\). Ile wynosi ryzyko portfela złożonego z dwóch aktywów z równymi wagami? Z trzech? Z czterech? Ile wynosi ryzyko (odchylenie standardowe) w przypadku portfela z nieskończoną liczbą aktywów (granica)? Ile aktywów należy minimalnie wziąć do portfela, żeby odchylenie standardowe stanowiło nie więcej niż 110% granicy? 105%? 101%?