Rozdział 4 Modele wędrówki cen
4.1 Model siatki dwumianowej
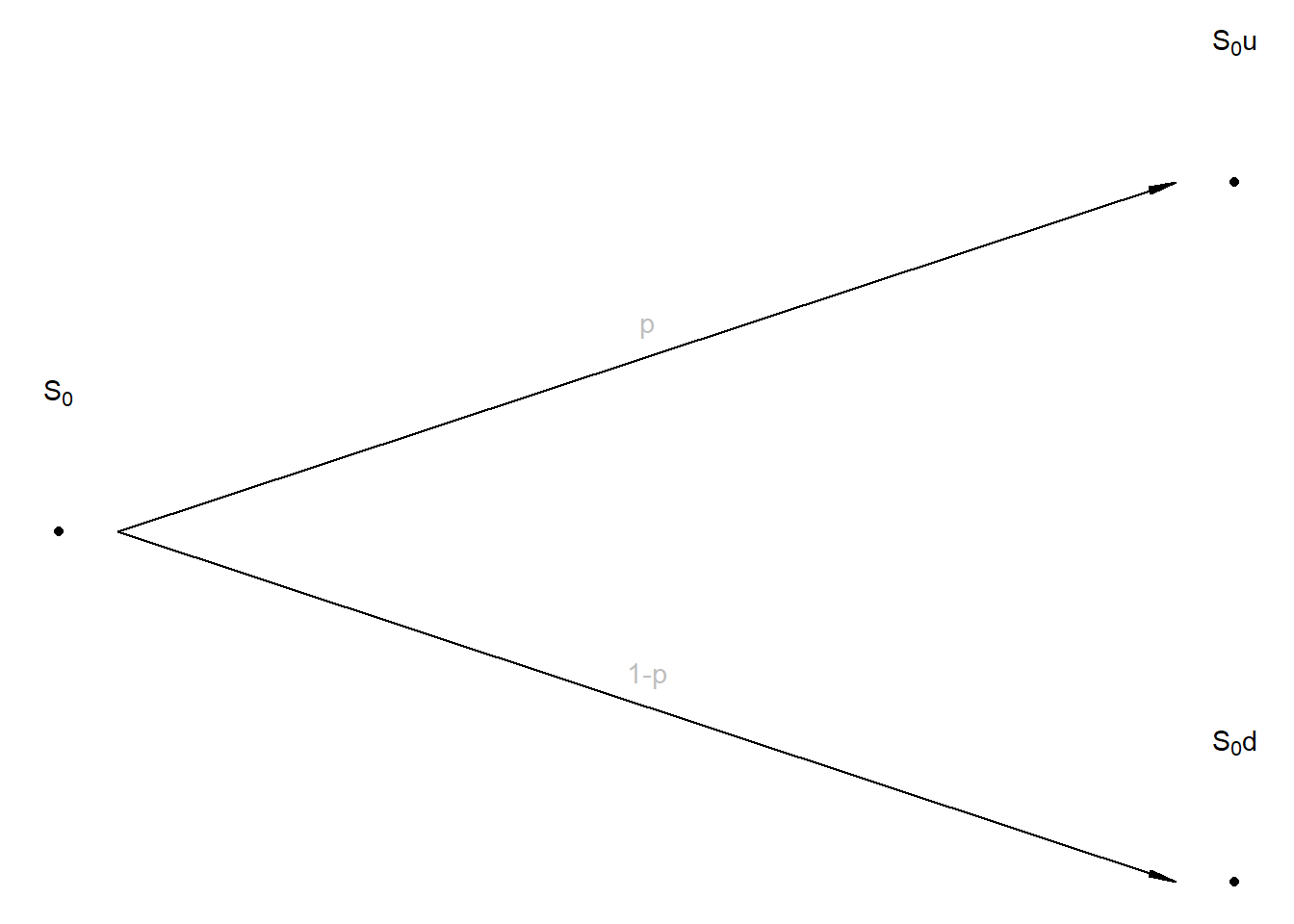
Rysunek 4.1: Początek siatki dwumianowej – cena rośnie o mnożnik u>1 z prawdopodobieństwem p lub spada (mnożnik 0<d<1) z prawdopodobieństwem 1-p
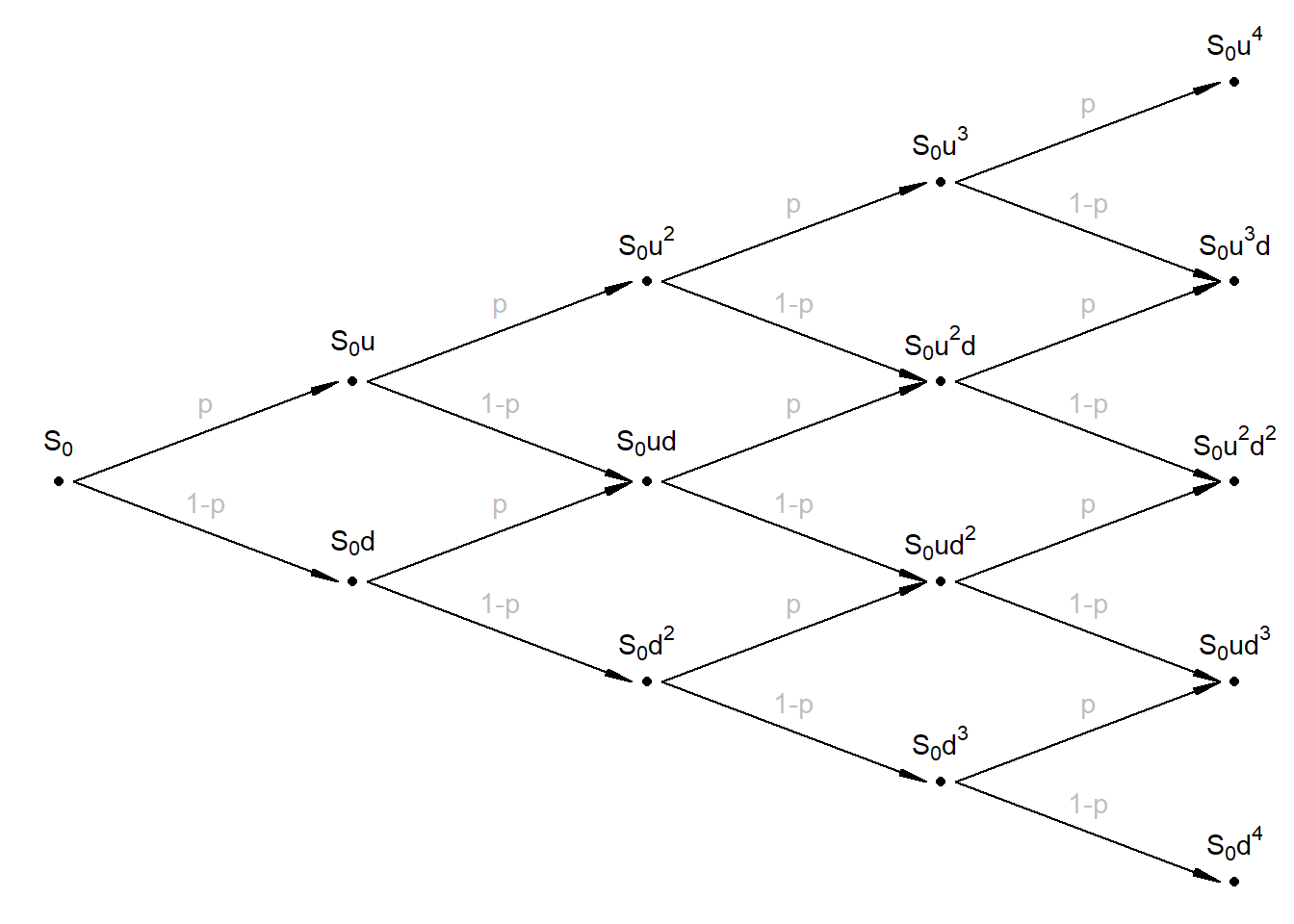
Rysunek 4.2: Model siatki dwumianowej
Jeżeli:
- \(\nu\) to oczekiwana roczna stopa wzrostu:
\[\begin{equation} \nu = E[ln(S_T/S_0)] \tag{4.1} \end{equation}\],
gdzie \(S_T\) to cena akcji po roku, a \(S_0\) to bieżąca cena;
- \(\sigma\) to roczne odchylenie standardowe stopy wzrostu (jako miara jej niepewności):
\[\begin{equation} \sigma = \sqrt{V[ln(S_T/S_0)]} \tag{4.2} \end{equation}\]
- okres \(\Delta t\) jest znikomo mały w porównaniu z 1 rokiem,
to parametry modelu siatki dwumianowej można wyznaczyć w następujący sposób:
\[\begin{equation} p = \frac{1}{2} + \frac{1}{2} \cdot \frac{\nu}{\sigma}\sqrt{\Delta t} \tag{4.3} \end{equation}\]
\[\begin{equation} u = e^{\sigma\sqrt{\Delta t}} \tag{4.4} \end{equation}\]
\[\begin{equation} d = e^{-\sigma\sqrt{\Delta t}} \tag{4.5} \end{equation}\]
4.2 Model addytywny
Model addytywny to model z czasem dyskretnym, to znaczy model pokazujący cenę dla równo oddalonych od siebie punktów w czasie (momentów).
Załóżmy, że mamy \(N+1\) momentów, oznaczamy je przez \(k\) (\(k = 0, 1, 2, ..., N\)). Cena aktywów w momencie \(k+1\) zależy od \(S_k\) (ceny w poprzednim momencie) i wynosi, zgodnie z tym modelem:
\[\begin{equation} S_{k+1} = a S_k + u_k, \tag{4.6} \end{equation}\]
gdzie \(a\) to pewna stała, a \(u_k\) to zakłócenia losowe.
Załóżmy, że zakłócenia \(u_k\) mają taki sam rozkład rozkład normalny, wartość oczekiwaną równą zero, wariancję \(\sigma^2\) i są niezależne. Można pokazać, że przy takich założeniach wartość oczekiwana ceny po \(k\) okresach wynosi:
\[\begin{equation} E(S_k) = a^k S_0, \tag{4.7} \end{equation}\]
Wariancja zaś wynosi:
\[\begin{equation} V(S_k) = \sigma^2\sum_{i=0}^k a^{2i} . \tag{4.8} \end{equation}\]
Parametry rozkładu prostych \(k\)-okresowych stóp zwrotu netto są następujące. Wartość oczekiwana:
\[\begin{equation} E\left[R(k)\right] = E\left[\frac{S_k}{S_0}-1\right] = a^k - 1 \tag{4.9} \end{equation}\]
Wariancja:
\[\begin{equation} V\left[R(k)\right] = V\left[\frac{S_k}{S_0}\right] = \frac{\sigma^2\sum_{i=0}^k a^{2i}}{S_0^2} \tag{4.10} \end{equation}\]
Model addytywny jest prosty w założeniach, jednak nie przystaje do rzeczywistości w dwóch podstawowych aspektach:
Według modelu ceny mogą spaść poniżej zera (w rzeczywistości zwykle nie mogą).
Odchylenie standardowe jest stałe niezależnie od rzędu wielkości ceny (jeżeli cena wzrośnie 100-krotnie, odchylenie standardowe względem ceny będzie 100 razy mniejsze).
4.3 Model multiplikatywny
Model multiplikatywny ma postać:
\[\begin{equation} S_{k+1} = S_k \cdot u_k, \tag{4.11} \end{equation}\]
gdzie \(u_k\) to zmienna zakłócająca inna niż w przypadku modelu addytywnego.
W postaci logarytmicznej:
\[\begin{equation} \ln S_{k+1} = \ln S_k + \ln u_k. \tag{4.12} \end{equation}\]
Zakładamy, że zmienne losowe \(w_k\)
\[\begin{equation} w_k = \ln u_k \tag{4.13} \end{equation}\]
mają rozkład normalny, są wzajemnie niezależne, a wartość oczekiwana każdej z nich wynosi \(E(w_k) = \nu\) przy wariancji równej \(\sigma^2\).
Czynnik zakłócający \(u_k\) można zapisać jako
\[\begin{equation} u_k = e^{w_k} \tag{4.14} \end{equation}\]
Ma on rozkład logarytmiczno-normalny.
Model multiplikatywny pozwala pozbyć się dwóch poprzednio wspomnianych problemów modelu addytywnego: ceny nie mogą spaść poniżej zera i zmienna \(u_k\) powoduje, że rozproszenie stóp zwrotu rośnie z ceną.
Cena instrumentu po k okresach, \(S_k\), ma rozkład log-normalny. Oznacza to, że logarytm ceny ma rozkład normalny z następującą wartością oczekiwaną:
\[\begin{equation} E(\ln S_k) = \ln S_0 + \nu k \tag{4.15} \end{equation}\]
i wariancją:
\[\begin{equation} V(\ln S_k) = k \sigma^2 \tag{4.16} \end{equation}\]
Logarytmiczna \(k\)-okresowa stopa zwrotu \(r(k)\) ma również rozkład normalny o wartości oczekiwanej:
\[\begin{equation} E[r(k)] = E\left[ln \frac{S_k}{S_0}\right] = k\nu \tag{4.17} \end{equation}\]
i wariancji:
\[\begin{equation} V[r(k)] = V\left[\ln \frac{S_k}{S_0}\right] = V\left[\ln S_k-S_0\right] = k \sigma^2 \tag{4.18} \end{equation}\]
Warto zauważyć, że wartość oczekiwana i wariancja \(k\)-okresowej logarytmicznej stopy zwrotu rosną proporcjonalnie do \(k\), zaś odchylenie standardowe rośnie jak \(\sqrt{k}\).
Jeżeli chcemy wyliczyć wartość oczekiwaną i odchylenie standardowe dla okresu ułamkowego oznaczonego przez \(p\) (np. chcielibyśmy przejść z rozkładu rocznych stóp o parametrach \(\nu\) i \(\sigma\) do rozkładu stóp miesięcznych \(p=1/12\)), postępujemy analogicznie:
\[\begin{equation} E(r_p) = \nu_p = p \nu \tag{4.19} \end{equation}\]
\[\begin{equation} V(r_p) = \sigma^2_p = p \sigma^2 \tag{4.20} \end{equation}\]
\[\begin{equation} \sigma_p = \sqrt{p} \sigma \tag{4.21} \end{equation}\]
4.4 Geometryczne ruchy Browna
W powyższych modelach ceny były dyskretne lub ciągłe, ale czas pozostawał dyskretny (zbiór oddzielonych od siebie momentów). Model przedstawiony w tym podrozdziale to model, w którym czas jest również ciągły.
Jeżeli będziemy skracać okres podstawowy tak, aby dążył do zera, model multiplikatywny przechodzi w tzw. proces Ito nazwany geometrycznymi ruchami Browna (\(S(t)\) albo \(S_t\) to cena w momencie \(t\), gdzie \(t\) przyjmuje dowolną wartość z określonego przedziału, \(z_t\) to znormalizowany proces Wienera):
\[\begin{equation} d \ln S_t = \nu d t + \sigma dz_t \tag{4.22} \end{equation}\]
Alternatywna równoważna postać modelu (w którym \(\mu = \nu+{\sigma^2}/{2}\)):
\[\begin{equation} d S_t = \mu S_t dt + \sigma S_t dz_t \tag{4.23} \end{equation}\]
Alternatywna postać modelu może być zapisana również w ten sposób:
\[\begin{equation} \frac{d S_t}{S_t} = \mu dt + \sigma dz_t \tag{4.24} \end{equation}\]
W przypadku geometrycznych ruchów Browna opisanych równaniem (4.24) oczekiwana logarytmiczna stopa za cały czas \(t\) wynosi:
\[\begin{equation} E\left(r(t)\right) = E\left(\ln\frac{S_t}{S_0}\right) = \nu t, \tag{4.25} \end{equation}\]
zaś jej odchylenie standardowe wynosi
\[\begin{equation} SD(r(t)) = SD\left(\ln\frac{S_t}{S_0}\right) = \sigma \sqrt{t}, \tag{4.26} \end{equation}\]
Oczekiwana prosta stopa netto za cały czas \(t\) wynosi
\[\begin{equation} E\left(R(t)\right) = E\left(\frac{S_t}{S_0}-1\right) = e^{\mu t}-1, \tag{4.27} \end{equation}\]
zaś jej odchylenie standardowe wynosi
\[\begin{equation} SD(R(t)) = SD\left(\frac{S_t}{S_0}-1\right) = e^{\mu t}\left(e^{\sigma^2 t}-1\right)^{1/2}, \tag{4.26} \end{equation}\]
Symulując ten proces, który w teorii jest w czasie ciągłym, musimy się jednak siłą rzeczy odwołać do obliczeń w czasie dyskretnym. Symulacje będą więc oparte na krótkich okresach \(\Delta t\) (w poniższym wzorze \(\epsilon(t_k)\) to realizacje niezależnych zmiennych losowowych o standaryzowanym rozkładzie normalnym):
\[\begin{equation} S(t_{k+1}) = S(t_{k})e^{\nu \Delta t + \sigma \epsilon(t_k)\sqrt{\Delta t}} \tag{4.28} \end{equation}\]
4.5 Szacowanie parametrów modeli multiplikatywnych
Jednookresową stopę zwrotu brutto w okresie \(k+1\) (od momentu \(k\) do momentu \(k+1\)) oznaczamy przez \(\mathcal{R}_{k+1}=\frac{S_{k+1}}{S_k}\). W modelu multiplikatywnym jednookresowa stopa zwrotu brutto z inwestycji równa jest zmiennej \(u_k\). Wartość \(w_k = \ln(u_k)\) to logarytm stopy brutto, czyli logarytmiczna stopa zwrotu \(r_k\). Wartość oczekiwana zmiennej \(w_k\) to \(\nu\), a wariancja to \(\sigma^2\).
Jak oszacować te parametry na podstawie danych z \(n\) okresów z przeszłości? Można obliczyć średnią logarytmiczną stopę zwrotu – to będzie estymator parametru \(\nu\):
\[ \bar{\nu} = \frac{1}{n}\sum_{i=1}^{n} r_i = \frac{1}{n}\sum_{i=1}^{n} \ln \frac{S_i}{S_{i-1}} = \frac{1}{n}\ln\frac{S_n}{S_0}\]
Błąd oszacowania \(V(\bar{\nu})\) wynosi
\[ V(\bar{\nu}) = \frac{\sigma^2}{n}. \]
Standardowy błąd oszacowania, czyli pierwiastek z wariancji estymatora wyniesie:
\[ SE(\bar{\nu}) = \frac{\sigma}{\sqrt{n}} \]
Możemy również oszacować parametr \(\sigma^2\). Estymator będzie wyglądał następująco:
\[ \hat{\sigma}^2 = \frac{1}{n-1}\sum_{i=1}^{n}\left[r_i - \bar{\nu}\right]^2 = \frac{1}{n-1}\sum_{i=1}^{n}\left[ \ln \frac{S_i}{S_{i-1}} - \bar{\nu}\right]^2 \]
Jego wariancja natomiast będzie wynosić:
\[ V(\hat{\sigma}^2) = \frac{2 \sigma^4}{n-1} \]
Błąd standardowy, czyli pierwiastek z wariancji estymatora wyniesie:
\[ SE(\hat{\sigma}^2) = \frac{\sqrt{2} \sigma^2}{\sqrt{n-1}} \]
Estymatorem parametru \(\sigma\) jest, jak się można domyślić pierwiastek z \(\hat{\sigma}^2\):
\[ \hat{\sigma} = \sqrt{\hat{\sigma}^2} \]
Jego błąd standardowy to w przybliżeniu, które można uznać za wystarczająco dobre dla \(n>10\) (Ahn and Fessler 2003):
\[ SE(\hat{\sigma}) = \frac{\sigma}{\sqrt{2(n-1)}} \]
4.6 Ćwiczenia
Zadanie 4.1 (Luenberger 2003) Akcja, której cena bieżąca wynosi \(S_0\)=100, ma oczekiwaną logarytmiczną stopę zwrotu \(\nu\) równą = 12%. Zmienność tej stopy wynosi \(\sigma\) = 20%. Wyznacz odpowiednie wartości parametrów niezbędnych do zbudowania siatki dwumianowej pokazującej zmiany cen tej akcji, jeżeli okresem podstawowym miałyby być 3 miesiące. Narysuj tę siatkę dla pierwszego roku, uzupełniając wartości w poszczególnych węzłach. Jakie jest prawdopodobieństwo osiągnięcia poszczególnych węzłów końcowych?
Zadanie 4.2 Na podstawie Ruppert and Matteson (2015). Dzienne logarytmiczne zwroty z akcji ZZZ są niezależne i mają rozkład normalny ze średnią 0,001 i odchyleniem standardowym 0,015. Załóżmy, że kupujemy te akcje za 1000 USD. Jakie jest prawdopodobieństwo, że po pięciu dniach handlowych inwestycja będzie warta mniej niż 980 USD?
Zadanie 4.3 Przygotuj symulację procesu zmieny cen według modelu addytywnego i multiplikatywnego w arkuszu kalkulacyjnym.
Zadanie 4.4 (Na podstawie Luenberger 2003) Załóżmy, że proces kształtowania się cen jest zgodny z modelem multiplikatywnym z parametrami \(\nu=0{,}1\) i \(\sigma=0{,}18\). Do celów oszacowania parametrów zbieramy dane z 10 lat.
Ile wynosi błąd standardowy oszacowania parametru \(\nu\)?
Ile wynosi przybliżony błąd standardowy oszacowania parametru \(\sigma\), jeżeli weźmiemy dane za 10 lat?
Ile wynosi błąd standardowy oszacowania parametru \(\sigma\), jeżeli skorzystamy ze 120 stóp miesięcznych: \(SE(\hat{\sigma}) = \sqrt{12} SE(\hat{\sigma}_{m})\)?
Ile wynosi błąd standardowy oszacowania parametru \(\sigma^2\), jeżeli skorzystamy ze \(52\cdot 10=520\) stóp tygodniowych: \(SE(\hat{\sigma}) = \sqrt{52} SE(\hat{\sigma}_{w})\)?
Ile wynosi błąd standardowy oszacowania parametru \(\sigma^2\), jeżeli skorzystamy z \(252\cdot 10=2520\) stóp dziennych: \(SE(\hat{\sigma}) = \sqrt{252} SE(\hat{\sigma}_{d})\)?
Zadanie 4.5 (Luenberger 2003) Symulacja komputerowa geometrycznych ruchów Browna Rozważ akcję, której cena \(S\) podlega geometrycznym ruchom Browna: \[ \frac{d S}{S(t)} = 0,10 dt + 0,30 dz\] a. Podstawiając \(\Delta t = 1/12\) i \(S(0)=1\) przeprowadź symulację kilku (a raczej wielu) lat przebiegu procesu. Zbadaj funkcję \(\frac{1}{t}\ln S(t)\) w zależności od \(t\). Zauważ, że funkcja ta dąży do \(p\). Jaka jest teoretyczna wartość tej granicy?
Jak duże musi być \(t\), aby możliwe było uzyskanie wyniku z dokładnością do dwóch miejsc po przecinku?
Zbadaj funkcję zmiennej \(t\): \[ \frac{1}{t} \left[\ln S(t) - pt \right]^2 \] Czy funkcja ta ma granicę skończoną? Jeśli tak, to jaka jest jej wartość?