Rozdział 6 Model CAPM
6.1 Linia rynku kapitałowego
Model CAPM zakłada, że wszyscy inwestorzy mają ten sam okres utrzymywania aktywów oraz jednakowo przewidują rozkład stóp zwrotu (oczekiwane stopy zwrotu, wariancje, kowariancje).
Zgodnie z modelem CAPM, który jest wynikiem analizy średniej-wariancji, racjonalni inwestorzy będą chcieli zbudować portfel oparty na portfelu stycznym T. Portfel styczny staje się portfelem rynkowym M, ponieważ jest on wspólny dla wszystkich inwestorów. Aby zbudować portfele o różnym poziomie ryzyka będą łączyć go portfel rynkowy z aktywami wolnymi od ryzyka. Takie portfele efektywne przedstawia linia rynku kapitałowego (CML).
Na wykresie, na którym na osi \(x\) jest odchylenie standardowe, a na osi \(y\) oczekiwana stopa zwrotu, można narysować linię rynku kapitałowego (capital market line, CML). Jest to linia prosta przechodząca przez punkt oznaczający aktywo wolne od ryzyka i portfel rynkowy M.
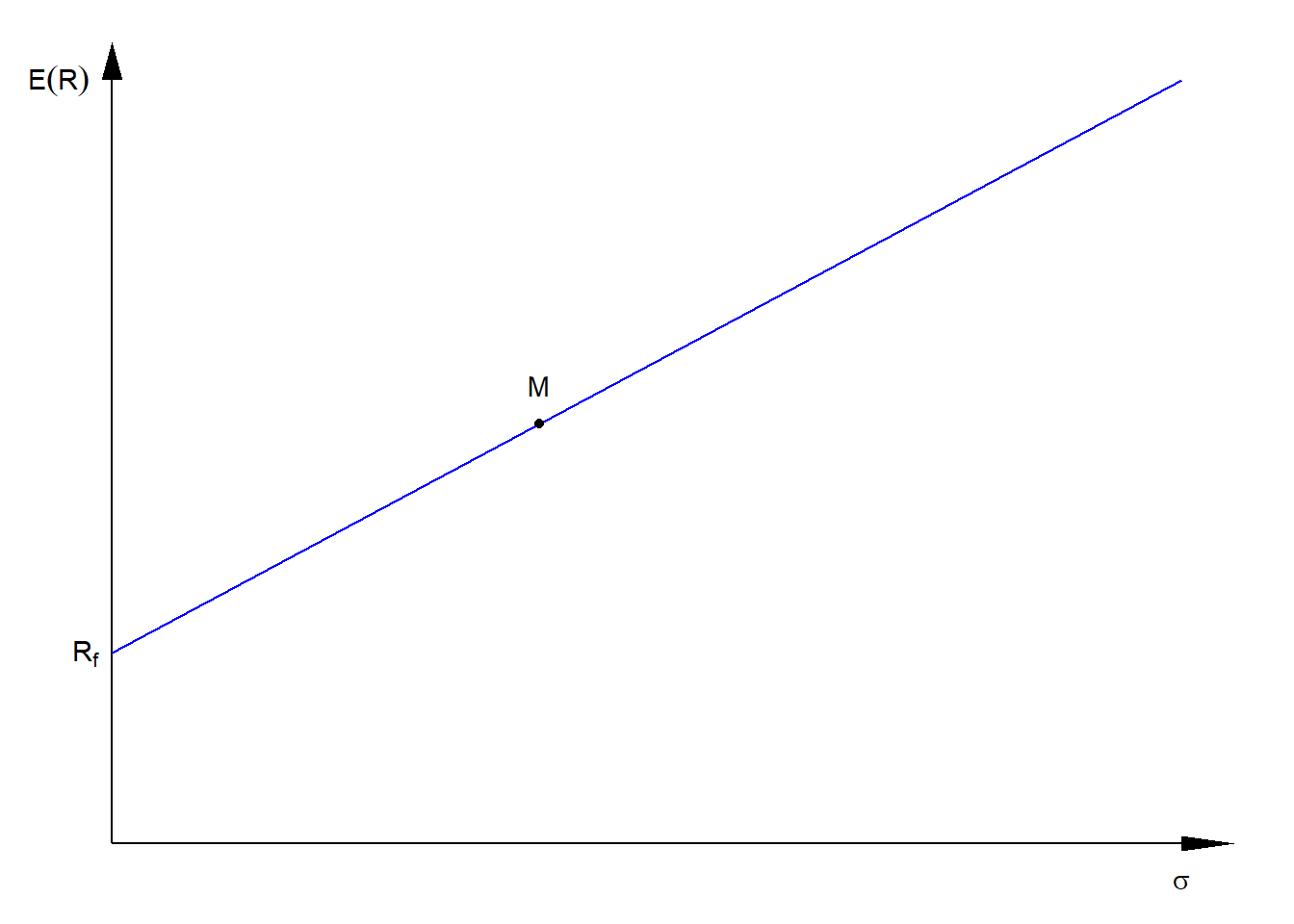
Rysunek 6.1: Linia rynku kapitałowego
Portfele efektywne leżą na linii rynku kapitałowego.
Formuła linii rynku kapitałowego:
\[E(R) = R_f + \frac{E(R_M)-R_f}{\sigma_M}\sigma\]
Współczynnik kierunkowy linii rynku kapitałowego (\(E(R_M)-R_f)/\sigma_M\)) to cena ryzyka (price of risk). Pokazuje ile dodatkowego zwrotu inwestorzy powinni oczekiwać od dodatkowej jednostki ryzyka mierzonego odchyleniem standardowym.
Nie wszystkie aktywa znajdują się na linii CML, nawet w stanie równowagi rynkowej. Znajdują się na niej tylko portfele efektywne.
6.2 Wycena aktywów kapitałowych CAPM
Model wyceny aktywów kapitałowych (Capital Asset Pricing Model, CAPM) może zostać wyprowadzony z analizy średniej-wariancji, założenia o efektywności portfela rynkowego oraz z założenia o istnieniu aktywa wolnego od ryzyka.
6.2.1 Równanie CAPM
Równanie modelu wyceny aktywów kapitałowych wygląda następująco:
\[ E(R_i) = R_f + \beta_i \left(E(R_M) - R_f\right), \]
gdzie \(E(R_i)\) to oczekiwana stopa zwrotu z aktywa (portfela) \(i\), \(R_f\) to stopa wolna od ryzyka, \(E(R_M)\) oczekiwana rynkowa stopa zwrotu.
Różnica \(E(R_M) - R_f\) nazywana jest premią za ryzyko rynkowe, a różnica \(E(R_i)-R_f\) nazywana jest premią za ryzyko aktywa \(i\).
Ze wzoru widzimy, że premia za ryzyko aktywa \(i\) zależy od współczynnika \(\beta_i\).
6.2.2 Współczynnik beta
Współczynnik \(\beta_i\) znany jest jako beta. Jest to znormalizowana kowariancja stóp zwrotu aktywa \(i\) oraz portfela rynkowego. Normalizacja polega na podzieleniu kowariancji stóp zwrotu aktywa \(i\) oraz rynkowej przez wariancję rynkowej stopy zwrotu:
\[\beta_i = \frac{\sigma_{iM}}{\sigma_M^2} = \frac{\rho_{iM} \sigma_i}{\sigma_M}\]
Dla przypomnienia, w powyższym wzorze \(\sigma_{iM}\) to kowariancja pomiędzy stopą zwrotu aktywa \(i\) a rynkową stopą zwrotu, \(\sigma^2_{M}\) to wariancja rynkowej stopy zwrotu, \(\sigma_i\) to odchylenie standardowe stopy zwrotu aktywa \(i\), zaś \(\rho_{iM}\) to korelacja pomiędzy rynkową stopą zwrotu a stopą zwrotu aktywa \(i\).
6.3 Linia rynku papierów wartościowych
Linia rynku papierów wartościowych (security market line, SML) pokazuje zależność pomiędzy betą a oczekiwaną stopą zwrotu. Jest to równanie CAPM przedstawione na wykresie. W warunkach równowagi rynkowej na SML powinny leżeć wszystkie aktywa i portfele (nie tylko portfele efektywne).
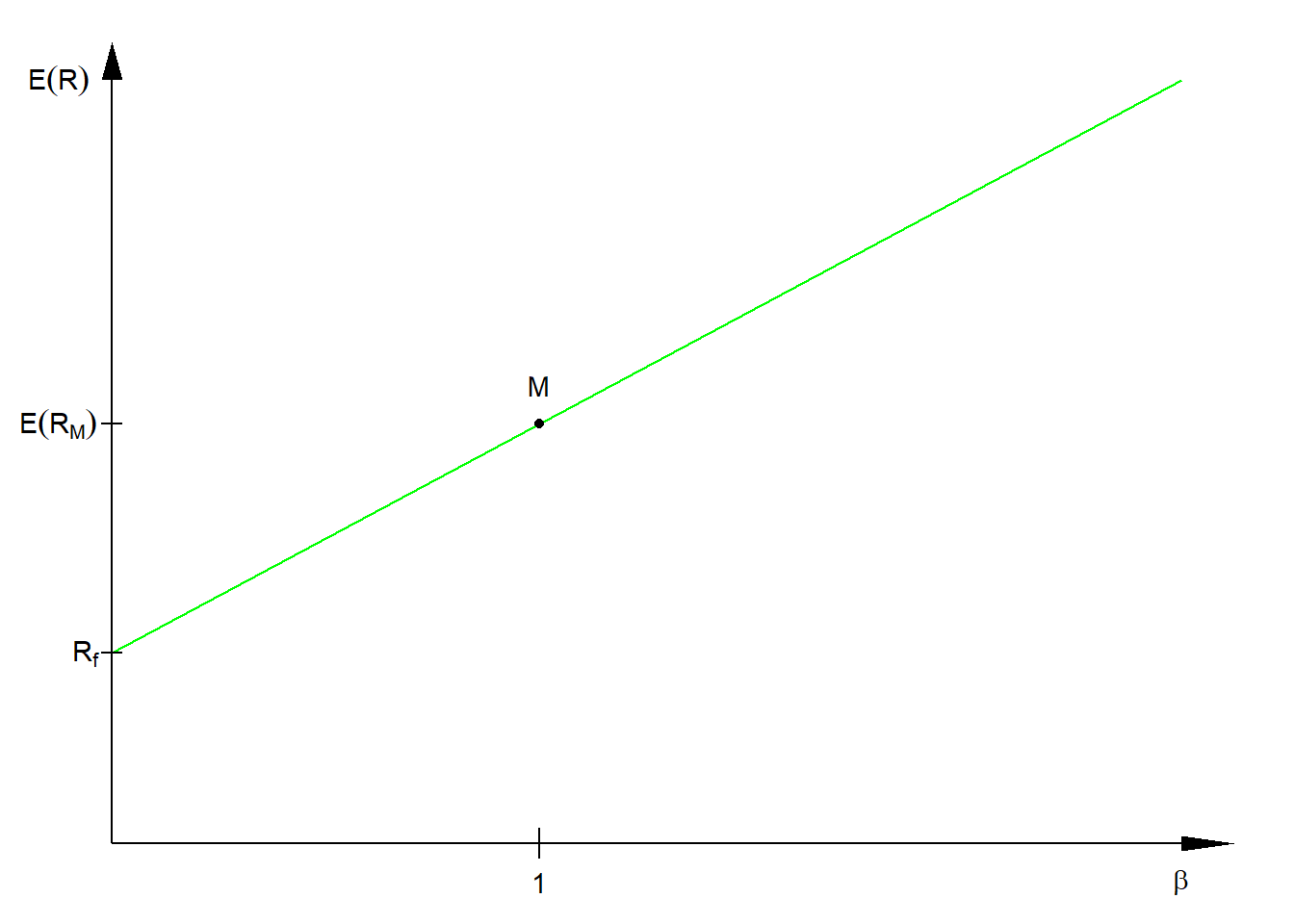
Rysunek 6.2: Linia rynku papierów wartościowych
6.4 Ryzyko systematyczne i specyficzne
Według modelu CAPM rzeczywiste stopy zwrotu z poszczególnych aktywów kształtują się według następującego wzoru:
\[ R_i = R_f + \beta_i (R_M - R_f) + \epsilon_i \]
Wartość oczekiwana składnika losowego \(\epsilon_i\) to według CAPM \(E(\epsilon_i)=0\).
Można wyprowadzić następujący wzór na wariancję stopy zwrotu \(V(R_i)=\sigma_i^2\):
\[ \sigma_i^2=\beta_i^2 \sigma^2_M + \sigma^2_{\epsilon_i} \]
Ten wzór można interpretować w ten sposób, że wariancja stopy zwrotu każdego aktywa składa się z części \(\beta_i^2 \sigma^2_M\) związanej z ryzykiem rynku jako całości (ryzyko systematyczne, niedywersyfikowalne) oraz z części dywersyfikowalnej \(\sigma^2_{\epsilon_i}\) (ryzyko niesystematyczne, idiosynkratyczne, specyficzne).
Część specyficzna nie jest istotna dla inwestora – jeżeli dane aktywo stanowi składnik dobrze zdywersyfikowanego portfela, w jego wycenie według modelu CAPM brane pod uwagę jest wyłącznie ryzyko systematyczne.
6.5 Model CAPM a decyzje inwestorów
Jeżeli model CAPM jest prawdziwy, najlepsza decyzja dla inwestorów to utrzymywanie portfela zbliżonego do portfela rynkowego. Stąd inwestorzy powinni chętnie korzystać z tak zwanych funduszy indeksowych, na przykład w formie tzw. ETF-ów.
Indeks Jensena i współczynnik Sharpe’a pomagają porównać rzeczywiste wyniki z założeniami modelu CAPM.
Indeks Jensena aktywa/portfela \(i\) to:
\[ J_i = \bar{R_i} - R_f - \hat{\beta}_i (\bar{R}_M - R_f), \]
gdzie \(\bar{R_i}\) to średnia zaobserwowana historyczna stopa zwrotu aktywa \(i\), \(R_f\) to stopa wolna od ryzyka z tego okresu, \(\hat{\beta}_i\) to oszacowana na podstawie danych historycznych beta aktywa \(i\), a \(\bar{R}_M\) to średnia zaobserwowana historyczna rynkowa stopa zwrotu.
Indeks Jensena pokazuje, czy zwrot z danego aktywa (portfela, funduszu) jest wyższy (J>0) czy niższy (J<0) niż zwrot wynikający z bety funduszu. Jeżeli model CAPM działa, średnio indeks Jensena powinien wynosić zero.
Uwaga! Indeks Jensena wynoszący 0 nie oznacza, że portfel jest efektywny.
Indeks Sharpe’a ex post aktywa/portfela \(i\) to:
\[ \text{Sharpe } ex\: post = \frac{\bar{R}_i-R_f}{{s}_i}, \]
gdzie \(s_i\) to historyczne zaobserwowane odchylenie standardowe stóp zwrotu aktywa \(i\).
Indeks Sharpe’a stanowi próbę oszacowania czy dany portfel/aktywo jest porfelem efektywnym (leżącym na granicy efektywnej przechodzącej przez portfel rynkowy oraz aktywo wolne od ryzyka). Uzyskaną wartość należy porównać z odpowiednią wartością dla portfela rynkowego.
6.6 CAPM jako model wyceny
Jeżeli rynek pozostaje w równowadze, według modelu CAPM powinna zostać spełniona następująca zależność.
\[ \frac{E(P_1)-P_0}{P_0}=R_f + \beta \left(E(R_M)-R_f\right),\]
gdzie \(E(P_1)\) to wartość oczekiwana aktywów (oczekiwana cena) na koniec okresu utrzymywania aktywów, \(P_0\) to cena bieżąca, \(\beta\) to odpowiednia beta danych aktywów.
Stąd jeżeli założymy, że znamy wszystkie wartości, łącznie z \(E(P_1)\), uzyskujemy formułę na cenę bieżącą:
\[ P_0 = \frac{E(P_1)}{1+R_f+\beta\left(E(R_M)-R_f\right)} \]
Pomijamy tutaj dywidendy (albo wliczamy je odpowiednio do ceny, tworząc adjusted price).
6.7 Ćwiczenia
Zadanie 6.1 (Ruppert and Matteson 2015) Ile wynosi beta portfela, jeżeli \(E(R_P)=16\%\), \(R_f = 5{,}5\%\) i \(E(R_M)=11\%\)?
Zadanie 6.2 (Ruppert and Matteson 2015) Załóżmy, że stopa wolna od ryzyka to 0,03, a oczekiwana stopa zwrotu portfela rynkowego wynosi 0,14. Odchylenie standardowe portfela rynkowego to 0,12.
Zgodnie z CAPM, jaki jest efektywny sposób zainwestowania z oczekiwaną stopą zwrotu równą 0,11?
Ile wynosi ryzyko (odchylenie standardowe) takiego portfela?
Zadanie 6.3 (Ruppert and Matteson 2015) Załóżmy, że stopa wolna od ryzyka to \(R_f=0{,}023\), oczekiwana wartość stopy zwrotu z portfela rynkowego to \(E(R_M)=0{,}10\) i ryzyko portfela rynkowego wynosi \(\sigma_M=0{,}12\).
Ile wynosi oczekiwany zwrot z portfela efektywnego, którego odchylenie standardowe wynosi \(\sigma_P = 0,05\)?
Stopy zwrotu z akcji A mają kowariancję ze zwrotami rynkowymi na poziomie \(\sigma_{AM} = 0{,}004\). Ile wynosi beta akcji A?
Akcje B mają betę równą 1,5, a \(\sigma_{\epsilon_B}=0,18\). Akcje C mają betę równą 1,8, zaś \(\sigma_{\epsilon_B}=0,28\). Ile wynosi oczekiwana stopa zwrotu z portfela składającego się z w połowie z akcji B i w połowie z akcji C? Ile wynosi ryzyko tego portfela przy założeniu, że stopy zwrotu z akcji B i C są niezależne.
Zadanie 6.4 (Ruppert and Matteson 2015) Załóżmy, że stopa wolna od ryzyka wynosi 4%, a rynkowa oczekiwana stopa zwrotu wynosi 12%. Odchylenie standardowe rynkowych stóp zwrotu to 11%. Załóżmy również, że kowariancja stóp zwrotu akcji A z rynkiem wynosi 165[%2] (=\(165 \cdot (1/100)^2\) = 0,0165).
Ile wynosi beta akcji A?
Ile wynosi oczekiwana stopa zwrotu akcji A?
Jeżeli wariancja stóp zwrotu akcji A wynosi 440[%2], jaki jest procentowy udział składnika systematycznego w tej wariancji?
Zadanie 6.5 (Ruppert and Matteson 2015) Załóżmy, że są trzy aktywa ryzykowne z następującymi wartościami bet oraz wariancjami składnika losowego (idiosykratycznego) \(\sigma^2_{\epsilon_j}\).
| j | beta akcji j | wariancja składnika losowego akcji j |
|---|---|---|
| 1 | 0,9 | 0,010 |
| 2 | 1,1 | 0,015 |
| 3 | 0,6 | 0,011 |
Załóżmy również, że wariancja rynkowej stopy zwrotu \(R_M\) wynosi 0,014.
- Ile wynosi beta portfela złożonego w równych częściach z tych trzech aktywów?
- Ile wynosi wariancja takiego portfela?
- Jaka jest udział składnika systematycznego wynikającego z ryzyka rynkowego w całościowej wariancji aktywa 1?
Zadanie 6.6 (Ruppert and Matteson 2015) Załóżmy, że istnieją dwa aktywa obarczone ryzykiem: C i D. Portfel styczny składa się w 60% z C i w 40% z D. Oczekiwana roczna stopa zwrotu to odpowiednio 4% i 6%. Odchylenie standardowe rocznych stóp zwrotu to 10% and 18%. Korelacja pomiędzy stopami zwrotu C i D to 0.5. Stopa wolna od ryzyka wynosi 1.2%.
Ile wynosi oczekiwana roczna stopa zwrotu z portfela stycznego?
Ile wynosi odchylenie standardowe rocznych stóp zwrotu z portfela stycznego?
Jeżeli chcemy uzyskać portfel efektywny z odchyleniem standardowym rocznych zwrotów w wysokości 3%, jaki powinien być udział w takim portfelu aktywa wolnego od ryzyka?
Jeżeli chcemy mieć portfel efektywny z oczekiwaną stopą zwrotu 7%, w jakich proporcjach powinniśmy mieć w portfelu aktywo C, aktywo D i aktywo wolne od ryzyka?
Zadanie 6.7 (Ruppert and Matteson 2015) Ile wynosi beta portfela, jeżeli oczekiwana stopa zwrotu tego portfela to \(E(R_P)=15\%\), stopa wolna od ryzyka to \(R_f=6\%\), a oczekiwana rynkowa stopa zwrotu to \(E(R_M)=12\%\)? Należy założyć, że działa model CAPM, a rynek jest w równowadze.
Zadanie 6.8 (Luenberger 2003) (Linia rynku kapitałowego) Załóżmy, że oczekiwana stopa zwrotu z portfela rynkowego wynosi 23%, a stopa zwrotu bonów skarbowych (wolnych od ryzyka) wynosi 7%. Odchylenie standardowe portfela rynkowego 32%. Załóżmy, że portfel rynkowy jest efektywny.
Napisz równanie linii rynku kapitałowego.
Jakie powinno być odchylenie standardowe, jeżeli wymagana stopa zwrotu wynosi 39%? Gdybyś miała do zainwestowania 1 000 USD, jak powinnaś ulokować swój kapitał, żeby osiągnąć taką stopę zwrotu?
Jakiej wypłaty powinnaś oczekiwać na koniec roku, jeżeli zainwestowałaś 300 USD w aktywa wolne od ryzyka i 700 dol. w portfel rynkowy?
Zadanie 6.9 (Luenberger 2003) Rozważmy świat, w którym są tylko dwa aktywa ryzykowna A i B oraz aktywa wolne od ryzyka, F. Podaży na rynku obu ryzykownych aktywów jest równa, tzn. M = 0,5A + 0,5B. Dane są następujące informacje: \(R_f = 0,10\), \(\sigma_A^2=0,04\), \(\sigma_{AB}=0,01\), \(\sigma_B^2=0,02\) i \(E(R_M)=0,18\).
Zapisz ogólne wyrażenia (nie podstawiając wartości) dla \(\sigma_M^2\), \(\beta_A\), \(\beta_B\).
Jakie, według CAPM, są wartości liczbowe \(E(R_A)\) i \(E(R_B)\)?
Zadanie 6.10 (Luenberger 2003) W Prostolandii istnieją tylko dwie ryzykowne akcje A i B, które opisano w tabeli:
| Akcja | Liczba akcji w obrocie | Cena 1 akcji (USD) | Oczekiwana stopa zwrotu (proc.) | Odchylenie standardowe stopy zwrotu (proc.) |
|---|---|---|---|---|
| Akcja A | 100 | 1,5 | 15 | 15 |
| Akcja B | 150 | 2,0 | 12 | 9 |
Współczynnik korelacji pomięDzy stopą zwrotu z akcji A a stopą zwrotu z akcji B wynosi \(\rho = 1/3\). Istnieją również aktywa wolne od ryzyka, a Prostolandia spełnia wszystkie założenia modelu CAPM.
Jaka jest oczekiwana stopa zwrotu z portfela rynkowego?
Jakie jest odchylenie standardowe portfela rynkowego?
Ile wynosi współczynnik beta akcji A?
Ile wynosi stopa wolna od ryzyka w Prostolandii?
Zadanie 6.11 (Luenberger 2003) W tabeli przedstawiono 10-letnią historię stóp zwrotu uzyskanych przez fundusz inwestycyjny ABC. Mamy ocenić te wyniki na podstawie teorii dochodu i ryzyka oraz modelu CAPM. Czy jest to dobry fundusz, który można zarekomendować inwestorom? Czy przez inwestora kierującego się wartością oczekiwaną i wariancją może być używany jako substytut portfela rynkowego?
| Rok | ABC - stopa zwrotu (proc.) | S & P - stopa zwrotu (proc.) | bony skarbowe - oprocentowanie (proc.) |
|---|---|---|---|
| 1 | 14 | 12 | 7,0 |
| 2 | 10 | 7 | 7,5 |
| 3 | 19 | 20 | 7,7 |
| 4 | -8 | -2 | 7,5 |
| 5 | 23 | 12 | 8,5 |
| 6 | 28 | 23 | 8,0 |
| 7 | 20 | 17 | 7,3 |
| 8 | 14 | 20 | 7,0 |
| 9 | -9 | -5 | 7,5 |
| 10 | 19 | 16 | 8,0 |
Ile wynosi historyczna średnia arytmetyczna i średnia geometryczna (CAGR) stóp zwrotu poszczególnych aktywów?
Ile wynosi historyczne odchylenie standardowe stóp zwrotu tych aktywów?
Ile wynosi kowariancja pomiędzy nadwyżkową stopą zwrotu funduszu ABC (\(R_{ABC} - R_{f}\)) a nadwyżkową stopą zwrotu rynkową (\(R_{M} - R_{f}\))? Jako rynek przyjmujemy indeks S&P.
Ile wynosi współczynnik beta funduszu ABC?
Ile wynosi indeks Jensena dla funduszu ABC i dla całego rynku?
Ile wynosi współczynnik Sharpe’a ex post dla funduszu ABC i dla całego rynku?
Co na tej podstawie możemy powiedzieć o funduszu ABC?
Zadanie 6.11 Rozważmy możliwość zainwestowania w akcje spółki naftowej, której dochody można traktować jak zmienną losową z uwagi na niepewność związaną z wielkością złoża i przyszłymi zmianami cen ropy. Oczekiwana wartość dochodu z posiadania tych akcji jest równa 1 000 USD przy relatywnie wysokim odchyleniu standardowym na poziomie 40%. Współćzynnik beta wynosi 0,6 i jest stosunkowo niski, ponieważ o ile ryzyko związane ze zmianami cen ropy jest skorelowane z rynkiem, o tyle poziom wydobycia ropy skorelowany nie jest. Stopa wolna od ryzyka jest