Capítulo8 DMAIC5. Controlar

8.1 Objetivos de aprendizaje

En este capítulo trabajaremos sobre los siguientes objetivos de aprendizaje:

• Descubrir las actividades a realizar en la etapa Controlar de un proyecto Lean Seis Sigma.
• Repasar conceptos y técnicas de Control Estadístico de los Procesos (CEP).
• Conocer los requisitos en la confección de un Plan de Control.
• Conocer las necesidades para la transferencia del proyecto y la finalización del Proyecto de Mejora Lean Seis Sigma.

8.2 Introducción

Los objetivos en la etapa CONTROLAR de un proceso DMAIC son:

• Implantar las soluciones de mejora de forma definitiva.
• Diseñar un sistema de control del proceso, para lo que habremos de tener claro cuándo un proceso está bajo control y cómo identificar “escapes” del control para intervenir. Para ello será esencial aplicar herramientas de Control Estadístico de Procesos (CEP).
• Completar y cerrar el informe del proyecto de mejora, comunicarlo y transferirlo con efectividad.

En este capítulo describiremos en profundidad en qué consiste y cómo se realiza el plan de control de los procesos, una vez implantada una solución de mejora. Estudiaremos a continuación los conceptos básicos del Control Estadístico de los Procesos, con el que monitorizar el funcionamiento de un proceso, arbitrando mecanismos de detección automática de variaciones especiales sobre las que sea preciso intervenir. Finalizaremos detallando cómo ultimar y transferir el proyecto de mejora, para darlo por finalizado.

Con esto, damos por terminado este manual, a través del cual hemos realizado un recorrido a través de las diversas etapas y herramientas básicas a considerar en la aplicación de la metodología Lean Seis Sigma para la mejora de los procesos.

8.3 El plan de control de procesos

El control de calidad se puede expresar como un proceso en el que:

• Se selecciona el objeto de control, es decir, la característica del producto que queremos asegurar (Y) o el parámetro del proceso que condiciona dicha características (X).
• Se establece la unidad de medida, especificando los medios o instrumentos que se van a utilizar para medir (sensores), la frecuencia con la que se va medir, el tamaño de muestra y la forma en la que se registrarán los resultados de las mediciones. Para establecer esta frecuencia, conviene tener en cuenta la “estabilidad” del proceso; si el proceso es estable el control se puede espaciar, pero si el proceso no es estable conviene realizar controles periódicamente.
• Se establece el nivel de rendimiento objetivo, es decir, cuál es el valor o gama de valores que se deben obtener cuando se realizan mediciones del objeto de control.
• Se aplica el método utilizando el sensor par realizar las medidas establecidas
• Se compara el valor obtenido en la medición con respecto al valor o intervalo de valores objetivo
• Se decide, en consecuencia del resultado, dejar que el proceso siga funcionando o actuar sobre la diferencia observada, corrigiendo el proceso.

Todos estos puntos se detallan en la Figura 8.1.

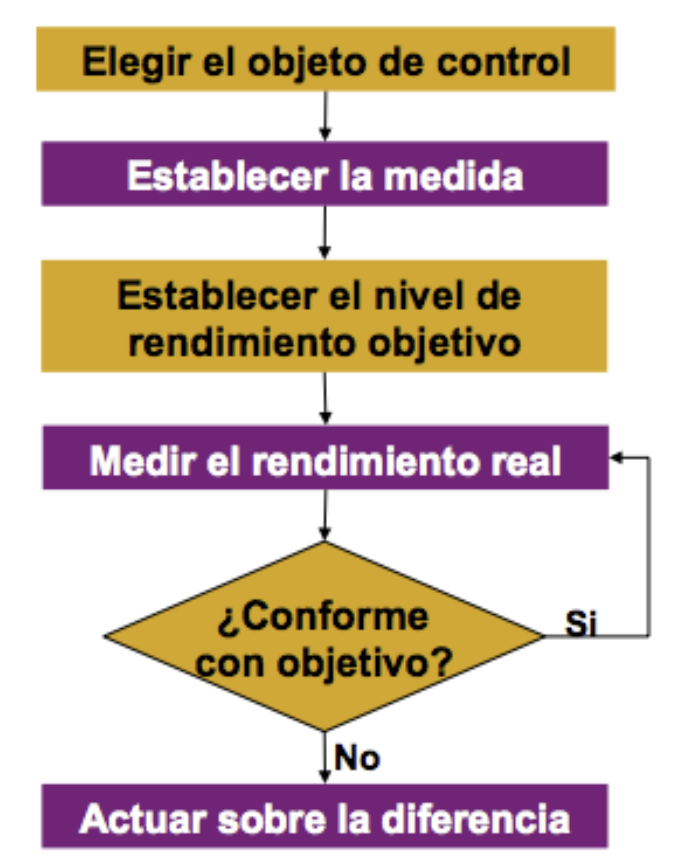
Figura 8.1: Esquema de la dinámica para el control de un proceso.

Esta etapa en un proyecto de mejora ha de culminar necesariamente en la redacción de un plan de control en el que se especifiquen todas las características del proceso mejorado y todos los requerimientos para asegurar el control de su funcionamiento bajo los estándares ajustados en la mejora. Indica además las instrucciones de trabajo para realizar el control de la calidad (frecuencia y modo de muestreo), establece los métodos de detección de situaciones fuera de control y las medidas consecuentes a tomar en función de dichas desviaciones.

8.3.1 Conceptos clave

Variables a controlar

Recordemos la estructura que hemos utilizado en secciones anteriores para describir un “proceso,” representada en la Figura 5.1, donde visualizábamos los condicionantes \(X\) que afectan al proceso para generar unas salidas o resultados \(Y\). Dado que los resultados siguen una relación del tipo \(Y = f (X)\), parece lógico que nuestro objeto de control se centre en las variables o parámetros del proceso (\(X\)’s) más que en las salidas, puesto que su variación repercute directamente sobre la \(Y\).

Los elementos del proceso, entre los que se encuentran nuestros objetos de control, pueden ser “factores” que se pueden medir y regular, pero también pueden ser “alternativas” que no se pueden medir, ni observar o comprobar, y por lo tanto no se podrán regular. Al determinar la forma de controlar, será necesario tener en cuenta estos aspectos, ya que no siempre podremos “controlar” determinadas variables del proceso. También hemos de recordar ahora que no todas las variables o parámetros del proceso influyen de la misma forma en su rendimiento. Hay unas pocas variables vitales (regla de Pareto) que son las que afectan en mayor medida al resultado. Sobre esas variables, que ya han sido identificadas a lo largo del proyecto, y especialmente en la etapa Analizar, se habrán de aplicar los esfuerzos de control.

Instantes a controlar

Si hablamos de instantes o momentos del proceso en los que aplicar medidas de control, cabe considerarlas en:

• El inicio del proceso, o puesta a punto, donde es preciso asegurar la disponibilidad y funcionalidad de todos los elementos necesarios para que el proceso pueda comenzar a funcionar eficaz y eficientemente. Esto afecta a materiales, equipos, sistemas, documentos, etc.
• Durante el proceso, verificando si las variables de control se mantienen dentro de los valores objetivo, para intervenir o detener el proceso en caso de que no fuera así.
• Al final del proceso, controlando el resultado para verificar su conformidad con respecto a los objetivos.
• También será preciso establecer revisiones periódicas de las instalaciones y medios para asegurar su disponibilidad y funcionalidad durante el tiempo que ha de funcionar el proceso.

Tipos de error que genera defectos

Otro aspecto a tener en cuenta en el control de los procesos es el modo en que pueden generarse los errores que conducen a defectos. Podemos distinguir básicamente tres tipos:

• El error inadvertido, que se suele producir por descuidos, falta de atención o, a veces, por limitaciones fisiológicas o psicológicas de las personas. Por ejemplo, una persona con dificultades de visión puede cometer errores inadvertidos de lectura y transcribir un dato erróneo.

• El error técnico se produce por falta de las habilidades necesarias para evitarlo o prevenirlo. Igual que el anterior es un error no intencionado, pero en este caso la persona es consciente de su falta de habilidad. Una tarea compleja, para la cual la persona no ha sido suficientemente entrenada, producirá este tipo de errores.

• El error consciente se produce por numerosas causas. Instrucciones de trabajo cambiantes o conflictivas pueden generar el “camino fácil” de realizar las actividades de una forma determinada, y cometer errores. Otras veces, las personas tienden a saltarse las normas, asumiendo que no son necesarias para realizar la actividad, con las lógicas consecuencias.

A veces el error, inconsciente o no, se produce en los propios equipos directivos. Una comunicación inadecuada, unas instrucciones vagas, comunicadas de manera informal, una actitud diferente, si no opuesta, a la que se pretende inculcar en los demás, etc., son algunos ejemplos de errores que se deben evitar. En la Figura 8.2 se muestran, caracterizados, estos tres tipos de error controlables, y se aportan soluciones o remedios para evitarlos o reducirlos.

Figura 8.2: Tipos de error humano, características y remedios para evitarlos y/o reducirlos.

Mecanismos de control, reducción o eliminación del error

Existen distintos tipos de mecanismos, más y menos eficientes, para la eliminación y/o reducción de errores: los que impiden el error, los que avisan de un error y los que detectan el defecto.

• Mecanismos para impedir el error. El mejor sistema para evitar los errores es impedirlos. Para ello, el mundo de la manufactura ha desarrollado numerosos mecanismos. Uno de los más típicos lo encontramos en las clavijas para conexiones de equipos informáticos. Al ser diferentes, se impide la conexión inadvertida de un elemento en la clavija que no le corresponde.

• Mecanismos de aviso. En segundo lugar se sitúan los métodos que avisan del error antes de que se produzca, aunque no lo impiden. En general se trata de dispositivos (sensores, indicadores, etc.) que generan señales de alarma para advertir del posible error.

• Mecanismos detectores del defecto. Los sistemas menos eficaces, aunque a veces son los únicos que podemos aplicar, son los que detectan el defecto (no el error), cuando ya se ha producido, pero permiten evitar que dicho defecto continúe a lo largo del proceso.

En cualquier caso, los controles o inspecciones en la fuente son los mecanismos más habituales para evitar que un defecto progrese hacia las operaciones siguientes a la que se ha producido.

La aplicación de métodos o mecanismos para impedir o prevenir los errores es un proceso simple que consiste en aplicar los siguientes pasos:

1. Describir el defecto real o potencial y la frecuencia de aparición.
2. Identificar la operación en la que se produce o puede producir el defecto.
3. Analizar las tareas necesarias para realizar la operación, de acuerdo con los procedimientos o instrucciones establecidas.
4. Identificar las condiciones de error que pudieran contribuir a producir el defecto.
5. Aplicar la técnica de “los 5 porqués” a las condiciones de error con el fin de identificar causas potenciales. Esta técnica consiste en partir de la pregunta “¿Por qué se produce el fallo?” y formular hasta un total de 5 preguntas que añadan el “por qué” a cada una de las respuestas consecutivas proporcionadas. Ejemplo: ¿Por qué se averió la máquina? Porque falló una pieza de rodaje. ¿Por qué falló la pieza? Porque hacía mucho que se había revisado. ¿Por qué hacía mucho que se había revisado? ….
6. Definir y aplicar un mecanismo o estrategia para impedir o prevenir el error.

El paso a nivel nos proporciona un buen ejemplo de diferentes alternativas de sistemas de prevención o protección del error, con:

• Normas implícitas. El conductor o peatón es consciente de que el paso a nivel puede suponer un riesgo, por lo que suele adoptar precauciones antes de atravesarlo.
• Normas explícitas. Para evitar el descuido, las autoridades de tráfico colocan señales de advertencia de la proximidad de un paso a nivel. Estas señales avisan pero no impiden el error de cruzar indebidamente el paso a nivel.
• Bajo nivel de intervención física. La compañía de ferrocarril coloca dispositivos de restricción y bloqueo, como semáforos y barreras que impiden o dificultan el paso (no lo llegan a impedir para peatones).
• Alto nivel de intervención física. El mejor sistema es desviar el paso de automóviles y peatones, impidiendo que pasen por la misma zona por donde pasa el tren, e incluso vallando la vía. De esta forma se impide definitivamente la posibilidad de accidente.**

Lógicamente estos últimos sistemas de intervención física son más costosos que los anteriores, pero son altamente eficaces. Un balance entre el coste de impedir (o dificultar) el error y el de las consecuencias cuando se produce, puede ayudar a optar por el sistema más adecuado.

En entornos industriales, especialmente cuando hay máquinas que entrañan riesgos para las personas, ya es una práctica habitual proteger espacios para que no sean accesibles, o utilizar mecanismos que paran la máquina si hay algún obstáculo en su trayectoria de desplazamiento. También en otros entornos no industriales se utilizan mecanismos para evitar errores, tales como listas de comprobación previas al inicio de una tarea, aplicaciones informáticas que impiden introducir datos diferentes a los previstos, etc.

A modo de conclusión, podemos representar el control estadístico de los procesos con la pirámide que se muestra en la Figura 8.3. En la base, siendo los más numerosos, han de estar los controles automáticos, que son métodos no humanos que proporcionan control sobre muchos equipos, instalaciones, procesos y se realizan en tiempo real, autorregulando el proceso o, en el peor de los casos, proporcionando alarmas.

El resto de los controles (autocontrol, auditoría y pocos vitales) requieren de la intervención humana y el área de pirámide que ocupan representa el volumen que han de representar en un plan de control del proceso.

En muchos casos, con independencia o de forma complementaria al autocontrol, se realizan auditorías para verificar el funcionamiento de los procesos o para verificar la adecuación de métodos o sistemas.

Finalmente, la dirección de la empresa supervisa los pocos procesos vitales mediante los informes de resultados, cuadros de mando, etc., y actúa cuando observa desviaciones de los objetivos.

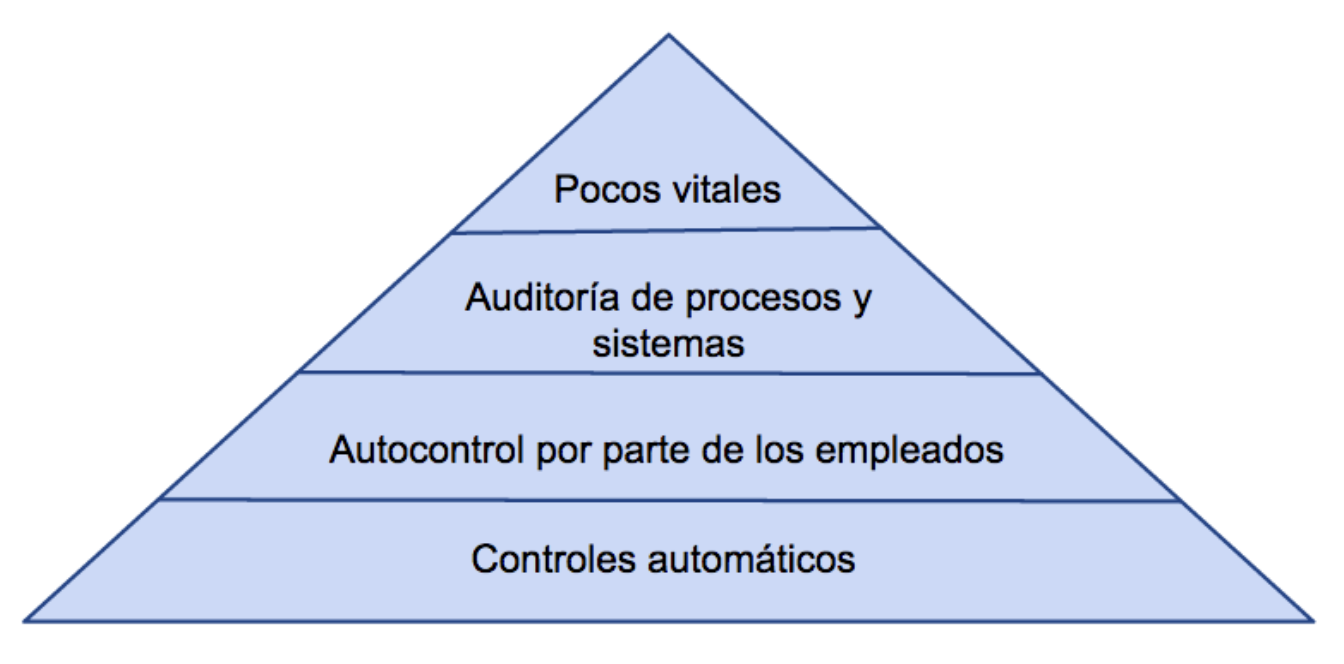
Figura 8.3: Pirámide de control de un proceso.

Se detalla a continuación en qué consisten cada uno de estos tipos de controles del error para reducir o evitar los defectos.

8.3.2 Sistemas a prueba de error: Poka-Yoke

Poka-Yoke proviene del japonés yokeru (evitar) y poka (errores inadvertidos), para generar el concepto “evitar los errores inadvertidos.” Los sistemas poka-yoke constituyen un sistema de control automático-autorregulado para evitar los errores.

Son ejemplos de sistemas a prueba de error:

• las conexiones de tamaños y formas diferentes,
• las etiquetas de colores diferentes,
• las listas de comprobación, etc.

La forma de una tarjeta SIM y su receptáculo en un dispositivo móvil, son un ejemplo de sistema poka-yoke, pues sólo es posible su colocación en la posición adecuada.

8.3.3 El autocontrol

El autocontrol es el motor que ha permitido a muchas empresas de manufactura incrementar sus tasas de productividad y, al tiempo, disminuir los defectos o rechaces en los procesos, aunque no siempre se aplica a los procesos transaccionales y de servicio, a pesar de su utilidad.

Para aplicar el autocontrol y como paso previo, es preciso que el proceso sea capaz de cumplir con los niveles de rendimiento requeridos, aunque no lo haga siempre. Precisamente uno de los motivos de controlarlo es ése: que no siempre el proceso funciona de la misma forma y necesita cierta regulación.

El autocontrol se basa en tres elementos o requisitos:

• Las personas que intervienen en el proceso saben lo que han de hacer y en consecuencia, lo que se espera que hagan. Esto significa que conocen los objetivos de su actividad y las instrucciones para conseguirlos.
• Las personas saben lo que están haciendo y por lo tanto lo que están rindiendo en relación a los objetivos. En otras palabras, han de disponer de las herramientas de medición que les permitan evaluar el resultado de su actividad para compararlo con los objetivos.
• Por último, las personas tienen la capacidad y autoridad para regular el proceso, realizando los ajustes necesarios cuando el resultado de la actividad no es conforme con respecto a los objetivos.

Estos tres elementos son la clave para conseguir que las personas se sientan “propietarias” de sus tareas y apliquen sus esfuerzos para alcanzar los objetivos.

8.3.4 La auditoría de proceso

Cuando el “sujeto” de control no es una variable que se pueda medir, sino una alternativa de funcionamiento, el control se suele transformar en auditoría.

Una auditoría de proceso es una revisión o comprobación que se realiza de forma periódica y sistemática (siguiendo un método) para comprobar que:

• Se utilizan los medios materiales y humanos establecidos.
• Las actividades siguen la secuencia establecida y se realizan de acuerdo con las instrucciones y/o métodos aprobados.
• Los controles del proceso se realizan con la frecuencia establecida.
• Los resultados del control se registran en la forma establecida.

La auditoría puede ser presencial, de modo que el auditor “ve” cómo está funcionando el proceso y verifica si se ajusta a lo establecido o testimonial, o no presencial, en la que el auditor pregunta acerca del funcionamiento del proceso y verifica los registros oportunos para asegurar que se ha ajustado a los establecido.

En la medida que sea posible es preferible la auditoría presencial, aunque muchos procesos, dada su naturaleza, dificultan la presencia del auditor, que puede interferir en el funcionamiento del proceso.

8.4 Control estadístico de los procesos

Desde el punto de vista estadístico a partir de los datos, el control de los procesos se realiza a través de diversas técnicas que conforman lo que se denomina Control Estadístico de los Procesos. Para empezar, cabe mencionar que los resultados observables de un proceso tienen variaciones originadas por dos tipos de causas:

• Las causas comunes o aleatorias, se refieren a las muchas fuentes de variación que están en el proceso y que hacen que su resultado tenga una distribución estable y predecible a lo largo del tiempo.

• Las causas especiales o asignables se refieren a fuentes de variación que no están siempre presentes en el proceso. Cuando intervienen dichas fuentes, la distribución del proceso cambia en el tiempo y el proceso se inestabiliza.

Cuando un proceso está afectado solamente por sus causas comunes de variación, se dice que está bajo control estadístico, o simplemente “bajo control”. Cuando un proceso está bajo control, su resultado es predecible.

Si el proceso está afectado, además de por sus causas comunes, por alguna causa especial, deja de ser estable y entonces se dice que está “fuera de control”. Cuando un proceso está fuera de control su resultado es impredecible.

8.4.1 ¿Qué es el CEP?

El Control Estadístico de los Procesos o CEP (Statistical Process Control, SPC, en inglés) es un método de control de los procesos, basado en el tratamiento estadístico de los datos que permite estudiar la variabilidad de los procesos y determinar cuándo aparecen cambios (variables especiales) que justifiquen una intervención para corregirlos.

El CEP trabaja sobre las fuentes de variabilidad posibles (comunes y especiales) y permite identificar cuándo el proceso cambia sus pautas de variabilidad y genera situaciones fuera de control, y así poder intervenir para investigar sus causas y actuar en consecuencia, reajustándolo para evitar que produzca defectos. Utiliza fundamentalmente gráficos de control que comparan el valor actual del proceso respecto a los patrones de variabilidad aleatoria, y así permiten detectar la variación producida por causas especiales, a través de “señales de fuera de control”.

Cuando un proceso está funcionando bajo control, y no presenta síntomas o tendencias en sus resultados la decisión más acertada es dejarlo funcionar, sin actuar sobre sus variables de funcionamiento. Lo contrario se conoce como “sobrecontrol.”

Cuando el proceso se ve afectado por causas especiales la decisión acertada es intervenir en el proceso, actuando sobre dicha causa especial. Si la presencia de esta causa no se detecta, se produce el “infracontrol.”

8.4.2 Ventajas del CEP

Las ventajas básicas del CEP son:

• Se trata de una técnica probada para la mejora de la productividad en el entorno industrial y en los servicios.
• Es eficaz para la prevención de defectos o fallos.
• Evita ajustes o “retoques” innecesarios del proceso.
• Proporciona información de diagnóstico.
• Proporciona información sobre la capacidad del proceso.
• Puede utilizarse tanto para variables cuantitativas como cualitativas.

A pesar de las ventajas descritas del hecho de llevar a cabo un control estadístico de los procesos, la práctica de estos métodos de control no es generalizada.

Algunos sectores de actividad, como el de automoción, química, farmacia, electrónica de consumo, etc., son usuarios del CEP, pero en otras industrias y, sobre todo en los servicios, no se está utilizando en la medida que podría. Quizás el término “estadístico” hace que se perciba como un método complejo que sólo puede ser aplicado por especialistas, si bien está basado en procedimientos gráficos muy estandarizados y accesibles.

En esta sección trataremos de explicar estos métodos de forma simple.

8.4.3 Necesidades del CEP

El control estadístico de los procesos tiene una serie de necesidades que son compensadas por las ventajas de su utilización.

• En primer lugar precisa de una formación básica y sencilla de las personas que van a utilizar el método, enfocada a cómo aplicar el método al proceso concreto.
• Requiere una sistematización en la recogida de información, con unos protocolos estandarizados sobre el modo de recoger los datos y una frecuencia fijada.
• Precisa de representaciones gráficas y análisis estadísticos adecuados, basados en gráficos de control pertinentes.
• Y por último, y en la línea del autocontrol, necesita que las personas que lo utilizan reaccionen ante cualquiera de las señales de aviso que proporciona el CEP, realizando los ajustes pertinentes en el proceso.

8.4.4 Cómo funciona el CEP

El CEP see realiza en dos fases, preparar y explotar, cuyos pasos se describen a continuación.

Fase I. PREPARAR

Básicamente se refiere a preparar el escenario para hacer visible el funcionamiento del sistema a partir de gráficos de control (que enseguida definiremos).

• Paso 1. Seleccionar la variable a monitorizar, el modo de muestreo (tamaño, frecuencia y método de medición) y el gráfico adecuado en función del control a realizar.
• Paso 2. Seleccionar una muestra inicial representativa del proceso bajo control para fijar, con ellos, los límites de control, esto es, las fronteras entre las que han de discurrir los datos cuando el proceso está bajo control, esto es, los límites de control, y la línea central, en torno a la que se distribuirán dichos datos.

Fase II. EXPLOTAR

• Paso 3. Obtener los valores de la variable a observar y monitorizarla a lo largo del tiempo según los gráficos elegidos, con la línea central y límites de control prefijados con la muestra bajo control.
• Paso 4. Interpretar los resultados y comprobar las condiciones para los datos-periodos que quedan fuera de control, para decidir las intervenciones oportunas.

8.4.5 Gráficos de control

Un gráfico de control es un gráfico bidimensional que representa en el eje \(Y\) la variable monitoreada y en el eje \(X\) la secuencia temporal del monitoreo. Añade tres líneas útiles para identificar si el proceso está bajo control o no: una línea central que marca la tendencia media (y se construye con la media de la variable monitorizada para los datos bajo control), y unos límites de control inferior y superior, que marcan el margen de variación esperado bajo circunstancias de control, y que se construyen generalmente en términos de numeros de desviaciones típicas a la media, utilizando la desviación típica calculada en la muestra bajo control; normalmente se usan tres desviaciones típicas en torno a la media \(\pm 3 \sigma\), siguiendo el modelo de distribución habitual en una distribución normal.

Un ejemplo de gráficos de control se muestra en la Figura 8.4, con dos descriptivos de una misma variable: las observaciones individualizadas (gráfico superior) y los recorridos móviles (gráfico inferior), esto es, las distancias entre observaciones consecutivas. En estos gráficos en particular se aprecia una tendencia estable en el tiempo, con todas las observaciones entre los límites de control (líneas rojas) y en torno a la línea central (en azul).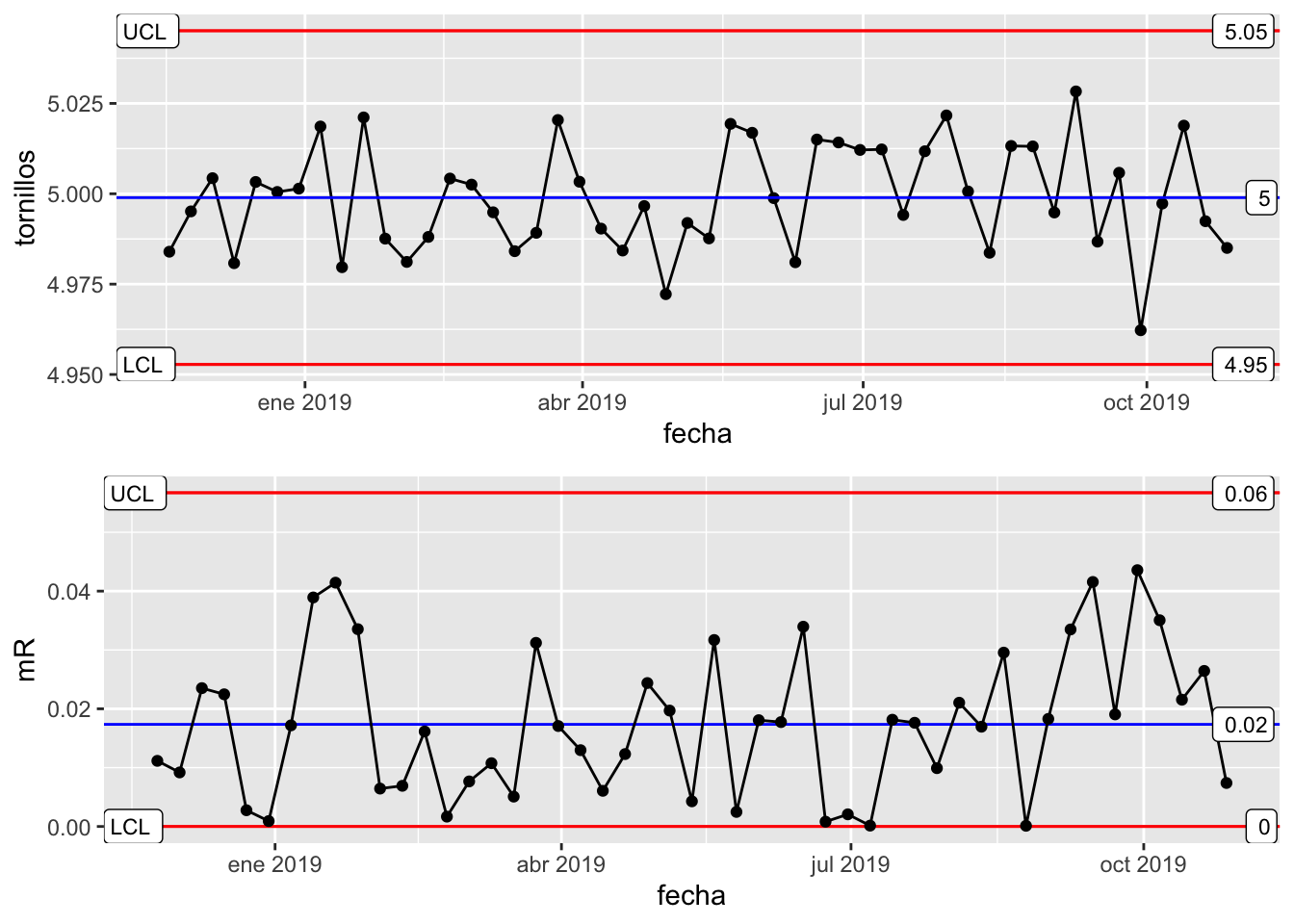

Figura 8.4: Gráficos de control de datos individualizados y recorridos móviles para las longitudes de tornillos.

Una vez representados los datos, en función de ciertas “señales” se determina si el proceso está variando de acuerdo con su patrón de variación natural, lo que indicaría que solamente están interviniendo las causas comunes de variación, o si la variación del proceso ha cambiado de patrón y ha aparecido alguna causa especial a investigar y, en su caso, a corregir. Las causas especiales también pueden identificarse a través de patrones en el gráfico de control: tendencias, ciclos, variación y estacionalidad. Cuando se identifica una desviación destacable respecto de los límites de control, se ha de emprender una investigación para identificar las causas, analizarlas y erradicarlas. Una descripción detallada de las opciones para detectar desviaciones del control se da en la Sección 8.4.8.

El CEP funciona como una prueba de hipótesis que compara, gráficamente, el resultado actual de una variable del proceso, respecto a unos valores o límites centrales y de control, que identifican la variabilidad natural del proceso y se construyen con datos bajo control. En principio, la hipótesis nula (\(H_0\)) es que el proceso está funcionando dentro de su patrón de variación natural y la hipótesis alternativa (\(H_1\)) es que el patrón de variación ha cambiado.

Al comparar el resultado actual con los límites de control y la línea central, existen una serie de señales, conocidas como situaciones fuera de control, que permiten rechazar la hipótesis nula y concluir que el proceso ha cambiado su patrón de variación y, por tanto, es necesario investigar la variación especial que ha aparecido para, caso de ser necesario, actuar sobre ella para “reconducir” al proceso hacia su patrón de variación natural.

En función del tipo de la variable que se va a controlar (cuantitativa o cualitativa) y también del tamaño de los lotes muestreados, esto es, si se inspeccionan unidades o lotes de varias unidades, existen diferentes gráficos de control, y los básicos se resumen en la Figura 8.5.

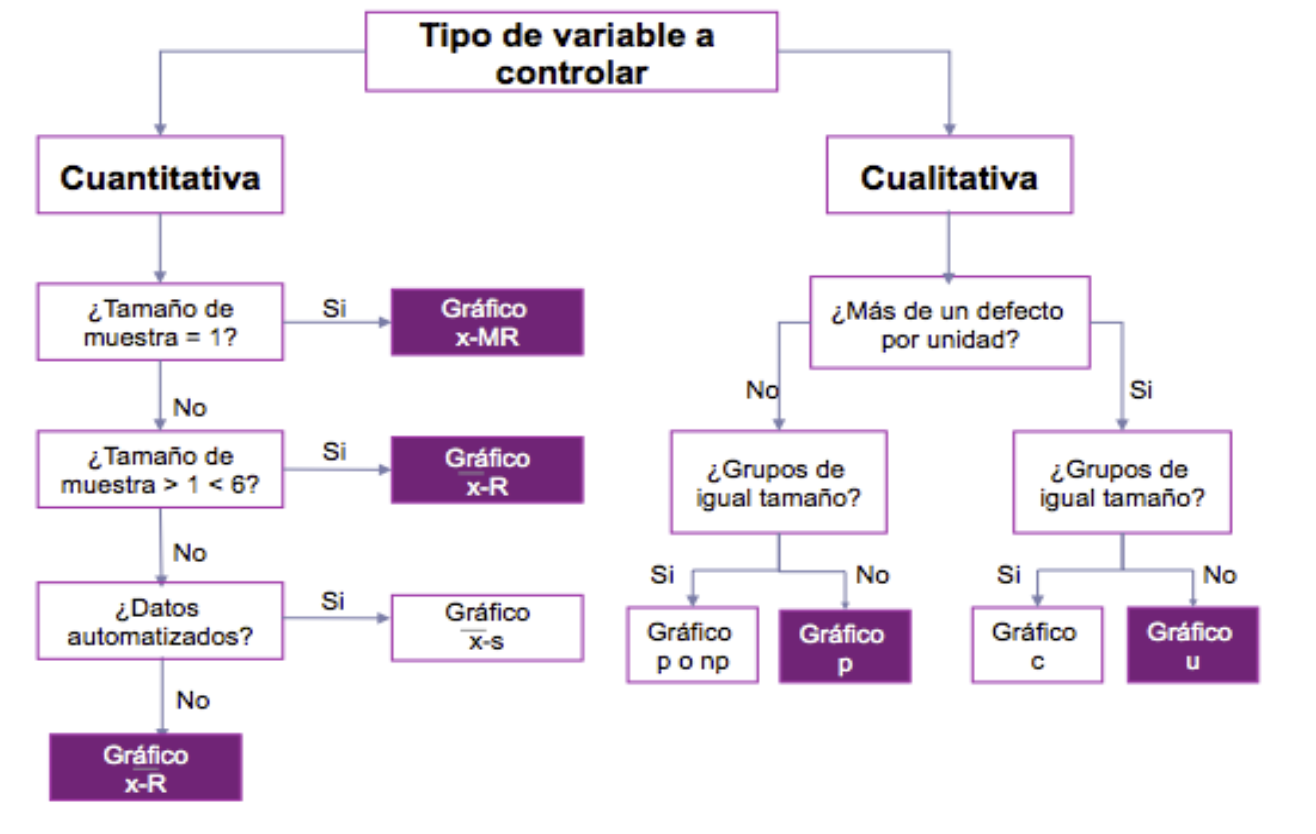
Figura 8.5: Tipos de gráficos de control en función de las características de los datos.

Básicamente la diferenciación primera la da el tipo de la variable a controlar, si es cuantitativa o cualitativa. En el caso de ser cuantitativa, se distingue entre que las muestras sean individuales, situación en que se grafican todos los datos, o no, y los datos vengan agrupados por lotes, situación en la que se grafica un descriptivo de cada lote. Si las variables son cualitativas, se grafican generalmente los volúmenes o proporciones de defectos.

También son varias las librerías con las que realizar estos gráficos en R (R Core Team 2021). Utilizaremos en este manual las librerías qicharts2 (Anhoej 2021), qcc (Scrucca 2017) y ggQC (Grey 2018).

Pasemos pues, a describir en primer lugar los diferentes tipos de gráficos, y luego detallaremos cómo identificar variaciones especiales (desviación del control), ejemplificándolo todo en R.

8.4.6 Gráficos de control para variables cuantitativas

Si la variable es cuantitativa, el control se centrará en los valores individuales observados o en los recorridos móviles entre observaciones consecutivas, y cuando el muestreo se realiza por lotes, en los estadísticos media, rango o recorrido, y desviación típica.

• Gráficos de individuos \(i\) y recorridos móviles \(mR\) (también identificados en ocasiones como gráficos \(x-mR\)), que muestran, respectivamente, las mediciones individualizadas de las unidades monitorizadas y las diferencias entre cada valor y el anterior (recorridos), en valor absoluto.

Simulamos en el ejemplo a continuación, tres procesos normales con 5 lotes cada uno de ellos. El tamaño de los lotes es de 20 y el número de observaciones para cada proceso es de 100. El primero se simula bajo control com media 0 y desviación típica (s) 1 (las 100 primeras observaciones), el segundo con más variabilidad (s=4) (las 100 siguientes) y el tercero (las 100 últimas), además de con más variabilidad, con distinta media (media=3 y s=4).

# Simulamos tres procesos: el primero bajo control
# semilla aleatoria para obtener siempre las mismas simulaciones
set.seed(0123) 
n=100
proc1=data.frame(proc=factor(rep(1,n)),
                 metric=rnorm(n,sd=1),
                 lote=rep(1:5,each=n/5),
                 run_id=1:n)
# el segundo con más variabilidad
set.seed(1234)
proc2=data.frame(proc=factor(rep(2,20)),
                 metric=rnorm(n,sd=4),
                 lote=rep(6:10,each=n/5),
                 run_id=(n+1):(2*n))
# el tercero con más variabilidad y distinta media
set.seed(3456)
proc3=data.frame(proc=factor(rep(3,20)),
                 metric=rnorm(n,mean=3,sd=4),
                 lote=rep(11:15,each=n/5),
                 run_id=(2*n+1):(3*n))
datos=rbind(proc1,proc2,proc3)
datos$control=factor(rep(c("Bajo control","Fuera control"),
                         c(20,40)))

Representamos los datos simulados en la Figura 8.6 para ver cómo se comportan los valores individualizados (en el i-chart) y los recorridos (en el mR-chart). El cambio en medias entre los procesos 1-2 (media en torno a cero) y el proceso 3 (media en torno a 3) es más fácil de apreciar en los gráficos i-chart, así como el cambio en varianza al pasar del proceso 1 al 2 (franjas de control más amplias para el proceso 2); el gráfico de recorridos mR-chart da mejor información sobre los cambios en variabilidad al rebasar el proceso bajo control, como muestran las bandas grises de control para el proceso 1, y las franjas mucho más amplias pero similares para los procesos 2-3 (con varianza similar).

library(qicharts2)
library(gridExtra)
# Representamos los datos individualizados con los datos
q1=qic(x=run_id,y=metric,data=datos,
       freeze=n, # identificando la zona bajo control
       chart="i",xlab="Observaciones",ylab="Valor",
       part=c(100,200),# identificando los tres procesos
       show.labels=TRUE,
       part.labels=c("Proceso1","Proceso2","Proceso3"))
#y con los recorridos móviles
q2=qic(x=run_id,y=metric,data=datos,
       freeze=n, # identificando la zona bajo control
       chart="mr",xlab="Observaciones",ylab="Valor",
       show.labels = TRUE,
       part=c(100,200),# identificando los tres procesos
       part.labels=c("Proceso1","Proceso2","Proceso3"))

grid.arrange(q1,q2,ncol=2)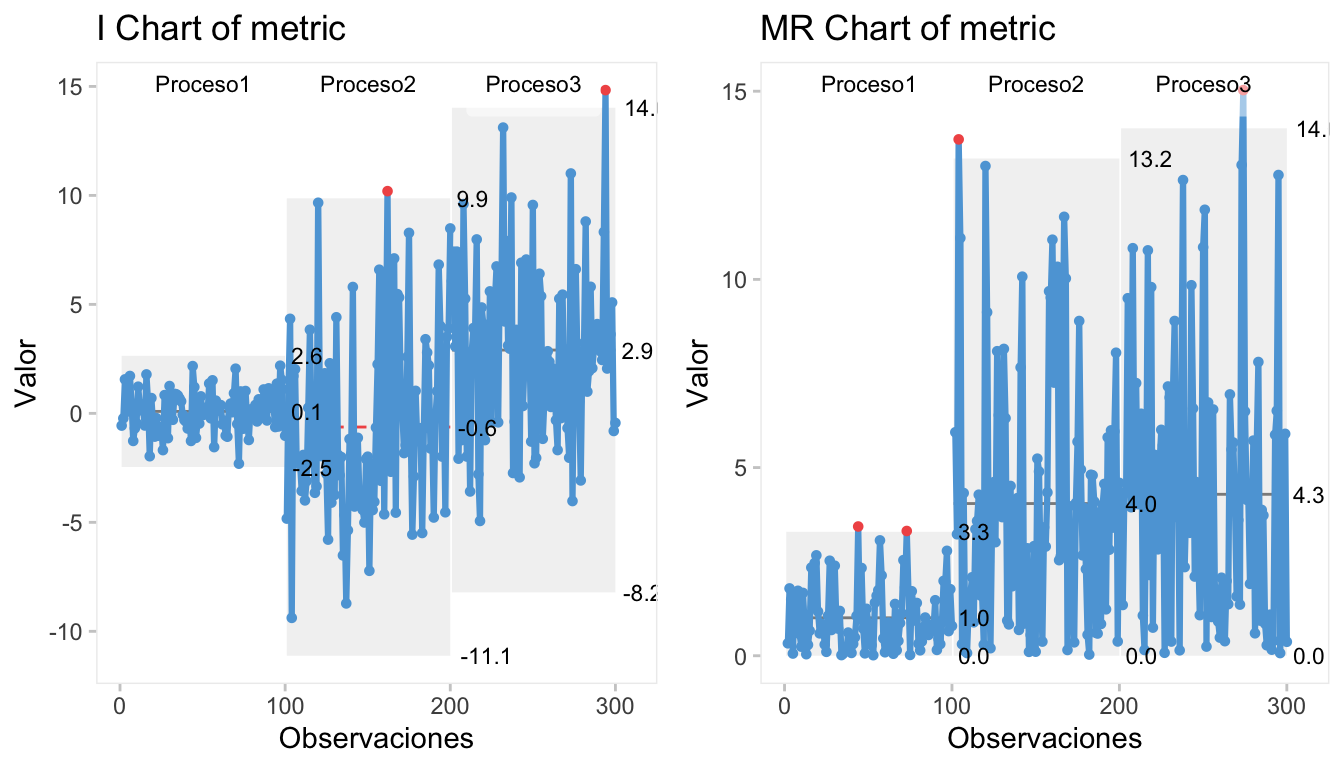

Figura 8.6: Gráfico individualizado y de recorridos móviles i-mR para tres procesos distintos consecutivos en el tiempo.

• Gráficos de medias y recorridos móviles \(\bar{x}-mR\) o medias y desviaciones \(\bar{x}-s\). Cuando las mediciones se realizan por lotes de unidades, y estamos interesados en el comportamiento de los lotes, se grafican los descriptivos por lotes a partir de descriptivos que resumen el comportamiento en cada lote. Así, para la tendencia se utilizan los gráficos de medias Xbar-chart o medianas calculadas en cada lote, y para la dispersión, los de recorridos móviles o mR-chart, calculados con la diferencia entre medias de dos lotes consecutivos, o el de desviaciones típicas en cada lote, s-chart.

En la Figura 8.7 se aprecia el cambio en media en los lotes del proceso 3 (lotes 11-15) y el cambio en varianza en los lotes del proceso 2 y 3 (lotes 6 al 15). En la Figura 8.8 se percibe el cambio en variabilidad de la zona bajo control a la zona fuera de control a través de los gráficos de recorridos (mR-chart) y de desviaciones típicas (s-chart), con valores en los lotes 6 al 15 (fuera de control), muy superiores a los de los lotes 1 al 5 (bajo control).

# xbar-chart
qic(x=lote,y=metric,data=datos,
       freeze=5, # identificando la zona bajo control (lote)
       chart="xbar",xlab="Lotes",
       show.labels = TRUE,
        part=c(5,10),
       part.labels=c("Proceso1","Proceso2","Proceso3"),
    # print.summary=TRUE,  # muestra una tabla-resumen del CEP
       point.size=2)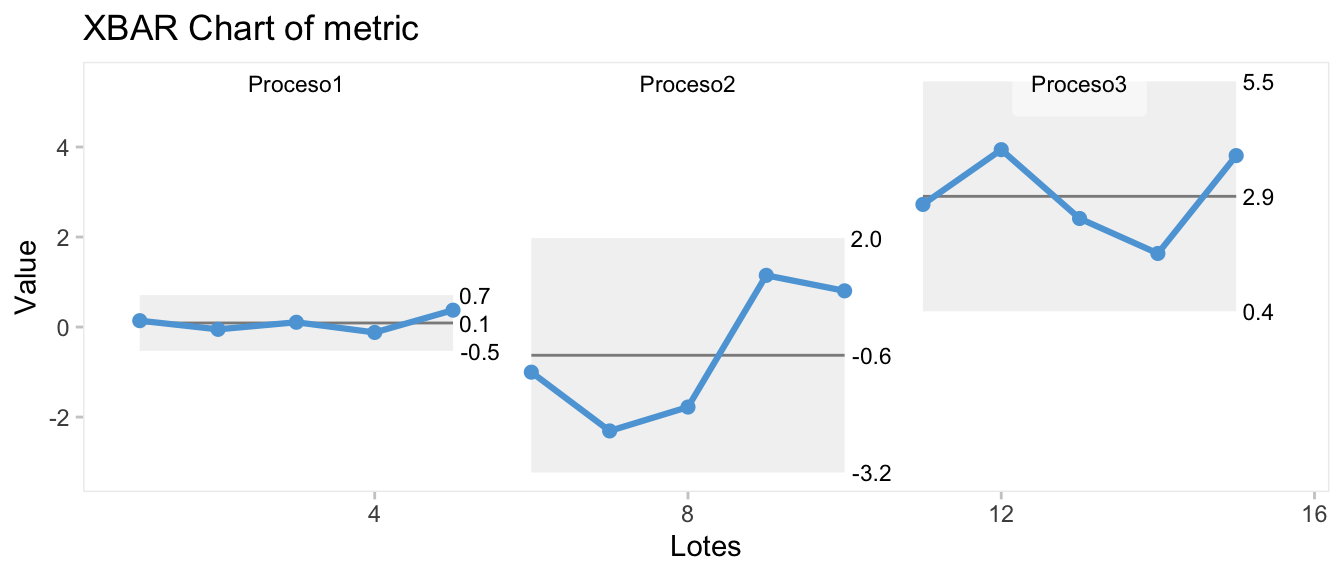

Figura 8.7: Gráfico xbar-chart con las medias de los lotes en tres procesos distintos consecutivos en el tiempo.

# mr-chart con los recorridos entre lotes
q3=qic(x=lote,y=metric,data=datos,
       chart="mr",xlab="Lotes",
       freeze=5, # identificando la zona bajo control (lote)
       point.size=2)
# s-chart con las desviaciones típicas en cada lote
q4=qic(x=lote,y=metric,data=datos,
       part=c(5,10),
        point.size=2,
       chart="s",xlab="Lotes")
grid.arrange(q3,q4,ncol=2)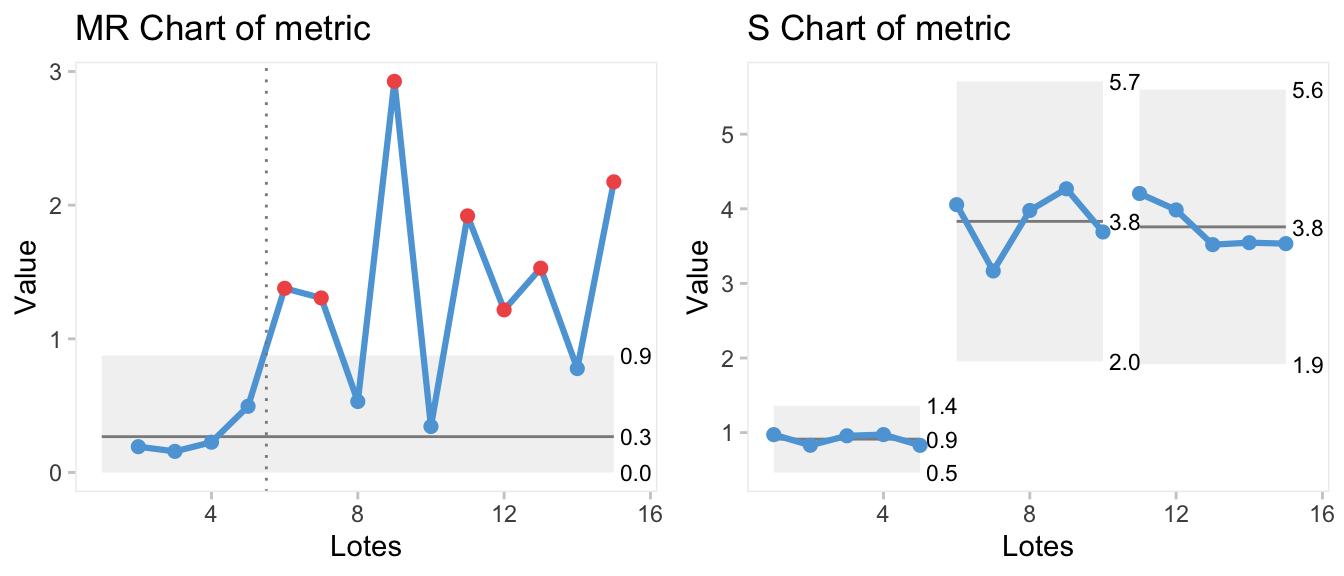

Figura 8.8: Gráficos mr-chart y s-chart con los recorridos móviles entre medias y las desviaciones típicas por lotes en tres procesos distintos consecutivos en el tiempo.

8.4.7 Gráficos de control para variables cualitativas

Si la variable es cualitativa, el CEP se realiza en términos de conteos y proporciones de defectos en el proceso. Así son comunes los:

• Gráficos c y u, que muestran la cantidad total de defectos en cada unidad de muestreo o (c-chart), o la tasa de defectos (defectos/n) o u-chart.

Utilizamos para visualizar estos gráficos, los datos cdi de la librería qicharts2, que registra el número de infecciones adquiridas en el hospital por los pacientes hospitalizados (variable \(n\)), así como el número de pacientes-día sin infección (variable day), antes y después de cierta intervención para reducir el riesgo de infecciones (period).

En la Figura 8.9 se muestran los gráficos c-chart con el conteo de infecciones y u-chart con la tasa de infecciones por 100.000 pacientes-día. Claramente se aprecia una reducción importante en el número de infecciones tras el tratamiento (c-chart), reflejada también en la tasa por 10.000 casos (u-chart)

# DATOS "cdi": #infecciones adquiridas en un hospital
library(qicharts2)
data("cdi")  # en la librería qicharts2 
# c-chart
q5=qic(month, n,data  = cdi, chart = 'c', 
    part  = 24, #frontera pre-post tratamiento
    part.labels=c("pre-tratamiento","post-tratamiento"),
    title="C-Chart ",ylab  = 'Casos', xlab  = 'Mes')
#u-chart (tasa por 100.000 casos)
q6=qic(month, n, n= days, data=cdi,
    multiply = 10000, # razón de la tasa (por 10000 pacientes)
    chart= 'u', part= 24,
    part.labels=c("pre-tratamiento","post-tratamiento"),
    title="U-Chart",ylab= 'Casos por 10.000 pacientes-día',
    xlab= 'Mes')

grid.arrange(q5,q6,ncol=2)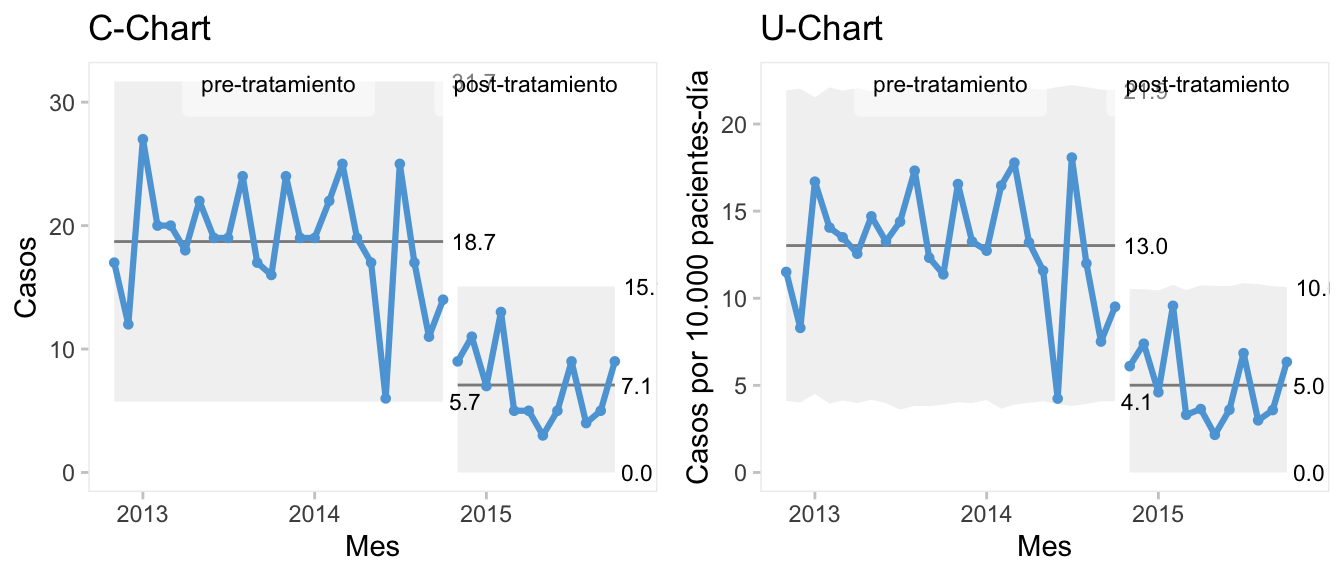

Figura 8.9: Gráficos c-chart con el número de infecciones y u-chart con la tasa de infecciones por 10.000 pacientes-día. Datos ‘cdi’ en qicharts2.

• Gráficos p y np, se utilizan cuando sólo es viable un tipo de defecto por unidad y disponemos de lotes. Los gráficos p-chart muestran la proporción de defectos y los gráficos np-chart el número total de unidades defectuosas en cada uno de los lotes inspeccionados.

Utilizamos para ejemplificar estos gráficos, la base de datos cabg de la librería qicharts2, que contiene registros de los resultados de operaciones de inserción de bypass en la arteria coronaria. Podemos calcular con ellos la proporción de pacientes fallecidos entre la fecha de la cirugía y 30 días más tarde. En la Figura 8.10 está representado el número de muertes (30 días después de la cirugía) por mes, en escala porcentual, con el gráfico p-chart. Si modificamos el argumento y.percent=FALSE obtenemos el gráfico del total de muertes np-chart.

library(qicharts2)
data("cabg") # coronary artery bypass graft operations,in qicharts2
library(tidyverse)
library(lubridate) # gestión de fechas

# calculamos el número de muertes (deaths) y 
# el total de pacientes operados (n) por mes en una nueva BD
cabg_by_month <- cabg %>% 
  mutate(month = as.Date(cut(date, 'month'))) %>%
  group_by(month) %>% 
  summarise(deaths = sum(death),n= n())

# Graficamos el porcentaje de muertes
qic(month, deaths, n,data= cabg_by_month,
    chart     = 'p',
    y.percent = TRUE,  # en escala porcentual
    title     = 'P chart',xlab= 'Mes',
    ylab= "Pacientes fallecidos 30 días tras la cirugía")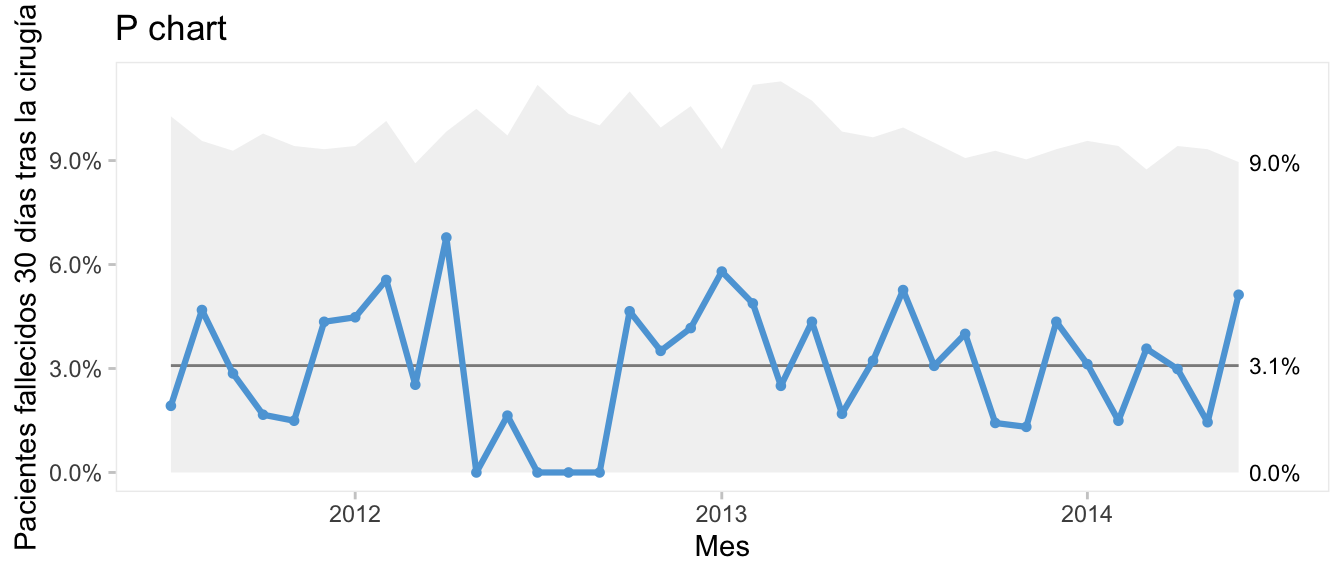

Figura 8.10: P-chart con la proporción de fallecimientos por mes. Datos ‘cdi’ en qicharts2.

• Gráficos T-chart. Si queremos graficar/controlar el tiempo entre eventos/defectos, acudimos a un gráfico T-chart.

En la Figura 8.11 se han representado los tiempos entre fallecimientos de los pacientes en la base de datos cabg, en función de cómo evoluciona el número total de fallecidos tras la cirugía de bypass.

# filtramos los fallecidos y calculamos el número de días desde 
# el inicio del estudio hasta la muerte 
fatalities=cabg %>%
  filter(death) %>%
  mutate(dt=date-lag(date)) # número de días desde inicio

qic(dt, data  = fatalities,chart = 't', title = 'T chart',
    ylab  = 'Días entre fallecimientos',
    xlab  = 'Número de fallecimientos')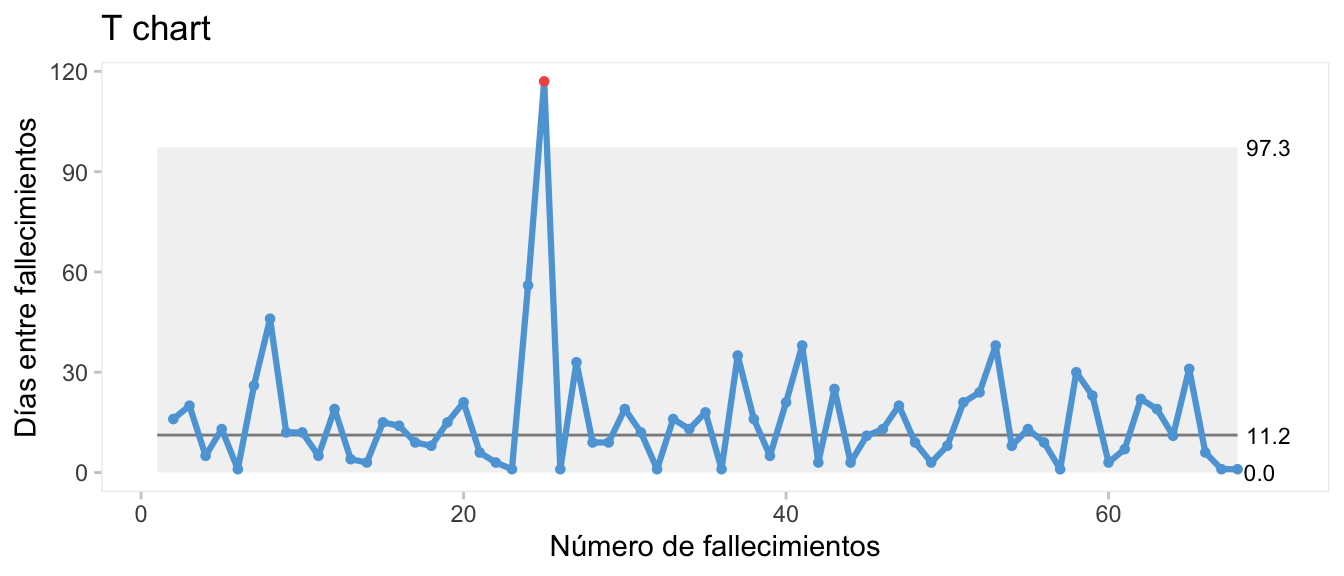

Figura 8.11: T-Chart con el tiempo entre fallecimientos. Datos ‘cdi’ en qicharts2.

8.4.8 Detección de la variación especial

Las causas especiales de variación, o variación no aleatoria se presentan en algunos procesos causadas por fenómenos que no son habituales en el sistema y provocan incertidumbre en la predicción. Veamos a continuación cómo interpretar los gráficos de control que construimos con nuestros datos, para identificar situaciones de variación especial que sacan fuera de control al proceso, y en las que será preciso intervenir para recuperar el control.

Las reglas más comunes para la identificación de variaciones especiales son:

1. Cambios de tendencias, como los que se muestran en la Figura 8.12. La fatiga, los desgastes o envejecimiento de materiales suelen producir señales de este tipo que, no necesariamente indican que el proceso esté fuera de control, especialmente cuando dicho ”desgaste” es lógico. Lo que sí nos indica esta señal es que hemos de estar vigilantes para parar el proceso y cambiar el elemento que está originando el cambio de tendencia, cuando exista riesgo de producir unidades defectuosas.

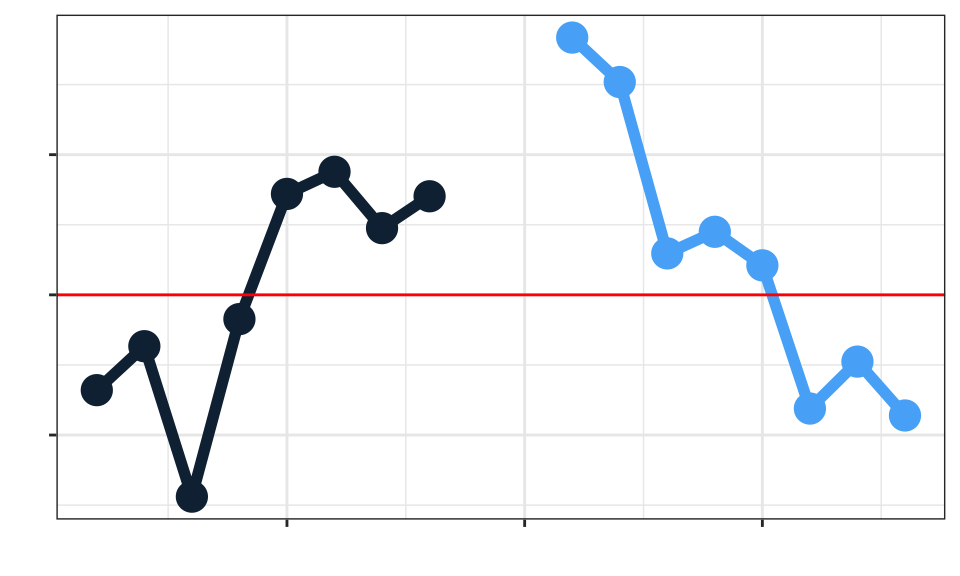
Figura 8.12: Cambio de tendencia en el control de procesos.

2. La regla de las 3sigmas de Shewhart, que identifica todos los puntos a 3 sigmas de la media o valor central, donde el sigma se calcula a partir de las constantes de Shewhart (Cano, Moguerza, and Corcoba 2015b).

Por ejemplo, en el caso de representar observaciones individualizadas, la línea central se calcula con la media \(\bar{x}\) de todas las observaciones y los límites de control con \(\bar{x}\pm 3 \bar{R}/d_2\), donde \(\bar{R}\) es el recorrido (rango) medio entre observaciones consecutivas, y \(d_2\) es una de las constantes de Shewhart.

Veamos cómo se consiguen estos gráficos con la librería qcc y la base de datos pistonrings incluida en ella. Esta base de datos contiene los registros del diámetro de los pistones de un motor, medido en 25 muestras (sample) de tamaño 5 para la fase de control, y 15 muestras posteriores, también de tamaño 5. En la Figura 8.13 aparecen representadas las medias de cada una de las muestras (lotes), y en la Figura 8.14 aparecen los datos individualizados. En rojo se remarcan los puntos que rebasan las línea de control a tres sigmas de la media.

library(qcc)
data(pistonrings)
diameter <- qcc.groups(pistonrings$diameter, pistonrings$sample) 
# identificamos los lotes/muestras
q=qcc(diameter[1:25,], type="xbar", newdata=diameter[26:40,],
       plot=FALSE)
plot(q,title="Datos agrupados por lotes",)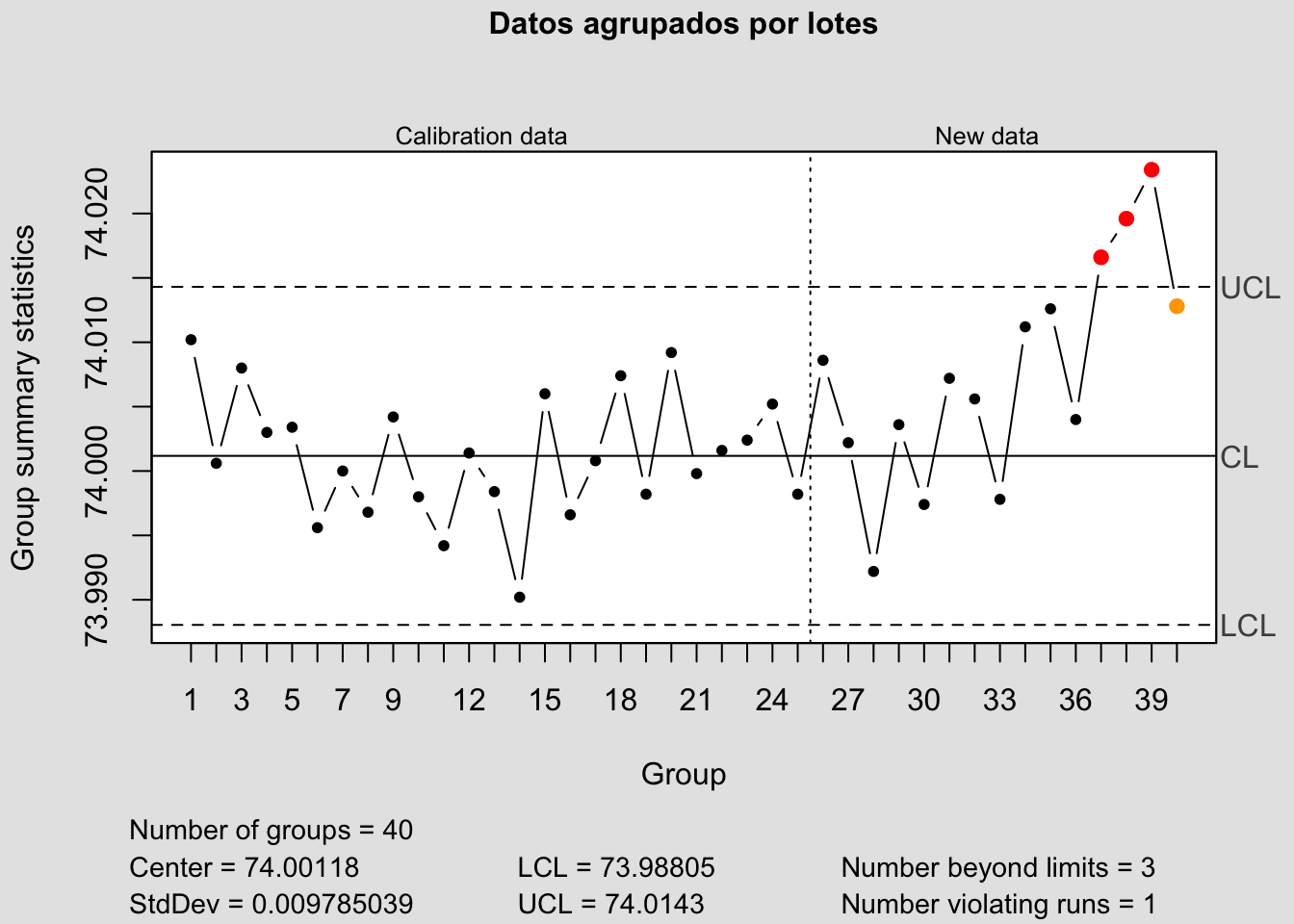

Figura 8.13: Gráfico de control (qcc) y regla de las 3sigmas con datos agrupados por lotes.

library(qcc)
data(pistonrings)
# PINTAMOS LOS datos individualizados
q=qcc(pistonrings$diameter[1:100],
    type="xbar.one",newdata=pistonrings$diameter[101:200],
    plot=FALSE)
plot(q,title="Datos individualizados")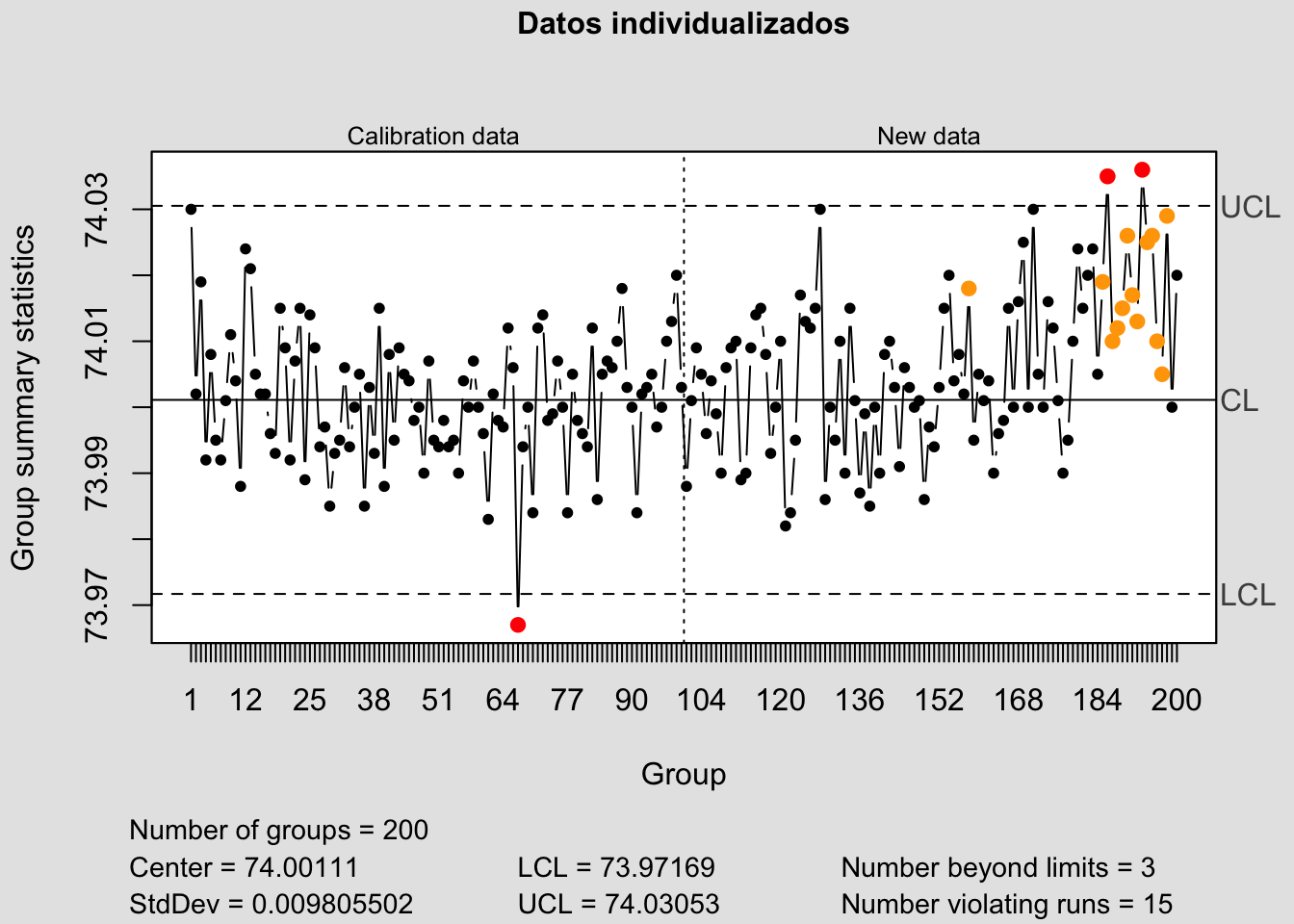    

Figura 8.14: Gráfico de control (qcc) y regla de las 3sigmas, con datos individualizados.

3. Las reglas de Western Electric (Wikipedia.org n.d.): Al representar los datos, quedan:

• al menos 1 punto fuera de los límites \(\pm 3 \sigma\) alrededor de la media
• al menos 2 puntos consecutivos más allá de los límites \(\pm 2 \sigma\)
• al menos 4 puntos consecutivos más allá de los límites \(\pm 1 \sigma\)
• al menos 8 puntos consecutivos a un lado de la línea central.

Estas reglas se han demostrado más efectivas en gráficos de control que tienen entre 20 y 30 puntos muestreados. Con menos datos pierden especificidad (más falsos negativos) y con más datos pierden sensibilidad (más falsos positivos).

Veamos cómo conseguir las violaciones a las reglas de Western Electric con gráficos de control generados con la librería ggQC en R, a partir de datos simulados. En la Figura 8.15 se remarcan en rojo los puntos que infringen cada una de estas reglas para el conjunto de datos simulados.

library(ggQC)
#Ssimulamos datos con outliers
set.seed(5555)
 QC_XmR <- data.frame(
 data = c(c(-1, 2.3, 2.4, 2.5),            #Outlier Data
   sample(c(rnorm(60),5,-5), 62, replace = FALSE), #Normal Data
   c(-0.85,-.5,-.75,-.25,-2.4,-2.6,-2.5,-2.7)), #Outlier Data
   Run_Order = 1:74   #Run Order
    )
# Render QC Violation Plot 
ggplot(QC_XmR, aes(x = Run_Order, y = data)) +
           stat_qc_violations(method = "XmR")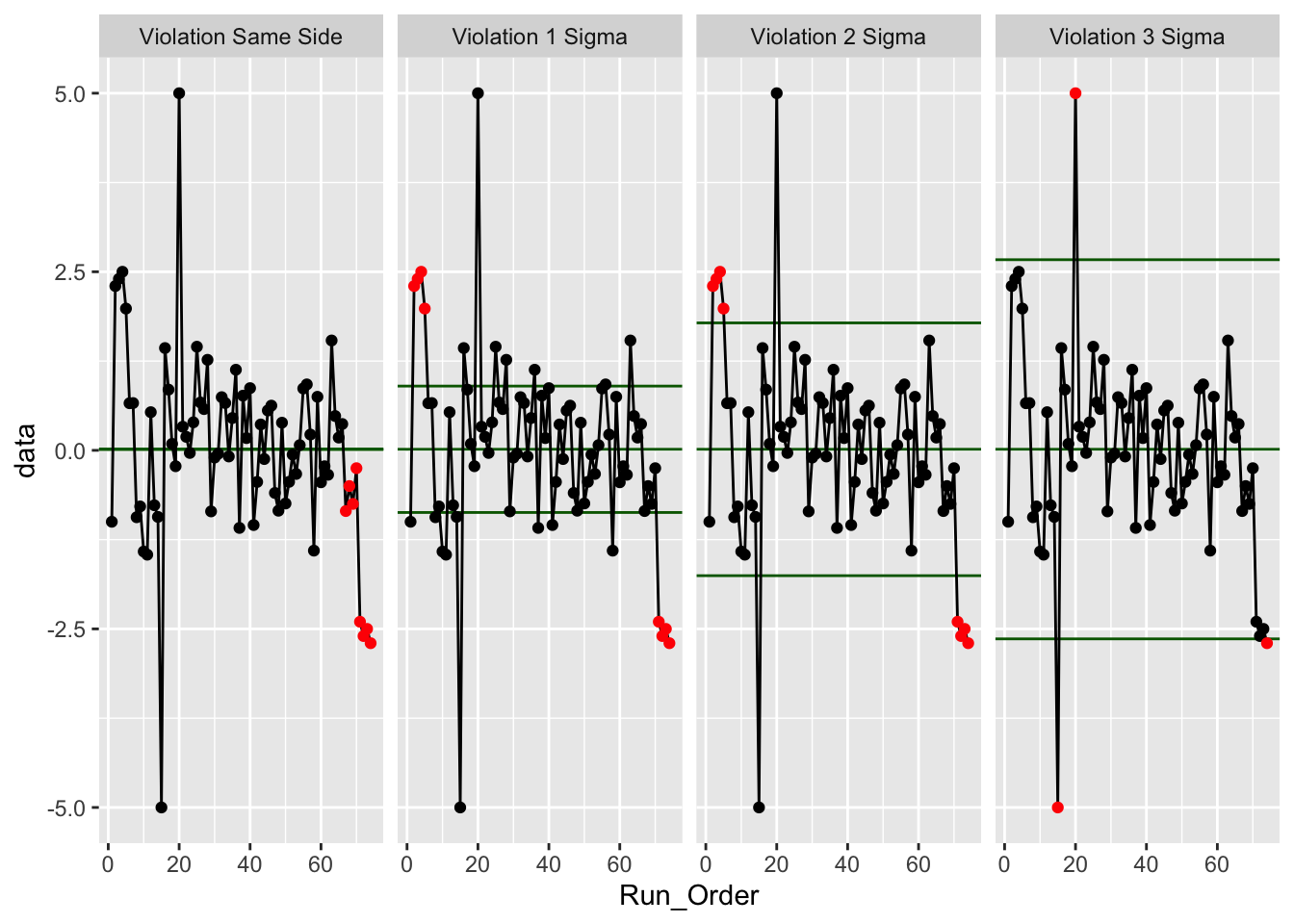   

Figura 8.15: Violaciones de las reglas de la Western Electric en datos simulados.

4. Las reglas Anhøj (A. V. Anhøj Jacob AND Olesen (2014) y J. Anhøj (2015)) consisten en dos tests basados exclusivamente en la distribución de los datos en relación al centro de la línea:

• cadenas de puntos consecutivos inusualmente largas al mismo lado de la línea central; el límite superior para la predicción del tamaño de este tipo de cadenas es aproximadamente \(log_2(n)+3\), con \(n\) el número de datos útiles;
• poca frecuencia de cruces de los datos a los dos lados de la línea central. El número de cruces tiene una distribución binomial \(Bin(n-1,0.5)\), luego el límite de predicción al 5% para el número de cruces es qbinom(p=0.05, n-1,prob=0.5).

Estas reglas tienen algunas ventajas, como son el hecho de que no dependen de los límites sigma, y por otro que se adaptan al número de datos disponibles sin perder sensibilidad ni especificidad.

La función qic en la librería qicharts2 proporciona, a través de la descripción summary, los valores con los que verificar si hay violaciones de las reglas de Anhøj. Visualizamos el resultado para los datos pistonrings (de la librería qcc) en la Tabla 8.1, donde el valor 1 en la fila 5 implica que hay alguna violación; de hecho, la longitud de la cadena más larga (20) rebasa el límite superior esperado (11), y los datos no llegan a cruzar la línea central tanto como se espera (86 veces cuando el mínimo es 88).

# Violaciones de las reglas de Anhøj
library(qicharts2)
a=summary(qic(pistonrings$diameter,chart="i"))
Descriptor=c(
  "Longitud de la cadena más larga de datos al mismo lado 
  de la línea central", 
  "Límite superior de la longitud esperada de la cadena 
  más larga 
  al mismo lado de la línea central",
  "Número de veces que los datos cruzan la línea central",
  "Límite inferior del número esperado de cruces de la 
  línea central",
  "Se viola la longitud de la cadena más larga o el 
  número de cruces",
  "Número de datos fuera de los límites de control")
Valor=c(a$longest.run,a$longest.run.max,a$n.crossings,
a$n.crossings.min,a$runs.signal,a$sigma.signal)
resultados=data.frame(Descriptor,Valor)
# Formateado de la tabla de resultados
library(kableExtra)
kbl(resultados,
  caption="Violaciones de las reglas de Anhøj en 
  pistonrings (qcc).")%>%
  kable_paper(full_width=FALSE)%>%
  column_spec(1,border_right =T,width="30em" ) %>%
  column_spec(2,bold=T)%>%
  row_spec(0,bold=T,background = "#EBD3CE")%>%
  row_spec(5,background = "#EBA191",color="black")

Tabla 8.1: Violaciones de las reglas de Anhøj en pistonrings (qcc).

Descriptor	Valor
Longitud de la cadena más larga de datos al mismo lado de la línea central	20
Límite superior de la longitud esperada de la cadena más larga al mismo lado de la línea central	11
Número de veces que los datos cruzan la línea central	86
Límite inferior del número esperado de cruces de la línea central	88
Se viola la longitud de la cadena más larga o el número de cruces	1
Número de datos fuera de los límites de control	3

La descripción completa de gráficos o fórmulas para los límites de control, así como una ampliación del tema se pueden encontrar en libros relacionados con el control de la calidad y el control estadístico de los procesos, como Cano, Moguerza, and Corcoba (2015c), Montgomery (2013), Langley et al. (2009) y Howard (2003), cuya consulta recomendamos al lector que desee ampliar conocimientos.

8.5 Transferencia del proyecto

Una vez redactado el plan de control, el proyecto está casi terminado. Los pasos finales a dar para zanjarlo definitivamente son:

1. Prever los mecanismos para que el proceso funcione en el futuro tal como lo hizo en las pruebas. Para ello será necesario elaborar las nuevas (o revisadas) instrucciones del proceso así como formar a las personas afectadas por los cambios del proceso.

En general las instrucciones de un proceso se suelen formalizar en procedimientos que describen el funcionamiento del proceso. Algunas de las actividades suelen estar también formalizadas mediante guías, especificaciones, fichas técnicas, etc. En cualquier caso, se trata de que los cambios introducidos en el proceso queden formalizados en la empresa. El documento con las instrucciones del proceso ha de satisfacer las siguientes características:

• han de estar físicamente disponibles y accesibles en una ubicación conocida y de fácil acceso,
• han de contener unos protocolos de revisión y actualización periódica para estar siempre adaptadas al proceso actual,
• han de ser diseñadas para el usuario, y por lo tanto ser comprensibles, por lo que es importante contar en su redacción con las personas que las utilizarán.

A veces, además de preparar instrucciones del proceso, es necesario realizar acciones formativas complementarias, sobre todo cuando el colectivo de personas afectadas por los cambios en el proceso es numeroso. Esta formación ha de tener necesariamente unos objetivos claros y una orientación práctica. La selección de los instructores, la programación y la planificación, así como la elaboración de una documentación completa pero simple, será crucial.

En los departamentos de formación de las empresas encontraremos técnicos que nos pueden ayudar a diseñar adecuadamente la acción formativa que necesitamos y los materiales para llevarla a cabo.

2. De forma complementaria y, sobre todo, para asegurar la implicación del Champion, propietario del proceso y mandos que intervienen en el proceso, es importante que el Black Belt prepare una presentación del proyecto que utilizará para comunicar los resultados del proyecto.
3. Finalmente, de cara al futuro, es conveniente que este también prepare un dossier del proyecto con los elementos básicos, para que otras personas con conocimiento de la metodología Seis Sigma puedan comprender el proyecto realizado y, sobre todo, ver las posibilidades de aplicación de los trabajos realizados en este proyecto a otros similares.

Bibliografía

Anhoej, Jacob. 2021. Qicharts2: Quality Improvement Charts. https://github.com/anhoej/qicharts2.

Anhøj, Anne Vingaard, Jacob AND Olesen. 2014. “Run Charts Revisited: A Simulation Study of Run Chart Rules for Detection of Non-Random Variation in Health Care Processes.” PLOS ONE 9 (11): 1–13. https://doi.org/10.1371/journal.pone.0113825.

Anhøj, Jacob. 2015. “Diagnostic Value of Run Chart Analysis: Using Likelihood Ratios to Compare Run Chart Rules on Simulated Data Series.” PLOS ONE 10 (3): 1–9. https://doi.org/10.1371/journal.pone.0121349.

———. 2015b. “Quality Control with r. An ISO Standards Approach.” In. Springer. https://link.springer.com/content/pdf/bbm%3A978-3-319-24046-6%2F1.pdf.

———. 2015c. Quality Control with r. An ISO Standards Approach. Springer. https://link.springer.com/content/pdf/bbm%3A978-3-319-24046-6%2F1.pdf.

Grey, Kenith. 2018. ggQC: Quality Control Charts for Ggplot. https://CRAN.R-project.org/package=ggQC.

Howard, David. 2003. The Basics of Statistical Process Control and Process Behaviour Charting. A User’s Guide to SPC. Management-Newstyle.

Langley, G. J., R. Moen, K. M. Nolan, T. W. Nola, C. L. Norman, and L. P. Provost. 2009. The Improvement Guide: A Practical Approach to Enhancing Organizational Performance, 2nd Edition. Jossey-Bass, a Wiley imprint.

Montgomery, D. C. 2013. Introduction to Statistical Quality Control. 7th Edition. John Wiley; Sons, New York.

R Core Team. 2021. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Scrucca, Luca. 2017. Qcc: Quality Control Charts. https://github.com/luca-scr/qcc.

Wikipedia.org. n.d. “Western Electric Rules.” Web. https://en.wikipedia.org/wiki/Western_Electric_rules.