Capítulo6 DMAIC3. Analizar

6.1 Objetivos de aprendizaje

En este capítulo trabajaremos sobre los siguientes objetivos de aprendizaje:

• Descubrir los objetivos y procesos en la etapa ANALIZAR de DMAIC.
• Descubrir la utilidad de los análisis gráficos e inferenciales para encontrar las causas de los defectos.
• Repasar los principales análisis gráficos e inferenciales en función del tipo de variables y problemas.
• Presentar el diseño de experimentos, en concreto el diseño factorial completo y sus desarrollos analíticos, como una herramienta para determinar las principales causas de variación en la respuesta. Se utilizará también después en la etapa de Mejorar.

6.2 Introducción

Los objetivos de la etapa Analizar en DMAIC son:

• Identificar todas las causas posibles que pueden provocar defectos.
• Seleccionar las que en principio parecen más probables mediante análisis gráficos.
• Confirmar las pocas causas vitales que realmente están provocando defectos mediante análisis estadísticos inferenciales.

Cuanta más y mejor información numérica tengamos disponible sobre las X’s e Y’s del proceso, más eficiente resultará esta etapa, en la que pretendemos identificar cuáles son las causas \(X\) principales de los outputs \(Y\), y en consecuencia de los defectos que se están generando, para así determinar cómo afectarlas para reducir el número de defectos.

Toda la información recopilada para comprender el funcionamiento del proceso nos permitirá identificar las causas probables. A continuación se muestran distintos gráficos y análisis nos facilitan esta labor, dependiendo del tipo de variables disponibles y objetivos, y con los que identificar qué variables están generando mayor variabilidad en los resultados (recordemos que la variabilidad está íntimamente relacionada con los defectos, y la reducción de los defectos la conseguiremos a través de una reducción de la variabilidad).

El siguiente paso en la etapa Mejorar, identificadas las causas, vendrá dado por aprovechar los resultados del análisis para diseñar nuevas configuraciones de las variables que afectan las respuestas (a través del Diseño de Experimentos, DOE -Design of Experiments-, entre otras herramientas) y así encontrar la óptima que reduce al máximo la variabilidad y por lo tanto los defectos. Dado el carácter analítico del DOE, será desarrollado también en este capítulo.

6.3 Análisis gráfico

Existen muy diversas posibilidades para realizar un análisis gráfico de los datos, en función del tipo de datos y objetivos. Este análisis gráfico ha de sernos útil para orientar qué variables están relacionadas y cómo con la respuesta. Después, en el análisis inferencial, verificaremos las relaciones estadísticamente significativas y confirmaremos las causas vitales en la variabilidad del proceso.

6.3.1 Diagrama de causa-efecto.

Nos permite organizar la información para identificar las causas X y los efectos en el proceso que tratamos. Se denomina diagrama de la espina de pescado (fishbone) o gráfico de Ishikawa, y se muestra un ejemplo en la Figura 6.1. Para crear un diagrama de causa-efecto basta seguir los pasos a continuación:

• crear la cabeza, con el problema a estudiar
• crear la espina central del pescado
• identificar al menos 4 causas que contribuyan al problema y conectarlas a la espina
• tormenta de ideas alrededor de cada causa, para documentar qué contribuye a que aparezca, y continuar añadiendo espinas hasta que las causas raíz aparezcan.

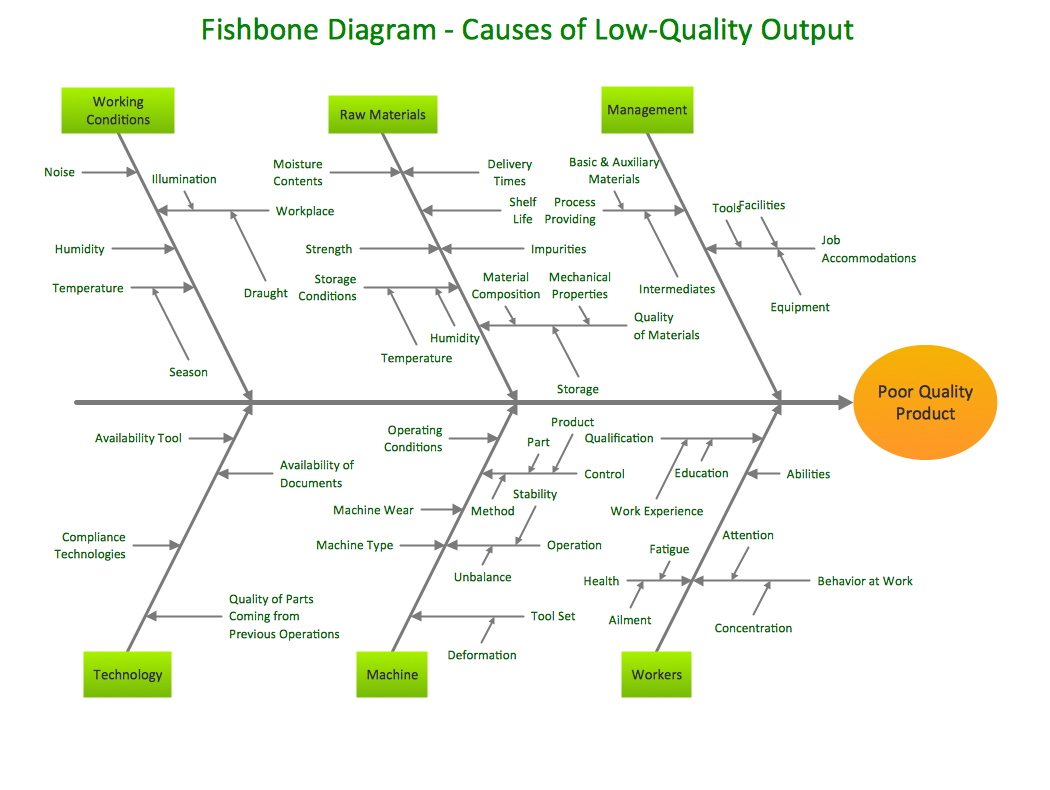
Figura 6.1: Ejemplo de gráfico Fishbone o espina de pescado. Fte: (https://conceptdraw.com/samples/fishbone-diagram).

Al utilizar el diagrama de causa-efecto se pueden cometer tres errores que pueden llevar a conclusiones equivocadas:

• El diagrama sirve para identificar “posibles” causas de un efecto o síntoma, es decir, para formular teorías sobre los “porqués” del problema, pero no significa que estas causas posibles sean realmente las que están originando el efecto. Más adelante será necesario comprobar que estas teorías son realidades o hechos.
• Si se realiza el diagrama sin conocer suficientemente el efecto o síntoma, sin haber tomado datos o analizado el flujo del proceso, es posible que el resultado del diagrama se quede en un nivel superficial, y no sirva para identificar las verdaderas causas raíz del problema.
• Cuando se realiza el diagrama limitando las posibilidades, asumiendo de entrada que las causas están localizadas en un grupo, es posible que se pierda información sobre las verdaderas causas del problema. En cualquier caso, si se va a recurrir a esta herramienta, es necesario tener en cuenta toda la información del proceso que se ha recopilado y estudiado durante la fase de Medir.

6.3.2 Gráfico de Pareto

El análisis de Pareto se puede utilizar en cualquiera de las distintas etapas de un proyecto Seis Sigma. Su finalidad es identificar las posibles causas de los defectos para focalizarse en las más importantes y vitales para el proceso. Este gráfico ya se presentó en la Sección 3.5.4 para la selección de procesos susceptibles de mejora.

Se basa en el principio de Pareto o regla 80/20: La mayor parte del esfuerzo/beneficio (aprox. 80%) es debido a un número limitado de acciones clave (aprox. 20%).

El gráfico de Pareto (ver Figura 6.2) es un diagrama de barras útil para representar la magnitud del efecto en función de causas posibles y detectar con él qué causas son las vitales.

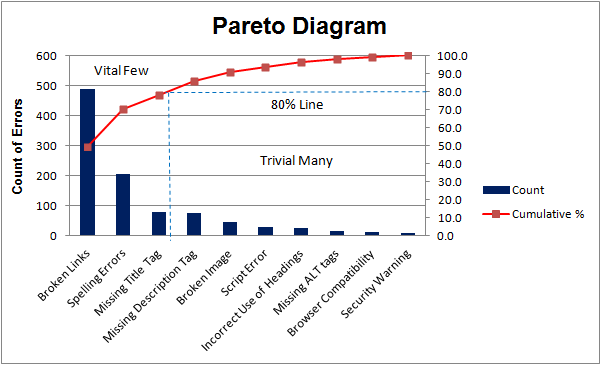
Figura 6.2: Diagrama de Pareto. Fte. (https://www.projectsmart.co.uk/pareto-analysis-step-by-step.php).

Elegido un factor como posible desencadenante de cierto evento (defecto, cumplimiento con los requerimientos de un cliente, …), se representa la variable que contiene la frecuencia o conteo de los eventos, clasificada para los diferentes niveles del factor desencadenante, y se superpone una línea que contiene información sobre las frecuencias acumuladas. Así es fácil discernir si los eventos se reparten de forma homogénea a lo largo del rango de categorías/niveles del factor desencadenante, o por el contrario, algún/os nivel/es favorecen con mayor intensidad la aparición de eventos. En el eje X ordena las categorías de mayor a menor frecuencia.

Es útil tanto para identificar las causas más importantes de los defectos, como para discernir cuáles son los requerimientos más demandados por los clientes, o qué categorías provocan un mayor volumen de defectos, tiempo, energía, recursos, etc.

6.3.3 Otros gráficos

Otros tipos de gráficos que nos resultarán útiles para descubrir causas, son los habituales en los análisis estadísticos:

• Diagramas de barras (barchart), para representar frecuencias (como número de defectos por máquina/operario, …).
• Histogramas, para representar el comportamiento de variables continuas (como tiempos de entrega, longitud de tornillos, …).
• Diagramas de dispersión (scatterplot), para investigar relaciones entre variables \(X/Y\) de tipo continuo (como grosor de una pieza en función de la concentración de acero en la aleación, …).
• Diagramas de líneas (run chart), para investigar la evolución a lo largo del tiempo de cualquier variable (como el número de defectos muestreados en días consecutivos, …).
• Diagramas de cajas y bigotes (Box-Whisker chart), para investigar diferencias en localización y variabilidad.
• Gráficos multivariantes y condicionados, para estudiar correlaciones y efectos \(X\) condicionantes sobre alguna variable output \(Y\).

Para análisis descriptivos y gráficos recomendamos las librerías de R: skimr (R-skimr?), ggplot2 (Wickham et al. 2021) y sjPlot (R-sjPlot?).

Ejemplos

Veamos cómo representar estos gráficos propuestos, con R, utilizando un ejemplo con datos relativos a concentraciones de amonio en residuos, tomados en distintos instantes de tiempo en dos ubicaciones distintas, por dos operadores. El objetivo inicial con estos datos es indagar si la concentración de amonio está relacionada con la ubicación y con el operador que ha tomado la medida. Veamos la estructura del banco de datos.

# Cargamos los datos y visualizamos
load("datos/datosamonio.RData")
head(datos)

##     amonio operador ubicacion tiempo
## 1 25.16269        A        u1      1
## 2 23.41408        A        u1      2
## 3 25.78547        A        u1      3
## 4 22.66741        A        u1      4
## 5 23.55343        A        u1      5
## 6 24.56961        A        u1      6

# cargamos librerías
require(tidyverse)

Con el gráfico de barras (Figura 6.3) visualizamos el número de observaciones realizadas en cada ubicación: el mismo número en ambas.

# Gráfico de barras
ggplot(datos,aes(x=ubicacion))+
  geom_bar(aes(fill=ubicacion))+
  theme_minimal()+
  theme(legend.position = "none")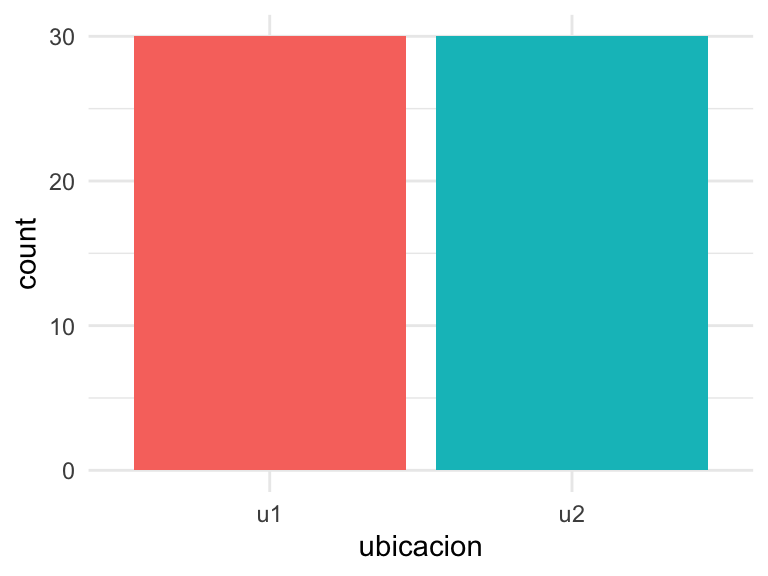

Figura 6.3: Gráfico de barras con los conteos.

Con el histograma (Figura 6.4) apreciamos cierta normalidad en los datos (niveles de amonio), si bien con algo de asimetría en la cola derecha.

# Histograma
ggplot(datos,aes(x=amonio))+
  geom_histogram(fill="skyblue",color="blue")+
  theme_classic()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.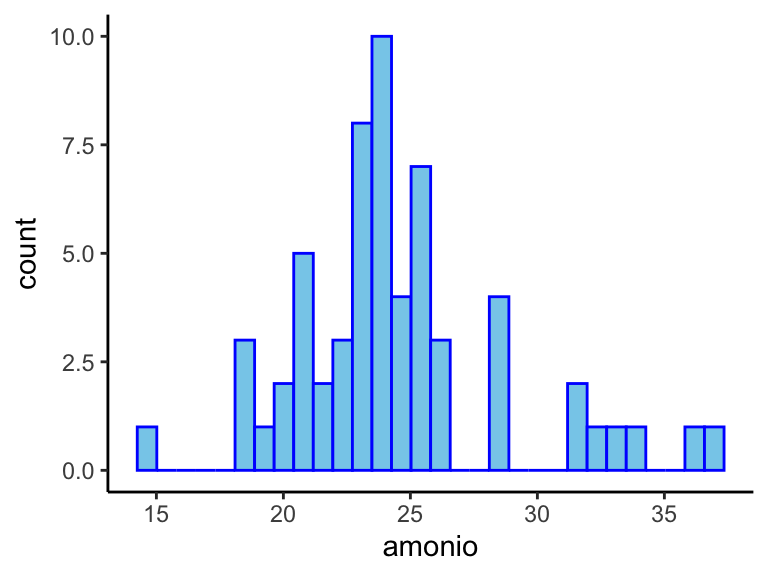

Figura 6.4: Histograma con las mediciones de amonio.

Si utilizamos la variable ‘tiempo’ que marca los instantes en que se han tomado consecutivamente las mediciones, no apreciamos ninguna tendencia en su relación con el amonio en el gráfico de dispersión (Figura 6.5).

# Gráfico de dispersión
ggplot(datos,aes(x=tiempo,y=amonio))+
  geom_point(color="blue")+
  theme_classic()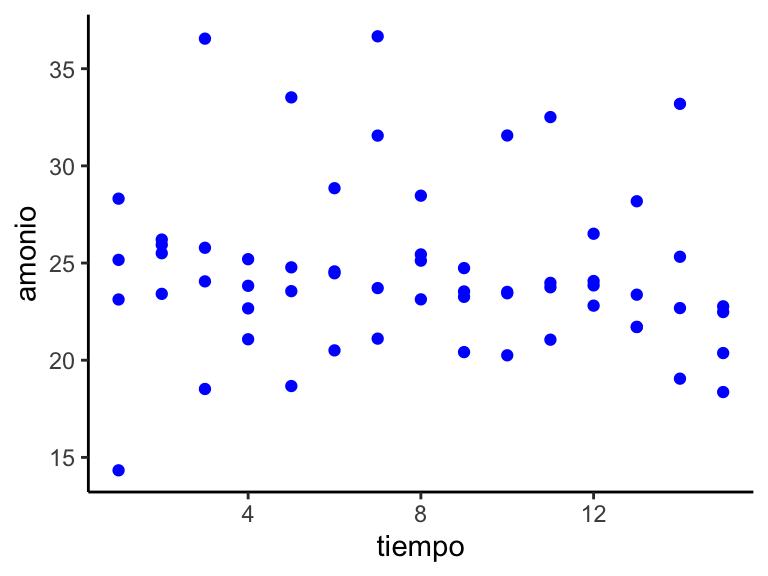

Figura 6.5: Gráfico de dispersión de las mediciones en función del tiempo.

Un resultado similar nos proporciona el gráfico de líneas (Figura 6.6) con la variable ‘tiempo.’

# Gráfico de puntos y líneas
ggplot(datos,aes(x=tiempo,y=amonio))+
  geom_point(color="skyblue")+
  geom_line(color="blue")+
  theme_classic()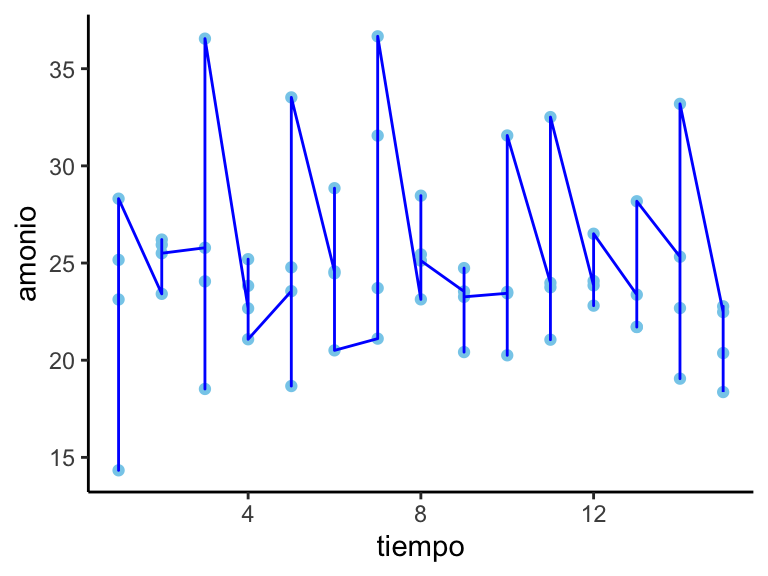

Figura 6.6: Gráfico de líneas (y puntos) del amonio versus el tiempo.

Con el diagrama de cajas podemos identificar relaciones, por ejemplo, entre las mediciones proporcionadas por cada operador. En la Figura 6.7 se aprecia que las mediciones en promedio son bastante similares (línea central de la caja), pero sin embargo, la variabilidad del operador B es mucho mayor que la del operador A.

# Gráfico de cajas 
ggplot(datos,aes(x=operador,y=amonio))+
  geom_boxplot(aes(fill=operador))+
  theme_minimal()+
  theme(legend.position = "none")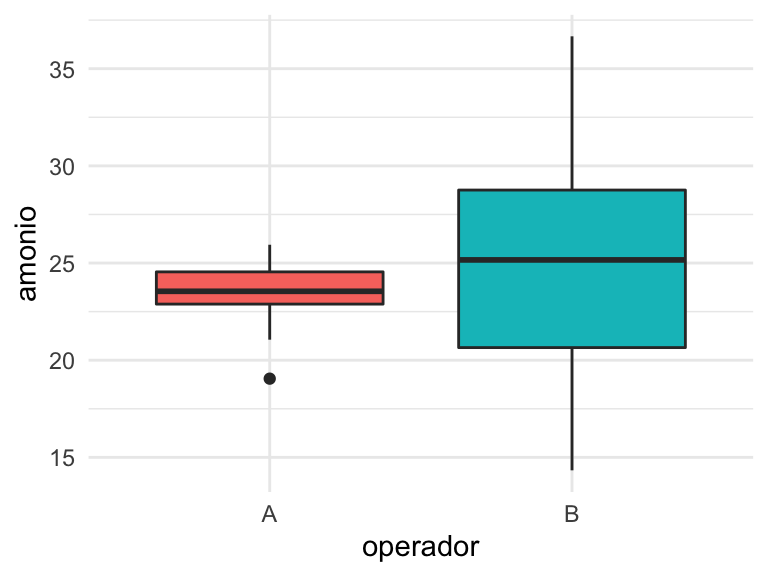

Figura 6.7: Gráfico de cajas (boxplot) de las mediciones de amonio según el operador.

# Gráfico de cajas condicionado
ggplot(datos,aes(x=operador,y=amonio))+
  geom_boxplot(aes(fill=ubicacion))+
  theme_minimal()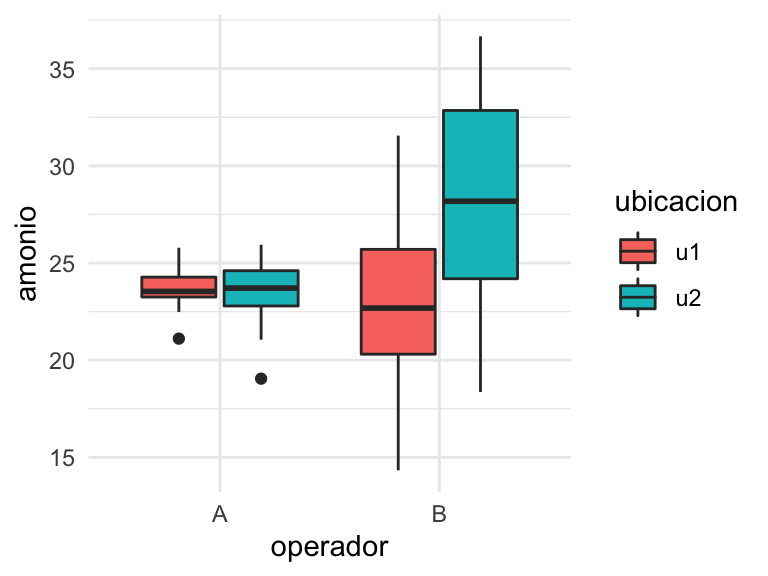

Figura 6.8: Gráfico de cajas condicionado: amonio según ubicación y operador.

En cuanto a gráficos condicionados, tenemos muchas variantes y posibilidades. En concreto en estos datos podemos intentar visualizar cómo están afectando conjuntamente ubicaciones y operadores, a las mediciones de amonio. Nos percatamos en la Figura 6.8 de que el operador A mide igual en cualesquiera de las dos ubicaciones, además con poca dispersión, mientras que el operador B recaba niveles de amonio bastante superiores en la ubicación u2 que en la u1, manteniendo en ambas una variabilidad similar y muy superior a la del operador A. Este hecho anticipa la posibilidad de un efecto de interacción ubicación:operador que explique la variabilidad de las mediciones de amonio. También da pautas sobre la posibilidad de medir con precisión, como lo hace el operador A.

6.4 Análisis inferencial

El análisis gráfico siempre nos da una orientación sobre por dónde iniciar el análisis inferencial, o lo que es lo mismo, la construcción de modelos estadísticos con los que evidenciar relaciones significativas y confirmar la magnitud del efecto que provocan sobre los resultados \(Y\) aquellas variables \(X\) que realmente están afectando a que se produzcan.

La fase de ANÁLISIS ha de ayudar a contestar las preguntas:

• ¿El tiempo afecta a los resultados (estabilidad)?
• ¿Qué causas principales están provocando mayor variación y desviación del objetivo?
• ¿Cómo afectan en el resultado las variaciones en las condiciones base (causas)?

Como indicaciones básicas, la Figura 6.9 muestra una posible hoja de ruta sobre cuestiones a investigar.

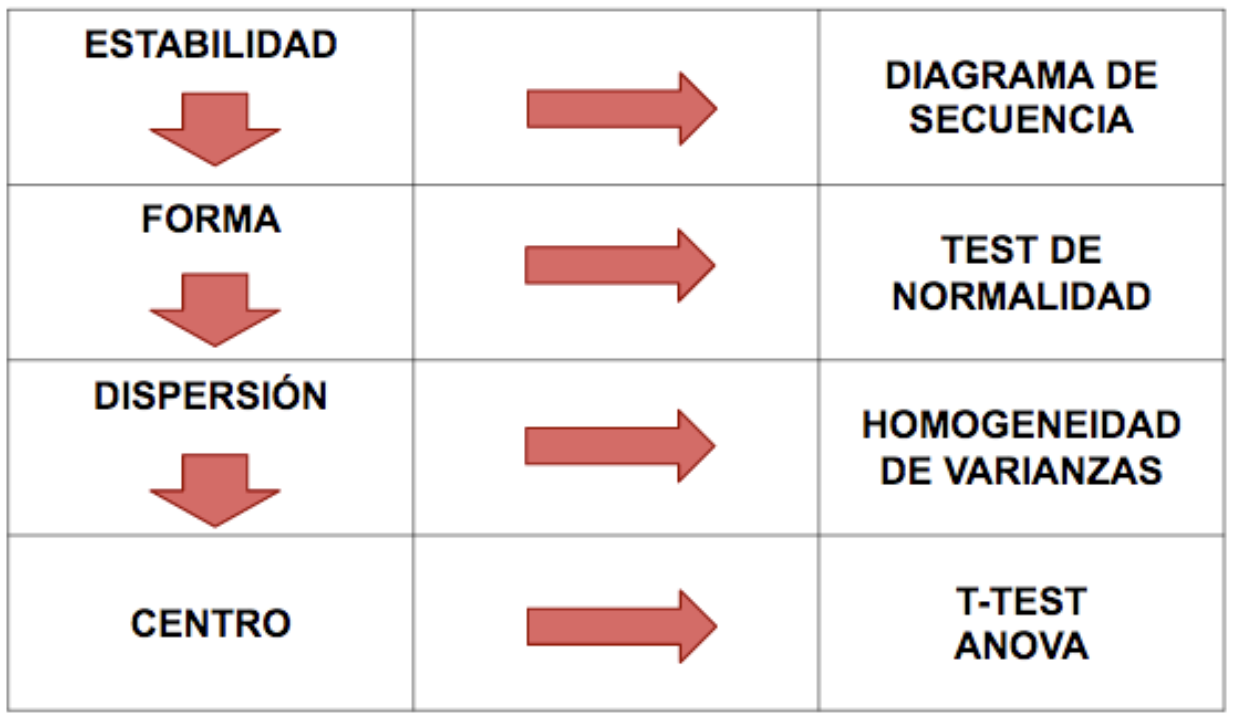
Figura 6.9: Cuestiones a investigar y análisis estadísticos útiles.

El análisis inferencial se orientará en función de los objetivos, el tipo de datos y el tipo de conclusiones pretendidos. Tiene sentido realizarlo para comprender de modo más preciso el proceso actual e identificar las causas reales del exceso de variabilidad detectado. Identificados los factores que provocan dicha variabilidad, cabrá reaccionar para controlarlos de modo eficiente, provocando una reducción de varianza sobre la respuesta.

6.4.1 Contrastes de hipótesis

Los pasos a dar en la formulación de un contraste de hipótesis son los siguientes:

1. Formular el problema/cuestión práctica.
2. Establecer las hipótesis: nula y alternativa. La hipótesis alternativa contiene la hipótesis que defendemos, lo que querríamos demostrar. La hipótesis nula lo contrario.
3. Decidir el test estadístico apropiado
4. Fijar el nivel alpha. Fijar el nivel beta. Calcular la potencia.
5. Determinar el tamaño muestra inicial.
6. Desarrollar el plan de muestreo y recolección de los datos.
   
7. Representar gráficamente los datos y realizar los tests estadísticos correspondientes. Extraer la conclusión estadística.
8. Traducir la conclusión estadística a una conclusión práctica respecto del problema propuesto.

Cuando planteamos un contraste de hipótesis es preciso considerar el error de tipo I, \(\alpha\) y de tipo II, \(\beta\), tolerables, que nos llevan al nivel de confianza, \(1-\alpha\) de las conclusiones, y a la potencia estadística, \(1-\beta\), respectivamente. Ver Figura 6.10.

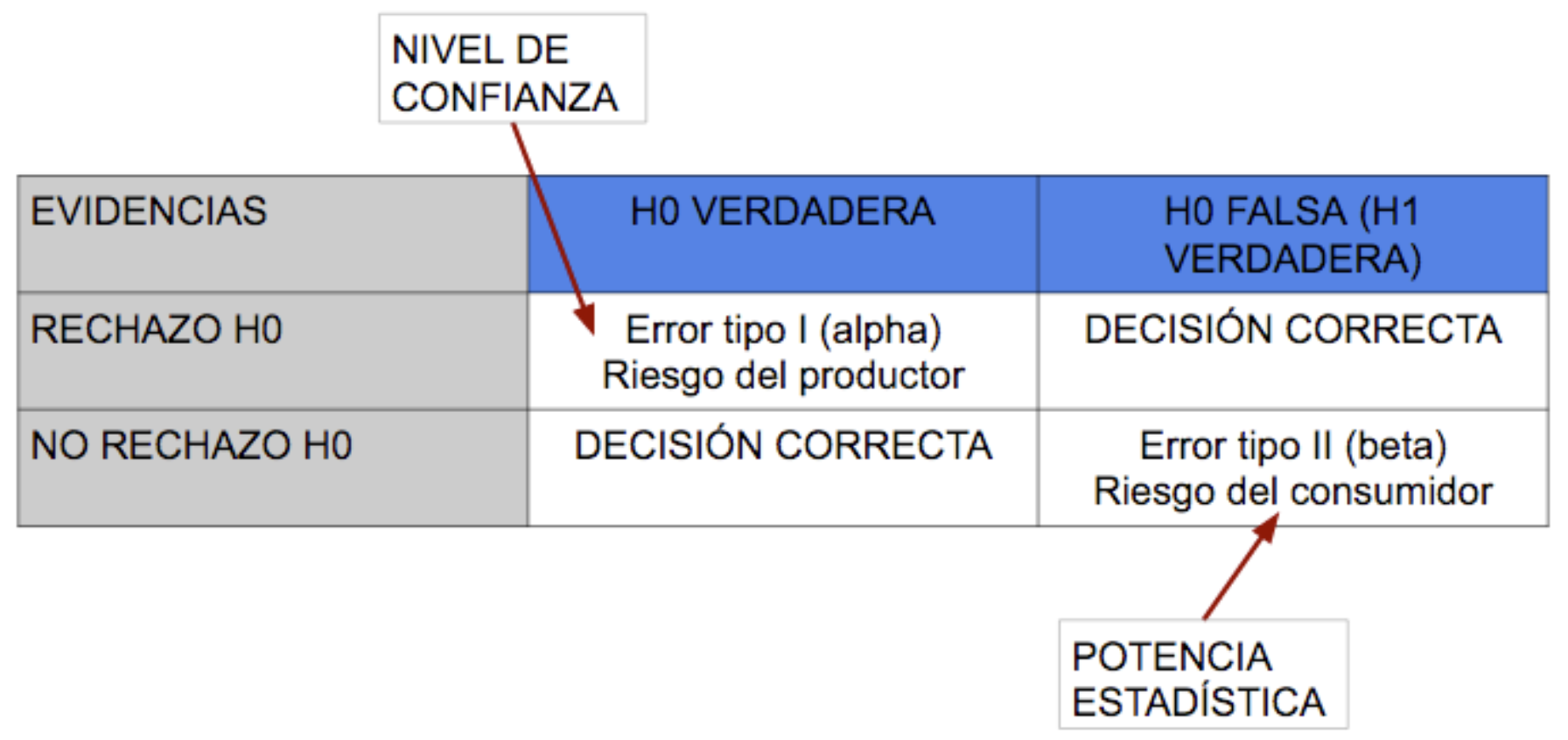
Figura 6.10: Error tipo I y tipo II en un contraste de hipótesis. Potencia estadística=1-beta. Nivel de confianza=1-alpha.

En función de las hipótesis a contrastar y de la tipología de las variables involucradas en las X’s y en las Y’s, habremos de optar por unos u otros contrastes. En las Figuras 6.11 y 6.12 se muestran los test más habituales bajo distintas configuraciones de X e Y.

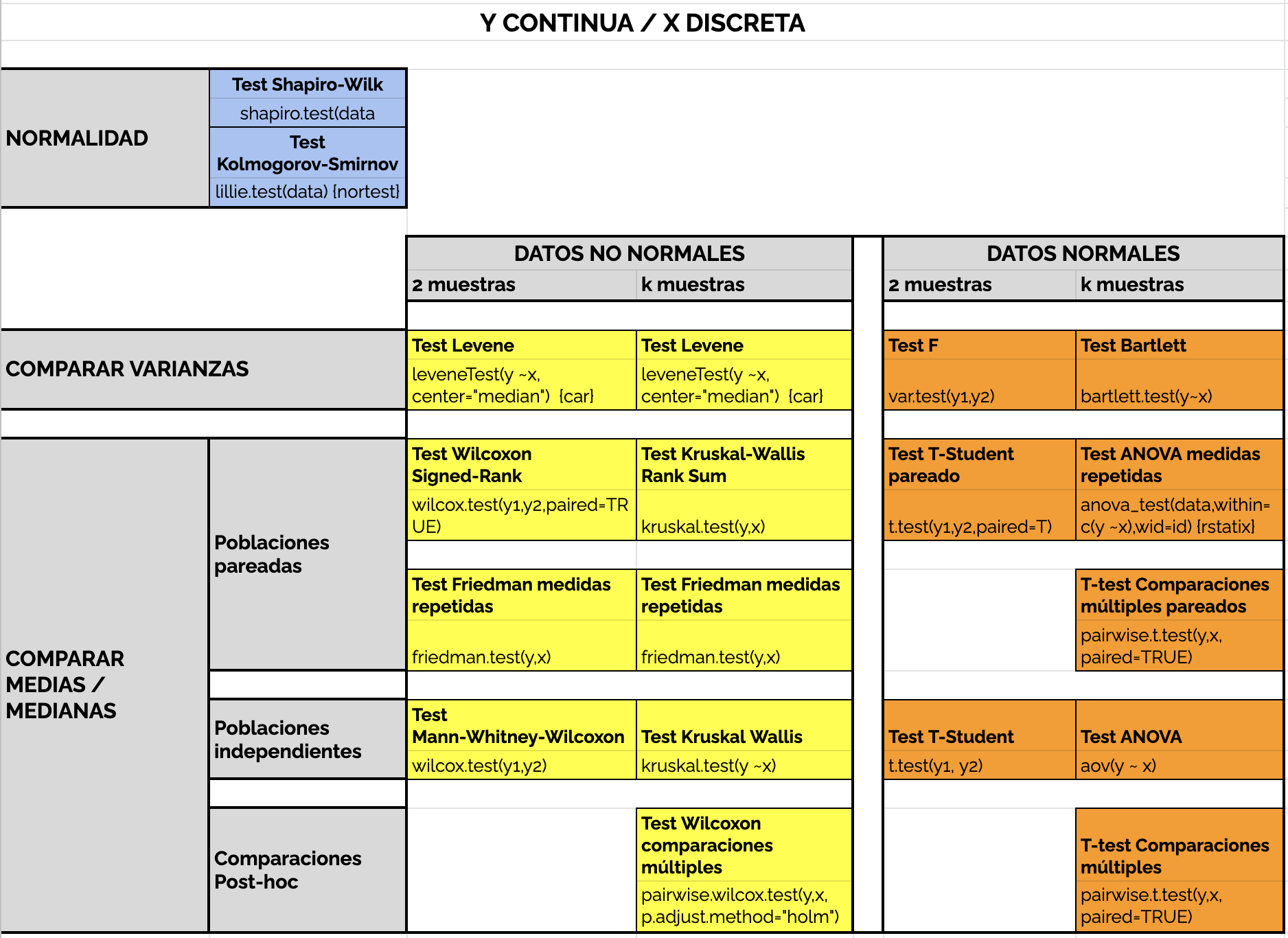
Figura 6.11: Contrastes de hipótesis para Y continua y X discreta.

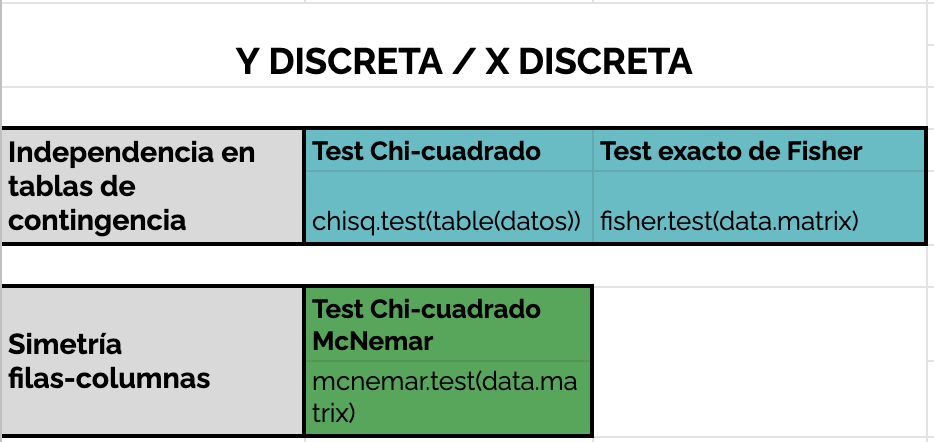
Figura 6.12: Contrastes de hipótesis para Y discreta y X discreta.

6.4.2 Modelización

En ocasiones, especialemente cuando tenemos muchas variables \(X\) involucradas y nos interesa investigar su relación con la respuesta \(Y\), no será suficiente resolver contrastes de hipótesis (generalmente para discernir la asociación con una sola variable), y será preciso abordar modelos estadísticos de predicción. En la Figura 6.13 se presenta una hoja de ruta sencilla con alternativas de análisis/modelos a ajustar para derivar conclusiones.

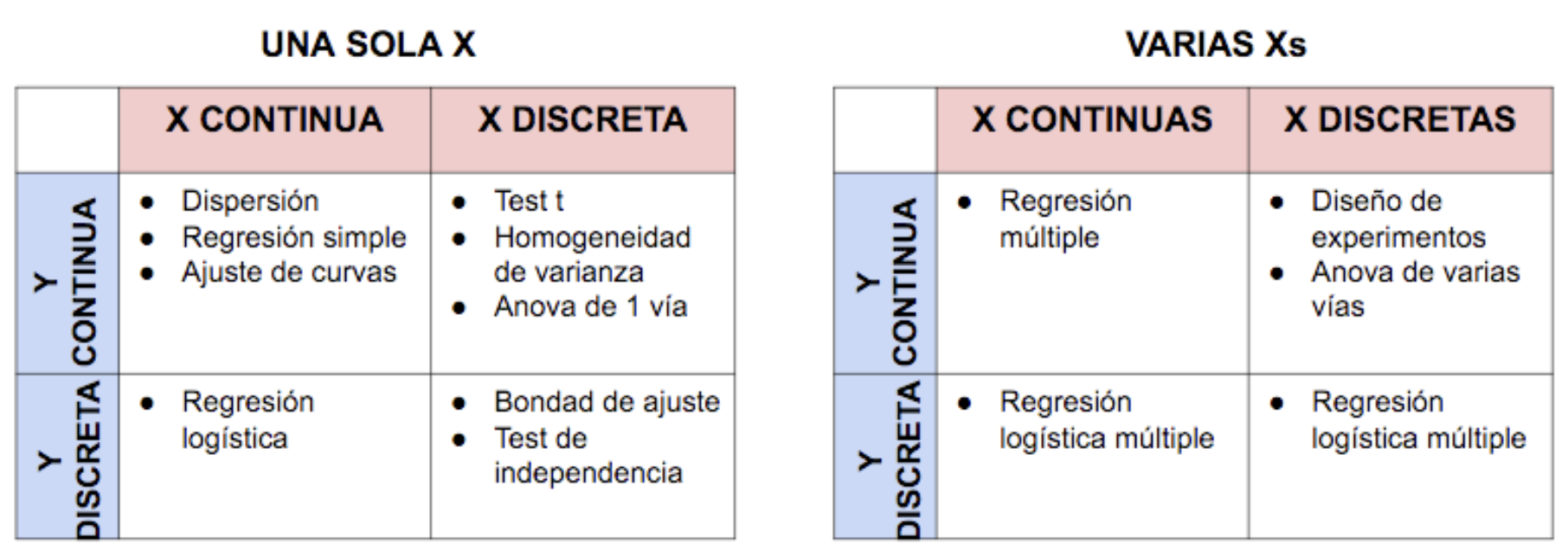
Figura 6.13: Alternativas de análisis con X e Y según tipología.

Puesto que en este curso no es factible hacer una revisión exhaustiva de las distintas técnicas de análisis y modelización estadística, te recomendamos las siguientes fuentes como material de consulta para abordar la modelización estadística con la que identificar variables \(X\) críticas para los resultados \(Y\):

• Análisis estadísticos con R (A. M. Mayoral and Morales 2015).
• R in Action (Kabacoff 2011).
• R para ciencia de Datos (Wickham and Grolemund n.d.).
• Modelos estadísticos con R (Morales and Mayoral 2021). Incluye Modelos Lineales Generalizados.
• Modelos lineales generalizados (A. M. Mayoral and Morales 2001)
• Pruebas no paramétricas (Berlanga and Rubio 2012).
• Recursos en línea para Data Science (Morales 2021).

6.5 Ejemplo: análisis de amonio

Seguimos con el ejemplo del amonio. Al disponer de dos variables causales de tipo factor, operador y ubicación, elegimos obviar el tiempo y estudiar la relación de ellas con el nivel de amonio medido. Puesto que ya identificamos en el análisis gráfico una posible interacción entre operador y ubicación, y además no teníamos demasiada desviación de normalidad en la variable respuesta (amonio), planteamos una modelización conjunta con un modelo lineal de Anova con interacción: \[amonio \sim operador + ubicacion + operador:ubicacion\]

fit=lm(amonio ~ operador * ubicacion,data=datos)
anova(fit)

## Analysis of Variance Table
## 
## Response: amonio
##                    Df Sum Sq Mean Sq F value   Pr(>F)   
## operador            1  59.04  59.036  3.9826 0.050845 . 
## ubicacion           1  84.95  84.949  5.7307 0.020045 * 
## operador:ubicacion  1 107.03 107.031  7.2204 0.009472 **
## Residuals          56 830.11  14.823                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Como vemos en el análisis de la varianza, la interacción resulta significativa (con el test \(F\) del Anova), de modo que ratifica el efecto conjunto que tienen estas dos variables sobre la medición de amonio. Ambas están afectando a la variabilidad, especialmente ubicación (las mediciones en las dos ubicaciones son significativamente distintas) y la mayor parte de esta está explicada por la interacción, como se muestra en la tabla de Anova anterior (los dos operadores no están midiendo igual en las dos ubicaciones).

Validamos por último el modelo con un test de normalidad para los residuos, que como vemos no permite rechazar la normalidad.

res=residuals(fit)
shapiro.test(res)

## 
##  Shapiro-Wilk normality test
## 
## data:  res
## W = 0.96273, p-value = 0.06404

El modelo de predicción se obtiene ya a partir de los coeficientes estimados en el modelo.

coefficients(fit)

##           (Intercept)             operadorB           ubicacionu2 
##            23.6919945            -0.6873489            -0.2914540 
## operadorB:ubicacionu2 
##             5.3424430

• Operador (A) - Ubicacion (U1): \(amonio \sim 23,69\)
• Operador (A) - Ubicacion (U2): \(amonio \sim 23,69-0,29=23,40\)
• Operador (B) - Ubicacion (U1): \(amonio \sim 23,69-0,69=23,00\)
• Operador (B) - Ubicacion (U2): \(amonio \sim 23,69-0,29-0,69+5,34=28,06\)

residuos=cbind(datos,res=res)
ggplot(residuos,aes(x=ubicacion,y=res,fill=operador))+
  geom_boxplot()+
  labs(y="Residuos")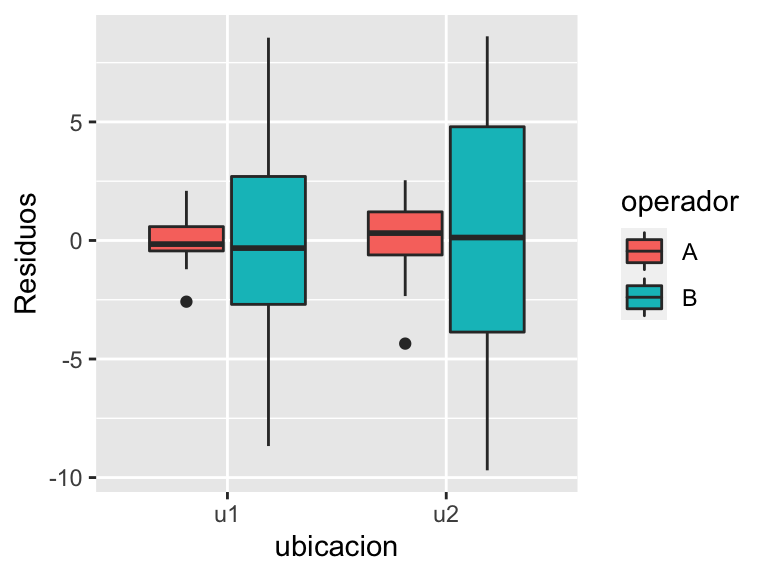

Figura 6.14: Gráfico condicionado de los residuos del modelo.

Así la medición más baja de amonio la genera el operador B en la ubicación 1, y también la más alta pero en la ubicacion 2. Sin embargo las dos más parecidas entre sí las genera el operador A. El análisis gráfico de los residuos (Figura 6.14) completa las conclusiones del análisis respecto a la gran variabilidad que queda sin explicar por el modelo ajustado para el medidor B, especialmente en la ubicación 2.

6.6 Diseño de experimentos

Una vez identificadas las causas vitales de la variabilidad en la respuesta, el paso siguiente es encontrar la configuración óptima de dichas variables condicionantes para reducir al máximo la variabilidad en la respuesta, y en consecuencia los defectos que se generen. Realmente el diseño de experimentos (Design of Experiments, DOE) se utiliza en la fase de Mejora, pero lo introducimos aquí por su estrecha vinculación con el análisis estadístico de datos, y por tanto para compendiar en este capítulo titulado ANALIZAR, todo lo que tiene que ver con el análisis de información.

Para estudiar de un modo más detallado el diseño de experimentos, proponemos varias lecturas alternativas como son Daniel (1976), Lawson (2015) y Lawson (2021), y alguna librería en R como DoE.base (Groemping 2021b), desarrollada por Groemping (2018), así como recopilaciones varias por este autor (Groemping 2021a). Para ampliar información sobre el diseño factorial fraccional, relativamente común en procesos industriales en los que no se pueden conseguir suficientes datos para estimar todos los efectos posibles cuando el número de factores a estudiar es muy amplio, se recomienda consultar Groemping (2014) y Natrella (2012).

Partimos del problema de diseñar un experimento en el que contamos con ciertos factores en los cuales queremos probar distintas configuraciones para investigar cómo afectan a la variable respuesta objetivo. Vamos a proponer realizar un diseño de experimentos bajo el supuesto más simple: queremos identificar todos los efectos principales e interacciones existentes porque tenemos suficiente presupuesto para probar y testar todas las posibilidades de combinación entre los factores disponibles, con repeticiones. Hablamos entonces del diseño factorial completo

Para obtener en R (R Core Team 2021) la matriz de diseño básica en un diseño factorial completo, introducimos como argumentos los factores a utilizar y sus niveles en el comando expand.grid(). Por ejemplo, supongamos 3 factores f1, f2 y f3, con 3, 2 y 2 niveles respectivamente. Conseguimos la matriz de diseño, para un diseño factorial completo, con:

expand.grid(f1=c("a", "b","c"),f2=c(-1,1),f3=c(0,1))

##    f1 f2 f3
## 1   a -1  0
## 2   b -1  0
## 3   c -1  0
## 4   a  1  0
## 5   b  1  0
## 6   c  1  0
## 7   a -1  1
## 8   b -1  1
## 9   c -1  1
## 10  a  1  1
## 11  b  1  1
## 12  c  1  1

Veamos, para ilustrar, dos diseños factoriales completos, el \(2^2\) y el \(2^k\).

6.6.1 Diseño factorial completo \(2^2\)

Consideramos dos factores, A y B, con dos niveles/categorías cada uno de ellos. Los efectos a estimar son:

• \(\mu\) la media global
  
• 2 efectos principales: \(\alpha\) para el factorA y \(\beta\) para el factorB
  
• 1 efecto de interacción \(\alpha\beta\) para la interacción AB.

Los grados de libertad que consume el modelo son por lo tanto 4, lo que requerirá un mínimo de 4 observaciones en total para tener estimaciones de todos los efectos.

El modelo lineal que representa cómo ambos factores y su interacción explican una respuesta \(y\) viene dado por: \[y=\mu+\alpha A + \beta B + (\alpha\beta) AB + \epsilon\] donde \(\epsilon\) representa un error aleatorio que se distribuye \(N(0,\sigma^2)\).

El hecho de tener dos niveles para cada factor nos da un total de \(2^2=4\) combinaciones posibles y distintas entre los diferentes niveles de los factores. Representando los dos niveles de los factores A y B con signos “+/-,” es muy fácil construir el término de interacción AB a partir del producto de los signos en los factores A y B. Asimismo, la matriz de diseño (Tabla 6.1) definida en las tres primeras columnas nos permite obtener fácilmente la predicción media para cada una de las combinaciones existentes, utilizando la expresión del modelo anterior:

Tabla 6.1: Matriz de diseño en el diseño \(2^2\).

A	B	AB	Estimación
+	+	+	\(\hat{\mu}+\hat{\alpha}+\hat{\beta}+ \hat{\alpha\beta}\)
+	-	-	\(\hat{\mu}+\hat{\alpha}-\hat{\beta}- \hat{\alpha\beta}\)
-	+	-	\(\hat{\mu}-\hat{\alpha}+\hat{\beta}- \hat{\alpha\beta}\)
-	-	+	\(\hat{\mu}-\hat{\alpha}-\hat{\beta}+ \hat{\alpha\beta}\)

Consideremos obtener dos observaciones de una variable respuesta \(Y\) por cada una de las combinaciones posibles en la Tabla 6.1, de manera que podamos estimar el error. Calculamos a continuación en la Tabla 6.2 los promedios para cada combinación.

Tabla 6.2: Cálculo de los promedios en cada combinación de los factores A y B.

A	B	AB	obs1	obs2	promedio
1	1	1	89.0	89.50	89.250
1	-1	-1	126.5	127.50	127.000
-1	1	-1	118.0	117.50	117.750
-1	-1	1	173.0	171.75	172.375

A continuación se calcula el efecto positivo/negativo en cada uno de los factores A, B e interacción AB, utilizando todos los datos en cada uno de dichos niveles (1/-1). Ver Tabla 6.3:

Tabla 6.3: Estimación del efecto (diferencia entre niveles) de cada factor.

	A	B	AB
(+1)	108.12	103.50	130.81
(-1)	145.06	149.69	122.38
Delta	-36.94	-46.19	8.44
Delta/2	-18.47	-23.09	4.22

La fila “(+1)” contiene, para cada factor (A, B y la interacción AB), el promedio de los promedios en la 6.3 que van asociados a los niveles ‘+1.’ Por ejemplo, \[\mbox{(+1)}^A=108.1=(89.25+127)/2\]

La fila Delta contiene, en cada columna, el incremento o cambio que sufre la variable respuesta cuando varía el factor correspondiente de su nivel “+1” a su nivel “-1,” Delta=(+1)-(-1).

Por último, la fila Delta/2 muestra el valor de la pendiente en la recta que une los dos puntos observados, calculada como el incremento en el eje \(Y\), Delta, dividido por el incremento en el eje \(X\), \((2=(1-(-1)))\). Se entiende claramente a partir la Figura 6.15, cómo se calcula la pendiente de la recta: \[pendiente=tangente(\theta)=Delta/2\]

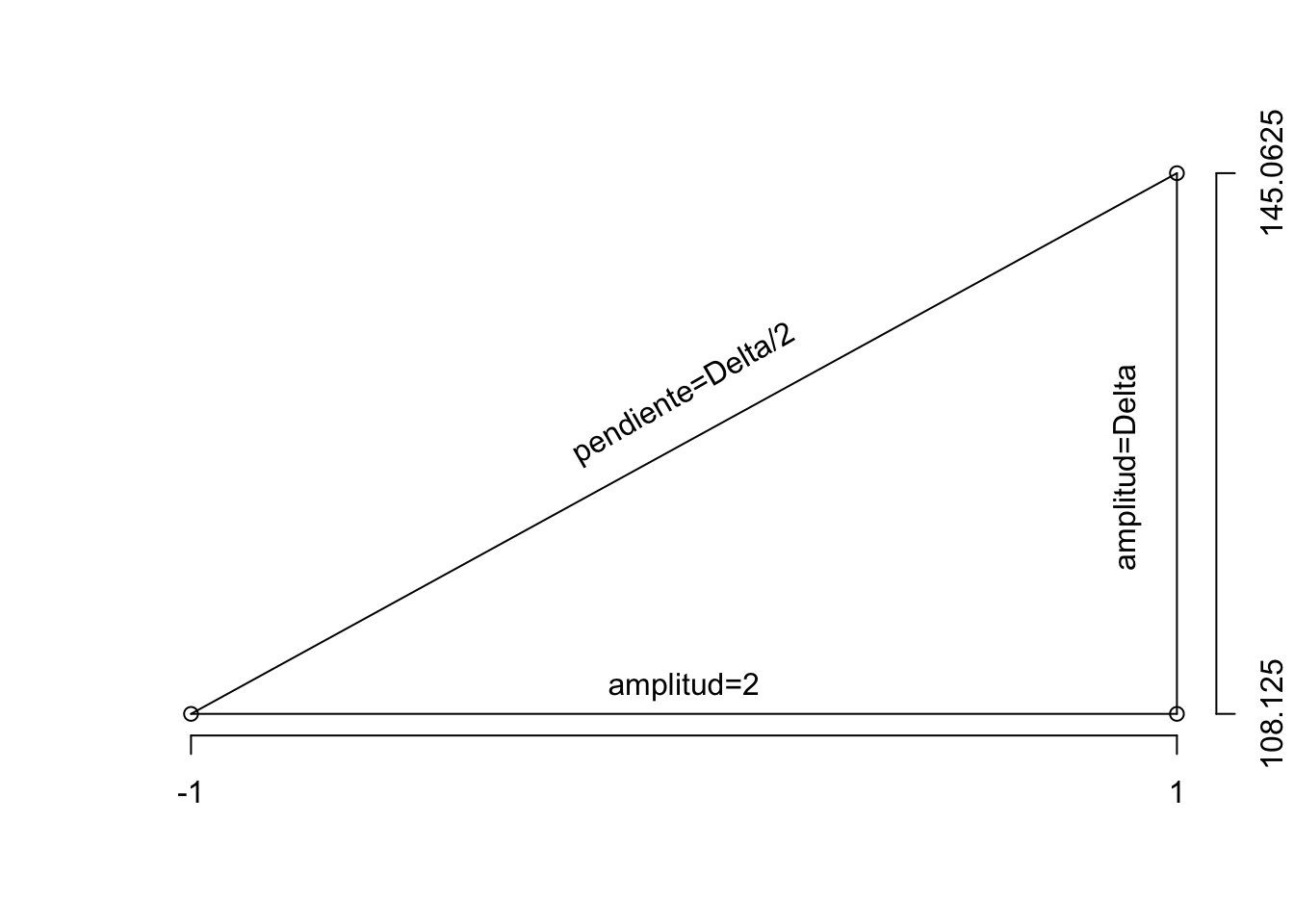
Figura 6.15: Ilustración del cálculo de la pendiente de una recta que pasa por dos puntos.

Así el modelo resultante estima un efecto \(\alpha\) para el factor \(A\), \(\beta\) para el factor \(B\) y \(\gamma\) para la interacción \(AB\): \[\hat{\alpha}=\frac{Delta_{A}}{2}, \ \hat{\beta}=\frac{Delta_{B}}{2}, \ \hat{\gamma}=\frac{Delta_{AB}}{2}.\] Así, el modelo de ajuste-predicción viene dado por:

\[\hat{y}=\hat{\mu}+\hat{\alpha} A + \hat{\beta} B + \hat{\gamma} AB\] y a partir de él podremos evaluar fácilmente la predicción en cualquiera de los puntos de muestreo (+1/-1), tal y como se deriva de los promedios en la Tabla 6.2. Finalmente, si queremos predecir la respuesta en el nivel intermedio entre los dos considerados, (\(A=B=0\)), bastará con utilizar \(A=0\) y \(B=0\), de donde la predicción de la respuesta resultará: \[\hat{y}(0)=\hat{\mu}=126.6\]

En R estos cálculos los hacemos directamente a través del ajuste del modelo lineal.

Construimos la matriz de datos

A=factor(c(1,1,1,1,-1,-1,-1,-1))
B=factor(c(1,1,-1,-1,1,1,-1,-1))
obs=rep(c(1,2),4)
datos=data.frame(A,B,obs,y);datos

##    A  B obs      y
## 1  1  1   1  89.00
## 2  1  1   2  89.50
## 3  1 -1   1 126.50
## 4  1 -1   2 127.50
## 5 -1  1   1 118.00
## 6 -1  1   2 117.50
## 7 -1 -1   1 173.00
## 8 -1 -1   2 171.75

Ajustamos el modelo lineal para estimar y con los factores A y B y la interacción AB, y obtenemos las estimaciones de los coeficientes del modelo que, en este caso, son diferencias entre las medias estimadas para los dos niveles de cada factor (\(A1=A_{+1}-A_{-1}\) y \(B1=B_{+1}-B_{-1}\)).

fit=lm(y~A*B,data=datos)
summary(fit)

## 
## Call:
## lm.default(formula = y ~ A * B, data = datos)
## 
## Residuals:
##      1      2      3      4      5      6      7      8 
## -0.250  0.250 -0.500  0.500  0.250 -0.250  0.625 -0.625 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 172.3750     0.4375  394.00 2.49e-10 ***
## A1          -45.3750     0.6187  -73.34 2.07e-07 ***
## B1          -54.6250     0.6187  -88.29 9.87e-08 ***
## A1:B1        16.8750     0.8750   19.29 4.26e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6187 on 4 degrees of freedom
## Multiple R-squared:  0.9998, Adjusted R-squared:  0.9996 
## F-statistic:  6215 on 3 and 4 DF,  p-value: 8.625e-08

Y predecimos con el modelo las medias sobre la matriz de diseño base, para cada una de las combinaciones de niveles de factores posibles:

newdata=expand.grid(A=factor(c(-1,1)),B=factor(c(-1,1)))
cbind(newdata,pred=predict(fit,newdata))

##    A  B    pred
## 1 -1 -1 172.375
## 2  1 -1 127.000
## 3 -1  1 117.750
## 4  1  1  89.250

Obtenemos, como era de esperar, las mismas predicciones promedio que en la Tabla 6.2 que ajustamos manualmente arriba, para cada una de las combinaciones posibles de los factores A y B.

6.6.2 Diseño factorial Completo \(2^k\)

En un modelo con \(k\) factores, \(A_1, A_2, ... , A_k\), cada uno de ellos con 2 niveles, los efectos a estimar son:

• \(\mu\) la media global
  
• \(k\) efectos principales
• \(\sum_{i=1}^{k-1} (k-i)\) efectos para las interacciones de orden 2
• \(\sum_{i=2}^{k-1} (k-i)\) efectos para las interacciones de orden 3,
• y así sucesivamente.

Tendremos en consecuencia \(2^k\) combinaciones posibles entre todos los niveles de todos los factores, lo que requerirá de al menos \(n=2^k\) datos para al menos estimar cada una de estas combinaciones con el dato recogido. Si requerimos al menos dos datos en cada combinación, necesitaremos \(n=2 \times 2^k\) observaciones; si requerimos tres, \(n=3 \times 2^k\), etc.

Una vez observados los datos, la estimación se realiza de igual modo que en el modelo \(2^2\) anterior, a partir del ajuste de un modelo lineal y su predicción.

fit=lm(y~A1*A2*...*Ak,data=datos)
m.pred=cbind(m,pred=predict(fit,m))

Como hemos comentado, cuando \(k\) es grande, el número de observaciones que necesita un diseño factorial completo \(2^k\) es muy grande. Esto ocurre con relativa frecuencia en procesos industriales, con el obstáculo añadido de que es inviable conseguir una muestra suficientemente grande para estimar todos los efectos de interés. Se introducen entonces los diseños factoriales fraccionales \(2^{k-p}\), en los que las interacciones de orden alto se suponen nulas, y se confunden con los efectos simples, por lo que no es viable estimarlas. Se reduce pues a un mínimo de \(n=2^{k-p}\) el número de observaciones precisas para estimar los efectos no despreciables.

Para concluir, comentar que el diseño de experimentos será una herramienta estadística útil en la siguiente etapa DMAIC: Mejorar, destinada a buscar alternativas de mejora para reducir la variabilidad del proceso y en consecuencia los defectos. Con pocos datos se podrán testar unos pocos escenarios o condiciones alternativas en las variables predictoras, e interpolar los resultados para inferir cuáles son los escenarios óptimos respecto a la reducción de la varianza en la variable respuesta, y en consecuencia del número de defectos. Comentaremos cómo utilizarlo en el Capítulo 7.

Bibliografía

Berlanga, Vanesa, and María José Rubio. 2012. “Clasificación de Pruebas No Paramétricas. Cómo Aplicarlas En SPSS.” Revista d’Innovació i Recerca En Educació 5 (2). https://doi.org/10.1344/reire2012.5.2528.

Daniel, Cuthbert. 1976. Applications of Statistics to Industrial Experimentation. NY Wiley.

Groemping, Ulrike. 2014. “R Package FrF2 for Creating and Analyzing Fractional Factorial 2-Level Designs.” Journal of Statistical Software 56 (1): 1–56. https://doi.org/10.18637/jss.v056.i01.

———. 2018. “R Package DoE.base for Factorial Experiments.” Journal of Statistical Software 85 (5): 1–41. https://doi.org/10.18637/jss.v085.i05.

———. 2021a. CRAN Task View: Design of Experiments (DoE) and Analysis of Experimental Data. https://cran.r-project.org/web/views/ExperimentalDesign.html.

———. 2021b. DoE.base: Full Factorials, Orthogonal Arrays and Base Utilities for DoE Packages. https://CRAN.R-project.org/package=DoE.base.

Kabacoff, Robert I. 2011. R in Action. Data Analysis and Graphics with r, 1st Ed. Manning.

Lawson, John. 2015. Design and Analysis of Experiments with r. CRC Press. http://www.ru.ac.bd/stat/wp-content/uploads/sites/25/2019/03/502_07_00_Lawson_Design-and-Analysis-of-Experiments-with-R-2017.pdf.

———. 2021. An Introduction to Acceptance Sampling and SPC with r. Chapman; Hall/CRC. https://bookdown.org/lawson/an_introduction_to_acceptance_sampling_and_spc_with_r26/.

Mayoral, A. M., and J. Morales. 2001. Modelos Lineales Generalizados. Universidad Miguel Hernández. https://drive.google.com/file/d/0B3JR7lZLWR_UTkQtcTVHOEpaSE0/view?resourcekey=0-U4-m_7AhIofwK1Y7SG6Kmw.

———. 2015. “Análisis Estadísticos Con r.” Documento online. https://drive.google.com/file/d/0B3JR7lZLWR_UYUtjWXE3R0lOenM/view?resourcekey=0-w88UvNFXE9CXZBPT7p-iwg.

Morales, J. 2021. “Recursos En línea Para Data Science.” Web. https://sites.google.com/umh.es/recursos-datascience/.

Morales, J., and A. M. Mayoral. 2021. “Modelos Estadísticos Con r.” Web. https://bookdown.org/j_morales/weblinmod/.

Natrella, Mary. 2012. “NIST/SEMATECH e-Handbook of Statistical Methods.” In, edited by Paul Tobias Carroll Croarkin. https://doi.org/10.18434/M32189.

R Core Team. 2021. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Wickham, Hadley, Winston Chang, Lionel Henry, Thomas Lin Pedersen, Kohske Takahashi, Claus Wilke, Kara Woo, Hiroaki Yutani, and Dewey Dunnington. 2021. Ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics. https://CRAN.R-project.org/package=ggplot2.

Wickham, Hadley, and Garrett Grolemund. n.d. “R Para Ciencia de Datos (Traducción de r for Data Science).” Edited by Riva Quiroga. https://es.r4ds.hadley.nz/.