Unidad 5 DMAIC2.MEDIR

5.1 Introducción

En esta unidad trabajaremos sobre los siguientes objetivos de aprendizaje:

Descubrir los objetivos y procesos en la etapa MEDIR de DMAIC.
Descubrir la necesidad de un análisis de fiabilidad del sistema de medida e implementarlo.
Identificar los objetivos de un análisis de capacidad e implementarlo.
Conocer la hoja de ruta en la etapa MEDIR del DMAIC.

5.2 Objetivos

Medir un proceso susceptible de mejora es útil y necesario para caracterizarlo y comprender cómo está funcionando, obtener datos precisos para evaluar su rendimiento o capacidad, y contrastar teorías sobre los condicionantes y las pautas de variación que ocasionan defectos. Recordemos una cita de Lord Kelvin, en University of Glasgow (n.d.):

“A menudo digo que cuando podemos medir aquello de lo que estamos hablando, y expresarlo mediante números, sabemos algo acerca de ello, cuando no podemos expresarlo mediante números, nuestro conocimiento es escaso e insatisfactorio; puede ser un principio de conocimiento pero apenas avanzamos todo lo que debemos hacia el estado de la Ciencia”.”

En ocasiones dispondremos de datos medidos sistemáticamente e incluso de forma automatizada en una empresa. En otras ocasiones habremos de diseñar el modo de medir un determinado proceso, para capturar la información que precisemos.

Los objetivos que se plantean en la etapa MEDIR son:

Identificar los resultados a medir sobre el proceso y cada una de sus etapas.
Determinar el método más adecuado para medir los resultados.
Evaluar el sistema de medida.
Recopilar datos y determinar la magnitud del problema.
Identificar qué área en el sistema de medida está provocando mayor variación.
Analizar la capacidad actual/potencial del proceso.

Proponemos un ejercicio:

Accede a continuación y sólo durante 1 minuto, a este DOCUMENTO con un texto en inglés. Has de contar individualmente la cantidad de letras F que aparecen en el texto y anotar el resultado. Cuando el instructor lo solicite, has de compartir en grupo tus anotaciones.

Y ahora comenta: ¿ha habido consenso?, ¿ha habido variabilidad? Justifica los resultados. ¿Sería posible articular un procedimiento de conteo que facilite dicho conteo y permita conseguir a todos el mismo resultado (o al menos reducir la variabilidad)? Intenta concretarlo y téstalo. ¿Qué conclusiones derivas de esta experiencia?

5.3 CTQ’s e Y’s

En todo proceso tendremos una serie de requisitos o necesidades del cliente que reexpresamos, durante la etapa DEFINIR, en términos de requisitos, atributos o prestaciones del producto o servicio producido. Los que realmente son críticos para la calidad, CTQ, nos ayudan a definir y concretar el proyecto. El siguiente paso es el de relacionar estos CTQ con variables o características cuantificables numéricamente y que nos permitan evaluar los logros del proyecto, esto es, la capacidad del proceso para satisfacer las necesidades “críticas” de los clientes o el grado de cumplimiento de estas necesidades. A estas variables las denominaremos variables $Y$, vinculadas a los observables en las salidas del proceso o procesos involucrados en el proyecto de mejora. Las $Y$ serán las variables o características sobre las que recabamos información (numérica) para poder evaluar el cumplimiento o grado de cumplimiento del CTQ.

A su vez, el proceso dependerá de una serie de condiciones controlables de puesta en marcha y funcionamiento (entradas, métodos, recursos), que habremos de cuantificar en variables $X$ para a continuación encontrar el modo en que se relacionan con las salidas $Y$ y predecir cómo las condicionan. El control sobre estas variables $X$ permitirá modificar las salidas $Y$ para cumplir con los requisitos del cliente. Conseguir unas salidas adecuadas será consecuencia pues, de regular y controlar las condiciones de funcionamiento del proceso que influyen sobre éstas.

Expresado matemáticamente, los resultados $Y$ serán función de las entradas $X$, $Y=f(X)$.

Para conocer bien el proceso necesitamos identificar todas las variables $Y$’s y $X$’s, y medirlas. En la Figura 5.1 se representa la interrelación entre las $X$ y las $Y$ en un proceso cualquiera.

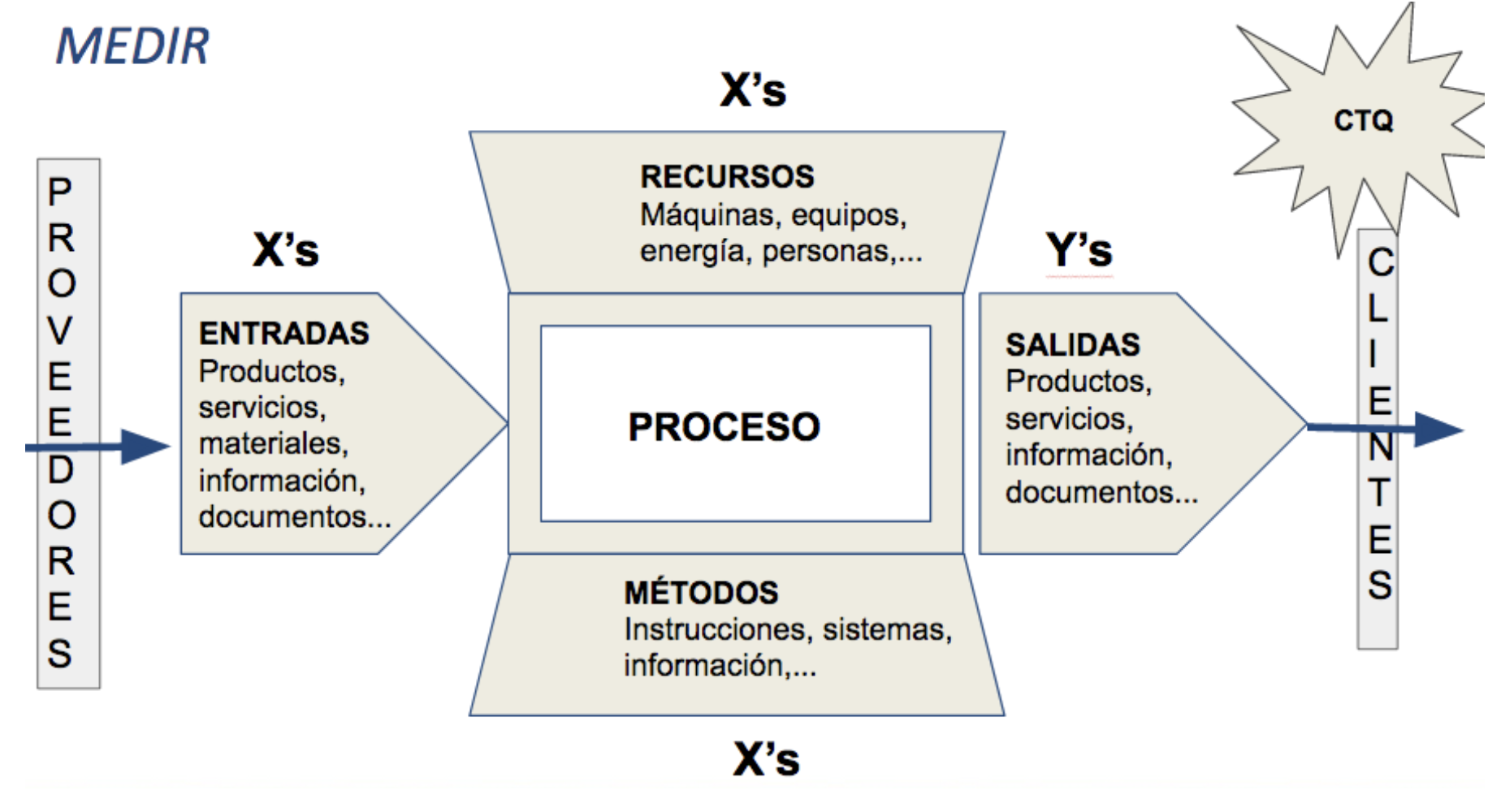
Figura 5.1: Relación entre variables X y variables Y en un proceso.

Para definir correctamente las $Y$’s conviene tener en cuenta las siguientes premisas:

Es preciso relacionar las $Y$’s con los CTQ’s. De hecho, un mismo CTQ puede tener varias $Y$’s
Hay que expresar las $Y$’s con claridad, de forma operativa, según el modo en que se utilicen en el proceso.
Hay que identificar los valores y rangos en los que hemos de acotar las $Y$’s para satisfacer los CTQ’s.
Hay que considerar el concepto de DEFECTO para definir las $Y$’s. Un defecto será una $Y$ que no cumple con los requisitos.

En ocasiones los CTQ y las $Y$’s coincidirán, pero no siempre será así.

Por ejemplo, en un proyecto de reducción del tiempo de entrega, el CTQ (tiempo de entrega) coincide con la $Y$, si bien ésta se podría medir en diferentes unidades. En un proyecto planteado para conseguir habitaciones confortables en un hotel, tendremos varios CTQ como el tamaño de la habitación, mobiliario, condiciones del baño, tipo de cama, ligadas asimismo a diferentes Y, como el largo y ancho de la habitación, espacio entre mobiliario, cantidad de mobiliario, tamaño de la cama, dureza del colchón, largo y ancho de la ducha, largo y ancho del baño, ….

Cuando encontramos muchas $Y$’s ligadas a un CTQ, podemos utilizar las siguientes preguntas para seleccionar las $Y$’s más adecuadas:

¿Está íntimamente ligada a alguno de los CTQ’s?
¿Se puede expresar en forma de objetivos o requisitos?
¿Es fácilmente medible?
¿Permite expresar o está asociada a un DEFECTO?
¿Es una medida directa del proceso?
¿Corresponde a un indicador importante del proceso?

El diagrama de flujo del proceso nos servirá asimismo de ayuda para concretar estas $Y$’s a medir. Habremos de profundizar en el conocimiento del proceso observando con mayor detalle cada paso o actividad y descubriendo qué tareas o etapas afectan más a las $Y$’s y a su variabilidad.

Sobre el mapa del proceso habremos de realizar una serie de preguntas típicas:

¿Cómo funciona cada etapa del proceso?
¿Cómo se producen los defectos?
¿Cómo se está midiendo el resultado de cada tarea?
¿Cómo se está midiendo el resultado final del proceso?
¿Cómo afectan los resultados por etapas al resultado final?
¿El funcionamiento del sistema, es estable o varía?
¿Estabilidad o inestabilidad de los resultados parciales/finales?
¿Qué factores pueden afectar al funcionamiento y resultados del proceso?
¿Cómo se producen los defectos: uniformemente o ante ciertas circunstancias?

Con todo, siempre habremos de adaptar esta batería de preguntas para comprender con profundidad el funcionamiento y resultados de cada proceso particular. Como recomendaciones generales hay que recopilar toda la documentación (procedimientos, normas, especificaciones, etc.) que describa el funcionamiento del proceso o que contengan instrucciones relativas a la forma de realizar las actividades, trabajar con las personas que están en el día a día del proceso, observar el proceso si es posible, identificar las relaciones del proceso con otros procesos o con los sistemas de medición, identificar los pasos o sistemas que contienen información o datos acerca del resultado de las tareas o actividades y conocer en detalle los recursos (materiales, humanos, tecnológicos, etc.) que utiliza el proceso.

Una vez que conozcamos en detalle el funcionamiento del proceso surgirá inmediatamente la necesidad de recopilar datos, y no siempre tendremos los datos adecuados para conseguir las respuestas que buscamos. En la medida que dispongamos de datos podremos comprender el proceso y determinar su capacidad para cumplir con los requisitos de los clientes. Por el momento en estas etapas previas, necesitaremos los datos para responder a una serie de preguntas básicas que nos van a permitir comprender, con cierto detalle, el funcionamiento y rendimiento del proceso.

5.4 Muestreo

Cuando medimos un proceso, generalmente hemos de recurrir al muestreo, pues será inviable observarlo infinitamente y en todas sus componentes.

Habrá que tomar una serie de precauciones para garantizar que la muestra elegida es buena para descubrir nuestros intereses. Una muestra es buena cuando no tiene sesgos, es aleatoria y es representativa de la población que nos interesa:

Representativa. En una muestra representativa los datos reflejan con precisión la población o proceso. Las muestras representativas ayudan a evitar sesgos específicos de los segmentos o partes de la población o proceso.
Aleatoria. En una muestra aleatoria los datos se recogen sin ningún orden predeterminado, cada elemento tiene la misma posibilidad de ser seleccionado. El muestreo aleatorio ayuda a evitar sesgos específicos relativos al tiempo y orden de la recogida de datos o de la persona que los recoge.
Sin sesgos. Un sesgo en una muestra es la presencia o influencia de algún factor que origina que la población o proceso aparezcan sistemáticamente diferentes de lo que realmente son. Será preciso evitar la exclusión de datos relevantes, la subjetividad y la interacción entre los sujetos que recogen la información y las fuentes de información y marcar un método protocolarizado de recogida de datos. Por supuesto, en la etapa de análisis, habrá que evitar estimadores sesgados.

Será importante especificar una metodología para la recogida de datos, esto es, un procedimiento lógico y estructurado que indique:

qué datos recoger
cuántos datos recoger (tamaño de muestra)
cómo (método y herramientas)
cuándo (frecuencia de muestreo)
dónde recogerlos (puntos de recogida)
y cómo guardarlos.

La especificación de qué datos recoger ha de provenir del análisis previo que se ha realizado entre los CTQ y las Y del proceso. Identificar cuáles son los outputs con los que comprobar el cumplimiento de los CTQ, e identificar así mismo, qué otros factores X pueden estar condicionando las Y, es crítico. Es preciso pues, estudiar de modo detallado el proceso para concretar estas variables a medir.

El método para obtener los datos vendrá definido a través del tipo de muestreo a utilizar. El más común es el aleatorio simple, en el que todas las unidades tienen idéntica probabilidad de ser seleccionadas, pero también es habitual en gestión de calidad, el muestreo estratificado. La estratificación es una técnica de clasificación y organización de datos para encontrar diferencias en los resultados ocasionados por factores de clasificación, que provocan diferencias entre categorías. Para estratificar basta tener claro cuáles son los factores que pueden influir en diferenciar los datos que se tienen (temporales, geográficos, humanos, tecnológicos, etc.) y establecer las categorías lógicas de dichos factores, como pueden ser los turnos, los días o meses, las comunidades o provincias, los diferentes grados de formación, los sistemas informáticos utilizados, etc. Si se encuentran diferencias entre estratos, habrá que investigar para determinar sus causas. Cuando estratifiquemos será preciso seleccionar muestras representativas en cada uno de los estratos que se definan.

El muestreo sistemático también es muy común en gestión de procesos y servicios. Consiste en escoger un primer registro de forma aleatoria y a continuación dinamizar una recogida sistemática de los subsecuentes registros, como por ejemplo uno cada n unidades producidas, uno cada n instantes de tiempo transcurridos, etc. Siempre y cuando la frecuencia de recogida no responda a algún patrón previo de comportamiento (como sería sólo recoger datos cada 24 horas y así coincidir idénticas condiciones), este tipo de muestreo se puede considerar como aleatorio y generar muestras representativas.

Para determinar el tamaño de la muestra necesaria para obtener datos confiables con los que trabajar habremos de considerar, tanto el parámetro de interés, como el tipo de análisis/contraste a utilizar en la etapa de análisis, como el tipo de muestreo (aleatorio simple, estratificado, …). Existen fórmulas específicas para calcular el tamaño muestral en muestreos estratificados.

Como recomendaciones básicas y sencillas para un muestreo aleatorio simple, podemos guiarnos por la Tabla 5.1.

Tabla 5.1: Recomendaciones simples sobre tamaños de muestra en función del estadístico/herramienta a utilizar.
Estadístico/Herramienta	Tamaño de muestra mínimo
Media	25
Desviación estándar	25
Proporción de defectos	100
Histogramas, Gráfico Pareto, Box-Plot	40
Diagrama de dispersión	25

Hay recursos ya desarrollados para conseguir el cálculo de tamaño requerido en función de las condiciones especificadas por el investigador (error tolerable, confiabilidad, tamaño de la población, …), como los que proporciona Select Statistical Services (si bien hay muchos más en internet). En cualquier caso, para el cálculo del tamaño de muestra es preciso tener en cuenta el contraste y tipo de muestreo a realizar, así como el error tipo I a tolerar (probabilidad de equivocarse cuando la hipótesis $H_0$ es cierta) y la potencia del contraste o error de tipo II (probabilidad de equivocarse cuando $H_0$ es falsa).

\[ \alpha=Pr(\mbox{error tipo I})=Pr(\mbox{rechazar } H_0|H_0 \mbox{ cierta}) \] \[ \beta=Pr(\mbox{error tipo II})=Pr(\mbox{no rechazar } H_0|H_0 \mbox{ falsa}).\]

Las herramientas de recogida de información serán máquinas en ocasiones, y personas en otras. En el caso de que intervengan personas, será preciso dar instrucciones simples y claras para evitar sesgos y asegurar que todos recopilan del mismo modo y correctamente la información requerida (protocolos de medición). Es siempre necesario en ese caso, diseñar hojas de registro o formularios -digitales a ser posible- que faciliten la recogida de datos. Actualmente casi todas las empresas están informatizadas y son las máquinas las que recopilan la información. Convendrá asegurar que se está recopilando información útil y precisa.

Respecto a la frecuencia para realizar las mediciones, cabe considerar las siguientes recomendaciones generales:

Distribuir la toma de muestras para garantizar representatividad.
Varias muestras pequeñas en momentos diferentes es mejor que una sola muestra grande en un momento dado.
Definir el plan/frecuencia de muestreo en función del objetivo del análisis y lo estable-inestable que sea el proceso.

Como regla práctica, interesa tomar muestras con frecuencia dos veces mayor a la frecuencia a la que se supone que cambia el proceso (si varía cada semana, tomar dos muestras semanales). En procesos inestables será preciso tomar datos con una mayor frecuencia que en procesos estables que se comportan de modo mantenido a lo largo del tiempo.

Respecto a los puntos de recogida de datos, idealmente los datos se han de recoger en aquellos pasos del proceso en que se produce una alteración en su funcionamiento. Generalmente será difícil/compleja la toma de datos, pues el proceso a estudio tiene un problema crónico (por eso se eligió para mejorar). Un buen mapa del proceso ayudará a detectar puntos conflictivos y de interés para la recogida de datos.

Finalmente, aunque parezca trivial, el almacenamiento efectivo y organizado de la información es crucial para luego poder acceder a ella de una manera eficaz. Es preciso tener en mente qué variables se están registrando, cómo se están codificando sus respuestas, y cómo nos serán útiles para analizarlas. Las hojas de cálculo son básicas cuando se trate de estructuras de datos sencillas. Cuando las estructuras son más sofisticadas, se requerirán bases de datos, con las que además se podrán hacer informes. En cualquier caso, la forma de volcar la información para su tratamiento estadístico será a través de hojas de cálculo.

En cualquier manual de muestreo estadístico se pueden encontrar fórmulas para el cálculo del tamaño de muestra y otras consideraciones. Para ampliar información sobre tipos de muestreo y cálculo del tamaño de muestra, consultar el tutorial de Cheng et al. (2018) y el libro de Lawson (2021).

5.5 Análisis del sistema de medida

Una vez recopilados los datos necesarios tenemos que plantearnos si dichos datos son suficientemente buenos para responder a las preguntas que nos hemos formulado sobre el funcionamiento del proceso. Nuestro plan de recogida de datos puede estar sometido a sesgos que provoquen errores en las conclusiones que obtengamos con los datos. Para evitar cualquier tipo de problema con los datos, en esta sección trataremos métodos que nos van a permitir evaluar la “calidad” de los datos recopilados. Hemos de tener en cuenta que no siempre es necesario evaluar el sistema de medida. En muchos casos recogemos los datos de forma estándar, como se recogen el resto de los datos sobre el funcionamiento de los procesos, por lo que no parece necesario que pongamos en duda la calidad de dichos datos. En cualquier caso, será el Green Belt quien, a la luz de los datos recopilados, se plantee la necesidad de evaluar el sistema de medida o no.

Para entender todo esto, es preciso entender que cuando medimos encontraremos irremediablemente variabilidad, y además esta variabilidad puede tener diversos orígenes, esto es:

del proceso mismo, como por ejemplo una máquina que genera piezas distintas;
del sistema de medida o procedimiento de medición, en el que se están produciendo errores de exactitud o de precisión.

Estos últimos errores tergiversarán las diferencias que se encuentren entre las piezas que se estén produciendo y por tanto los datos no permitirán valorar de modo adecuado la variabilidad del proceso.

5.5.1 Errores de medida

El objetivo de la etapa medir es conseguir datos que reflejen de modo preciso el comportamiento de un proceso. Si hay errores de medición, este objetivo no se estará consiguiendo, y las variaciones reales quedarán camufladas con los errores de medición. Los tipos de error de medición a evitar son:

Errores de exactitud, esto es, se generan diferencias entre el valor registrado y el real. Se refieren a errores por
- sesgos: diferencias sistemáticas entre el valor medio de las observaciones y la medida real;
- linealidad: errores que dependen de la magnitud que se mide y que están relacionados con el dispositivo de medida;
- estabilidad: diferencias en las mediciones realizadas en idénticas condiciones y en instantes distintos de tiempo (provocadas a veces por el cansancio del operador que realiza la medición o el desgaste/descalibración de los aparatos de medida);
- discriminación: relacionada con la capacidad del aparato de medida para discriminar variaciones; un sistema/equipo de medida con buena capacidad de discriminación será aquel que discrimina hasta una décima parte del valor de especificación del elemento a medir, si bien también se aceptan equipos con una discriminación de una cuarta parte (ver 5.2).

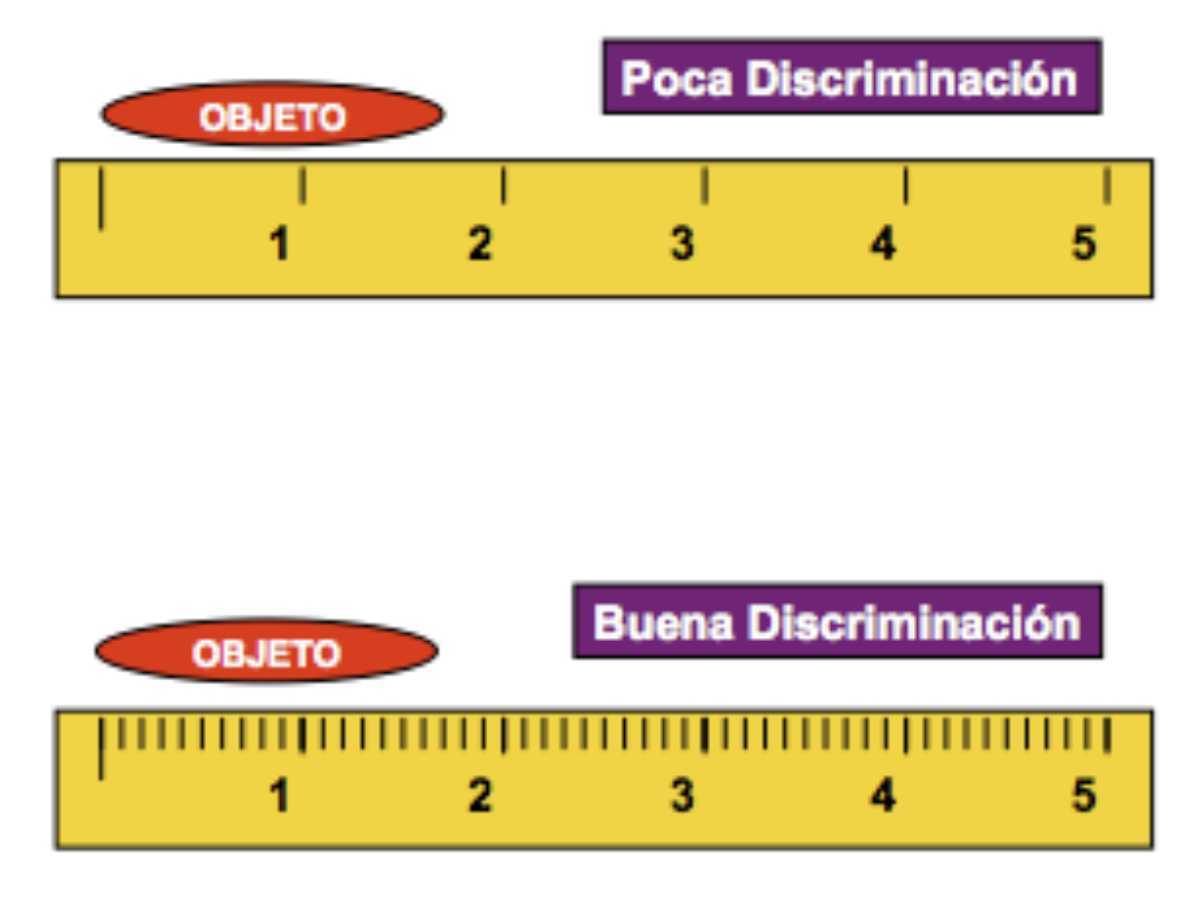
Figura 5.2: Discriminación del instrumento de medida

Los errores por sesgos y linealidad se corrigen generalmente con una correcta calibración del aparato de medida, así como los de estabilidad. Los de discriminación se corrigen utilizando instrumentos de medida con mayor discriminación.

Errores de precisión, relacionados con la fiabilidad del sistema de medida, es decir, con su capacidad para producir siempre las mismas mediciones bajo idénticas condiciones, y aluden a problemas de repetitividad y reproducibilidad (que veremos a continuación).

Podemos encontrarnos sistemas de medida que adolezcan de cualquier combinación posible entre error de exactitud y de precisión, como se muestra en la Figura 5.3.

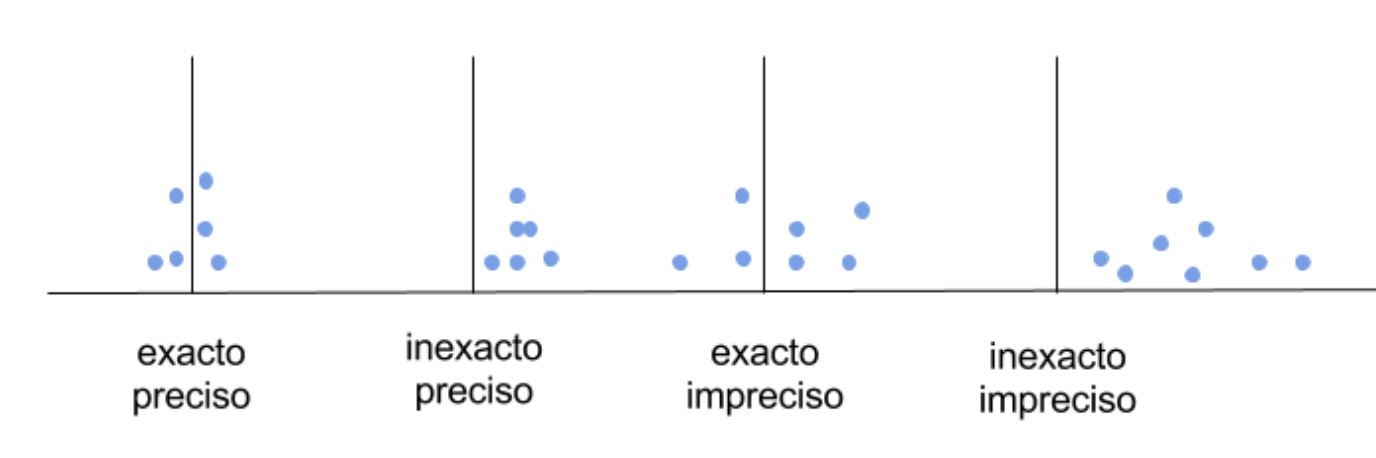
Figura 5.3: Tipos de errores en un sistema de medida

5.5.2 Fiabilidad

Un sistema de medida es fiable si devuelve el mismo valor de un atributo o característica cada vez que se toma una medición utilizando el mismo método de medición, esto es, si los errores de precisión son mínimos. La fiabilidad, o lo que es lo mismo, la precisión de un sistema de medida, se comprueba a través de la cuantificación de los siguientes tipos de error:

Repetitividad: se refiere a la habilidad de un operador (o un aparato de medida) de repetir consistentemente la misma medición del mismo elemento, utilizando idénticas herramientas y condiciones. La variación por repetitividad alude a la variación debida al aparato/sistema de medida. En la Fig 5.4 se muestran las mediciones realizadas con dos herramientas, A y B; la herramienta A (puntos abajo en azul) tiene mayor variación que la B (puntos arriba en rojo), y en consecuencia presenta problemas de repetitividad.

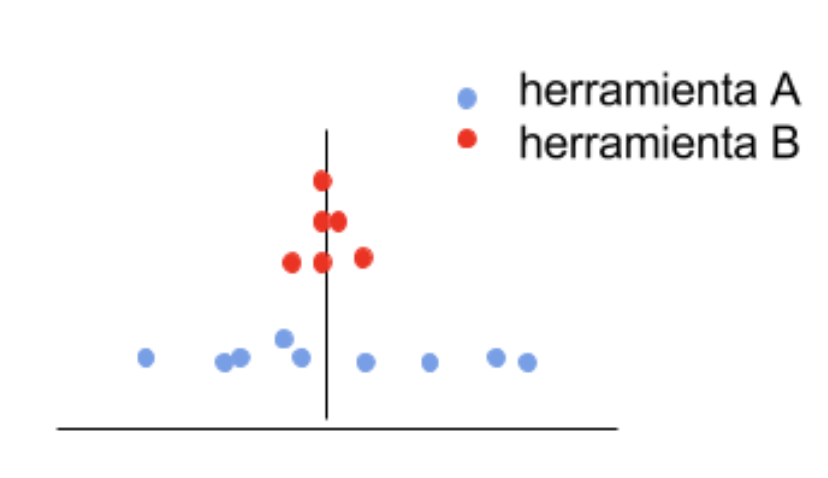
Figura 5.4: Problemas de repetitividad en la herramienta A.

Reproducibilidad: se refiere a la habilidad de una herramienta, utilizada por varios operadores, de reproducir consistentemente la misma medición del mismo elemento bajo idénticas condiciones. Alude a la variación entre los operarios que realizan las mediciones utilizando un mismo aparato de medida y condiciones. En la Figura 5.5 se muestran las mediciones realizadas por 3 operarios; si bien no hay excesivas diferencias entre las mediciones de los operarios 1 y 2 (en torno a la línea vertical), sí las hay entre éstos y el operario 3, que induce pues, problemas de preproducibilidad.

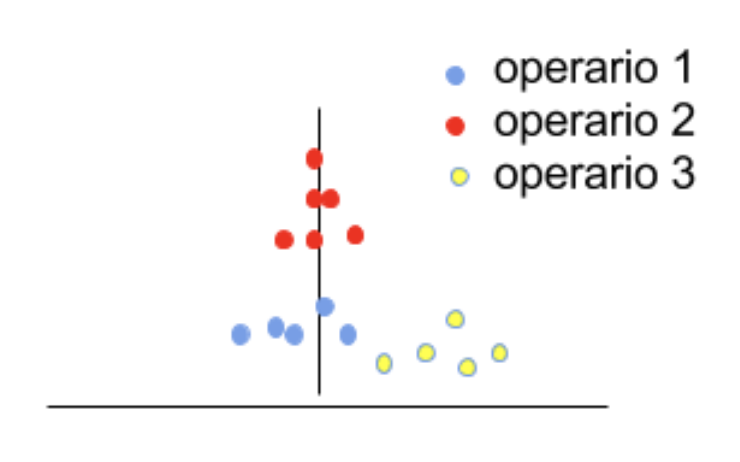
Figura 5.5: Problemas de reproducibilidad de los operarios 2 y 3.

5.5.3 Análisis Gage R&R

El análisis Gage R&R es útil para evaluar la habilidad de un sistema de medida para medir un producto o proceso de una forma precisa y consistente. Un análisis Gage R&R nos permite investigar:

si la variabilidad del sistema de medida es pequeña comparada con la variabilidad del proceso, esto es, si los errores de medida son pequeños y asumibles;
cuánta de la variabilidad en el sistema de medida está causada por diferencias entre los operadores o aparatos de medida;
si las mediciones realizadas por el mismo operario o aparato de medida son consistentes;
si el sistema de medida es capaz de discriminar entre productos del proceso que son distintos entre sí.

Gage R&R calcula la variación total (VT) a partir de tres fuentes, representadas en la Figura 5.6:

Diferencias entre los elementos que son medidos.
Diferencias entre operarios/aparatos de medida.
Diferencias entre mediciones del mismo elemento por el mismo operario/aparato de medida.

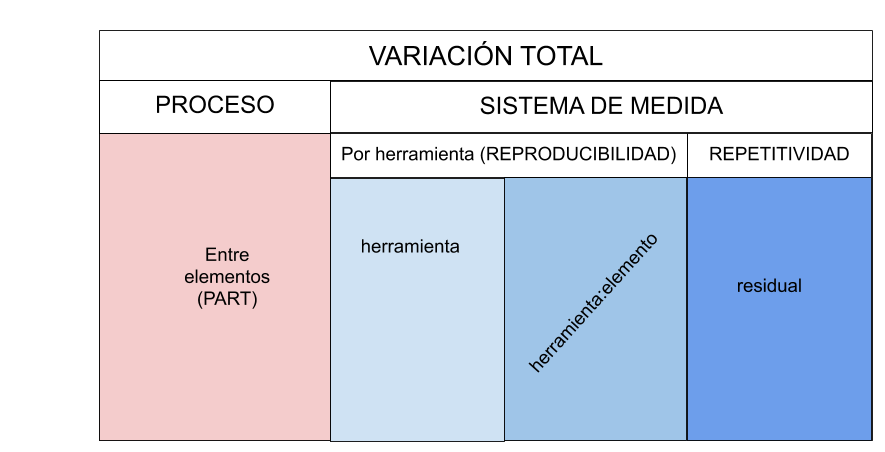
Figura 5.6: Descomposición de la variabilidad total

El análisis Gage R&R utiliza la variación total para determinar cuánta de esta variación es atribuíble a los aparatos (repetitividad: habilidad de un operador de repetir consistentemente la misma medida del mismo elemento, utilizando la misma equipación bajo las mismas condiciones) y cuánta a los operarios (reproducibilidad: capacidad de que diferentes equipaciones de medida/operadores puedan reproducir consistentemente la misma medición del mismo elemento bajo las mismas condiciones).

En un análisis Gage consideraremos siempre un factor operario (appraiser) con $n_o$ niveles, que representa quién hace la medición (o el aparato de medida), un factor elemento (part) con $n_p$ niveles, que representa a cada uno de los elementos (productos generados en el proceso) distintos que se miden, y asumiremos un diseño cruzado (cross) en el que cada operario mide todos los elementos, y cada uno de ellos un número $n_{run}$ de veces.

Si realizamos un análisis de la varianza en el que hemos incluido como factores de variación los elementos que hemos medido (part), los operarios (appraiser), y la interacción de los operarios con los elementos (appraiser:part), la tabla de ANOVA nos proporcionará una descomposición de la varianza según: \[\sigma^2=\sigma^2_{part}+\sigma^2_{appraiser}+\sigma^2_{appraiser:part}+\sigma^2_{error}\] donde $\sigma^2_{error}$ estará representando el error inherente a la medición, no explicable por variaciones entre los operarios/aparatos que miden, y por lo tanto identifica la consistencia en la medición de un mismo elemento por un mismo operario, esto es, el error de repetitividad o cuadrado medio de los residuos MSE.

\[\sigma^2_{repetitividad}=\sigma^2_{error}=MSE.\]

Cuando la interacción ‘operador:part’ no es significativa (distintos operarios miden de forma diferente distintos elementos), calculamos $\sigma^2_{appraiser}$ a partir del cuadrado medio del operador, $MSA$ y del cuadrado medio del error, $MSE$, y considerando el número total de mediciones que ha realizado cada operador, que es el producto del número de elementos (parts), $n_p$ y del número de veces que ha medido cada elemento, $n_{run}$: \[\sigma^2_{appraiser}=\frac{MSA-MSE}{n_p \times n_{run}}\] La variabilidad atribuíble a las diferencias entre los elementos (parts) proviene del cuadrado medio $MSP$, y se calcula considerando en el denominador el número de mediciones que se han realizado de cada elemento, esto es, el número de operadores (appraisers) $n_a$, por el número de repeticiones de cada elemento por el mismo operador, $n_{run}$: \[\sigma^2_{part}=\frac{MSP-MSE}{n_a \times n_{run}}.\]

Cuando hay interacción, la variabilidad atribuíble a reproducibilidad se obtiene de la del operador y la de su interacción con los elementos (considerando posibles variaciones en el comportamiento del operador al medir distintos elementos): \[\sigma^2_{reproducibilidad}=\sigma^2_{appraiser}+\sigma^2_{appraiser:part}\]

La variabilidad Gage se calcula con las componentes de repetitividad y reproducibilidad: \[\sigma^2_{Gage}=\sigma^2_{repetitividad}+\sigma^2_{reproducibilidad}\]

5.5.3.1 Indicadores Gage

Una vez calculada la descomposición de la varianza del proceso, la fiabilidad del sistema de medida es evaluado en términos de los siguientes indicadores:

El porcentaje de contribución de la varianza (%Contrib) es el porcentaje de la variación del proceso que proviene de cada una de las fuentes posibles. Se calcula como la varianza de cada componente, dividida por la varianza total y multiplicada por 100. Cuanto mayor sea %Contrib(Gage), bien en la componente de repetitividad, reproducibilidad, o en ambas, mayores serán los problemas manifiestos sobre el sistema de medida.

\[\% Contrib(Gage)=\frac{Varianza.Gage}{Var.total} \times 100 \%,\]

El porcentaje de variación del estudio, %StudyVar, se calcula como el porcentaje de varianza del estudio asumido por cada una de las fuentes sobre la variación del estudio total, o lo que es lo mismo, el porcentaje de desviación estándar que aporta cada fuente respecto de la desviación estándar total. La variación del estudio (StudyVar) se calcula a partir de la desviación estándar (raíz cuadrada de la varianza), multiplicada por el nivel sigma asumido (habitualmente 6). \[\% StudyVar(Gage)=\frac{se.Gage}{se.total} \times 100 \%,\] con $se$ el error estándar.
- El porcentaje de tolerancia, %Tolerance, se calcula como el porcentaje del rango de tolerancia del proceso (distancia entre los límites de especificación) que es consumido por el error de cada una de las fuentes. Para su cálculo hay que especificar la tolerancia.

\[\% Tolerancia(Gage)=\frac{se.Gage}{Rango.tolerancia} \times 100\%.\] - Un análisis Gage también devuelve el número de categorías distintas, que representa el número de grupos de elementos que la herramienta de medida puede distinguir a partir de los datos. Cuanto mayor sea este número, mayor es la posibilidad de que la herramienta de medida pueda discriminar entre elementos diferentes. Un valor de 1, por ejemplo, indica que el sistema de medida no puede discriminar ni siquiera dos elementos distintos.

En Soporte de Minitab (n.d.) se proporciona una detallada descripción e interpretación de los resultados de un análisis Gage R&R.

En general, los resultados que nos den los indicadores Gage serán coherentes, con todo, caben considerar ciertas preferencias en función de los objetivos:

Si el sistema de medida se utiliza para mejora de procesos, esto es, para reducir la variabilidad entre elementos,%StudyVar es un mejor estimador de la precisión de la medición.
Si el sistema de medida evalúa los elementos respecto de las especificaciones, %Tolerance es una métrica más apropiada.

Como regla de decisión para concluir sobre la fiabilidad del sistema de Medida, Soporte de Minitab (n.d.) recomienda los que se muestran en la Tabla 5.2:

Tabla 5.2: Valores frontera para concluir sobre el análisis Gage global y/o en cualquiera de sus componentes (reproducibilidad/repetitividad) (Soporte de Minitab n.d.).
%StudyVar	%Contrib	#Categorías distintas	Decision
menor al 10%	menor al 1%	5 o más	el sistema de medida es aceptable
entre el 10% y el 30%	entre el 1% y el 9%	entre 2 y 4	el sistema de medida es crítico, pero podría ser aceptable en función de costes
mayor del 30%	mayor del 9%	menor a 2	el sistema de medida es inaceptable y debería ser mejorado.

5.5.3.2 Gráficos Gage

También los gráficos que se generan en un análisis Gage ayudan a visualizar problemas en el sistema de medida. En un análisis gráfico es importante visualizar la variabilidad por elementos y por herramientas de medida, así como posibles interacciones entre estos, cuestión que se resuelve a través de diagramas de barras, puntos y líneas, y gráficos R-chart y $\bar{x}$-chart.

El gráfico de Components of variation representa el %Contribution (contribución a la varianza total) y %StudyVar (contribución a la desviación típica) asociadas al sistema de medida.
El gráfico Var by part representa con puntos todas las mediciones de cada uno de los elementos (parts) medidos, sin diferenciar por el aparato de medida o appraiser. Superpone una línea que pasa por los puntos medios de las mediciones de cada elemento. Una línea horizontal implicará que en promedio todos los elementos son similares (se han medido de modo similar). Mayor dispersión de los puntos en la vertical implicará que las mediciones de ese elemento han sido más dispares entre sí.
El gráfico Var by appraiser representa con puntos todas las mediciones realizadas con cada uno de los aparatos de medida (appraiser), sin diferenciar por elemento (part*). Superpone una línea que pasa por los puntos medios de las mediciones de cada herramienta. Una línea horizontal implicará que en promedio todas los herramientas han medido de forma similar (los elementos son similares). Mayor dispersión de los puntos en la vertical implicará que las mediciones con esa herramienta han sido más dispares entre sí, disparidad que puede venir justificada por diferencias entre los elementos o por inconsistencia de la herramienta.
El gráfico Var by part:appraiser interaction representa con puntos las mediciones medias de cada elemento (part) realizadas por cada herramienta (appraiser*). Une con líneas las medias para cada herramienta. Diferencias entre los puntos implican elementos diferentes o mediciones diferentes. Tendencias distintas en las líneas implican que cada herramienta mide de forma diferente cada elemento (interacción). Proximidad de los puntos en una vertical significa que ese elemento ha sido medido de forma similar con todas las herramientas (sin problemas de reproducibilidad). Alineación en la horizontal de todas las mediciones medias conseguidas con la misma herramienta implica similaridad entre los elementos medidos.
El gráfico $\bar{x}$ Chart) by appraiser proporciona la misma representación del gráfico anterior, pero con las mediciones separadas por herramientas (appraiser), esto es, sin superponer las líneas. Añade además una línea central con el promedio de todas las mediciones ($\bar{x}$), y unos límites inferior y superior obtenidos a partir de la constante de Shewhart $d_2$, el rango medio observado $\bar{R}$ y el número de observaciones disponibles $n$. \[lim_{sup}=\bar{x} +3 \cdot \bar{R}/(d_2 \sqrt{n}); \ \ \ \ lim_{inf}=\bar{x} -3 \cdot \bar{R}/(d_2 \sqrt{n})\]
El gráfico R Chart by appraiser representa el rango de variación (máximo-mínimo) entre las mediciones de un mismo elemento, diferenciadas para cada una de las herramientas de medida. Superpone además una línea central con el rango medio observado para todas las mediciones ($\bar{R}$), y unos límites obtenidos a partir de este y las constantes de Shewhart $d_2$ y $d_3$ (Cano, Moguerza, and Corcoba 2015b).

\[lim_{sup}=\bar{R} \cdot ( 1+d_3/d_2); \ \ \ \ lim_{inf}=\bar{R} \cdot( 1-d_3/d_2)\] Este gráfico da información sobre la consistencia en las medidas de cada operador/herramienta en cada elemento medido, en términos de rangos (diferencia entre el mayor valor medido y el menor). Si los rangos de cada operador/herramienta son próximos a cero, las medidas realizadas son consistentes y no presentan problemas de repetitividad. Que las mediciones queden entre los límites no implica que no haya problemas de error del sistema de medida; de hecho podríamos tener límites amplios cuando hubiera operadores/elementos con mediciones muy precisas y otros con mucha variabilidad.

Resumiendo, los gráficos de puntos “var by part”/“var by appraiser” son útiles para identificar qué elementos/herramientas de medida (respectivamente) provocan mayor variabilidad en las mediciones; el de interacción “part:appraiser” permite identificar si todos los operadores/herramientas miden igual todos los elementos, o por el contrario hay diferencias debido a elementos diferentes o a problemas de reproducibilidad entre operadores/herramientas.

5.5.4 Ejemplo Gage R&R

Cano, Moguerza, and Redchuk (2013) proporcionan un ejemplo desarrollado para el cálculo del estudio Gage R&R completo. Un fabricante de baterías hace varios tipos de pilas para uso doméstico. El BB de la compañía quiere empezar un proyecto Seis Sigma para mejorar la línea de producción de las pilas de voltaje 1.5, habiendo identificado la CTQ con la variable voltaje. Pretende iniciar el estudio analizando el sistema de medida, para lo que ha diseñado un experimento con 2 voltímetros, 3 pilas diferentes y 3 mediciones para cada combinación pila-voltímetro. Los datos son los siguientes:

voltimetro = factor(rep(1:2, each = 9))
pila = factor(rep(rep(1:3, each = 3), 2))
run = factor(rep(1:3, 6))
voltaje = c(1.4727, 1.4206, 1.4754, 1.5083, 1.5739, 1.4341, 1.5517, 
            1.5483, 1.4614, 1.3337,1.6078, 1.4767, 1.4066, 1.5951, 
            1.8419,1.7087, 1.8259, 1.5444)
pilas = data.frame(voltimetro, pila,run, voltaje)

El objetivo del proceso de medición es poder discriminar entre pilas (parts) que son diferentes. El voltímetro hace el papel de operador/aparato que realiza la medida (appraiser). Las mediciones (var) están contenidas en la variable voltaje.

Utilizamos la función de la librería SixSigma (Cano, Moguerza, and Corcoba 2015a) que proporciona el análisis Gage R&R íntegro, incluida la tabla de ANOVA y la descomposición Gage de la varianza.

library(SixSigma)
# ss.rr(var, part, appr, data, main, sub)
my.rr <- ss.rr(var = voltaje, part = pila,
               appr = voltimetro,
               data = pilas,
               main = "Análisis Gage R&R SixSigma",
               sub = "Batteries Project MSA")

## Complete model (with interaction):
## 
##                 Df  Sum Sq Mean Sq F value Pr(>F)
## pila             2 0.06308 0.03154   3.415  0.227
## voltimetro       1 0.04444 0.04444   4.812  0.160
## pila:voltimetro  2 0.01847 0.00924   0.584  0.573
## Repeatability   12 0.18982 0.01582               
## Total           17 0.31582                       
## 
## alpha for removing interaction: 0.05 
## 
## 
## Reduced model (without interaction):
## 
##               Df  Sum Sq Mean Sq F value Pr(>F)
## pila           2 0.06308 0.03154   2.120  0.157
## voltimetro     1 0.04444 0.04444   2.987  0.106
## Repeatability 14 0.20829 0.01488               
## Total         17 0.31582                       
## 
## Gage R&R
## 
##                       VarComp %Contrib
## Total Gage R&R    0.018162959    86.74
##   Repeatability   0.014878111    71.05
##   Reproducibility 0.003284848    15.69
##     voltimetro    0.003284848    15.69
## Part-To-Part      0.002777127    13.26
## Total Variation   0.020940086   100.00
## 
##                       StdDev  StudyVar %StudyVar
## Total Gage R&R    0.13477002 0.8086201     93.13
##   Repeatability   0.12197586 0.7318552     84.29
##   Reproducibility 0.05731359 0.3438816     39.61
##     voltimetro    0.05731359 0.3438816     39.61
## Part-To-Part      0.05269846 0.3161907     36.42
## Total Variation   0.14470690 0.8682414    100.00
## 
## Number of Distinct Categories = 1

## Warning in widths.x[pos.widths[[nm]]] <- widths.settings[[nm]] *
## widths.defaults[[nm]]$x: número de items para para sustituir no es un múltiplo
## de la longitud del reemplazo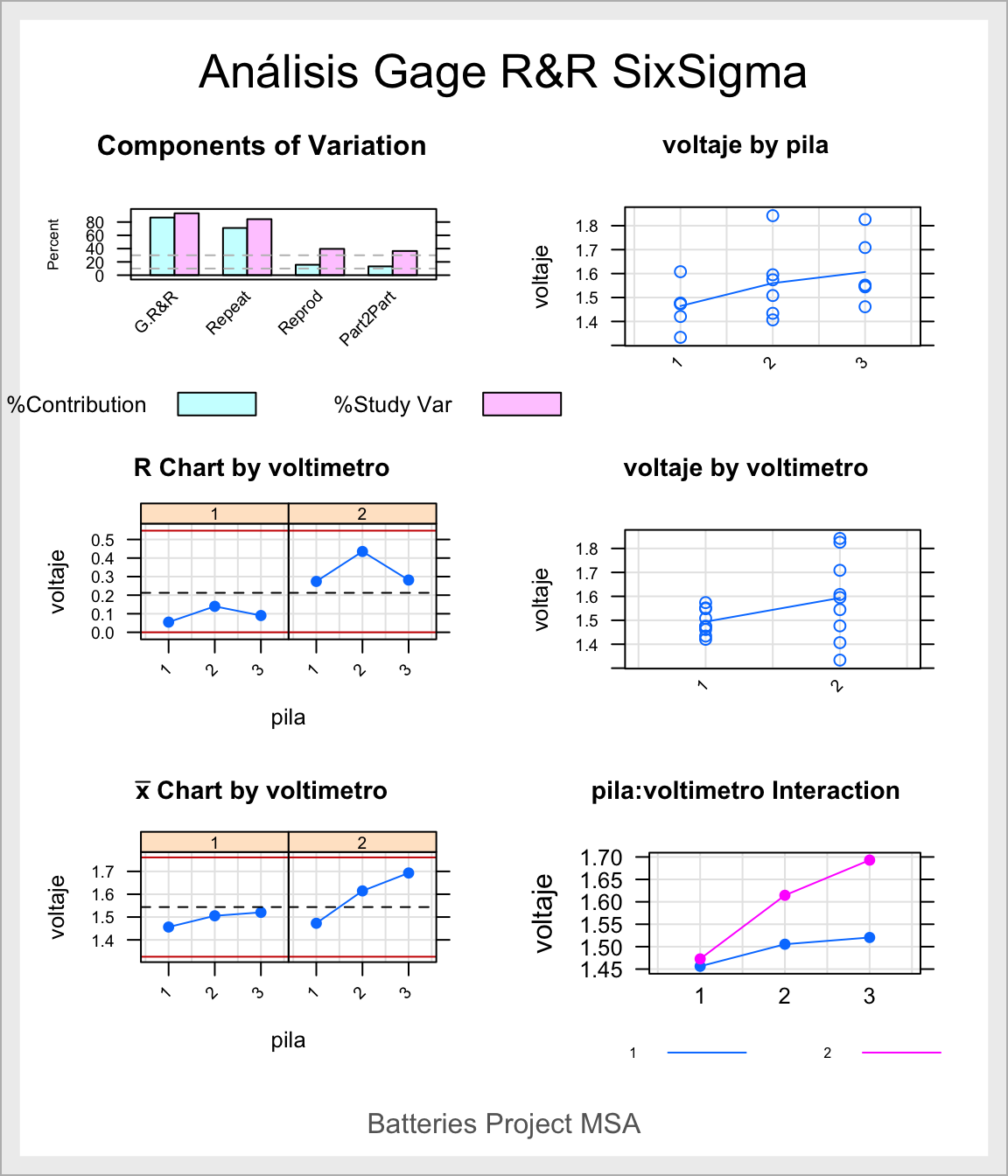

Interpretemos los resultados:

Respecto a los resultados numéricos, en primer lugar la tabla de Anova indica que no se detectan diferencias significativas entre las pilas (elementos de medida), ni entre las voltímetros (instrumentos de medida). La interacción tampoco resulta significativa y ha sido excluida.
La componente de la varianza en el análisis Gage asociada al sistema de medida, %Contrib, supone un 86.74% de la variabilidad total. El sistema de medida tiene problemas, y es especialmente crítico en la componente de repetitividad (71.05% de contribución de la varianza). En términos de Variación del estudio, %StudyVar, es igual de claro el problema de fiabilidad, con un valor para la componente Gage del 93.13%, y del 84.29% para la repetitividad. El número de categorías distinta es 1, de modo que el sistema de medida no es capaz de discriminar siquiera dos pilas distintas. Tanto los valores de variabilidad como los de discriminación, nos llevan a concluir que el sistema de medida no es aceptable.
Respecto a los gráficos, apreciamos lo siguiente:
- En el gráfico de Components of variation queda patente lo anteriormente concluido a partir de la tabla de contribuciones a la varianza: la escasa fiabilidad del sistema de medida, con varianzas Gage sumamente altas, especialmente en la componente de repetitividad.
- Var By Part (voltage by battery). Las mediciones de la pila 2 presentan mayor dispersión que las realizadas con la 1, especialmente debido a una medición que es muy alta respecto del resto; en general las mediciones de la pila 3 son más elevadas que el resto. Hay diferencias claras entre las pilas, al presentar líneas de tendencia oblicuas entre las medias.
- Var By Appraiser. Las mediciones realizadas con el voltímetro 2 son mucho más variables que las realizadas con el voltímetro 1, y en promedio algo superiores (línea tendencia oblícua). Hay diferencias claras entre los voltímetros, y problemas de consistencia/repetitividad en el voltímetro 2.
- Part x Appraiser Interaction. El voltímetro 2 mide de forma diferente (en promedio) cada una de las tres pilas, mientras que el voltímetro 1 es más estable en las mediciones de las tres pilas. Sin embargo, la tendencia en las mediciones es similar para los dos voltímetros: la magnitud de la pila 1 es la más pequeña, mediana la pila 2 y mayor la pila 3. La interacción es irrelevante, como se aprecia en la tabla de Anova mostrada al inicio.
- R Chart by Appraiser: Claramente el voltímetro 2 ha generado mucha más variabilidad al medir cualquiera de las tres pilas que el voltímetro 2, con rangos por encima del promedio de rangos. Ratifica el problema de repetitividad provocado por la variabilidad con la que mide el voltímetro 2.
- xbar Chart by appraiser: Este gráfico coincide con el de interacción, descompuesto en dos partes, una por cada voltímetro. El voltímetro 1 es más estable en sus mediciones de las tres pilas que el voltímetro 2. Ratifica el problema de reproducibilidad provocado por el voltímetro 2, especialmente en las pilas 2 y 3.

La conclusión final es que el sistema de medida tiene serios problemas de fiabilidad, provocados principalmente por el voltímetro 2. Sería preciso pues, recalibrar el voltímetro 2 en conjunción con el 1 (que parece funcionar adecuadamente), y repetir las mediciones. Tras un nuevo análisis del sistema de medida, si no se aprecian problemas, procederíamos a utilizar los datos para evaluar la variabilidad procedente del proceso en sí.

5.5.5 Análisis Gage R&R cualitativo

Cuando las variables son de tipo cualitativo, con datos que no se miden sino que se cuentan, también se pueden cometer errores de recuento. Un ejemplo sencillo de sistemas de medida con datos categóricos es la revisión de un conjunto de piezas y su clasificación como defectuosas o no defectuosas.

Veamos a continuación cómo validar un sistema de medida para este tipo de datos.

En este tipo de sistemas hemos de preocuparnos, además de por la repetitividad (suponer que un observador va a ver lo mismo en dos o más observaciones distintas del mismo elemento) y la reproducibilidad (suponer que dos observadores van a ver lo mismo cuando observan el mismo elemento), por la exactitud. La exactitud está ligada a la decisión que toma un observador cuando discrimina un defecto: puede ver un defecto que no existe, o no ver un defecto que existe. Un mismo observador puede ser consistente en sus observaciones de un mismo elemento (no repetitividad), pero dar una clasificación (defecto/no defecto) incorrecta. El sistema será repetible pero no exacto. Asimismo, varios observadores pueden ser consistentes en sus observaciones, pero éstas no ser correctas porque no han discriminado correctamente el defecto; el sistema sería reproducible pero no exacto.

El análisis del sistema de medida con datos categóricos tiene en cuenta ambos conceptos:

el de desviación, para juzgar si la decisión adoptada es correcta, y
el de dispersión, para comprobar si adoptan la misma decisión de dos observaciones diferentes, provengan del mismo observador o de observadores distintos.

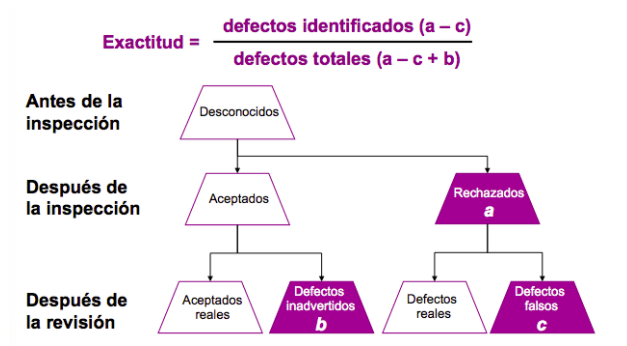
Figura 5.7: Exactitud en la medición de variables cualitativas. Identificación de defectos.

La exactitud de una inspección se mide, como se muestra en la Figura 5.7, a través de los defectos identificados correctamente, esto es, con el cociente entre:

(numerador) los defectos reales que fueron identificados por el observador: los rechazados por el observador (a) menos los que han sido rechazados sin tener defectos (c),
(denominador) los defectos totales, esto es, todos los errores detectados al compararlos con el patrón o hacer una inspección de la medición: los defectos clasificados como defectos (a-c), más los que no se identificaron como defectos en la medición y pasaron inadvertidos (b).

\[Exactitud = \frac{\mbox{defectos reales identificados} }{\mbox{defectos totales} }=\frac{(a-c)}{(a-c+b)}\]

Al pretender testar también la repetitividad y la reproducibilidad, será necesario comparar las decisiones de un mismo observador en diferentes observaciones, y las de diferentes observadores en varias mediciones. Con todo ello podremos evaluar de modo completo, respecto a exactitud y repetitividad-reproducibilidad, $E+ R\&R$, el método de recogida de información o sistema de medida.

El método para realizar estudios $E+R\&R$ con variables categóricas es sencillo. Básicamente se trata de realizar diferentes observaciones y revisiones de un conjunto de elementos y clasificarlos en la categoría que corresponda:

Trata datos binarios (mal/bien-defecto/no defecto) o una cantidad limitada de atributos.
Compara los elementos observados con respecto a un “patrón” para aceptar/rechazar o asociar a una categoría y así poder reconocer la exactitud del método y de los observadores. El patrón podría proporcionarlo la medición/revisión por un inspector.
Focaliza también la eficacia para diferenciar entre categorías.
Se realiza con al menos 2 observadores, 2 observaciones cada uno, de unos 20 elementos representativos del objetivo a evaluar, con el fin de poder concluir sobre repetitividad y reproducibilidad.

Para evaluar el sistema disponemos de una función propia en gagerr-binario.R, que requiere los datos en el formato:

part= variable que identifica elementos
appr=variable que identifica al observador/medidor que realiza la medición
rep=variable ordinal de las mediciones (réplicas) que realiza cada observador
result=variable de clasificación del observador (1=ok, 0=defectuoso)
patt=variable con el patrón o clasificación correcta (1=ok, 0=defectuoso)

5.5.6 Ejemplo Gage cualitativo

Se considera una muestra de 20 Lacasitos que son evaluados cuidadosamente por un inspector externo para reconocer los defectuosos de los no defectuosos; esta clasificación se reconoce como el patrón de clasificación. A continuación dos observadores realizan su clasificación de los 20 lacasitos en dos momentos diferentes.

load("datos/lacasitos.RData")
 # part= identificador del lacasito (de 1 a 20)
 # appr=observador/inspector (1 y 2)
 # rep=ordinal de la medición que realiza cada observador (1 y 2)
 # result=clasificación del observador (1=ok, 0=defectuoso)
 # patt=patrón o clasificación correcta (1=ok, 0=defectuoso)

# Y cargamos la función gagerr-binario.R, también en Github
source("datos/gagerr-binario.R")
# source("https://raw.githubusercontent.com/asunmayoral/leanseissigma/main/gagerr-binario.R")
gage.rr.binary(part,appr,result,rep,patt,lacasitos)

## $Repetitivity
##             inspected matched Repetitivity            IC95
## Observador1        20      10          50% (29.93%,70.07%)
## Observador2        20      19          95% (73.06%,99.74%)
## 
## $Repetitivity.Exact
##             inspected matched Repet.Exact            IC95
## Observador1        20       6         30% (12.84%,54.33%)
## Observador2        20      11         55% (32.05%,76.17%)
## 
## $Reproducibility
##         inspected matched Reproducibility              IC95
## Results        40      25           62.5% (45.81 %,76.83 %)
## 
## $Reproducibility.Exact
##         inspected matched Reprod.Exact              IC95
## Results        40      21        52.5% (36.34 %,68.18 %)

Las conclusiones son las siguientes:

Repetitividad. El observador1 es menos consistente en sus dos mediciones (sólo coinciden las mediciones de un 50% de los lacasitos que revisa), mientras que el observador2 resulta bastante consistente, con un 95% de coincidencias entre ambas mediciones. Los intervalos de confianza no solapan, por lo que los dos observadores se reconocen diferentes respecto a coherencia. El observador1 muestra problemas de repetitividad.

Repetitividad y Exactitud. El observador1 además de inconsistente es poco fiable a la hora de identificar lacasitos defectuosos, pues sólo consigue un 30% de clasificaciones correctas. El observador2, aunque consistente según lo anterior, es poco preciso al identificar los fallos y sólo identifica correctamente un 55% de los lacasitos. Respecto a exactitud no son especialmente buenos ninguno de los dos.

Reproducibilidad. De las 40 inspecciones realizadas por cada uno de los 2 observadores, ambos han coincidido en un 62,5% de las mediciones que han realizado. Al ser tan amplio el intervalo de confianza, (45.8%,76.8%), reconocemos ciertos problemas de reproducibilidad.

Reproducibilidad y Exactitud. El porcentaje baja al 52.5% cuando exigimos a la par coincidencia en los juicios de los observadores e identificación correcta de los errores. El IC igualmente es muy amplio, (36.34 %,68.18 %), por lo que se reconocen problemas de reproducibilidad vinculados a exactitud.

5.6 Capacidad de un proceso

Medir la capacidad del proceso consiste en cuantificar cuánto concuerdan los resultados con las especificaciones del proceso (dadas por los requisitos del cliente) en términos del número de defectos y/o la producción observada y esperada.

Explicado de otro modo, la capacidad del proceso es una medida del grado en que el rendimiento real de un proceso (sus resultados) está dentro de las especificaciones. Un proceso será capaz si todos los posibles resultados caen dentro de los límites de especificación.

El estudio de capacidad del proceso se realiza en distintas fases de un proyecto de mejora, y en cada una de ellas con una finalidad concreta:

en la fase MEDIR, para determinar el rendimiento real y potencial del sistema,
en la fase MEJORAR, cuando se optimiza el proceso, para confirmar la solución como una solución de mejora que satisface las especificaciones,
en la fase CONTROL, cuando se compara la mejora actual con el objetivo de mejora.

La baja capacidad de un proceso puede proceder de dos fenómenos, o de la combinación entre ambos: precisión y centrado. Un proceso puede estar centrado, de forma que el valor medio de su resultado esté próximo al centro del intervalo de la especificación, pero ser impreciso (disperso), por lo que algunos valores estarán fuera de dicho intervalo, en cualquier extremo. Por otra parte, un proceso puede ser preciso, tener poca dispersión, pero estar descentrado, de forma que el valor medio de su resultado estará próximo a uno de los extremos del intervalo de especificación y, a pesar de su pequeña dispersión, alguno de los valores estará fuera del intervalo. Ver Figura 5.8.

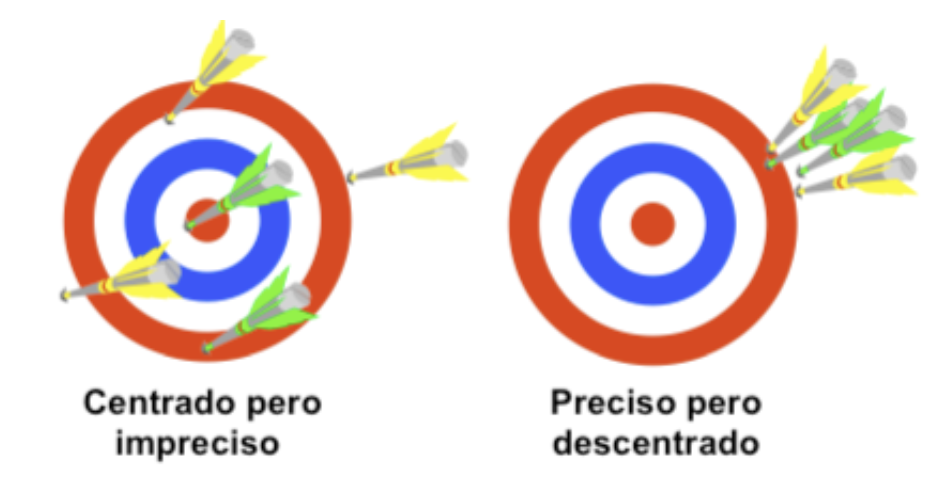
Figura 5.8: Capacidad de un proceso en términos de centralización y precisión.

La cantidad de valores fuera del intervalo de especificación puede ser la misma en ambos casos, pero el comportamiento del proceso, y las posibilidades de mejora, son diferentes. En principio, sin conocer causas concretas, es más fácil mejorar un proceso preciso y descentrado que uno centrado e impreciso. Estos dos fenómenos obligan a evaluar la capacidad de un proceso bajo dos aspectos: uno que solamente tiene en cuenta la dispersión (precisión) y otro que combina ambos elementos, centrado y dispersión. Cuando profundicemos en la medición de la capacidad del proceso para respuesta continua, introduciremos además otro factor importante para concluir sobre dicha capacidad, que será la estabilidad del sistema.

5.6.1 Medir la capacidad

La medición de la capacidad se realiza de uno u otro modo (con distintas herramientas) en función de si los datos que medimos son de tipo numérico o consisten exclusivamente en conteos (defectos/no defectos).

Gráficamente podemos explorar la capacidad del proceso representando en un gráfico los datos numéricos superpuestos sobre los límites de especificación del proceso, o mediante gráficos de barras si se trata de datos de tipo categórico (defectos/no-defectos). Si hay muchos datos fuera de los límites de especificación, o el porcentaje de defectos es demasiado grande, el proceso será poco capaz.

Numéricamente evaluaremos la capacidad del proceso en función de “índices de capacidad,” que se calcularán de uno u otro modo en función de la naturaleza de los resultados $Y$ medidos en el proceso. Así, en datos discretos (defectos/no-defectos) se calcularán a través del número de defectos y de oportunidades, y en datos continuos se calcularán en función de medias, desviaciones típicas y de los propios límites de especificación del proceso.

Distinguimos pues, entre la evaluación de la capacidad del proceso, en función de si los datos disponibles son categóricos (defectos/no defectos) o continuos. En cualquier caso, es imprescindible definir los siguientes conceptos:

UNIDAD: es el producto que se procesa o el producto/servicio final que se entrega.
DEFECTO es cualquier fallo que impide alcanzar el estándar o los requisitos del cliente.
OPORTUNIDAD representa cuántos defectos se podrían encontrar en una sola unidad.
RETRABAJO el producto defectuoso devuelto a la cadena de producción para reprocesarlo y rectificar los defectos. Multiplica los costes de producción.
COSTES DE MALA CALIDAD identifican los costes asociados a la ineficiencia del sistema de producción.

5.6.2 Capacidad versus defectos

Cuando los datos $Y$ disponibles conciernen al número de defectos encontrados, será preciso medir la capacidad basada exclusivamente en dichos defectos. Esta aproximación es:

simple: se comprende bien la diferencia entre bueno y defectuoso;
consistente: siempre que hay requisitos del cliente, aparecen defectos;
comparable entre procesos, compañías, …

Los principales índices de capacidad cuando sólo tenemos información sobre el número de defectos, son:

Rendimiento (YIELD). Es el volumen de buenos resultados sobre el total de resultados (unidades por oportunidades). \[YIELD=\frac{total-defectos}{total}\]
Rendimiento de primera mano (FTY). Es el volumen de buenos resultados obtenidos sin necesidad de retrabajo. \[FTY=\frac{total-retrabajo-defectos}{total}\]
Rendimiento acumulado de primera mano (RTY). Es el volumen de primeros buenos resultados acumulados en el proceso completo, cuando un proceso está compuesto de varios subprocesos. \[RTY=\prod_{i=1}^n FTY_i=FTY_1 \times FTY_2 \times ... \times FTY_n\]
Defectos por unidad (DPU). Es el ratio de defectos entre el número total de unidades inspeccionadas. \[DPU=\frac{defectos}{unidades}\]
Defectos por oportunidad (DPO). Es el ratio de defectos por el total de oportunidades. \[DPO=\frac{defectos}{unidades \times oportunidades}=1-YIELD\]
Defectos por millón de oportunidades (DPMO). Es el número de defectos por oportunidad multiplicado por un millón. \[DPMO=DPO \times 10^6\]

Una vez tenemos calculadas estas medidas en términos de defectos, podemos utilizar las tablas de conversión (ver tabla en la Figura 5.9) para concluir sobre el nivel Sigma del proceso, o directamente utilizar una calculadora digital u hoja de cálculo, como las disponibles en GoodCalculators.com (n.d.) GoodCalculators.com o GigaCalculator.com

Figura 5.9: Tabla de conversión a nivel 6sigma (Basu 2011).

Con todos los índices evaluados (ver Figura 5.10), se puede concluir sobre cómo está funcionando el proceso y en consecuencia qué costes origina, para obtener una evaluación completa del proceso. Los pasos a dar en este punto son:

Concretar un periodo de tiempo y contar el número de incidentes.
Determinar el coste asociado a todos esos incidentes, incluidos los costes por retrabajo (nº defectos o revisiones/producción x nº trabajadores x horas retrabajo x coste hora), almacenamiento, reparaciones,….
Determinar el coste material por los defectos (coste producto x defectuosos).
Sumar todos los costes.

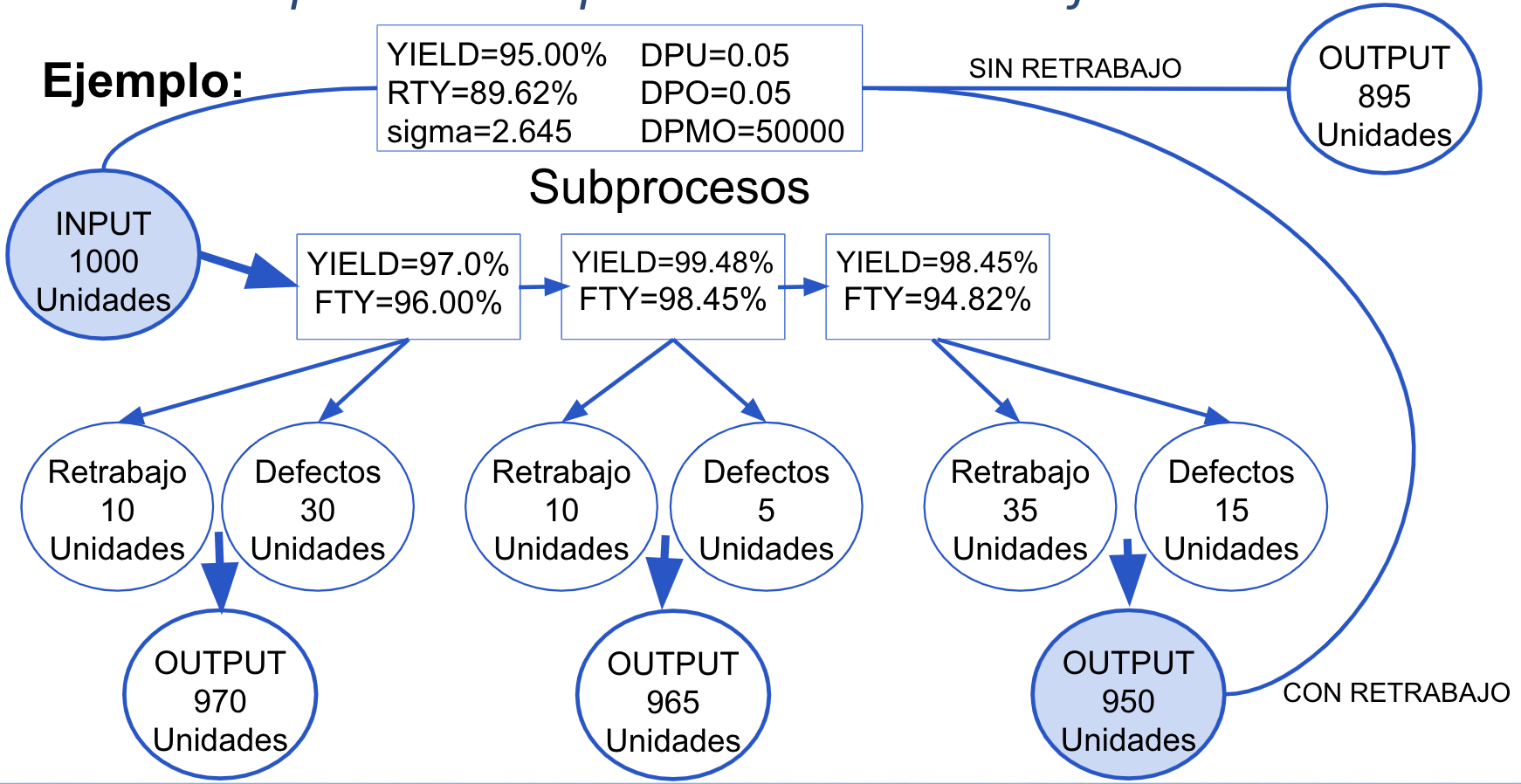
Figura 5.10: Ejemplo de evaluación de un proceso descompuesto en subprocesos.

5.6.3 Capacidad en continuo

Como ya comentamos anteriormente, una baja capacidad del sistema viene identificada por observaciones que se manifiestan:

descentradas y precisas, que resultan fáciles de corregir por lo general,
centradas pero dispersas, en cuyo caso la solución suele ser más difícil. Ambas situaciones se ilustran en la Figura 5.11.

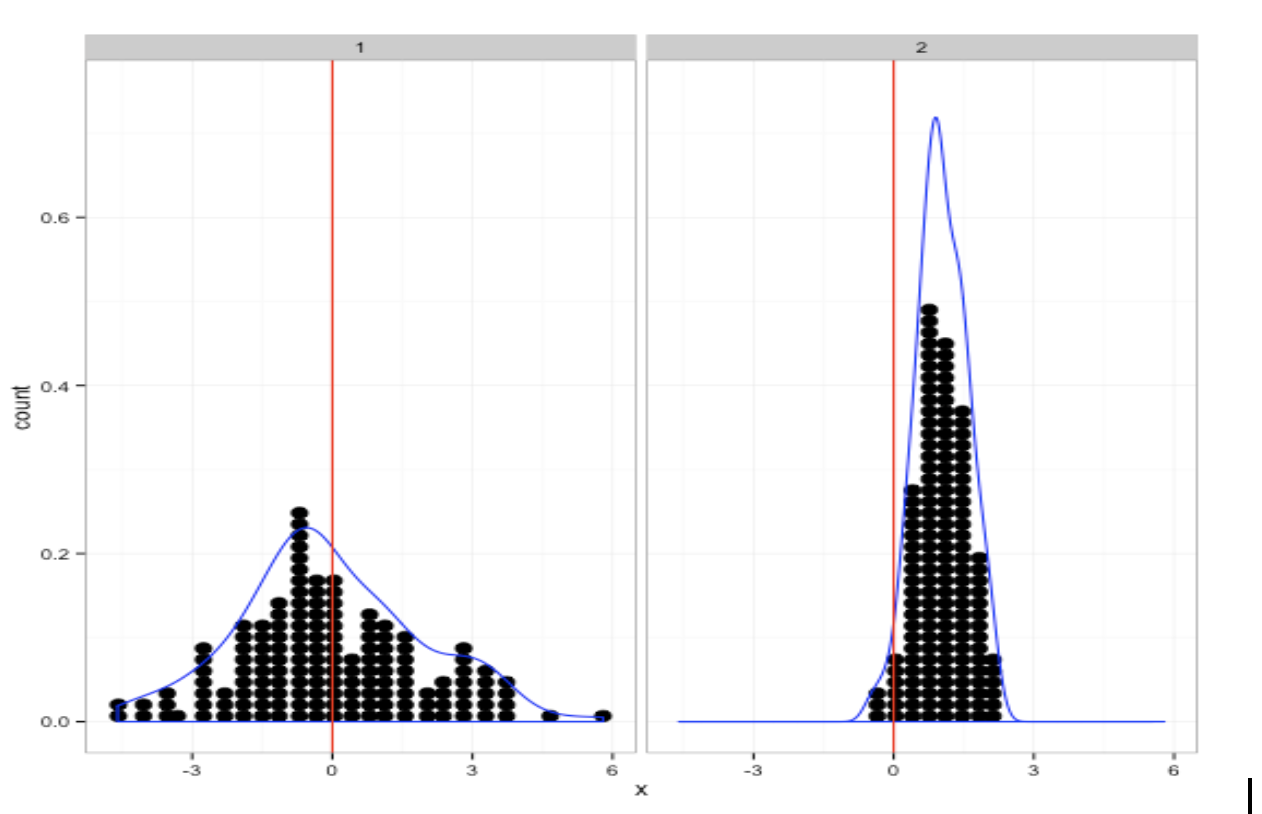
Figura 5.11: Izquierda: proceso centrado y disperso. Derecha: proceso descentrado y preciso.

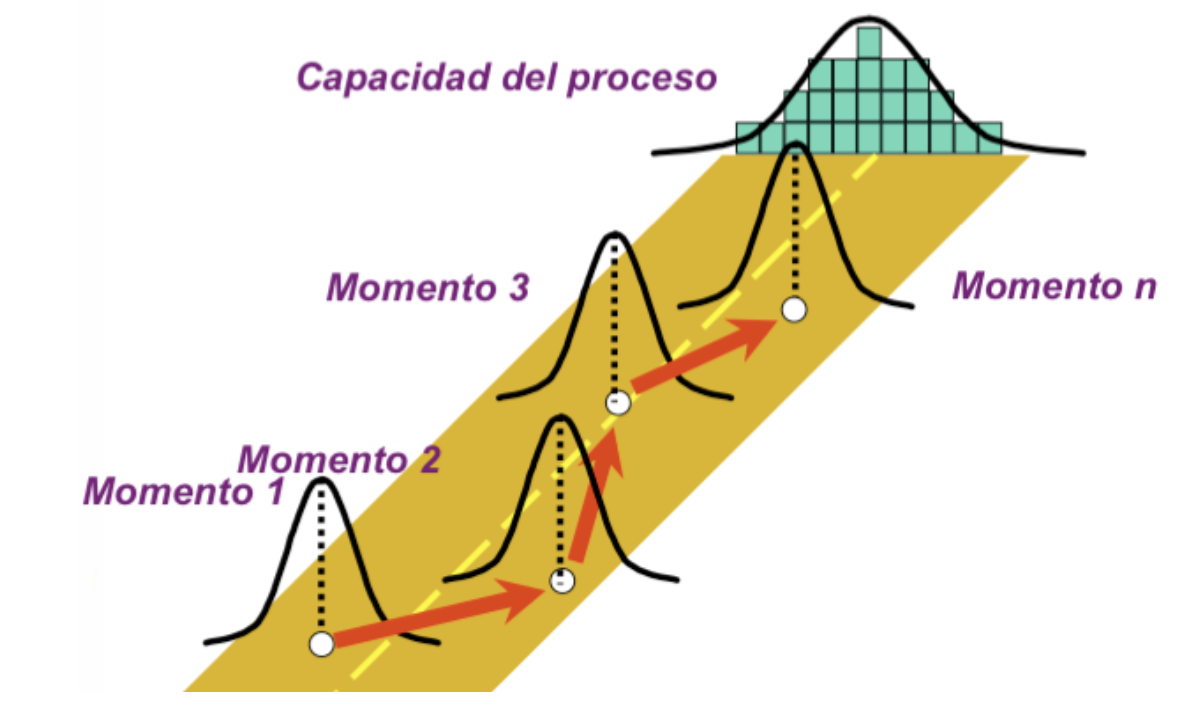
La varianza a corto plazo es la varianza en cada una de las curvas normales del camino naranja. La varianza a largo plazo es la varianza acumulada a lo largo del tiempo (en la curva normal al fondo).

Figura 5.12: La varianza a corto plazo es la varianza en cada una de las curvas normales del camino naranja. La varianza a largo plazo es la varianza acumulada a lo largo del tiempo (en la curva normal al fondo).

Puesto que la variación es el mayor de los problemas en proyectos de mejora, la medición de la capacidad de un proceso se basará fundamentalmente en cuantificar la variabilidad existente en el proceso, variabilidad que se puede medir en un instante determinado y nos proporciona la variabilidad a corto plazo, o sucesivamente a lo largo del tiempo en distintos instantes, generando lo que se denomina variabilidad a largo plazo (ver Editor (2017b)). Ahora bien, al medir el proceso en un determinado instante de tiempo, cabe esperar que la variabilidad de los datos resulte inferior a la obtenida si se mide a lo largo de un periodo de tiempo más prolongado. Es lo que se aprecia en la Figura 5.12, donde las curvas de variación en el camino naranja representan distintas mediciones puntuales a lo largo del tiempo (variabilidad a corto plazo), con menor variabilidad que la última curva de variación (variabilidad a largo plazo), que acumula toda la variación generada en el camino.

Si hemos realizado ese tipo de mediciones a lo largo del tiempo, comparar la varianza puntual o a corto plazo con la varianza a largo plazo, permitirá concluir sobre la capacidad (a corto plazo o potencial), con la capacidad global o a largo plazo, y así determinar si el sistema es estable, si está controlado, describir cómo se comporta actualmente, y predecir cómo se va a comportar en el futuro. Distinguimos pues entre:

Capacidad a corto plazo (short term capability o simplemente capability), se refiere a cómo funciona/rinde el proceso en un momento dado y muestra la capacidad potencial del proceso: a lo que puede llegar. Se calcula con la varianza a corto plazo $\sigma^2_{ST}$, disponible cuando sólo se ha observado el proceso en un momento concreto o en un corto espacio de tiempo. La variación a corto plazo ($\sigma^2_{ST}$) refleja cómo varían los resultados (y sus causas) en un período corto de tiempo.
Capacidad a largo plazo (long term capability), también llamada rendimiento del sistema, o capacidad global (performance or overall capability), se refiere a cómo percibe realmente el cliente el rendimiento del proceso, esto es, cómo se mantiene la reproducibilidad de un proceso. Se calcula con la varianza a largo plazo, $\sigma^2_{LT}$, disponible cuando se han observado varios lotes del proceso en diferentes instantes a lo largo del tiempo, durante un periodo de tiempo largo. La variación a largo plazo ($\sigma^2_{LT}$) refleja cómo varían los resultados (y sus causas) en un período de tiempo largo.

Con datos continuos es posible analizar la capacidad del sistema a través de una tabla de descomposición de la varianza, al relacionar la varianza a largo plazo $\sigma^2_{LT}$ con la suma de cuadrados total, $SST$, y la varianza a corto plazo $\sigma^2_{ST}$ con la suma de cuadrados WITHIN (dentro de los grupos), $SSW$. Recordemos que en la descomposición de la varianza se añadía la suma de cuadrados BETWEEN, SSB (entre los grupos), y se tenía: \[SST=SSB+SSW\] Extrapolando esta relación a un análisis de capacidad, cuando se habla de capacidad de que un proceso opere conforme a los límites de especificación, se está hablando implícitamente de que el proceso sea “exacto” y a la vez sea “preciso,” como ya se comentó previamente. La capacidad global se convierte pues en una suma de la exactitud del proceso, cuantificada por la variación que se produce en las mediciones en distintos instantes de tiempo ($SSB$), y la variación apreciada dentro de cada instante medido ($SSW$), tal y como se muestra en la Figura 5.13.

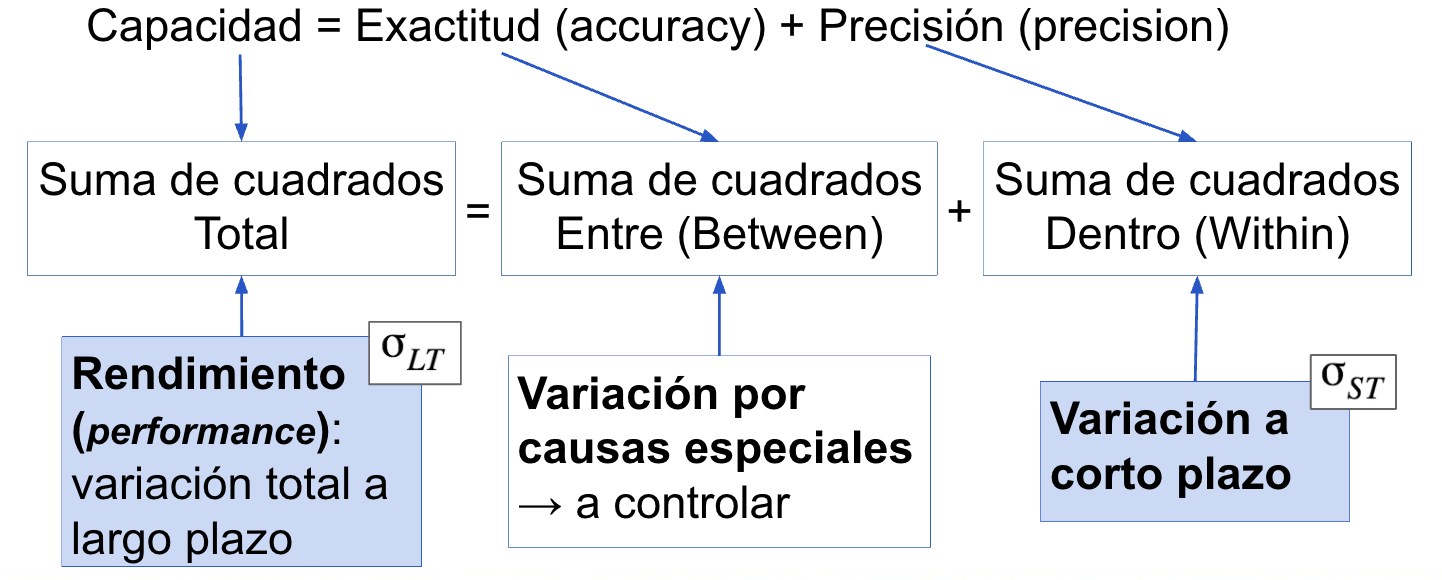
Figura 5.13: Relación entre capacidad y variabilidad.

Si en los datos obtenidos de la medición del proceso surge un modo razonable de agrupar los datos en función del momento en que se han tomado, se podrán estimar las varianzas a largo y corto plazo con las sumas de cuadrados $SST$ y $SSW$ respectivamente. De no ser el caso, por defecto estaremos calculando capacidad a corto plazo, y las conclusiones vendrán expresadas en términos del nivel sigma al que está funcionando el proceso. La diferencia de concluir con una varianza a corto plazo o una largo plazo sobre el nivel sigma del proceso se denomina $Sigma Shift$ y viene a ser, según aproximaciones empíricas, de $1.5\sigma$.

Simplemente comparando las varianzas a corto y largo plazo ya se pueden extraer conclusiones. Una diferencia grande entre la variación a largo y a corto plazo indica que el rendimiento del proceso puede mejorar si se controla mejor: el proceso no es estable y no está manteniendo el rendimiento. Una diferencia pequeña entre la variación a largo y corto plazo indica que el proceso ya ha sido controlado a lo largo del tiempo (es estable), de modo que si es preciso un mejor rendimiento, es improbable que se consiga: el proceso estaría en el límite de su potencial y si se precisaría mayor rendimiento, por lo que habría de ser rediseñado.

5.6.3.1 Índices de capacidad

Con todo, estudiaremos a continuación de un modo más objetivo la capacidad de un sistema a través de los índices de capacidad, que se calculan a partir de medias, varianzas y límites de especificación, y al estar libres de unidad de medida permiten comparar la capacidad de procesos diferentes. Los índices de capacidad comparan las especificaciones del cliente con la dispersión de los datos cuando éstos siguen una distribución normal.

Si USL (Upper Specification Limit) y LSL (Lower Specification Limit) son los límites de especificación en nuestro proceso que acotan la región de aceptación de un resultado (output), entonces tenemos defectos cuando el output $Y$ queda fuera del intervalo que definen estos límites: \[DEFECTO \rightarrow Y \notin (LSL,USL)\]

Se definen los siguientes índices de capacidad:

los índices Z-score $Z_L$ y $Z_U$, son las diferencias estandarizadas de los límites de especificación a la media; se calculan con la respuesta media observada $\bar{y}$ y la varianza de los datos $\sigma$, bien a corto o a largo plazo, para dar lugar a los respectivos índices a corto o largo plazo: \[ Z_L=\frac{\bar{y}-LSL}{\sigma}, \ \ \ Z_U=\frac{USL-\bar{y}}{\sigma}.\]
Z del proceso (Process Z, nivel Z o Z-Bench). Se interpreta como el punto en una distribución normal tal que el área a la derecha de ese punto representa la proporción de unidades defectuosas en el proceso bajo estudio. Cuanto mayor es el valor Z del proceso, mejor funciona este puesto que produce menos defectos. Se obtiene a partir de los Z-scores, basados en la media y varianza de los datos observados y de los límites de especificación. Se calcula pues, la probabilidad acumulada por una distribución normal $N$ fuera de los Z-scores, \[ PDFE = Pr\left(N<Z_L\right)+Pr\left(N>Z_U\right) \] y a partir de ahí se determina el cuantil $Z$ que acumula a su derecha toda esta probabilidad, \[Z_{\sigma} = F_{N(0,1)}^{-1}(PDFE).\]

Representa así el número de desviaciones estándar hasta el centro de los datos por encima de las cuales se acumularían todos los defectos del sistema. Es pues un buen representante del nivel sigma de un proceso cuando hay cierta normalidad en los datos.

Si se utiliza la varianza a corto plazo, $\sigma=\sigma_{ST}$, el valor $Z_{\sigma_{ST}}$ describe lo preciso que es el proceso en un momento dado en el tiempo, esto es, cómo funcionaría el proceso si se mantuviera constante la varianza a corto plazo. Se denomina “capacidad instantánea” o “capacidad a corto plazo.” Es el valor comúnmente utilizado en contexto Seis Sigma para referirse al nivel SIGMA del proceso. Representa el verdadero potencial de la tecnología del proceso para cumplir con las especificaciones de rendimiento.

Al utilizar $\sigma=\sigma_{LT}$, el valor $Z_{\sigma_{LT}}$ describe la reproducibilidad sostenida de un proceso, esto es, da una mejor medida de la realidad al incluir variación debida a causas comunes y también por causas especiales surgidas durante un perido de tiempo largo. Se denomina “capacidad a largo plazo” y valora la percepción del cliente.

Para la Z del proceso habitualmente se asume, cuando no se tiene información sobre la varianza a corto plazo, una corrección fija de 1.5 puntos para relacionar las Z’s a largo y corto plazo. Esto implica que a largo plazo el sistema es menos capaz que a largo plazo. \[Z_{ST}=Z_{LT}+1.5\]

Z-Shift (o desplazamiento Z) es la diferencia entre la $Z_{ST}$ y la $Z_{LT}$ y proporciona una aproximación de lo bien (o mal) controlado que está el proceso. \[Z_{Shift}=Z_{ST}-Z_{LT}\] Cuanto mayor es el Z-Shift, más oportunidades de mejora existen, si se puede controlar mejor el proceso y eliminar o reducir las causas específicas que generan la variación entre los diferentes grupos de datos (Soporte Minitab n.d.).

La conversión de los valores de estos índices a DPMO se realiza a través de tablas como la que se obtiene en six-sigma-material.com (n.d.) DPMO, Z-Score, Cpk, Yield Conversion Table Short Term Sigma Conversion Table.

Los índices de capacidad más populares son, sin embargo, los $P_p$ y $C_p$. Los índices de capacidad que calculan la capacidad potencial, esto es, basados en la varianza a corto plazo, son $C_p$, $C_{pU}$, $C_{pL}$ y $C_{pk}$. La capacidad que percibe el cliente y que explica (contiene) las diferencias entre grupos, se calcula con la varianza a largo plazo a través de los índices $P_p$, $P_{pU}$, $P_{pL}$ y $P_{pk}$.

Índice de capacidad del proceso, o margen del diseño. A mayor margen en el diseño, menor número de defectos por unidad, DPU. El índice de capacidad dice qué es capaz de hacer el proceso en el futuro, asumiendo que permanece bajo control.

\[C_p=\frac{USL-LSL}{6\sigma}\]

Índice de capacidad del proceso ajustado, que incluye una corrección con el centro de los datos, \[C_{pk}=min\{C_{pL},C_{pU}\},\]

donde \[C_{pU}=\frac{USL-\bar{y}}{3\sigma}, \ \mbox{ y } \ C_{pL}=\frac{\bar{y}-LSL}{3\sigma}\]

$C_{pk}$ da una corrección del índice $C_p$, ajustando por un posible efecto de no centrado en la distribución de los datos respecto de los límites de especificación. Cuando el proceso está centrado, los valores de ambos índices coinciden.

A mayor valor del $C_{pk}$, menos probable es que un producto se salga de las especificaciones (generando un defecto). $C_{pk}$ mide lo cercano que está el proceso al objetivo y lo consistente que está en torno al rendimiento promedio.

Cuando se utiliza la sigma a largo plazo, los índices se denominan $P_p$ y $P_{pk}$, y miden el rendimiento (performance) del proceso, informando sobre la capacidad del proceso para conseguir los requerimientos del cliente en base a la información disponible (histórico). $C_{pk}$ y $P_{pk}$ convergerán a casi el mismo valor cuando el proceso esté bajo control.

Puesto que el cálculo está asociado a estimaciones, se suele dar una banda de confianza basada en estimaciones MonteCarlo. Ampliar en Editorial (n.d.).

Para interpretar los índices de capacidad, son ilustrativas las Figuras 5.14 y 5.15, donde la variabilidad del proceso viene representada por la longitud de un coche que quiere aparcar y las líneas rojas proporcionan los límites de especificación, en este caso la longitud de la plaza de parking.

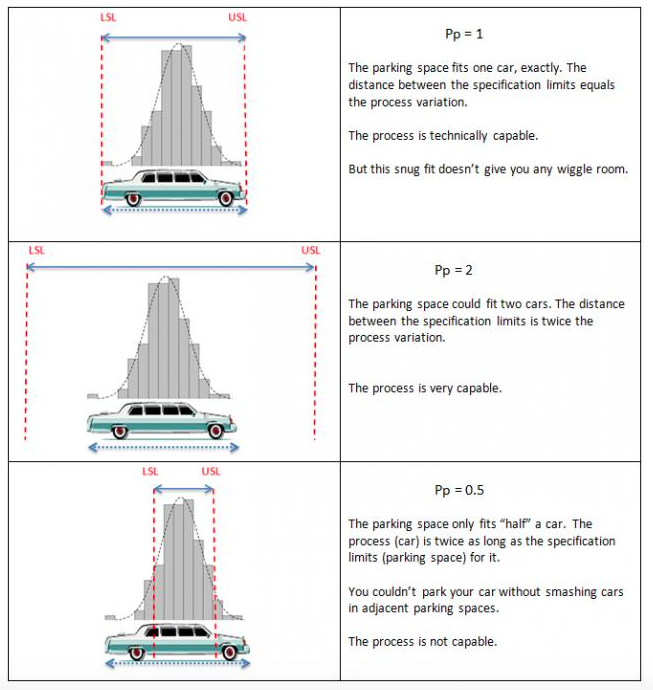
Figura 5.14: Interpretación del índice de capacidad Pp.

Figura 5.15: Interpretación del índice de capacidad Ppk.

Un valor del índice próximo a 1 indica que el hueco para aparcar está ajustado, pero el coche cabe: el proceso encaja en los límites de especificación -es técnicamente capaz-, pero de modo ajustado o comprometido. Para un valor de 2 el hueco de aparcar tiene una longitud doble a la del coche, de modo que este puede aparcar de modo holgado: el proceso es capaz de cumplir perfectamente con las especificaciones. Para un valor de 0.5, el parking es la mitad de la longitud del coche, de modo que de ninguna manera puede aparcar: el proceso no va a cumplir los límites de especificación y no es capaz.

Remarcar que comparar los valores $C_p$ y $C_{pk}$ permite identificar problemas de centrado (si difieren entre sí) y de variabilidad (si proporcionan conclusiones insatisfactorias). Comparar los valores $C_p$ y $P_p$ permite extraer conclusiones sobre la capacidad actual o potencial del proceso y la capacidad a largo plazo. Es posible calcular intervalos de confianza para los índices de capacidad, a partir de aproximaciones a normalidad. Se puede ampliar información en Soporte Minitab (n.d.).

En otras fuentes, entre ellas 1Factory (n.d.), podemos encontrar los valores de referencia para interpretar los índices de capacidad que se muestran en la Tabla 5.3, así como una interpretación visual interesante con coches y garages.

Tabla 5.3: Valores frontera para la interpretación de los índices de capacidad.
Índice	Interpretación proceso
$C_p<1$	no adecuado
$1 \leq C_p \leq 1.33$	adecuado
$C_p>1.33$	satisfactorio para los procesos existentes
$C_p >1.50$	satisfactorio para variables críticas
$C_p >1.67$	satisfactorio para nuevos procesos con una variable crítica.

5.6.4 Ejemplo Capacidad

Proponemos dos librerías básicas para realizar el análisis de capacidad en R: SixSigma (Cano, Moguerza, and Corcoba 2015a) y qcc (Scrucca 2017), y para ilustrarlo ofrecemos dos ejemplos. El primero extraído de Cano, Moguerza, and Redchuk (2013) para ilustrar el análisis de capacidad con SixSigma, y el segundo obtenido de la propia librería qcc.

Ejemplo SixSigma La librería SixSigma tiene diversas funciones implementadas para resolver el análisis de capacidad. Entre ellas:

ss.ca.yield() proporciona las medidas de rendimiento Yield, FTY, RTY y DPMO.
ss.ca.z(), ss.ca.cp(). ss.ca.cpk() calcula los índices de capacidad del proceso Z, Cp y Cpk.
ss.study.ca() resuelve el estudio de capacidad mostrando histogramas con los datos y límites de especificación, tests de normalidad y valores para los índices de capacidad.

Veamos cómo resuelven un ejemplo propuesto en Cano, Moguerza, and Redchuk (2013) con datos para el corto plazo y simulados para el largo plazo, en los que el target objetivo es 750 y los límites de especificación vienen dados por el intervalo $[740,760]$.

# Análisis de capacidad con SixSigma
library(SixSigma)
ss.study.ca(ss.data.ca$Volume, rnorm(40, 753, 3), 
        LSL = 740, USL = 760, T = 750, alpha = 0.05, 
            f.sub = "Winery Project")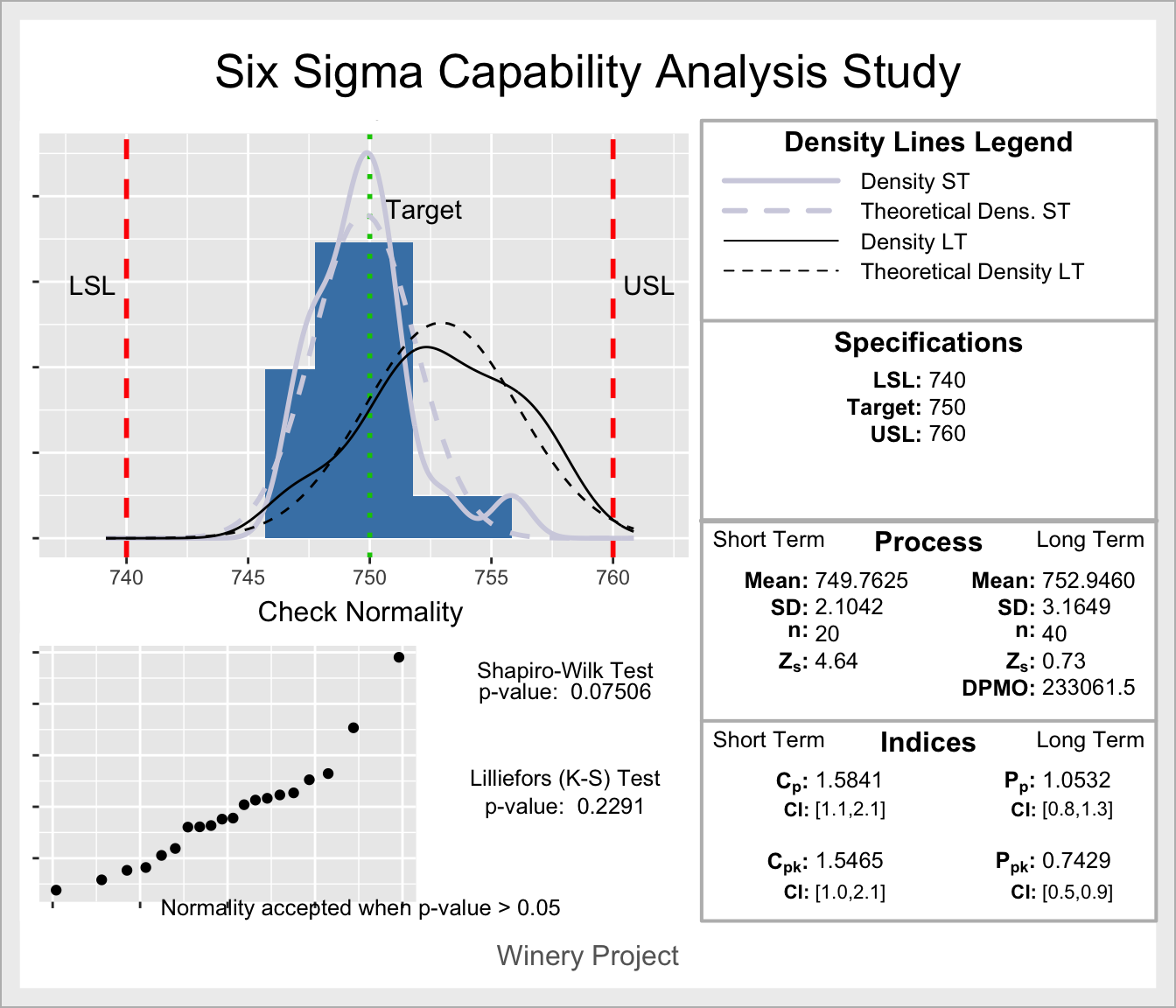

Figura 5.16: Análisis de capacidad con la librería SixSigma.

El histograma en la Figura 5.16 representa los datos disponibles (a corto plazo) y superpone líneas de densidad para la distribución de estos y de los utilizados en el largo plazo (desplazados a la derecha respecto de los primeros). Describe con medias, desviaciones típicas, tamaño de muestra e índices de capacidad, los procesos a corto y largo plazo, y también resuelve los tests de normalidad para los datos proporcionados. Como conclusiones, se derivan las siguientes:

Corto plazo: No se rechaza normalidad y los datos están centrados respecto de los límites de especificación, por lo que los índices $C_p$ y $C_{pk}$ prácticamente coinciden. Además, al dar valores superiores a 1.5, podemos afirmar que el proceso es satisfactorio en el corto plazo. Actualmente está operando bastante bien dentro de los límites de especificación. El valor Z del proceso, que da una aproximación del nivel sigma, es de 4.64, lo cual apoya las conclusiones basadas en el índice $C_p$.
Largo plazo: El proceso está ligeramente descentrado al dar una media de 752.8, desviada del target 750 y la varianza es ligeramente superior a la apreciada en el corto plazo. Los índices $P_p$ y $P_{pk}$ difieren, avalando el descentrado de los datos respecto de los límites de especificación, por lo que para corregir el proceso ya es preciso centrarlo. Respecto del índice $P_p$ el proceso es adecuado, es decir, en caso de estar centrado, la varianza que se aprecia es permisible para evaluar el proceso como adecuado. Sin embargo, el índice $P_{pk}$ da un valor inferior a 1, lo que implica que el proceso no es capaz de cumplir con las especificaciones y para hacerlo habría de ser centrado.
Corto y largo plazo: las diferencias que se aprecian entre los valores $C_p$ y $P_p$ hablan de cierta inestabilidad en el proceso; si bien es potencialmente capaz de funcionar de modo satisfactorio (en el corto plazo), perdería cierta capacidad en el largo plazo en el caso de estar centrado, porque la varianza ha aumentado respecto del corto plazo. Por otro lado, al comparar $C_{pk}$ y $P_{pk}$, la conclusión es claramente que el proceso a largo plazo ha perdido capacidad para cumplir con las especificaciones y necesariamente ha de ser centrado; si además se invierte algo de esfuerzo en reducir variabilidad, el proceso podría alcanzar el comportamiento satisfactorio que ha manifestado en el corto plazo.

Ejemplo qcc. Utilizamos el ejemplo que proporciona la librería en la documentación para qcc, ampliada en Scrucca (2021). Proporciona un ejemplo, pistonrings, en el que se ha realizado un muestreo del diámetro de anillos de pistones en 40 lotes/muestreos a lo largo del tiempo, cada uno de tamaño 5. Las primeras 10 muestras se consideran bajo control. La variable objetivo es diameter, y sample identifica los lotes o muestras.

Para iniciar el análisis es preciso agrupar los datos por lotes, lo que se hace con la función qcc.groups. La función qcc genera un objeto analítico a partir del cual se puede realizar el estudio de capacidad con la función process.capability, especificando los límites y el objetivo.

# Análisis de capacidad con qcc
library(qcc)
data(pistonrings)
attach(pistonrings)
# agrupa los datos por lotes/muestras
diameter <- qcc.groups(diameter, sample)
# análisis de capacidad sólo con las 25 primeras muestras
q <- qcc(diameter[1:25,], type="xbar",plot=FALSE)
process.capability(q, spec.limits=c(73.95,74.05), target=74.02)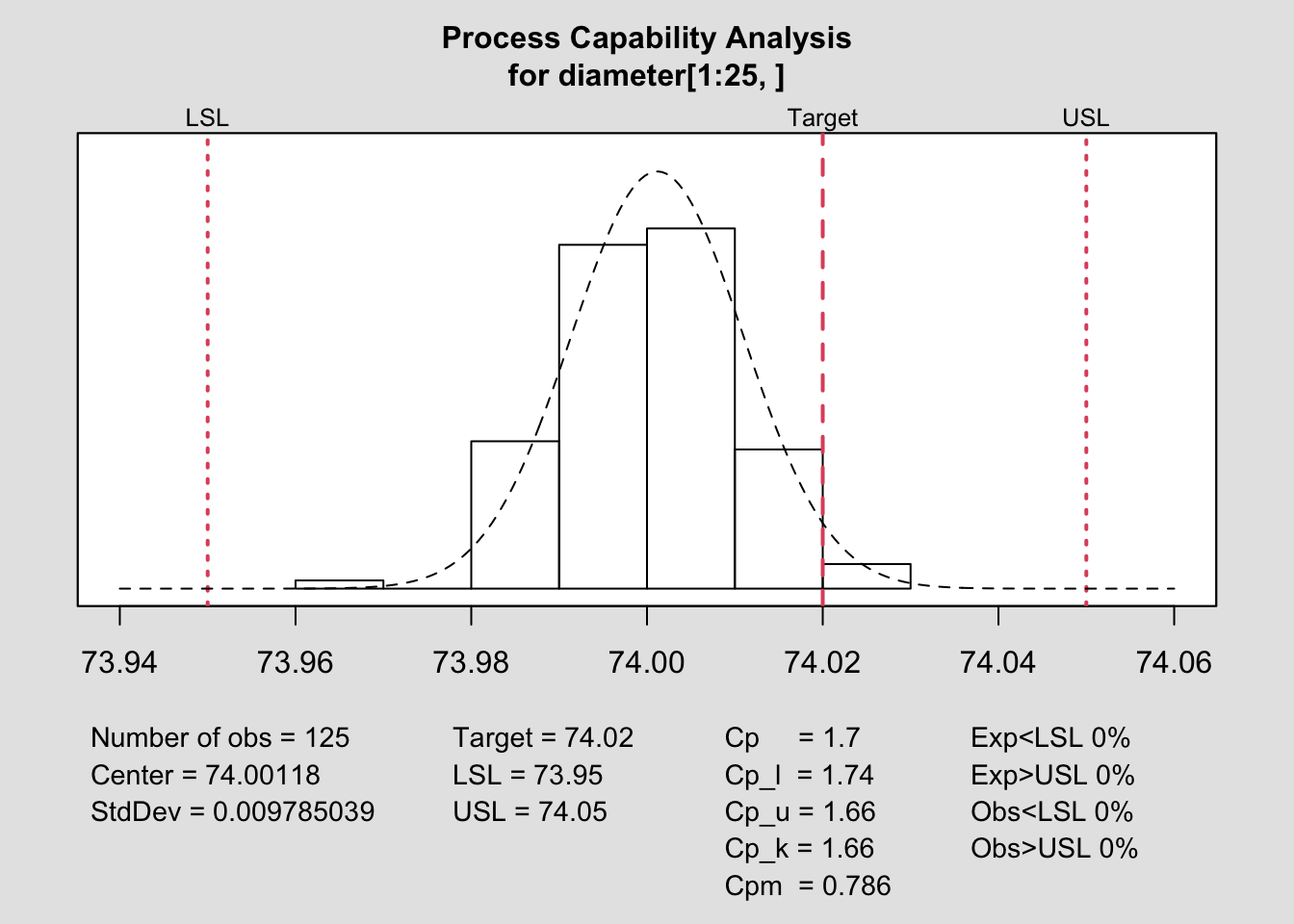

Figura 5.17: Análisis de capacidad con la librería qcc.

## 
## Process Capability Analysis
## 
## Call:
## process.capability(object = q, spec.limits = c(73.95, 74.05),     target = 74.02)
## 
## Number of obs = 125          Target = 74.02
##        Center = 74              LSL = 73.95
##        StdDev = 0.009785        USL = 74.05
## 
## Capability indices:
## 
##        Value    2.5%   97.5%
## Cp    1.7033  1.4914  1.9148
## Cp_l  1.7433  1.5548  1.9319
## Cp_u  1.6632  1.4827  1.8437
## Cp_k  1.6632  1.4481  1.8783
## Cpm   0.7856  0.6556  0.9154
## 
## Exp<LSL 0%    Obs<LSL 0%
## Exp>USL 0%    Obs>USL 0%

La función qcc resuelve el análisis de capacidad a corto plazo con los datos introducidos y proporciona el output que se muestra en la 5.17. Proporciona información numérica sobre ellos, como la media, desviación típica y número de observaciones y, tras mostrar las especificaciones y objetivos del proceso, presenta bajo el gráfico con el histograma y líneas rojas para límites, los valores de los índices de capacidad relacionados con el $C_p$. Calcula también el porcentaje de valores observados y esperados fuera de los límites de especificación.

Las conclusiones derivadas del análisis de pistonrings son:

El proceso está dentro de los límites de especificación, si bien está algo descentrado respecto del objetivo o target: las medias difieren en 0.02u. Los valores de $C_p$ y $C_{pk}$ difieren, pero no excesivamente, y ambos dan resultados adecuados, si bien corrigiendo el descentrado, el proceso ganaría capacidad para cumplir con las especificaciones y sería calificado mejor, como satisfactorio.
Asumiendo normalidad, no se espera que los datos queden fuera de los límites de especificación, y tampoco con los datos observados se ha dado el caso.

5.7 Hoja de ruta: MEDIR

A continuación, y a modo de resumen, se da una serie de hojas de ruta para las distintas fases/procesos en la etapa MEDIR.

5.7.1 Planificación de la medición

¿Qué tratamos de aprender, rastrear o evaluar?
¿Qué es lo que vamos a contar o a medir? ¿En qué unidades se expresa esa medición y de qué tipo es la variable que representa?
Da una definición operacional de la medición.
¿Necesitamos recoger datos nuevos o hay ya históricos disponibles?
¿Cómo planeas utilizar/visualizar estos datos?
¿Cuál es el plan para asegurar precisión, repetibilidad y reproducibilidad?

5.7.2 Árbol CTQ

Para identificar los CTQ de un proceso, se puede utilizar un árbol CTQ siguiendo estos pasos:

Identificar un output que es importante para los clientes.
Identificar una característica de dicho output que es “critical to quality.” Se completa un recuadro a la izquierda.
Tormenta de ideas sobre tipos de datos asociados a la característica ctq, ordenándolos de modo lógico en ramas que emergen del cuadro inicial.
¿Es sensato y útil recopilar todos los datos especificados en el árbol?
Confirmar los datos a recopilar.

5.7.3 Factores de estratificación

Para identificar factores de estratificación a utilizar en el muestreo, podemos resolver las siguientes cuestiones.

1.Identificar preguntas que te gustaría investigar una vez tuvieras los datos a mano:

*  ¿Quién? (dpto, individuo, tipo de cliente,...).
* ¿Qué?  (tipo de reclamación, tipo de defecto, razón para una reclamación,... ).
* ¿Cuándo? (mes, cuatrimestre, día de la semana, hora del día, ... ).
* ¿Dónde? (región, ciudad, localización específica del producto, ...).

2.Decidir qué factores de estratificación son más importantes y qué cuestiones más pertinentes, claves para resolver el problema a estudio.

3.Documentar estas decisiones.

5.7.4 Plan de muestreo

Para concretar el plan de muestreo, es conveniente seguir las siguientes indicaciones.

Identificar y definir

1.¿Qué vas a contar (la unidad)? 2.¿Cuántas unidades?

¿Cuál es el tamaño de la población en cada estrato? $N=...$
¿Cuántas unidades son procesadas por semana, por día, …? Frecuencia de procesado $FP=...$

¿Cuál es la característica de interés (ej. defecto, tiempo, …)?
¿Esta medida es discreta o continua?

Si es discreta, ¿qué proporción de la población estimas que tiene ese defecto/característica? $p=...$ (entre 0 y 1)
Si es continua, ¿qué estimación das para su desviación típica en la población? $s=...$ (piensa en normalidad y en un intervalo $ 2s$ para albergar al 95% de la población -datos-).

¿Con qué precisión/fiabilidad haces esa estimación? $\pm \rightarrow d=...$
¿Cuántos ciclos de trabajo se hacen por día o por semana? $nciclos=...$

Seleccionar una estrategia de muestreo

Estrategia seleccionada: __ Aleatoria / __ Sistemática
¿Cómo vas a identificar a las unidades de la muestra (están numeradas, usarás números aleatorios)?

En el caso de utilizar las frecuencias de procesado, aplica muestreo sistemático aunque el aleatorio sea factible.

Determinar el tamaño muestral mínimo

Si la característica es discreta: $n=(2/d)*2 p (1-p) \rightarrow n=...$
Si la característica es continua: $n=(2s/d)^2 \rightarrow n=...$

En el caso de utilizar las frecuencias de procesado, FP:

¿$FP>10$ por día?

SÍ: usa estrategia de muestreo diario;
NO: usa estrategia de muestreo semanal

Utiliza los Gráficos de selección del tamaño de muestra (diarios o semanales) para determinar el tamaño de muestra mínimo:

estrategia semanal: $n.min=(FP+110)/12$
estrategia diaria: $n.min=(FP+870)/90$

Ajustar por población finita para el caso de muestreo aleatorio

Calcula la proporción de muestra respecto al tamaño de la población, n/N=…
Si $n/N>0.05$ realizar el ajuste por población finita según la siguiente fórmula: $n_{finito}= n/(1+n/N) \rightarrow$ nfinito=…

Seleccionar tamaño del subgrupo y frecuencia de muestreo

¿Es tu característica continua?

SÍ: usa subgrupos de tamaño 1. Muestrea a intervalos apropiados (cada hora, cada n-ésimo ítem,…).
NO: usa los siguientes pasos para identificar el tamaño de los subgrupos y la frecuencia de muestreo:
1. tamaño del subgrupo $TS= 5/p$
2. ¿$TS \geq FP$?
  - SÍ: Es preciso muestrear todos los ítems o reconsiderar la característica.
  - NO: calcula la frecuencia de muestreo con: frecuencia base= $n.min / TS$.

Si hay un ciclo en el proceso, nciclos=1, incrementa la frecuencia a dos veces el número de ciclos por día o semana (ej: 3 ciclos en un día precisarán 6 muestreos al día).

5.7.5 Conteo de defectos y cálculo del nivel Sigma

Los niveles sigma de un proceso se pueden determinar de varios modos. Los siguientes pasos utilizan el método más simple, basado en el número de defectos al final de un proceso.

PASO1. Selecciona:

el proceso a evaluar,
la unidad: la primera “cosa” producida por el proceso
los requisitos del cliente para dicha unidad.

PASO 2. Define el defecto y el número de oportunidades.

Defectos: basándote en los requisitos, lista de modo objetivo todos los posibles defectos en una unidad individual.
Oportunidades: ¿Cuántos defectos se pueden encontrar en una unidad individual?

PASO 3. Recaba datos y calcula DPMO

Al final del proceso se tienen … unidades contadas y … defectos contados.
Calcula el total de oportunidades en los datos recogidos: $unidades \times oportunidades$
Calcula el número de defectos por millón de oportunidades: $DPMO$

PASO 4. Convierte DPMO a nivel Sigma con las tablas o calculadoras de conversión.

5.7.6 Checklist MEDIR

Los siguientes puntos secuenciados proporcionan una hoja de ruta genérica o checklist en la fase MEDIR, que puedes descargar en este enlace.

EN NUESTRO PROYECTO HEMOS …

Determinado sobre qué queremos aprender sobre nuestro problema y proceso y dónde podemos ir en el proceso para conseguir la respuestas.
Identificado los tipos de medidas que queremos recopilar y conseguido un equilibrio entre efectividad/eficiencia y input/proceso/output.
Desarrollado definiciones operacionales de las cosas o atributos que queremos medir de forma clara y no ambigua.
Testado nuestras definiciones operacionales con otros para asegurar su claridad e interpretación consistente.
Hecho una elección clara y razonable entre conseguir datos nuevos y aprovechar otros previamente recopilados en la organización.
Clarificado los factores de estratificación que necesitamos identificar para facilitar el análisis de nuestros datos.
Desarrollado y testado los formularios y hojas de chequeo para la recogida de datos, y son fáciles de cumplimentar y proporcionar datos completos y consistentes.
Identificado un tamaño de muestra apropiado, una cantidad de subgrupo y una frecuencia de muestreo apropiadas para asegurar la representación válida del proceso que estamos midiendo.
Preparado y testado nuestro sistema de medida, incluyendo entrenamiento de los recolectores de datos y evaluado la estabilidad del proceso de recopilación de datos.
Utilizado datos para preparar las medidas de rendimiento base del proceso, incluyendo la proporción de defectos y la producción (yield).

Bibliografía

1Factory. n.d. “Process Capability Analysis Cp, Cpk, Pp, Ppk - a Guide.” Web publication. https://www.1factory.com/quality-academy/guide-to-process-capability-analysis-cp-cpk-pp-ppk.html.

Basu, Ron. 2011. “Fit Sigma: A Lean Approach to Building Sustainable Quality Beyond Six Sigma.” In. Wiley. https://www.oreilly.com/library/view/fit-sigma-a/9780470666210/OEBPS/9780470666210_epub_a_3.htm.

Cano, Emilio L., Javier M. Moguerza, and Mariano Prieto Corcoba. 2015a. Quality Control with r. Use r! New York: Springer.

———. 2015b. “Quality Control with r. An ISO Standards Approach.” In. Springer. https://link.springer.com/content/pdf/bbm%3A978-3-319-24046-6%2F1.pdf.

Cano, Emilio L., Javier M. Moguerza, and A. Redchuk. 2013. Six Sigma with r. Springer Use R! Series. http://sixsigmawithr.com/, https://www.springer.com/gp/book/9781461436515.

Cheng, S., K. Kupfer, M. Dixon, and S. Shammas. 2018. “Optimized Sampling Design and Rationale for Verification and Validation.” Quality and Reliability Engineering International 35: 483–502. https://doi.org/https://doi.org/10.1002/qre.2353.

———. 2017b. “Six Sigma Concepts and Metrics (Part 2 of 2).” Web publication; Minitab. https://blog.minitab.com/en/quality-business/six-sigma-concepts-and-metrics-part-2-of-2#.

Editorial, iSixSigma. n.d. “Process Capability (Cp,cpk) and Process Performance (Pp,ppk). What Is the Difference?” Web publication; iSixSigma. https://www.isixsigma.com/tools-templates/capability-indices-process-capability/process-capability-cp-cpk-and-process-performance-pp-ppk-what-difference/.

GoodCalculators.com. n.d. “Six Sigma Calculator.” Web publication. https://goodcalculators.com/six-sigma-calculator/.

———. 2021. An Introduction to Acceptance Sampling and SPC with r. Chapman; Hall/CRC. https://bookdown.org/lawson/an_introduction_to_acceptance_sampling_and_spc_with_r26/.

Minitab, Soporte. n.d. “Nivel z Como Una Estimación de La Capacidad Sigma.” Web publication; Minitab. https://support.minitab.com/es-mx/minitab/18/help-and-how-to/quality-and-process-improvement/capability-analysis/supporting-topics/capability-metrics/z-bench-as-an-estimate-of-sigma-capability/.

———. n.d. “Potential (Within) Capability for Normal Capability Analysis.” Web publication; Minitab. https://support.minitab.com/en-us/minitab/18/help-and-how-to/quality-and-process-improvement/capability-analysis/how-to/capability-analysis/normal-capability-analysis/interpret-the-results/all-statistics-and-graphs/potential-within-capability/.

Minitab, Soporte de. n.d. “¿Es Aceptable Mi Sistema de Medición?” Web publication; Minitab.com. https://support.minitab.com/es-mx/minitab/19/help-and-how-to/quality-and-process-improvement/measurement-system-analysis/supporting-topics/gage-r-r-analyses/is-my-measurement-system-acceptable/.

———. n.d. “Interpretar Los Resultados Clave Para Estudio Gage Cruzado Del Sistema de Medición.” Web publication; Minitab.com. https://support.minitab.com/es-mx/minitab/18/help-and-how-to/quality-and-process-improvement/measurement-system-analysis/how-to/gage-study/crossed-gage-r-r-study/interpret-the-results/key-results/.

Scrucca, Luca. 2017. Qcc: Quality Control Charts. https://github.com/luca-scr/qcc.

———. 2021. A Quick Tour of Qcc. https://github.com/luca-scr/qcc/blob/master/vignettes/qcc.Rmd.

six-sigma-material.com. n.d. “Short Term Sigma Conversion Table.” Web publication; Six Sigma Material. https://www.six-sigma-material.com/Tables.html.

University of Glasgow, Library of the. n.d. “William Thomson, Lord Kelvin 1824-1907.” Web publication. https://www.gla.ac.uk/myglasgow/library/files/special/exhibns/Kelvin/kelvinindex.html.

Índice	Interpretación proceso
\(C_p<1\)	no adecuado
\(1 \leq C_p \leq 1.33\)	adecuado
\(C_p>1.33\)	satisfactorio para los procesos existentes
\(C_p >1.50\)	satisfactorio para variables críticas
\(C_p >1.67\)	satisfactorio para nuevos procesos con una variable crítica.