Chapter 10 Tests and modelling in R

In this section we will look very closely at the assessment of the relationships that are based on variation in your data. We will also discuss the importance of variability as an important ingredient for conducting statistical tests that do not just scream of significance but also make an appropriate use of the tools.

In a previous section we have introduced you to plenty of ways to visualise your data in R, organise it and tidy it. Visualisations in fact are not just there for fun graphics, they are an essential part of data examination that can highlight problems related to lack of variability in your data sooner than later.

We expect that you may have seen the tools we will be discussing below but may know how to use them in SPSS or Excel, we thus will focus more on application of these in R, very quick results interpretation, diagnostics set up and the assumptions checking.

We will use the mix of tool you have already seen but will also cover simple plot() function and more of psych descriptive tools.

10.1 Hypothesis testing

In R, we can generate distributions, visualise them, study them and also find critical values if we are interested with testing the probability of data to occur under null distribution. For continuous variables we will be dealing with t and Z distributions.

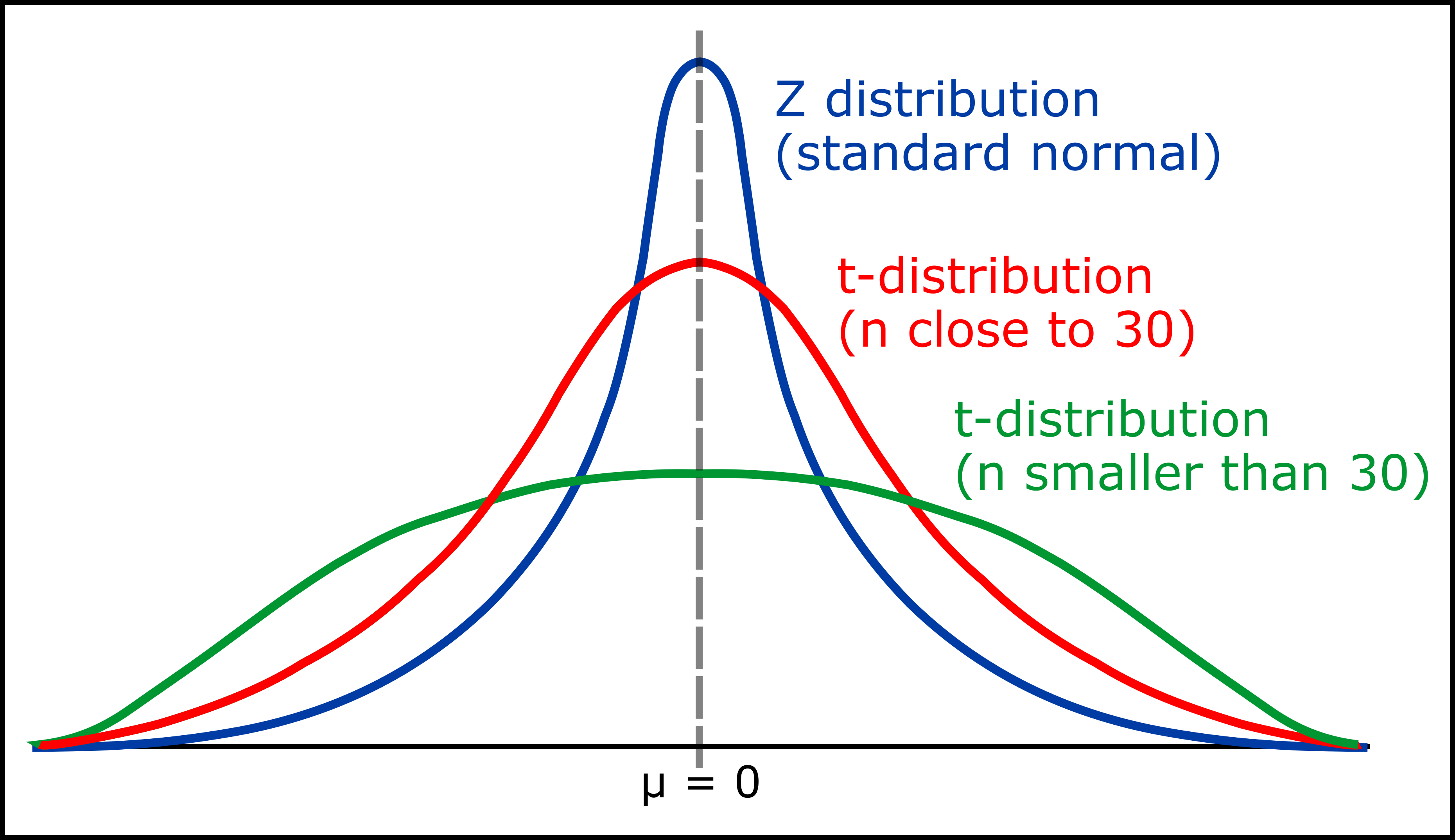Image courtesy: Andy Connelly

We will present one here with a continuous variable. Let us generate a normal distribution of grades.

grades_generated<-rnorm(n=20, mean=60, sd=4)
summary(grades_generated)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   51.35   57.04   58.11   58.78   61.64   63.92

We can also create it by imputing some data:

grades<-c(63, 68, 72, 53, 43, 59, 56, 58, 76, 54, 46, 62, 58, 54, 45, 
          53, 82, 69, 51, 58, 45, 50, 60, 73, 62, 56, 60, 53, 61, 56,
          43, 39, 61, 68, 60, 60, 58, 61, 63, 59, 58, 73, 54, 55, 57, 62, 71, 58, 84, 68)
summary(grades)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   39.00   54.00   58.50   59.36   62.75   84.00

Lets visualise the grades so we can imagine what our distribution looks like:

hist(grades)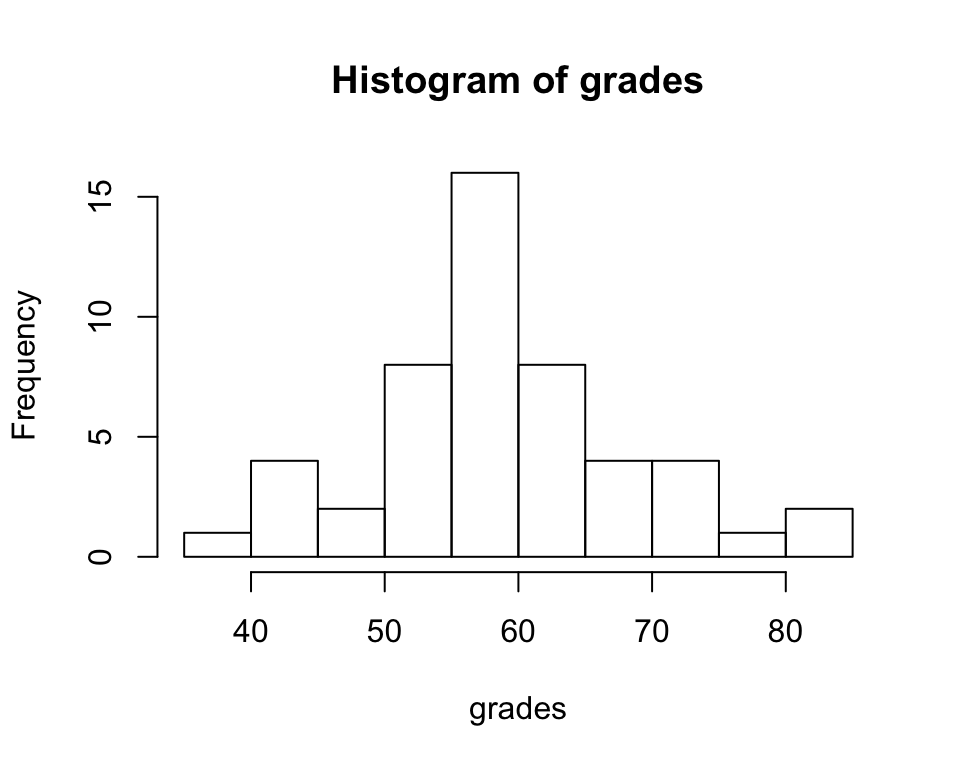

#We can also present it as density function
plot(density(grades))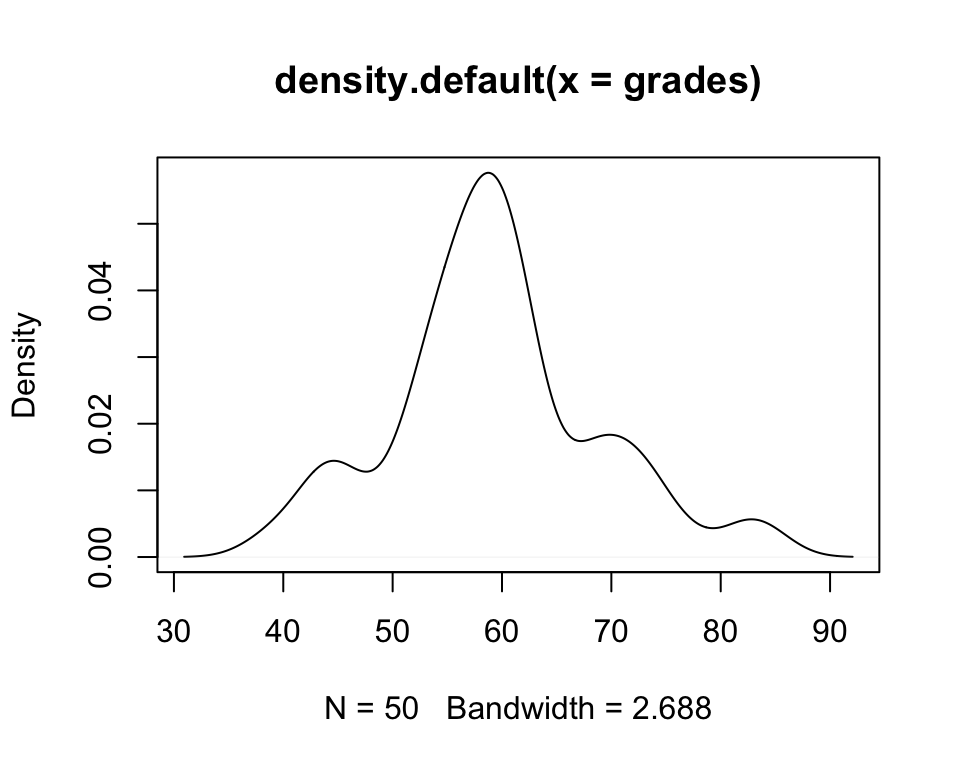

We can perform a one test sample using R. I want to test how likely it is to observe mean of 85 under the null distribution.

t.test(grades, mu = 85, alternative = "two.sided")

## 
##  One Sample t-test
## 
## data:  grades
## t = -19.103, df = 49, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 85
## 95 percent confidence interval:
##  56.6628 62.0572
## sample estimates:
## mean of x 
##     59.36

What about 55?

t.test(grades, mu = 60, alternative = "two.sided")

## 
##  One Sample t-test
## 
## data:  grades
## t = -0.47684, df = 49, p-value = 0.6356
## alternative hypothesis: true mean is not equal to 60
## 95 percent confidence interval:
##  56.6628 62.0572
## sample estimates:
## mean of x 
##     59.36

We can also test whether true mean is greater than the sample mean of 65 under the null distribution:

t.test(grades, mu = 65, alternative = "greater")

## 
##  One Sample t-test
## 
## data:  grades
## t = -4.2021, df = 49, p-value = 0.9999
## alternative hypothesis: true mean is greater than 65
## 95 percent confidence interval:
##  57.10977      Inf
## sample estimates:
## mean of x 
##     59.36

We can also test whether true mean is smaller than the sample mean of 65 under the null distribution:

t.test(grades, mu = 65, alternative = "less")

## 
##  One Sample t-test
## 
## data:  grades
## t = -4.2021, df = 49, p-value = 5.576e-05
## alternative hypothesis: true mean is less than 65
## 95 percent confidence interval:
##      -Inf 61.61023
## sample estimates:
## mean of x 
##     59.36

We can reject the null, meaning that true mean is less than 65, but certainly not greater than 65. Looks good! Make a note of key outputs, most of them will reappear in other setting (i.e. p-value, test statistics, df).