7.4 高级函数
高级函数并不是指使用难度,而是使用频率可能不高,但在实现某些功能时特别便利的函数。
如分组聚合的groupingsets,前后移动的shift等函数。
7.4.1 groupingsets
产生多个层次的合计数据,与sql中的grouping set功能相似。
用法
rollup(x, j, by, .SDcols, id = FALSE, ...)
groupingsets(x, j, by, sets, .SDcols, id = FALSE, jj, ...)
# rollup
rollup(DT, j = lapply(.SD, sum), by = c("color","year","status"), id=TRUE, .SDcols="value")
rollup(DT, j = c(list(count=.N), lapply(.SD, sum)), by = c("color","year","status"), id=TRUE)如果要达到像Excel中透视表一样的效果,如下所示:
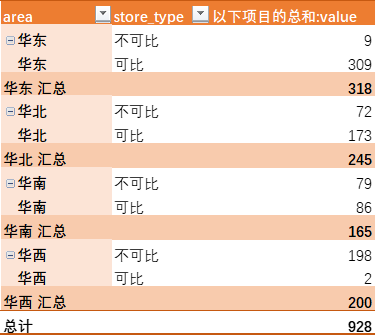
Excel groupingsets透视表
- rollup
library(magrittr)
#>
#> 载入程辑包:'magrittr'
#> The following object is masked from 'package:purrr':
#>
#> set_names
#> The following object is masked from 'package:tidyr':
#>
#> extract
DT <- fread('./data/data-table-groupingsets.csv',encoding = 'UTF-8')
(rollup(DT,j =list(以下项目的总和 =sum(value)),by = c("area","store_type"),id = TRUE) %>% setorderv(cols=c('area','grouping'),na.last = TRUE))
#> grouping area store_type 以下项目的总和
#> 1: 0 华东 不可比 9
#> 2: 0 华东 可比 309
#> 3: 1 华东 <NA> 318
#> 4: 0 华北 不可比 72
#> 5: 0 华北 可比 173
#> 6: 1 华北 <NA> 245
#> 7: 0 华南 可比 86
#> 8: 0 华南 不可比 79
#> 9: 1 华南 <NA> 165
#> 10: 0 华西 可比 2
#> 11: 0 华西 不可比 198
#> 12: 1 华西 <NA> 200
#> 13: 3 <NA> <NA> 928通过上述计算,发现计算结果与Excel透视表一样。
- cube
观察cube()计算结果与rollup()差异,发现cube()聚合层次更多。
cube(DT,j = sum(value),by = c("area","store_type"),id = TRUE)
#> grouping area store_type V1
#> 1: 0 华东 不可比 9
#> 2: 0 华东 可比 309
#> 3: 0 华西 可比 2
#> 4: 0 华西 不可比 198
#> 5: 0 华南 可比 86
#> 6: 0 华北 不可比 72
#> 7: 0 华南 不可比 79
#> 8: 0 华北 可比 173
#> 9: 1 华东 <NA> 318
#> 10: 1 华西 <NA> 200
#> 11: 1 华南 <NA> 165
#> 12: 1 华北 <NA> 245
#> 13: 2 <NA> 不可比 358
#> 14: 2 <NA> 可比 570
#> 15: 3 <NA> <NA> 928- groupingsets
根据需要指定指定聚合的层次。
# 与本例中rollup 结果一致
groupingsets(DT,j = sum(value),by = c("area","store_type"),sets = list('area',c("area","store_type"), character()),id = TRUE)
#> grouping area store_type V1
#> 1: 1 华东 <NA> 318
#> 2: 1 华西 <NA> 200
#> 3: 1 华南 <NA> 165
#> 4: 1 华北 <NA> 245
#> 5: 0 华东 不可比 9
#> 6: 0 华东 可比 309
#> 7: 0 华西 可比 2
#> 8: 0 华西 不可比 198
#> 9: 0 华南 可比 86
#> 10: 0 华北 不可比 72
#> 11: 0 华南 不可比 79
#> 12: 0 华北 可比 173
#> 13: 3 <NA> <NA> 928
# 与本例中cube 结果一致
groupingsets(DT,j = sum(value),by = c("area","store_type"),sets = list('area',c("area","store_type"),"store_type", character()),id = TRUE)
#> grouping area store_type V1
#> 1: 1 华东 <NA> 318
#> 2: 1 华西 <NA> 200
#> 3: 1 华南 <NA> 165
#> 4: 1 华北 <NA> 245
#> 5: 0 华东 不可比 9
#> 6: 0 华东 可比 309
#> 7: 0 华西 可比 2
#> 8: 0 华西 不可比 198
#> 9: 0 华南 可比 86
#> 10: 0 华北 不可比 72
#> 11: 0 华南 不可比 79
#> 12: 0 华北 可比 173
#> 13: 2 <NA> 不可比 358
#> 14: 2 <NA> 可比 570
#> 15: 3 <NA> <NA> 928groupingsets: sets参数,用list()包裹想要聚合的字段组合,最后character(),加上该部分相当于不区分层级全部聚合,用法类似sql中“().”
SELECT brand, size, sum(sales) FROM items_sold GROUP BY GROUPING SETS ((brand), (size), ());
7.4.2 rleid
该函数根据分组生成长度列。
即将0011001110111101类似这种分组成1 1 2 2 3 3 4 4 4 5 6 6 6 6 7 8。在特定时候是很便捷的一个函数。如在计算股票连续上涨或下跌天数时。
rleid(c(0,0,1,1,0,0,1,1,1,0,1,1,1,1,0,1))
#> [1] 1 1 2 2 3 3 4 4 4 5 6 6 6 6 7 8用法:
rleid(..., prefix=NULL)
rleidv(x, cols=seq_along(x), prefix=NULL)DT = data.table(grp=rep(c("A", "B", "C", "A", "B"), c(2,2,3,1,2)), value=1:10)
rleid(DT$grp) # get run-length ids
#> [1] 1 1 2 2 3 3 3 4 5 5
rleidv(DT, "grp") # same as above
#> [1] 1 1 2 2 3 3 3 4 5 5
rleid(DT$grp, prefix="grp") # prefix with 'grp'
#> [1] "grp1" "grp1" "grp2" "grp2" "grp3" "grp3" "grp3" "grp4" "grp5" "grp5"7.4.3 shift
向前或向后功能,通俗来说就是向前或向后移动位置。
示例如下:
x = 1:5
# lag with n=1 and pad with NA (returns vector)
shift(x, n=1, fill=NA, type="lag")
#> [1] NA 1 2 3 4其中参数n控制偏移量,n正负数和type的参数相对应。, n=-1 and type=‘lead’ 与 n=1 and type=’lag’效果相同。
在data.table上使用:
DT = data.table(year=2010:2014, v1=runif(5), v2=1:5, v3=letters[1:5])
cols = c("v1","v2","v3")
anscols = paste("lead", cols, sep="_")
DT[, (anscols) := shift(.SD, 1, 0, "lead"), .SDcols=cols]例如求某人连续消费时间间隔天数时:
DT = data.table(dates =lubridate::ymd(c(20210105,20210115,20210124,20210218,20210424)))
DT[,newdate:=shift(dates)]
DT
#> dates newdate
#> 1: 2021-01-05 <NA>
#> 2: 2021-01-15 2021-01-05
#> 3: 2021-01-24 2021-01-15
#> 4: 2021-02-18 2021-01-24
#> 5: 2021-04-24 2021-02-18通过构造新列newdate,然后将两列相减dates-newdate即可得到每次购物间隔天数。
7.4.4 J
J 是.(),list()等的别名。SJ是排序连接,CJ是交叉连接。
用法:
# DT[J(...)] # J() only for use inside DT[...]
# DT[.(...)] # .() only for use inside DT[...]
# DT[list(...)] # same; .(), list() and J() are identical
SJ(...) # DT[SJ(...)]
CJ(..., sorted=TRUE, unique=FALSE) # DT[CJ(...)]- CJ
我喜欢用CJ()函数创建笛卡尔积表。例如在商品运营中,时常需要将门店和商品形成笛卡尔积表,相比起dplyr::full_join() ,data.table::merge.data.table(allow.cartesian = TRUE ),CJ更加方便快捷。
# CJ usage examples
CJ(c(5, NA, 1), c(1, 3, 2)) # sorted and keyed data.table
#> V1 V2
#> 1: NA 1
#> 2: NA 2
#> 3: NA 3
#> 4: 1 1
#> 5: 1 2
#> 6: 1 3
#> 7: 5 1
#> 8: 5 2
#> 9: 5 3
# do.call(CJ, list(c(5, NA, 1), c(1, 3, 2))) # same as above
# CJ(c(5, NA, 1), c(1, 3, 2), sorted=FALSE) # same order as input, unkeyed- SJ
SJ : Sorted Join. The same value as J() but additionally setkey() is called on all columns in the order they were passed to SJ. For efficiency, to invoke a binary merge rather than a repeated binary full search for each row of i.