Chapter 14 Correlation

14.1 Introduction

Understanding relationships between variables is crucial in food science, where we often deal with complex datasets, such as chemical properties, sensory attributes, or production parameters. Correlation analysis quantifies the degree to which two variables are related, while heatmaps provide an intuitive plot of these relationships, enabling easy identification of patterns and clusters.

In this chapter, we will:

  1. Perform correlation analysis on a sample dataset.

  2. Visualize the results using a heatmap.

  3. Discuss practical applications of correlation analysis in food science.

14.1.1 Setting Up the Environment

First, ensure that the necessary libraries are installed. Install any missing libraries using:

install.packages(c("tidyverse", "corrplot", "pheatmap"))

Load the libraries:

library(tidyverse)
library(corrplot)
library(pheatmap)

14.2 Preparing the Dataset

For demonstration, we will use the mtcars dataset, a built-in dataset in R that provides data on various car attributes. While not directly related to food science, the structure of this dataset is analogous to real-world datasets with multiple numeric variables.

# Load the dataset
data("mtcars")

# Inspect the data
head(mtcars)
##                    mpg cyl disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
## Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
## Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1
# Select numeric variables for correlation analysis
correlation_data <- mtcars %>% select_if(is.numeric)

14.3 Correlation Analysis

We calculate the correlation matrix for the selected numeric variables. Correlation coefficients range from -1 (perfect negative correlation) to +1 (perfect positive correlation), with 0 indicating no correlation.

# Calculate the correlation matrix
cor_matrix <- cor(correlation_data, use = "complete.obs")

# Display the correlation matrix
print(cor_matrix)
##             mpg        cyl       disp         hp        drat         wt
## mpg   1.0000000 -0.8521620 -0.8475514 -0.7761684  0.68117191 -0.8676594
## cyl  -0.8521620  1.0000000  0.9020329  0.8324475 -0.69993811  0.7824958
## disp -0.8475514  0.9020329  1.0000000  0.7909486 -0.71021393  0.8879799
## hp   -0.7761684  0.8324475  0.7909486  1.0000000 -0.44875912  0.6587479
## drat  0.6811719 -0.6999381 -0.7102139 -0.4487591  1.00000000 -0.7124406
## wt   -0.8676594  0.7824958  0.8879799  0.6587479 -0.71244065  1.0000000
## qsec  0.4186840 -0.5912421 -0.4336979 -0.7082234  0.09120476 -0.1747159
## vs    0.6640389 -0.8108118 -0.7104159 -0.7230967  0.44027846 -0.5549157
## am    0.5998324 -0.5226070 -0.5912270 -0.2432043  0.71271113 -0.6924953
## gear  0.4802848 -0.4926866 -0.5555692 -0.1257043  0.69961013 -0.5832870
## carb -0.5509251  0.5269883  0.3949769  0.7498125 -0.09078980  0.4276059
##             qsec         vs          am       gear        carb
## mpg   0.41868403  0.6640389  0.59983243  0.4802848 -0.55092507
## cyl  -0.59124207 -0.8108118 -0.52260705 -0.4926866  0.52698829
## disp -0.43369788 -0.7104159 -0.59122704 -0.5555692  0.39497686
## hp   -0.70822339 -0.7230967 -0.24320426 -0.1257043  0.74981247
## drat  0.09120476  0.4402785  0.71271113  0.6996101 -0.09078980
## wt   -0.17471588 -0.5549157 -0.69249526 -0.5832870  0.42760594
## qsec  1.00000000  0.7445354 -0.22986086 -0.2126822 -0.65624923
## vs    0.74453544  1.0000000  0.16834512  0.2060233 -0.56960714
## am   -0.22986086  0.1683451  1.00000000  0.7940588  0.05753435
## gear -0.21268223  0.2060233  0.79405876  1.0000000  0.27407284
## carb -0.65624923 -0.5696071  0.05753435  0.2740728  1.00000000

14.4 Correlations with a Heatmap

A heatmap is a powerful way to visualize correlations between variables. High correlations are typically represented with stronger colors, making patterns easier to identify.

Using the corrplot package:

# Basic heatmap using corrplot
c1 <- corrplot(cor_matrix, method = "color", addCoef.col = "black", 
         tl.col = "black", tl.cex = 0.8, number.cex = 0.7, 
         title = "Correlation Heatmap (mtcars)", mar = c(0, 0, 1, 0))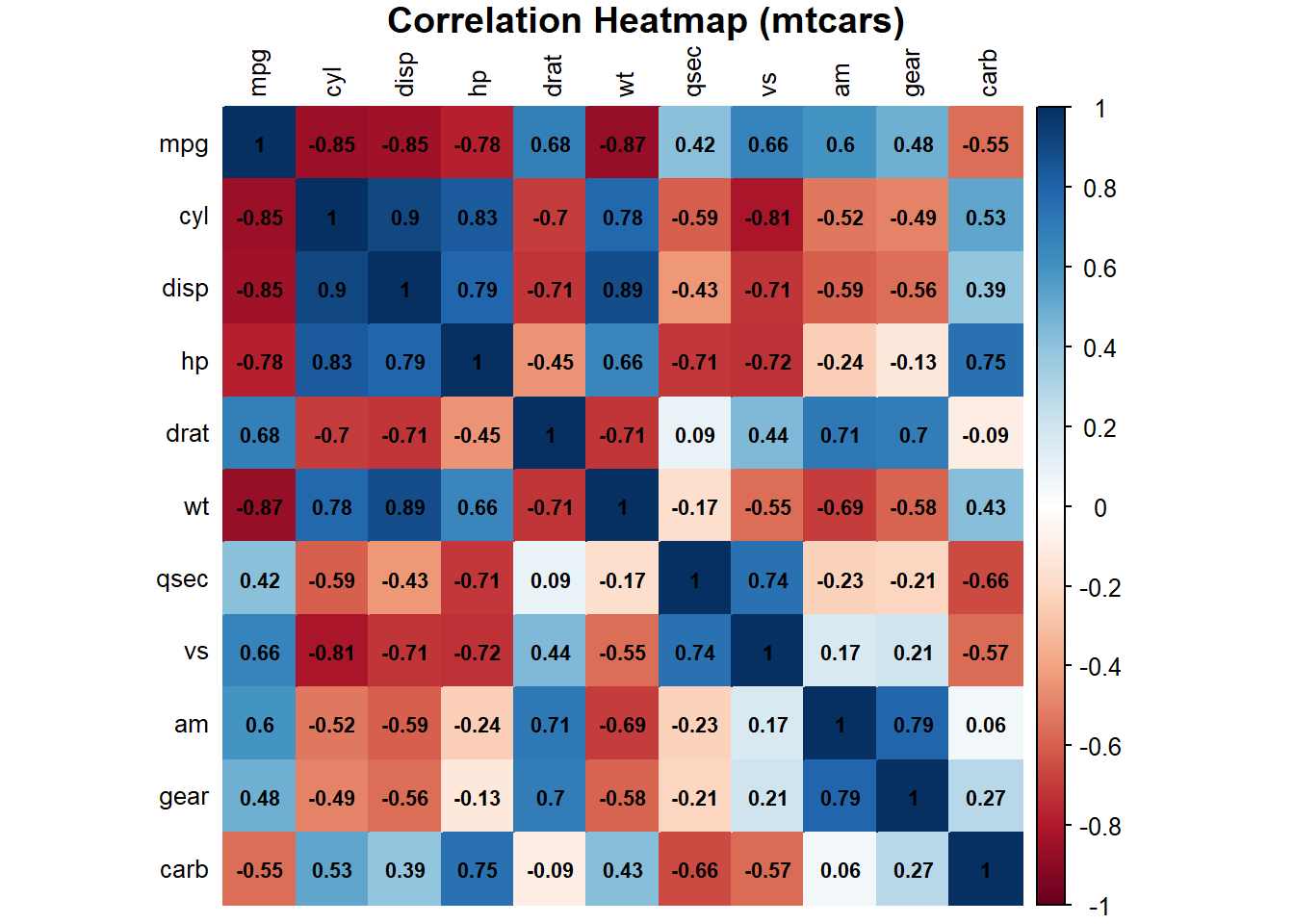

c1
## $corr
##             mpg        cyl       disp         hp        drat         wt
## mpg   1.0000000 -0.8521620 -0.8475514 -0.7761684  0.68117191 -0.8676594
## cyl  -0.8521620  1.0000000  0.9020329  0.8324475 -0.69993811  0.7824958
## disp -0.8475514  0.9020329  1.0000000  0.7909486 -0.71021393  0.8879799
## hp   -0.7761684  0.8324475  0.7909486  1.0000000 -0.44875912  0.6587479
## drat  0.6811719 -0.6999381 -0.7102139 -0.4487591  1.00000000 -0.7124406
## wt   -0.8676594  0.7824958  0.8879799  0.6587479 -0.71244065  1.0000000
## qsec  0.4186840 -0.5912421 -0.4336979 -0.7082234  0.09120476 -0.1747159
## vs    0.6640389 -0.8108118 -0.7104159 -0.7230967  0.44027846 -0.5549157
## am    0.5998324 -0.5226070 -0.5912270 -0.2432043  0.71271113 -0.6924953
## gear  0.4802848 -0.4926866 -0.5555692 -0.1257043  0.69961013 -0.5832870
## carb -0.5509251  0.5269883  0.3949769  0.7498125 -0.09078980  0.4276059
##             qsec         vs          am       gear        carb
## mpg   0.41868403  0.6640389  0.59983243  0.4802848 -0.55092507
## cyl  -0.59124207 -0.8108118 -0.52260705 -0.4926866  0.52698829
## disp -0.43369788 -0.7104159 -0.59122704 -0.5555692  0.39497686
## hp   -0.70822339 -0.7230967 -0.24320426 -0.1257043  0.74981247
## drat  0.09120476  0.4402785  0.71271113  0.6996101 -0.09078980
## wt   -0.17471588 -0.5549157 -0.69249526 -0.5832870  0.42760594
## qsec  1.00000000  0.7445354 -0.22986086 -0.2126822 -0.65624923
## vs    0.74453544  1.0000000  0.16834512  0.2060233 -0.56960714
## am   -0.22986086  0.1683451  1.00000000  0.7940588  0.05753435
## gear -0.21268223  0.2060233  0.79405876  1.0000000  0.27407284
## carb -0.65624923 -0.5696071  0.05753435  0.2740728  1.00000000
## 
## $corrPos
##     xName yName  x  y        corr
## 1     mpg   mpg  1 11  1.00000000
## 2     mpg   cyl  1 10 -0.85216196
## 3     mpg  disp  1  9 -0.84755138
## 4     mpg    hp  1  8 -0.77616837
## 5     mpg  drat  1  7  0.68117191
## 6     mpg    wt  1  6 -0.86765938
## 7     mpg  qsec  1  5  0.41868403
## 8     mpg    vs  1  4  0.66403892
## 9     mpg    am  1  3  0.59983243
## 10    mpg  gear  1  2  0.48028476
## 11    mpg  carb  1  1 -0.55092507
## 12    cyl   mpg  2 11 -0.85216196
## 13    cyl   cyl  2 10  1.00000000
## 14    cyl  disp  2  9  0.90203287
## 15    cyl    hp  2  8  0.83244745
## 16    cyl  drat  2  7 -0.69993811
## 17    cyl    wt  2  6  0.78249579
## 18    cyl  qsec  2  5 -0.59124207
## 19    cyl    vs  2  4 -0.81081180
## 20    cyl    am  2  3 -0.52260705
## 21    cyl  gear  2  2 -0.49268660
## 22    cyl  carb  2  1  0.52698829
## 23   disp   mpg  3 11 -0.84755138
## 24   disp   cyl  3 10  0.90203287
## 25   disp  disp  3  9  1.00000000
## 26   disp    hp  3  8  0.79094859
## 27   disp  drat  3  7 -0.71021393
## 28   disp    wt  3  6  0.88797992
## 29   disp  qsec  3  5 -0.43369788
## 30   disp    vs  3  4 -0.71041589
## 31   disp    am  3  3 -0.59122704
## 32   disp  gear  3  2 -0.55556920
## 33   disp  carb  3  1  0.39497686
## 34     hp   mpg  4 11 -0.77616837
## 35     hp   cyl  4 10  0.83244745
## 36     hp  disp  4  9  0.79094859
## 37     hp    hp  4  8  1.00000000
## 38     hp  drat  4  7 -0.44875912
## 39     hp    wt  4  6  0.65874789
## 40     hp  qsec  4  5 -0.70822339
## 41     hp    vs  4  4 -0.72309674
## 42     hp    am  4  3 -0.24320426
## 43     hp  gear  4  2 -0.12570426
## 44     hp  carb  4  1  0.74981247
## 45   drat   mpg  5 11  0.68117191
## 46   drat   cyl  5 10 -0.69993811
## 47   drat  disp  5  9 -0.71021393
## 48   drat    hp  5  8 -0.44875912
## 49   drat  drat  5  7  1.00000000
## 50   drat    wt  5  6 -0.71244065
## 51   drat  qsec  5  5  0.09120476
## 52   drat    vs  5  4  0.44027846
## 53   drat    am  5  3  0.71271113
## 54   drat  gear  5  2  0.69961013
## 55   drat  carb  5  1 -0.09078980
## 56     wt   mpg  6 11 -0.86765938
## 57     wt   cyl  6 10  0.78249579
## 58     wt  disp  6  9  0.88797992
## 59     wt    hp  6  8  0.65874789
## 60     wt  drat  6  7 -0.71244065
## 61     wt    wt  6  6  1.00000000
## 62     wt  qsec  6  5 -0.17471588
## 63     wt    vs  6  4 -0.55491568
## 64     wt    am  6  3 -0.69249526
## 65     wt  gear  6  2 -0.58328700
## 66     wt  carb  6  1  0.42760594
## 67   qsec   mpg  7 11  0.41868403
## 68   qsec   cyl  7 10 -0.59124207
## 69   qsec  disp  7  9 -0.43369788
## 70   qsec    hp  7  8 -0.70822339
## 71   qsec  drat  7  7  0.09120476
## 72   qsec    wt  7  6 -0.17471588
## 73   qsec  qsec  7  5  1.00000000
## 74   qsec    vs  7  4  0.74453544
## 75   qsec    am  7  3 -0.22986086
## 76   qsec  gear  7  2 -0.21268223
## 77   qsec  carb  7  1 -0.65624923
## 78     vs   mpg  8 11  0.66403892
## 79     vs   cyl  8 10 -0.81081180
## 80     vs  disp  8  9 -0.71041589
## 81     vs    hp  8  8 -0.72309674
## 82     vs  drat  8  7  0.44027846
## 83     vs    wt  8  6 -0.55491568
## 84     vs  qsec  8  5  0.74453544
## 85     vs    vs  8  4  1.00000000
## 86     vs    am  8  3  0.16834512
## 87     vs  gear  8  2  0.20602335
## 88     vs  carb  8  1 -0.56960714
## 89     am   mpg  9 11  0.59983243
## 90     am   cyl  9 10 -0.52260705
## 91     am  disp  9  9 -0.59122704
## 92     am    hp  9  8 -0.24320426
## 93     am  drat  9  7  0.71271113
## 94     am    wt  9  6 -0.69249526
## 95     am  qsec  9  5 -0.22986086
## 96     am    vs  9  4  0.16834512
## 97     am    am  9  3  1.00000000
## 98     am  gear  9  2  0.79405876
## 99     am  carb  9  1  0.05753435
## 100  gear   mpg 10 11  0.48028476
## 101  gear   cyl 10 10 -0.49268660
## 102  gear  disp 10  9 -0.55556920
## 103  gear    hp 10  8 -0.12570426
## 104  gear  drat 10  7  0.69961013
## 105  gear    wt 10  6 -0.58328700
## 106  gear  qsec 10  5 -0.21268223
## 107  gear    vs 10  4  0.20602335
## 108  gear    am 10  3  0.79405876
## 109  gear  gear 10  2  1.00000000
## 110  gear  carb 10  1  0.27407284
## 111  carb   mpg 11 11 -0.55092507
## 112  carb   cyl 11 10  0.52698829
## 113  carb  disp 11  9  0.39497686
## 114  carb    hp 11  8  0.74981247
## 115  carb  drat 11  7 -0.09078980
## 116  carb    wt 11  6  0.42760594
## 117  carb  qsec 11  5 -0.65624923
## 118  carb    vs 11  4 -0.56960714
## 119  carb    am 11  3  0.05753435
## 120  carb  gear 11  2  0.27407284
## 121  carb  carb 11  1  1.00000000
## 
## $arg
## $arg$type
## [1] "full"

Using the pheatmap package for clustering:

# Heatmap with hierarchical clustering
c2 <- pheatmap(cor_matrix, 
         display_numbers = TRUE, 
         color = colorRampPalette(c("blue", "white", "red"))(50),
         fontsize = 10, 
         main = "Correlation Heatmap with Clustering")

c2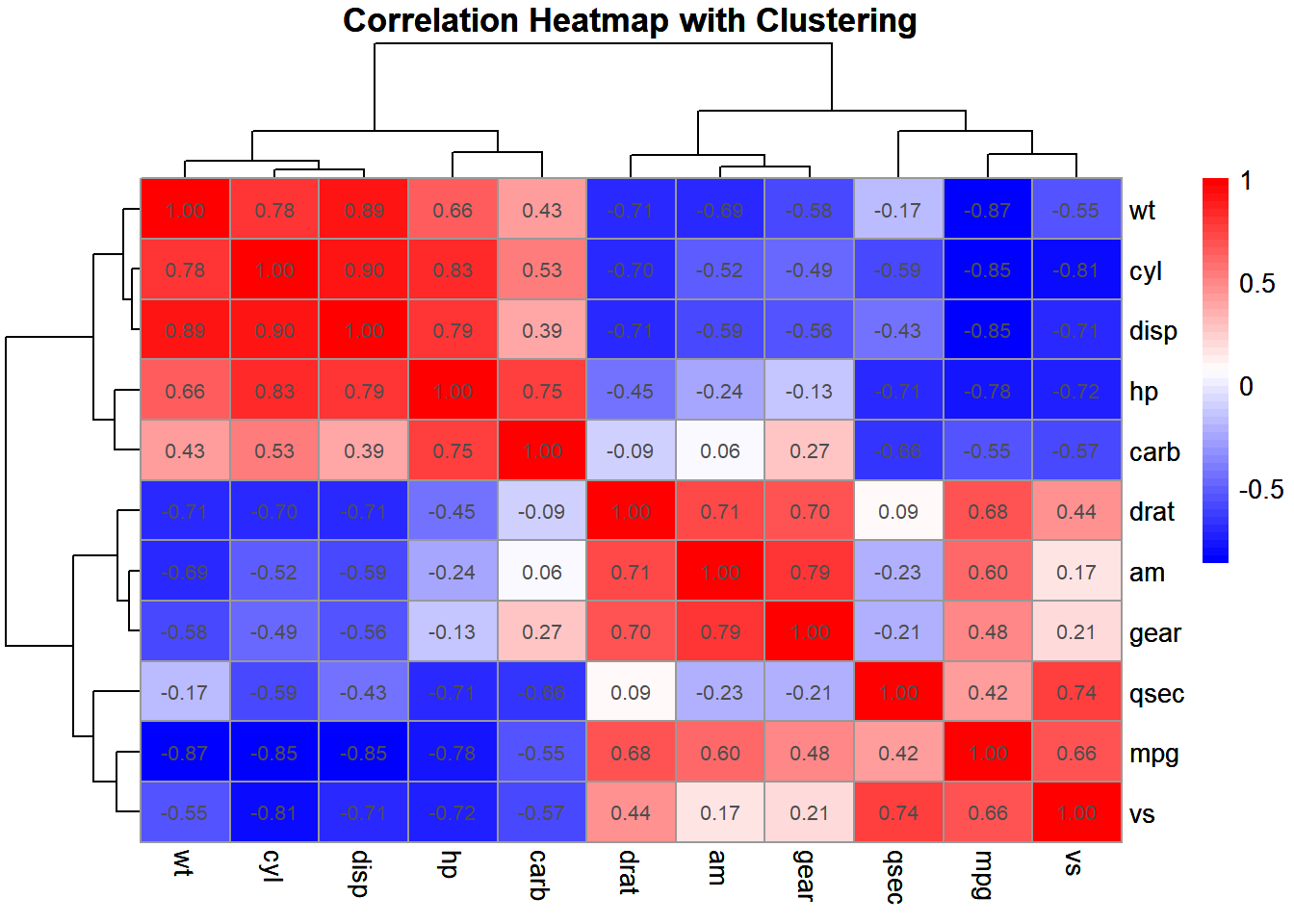

14.4.1 Interpreting the Results

  • Positive Correlations: Variables that increase together. For instance, in the mtcars dataset, disp (engine displacement) and wt (weight) may show a strong positive correlation.

  • Negative Correlations: Variables that move inversely. For example, mpg (miles per gallon) might have a negative correlation with wt.

  • Clusters: Groups of variables that are highly correlated with each other. These clusters can reveal underlying relationships, such as similar chemical properties or sensory profiles in food science.

14.5 Summary

Correlation analysis and heatmap visualization are powerful tools for understanding complex datasets in food science. By identifying relationships between variables, researchers can derive actionable insights, optimize processes, and improve product quality.

Try applying these techniques to your own datasets, whether analyzing chemical compositions, sensory data, or production parameters, and unlock valuable patterns hidden in the data.