Acknowledgement: 본 절의 구성에는 다음 교재를 발췌하였다.
주 출처
김양진 (2020). R과 SAS를 활용한 경시적 자료분석. 자유아카데미. - 4장 선형혼합모형
보조 출처
이근백 (2022). 경시적 자료분석 - R 활용. 자유아카데미. - 5장 연속형 경시적 자료분석을 위한 선형혼합모형
선형 혼합 모형 이론
개요
선형 혼합 모형은 개체마다 반복횟수가 다른 것을 허용한다는 점에서 유용하다.
Laird and Ware(1982)에 의해 처음 제안되었다.
이제 다룰 자료의 형태는 다음과 같다.
1
\(y_{11}\) \(t_{11}\) \(x_{111}\) \(\ldots\) \(x_{11 p}\)
1
\(y_{12}\) \(t_{12}\) \(x_{121}\) \(\ldots\) \(x_{12 p}\)
\(\vdots\) \(\vdots\) \(\vdots\) \(\vdots\) \(\vdots\) \(\vdots\)
\(\vdots\) \(\vdots\) \(\vdots\) \(\vdots\) \(\vdots\) \(\vdots\)
\(n\) \(y_{n m_{n}}\) \(t_{n m_{n}}\) \(x_{n m_{n} 1}\) \(\cdots\) \(x_{n m_{2} p}\)
모형식: random intercept model
개체 \(i\) 에 대한 관찰 횟수가 \(m_i\) 번이라고 하자. 공변량 \(x_{ij}\) 로는 설명되지 않지만 개체 공통의 효과가 있다고 가정하고 싶은 경우, 아래와 같은 확률 모형을 고려할 수 있다.
\[
y_{ij}= \beta_0 + {\bf x}_{ij}^T \boldsymbol{\beta} + b_i + \epsilon_{ij}, \quad j=1,\ldots, m_i, \quad i=1, \ldots, N
\] - 행렬/벡터 표현:
\[
{\bf y}_i = {\bf X}_i \boldsymbol{\beta} + {\bf 1}b_i + \boldsymbol{\epsilon}_i, \quad i=1, \cdots, N
\]
여기서, 아래처럼 \(b_i\) 가 모수(parameter)가 아닌 확률변수임을 가정할 경우 random intercept model이 된다:
\[
\begin{aligned}
E(b_i) = 0, \qquad & {\rm Var}(b_i) = \rho^2, \\
E(\epsilon_{ij}) = 0, \qquad & {\rm Var}(\epsilon_{ij}) = \sigma^2, \\
b_i~~ {\rm iid}, ~~ \epsilon_{ij} ~~ {\rm iid}, & \quad b_i \perp \epsilon_{ij}
\end{aligned}
\]
사실 위 모형은 general linear model에서 오차항의 분산-공분산 행렬에 compound symmetry model을 가정하는 것과 동치이다. 왜냐 하면, \({\bf y}_i := (y_{i1}, y_{i2}, \ldots, y_{im_i}^T)\) 에 대해,
\[
{\rm Var}({\bf y}_i ) = {\rm Var}({\bf X}_i \boldsymbol{\beta} + {\bf 1}b_i + \boldsymbol{\epsilon}_i) = {\rm Var}\left( {\bf 1}b_i + \boldsymbol{\epsilon}_i \right) =
\] \[
\rho^2 {\bf 1} {\bf 1}^T + \sigma^2{\bf I} =
\begin{bmatrix} \rho^2 + \sigma^2 & \rho^2 &\cdots & \rho^2 \\ \rho^2 & \rho^2 + \sigma^2 & \cdots & \rho^2 \\ \vdots & \vdots & \ddots & \vdots \\ \rho^2 & \rho^2 & \cdots & \rho^2 + \sigma^2 \end{bmatrix}.
\]
모형식: 일반화
위 random intercept model은 아래의 일반적인 선형혼합모형 식에서 \({\bf z}_{ij} = 1\) , \({\bf u}_{i} = b_i\) 인 사례에 해당한다:
\[
y_{ij}= \beta_0 + {\bf x}_{ij}^T \boldsymbol{\beta} + {\bf z}_{ij}^T {\bf u}_{i} + \epsilon_{ij}, \quad j=1,\ldots, m_i, \quad i=1, \cdots, N
\]
\[
{\bf y}_i = {\bf X}_i \boldsymbol{\beta} + {\bf Z}_i {\bf u}_{i} + \boldsymbol{\epsilon}_i, \quad i=1, \cdots, N
\]
\[
\begin{aligned}
E({\bf u}_i) = {\bf 0}, \qquad & {\rm Var}({\bf u}_i) = {\bf R}_i, \\
E(\boldsymbol{\epsilon}_i) = {\bf 0}, \qquad & {\rm Var}(\boldsymbol{\epsilon}_i) = {\bf \Sigma}_i, \\
{\bf u}_i ~~ {\rm iid}, ~~ \boldsymbol{\epsilon}_i ~~ {\rm iid}, & \quad {\bf u}_i \perp \boldsymbol{\epsilon}_i
\end{aligned}
\] - 여기서 \({\bf R}_i\) 과 \({\bf \Sigma}_i\) 에 대하여는 \(\rho^2 {\bf I}\) , \(\sigma^2 {\bf I}\) 등의 간단한 가정이 보통 주입되나, 원리적으로는 더 복잡한 공분산 고려도 고려할 수 있다. (가령 \({\bf \Sigma}\) 에 시간적인 효과를 넣어 AR(1) 등을 고려할 수 있다.) - nlme 라이브러리의 lme 함수 기준으로, \({\rm Var}({\bf u}_i) = {\bf R}_i\) 의 모델링은 lme(... random=XXX)에서 지원하고, \({\rm Var}(\boldsymbol{\epsilon}_i) = {\bf \Sigma}_i\) 의 모델링은 lme(... correlation=XXX)에서 지원한다. 아래 자료분석 예제에서 다시 언급하겠다. - 반응변수 공분산 구조:
\[
{\rm Var}({\bf y}_i ) = {\rm Var}({\bf X}_i \boldsymbol{\beta} + {\bf Z}_i{\bf u}_i + \boldsymbol{\epsilon}_i) = {\rm Var}\left( {\bf Z}_i{\bf u}_i + \boldsymbol{\epsilon}_i \right) = {\bf Z}_i^T {\bf R}_i {\bf Z}_i + {\bf \Sigma}_i
\] \[
\rho^2 {\bf 1} {\bf 1}^T + \sigma^2{\bf I} =
\begin{bmatrix} \rho^2 + \sigma^2 & \rho^2 &\cdots & \rho^2 \\ \rho^2 & \rho^2 + \sigma^2 & \cdots & \rho^2 \\ \vdots & \vdots & \ddots & \vdots \\ \rho^2 & \rho^2 & \cdots & \rho^2 + \sigma^2 \end{bmatrix}.
\]
모수 \(\boldsymbol{\beta}\) , \({\bf R}_i\) 과 \({\bf \Sigma}_i\) 의 추정
\({\bf R}_i\) 과 \({\bf \Sigma}_i\) 이 간단한 구조인 경우, 이전 장에서 언급한 최대가능도 방법(maximum likelihood method) 또는 제한된 최대가능도방법 (restricted maximum likelkhood method; REML)을 사용한다.\({\bf R}_i\) 과 \({\bf \Sigma}_i\) 의 구조가 복잡해지면 추가적인 계산적 복잡함이 존재한다. (즉 더 오래 걸린다)
random effect \({\bf U}_i\) 의 예측값
\({\bf U}_i\) 는 확률변수이지 unknown fixed value가 아니기 때문에, “추정값”이라는 개념이 따로 존재하지는 않는다.다만 \(E({\bf U}_i | X_i)\) 은 unknown fixed value이므로 추정이 가능하고, 이를 \({\bf U}_i\) 의 예측값으로 사용한다. 자세한 식은 생략하나, 대부분의 라이브러리에서 지원한다.
자료 분석 예제
Recall: 가문비나무 성장 곡선 자료
연구 목적: 오존이 식물의 성장에 미치는 영향을 조사
\(N=79\) 측정 시점: 152일(baseline), 174, 201, 227, 258일
반응변수: \(\log \left(h d^{2}\right)\) , \(h\) 는 키, \(d\) 는 지름
실험군은 1번-54번(오존 노출) ,대조군은 55번-79번(오존 비노출)
= read.table ("data/spruce_data.txt" , col.names= c ("day152" , "day174" , "day201" , "day227" , "day258" ))head (spruce)
day152 day174 day201 day227 day258
1 4.515 4.982 5.408 5.903 6.145
2 4.235 4.199 4.683 4.915 4.957
3 3.980 4.364 4.792 4.986 5.032
4 4.357 4.772 5.098 5.298 5.356
5 4.340 4.953 5.423 5.974 6.276
6 4.586 5.081 5.362 5.764 5.995
= (1 : 79 )= as.data.frame (cbind (id,spruce))library (reshape2)= melt (spruce2, id= "id" )$ trt = ifelse (spruce3$ id < 55 , 1 , 0 )names (spruce3) = c ("id" ,"time" ,"growth" , "trt" )print (spruce3[1 : 10 ,])
id time growth trt
1 1 day152 4.515 1
2 2 day152 4.235 1
3 3 day152 3.980 1
4 4 day152 4.357 1
5 5 day152 4.340 1
6 6 day152 4.586 1
7 7 day152 4.406 1
8 8 day152 4.243 1
9 9 day152 4.815 1
10 10 day152 3.840 1
'data.frame': 395 obs. of 4 variables:
$ id : int 1 2 3 4 5 6 7 8 9 10 ...
$ time : Factor w/ 5 levels "day152","day174",..: 1 1 1 1 1 1 1 1 1 1 ...
$ growth: num 4.51 4.24 3.98 4.36 4.34 ...
$ trt : num 1 1 1 1 1 1 1 1 1 1 ...
$ id = as.factor (spruce3$ id)$ trt = as.factor (spruce3$ trt)str (spruce3)
'data.frame': 395 obs. of 4 variables:
$ id : Factor w/ 79 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
$ time : Factor w/ 5 levels "day152","day174",..: 1 1 1 1 1 1 1 1 1 1 ...
$ growth: num 4.51 4.24 3.98 4.36 4.34 ...
$ trt : Factor w/ 2 levels "0","1": 2 2 2 2 2 2 2 2 2 2 ...
Random intercept (임의 절편) 모형
R 패키지에서 lme4에서 제공되는 lmer 함수를 사용하자.
이번 분석에서는 모든 공변량(시간(time)과 처리(trt))를 질적인 범주형 변수로 간주해본다.
모형식:
\[
\begin{aligned}
\log (y_{i j}) & =\beta_{0}+\beta_{11} \mathbb{I}(t_{i j}={\rm day}_{174})+\beta_{12} \mathbb{I} (t_{i j}=\operatorname{day}_{201})+\beta_{13} \mathbb{I} (t_{i j}={\rm day}_{227})+\beta_{14} \mathbb{I} (t_{i j}={\rm day}_{258}) \\
& +\beta_{2} \mathbb{I} ({\rm trt}_{i})+\beta_{21} \mathbb{I} (t_{i j}={\rm day}_{174}) \mathbb{I} ({\rm trt}_{i}) + \beta_{22} \mathbb{I} (t_{i j}={\rm day}_{201}) \mathbb{I} ({\rm trt}_{i}) \\
& +\beta_{23} \mathbb{I} (t_{i j}={\rm day}_{227}) \mathbb{I} ({\rm trt}_{i})+\beta_{24} \mathbb{I} (t_{i j}={\rm day}_{258}) \mathbb{I} ({\rm trt}_{i})+b_{i}+\epsilon_{i j}
\end{aligned}
\]
위 모형의 회귀계수를 설명하기 전에 교호작용의 유의성을 먼저 검정해 보자. (\(H_0: \beta_{21} = \beta_{22} = \beta_{23} = \beta_{24} = 0\) )
아래 스크립트에서 mod11 은 교호작용을 포함한 모형, mod21 는 교호작용이 제거된 축소 모형(nested model)이다. \(b_i\) 를 모형에 더하는 방법은 (1|id)이다.
이 두모형의 가능도값을 비교하는 방식으로 \(H_0\) 에 대한 검정이 가능하다. (“가능도비 검정(likelihood ratio test)”이라 한다.) 가능도비 검정은 anova(mod11,mod21) 함수로 가능하다.
원리상 ML 방법을 이용해 fitting 했을때만 가능도비 검정이 지원되고 REML 방법에 대해서는 지원되지 않는다. anova 함수가 알아서 ML 방법으로 재적합 해준다. (출력 메시지 참고)
출력 화면 우측 아래의 p값 0.02221로부터, 유의수준 5%에서 귀무가설 \(H_0\) 을 기각할 수 있다. 즉 교호작용이 유의함을 알 수 있다.
Loading required package: Matrix
= lmer (log (growth) ~ time + trt + time* trt + (1 | id), data= spruce3)#summary(mod11) = lmer (log (growth) ~ time + trt + (1 | id), data= spruce3)#summary(mod21) anova (mod11,mod21)
refitting model(s) with ML (instead of REML)
Data: spruce3
Models:
mod21: log(growth) ~ time + trt + (1 | id)
mod11: log(growth) ~ time + trt + time * trt + (1 | id)
npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
mod21 8 -1072.9 -1041.0 544.44 -1088.9
mod11 12 -1076.3 -1028.5 550.15 -1100.3 11.421 4 0.02221 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
그러면 교호작용이 포함된 모형에 해당되는 회귀계수를 해석해 보자.
nlme 패키지의 lme 함수를 이용하자. 문법이 약간 다름에 주의하라.
위에서 작동시켰던 lme4 라이브러리의 lmer 함수는 p값을 제공하지 않는다.
Attaching package: 'nlme'
The following object is masked from 'package:lme4':
lmList
= lme (log (growth) ~ time + trt + time* trt, random= ~ 1 | id, data= spruce3)summary (mod1)
Linear mixed-effects model fit by REML
Data: spruce3
AIC BIC logLik
-1002.532 -955.0932 513.266
Random effects:
Formula: ~1 | id
(Intercept) Residual
StdDev: 0.1346122 0.04073224
Fixed effects: log(growth) ~ time + trt + time * trt
Value Std.Error DF t-value p-value
(Intercept) 1.4072489 0.02812796 308 50.03025 0.0000
timeday174 0.1125474 0.01152082 308 9.76905 0.0000
timeday201 0.2002952 0.01152082 308 17.38550 0.0000
timeday227 0.2780214 0.01152082 308 24.13209 0.0000
timeday258 0.3170184 0.01152082 308 27.51700 0.0000
trt1 -0.0172301 0.03402161 77 -0.50645 0.6140
timeday174:trt1 -0.0145361 0.01393477 308 -1.04316 0.2977
timeday201:trt1 -0.0186735 0.01393477 308 -1.34007 0.1812
timeday227:trt1 -0.0302962 0.01393477 308 -2.17414 0.0305
timeday258:trt1 -0.0439608 0.01393477 308 -3.15476 0.0018
Correlation:
(Intr) tmd174 tmd201 tmd227 tmd258 trt1 t174:1 t201:1 t227:1
timeday174 -0.205
timeday201 -0.205 0.500
timeday227 -0.205 0.500 0.500
timeday258 -0.205 0.500 0.500 0.500
trt1 -0.827 0.169 0.169 0.169 0.169
timeday174:trt1 0.169 -0.827 -0.413 -0.413 -0.413 -0.205
timeday201:trt1 0.169 -0.413 -0.827 -0.413 -0.413 -0.205 0.500
timeday227:trt1 0.169 -0.413 -0.413 -0.827 -0.413 -0.205 0.500 0.500
timeday258:trt1 0.169 -0.413 -0.413 -0.413 -0.827 -0.205 0.500 0.500 0.500
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.52693447 -0.44329125 -0.03964318 0.48673582 5.22872974
Number of Observations: 395
Number of Groups: 79
위 결과에 대한 김양진 (2020) 67쪽의 해석은 다음과 같다. (일부 표현 수정)
연구 초기 시점(153일)에는 오존 노출 그릅과 비노출 그룹의 평균 성장 정도 차이(로그 scale)는 -0.01732 이었으며 그 정도는 유의하지 않았다(t-value = -0.506, p=0.614).
각 그룹별 성장 정도를 검토해 보자.
오존 비노출군
timeday174-timeday258 변수들은 trt=0 그릅에 대한 timeday152와 비교하여 얼마나 성장했는 지와 유의성을 보여준다.
timeday174에서는 평균적으로 0.1125 만큼 성장하였으며 그 성장정도는 매우 유의하였다.
timeday201, timeday227, timeday258의 회귀계수도 비슷한 해석이 적용될 수 있다. >> 여기서 해당 계수(0.11255 < 0.2003 < 0.2780 < 0.3172)는 152일과 비교한 평균 성장 증가분을 보여 주는 것이므로, 시간이 경과할수록 큰 값을 가지는 것은 당연한 것이다. 또한 해당 추정값을 이용하여 day152부터 day258의 평균 성장을 추정할 수 있다(아래 표 참조).
오존 노출군
timeday174:trt-timeday258:trt는 비노출 그룹와 비교하여 오존 노출 그룹 \((\mathrm{trt}=1)\) 그룹 의 시간별 증감 정도를 보여 준다. 예를들어, 기저 시간대 day152에서 비노출 그룹과 노출 그룹의 차이는 trt의 회귀계수 -0.017이다.
fixed effect의 timeday 174:trt는 day174에서 비노출 그릅 (trt=0)에 비교하여 얼마나 더 성장했는지 여부와 그 유의성을 보여 준다. 즉, 오존 노출 그룹 (trt=1) 과 비노출 그룹 (trt=0)의 성장 차이는 로그 scale으로 -0.01454 이었다. 하지만 이 차이는 통계적으로 유의적인지 않았다(p=0.2977).
비슷하게 day201에서도 두 그룹의 성장 차이는 -0.0186 이었고 역시 유의적이지 않았다(p=0.1812).
하지만 day227 과 day258에서의 오존 노출 그룹과 비노출 그룹의 성장 정도는 유의적으로 차이가 남을 알 수 있다(day227 p=0.0305, day258 p=0.0018).
따라서 자료분석을 통해 두 그릅의 성장 정도(growth rate)는 연구 중반 (day 201)까지는 유의한 차이가 없었으나 그 이후에 오존 처리를 받은 나무 그룹이 정상 대기 하에서 자란 나무 그룹보다 성장이 느림을 알 수 있다.
아래 표는 위 모형에서 구한 회귀계수를 이용하여 시간별 그릅별 평균 성장을 계산하였다. 시간이 갈수록 평균간격이 점차적으로 커진다.
day152
\(1.407\) \(1.407-0.0172\)
day174
\(1.407+0.112\) \(1.407-0.0172+0.112-0.0145\)
day201
\(1.407+0.200\) \(1.407-0.0172+0.200-0.0187\)
day227
\(1.407+0.278\) \(1.407-0.0172+0.278-0.0303\)
day239
\(1.407+0.317\) \(1.407-0.0172+0.317-0.0439\)
(표: 가문비나무의 오존 처리 여부에 따른 시간별 평균 성장도)
Random intercept and random slope (임의 절편 및 임의 기울기) 모형
위 분석에서는 day를 전부 질적 확률변수로 취급하였다. 이 결과 day의 5범주가 4개의 변수로 더미 코딩되어, 최종 분석에서 총 10개의 회귀계수 (\(\beta\) )가 적합되었다.
day를 연속형으로 취급한 random effect를 삽입해 보자. \(b_{i0}\) 가 임의 절편항, \(b_{i1}t_{ij}\) 가 임의 기울기항이다.
\[
\begin{aligned}
\log (y_{i j}) & =\beta_{0}+\beta_{11} \mathbb{I}(t_{i j}={\rm day}_{174})+\beta_{12} \mathbb{I} (t_{i j}=\operatorname{day}_{201})+\beta_{13} \mathbb{I} (t_{i j}={\rm day}_{227})+\beta_{14} \mathbb{I} (t_{i j}={\rm day}_{258}) \\
& +\beta_{2} \mathbb{I} ({\rm trt}_{i})+\beta_{21} \mathbb{I} (t_{i j}={\rm day}_{174}) \mathbb{I} ({\rm trt}_{i}) + \beta_{22} \mathbb{I} (t_{i j}={\rm day}_{201}) \mathbb{I} ({\rm trt}_{i}) \\
& +\beta_{23} \mathbb{I} (t_{i j}={\rm day}_{227}) \mathbb{I} ({\rm trt}_{i})+\beta_{24} \mathbb{I} (t_{i j}={\rm day}_{258}) \mathbb{I} ({\rm trt}_{i})+b_{i0}+ b_{i1}t_{ij} + \epsilon_{i j}
\end{aligned}
\]
아래 스크립트에서 time2가 연속형으로 변환된 관측 시점을 가리킨다. time변수를 문자열로 변환한 뒤 gsub 명령문을 이용해 day를 잘라냈다.
= gsub ("day" , " " , spruce3$ time)= as.numeric (time2)$ time2 = as.numeric (time2) # time2는 연속형 변수 head (spruce3)
id time growth trt time2
1 1 day152 4.515 1 152
2 2 day152 4.235 1 152
3 3 day152 3.980 1 152
4 4 day152 4.357 1 152
5 5 day152 4.340 1 152
6 6 day152 4.586 1 152
아래 코드를 보면, mod1s는 임의 절편항 모형(mod1)과 비교했을 때 random 부분의 인풋이 달라졌다. 문법을 보면 따로 random effect 및 error term의 공분산 구조를 명시하지 않았다. 이 경우에는 따로 구조가정이 없는 모형을 적합한다.
각 개체 \(i\) 에 대해서 관측횟수가 적은 경우에 가장 손쉽게 적용할 수 있다. 관측횟수가 많아지면 공분산 구조의 명시되지 않을 경우 추정이 수학적/계산적으로 어려워질 수 있다.
mod1과의 anova를 통해 추가된 항 (임의 절편항)의 유의성을 평가할 수 있다.anova 결과를 통해, mod1보다 mod1s가 핏의 적합도가 더 좋음을 알 수 있다. (대표적인 모형 적합도 지표인 AIC, BIC 값들이 더 낮음)
= lme (log (growth) ~ time+ trt+ time* trt, random= ~ time2| id, data= spruce3)anova (mod1s,mod1)
Model df AIC BIC logLik Test L.Ratio p-value
mod1s 1 14 -1156.906 -1101.5603 592.4529
mod1 2 12 -1002.532 -955.0932 513.2660 1 vs 2 158.3737 <.0001
이제 모형 계수를 해석해 보자. 김양진 (2020) 70쪽의 해석을 인용하겠다.
Linear mixed-effects model fit by REML
Data: spruce3
AIC BIC logLik
-1156.906 -1101.56 592.4529
Random effects:
Formula: ~time2 | id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 0.251831132 (Intr)
time2 0.000759223 -0.888
Residual 0.025374547
Fixed effects: log(growth) ~ time + trt + time * trt
Value Std.Error DF t-value p-value
(Intercept) 1.4072489 0.03211281 308 43.82204 0.0000
timeday174 0.1125474 0.00791637 308 14.21705 0.0000
timeday201 0.2002952 0.01033773 308 19.37515 0.0000
timeday227 0.2780214 0.01346120 308 20.65354 0.0000
timeday258 0.3170184 0.01762315 308 17.98875 0.0000
trt1 -0.0172301 0.03884141 77 -0.44360 0.6586
timeday174:trt1 -0.0145361 0.00957509 308 -1.51812 0.1300
timeday201:trt1 -0.0186735 0.01250380 308 -1.49343 0.1363
timeday227:trt1 -0.0302962 0.01628172 308 -1.86075 0.0637
timeday258:trt1 -0.0439608 0.02131573 308 -2.06237 0.0400
Correlation:
(Intr) tmd174 tmd201 tmd227 tmd258 trt1 t174:1 t201:1 t227:1
timeday174 -0.386
timeday201 -0.562 0.618
timeday227 -0.629 0.599 0.794
timeday258 -0.661 0.570 0.799 0.881
trt1 -0.827 0.319 0.465 0.520 0.546
timeday174:trt1 0.319 -0.827 -0.511 -0.495 -0.471 -0.386
timeday201:trt1 0.465 -0.511 -0.827 -0.656 -0.660 -0.562 0.618
timeday227:trt1 0.520 -0.495 -0.656 -0.827 -0.729 -0.629 0.599 0.794
timeday258:trt1 0.546 -0.471 -0.660 -0.729 -0.827 -0.661 0.570 0.799 0.881
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.74007428 -0.40946479 0.03512045 0.37030384 4.70251638
Number of Observations: 395
Number of Groups: 79
Random effects: 다음의 결과를 보면, 두 확률변수의 상관계수는 corr(b_{i0}, b_{i1})=-0.88$ 으로 음의 값을 가지는데, 이는 랜덤 절편이 큰 나무의 기울기가 랜덤 절편이 작은 나무의 기울기보다 작음을 의미한다. 즉, 초기에 키가 큰 나무의 성장 변화가 초기에 작은 키를 가진 나무의 성장 변화보다 더 작음을 의미한다. 이러한 현상은 성장 곡선(growth curve)과 관련된 자료분석에서 자주 발생된다.
랜덤 기울기를 포함함으로써 고정효과 중 day227:trt의 효과가 유의적이지 않는 것으로 바뀌었다.
Random intercept (임의 절편) 모형에서 오차항의 상관성을 반영하기
지금까지의 분석에서는 error term \(\epsilon_{ij}\) 가 개체 \(i\) , 시점 \(j\) 에 대해 모두 독립임을 가정했다. 즉 \({\rm Var}(\boldsymbol{\epsilon}_i) = \sigma^2 {\bf I}\) 임을 가정했다. 여기서 개체 측정치 간의 상관성(개체 내 변동의 상관성)을 모형에 더 반영하기 위하여는 아래처럼, correlation=xxx 를 삽입하면 된다.
여기서 적용한 상관구조 외에도 lme 함수에서는 corARMA, corCAR1, corCompSymm, corExp, corGaus, corLin, corRatio, corSpher를 사용할 수 있다 한다. 자세한 설명은 help(lme)를 참고할 수 있다.
아래는 임의 절편에 더하여 \({\rm Var}(\boldsymbol{\epsilon}_i)\) 에 AR(1) 상관모형 및 무구조(unstructured) 모형을 적용한 결과이다.
AIC 값을 보면 둘 다 mod1보다는 낮다. 즉, 개체 내 변동의 상관성이 반영되는 것이 데이터를 더 잘 설명함을 알 수 있다.
# AR(1) 상관모형 = lme (log (growth) ~ time* trt, random= ~ 1 | id, correlation= corAR1 (),data= spruce3)summary (mod2s)
Linear mixed-effects model fit by REML
Data: spruce3
AIC BIC logLik
-1176.578 -1125.185 601.2888
Random effects:
Formula: ~1 | id
(Intercept) Residual
StdDev: 1.286214e-06 0.1487104
Correlation Structure: AR(1)
Formula: ~1 | id
Parameter estimate(s):
Phi
0.9692572
Fixed effects: log(growth) ~ time * trt
Value Std.Error DF t-value p-value
(Intercept) 1.4072489 0.02974208 308 47.31508 0.0000
timeday174 0.1125474 0.00737493 308 15.26081 0.0000
timeday201 0.2002952 0.01034926 308 19.35358 0.0000
timeday227 0.2780214 0.01257792 308 22.10393 0.0000
timeday258 0.3170184 0.01441284 308 21.99555 0.0000
trt1 -0.0172301 0.03597394 77 -0.47896 0.6333
timeday174:trt1 -0.0145361 0.00892020 308 -1.62958 0.1042
timeday201:trt1 -0.0186735 0.01251774 308 -1.49176 0.1368
timeday227:trt1 -0.0302962 0.01521337 308 -1.99142 0.0473
timeday258:trt1 -0.0439608 0.01743276 308 -2.52174 0.0122
Correlation:
(Intr) tmd174 tmd201 tmd227 tmd258 trt1 t174:1 t201:1 t227:1
timeday174 -0.124
timeday201 -0.174 0.702
timeday227 -0.211 0.569 0.810
timeday258 -0.242 0.489 0.696 0.859
trt1 -0.827 0.103 0.144 0.175 0.200
timeday174:trt1 0.103 -0.827 -0.580 -0.470 -0.404 -0.124
timeday201:trt1 0.144 -0.580 -0.827 -0.670 -0.576 -0.174 0.702
timeday227:trt1 0.175 -0.470 -0.670 -0.827 -0.710 -0.211 0.569 0.810
timeday258:trt1 0.200 -0.404 -0.576 -0.710 -0.827 -0.242 0.489 0.696 0.859
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-4.0790258 -0.4933538 0.1866468 0.6012721 1.9526748
Number of Observations: 395
Number of Groups: 79
numDF denDF F-value p-value
(Intercept) 1 308 9008.931 <.0001
time 4 308 354.755 <.0001
trt 1 77 1.260 0.2652
time:trt 4 308 1.797 0.1293
Model df AIC BIC logLik Test L.Ratio p-value
mod2s 1 13 -1176.578 -1125.1854 601.2888
mod1 2 12 -1002.532 -955.0932 513.2660 1 vs 2 176.0455 <.0001
# 무구조(unstructured) 상관모형 = lme (log (growth) ~ time* trt, random = ~ 1 | id, correlation= corSymm (), data= spruce3)summary (mod3s)
Linear mixed-effects model fit by REML
Data: spruce3
AIC BIC logLik
-1239.445 -1152.473 641.7224
Random effects:
Formula: ~1 | id
(Intercept) Residual
StdDev: 0.1428293 0.04987735
Correlation Structure: General
Formula: ~1 | id
Parameter estimate(s):
Correlation:
1 2 3 4
2 0.457
3 -0.070 0.750
4 -0.396 0.522 0.776
5 -0.474 0.468 0.699 0.922
Fixed effects: log(growth) ~ time * trt
Value Std.Error DF t-value p-value
(Intercept) 1.4072489 0.03025753 308 46.50905 0.0000
timeday174 0.1125474 0.01039366 308 10.82847 0.0000
timeday201 0.2002952 0.01459529 308 13.72327 0.0000
timeday227 0.2780214 0.01666665 308 16.68130 0.0000
timeday258 0.3170184 0.01712870 308 18.50802 0.0000
trt1 -0.0172301 0.03659739 77 -0.47080 0.6391
timeday174:trt1 -0.0145361 0.01257145 308 -1.15628 0.2485
timeday201:trt1 -0.0186735 0.01765344 308 -1.05778 0.2910
timeday227:trt1 -0.0302962 0.02015881 308 -1.50288 0.1339
timeday258:trt1 -0.0439608 0.02071768 308 -2.12190 0.0346
Correlation:
(Intr) tmd174 tmd201 tmd227 tmd258 trt1 t174:1 t201:1 t227:1
timeday174 -0.172
timeday201 -0.241 0.894
timeday227 -0.275 0.839 0.917
timeday258 -0.283 0.830 0.893 0.973
trt1 -0.827 0.142 0.199 0.228 0.234
timeday174:trt1 0.142 -0.827 -0.739 -0.694 -0.686 -0.172
timeday201:trt1 0.199 -0.739 -0.827 -0.758 -0.738 -0.241 0.894
timeday227:trt1 0.228 -0.694 -0.758 -0.827 -0.805 -0.275 0.839 0.917
timeday258:trt1 0.234 -0.686 -0.738 -0.805 -0.827 -0.283 0.830 0.893 0.973
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-4.132904562 -0.525087792 0.008529093 0.566621296 3.130291936
Number of Observations: 395
Number of Groups: 79
numDF denDF F-value p-value
(Intercept) 1 308 9323.260 <.0001
time 4 308 266.492 <.0001
trt 1 77 1.339 0.2508
time:trt 4 308 2.778 0.0271
Model df AIC BIC logLik Test L.Ratio p-value
mod3s 1 22 -1239.445 -1152.4735 641.7224
mod1 2 12 -1002.532 -955.0932 513.2660 1 vs 2 256.9128 <.0001
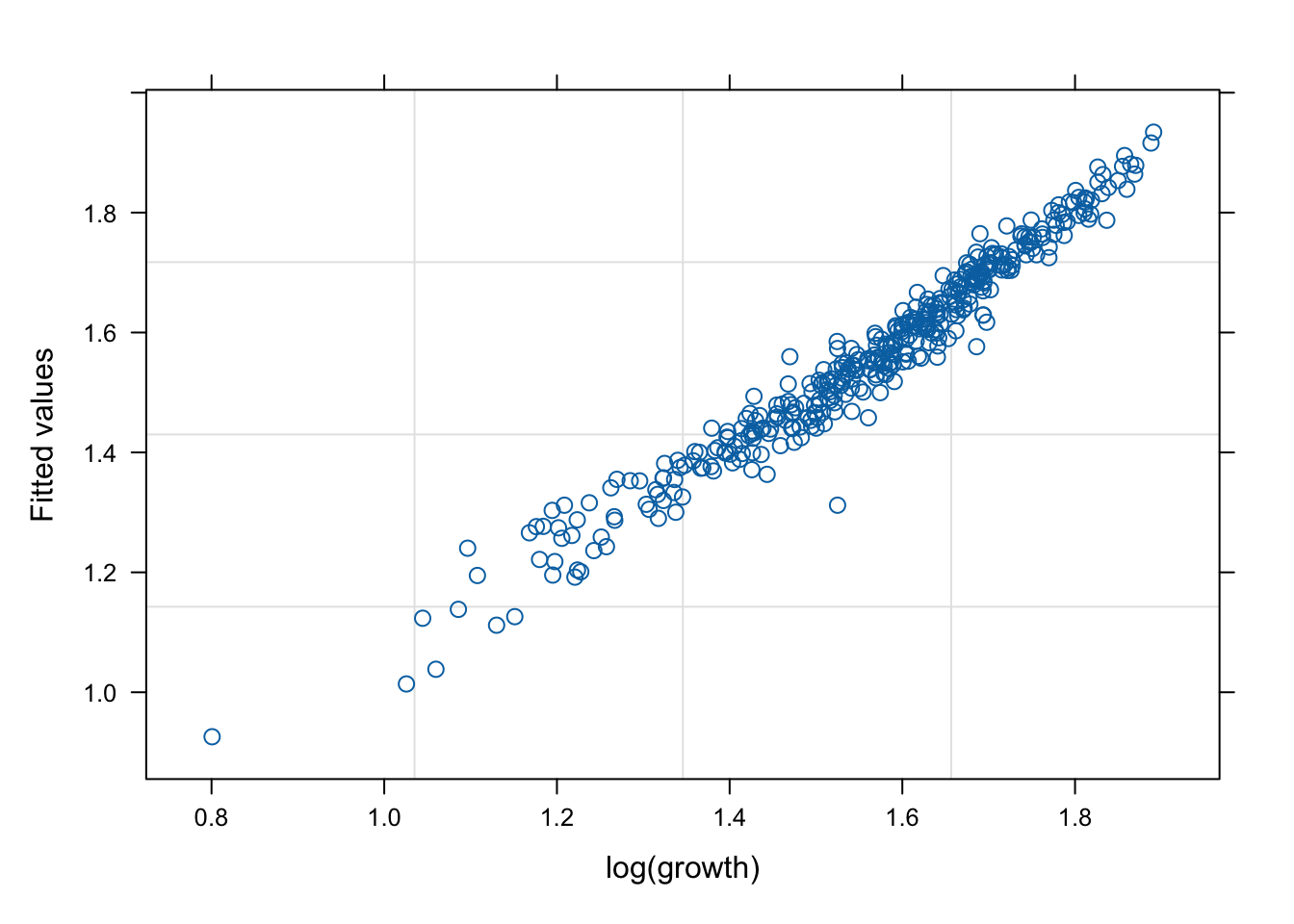
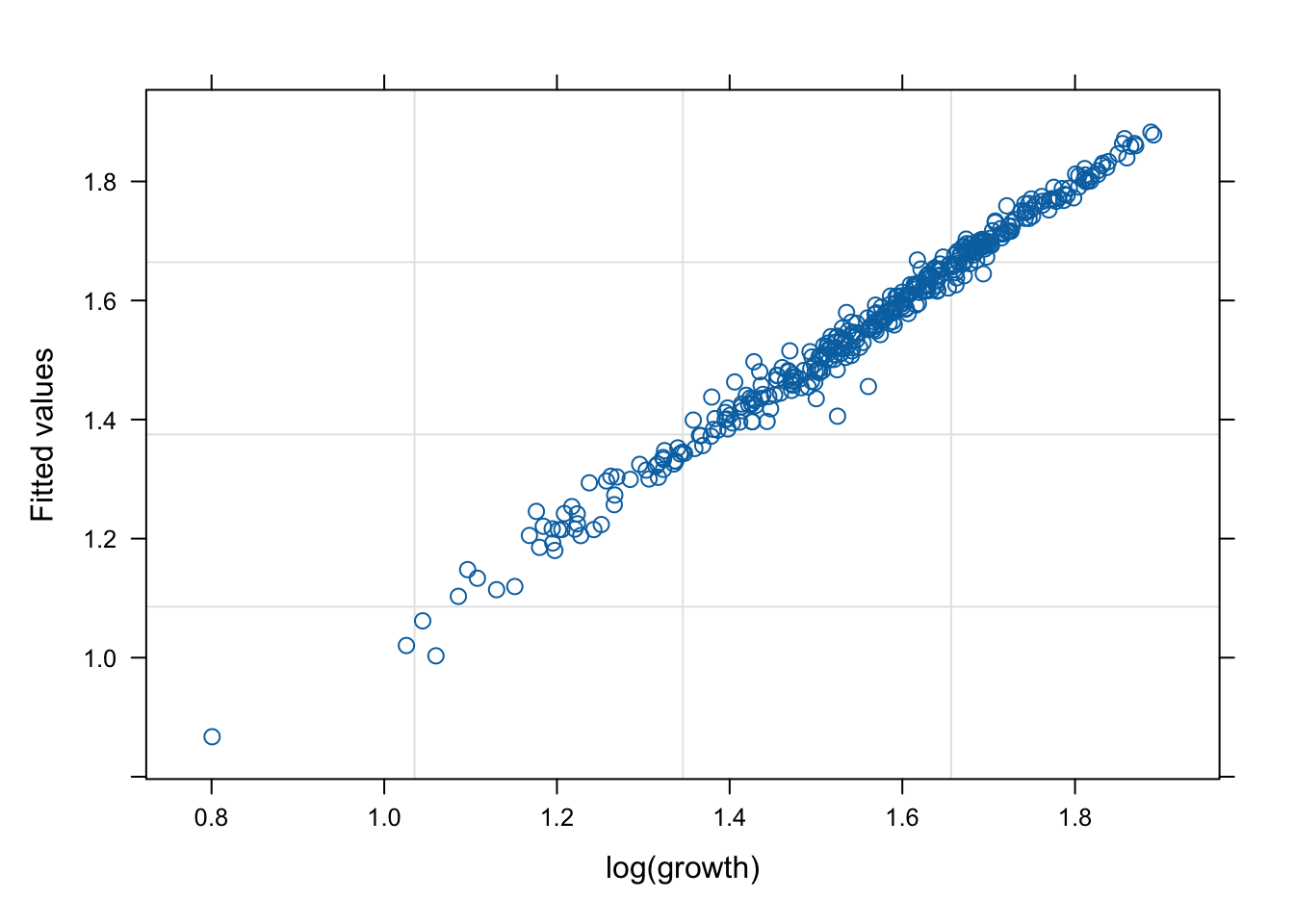
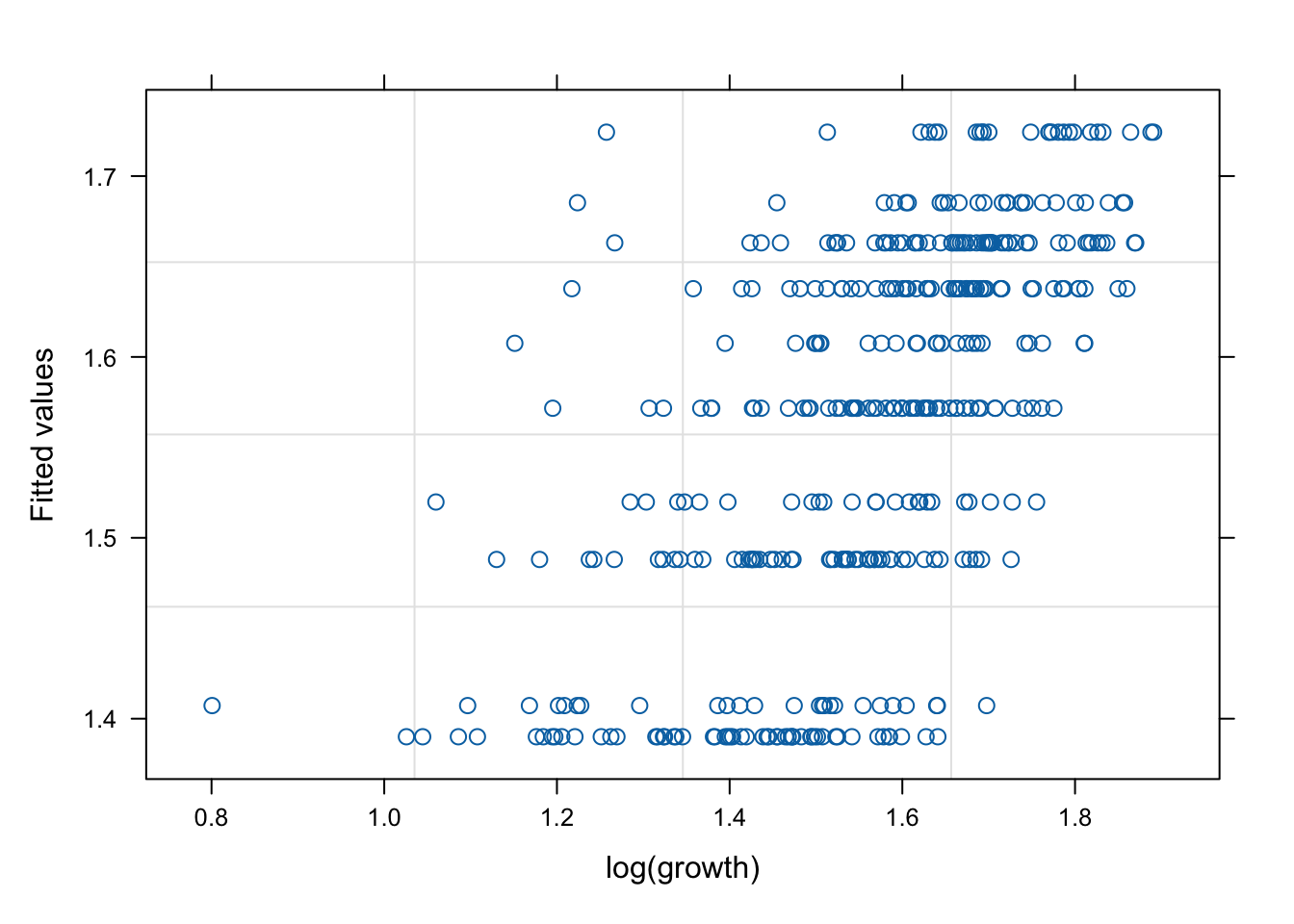
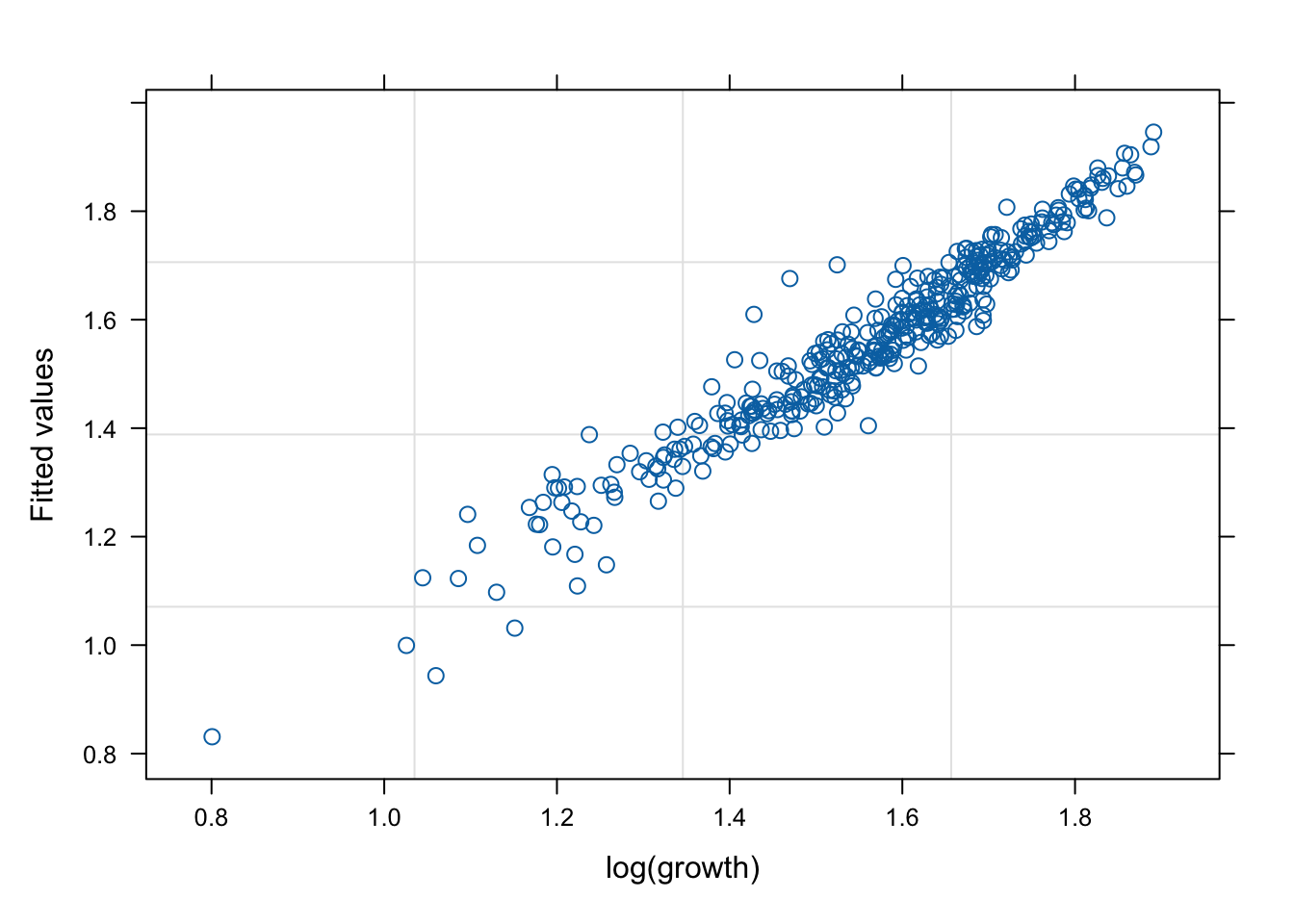
네 모형의 적합 정도 비교 시각화
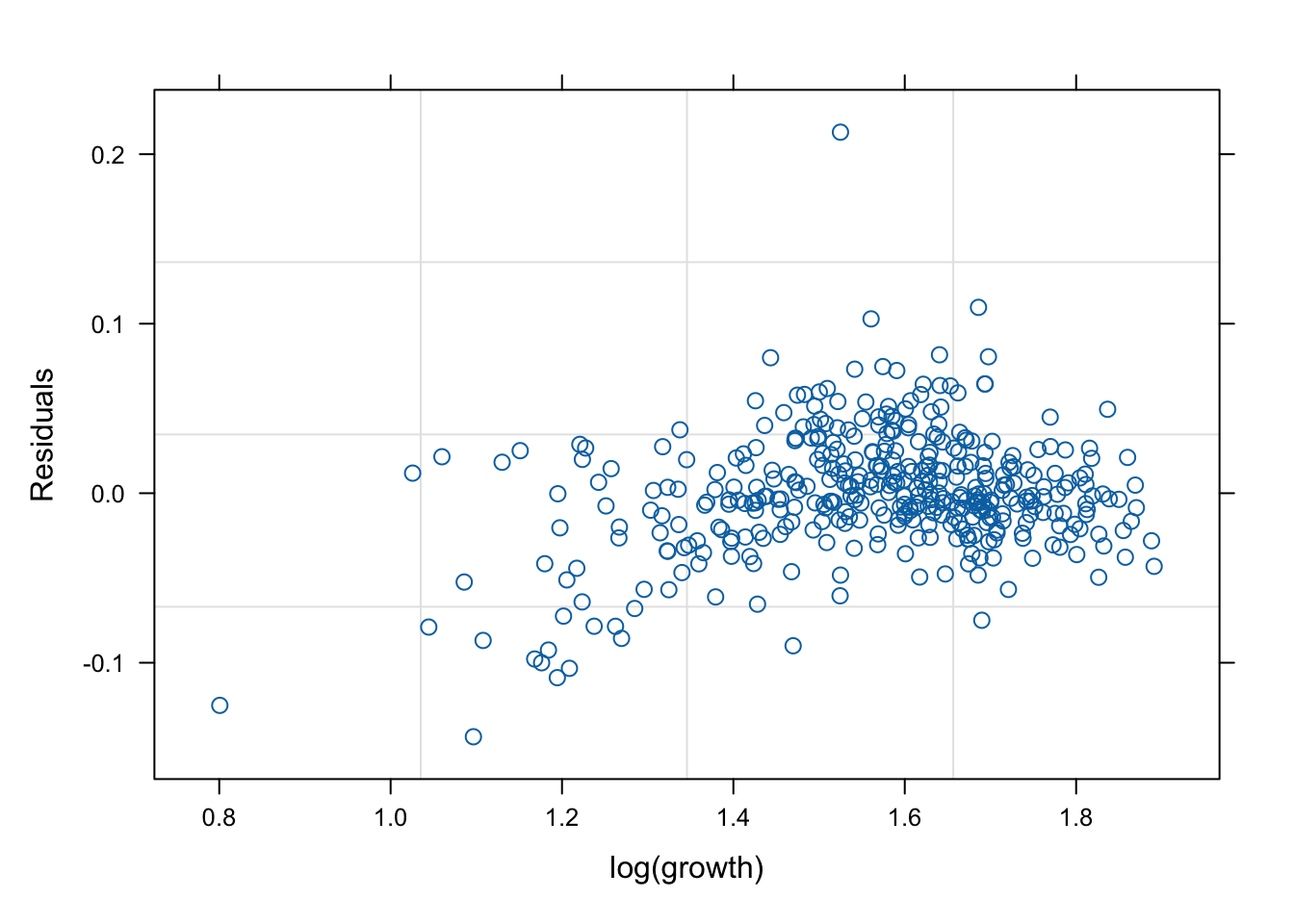
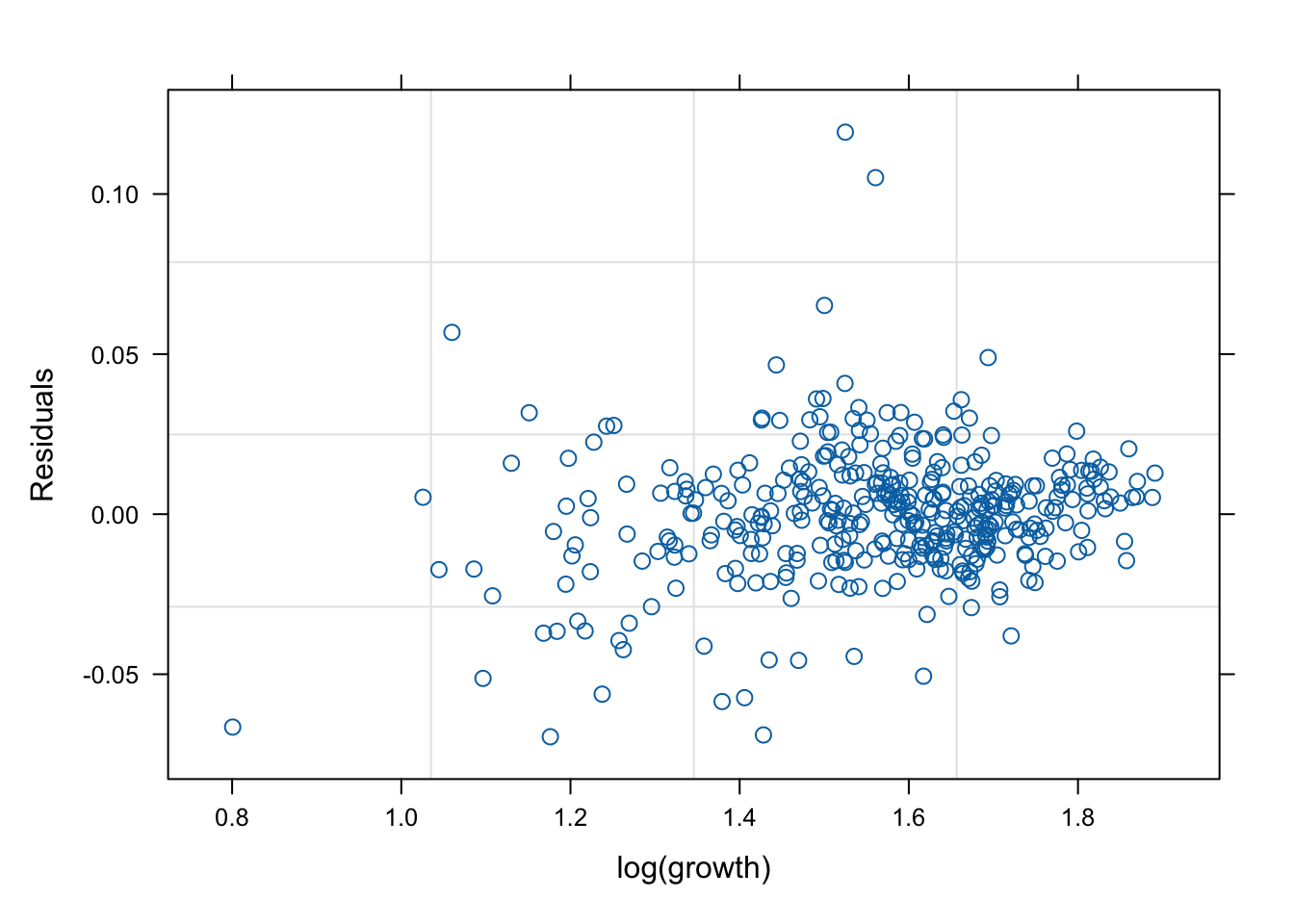
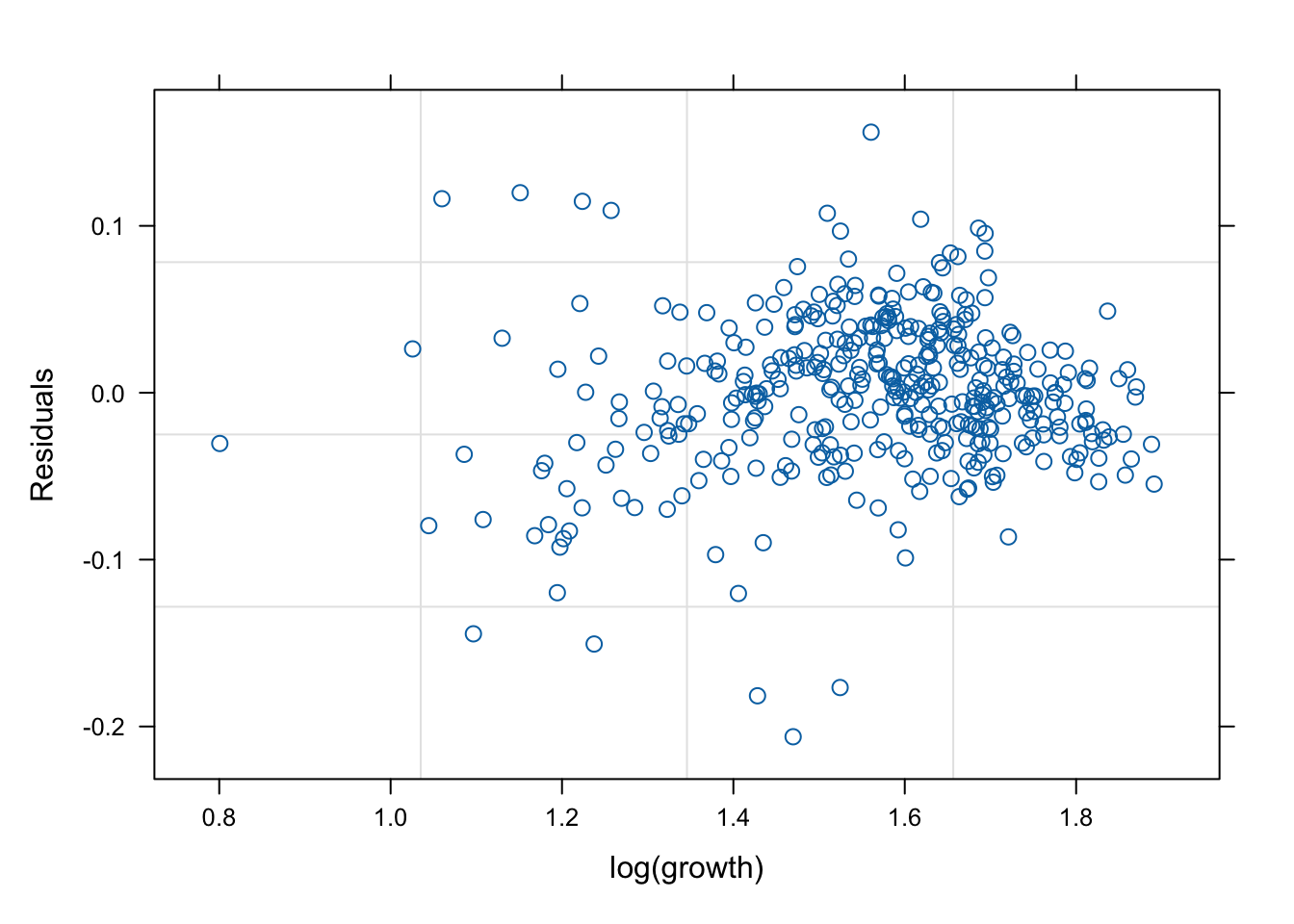
잔차(residual, \(\hat{y}\) ) vs. 반응변수(response, \(y\) )의 관계를 살펴 보자. 모형 가정이 맞다면, 둘은 독립적으로 행동하여야 한다.
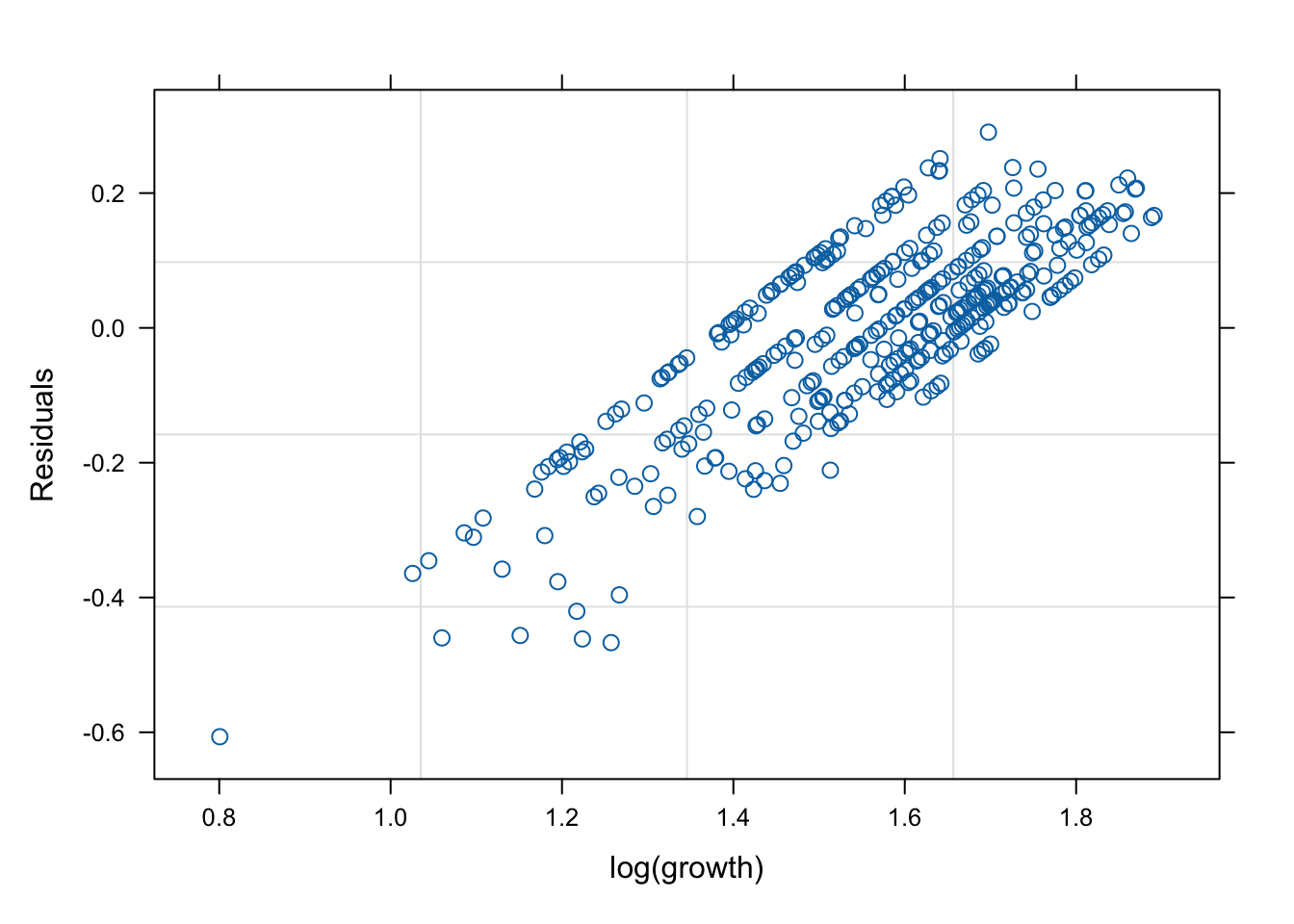
그런데 mod2s (랜덤 절편 + 개체 내 AR(1) 상관성)의 경우 잔차의 trend가 반응변수에 독립적이지 않다. 따라서 이 모형은 적절하지 않을 수 있다.
mod1s (랜덤 절편 + 랜덤 기울기)가 전반적으로 적합도가 좋다. (residual이 작다).
# fitted value (y_hat) vs. response (y) # a line + noise trend is good plot (mod1, fitted (.) ~ log (growth))plot (mod1s, fitted (.) ~ log (growth))plot (mod2s, fitted (.) ~ log (growth))plot (mod3s, fitted (.) ~ log (growth))# residual (y-y_mat) vs. response (y) # white-noise trend is preferred good plot (mod1, resid (.) ~ log (growth))plot (mod1s, resid (.) ~ log (growth))plot (mod2s, resid (.) ~ log (growth))plot (mod3s, resid (.) ~ log (growth))## for more information, # try ?plot.lme # try plot(mod3s, fitted(.) ~ log(growth) | id)