Acknowledgement: 본 절의 구성에는 다음 교재를 발췌하였다.
- 김양진 (2020). R과 SAS를 활용한 경시적 자료분석. 자유아카데미. - 1장 경시적 자료 구조의 이해, 2장 탐색적 자료분석
- 이근백 (2022). 경시적 자료분석 - R 활용. 자유아카데미. - 3장 탐색적 자료분석
- 황선재 (2019), 패널 다층모형 & 성장곡선분석 (Panel Multilevel Models & Growth Curve Analysis). https://repository.kihasa.re.kr/bitstream/201002/43529/4/p20190926-01-02.pdf
경시적 자료 구조의 이해
- 경시적 자료(longitudinal data): 관심 있는 반응변수를 일정 기간 동안 반복적으로 측정하는 모든 유형의 자료를 일컬음. 예를 들어 아래 자료를 포함한다.
- 반복측정 자료(repeatedly measured data)
- 사건사 자료(Event history data)
- 패널 자료(panel data),
- 시계열적 교차 자료(time series cross-sectional data)
- 다층 자료 (multi-level data): (복수의) 관측값이 특정 개체/집단에 속하거나 군집되어 있는 자료
- 일반적인 회귀분석, 분산분석, 범주형 자료분석은 반응변수(response variable)가 일변량 자료(univariate data)임.
- 경시적 자료의 관심은 주로 반응변수가 다변량 자료(multivariate data)임
- e.g. 한 단위에게서 여러 값을 측정한 경우, 이를테면 신생아 출생시 몸무게, 키, 머리둘레 \(\left(Y_{1}, Y_{2}, Y_{3}\right)\)
- e.g. 시간을 두고 반복적으로 측정된 값들로 이루어져 있는 경우, 이를테면 매년 측정된 키
- e.g. 가족 별 가족 구성원을 관측한 횡단 다층 자료
- Level 1: 가족구성원, Level 2: 가족
- e.g. 학군 별, 학교 별, 학생들을 관측한 횡단 다층자료
- Level 1: 학생, Level 2: 학교, Level 3: 학군
- e.g. 패널자료
- Level 1: 개체내 시계열 관측치, Level 2: 개체
- 위 예시들 모두, 상위 개체로부터 파생된 관찰값들은 서로 연관되어 있음. 이들 간의 연관성을 고려한 모형이 적용되어야.
경시적 자료를 위한 분석기법은 왜 필요한가?
- 대부분의 사회과학 자료는 개체의 속성, 개체가 속한 집단/구조의 속성, 그리고 상위수준과 하위수준의 상호관계를 모두 다루고 싶어함. 경시적 자료를 위한 분석기법은 같은 층위에 속한 변수들, 다른 층위에 속한 변수들 간의 관계를 동시에 모형에 반영할 수 있음.
- 다만, 관찰값들 간의 동시적 상관(주로 횡단자료의 경우)과 자기상관(주로 종단자료의 경우)의 문제를 모형에서 다루어야 \(\beta\)의 비편향된 추정이 가능하기 때문에, 단순한 선형회귀/로지스틱 선형회귀보다 진전된 방법이 필요해짐.
경시적 자료의 예와 시각화
연속형 반응변수 - 가문비 나무(stika spruce) 자료
- 오존이 나무의 성장에 미치는 영향?
- 나무 79그루의 나무 –> ozone-treated vs. control
- 두 그릅의 성장 패턴에 차이가 존재? (Diggle et al., 2002).
- 반응변수: 나무의 높이 * (지름의 제곱근)
- 측정횟수는 5회
- spruce 자료 관측개체의 관측 시점과 관측 횟수가 동일함 (가장 고전적)
- data는 wide format을 제공된었다. 다만 경시자료분석에 대한 많은 통계 패키지를 사용하기 위하여는 아래처럼 long format으로 변환해야 할 수도 있다.
spruce = read.table("data/spruce_data.txt", col.names=c("day152", "day174", "day201", "day227", "day258"))
head(spruce)
day152 day174 day201 day227 day258
1 4.515 4.982 5.408 5.903 6.145
2 4.235 4.199 4.683 4.915 4.957
3 3.980 4.364 4.792 4.986 5.032
4 4.357 4.772 5.098 5.298 5.356
5 4.340 4.953 5.423 5.974 6.276
6 4.586 5.081 5.362 5.764 5.995
id = (1:79)
spruce2 = as.data.frame(cbind(id,spruce))
library(reshape2)
spruce3 = melt(spruce2, id="id")
spruce3$trt = ifelse(spruce3$id < 55, 1, 2)
names(spruce3) = c("id","time","growth", "trt")
print(spruce3[1:10,])
id time growth trt
1 1 day152 4.515 1
2 2 day152 4.235 1
3 3 day152 3.980 1
4 4 day152 4.357 1
5 5 day152 4.340 1
6 6 day152 4.586 1
7 7 day152 4.406 1
8 8 day152 4.243 1
9 9 day152 4.815 1
10 10 day152 3.840 1
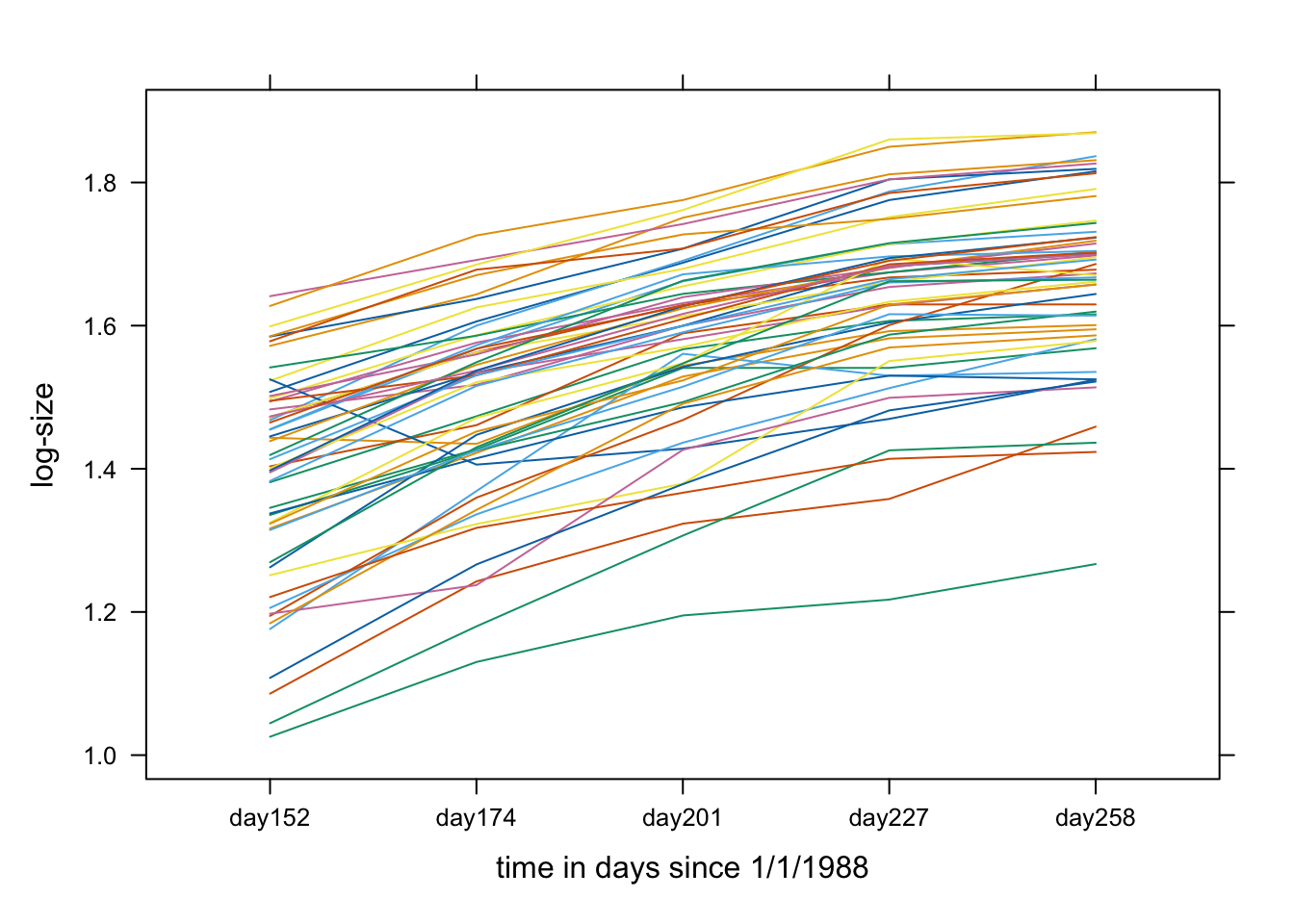
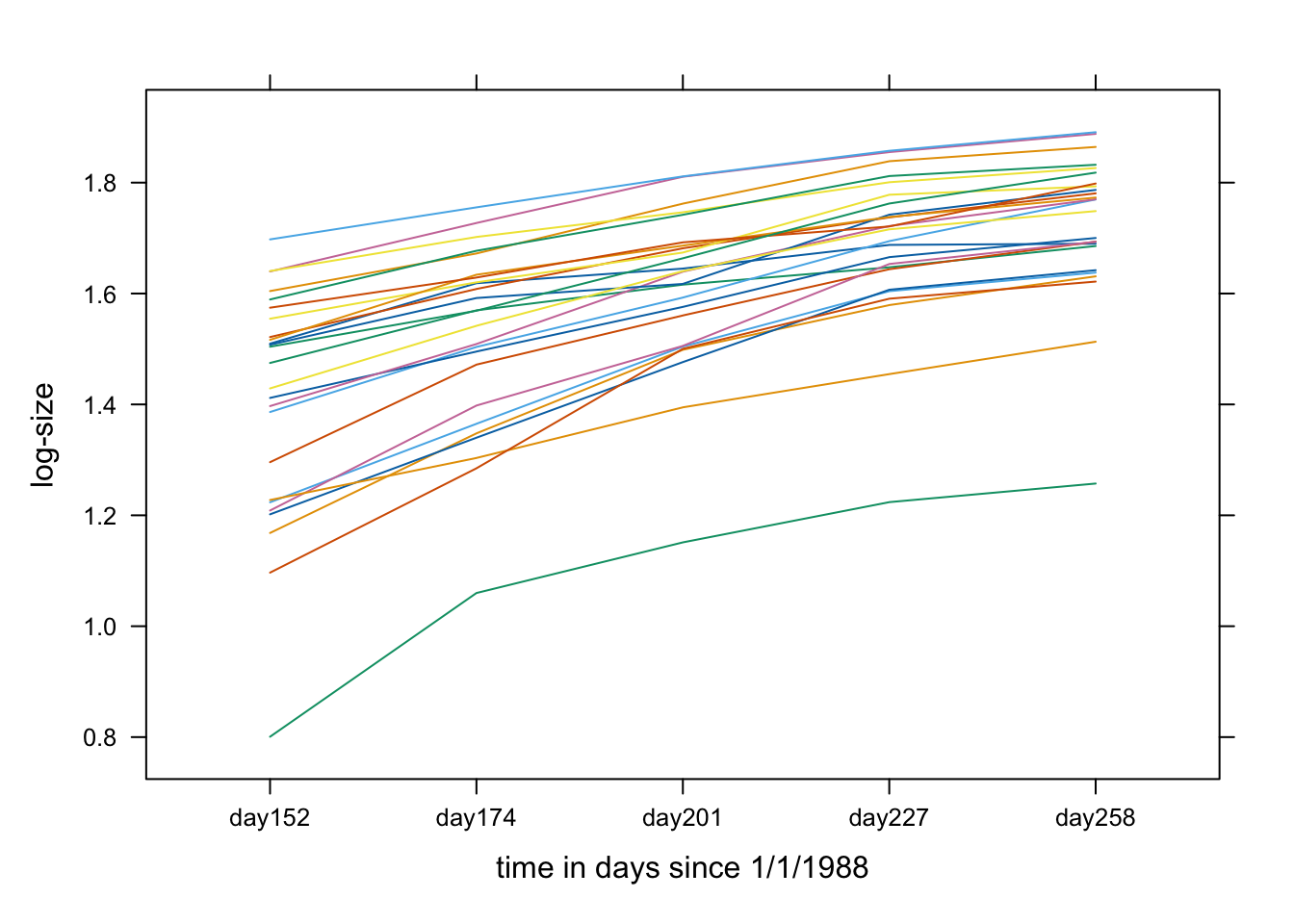
스파게티 플랏(spagetti plot)
- 각 개체들의 응답시간(가로축)과 응답변수(세로축)에 따라 점을 찍고 이어서 만든다.
- 장점: boxplot과 비교하면, 각 개체의 반응변수가 어떻게 변화하는지 추적하기 용이하다.
- 단점: 여전히 두 그룹이 통계적으로 유의하게 다른지는 알 수 없다. (통계적 검정나 모형 피팅이 필요하다.)
library(lattice)
par(mfrow=c(1,2))
xyplot(log(spruce3[id < 55, 3]) ~ spruce3[id < 55, 2], groups=spruce3[id < 55, 1], type="l", xlab="time in days since 1/1/1988", ylab="log-size")
xyplot(log(spruce3[id >= 55, 3]) ~ spruce3[id >= 55, 2], groups=spruce3[id >= 55, 1], type="l", xlab="time in days since 1/1/1988", ylab="log-size")
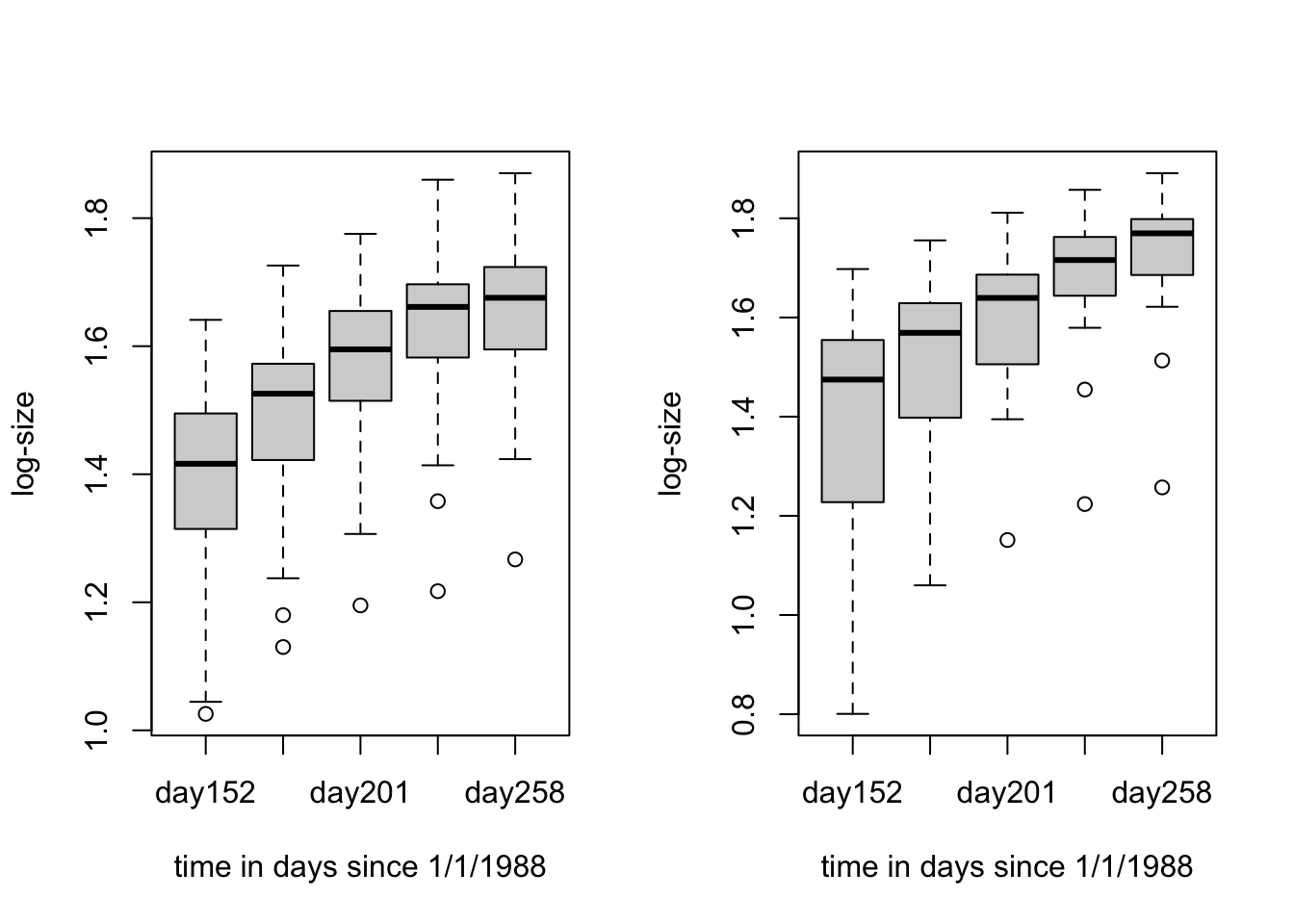
par(mfrow=c(1,2))
boxplot(log(spruce3[id < 55, 3]) ~ spruce3[id < 55, 2], groups=spruce3[id < 55, 1], type="l", xlab="time in days since 1/1/1988", ylab="log-size")
boxplot(log(spruce3[id >= 55, 3]) ~ spruce3[id >= 55, 2], groups=spruce3[id >= 55, 1], type="l", xlab="time in days since 1/1/1988", ylab="log-size") # ozone-control group (ID:55-79)
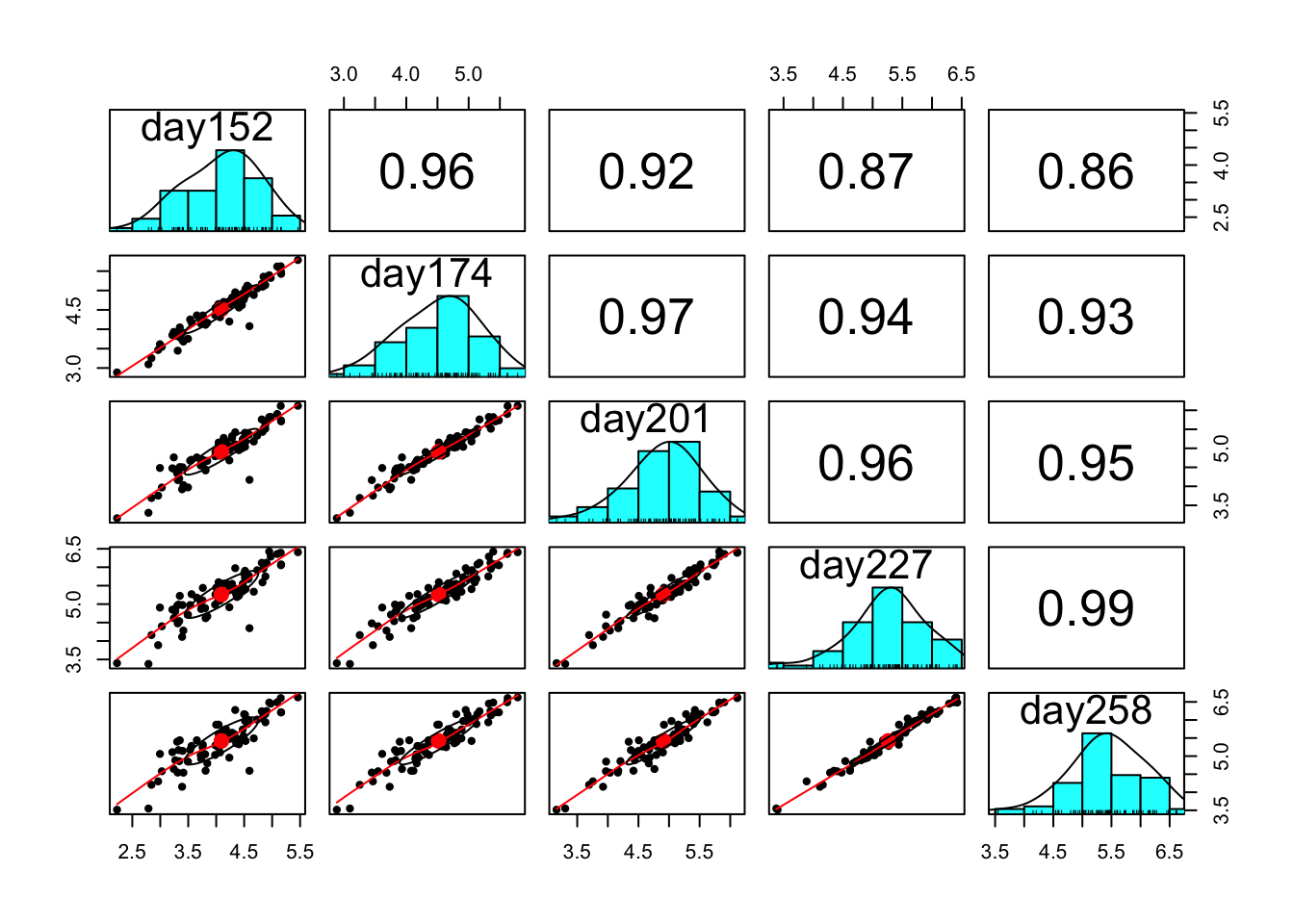
상관계수 구조의 탐색
- 다섯 번의 측정값을 나타내는 확률벡터를 \((Y_1, \ldots, Y_5)\)라 하자. 아래 그림에 의하면 가까운 시점일수록 (즉 \(|t_1 - t_2|\))가 작을수록 \({\rm Corr}(Y_{t_1}, Y_{t_2})\)의 추정값이 커지고 있다.
- 반응변수들끼리 독립이 아니라는 점에 주목하자.
library(psych)
pairs.panels(spruce[ ,c("day152", "day174", "day201", "day227", "day258")])
결측이 있는 순서형 반응변수 - 우울증 신약 자료
- NIMH(National Institute of Mental Health) schizophrenia Collaborative study
- 437명의 우울증 환자
- 신약이 환자의 상태 호전에 도움을 주는가? (Hedeker and Gibbs, 2006).
- 위약군(
tx=0), 신약군(tx=1)에 각각 108명과 329명 임의배분 후 6회 반복측정
- 반응변수: 상태의 심각정도를 보여 주는 지표로 IMPS(Impatient Multidimensional Psychiatric Scale)의 79 항목을 사용, 1(정상) - 7(매우 심각)점의 범위를 가짐
# header column이 없는 테이블임.
IMPS = read.table("data/SCHIZX1.DAT.txt", col.names = c("id", "imps79", "imps79b", "imps790", "int", "tx", "week", "sweek", "txswk"))
Warning in scan(file = file, what = what, sep = sep, quote = quote, dec = dec,
: number of items read is not a multiple of the number of columns
id imps79 imps79b imps790 int tx week sweek txswk
1 1103 5.5 1 4 1 1 0 0.0000 0.0000
2 1103 3.0 0 2 1 1 1 1.0000 1.0000
3 1103 -9.0 -9 -9 1 1 2 1.4142 1.4142
4 1103 2.5 0 2 1 1 3 1.7321 1.7321
5 1103 -9.0 -9 -9 1 1 4 2.0000 2.0000
6 1103 -9.0 -9 -9 1 1 5 2.2361 2.2361
'data.frame': 3060 obs. of 9 variables:
$ id : chr "1103" "1103" "1103" "1103" ...
$ imps79 : num 5.5 3 -9 2.5 -9 -9 4 6 3 -9 ...
$ imps79b: int 1 0 -9 0 -9 -9 1 1 0 -9 ...
$ imps790: int 4 2 -9 2 -9 -9 2 4 2 -9 ...
$ int : int 1 1 1 1 1 1 1 1 1 1 ...
$ tx : int 1 1 1 1 1 1 1 1 1 1 ...
$ week : int 0 1 2 3 4 5 6 0 1 2 ...
$ sweek : num 0 1 1.41 1.73 2 ...
$ txswk : num 0 1 1.41 1.73 2 ...
table(IMPS[IMPS$week==0, ]$tx)
## 결측치는 -9로 코딩되어 있음. NA로 바꿔주자.
IMPS[ ,2] = ifelse(IMPS[ ,2] == -9, NA, IMPS[ ,2])
IMPS[ ,3] = ifelse(IMPS[ ,3] == -9, NA, IMPS[ ,3])
IMPS[ ,4] = ifelse(IMPS[ ,4] == -9, NA, IMPS[ ,4])
table(IMPS$imps79) ## 원자료의 점수별 빈도
1 1.5 1.7 2 2.3 2.5 3 3.3 3.5 3.7 4 4.3 4.5 4.7 5 5.3 5.5 5.7 6 6.5
51 47 3 87 2 83 97 2 93 1 197 1 171 1 239 1 233 1 206 57
7
30
cumsum(table(IMPS$imps79)) ## 누적빈도
1 1.5 1.7 2 2.3 2.5 3 3.3 3.5 3.7 4 4.3 4.5 4.7 5 5.3
51 98 101 188 190 273 370 372 465 466 663 664 835 836 1075 1076
5.5 5.7 6 6.5 7
1309 1310 1516 1573 1603
## 원자료를 이분화함 (0: imps79 < 3.5, 1: imps79 >=3.5)
table(IMPS$imps79o)
## 원자료를 순서화함 (0 imps79 <= 2.3, 1: 2.5<-imps79<4.7,
## 3: 4.7 <= imps79 < 5.3, 4: 5.5 <= imps79
- 이 자료에는 간헐적 결측이 포함됨.
- 대부분의 자료가 week=0,1,3,6에 측정됨.
- 또한 437명의 환자 중 102명의 환자가 연구 도중에 탈퇴(drop out)하였다.
- 분석에서는 2, 4, 5주의 자료를 제외하는 것이 좋을 수 있고, 다른 주차에 대하여도 결측을 적절하게 보정하기 위한 고민이 필요할 수 있다. 특히 반응변수와 결측 발생여부의 연관관계 존재 여부에 따라 적용되는 분석 방법이 달라진다.
IMPS1 = IMPS[IMPS$imps79 != -9, ]
# you can also try
# library(tidyr)
# IMPS1 = drop_na(IMPS)
table(IMPS1$tx, IMPS1$week)
0 1 2 3 4 5 6
0 107 105 5 87 2 2 70
1 327 321 9 287 9 7 265
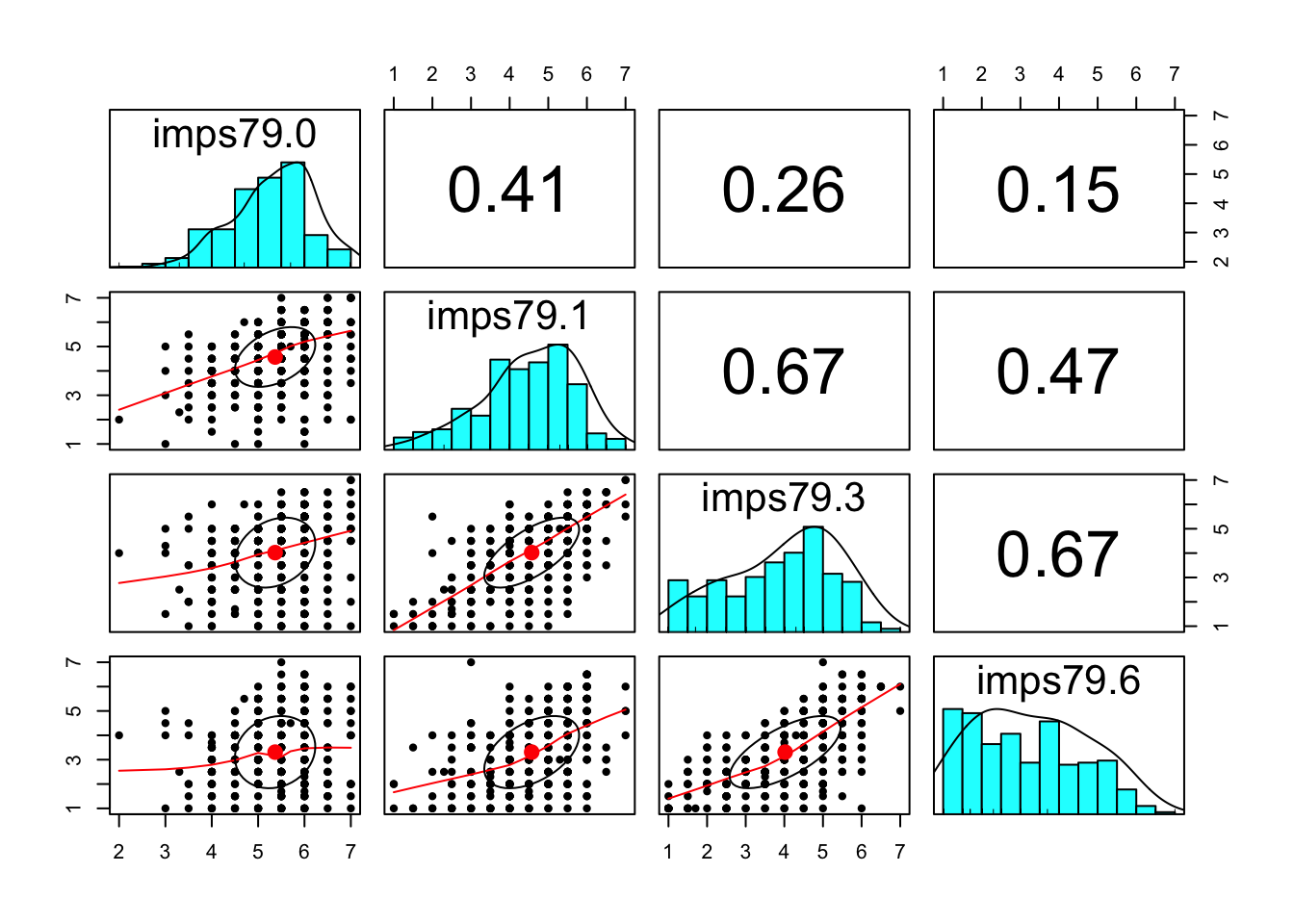
상관계수 구조의 탐색
IMPS2 = IMPS1[IMPS1$week %in% c(0,1,3,6), ]
# reshape
IMPS2a = reshape(IMPS2[ ,c("id" , "week", "imps79")],
direction="wide", v.names="imps79",
timevar="week", idvar="id")
head(IMPS2a)
id imps79.0 imps79.1 imps79.3 imps79.6
1 1103 5.5 3 2.5 4.0
8 1104 6.0 3 1.5 2.5
15 1105 4.0 3 1.0 NA
22 1106 3.0 1 1.5 1.0
29 1107 5.0 5 5.0 5.5
36 1108 6.0 6 3.5 4.5
library(psych)
pairs.panels(IMPS2a[ ,-1])
이항 반응변수 - 인도네시아 아동 호흡기 질환 자료
ichs = read.table("data/ichs.dat", header=T)
dim(ichs)
ID RESPONSE TIME GENDER VITA AGE
1 1 0 0 1 0 4
2 1 0 3 1 0 4
3 1 0 6 1 0 4
4 1 1 9 1 0 4
5 1 0 12 1 0 4
6 1 0 15 1 0 4
table(ichs[ichs$TIME==0, ]$VITA)
table(ichs$RESPONSE, ichs$TIME)
0 3 6 9 12 15
0 183 182 172 176 174 169
1 67 68 78 74 76 81
다양한 모형들
회귀분석의 (단순) 확장
아래 수식에서
- \(\varepsilon_{i j}\)은 random independent error을 의미하는 확률변수이다.
- \(\alpha\), \(\beta\), \(\alpha_i\), \(\beta_i\)들은 맥락에 따라 고정된 모수(parameter)로 취급되기도 하고, 가변적인 확률변수(random variable)로 취급되기도 한다.
- \(i\)가 더 상위 수준, \(j\)가 하위수준의 index이다. 책이나 패키지 매뉴얼에 따라서는 반대의 표기법을 택하기도 하므로, 특정 패키지를 적용하기 전에는 해당 패키지가 구현하는 모형식을 확인하세요.
- 선형회귀 모형 (linear regression model)
\[
y_{i j}=\alpha+\beta x_{i j}+\varepsilon_{i j}
\]
- 임의절편 모형 (random-intercept model)
\[
y_{i j}=\alpha_i +\beta x_{i j}+\varepsilon_{i j}
\]
- 임의계수 모형 (random-coefficient model)
\[
y_{i j}=\alpha_i+\beta_i x_{i j}+\varepsilon_{i j}
\]
- 다층/혼합효과 모형
\[
y_{i j}=\alpha_i+\beta_i x_{i j}+\varepsilon_{i j}
\]
(4-1) 다층/혼합효과 ‘기본’ 모형: 분리형
\[
\begin{array}{cc}
\text{(Level 1)} \qquad \qquad \qquad & \\
y_{i j}=\alpha_i+\beta_i x_{i j}+\varepsilon_{i j} & \left(\varepsilon_{i j} \sim \mathrm{~N}\left(0, \sigma_{\varepsilon}^2\right)\right) \\
\text{(Level 2)} \qquad \qquad \qquad & \\
\alpha_i=\gamma_0+\gamma_1 z_i+u_{1 i} & \left(u_{1 i} \sim N\left(0, \sigma_{u1}^2\right)\right) \\
\beta_i=\delta_0+\delta_1 k_i+u_{2 i} & \left(u_{2 i} \sim \mathrm{~N}\left(0, \sigma_{u 2}^2\right)\right)
\end{array}
\]
(4-2) 다층/혼합효과 ‘기본’ 모형: 결합형
\[
\begin{gathered}
y_{i j}=\left(\gamma_0+\gamma_1 z_i+u_{1 i}\right)+\left(\delta_0+\delta_1 k_i+u_{2 i}\right) x_{i j}+\varepsilon_{i j} \\
= \left(\underbrace{\gamma_0+\gamma_1 z_i+\delta_0 x_{i j}+\delta_1 k_i x_{i j}}_{\text { '고정요소' }}\right)+\left( \underbrace{u_{1 i}+u_{2 i} x_{i j}+\varepsilon_{i j}}_{\text { '임의요소' }}\right) \\
\end{gathered}
\]
예. 성장곡선 모형 (growth curve model)
- 개체의 특정 변수가 시간에 따라 어떻게 변해가는지, 그 변화의 양상이 개체별로 다른지 분석하는 기법이다. 여기서 개체별 변화양상의 차이를 다른 독립변수로 설명한다.
- \(i\)번째 개체를 \(t=1,\ldots, T\) 시각에 관찰하였다고 가정하자.
- 성장곡선모형의 모형식은 다층모형에서 설명변수 \(x_{i j}\)만 시각 \({\rm Time}_{i t}\)으로 바뀌었다.
- 성장곡선 모형의 ‘분리형’ 모형식:
\[
\begin{array}{cc}
\text{(Level 1)} \qquad \qquad \qquad & \\
y_{i t}=\alpha_i+\beta_i {\rm Time}_{i t}+\varepsilon_{i t} & \left(\varepsilon_{i t} \sim \mathrm{~N}\left(0, \sigma_{\varepsilon}^2\right)\right) \\
\text{(Level 2)} \qquad \qquad \qquad & \\
\alpha_i=\gamma_0+\gamma_1 z_i+u_{1 i} & \left(u_{1 i} \sim N\left(0, \sigma_{u1}^2\right)\right) \\
\beta_i=\delta_0+\delta_1 k_i+u_{2 i} & \left(u_{2 i} \sim \mathrm{~N}\left(0, \sigma_{u 2}^2\right)\right)
\end{array}
\]
\[
\begin{gathered}
y_{i t}=\left(\gamma_0+\gamma_1 z_i+u_{1 i}\right)+\left(\delta_0+\delta_1 k_i+u_{2 i}\right) x_{i t}+\varepsilon_{i t} \\
= \left(\underbrace{\gamma_0+\gamma_1 z_i+\delta_0 {\rm Time}_{i t}+\delta_1 k_i {\rm Time}_{i t}}_{\text { '고정요소' }}\right)+\left( \underbrace{u_{1 i}+u_{2 i} {\rm Time}_{i t}+\varepsilon_{i t}}_{\text { '임의요소' }}\right) \\
\end{gathered}
\]